Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T13:00:01.969Z Has data issue: false hasContentIssue false
  • English
  • Français

Gibbs partitions, Riemann–Liouville fractional operators, Mittag–Leffler functions, and fragmentations derived from stable subordinators

Part of: Nonparametric inference Parametric inference

Published online by Cambridge University Press:  23 June 2021

Man-Wai Ho ,
Lancelot F. James  and
John W. Lau
Man-Wai Ho*
Affiliation:
The Chinese University of Hong Kong
Lancelot F. James*
Affiliation:
The Hong Kong University of Science and Technology
John W. Lau*
Affiliation:
The University of Western Australia
*
*Postal address: Stanley Ho Big Data Decision Analytics Research Centre, Chen Yu Tung Building, The Chinese University of Hong Kong, Shatin, N.T., Hong Kong SAR.
**Postal address: Department of Information Systems, Business Statistics and Operations Management, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong SAR. Email address: lancelot@ust.hk
***Postal address: UWA Centre for Applied Statistics, The University of Western Australia (M019), 35 Stirling Highway, CRAWLEY WA 6009, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

Pitman (2003), and subsequently Gnedin and Pitman (2006), showed that a large class of random partitions of the integers derived from a stable subordinator of index 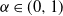$\alpha\in(0,1)$ have infinite Gibbs (product) structure as a characterizing feature. The most notable case are random partitions derived from the two-parameter Poisson–Dirichlet distribution, 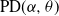$\textrm{PD}(\alpha,\theta)$, whose corresponding $\alpha$-diversity/local time have generalized Mittag–Leffler distributions, denoted by 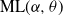$\textrm{ML}(\alpha,\theta)$. Our aim in this work is to provide indications on the utility of the wider class of Gibbs partitions as it relates to a study of Riemann–Liouville fractional integrals and size-biased sampling, and in decompositions of special functions, and its potential use in the understanding of various constructions of more exotic processes. We provide characterizations of general laws associated with nested families of 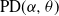$\textrm{PD}(\alpha,\theta)$ mass partitions that are constructed from fragmentation operations described in Dong et al. (2014). These operations are known to be related in distribution to various constructions of discrete random trees/graphs in [n], and their scaling limits. A centerpiece of our work is results related to Mittag–Leffler functions, which play a key role in fractional calculus and are otherwise Laplace transforms of the $\textrm{ML}(\alpha,\theta)$ variables. Notably, this leads to an interpretation within the context of 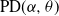$\textrm{PD}(\alpha,\theta)$ laws conditioned on Poisson point process counts over intervals of scaled lengths of the $\alpha$-diversity.

Keywords

beta-gamma algebraBrownian and Bessel processesGibbs partitionsMittag–Leffler functionsstable Poisson–Kingman distributions

MSC classification

Primary: 62G05: Estimation
Secondary: 62F15: Bayesian inference
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 2 , June 2021 , pp. 314 - 334
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. (1991). The continuum random tree. I. Ann. Prob. 19, 1–28.Google Scholar
Aldous, D. (1993). The continuum random tree. III. Ann. Prob. 21, 248–289.Google Scholar
Bacallado, S., Battiston, M., Favaro, S. and Trippa, L. (2017). Sufficientness postulates for Gibbs-type priors and hierarchical generalizations. Statist. Sci. 32, 487–500.CrossRefGoogle Scholar
Barlow, M., Pitman, J. and Yor, M. (1989). Une extension multidimensionnelle de la loi de l’arc sinus. In Séminaire de Probabilités XXIII, eds J. Azema, P.-A. Meyer and M. Yor, Lecture Notes in Math. 1372, Springer, Berlin, pp. 294–314.CrossRefGoogle Scholar
Bertoin, J. (2006). Random Fragmentation and Coagulation Processes, Cambridge University Press.10.1017/CBO9780511617768CrossRefGoogle Scholar
Bertoin, J. and Yor, M. (2001). On subordinators, self-similar Markov processes and some factorizations of the exponential variable. Electron. Commun. Prob. 6, 95–106.CrossRefGoogle Scholar
Bloem-Reddy, B. and Orbanz, P. (2017). Preferential attachment and vertex arrival times. arXiv:1710.02159 [math.PR].Google Scholar
Caron, F. and Fox, E. B. (2017). Sparse graphs using exchangeable random measures. J. R. Statist. Soc. B 79, 1–44.10.1111/rssb.12233CrossRefGoogle ScholarPubMed
Chaumont, L. and Yor, M. (2003). Exercises in Probability. A Guided Tour From Measure Theory to Random Processes, via Conditioning. Cambridge Series in Statistical and Probabilistic Mathematics 13, Cambridge University Press.Google Scholar
De Blasi, P., Favaro, S., Lijoi, A., Mena, R., Prünster, I. and Ruggiero, M. (2015). Are Gibbs-type priors the most natural generalization of the Dirichlet Process? IEEE Trans. Pattern Anal. Mach. Intell. 37, 212–229.10.1109/TPAMI.2013.217CrossRefGoogle ScholarPubMed
Devroye, L. (2009). Random variate generation for exponentially and polynomially tilted stable distributions. ACM Trans. Model. Comput. Simul. 19, 18.10.1145/1596519.1596523CrossRefGoogle Scholar
Devroye, L. and James, L. F. (2014). On simulation and properties of the stable law. Stat. Meth. Appl. 23, 307–343.CrossRefGoogle Scholar
Dong, R., Goldschmidt, C. and Martin, J. (2006). Coagulation-fragmentation duality, Poisson–Dirichlet distributions and random recursive trees. Ann. Appl. Prob. 16, 1733–1750.CrossRefGoogle Scholar
Favaro, S., Lijoi, A., Mena, R. H. and Prünster, I. (2009). Bayesian non-parametric inference for species variety with a two-parameter Poisson–Dirichlet process prior. J. R. Statist. Soc. B 71, 993–1008.CrossRefGoogle Scholar
Feng, S. (2010). The Poisson–Dirichlet Distribution and Related Topics: Models and Asymptotic Behaviors. Springer, Berlin.CrossRefGoogle Scholar
Gnedin, A. and Pitman, J. (2006). Exchangeable Gibbs partitions and Stirling triangles. J. Math. Sci. 138, 5674–5685.CrossRefGoogle Scholar
Goldschmidt, C. and Haas, B. (2015). A line-breaking construction of the stable trees. Electron. J. Prob. 20, 1–24.10.1214/EJP.v20-3690CrossRefGoogle Scholar
Gorenflo, R., Kilbas, A. A., Mainardi, F. and Rogosin, S. V. (2014). Mittag–Leffler Functions, Related Topics and Applications. Springer, Berlin.10.1007/978-3-662-43930-2CrossRefGoogle Scholar
Griffiths, R. C. and Spanò, D. (2007). Record indices and age-ordered frequencies in exchangeable Gibbs partitions. Electron. J. Prob. 12, 1101–1130.CrossRefGoogle Scholar
Haas, B., Miermont, G., Pitman, J. and Winkel, M. (2008). Continuum tree asymptotics of discrete fragmentations and applications to phylogenetic models. Ann. Prob. 36, 1790–1837.10.1214/07-AOP377CrossRefGoogle Scholar
Haas, B., Pitman, J. and Winkel, M. (2009). Spinal partitions and invariance under re-rooting of continuum random trees. Ann. Prob. 37, 1381–1411.CrossRefGoogle Scholar
Ho, M.-W., James, L. F. and Lau, J. W. (2007). Gibbs partitions (EPPFs) derived from a stable subordinator are Fox H and Meijer G transforms. arXiv:0708.0619[math.PR].Google Scholar
James, L. F. (2010). Lamperti type laws. Ann. Appl. Prob. 20, 1303–1340.10.1214/09-AAP660CrossRefGoogle Scholar
James, L. F. (2013). Stick-breaking $\textrm{PG}(\alpha,\zeta)$-generalized gamma processes. arXiv:1308.6570 [math.PR].Google Scholar
James, L. F. (2015). Generalized Mittag–Leffler distributions arising as limits in preferential attachment models. arXiv:1509.07150 [math.PR].Google Scholar
James, L. F. (2019). Stick-breaking Pitman–Yor processes given the species sampling size. arXiv:1908.07186 [math.ST].Google Scholar
James, L. F and Ross, N. (2017). Multicolor triangular Pólya urn schemes and the generalized Mittag–Leffler distribution. Manuscript in preparation.Google Scholar
Janson, S. (2006). Limit theorems for triangular urn schemes. Prob. Theory Relat. Fields 134, 417–452.10.1007/s00440-005-0442-7CrossRefGoogle Scholar
Janson, S., Kuba, M. and Panholzer, A. (2011). Generalized Stirling permutations, families of increasing trees and urn models. J. Combinatorial Theory A 118, 94–114.CrossRefGoogle Scholar
Jedidi, W., Simon, T. and Wang, M. (2017). Density solutions to a class of integro-differential equations. J. Math. Anal. Appl. 458, 134–152.CrossRefGoogle Scholar
Kingman, J. F. C. (1975). Random discrete distributions. J. R. Statist. Soc. B 37, 1–22.Google Scholar
Lamperti, J. (1958). An occupation time theorem for a class of stochastic processes. Trans. Amer. Math. Soc. 88, 380–387.CrossRefGoogle Scholar
Lomeli, M., Favaro, S. and Teh, Y. W. (2017). A marginal sampler for $\sigma$-stable Poisson–Kingman mixture models. J. Comput. Graph. Statist. 26, 44–53.Google Scholar
Mathai, A. M., Saxena, R. K. and Haubold, H. J. (2010). The H-Function. Theory and Applications. Springer, New York.Google Scholar
Pakes, A. G. (2014). On generalized stable and related laws. J. Math. Anal. Appl. 411, 201–222.10.1016/j.jmaa.2013.09.041CrossRefGoogle Scholar
Patie, P. (2011). A refined factorization of the exponential law. Bernoulli 17, 814–826.10.3150/10-BEJ292CrossRefGoogle Scholar
Peköz, E., Röllin, A. and Ross, N. (2013). Degree asymptotics with rates for preferential attachment random graphs. Ann. Appl. Prob. 23, 1188–1218.CrossRefGoogle Scholar
Peköz, E., Röllin, A. and Ross, N. (2016). Generalized gamma approximation with rates for urns, walks and trees. Ann. Prob. 44, 1776–1816.CrossRefGoogle Scholar
Peköz, E., Röllin, A. and Ross, N. (2017). Joint degree distributions of preferential attachment random graphs. Adv. Appl. Prob. 49, 368–387.CrossRefGoogle Scholar
Peköz, E., Röllin, A. and Ross, N. (2019). Pólya urns with immigration at random times. Bernoulli 25, 189–220.CrossRefGoogle Scholar
Perman, M., Pitman, J. and Yor, M. (1992). Size-biased sampling of Poisson point processes and excursions. Prob. Theory Relat. Fields 92, 21–39.CrossRefGoogle Scholar
Pitman, J. (1995). Exchangeable and partially exchangeable random partitions. Prob. Theory Relat. Fields, 102, 145–158.10.1007/BF01213386CrossRefGoogle Scholar
Pitman, J. (1996). Some developments of the Blackwell–MacQueen urn scheme. In Statistics, Probability and Game Theory. IMS Lecture Notes Monogr. Ser. 30. Inst. Math. Statist., Hayward, CA, pp. 245–267.CrossRefGoogle Scholar
Pitman, J. (1997). Partition structures derived from Brownian motion and stable subordinators. Bernoulli 3, 79–96.10.2307/3318653CrossRefGoogle Scholar
Pitman, J. (1999). Brownian motion, bridge, excursion, and meander characterized by sampling at independent uniform times. Electron. J. Prob. 4, 11.CrossRefGoogle Scholar
Pitman, J. (2003). Poisson–Kingman partitions. In Statistics and Science: A Festschrift for Terry Speed. IMS Lecture Notes Monogr. Ser. 40. Inst. Math. Statist., Beachwood, OH, pp. 1–34.CrossRefGoogle Scholar
Pitman, J. (2006). Combinatorial Stochastic Processes. Lecture Notes Math. 1875. Springer, Berlin.Google Scholar
Pitman, J. (2016). Gamma transforms of maxima and path decompositions for reflecting Brownian depth processes. Manuscript in preparation.Google Scholar
Pitman, J. (2017). Mixed Poisson and negative binomial models for clustering and species sampling. Manuscript in preparation.Google Scholar
Pitman, J. and Winkel, M. (2009) Regenerative tree growth: binary self-similar continuum random trees and Poisson–Dirichlet compositions. Ann. Probab. 37, 1999–2041.10.1214/08-AOP445CrossRefGoogle Scholar
Pitman, J. and Winkel, M. (2015) Regenerative tree growth: Markovian embedding of fragmenters, bifurcators, and bead splitting processes. Ann. Prob. 43, 2611–2646.CrossRefGoogle Scholar
Pitman, J. and Yakubovich, Y. (2018). Ordered and size-biased frequencies in GEM and Gibbs models for species sampling. Ann. Appl. Prob. 28, 1793–1820.CrossRefGoogle Scholar
Pitman, J. and Yor, M. (1992). Arcsine laws and interval partitions derived from a stable subordinator. Proc. London Math. Soc. 65, 326–356.10.1112/plms/s3-65.2.326CrossRefGoogle Scholar
Pitman, J. and Yor, M. (1997). The two-parameter Poisson–Dirichlet distribution derived from a stable subordinator. Ann. Prob. 25, 855–900.CrossRefGoogle Scholar
Prabhakar, T. R. (1970). On a set of polynomials suggested by Laguerre polynomials. Pacific J. Math. 35, 213–219.CrossRefGoogle Scholar
Rembart, F. and Winkel, M. (2016). A binary embedding of the stable line-breaking construction. arXiv:1611.02333 [math.PR].Google Scholar
Rembart, F. and Winkel, M. (2018). Recursive construction of continuum random trees. Ann. Prob. 46, 2715–2748.CrossRefGoogle Scholar
Schneider, W. R. (1986). Stable distributions: Fox functions representation and generalization. In Stochastic Processes in Classical and Quantum Systems (Ascona 1985), eds S. Albeverio, G. Casati and D. Merlini, Lecture Notes Phys. 262. Springer, Berlin, pp. 497–511.Google Scholar
Schneider, W. R. (1987). Generalized one sided stable distributions. In Stochastic Processes – Mathematics and Physics II, eds Albeverio, S., Blanchard, P. and Streit, L., Lecture Notes Math. 1250. Springer, Berlin, pp. 269–287.Google Scholar
Steutel, F. W. and van Harn, K. (2003). Infinite Divisibility of Probability Distributions on the Real Line. Marcel Dekker, New York.10.1201/9780203014127CrossRefGoogle Scholar
Zolotarev, V. M. (1957). Mellin–Stieltjes transforms in probability theory. Theory Prob. Appl. 2, 433–460.10.1137/1102031CrossRefGoogle Scholar