Article contents
Characterizations of Morrey type spaces
Published online by Cambridge University Press: 14 May 2021
Abstract
For a nondecreasing function  $K: [0, \infty)\rightarrow [0, \infty)$
and
$K: [0, \infty)\rightarrow [0, \infty)$
and 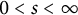 $0<s<\infty $
, we introduce a Morrey type space of functions analytic in the unit disk
$0<s<\infty $
, we introduce a Morrey type space of functions analytic in the unit disk 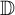 $\mathbb {D}$
, denoted by
$\mathbb {D}$
, denoted by 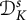 $\mathcal {D}^s_K$
. Some characterizations of
$\mathcal {D}^s_K$
. Some characterizations of 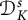 $\mathcal {D}^s_K$
are obtained in terms of K-Carleson measures. A relationship between two spaces
$\mathcal {D}^s_K$
are obtained in terms of K-Carleson measures. A relationship between two spaces 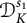 $\mathcal {D}^{s_1}_K$
and
$\mathcal {D}^{s_1}_K$
and 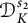 $\mathcal {D}^{s_2}_K$
is given by fractional order derivatives. As an extension of some known results, for a positive Borel measure
$\mathcal {D}^{s_2}_K$
is given by fractional order derivatives. As an extension of some known results, for a positive Borel measure 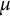 $\mu $
on
$\mu $
on 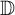 $\mathbb {D}$
, we find sufficient or necessary condition for the embedding map
$\mathbb {D}$
, we find sufficient or necessary condition for the embedding map 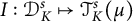 $I: \mathcal {D}^{s}_{K}\mapsto \mathcal {T}^s_{K}(\mu)$
to be bounded.
$I: \mathcal {D}^{s}_{K}\mapsto \mathcal {T}^s_{K}(\mu)$
to be bounded.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
This research is supported by the National Natural Science Foundation of China (Grant Number 11720101003)
References
- 2
- Cited by





