Let n and k be positive integers with
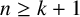 $n\ge k+1$
and let
$n\ge k+1$
and let
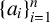 $\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Let
$\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Let
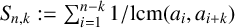 $S_{n, k}:=\sum _{i=1}^{n-k} {1}/{\mathrm {lcm}(a_{i},a_{i+k})}$
. In 1978, Borwein [‘A sum of reciprocals of least common multiples’, Canad. Math. Bull. 20 (1978), 117–118] confirmed a conjecture of Erdős by showing that
$S_{n, k}:=\sum _{i=1}^{n-k} {1}/{\mathrm {lcm}(a_{i},a_{i+k})}$
. In 1978, Borwein [‘A sum of reciprocals of least common multiples’, Canad. Math. Bull. 20 (1978), 117–118] confirmed a conjecture of Erdős by showing that
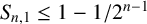 $S_{n,1}\le 1-{1}/{2^{n-1}}$
. Hong [‘A sharp upper bound for the sum of reciprocals of least common multiples’, Acta Math. Hungar. 160 (2020), 360–375] improved Borwein’s upper bound to
$S_{n,1}\le 1-{1}/{2^{n-1}}$
. Hong [‘A sharp upper bound for the sum of reciprocals of least common multiples’, Acta Math. Hungar. 160 (2020), 360–375] improved Borwein’s upper bound to
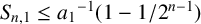 $S_{n,1}\le {a_{1}}^{-1}(1-{1}/{2^{n-1}})$
and derived optimal upper bounds for
$S_{n,1}\le {a_{1}}^{-1}(1-{1}/{2^{n-1}})$
and derived optimal upper bounds for
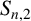 $S_{n,2}$
and
$S_{n,2}$
and
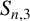 $S_{n,3}$
. In this paper, we present a sharp upper bound for
$S_{n,3}$
. In this paper, we present a sharp upper bound for
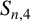 $S_{n,4}$
and characterise the sequences
$S_{n,4}$
and characterise the sequences
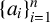 $\{a_i\}_{i=1}^n$
for which the upper bound is attained.
$\{a_i\}_{i=1}^n$
for which the upper bound is attained.
 $\mathbb {Z}_m$ IN AVERAGE
$\mathbb {Z}_m$ IN AVERAGE
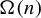 $\Omega (n)$
$\Omega (n)$