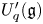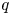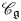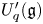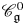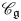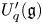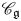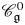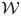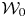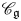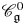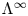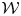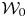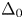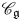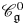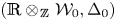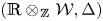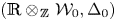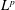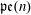Let $U_q'({\mathfrak {g}})$ be a quantum affine algebra with an indeterminate $q$, and let $\mathscr {C}_{\mathfrak {g}}$ be the category of finite-dimensional integrable $U_q'({\mathfrak {g}})$-modules. We write $\mathscr {C}_{\mathfrak {g}}^0$ for the monoidal subcategory of $\mathscr {C}_{\mathfrak {g}}$ introduced by Hernandez and Leclerc. In this paper, we associate a simply laced finite-type root system to each quantum affine algebra $U_q'({\mathfrak {g}})$ in a natural way and show that the block decompositions of $\mathscr {C}_{\mathfrak {g}}$ and $\mathscr {C}_{\mathfrak {g}}^0$ are parameterized by the lattices associated with the root system. We first define a certain abelian group $\mathcal {W}$ (respectively $\mathcal {W} _0$) arising from simple modules of $\mathscr {C}_{\mathfrak {g}}$ (respectively $\mathscr {C}_{\mathfrak {g}}^0$) by using the invariant $\Lambda ^\infty$ introduced in previous work by the authors. The groups $\mathcal {W}$ and $\mathcal {W} _0$ have subsets $\Delta$ and $\Delta _0$ determined by the fundamental representations in $\mathscr {C}_{\mathfrak {g}}$ and $\mathscr {C}_{\mathfrak {g}}^0$, respectively. We prove that the pair $( \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} _0, \Delta _0)$ is an irreducible simply laced root system of finite type and that the pair $( \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} , \Delta )$ is isomorphic to the direct sum of infinite copies of $( \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} _0, \Delta _0)$ as a root system.

Block decomposition of $L^{p}$ spaces with weighted Hausdorff content is established for $0<p\leqslant 1$ and the Fefferman–Stein type inequalities are shown for fractional integral operators and some variants of maximal operators.

We solve two problems in representation theory for the periplectic Lie superalgebra 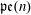$\mathfrak{p}\mathfrak{e}(n)$, namely, the description of the primitive spectrum in terms of functorial realisations of the braid group and the decomposition of category 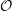${\mathcal{O}}$ into indecomposable blocks.

To solve the first problem, we establish a new type of equivalence between category 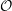${\mathcal{O}}$ for all (not just simple or basic) classical Lie superalgebras and a category of Harish-Chandra bimodules. The latter bimodules have a left action of the Lie superalgebra but a right action of the underlying Lie algebra. To solve the second problem, we establish a BGG reciprocity result 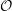for the periplectic Lie superalgebra.