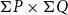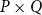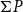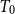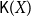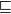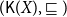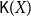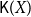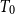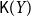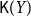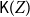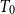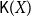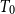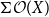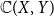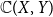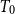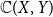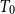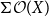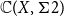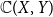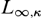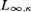In this paper, we mainly study the function spaces related to H-sober spaces. For an irreducible subset system H and
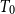 $T_{0}$
spaces X and Y, it is proved that the following three conditions are equivalent: (1) the Scott space
$T_{0}$
spaces X and Y, it is proved that the following three conditions are equivalent: (1) the Scott space
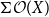 $\Sigma \mathcal O(X)$
of the lattice of all open sets of X is H-sober; (2) for every H-sober space Y, the function space
$\Sigma \mathcal O(X)$
of the lattice of all open sets of X is H-sober; (2) for every H-sober space Y, the function space
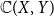 $\mathbb{C}(X, Y)$
of all continuous mappings from X to Y equipped with the Isbell topology is H-sober; (3) for every H-sober space Y, the Isbell topology on
$\mathbb{C}(X, Y)$
of all continuous mappings from X to Y equipped with the Isbell topology is H-sober; (3) for every H-sober space Y, the Isbell topology on
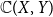 $\mathbb{C}(X, Y)$
has property S with respect to H. One immediate corollary is that for a
$\mathbb{C}(X, Y)$
has property S with respect to H. One immediate corollary is that for a
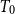 $T_{0}$
space X, Y is a d-space (resp., well-filtered space) iff the function space
$T_{0}$
space X, Y is a d-space (resp., well-filtered space) iff the function space
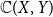 $\mathbb{C}(X, Y)$
equipped with the Isbell topology is a d-space (resp., well-filtered space). It is shown that for any
$\mathbb{C}(X, Y)$
equipped with the Isbell topology is a d-space (resp., well-filtered space). It is shown that for any
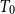 $T_0$
space X for which the Scott space
$T_0$
space X for which the Scott space
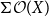 $\Sigma \mathcal O(X)$
is non-sober, the function space
$\Sigma \mathcal O(X)$
is non-sober, the function space
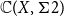 $\mathbb{C}(X, \Sigma 2)$
equipped with the Isbell topology is not sober. The function spaces
$\mathbb{C}(X, \Sigma 2)$
equipped with the Isbell topology is not sober. The function spaces
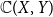 $\mathbb{C}(X, Y)$
equipped with the Scott topology, the compact-open topology and the pointwise convergence topology are also discussed. Our study also leads to a number of questions, whose answers will deepen our understanding of the function spaces related to H-sober spaces.
$\mathbb{C}(X, Y)$
equipped with the Scott topology, the compact-open topology and the pointwise convergence topology are also discussed. Our study also leads to a number of questions, whose answers will deepen our understanding of the function spaces related to H-sober spaces.
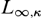 ${L_{\infty ,\kappa }}$
${L_{\infty ,\kappa }}$