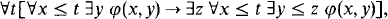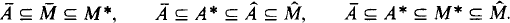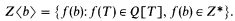10 results
EXISTENTIALLY CLOSED MODELS IN THE FRAMEWORK OF ARITHMETIC
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 May 2016, pp. 774-788
- Print publication:
- June 2016
-
- Article
- Export citation
Truth definitions without exponentiation and the Σ1 collection scheme
-
- Journal:
- The Journal of Symbolic Logic / Volume 77 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 March 2014, pp. 649-655
- Print publication:
- June 2012
-
- Article
- Export citation
Existentially closed structures and Gödel's second incompleteness theorem
-
- Journal:
- The Journal of Symbolic Logic / Volume 66 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 12 March 2014, pp. 349-356
- Print publication:
- March 2001
-
- Article
- Export citation
A sharp version of the bounded Matijasevich conjecture and the end-extension problem
-
- Journal:
- The Journal of Symbolic Logic / Volume 57 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 March 2014, pp. 597-616
- Print publication:
- June 1992
-
- Article
- Export citation
On maximal theories
-
- Journal:
- The Journal of Symbolic Logic / Volume 56 / Issue 3 / September 1991
- Published online by Cambridge University Press:
- 12 March 2014, pp. 885-890
- Print publication:
- September 1991
-
- Article
- Export citation
Open induction and the true theory of rationals
-
- Journal:
- The Journal of Symbolic Logic / Volume 52 / Issue 3 / September 1987
- Published online by Cambridge University Press:
- 12 March 2014, pp. 793-801
- Print publication:
- September 1987
-
- Article
- Export citation
A recursive model for arithmetic with weak induction
-
- Journal:
- The Journal of Symbolic Logic / Volume 50 / Issue 1 / March 1985
- Published online by Cambridge University Press:
- 12 March 2014, pp. 49-54
- Print publication:
- March 1985
-
- Article
- Export citation
On finite lattices of degrees of constructibility
-
- Journal:
- The Journal of Symbolic Logic / Volume 42 / Issue 3 / September 1977
- Published online by Cambridge University Press:
- 12 March 2014, pp. 349-371
- Print publication:
- September 1977
-
- Article
- Export citation
On finite lattices of degrees of constructibility of reals
-
- Journal:
- The Journal of Symbolic Logic / Volume 41 / Issue 2 / June 1976
- Published online by Cambridge University Press:
- 12 March 2014, pp. 313-322
- Print publication:
- June 1976
-
- Article
- Export citation
One more aspect of forcing and omitting types
-
- Journal:
- The Journal of Symbolic Logic / Volume 41 / Issue 1 / March 1976
- Published online by Cambridge University Press:
- 12 March 2014, pp. 73-80
- Print publication:
- March 1976
-
- Article
- Export citation



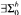 sentences.
sentences.