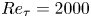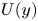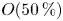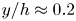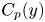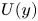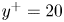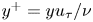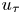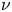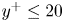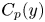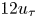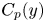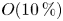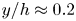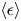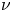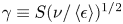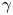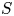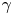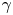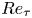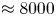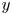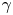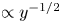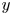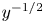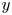We study the application of Taylor's frozen hypothesis to the pressure fluctuations in turbulent channels by means of spatio-temporal data from direct numerical simulations with large computational domains up to the friction Reynolds number 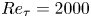$R{e_\tau } = 2000$. The applicability of the hypothesis is quantitatively verified by comparing the wavenumber and Taylor (frequency) premultiplied spectra of the pressure fluctuations at each distance y from the wall. Using the local mean velocity 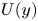$U(y)$ for the hypothesis leads to a large difference between both spectra with a value of 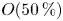$O(50\,{\%})$ for its maximum from the wall to 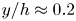$y/h \approx 0.2$, where h is the channel half-depth. Alternatively, the convection velocity of the pressure fluctuations 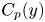${C_p}(y)$, originally defined by Del Álamo & Jiménez (J. Fluid Mech., vol. 640, 2009, pp. 5–26) as a function of y, is investigated and adopted for the hypothesis. It is nearly equal to 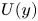$U(y)$ from 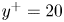${y^ + } = 20$ to the channel centre, where 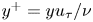${y^ + } = y{u_\tau }/\nu $, in which 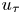${u_\tau }$ and 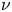$\nu $ represent the friction velocity and kinematic viscosity, respectively. For 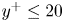${y^ + } \le 20$, 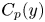${C_p}(y)$ is almost constant with a value of around 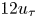$12{u_\tau }$. Applying 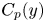${C_p}(y)$ for the hypothesis decreases the difference between both spectra down to a value of 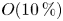$O(10\,{\%})$ for its maximum from the wall to 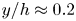$y/h \approx 0.2$. Finally, the difference between the pressure wavenumber and frequency premultiplied spectra near the wall is reduced further via applying a wavenumber-dependent convection velocity. This wavenumber-dependent convection velocity is the linear combination of the convection velocities of the turbulent structures associated with the pressure field weighted by their relative contributions to the pressure variance.

This paper presents an extension of Kolmogorov's local similarity hypotheses of turbulence to include the influence of mean shear on the statistics of the fluctuating velocity in the dissipation range of turbulent shear flow. According to the extension, the moments of the fluctuating velocity gradients are determined by the local mean rate of the turbulent energy dissipation $\left \langle \epsilon \right \rangle$ per unit mass, kinematic viscosity $\nu$ and parameter $\gamma \equiv S (\nu /\left \langle \epsilon \right \rangle )^{1/2}$, provided that $\gamma$ is small in an appropriate sense, where $S$ is an appropriate norm of the local gradients of the mean flow. The statistics of the moments are nearly isotropic for sufficiently small $\gamma$, and the anisotropy of moments decreases approximately in proportion to $\gamma$. This paper also presents a report on the second-order moments of the fluctuating velocity gradients in direct numerical simulations (DNSs) of turbulent channel flow (TCF) with the friction Reynolds number $Re_\tau$ up to $\approx 8000$. In the TCF, there is a range $y$ where $\gamma$ scales approximately $\propto y^ {-1/2}$, and the anisotropy of the moments of the gradients decreases with $y$ nearly in proportion to $y^ {-1/2}$, where $y$ is the distance from the wall. The theoretical conjectures proposed in the first part are in good agreement with the DNS results.

Various compositions of Li1-2xCaxSi2N3 (x = 0–0.2) were synthesized by the reaction of Li3N, Si3N4, and Ca3N2 at temperatures of 1873–2073 K. Ca was incorporated into the LiSi2N3 host lattice to form a solid solution of Li1-2xCaxSi2N3. The activation energy for ionic conduction was decreased and ionic conductivity at room temperature was enhanced by Ca doping. At 298 K, the ionic conductivity of densified Li1-2xCaxSi2N3 (x = 0.075) ceramic reached 1.6 × 10−5 S m−1, almost four orders of magnitude higher than that of densified Li1-2xCaxSi2N3 (x = 0) ceramic (3.1 × 10−9 S m−1). The change in the LiSi2N3 framework upon Ca doping decreased the interaction between the ions and increased the number of defects in the structure, making it easier for mobile Li+ ions to migrate. Moreover, the incorporation of aliovalent substitutional Ca2+ ions in the LiSi2N3 lattice is expected to create Li+ vacancies (VLi) for charge compensation (Li1-2xCaxVLiSi2N3), thereby increasing the number of mobile Li+ ions.

We report Fermi surface and magnetic properties of a cubic PuIn3 grown by the indium flux method. Fermi surfaces detected by the de Haas-van Alphen effect can be well explained by the band calculations assuming itinerant 5f electrons.

We studied tensile creep behavior in two silicon nitride ceramics, i.e., 4.8 mol% Lu2O3 (SN48) and 1.2 mol% Lu2O3 (SN12), at 1400–1500 °C under applied stress of 137–300 MPa. Time to failure of SN48 increased with decreasing applied stress and minimum strain rate. The stress–rupture parameter was 10.7 at 1400 °C and 11.4 at 1500 °C. Pore formation was confirmed in a creep-tested specimen of SN48 by transmission electron microscopy. These results suggest that SN48 was fractured by creep rupture. The minimum strain rate of SN12 was almost below the measurement system limitation at temperatures below 1500 °C. Time to failure tended to increase with decreasing applied stress. The stress–rupture parameter was 41 at 1400 °C and 73 at 1500 °C. These results suggest that SN12 was fractured by subcritical crack growth.

Lutetium nitride (LuN), an end member of a new quaternary system Si3N4–SiO2–Lu2O3–LuN, was synthesized by direct nitridation of a lutetium metal. The nitridation extent of the lutetium ingot (10 × 5 × 2 mm) reached about 97% by heating at 1600 °C for 8 h with an applied N2 pressure of 0.92 MPa; the initial shape of the bulk metal was maintained in the course of nitridation. The resulting nitrided lutetium possessed a moderately low oxygen content (∼0.7 wt%), which enables the preparation of uncharacterized high nitrogen-containing phases in the Lu–Si–O–N system.

High-temperature fracture behavior of a Yb2O3–SiO2–doped hot-pressed silicon nitride (Si3N4) ceramic was investigated in four-point flexure between 1000 and 1500 °C at five crosshead speeds, using the specimens precracked with three indentation loads. Above 1000 °C, a temperature and stressing rate dependence of fracture stress was seen. At 1200 °C the fracture stress of the precracked specimens increased with decreasing stressing rates due to a toughening effect, the absence of slow crack growth (SCG). However, at 1400 and 1500 °C the fracture stress decreased with decreasing stressing rate. In particular, this dependence was stronger at 1500 °C than at 1400 °C. The SCG was observed only in the specimens precracked with indentation loads of 98 and 196 N. This crack extended with increasing test temperature and/or decreasing stressing rate. The dependence of fracture stress on stressing rate was attributed to a SCG behavior at higher temperatures.

Epitaxially grown CeO2 layers on (100)Si substrates are studied using the RBS/channeling technique. The crystallographic correlation between the overgrown layers and off-oriented Si substrates is precisely analyzed by means of constructing stereographic projections obtained from the planar channeling dips. From the stereographic projections for the CeO2 layer on the 4° off-oriented Si substrate, it is clearly seen not only that the epitaxial (110)CeO2 layer is single crystal with the direction defined as [001]CeO2 ║ [011]Si, but also that the crystalline quality of (110)CeO2 on (100)Si can be improved by use of the off-oriented substrate. The inclined epitaxial direction is also detected as the depth information.

The aims of this paper are (a) to construct probability models for peacetime and wartime alliance formation, (b) to provide international political interpretations of the probability models, and (c) to obtain some policy implications from these models.

Since Horvath and Foster published their seminal work in 1963 on probability models of wartime alliance sizes, no further research has been undertaken to elaborate their ideas (except for Yamamoto, 1974; and Yamamoto and Bremer, 1980), even though varied probability models have been applied to the analysis of war occurrences (see Richardson; Singer and Small, 1972; and Wilkinson) and of peacetime alliance formation (see McGowan and Rood, and Siverson and Duncan). Horvath and Foster found that the frequency distribution of wartime alliance sizes is accounted for by a Yule distribution which has a long tail (meaning that large alliances are likely to form in war) and that a Yule distribution can be derived from a process in which a war alliance will acquire new members with.a probability directly proportional to its current size (i.e., the number of participating nations in the alliance) and in which the members of alliances are not allowed to leave until war ends.