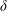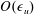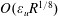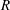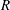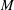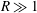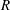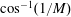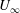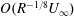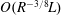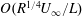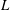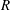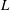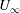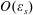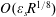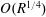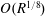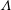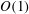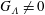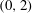57 results
Excitation and evolution of radiating modes in supersonic boundary layers. Part 1. Fundamental resonance with impinging sound waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 985 / 25 April 2024
- Published online by Cambridge University Press:
- 18 April 2024, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Excitation and evolution of radiating modes in supersonic boundary layers. Part 2. Back effect of spontaneously radiated Mach waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 985 / 25 April 2024
- Published online by Cambridge University Press:
- 18 April 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear dynamics and acoustic radiation of coherent structures consisting of multiple ring–helical modes in the near-nozzle region of a subsonic turbulent circular jet
-
- Journal:
- Journal of Fluid Mechanics / Volume 973 / 25 October 2023
- Published online by Cambridge University Press:
- 11 October 2023, A8
-
- Article
- Export citation
Spatial–temporal transformation for primary and secondary instabilities in weakly non-parallel shear flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 959 / 25 March 2023
- Published online by Cambridge University Press:
- 17 March 2023, A21
-
- Article
- Export citation
Nonlinear evolution and low-frequency acoustic radiation of ring-mode coherent structures on subsonic turbulent circular jets
-
- Journal:
- Journal of Fluid Mechanics / Volume 940 / 10 June 2022
- Published online by Cambridge University Press:
- 12 April 2022, A39
-
- Article
- Export citation
Effects of spanwise-periodic surface heating on supersonic boundary-layer instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 940 / 10 June 2022
- Published online by Cambridge University Press:
- 08 April 2022, A20
-
- Article
- Export citation
Elevated low-frequency free-stream vortical disturbances eliminate boundary-layer separation
-
- Journal:
- Journal of Fluid Mechanics / Volume 920 / 10 August 2021
- Published online by Cambridge University Press:
- 08 June 2021, A14
-
- Article
- Export citation
Görtler vortices and streaks in boundary layer subject to pressure gradient: excitation by free stream vortical disturbances, nonlinear evolution and secondary instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 900 / 10 October 2020
- Published online by Cambridge University Press:
- 06 August 2020, A15
-
- Article
- Export citation
Effects of streamwise-elongated and spanwise-periodic surface roughness elements on boundary-layer instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 899 / 25 September 2020
- Published online by Cambridge University Press:
- 27 July 2020, A34
-
- Article
- Export citation
Receptivity of inviscid modes in supersonic boundary layers due to scattering of free-stream sound by localised wall roughness
-
- Journal:
- Journal of Fluid Mechanics / Volume 896 / 10 August 2020
- Published online by Cambridge University Press:
- 04 June 2020, A23
-
- Article
- Export citation
Generation of first Mack modes in supersonic boundary layers by slow acoustic waves interacting with streamwise isolated wall roughness
-
- Journal:
- Journal of Fluid Mechanics / Volume 888 / 10 April 2020
- Published online by Cambridge University Press:
- 06 February 2020, A10
-
- Article
- Export citation
Nonlinear evolution and acoustic radiation of coherent structures in subsonic turbulent free shear layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 884 / 10 February 2020
- Published online by Cambridge University Press:
- 05 December 2019, A10
-
- Article
- Export citation
Receptivity of supersonic boundary layers over smooth and wavy surfaces to impinging slow acoustic waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 872 / 10 August 2019
- Published online by Cambridge University Press:
- 14 June 2019, pp. 849-888
-
- Article
- Export citation
Effects of distributed roughness on crossflow instability through generalized resonance mechanisms
-
- Journal:
- Journal of Fluid Mechanics / Volume 858 / 10 January 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 787-831
-
- Article
- Export citation
Assessing the impact of antibiotic stewardship program elements on antibiotic use across acute-care hospitals: an observational study
-
- Journal:
- Infection Control & Hospital Epidemiology / Volume 39 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 12 June 2018, pp. 941-946
- Print publication:
- August 2018
-
- Article
- Export citation
Stationary crossflow vortices near the leading edge of three-dimensional boundary layers: the role of non-parallelism and excitation by surface roughness
-
- Journal:
- Journal of Fluid Mechanics / Volume 845 / 25 June 2018
- Published online by Cambridge University Press:
- 20 April 2018, pp. 93-140
-
- Article
- Export citation
Nonlinear evolution and secondary instability of steady and unsteady Görtler vortices induced by free-stream vortical disturbances
-
- Journal:
- Journal of Fluid Mechanics / Volume 829 / 25 October 2017
- Published online by Cambridge University Press:
- 25 September 2017, pp. 681-730
-
- Article
- Export citation
A local scattering approach for the effects of abrupt changes on boundary-layer instability and transition: a finite-Reynolds-number formulation for isolated distortions
-
- Journal:
- Journal of Fluid Mechanics / Volume 822 / 10 July 2017
- Published online by Cambridge University Press:
- 06 June 2017, pp. 444-483
-
- Article
- Export citation
Nonlinear unsteady streaks engendered by the interaction of free-stream vorticity with a compressible boundary layer
-
- Journal:
- Journal of Fluid Mechanics / Volume 817 / 25 April 2017
- Published online by Cambridge University Press:
- 15 March 2017, pp. 80-121
-
- Article
- Export citation
Response and receptivity of the hypersonic boundary layer past a wedge to free-stream acoustic, vortical and entropy disturbances
-
- Journal:
- Journal of Fluid Mechanics / Volume 797 / 25 June 2016
- Published online by Cambridge University Press:
- 26 May 2016, pp. 874-915
-
- Article
- Export citation