18 results
Coupling the Kolmogorov diffusion: maximality and efficiency considerations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 15-35
- Print publication:
- July 2016
-
- Article
- Export citation
Perfect simulation of M/G/c queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1039-1063
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Return to the Poissonian city
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 297-309
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Dietrich Stoyan: A Tribute on the Occasion of his Seventieth Birthday
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. i-iv
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Short-length routes in low-cost networks via Poisson line patterns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-21
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Simulation of cluster point processes without edge effects
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 267-280
- Print publication:
- June 2002
-
- Article
- Export citation
Perfect simulation using dominating processes on ordered spaces, with application to locally stable point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 844-865
- Print publication:
- September 2000
-
- Article
- Export citation
Stationary countable dense random sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 86-100
- Print publication:
- March 2000
-
- Article
- Export citation
Riemannian barycentres and geodesic convexity
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 127 / Issue 2 / September 1999
- Published online by Cambridge University Press:
- 01 September 1999, pp. 253-269
- Print publication:
- September 1999
-
- Article
- Export citation
A diffusion model for bookstein triangle shape
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 317-334
- Print publication:
- June 1998
-
- Article
- Export citation
A diffusion model for Bookstein triangle shape
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 334-335
- Print publication:
- June 1996
-
- Article
- Export citation
On the empty cells of Poisson histograms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 561-574
- Print publication:
- September 1993
-
- Article
- Export citation
A remark on the proof of Itô's formula for C2 functions of continuous semimartingales
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 216-221
- Print publication:
- March 1992
-
- Article
- Export citation
Symbolic computation and the diffusion of shapes of triads
-
- Journal:
- Advances in Applied Probability / Volume 20 / Issue 4 / December 1988
- Published online by Cambridge University Press:
- 01 July 2016, pp. 775-797
- Print publication:
- December 1988
-
- Article
- Export citation
The range of the mean-value quantities of planar tessellations
-
- Journal:
- Journal of Applied Probability / Volume 24 / Issue 2 / June 1987
- Published online by Cambridge University Press:
- 14 July 2016, pp. 411-421
- Print publication:
- June 1987
-
- Article
- Export citation
One-dimensional classical scattering processes and the diffusion limit
-
- Journal:
- Advances in Applied Probability / Volume 19 / Issue 1 / March 1987
- Published online by Cambridge University Press:
- 01 July 2016, pp. 81-105
- Print publication:
- March 1987
-
- Article
- Export citation
Coupling methods and the storage equation
-
- Journal:
- Journal of Applied Probability / Volume 20 / Issue 2 / June 1983
- Published online by Cambridge University Press:
- 14 July 2016, pp. 436-441
- Print publication:
- June 1983
-
- Article
- Export citation
Alignments in two-dimensional random sets of points
-
- Journal:
- Advances in Applied Probability / Volume 12 / Issue 2 / June 1980
- Published online by Cambridge University Press:
- 01 July 2016, pp. 380-424
- Print publication:
- June 1980
-
- Article
- Export citation

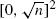 satisfying a weak equidistribution assumption. We show that if the first excess is
satisfying a weak equidistribution assumption. We show that if the first excess is 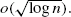
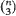 resulting triads form triangles with largest angle ≧ π – ∊. The main object of the paper is to obtain asymptotic formulae for
resulting triads form triangles with largest angle ≧ π – ∊. The main object of the paper is to obtain asymptotic formulae for 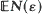 and Var (
and Var (