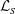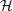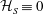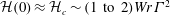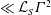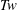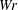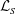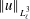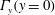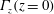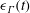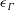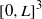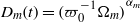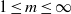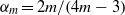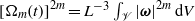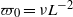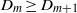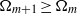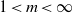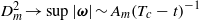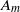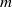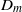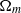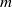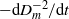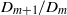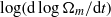16 results
Topology of interacting coiled vortex rings
-
- Journal:
- Journal of Fluid Mechanics / Volume 854 / 10 November 2018
- Published online by Cambridge University Press:
- 03 September 2018, R2
-
- Article
- Export citation
Enstrophy and circulation scaling for Navier–Stokes reconnection
-
- Journal:
- Journal of Fluid Mechanics / Volume 839 / 25 March 2018
- Published online by Cambridge University Press:
- 25 January 2018, R2
-
- Article
- Export citation
X-Ray and Optical Properties of Black Widows and Redbacks
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 13 / Issue S337 / September 2017
- Published online by Cambridge University Press:
- 04 June 2018, pp. 43-46
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
AUGUSTINE'S CANAANITES1
-
- Journal:
- Papers of the British School at Rome / Volume 82 / October 2014
- Published online by Cambridge University Press:
- 02 October 2014, pp. 175-197
- Print publication:
- October 2014
-
- Article
- Export citation
Contributors
-
-
- Book:
- Handbook of Research Methods in Social and Personality Psychology
- Published online:
- 05 June 2014
- Print publication:
- 24 February 2014, pp vii-viii
-
- Chapter
- Export citation
Vorticity moments in four numerical simulations of the 3D Navier–Stokes equations
-
- Journal:
- Journal of Fluid Mechanics / Volume 732 / 10 October 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 316-331
-
- Article
- Export citation
Bounds for Euler from vorticity moments and line divergence
-
- Journal:
- Journal of Fluid Mechanics / Volume 729 / 25 August 2013
- Published online by Cambridge University Press:
- 24 July 2013, R2
-
- Article
- Export citation
Contributors
-
-
- Book:
- Rehabilitation in Movement Disorders
- Published online:
- 05 June 2013
- Print publication:
- 23 May 2013, pp viii-x
-
- Chapter
- Export citation
2 - Structure and Dynamics of Vorticity in Turbulence
-
-
- Book:
- Ten Chapters in Turbulence
- Published online:
- 05 February 2013
- Print publication:
- 06 December 2012, pp 43-86
-
- Chapter
- Export citation
Chandra observations of black widow pulsars
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 8 / Issue S291 / August 2012
- Published online by Cambridge University Press:
- 20 March 2013, pp. 389-391
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
Contributors
-
-
- Book:
- The Cambridge Dictionary of Christianity
- Published online:
- 05 August 2012
- Print publication:
- 20 September 2010, pp xi-xliv
-
- Chapter
- Export citation
Velocity, scalar and transfer spectra in numerical turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 211 / February 1990
- Published online by Cambridge University Press:
- 26 April 2006, pp. 309-332
-
- Article
- Export citation
Rayleigh number scaling in numerical convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 310 / 10 March 1996
- Published online by Cambridge University Press:
- 26 April 2006, pp. 139-179
-
- Article
- Export citation
Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 153 / April 1985
- Published online by Cambridge University Press:
- 20 April 2006, pp. 31-58
-
- Article
- Export citation
Comparison of direct numerical simulations with predictions of two-point closures for isotropic turbulence convecting a passive scalar
-
- Journal:
- Journal of Fluid Mechanics / Volume 118 / May 1982
- Published online by Cambridge University Press:
- 20 April 2006, pp. 205-219
-
- Article
- Export citation
Prandtl number dependence of Nusselt number in direct numerical simulations
-
- Journal:
- Journal of Fluid Mechanics / Volume 419 / 25 September 2000
- Published online by Cambridge University Press:
- 20 October 2000, pp. 325-344
-
- Article
- Export citation