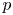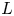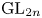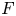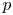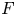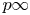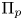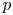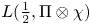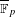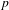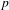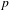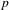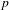4 results
L-functions of GL2n: p-adic properties and non-vanishing of twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2437-2468
- Print publication:
- December 2020
-
- Article
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ATTACHED TO HILBERT MODULAR FORMS MOD
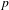 $p$ OF WEIGHT 1
$p$ OF WEIGHT 1
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 23 April 2018, pp. 281-306
- Print publication:
- March 2020
-
- Article
- Export citation
1 - On the local structure of ordinary Hecke algebras at classical weight one points
-
-
- Book:
- Automorphic Forms and Galois Representations
- Published online:
- 05 October 2014
- Print publication:
- 16 October 2014, pp 1-16
-
- Chapter
- Export citation
On Ihara’s lemma for Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 09 September 2009, pp. 1114-1146
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation