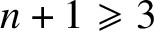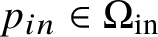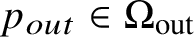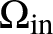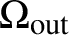4 results
Inverse problems for nonlinear hyperbolic equations with disjoint sources and receivers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 November 2021, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evaluation of the orientation distribution of fibers from reflection images of fibrous samples
-
- Journal:
- The European Physical Journal - Applied Physics / Volume 65 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 January 2014, 10703
- Print publication:
- January 2014
-
- Article
-
- You have access
- Open access
- Export citation
Hyperbolic inverse boundary-value problem and time-continuation of the non-stationary Dirichlet-to-Neumann map
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 4 / August 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 931-949
- Print publication:
- August 2002
-
- Article
- Export citation
Analysis of the PML equations in general convex geometry
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 131 / Issue 5 / October 2001
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1183-1207
- Print publication:
- October 2001
-
- Article
- Export citation