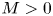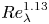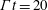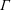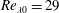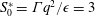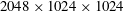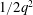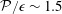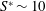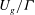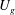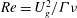8 results
The merger of co-rotating vortices in dusty flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 981 / 25 February 2024
- Published online by Cambridge University Press:
- 26 February 2024, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability of a dusty vortex
-
- Journal:
- Journal of Fluid Mechanics / Volume 948 / 10 October 2022
- Published online by Cambridge University Press:
- 20 September 2022, A56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Accelerated decay of a Lamb–Oseen vortex tube laden with inertial particles in Eulerian–Lagrangian simulations
-
- Journal:
- Journal of Fluid Mechanics / Volume 936 / 10 April 2022
- Published online by Cambridge University Press:
- 07 February 2022, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reynolds number scaling of burning rates in spherical turbulent premixed flames
-
- Journal:
- Journal of Fluid Mechanics / Volume 906 / 10 January 2021
- Published online by Cambridge University Press:
- 05 November 2020, A2
-
- Article
- Export citation
The rapid distortion of two-way coupled particle-laden turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 877 / 25 October 2019
- Published online by Cambridge University Press:
- 19 August 2019, pp. 82-104
-
- Article
- Export citation
Clustering in Euler–Euler and Euler–Lagrange simulations of unbounded homogeneous particle-laden shear
-
- Journal:
- Journal of Fluid Mechanics / Volume 859 / 25 January 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 174-203
-
- Article
- Export citation
An algorithm for solving the Navier–Stokes equations with shear-periodic boundary conditions and its application to homogeneously sheared turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 833 / 25 December 2017
- Published online by Cambridge University Press:
- 08 November 2017, pp. 687-716
-
- Article
- Export citation
Preferential concentration driven instability of sheared gas–solid suspensions
-
- Journal:
- Journal of Fluid Mechanics / Volume 770 / 10 May 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 85-123
-
- Article
- Export citation