29 results
A VARIANT OF HOFSTADTER’S SEQUENCE AND FINITE AUTOMATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1-8
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Periodic unique beta-expansions: the Sharkovskiĭ ordering
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 29 / Issue 4 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1055-1074
- Print publication:
- August 2009
-
- Article
- Export citation
A note on univoque self-Sturmian numbers
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 04 January 2008, pp. 659-662
- Print publication:
- October 2008
-
- Article
- Export citation
8 - Frequency of Letters
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 247-282
-
- Chapter
- Export citation
Contents
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp vii-xii
-
- Chapter
- Export citation
4 - Finite Automata and Other Models of Computation
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 128-151
-
- Chapter
- Export citation
9 - Characteristic Words
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 283-297
-
- Chapter
- Export citation
11 - Cobham's Theorem
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 345-350
-
- Chapter
- Export citation
Index
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 555-571
-
- Chapter
- Export citation
Preface
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp xiii-xvi
-
- Chapter
- Export citation

Automatic Sequences
- Theory, Applications, Generalizations
-
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003
Appendix - Hints, References, and Solutions for Selected Exercises
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 471-480
-
- Chapter
- Export citation
5 - Automatic Sequences
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 152-172
-
- Chapter
- Export citation
3 - Numeration Systems
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 70-127
-
- Chapter
- Export citation
15 - Automaticity
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 428-437
-
- Chapter
- Export citation
6 - Uniform Morphisms and Automatic Sequences
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 173-211
-
- Chapter
- Export citation
10 - Subwords
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 298-344
-
- Chapter
- Export citation
7 - Morphic Sequences
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 212-246
-
- Chapter
- Export citation
12 - Formal Power Series
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 351-378
-
- Chapter
- Export citation
14 - Multidimensional Automatic Sequences
-
- Book:
- Automatic Sequences
- Published online:
- 13 October 2009
- Print publication:
- 21 July 2003, pp 405-427
-
- Chapter
- Export citation

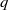
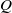
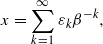
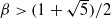 , then, as is well known, there always exist
, then, as is well known, there always exist 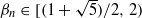 such that there are no unique periodic
such that there are no unique periodic 