Article contents
A VARIANT OF HOFSTADTER’S SEQUENCE AND FINITE AUTOMATA
Published online by Cambridge University Press: 03 May 2013
Abstract
Following up on a paper of Balamohan et al. [‘On the behavior of a variant of Hofstadter’s 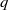 $q$-sequence’, J. Integer Seq. 10 (2007)], we analyze a variant of Hofstadter’s
$q$-sequence’, J. Integer Seq. 10 (2007)], we analyze a variant of Hofstadter’s 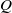 $Q$-sequence and show that its frequency sequence is 2-automatic. An automaton computing the sequence is explicitly given.
$Q$-sequence and show that its frequency sequence is 2-automatic. An automaton computing the sequence is explicitly given.
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
- 6
- Cited by


