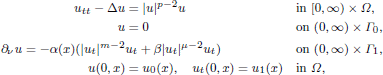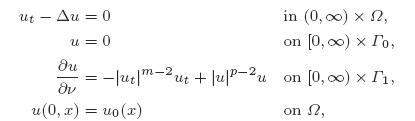The paper deals with local existence, blow-up and global existence for the solutions of a wave equation with an internal nonlinear source and a nonlinear boundary damping. The typical problem studied is\cases{u_{tt}-\Delta u=|u|^{p-2}u \hfill & \rm{~}OPEN~7~in <hsp sp=0.25>[0,\rm{inf}ty )\times \Omega ,}\hfill \cr u=0 \hfill & \rm{~}OPEN~6~on <hsp sp=0.25>[0,\rm{inf}ty )\times \Gamma _0,}\hfill \cr \frac {\partial u}{\partial \nu }=-\alpha (x)|u_t|^{m-2}u_t \hfill & \rm{~}OPEN~2~on <hsp sp=0.25>[0,\rm{inf}ty )\times \Gamma _1,}\cr u(0,x)=u_0(x),u_t(0,x)=u_1(x) & \rm{~}OPEN~1~on<hsp sp=0.25>\Omega ,}\hfill }
where \Omega \subset ℝ^n (n\ge 1) is a regular and bounded domain, \partial \Omega =\Gamma _0\cup \Gamma _1, \lambda _{n-1}(\Gamma _0)>>;0, 2<>;p\le 2(n-1)/(n-2) (when n\ge 3), m>>;1, \alpha \in L^\rm{inf}ty (\Gamma _1), \alpha \ge 0, and the initial data are in the energy space. The results proved extend the potential well theory, which is well known when the nonlinear damping acts in the interior of \Omega, to this problem.