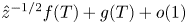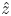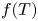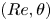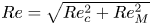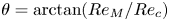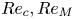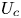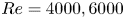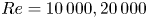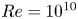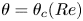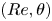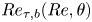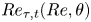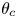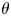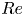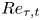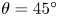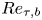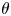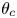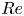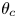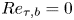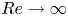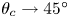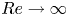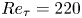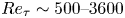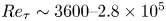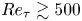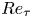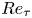We present numerical simulation and mean-flow modelling of statistically stationary plane Couette–Poiseuille flow in a parameter space 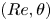 $(Re,\theta )$ with
$(Re,\theta )$ with 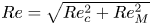 $Re=\sqrt {Re_c^2+Re_M^2}$ and
$Re=\sqrt {Re_c^2+Re_M^2}$ and 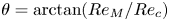 $\theta =\arctan (Re_M/Re_c)$, where
$\theta =\arctan (Re_M/Re_c)$, where 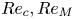 $Re_c,Re_M$ are independent Reynolds numbers based on the plate speed
$Re_c,Re_M$ are independent Reynolds numbers based on the plate speed 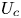 $U_c$ and the volume flow rate per unit span, respectively. The database comprises direct numerical simulations (DNS) at
$U_c$ and the volume flow rate per unit span, respectively. The database comprises direct numerical simulations (DNS) at 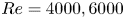 $Re=4000,6000$, wall-resolved large-eddy simulations at
$Re=4000,6000$, wall-resolved large-eddy simulations at 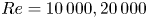 $Re = 10\,000, 20\,000$, and some wall-modelled large-eddy simulations (WMLES) up to
$Re = 10\,000, 20\,000$, and some wall-modelled large-eddy simulations (WMLES) up to 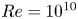 $Re=10^{10}$. Attention is focused on the transition (from Couette-type to Poiseuille-type flow), defined as where the mean skin-friction Reynolds number on the bottom wall
$Re=10^{10}$. Attention is focused on the transition (from Couette-type to Poiseuille-type flow), defined as where the mean skin-friction Reynolds number on the bottom wall  $Re_{\tau,b}$ changes sign at
$Re_{\tau,b}$ changes sign at 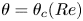 $\theta =\theta _c(Re)$. The mean flow in the
$\theta =\theta _c(Re)$. The mean flow in the 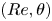 $(Re,\theta )$ plane is modelled with combinations of patched classical log-wake profiles. Several model versions with different structures are constructed in both the Couette-type and Poiseuille-type flow regions. Model calculations of
$(Re,\theta )$ plane is modelled with combinations of patched classical log-wake profiles. Several model versions with different structures are constructed in both the Couette-type and Poiseuille-type flow regions. Model calculations of 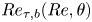 $Re_{\tau,b}(Re,\theta )$,
$Re_{\tau,b}(Re,\theta )$, 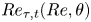 $Re_{\tau,t}(Re,\theta )$ (the skin-friction Reynolds number on the top wall) and
$Re_{\tau,t}(Re,\theta )$ (the skin-friction Reynolds number on the top wall) and 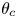 $\theta _c$ show general agreement with both DNS and large-eddy simulations. Both model and simulation indicate that, as
$\theta _c$ show general agreement with both DNS and large-eddy simulations. Both model and simulation indicate that, as 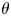 $\theta$ is increased at fixed
$\theta$ is increased at fixed 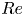 $Re$,
$Re$, 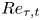 $Re_{\tau,t}$ passes through a peak at approximately
$Re_{\tau,t}$ passes through a peak at approximately 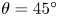 $\theta = 45^{\circ }$, while
$\theta = 45^{\circ }$, while 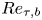 $Re_{\tau,b}$ increases monotonically. Near the bottom wall, the flow laminarizes as
$Re_{\tau,b}$ increases monotonically. Near the bottom wall, the flow laminarizes as 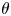 $\theta$ passes through
$\theta$ passes through 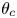 $\theta _c$ and then re-transitions to turbulence. As
$\theta _c$ and then re-transitions to turbulence. As 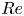 $Re$ increases,
$Re$ increases, 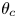 $\theta _c$ increases monotonically. The transition from Couette-type to Poiseuille-type flow is accompanied by the rapid attenuation of streamwise rolls observed in pure Couette flow. A subclass of flows with
$\theta _c$ increases monotonically. The transition from Couette-type to Poiseuille-type flow is accompanied by the rapid attenuation of streamwise rolls observed in pure Couette flow. A subclass of flows with 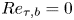 $Re_{\tau,b}=0$ is investigated. Combined WMLES with modelling for these flows enables exploration of the
$Re_{\tau,b}=0$ is investigated. Combined WMLES with modelling for these flows enables exploration of the 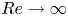 $Re\to \infty$ limit, giving
$Re\to \infty$ limit, giving 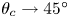 $\theta _c \to 45^\circ$ as
$\theta _c \to 45^\circ$ as 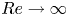 $Re\to \infty$.
$Re\to \infty$.