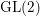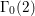The aim of this paper is to carry out an explicit construction of CAP representations of 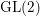 $\text{GL}(2)$ over a division quaternion algebra with discriminant two. We first construct cusp forms on such a group explicitly by lifting from Maass cusp forms for the congruence subgroup
$\text{GL}(2)$ over a division quaternion algebra with discriminant two. We first construct cusp forms on such a group explicitly by lifting from Maass cusp forms for the congruence subgroup 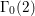 ${\rm\Gamma}_{0}(2)$. We show that this lifting is nonzero and Hecke-equivariant. This allows us to determine each local component of a cuspidal representation generated by such a lifting. We then show that our cuspidal representations provide examples of CAP (cuspidal representation associated to a parabolic subgroup) representations, and, in fact, counterexamples to the Ramanujan conjecture.
${\rm\Gamma}_{0}(2)$. We show that this lifting is nonzero and Hecke-equivariant. This allows us to determine each local component of a cuspidal representation generated by such a lifting. We then show that our cuspidal representations provide examples of CAP (cuspidal representation associated to a parabolic subgroup) representations, and, in fact, counterexamples to the Ramanujan conjecture.