15 results
Krieger’s type for ergodic non-singular Poisson actions of non-(T) locally compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2317-2353
- Print publication:
- July 2023
-
- Article
- Export citation
Generic non-singular Poisson suspension is of type III1
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 1415-1445
- Print publication:
- April 2022
-
- Article
- Export citation
Ergodic cocycles of IDPFT systems and non-singular Gaussian actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 18 February 2021, pp. 1624-1654
- Print publication:
- May 2022
-
- Article
- Export citation
K-property for Maharam extensions of non-singular Bernoulli and Markov shifts
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 39 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 05 April 2018, pp. 3292-3321
- Print publication:
- December 2019
-
- Article
- Export citation
Directional recurrence and directional rigidity for infinite measure preserving actions of nilpotent lattices
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 37 / Issue 6 / September 2017
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1841-1861
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Actions of finite rank: weak rational ergodicity and partial rigidity
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 36 / Issue 7 / October 2016
- Published online by Cambridge University Press:
- 13 April 2015, pp. 2138-2171
- Print publication:
- October 2016
-
- Article
- Export citation
Mixing actions of the Heisenberg group
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 34 / Issue 4 / August 2014
- Published online by Cambridge University Press:
- 21 January 2013, pp. 1142-1167
- Print publication:
- August 2014
-
- Article
- Export citation
A survey on spectral multiplicities of ergodic actions
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 33 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 09 December 2011, pp. 81-117
- Print publication:
- February 2013
-
- Article
- Export citation
New spectral multiplicities for mixing transformations
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 32 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 14 March 2011, pp. 517-534
- Print publication:
- April 2012
-
- Article
- Export citation
Mixing constructions with infinite invariant measure and spectral multiplicities
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 31 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 10 May 2010, pp. 853-873
- Print publication:
- June 2011
-
- Article
- Export citation
Explicit solution of Rokhlin's problem on homogeneous spectrum and applications
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 26 / Issue 5 / October 2006
- Published online by Cambridge University Press:
- 11 September 2006, pp. 1467-1490
- Print publication:
- October 2006
-
- Article
- Export citation
MULTIPLE AND POLYNOMIAL RECURRENCE FOR ABELIAN ACTIONS IN INFINITE MEASURE
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 28 January 2004, pp. 183-200
- Print publication:
- February 2004
-
- Article
- Export citation
Generators and Bernoullian factors for amenable actions and cocycles on their orbits
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 22 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 06 November 2002, pp. 1715-1745
- Print publication:
- December 2002
-
- Article
- Export citation
Endomorphisms of measured equivalence relations, cocycles with values in non-locally compact groups and applications
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 19 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 01 June 1999, pp. 571-590
- Print publication:
- June 1999
-
- Article
- Export citation
Comparison of cocycles of measured equivalence relations and lifting problems
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 18 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 01 February 1998, pp. 125-151
- Print publication:
- February 1998
-
- Article
- Export citation



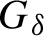

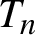
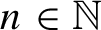
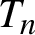
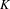
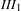
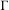
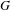

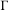
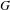

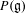

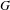


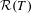

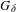
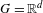
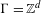
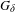
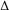
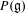
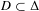

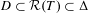
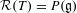

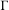
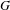
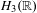
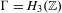
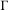

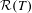
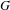
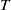
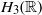
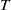
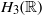
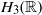
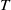
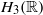
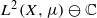 by
by  are realizable as ℳ(
are realizable as ℳ(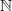 such that 1∈
such that 1∈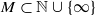 as the set of essential values of the multiplicity function for the Koopman operator of a mixing ergodic infinite measure preserving transformation, (ii) construct mixing power weakly mixing infinite measure preserving transformations, and (iii) construct mixing Poissonian automorphisms with a simple spectrum, etc.
as the set of essential values of the multiplicity function for the Koopman operator of a mixing ergodic infinite measure preserving transformation, (ii) construct mixing power weakly mixing infinite measure preserving transformations, and (iii) construct mixing Poissonian automorphisms with a simple spectrum, etc.