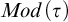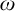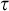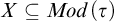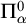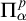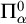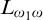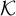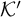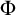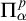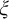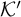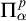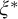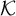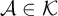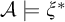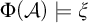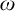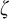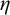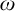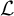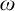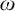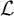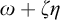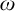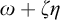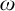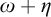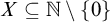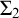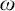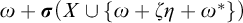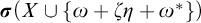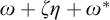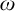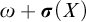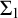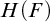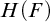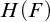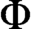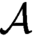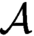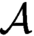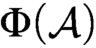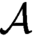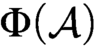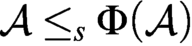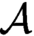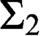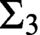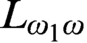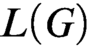Cohesive powers of computable structures are effective analogs of ultrapowers, where cohesive sets play the role of ultrafilters. Let 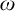 $\omega $,
$\omega $, 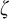 $\zeta $, and
$\zeta $, and 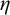 $\eta $ denote the respective order-types of the natural numbers, the integers, and the rationals when thought of as linear orders. We investigate the cohesive powers of computable linear orders, with special emphasis on computable copies of
$\eta $ denote the respective order-types of the natural numbers, the integers, and the rationals when thought of as linear orders. We investigate the cohesive powers of computable linear orders, with special emphasis on computable copies of 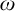 $\omega $. If
$\omega $. If 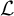 $\mathcal {L}$ is a computable copy of
$\mathcal {L}$ is a computable copy of 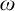 $\omega $ that is computably isomorphic to the usual presentation of
$\omega $ that is computably isomorphic to the usual presentation of 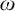 $\omega $, then every cohesive power of
$\omega $, then every cohesive power of 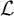 $\mathcal {L}$ has order-type
$\mathcal {L}$ has order-type 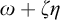 $\omega + \zeta \eta $. However, there are computable copies of
$\omega + \zeta \eta $. However, there are computable copies of 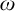 $\omega $, necessarily not computably isomorphic to the usual presentation, having cohesive powers not elementarily equivalent to
$\omega $, necessarily not computably isomorphic to the usual presentation, having cohesive powers not elementarily equivalent to 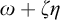 $\omega + \zeta \eta $. For example, we show that there is a computable copy of
$\omega + \zeta \eta $. For example, we show that there is a computable copy of 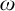 $\omega $ with a cohesive power of order-type
$\omega $ with a cohesive power of order-type 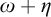 $\omega + \eta $. Our most general result is that if
$\omega + \eta $. Our most general result is that if 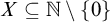 $X \subseteq \mathbb {N} \setminus \{0\}$ is a Boolean combination of
$X \subseteq \mathbb {N} \setminus \{0\}$ is a Boolean combination of 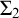 $\Sigma _2$ sets, thought of as a set of finite order-types, then there is a computable copy of
$\Sigma _2$ sets, thought of as a set of finite order-types, then there is a computable copy of 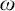 $\omega $ with a cohesive power of order-type
$\omega $ with a cohesive power of order-type 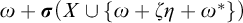 $\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$, where
$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$, where 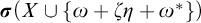 $\boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$ denotes the shuffle of the order-types in X and the order-type
$\boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$ denotes the shuffle of the order-types in X and the order-type 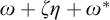 $\omega + \zeta \eta + \omega ^*$. Furthermore, if X is finite and non-empty, then there is a computable copy of
$\omega + \zeta \eta + \omega ^*$. Furthermore, if X is finite and non-empty, then there is a computable copy of 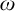 $\omega $ with a cohesive power of order-type
$\omega $ with a cohesive power of order-type 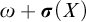 $\omega + \boldsymbol {\sigma }(X)$.
$\omega + \boldsymbol {\sigma }(X)$.