102 results
Singular matrices and pairwise-tangent circles
-
- Journal:
- The Mathematical Gazette / Volume 108 / Issue 571 / March 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 12-19
- Print publication:
- March 2024
-
- Article
- Export citation
107.28 Sums, and sums of squares
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 570 / November 2023
- Published online by Cambridge University Press:
- 11 October 2023, pp. 488-490
- Print publication:
- November 2023
-
- Article
- Export citation
107.36 Similarities and circle-preserving bijections of the plane
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 570 / November 2023
- Published online by Cambridge University Press:
- 11 October 2023, pp. 508-511
- Print publication:
- November 2023
-
- Article
- Export citation
Groups, conics and recurrence relations
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 569 / July 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 193-203
- Print publication:
- July 2023
-
- Article
- Export citation
106.33 Fibonacci numbers and Cassini’s identity
-
- Journal:
- The Mathematical Gazette / Volume 106 / Issue 567 / November 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 498-501
- Print publication:
- November 2022
-
- Article
- Export citation
The real solutions of x = ax
-
- Journal:
- The Mathematical Gazette / Volume 106 / Issue 566 / July 2022
- Published online by Cambridge University Press:
- 22 June 2022, pp. 206-211
- Print publication:
- July 2022
-
- Article
- Export citation
105.26 Areas above and below a curve
-
- Journal:
- The Mathematical Gazette / Volume 105 / Issue 563 / July 2021
- Published online by Cambridge University Press:
- 21 June 2021, pp. 309-311
- Print publication:
- July 2021
-
- Article
- Export citation
Pitot's theorem, dynamic geometry and conics
-
- Journal:
- The Mathematical Gazette / Volume 105 / Issue 562 / March 2021
- Published online by Cambridge University Press:
- 17 February 2021, pp. 52-60
- Print publication:
- March 2021
-
- Article
- Export citation
Surjective isometries of metric geometries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 828-839
- Print publication:
- December 2021
-
- Article
- Export citation
Repeated vector products
-
- Journal:
- The Mathematical Gazette / Volume 104 / Issue 561 / November 2020
- Published online by Cambridge University Press:
- 08 October 2020, pp. 460-468
- Print publication:
- November 2020
-
- Article
- Export citation
104.24 Surveying in the hyperbolic plane
-
- Journal:
- The Mathematical Gazette / Volume 104 / Issue 560 / July 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 341-343
- Print publication:
- July 2020
-
- Article
- Export citation
The convexity of the function y = E(x) defined by xy = yx
-
- Journal:
- The Mathematical Gazette / Volume 104 / Issue 559 / March 2020
- Published online by Cambridge University Press:
- 02 March 2020, pp. 36-43
- Print publication:
- March 2020
-
- Article
- Export citation
The three Steiner-Lehmus theorems
-
- Journal:
- The Mathematical Gazette / Volume 103 / Issue 557 / July 2019
- Published online by Cambridge University Press:
- 06 June 2019, pp. 293-304
- Print publication:
- July 2019
-
- Article
- Export citation
102.54 Unravelling Simpson's paradox
-
- Journal:
- The Mathematical Gazette / Volume 102 / Issue 555 / November 2018
- Published online by Cambridge University Press:
- 17 October 2018, pp. 534-535
- Print publication:
- November 2018
-
- Article
- Export citation
102.05 Remarks on Problem 100.I
-
- Journal:
- The Mathematical Gazette / Volume 102 / Issue 553 / March 2018
- Published online by Cambridge University Press:
- 08 February 2018, pp. 102-104
- Print publication:
- March 2018
-
- Article
- Export citation
101.34 The area of a quadrilateral
-
- Journal:
- The Mathematical Gazette / Volume 101 / Issue 552 / November 2017
- Published online by Cambridge University Press:
- 16 October 2017, pp. 492-494
- Print publication:
- November 2017
-
- Article
- Export citation
101.03 Products of 3 × 3 magic matrices
-
- Journal:
- The Mathematical Gazette / Volume 101 / Issue 550 / March 2017
- Published online by Cambridge University Press:
- 03 February 2017, pp. 96-98
- Print publication:
- March 2017
-
- Article
- Export citation

Mathematical Explorations
-
- Published online:
- 12 January 2017
- Print publication:
- 13 October 2016
4 - Intersecting chords
-
- Book:
- Mathematical Explorations
- Published online:
- 12 January 2017
- Print publication:
- 13 October 2016, pp 26-33
-
- Chapter
- Export citation
Preface
-
- Book:
- Mathematical Explorations
- Published online:
- 12 January 2017
- Print publication:
- 13 October 2016, pp ix-ix
-
- Chapter
- Export citation



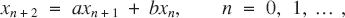
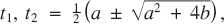
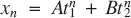 when
when 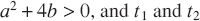 are real and distinct;
are real and distinct;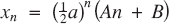 when
when