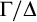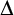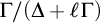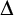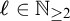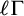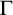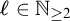1 Introduction
The model theory of ordered abelian groups has been studied since the sixties, and was initiated by Robinson and Zakon in [Reference Robinson and Zakon15] who studied the completions of regular ordered abelian groups (see Definition 2.10). Later, the study of the elementary properties of ordered abelian groups was continued by Belegradek in [Reference Belegradek2] for the class of poly-regular ordered abelian groups (see Definition 2.13). Significant achievements on (relative) quantifier elimination, model completion, and definability of convex subgroups were achieved by Schmitt in [Reference Schmitt16] for the general class of ordered abelian groups. More recently, Cluckers and Halupczok obtained a (relative) quantifier elimination for ordered abelian groups in [Reference Cluckers and Halupczok3] in a language that is more aligned with Shelah’s imaginary expansion than the one introduced by Schmitt.
The model theoretic classification of certain classes of ordered abelian groups is an active research area. Results include: the well-known result of Gurevich–Schmitt that no ordered abelian group has the independence property in [Reference Gurevich and Schmitt6]; the dp-minimal case characterized by Jahnke, Simon, and Walsberg in [Reference Jahnke, Simon and Walsberg11]; the strongly dependent case independently obtained by Dolich–Goodrick, Farré, and Halevi–Hasson in [Reference Dolich and Goodrick4, Reference Farré5, Reference Halevi and Hasson7], respectively, and the distal case in [Reference Aschenbrenner, Chernikov, Gehret and Ziegler1] due to Aschenbrenner, Chernikov, Gehret, and Ziegler.
The next natural step regarding the model theory of ordered abelian groups was understanding a reasonable language where one will have elimination of imaginaries. The answer to this problem, interesting in its own sake, has a significant impact in clarifying the problem of elimination of imaginaries for henselian valued fields. At the heart of the model theory of henselian valued fields is the well known Ax-Kochen/Ershov theorem, that broadly states that the first-order theory of a henselian finitely ramified valued field is completely determined by the first-order theory of its residue field and its value group. In a pure henselian valued field, the value group is a pure ordered abelian group and it is interpretable in the structure.
Following the Ax-Kochen principle one can first attempt to solve the problem of elimination of imaginaries for henselian valued fields by following two orthogonal directions:
-
1. The first one is to make the value group as tame as possible (e.g., to assume that it is definably complete) and to understand the obstacles that the residue field naturally contributes to the problem. This research path was successfully finalized by Hils and Rideau-Kikuchi in [Reference Hils and Rideau-Kikuchi9].
-
2. Alternatively, one can make the residue field very tame (e.g., algebraically closed) and study the issues that the complexity of the value group brings to the problem. The work in [Reference Vicaría19] clarifies the picture for the equicharacteristic zero case, and this paper is the first milestone towards the solution.
We use an abstract criterion isolated by Hrushovski in [Reference Hrushovski10] to show the following two results:
Theorem. Let
![]() $\Gamma $
be an ordered abelian group of bounded regular rank (equivalently with finite spines). Then
$\Gamma $
be an ordered abelian group of bounded regular rank (equivalently with finite spines). Then
![]() $\Gamma $
admits weak-elimination of imaginaries once the quotient sorts are added.
$\Gamma $
admits weak-elimination of imaginaries once the quotient sorts are added.
Theorem. Let
![]() $\Gamma $
be a dp-minimal ordered abelian group. Then
$\Gamma $
be a dp-minimal ordered abelian group. Then
![]() $\Gamma $
admits elimination of imaginaries once the quotient sorts are added, and we add constants to distinguish the cosets of
$\Gamma $
admits elimination of imaginaries once the quotient sorts are added, and we add constants to distinguish the cosets of
![]() $\ell \Gamma $
in
$\ell \Gamma $
in
![]() $\Gamma $
, where
$\Gamma $
, where
![]() $\ell \in \mathbb {N}_{\geq 2}$
.
$\ell \in \mathbb {N}_{\geq 2}$
.
This paper is organized as follows:
-
1. Section 2: We present the state of model theory of ordered abelian groups and introduce the class of ordered abelian groups with bounded regular rank.
-
2. Section 3: We characterize the definable end-segments in an ordered abelian group with bounded regular rank and show that they can be coded in the quotient sorts.
-
3. Section 4: We introduce Hrushovski’s theorem to achieve a weak elimination of imaginaries result for the class of ordered abelian groups with bounded regular rank. This criterion requires us to check two conditions: the density of definable types, proved in Proposition 4.4; and the coding of definable types, proved in Proposition 4.2.
-
4. Section 5: We briefly summarize the main results for pure ordered abelian groups.
The case of direct sums of the integers with the lexicographic order has been done independently by Liccardo in [Reference Liccardo13], as part of her Ph.D. thesis under D’Aquino. Hils and Mennuni in [Reference Hils and Mennuni8] have independently obtained the result for the regular case.
2 Preliminaries
2.1 Elimination of imaginaries
Let T be a first-order theory and let
![]() $\mathfrak {M}$
be its monster model. Let
$\mathfrak {M}$
be its monster model. Let
![]() $D \subseteq \mathfrak {M}^{k}$
be some definable set and E some definable equivalence relation over D. The equivalence class
$D \subseteq \mathfrak {M}^{k}$
be some definable set and E some definable equivalence relation over D. The equivalence class
![]() $e=a/E$
is said to be an imaginary element. Imaginaries in model theory were introduced by Shelah in [Reference Shelah18]. Later in [Reference Makkai14], Makkai proposed to construct the many sorted structure
$e=a/E$
is said to be an imaginary element. Imaginaries in model theory were introduced by Shelah in [Reference Shelah18]. Later in [Reference Makkai14], Makkai proposed to construct the many sorted structure
![]() $\mathfrak {M}^{eq}$
, where we add a sort
$\mathfrak {M}^{eq}$
, where we add a sort
![]() $S_{E}$
for each definable equivalence relation E and a map
$S_{E}$
for each definable equivalence relation E and a map
![]() $\pi _{E}$
sending each element to its class. Since then, the model theoretic community has presented and studied imaginary elements in this way and refers to the multi-sorted structure
$\pi _{E}$
sending each element to its class. Since then, the model theoretic community has presented and studied imaginary elements in this way and refers to the multi-sorted structure
![]() $\mathfrak {M}^{eq}$
as the imaginary expansion of
$\mathfrak {M}^{eq}$
as the imaginary expansion of
![]() $\mathfrak {M}$
. We call the sorts
$\mathfrak {M}$
. We call the sorts
![]() $S_{E}$
imaginary sorts while we refer to
$S_{E}$
imaginary sorts while we refer to
![]() $\mathfrak {M}$
as the home sort.
$\mathfrak {M}$
as the home sort.
Any formula
![]() $\phi (\mathbf {x},\mathbf {y})$
induces an equivalence relation in
$\phi (\mathbf {x},\mathbf {y})$
induces an equivalence relation in
![]() $\mathfrak {M}^{|\mathbf {y}|}$
defined as
$\mathfrak {M}^{|\mathbf {y}|}$
defined as
Let
![]() $\mathbf {b} \in \mathfrak {M}^{|\mathbf {y}|}$
and
$\mathbf {b} \in \mathfrak {M}^{|\mathbf {y}|}$
and
![]() $X:= \phi (\mathbf {x}, \mathbf {b})$
. We call the class
$X:= \phi (\mathbf {x}, \mathbf {b})$
. We call the class
![]() $\mathbf {b}/ E_{\phi }$
the code of X and denote it as
$\mathbf {b}/ E_{\phi }$
the code of X and denote it as
![]() $\ulcorner X \urcorner $
. We denote by
$\ulcorner X \urcorner $
. We denote by
![]() $\operatorname {dcl}^{eq}$
and
$\operatorname {dcl}^{eq}$
and
![]() $\operatorname {acl}^{eq}$
the definable closure and the algebraic closure in the expansion
$\operatorname {acl}^{eq}$
the definable closure and the algebraic closure in the expansion
![]() $\mathfrak {M}^{eq}$
.
$\mathfrak {M}^{eq}$
.
Definition 2.1.
-
1. We say that T has elimination of imaginaries if for any imaginary element e there is a tuple a in the home sort such that
 $e \in \operatorname {dcl}^{eq}(a)$
and
$e \in \operatorname {dcl}^{eq}(a)$
and
 $a \in \operatorname {dcl}^{eq}(e)$
.
$a \in \operatorname {dcl}^{eq}(e)$
. -
2. We say that T has weak elimination of imaginaries if for any imaginary element e there is a tuple a in the home sort such that
 $e \in \operatorname {dcl}^{eq}(a)$
and
$e \in \operatorname {dcl}^{eq}(a)$
and
 $a \in \operatorname {acl}^{eq}(e)$
.
$a \in \operatorname {acl}^{eq}(e)$
. -
3. We say that T codes finite sets if for every model
 $M \vDash T$
and every finite subset S of M, the code
$M \vDash T$
and every finite subset S of M, the code
 $\ulcorner S \urcorner $
is interdefinable with a tuple of elements in M.
$\ulcorner S \urcorner $
is interdefinable with a tuple of elements in M.
The following is a folklore fact.
Fact 2.2. Let T be a complete multi-sorted theory. If T has weak elimination of imaginaries and codes finite sets then T eliminates imaginaries.
2.2 Ordered abelian groups of bounded regular rank
In this section we summarize several results about the classification of ordered abelian groups and their model theoretic behavior. We start by recalling the following folklore fact.
Fact 2.3. Let
![]() $(\Gamma ,< ,+, 0)$
be a non-trivial ordered abelian group. Then the topology induced by the order in
$(\Gamma ,< ,+, 0)$
be a non-trivial ordered abelian group. Then the topology induced by the order in
![]() $\Gamma $
is discrete if and only if
$\Gamma $
is discrete if and only if
![]() $\Gamma $
has a minimal positive element. In this case we say that
$\Gamma $
has a minimal positive element. In this case we say that
![]() $\Gamma $
is discrete, otherwise we say that it is dense.
$\Gamma $
is discrete, otherwise we say that it is dense.
The following notions were isolated in the sixties by Robinson and Zakon in [Reference Robinson and Zakon15] to understand some complete extensions of the theory of ordered abelian groups.
Definition 2.4. Let
![]() $\Gamma $
be an ordered abelian group and
$\Gamma $
be an ordered abelian group and
![]() $n \in \mathbb {N}_{\geq 2}$
.
$n \in \mathbb {N}_{\geq 2}$
.
-
1. Let
 $\gamma \in \Gamma $
. We say that
$\gamma \in \Gamma $
. We say that
 $\gamma $
is n-divisible if there is some
$\gamma $
is n-divisible if there is some
 $\beta \in \Gamma $
such that
$\beta \in \Gamma $
such that
 $\gamma =n\beta $
.
$\gamma =n\beta $
. -
2. We say that
 $\Gamma $
is n-divisible if every element
$\Gamma $
is n-divisible if every element
 $\gamma \in \Gamma $
is n-divisible.
$\gamma \in \Gamma $
is n-divisible. -
3.
 $\Gamma $
is said to be n-regular if any interval with at least n points contains an n-divisible element.
$\Gamma $
is said to be n-regular if any interval with at least n points contains an n-divisible element.
Example 2.5. We include some examples to illustrate the previous definitions.
-
1. Consider the ordered abelian group
 $(\mathbb {Z},+, \leq , 0)$
, the elements
$(\mathbb {Z},+, \leq , 0)$
, the elements
 $2,4,6$
are
$2,4,6$
are
 $2$
-divisible while
$2$
-divisible while
 $1$
is not.
$1$
is not. -
2. The groups
 $(\mathbb {Q},+,\leq , 0)$
and
$(\mathbb {Q},+,\leq , 0)$
and
 $(\mathbb {Z}, +, \leq , 0)$
are n-regular for each natural number
$(\mathbb {Z}, +, \leq , 0)$
are n-regular for each natural number
 $n \in \mathbb {N}_{\geq 2}$
. The group
$n \in \mathbb {N}_{\geq 2}$
. The group
 $(\mathbb {Z} \oplus \mathbb {Z}, \leq _{lex}, +, 0)$
, where
$(\mathbb {Z} \oplus \mathbb {Z}, \leq _{lex}, +, 0)$
, where
 $\leq _{lex}$
is the lexicographic order, is not
$\leq _{lex}$
is the lexicographic order, is not
 $2$
-regular, because the interval
$2$
-regular, because the interval
 $\big ((1,-1),(1,4)\big )=\{ (1,0), (1,1), (1,2),(1,3)\}$
does not contain a
$\big ((1,-1),(1,4)\big )=\{ (1,0), (1,1), (1,2),(1,3)\}$
does not contain a
 $2$
-divisible element.
$2$
-divisible element.
The following definitions were introduced by Schmitt in [Reference Schmitt16, Reference Schmitt, Müller and Richter17].
Definition 2.6. We fix an ordered abelian group
![]() $\Gamma $
and
$\Gamma $
and
![]() $n\in \mathbb {N}_{\geq 2}$
. Let
$n\in \mathbb {N}_{\geq 2}$
. Let
![]() $\gamma \in \Gamma $
. We define:
$\gamma \in \Gamma $
. We define:
-
•
 $A(\gamma )=$
the largest convex subgroup of
$A(\gamma )=$
the largest convex subgroup of
 $\Gamma $
not containing
$\Gamma $
not containing
 $\gamma $
.
$\gamma $
. -
•
 $B(\gamma )=$
the smallest convex subgroup of
$B(\gamma )=$
the smallest convex subgroup of
 $\Gamma $
containing
$\Gamma $
containing
 $\gamma $
.
$\gamma $
. -
•
 $C(\gamma )=B(\gamma )/A(\gamma )$
.
$C(\gamma )=B(\gamma )/A(\gamma )$
. -
•
 $A_{n}(\gamma )=$
the smallest convex subgroup C of
$A_{n}(\gamma )=$
the smallest convex subgroup C of
 $\Gamma $
such that
$\Gamma $
such that
 $B(\gamma )/C$
is n-regular.
$B(\gamma )/C$
is n-regular. -
•
 $B_{n}(\gamma )=$
the largest convex subgroup C of
$B_{n}(\gamma )=$
the largest convex subgroup C of
 $\Gamma $
such that
$\Gamma $
such that
 $C/A_{n}(\gamma )$
is n-regular.
$C/A_{n}(\gamma )$
is n-regular.
In [Reference Schmitt16, Chapter 2], Schmitt shows that the groups
![]() $A_{n}(\gamma )$
and
$A_{n}(\gamma )$
and
![]() $B_{n}(\gamma )$
are definable in the language of ordered abelian groups
$B_{n}(\gamma )$
are definable in the language of ordered abelian groups
![]() $\mathcal {L}_{OAG}=\{ +,-, \leq , 0\}$
by a first-order formula using only the parameter
$\mathcal {L}_{OAG}=\{ +,-, \leq , 0\}$
by a first-order formula using only the parameter
![]() $\gamma $
.
$\gamma $
.
We recall that the set of convex subgroups of an ordered abelian group is totally ordered by inclusion.
Definition 2.7. Let
![]() $\Gamma $
be an ordered abelian group and
$\Gamma $
be an ordered abelian group and
![]() $n \in \mathbb {N}_{\geq 2}$
, we define the n-regular rank to be the order type of
$n \in \mathbb {N}_{\geq 2}$
, we define the n-regular rank to be the order type of
The n-regular rank of an ordered abelian group
![]() $\Gamma $
is a linear order, and when it is finite we can identify it with its cardinal. In [Reference Farré5], Farré emphasizes that we can characterize it without mentioning the subgroups
$\Gamma $
is a linear order, and when it is finite we can identify it with its cardinal. In [Reference Farré5], Farré emphasizes that we can characterize it without mentioning the subgroups
![]() $A_{n}(\gamma )$
. The following is [Reference Farré5, Remark 2.2].
$A_{n}(\gamma )$
. The following is [Reference Farré5, Remark 2.2].
Fact 2.8. Let
![]() $\Gamma $
be an ordered abelian group and
$\Gamma $
be an ordered abelian group and
![]() $n \in \mathbb {N}_{\geq 2}$
, then:
$n \in \mathbb {N}_{\geq 2}$
, then:
-
1.
 $\Gamma $
has n-regular rank equal to
$\Gamma $
has n-regular rank equal to
 $0$
if and only if
$0$
if and only if
 $\Gamma =\{0\}$
.
$\Gamma =\{0\}$
. -
2.
 $\Gamma $
has n-regular rank equal to
$\Gamma $
has n-regular rank equal to
 $1$
if and only if
$1$
if and only if
 $\Gamma $
is n-regular and not trivial.
$\Gamma $
is n-regular and not trivial. -
3.
 $\Gamma $
has n-regular rank equal to m if there are
$\Gamma $
has n-regular rank equal to m if there are
 $\Delta _{0}, \dots , \Delta _{m}$
convex subgroups of
$\Delta _{0}, \dots , \Delta _{m}$
convex subgroups of
 $\Gamma $
, such that:
$\Gamma $
, such that:-
•
 $\{0\}=\Delta _{0} < \Delta _{1} < \dots < \Delta _{m}=\Gamma $
.
$\{0\}=\Delta _{0} < \Delta _{1} < \dots < \Delta _{m}=\Gamma $
. -
• For each
 $0 \leq i< m$
, the quotient group
$0 \leq i< m$
, the quotient group
 $\Delta _{i+1}/\Delta _{i}$
is n-regular.
$\Delta _{i+1}/\Delta _{i}$
is n-regular. -
• The quotient group
 $\Delta _{i+1}/\Delta _{i}$
is not n-divisible for
$\Delta _{i+1}/\Delta _{i}$
is not n-divisible for
 $0 < i < m$
.
$0 < i < m$
.
In this case we define
 $RJ_{n}(\Gamma )=\{\Delta _{0}, \dots , \Delta _{m-1}\}$
. The elements of this set are called the n-regular jumps.
$RJ_{n}(\Gamma )=\{\Delta _{0}, \dots , \Delta _{m-1}\}$
. The elements of this set are called the n-regular jumps. -
Example 2.9. Let
![]() $G=\underbrace {\mathbb {Z} \oplus \dots \oplus \mathbb {Z}}_{n- \text {times}}$
with the lexicographic order
$G=\underbrace {\mathbb {Z} \oplus \dots \oplus \mathbb {Z}}_{n- \text {times}}$
with the lexicographic order
![]() $\leq _{lex}$
. The
$\leq _{lex}$
. The
![]() $3$
-regular rank of G is equal to n. This is witnessed by the sequence:
$3$
-regular rank of G is equal to n. This is witnessed by the sequence:
2.2.1 Regular groups and poly-regular groups.
Definition 2.10. An ordered abelian group
![]() $\Gamma $
is said to be regular if it is n-regular for all
$\Gamma $
is said to be regular if it is n-regular for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Example 2.11.
![]() $\displaystyle {(\mathbb {Z}, +,\leq , 0)}$
and
$\displaystyle {(\mathbb {Z}, +,\leq , 0)}$
and
![]() $\displaystyle {(\mathbb {Q},+,\leq , 0)}$
are standard examples of regular groups. By [Reference Belegradek2, Theorem 1.2] any archimedean group is regular.
$\displaystyle {(\mathbb {Q},+,\leq , 0)}$
are standard examples of regular groups. By [Reference Belegradek2, Theorem 1.2] any archimedean group is regular.
Robinson and Zakon in their seminal paper [Reference Robinson and Zakon15] completely characterized the possible completions of the theory of regular groups, obtained by extending the first-order theory of ordered abelian groups with axioms asserting that for each
![]() $n \in \mathbb {N}$
if an interval contains at least n-elements then it contains an n-divisible element. The following is [Reference Robinson and Zakon15, Theorem 4.7].
$n \in \mathbb {N}$
if an interval contains at least n-elements then it contains an n-divisible element. The following is [Reference Robinson and Zakon15, Theorem 4.7].
Theorem 2.12. The possible completions of the theory of regular groups are:
-
1. the theory of discrete regular groups, and
-
2. the completions of the theory of dense regular groups
 $T_{\chi }$
where
$T_{\chi }$
where  $$ \begin{align*} \chi&=:\operatorname{Primes} \rightarrow \mathbb{N} \cup \{\infty\} \end{align*} $$
$$ \begin{align*} \chi&=:\operatorname{Primes} \rightarrow \mathbb{N} \cup \{\infty\} \end{align*} $$
is a function specifying the index
 $\chi (p)= [\Gamma : p\Gamma ]$
.
$\chi (p)= [\Gamma : p\Gamma ]$
.
Robinson and Zakon proved as well that each of these completions is the theory of some archimedean group. In particular, any discrete regular group is elementarily equivalent to
![]() $(\mathbb {Z},\leq , +, 0)$
. This theory is known as Presburger arithmetic, introduced in
$(\mathbb {Z},\leq , +, 0)$
. This theory is known as Presburger arithmetic, introduced in
![]() $1929$
by M. Presburger, who proved that it admits quantifier elimination in the well-known Presburger Language
$1929$
by M. Presburger, who proved that it admits quantifier elimination in the well-known Presburger Language
Given an ordered abelian group
![]() $\Gamma $
we naturally see it as an
$\Gamma $
we naturally see it as an
![]() $\mathcal {L}_{\operatorname {Pres}}$
-structure. The symbols
$\mathcal {L}_{\operatorname {Pres}}$
-structure. The symbols
![]() $\{0,+,- ,<\}$
take their obvious interpretation. If
$\{0,+,- ,<\}$
take their obvious interpretation. If
![]() $\Gamma $
is discrete, the constant symbol
$\Gamma $
is discrete, the constant symbol
![]() $1$
is interpreted as the least positive element of
$1$
is interpreted as the least positive element of
![]() $\Gamma $
, and by
$\Gamma $
, and by
![]() $0$
otherwise. For each
$0$
otherwise. For each
![]() $m \in \mathbb {N}_{\geq 2}$
the binary relation symbol
$m \in \mathbb {N}_{\geq 2}$
the binary relation symbol
![]() $\equiv _{m}$
is interpreted as the equivalence modulo m, i.e., for any
$\equiv _{m}$
is interpreted as the equivalence modulo m, i.e., for any
![]() $g,h \in \Gamma \ \displaystyle {g \equiv _{m} h \ \text {if and only if } \ g-h \in m\Gamma }$
.
$g,h \in \Gamma \ \displaystyle {g \equiv _{m} h \ \text {if and only if } \ g-h \in m\Gamma }$
.
The theory of a dense ordered abelian group admits quantifier elimination in the Presburger language if and only if it is regular. This is a result of Weispfenning in [Reference Weispfenning20, Theorem 2.9].
Definition 2.13. Let
![]() $\Gamma $
be an ordered abelian group. We say that it is poly-regular if it is elementarily equivalent to a subgroup of the lexicographically ordered group
$\Gamma $
be an ordered abelian group. We say that it is poly-regular if it is elementarily equivalent to a subgroup of the lexicographically ordered group
![]() $\mathbb {R}^{n}$
.
$\mathbb {R}^{n}$
.
In [Reference Belegradek2] Belegradek studied poly-regular groups and proved that an ordered abelian group is poly-regular if and only if it has finitely many proper definable convex subgroups, and all the proper convex subgroups are definable over the empty set. In [Reference Weispfenning20, Theorem 2.9] Weispfenning obtained quantifier elimination for the class of poly-regular groups in the language of ordered abelian groups extended with predicates to distinguish the subgroups
![]() $\Delta +\ell \Gamma $
where
$\Delta +\ell \Gamma $
where
![]() $\Delta $
is a convex subgroup and
$\Delta $
is a convex subgroup and
![]() $\ell \in \mathbb {N}_{\geq 2}$
.
$\ell \in \mathbb {N}_{\geq 2}$
.
2.2.2 Ordered abelian groups with bounded regular rank.
Definition 2.14. Let
![]() $\Gamma $
be an ordered abelian group. We say that it has bounded regular rank if it has finite n-regular rank for each
$\Gamma $
be an ordered abelian group. We say that it has bounded regular rank if it has finite n-regular rank for each
![]() $n \in \mathbb {N}_{\geq 2}$
. For notation, we will use
$n \in \mathbb {N}_{\geq 2}$
. For notation, we will use
 $\displaystyle {RJ(\Gamma )= \bigcup _{n \in \mathbb {N}_{\geq 2}} RJ_{n}(\Gamma )}$
.
$\displaystyle {RJ(\Gamma )= \bigcup _{n \in \mathbb {N}_{\geq 2}} RJ_{n}(\Gamma )}$
.
The class of ordered abelian groups of bounded regular rank extends the class of poly-regular groups and regular groups. The terminology of bounded regular rank becomes clear with the following Proposition (item
![]() $3$
).
$3$
).
Proposition 2.15. Let
![]() $\Gamma $
be an ordered abelian group. The following are all equivalent:
$\Gamma $
be an ordered abelian group. The following are all equivalent:
-
1.
 $\Gamma $
has finite p-regular rank for each prime number p.
$\Gamma $
has finite p-regular rank for each prime number p. -
2.
 $\Gamma $
has finite n-regular rank for each natural number
$\Gamma $
has finite n-regular rank for each natural number
 $n \geq 2$
.
$n \geq 2$
. -
3. There is some cardinal
 $\kappa $
such that for any
$\kappa $
such that for any
 $H \equiv \Gamma $
,
$H \equiv \Gamma $
,
 $|RJ(H)|\leq \kappa $
.
$|RJ(H)|\leq \kappa $
. -
4. For any
 $H \equiv \Gamma $
, any definable convex subgroup of H has a definition without parameters.
$H \equiv \Gamma $
, any definable convex subgroup of H has a definition without parameters. -
5. There is some cardinal
 $\kappa $
such that for any
$\kappa $
such that for any
 $H \equiv \Gamma $
, H has at most
$H \equiv \Gamma $
, H has at most
 $\kappa $
definable convex subgroups.
$\kappa $
definable convex subgroups.
Moreover, in this case
![]() $RJ(\Gamma )$
is the collection of all proper definable convex subgroups of
$RJ(\Gamma )$
is the collection of all proper definable convex subgroups of
![]() $\Gamma $
and all are definable without parameters. In particular, there are only countably many definable convex subgroups.
$\Gamma $
and all are definable without parameters. In particular, there are only countably many definable convex subgroups.
Proof This is [Reference Farré5, Proposition 2.3].
2.2.3 Quantifier elimination and the quotient sorts.
In [Reference Cluckers and Halupczok3] Cluckers and Halupczok introduced a language
![]() $\mathcal {L}_{qe}$
to obtain quantifier elimination for ordered abelian groups relative to the auxiliary sorts
$\mathcal {L}_{qe}$
to obtain quantifier elimination for ordered abelian groups relative to the auxiliary sorts
![]() $S_{n}$
,
$S_{n}$
,
![]() $T_{n}$
, and
$T_{n}$
, and
![]() $T_{n}^{+}$
, whose precise description can be found in [Reference Cluckers and Halupczok3, Definition 1.5]. This language is similar in spirit to the one introduced by Schmitt in [Reference Schmitt16], but has lately been preferred by the community as it is more in line with the many-sorted language of Shelah’s imaginary expansion
$T_{n}^{+}$
, whose precise description can be found in [Reference Cluckers and Halupczok3, Definition 1.5]. This language is similar in spirit to the one introduced by Schmitt in [Reference Schmitt16], but has lately been preferred by the community as it is more in line with the many-sorted language of Shelah’s imaginary expansion
![]() $\mathfrak {M}^{eq}$
. Schmitt does not distinguish between the sorts
$\mathfrak {M}^{eq}$
. Schmitt does not distinguish between the sorts
![]() $S_{n}$
,
$S_{n}$
,
![]() $T_{n}$
, and
$T_{n}$
, and
![]() $T_{n}^{+}$
. Instead for each
$T_{n}^{+}$
. Instead for each
![]() $n \in \mathbb {N}$
he works with a single sort
$n \in \mathbb {N}$
he works with a single sort
![]() $Sp_{n}(\Gamma ) $
called the n-spine of
$Sp_{n}(\Gamma ) $
called the n-spine of
![]() $\Gamma $
, whose description can be found in [Reference Gurevich and Schmitt6, Section 2]. In [Reference Cluckers and Halupczok3, Section 1.5] it is explained how the auxiliary sorts of Cluckers and Halupczok are related to the n-spines
$\Gamma $
, whose description can be found in [Reference Gurevich and Schmitt6, Section 2]. In [Reference Cluckers and Halupczok3, Section 1.5] it is explained how the auxiliary sorts of Cluckers and Halupczok are related to the n-spines
![]() $Sp_{n}(\Gamma )$
of Schmitt. In [Reference Farré5, Section 2], it is shown that an ordered abelian group
$Sp_{n}(\Gamma )$
of Schmitt. In [Reference Farré5, Section 2], it is shown that an ordered abelian group
![]() $\Gamma $
has bounded regular rank if and only if all the n-spines are finite, and
$\Gamma $
has bounded regular rank if and only if all the n-spines are finite, and
![]() $Sp_{n}(\Gamma )=RJ_{n}(\Gamma )$
. In this case, we define the regular rank of
$Sp_{n}(\Gamma )=RJ_{n}(\Gamma )$
. In this case, we define the regular rank of
![]() $\Gamma $
as the cardinal
$\Gamma $
as the cardinal
![]() $|RJ(\Gamma )|$
, which is either finite or
$|RJ(\Gamma )|$
, which is either finite or
![]() $\aleph _{0}$
. Instead of saying that
$\aleph _{0}$
. Instead of saying that
![]() $\Gamma $
is an ordered abelian group with finite spines, we prefer to use the classical terminology of bounded regular rank, as it emphasizes the relevance of the n-regular jumps and the role of the divisibilities to describe the definable convex subgroups.
$\Gamma $
is an ordered abelian group with finite spines, we prefer to use the classical terminology of bounded regular rank, as it emphasizes the relevance of the n-regular jumps and the role of the divisibilities to describe the definable convex subgroups.
Definition 2.16 (The language
 $\mathcal {L}$
).
$\mathcal {L}$
).
Let
![]() $\Gamma $
be an ordered abelian group with bounded regular rank. We view
$\Gamma $
be an ordered abelian group with bounded regular rank. We view
![]() $\Gamma $
as a multi-sorted structure in the language
$\Gamma $
as a multi-sorted structure in the language
![]() $\mathcal {L}$
, where:
$\mathcal {L}$
, where:
-
1. We add a sort for the ordered abelian group
 $\Gamma $
, and we equip it with a copy of the language
$\Gamma $
, and we equip it with a copy of the language
 $\mathcal {L}_{\operatorname {Pres}}$
extended with predicates to distinguish each of the convex subgroups
$\mathcal {L}_{\operatorname {Pres}}$
extended with predicates to distinguish each of the convex subgroups
 $\Delta \in RJ(\Gamma )$
. We refer to this sort as the main sort.
$\Delta \in RJ(\Gamma )$
. We refer to this sort as the main sort. -
2. For each
 $\Delta \in RJ(\Gamma )$
we add a sort for the ordered abelian group
$\Delta \in RJ(\Gamma )$
we add a sort for the ordered abelian group
 $\Gamma /\Delta $
, equipped with a copy of the Presburger language
$\Gamma /\Delta $
, equipped with a copy of the Presburger language $\mathcal {L}_{\operatorname {Pres}}^{\Delta }=\{ 0^{\Delta }, 1^{\Delta }, +^{\Delta }, -^{\Delta }, <^{\Delta }, (\equiv _{m}^{\Delta })_{m \in \mathbb {N}_{\geq 2}}\}$
.
$\mathcal {L}_{\operatorname {Pres}}^{\Delta }=\{ 0^{\Delta }, 1^{\Delta }, +^{\Delta }, -^{\Delta }, <^{\Delta }, (\equiv _{m}^{\Delta })_{m \in \mathbb {N}_{\geq 2}}\}$
.We add as well a map
 $\rho _{\Delta }: \Gamma \rightarrow \Gamma /\Delta $
, interpreted as the natural quotient map.
$\rho _{\Delta }: \Gamma \rightarrow \Gamma /\Delta $
, interpreted as the natural quotient map.
In [Reference Farré5, Theorem 2.4] Farré obtained a quantifier elimination statement for the class of ordered abelian groups with bounded regular rank in the language
![]() $\mathcal {L}$
extended with a set of constants in the home sort. However, we present a slightly different language where we add the constants for the minimal element in
$\mathcal {L}$
extended with a set of constants in the home sort. However, we present a slightly different language where we add the constants for the minimal element in
![]() $\Gamma /\Delta $
(if it exists) instead of adding a representative in the home sort whose projection is the minimal class in
$\Gamma /\Delta $
(if it exists) instead of adding a representative in the home sort whose projection is the minimal class in
![]() $\Gamma /\Delta $
. For this purpose we highlight that the following statement is a direct consequence of [Reference Aschenbrenner, Chernikov, Gehret and Ziegler1, Proposition 3.14].
$\Gamma /\Delta $
. For this purpose we highlight that the following statement is a direct consequence of [Reference Aschenbrenner, Chernikov, Gehret and Ziegler1, Proposition 3.14].
Theorem 2.17. Let
![]() $\Gamma $
be an ordered abelian group with bounded regular rank. Then
$\Gamma $
be an ordered abelian group with bounded regular rank. Then
![]() $\Gamma $
admits quantifier elimination in the language
$\Gamma $
admits quantifier elimination in the language
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Notation 2.18. We will be mainly interested in the description of the definable sets in the main sort. For this purpose we will slightly abuse the language, to simplify the notation. For each
![]() $k \in \mathbb {Z}$
and
$k \in \mathbb {Z}$
and
![]() $\Delta \in RJ(\Gamma )$
we define
$\Delta \in RJ(\Gamma )$
we define
![]() $k^{\Delta }= k \cdot 1^{\Delta }$
, where
$k^{\Delta }= k \cdot 1^{\Delta }$
, where
![]() $1^{\Delta }$
is the minimal element in
$1^{\Delta }$
is the minimal element in
![]() $\Gamma /\Delta $
if it exists. We will sometimes indicate
$\Gamma /\Delta $
if it exists. We will sometimes indicate
![]() $k^{\Delta }$
simply as
$k^{\Delta }$
simply as
![]() $k+\Delta $
. We introduce the following notation:
$k+\Delta $
. We introduce the following notation:
-
1. We write
 $\tau (\mathbf {x}) + \Delta < \beta + k+ \Delta $
for the formula
$\tau (\mathbf {x}) + \Delta < \beta + k+ \Delta $
for the formula
 $\rho _{\Delta }(\tau (\mathbf {x}))<^{\Delta } \rho _{\Delta }(\beta )+k^{\Delta }$
.
$\rho _{\Delta }(\tau (\mathbf {x}))<^{\Delta } \rho _{\Delta }(\beta )+k^{\Delta }$
. -
2. We write
 $\tau (\mathbf {x}) \equiv _{\Delta } \beta +k$
for the formula
$\tau (\mathbf {x}) \equiv _{\Delta } \beta +k$
for the formula
 $\rho _{\Delta }(\tau (\mathbf {x}))= \rho _{\Delta }(\beta )+k^{\Delta }$
.
$\rho _{\Delta }(\tau (\mathbf {x}))= \rho _{\Delta }(\beta )+k^{\Delta }$
. -
3. We write
 $\tau (\mathbf {x}) \equiv _{\Delta + m\Gamma } \beta + k$
for the formula
$\tau (\mathbf {x}) \equiv _{\Delta + m\Gamma } \beta + k$
for the formula
 $\rho _{\Delta }(\tau (\mathbf {x})) \equiv _{m}^{\Delta } \rho _{\Delta }(\beta )+ k^{\Delta }$
. The latter is interpreted as
$\rho _{\Delta }(\tau (\mathbf {x})) \equiv _{m}^{\Delta } \rho _{\Delta }(\beta )+ k^{\Delta }$
. The latter is interpreted as
 $\rho _{\Delta }(\tau (\mathbf {x})) - (\rho _{\Delta }(\beta )+k^{\Delta }) \in m \big (\Gamma / \Delta )$
.
$\rho _{\Delta }(\tau (\mathbf {x})) - (\rho _{\Delta }(\beta )+k^{\Delta }) \in m \big (\Gamma / \Delta )$
.
Here
![]() $\tau (\mathbf {\mathbf {x}})$
is a term in the language of ordered abelian groups in m variables,
$\tau (\mathbf {\mathbf {x}})$
is a term in the language of ordered abelian groups in m variables,
![]() $\mathbf {x}\,{=}\,(x_{1}, \dots , x_{m})$
and
$\mathbf {x}\,{=}\,(x_{1}, \dots , x_{m})$
and
![]() $\beta \in \Gamma $
.
$\beta \in \Gamma $
.
Definition 2.19.
-
1. A set
 $S \subset \Gamma $
is said to be an end-segment (respectively, an initial segment) if for any
$S \subset \Gamma $
is said to be an end-segment (respectively, an initial segment) if for any
 $x \in S$
and
$x \in S$
and
 $y \in \Gamma $
,
$y \in \Gamma $
,
 $x < y$
(respectively,
$x < y$
(respectively,
 $y < x$
) we have that
$y < x$
) we have that
 $y \in S$
.
$y \in S$
. -
2. Let
 $n \in \mathbb {N}_{\geq 2}$
,
$n \in \mathbb {N}_{\geq 2}$
,
 $\Delta \in RJ(\Gamma )$
,
$\Delta \in RJ(\Gamma )$
,
 $\beta \in \Gamma \cup \{ -\infty , +\infty \}$
, and
$\beta \in \Gamma \cup \{ -\infty , +\infty \}$
, and
 $\square \in \{ \geq ,>\} $
.
$\square \in \{ \geq ,>\} $
. $\{ \eta \in \Gamma \ | \ n\eta + \Delta \square \beta +\Delta \}$
is an end-segment of
$\{ \eta \in \Gamma \ | \ n\eta + \Delta \square \beta +\Delta \}$
is an end-segment of
 $\Gamma $
. We call the end-segments of this form divisibility end-segments. We define divisibility initial segments analogously.
$\Gamma $
. We call the end-segments of this form divisibility end-segments. We define divisibility initial segments analogously. -
3. A mid-segment is a nonempty set C of the form
 $C= U \cap L$
where U is a divisibility end-segment and L is a divisibility initial segment.
$C= U \cap L$
where U is a divisibility end-segment and L is a divisibility initial segment. -
4. A basic positive congruence formula is a formula of the form
 $zx \equiv _{\Delta +l\Gamma } \beta + k$
where
$zx \equiv _{\Delta +l\Gamma } \beta + k$
where
 $\beta \in \Gamma $
,
$\beta \in \Gamma $
,
 $z,k \in \mathbb {Z}$
,
$z,k \in \mathbb {Z}$
,
 $l \in \mathbb {N}_{\geq 2}$
, and
$l \in \mathbb {N}_{\geq 2}$
, and
 $\Delta \in RJ(\Gamma )$
. Likewise, a basic negative formula is a formula of the form
$\Delta \in RJ(\Gamma )$
. Likewise, a basic negative formula is a formula of the form
 $zx \not \equiv _{\Delta +l\Gamma } \beta + k$
. A basic congruence formula is either a basic positive congruence formula or a basic negative formula.
$zx \not \equiv _{\Delta +l\Gamma } \beta + k$
. A basic congruence formula is either a basic positive congruence formula or a basic negative formula. -
5. A finite congruence restriction is a finite conjunction of basic congruence formulas.
-
6. A nice set is a set of the form
 $C \cap X$
, where C is a mid-segment and X is defined by a finite congruence restriction.
$C \cap X$
, where C is a mid-segment and X is defined by a finite congruence restriction.
The following is a direct consequence of quantifier elimination.
Corollary 2.20. Let
![]() $\Gamma $
be an ordered abelian group with bounded regular rank. Let
$\Gamma $
be an ordered abelian group with bounded regular rank. Let
![]() $X \subseteq \Gamma $
be a definable set. Then X is a finite union of nice sets.
$X \subseteq \Gamma $
be a definable set. Then X is a finite union of nice sets.
We will consider an extension
![]() $\mathcal {L}_{Q}$
of the language
$\mathcal {L}_{Q}$
of the language
![]() $\mathcal {L}$
, where for each natural number
$\mathcal {L}$
, where for each natural number
![]() $n \in \mathbb {N}_{\geq 2}$
and
$n \in \mathbb {N}_{\geq 2}$
and
![]() $\Delta \in RJ(\Gamma )$
we add a sort for the quotient group
$\Delta \in RJ(\Gamma )$
we add a sort for the quotient group
![]() $\Gamma / (\Delta +n\Gamma )$
and a map
$\Gamma / (\Delta +n\Gamma )$
and a map
![]() $\pi _{\Delta }^{n}:\Gamma \rightarrow \Gamma /(\Delta +n\Gamma )$
. We refer to the sorts in the language
$\pi _{\Delta }^{n}:\Gamma \rightarrow \Gamma /(\Delta +n\Gamma )$
. We refer to the sorts in the language
![]() $\mathcal {L}_{Q}$
as quotient sorts.
$\mathcal {L}_{Q}$
as quotient sorts.
The following fact will be very useful to show weak elimination of imaginaries for ordered abelian groups with bounded regular rank.
Fact 2.21. Let
![]() $\Gamma $
be an ordered abelian group of finite n-regular rank witnessed by the sequence
$\Gamma $
be an ordered abelian group of finite n-regular rank witnessed by the sequence
![]() $\{ 0 \}=\Delta _{0} < \Delta _{1} < \cdots < \Delta _{l}=\Gamma $
and fix some definable convex subgroup H. Then
$\{ 0 \}=\Delta _{0} < \Delta _{1} < \cdots < \Delta _{l}=\Gamma $
and fix some definable convex subgroup H. Then
![]() $\Gamma /H$
is also a group of finite n-regular rank. Moreover, if
$\Gamma /H$
is also a group of finite n-regular rank. Moreover, if
![]() $\Gamma $
is an ordered abelian group of bounded regular rank, then
$\Gamma $
is an ordered abelian group of bounded regular rank, then
![]() $H \in RJ(\Gamma )$
and each coset of
$H \in RJ(\Gamma )$
and each coset of
![]() $\Delta _{i}/H$
in
$\Delta _{i}/H$
in
![]() $\Gamma /H$
is interdefinable with an element of
$\Gamma /H$
is interdefinable with an element of
![]() $\Gamma /\Delta _{i}$
.
$\Gamma /\Delta _{i}$
.
Proof Let
![]() $\Gamma $
be an ordered abelian group and H a convex subgroup. Assume that
$\Gamma $
be an ordered abelian group and H a convex subgroup. Assume that
![]() $\Gamma $
has finite n-regular rank, witnessed by the sequence
$\Gamma $
has finite n-regular rank, witnessed by the sequence
![]() $\{ 0 \}=\Delta _{0} < \Delta _{1} < \cdots < \Delta _{l}=\Gamma $
and let r be the smallest index such that
$\{ 0 \}=\Delta _{0} < \Delta _{1} < \cdots < \Delta _{l}=\Gamma $
and let r be the smallest index such that
![]() $\Delta _{r} \subseteq H \subseteq \Delta _{r+1}$
. We aim to show that
$\Delta _{r} \subseteq H \subseteq \Delta _{r+1}$
. We aim to show that
![]() $\Delta _{r+1}/H < \dots < \Delta _{l}/H=\Gamma /H$
witnesses that
$\Delta _{r+1}/H < \dots < \Delta _{l}/H=\Gamma /H$
witnesses that
![]() $\Gamma /H$
has finite n-regular rank. For each
$\Gamma /H$
has finite n-regular rank. For each
![]() $r\leq i< l$
, by the isomorphism theorem
$r\leq i< l$
, by the isomorphism theorem
![]() $(\Delta _{i+1}/H) / (\Delta _{i}/H) \cong \Delta _{i+1}/\Delta _{i}$
. As
$(\Delta _{i+1}/H) / (\Delta _{i}/H) \cong \Delta _{i+1}/\Delta _{i}$
. As
![]() $\Delta _{i+1}/\Delta _{i}$
is n-regular and not n-divisible, so is
$\Delta _{i+1}/\Delta _{i}$
is n-regular and not n-divisible, so is
![]() $(\Delta _{i+1}/H) / (\Delta _{i}/H)$
.
$(\Delta _{i+1}/H) / (\Delta _{i}/H)$
.
The second part of the statement follows immediately by the isomorphism theorem and Proposition 2.15.
2.3 A survey of model theoretic results on ordered abelian groups
In
![]() $1984$
the classification of the model theoretic complexity of ordered abelian groups was initiated by Gurevich and Schmitt in [Reference Gurevich and Schmitt6], who proved that no ordered abelian group has the independence property. During the last years finer classifications have been achieved, and we present the state of the field in this subsection.
$1984$
the classification of the model theoretic complexity of ordered abelian groups was initiated by Gurevich and Schmitt in [Reference Gurevich and Schmitt6], who proved that no ordered abelian group has the independence property. During the last years finer classifications have been achieved, and we present the state of the field in this subsection.
Definition 2.22. Let
![]() $\Gamma $
be an ordered abelian group and let p be a prime number. We say that p is a singular prime if
$\Gamma $
be an ordered abelian group and let p be a prime number. We say that p is a singular prime if
![]() $[\Gamma : p\Gamma ]= \infty $
. If
$[\Gamma : p\Gamma ]= \infty $
. If
![]() $\Gamma $
does not have singular primes we call it non-singular.
$\Gamma $
does not have singular primes we call it non-singular.
The following result corresponds to [Reference Jahnke, Simon and Walsberg11, Proposition 5.1].
Proposition 2.23. Let
![]() $\Gamma $
be an ordered abelian group. The following conditions are equivalent:
$\Gamma $
be an ordered abelian group. The following conditions are equivalent:
-
1.
 $\Gamma $
is non-singular.
$\Gamma $
is non-singular. -
2.
 $\Gamma $
is
$\Gamma $
is
 $dp$
-minimal.
$dp$
-minimal.
The following is [Reference Aschenbrenner, Chernikov, Gehret and Ziegler1, Theorem 3.13].
Proposition 2.24. Let
![]() $\Gamma $
be an ordered abelian group with bounded regular rank (i.e., each
$\Gamma $
be an ordered abelian group with bounded regular rank (i.e., each
![]() $Sp_{n}(\Gamma )$
is finite). The following statements are equivalent:
$Sp_{n}(\Gamma )$
is finite). The following statements are equivalent:
-
1.
 $\Gamma $
is distal.
$\Gamma $
is distal. -
2.
 $\Gamma $
is
$\Gamma $
is
 $dp$
-minimal.
$dp$
-minimal.
The following statement was independently achieved in [Reference Dolich and Goodrick4, Reference Farré5, Reference Halevi and Hasson7].
Proposition 2.25. Let
![]() $\Gamma $
be an ordered abelian group. The following conditions are equivalent:
$\Gamma $
be an ordered abelian group. The following conditions are equivalent:
-
1.
 $\Gamma $
is strongly dependent.
$\Gamma $
is strongly dependent. -
2.
 $\Gamma $
has finite
$\Gamma $
has finite
 $dp$
-rank.
$dp$
-rank. -
3.
 $\Gamma $
has bounded regular rank and finitely many singular primes.
$\Gamma $
has bounded regular rank and finitely many singular primes.
Moreover, let
![]() $\mathcal {P}= \{ p \in \mathbb {N} \ | \ p$
is a singular prime
$\mathcal {P}= \{ p \in \mathbb {N} \ | \ p$
is a singular prime
![]() $\}$
. Then
$\}$
. Then
3 Definable end-segments
In this subsection we characterize the definable end-segments (or initial segments) in an ordered abelian group with bounded regular rank (equivalently with finite spines). We also show that they can be coded in the quotient sorts.
Definition 3.1. Let
![]() $\Gamma $
be an ordered abelian group with bounded regular rank:
$\Gamma $
be an ordered abelian group with bounded regular rank:
-
1. Given
 $S \subseteq \Gamma $
an end-segment (or an initial segment) we denote by
$S \subseteq \Gamma $
an end-segment (or an initial segment) we denote by
 $\Delta _{S}$
the stabilizer of S, i.e.,
$\Delta _{S}$
the stabilizer of S, i.e.,
 $\Delta _{S}:= \{ \beta \in \Gamma \ | \ \beta +S= S\}$
.
$\Delta _{S}:= \{ \beta \in \Gamma \ | \ \beta +S= S\}$
. -
2. Let
 $S \subseteq \Gamma $
be an end-segment and
$S \subseteq \Gamma $
be an end-segment and
 $\Delta \in RJ(\Gamma )$
. We consider the projection map
$\Delta \in RJ(\Gamma )$
. We consider the projection map
 $\displaystyle {\rho _{\Delta }: \Gamma \rightarrow \Gamma /\Delta }$
, and we write
$\displaystyle {\rho _{\Delta }: \Gamma \rightarrow \Gamma /\Delta }$
, and we write
 $S_{\Delta }$
to indicate
$S_{\Delta }$
to indicate
 $\rho _{\Delta }(S)$
. The set
$\rho _{\Delta }(S)$
. The set  $$ \begin{align*} \displaystyle{S_{\Delta}=\{ \gamma \in \Gamma/\Delta \ | \ \exists y \in S \ \rho_{\Delta}(y)=\gamma\}} \end{align*} $$
$$ \begin{align*} \displaystyle{S_{\Delta}=\{ \gamma \in \Gamma/\Delta \ | \ \exists y \in S \ \rho_{\Delta}(y)=\gamma\}} \end{align*} $$
is a definable end-segment of
 $\Gamma /\Delta $
, as it is the projection of an end-segment.
$\Gamma /\Delta $
, as it is the projection of an end-segment. -
3. Let
 $\Delta \in RJ(\Gamma )$
and
$\Delta \in RJ(\Gamma )$
and
 $S \subseteq \Gamma $
be an end-segment. We say that S is
$S \subseteq \Gamma $
be an end-segment. We say that S is
 $\Delta $
-decomposable if it is a union of
$\Delta $
-decomposable if it is a union of
 $\Delta $
-cosets.
$\Delta $
-cosets. -
4. Let X and Y be definable sets. We say that Y is coinitial (or cofinal) in X if for any
 $y \in X$
there is some element
$y \in X$
there is some element
 $z \in X \cap Y$
such that
$z \in X \cap Y$
such that
 $z \leq y$
(respectively,
$z \leq y$
(respectively,
 $z \geq y$
).
$z \geq y$
).
Fact 3.2. Let
![]() $S \subseteq \Gamma $
be a definable end-segment. Then
$S \subseteq \Gamma $
be a definable end-segment. Then
![]() $\Delta _{S}$
is a definable convex subgroup of
$\Delta _{S}$
is a definable convex subgroup of
![]() $\Gamma $
, and therefore
$\Gamma $
, and therefore
![]() $\Delta _{S} \in RJ(\Gamma )$
. Furthermore,
$\Delta _{S} \in RJ(\Gamma )$
. Furthermore,
![]() $\displaystyle {\Delta _{S}= \bigcup _{\Delta \in \mathcal {C}} \Delta }$
, where
$\displaystyle {\Delta _{S}= \bigcup _{\Delta \in \mathcal {C}} \Delta }$
, where
Proof We first show that
![]() $\displaystyle {\Delta _{S} \subseteq \bigcup _{\Delta \in \mathcal {C}} \Delta }$
. Note
$\displaystyle {\Delta _{S} \subseteq \bigcup _{\Delta \in \mathcal {C}} \Delta }$
. Note
![]() $\Delta _{S}$
is a definable convex subgroup, so
$\Delta _{S}$
is a definable convex subgroup, so
![]() $\Delta _{S} \in RJ(\Gamma )$
. We aim to show that S is
$\Delta _{S} \in RJ(\Gamma )$
. We aim to show that S is
![]() $\Delta _{S}$
-decomposable, so it is sufficient to show that for any
$\Delta _{S}$
-decomposable, so it is sufficient to show that for any
![]() $\gamma \in S$
,
$\gamma \in S$
,
![]() $\gamma +\Delta _{S} \subseteq S$
. Fix some
$\gamma +\Delta _{S} \subseteq S$
. Fix some
![]() $\gamma \in \Gamma $
. If
$\gamma \in \Gamma $
. If
![]() $\delta \in \Delta _{S}$
then
$\delta \in \Delta _{S}$
then
![]() $\gamma +\delta \in S$
, so
$\gamma +\delta \in S$
, so
![]() $\gamma + \Delta _{S}\subseteq S$
.
$\gamma + \Delta _{S}\subseteq S$
.
We now prove that
![]() $\displaystyle {\bigcup _{\Delta \in \mathcal {C}}} \Delta \subseteq \Delta _{S}$
. Let
$\displaystyle {\bigcup _{\Delta \in \mathcal {C}}} \Delta \subseteq \Delta _{S}$
. Let
![]() $\Delta \in \mathcal {C}$
and fix some
$\Delta \in \mathcal {C}$
and fix some
![]() $\delta \in \Delta $
. We want to show that
$\delta \in \Delta $
. We want to show that
![]() $\delta +S \subseteq S$
and
$\delta +S \subseteq S$
and
![]() $S \subseteq \delta +S$
. Because S is
$S \subseteq \delta +S$
. Because S is
![]() $\Delta $
-decomposable,
$\Delta $
-decomposable,
![]() $\gamma +\Delta \subseteq S$
for any
$\gamma +\Delta \subseteq S$
for any
![]() $\gamma \in S$
. In particular,
$\gamma \in S$
. In particular,
![]() $\gamma +\delta \in S$
. As
$\gamma +\delta \in S$
. As
![]() $\gamma $
is an arbitrary element in S, we conclude that
$\gamma $
is an arbitrary element in S, we conclude that
![]() $\delta +S \subseteq S$
. It is only left to show that
$\delta +S \subseteq S$
. It is only left to show that
![]() $S \subseteq \delta +S$
. Let
$S \subseteq \delta +S$
. Let
![]() $\gamma \in S$
, then
$\gamma \in S$
, then
![]() $\gamma -\delta \in S$
because
$\gamma -\delta \in S$
because
![]() $\gamma +\Delta \subseteq S$
. As
$\gamma +\Delta \subseteq S$
. As
![]() $\gamma =\delta +(\gamma -\delta )\in \delta +S$
, we have
$\gamma =\delta +(\gamma -\delta )\in \delta +S$
, we have
![]() $S \subseteq \delta +S$
, as required.
$S \subseteq \delta +S$
, as required.
Proposition 3.3. Let
![]() $\Gamma $
be an ordered abelian group of bounded regular rank. Any definable end-segment is a divisibility end-segment.
$\Gamma $
be an ordered abelian group of bounded regular rank. Any definable end-segment is a divisibility end-segment.
Proof Let
![]() $S \subseteq \Gamma $
be a definable end-segment such that
$S \subseteq \Gamma $
be a definable end-segment such that
![]() $S \neq \Gamma $
. By Fact 3.2,
$S \neq \Gamma $
. By Fact 3.2,
![]() $\Delta _{S}$
is a definable convex subgroup of
$\Delta _{S}$
is a definable convex subgroup of
![]() $\Gamma $
and S is
$\Gamma $
and S is
![]() $\Delta _{S}$
-decomposable. To simplify the notation we will denote
$\Delta _{S}$
-decomposable. To simplify the notation we will denote
![]() $\hat {\Gamma }=\Gamma /\Delta _{S}$
and
$\hat {\Gamma }=\Gamma /\Delta _{S}$
and
![]() $\hat {S}=S_{\Delta _{S}}= \rho _{\Delta _{S}}(S)$
. It is sufficient to prove that
$\hat {S}=S_{\Delta _{S}}= \rho _{\Delta _{S}}(S)$
. It is sufficient to prove that
![]() $\hat {S}$
is a divisibility end-segment in
$\hat {S}$
is a divisibility end-segment in
![]() $\hat {\Gamma }$
.
$\hat {\Gamma }$
.
Claim 3.3.1. Note that for any
![]() $k \in \mathbb {N}$
exactly one of the following occurs:
$k \in \mathbb {N}$
exactly one of the following occurs:
-
•
 $\hat {\Gamma }$
is k-regular.
$\hat {\Gamma }$
is k-regular. -
• There is a nontrivial k-regular convex subgroup
 $\Lambda _{k}$
of
$\Lambda _{k}$
of
 $\hat {\Gamma }$
and a coset
$\hat {\Gamma }$
and a coset
 $\eta +\Lambda _{k}$
such that
$\eta +\Lambda _{k}$
such that
 $\hat {S} \cap (\eta + \Lambda _{k}) \neq \emptyset $
and
$\hat {S} \cap (\eta + \Lambda _{k}) \neq \emptyset $
and
 $\hat {S}^{c} \cap (\eta + \Lambda _{k}) \neq \emptyset $
.
$\hat {S}^{c} \cap (\eta + \Lambda _{k}) \neq \emptyset $
.
Proof Let
![]() $\{0\}=\Delta _{0} < \Delta _{1} < \dots < \Delta _{l}=\Gamma $
be the sequence of convex subgroups witnessing that
$\{0\}=\Delta _{0} < \Delta _{1} < \dots < \Delta _{l}=\Gamma $
be the sequence of convex subgroups witnessing that
![]() $\Gamma $
has k-finite regular rank equal to l. Let
$\Gamma $
has k-finite regular rank equal to l. Let
![]() $r \leq l$
be the smallest index such that
$r \leq l$
be the smallest index such that
![]() $\Delta _{S} \subsetneq \Delta _{r}$
. If
$\Delta _{S} \subsetneq \Delta _{r}$
. If
![]() $r=l$
then
$r=l$
then
![]() $\hat {\Gamma }$
is k-regular. Otherwise the quotient group
$\hat {\Gamma }$
is k-regular. Otherwise the quotient group
![]() $\Lambda _{k}=\Delta _{r}/ \Delta _{S}$
satisfies the required conditions. Indeed, as
$\Lambda _{k}=\Delta _{r}/ \Delta _{S}$
satisfies the required conditions. Indeed, as
![]() $\Delta _{r}/\Delta _{r-1}$
is k-regular so is
$\Delta _{r}/\Delta _{r-1}$
is k-regular so is
![]() $\Delta _{r}/ \Delta _{S}$
. Additionally, S is not
$\Delta _{r}/ \Delta _{S}$
. Additionally, S is not
![]() $\Delta _{r}$
-decomposable. If it were, then we would have
$\Delta _{r}$
-decomposable. If it were, then we would have
![]() $\Delta _{r} \subseteq \Delta _{S}$
which contradicts
$\Delta _{r} \subseteq \Delta _{S}$
which contradicts
![]() $\Delta _{S} \subsetneq \Delta _{r}$
. Then there is some coset
$\Delta _{S} \subsetneq \Delta _{r}$
. Then there is some coset
![]() $\eta + \Delta _{r}$
such that
$\eta + \Delta _{r}$
such that
![]() $S \cap (\eta +\Delta _{r}) \neq \emptyset $
and
$S \cap (\eta +\Delta _{r}) \neq \emptyset $
and
![]() $S^{c} \cap (\eta +\Delta _{r}) \neq \emptyset $
because otherwise S would be
$S^{c} \cap (\eta +\Delta _{r}) \neq \emptyset $
because otherwise S would be
![]() $\Delta _{r}$
-decomposable. Thus
$\Delta _{r}$
-decomposable. Thus
![]() $\hat {S} \cap (\hat {\eta }+\Lambda _{k} )\neq \emptyset $
and
$\hat {S} \cap (\hat {\eta }+\Lambda _{k} )\neq \emptyset $
and
![]() $\hat {S}^{c} \cap (\hat {\eta }+ \Lambda _{k} )\neq \emptyset $
, where
$\hat {S}^{c} \cap (\hat {\eta }+ \Lambda _{k} )\neq \emptyset $
, where
![]() $\hat {\eta }= \eta + \Delta _{S}$
.
$\hat {\eta }= \eta + \Delta _{S}$
.
We may assume that
![]() $\hat {S}$
does not have a minimum because otherwise the statement follows immediately. By Corollary 2.20 applied to
$\hat {S}$
does not have a minimum because otherwise the statement follows immediately. By Corollary 2.20 applied to
![]() $\hat {\Gamma }$
,
$\hat {\Gamma }$
,
![]() $\hat {S}$
is a finite union of nice sets
$\hat {S}$
is a finite union of nice sets
![]() $C_{i} \cap X_{i}$
, where
$C_{i} \cap X_{i}$
, where
![]() $C_{i}=U_{i}\cap L_{i}$
. As
$C_{i}=U_{i}\cap L_{i}$
. As
![]() $\hat {S}$
is a definable end-segment, it is sufficient to understand the co-initial description of
$\hat {S}$
is a definable end-segment, it is sufficient to understand the co-initial description of
![]() $\hat {S}$
. Without loss of generality we may assume that
$\hat {S}$
. Without loss of generality we may assume that
![]() $U_{i} \subseteq U_{1}$
for all i. Let
$U_{i} \subseteq U_{1}$
for all i. Let
![]() $\hat {\Delta } \in RJ(\hat {\Gamma })$
. Then
$\hat {\Delta } \in RJ(\hat {\Gamma })$
. Then
![]() $\hat {\Delta }=\Delta /\Delta _{S}$
for some
$\hat {\Delta }=\Delta /\Delta _{S}$
for some
![]() $\Delta _{S} \subsetneq \Delta \in RJ(\Gamma )$
. Thus there is a coset
$\Delta _{S} \subsetneq \Delta \in RJ(\Gamma )$
. Thus there is a coset
![]() $\eta + \hat {\Delta }$
such that
$\eta + \hat {\Delta }$
such that
![]() $\hat {S} \cap (\eta + \hat {\Delta }) \neq \emptyset $
and
$\hat {S} \cap (\eta + \hat {\Delta }) \neq \emptyset $
and
![]() $\hat {S}^{c} \cap (\eta + \hat {\Delta }) \neq \emptyset $
because S is not
$\hat {S}^{c} \cap (\eta + \hat {\Delta }) \neq \emptyset $
because S is not
![]() $\Delta $
-decomposable.
$\Delta $
-decomposable.
Hence, each of the congruence formulas involving the groups
![]() $\hat {\Delta }+ k \hat {\Gamma }$
does not change its truth value over
$\hat {\Delta }+ k \hat {\Gamma }$
does not change its truth value over
![]() $U_{1} \cap (\eta + \hat {\Delta })$
. Therefore it does not change its truth value co-initially in
$U_{1} \cap (\eta + \hat {\Delta })$
. Therefore it does not change its truth value co-initially in
![]() $U_{1}$
.
$U_{1}$
.
Consider a conjunction of congruence restrictions of the form:
 $$ \begin{align*} C(x):=\bigg( \bigwedge_{i\leq s} x \equiv_{k_{i}\hat{\Gamma} } c_{i} \bigg)\wedge \bigg( \bigwedge_{j \leq l } \neg(x \equiv_{r_{j} \hat{\Gamma}} d_{j}) \bigg). \end{align*} $$
$$ \begin{align*} C(x):=\bigg( \bigwedge_{i\leq s} x \equiv_{k_{i}\hat{\Gamma} } c_{i} \bigg)\wedge \bigg( \bigwedge_{j \leq l } \neg(x \equiv_{r_{j} \hat{\Gamma}} d_{j}) \bigg). \end{align*} $$
Let M be the least common multiple of all the
![]() $k_{i}$
’s and
$k_{i}$
’s and
![]() $r_{j}$
’s involved in the definition of
$r_{j}$
’s involved in the definition of
![]() $C(x)$
. By the previous Claim 3.3.1,
$C(x)$
. By the previous Claim 3.3.1,
![]() $\Gamma $
is M-regular or we can find an M-regular group
$\Gamma $
is M-regular or we can find an M-regular group
![]() $\Lambda _{M}$
and a coset that intersects
$\Lambda _{M}$
and a coset that intersects
![]() $\hat {S}$
and its complement. We first assume the existence of a non-trivial convex subgroup
$\hat {S}$
and its complement. We first assume the existence of a non-trivial convex subgroup
![]() $\Lambda _{M}$
and a coset
$\Lambda _{M}$
and a coset
![]() $\eta +\Lambda _{M}$
such that
$\eta +\Lambda _{M}$
such that
![]() $\hat {S} \cap (\eta + \Lambda _{M}) \neq \emptyset $
and
$\hat {S} \cap (\eta + \Lambda _{M}) \neq \emptyset $
and
![]() $\hat {S}^{c} \cap (\eta + \Lambda _{M}) \neq \emptyset $
. Let
$\hat {S}^{c} \cap (\eta + \Lambda _{M}) \neq \emptyset $
. Let
![]() $Y=C(x) \cap (U_{1} \cap (\eta + \Lambda _{M}) )$
.
$Y=C(x) \cap (U_{1} \cap (\eta + \Lambda _{M}) )$
.
Claim 3.3.2. If
![]() $Y \neq \emptyset $
, then
$Y \neq \emptyset $
, then
![]() $C(x)$
is co-initial in
$C(x)$
is co-initial in
![]() $U_{1}$
.
$U_{1}$
.
Proof Let
![]() $x_{0} \in Y$
and
$x_{0} \in Y$
and
![]() $ U'= \big (U_{1} \cap (\eta + \Lambda _{M})\big )-x_{0}$
.
$ U'= \big (U_{1} \cap (\eta + \Lambda _{M})\big )-x_{0}$
.
![]() $U'$
is a definable end-segment of
$U'$
is a definable end-segment of
![]() $\Lambda _{M}$
without a minimum. Fix an element
$\Lambda _{M}$
without a minimum. Fix an element
![]() $\delta \in U'$
. As
$\delta \in U'$
. As
![]() $U'$
does not have a minimum and
$U'$
does not have a minimum and
![]() $\Lambda _{M}$
is M-regular, we can find an element
$\Lambda _{M}$
is M-regular, we can find an element
![]() $\gamma \in \Lambda _{M}$
such that
$\gamma \in \Lambda _{M}$
such that
![]() $M\gamma \in U'$
and
$M\gamma \in U'$
and
![]() $M\gamma <\delta $
. Then
$M\gamma <\delta $
. Then
![]() $z= M\gamma +x_{0} \in Y$
and
$z= M\gamma +x_{0} \in Y$
and
![]() $z< x_{0}+\delta $
. Thus
$z< x_{0}+\delta $
. Thus
![]() $C(x)$
is co-initial in
$C(x)$
is co-initial in
![]() $U_{1}$
.
$U_{1}$
.
Likewise, if
![]() $\hat {\Gamma }$
is M-regular we can conclude that
$\hat {\Gamma }$
is M-regular we can conclude that
![]() $C(x)$
is co-initial in
$C(x)$
is co-initial in
![]() $U_{1}$
. Consequently, the congruence restrictions are irrelevant in the definition of the end-segment S. It must be the case then that
$U_{1}$
. Consequently, the congruence restrictions are irrelevant in the definition of the end-segment S. It must be the case then that
![]() $S=U_{1}$
, as desired.
$S=U_{1}$
, as desired.
Even though it may seem like any divisibility cut defined by a formula of the form
![]() $nx \square \beta $
where
$nx \square \beta $
where
![]() $n \in \mathbb {N}_{\geq 2}$
,
$n \in \mathbb {N}_{\geq 2}$
,
![]() $\square \in \{ \geq ,>\}$
and
$\square \in \{ \geq ,>\}$
and
![]() $\beta \in \Gamma $
could be coded by
$\beta \in \Gamma $
could be coded by
![]() $\beta $
, this statement is false and requires a slightly more delicate treatment. We introduce the following example to motivate the reader to not dismiss the technical work in Proposition 3.3.
$\beta $
, this statement is false and requires a slightly more delicate treatment. We introduce the following example to motivate the reader to not dismiss the technical work in Proposition 3.3.
Example 3.4. Consider the ordered abelian group
![]() $(\mathbb {Z}\oplus \mathbb {Z},\leq _{lex},+,0)$
where
$(\mathbb {Z}\oplus \mathbb {Z},\leq _{lex},+,0)$
where
![]() $\leq _{lex}$
is the lexicographic order. Let
$\leq _{lex}$
is the lexicographic order. Let
![]() $\displaystyle {S=\{ z \in \mathbb {Z}^{2} \ | \ 2z \geq (1,1)\}}$
. Note that for any
$\displaystyle {S=\{ z \in \mathbb {Z}^{2} \ | \ 2z \geq (1,1)\}}$
. Note that for any
![]() $\beta \in \mathbb {Z}$
, S is also defined by the formula
$\beta \in \mathbb {Z}$
, S is also defined by the formula
![]() $2z \geq (1, \beta )$
.
$2z \geq (1, \beta )$
.
Lemma 3.5. Let
![]() $\Gamma $
be an ordered abelian group of bounded regular rank. Let
$\Gamma $
be an ordered abelian group of bounded regular rank. Let
![]() ${\{0\}=\Delta _{0} \leq \Delta _{1} \leq \dots \leq \Delta _{l}=\Gamma }$
be the sequence of convex subgroups witnessing that
${\{0\}=\Delta _{0} \leq \Delta _{1} \leq \dots \leq \Delta _{l}=\Gamma }$
be the sequence of convex subgroups witnessing that
![]() $\Gamma $
has finite n-regular rank. Then any divisibility end-segment S defined by a formula
$\Gamma $
has finite n-regular rank. Then any divisibility end-segment S defined by a formula
![]() $nx \ \square \ \beta $
where
$nx \ \square \ \beta $
where
![]() $n \in \mathbb {N}_{\geq 1}$
,
$n \in \mathbb {N}_{\geq 1}$
,
![]() $\square \in \{ \geq ,>\}$
and
$\square \in \{ \geq ,>\}$
and
![]() $\beta \in \Gamma $
is coded by a tuple of elements in the sorts
$\beta \in \Gamma $
is coded by a tuple of elements in the sorts
![]() $\Gamma \cup \{ \Gamma /\Delta _{i} \ | \ i \leq l\}$
.
$\Gamma \cup \{ \Gamma /\Delta _{i} \ | \ i \leq l\}$
.
Proof We argue by induction in the n-regular rank of
![]() $\Gamma $
that S can be coded in the sorts
$\Gamma $
that S can be coded in the sorts
![]() $\Gamma \cup \{ \Gamma /\Delta _{i} \ | \ i \leq l\}$
. For the base case, we suppose that
$\Gamma \cup \{ \Gamma /\Delta _{i} \ | \ i \leq l\}$
. For the base case, we suppose that
![]() $\Gamma $
is n-regular. We first assume that
$\Gamma $
is n-regular. We first assume that
![]() $\Gamma $
is dense, and we aim to prove that
$\Gamma $
is dense, and we aim to prove that
![]() $\beta $
and
$\beta $
and
![]() $\ulcorner S \urcorner $
are interdefinable. It is clear that
$\ulcorner S \urcorner $
are interdefinable. It is clear that
![]() $\ulcorner S \urcorner \in dcl^{eq}(\beta )$
. For the converse let
$\ulcorner S \urcorner \in dcl^{eq}(\beta )$
. For the converse let
![]() $\sigma $
be any automorphism of the monster model
$\sigma $
be any automorphism of the monster model
![]() $\mathfrak {M}$
and suppose that
$\mathfrak {M}$
and suppose that
![]() $\sigma (\beta ) \neq \beta $
. Without loss of generality,
$\sigma (\beta ) \neq \beta $
. Without loss of generality,
![]() $\beta < \sigma (\beta )$
. By density we can find n-elements in the interval
$\beta < \sigma (\beta )$
. By density we can find n-elements in the interval
![]() $(\beta , \sigma (\beta ))$
. By n-regularity and density there is an element
$(\beta , \sigma (\beta ))$
. By n-regularity and density there is an element
![]() $\delta $
such that
$\delta $
such that
![]() $\beta < n\delta < \sigma (\beta )$
. Thus
$\beta < n\delta < \sigma (\beta )$
. Thus
![]() $\sigma (S) \subsetneq S$
.
$\sigma (S) \subsetneq S$
.
We now assume that
![]() $\Gamma $
is discrete and let
$\Gamma $
is discrete and let
![]() $1$
be its minimal element. There is a unique natural number
$1$
be its minimal element. There is a unique natural number
![]() $0 \leq i \leq n-1$
such that
$0 \leq i \leq n-1$
such that
![]() $\beta +i$
is n-divisible, because
$\beta +i$
is n-divisible, because
![]() $\{ \beta , \beta +1, \dots , \beta +(n-1)\}$
is an interval with at least n-elements. Let
$\{ \beta , \beta +1, \dots , \beta +(n-1)\}$
is an interval with at least n-elements. Let
![]() $i_{0}$
be the index such that
$i_{0}$
be the index such that
![]() $\beta +i_{0}$
is n-divisible. Then
$\beta +i_{0}$
is n-divisible. Then
![]() $x \in S$
if and only if
$x \in S$
if and only if
![]() $nx \geq \beta +i_{0}$
. Thus
$nx \geq \beta +i_{0}$
. Thus
![]() $\frac {\beta +i_{0}}{n}$
is the minimal element of S and thereby it is a code for S.
$\frac {\beta +i_{0}}{n}$
is the minimal element of S and thereby it is a code for S.
We proceed to show the inductive step, and we consider the sequence
![]() $\{0\}=\Delta _{0} < \Delta _{1} < \dots < \Delta _{l+1}=\Gamma $
witnessing that
$\{0\}=\Delta _{0} < \Delta _{1} < \dots < \Delta _{l+1}=\Gamma $
witnessing that
![]() $\Gamma $
has n-regular rank equal to
$\Gamma $
has n-regular rank equal to
![]() $l+1$
. Let
$l+1$
. Let
![]() $\rho _{\Delta _{1}}: \Gamma \rightarrow \Gamma /\Delta _{1}$
be the canonical projection map, and note that
$\rho _{\Delta _{1}}: \Gamma \rightarrow \Gamma /\Delta _{1}$
be the canonical projection map, and note that
![]() $\Gamma /\Delta _{1}$
is an ordered abelian group of n-regular rank l. First we suppose that
$\Gamma /\Delta _{1}$
is an ordered abelian group of n-regular rank l. First we suppose that
![]() $\rho _{\Delta _{1}}(\beta )$
is not n-divisible. Then S is interdefinable with
$\rho _{\Delta _{1}}(\beta )$
is not n-divisible. Then S is interdefinable with
![]() $S_{\Delta _{1}}=\{ \eta \in \Gamma /\Delta _{1} \ | \ n\eta> \rho _{\Delta _{1}}(\beta )\}$
. By the induction hypothesis, such end-segment can be coded in the sorts
$S_{\Delta _{1}}=\{ \eta \in \Gamma /\Delta _{1} \ | \ n\eta> \rho _{\Delta _{1}}(\beta )\}$
. By the induction hypothesis, such end-segment can be coded in the sorts
![]() $\Gamma / \Delta _{1} \cup \{ (\Gamma /\Delta _{1})/ (\Delta _{i}/\Delta _{1}) \ | \ 2 \leq i \leq l\}$
. As each of the sorts
$\Gamma / \Delta _{1} \cup \{ (\Gamma /\Delta _{1})/ (\Delta _{i}/\Delta _{1}) \ | \ 2 \leq i \leq l\}$
. As each of the sorts
![]() $(\Gamma /\Delta _{1})/ (\Delta _{i}/\Delta _{1})$
can be canonically identified with
$(\Gamma /\Delta _{1})/ (\Delta _{i}/\Delta _{1})$
can be canonically identified with
![]() $\Gamma /\Delta _{i}$
, the conclusion of the statement follows.
$\Gamma /\Delta _{i}$
, the conclusion of the statement follows.
We consider the case where
![]() $\rho _{\Delta _{1}}(\beta )$
is n-divisible, i.e., there is some
$\rho _{\Delta _{1}}(\beta )$
is n-divisible, i.e., there is some
![]() $\eta \in \Gamma $
such that
$\eta \in \Gamma $
such that
![]() $n \rho _{\Delta _{1}}(\eta )=\rho _{\Delta _{1}}(\beta )$
. Note that
$n \rho _{\Delta _{1}}(\eta )=\rho _{\Delta _{1}}(\beta )$
. Note that
![]() $\rho _{\Delta _{1}}(\eta )= \min (S_{\Delta _{1}})$
. If
$\rho _{\Delta _{1}}(\eta )= \min (S_{\Delta _{1}})$
. If
![]() $\Delta _{1}$
is discrete, then S has a minimum and this minimal element is a code for S. Thus without loss of generality
$\Delta _{1}$
is discrete, then S has a minimum and this minimal element is a code for S. Thus without loss of generality
![]() $\Delta _{1}$
is dense. We aim to show that
$\Delta _{1}$
is dense. We aim to show that
![]() $\beta $
and
$\beta $
and
![]() $\ulcorner S \urcorner $
are interdefinable. In fact, let
$\ulcorner S \urcorner $
are interdefinable. In fact, let
![]() $\sigma $
be an automorphism of the monster model
$\sigma $
be an automorphism of the monster model
![]() $\mathfrak {M}$
fixing
$\mathfrak {M}$
fixing
![]() $\ulcorner S \urcorner $
. We want to show that it fixes also
$\ulcorner S \urcorner $
. We want to show that it fixes also
![]() $\beta $
. We argue by contradiction, and we assume that
$\beta $
. We argue by contradiction, and we assume that
![]() $\beta <\sigma (\beta )$
. As
$\beta <\sigma (\beta )$
. As
![]() $\rho _{\Delta _{1}}(\beta )\in dcl^{eq}( \ulcorner S\urcorner )$
, we have
$\rho _{\Delta _{1}}(\beta )\in dcl^{eq}( \ulcorner S\urcorner )$
, we have
![]() $\sigma (\beta )- \beta \in \Delta _{1}$
. Fix some element
$\sigma (\beta )- \beta \in \Delta _{1}$
. Fix some element
![]() $\eta \in \Gamma $
such that
$\eta \in \Gamma $
such that
![]() $n\eta +\Delta _{1}=\beta +\Delta _{1}$
. We can find elements
$n\eta +\Delta _{1}=\beta +\Delta _{1}$
. We can find elements
![]() $\delta _{1}<\delta _{2} \in \Delta _{1}$
such that
$\delta _{1}<\delta _{2} \in \Delta _{1}$
such that
![]() $\beta =n \eta +\delta _{1}$
and
$\beta =n \eta +\delta _{1}$
and
![]() $\sigma (\beta )=n\eta +\delta _{2}$
. By n-regularity and density of
$\sigma (\beta )=n\eta +\delta _{2}$
. By n-regularity and density of
![]() $\Delta _{1}$
we can find an element
$\Delta _{1}$
we can find an element
![]() $\gamma \in \Delta _{1}$
such that
$\gamma \in \Delta _{1}$
such that
![]() $\delta _{1}< n\gamma < \delta _{2}$
, so we have
$\delta _{1}< n\gamma < \delta _{2}$
, so we have
![]() $ \beta < n(\gamma +\eta )< \sigma (\beta )$
and hence
$ \beta < n(\gamma +\eta )< \sigma (\beta )$
and hence
![]() $S \subsetneq \sigma (S)$
, as desired.
$S \subsetneq \sigma (S)$
, as desired.
Proposition 3.6. Let
![]() $\Gamma $
be an ordered abelian group of bounded regular rank and let
$\Gamma $
be an ordered abelian group of bounded regular rank and let
![]() $S \subseteq \Gamma $
be a definable end-segment. Then
$S \subseteq \Gamma $
be a definable end-segment. Then
![]() $\ulcorner S \urcorner $
is interdefinable with a tuple of elements in the sorts
$\ulcorner S \urcorner $
is interdefinable with a tuple of elements in the sorts
![]() $\Gamma \cup \{ \Gamma / \Delta \ | \ \Delta \in RJ(\Gamma )\}$
. Consequently, any initial segment is also coded in the sorts
$\Gamma \cup \{ \Gamma / \Delta \ | \ \Delta \in RJ(\Gamma )\}$
. Consequently, any initial segment is also coded in the sorts
![]() $\Gamma \cup \{ \Gamma / \Delta \ | \ \Delta \in RJ(\Gamma )\}$
.
$\Gamma \cup \{ \Gamma / \Delta \ | \ \Delta \in RJ(\Gamma )\}$
.
Proof By Proposition 3.3 it is sufficient to code divisibility end-segments. We may assume that
![]() $S= \{ \eta \in \Gamma \ | \ n \eta +\Delta \geq \beta +\Delta \}$
. Therefore S is interdefinable with
$S= \{ \eta \in \Gamma \ | \ n \eta +\Delta \geq \beta +\Delta \}$
. Therefore S is interdefinable with
![]() $S_{\Delta }=\{ z \in \Gamma /\Delta \ | \ nz \geq \rho _{\Delta }(\beta )\}$
; this is a definable end-segment of
$S_{\Delta }=\{ z \in \Gamma /\Delta \ | \ nz \geq \rho _{\Delta }(\beta )\}$
; this is a definable end-segment of
![]() $\Gamma /\Delta $
. The statement follows immediately from Lemma 3.5 combined with Fact 2.21.
$\Gamma /\Delta $
. The statement follows immediately from Lemma 3.5 combined with Fact 2.21.
The second part of the statement follows by noticing that any initial segment is the complement of an end-segment.
4 An abstract criterion to eliminate imaginaries
The following is [Reference Hrushovski10, Lemma 1.17].
Theorem 4.1. Let T be a first-order theory with home sort K. Let
![]() $\mathcal {G}$
be some collection of sorts. If the following conditions all hold, then T has weak elimination of imaginaries in the sorts
$\mathcal {G}$
be some collection of sorts. If the following conditions all hold, then T has weak elimination of imaginaries in the sorts
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
-
1. Density of definable types: for every non-empty definable set
 $X \subseteq K$
there is an
$X \subseteq K$
there is an
 $acl^{eq}(\ulcorner X \urcorner )$
-definable type in X.
$acl^{eq}(\ulcorner X \urcorner )$
-definable type in X. -
2. Coding definable types: every definable type in
 $K^{n}$
has a code in
$K^{n}$
has a code in
 $\mathcal {G}$
(possibly infinite). That is, if p is any (global) definable type in
$\mathcal {G}$
(possibly infinite). That is, if p is any (global) definable type in
 $K^{n}$
, then the set
$K^{n}$
, then the set
 $\ulcorner p \urcorner $
of codes of the definitions of p is interdefinable with some (possibly infinite) tuple from
$\ulcorner p \urcorner $
of codes of the definitions of p is interdefinable with some (possibly infinite) tuple from
 $\mathcal {G}$
.
$\mathcal {G}$
.
Proof A very detailed proof can be found in [Reference Johnson12, Theorem 6.3]. The first part of the proof shows weak elimination of imaginaries as it is shown that for any imaginary element e we can find a tuple
![]() $a \in \mathcal {G}$
such that
$a \in \mathcal {G}$
such that
![]() $e \in dcl^{eq}(a)$
and
$e \in dcl^{eq}(a)$
and
![]() $a \in acl^{eq}(e)$
.
$a \in acl^{eq}(e)$
.
We will use this criterion to prove that any pure ordered abelian group with bounded regular rank admits weak elimination of imaginaries once the quotient sorts are added.
4.1 Coding of definable types
In this subsection we show that any definable type
![]() $p(\mathbf {x})$
can be coded in the quotient sorts.
$p(\mathbf {x})$
can be coded in the quotient sorts.
Proposition 4.2. Let
![]() $\Gamma $
be an ordered abelian group and let
$\Gamma $
be an ordered abelian group and let
![]() $p(\mathbf {x}) \in S_{n}(\Gamma )$
be a definable type. Then
$p(\mathbf {x}) \in S_{n}(\Gamma )$
be a definable type. Then
![]() $p(\mathbf {x})$
can be coded in the quotient sorts.
$p(\mathbf {x})$
can be coded in the quotient sorts.
Proof Let
![]() $p(\mathbf {x})$
be a definable type in n variables over
$p(\mathbf {x})$
be a definable type in n variables over
![]() $\Gamma $
. By quantifier elimination (Theorem 2.17),
$\Gamma $
. By quantifier elimination (Theorem 2.17),
![]() $p(\mathbf {x})$
is completely determined by formulas of the following forms:
$p(\mathbf {x})$
is completely determined by formulas of the following forms:
-
• First kind:
or $$ \begin{align*} \phi_{1}(\mathbf{x}, \beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i} +\Delta < \beta+k +\Delta} \end{align*} $$
where
$$ \begin{align*} \phi_{1}(\mathbf{x}, \beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i} +\Delta < \beta+k +\Delta} \end{align*} $$
where $$ \begin{align*} \psi_{1}(\mathbf{x}, \beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i} +\Delta> \beta+k+\Delta}, \end{align*} $$
$$ \begin{align*} \psi_{1}(\mathbf{x}, \beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i} +\Delta> \beta+k+\Delta}, \end{align*} $$
 $\beta \in \Gamma $
,
$\beta \in \Gamma $
,
 $\Delta \in RJ(\Gamma )$
, and
$\Delta \in RJ(\Gamma )$
, and
 $k, z_{i} \in \mathbb {Z}$
.
$k, z_{i} \in \mathbb {Z}$
.
-
• Second kind:
where $$ \begin{align*} \phi_{2}(\mathbf{x}, \beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i}\equiv_{\Delta+ l\Gamma} \beta+k}, \end{align*} $$
$$ \begin{align*} \phi_{2}(\mathbf{x}, \beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i}\equiv_{\Delta+ l\Gamma} \beta+k}, \end{align*} $$
 $\beta \in \Gamma $
,
$\beta \in \Gamma $
,
 $\Delta \in RJ(\Gamma )$
,
$\Delta \in RJ(\Gamma )$
,
 $k, z_{i} \in \mathbb {Z}$
, and
$k, z_{i} \in \mathbb {Z}$
, and
 $l \in \mathbb {N}_{\geq 2}$
.
$l \in \mathbb {N}_{\geq 2}$
.
-
• Third kind:
where $$ \begin{align*} \phi_{3}(\mathbf{x},\beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i}\equiv_{\Delta} \beta+k}, \end{align*} $$
$$ \begin{align*} \phi_{3}(\mathbf{x},\beta):=\displaystyle{\sum_{i\leq n} z_{i} x_{i}\equiv_{\Delta} \beta+k}, \end{align*} $$
 $\beta \in \Gamma $
,
$\beta \in \Gamma $
,
 $\Delta \in RJ(\Gamma )$
, and
$\Delta \in RJ(\Gamma )$
, and
 $z_{i} \in \mathbb {Z}$
.
$z_{i} \in \mathbb {Z}$
.
The set
![]() $\{ \beta \in \Gamma \ | \ \phi _{1}(\mathbf {x},\beta ) \in p(\mathbf {x}) \}$
is an end-segment of
$\{ \beta \in \Gamma \ | \ \phi _{1}(\mathbf {x},\beta ) \in p(\mathbf {x}) \}$
is an end-segment of
![]() $\Gamma $
, so it can be coded in the quotient sorts by Propositions 3.3 and 3.6. Likewise, the set
$\Gamma $
, so it can be coded in the quotient sorts by Propositions 3.3 and 3.6. Likewise, the set
![]() $\displaystyle {\{\beta \in \Gamma \ | \ \psi _{1}(\mathbf {x},\beta ) \in p(\mathbf {x}) \}}$
is an initial segment of
$\displaystyle {\{\beta \in \Gamma \ | \ \psi _{1}(\mathbf {x},\beta ) \in p(\mathbf {x}) \}}$
is an initial segment of
![]() $\Gamma $
, and it admits a code in the quotient sorts.
$\Gamma $
, and it admits a code in the quotient sorts.
Let
![]() $X=\{ \beta \in \Gamma \ | \ \phi _{2}(\mathbf {x},\beta ) \in p(\mathbf {x})\}$
, then X is either empty or we can take
$X=\{ \beta \in \Gamma \ | \ \phi _{2}(\mathbf {x},\beta ) \in p(\mathbf {x})\}$
, then X is either empty or we can take
![]() $\beta _{0} \in X$
and
$\beta _{0} \in X$
and
![]() $\ulcorner X \urcorner $
is interdefinable with
$\ulcorner X \urcorner $
is interdefinable with
![]() $\pi _{\Delta }^{l}(\beta _{0}) \in \Gamma /(\Delta +l\Gamma )$
.
$\pi _{\Delta }^{l}(\beta _{0}) \in \Gamma /(\Delta +l\Gamma )$
.
Lastly,
![]() $\displaystyle {Z=\{ \beta \in \Gamma \ | \ \phi _{3}(\mathbf {x},\beta ) \in p(\mathbf {x})\}}$
is either empty or for any element
$\displaystyle {Z=\{ \beta \in \Gamma \ | \ \phi _{3}(\mathbf {x},\beta ) \in p(\mathbf {x})\}}$
is either empty or for any element
![]() $\beta _{0} \in Z$
, we have that
$\beta _{0} \in Z$
, we have that
![]() $\ulcorner Z \urcorner $
is interdefinable with
$\ulcorner Z \urcorner $
is interdefinable with
![]() $\rho _{\Delta }(\beta _{0}) \in \Gamma / \Delta $
.
$\rho _{\Delta }(\beta _{0}) \in \Gamma / \Delta $
.
4.2 Density of definable types
In this subsection we prove the first condition required in Hrushovski’s criterion: the density of definable types in algebraically closed sets.
The following will be a useful fact to obtain our result.
Fact 4.3. Let
![]() $X\subseteq \Gamma $
be a definable set without a minimum element. Then there is a
$X\subseteq \Gamma $
be a definable set without a minimum element. Then there is a
![]() $\ulcorner X \urcorner $
definable end-segment S such that X is co-initial in S.
$\ulcorner X \urcorner $
definable end-segment S such that X is co-initial in S.
Proof Let
![]() $I=\{ \beta \in \Gamma \ | \ (-\infty , \beta ]\cap X=\emptyset \}$
. I is a
$I=\{ \beta \in \Gamma \ | \ (-\infty , \beta ]\cap X=\emptyset \}$
. I is a
![]() $\ulcorner X \urcorner $
-definable initial segment of
$\ulcorner X \urcorner $
-definable initial segment of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $S=\Gamma \backslash I$
, it is sufficient to verify that X is co-initial in S. Let
$S=\Gamma \backslash I$
, it is sufficient to verify that X is co-initial in S. Let
![]() $\beta \in S$
, then
$\beta \in S$
, then
![]() $(-\infty , \beta ] \cap X \neq \emptyset $
. Because X does not have a minimum, we can find an element
$(-\infty , \beta ] \cap X \neq \emptyset $
. Because X does not have a minimum, we can find an element
![]() $x \in X$
such that
$x \in X$
such that
![]() $x < \beta $
, as required.
$x < \beta $
, as required.
Proposition 4.4. Let
![]() $\Gamma $
be an ordered abelian group of bounded regular rank and
$\Gamma $
be an ordered abelian group of bounded regular rank and
![]() $X \subseteq \Gamma $
a definable set. There is a global type
$X \subseteq \Gamma $
a definable set. There is a global type
![]() $p(x) \vdash x \in X$
such that
$p(x) \vdash x \in X$
such that
![]() $p(x)$
is definable over
$p(x)$
is definable over
![]() $\operatorname {acl}^{eq} (\ulcorner X \urcorner )$
.
$\operatorname {acl}^{eq} (\ulcorner X \urcorner )$
.
Proof Let
![]() $X \subseteq \Gamma $
be a
$X \subseteq \Gamma $
be a
![]() $1$
-definable set. If X has a minimum element a, the statement follows immediately by taking the type of this element. Thus we may assume that X does not have a minimum, by Fact 4.3 there is a
$1$
-definable set. If X has a minimum element a, the statement follows immediately by taking the type of this element. Thus we may assume that X does not have a minimum, by Fact 4.3 there is a
![]() $\ulcorner X \urcorner $
-definable end-segment S such that X is co-initial in S. In particular, the type
$\ulcorner X \urcorner $
-definable end-segment S such that X is co-initial in S. In particular, the type
is a consistent partial type which is
![]() $\ulcorner S \urcorner $
-definable.
$\ulcorner S \urcorner $
-definable.
Let
![]() $\pi : \mathbb {N} \rightarrow \mathbb {N}\times \mathbb {N}_{\geq 1}$
be some fixed bijection. We now build by induction an increasing sequence of partial consistent types
$\pi : \mathbb {N} \rightarrow \mathbb {N}\times \mathbb {N}_{\geq 1}$
be some fixed bijection. We now build by induction an increasing sequence of partial consistent types
![]() $(\Sigma _{i}(x) \ | \ i < \omega )$
in the following way:
$(\Sigma _{i}(x) \ | \ i < \omega )$
in the following way:
-
• Stage
 $0$
: Set
$0$
: Set
 $\Sigma _{0}(x)=\Sigma _{S}^{gen}(x)$
.
$\Sigma _{0}(x)=\Sigma _{S}^{gen}(x)$
. -
• Stage
 $i+1$
: Let
$i+1$
: Let
 $\pi (i)=(k,l)$
, at this stage we want to decide the congruence modulo the subgroup
$\pi (i)=(k,l)$
, at this stage we want to decide the congruence modulo the subgroup
 $\Delta _{k}+l\Gamma $
. To keep the notation simple we assume that
$\Delta _{k}+l\Gamma $
. To keep the notation simple we assume that
 $l\geq 2$
and we use the projection map
$l\geq 2$
and we use the projection map
 $\pi _{\Delta _{k}}^{l}:=\Gamma \rightarrow \Gamma / (\Delta _{k}+l\Gamma )$
. If
$\pi _{\Delta _{k}}^{l}:=\Gamma \rightarrow \Gamma / (\Delta _{k}+l\Gamma )$
. If
 $l=1$
we argue in the same manner to fix the coset of
$l=1$
we argue in the same manner to fix the coset of
 $\Delta _{k}$
and instead we use the projection map
$\Delta _{k}$
and instead we use the projection map
 $\rho _{\Delta _{k}}:\Gamma \rightarrow \Gamma /\Delta _{k}$
.
$\rho _{\Delta _{k}}:\Gamma \rightarrow \Gamma /\Delta _{k}$
.We proceed by cases:
-
a) Set
 $\Sigma _{i+1}(x)=\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x) \neq \pi _{\delta _{k}}^{l}(\beta ) \ | \ \beta \in \Gamma \}$
if it is consistent.
$\Sigma _{i+1}(x)=\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x) \neq \pi _{\delta _{k}}^{l}(\beta ) \ | \ \beta \in \Gamma \}$
if it is consistent. -
b) Otherwise, let
 $A_{i}=\{\eta _{1},\dots ,\eta _{r_{i}}\} \subseteq \Gamma /(\Delta _{k}+l\Gamma )$
be the finite set of cosets such that
$A_{i}=\{\eta _{1},\dots ,\eta _{r_{i}}\} \subseteq \Gamma /(\Delta _{k}+l\Gamma )$
be the finite set of cosets such that
 $\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x)=\eta _{j}\}$
is consistent. Take an element
$\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x)=\eta _{j}\}$
is consistent. Take an element
 $\hat {\eta }\in A_{i}$
and set
$\hat {\eta }\in A_{i}$
and set
 $\Sigma _{i+1}(x)=\Sigma _{i}(x) \cup \{ \pi _{\Delta _{k}}^{l}(x)=\hat {\eta }\}$
.
$\Sigma _{i+1}(x)=\Sigma _{i}(x) \cup \{ \pi _{\Delta _{k}}^{l}(x)=\hat {\eta }\}$
.
Let
 $\mathfrak {M}$
be the monster model and
$\mathfrak {M}$
be the monster model and  $$ \begin{align*} \mathcal{J}&=\{ i \in \mathbb{N} \ | \ \Sigma_{i}(x)\cup \{ \pi_{\Delta_{k}}^{l}(x) \neq \pi_{\delta_{k}}^{l}(\beta) \ | \ \beta \in \Gamma\} \ \text{is inconsistent}\}. \end{align*} $$
$$ \begin{align*} \mathcal{J}&=\{ i \in \mathbb{N} \ | \ \Sigma_{i}(x)\cup \{ \pi_{\Delta_{k}}^{l}(x) \neq \pi_{\delta_{k}}^{l}(\beta) \ | \ \beta \in \Gamma\} \ \text{is inconsistent}\}. \end{align*} $$
Claim 4.4.1. For any
 $\sigma \in Aut(\mathfrak {M}/ \operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
the following conditions hold:
$\sigma \in Aut(\mathfrak {M}/ \operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
the following conditions hold:-
1. For any
 $i \in \mathbb {N} \ \sigma (\Sigma _{i}(x))=\Sigma _{i}(x)$
.
$i \in \mathbb {N} \ \sigma (\Sigma _{i}(x))=\Sigma _{i}(x)$
. -
2. For any
 $i \in \mathcal {J} \ \sigma (A_{i})=A_{i}$
.
$i \in \mathcal {J} \ \sigma (A_{i})=A_{i}$
.
In particular, as
 $\sigma $
is arbitrary, then
$\sigma $
is arbitrary, then
 $A_{i}\subseteq \operatorname {acl}^{eq}(\ulcorner X \urcorner )$
.
$A_{i}\subseteq \operatorname {acl}^{eq}(\ulcorner X \urcorner )$
.Proof We argue by induction on i to show that for any
 $\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
we have that
$\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
we have that
 $\sigma (\Sigma _{i}(x))=\Sigma _{i}(x)$
and if
$\sigma (\Sigma _{i}(x))=\Sigma _{i}(x)$
and if
 $i \in \mathcal {J}$
then
$i \in \mathcal {J}$
then
 $\sigma (A_{i})=A_{i}$
. For the base case, fix some
$\sigma (A_{i})=A_{i}$
. For the base case, fix some
 $\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
. Then
$\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
. Then
 $\sigma (\Sigma _{0}(x))=\Sigma _{0}(x)$
because
$\sigma (\Sigma _{0}(x))=\Sigma _{0}(x)$
because
 $\Sigma _{S}^{gen}(x)$
is
$\Sigma _{S}^{gen}(x)$
is
 $\ulcorner S \urcorner $
-definable and
$\ulcorner S \urcorner $
-definable and
 $\ulcorner S \urcorner \in \operatorname {dcl}^{eq}(\ulcorner X \urcorner )$
. Suppose the statement holds for i and fix some
$\ulcorner S \urcorner \in \operatorname {dcl}^{eq}(\ulcorner X \urcorner )$
. Suppose the statement holds for i and fix some
 $\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner )).$
If
$\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner )).$
If
 $\Sigma _{i+1}(x)=\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x) \neq \pi _{\Delta _{k}}^{l}(\beta ) \ | \ \beta \in \Gamma \}$
, then
$\Sigma _{i+1}(x)=\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x) \neq \pi _{\Delta _{k}}^{l}(\beta ) \ | \ \beta \in \Gamma \}$
, then  $$ \begin{align*} \sigma(\Sigma_{i+1}(x))&= \sigma(\Sigma_{i}(x)) \cup\{ \pi_{\Delta_{k}}^{l}(x)\neq \pi_{\Delta_{k}}^{l}(\sigma(\beta)) \ | \ \beta \in \Gamma\}\\ &=\Sigma_{i}(x)\cup\{ \pi_{\Delta_{k}}^{l}(x)\neq \pi_{\Delta_{k}}^{l}(\sigma(\beta)) \ | \ \beta \in \Gamma\}=\Sigma_{i+1}(x). \end{align*} $$
$$ \begin{align*} \sigma(\Sigma_{i+1}(x))&= \sigma(\Sigma_{i}(x)) \cup\{ \pi_{\Delta_{k}}^{l}(x)\neq \pi_{\Delta_{k}}^{l}(\sigma(\beta)) \ | \ \beta \in \Gamma\}\\ &=\Sigma_{i}(x)\cup\{ \pi_{\Delta_{k}}^{l}(x)\neq \pi_{\Delta_{k}}^{l}(\sigma(\beta)) \ | \ \beta \in \Gamma\}=\Sigma_{i+1}(x). \end{align*} $$
Let’s assume that
 $\Sigma _{i+1}(x)=\Sigma _{i}(x) \cup \{ \pi _{\Delta _{k}}^{l}(x)=\eta \}$
for some
$\Sigma _{i+1}(x)=\Sigma _{i}(x) \cup \{ \pi _{\Delta _{k}}^{l}(x)=\eta \}$
for some
 $\eta \in A_{i}$
. We first argue that
$\eta \in A_{i}$
. We first argue that
 $\sigma (A_{i})=A_{i}$
. By definition of
$\sigma (A_{i})=A_{i}$
. By definition of
 $A_{i}$
:
$A_{i}$
:  $$ \begin{align*} \mu \in A_{i}& \ \text{if and only if} \ \Sigma_{i}(x) \cup \{ \pi_{\Delta_{k}}^{l}(x)=\mu \} \ \text{is consistent.} \end{align*} $$
$$ \begin{align*} \mu \in A_{i}& \ \text{if and only if} \ \Sigma_{i}(x) \cup \{ \pi_{\Delta_{k}}^{l}(x)=\mu \} \ \text{is consistent.} \end{align*} $$
Let
 $\mu \in A_{i}$
, then
$\mu \in A_{i}$
, then
 $\displaystyle {\Sigma _{i}(x) \cup \{ \pi _{\Delta _{k}}^{l}(x)=\mu \}}$
is consistent. As
$\displaystyle {\Sigma _{i}(x) \cup \{ \pi _{\Delta _{k}}^{l}(x)=\mu \}}$
is consistent. As
 $\sigma $
is an automorphism, then
$\sigma $
is an automorphism, then  $$ \begin{align*} \sigma(\Sigma_{i}(x)) &\cup \{ \pi_{\Delta_{k}}^{l}(x)=\sigma(\mu)\} \ \text{is consistent.} \end{align*} $$
$$ \begin{align*} \sigma(\Sigma_{i}(x)) &\cup \{ \pi_{\Delta_{k}}^{l}(x)=\sigma(\mu)\} \ \text{is consistent.} \end{align*} $$
By the induction hypothesis,
 $\sigma (\Sigma _{i}(x))=\Sigma _{i}(x)$
. Hence,
$\sigma (\Sigma _{i}(x))=\Sigma _{i}(x)$
. Hence,  $$ \begin{align*} \Sigma_{i}(x) \cup \{ \pi_{\Delta_{k}}^{l}(x)=\sigma(\mu)\}\ \ \text{is consistent.} \end{align*} $$
$$ \begin{align*} \Sigma_{i}(x) \cup \{ \pi_{\Delta_{k}}^{l}(x)=\sigma(\mu)\}\ \ \text{is consistent.} \end{align*} $$
Consequently,
 $\sigma (\mu ) \in A_{i}$
and we conclude that
$\sigma (\mu ) \in A_{i}$
and we conclude that
 $\sigma (A_{i}) \subseteq A_{i}$
. We argue in a similar manner with
$\sigma (A_{i}) \subseteq A_{i}$
. We argue in a similar manner with
 $\sigma ^{-1}$
to show that
$\sigma ^{-1}$
to show that
 $A_{i}\subseteq \sigma (A_{i})$
.
$A_{i}\subseteq \sigma (A_{i})$
.As for any
 ${\sigma \in Aut(\mathfrak {M}/ \operatorname {acl}^{eq}(\ulcorner X \urcorner ))}$
,
${\sigma \in Aut(\mathfrak {M}/ \operatorname {acl}^{eq}(\ulcorner X \urcorner ))}$
,
 $\sigma (A_{i})=A_{i}$
and
$\sigma (A_{i})=A_{i}$
and
 $A_{i}$
is a finite set, then
$A_{i}$
is a finite set, then
 $ A_{i} \subseteq \operatorname {acl}^{eq}(\ulcorner X \urcorner )$
. In particular,
$ A_{i} \subseteq \operatorname {acl}^{eq}(\ulcorner X \urcorner )$
. In particular,
 $\eta \in \operatorname {acl}^{eq}(\ulcorner X \urcorner )$
where
$\eta \in \operatorname {acl}^{eq}(\ulcorner X \urcorner )$
where
 $\Sigma _{i+1}(x)=\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x)=\eta \}$
. Then for any
$\Sigma _{i+1}(x)=\Sigma _{i}(x)\cup \{ \pi _{\Delta _{k}}^{l}(x)=\eta \}$
. Then for any
 $\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
we have that
$\sigma \in Aut(\mathfrak {M}/\operatorname {acl}^{eq}(\ulcorner X \urcorner ))$
we have that
 $\displaystyle {\sigma (\Sigma _{i+1}(x))=\Sigma _{i+1}(x)}$
, as required.
$\displaystyle {\sigma (\Sigma _{i+1}(x))=\Sigma _{i+1}(x)}$
, as required. -
Let
![]() $\displaystyle {\Sigma _{\infty }(x)=\bigcup _{i \in \mathbb {N}} \Sigma _{i}(x)}$
, this is a partial consistent type and
$\displaystyle {\Sigma _{\infty }(x)=\bigcup _{i \in \mathbb {N}} \Sigma _{i}(x)}$
, this is a partial consistent type and
![]() $\Sigma _{\infty }(x) \vdash x \in X$
. By quantifier elimination
$\Sigma _{\infty }(x) \vdash x \in X$
. By quantifier elimination
![]() $\Sigma _{\infty }(x)$
determines a complete type
$\Sigma _{\infty }(x)$
determines a complete type
![]() $p(x)$
. Then
$p(x)$
. Then
![]() $p(x) \vdash x \in X$
, and
$p(x) \vdash x \in X$
, and
![]() $p(x)$
is
$p(x)$
is
![]() $acl^{eq}(\ulcorner X \urcorner )$
-definable because
$acl^{eq}(\ulcorner X \urcorner )$
-definable because
![]() $p(x)$
is completely determined by the data in
$p(x)$
is completely determined by the data in
![]() $\Sigma _{\infty }(x)$
, which is definable over
$\Sigma _{\infty }(x)$
, which is definable over
![]() $\operatorname {acl}^{eq}(\ulcorner X \urcorner )$
by Claim 4.4.1.
$\operatorname {acl}^{eq}(\ulcorner X \urcorner )$
by Claim 4.4.1.
5 Main Results
Theorem 5.1. Let
![]() $\Gamma $
be an ordered abelian group of bounded regular rank (equivalently with finite spines). Then
$\Gamma $
be an ordered abelian group of bounded regular rank (equivalently with finite spines). Then
![]() $\Gamma $
admits weak-elimination of imaginaries in the language
$\Gamma $
admits weak-elimination of imaginaries in the language
![]() $\mathcal {L}_{Q}$
, once the quotient sorts are added.
$\mathcal {L}_{Q}$
, once the quotient sorts are added.
Proof By 4.1 it is sufficient to check that we have density of definable types and that we can code definable types in the quotient sorts. The first condition is Proposition 4.4 and the second one is Proposition 4.2.
5.1 The dp-minimal case
In this section we show that a better statement can be achieved for the
![]() $dp$
-minimal case.
$dp$
-minimal case.
Definition 5.2. Let
![]() $\Gamma $
be an ordered abelian group and H some definable subgroup. A subset
$\Gamma $
be an ordered abelian group and H some definable subgroup. A subset
![]() $\mathcal {C} \subseteq \Gamma $
is said to be a complete set of representatives modulo H if:
$\mathcal {C} \subseteq \Gamma $
is said to be a complete set of representatives modulo H if:
-
1. Given any
 $\gamma \in \Gamma $
there is some
$\gamma \in \Gamma $
there is some
 $\beta \in \mathcal {C}$
such that
$\beta \in \mathcal {C}$
such that
 $\gamma -\beta \in H$
.
$\gamma -\beta \in H$
. -
2. For any
 $\beta \neq \eta \in \mathcal {C}$
we have that
$\beta \neq \eta \in \mathcal {C}$
we have that
 $\beta +H\neq \eta +H$
.
$\beta +H\neq \eta +H$
.
Fact 5.3. Let
![]() $\Gamma $
be an ordered abelian group,
$\Gamma $
be an ordered abelian group,
![]() $\Delta $
a convex subgroup, and
$\Delta $
a convex subgroup, and
![]() $k \in \mathbb {N}$
. Let
$k \in \mathbb {N}$
. Let
![]() $\mathcal {C}$
be a complete set of representatives of
$\mathcal {C}$
be a complete set of representatives of
![]() $\Gamma $
modulo
$\Gamma $
modulo
![]() $k\Gamma $
, then some subset
$k\Gamma $
, then some subset
![]() $\mathcal {C}_{0} \subseteq \mathcal {C}$
is a complete set of representatives modulo
$\mathcal {C}_{0} \subseteq \mathcal {C}$
is a complete set of representatives modulo
![]() $\Delta +k\Gamma $
.
$\Delta +k\Gamma $
.
Proof Let
![]() $\mathcal {C} \subseteq \Gamma $
be a complete set of representatives of
$\mathcal {C} \subseteq \Gamma $
be a complete set of representatives of
![]() $\Gamma $
modulo
$\Gamma $
modulo
![]() $k\Gamma $
and let
$k\Gamma $
and let
![]() $\pi _{\Delta }^{k}: \Gamma \rightarrow \Gamma /(\Delta +k\Gamma )$
be the projection map.
$\pi _{\Delta }^{k}: \Gamma \rightarrow \Gamma /(\Delta +k\Gamma )$
be the projection map.
![]() $\pi _{\Delta }^{k}(\mathcal {C})=\Gamma /(\Delta +k\Gamma )$
, because for any
$\pi _{\Delta }^{k}(\mathcal {C})=\Gamma /(\Delta +k\Gamma )$
, because for any
![]() $\gamma \in \Gamma $
, there is some
$\gamma \in \Gamma $
, there is some
![]() $\beta \in \mathcal {C}$
such that
$\beta \in \mathcal {C}$
such that
![]() $\gamma -\beta \in k\Gamma $
, in particular,
$\gamma -\beta \in k\Gamma $
, in particular,
![]() $\gamma -\beta \in \Delta +k\Gamma $
. For each coset
$\gamma -\beta \in \Delta +k\Gamma $
. For each coset
![]() $\eta \in \Gamma /(\Delta +k\Gamma )$
choose an element
$\eta \in \Gamma /(\Delta +k\Gamma )$
choose an element
![]() $c_{\eta }\in \mathcal {C}$
such that
$c_{\eta }\in \mathcal {C}$
such that
![]() $\pi _{\Delta }^{k}(c_{\eta })=\eta $
. The set
$\pi _{\Delta }^{k}(c_{\eta })=\eta $
. The set
![]() $\mathcal {C}_{0}=\{ c_{\eta }\ | \ \eta \in \Gamma /(\Delta +k\Gamma )\}$
is a complete set of representatives.
$\mathcal {C}_{0}=\{ c_{\eta }\ | \ \eta \in \Gamma /(\Delta +k\Gamma )\}$
is a complete set of representatives.
By Proposition 2.23, an ordered abelian group is
![]() $dp$
-minimal if and only if it does not have singular primes, i.e., for any p prime number
$dp$
-minimal if and only if it does not have singular primes, i.e., for any p prime number
![]() $[\Gamma :p\Gamma ]< \infty $
. We consider the language
$[\Gamma :p\Gamma ]< \infty $
. We consider the language
![]() $\mathcal {L}_{dp}$
extending
$\mathcal {L}_{dp}$
extending
![]() $\mathcal {L}_{Q}$
, where for each
$\mathcal {L}_{Q}$
, where for each
![]() $k \in \mathbb {N}_{\geq 2}$
we add constants for the elements of the finite groups
$k \in \mathbb {N}_{\geq 2}$
we add constants for the elements of the finite groups
![]() $\Gamma /k\Gamma $
.
$\Gamma /k\Gamma $
.
Corollary 5.4. Let
![]() $\Gamma $
be a dp-minimal ordered group. Then
$\Gamma $
be a dp-minimal ordered group. Then
![]() $\Gamma $
admits elimination of imaginaries in the language
$\Gamma $
admits elimination of imaginaries in the language
![]() $\mathcal {L}_{dp}$
, where the quotient sorts are added.
$\mathcal {L}_{dp}$
, where the quotient sorts are added.
Proof By Theorem 5.1 and Fact 2.2 it is sufficient to show that we can also code finite sets. Let
![]() $\Delta $
definable convex subgroup and
$\Delta $
definable convex subgroup and
![]() $k \in \mathbb {N}$
, the group
$k \in \mathbb {N}$
, the group
![]() $\Gamma /(\Delta +k\Gamma )$
is also finite. We first argue that
$\Gamma /(\Delta +k\Gamma )$
is also finite. We first argue that
![]() $\Gamma /(\Delta +k\Gamma ) \subseteq \operatorname {dcl}(\emptyset )$
. Consider the
$\Gamma /(\Delta +k\Gamma ) \subseteq \operatorname {dcl}(\emptyset )$
. Consider the
![]() $\emptyset $
-definable function
$\emptyset $
-definable function
 $$ \begin{align*} f:& \Gamma/k\Gamma \rightarrow \Gamma/(\Delta+k\Gamma)\\ & \gamma+k\Gamma \rightarrow \gamma+(\Delta+k\Gamma). \end{align*} $$
$$ \begin{align*} f:& \Gamma/k\Gamma \rightarrow \Gamma/(\Delta+k\Gamma)\\ & \gamma+k\Gamma \rightarrow \gamma+(\Delta+k\Gamma). \end{align*} $$
By Fact 5.3 f is surjective.
Hence, it is enough to prove that finite sets of tuples in
![]() $\mathcal {S}=\{ \Gamma /\Delta \ | \ \Delta \in RJ(\Gamma )\}$
can be coded in the quotient sorts. As each of the sorts
$\mathcal {S}=\{ \Gamma /\Delta \ | \ \Delta \in RJ(\Gamma )\}$
can be coded in the quotient sorts. As each of the sorts
![]() $\Gamma /\Delta $
is linearly ordered, there is a definable order induced over the finite products of quotients of
$\Gamma /\Delta $
is linearly ordered, there is a definable order induced over the finite products of quotients of
![]() $\Gamma /\Delta $
, and thereby any finite set of tuples in
$\Gamma /\Delta $
, and thereby any finite set of tuples in
![]() $\mathcal {S}$
is already coded in
$\mathcal {S}$
is already coded in
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Acknowledgments
The author would like to express her gratitude to Thomas Scanlon and Pierre Simon, for many insightful conversations and their time. The author is grateful to R. Mennuni for his comments in a previous draft, J. Brown and A. Padgett for their careful reading, their time and the extensive detailed grammar corrections that allowed me to significantly improve the presentation of this paper written in my third language. Lastly, the author is also grateful to the anonymous referee for a careful reading, all the provided comments and a very fast feedback.
Funding
The author would like to thank particularly the financial support given by the NSF Grant 1848562.