No CrossRef data available.
Article contents
THE REVERSE MATHEMATICS OF  ${\mathsf {CAC\ FOR\ TREES}}$
${\mathsf {CAC\ FOR\ TREES}}$
Published online by Cambridge University Press: 28 April 2023
Abstract
 ${\mathsf {CAC\ for\ trees}}$
is the statement asserting that any infinite subtree of
${\mathsf {CAC\ for\ trees}}$
is the statement asserting that any infinite subtree of
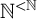 $\mathbb {N}^{<\mathbb {N}}$
has an infinite path or an infinite antichain. In this paper, we study the computational strength of this theorem from a reverse mathematical viewpoint. We prove that
$\mathbb {N}^{<\mathbb {N}}$
has an infinite path or an infinite antichain. In this paper, we study the computational strength of this theorem from a reverse mathematical viewpoint. We prove that
 ${\mathsf {CAC\ for\ trees}}$
is robust, that is, there exist several characterizations, some of which already appear in the literature, namely, the statement
${\mathsf {CAC\ for\ trees}}$
is robust, that is, there exist several characterizations, some of which already appear in the literature, namely, the statement
 $\mathsf {SHER}$
introduced by Dorais et al. [8], and the statement
$\mathsf {SHER}$
introduced by Dorais et al. [8], and the statement
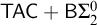 $\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
where
$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
where
 $\mathsf {TAC}$
is the tree antichain theorem introduced by Conidis [6]. We show that
$\mathsf {TAC}$
is the tree antichain theorem introduced by Conidis [6]. We show that
 ${\mathsf {CAC\ for\ trees}}$
is computationally very weak, in that it admits probabilistic solutions.
${\mathsf {CAC\ for\ trees}}$
is computationally very weak, in that it admits probabilistic solutions.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic





