Let f be an arbitrary transcendental entire or meromorphic function in the class 𝒮 (i.e. with finitely many singularities). We show that the topological pressure P(f,t) for t>0 can be defined as the common value of the pressures P(f,t,z) for all z∈ℂ up to a set of Hausdorff dimension zero. Moreover, we prove that P(f,t) equals the supremum of the pressures of f∣X over all invariant hyperbolic subsets X of the Julia set, and we prove Bowen’s formula for f, i.e. we show that the Hausdorff dimension of the radial Julia set of f is equal to the infimum of the set of t, for which P(f,t) is non-positive. Similar results hold for (non-exceptional) transcendental entire or meromorphic functions f in the class ℬ (i.e. with a bounded set of singularities), for which the closure of the post-singular set does not contain the Julia set.

In the last two decades, considerable attention has been paid to the dimension theory of self-affine sets. In the case of generalized 4-corner sets (see Figure 1), the iterated function systems obtained as the projections of self-affine systems have maps of common fixed points. In this paper, we extend our result [B. Bárány. On the Hausdorff dimension of a family of self-similar sets with complicated overlaps. Fund. Math. 206 (2009), 49–59], which introduced a new method of computation of the box and Hausdorff dimensions of self-similar families where some of the maps have common fixed points. The extended version of our method presented in this paper makes it possible to determine the box dimension of the generalized 4-corner set for Lebesgue-typical contracting parameters.

Let α1,…,αn be irrational numbers which are linearly independent over the rationals, and f1,…,fn commuting germs of holomorphic diffeomorphisms in ℂ such that fk(0)=0,f′k(0)=e2πiαk,k=1,…,n. Moser showed that f 1,…,fn are simultaneously linearizable (i.e. conjugate by a germ of holomorphic diffeomorphism h to the rigid rotations Rαk(z)=e2πiαkz) if the vector of rotation numbers (α 1,…,αn) satisfies a Diophantine condition. Adapting Yoccoz’s renormalization to the setting of commuting germs, we show that simultaneous linearization holds in the presence of a weaker Brjuno-type condition ℬ(α1,…,αn)<+∞, where ℬ(α1,…,αn) is a multivariable analogue of the Brjuno function. If there are no periodic orbits for the action of the germs f1,…,fn in a neighbourhood of the origin, then a weaker arithmetic condition ℬ′ (α 1,…,αn)<+∞ analogous to Perez-Marco’s condition for linearization in the absence of periodic orbits is shown to suffice for linearizability. Normalizing the germs to be univalent on the unit disc, in both cases the Siegel discs are shown to contain discs of radii 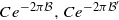for some universal constant C.

In this paper we investigate the ideal structure of the C*-algebra of a locally injective surjection introduced by the second-named author. Our main result is that a simple quotient of the C*-algebra of a locally injective surjection on a compact metric space of finite covering dimension is either a full matrix algebra, a crossed product of a minimal homeomorphism of a compact metric space of finite covering dimension, or it is purely infinite and hence covered by the classification result of Kirchberg and Phillips. It follows in particular that if the C*-algebra of a locally injective surjection on a compact metric space of finite covering dimension is simple, then it is automatically purely infinite, unless the map in question is a homeomorphism. A corollary of this result is that if the C*-algebra of a one-sided subshift is simple, then it is also purely infinite.

We construct a countable family of open intervals contained in (0,1] whose endpoints are quadratic surds and such that their union is a full measure set. We then show that these intervals are precisely the monotonicity intervals of the entropy of α-continued fractions, thus proving a conjecture of Nakada and Natsui.

We study the relation between escape rates and pressure in general dynamical systems with holes, where pressure is defined to be the difference between entropy and the sum of positive Lyapunov exponents. Central to the discussion is the formulation of a class of invariant measures supported on the survivor set over which we take the supremum to measure the pressure. Upper bounds for escape rates are proved for general diffeomorphisms of manifolds, possibly with singularities, for arbitrary holes and natural initial distributions, including Lebesgue and Sinai–Reulle–Bowen (SRB) measures. Lower bounds do not hold in such a generality, but for systems admitting Markov tower extensions with spectral gaps, we prove the equality of the escape rate with the absolute value of the pressure and the existence of an invariant measure realizing the escape rate, i.e. we prove a full variational principle. As an application of our results, we prove a variational principle for the billiard map associated with a planar Lorentz gas of finite horizon with holes.

We consider the functional in a periodic setting. We discuss whether the minimizers or the stable solutions satisfy some symmetry or monotonicity properties, with special emphasis on the autonomous case when F is x-independent. In particular, we give an answer to a question posed by Victor Bangert when F is autonomous in dimension n≤3 and in any dimension for non-zero rotation vectors.

We discuss recurrence and ergodicity properties of random walks and associated skew products for large classes of locally compact groups and homogeneous spaces. In particular, we show that a closed subgroup of a product of finitely many linear groups over local fields supports an adapted recurrent random walk if and only if it has at most quadratic growth. We give also a detailed analysis of ergodicity properties for special classes of random walks on homogeneous spaces and for associated homeomorphisms with infinite invariant measure. The structural properties of closed subgroups of linear groups over local fields and the properties of group actions with respect to certain Radon measures associated with random walks play an important role in the proofs.

The derivation of Ruelle’s derivative formula of the SRB measure depends largely on the calculation of the derivative of the unstable Jacobian. Although Ruelle’s derivative formula is correct, the proofs in the original paper and its corrigendum are not complete. In this paper, we re-visit the differentiation process of the unstable Jacobian and provide a complete derivation of its derivative formula. Our approach is to extend the volume form provided by the SRB measure on local unstable manifolds to a system of Hölder continuous local Riemannian metrics on the manifold so that under this system of local metrics, the unstable Jacobian becomes differentiable with respect to the base point and its derivative with respect to the map can be obtained by the chain rule.

We study invariants for shifts of finite type obtained as the K-theory of various C*-algebras associated with them. These invariants have been studied intensively over the past thirty years since their introduction by Wolfgang Krieger. They may be given quite concrete descriptions as inductive limits of simplicially ordered free abelian groups. Shifts of finite type are special cases of Smale spaces and, in earlier work, the second author has shown that the hyperbolic structure of the dynamics in a Smale space induces natural ring and module structures on certain of these K-groups. Here, we restrict our attention to the special case of shifts of finite type and obtain explicit descriptions in terms of the inductive limits.

Burguet [A direct proof of the tail variational principle and its extension to maps. Ergod. Th. & Dynam. Sys.29 (2009), 357–369] presented a direct proof of the variational principle of tail entropy and extended Downarowicz’s results to a non-invertible case. This paper defines and discusses tail pressure, which is an extension of tail entropy for continuous transformations. This study reveals analogs of many known results of topological pressure. Specifically, a variational principle is provided and some applications of tail pressure, such as the investigation of invariant measures and equilibrium states, are also obtained.

Let ℱn be families of entire functions, holomorphically parameterized by a complex manifold M. We consider those parameters in M that correspond to non-escaping hyperbolic functions, i.e. those maps f∈ℱn for which the postsingular set P(f) is a compact subset of the Fatou set ℱ(f) of f. We prove that if ℱn→ℱ∞ in the sense of a certain dynamically sensible metric, then every non-escaping hyperbolic component in the parameter space of ℱ∞ is a kernel of a sequence of non-escaping hyperbolic components in the parameter spaces of ℱn. Parameters belonging to such a kernel do not always correspond to hyperbolic functions in ℱ∞. Nevertheless, we show that these functions must be J-stable. Using quasiconformal equivalences, we are able to construct many examples of families to which our results can be applied.

We consider ℝn skew-products of a class of hyperbolic dynamical systems. It was proved by Niţică and Pollicott [Transitivity of Euclidean extensions of Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 25 (2005), 257–269] that for an Anosov diffeomorphism ϕ of an infranilmanifold Λ there is (subject to avoiding natural obstructions) an open and dense set f:Λ→ℝN for which the skew-product ϕf(x,v)=(ϕ(x),v+f(x)) on Λ×ℝN has a dense orbit. We prove a similar result in the context of an Axiom A hyperbolic flow on an attractor.

We consider the multifractal analysis of Birkhoff averages of continuous potentials on a self-affine Sierpiński sponge. In particular, we give a variational principle for the packing dimension of the level sets. Furthermore, we prove that the packing spectrum is concave and continuous. We give a sufficient condition for the packing spectrum to be real analytic, but show that for general Hölder continuous potentials, this need not be the case. We also give a precise criterion for when the packing spectrum attains the full packing dimension of the repeller. Again, we present an example showing that this is not always the case.

We prove the existence of two Alexandrov-embedded closed magnetic geodesics on any two-dimensional sphere with non-negative Gauß curvature.