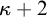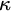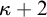1 Introduction
Theorems like compactness for first-order logic tell us there is a great degree of ambiguity for mathematical and set theoretic concepts. But much of this disappears if we restrict ourselves to only considering models that are transitive. But this does not get rid of all ambiguity. The advent of forcing as a method of set theory has revealed that even with this restriction, there’s a great amount of ambiguity not about the membership relation, but instead about what sets exist.
One response to this is to come up with axioms that help sharpen our conception of the universe so as to become immune to methods of forcing in some sense, and say more definitively what exists. For example, the axiom of “
$\mathrm {V}=\mathrm {L}$
” yields models that are immune to forcing. Under certain assumptions, the core model
$\mathrm {K}$
has this property too. Forcing axioms can be considered in a similar way, essentially stating that we’ve already forced as much as we can.
The consistency of most of these axioms is unfortunately not something we can know, as they often carry with them large cardinal hypotheses. Such hypotheses are used as a standard measure of the strength of statements: if we want to know how strong a statement is, we show it is equiconsistent with some large cardinal axiom. The question then becomes to what extent can these large cardinals be immune to forcing?
Generally speaking, we cannot ensure large cardinal properties are immune to forcing—indestructible—because we may simply add via forcing a bijection between the cardinal
$\kappa $
and
$\aleph _0$
. But if we restrict our forcing to be, say, smaller than
$\kappa $
, we can get preservation of some properties, especially those involving elementary embeddings since measures in the ground model generate measures in the generic extension. Large forcings can still pose a problem, but the answer isn’t as clear if we restrict our attention to large posets that don’t affect anything “small.” These are the notions we will investigate here, and mostly we will consider
$<\kappa $
-strategically closed,
$\le \kappa $
-distributive posets.
This topic starts with Laver’s preparation for making a supercompact cardinal
$\kappa $
indestructible (by
$<\kappa $
-directed closed forcings) in [Reference Kanamori9]. Since then, there has been a great deal of literature about the limits of this for other cardinals and varying degrees of strength.Footnote
1
Ignoring for the moment what exactly a lot of this terminology means, a short selection of results in this area is the following.
-
• [Reference Apter and Hamkins2] explores making all degrees of supercompactness and strength indestructible while there is a supercompact.
-
• [Reference Hamkins5] explores the ways in which indestructible cardinals can be made destructible and subsequently resurrected.
-
• [Reference Apter and Sargsyan3] explores a weaker version of indestructibility for strength while there is a strong cardinal, and gets an equiconsistency result: universal weak indestructibility (while there is a strong cardinal) is equiconsistent with a hyperstrong cardinal.
-
• [Reference Apter1] further explores this weaker version of indestructibility for strength to get (weak) indestructibility for lots of (strong) supercompact cardinals, and again establishes an equiconsistency for this indestructibility for many strongs from a hyperstrong cardinal (a proper class if we cut off the universe at the hyperstrong).
Part of what these works show is that there is a balance to the amount of indestructibility one can have: due to a limiting result of [Reference Apter and Hamkins2], full indestructibility for degrees of strength (or supercompactness) for all
$\delta <\kappa $
implies
$\kappa $
is not indestructible if
$\kappa $
is strong (or supercompact) and a measurable above
$\kappa $
exists. So [Reference Apter and Hamkins2, Reference Apter and Sargsyan3] critically proceed by making sure there is no measurable above the resulting strong or supercompact cardinal, thus being incompatible with the existence of multiple strong or supercompact cardinals. The work in [Reference Apter1] considers multiple strong and supercompact cardinals with indestructibility, but as a consequence, ignores indestructibility for partial degrees of strength.
This work further explores [Reference Apter1, Reference Apter and Sargsyan3] by considering indestructibility for these partial degrees of strength in the presence of multiple strong cardinals. It is also shown that to get universal weak indestructibility for small degrees of strength and supercompactness, we actually need a large increase in consistency strength, much more than a proper class of hyperstrong or hypercompact cardinals, just one of which is used in [Reference Apter1, Reference Apter and Sargsyan3] to get (many) weakly indestructible strongs and supercompacts. By “small” degrees, I mean degrees of strength below the next measurable cardinal.
The following theorem was the main goal of [Reference Apter and Sargsyan3].
Theorem 1.1 (Apter–Sargsyan).
The following are equiconsistent with
$\mathsf {ZFC}$
:
-
1. There is a hyperstrong cardinal.
-
2. There is a strong cardinal and universal weak indestructibility for all degrees of strength holds.
Hence a hyperstrong cardinal is able to yield indestructibility for all small degrees of strength,Footnote 2 and produce a strong cardinal (with also indestructible strength). A natural strengthening of (2) is having multiple strong cardinals while still ensuring universal weak indestructibility, but this is inconsistent by Result 1.17. A revised strengthening of (2) is having multiple strong cardinals while still ensuring universal weak indestructibility for small degrees of strength. A natural guess at the consistency strength of this is the existence of many hyperstrong cardinals. But this is insufficient, and indeed the consistency strength of this is strictly larger than a proper class of hyperstrong cardinals. The following is one of the main results of the document that ensures this increase in strength, assuming for the moment that a single strong reflecting strongs cardinal with a strong above it gives the consistency of a proper class of hyperstrongs, proven with Result 1.23.
Theorem 1.2 (Main goal).
The following are equiconsistent with
$\mathsf {ZFC}$
:
-
1. There is a proper class of strongs reflecting strongs.
-
2. There is a proper class of strong cardinals and weak indestructibility for any cardinal
$\kappa $
’s
$\kappa +2$
-strength. -
3. There is a proper class of strong cardinals and weak indestructibility for any cardinal
$\kappa $
’s
$\lambda $
-strength where
$\lambda $
is below the next measurable limit of measurables above
$\kappa $
.
In my thesis [Reference Holland7], we also establish a similar result for supercompactness, and the following just by continuing the preparation from Theorem 1.2 through to a Woodin cardinal, and a separate preparation where we ignore small degrees of strength.
Corollary 1.3 (Side result).
The following are equiconsistent with
$\mathsf {ZFC}$
:
-
1. There is a Woodin cardinal.
-
2. There is a Woodin cardinal
$\delta $
such that weak indestructibility for any
$\kappa $
’s
$\kappa +2$
-strength holds below
$\delta $
. -
3. There is a Woodin cardinal
$\delta $
such that every
$<\delta $
-strong cardinal has weakly indestructible
$<\delta $
-strength.
This gives the consistency of a large number of weakly indestructible strong cardinals from a Woodin cardinal. Moreover, it tells us that weak indestructibility for large degrees of strength and for small degrees of strength below a Woodin cardinal are equiconsistent. This contrasts with weak indestructibility for small degrees in the presence of, say, two strong cardinals, which is strictly stronger than for a proper class of weakly indestructible strong cardinals.
1.1 Background
Throughout we will use the following notation.
Definition 1.4.
-
• For
$\delta \in \mathrm {Ord}$
, write
$\delta ^{+\sharp }$
for the least measurable cardinal
$\kappa>\delta $
. -
• Write
$\delta ^{+\sharp \sharp }$
for the least cardinal
$\kappa>\delta $
that is
$\kappa +2$
-strong. -
• Write
for the least strong cardinal
$\kappa>\delta $
. -
• For a transitive model of set theory,
$\mathrm {M}$
, and
$\lambda \in \mathrm {Ord}^{\mathrm {M}}$
, we write
$\mathrm {M}\mid \lambda $
for
$\mathrm {V}_\lambda ^{\mathrm {M}}$
, the
$\lambda $
-th stage of the cumulative hierarchy in
$\mathrm {M}$
. -
• For a poset
$\mathbb {R}\in \mathrm {V}$
, we write
$\mathrm {V}^{\mathbb {R}}$
for an arbitrary generic extension of
$\mathrm {V}$
by
$\mathbb {R}$
, occasionally working below some particular condition in
$\mathbb {R}$
.
Definition 1.5. Let
$\kappa $
be a cardinal,
$\varphi $
a property of cardinals, and
a property of posets.
-
•
$\kappa $
has
$\varphi $
as indestructible by posets with
iff
$\varphi (\kappa )$
holds and -
•
$\kappa $
has
$\varphi $
as weakly indestructible by posets with
iff it’s indestructible by
$\le \kappa $
-distributive posets with
.
So the usual Laver indestructibility refers to indestructibility for all degrees of supercompactness of a single (supercompact) cardinal
$\kappa $
by
$<\kappa $
-directed closed posets. For strength, we usually consider weak indestructibility by
$<\kappa $
-strategically closed posets, and thus indestructibility by
$<\kappa $
-strategically closed,
$\le \kappa $
-distributive posets.
$<\kappa $
-strategic closure is a significant weakening of
$<\kappa $
-directed closure and is defined as follows.
Definition 1.6. Let
$\mathbb {P}$
be a poset and
$\kappa ,\lambda $
ordinals. The game
$\mathcal {G}_{\mathbb {P}}^\lambda $
is the two person game of length
$\le \lambda $
$$\begin{align*}\begin{array}{r *{20}{c}} {\mathbf{I}}:& p_0=\textbf{1}^{\mathbb{P}}&& p_2&& \cdots && p_\omega && p_{\omega+2}&&\cdots \\ {\mathbf{I\hspace{-.7pt}I}}:&& p_1&& p_3&&\cdots && p_{\omega+1}&&\cdots \text{,} \end{array} \end{align*}$$
where
$p_\alpha \le ^{\mathbb {P}} p_\beta $
for
$\alpha \ge \beta $
, and assuming such a
$p_\alpha $
exists,
${\mathbf {I}}$
plays
$p_\alpha $
for even
$\alpha < \lambda ($
including limit
$\alpha $
) and
${\mathbf {II}}$
plays
$p_\alpha \in \mathbb {P}$
for odd
$\alpha <\lambda $
.
${\mathbf {I}}$
wins iff players play on each turn: the resulting sequence of
$p_\alpha $
s has length
$\lambda $
.
-
•
$\mathbb {P}$
is
$\le \kappa $
-strategically closed iff
${\mathbf {I}}$
has a winning strategy in
$\mathcal {G}_{\mathbb {P}}^{\kappa +1}$
. -
•
$\mathbb {P}$
is
$\kappa $
-strategically closed iff
${\mathbf {I}}$
has a winning strategy in
$\mathcal {G}_{\mathbb {P}}^\kappa $
. -
•
$\mathbb {P}$
is
$<\kappa $
-strategically closed iff
$\mathbb {P}$
is
$\le \alpha $
-strategically closed for all ordinals
$\alpha <\kappa $
.
Basically whereas
$<\kappa $
-closure ensures we can always extend a
$\leqslant ^{\mathbb {P}}$
-decreasing sequence
$\langle p_\alpha :\alpha <\lambda \rangle $
whenever
$\lambda <\kappa $
,
$\kappa $
-strategic closure only gives control over half of the sequence, relying on
${\mathbf {I}}$
’s strategy to extend at limits.
Despite their differences, the similarities between
$<\kappa $
-closed and
$\kappa $
-strategically closed preorders are enough to allow some arguments about
$<\kappa $
-closure to go through. For example,
$\kappa $
-strategically closed preorders are
$\le \kappa $
-distributive by basically the same proof as with full closure. There are many other common results in iterated forcing where using strategic closure vs. full closure makes no difference [Reference Cummings, Foreman and Kanamori4, Propositions 7.9 and 7.12].
Definition 1.7. Let
$\kappa $
be a cardinal. A preorder
$\mathbb {P}$
is
$<\kappa $
-distributive iff for every collection
$\mathcal {D}$
of open, dense sets of
$\mathbb {P}$
, if
$|\mathcal {D}|<\kappa $
then
$\bigcap \mathcal {D}\neq \emptyset $
is open, dense. We may similarly define
$\le \kappa $
-distributive.
Corollary 1.8. For any infinite cardinal
$\kappa $
, if
$\mathbb {P}$
is
$<\kappa $
-strategically closed, then
$\mathbb {P}$
is
$<\kappa $
-distributive.
It’s not hard to see that if
$\kappa $
is measurable, its
$\kappa +1$
-strength is weakly indestructible. So easy models of universal indestructibility for small degrees of strength are those with no large cardinals, or those with only measurables. Obviously if a poset isn’t
$<\kappa $
-distributive, it can collapse the strength of
$\kappa $
, e.g., through a trivial collapse
$\mathrm {Col}(\omega ,\kappa )$
.
Corollary 1.9. Let
$\kappa $
be measurable. Then
$\kappa $
’s measurability (i.e., its
$\kappa +1$
-strength) is weakly indestructible.
Proof If
$U\in \mathrm {V}$
is a measure on
$\kappa $
and
$\mathbb {P}\in \mathrm {V}$
is a
$\le \kappa $
-distributive poset, no subsets of
$\kappa $
are added by
$\mathbb {P}$
. Then
$U\in \mathrm {V}\subseteq \mathrm {V}^{\mathbb {P}}$
is still a measure in
$\mathrm {V}^{\mathbb {P}}$
.
The rest of this document will assume familiarity with strong cardinals and their fundamental properties.
Definition 1.10.
-
• A cardinal
$\kappa $
is
$\lambda $
-strong iff there is an elementary embedding
$j:\mathrm {V}\rightarrow \mathrm {M}$
(as witnessed by a
$(\kappa ,\lambda )$
-extender) with
$\operatorname {\mathrm {cp}}(j)=\kappa $
,
$j(\kappa )>\lambda $
, and
$\mathrm {V}\mid \lambda =\mathrm {M}\mid \lambda $
. -
• A cardinal is strong iff it is
$\lambda $
-strong for every
$\lambda \in \mathrm {Ord}$
. -
• We call embeddings (extenders) witnessing
$\lambda $
-strength
$\lambda $
-strong embeddings (extenders).
Beyond their definition, strong cardinals are useful for the following reflection principle.
Lemma 1.11 (
$\Sigma _2$
-reflection).
Let
$\kappa $
be a strong cardinal and
$\delta \ge \kappa $
. Suppose
$\mathrm {V}\mid \delta \vDash "{\varphi (\vec {x})}\text {"}$
for some formula
$\varphi $
and parameters
$\vec {x}\in \mathrm {V}\mid \kappa $
. Then there are unboundedly many
$\alpha <\kappa $
such that
$\mathrm {V}\mid \alpha \vDash "{\varphi (\vec {x})}.\text {"}$
Proof Let
$j:\mathrm {V}\rightarrow \mathrm {M}$
be a
$\delta $
-strong embedding so that
$j(\vec {x})=\vec {x}$
,
$\delta <j(\kappa )$
, and
$\mathrm {M}\mid \delta =\mathrm {V}\mid \delta \vDash "{\varphi (\vec {x})}.\text {"}$
In
$\mathrm {M}$
, there is then some level of the cumulative hierarchy below
$j(\kappa )$
that satisfies
$\varphi (j(\vec {x}))$
and so by elementarity, in
$\mathrm {V}$
there’s a level
$\mathrm {V}\mid \alpha $
of the cumulative hierarchy with
$\operatorname {\mathrm {rank}}(\vec {x})<\alpha <\kappa $
satisfying
$\varphi (\vec {x})$
. Because
$\delta>\kappa $
, we could have thrown in any fixed ordinal
$\beta <\kappa $
as a useless parameter into
$\vec {x}$
so the idea above gives an
$\alpha>\beta $
with this property. here
In searching for extenders, it’s useful to know the following fact which tells us generally that we only need to search up to the next strong limit after
$\lambda $
limit to find
$\lambda $
-strong extenders. In particular, if
$\lambda $
itself is already a strong limit,
$\kappa $
being
$\lambda $
-strong is equivalent to
$\kappa $
having a
$\lambda $
-strong
$(\kappa ,\lambda )$
-extender.
Lemma 1.12. Let
$\kappa $
be
$\lambda $
-strong, as witnessed by the elementary
$j:\mathrm {V}\rightarrow \mathrm {M}$
. Suppose
$\mu \ge |\mathrm {V}\mid \lambda |^+$
. Therefore the derived
$(\kappa ,\mu )$
-extender is
$\lambda $
-strong.
Proof Let E be the derived
$(\kappa ,\mu )$
-extender:
$E=\{\langle r,X\rangle \in [\mu ]^{<\omega }\times \mathcal {P}([\kappa ]^{|r|}):r\in j(X)\}$
. We form the ultrapower
$\mathrm {Ult}_E(\mathrm {V})$
with elementary
$j_E:\mathrm {V}\rightarrow \mathrm {Ult}_E(\mathrm {V})$
and can factor
$j=j_E\circ k_E$
where
$\mathrm {cp}(k_E)\ge \mu $
. Note that
$|\mathrm {Ult}_E(\mathrm {V})\mid \gamma |^{\mathrm {Ult}_E(\mathrm {V})}=\nu \le |\mathrm {V}\mid \gamma |<\mu $
for some
$\nu $
. In particular, we can code
$\langle \mathrm {Ult}_E(\mathrm {V})\mid \gamma ,\in \rangle $
as a subset of
$\nu $
. This subset
$R\subseteq \nu $
must also be in
$\mathrm {M}$
because
$\operatorname {\mathrm {cp}}(k_E)\ge \mu $
:
$$\begin{align*}k_E(R)=\{\beta\in k_E(\nu):\beta\in k_E(R)\}=\{\beta\in \nu:k_E(\beta)\in k_E(R)\}=R\text{.}\end{align*}$$
But then in
$\mathrm {M}$
, by elementarity,
$k_E(R)=R$
codes
$\langle \mathrm {M}\mid \gamma ,\in \rangle =\langle \mathrm {V}\mid \gamma ,\in \rangle $
for every
$\gamma <\lambda $
. This shows
$\mathrm {V}\mid \lambda =\mathrm {Ult}_E(\mathrm {V})\mid \lambda $
, meaning E is
$\lambda $
-strong.
Corollary 1.13. Suppose
exists. Then
$\kappa $
is strong iff
$\kappa $
is
-strong.
We now establish some definitions related to [Reference Apter and Sargsyan3], explaining Theorem 1.1.
Definition 1.14. Let
$\kappa $
and
$\alpha>0$
be ordinals. We define by transfinite recursion what it means for
$\kappa $
to be
$\alpha $
-hyperstrong.
-
•
$\kappa $
is
$0$
-hyperstrong iff
$\kappa $
is strong. -
•
$\kappa $
is
$<\alpha $
-hyperstrong iff
$\kappa $
is
$\xi $
-hyperstrong for every
$\xi <\alpha $
. -
•
$\kappa $
is
$\alpha $
-hyperstrong iff for any
$\lambda>\kappa $
, there is a
$(\kappa ,\lambda )$
-extender E giving an ultrapower embedding
$j_E:\mathrm {V}\rightarrow \mathrm {M}$
with
$\operatorname {\mathrm {cp}}(j_E)=\kappa $
,
$j_E(\kappa )>|\mathrm {V}\mid \lambda |$
,
$\mathrm {V}\mid \lambda \subseteq \mathrm {M}$
, and
$\mathrm {M}\vDash "{\kappa \text { is }<\alpha \text {-hyperstrong}}.\text {"}$
-
•
$\kappa $
is hyperstrong iff
$\kappa $
is
$\xi $
-hyperstrong for every ordinal
$\xi $
.
We will work with hyperstrongs mostly to show that they are insufficient in establishing the main result of Theorem 1.2. We will also make use of strongs reflecting strongs. We will discuss the interaction between these two definitions in the next subsection.
Definition 1.15. Let
$\kappa $
be a cardinal and
$\lambda $
an ordinal.
-
• We say
$\kappa $
is
$\lambda $
-strong reflecting strongs (
$\lambda $
-srs) iff there’s a
$\lambda $
-strong extender E with critical point
$\kappa $
giving an elementary
$j_E:\mathrm {V}\rightarrow \mathrm {M}=\operatorname {\mathrm {Ult}}_E(\mathrm {V})$
with
$$\begin{align*}\{\xi<\lambda :\xi \text{ is strong}\}=\{\xi<\lambda :\mathrm{M}\vDash "{\xi \text{ is strong}}\text{"}\}\text{.}\end{align*}$$
-
• We call such an embedding (extender) a
$\lambda $
-srs embedding (extender). -
• We say
$\kappa $
is srs iff
$\kappa $
is
$\lambda $
-srs for every
$\lambda>\kappa ;$
and we say
$\kappa $
is
$<\lambda $
-srs if
$\kappa $
is
$\alpha $
-srs for each
$\alpha <\lambda $
.
For the most part, we only care about strongs reflecting strongs when they have strongs above them since if there is no strong above
$\kappa $
,
$\kappa $
is srs iff
$\kappa $
is
$1$
-hyperstrong (as we will show with Corollary 1.24). But under the not-uncommon assumption of a strong above, this is a strengthening of hyperstrong cardinals both in the sense of being hyperstrong and in having a consistency strength higher than a class of hyperstrong cardinals. (2) implies (1) direction of Theorem 1.2 then tells us that a proper class of hyperstrong cardinals is insufficient to ensure universal weak indestructibility for very small degrees of strength with a proper class of strongs.
For now, we end this subsection with the following definition.
Definition 1.16.
$\mathsf {UWISS}$
(Universal weak indestructibility for small degrees of strength) is the proposition that for all
$\kappa $
, if
$\kappa $
is
$\kappa +2$
-strong, then
$\kappa $
’s
$\kappa +2$
-strength is weakly indestructible by
$<\kappa $
-strategically closed posets.
This will be equiconsistent with every
$\rho $
-strong
$\kappa $
having weakly indestructible
$\rho $
-strength for
$\rho $
below the next measurable limit of measurables above
$\kappa $
.
1.2 Limiting results
The limit imposed on universal indestructibility was explored in [Reference Apter and Hamkins2] for full indestructibility, but we may consider weak indestructibility in a similar way. The main limiting result is the following with the proof adapted from [Reference Apter and Hamkins2, Theorem 11] and [Reference Hamkins5, Superdestruction Theorem III].
Result 1.17. Suppose
$\kappa $
is strong and this is not destroyed by
$\mathrm {Add}(\kappa ^+,1)$
. Suppose
$\kappa ^{+\sharp \sharp }$
exists. Then, there are arbitrarily large
$\delta <\kappa $
whose
$\delta +2$
-strength is destroyed by
$\mathrm {Add}(\delta ^+,1)$
.
Proof Let A be
$\mathrm {Add}(\kappa ^+,1)$
-generic over
$\mathrm {V}$
. By hypothesis,
$\kappa $
is still strong in
$\mathrm {V}[A]$
and so we get a sufficiently strong embedding
$j:\mathrm {V}[A]\rightarrow \mathrm {M}[j(A)]$
with
$\operatorname {\mathrm {cp}}(j)=\kappa $
so that
$\lambda =\kappa ^{+\sharp \sharp }$
is still
$\lambda +2$
-strong in
$\mathrm {M}[j(A)]$
.
Claim 1.18.
$\lambda $
’s
$\lambda +2$
-strength is destroyed by
$\mathrm {Add}(\lambda ^+,1)$
in
$\mathrm {V}[A]$
.
Proof Suppose not. Let G be
$\mathrm {Add}(\lambda ^+,1)$
-generic over
$\mathrm {V}[A]$
and let
$i:\mathrm {V}[A*G]\rightarrow \mathrm {N}[i(A*G)]$
be
$\lambda +2$
-strong with
$\operatorname {\mathrm {cp}}(i)=\lambda $
. Since
$A\subseteq \kappa ^+<\operatorname {\mathrm {cp}}(i)$
,
$i(A*G)=A*i(G)$
. Without loss of generality, i is generated by extenders such that
$\mathrm {N}[A*i(G)]$
is closed under
$\lambda $
-sequences of
$\mathrm {V}[A*G]$
.
Note that there is a gap at
$(2^{\kappa })^+$
, so by gap forcing [Reference Hamkins6],
$i\upharpoonright \mathrm {V}:\mathrm {V}\rightarrow \mathrm {N}$
is a class of
$\mathrm {V}$
, is closed under
$\lambda $
-sequences, and is still
$\lambda +2$
-strong. It follows that
$G\subseteq \lambda ^+$
is in
$\mathrm {H}_{\lambda ^{++}}^{\mathrm {V}[A*G]}=\mathrm {H}_{\lambda ^{++}}^{\mathrm {N}[A*i(G)]}$
and hence in
$\mathrm {N}[A*i(G)]$
, but wasn’t added by
$i(\mathrm {Add}(\lambda ^+,1))$
by
$<i(\lambda ^+)$
-distributivity in
$\mathrm {N}[A]$
. Thus
$G=\dot G_A\in \mathrm {N}[A]$
for some
$\mathrm {Add}(\kappa ^+,1)$
-name
$\dot G$
which can be thought of as a function from
$(\lambda ^+)^{\mathrm {V}}=(\lambda ^+)^{\mathrm {N}}$
to antichains of
$\mathrm {Add}(\kappa ^+,1)$
. Since this poset is
$\kappa ^+$
-cc and has size
$2^\kappa $
,
$\dot G$
has size
$\le (2^{\kappa })^{\kappa }\cdot {\lambda ^+}=\lambda ^+$
and is therefore in the hereditarily
$<(\lambda ^{++})^{\mathrm {N}}=(\lambda ^{++})^{\mathrm {V}}$
-sized sets
$\mathrm {H}_{\lambda ^{++}}^{\mathrm {N}}=\mathrm {H}_{\lambda ^{++}}^{\mathrm {V}}$
. The ability to consider all of this in
$\mathrm {V}$
means
$G\in \mathrm {V}[A]$
, a contradiction.
Without loss of generality,
$\mathrm {M}[j(A)]$
has enough agreement with
$\mathrm {V}[A]$
to witness this fact as well. Since
$\kappa <\lambda <j(\kappa )$
, this is reflected down into
$\mathrm {V}[A]$
: there are arbitrarily large
$\delta <\kappa $
such that
$\delta $
’s
$\delta +2$
-strength is destroyed by
$\mathrm {Add}(\delta ^+,1)$
in
$\mathrm {V}[A]$
. It follows that
$\mathrm {Add}(\kappa ^+,1)*\mathrm {Add}(\delta ^+,1)$
is
$<\delta $
-directed closed and
$\le \delta $
-distributive in
$\mathrm {V}$
but destroys
$\delta $
’s
$\delta +2$
-strength. Since
$\mathrm {Add}(\kappa ^+,1)$
is sufficiently distributive, it can’t add to nor destroy
$\delta $
’s
$\delta +2$
-strength. So it must be that
$\mathrm {Add}(\delta ^+,1)^{\mathrm {V}[A]}$
destroyed it. Since
$\mathrm {Add}(\kappa ^+,1)$
is
$\le \kappa $
-distributive,
$\mathrm {Add}(\delta ^+,1)^{\mathrm {V}[A]}=\mathrm {Add}(\delta ^+,1)^{\mathrm {V}}$
destroyed
$\delta $
’s
$\delta +2$
-strength in
$\mathrm {V}$
.
And this result generalizes to larger degrees of strength with the same proof.
Corollary 1.19. Let
$\mu \in \mathrm {Ord}$
. Suppose
$\kappa $
is strong, and this is not destroyed by
$\mathrm {Add}(\kappa ^{+\mu },1)$
. Suppose there is a
$\lambda>\kappa ^{+\mu +1}$
that is
$\lambda +\mu +1$
-strong. Then:
-
1. There are unboundedly many
$\delta <\kappa $
such that
$\delta $
is
$\delta +\rho $
-strong for some
$\rho $
, but this is destructible by
$\mathrm {Add}(\delta ^{+\rho },1)$
. -
2. If
$\mu <\kappa $
, then there are arbitrarily large
$\delta <\kappa $
such that
$\delta $
’s
$\delta +\mu +1$
-strength is destructible by
$\mathrm {Add}(\delta ^{+\mu },1)$
.
In particular, with two strong cardinals, one cannot have universal weak indestructibility for all degrees of strength, contrasting with Theorem 1.1 from [Reference Apter and Sargsyan3, Theorems 3 and 4]. Corollary 1.19 also easily generalizes to supercompactness in place of strength.
The contrapositive to Result 1.17 details one aspect of what goes wrong if one naïvely tries to continue the preparation from either [Reference Apter and Hamkins2] or [Reference Apter and Sargsyan3].
Corollary 1.20. Suppose
$\kappa $
is strong and
$\kappa ^{+\sharp \sharp }$
exists. Suppose every
$\delta <\kappa $
that is
$\delta +2$
-strong has this indestructible by
$\mathrm {Add}(\delta ^+,1)$
. Then
$\kappa $
’s strength is destroyed by
$\mathrm {Add}(\kappa ^+,1)$
.
All of this is just to justify that one simultaneously cannot have
$\mathsf {UWISS}$
with any reasonable amount of indestructibility for large degrees of strength. Moreover, versions of Result 1.17 and Corollary 1.20 with these weaker notions of indestructibility replaced with full indestructibility hold as noted in the original Theorems 10–12 of [Reference Apter and Hamkins2]. A corollary of Corollary 1.20 and Result 1.17 is that achieving universal indestructibility for all degrees of strength with a strong cardinal
$\kappa $
requires that
$\kappa ^{+\sharp \sharp }$
doesn’t exist. And this is exactly what [Reference Apter and Hamkins2, Reference Apter and Sargsyan3] do.
Let us now show why—assuming the equiconsistency of Theorem 1.2—hyperstrongs are insufficient to establish
$\mathsf {UWISS}$
with a proper class of (weakly destructible) strongs. To do this, we need to unfortunately look at the fine details of calculating hyperstrongs and strongs reflecting strongs inside the cumulative hierarchy. A straightforward, somewhat tedious induction gives the following, recalling Definition 1.14 for the definition of a hyperstrong cardinal.
Corollary 1.21. Fix ordinals
$\kappa ,\alpha>0$
with
$\kappa $
infinite. Then the following are equivalent.
-
1.
$\kappa $
is
$<\alpha $
-hyperstrong. -
2.
$\mathrm {V}\mid \delta \vDash \textit{"}{\kappa \text { is }<\alpha \text {-hyperstrong}}\text {"}$
for all
$\delta \ge |\kappa +\alpha |^+$
closed under the map
$\lambda \mapsto |\mathrm {V}\mid \lambda |^+$
.
Proof (2) always implies (1) since any failure of hyperstrength is reflected to
$\mathrm {V}\mid \delta $
for arbitrarily large
$\delta $
. So we assume (1) and aim to show (2) by induction. For
$\alpha =1$
—i.e.,
$0$
-hyperstrength or just being strong—this follows by the absoluteness of strength of extenders between levels of the cumulative hierarchy. Extenders witnessing the
$\lambda $
-strength of
$\kappa $
for
$\lambda <\delta $
can be found with length
$\mu =|\mathrm {V}\mid \lambda |^+$
by Lemma 1.12 and so are in
$\mathrm {V}\mid {\mu +\omega }\subseteq \mathrm {V}\mid \delta $
with
$\delta $
a strong limit. So
$\kappa $
being strong implies it is strong in
$\mathrm {V}\mid \delta $
.
For limit
$\alpha $
, this follows inductively: for each
$\xi <\alpha $
,
$\kappa $
is
$<\xi +1$
-hyperstrong iff
$\mathrm {V}\mid \delta \vDash $
“
$\kappa $
is
$<\xi +1$
-hyperstrong” for all strong limit
$\delta>|\kappa +\xi |^+$
closed under
$\lambda \mapsto |\mathrm {V}\mid \lambda |^+$
. Hence
$\kappa $
is
$<\alpha $
-hyperstrong implies
$\mathrm {V}\mid \delta $
satisfies this for such
$\delta $
greater than
$\sup _{\xi <\alpha }|\kappa +\xi |^+\le |\kappa +\alpha |^+$
.
For successor
$\alpha $
, assume the results for
$<\alpha $
-hyperstrength. In fact, we take the inductive hypothesis as this holding for any transitive model of
$\mathsf {ZFC}$
containing
$|\kappa +\alpha |^+$
. But without loss of generality, and for the sake of notation, take our model as
$\mathrm {V}$
. As notation, for E an extender, let
$j_E:\mathrm {V}\rightarrow \operatorname {\mathrm {Ult}}_E(\mathrm {V})$
be the canonical embedding.
Suppose
$\kappa $
is
$\alpha $
-hyperstrong and let
$\delta \ge |\kappa +\alpha |^+$
be an arbitrary strong limit closed under
$\lambda \mapsto |\mathrm {V}\mid \lambda |^+$
. Inductively,
$\mathrm {V}\mid \delta \vDash "{\kappa \text { is }< \alpha \text {-hyperstrong.}}\text {"}$
Let
$\lambda <\delta $
be arbitrary. In
$\mathrm {V}$
, there’s a
$\lambda $
-strong extender E on
$\kappa $
such that
$\mathrm {Ult}_E(\mathrm {V})\vDash "{\kappa \text { is }<\alpha \text {-hyperstrong.}}\text {"}$
Consider
$\gamma =\sup _{\beta <\delta }j_E(\beta )$
which is a strong limit in
$\mathrm {Ult}_E(\mathrm {V})$
because
$\delta $
is a strong limit in
$\mathrm {V}$
. Moreover,
$$\begin{align*}\gamma \ge \delta \ge|\kappa+\alpha |^+\ge(|\kappa+\alpha |^{+})^{\mathrm{Ult}_E(\mathrm{V})}\text{.}\end{align*}$$
To see that
$\gamma $
is closed under
$\lambda '\mapsto |\mathrm {V}\mid \lambda '|^+$
in
$\mathrm {Ult}_E(\mathrm {V})$
, let
$\lambda '<\gamma $
be arbitrary. Then
$\lambda '<j_E(\beta )$
for some
$\beta <\delta $
. Since
$|\mathrm {V}\mid \beta |^+<\delta $
, we have by elementarity
$$\begin{align*}\mathrm{Ult}_E(\mathrm{V})\models"{|\mathrm{Ult}_E(\mathrm{V})\mid\lambda'|\le |\mathrm{Ult}_E(\mathrm{V})\mid j_E(\beta)|=j_E(|\mathrm{V}\mid \beta|)<\gamma}.\text{"}\end{align*}$$
As a strong limit in
$\mathrm {Ult}_E(\mathrm {V})$
,
$(|\mathrm {V}\mid \lambda '|^+)^{\mathrm {Ult}_E(\mathrm {V})}<\gamma $
. So by the inductive hypothesis on
$\alpha $
,
$$\begin{align*}\mathrm{Ult}_E(\mathrm{V})\mid\gamma \vDash "{\kappa \text{ is }<\alpha \text{-hyperstrong.}}\text{"}\end{align*}$$
Yet
$E\in \mathrm {V}\mid \delta $
and taking the ultrapower there yields
$\mathrm {Ult}_E^{\mathrm {V}\mid \delta }(\mathrm {V}\mid \delta )=\mathrm {Ult}_E(\mathrm {V})\mid \gamma $
. Hence E witnesses the
$\alpha $
-hyperstrength of
$\kappa $
in
$\mathrm {V}\mid \delta $
.
We also make use of the following lemma.
Lemma 1.22. Let
$\kappa $
be strong such that
exists. Then:
-
1.
$\kappa $
is
-hyperstrong iff
$\kappa $
is hyperstrong. -
2.
iff
$\kappa $
is
-hyperstrong and hence hyperstrong by
$(1)$
.
Proof
-
1. Suppose
$\kappa $
is not hyperstrong. By reflection, (*)for some
$$ \begin{align} \mathrm{V}\mid \delta \vDash "{\exists \gamma \ (\kappa \text{ is not }\gamma \text{-hyperstrong})\wedge \forall\alpha\in\mathrm{Ord}\ (\beth_\alpha\text{ and }|\mathrm{V}\mid\alpha|^+\text{ exists})}\text{"} \end{align} $$
$\delta $
. By Lemma 1.11, we get some
such that (
$*$
) holds. Since
$\beth _\alpha <\delta $
for every
$\alpha <\delta $
,
$\delta $
is a strong limit with then
$\delta>|\kappa +\gamma |^+$
for any
$\gamma $
as in (
$*$
). Corollary 1.21 therefore implies
$\kappa $
is not
$\gamma $
-hyperstrong for some
, a contradiction.
-
2. Suppose
$\kappa $
is not
$\alpha $
-hyperstrong for some
. This fact can be reflected to some level
$\mathrm {V}\mid \delta $
where
$\delta $
is a strong limit, and by Lemma 1.11, to
$\mathrm {V}\mid \delta $
for arbitrarily large strong limit
. In particular, we get some strong limit
$\delta _0$
with
such that
$\mathrm {V}\mid {\delta _0}\vDash $
“
$\kappa $
is not
$\alpha $
-hyperstrong.” But applying Corollary 1.21 in
, by the hypothesis,
for all limit
$\delta>|\kappa +\alpha |^+$
, a contradiction with the hypothesis on
$\delta _0$
. Hence
$\kappa $
must be
$\alpha $
-hyperstrong for each
, and so hyperstrong by (1).
This lemma allows us to show that the existence of an srs (with a strong above it) is strictly stronger than a proper class of hyperstrongs.
Result 1.23. Let
$\kappa $
be srs such that
exists. Then
$\kappa $
is hyperstrong. In fact, any single
-srs embedding witnesses all degrees of hyperstrength of
$\kappa $
. Moreover, in
$\mathrm {V}\mid \kappa $
, there is a proper class of hyperstrongs.
Proof Let
$\kappa $
be srs.
$\kappa $
is already
$0$
-hyperstrong. There is then a
-srs embedding
$j:\mathrm {V}\rightarrow \mathrm {M}$
with
$\operatorname {\mathrm {cp}}(j)=\kappa $
. We proceed by induction on
$\alpha $
to show
$\kappa $
is
$<\alpha $
-hyperstrong in
$\mathrm {V}$
and
$\mathrm {M}$
, with the base case of
$\alpha =1$
already true. The limit case is trivial, so we consider only the successor case: showing
$\alpha $
-hyperstrength in
$\mathrm {V}$
and
$\mathrm {M}$
. By Lemma 1.22 (1), we may assume
.
Suppose
$\kappa $
is
$<\alpha $
-hyperstrong in
$\mathrm {V}$
and
$\mathrm {M}$
so that
$\kappa $
is
$\alpha $
-hyperstrong in
$\mathrm {V}$
. If there is some
$\lambda $
with no
$\lambda $
-strong extender in
$\mathrm {M}$
witnessing
$\alpha $
-hyperstrength of
$\kappa $
, then by reflection, some
$\mathrm {M}\mid \delta $
(correctly) satisfies there’s no such extender. By Lemma 1.11, we can assume
with
$\delta $
a strong limit so that
$\mathrm {M}\mid \delta =\mathrm {V}\mid \delta $
also has no such extender. Corollary 1.21 tells us
$\mathrm {V}$
must satisfy
$\kappa $
isn’t
$\alpha $
-hyperstrong, a contradiction.
We also can show that
$\kappa $
is the limit of hyperstrongs, giving
$\mathrm {V}\mid \kappa $
as a model of a proper class of hyperstrongs. Suppose not:
$\kappa $
is the least hyperstrong above some
$\lambda $
. By elementarity,
$j(\kappa )$
is still the least hyperstrong above
$j(\lambda )=\lambda $
in
$\mathrm {M}$
but
So by Lemma 1.22 (2),
$\kappa $
is hyperstrong in
$\mathrm {M}$
. But
$\lambda <\kappa <j(\kappa )$
contradicts that
$j(\kappa )$
is the least hyperstrong above
$\lambda $
in
$\mathrm {M}$
.
When there is no strong above an srs, then being hyperstrong is a stronger property.
Corollary 1.24. Suppose there is no strong above
$\kappa $
. Then
$\kappa $
is srs iff
$\kappa $
is
$1$
-hyperstrong.
Proof Clearly if
$\kappa $
is srs, any
$\lambda $
-srs embedding
$j:\mathrm {V}\rightarrow \mathrm {M}$
has
$\kappa $
as strong in both
$\mathrm {V}$
and
$\mathrm {M}$
, meaning
$\kappa $
is
$1$
-hyperstrong. For the other direction, let
$\lambda>\kappa $
be arbitrary, and let
$j:\mathrm {V}\rightarrow \mathrm {M}$
be
$\lambda $
-strong where
$\kappa $
is strong in
$\mathrm {M}$
. If some
$\delta $
is strong in
$\mathrm {M}$
for
$\kappa <\delta <\lambda $
, let
$\delta $
be least. Then there is a
$\lambda $
-strong embedding
$h:\mathrm {M}\rightarrow \mathrm {N}$
with
$\mathrm {cp}(h)=\delta $
such that
$\delta $
is not strong in
$\mathrm {N}$
, e.g., using the Mitchell-least
$\lambda $
-strong embedding. It follows that in
$\mathrm {N}$
, there are no strongs in the interval
$(\kappa ,j(\delta ))\supseteq (\kappa ,\lambda )$
. Hence
$h\circ j:\mathrm {V}\rightarrow \mathrm {N} \lambda $
-strong and
$\mathrm {V}$
,
$\mathrm {N}$
agree that the only strong below
$\lambda $
is
$\kappa $
, so
$\kappa $
is
$\lambda $
-srs.
2 Strongs reflecting strongs in the core model
We begin with proving the “easy” direction of Theorem 1.2 through core model techniques. We show (2) implies (1), meaning that from a model with
$\mathsf {UWISS}$
and a proper class of strongs, we can find a model with a proper class of srs cardinals. Firstly, note that a Woodin cardinal implies the existence of a proper class of srs cardinals by an easy proof.
Lemma 2.1. The existence of a Woodin cardinal implies
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}\mathrel {+}$
“There is a proper class of srs cardinals”).
Proof Let
$\delta $
be Woodin and
$A=\{\kappa <\delta :\kappa \text { is strong}\}$
. By Woodin-ness and [Reference Jech8, Theorem 26.14], there is an unbounded (in fact, stationary) set
$$\begin{align*}\{\kappa<\delta :\kappa \text{ is }\lambda \text{-strong reflecting }A\text{ for all }\lambda<\delta \}\subseteq \mathrm{V}\mid \delta \text{.}\end{align*}$$
But this just means we get
$\lambda $
-strong extenders
$E_\lambda \in \mathrm {V}\mid \delta $
for
$\lambda <\delta $
on each
$\kappa $
in this set such that the resulting embedding
$j_\lambda :\mathrm {V}\rightarrow \mathrm {M}_\lambda $
has
$j_\lambda (A)\cap \mathrm {V}\mid \lambda =A\cap \mathrm {V}\mid \lambda $
, i.e.,
$\{\alpha <\lambda :\mathrm {M}\vDash "{\alpha \text { is strong}}\text {"}\}=\{\alpha <\lambda :\alpha \text { is strong}\}$
. Hence
$\mathrm {V}\mid \delta $
witnesses the consistency statement.
Hence we may assume without loss of generality that there is no inner model with a Woodin and thus may work with the core model
$\mathrm {K}$
below a Woodin as presented in [Reference Martin and Steel11, Reference Perlmutter13]. There are a few standard facts about
$\mathrm {K}$
that we will use.
Lemma 2.2. Suppose there is no inner model with a Woodin cardinal. Then the core model
$\mathrm {K}$
is such that:
-
1. (Local definability) For every regular
$\kappa>\aleph _1$
,
$\mathrm {K}^{\mathrm {H}_\kappa }=\mathrm {K}\cap \mathrm {H}_\kappa $
. -
2. (Generic absoluteness) For every poset
$\mathbb {P}\in \mathrm {V}$
, and every
$\mathbb {P}$
-generic G over
$\mathrm {V}$
,
$\mathrm {K}^{\mathrm {V}}=\mathrm {K}^{\mathrm {V}[G]}$
. -
3. (Initial segment condition) If E is an extender on the sequence of
$\mathrm {K}$
, then for every
$\alpha <\operatorname {\mathrm {lh}}(E)$
,
$E\upharpoonright \alpha \in \mathrm {K}$
is on the sequence of
$\mathrm {K}$
.
We will also make use of some basic facts of iteration trees, and in particular, normal iteration trees. The facts we use are essentially a fragment of the definition of normal in iteration trees [Reference Laver10], namely that they are
$+2$
-trees.
Result 2.3. Let
$\mathcal {T}$
be an iteration tree with models
$\langle \mathcal {M}^{\mathcal {T}}_\alpha :\alpha <\mathrm {lh}(\mathcal {T})\rangle $
, embeddings
$i_{\alpha ,\beta }:\mathcal {M}^{\mathcal {T}}_\alpha \rightarrow \mathcal {M}^{\mathcal {T}}_\beta $
for
$\alpha <^{\mathcal {T}}\beta $
, and extender sequence
$\langle E_\alpha :\alpha +1<\mathrm {lh}(\mathcal {T})\rangle $
. If
$\mathcal {T}$
is normal then for
$\alpha <^{\mathcal {T}}\beta <^{\mathcal {T}}\gamma $
:
-
•
$\mathrm {cp}(i_{\alpha ,\beta })<\mathrm {cp}(i_{\beta ,\gamma })$
. -
• If
$\mathcal {M}^{\mathcal {T}}_\alpha \mid \lambda =\mathcal {M}^{\mathcal {T}}_\beta \mid \lambda $
, then
$\lambda <\mathrm {cp}(i_{\beta ,\gamma })$
. -
• If the extender E is applied to
$\mathcal {M}^{\mathcal {T}}_\alpha $
in the iteration tree, then
$\mathcal {M}^{\mathcal {T}}_\alpha \mid \mathrm {str}(E)=\mathcal {M}^{\mathcal {T}}_\beta \mid \mathrm {str}(E)$
, where
$\mathrm {str}(E)$
is the strength of E. Hence
$\mathrm {str}(E)<\mathrm {cp}(i_{\beta ,\gamma })$
.
When working with
$\mathrm {K}$
, it will be useful to know when an extender is on the sequence of
$\mathrm {K}$
, so we make use of the following lemma.
Lemma 2.4. Let E be a
$(\kappa ,\lambda )$
-extender with strength
$\lambda =\kappa +\delta $
such that
$(\kappa ^{+\delta })^{\mathrm {V}}$
is regular. Then:
-
1. For
$j:\mathrm {V}\rightarrow \mathrm {M}$
the canonical ultrapower map given by E, we have
, where
is the main branch of some normal iteration tree
$\mathcal {T}$
on
$\mathrm {K}$
with last model
$\mathrm {K}^{\mathrm {M}}$
. -
2.
$F=E\cap \mathrm {K}\in \mathrm {K}$
is on the sequence of
$\mathrm {K}$
and in fact,
$\mathrm {K}\vDash $
“F is a
$(\kappa ,\lambda )$
-extender with
$\mathrm {str}(F)=\lambda $
.” We can also factor
$j\upharpoonright \mathrm {K}=j_F\circ k_F$
where
$j_F:\mathrm {K}\rightarrow \operatorname {\mathrm {Ult}}_F(\mathrm {K})$
is the canonical ultrapower map and
$\operatorname {\mathrm {cp}}(k_F)>\lambda $
. -
3. Moreover, for each regular
$\mu <(\kappa ^{+\delta })^{\mathrm {V}}$
in
$\mathrm {K}$
, there is an extender
$F_\mu $
such that
$\mathrm {Ult}_{F_\mu }(\mathrm {K})$
and
$\mathrm {K}$
agree on
$\mathrm {H}_{\mu }$
.
Proof Let
$\mathrm {M}=\operatorname {\mathrm {Ult}}_E(\mathrm {V})$
so that
${}^\omega M\subseteq M$
. Let
$j:\mathrm {V}\rightarrow \mathrm {M}$
be the canonical ultrapower map. The hypotheses of [Reference Mitchell and Steel12] are satisfied and hence
$\mathrm {K}^{\mathrm {M}}$
(i.e.,
$j(\mathrm {K})$
) is an iterate of
$\mathrm {K}$
. Moreover
for some normal iteration tree
$\mathcal {T}$
on
$\mathrm {K}$
of successor length where
is the iteration map for the main branch of
$\mathcal {T}$
, and
$\mathcal {T}$
has last model
$\mathrm {K}^{\mathrm {M}}$
, giving (1). More explicitly, let
$\operatorname {\mathrm {lh}}(\mathcal {T})=\gamma +1$
. Let
$\xi $
be such that the
$\mathcal {T}$
-predecessor of
$\xi +1$
is
$0$
and
$\xi +1$
lies on the branch of
$\gamma $
. We have models
$\langle \mathcal {M}_\alpha ^{\mathcal {T}}:\alpha <\operatorname {\mathrm {lh}}(\mathcal {T})\rangle $
with extender sequence
$\langle E_\alpha :\alpha <\operatorname {\mathrm {lh}}(\mathcal {T})-1\rangle $
, iteration maps
$i_{\alpha ,\beta }:\mathcal {M}_\alpha ^{\mathcal {T}}\rightarrow \mathcal {M}_\beta ^{\mathcal {T}}$
for
$\alpha \le _{\mathcal {T}}\beta $
, and the following branch
$$\begin{align*}\mathrm{K}=\mathcal{M}_0^{\mathcal{T}}\rightarrow _{E_\xi }\mathcal{M}_{\xi+1}^{\mathcal{T}}\rightarrow \cdots \rightarrow \mathcal{M}_\gamma^{\mathcal{T}}=\mathrm{K}^{\mathrm{M}}\text{.}\end{align*}$$
We now show that
$E_\xi \upharpoonright \lambda =F$
. [Reference Mitchell and Steel12] tells us that
$i_{0,\gamma }=j\upharpoonright \mathrm {K}$
. Since
$\mathrm {V}\mid \lambda =\mathrm {M}\mid \lambda $
and
$\lambda =\kappa +\delta $
,
$\mathrm {H}_{\kappa ^{+\delta }}^{\mathrm {V}}=\mathrm {H}_{\kappa ^{+\delta }}^{\mathrm {M}}$
so by local definability from Lemma 2.2,
$\mathrm {K}^{\mathrm {M}}\cap \mathrm {H}_{\kappa ^{+\delta }}^{\mathrm {M}} = \mathrm {K}\cap \mathrm {H}_{\kappa ^{+\delta }}$
. It follows that
$\operatorname {\mathrm {str}}(E_\xi )\ge \lambda $
. By normality of
$\mathcal {T}$
, Result 2.3 tells us
$\operatorname {\mathrm {cp}}(i_{\xi +1,\gamma })>\operatorname {\mathrm {lh}}(E_\xi )\ge \lambda $
. So for any given
$\langle a,A\rangle \in [\lambda ]^{<\omega }\times \mathcal {P}([\kappa ]^{|a|})$
in
$\mathrm {K}$
,
$$ \begin{align*} \langle a,A\rangle \in F&\quad\text{iff}\quad a\in j(A)=i_{0,\gamma }(A)\\ &\quad\text{iff}\quad i_{\xi+1,\gamma }(a)\in i_{\xi+1,\gamma }(i_{0,\xi+1}(A))\\ &\quad\text{iff}\quad a\in i_{0,\xi+1}(A)\quad\text{iff}\quad \langle a,A\rangle \in E_\xi. \end{align*} $$
Hence
$E_\xi $
and F agree up to
$\lambda $
. By the initial segment condition,
$E_\xi \upharpoonright \lambda =F$
ensures F is on the sequence of
$\mathrm {K}$
. The strength of F being
$\lambda $
in
$\mathrm {K}$
follows from
$\mathrm {str}(E_\xi )\ge \lambda $
by Result 2.3. Moreover, restricting
$E_\xi $
appropriately yields
$F_\mu $
as in (3), with these in
$\mathrm {K}$
again by the initial segment condition.
We can show the factorization part of (2) from all of this. Firstly, let
$j_F:\mathrm {K}\rightarrow \operatorname {\mathrm {Ult}}_F(\mathrm {K})$
be the canonical embedding, and factor
$i_{0,\xi +1}=j_{F}\circ k_{F,\xi +1}$
in the usual way with
$k_{F,\xi +1}:\operatorname {\mathrm {Ult}}_F(\mathrm {K})\rightarrow \mathcal {M}_{\xi +1}$
, because we now know the
$(\kappa ,\lambda )$
-extender derived from
$i_{0,\xi +1}$
is F. Then we get
So
$k_F=k_{F,\xi +1}\circ i_{\xi +1,\gamma }$
gives the factorization for (2).
Simply put, if
$\kappa $
is
$\kappa +\delta $
-strong in
$\mathrm {V}$
, then
$\kappa $
is
$<\kappa ^{+\delta }$
-strong in
$\mathrm {K}$
according to the
$\mathrm {H}$
-hierarchy:
$\mathrm {K}\vDash $
“there are extenders
$F_\mu $
such that
$\mathrm {H}_\mu \in \operatorname {\mathrm {Ult}}_{F_\mu }(\mathrm {K})$
for each regular
$\mu <\kappa ^{+\delta }$
.”
In particular, any
$\kappa $
strong in
$\mathrm {V}$
is strong in
$\mathrm {K}$
: to get
$\kappa $
as
$\lambda $
-strong in
$\mathrm {K}$
, we just need a sufficiently large
$\mu $
such that
$\mathrm {K}\mid \lambda \subseteq \mathrm {H}_\mu ^{\mathrm {K}}$
. Then
$\kappa $
being
$\mu ^+$
-strong in
$\mathrm {V}$
implies being
$\lambda $
-strong in
$\mathrm {K}$
.
But we can actually say much more than
$\mathrm {V}$
-strongs being
$\mathrm {K}$
-strong assuming
$\mathsf {UWISS}$
: any cardinal
$\kappa $
that is
$\kappa +2$
-strong in
$\mathrm {V}$
will be strong in
$\mathrm {K}$
, as we will prove below. As a result, any
$\mathrm {V}$
-strong cardinal is a limit of
$\mathrm {K}$
-strong cardinals, for example. Indeed, we will show that any
$\mathrm {V}$
-strong cardinal is srs in
$\mathrm {K}$
. These ideas will be central for the (2) implies (1) direction of Theorem 1.2.
Theorem 2.5. (2) implies (1) where these stand for:
-
1.
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}+\textit{"}{\text {There is a proper class of strongs reflecting strongs}}\text {"});$
-
2.
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}+\textit{"}{\text {There is a proper class of strong cardinals}}\text {"}+\mathsf {UWISS})$
.
Proof We’re done if there is an inner model with a Woodin cardinal, so assume otherwise. Let
$ \mathrm {V}\vDash \mathsf {ZFC}+\mathsf {UWISS}$
have a proper class of strong cardinals. It will be useful to understand what cardinals are strong in the core model
$\mathrm {K}$
.
Claim 2.6. Suppose
$\kappa $
is
$\kappa +2$
-strong in
$\mathrm {V}$
. Then
$\kappa $
is strong in
$\mathrm {K}$
.
Proof Let
$\delta>\kappa ^+$
be arbitrarily large. Write
$\lambda =\beth _{\delta }^+\ge \delta $
. Consider
$\mathbb {P}=\mathrm {Col}(\kappa ^+,\lambda )$
. By indestructibility,
$\kappa $
is still
$\kappa +2$
-strong in
$\mathrm {V}^{\mathbb {P}}$
as witnessed by some
$(\kappa ,\kappa +2)$
-extender E and notice
$\lambda <(\lambda ^+)^{\mathrm {V}}=(\kappa ^{++})^{\mathrm {V}^{\mathbb {P}}}$
. By generic absoluteness,
$\mathrm {K}^{\mathrm {V}^{\mathbb {P}}}=\mathrm {K}^{\mathrm {V}}$
and so
$\lambda $
is regular in
$\mathrm {K}$
. By Lemma 2.4, there is an extender
$F=F_{\lambda }\in \mathrm {K}$
such that
$\mathrm {K}$
and
$\operatorname {\mathrm {Ult}}_F(\mathrm {K})$
agree on
$\mathrm {H}_{\lambda }$
. As
$\beth _\delta <\lambda $
is a strong limit in
$\mathrm {V}$
, this also holds in
$\mathrm {K}$
, so that
$\mathrm {K},\mathrm {Ult}_F(\mathrm {K})\vDash $
“
$\mathrm {H}_\lambda \supseteq \mathrm {V}_\delta $
.” This means
$\mathrm {K}\mid \delta =\mathrm {Ult}_{F}(\mathrm {K})\mid \delta $
so that
$\kappa $
is
$\delta $
-strong in
$\mathrm {K}$
.
We now aim to show any
$\kappa $
strong in
$\mathrm {V}$
is actually srs in
$\mathrm {K}$
. Let
$\kappa $
be strong in
$ \mathrm {V}$
and let the
$\lambda $
-strength of
$\kappa $
, for some strong
, be witnessed by a
$(\kappa ,\lambda )$
-extender
$E\in \mathrm {V}$
and embedding
$j_E:\mathrm {V}\rightarrow \operatorname {\mathrm {Ult}}_E(\mathrm {V})$
. Note that
$j_E$
restricts down to
$j_E\upharpoonright \mathrm {K}:\mathrm {K}\rightarrow \mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}$
. Consider
$F=E\cap \mathrm {K}$
which is in
$\mathrm {K}$
and on the
$\mathrm {K}$
-sequence by Lemma 2.4. So consider the resulting ultrapower
$\mathrm {Ult}_{F}(\mathrm {K})$
via
$j_{F}:\mathrm {K}\rightarrow \operatorname {\mathrm {Ult}}_{F}(\mathrm {K})$
which then factors
$j_E=k_F\circ j_F$
via
$k_{F}:\operatorname {\mathrm {Ult}}_{F}(\mathrm {K})\rightarrow \mathrm {K}^{\mathrm {Ult}_E( \mathrm {V})}$
as seen in Figure 1. This is due to (1) and (2) of Lemma 2.4.
Figure 1 Factoring ultrapower embeddings with
$\mathrm {K}$
.
Note that
$\operatorname {\mathrm {cp}}(k_{F})\ge \lambda $
so that for any cardinal
$\xi <\lambda $
,
$$\begin{align*}\mathrm{Ult}_{F}(\mathrm{K})\vDash "{\xi \text{ is strong}}\text{"}\quad\text{iff}\quad \mathrm{K}^{\mathrm{Ult}_E(\mathrm{V})}\vDash "{k_{F}(\xi )=\xi \text{ is strong.}}\text{"}\end{align*}$$
Thus it suffices to show
$\mathrm {K}$
and
$\mathrm {K}^{\operatorname {\mathrm {Ult}}_E(\mathrm {V})}$
agree on strongs below
$\lambda $
, because then all three would agree and so F would witness a
$\lambda $
-srs embedding for
$\kappa $
in
$\mathrm {K}$
. By local definability,
$\mathrm {K}\mid \lambda =\mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}\mid \lambda $
and hence we get that
$\mathrm {K}$
and
$\mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}$
agree on
$"{\xi \text { is }<\lambda \text {-strong}}\text {"}$
whenever
$\xi <\lambda $
. So it suffices to show
$$ \begin{align} \mathrm{K},\mathrm{K}^{\mathrm{Ult}_E(\mathrm{V})}\vDash "{\forall \xi<\lambda \ (\xi \text{ is }<\lambda \text{-strong}\rightarrow \xi \text{ is strong}).}\text{"} \end{align} $$
Since
$\lambda $
is strong (in
$\mathrm {V}$
),
$\lambda $
is a limit of cardinals
$\xi $
that are
$\xi +2$
-strong. By the strength of E, if
$\xi $
is
$\xi +2$
-strong in
$\mathrm {V}$
, then
$\xi $
is
$\xi +2$
-strong in
$\mathrm {Ult}_E(\mathrm {V})$
, and hence
$\lambda $
is a limit of cardinals
$\xi $
that are
$\xi +2$
-strong in
$\mathrm {Ult}_E(\mathrm {V})$
. So by Claim 2.6,
$\lambda $
is a limit of
$\mathrm {K}$
-strongs and
$\mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}$
-strongs. As a result, if
$\xi <\lambda $
is not
$\beta $
-strong in either
$\mathrm {K}$
or
$\mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}$
for some
$\beta $
, then by Lemma 1.11, this is reflected by some strong below
$\lambda $
in
$\mathrm {K}$
or
$\mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}$
, showing (
$*$
) holds. It follows that
$\mathrm {K}$
and
$\mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}$
agree on strongs below
$\lambda $
, and since
$\mathrm {K}^{\mathrm {Ult}_E(\mathrm {V})}$
and
$\mathrm {Ult}_F(\mathrm {K})$
agree on strongs below
$\lambda $
, we get that
$F\in \mathrm {K}$
witnesses that
$\kappa $
is
$\lambda $
-srs. A proper class of strongs in
$\mathrm {V}$
then gives a proper class of srs cardinals in
$\mathrm {K}$
.
3 The forcing direction
Now we show the harder direction of Theorem 1.2. We show we can force a proper class of strongs with
$\mathsf {UWISS}$
from a proper class of srs cardinals. The general idea behind the poset, as with most indestructibility results, is a trial by fire to kill all degrees of strength.
The result will be that the srs cardinals remain strong after forcing with the preparation, and small degrees of strength are, by virtue of surviving the trial by fire, weakly indestructible. We do not get universal indestructibility for all degrees of strength both because that’s impossible by Result 1.17 and because it’s possible for the tail poset to resurrect degrees of strength that were destroyed, something avoided in [Reference Apter and Hamkins2, Reference Apter and Sargsyan3] by cutting off the universe and declaring success anytime this might happen.
Our trial proceeds with appropriate posets via a lottery in an Easton iteration, that is to say direct limits are taken at (weakly) inaccessible stages and inverse limits elsewhere. What posets are appropriate? Well, the ones that destroy the strength of a cardinal
$\kappa $
and also are simultaneously
$<\kappa $
-strategically closed and
$\le \kappa $
-distributive, basically violating
$\mathsf {UWISS}$
.
Definition 3.1. For
$\delta $
a cardinal of strength
$\ge \rho $
, we say a poset
$\mathbb {Q}$
is
$\delta ,\rho $
-appropriate iff:
-
1.
$\mathbb {Q}$
is
$<\delta $
-strategically closed
$;$
-
2.
$\mathbb {Q}$
is
$\le \delta $
-distributive
$;$
and -
3.
$\mathbb {Q}$
destroys the
$\rho $
-strength of
$\delta $
.
If just (1) and (2) hold, we say
$\mathbb {Q}$
is
$\delta $
-appropriate.
So the destructibility of a cardinal
$\delta $
’s degree of strength
$\rho $
by a
$<\delta $
-strategically closed and
$\le \delta $
-distributive poset is obviously equivalent to the existence of a
$\delta ,\rho $
-appropriate poset. Hence we can restate
$\mathsf {UWISS}$
as the lack of any
$\delta ,\delta +2$
-appropriate posets for any
$\delta $
. We will show that the existence of appropriate posets is equivalent to the existence of “small” appropriate posets, basically meaning that we can bound the rank of
$\mathbb {Q}$
and
$\rho $
by
.
In examining Definition 3.1, we have the following easy, useful result.
Corollary 3.2. Let
$\mathbb {P}\in \mathrm {V}\mid \alpha $
be a poset. Then:
-
•
$\mathbb {P}$
is
$\delta ,\rho $
-appropriate iff for some (any) strong limit
$\lambda \ge |\alpha +\rho |^+$
,
$\mathrm {V}\mid {\lambda }\mathrel {\vDash }$
“
$\mathbb {P}$
is
$\delta ,\rho $
-appropriate.” -
• For
$\dot {\mathbb {Q}}$
a
$\mathbb {P}$
-name for a poset,
$\mathbb {P}\Vdash \textit{"}{\mathbb {Q}\text { is }\check \delta ,\check \rho \text {-appropriate with rank }\check \beta }\text {"}$
iff
$\mathrm {V}\mid \lambda $
satisfies this for strong limit
$\lambda \ge |\max (\alpha ,\rho ,\beta )|^+$
.
Proof It suffices to show the second since the first follows from it in the case that
$\mathbb {P}$
is trivial. Let
$\kappa =|\max (\alpha ,\rho ,\beta )|^+$
.
$\mathbb {Q}$
is forced to be a subset of
$(\mathrm {V}\mid \beta )^{\mathbb {P}}$
. So without loss of generality,
$\dot {\mathbb {Q}}$
is a nice
$\mathbb {P}$
-name for a subset of
$(\mathrm {V}\mid \beta )^{\mathbb {P}}$
which therefore has rank
$<\kappa $
.
$<\delta $
-strategic closure and
$\delta $
-distributivity only make claims about
$\mathcal {P}(\mathcal {P}(\mathbb {Q}))$
. Nice names again mean that we only need access to
$\mathbb {P}$
-names of rank
$<\kappa $
, meaning these concepts are absolute between
$\mathrm {V}$
and
$\mathrm {V}\mid \lambda $
for
$\lambda \ge \kappa $
. So the remaining concepts we need absoluteness for are related to the (non)-existence of extenders and inaccessibles: we need
$$\begin{align*}\mathbb{P}\Vdash "{\dot{\mathbb{Q}}\Vdash `{\check \delta \text{ is no longer }\check \rho \text{-strong}}\text{'}}.\text{"}\end{align*}$$
Working in
$\mathrm {V}^{\mathbb {P}}$
, for
$\lambda>\kappa $
a strong limit, if
$\rho '<\lambda $
, then nice
$\mathbb {Q}$
-names for
$(\delta ,\rho ')$
-extenders will have rank
$<\rho '+\beta +\omega <\lambda $
. So in
$\mathrm {V}$
, we only need to consider nice names for subsets of
$(\mathrm {V}\mid {\rho +\beta +\omega })^{\mathbb {P}}$
, which all have rank
$<\lambda $
.
The search for a
$\delta ,\rho $
-appropriate poset—equivalently the weak destructibility of
$\delta $
’s strength—can be bounded in the presence of lots of strong cardinals: if there is some
$\delta ,\rho $
-appropriate poset, then we can choose
$\rho $
and the rank of the poset to be less than
just as in [Reference Apter and Sargsyan3]. This isn’t too difficult to show, and helps us in defining our forcing preparation later.
Lemma 3.3. Let
$\delta \in \mathrm {Ord}$
. Let
$\mathbb {R}\in \mathrm {V}\mid \alpha $
be a poset. Suppose there’s a
$\delta ,\rho ^{**}$
-appropriate
$\mathbb {Q}^{**}\in \mathrm {V}^{\mathbb {R}}$
. Then, there’s a
$\delta ,\rho $
-appropriate
where
and
$\rho \le \rho ^{**}$
.
Proof Let
$\mathbb {Q}^{**}$
have rank greater than
in
$ \mathrm {V}^{\mathbb {R}}$
. Corollary 3.2 tells us for sufficiently large
$\lambda $
,
$\mathbb {Q}^{**}$
is
$\delta ,\rho ^{**}$
-appropriate in
$\mathrm {V}^{\mathbb {R}}\mid \lambda $
. More precisely, we get a name
$\dot {\mathbb {Q}}^{**}\in \mathrm {V}\mid \lambda $
such that
$$\begin{align*}\mathrm{V}\mid \lambda \vDash "{\mathbb{R}\Vdash `{\dot{\mathbb{Q}}^{**}\text{ is }\check\delta ,\check\rho^{**}\text{-appropriate}}\text{'}}.\text{"}\end{align*}$$
Let
$j:\mathrm {V}\rightarrow \mathrm {M}$
witness the
$\lambda $
-strength of
$\gamma $
in
$ \mathrm {V}$
. It follows that
$$\begin{align*}\mathrm{V}\mid \lambda =\mathrm{M}\mid \lambda \vDash "{\mathbb{R}\Vdash `{\dot{\mathbb{Q}}^{**}\text{ is }\check{\delta },\check{\rho }^{**}\text{-appropriate}}\text{'}}.\text{"}\end{align*}$$
Since
$\rho ^{**}$
and the rank of
$\mathbb {Q}^{**}$
are below
$\lambda \le j(\gamma )$
,
$\mathrm {M}$
believes there’s an
$\mathbb {R}$
-name for a poset
$\dot {\mathbb {Q}}^*$
in
$\mathrm {M}\mid {j(\gamma )}$
that is
$\delta ,\rho ^*$
-appropriate for some
$\rho ^*<j(\gamma )$
and in particular,
$\rho ^*=\rho ^{**}\le j(\rho ^{**})$
. Elementarity then gives a name
$\dot {\mathbb {Q}}$
for a
$\delta ,\rho $
-appropriate poset in
$\mathrm {V}\mid \gamma $
with
$\rho <\gamma $
and
$\rho \le \rho ^{**}$
. The rank of this poset in
$ \mathrm {V}^{\mathbb {R}}$
is therefore below
$\gamma $
.
In particular, if
then
$\dot {\mathbb {Q}}$
will have rank
.
3.1 Forcing UWISS
We now attempt to prove the following, one of the directions from Theorem 1.2.
Theorem 3.4. (1) implies (2) where these stand for:
-
1.
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}\mathrel {+}$
“There is a proper class of srs cardinals”). -
2.
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}\mathrel {+}$
“There is a proper class of strongs”
$\mathrel {+}\mathsf {UWISS})$
.
Suppose
$ \mathrm {V}\vDash \mathsf {ZFC}+"{\text {there is a proper class of srs cardinals.}}\text {"}$
Without loss of generality, also assume that
$ \mathrm {V}\vDash \mathsf {GCH}$
.Footnote
3
The basic idea is a trial by fire where anything that emerges with some degree of strength should have its degree of strength weakly indestructible. A slight hiccup with this is that we don’t actually have much control over what the resulting strength is, so rather than all of its degrees of strength being weakly indestructible, just degrees smaller than the next stage of forcing are. A broad outline of the proof is as follows. Here
$\mathbb {P}$
is the whole preparation.
-
i. Show that if
$\kappa $
is
$\kappa +2$
-strong in
$\mathrm {V}^{\mathbb {P}}$
, then this is weakly indestructible, showing
$\mathrm {V}^{\mathbb {P}}\vDash \mathsf {UWISS}$
, proved with Result 3.10. -
ii. Show that if
$\kappa $
is
$\lambda $
-srs for
$\lambda $
a limit of strongs in
$\mathrm {V}$
then
$\kappa $
is
$\lambda $
-strong in
$\mathrm {V}^{\mathbb {P}}$
, implying that any
$\mathrm {V}$
-srs cardinal is
$\mathrm {V}^{\mathbb {P}}$
-strong, and there is a proper class of both, proved with Lemma 3.13.
A necessary consequence of Corollary 1.20, given that we force
$\mathsf {UWISS}$
for cardinals below
$\kappa $
by stage
$\kappa $
, is that an srs cardinal
$\kappa $
will have its strength destroyed by
$\mathbb {P}_{\kappa +1}$
, but will nevertheless have its
$\lambda $
-strength resurrected by stage
$\lambda $
(whenever
$\lambda $
is a limit of strongs).
More generally, showing that degrees of strength aren’t resurrected is not as simple a task as it might seem, and disregarding Result 1.17, this is partly why we can’t use this preparation to get indestructible strength for large strengths. Let me describe the situation in a little more detail to show what goes wrong. The basic idea is that these cardinals are not going through this “trial by fire” alone, and a later cardinal can act like a medic.
Naïvely, one will proceed destroying as much strength as possible: if
$\kappa $
is
$\rho $
-strong in
$\mathrm {V}^{\mathbb {P}_\kappa }$
, we try to destroy this with
$\kappa $
-appropriate posets if we can, and this constitutes the forcing done at stage
$\kappa $
. If we destroy
$\kappa $
’s strength down to be
$<\rho $
, but some non-trivial forcing is done at stage
$\delta <\rho $
, we might accidentally resurrect
$\kappa $
’s
$\rho $
-strength, as below with Figure 2.
Figure 2 Interaction resurrecting strength.
Moreover, there is a problem if a cardinal’s strength is merely playing dead. For suppose
$\kappa $
is
$\lambda $
-strong in
$\mathrm {V}$
. As we approach
$\kappa $
,
$\kappa $
might reduce its strength so that
$\kappa $
is merely
$\rho $
-strong in
$\mathrm {V}^{\mathbb {P}_\kappa }$
and weakly indestructible there. In that case, we would do nothing, for we don’t see any strength to destroy. But then, it may be that
$\rho $
is large enough that the next non-trivial stage of forcing occurs at some
$\delta <\rho $
, in which case,
$\kappa $
might “wake up” and we accidentally resurrect
$\kappa $
’s
$\lambda $
-strength. Because we never think to return to previously dealt with stages,
$\kappa $
might remain
$\lambda $
strong in
$\mathrm {V}^{\mathbb {P}}$
but not be weakly indestructible.
Any attempted solution to this will ultimately either result in no resulting large strength or further forcing that might again resurrect strength by Result 1.17. For example, we might try to collapse destroyed degrees of strength below the next stage of forcing. This is due to the general fact that if
$\kappa $
’s strength is
$\rho <\kappa ^{+\sharp \sharp }$
, then the subsequent stages won’t resurrect degrees of strength by distributivity of the tail forcing proven with Corollary 3.8, expressed with Figure 3.
Figure 3 Non-interaction leaving strength destroyed.
The forcing at
$\kappa ^{+\sharp \sharp }$
shouldn’t affect smaller degrees of strength by distributivity. But the collapse we’re considering done at stage
$\kappa $
could then resurrect degrees of strength. So this gives the following result, the proof of which is given later with Result 3.21.
Result 3.5. It’s consistent (relative to two srs cardinals and proper class of strong cardinals) that we can force a
$\kappa $
that is not
$\rho $
-strong to be
$\rho $
-strong by a collapse
$\mathrm {Col}(\kappa ^+,\rho )$
.
This problem isn’t an issue when we only care about finding one strong or supercompact cardinal with indestructibility properties: if we ever have a measurable between a cardinal and its remaining strength, we could have just cut off the universe and end up in the desired model; no need to deal with the resurrection. This is essentially the argument given in [Reference Apter and Hamkins2, Reference Apter and Sargsyan3]. Unfortunately for us, we can’t just stop our preparation and declare success, and this is partially why resurrected degrees of strength remain a fact of life.
Our partial ordering is a modification of the one used in the proof of [Reference Apter and Sargsyan3, Theorem 3]. Specifically, we define an iteration (of proper class length)
which begins by adding a Cohen subset of
$\omega $
to make use of gap forcing arguments. All other nontrivial stages of forcing can only occur at inaccessible
$\delta $
that are
$\delta +2$
-strong in
$\mathrm {V}$
.
Definition 3.6 (The preparation).
Define
$\mathbb {P}_{\omega +1}=\mathrm {Add}(\omega ,1)$
. Suppose
has been defined for
$\delta>\omega $
. We aim to define
$\dot {\mathbb {Q}}_\delta $
.
-
1. If no
$p\in \mathbb {P}_\delta $
forces that
$\delta $
is inaccessible, then
$\dot {\mathbb {Q}}_\delta =\dot {\textbf {1}}$
is trivial. -
2. Otherwise, suppose
$\delta $
is forced by some
$p\in \mathbb {P}_\delta $
to be
$<\lambda $
-strong for some (maximal)
$\lambda $
(allowing
$\lambda =\mathrm {Ord}$
if strong), and work below p.-
(a) If the
$<\lambda $
-strength of
$\delta $
is weakly indestructible via posets of rank
, then define
$\dot {\mathbb {Q}}_\delta =\dot {\textbf {1}}$
. -
(b) Otherwise, we let
$\rho <\lambda $
be the minimal degree of
$\delta $
’s strength that is weakly destructible and let
$\dot {\mathbb {Q}}_\delta $
be the lottery sum of all (what are forced to be) posets that take the form
$\dot {\mathbb {B}}*\dot {\mathbb {C}}$
where the following happen. -
(c)
$\dot {\mathbb {B}}$
is a
$\delta ,\rho $
-appropriate poset of rank
. -
(d) In
$\mathrm {V}^{\mathbb {P}_\delta *\dot {\mathbb {B}}}$
, if
$\rho <\delta ^{+\sharp \sharp }\le |\dot {\mathbb {B}}|$
, then
$\dot {\mathbb {C}}$
is a name for
$\mathrm {Col}(\rho ^{+\sharp },|\dot {\mathbb {B}}|)$
. If
$\delta ^{+\sharp \sharp }\le \rho ,|\dot {\mathbb {B}}|$
then
$\dot {\mathbb {C}}$
is a name for
$\mathrm {Col}(\delta ^{+\sharp },|\dot {\mathbb {B}}|)$
. Otherwise
$\dot {\mathbb {C}}$
is trivial.
-
Using Easton support for limit stages, we write
for the class iteration and
for the tail forcing of
$\mathbb {P}_\lambda $
whenever
$\delta <\lambda $
.
Some remarks about this preparation: note that we can then factor
$\mathbb {P}_{\omega +1}*\mathbb {R}_{(\omega +1,\delta )}$
and this admits a gap at
$\aleph _1$
. So it satisfies the hypothesis for the Gap Forcing Theorem [Reference Hamkins6]: for any elementary embedding
$j:\mathrm {V}^{\mathbb {P}_\delta }\rightarrow \mathrm {M}^{j(\mathbb {P}_\delta )}$
, we get
$j\upharpoonright \mathrm {V}:\mathrm {V}\rightarrow \mathrm {M}$
as a class of
$\mathrm {V}$
, meaning we don’t add any strength to any cardinal.
The preparation also only acts on
$\delta $
that are
$\delta +2$
-strong. So for any
$\kappa $
, the next non-trivial stage of forcing should be at least
$\kappa ^{+\sharp \sharp }$
, and this is made precise with Lemma 3.9.
Note that each
$\dot {\mathbb {Q}}_\delta $
is
$\delta ,\rho $
-appropriate for some
$\rho $
whenever it’s non-trivial. Secondly, it’s not hard to see that we can regard
for any
$\delta $
. In fact, we can regard
$\mathbb {P}_\delta \subseteq \mathrm {V}\mid \delta $
whenever
$\dot {\mathbb {Q}}_\delta $
is non-trivial, since
$\delta $
is therefore inaccessible and not collapsed by any previous stage, meaning every previous stage had a smaller cardinality and thus smaller rank.
The collapsing poset used for each poset in the lottery is used to give better control over the tail forcing, and in particular to show
$\mathbb {P}_{\delta }$
is
$\delta $
-cc whenever
$\delta $
is still inaccessible there. Moreover, the collapse allows us to ensure that once we collapse a small degree of strength with a small poset, the strength stays collapsed and won’t be resurrected. Larger degrees, however, can be resurrected.
There are several standard facts of tail forcings we need to use in order to prove that the tail forcings of the preparation are strategically closed. The use of this will be in showing that
$\dot {\mathbb {R}}_{[\delta ,\lambda )}$
is
$\delta $
-appropriate and thus can be used in arguments with
$\delta ,\rho $
-appropriate posets since it is close to being one. One background result used is the following [Reference Cummings, Foreman and Kanamori4, Theorem 7.12].
Theorem 3.7. Let
be a
$\lambda $
-stage iteration such that for some
$\delta <\lambda $
and some
$\mu $
:
-
1. inverse limits or direct limits are taken at every limit stage
$;$
-
2. inverse limits are taken at every limit stage
$\ge \delta $
of cofinality
$<\mu ;$
-
3.
$\dot {\mathbb {Q}}_\xi '$
is (forced to be)
$<\mu $
-strategically closed for every
$\xi $
with
$\delta \le \xi <\lambda ;$
and -
4.
$\mathbb {P}_\delta '$
is
$\mu $
-cc.
Then the tail forcing
$\dot {\mathbb {R}}_{[\delta ,\lambda )}$
is (forced to be)
$<\mu $
-strategically closed.
Corollary 3.8. Let
$\delta <\lambda $
. Then, the tail forcing of our preparation,
$\dot {\mathbb {R}}_{[\delta ,\lambda )}$
is (forced to be)
$<\delta $
-strategically closed and
$\le \delta $
-distributive.
Proof If
$\dot {\mathbb {Q}}_\delta $
is non-trivial, then below the appropriate conditions,
$\delta $
is inaccessible in
$\mathrm {V}^{\mathbb {P}_\delta }$
so we take a direct limit at stage
$\delta $
. It follows that
$\delta $
was not collapsed at some previous stage by a
$\kappa ,\rho $
-appropriate poset
$\mathbb {Q}$
where
$\kappa <\delta \le \max (\rho ,|\mathbb {Q}|)$
. So for each
$\kappa <\delta $
,
$\dot {\mathbb {Q}}_\kappa $
is equivalent to a poset with rank
$<\delta $
and in fact we can regard
$\mathbb {P}_\delta \subseteq \mathrm {V}\mid \delta $
and so
$\mathbb {P}_\delta $
is
$\delta $
-cc. Using Theorem 3.7, Easton support iterations clearly take inverse or direct limits everywhere, and only direct limits at certain regular stages. So at any
$\xi \ge \delta>\operatorname {\mathrm {cof}}(\xi )$
, we take an inverse limit. Thus (1) and (2) hold from Theorem 3.7. By hypothesis, (3) holds since lottery sums of
$<\kappa $
-strategically closed posets are
$<\kappa $
-strategically closed. (4) holds since
$\mathbb {P}_\delta $
is
$\delta $
-cc and thus
$\dot {\mathbb {R}}_{[\delta ,\lambda )}$
is
$<\delta $
-strategically closed.
If
$\dot {\mathbb {Q}}_\delta $
is trivial, then below the appropriate conditions, the next non-trivial stage (if there is one)
$\dot {\mathbb {Q}}_\mu $
has by the above argument that
$\dot {\mathbb {R}}_{[\mu ,\lambda )}\cong \dot {\mathbb {R}}_{[\delta ,\lambda )}$
is
$<\mu $
-strategically closed and hence
$<\delta $
-strategically closed. If there is no non-trivial stage above
$\delta $
, then the tail forcing is trivial and hence
$<\delta $
-strategically closed.
For
$\le \delta $
-distributivity, note that
$\dot {\mathbb {R}}_{[\delta ,\lambda )}\cong \dot {\mathbb {Q}}_\delta *\dot {\mathbb {R}}_{(\delta ,\lambda )}$
is the two-step iteration of two
$\le \delta $
-distributive posets.
Given that measurability is already indestructible by Corollary 1.9, the next non-trivial stage of forcing after
$\delta $
occurs at stage
$\delta ^{+\sharp \sharp }$
at the earliest.
Lemma 3.9. The first non-trivial stage of forcing after any
$\kappa \in \mathrm {Ord}$
is at least
$(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
.
Proof To have any degree of
$\delta $
’s strength weakly destructible over
$\mathrm {V}^{\mathbb {P}_\delta }$
, we require
$\delta $
to be at least
$\delta +2$
-strong. Hence the least
$\delta $
such that
$\mathbb {P}_{\delta }\cong \mathbb {P}_{\kappa +1}$
but
$\dot {\mathbb {Q}}_\delta $
is non-trivial must have that
$\delta $
is
$\delta +2$
-strong in
$\mathrm {V}^{\mathbb {P}_\delta }=\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
and hence
$\delta \ge (\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
.
Hence all the degrees of
$\kappa $
’s strength below
$(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
remain indestructible even if larger degrees are accidentally resurrected. The basic proof of this is that if we could destroy something, we would have destroyed it already.
Result 3.10. Let
$\kappa $
be such that
$\mathbb {P}_\kappa $
and
$\mathbb {P}_{\kappa +1}\Vdash $
“
$\check \kappa $
is
$\check \rho $
-strong for
$\check \rho <\kappa ^{+\sharp \sharp }$
.” Then
$\mathbb {P}\Vdash $
“
$\check \kappa $
’s
$\rho $
-strength is weakly indestructible.”
Proof By downward absoluteness, in
$\mathrm {V}^{\mathbb {P}_{\kappa }}$
,
$\kappa $
is still inaccessible. Hence we are in case (2) of Definition 3.6. As a poset of size
and by gap forcing [Reference Hamkins6],
$\kappa ^{+\sharp }$
,
$\kappa ^{+\sharp \sharp }$
, and
are all the same in
$\mathrm {V}$
and
$\mathrm {V}^{\mathbb {P}_\kappa }$
. (Such cardinals retain their large cardinal status by small forcing, and no new such cardinals are added above
$\aleph _1$
by [Reference Hamkins6].)
As a result, because
$\rho <\kappa ^{+\sharp \sharp }$
in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
, the tail forcing after
$\kappa $
is sufficiently distributive such that the
$\rho $
-strong extender on
$\kappa $
in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
is still
$\rho $
-strong in
$\mathrm {V}^{\mathbb {P}}$
. Thus it suffices to show weak indestructibility for this degree of strength. So suppose
$\dot {\mathbb {Q}}$
is
$\kappa ,\rho $
-appropriate in
$\mathrm {V}^{\mathbb {P}}$
. By distributivity of the tail forcing,
$\dot {\mathbb {Q}}\in \mathrm {V}^{\mathbb {P}_\lambda }$
for some
$\lambda>\kappa $
. The tail forcing
$\dot {\mathbb {R}}_{(\kappa ,\lambda )}$
is therefore
$\kappa $
-appropriate by Corollary 3.8.
This tells us that
$\dot {\mathbb {Q}}_\kappa $
must be non-trivial. To see this, otherwise
$\kappa $
must be
$\rho $
-strong in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}=\mathrm {V}^{\mathbb {P}_\kappa }$
. It follows that
$\dot {\mathbb {R}}_{[\kappa ,\lambda )}*\dot {\mathbb {Q}}$
is
$\kappa ,\rho $
-appropriate in
$\mathrm {V}^{\mathbb {P}_\kappa }$
so that by Lemma 3.3, we can find a
$\kappa ,\rho $
-appropriate poset of small size and so
$\dot {\mathbb {Q}}_\kappa $
should be non-trivial, a contradiction.
Since
$\dot {\mathbb {Q}}_\kappa $
is non-trivial, by Definition 3.6, we forced with some poset
$\dot {\mathbb {B}}*\dot {\mathbb {C}}$
at stage
$\kappa $
where
$\dot {\mathbb {B}}$
is
$\kappa ,\rho _\kappa $
-appropriate in
$\mathrm {V}^{\mathbb {P}_\kappa }$
with minimal
$\rho _\kappa $
. If
$\rho <\rho _\kappa $
, the
$\kappa ,\rho $
-appropriate
$\dot {\mathbb {R}}_{[\kappa ,\lambda )}*\dot {\mathbb {Q}}$
would violate minimality of
$\rho _\kappa $
(via Lemma 3.3 to ensure we stay below
in
$\mathrm {V}^{\mathbb {P}_{\kappa }}$
). So
$\rho \ge \rho _\kappa $
. We now break into cases.
-
• Suppose
$\dot {\mathbb {C}}$
is non-trivial. Thus
$\rho _\kappa <\kappa ^{+\sharp \sharp }\le |\dot {\mathbb {B}}|$
and
$\dot {\mathbb {C}}$
collapses
$|\dot {\mathbb {B}}|$
to be
$\rho _\kappa ^{+\sharp }$
(which is
$<\kappa ^{+\sharp \sharp }$
) in a way that is
$<\rho _\kappa ^{+\sharp }$
-distributive. In particular, this preserves the lack of
$\rho _\kappa $
-strong extenders, and so the lack of
$\rho $
-strong extenders in
$\mathrm {V}^{\mathbb {P}_\kappa *\dot {\mathbb {B}}}$
to
$\mathrm {V}^{\mathbb {P}_\kappa *\dot {\mathbb {B}}*\dot {\mathbb {C}}}$
, contradicting that
$\kappa $
is
$\rho $
-strong in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
-
• Suppose
$\dot {\mathbb {C}}$
is trivial so that because
$\dot {\mathbb {B}}$
is
$\kappa ,\rho _\kappa $
-appropriate,
$\kappa $
is not
$\rho _\kappa $
-strong in
$\mathrm {V}^{\mathbb {P}_{\kappa }*\dot {\mathbb {B}}}=\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
and hence not
$\rho $
-strong there, a contradiction.
Unfortunately, this does not guarantee weak indestructibility for
$\kappa $
’s degrees of strength
$<\kappa ^{+\sharp \sharp }$
in
$\mathrm {V}^{\mathbb {P}}$
, but merely for strength
$<(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
and so in particular
$\kappa +2$
-strength,
$\kappa ^{+\sharp }$
-strength, and
$<\lambda $
-strength for the first
$\lambda $
a measurable limit of measurables in
$\mathrm {V}^{\mathbb {P}}$
.
Corollary 3.11 (Forcing
$\mathsf {UWISS}$
).
Suppose
$\mathrm {V}\vDash $
“there is a proper class of strongs.” Then:
-
• The preparation
$\mathbb {P}$
is well defined and
$\mathbb {P}\Vdash \mathsf {UWISS}$
. -
• In fact, if
$\kappa $
is
$\rho $
-strong for
$\rho <(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
in
$\mathrm {V}^{\mathbb {P}}$
then this strength is weakly indestructible in
$\mathrm {V}^{\mathbb {P}}$
. -
• In particular, any cardinal
$\kappa $
’s strength that is below the least measurable limit of measurables above
$\kappa $
is weakly indestructible, e.g.,
$\kappa +2$
-strength,
$\kappa ^{+\sharp }$
-strength,
$(\kappa ^{+\sharp })^{+\sharp }$
-strength, etc.
Proof Let
$\gamma =(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
. Then the tail poset
$\mathbb {R}_{[\gamma ,\infty )}$
is
$\le \gamma $
-distributive. So for
$\rho <\gamma $
, any extender witnessing
$\kappa $
’s
$\rho $
-strength in
$\mathrm {V}^{\mathbb {P}}$
is in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
, and this is weakly indestructible by Result 3.10.
We may not get better than this, since we could have the following: in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
,
$\kappa $
is
$\rho $
-strong for
$\rho>\kappa ^{+\sharp \sharp }$
. Then at stage
$\mu =(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
we do some non-trivial forcing that destroys
$\mu $
’s
$\mu +2$
-strength, and subsequently resurrects
$\kappa $
’s
$\rho '$
-strength for
$\rho '>\mu $
in a way that the new
$(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\mu }}}>\rho '$
but
$\kappa $
’s
$\rho '$
-strength is now destructible. Nevertheless, this doesn’t affect degrees of strength below
$(\kappa ^{+\sharp \sharp })^{\mathrm {V}^{\mathbb {P}_{\kappa +1}}}$
as the above shows.
3.2 A proper class of strongs
So all that remains is to show that srs cardinals of
$\mathrm {V}$
are strong in
$\mathrm {V}^{\mathbb {P}}$
. We do this by working with partial degrees of reflecting strongs. The usefulness of reflecting strongs allows us to properly calculate the preparation up to limits of strongs.
Lemma 3.12. Let
$\lambda $
be a limit of strongs. Let
$j:\mathrm {V}\rightarrow \mathrm {M}$
be at least
$\lambda $
-strong such that
$\mathrm {V}$
and
$\mathrm {M}$
agree on strongs
$<\lambda $
. Then
$\mathbb {P}_{\lambda }^{ \mathrm {V}}=j(\mathbb {P})_{\lambda }=\mathbb {P}^{\mathrm {M}}_{\lambda }$
.
Proof Let
$\kappa =\operatorname {\mathrm {cp}}(j)$
. j will not affect the Easton support below
$\lambda $
, so it suffices to show
$\dot {\mathbb {Q}}_\delta ^{\mathrm {V}}=\dot {\mathbb {Q}}_\delta ^{\mathrm {M}}$
for all cardinals
$\delta <\lambda $
. Proceed by induction on
$\delta $
. In case (1) of Definition 3.6,
$\delta $
’s non-inaccessibility is easily absolute between
$\mathrm {V}$
and
$\mathrm {M}$
since inductively
$\mathbb {P}_\delta =\mathbb {P}_\delta ^{\mathrm {M}}$
.
Note that since
$\lambda $
is a limit of strongs and
$\mathrm {V}$
,
$\mathrm {M}$
agree on strongs
$<\lambda $
, if
$\delta <\lambda $
, then
and so we can unambiguously write
in such cases. Note also if
$\delta $
is
$<\lambda _0$
-strong in
$\mathrm {V}$
, then either
implies
$\delta $
is strong in both since the models agree on strongs below
$\lambda $
, or else
and so the lack of
$\lambda _0$
-strong extenders in
$\mathrm {V}\mid \lambda $
matches with
$\mathrm {M}\mid \lambda $
. Note also that all (names for) collapses we consider will exist in
and thus have the same interpretation in both models.
In case (2), by Corollary 3.2, the existence of
and a
$<\delta $
-strategically closed,
$\le \delta $
-distributive
such that
$\delta $
isn’t
$\rho $
-strong after forcing with
$\mathbb {P}_\delta *\dot {\mathbb {B}}$
can be calculated in
$\mathrm {V}\mid \lambda =\mathrm {M}\mid \lambda $
. Hence the two share the same such posets, and moreover, the minimal
$\rho $
witnessing this is the same for both. The calculation of
$\delta ^{+\sharp \sharp }$
in both will be below
and easily the same in both models. The collapse (also being below
) will also be the same, meaning
$\dot {\mathbb {Q}}_\delta $
is the same in both.
In particular, if
$j:\mathrm {V}\rightarrow \mathrm {M}$
is a
$\lambda $
-srs embedding, then
$\mathbb {P}_{\lambda }^{\mathrm {V}}=\mathbb {P}_{\lambda }^{\mathrm {M}}$
whenever
$\lambda $
is a limit of strongs. This gives us the edge over hyperstrength in generalizing [Reference Apter and Sargsyan3] which generally only gets agreement for
$\mathbb {P}_{\operatorname {\mathrm {cp}}(j)}$
, but the resulting argument is adapted from [Reference Apter and Sargsyan3].
Lemma 3.13. Let
$\kappa $
be strong and
$\lambda $
-srs where
$\lambda $
is a limit of strongs. Then
$\mathbb {P}_\lambda \Vdash $
“
$\kappa $
is
$\lambda $
-strong.”
Proof Let
$j:\mathrm {V}\rightarrow \mathrm {M}$
be
$\lambda $
-srs with
$\operatorname {\mathrm {cp}}(j)=\kappa $
so that
$\mathrm {M}=\operatorname {\mathrm {Ult}}_E(\mathrm {V})$
for some
$(\kappa ,\lambda )$
-extender E. We can factor by Lemma 3.12
$$ \begin{align*} j(\mathbb{P}_{\lambda })=\mathbb{P}_{j(\lambda )}^{\mathrm{M}}&\cong\mathbb{P}_\lambda^{\mathrm{M}}*\dot{\mathbb{R}}_{[\lambda ,j(\kappa ))}^{\mathrm{M}}*\dot{\mathbb{R}}_{[j(\kappa ),j(\lambda ))}^{\mathrm{M}}\\ &\cong \mathbb{P}_\lambda^{\mathrm{V}}*\dot{\mathbb{R}}_{[\lambda ,j(\kappa ))}^{\mathrm{M}}*\dot{\mathbb{R}}_{[j(\kappa ),j(\lambda ))}^{\mathrm{M}}\text{.} \end{align*} $$
Without loss of generality,
$\lambda $
isn’t
$\lambda +2$
-strong in
$\mathrm {M}$
(otherwise just taking another ultrapower by the Mitchell-least measure on
$\lambda $
) so that in
$\mathrm {M}^{\mathbb {P}_\lambda }$
,
$\lambda $
is at most measurable with therefore indestructible degrees of strength and its original strength already small:
$\dot {\mathbb {Q}}_\lambda ^{\mathrm {M}}=\dot {\textbf {1}}$
. Thus
$\dot {\mathbb {R}}_{[\lambda ,j(\lambda ))}^{\mathrm {M}}$
is actually
$\lambda ^+$
-strategically closed in
$\mathrm {M}$
(and indeed much more).
So let
$G=G_0*G_1$
be
$\mathbb {P}_\kappa *\dot {\mathbb {R}}_{[\kappa ,\lambda )}$
-generic over
$\mathrm {V}$
such that
$\mathrm {V}[G]\vDash $
“
$\kappa $
is not
$\lambda $
-strong.” Our goal is to lift j to
$j^+:\mathrm {V}[G]\rightarrow \mathrm {M}[G*H]$
in
$\mathrm {V}[G]$
for some
$H=H_0*H_1\in \mathrm {V}[G]$
that is
$(\dot {\mathbb {R}}_{[\lambda ,j(\kappa ))}^{\mathrm {M}}*\dot {\mathbb {R}}_{[j(\kappa ),j(\lambda ))}^{\mathrm {M}})_G$
-generic over
$\mathrm {M}[G]$
such that
$j^+$
remains
$\lambda $
-strong. This requires examining
$j"G$
, and beyond this there are only a couple steps in this lift-up argument: first building
$H_0$
arbitrarily and then generating
$H_1$
from
$j"G_1$
.
Claim 3.14. For
$j(p)\in j"G$
,
$j(p)\upharpoonright [\lambda ,j(\kappa ))$
—and in fact
$j(p)\upharpoonright [\kappa ,j(\kappa ))$
—is trivial. Hence the only non-trivial information
$j"G$
encodes occurs before
$\lambda $
and after
$j(\kappa )$
.
Proof Let
$p\in G$
be arbitrary. Since we take a direct limit at stage
$\kappa $
, there is some
$\alpha <\kappa $
where
$p\upharpoonright [\alpha ,\kappa )$
is just a sequence of
$\dot {\textbf {1}}$
s:
$p\upharpoonright [\alpha ,\kappa )$
is trivial in
$\dot {\mathbb {R}}_{[\alpha ,\kappa )}$
. By elementarity,
$j(p)$
is similarly trivial from
$j(\alpha )=\alpha <\kappa $
to
$j(\kappa )$
. In particular,
$j(p)\upharpoonright [\kappa ,j(\kappa ))$
is trivial.
As a result, any
$H_0$
that is
$\mathbb {R}_{[\lambda ,j(\kappa ))}^{\mathrm {M}[G]}=(\dot {\mathbb {R}}_{[\lambda ,j(\kappa ))}^{\mathrm {M}})_G$
-generic over
$\mathrm {M}[G]$
has
$j"G\upharpoonright j(\kappa )$
contained in
$G*H_0$
. So we merely need to find such a generic over
$\mathrm {M}[G]$
in
$\mathrm {V}[G]$
to get
$H_0$
. Then we find
$H_1$
. Claim 3.14 is partly why we need to break up the iteration as we do. The general idea is that
$j"G$
might have conditions with potentially unbounded support in
$j(\lambda )$
. So we must generate the generic over the end tail. Claim 3.14 ensures that the middle is left unaffected since
$j"G$
has no real information about it.
As an ultrapower, we can regard
$\mathrm {M}=\{j(f)(r):r\in [\lambda ]^{<\omega }\wedge f:[\kappa ]^{<\omega }\rightarrow \mathrm {V}\}$
so that there are elements of
$[\lambda ]^{<\omega }$
and functions from
$[\kappa ]^{<\omega }$
to
$\mathrm {V}$
that represent
$\mathbb {P}_\kappa ^{\mathrm {V}}$
,
$\dot {\mathbb {R}}_{(\kappa ,j(\lambda ))}^{\mathrm {M}}$
and
$\lambda $
. In fact, we can choose a single element
$r_0\in [\lambda ]^{<\omega }$
so that
$$\begin{align*}\mathbb{P}_\kappa^{\mathrm{V}},\dot{\mathbb{R}}_{(\kappa,j(\lambda))}^{\mathrm{M}},\lambda\in\{j(f)(r_0):f:[\kappa]^{<\omega}\rightarrow\mathrm{V}\}\text{.}\end{align*}$$
So now we consider
$$\begin{align*}\mathrm{N}=\{j(f)(r_0,\kappa ,\lambda ): f\colon[\kappa ]^{<\omega }\rightarrow \mathrm{V}\}\text{,}\end{align*}$$
which has the following nice properties.
Claim 3.15. The model
and
$\mathrm {V}\vDash \textit{"}{{}^{\kappa }\mathrm {N}\subseteq \mathrm {N}}.\text {"}$
Moreover,
$\mathbb {P}_\kappa ,\mathbb {P}_\lambda ,\dot {\mathbb {Q}}_\kappa ,\dot {\mathbb {R}}_{(\lambda ,j(\kappa ))}^{\mathrm {M}}, \kappa ,\lambda \in \mathrm {N}$
.
Proof To show
, we proceed by induction on formulas with the only interesting case being existential quantification. So suppose
$\mathrm {M}\models "{\exists x\ \varphi (x,j(f)(r_0,\kappa ,\lambda ))}\text {"}$
for some
$f:[\kappa ]^{<\omega }\rightarrow \mathrm {V}$
. By our choice of
$r_0$
, there are functions
$g,h$
such that
$\kappa =j(g)(r_0)$
and
$\lambda =j(h)(r_0)$
. Hence
$$ \begin{align*} \mathrm{M}&\models "{\exists x\ \varphi(x,j(f)(r_0,j(g)(r_0),j(h)(r_0))}\text{"}\\ \text{iff}\quad r_0&\in j\left(\{r\in[\lambda]^{<\omega}:\mathrm{V}\models "{\exists x\ \varphi(x,f(r,g(r),h(r)))}\text{"}\}\right)\text{.} \end{align*} $$
So for
$r\in [\lambda ]^{<\omega }$
, let
$\chi (r)$
, if it exists, be such that
$\mathrm {V}\models "{\varphi (\chi (r),f(r,g(r),h(r)))}.\text {"}$
It follows that
$$ \begin{align*} \mathrm{M}&\models "{\varphi(j(\chi)(r_0),j(f)(r_0,j(g)(r_0),j(h)(r_0))}\text{"}\\ \text{iff}\quad \mathrm{M}&\models "{\varphi(j(\chi)(r_0),j(f)(r_0,\kappa,\lambda))}.\text{"} \end{align*} $$
So such a witness
$j(\chi )(r_0)\in N$
yields
$N\models "{\exists x\ \varphi (x,j(f)(r_0,\kappa ,\lambda )).}\text {"}$
It follows inductively that
.
To see that
$\mathbb {P}_\kappa ,\mathbb {P}_\lambda ,\dot {\mathbb {Q}}_\kappa ,\dot {\mathbb {R}}_{(\lambda ,j(\kappa ))}^{\mathrm {M}},\kappa ,\lambda \in \mathrm {N}$
:
-
•
$f(x,y,z)=y$
witnesses
$\kappa \in \mathrm {N}$
. -
•
$f(x,y,z)=z$
witnesses
$\lambda \in \mathrm {N}$
. -
•
$f(x,y,z)=\mathbb {P}_y$
witnesses
$\mathbb {P}_\kappa \in \mathrm {N}$
. -
•
$f(x,y,z)=\mathbb {P}_z$
witnesses
$\mathbb {P}_\lambda \in \mathrm {N}$
. -
•
$f(x,y,z)=\dot {\mathbb {Q}}_y$
witnesses
$\dot {\mathbb {Q}}_\kappa \in \mathrm {N}$
. -
•
$f(x,y,z)=\dot {\mathbb {R}}_{(z,\kappa )}$
witnesses
$\dot {\mathbb {R}}_{(\lambda ,j(\kappa ))}^{\mathrm {M}}\in \mathrm {N}$
.
To see that
$\mathrm {N}^\kappa \cap \mathrm {V}\subseteq \mathrm {N}$
, suppose
$\langle j(f_\alpha )(r_0,\kappa ,\lambda ):\alpha <\kappa \rangle $
is arbitrary where each
$f_\alpha :[\kappa ]^{<\omega }\rightarrow \mathrm {V}$
. Then we can consider in the function g mapping
$r,y,z$
to
$F_{r,y,z}$
defined by
$F_{r,y,z}(\alpha )=f_\alpha (r,y,z)$
for
$\alpha <y$
so that for
$y\le \kappa $
,
$j(g)(r,y,z)=\langle j(f_\alpha )(r,y,z):\alpha <y\rangle $
. Hence
$j(g)(r_0,\kappa ,\lambda )=\langle j(f_\alpha )(r_0,\kappa ,\lambda ):\alpha <\kappa \rangle $
is therefore in
$\mathrm {N}$
.
We write
$\mathrm {N}[G]$
for
$\{\tau _G:\tau \in \mathrm {N}\}$
.
Claim 3.16. In
$\mathrm {V}[G]$
, there is an
$H_0\ \mathbb {R}_{(\lambda ,j(\kappa ))}^{\mathrm {M}[G]}$
-generic over
$\mathrm {N}[G]$
.
Proof
$\mathbb {R}_{(\lambda ,j(\kappa ))}^{\mathrm {M}[G]}$
is
$\lambda ^+$
-strategically closed in
$\mathrm {M}[G]$
and this translates to being merely
$\kappa ^+$
-strategically closed in
$\mathrm {V}[G]$
by the closure conditions of
$\mathrm {M}$
and
$\mathrm {N}$
in
$\mathrm {V}$
:
is closed under
$\kappa $
-sequences. Hence
$\mathbb {R}_{(\lambda ,j(\kappa ))}^{\mathrm {M}[G]}\cap \mathrm {N}[G]$
is still
$\kappa ^+$
-strategically closed in
$\mathrm {V}[G]$
. Since dense sets in
$\mathrm {N}[G]$
can be identified with functions
$f:[\kappa ]^{<\omega }\rightarrow \mathrm {V}\mid \kappa $
, a simple counting argument shows that in
$\mathrm {V}[G]$
, there are at most, due to
$\mathsf {GCH}$
in
$\mathrm {V}$
,
$\kappa ^\kappa =\kappa ^+$
-many antichains of the poset in
$\mathrm {N}[G]$
. Thus we can find in
$\mathrm {V}[G]$
an H that is
$\mathbb {R}_{(\kappa ,j(\kappa ))}^{\mathrm {M}[G]}\cap \mathrm {N}[G]$
-generic over
$\mathrm {N}[G]$
by standard techniques (extending into dense open sets one by one and leaving the other player in the strategic closure game to extend at limit stages).
Now we must show that
$H_0$
is actually generic over
$M[G]$
. Let D be a dense open set of
$\mathbb {R}_{(\lambda ,j(\kappa ))}^{\mathrm {M}[G]}$
. We can represent D by
$j(f)(r)$
for some
$f:[\kappa ]^{<\omega }\rightarrow \mathbb {P}_{\kappa }$
and
$r\in [\lambda ]^{<\omega }$
. So in
$\mathrm {M}[G]$
, consider the set
$\{j(f)(s)\text { dense open in }\mathbb {R}_{(\lambda ,j(\kappa ))}^{\mathrm {M}[G]}:s\in [\lambda ]^{<\omega }\}$
. Since
$\mathrm {M}[G]$
thinks that the tail
$\mathbb {R}_{(\lambda ,j(\kappa ))}^{\mathrm {M}[G]}$
is
$\lambda ^+$
-strategically closed, the intersection of all of these sets
$E=\bigcap _{s\in [\lambda ]^{<\omega }}j(f)(s)$
is dense open. Moreover,
$E\in \mathrm {N}[G]$
as follows: define
$g(x,y,\alpha )=\bigcap _{s\in [\alpha ]^{<\omega }}f(s)$
so that
$E=j(g)(r_0,\kappa ,\lambda )\in \mathrm {N}[G]$
. Therefore
$E\cap H_0\neq \emptyset $
and showing that
$H_0$
is generic over
$\mathrm {M}[G]$
.
Claim 3.17. Let
$H_1$
be the filter generated by
$j"G_1$
. Then
$H_1$
is
$\mathbb {R}_{[j(\kappa ),j(\lambda ))}^{\mathrm {M}[G*H_0]}$
-generic over
$\mathrm {M}[G*H_0]$
and as a result of Claim 3.14,
$j"G\subseteq G*H_0*H_1$
.
Proof Let
$D\in \mathrm {M}[G*H_0]$
be open dense with name
$\dot D$
. It follows that we can represent D as
$j(d)(r)_{G*H_0}$
for some
$d:[\kappa ]^{<\omega }\rightarrow \mathrm {V}$
and
$r\in [\lambda ]^{<\omega }$
where each
$d(s)$
is a name for a dense open set in
$\dot {\mathbb {R}}_{[\kappa ,\lambda )}$
. In
$\mathrm {V}[G_0]$
, since the tail forcing
$\mathbb {R}_{[\kappa ,\lambda )}^{\mathrm {V}[G_0]}$
is
$\le \kappa $
-distributive by Corollary 3.8, we can intersect all of these dense open sets
$\bigcap _{s\in [\kappa ]^{<\omega }}d(s)_{G_0}$
and get another dense open set that intersects
$G_1$
: there is a p such that for every
$s\in [\kappa ]^{<\omega }$
,
$p\in G_1\cap d(s)_{G_0}$
. Thus some
$q\in G_0$
has in
$\mathrm {M}$
that
$j(q)\Vdash $
“
$j(p)\in j(d)(s)$
for every
$s\in [j(\kappa )]^{<\omega }$
” and in particular
$j(q)\Vdash "{j(p)\in \dot D}.\text {"}$
Since
$q\in G_0\subseteq \mathbb {P}_\kappa $
,
$j(q)$
is just q with a bunch of
$\dot {\textbf {1}}$
s appended, meaning
$j(q)\in G*H_0$
and so indeed
$j(p)\in j"G_1\cap D\subseteq H_1\cap D$
in
$\mathrm {M}[G*H_0]$
.
Thus
$j"G\subseteq G*H_0*H_1$
and so
$j:\mathrm {V}\rightarrow \mathrm {M}$
lifts to
$j^+:\mathrm {V}[G]\rightarrow \mathrm {M}[G*H]$
. It’s not hard to see that
$j^+$
is still
$\lambda $
-strong since
$G\subseteq \mathrm {V}\mid \lambda =\mathrm {M}\mid \lambda $
and H adds no sets of rank
$<\lambda $
.
More generally what this shows is the following.
Corollary 3.18. If
$j:\mathrm {V}\rightarrow \mathrm {M}$
is
$\lambda $
-srs for
$\lambda $
a limit of strongs such that
$\lambda $
isn’t
$\lambda +2$
-strong in
$\mathrm {M}$
, then we can lift j to
$j^+:\mathrm {V}^{\mathbb {P}_\lambda }\rightarrow \mathrm {M}^{j(\mathbb {P}_\lambda )}$
.
And this gives the desired result.
Result 3.19. Assume there is a proper class of srs cardinals and
$\mathsf {GCH}$
holds. Then
$\mathbb {P}\Vdash \mathsf {UWISS}+\textit{"}{\text {there is a proper class of strongs.}}\text {"}$
Proof That
$\mathbb {P}\Vdash \mathsf {UWISS}$
follows from Corollary 3.11. For a proper class of strongs, let
$\kappa $
be srs and let
$\lambda>\kappa $
be a strong limit of strongs in
$\mathrm {V}$
. By Lemma 3.13, in
$\mathrm {V}^{\mathbb {P}_\lambda }$
,
$\kappa $
is
$\lambda $
-strong and this degree of strength is weakly indestructible, meaning
$\kappa $
is still
$\lambda $
-strong in all later stages (since, again, the tail forcings will be
$\le \lambda $
-distributive and
$<\lambda $
-strategically closed) and so
$\lambda $
-strong in
$\mathrm {V}^{\mathbb {P}}$
. Since there are a proper class of
$\mathrm {V}$
-strongs above
$\kappa $
, it follows that
$\kappa $
is strong in
$\mathrm {V}^{\mathbb {P}}$
. Hence any
$\kappa $
srs in
$\mathrm {V}$
is strong in
$\mathrm {V}^{\mathbb {P}}$
, and we have a proper class of both.
This completes the proof of Theorem 3.4, repeated below, and so in conjunction with Theorem 2.5, Theorem 1.2 holds.
Corollary 3.20. (1) implies (2) and (3) where these stand for:
-
1.
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}\mathrel {+}$
“There is a proper class of srs cardinals”). -
2.
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}\mathrel {+}$
“There is a proper class of strongs”
$\mathrel {+}\mathsf {UWISS})$
. -
3.
$\operatorname {\mathrm {Con}}(\mathsf {ZFC}\mathrel {+}$
“There is a proper class of strongs”
$+$
“Every
$\lambda $
-strong
$\kappa $
has weakly indestructible
$\lambda $
-strength whenever
$\lambda $
is below the least measurable limit of measurable cardinals larger than
$\kappa $
.”
Again, we can go further than even what (3) states; up to the next cardinal
$\lambda $
that has at least as many measurables below it as a
$\lambda +2$
-strong cardinal should (since it was
$\lambda +2$
-strong in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
).
The above results allow us to also prove Result 3.5, restated below.
Result 3.21. It’s consistent (relative to two srs cardinals and proper class of strong cardinals) that we can force a
$\kappa $
that is not
$\rho $
-strong to be
$\rho $
-strong by a collapse
$\mathrm {Col}(\kappa ^+,\rho )$
Proof Suppose toward a contradiction that these collapses never add strength. Consider the Easton support iteration
where
$\dot {\mathbb {Q}}_\kappa $
is defined by the following.
-
1. At every stage
$\kappa $
that is (forced to be)
$\kappa +2$
-strong, we force with the lottery of
$\kappa ,\rho $
-appropriate posets for minimal
$\rho $
(if any exist) of rank
. -
2. Then with
$\mathrm {Col}(\kappa ^+,\rho )$
if such a
$\rho $
exists. -
3. If there is no such
$\rho $
, and
$\kappa $
was originally
$<\lambda $
-strong in
$\mathrm {V}$
where
, then force with
$\mathrm {Col}(\kappa ^+,\lambda )$
. -
4. Otherwise force trivially.
If the collapses never resurrect degrees of strength, then the proof of Lemma 3.13 goes through to show that the original srs cardinals are strong. Moreover, weak indestructibility will hold for all degrees of strength, simply because the tail will be appropriate (by Corollary 3.8) and the following:
-
• Anytime we destroy
$\kappa $
’s
$\rho $
-strength with the lottery,
$\kappa $
’s remaining
$<\rho $
-strength would be weakly indestructible in
$\mathrm {V}^{\mathbb {P}_{\kappa +1}}$
(if there were some
$\kappa ,\rho '$
-appropriate
$\dot {\mathbb {Q}}$
for
$\rho '<\rho $
then in
$\mathrm {V}^{\mathbb {P}_\kappa }$
, we could force with the
$\kappa ,\rho '$
-appropriate
$\dot {\mathbb {Q}}_\kappa *\dot {\mathbb {Q}}$
). Moreover, this strength remains destroyed: the collapse
$\mathrm {Col}(\kappa ^+,\rho )$
ensures the next stage of forcing occurs far beyond
$\rho $
. So the lack of
$\rho $
-strong extenders continues through to the end of the preparation. By hypothesis, this collapse doesn’t add to
$\kappa $
’s strength. -
• If the lottery doesn’t destroy any of
$\kappa $
’s
$<\lambda $
-strength, then the collapse
$\mathrm {Col}(\kappa ^+,\lambda )$
again doesn’t add any degree of strength to
$\kappa $
and ensures the next stage of forcing occurs well beyond
$\lambda $
. Again, the lack of
$\lambda $
-strong extenders continues through to the end of the preparation.
The same proof as Corllary 3.18 with the previous preparation in Definition 3.6 tells us that the srs cardinals become strong in
$\mathrm {V}^{\mathbb {P}}$
. But two strong cardinals and weak indestructibility for all degrees of strength contradicts Result 1.17.
4 Small side results
It’s not hard to see that the forcing preparation
$\mathbb {P}$
from Definition 3.6 can be generalized and restricted to the following theorem when combined with the original proof from [Reference Apter and Sargsyan3]. The idea really is that [Reference Apter and Sargsyan3] only gives
$\mathsf {UWISS}$
and the only reason there is a weakly indestructible strong cardinal in the end is that all of its degrees of strength are small: there is no measurable cardinal above the strong.
Theorem 4.1. Let
$\alpha \in \mathrm {Ord}$
. Then the following are equiconsistent.
-
1.
$\mathsf {ZFC}+\textit{"}{\text {there are (at least) }\alpha \text { srs cardinals with a hyperstrong above them}}\text {"};$
-
2.
$\mathsf {ZFC}+\mathsf {UWISS}+\textit{"}{\text {there are (at least) }\alpha +1\text {-many strong cardinals}}.\text {"}$
In fact, the last of those
$\alpha +1$
-strong cardinals is weakly indestructible for all of its degrees of strength.
Proof That (2) is consistent relative to (1) follows from the techniques of [Reference Apter and Sargsyan3]. More precisely, consider the forcing
$\mathbb {P}$
from Definition 3.6 but cutting off the universe
$\mathrm {V}$
so that there is no measurable above the hyperstrong
$\delta $
. Because the set of strongs below a hyperstrong forms a stationary set, for each srs cardinal
$\kappa $
below the hyperstrong
$\delta $
, we have many
$\lambda <\delta $
such that
$\lambda \ge \kappa $
is a non-measurable limit of strongs. As a result, Lemma 3.13 tells us that if
$\kappa <\delta $
is srs in
$\mathrm {V}$
then
$\kappa $
will be
$<\delta $
-strong in
$\mathrm {V}^{\mathbb {P}}$
. But [Reference Apter and Sargsyan3, Lemma 1.4] shows that the hyperstrong
$\delta $
is strong in
$\mathrm {V}^{\mathbb {P}}$
and so being
$<\delta $
-strong implies being fully strong in
$\mathrm {V}^{\mathbb {P}}$
. Hence every srs
$\kappa <\delta $
in
$\mathrm {V}$
is also strong in
$\mathrm {V}^{\mathbb {P}}$
. Since
$\mathbb {P}$
still forces
$\mathsf {UWISS}$
, we get (2) in
$\mathrm {V}^{\mathbb {P}}$
.
That (1) is consistent relative to (2) follows again from the techniques of [Reference Apter and Sargsyan3]: if
$\mathrm {V}\vDash \mathsf {ZFC}+\mathsf {UWISS}$
, then the last
$\mathrm {V}$
-strong
$\delta $
is hyperstrong in the core model
$\mathrm {K}$
by [Reference Apter and Sargsyan3, Theorem 4]. Now without loss of generality, cut off
$\mathrm {K}$
such that there are no measurables above
$\delta $
. It follows that
$\delta $
is not only still hyperstrong, but now fully srs by Corollary 1.24. Yet
$\kappa $
being
$\delta $
-srs implies
$\kappa $
is fully srs in
$\mathrm {K}$
. To see this, let
$\lambda>\delta $
be arbitrary. Let
$j:\mathrm {K}\rightarrow \mathrm {M}$
witness that
$\delta $
is
$\lambda $
-srs in
$\mathrm {K}$
. So
$\mathrm {K}$
and
$\mathrm {M}$
agree on strongs below
$\lambda $
. In
$\mathrm {M}$
,
$j(\kappa )=\kappa $
is
$j(\delta )$
-srs and hence
$\lambda $
-srs as witnessed by some
$i:\mathrm {M}\rightarrow \mathrm {N}$
with
$\mathrm {cp}(i)=\kappa $
where
$\mathrm {M}$
and
$\mathrm {N}$
agree on strongs below
$\lambda $
. Thus
$\mathrm {K}$
,
$\mathrm {M}$
, and
$\mathrm {N}$
all agree on strongs below
$\lambda $
. It follows that
$i\circ j:\mathrm {K}\rightarrow \mathrm {N}$
is a
$\lambda $
-srs embedding of
$\mathrm {K}$
so that
$\kappa $
is
$\lambda $
-srs for our arbitrary
$\lambda>\delta $
. Thus the
$\alpha $
-many
$\mathrm {V}$
-strongs below
$\delta $
are srs in
$\mathrm {K}$
.
Reflecting strongs is just one kind of reflection, but in principle, we could also enforce that we reflect more. This essentially converges onto the idea of a Woodin cardinal. The following results are proven in my thesis [Reference Holland7].
Theorem 4.2. Let
$\mathbb {P}$
be as in Definition 3.6. Let
$\delta $
be a Woodin cardinal. Then
$\mathbb {P}_\delta \Vdash "{\delta \text { is Woodin.}}\text {"}$
Hence the existence of a Woodin cardinal
$\delta $
gives the consistency of a Woodin cardinal
$\delta $
where
$\mathrm {V}\mid \delta \vDash \mathsf {UWISS}$
.
This gives the consistency of
$\mathsf {UWISS}$
with a proper class of a large variety of large cardinal notions relative to the existence of a Woodin cardinal.
While on the topic of Woodins, consider the interaction of universal weak indestructibility for large degrees of strength with Woodin cardinals. For example, we used cardinals that are strong and reflect strongs to get some weak indestructibility results in the presence of strongs. We cannot have the same indestructibility for reflection properties.
Definition 4.3. An inaccessible cardinal
$\delta $
is Woodin for weak indestructibility iff for every
$A\subseteq \mathrm {V}\mid \delta $
, there is a
$\kappa <\delta $
that is
$<\delta $
-strong reflecting A such that this strength and reflection is weakly indestructible by
$<\kappa $
-strategically closed posets.
Result 4.4. It is not possible to have a cardinal that is Woodin for weak indestructibility.
Proof Suppose not: let
$\delta $
be Woodin for weak indestructibility. Let W be the set of all cardinals with weakly indestructible
$<\delta $
-strength in
$\mathrm {V}$
. Note that
$W\subseteq \delta $
is unbounded for the same reason Woodin cardinals
$\delta '$
are limits of
$<\delta '$
-strong cardinals. There is therefore an (arbitrarily large)
$\kappa <\delta $
that is
$<\delta $
-strong reflecting W such that this is weakly indestructible. In particular, after adding a Cohen subset
$A\subseteq \mathrm {Add}(\kappa ^+,1)$
,
$\kappa $
is still
$<\delta $
-strong reflecting W. Let
$j:\mathrm {V}[A]\rightarrow \mathrm {M}[j(A)]$
,
$\operatorname {\mathrm {cp}}(j)=\kappa $
witness this for some large
$\lambda <\delta $
. In
$\mathrm {M}[j(A)]$
,
$j(W)\cap \lambda =W\cap \lambda \ni \kappa $
. Consider the least element
$\mu \in W$
above
$\kappa $
that is
$<\delta $
-strong, and assume without loss of generality that
$\lambda $
is large enough that
$\mu <\lambda $
. By [Reference Hamkins5, Superdestruction Theorem III] in
$\mathrm {V}[A]$
, since
$\mathrm {Add}(\kappa ^+,1)$
is small relative to
$\mu $
,
$\mu $
’s strength is weakly destructible by
$\mathrm {Add}(\mu ^+,1)$
. Reflected in
$\mathrm {V}[A]$
, this means arbitrarily large cardinals
$\hat \mu \in W$
have their
$<\delta $
-strength destroyed by
$\mathrm {Add}(\hat \mu ^+,1)$
. Hence
$\mathrm {Add}(\kappa ^+,1)*\mathrm {Add}(\hat \mu ^+,1)$
destroys
$\hat \mu $
’s
$<\delta $
-strength in
$\mathrm {V}$
, contradicting that
$\hat \mu \in W$
.
Despite this result, we can still have a Woodin cardinal such that the cardinals witnessing this can always be chosen to have weakly indestructible strength.
Definition 4.5. A cardinal
$\delta $
is Woodin witnessed by (weak) indestructibility iff
$\delta $
is Woodin, and every
$<\delta $
-strong cardinal
$\kappa <\delta $
has (weakly) indestructible strength.
Using strongs reflecting strongs again, it’s possible to force any Woodin cardinal
$\delta $
to be witnessed by weak indestructibility, as proved in [Reference Holland7], with a slightly easier preparation than with Theorem 4.2 as one only forces at
$<\delta $
-strong stages.
Corollary 4.6. The following are equiconsistent with
$\mathsf {ZFC}$
.
-
1. There is a Woodin cardinal.
-
2. There is a Woodin witnessed by weak indestructibility.
-
3. There is a Woodin cardinal
$\delta $
such that
$\mathrm {V}\mid \delta \vDash \mathsf {UWISS}$
.
This suggests there is a delicate balance between (weak) indestructibility and reflection: one can have weakly indestructible strength with relative ease, but this cannot coincide with weakly indestructible reflection properties by Result 4.4. What kinds of non-trivial reflection can be indestructible is a subject of further research. For example, is it possible to have a proper class of strongs, and a strong reflecting strongs with this strength and reflection weakly indestructible? Below a Woodin witnessed by weak indestructibility,
$\delta $
, the answer is no, because in
$\mathrm {V}\mid \delta $
, the weakly indestructible strong cardinals are just all of the strong cardinals. But in a more general setting the answer is not as obvious to me.
Some of the open problems stated above are collected here for convenience.
Questions 4.7. All of the questions below can also be rephrased in terms of supercompactness.
-
1. Is it possible to have every
$\kappa $
’s
$<\kappa ^{+\sharp \sharp }$
-strength weakly indestructible in the presence of multiple strong cardinals? -
2. To what extent can the reflection properties in the embeddings of a measurable cardinal be (weakly) indestructible?
-
3. Is it possible to have a strong reflecting strongs cardinal (with a strong above it) such that this strength and reflection of (ground model) strongs is weakly indestructible?
-
4. To what extent can we control the resurrection of degrees after destroying degrees of strength in a preparation like Definition 3.6?
-
5. If a poset is
$\le \kappa $
-strategically closed, is it
$<\kappa ^+$
-strategically closed?
Open access
