1. Introduction
The intrusion of a liquid underneath an elastic sheet resting on a non-deformable solid has been utilized as a generic model to understand the formation of geological structures such as magmatic sills and laccoliths (Pollard & Johnson Reference Pollard and Johnson1973; Lister & Kerr Reference Lister and Kerr1991; Michaut Reference Michaut2011) and ice sheet relaxation (Lai et al. Reference Lai, Stevens, Chase, Creyts, Behn, Das and Stone2021). In models of e.g. sill and laccolith emplacement, the intruding magma is commonly assumed to be Newtonian, and the solid is assumed to deform by elastic bending and tensile fracturing. However, there is growing evidence that some magmas exhibit highly non-Newtonian behaviour (Balmforth et al. Reference Balmforth, Burbidge, Craster, Salzig and Shen2000; Caricchi et al. Reference Caricchi, Burlini, Ulmer, Gerya, Vassalli and Papale2007; Cordonnier et al. Reference Cordonnier, Caricchi, Pistone, Castro, Hess, Gottschaller, Manga, Dingwell and Burlini2012), such that the magma can transport as plug flow (Morgan et al. Reference Morgan, Stanik, Horsman, Tikoff, de Saint Blanquat and Habert2008). Moreover, rock layers along which magma is emplaced can also exhibit a complex viscoplastic rheological response to magma flow (Scheibert, Galland & Hafver Reference Scheibert, Galland and Hafver2017; Galland et al. Reference Galland, Spacapan, Rabbel, Mair, Soto, Eiken, Schiuma and Leanza2019). To what extent these nonlinear phenomena affect the dynamics of these geophysical systems is still unclear. To model the complex dynamics in geophysical flow, we consider an elastic sheet separated from a rigid substrate by a prewetted layer of viscoplastic fluid, and study the formation of a blister formed as we inject the same viscoplastic fluid in between the elastic sheet and the rigid substrate (see the illustration in figure 1a).

Figure 1. (a) Schematic drawing of the studied system. An incompressible elastic sheet, of Young's modulus ![]() $E$, thickness
$E$, thickness ![]() $d$, and Poisson ratio
$d$, and Poisson ratio ![]() $\nu$, rests on top of the prewetted layer with thickness
$\nu$, rests on top of the prewetted layer with thickness ![]() $h_0$, of yield stress fluid made from a solution of Carbopol mixed with water. A solution of the same Carbopol–water mixture as that in the prewetted layer is injected at a constant flux
$h_0$, of yield stress fluid made from a solution of Carbopol mixed with water. A solution of the same Carbopol–water mixture as that in the prewetted layer is injected at a constant flux ![]() $Q$ beneath the elastic sheet through a small tube of radius
$Q$ beneath the elastic sheet through a small tube of radius ![]() $r_t$. The resulting blister's height profile
$r_t$. The resulting blister's height profile ![]() $h(r,t)$ is measured by tracking a laser line (on top of the sheet). (b) An illustration of the two-dimensional cross-section along the lasing line from the injection point to the edge of the sheet. We define the apparent radius
$h(r,t)$ is measured by tracking a laser line (on top of the sheet). (b) An illustration of the two-dimensional cross-section along the lasing line from the injection point to the edge of the sheet. We define the apparent radius ![]() $R(t)$ as the first radial coordinate where the blister height profile matches the prewetted layer thickness,
$R(t)$ as the first radial coordinate where the blister height profile matches the prewetted layer thickness, ![]() $h(r=R(t),t) = h_0$. The region around this point is referred to as the intrusion tip. Note that the aspect ratio between the fluid depth
$h(r=R(t),t) = h_0$. The region around this point is referred to as the intrusion tip. Note that the aspect ratio between the fluid depth ![]() $h(r,t)$ and the thickness of the elastic sheet
$h(r,t)$ and the thickness of the elastic sheet ![]() $d$ is exaggerated for easier visualization of the intrusion.
$d$ is exaggerated for easier visualization of the intrusion.
Fluid models that account for viscoplasticity have provided a more realistic representation of mud, glacier and magma flows on the Earth's surface (Liu & Mei Reference Liu and Mei1989; Balmforth et al. Reference Balmforth, Burbidge, Craster, Salzig and Shen2000; Petford Reference Petford2003). Recently, viscoplastic fluids have also attracted interest in interfacial flows, where they were demonstrated to affect coating, drop spreading, bursting and coalescence (Smit et al. Reference Smit, Kusina, Joanny and Colin2019; Jalaal, Stoeber & Balmforth Reference Jalaal, Stoeber and Balmforth2021; Sanjay, Lohse & Jalaal Reference Sanjay, Lohse and Jalaal2021; Kern, Sæter & Carlson Reference Kern, Sæter and Carlson2022). For an elastic sheet resting on a solid prewetted by a Newtonian fluid film, it has been shown that the growth dynamics when injecting the same fluid underneath the sheet is determined by a coupling between local effects at the intrusion tip (see figure 1b) and the quasi-static shape of the sheet (Lister, Peng & Neufeld Reference Lister, Peng and Neufeld2013). The dynamic changes, e.g. if there is vapour at the intrusion tip (Wang & Detournay Reference Wang and Detournay2018), if there is dry adhesion between the elastic surface and the supporting solid (Hosoi & Mahadevan Reference Hosoi and Mahadevan2004; Ball & Neufeld Reference Ball and Neufeld2018; Lister, Skinner & Large Reference Lister, Skinner and Large2019), if gravitational effects dominate (Hewitt, Balmforth & De Bruyn Reference Hewitt, Balmforth and De Bruyn2015), if the ratio of the deformation and the prewetted film thickness changes (Pedersen et al. Reference Pedersen, Niven, Salez, Dalnoki-Veress and Carlson2019), if the supporting solid is porous (Chase, Lai & Stone Reference Chase, Lai and Stone2021; Lai et al. Reference Lai, Stevens, Chase, Creyts, Behn, Das and Stone2021), or in the case of the effect from thermal fluctuations at small scales (Carlson Reference Carlson2018). The influence of a deformable elastic sheet on the resulting flow has also been demonstrated in the presence of an interface, resulting in e.g. the suppression of viscous fingering in a Hele-Shaw geometry (Pihler-Puzović et al. Reference Pihler-Puzović, Peng, Lister, Heil and Juel2018). This paper looks at another elastohydrodynamic phenomenon, where a working fluid is viscoplastic. Large stresses near the solid surfaces and at the intrusion tip can fluidize the material locally, while the bulk of the viscoplastic liquid forming the blister may remain in a solid-like state. In this paper, we show that having yielded and unyielded regions of the viscoplastic fluid generates growth dynamics distinct from the case of Newtonian fluids.
2. Experimental set-up
Our experiments adapted the design and measurement technique from previous Newtonian elastohydrodynamics studies (Lister et al. Reference Lister, Peng and Neufeld2013; Berhanu et al. Reference Berhanu, Guérin, Courrech du Pont, Raoult, Perrier and Michaut2019). A schematic representation of the experimental system is shown in figure 1(a). An elastic sheet is placed atop a substrate prewetted with a thin film of Carbopol–water mixtures, which have well-characterized rheological properties and minor thixotropic effects (Coussot Reference Coussot2014). A thin elastic sheet covers the Plexiglas plate underneath the liquid film. The dynamics are generated by an influx of the same viscoplastic fluid used to prewet the substrate through an inlet at the centre of the elastic sheet. The sides of the elastic sheets facing the fluid are rough, as Carbopol is known to have significant slip effects on several smooth surfaces (Jalaal, Balmforth & Stoeber Reference Jalaal, Balmforth and Stoeber2015).
To avoid clumping, Carbopol 940 (CAS. 9003-01-4) was briefly mixed in deionized water using a Silverson L5M high shear laboratory mixer set to between 300 and 1000 revolutions per minute until the polymer dissolved. 1M NaOH was added to the dissolved solution in an 8 : 1 wt:wt% ratio of 1M NaOH:Carbopol 940. The solution was then gently mixed mechanically using a Kenwood Chef XL Titanium mixer for approximately 10 days. The amount of dissolved Carbopol was controlled to vary the yield stress, and ranged from ![]() $0.8\ {\rm g}\ {\rm l}^{-1}$ to
$0.8\ {\rm g}\ {\rm l}^{-1}$ to ![]() $2\ {\rm g}\ {\rm l}^{-1}$, resulting in yield stresses
$2\ {\rm g}\ {\rm l}^{-1}$, resulting in yield stresses ![]() $\tau _0=3.9, 11.3, 31.7, 47.3$ Pa. The Carbopol solutions were characterized using an Anton Paar Rheometer 702 with the striated parallel plate geometry (PP50/P2) to prevent slip. The surface roughness amplitude for the striated plate from Anton Paar was
$\tau _0=3.9, 11.3, 31.7, 47.3$ Pa. The Carbopol solutions were characterized using an Anton Paar Rheometer 702 with the striated parallel plate geometry (PP50/P2) to prevent slip. The surface roughness amplitude for the striated plate from Anton Paar was ![]() $500 \ \mathrm {\mu }{\rm m}$, with wavelength
$500 \ \mathrm {\mu }{\rm m}$, with wavelength ![]() $1$ mm. Before each measurement, a pre-shear step was included to break and reheal the material's microstructure (Medhi et al. Reference Medhi, Chowdhury, Gupta and Mazumdar2020). In figure 2(a), we have plotted the shear stress
$1$ mm. Before each measurement, a pre-shear step was included to break and reheal the material's microstructure (Medhi et al. Reference Medhi, Chowdhury, Gupta and Mazumdar2020). In figure 2(a), we have plotted the shear stress ![]() $\tau _0$ versus the shear rate
$\tau _0$ versus the shear rate ![]() $\dot {\gamma }$, and fitted the curves with the Herschel–Bulkley model,
$\dot {\gamma }$, and fitted the curves with the Herschel–Bulkley model, ![]() $\tau = \tau _0 + K \dot {\gamma }^n$. The results of this fit in terms of the yield stress
$\tau = \tau _0 + K \dot {\gamma }^n$. The results of this fit in terms of the yield stress ![]() $\tau _0$, consistency index
$\tau _0$, consistency index ![]() $K$ and flow index
$K$ and flow index ![]() $n$ are listed in table 2. Figure 2(b) shows the viscosity curves as a function of the shear rate for the different samples.
$n$ are listed in table 2. Figure 2(b) shows the viscosity curves as a function of the shear rate for the different samples.

Figure 2. (a) Experimental curves (markers) for ![]() $\tau$ versus
$\tau$ versus ![]() $\dot {\gamma }$, with a Herschel–Bulkley model (line) fitted with the values listed in table 1. (b) Plot of the viscosity
$\dot {\gamma }$, with a Herschel–Bulkley model (line) fitted with the values listed in table 1. (b) Plot of the viscosity ![]() $\mu$ versus
$\mu$ versus ![]() $\dot {\gamma }$. (c,d) Corresponding measurements of the two highest yield stress fluids, but with smooth and rough walls of elite double (ED) instead of the striated plate geometry.
$\dot {\gamma }$. (c,d) Corresponding measurements of the two highest yield stress fluids, but with smooth and rough walls of elite double (ED) instead of the striated plate geometry.
The prewetted layer was made by pouring the desired amount of Carbopol–water mixture over a surface area corresponding to the area of the elastic sheet, placing the sheet on top of this layer, and then covering it with a rigid plate with uniformly distributed weight ![]() $70$ kg for
$70$ kg for ![]() ${\approx }1$ h. Afterwards, excess fluid was removed at the edge of the sheet, and the system was weighed to obtain the deposited Carbopol mass, allowing us to calculate the prewetted film height. The height of the prewetted layer of the Carbopol–water mixture was
${\approx }1$ h. Afterwards, excess fluid was removed at the edge of the sheet, and the system was weighed to obtain the deposited Carbopol mass, allowing us to calculate the prewetted film height. The height of the prewetted layer of the Carbopol–water mixture was ![]() $h_0 \approx 0.2$ mm in experiments with the two lowest yield stress samples, and
$h_0 \approx 0.2$ mm in experiments with the two lowest yield stress samples, and ![]() $h_0 \approx 0.2\unicode{x2013}0.4$ mm in experiments with the two fluids with the highest yield stress. However, the results were insensitive to the precise value within this range of
$h_0 \approx 0.2\unicode{x2013}0.4$ mm in experiments with the two fluids with the highest yield stress. However, the results were insensitive to the precise value within this range of ![]() $h_0$ values.
$h_0$ values.
The elastic sheets were moulded on a coated rough wood plate (Huntonit Classique 1220 HV, product number 231001) using a silicone-based elastomer (Zhermack, Elite Double (ED)), thus ensuring roughness on one side of the sheets. Profilometry measurements of the rough surface were performed on an S Neox optical profiler controlled with the SensoSCAN 6.7 software (Sensofar, Barcelona, Spain). Samples were scanned in confocal mode with white, green, red and blue light with an EPI ![]() $20\times$ objective with lateral resolution
$20\times$ objective with lateral resolution ![]() $0.4 \mathrm {\mu }{\rm m}$. All images were levelled by the least squares method and had filled-in non-measured points (
$0.4 \mathrm {\mu }{\rm m}$. All images were levelled by the least squares method and had filled-in non-measured points (![]() ${<}5\,\%$) before analysis. The surface parameters were obtained from image analysis, and all image processing was done using SensoMap Standard 7.4 (Sensofar, Digital Surf's Mountains Technology
${<}5\,\%$) before analysis. The surface parameters were obtained from image analysis, and all image processing was done using SensoMap Standard 7.4 (Sensofar, Digital Surf's Mountains Technology![]() $\circledR$, Spain). Different roughness parameters measured by the profilometer can be found in table 2. In addition to the elastic sheet on top, made of ED 8, a very thin rough elastic sheet made of ED 32 with thickness
$\circledR$, Spain). Different roughness parameters measured by the profilometer can be found in table 2. In addition to the elastic sheet on top, made of ED 8, a very thin rough elastic sheet made of ED 32 with thickness ![]() $d = 1.7\ \textrm {mm} \pm 0.1\ \textrm {mm}$ was used to cover the Plexiglas plate underneath the prewetted Carbopol layer, to prevent slip at both surfaces. Strong adhesion forces between the Plexiglas and ED 32 render this layer immobile during the experiments. For ED 8,
$d = 1.7\ \textrm {mm} \pm 0.1\ \textrm {mm}$ was used to cover the Plexiglas plate underneath the prewetted Carbopol layer, to prevent slip at both surfaces. Strong adhesion forces between the Plexiglas and ED 32 render this layer immobile during the experiments. For ED 8, ![]() $E = 0.25\ \textrm {MPa}$, and for ED 32,
$E = 0.25\ \textrm {MPa}$, and for ED 32, ![]() $E = 1.2\ \textrm {MPa}$; both have a Poisson ratio
$E = 1.2\ \textrm {MPa}$; both have a Poisson ratio ![]() $\nu \approx 0.5$ (Coulais et al. Reference Coulais, Overvelde, Lubbers, Bertoldi and van Hecke2015). To study different deformation regimes, two versions of the top sheet of ED 8 were made, with thicknesses
$\nu \approx 0.5$ (Coulais et al. Reference Coulais, Overvelde, Lubbers, Bertoldi and van Hecke2015). To study different deformation regimes, two versions of the top sheet of ED 8 were made, with thicknesses ![]() $d = 9.5\ {\rm mm} \pm 0.5\ {\rm mm}$ (diameter
$d = 9.5\ {\rm mm} \pm 0.5\ {\rm mm}$ (diameter ![]() $D=600$ mm) and
$D=600$ mm) and ![]() $d = 1.5\ {\rm mm} \pm 0.1\ {\rm mm}$ (
$d = 1.5\ {\rm mm} \pm 0.1\ {\rm mm}$ (![]() $D= 400$ mm), resulting in a bending modulus of the sheets
$D= 400$ mm), resulting in a bending modulus of the sheets ![]() $B = {Ed^3}/{12(1-\nu ^2)}= 0.024$ N m and
$B = {Ed^3}/{12(1-\nu ^2)}= 0.024$ N m and ![]() $B= 9.4 \times 10^{-7}$ N m, respectively. In addition, to ensure our roughened elastomer minimized slip, similar measurements of the Carbopol properties as with the striated plates were carried out, but with small circular samples of the elastic sheets as bounding walls. Rough and smooth elastomer layers were tested to characterize how the surface roughness affected the measurements. In figures 2(c) and 2(d), the corresponding curves for the measured shear stress and viscosity versus the shear rate are plotted for Carbopol samples of the highest yield stresses with both smooth and rough ED surfaces. Figures 2(c) and 2(d) measurements suggest that the surface roughness reduces slip effects significantly. However, even with the rough surface configuration, the measured yield stress still deviates from the measurement on the striated plates. We note, however, that the form of the two curves is similar. The discrepancy can be caused by a slip or the custom-built set-up, e.g. a slight non-uniformity in the thickness of the ED samples. To quantify the effects of slip in our experiment, we compare experimental values using rough or smooth sides of the sheets in § 5.2. Otherwise, rough boundaries apply to the results reported.
$B= 9.4 \times 10^{-7}$ N m, respectively. In addition, to ensure our roughened elastomer minimized slip, similar measurements of the Carbopol properties as with the striated plates were carried out, but with small circular samples of the elastic sheets as bounding walls. Rough and smooth elastomer layers were tested to characterize how the surface roughness affected the measurements. In figures 2(c) and 2(d), the corresponding curves for the measured shear stress and viscosity versus the shear rate are plotted for Carbopol samples of the highest yield stresses with both smooth and rough ED surfaces. Figures 2(c) and 2(d) measurements suggest that the surface roughness reduces slip effects significantly. However, even with the rough surface configuration, the measured yield stress still deviates from the measurement on the striated plates. We note, however, that the form of the two curves is similar. The discrepancy can be caused by a slip or the custom-built set-up, e.g. a slight non-uniformity in the thickness of the ED samples. To quantify the effects of slip in our experiment, we compare experimental values using rough or smooth sides of the sheets in § 5.2. Otherwise, rough boundaries apply to the results reported.
Table 1. Values for ![]() $\tau _0$,
$\tau _0$, ![]() $K$ and
$K$ and ![]() $n$ after fitting the sample measurements from figure 2(a) with the Herschel–Bulkley model.
$n$ after fitting the sample measurements from figure 2(a) with the Herschel–Bulkley model.

Table 2. Different roughness parameters measured by the profilometer. Here, we present the mean, standard deviation (SD) and median values for five different measurements of different samples. Amplitude parameters (![]() $S_a$,
$S_a$, ![]() $S_q$,
$S_q$, ![]() $S_z$,
$S_z$, ![]() $S_{sk}$ and
$S_{sk}$ and ![]() $S_{ku}$) were calculated with advanced software (SensoMap Plus 4.1, Sensofar, Terrassa, Spain). Here,
$S_{ku}$) were calculated with advanced software (SensoMap Plus 4.1, Sensofar, Terrassa, Spain). Here, ![]() $S_a$ is the average height deviation from the mean plan,
$S_a$ is the average height deviation from the mean plan, ![]() $S_q$ is the root mean square value of ordinate values within the defined area,
$S_q$ is the root mean square value of ordinate values within the defined area, ![]() $S_z$ is defined as the sum of the largest peak height value and the largest pit depth value within the defined area,
$S_z$ is defined as the sum of the largest peak height value and the largest pit depth value within the defined area, ![]() $S_{sk}$ is the surface skewness, and
$S_{sk}$ is the surface skewness, and ![]() $S_{ku}$ is the surface kurtosis.
$S_{ku}$ is the surface kurtosis.

Our experiment is conducted by injecting the Carbopol–water mixture through a tube with radius ![]() $r_t = 2$ mm, at the centre of the plate at a controlled flux
$r_t = 2$ mm, at the centre of the plate at a controlled flux ![]() $Q=1.7,3.3,6.7\times 10^{-7}\ {\rm m}^3\ {\rm s}^{-1}$, using two Merck-Millipore-Sigma syringe pumps, injecting a total volume of approximately
$Q=1.7,3.3,6.7\times 10^{-7}\ {\rm m}^3\ {\rm s}^{-1}$, using two Merck-Millipore-Sigma syringe pumps, injecting a total volume of approximately ![]() $180\ {\rm ml}$. A laser line is used to visualize the sheet's deflection
$180\ {\rm ml}$. A laser line is used to visualize the sheet's deflection ![]() $h(r,t)$ as the blister grows in time and space, and we track the profile with a digital camera, imaging with angle
$h(r,t)$ as the blister grows in time and space, and we track the profile with a digital camera, imaging with angle ![]() $17^{\circ }$ relative to the horizontal plane. The experimental interface profiles are obtained by fitting a Gaussian distribution to the colour intensity along each column of pixels and extracting the mean vertical coordinate. We define the height at the centre of the blister,
$17^{\circ }$ relative to the horizontal plane. The experimental interface profiles are obtained by fitting a Gaussian distribution to the colour intensity along each column of pixels and extracting the mean vertical coordinate. We define the height at the centre of the blister, ![]() $h(0,t)$, as the maximum deformation of the profile, and the apparent spreading radius
$h(0,t)$, as the maximum deformation of the profile, and the apparent spreading radius ![]() $R(t)$ as described in figure 1(b). For each set of parameters, two experiments were carried out to demonstrate the reproducibility of the results. The error bars correspond to the standard deviation of measurements with the same parameter settings.
$R(t)$ as described in figure 1(b). For each set of parameters, two experiments were carried out to demonstrate the reproducibility of the results. The error bars correspond to the standard deviation of measurements with the same parameter settings.
3. Theoretical framework
3.1. Mathematical model
To give a theoretical description of the elastohydrodynamics of the viscoplastic intrusion, we assume a small aspect ratio, viscous flow and axial symmetry around the injection point, allowing us to adopt the lubrication theory. To capture the principal viscoplastic effect, we use the Bingham model, which can be combined with the integrated lubrication equations to derive an expression for the vertical yielding line ![]() $Y(r,t)$ of the fluid, where the shear stress
$Y(r,t)$ of the fluid, where the shear stress ![]() $|\tau _{rz}|$ equals the yield stress
$|\tau _{rz}|$ equals the yield stress ![]() $\tau _0$ (Liu & Mei Reference Liu and Mei1989; Balmforth et al. Reference Balmforth, Burbidge, Craster, Salzig and Shen2000, Reference Balmforth, Craster, Rust and Sassi2006):
$\tau _0$ (Liu & Mei Reference Liu and Mei1989; Balmforth et al. Reference Balmforth, Burbidge, Craster, Salzig and Shen2000, Reference Balmforth, Craster, Rust and Sassi2006):
 \begin{equation} Y(r,t) = \max \left(0,\frac{h(r,t)}{2} - \frac{\tau_0}{\left|\dfrac{\partial p(r,t)}{\partial r} \right|}\right). \end{equation}
\begin{equation} Y(r,t) = \max \left(0,\frac{h(r,t)}{2} - \frac{\tau_0}{\left|\dfrac{\partial p(r,t)}{\partial r} \right|}\right). \end{equation} Since we have two solid surfaces, we expect the shear profile ![]() $|\tau _{rz}|$ to be symmetric, so it will have another corresponding yielding position along
$|\tau _{rz}|$ to be symmetric, so it will have another corresponding yielding position along ![]() $z(r,t)= h(r,t)-Y(r,t)$. We have a plug flow between the two yielding lines that flows with a constant speed and zero shear rate (Balmforth & Craster Reference Balmforth and Craster1999). We follow the standard procedure to derive the thin film equation, where the additional term
$z(r,t)= h(r,t)-Y(r,t)$. We have a plug flow between the two yielding lines that flows with a constant speed and zero shear rate (Balmforth & Craster Reference Balmforth and Craster1999). We follow the standard procedure to derive the thin film equation, where the additional term ![]() $Y(r,t)$ appears from employing the Bingham model for
$Y(r,t)$ appears from employing the Bingham model for ![]() $|\tau _{rz}| >\tau _0$ (Liu & Mei Reference Liu and Mei1989; Oron, Davis & Bankoff Reference Oron, Davis and Bankoff1997; Balmforth et al. Reference Balmforth, Burbidge, Craster, Salzig and Shen2000, Reference Balmforth, Craster, Rust and Sassi2006):
$|\tau _{rz}| >\tau _0$ (Liu & Mei Reference Liu and Mei1989; Oron, Davis & Bankoff Reference Oron, Davis and Bankoff1997; Balmforth et al. Reference Balmforth, Burbidge, Craster, Salzig and Shen2000, Reference Balmforth, Craster, Rust and Sassi2006):
Here, we have introduced ![]() $w(r) = ({2Q}/{{\rm \pi} r_t^2})(1- ({r}/{r_t})^2)$ for
$w(r) = ({2Q}/{{\rm \pi} r_t^2})(1- ({r}/{r_t})^2)$ for ![]() $r\leq r_t$, which is the Poiseuille flow through the tube with radius
$r\leq r_t$, which is the Poiseuille flow through the tube with radius ![]() $r_t$, allowing us to prescribe the influx
$r_t$, allowing us to prescribe the influx ![]() $Q$. Note that a no-slip condition has been applied at both solid surfaces, and that
$Q$. Note that a no-slip condition has been applied at both solid surfaces, and that ![]() $\mu$ is the effective fluid viscosity. The pressure
$\mu$ is the effective fluid viscosity. The pressure ![]() $p(r,t)$ consists of two terms, with the first term representing the elastic bending (Landau et al. Reference Landau, Lifšic, Lifshitz, Kosevich and Pitaevskii1986), where
$p(r,t)$ consists of two terms, with the first term representing the elastic bending (Landau et al. Reference Landau, Lifšic, Lifshitz, Kosevich and Pitaevskii1986), where ![]() $\nabla ^4$ is the bi-Laplacian operator in cylindrical coordinates. The second term is the hydrostatic pressure with
$\nabla ^4$ is the bi-Laplacian operator in cylindrical coordinates. The second term is the hydrostatic pressure with ![]() $g$ the gravitational acceleration and
$g$ the gravitational acceleration and ![]() $\rho$ the density of the Carbopol solution, set equal to the water density. Note that the Föppl–von Kármán equations describe the effect of elastic stretching of the sheet, discussed further in § 4.2, but not considered in the numerical simulations of (3.2).
$\rho$ the density of the Carbopol solution, set equal to the water density. Note that the Föppl–von Kármán equations describe the effect of elastic stretching of the sheet, discussed further in § 4.2, but not considered in the numerical simulations of (3.2).
Equation (3.2) has two particularly interesting limits. If ![]() $Y(r,t)=h(r,t)/2$, then Newtonian flow is recovered, and the blister grows with a height
$Y(r,t)=h(r,t)/2$, then Newtonian flow is recovered, and the blister grows with a height ![]() $\sim t^{8/22}$ (Lister et al. Reference Lister, Peng and Neufeld2013). As
$\sim t^{8/22}$ (Lister et al. Reference Lister, Peng and Neufeld2013). As ![]() $Y(r,t)\rightarrow 0$, we expect a plug flow to form and the flow to be dominated by the effects of
$Y(r,t)\rightarrow 0$, we expect a plug flow to form and the flow to be dominated by the effects of ![]() $\tau _0$.
$\tau _0$.
3.2. Numerical simulations
The experiments are complemented by numerical solutions of the axisymmetric non-dimensional version of (3.2). The equation is discretized by linear finite elements and an implicit time marching method (Pedersen et al. Reference Pedersen, Niven, Salez, Dalnoki-Veress and Carlson2019). We make (3.1) and (3.2) non-dimensional by scaling ![]() $h(r,t)$ and
$h(r,t)$ and ![]() $r$ with length scale
$r$ with length scale ![]() $L = ({B}/{\tau _0})^{1/3}$, and time
$L = ({B}/{\tau _0})^{1/3}$, and time ![]() $t$ with time scale
$t$ with time scale ![]() $T = {B}/{Q\tau _0}$, giving a non-dimensional number
$T = {B}/{Q\tau _0}$, giving a non-dimensional number ![]() $\varPi _1 = {B}/{6\mu Q}$ in front of the first term on the right-hand side of (3.2), which describes the ratio between elastic and viscous forces. In the simulation that includes gravity, we get another non-dimensional number in front of the hydrostatic pressure term,
$\varPi _1 = {B}/{6\mu Q}$ in front of the first term on the right-hand side of (3.2), which describes the ratio between elastic and viscous forces. In the simulation that includes gravity, we get another non-dimensional number in front of the hydrostatic pressure term, ![]() $\varPi _2 = {\rho g B^{1/3}}/{\tau _0^{4/3}}$, representing the ratio between elasto-gravity and the yield stress. We assume that the shear rate will set the effective viscosity in our experiments in the regions where the fluid is yielded, determining the viscous time scale. We estimate the effective viscosity by assuming a parabolic velocity profile for
$\varPi _2 = {\rho g B^{1/3}}/{\tau _0^{4/3}}$, representing the ratio between elasto-gravity and the yield stress. We assume that the shear rate will set the effective viscosity in our experiments in the regions where the fluid is yielded, determining the viscous time scale. We estimate the effective viscosity by assuming a parabolic velocity profile for ![]() $z > h(r,t) - Y(r,t)$ and
$z > h(r,t) - Y(r,t)$ and ![]() $z< Y(r,t)$, and obtain
$z< Y(r,t)$, and obtain ![]() $\dot {\gamma }_{max} \approx ({\partial u}/{\partial z})|_{z=0, z = h} \sim {Q}/{R(t)\,Y(r,t)^2}$. Setting
$\dot {\gamma }_{max} \approx ({\partial u}/{\partial z})|_{z=0, z = h} \sim {Q}/{R(t)\,Y(r,t)^2}$. Setting ![]() $Q\approx 10^{-7}\ {\rm m}^3\ {\rm s}^{-1}$,
$Q\approx 10^{-7}\ {\rm m}^3\ {\rm s}^{-1}$, ![]() $R(t)\approx 10^{-1}\ {\rm m}$ and
$R(t)\approx 10^{-1}\ {\rm m}$ and ![]() $Y(r,t)\approx 10^{-4}\ {\rm m}$ gives
$Y(r,t)\approx 10^{-4}\ {\rm m}$ gives ![]() $\dot {\gamma }_{max} \approx 100 \ {\rm s}^{{-1}}$. This is a conservative estimate for the shear rate, and we therefore assume
$\dot {\gamma }_{max} \approx 100 \ {\rm s}^{{-1}}$. This is a conservative estimate for the shear rate, and we therefore assume ![]() $\dot {\gamma }\approx 10\unicode{x2013}100\ {\rm s}^{{-1}}$ in the experiments. From the rheological viscosity curves in figure 2, we can then estimate the effective viscosity
$\dot {\gamma }\approx 10\unicode{x2013}100\ {\rm s}^{{-1}}$ in the experiments. From the rheological viscosity curves in figure 2, we can then estimate the effective viscosity ![]() $\mu \approx 0.1\unicode{x2013}10\ {\rm Pa}\ {\rm s}$, which translates to
$\mu \approx 0.1\unicode{x2013}10\ {\rm Pa}\ {\rm s}$, which translates to ![]() $\varPi _1\approx 10^2\unicode{x2013}10^4$. We use an adaptive time-stepping routine with a time step limit
$\varPi _1\approx 10^2\unicode{x2013}10^4$. We use an adaptive time-stepping routine with a time step limit ![]() $\Delta t/T = 9\times 10^{-6}$, and discretization in space
$\Delta t/T = 9\times 10^{-6}$, and discretization in space ![]() $\Delta r/L \in [0.00025\unicode{x2013}0.015]$. We have defined
$\Delta r/L \in [0.00025\unicode{x2013}0.015]$. We have defined
 \begin{equation} Y(r,t)=\max\left(\epsilon,h(r,t)/2-\frac{1}{\left|\dfrac{\partial}{\partial r} \nabla^4h(r,t)\right|}\right), \end{equation}
\begin{equation} Y(r,t)=\max\left(\epsilon,h(r,t)/2-\frac{1}{\left|\dfrac{\partial}{\partial r} \nabla^4h(r,t)\right|}\right), \end{equation}
with a regularization parameter ![]() $\epsilon = 10^{-6}$ similar to that of Jalaal et al. (Reference Jalaal, Stoeber and Balmforth2021). We tested that the results are unaffected by this choice of
$\epsilon = 10^{-6}$ similar to that of Jalaal et al. (Reference Jalaal, Stoeber and Balmforth2021). We tested that the results are unaffected by this choice of ![]() $\epsilon$. The simulations are started with
$\epsilon$. The simulations are started with ![]() $Y(r,t)=h(r,t)/2$, and the plug flow is introduced gradually until
$Y(r,t)=h(r,t)/2$, and the plug flow is introduced gradually until ![]() $t/T = 10^{-4}$. We initialize the profile with the shape known from the Newtonian case (Lister et al. Reference Lister, Peng and Neufeld2013), taking the form of a small bump,
$t/T = 10^{-4}$. We initialize the profile with the shape known from the Newtonian case (Lister et al. Reference Lister, Peng and Neufeld2013), taking the form of a small bump,
 \begin{equation} \frac{h(r,t = 0)}{L} = \frac{h_0}{L}\left(1-\left(\frac{4r}{L}\right)^2\right)^2\quad {\rm for}\ r/L\leq 1/4, \end{equation}
\begin{equation} \frac{h(r,t = 0)}{L} = \frac{h_0}{L}\left(1-\left(\frac{4r}{L}\right)^2\right)^2\quad {\rm for}\ r/L\leq 1/4, \end{equation}
on top of a prewetted layer ![]() $h_0/L =0.007$. As boundary conditions, we set the first three odd derivatives of
$h_0/L =0.007$. As boundary conditions, we set the first three odd derivatives of ![]() $h(r,t)$ to vanish at the axis of symmetry,
$h(r,t)$ to vanish at the axis of symmetry,
and at the edge of the domain,
Note that in all simulations, the domain's boundary is far from the apparent spreading radius and does not affect the blister dynamics, nor does the choice of the boundary conditions at the edge (as long as they are also satisfied by the initial profile).
4. Scaling analysis
We investigate the dynamics when we have a balance between the driving pressure gradient and the opposing fluid's yield stress force, such that ![]() $Y \to 0$ in (3.1). We follow Balmforth et al. (Reference Balmforth, Burbidge, Craster, Salzig and Shen2000), who looked at the gravitational spreading of a viscoplastic dome. An assumption of a quasi-static equilibrium between the hydrostatic pressure gradient and the resisting yield stress leads to Nye's asymptotic solution (Nye Reference Nye1952), and gravity-driven viscoplastic spreading of the dome:
$Y \to 0$ in (3.1). We follow Balmforth et al. (Reference Balmforth, Burbidge, Craster, Salzig and Shen2000), who looked at the gravitational spreading of a viscoplastic dome. An assumption of a quasi-static equilibrium between the hydrostatic pressure gradient and the resisting yield stress leads to Nye's asymptotic solution (Nye Reference Nye1952), and gravity-driven viscoplastic spreading of the dome: ![]() $h(0,t)\sim t^{1/5}$ and
$h(0,t)\sim t^{1/5}$ and ![]() $R(t) \sim t^{2/5}$. New scaling laws are described below for the cases when bending or tension in the elastic sheet sets the fluid pressure of the viscoplastic blister.
$R(t) \sim t^{2/5}$. New scaling laws are described below for the cases when bending or tension in the elastic sheet sets the fluid pressure of the viscoplastic blister.
4.1. Elastic bending regime
We describe the regime where the pressure is dominated by elastic bending, giving ![]() $p(r,t) \sim B\,\nabla ^4h(r,t)$. If we scale the height
$p(r,t) \sim B\,\nabla ^4h(r,t)$. If we scale the height ![]() $h(r,t)$ with
$h(r,t)$ with ![]() $h(0,t)$, and the radial direction
$h(0,t)$, and the radial direction ![]() $r$ with
$r$ with ![]() $R(t)$, while assuming unidirectional flow from
$R(t)$, while assuming unidirectional flow from ![]() $r=0$ and outwards in the limit
$r=0$ and outwards in the limit ![]() $Y(r,t)\rightarrow 0$, then (3.1) gives
$Y(r,t)\rightarrow 0$, then (3.1) gives ![]() ${\partial p(r,t)}/{\partial r} \sim {B\,h(0,t)}/{R(t)^5}\sim 2\tau _0/h(0,t)$. We impose conservation of mass, where the volume
${\partial p(r,t)}/{\partial r} \sim {B\,h(0,t)}/{R(t)^5}\sim 2\tau _0/h(0,t)$. We impose conservation of mass, where the volume ![]() $V= \int _0^{R(t)}2{\rm \pi} \, h(r,t)\,r \,{\rm d}r\sim h(0,t)\,R(t)^2 \sim Qt$ is implicit in (3.2). Together, this gives the scaling laws for the blister height
$V= \int _0^{R(t)}2{\rm \pi} \, h(r,t)\,r \,{\rm d}r\sim h(0,t)\,R(t)^2 \sim Qt$ is implicit in (3.2). Together, this gives the scaling laws for the blister height ![]() $h(0,t)$ and radius
$h(0,t)$ and radius ![]() $R(t)$:
$R(t)$:
 \begin{gather} h(0,t) \sim \left(\frac{4\tau_0^2Q^5}{B^2}\right)^{1/9}t^{5/9} \sim LT^{{-}5/9}t^{5/9}, \end{gather}
\begin{gather} h(0,t) \sim \left(\frac{4\tau_0^2Q^5}{B^2}\right)^{1/9}t^{5/9} \sim LT^{{-}5/9}t^{5/9}, \end{gather} \begin{gather}R(t) \sim \left(\frac{Q^2B}{2\tau_0}\right)^{1/9}t^{2/9} \sim L T^{{-}2/9}t^{2/9}. \end{gather}
\begin{gather}R(t) \sim \left(\frac{Q^2B}{2\tau_0}\right)^{1/9}t^{2/9} \sim L T^{{-}2/9}t^{2/9}. \end{gather} The length scale ![]() $L = ({B}/{\tau _0})^{1/3}$ and time scale
$L = ({B}/{\tau _0})^{1/3}$ and time scale ![]() $T = {B}/{Q\tau _0}$ appear in (4.1) and (4.2), which characterize our system.
$T = {B}/{Q\tau _0}$ appear in (4.1) and (4.2), which characterize our system.
In the limit ![]() $Y(r,t)\rightarrow 0$, (3.1) reduces to a nonlinear ordinary differential equation (ODE)
$Y(r,t)\rightarrow 0$, (3.1) reduces to a nonlinear ordinary differential equation (ODE)
and the height prediction becomes independent of time, i.e. ![]() $h(r,t) \to h(r)$. By scaling
$h(r,t) \to h(r)$. By scaling ![]() $h(r)$ and
$h(r)$ and ![]() $r$ with
$r$ with ![]() $L$, (4.3) becomes parameter-free. Solving this (4.3) for
$L$, (4.3) becomes parameter-free. Solving this (4.3) for ![]() $h(r)$ should therefore yield the same universal shape as obtained when scaling the blister profile with the predicted scaling laws given by (4.1) and (4.2).
$h(r)$ should therefore yield the same universal shape as obtained when scaling the blister profile with the predicted scaling laws given by (4.1) and (4.2).
From Jalaal et al. (Reference Jalaal, Stoeber and Balmforth2021), it follows that the sign of the pressure gradient must correspond to the sign of ![]() $(h_{0}-h)$. To regularize the step function, we replace it with
$(h_{0}-h)$. To regularize the step function, we replace it with ![]() $\tanh (\varTheta (h_0-h))$ and solve the ODE numerically using
$\tanh (\varTheta (h_0-h))$ and solve the ODE numerically using ![]() $\varTheta = 10^{10}$, which is large enough for the solution to be insensitive to this parameter. We aid the numerical solver by starting with a guess based on a numerical profile from our numerical solution of (3.2). Five boundary conditions are needed to define our problem. We choose three conditions at the centreline, where we pin the height to the maximum height of the simulation profile
$\varTheta = 10^{10}$, which is large enough for the solution to be insensitive to this parameter. We aid the numerical solver by starting with a guess based on a numerical profile from our numerical solution of (3.2). Five boundary conditions are needed to define our problem. We choose three conditions at the centreline, where we pin the height to the maximum height of the simulation profile ![]() $h_{max}$, i.e.
$h_{max}$, i.e. ![]() ${h(0)} = h_{max}$, and set the odd derivatives
${h(0)} = h_{max}$, and set the odd derivatives ![]() ${\partial {h}(0)}/{\partial r} = 0$ and
${\partial {h}(0)}/{\partial r} = 0$ and ![]() ${\partial ^3 {h}(0)}/{\partial r^3} = 0$ at the symmetry axis. Defining
${\partial ^3 {h}(0)}/{\partial r^3} = 0$ at the symmetry axis. Defining ![]() $\tilde {R}$ as the radial coordinate corresponding to the minimum value
$\tilde {R}$ as the radial coordinate corresponding to the minimum value ![]() $h_{min}$ of the numerical blister profile
$h_{min}$ of the numerical blister profile ![]() $h(r,t)$, we apply the additional two boundary conditions
$h(r,t)$, we apply the additional two boundary conditions ![]() $h(\tilde {R}) = h_{min}$ and
$h(\tilde {R}) = h_{min}$ and ![]() ${\partial {h}(\tilde {R})}/{\partial r} = 0$. We solve (4.3) with the solver Solve_bvp retrieved from the scipy package in Python.
${\partial {h}(\tilde {R})}/{\partial r} = 0$. We solve (4.3) with the solver Solve_bvp retrieved from the scipy package in Python.
4.2. Elastic stretching regime
In order to predict how stretching of the sheet links to fluid pressure, we must consider the Föppl–von Kármán equations for the deformation of an axisymmetric sheet (Landau et al. Reference Landau, Lifšic, Lifshitz, Kosevich and Pitaevskii1986; Lister et al. Reference Lister, Peng and Neufeld2013; Peng et al. Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015; Pihler-Puzović et al. Reference Pihler-Puzović, Juel, Peng, Lister and Heil2015):
Here, ![]() $\varLambda (r,t) = {\rm d} \sigma _{rr}$ is the tension in the sheet, where
$\varLambda (r,t) = {\rm d} \sigma _{rr}$ is the tension in the sheet, where ![]() $\sigma$ is the Cauchy stress tensor, and the subscript refers to the radial stress component in the sheet. Equation (4.4) is the momentum balance on the elastic sheet and couples the vertical sheet deflection to the pressure exerted by the fluid,
$\sigma$ is the Cauchy stress tensor, and the subscript refers to the radial stress component in the sheet. Equation (4.4) is the momentum balance on the elastic sheet and couples the vertical sheet deflection to the pressure exerted by the fluid, ![]() $p(r,t)$. The second equation (4.5) describes the force balance along the radial direction of the sheet and is used to obtain the tension
$p(r,t)$. The second equation (4.5) describes the force balance along the radial direction of the sheet and is used to obtain the tension ![]() $\varLambda (r,t)$. If we consider intrusion processes where
$\varLambda (r,t)$. If we consider intrusion processes where ![]() $h(0,t) \gg d$, then the term
$h(0,t) \gg d$, then the term ![]() $p(r,t) \sim ({1}/{r})({\partial }/{\partial r})(r\,\varLambda (r,t)\, {\partial h(r,t)}/{\partial r})$ dominates the pressure. By scaling the pressure gradient with the tension from elastic stretching of the sheet, (3.1) in the limit
$p(r,t) \sim ({1}/{r})({\partial }/{\partial r})(r\,\varLambda (r,t)\, {\partial h(r,t)}/{\partial r})$ dominates the pressure. By scaling the pressure gradient with the tension from elastic stretching of the sheet, (3.1) in the limit ![]() $Y \to 0$ now gives
$Y \to 0$ now gives ![]() ${\partial p(r,t)}/{\partial r} \sim {\varLambda (r,t)\, h(0,t)}/{R(t)^3}\sim 2\tau _0/h(0,t)$. From (4.5), we obtain a scaling for the tension in the sheet,
${\partial p(r,t)}/{\partial r} \sim {\varLambda (r,t)\, h(0,t)}/{R(t)^3}\sim 2\tau _0/h(0,t)$. From (4.5), we obtain a scaling for the tension in the sheet, ![]() $\varLambda (r,t) \sim {Ed}/{2} ({h(0,t)}/{R(t)})^2$. Combining this with conservation of the blister's mass, the regime governed by the balance between the stretching of the elastic sheet and the opposing yield stress reads
$\varLambda (r,t) \sim {Ed}/{2} ({h(0,t)}/{R(t)})^2$. Combining this with conservation of the blister's mass, the regime governed by the balance between the stretching of the elastic sheet and the opposing yield stress reads
 \begin{gather} h(0,t) \sim \left(\frac{16 \tau_0^2 Q^5}{\left(Ed\right)^2}\right)^{1/13}t^{5/13}\sim L_{\varLambda}T_{\varLambda}^{{-}5/13}t^{5/13}, \end{gather}
\begin{gather} h(0,t) \sim \left(\frac{16 \tau_0^2 Q^5}{\left(Ed\right)^2}\right)^{1/13}t^{5/13}\sim L_{\varLambda}T_{\varLambda}^{{-}5/13}t^{5/13}, \end{gather} \begin{gather}R(t) \sim \left(\frac{Ed Q^4}{4 \tau_0}\right)^{1/13}t^{4/13}\sim L_{\varLambda}T_{\varLambda}^{{-}4/13}t^{4/13}. \end{gather}
\begin{gather}R(t) \sim \left(\frac{Ed Q^4}{4 \tau_0}\right)^{1/13}t^{4/13}\sim L_{\varLambda}T_{\varLambda}^{{-}4/13}t^{4/13}. \end{gather} This scaling yields new length and time scales ![]() $L_{\varLambda } = {Ed}/{\tau _0}$ and
$L_{\varLambda } = {Ed}/{\tau _0}$ and ![]() $T_{\varLambda } = {(Ed)^3}/{\tau _0^3 Q}$ . In the limit as
$T_{\varLambda } = {(Ed)^3}/{\tau _0^3 Q}$ . In the limit as ![]() $Y \to 0$, (3.1) becomes
$Y \to 0$, (3.1) becomes
In the case when the stretching of the sheet is isotropic, the equation takes the form similar to an arrested viscoplastic droplet (Jalaal et al. Reference Jalaal, Stoeber and Balmforth2021), with ![]() $\varLambda$ then interpreted as the surface tension coefficient.
$\varLambda$ then interpreted as the surface tension coefficient.
5. Results
5.1. Elastic bending
We use the blister's maximal height ![]() $h(0,t)$ as a metric to test the predictions from (4.1) and (4.2). In these experiments, we use the thick membrane (
$h(0,t)$ as a metric to test the predictions from (4.1) and (4.2). In these experiments, we use the thick membrane (![]() $d=9.5$ mm) with bending stiffness
$d=9.5$ mm) with bending stiffness ![]() $B = 0.024$ N m. Thus we can consider small deformations compared with the sheet thickness (
$B = 0.024$ N m. Thus we can consider small deformations compared with the sheet thickness (![]() $h(0,t) \leq d$), similar to those estimated in natural sills and laccoliths (e.g. Castro et al. Reference Castro, Cordonnier, Schipper, Tuffen, Baumann and Feisel2016; Magee et al. Reference Magee2016), and we expect the elastic bending pressure to dominate the tension in the sheet. The spatiotemporal growths of the blister for two Carbopol solutions,
$h(0,t) \leq d$), similar to those estimated in natural sills and laccoliths (e.g. Castro et al. Reference Castro, Cordonnier, Schipper, Tuffen, Baumann and Feisel2016; Magee et al. Reference Magee2016), and we expect the elastic bending pressure to dominate the tension in the sheet. The spatiotemporal growths of the blister for two Carbopol solutions, ![]() $\tau _0=3.9$ Pa and
$\tau _0=3.9$ Pa and ![]() $47.3$ Pa, are shown in figure 3(a). A distinct effect of
$47.3$ Pa, are shown in figure 3(a). A distinct effect of ![]() $\tau _0$ on the growth of the blister's apparent radius
$\tau _0$ on the growth of the blister's apparent radius ![]() $R(t)$ and its height at the centre
$R(t)$ and its height at the centre ![]() $h(0,t)$ is observed.
$h(0,t)$ is observed.

Figure 3. (a) Experimental profiles ![]() $h(r,t)$ of the elastic sheet at
$h(r,t)$ of the elastic sheet at ![]() $t= 100, 200, 300$ s when injecting a fluid with low (
$t= 100, 200, 300$ s when injecting a fluid with low (![]() $\tau _0=3.9\ {\rm Pa}$) and high (
$\tau _0=3.9\ {\rm Pa}$) and high (![]() $\tau _0=47.3\ {\rm Pa}$) yield stresses between the rough surfaces. (b) Plots of the experimental results with the rough surfaces for the blister height
$\tau _0=47.3\ {\rm Pa}$) yield stresses between the rough surfaces. (b) Plots of the experimental results with the rough surfaces for the blister height ![]() $h(0,t)-h_0$ for different yield stresses
$h(0,t)-h_0$ for different yield stresses ![]() $\tau _0$ and fluxes
$\tau _0$ and fluxes ![]() $Q$. (c) Results from (b) scaled by the length
$Q$. (c) Results from (b) scaled by the length ![]() $L = ({B}/{\tau _0})^{1/3}$ and the time
$L = ({B}/{\tau _0})^{1/3}$ and the time ![]() $T = {B}/{Q\tau _0}$ while comparing with the numerical simulations of the non-dimensional version of (3.2). The black dash-dotted line shows the derived scaling law of (4.1), where we have determined
$T = {B}/{Q\tau _0}$ while comparing with the numerical simulations of the non-dimensional version of (3.2). The black dash-dotted line shows the derived scaling law of (4.1), where we have determined ![]() $\alpha$ = 0.35.
$\alpha$ = 0.35.
To explore further the effects of the yield stress and the influx on the dynamics, we vary these parameters systematically while keeping the bending stiffness fixed. Figure 3(b) shows how ![]() $h(0,t)$ is affected by
$h(0,t)$ is affected by ![]() $\tau _0$ and
$\tau _0$ and ![]() $Q$. To see these effects clearly, the experimental data can be rescaled by
$Q$. To see these effects clearly, the experimental data can be rescaled by ![]() $h(0,t)/L$ and
$h(0,t)/L$ and ![]() $t/T$, as shown in figure 3(c). By scaling the data in figure 3(b), we notice that it collapses onto a single curve in figure 3(c), which has a slope in agreement with the proposed scaling law of (4.1).
$t/T$, as shown in figure 3(c). By scaling the data in figure 3(b), we notice that it collapses onto a single curve in figure 3(c), which has a slope in agreement with the proposed scaling law of (4.1).
The results of the numerical simulations based on (3.2) and (3.3) are plotted together with the experimental data in figure 3(c). These results show how the blistering growth is relatively insensitive to the non-dimensional numbers ![]() $\varPi _1$ and
$\varPi _1$ and ![]() $\varPi _2$, and recover the scaling law from (4.1). The time shift separating the experiments and the simulations (a factor of
$\varPi _2$, and recover the scaling law from (4.1). The time shift separating the experiments and the simulations (a factor of ![]() $1.33$ in time) can be caused by a combination of small slip effects, the simplified influx condition, or the minimal rheological model that we use to describe the Carbopol solutions (Coussot Reference Coussot2014). As shown in figure 2, the Carbopol solutions are shear-thinning fluids, and our samples are well fitted with a Herschel–Bulkley model using
$1.33$ in time) can be caused by a combination of small slip effects, the simplified influx condition, or the minimal rheological model that we use to describe the Carbopol solutions (Coussot Reference Coussot2014). As shown in figure 2, the Carbopol solutions are shear-thinning fluids, and our samples are well fitted with a Herschel–Bulkley model using ![]() $n\approx 0.4$. In our mathematical model, we neglect this shear-thinning effect, assuming the viscosity to be constant, which serves as a source for error.
$n\approx 0.4$. In our mathematical model, we neglect this shear-thinning effect, assuming the viscosity to be constant, which serves as a source for error.
Next, we check if the interfacial dynamics of the blister adopts a self-similar shape by using the predicted scaling laws (4.2) and (4.1) to rescale the height profiles. Figures 4(a)–4(d) show the experimental blister's evolution in time for four experiments when injecting fluids of different yield stress. In figures 4(e)–4(h), we scale ![]() $h(r,t)/h(0,t)$ with
$h(r,t)/h(0,t)$ with ![]() $h(0,t)$ as predicted by (4.1), and
$h(0,t)$ as predicted by (4.1), and ![]() $r/R(t)$ with
$r/R(t)$ with ![]() $R(t)$ given by (4.2). It is clear from scaling the experimental blister profiles that they collapse onto what appears to be a universal shape that becomes increasingly apparent as
$R(t)$ given by (4.2). It is clear from scaling the experimental blister profiles that they collapse onto what appears to be a universal shape that becomes increasingly apparent as ![]() $\tau _0$ increases.
$\tau _0$ increases.

Figure 4. (a–d) Plots of four experimental blister profiles from ![]() $t = 136$ s to
$t = 136$ s to ![]() $t = 376$ s, with time interval
$t = 376$ s, with time interval ![]() $80$ s between each profile, for the different yield stress values with rough surfaces. (e–h) Experimental profiles collapsed into a self-similar shape scaling, with the time
$80$ s between each profile, for the different yield stress values with rough surfaces. (e–h) Experimental profiles collapsed into a self-similar shape scaling, with the time ![]() $T$ and length
$T$ and length ![]() $L$ from (4.1) and (4.2).
$L$ from (4.1) and (4.2).
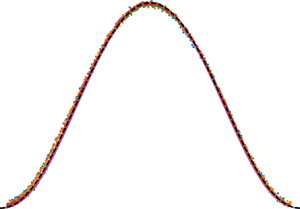
In figure 5(a), we show two numerical profiles at different time instants, and their corresponding yielding lines (dashed lines) from (3.1). A significant part of the fluid volume is between the yielding lines and moves as a plug flow, while the yielded flow with a viscous gradient is limited to narrow regions. For a shear-thinning fluid, the viscosity and the resistance to the flow will decrease in the small pockets close to the boundaries because of the high shear rate. Therefore, including shear-thinning effects in the viscosity could facilitate more fluid flowing radially inside the blister, leading to an even closer agreement with the experiments. We note that despite the simplification in the mathematical model, the simulations capture the elastohydrodynamic growth of the blister well, and the results show consistency concerning the scaling laws from (4.1) and (4.2), and the proposed physical picture based on a plug flow. In figure 5(b), we collapse nine numerical profiles in between these two time instants (![]() $t/T=0.12\unicode{x2013}0.3$) onto the universal shape by scaling the height profiles and the radial coordinate with (4.1) and (4.2), respectively. Apparent time independence of the shape is demonstrated. Furthermore, as shown in figure 5(c), the blister shape predicted by (4.3) is in excellent agreement with the profiles from experiments and the numerical model, normalized with
$t/T=0.12\unicode{x2013}0.3$) onto the universal shape by scaling the height profiles and the radial coordinate with (4.1) and (4.2), respectively. Apparent time independence of the shape is demonstrated. Furthermore, as shown in figure 5(c), the blister shape predicted by (4.3) is in excellent agreement with the profiles from experiments and the numerical model, normalized with
This suggests that the blister attains the self-similar shape.

Figure 5. (a) Blister profiles extracted from the numerical simulations based on the non-dimensional version of (3.2) with ![]() $\varPi _1 = 1000$. Dashed lines for each profile represent the corresponding non-dimensional yield limits
$\varPi _1 = 1000$. Dashed lines for each profile represent the corresponding non-dimensional yield limits ![]() $Y(r,t)/L$ and
$Y(r,t)/L$ and ![]() $(h(r,t)-Y(r,t))/L$; plug flow occurs in between the yield lines. (b) Two profiles from (a) collapsed together with nine profiles in between
$(h(r,t)-Y(r,t))/L$; plug flow occurs in between the yield lines. (b) Two profiles from (a) collapsed together with nine profiles in between ![]() $t/T = 0.12$ and
$t/T = 0.12$ and ![]() $t/T = 0.3$ by scaling with the time dependence of (4.1) and (4.2), which reveals the time-independent shape. (c) Normalization of our experimental and numerical similarity profiles from figures 4(h) and 5(b) (11 profiles for
$t/T = 0.3$ by scaling with the time dependence of (4.1) and (4.2), which reveals the time-independent shape. (c) Normalization of our experimental and numerical similarity profiles from figures 4(h) and 5(b) (11 profiles for ![]() $t/T\in [0.12\unicode{x2013}0.3]$) by using
$t/T\in [0.12\unicode{x2013}0.3]$) by using ![]() $h_{max} = (h(0,t)-h_0)T^{5/9}/Lt^{5/9}$ and
$h_{max} = (h(0,t)-h_0)T^{5/9}/Lt^{5/9}$ and ![]() $r_{max} =R(t)\,T^{2/9}/Lt^{2/9}$, where
$r_{max} =R(t)\,T^{2/9}/Lt^{2/9}$, where ![]() $L = ({B}/{\tau _0})^{1/3}$ and
$L = ({B}/{\tau _0})^{1/3}$ and ![]() $T = {B}/{Q\tau _0}$. The self-similar shape is described by the solution of the non-dimensional form of (4.3).
$T = {B}/{Q\tau _0}$. The self-similar shape is described by the solution of the non-dimensional form of (4.3).
5.2. Elastic bending: slip effect
To address the effect of slip in our experiment, we made a set of experiments with Carbopol–water mixtures of the lowest and highest yield stress on both rough and smooth surfaces, with ![]() $B = 0.024\ \textrm {N} \textrm {m}$ of the overlying elastic sheet, and
$B = 0.024\ \textrm {N} \textrm {m}$ of the overlying elastic sheet, and ![]() $Q=3.3 \times 10^{-7} \textrm {m}^3\ \textrm {s}^{-1}$. In figure 6(a), we show the results from these experiments in terms of
$Q=3.3 \times 10^{-7} \textrm {m}^3\ \textrm {s}^{-1}$. In figure 6(a), we show the results from these experiments in terms of ![]() $h(0,t)$ versus time, demonstrating that preventing slip by introducing a rough surface causes a significant increase in the maximum deformation for the high yield stress fluid. Slip decreases the resistance of the fluid along the walls, allowing for faster radial fluid flow in the blister. The effect of slip is less apparent for fluids of lower yield stress. In figure 6(b), we plot the data of figure 6(a) using logarithmic axes, and show that the power law is still recovered when there is slip at the surfaces, implying that only the time shift and not the power-law growth is a consequence of slip. Moreover, this further strengthens our argument that the dynamics is dominated by plug flow.
$h(0,t)$ versus time, demonstrating that preventing slip by introducing a rough surface causes a significant increase in the maximum deformation for the high yield stress fluid. Slip decreases the resistance of the fluid along the walls, allowing for faster radial fluid flow in the blister. The effect of slip is less apparent for fluids of lower yield stress. In figure 6(b), we plot the data of figure 6(a) using logarithmic axes, and show that the power law is still recovered when there is slip at the surfaces, implying that only the time shift and not the power-law growth is a consequence of slip. Moreover, this further strengthens our argument that the dynamics is dominated by plug flow.

Figure 6. (a) Comparison of experiments with rough and smooth surfaces of the elastic sheets for two fluids with different yield stress. (b) Results show that slip clearly introduces a time shift with respect to the results on the no-slip surfaces, but that the bending regime discovered in § 4.1 is still recovered. The marker configuration in (a) also applies in (b).
5.3. Elastic stretching
Next, we investigate experimentally the limit when the tension dominates elastic bending, ![]() $h(0,t) \gg d$, in the elastic sheet. The thin elastic sheet has thickness
$h(0,t) \gg d$, in the elastic sheet. The thin elastic sheet has thickness ![]() $d=1.5$ mm and Young's modulus
$d=1.5$ mm and Young's modulus ![]() $E = 0.25$ MPa, giving bending stiffness
$E = 0.25$ MPa, giving bending stiffness ![]() $B = 9.4\times 10^{-7}\ \textrm {N} \textrm {m}$. The influx
$B = 9.4\times 10^{-7}\ \textrm {N} \textrm {m}$. The influx ![]() $Q = 3.3 \times 10^{-7}\ \textrm {m}^3 \textrm {s}^{-1}$ and the yield stress
$Q = 3.3 \times 10^{-7}\ \textrm {m}^3 \textrm {s}^{-1}$ and the yield stress ![]() $\tau _0=47.3$ Pa are also used. The deformation of the sheet in the experiments reaches
$\tau _0=47.3$ Pa are also used. The deformation of the sheet in the experiments reaches ![]() $h(0,t) \approx 10d$. In figure 7(a), the scaling prediction from tension given by (4.6) is recovered, also demonstrated by the collapse of experimental profiles from figures 7(b) and 7(c), when scaling the vertical and horizontal coordinates with the respective time dependencies from (4.6) and (4.7). The shape of the profiles in figure 7(c) is in close agreement with the shape from the ODE describing an arrested viscoplastic droplet as solved by Jalaal et al. (Reference Jalaal, Stoeber and Balmforth2021) and discussed in § 4.2, which would hold only if the tension in the sheet is close to isotropic (
$h(0,t) \approx 10d$. In figure 7(a), the scaling prediction from tension given by (4.6) is recovered, also demonstrated by the collapse of experimental profiles from figures 7(b) and 7(c), when scaling the vertical and horizontal coordinates with the respective time dependencies from (4.6) and (4.7). The shape of the profiles in figure 7(c) is in close agreement with the shape from the ODE describing an arrested viscoplastic droplet as solved by Jalaal et al. (Reference Jalaal, Stoeber and Balmforth2021) and discussed in § 4.2, which would hold only if the tension in the sheet is close to isotropic (![]() ${\partial \varLambda }/{\partial r} \approx 0$).
${\partial \varLambda }/{\partial r} \approx 0$).

Figure 7. (a) Plots of ![]() $h(0,t)$ in experiments with rough walls (experimental parameters
$h(0,t)$ in experiments with rough walls (experimental parameters ![]() $d = 1.5$ mm,
$d = 1.5$ mm, ![]() $E = 0.25$ MPa,
$E = 0.25$ MPa, ![]() $B = 9.4\times 10^{-7}\ \textrm {N}\ \textrm {m}$,
$B = 9.4\times 10^{-7}\ \textrm {N}\ \textrm {m}$, ![]() $Q = 3.3 \times 10^{-7}\ \textrm {m}^3\ \textrm {s}^{-1}$ and
$Q = 3.3 \times 10^{-7}\ \textrm {m}^3\ \textrm {s}^{-1}$ and ![]() $\tau _0 = 47.3$ Pa),
$\tau _0 = 47.3$ Pa), ![]() $h(0,t) \gg d$, together with the scaling law in (4.6), where we have determined
$h(0,t) \gg d$, together with the scaling law in (4.6), where we have determined ![]() $\beta = 0.67$. (b) Plots of four experimental blister profiles from
$\beta = 0.67$. (b) Plots of four experimental blister profiles from ![]() $t = 80$ s to
$t = 80$ s to ![]() $t = 200$ s with time interval
$t = 200$ s with time interval ![]() $40$ s between each profile. (c) The self-similarity is shown by rescaling the horizontal and vertical axis of the experimental profiles using the scaling laws in (4.7) and (4.6), respectively. The results are non-dimensionalized using
$40$ s between each profile. (c) The self-similarity is shown by rescaling the horizontal and vertical axis of the experimental profiles using the scaling laws in (4.7) and (4.6), respectively. The results are non-dimensionalized using ![]() $\unicode{x0141} _{\varLambda } = Ed/\tau _0$ and
$\unicode{x0141} _{\varLambda } = Ed/\tau _0$ and ![]() $T_{\varLambda }=(Ed)^3/\tau _0^3Q$.
$T_{\varLambda }=(Ed)^3/\tau _0^3Q$.
6. Conclusion
The intrusion of flowing matter with complex rheological properties underneath an elastic layer or inside an elastic matrix appears in many geological processes. Both nonlinear magma plug flow (Morgan et al. Reference Morgan, Stanik, Horsman, Tikoff, de Saint Blanquat and Habert2008) and viscoplastic deformation of magma intrusions in host rocks (Galland et al. Reference Galland, Spacapan, Rabbel, Mair, Soto, Eiken, Schiuma and Leanza2019) have been documented to play a key role in magma emplacement in the Earth's crust. Our study quantifies the dynamics of a viscoplastic blister's growth underneath an elastic sheet when the pressure is dominated by bending or stretching of the sheet; see table 3. The blister adopts a self-similar quasi-static shape in time that is set by the balance between the pressure gradient induced by the deformation of the elastic sheet and the yield stress of the intruding fluid, independent of the slip in the system. The experimental results have a time shift with respect to the numerical simulations. This time shift could result from our use of the Bingham model, a simplified rheological model that neglects shear-thinning effects, or some remaining slip in our experimental system that would also lead to faster radial growth of the blister. These results point to how the growth of geological structures such as sills and laccoliths may exhibit distinct dynamics from those predicted by a Newtonian model if the intruding fluid can support critical stress before starting to flow. Our work gives a first look at the elastohydrodynamics of a growing viscoplastic blister. Clearly, however, there are many more configurations that remain to be studied, for instance, additional non-Newtonian effects in the bulk and the elastic sheet (Ball & Balmforth Reference Ball and Balmforth2021), or a combination of the yield stress intrusion model with an elastic fracture toughness at the tip.
Table 3. Summary of the elastoviscoplastic growth regimes of the blister with the influx ![]() $Q$, sheet thickness
$Q$, sheet thickness ![]() $d$, bending modulus
$d$, bending modulus ![]() $B$, Young's modulus
$B$, Young's modulus ![]() $E$ and yield stress
$E$ and yield stress ![]() $\tau _0$.
$\tau _0$.

Acknowledgements
We would like to thank V. Kern, M. Janssen and F. Renard for constructive feedback regarding the manuscript.
Funding
The authors acknowledge funding through the EarthFlow initiative at the University of Oslo.
Declaration of interests
The authors report no conflict of interest.