INTRODUCTION
Parasites are heterogeneously distributed within host populations (Anderson and May, Reference Anderson and May1991; Anderson, Reference Anderson and Cox1993). Usually, some of this heterogeneity will be spatially structured and explained by various ecological factors and species interactions that are themselves spatially structured. Improved understanding of the spatial patterns of infection and disease, and the processes behind them, can help predict spatial distributions in unsampled areas, assist in the geographical targeting of control interventions and improve our understanding of disease outbreaks.
A number of tools are now available to help us better quantify and understand spatial variation in the patterns of infection and disease. The recent application of global positioning systems (GPS), geographical information systems (GIS) combined with spatial statistical approaches, for example, has provided an improved understanding of spatial patterns and processes (Hay et al. Reference Hay, Omumbo, Craig and Snow2000; Simoonga et al. Reference Simoonga, Utzinger, Brooker, Vounatsou, Appleton, Stensgaard, Olsen and Kristensen2009; Machault et al. Reference Machault, Vignolles, Borchi, Vounatsou, Pages, Briolant, Lacaux and Rogier2011). This has, in turn, enabled us to predict spatial distributions using remotely sensed environmental data to assist the targeting of control and estimation of the burden of parasitic diseases (Brooker, Reference Brooker2007; Patil et al. Reference Patil, Gething, Piel and Hay2011; Soares Magalhães et al. Reference Soares Magalhães, Clements, Patil, Gething and Brooker2011c). In this review, we aim to provide an overview of available tools, methods and their applications for improving our understanding of the ecology and epidemiology of human parasitic diseases. As a framework, we consider separately the three major branches of spatial statistics: continuous spatial variation; discrete spatial variation; and spatial point processes (Cressie, Reference Cressie1991; Diggle, Reference Diggle, Armitage and David1996).
Approaches to spatial analysis
Any statistical approach that accounts for either absolute location and/or relative position (spatial arrangement) of the data can be referred to as spatial. There are three main approaches, illustrated in Fig. 1. The feature that distinguishes between them is the basic underlying statistical model, and the assumptions that this makes regarding the spatial processes involved (Diggle, Reference Diggle, Durr and Gatrell2004). For instance, spatial statistics investigating continuous spatial dependency assume that the outcome occurs and is potentially measurable throughout space and, as such, spatial variation in the outcome can be modelled explicitly. In contrast, discrete spatial statistics investigate proximity and are used when data are only available at an aggregate area level. Here, spatial structure is modelled by considering dependency between neighbouring discrete units. Both of these approaches rely upon spatially sampled measurement data, and can be described as global in the sense that they model the overall degree of spatial autocorrelation for a dataset. Spatial point processes, on the other hand, concern the physical location of events distributed within a study region and are used to investigate either the general (i.e. global) propensity for points to cluster or the location of individual (i.e. local) spatial clusters of infection, disease or vector and intermediate host populations, relative to the underlying population. Below, we describe each of these three approaches.
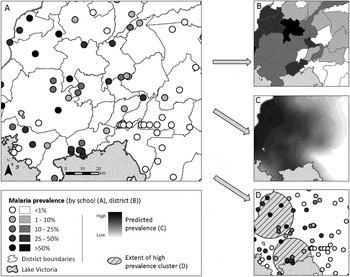
Fig. 1. An illustrated application of the three major branches of spatial statistics, using one dataset. (A) Data used for analysis: Point-level (school-level) malaria prevalence data for Western Kenya, collected during the National School Malaria Survey, 2010 (Gitonga et al. Reference Gitonga, Karanja, Kihara, Mwanje, Juma, Snow, Noor and Brooker2010). (B) Discrete spatial analysis: data are aggregated to the area level (in this case, mean district prevalence) for presentation and analysis. Discrete spatial statistics can be used to smooth between units, or investigate associations with covariates. (C) Continuous spatial analysis: characterizes spatial dependency (or autocorrelation) between points, and can be used to interpolate predicted outcomes across the entire study region (in this case, using Ordinary Kriging (Goovaerts, Reference Goovaerts1997)). (D) Spatial point processes: used to investigate the location of individual spatial clusters (indicated as hatched circles) in the outcome (in this case, Kulldorf's spatial scan statistic (Kulldorff and Nagarwalla, Reference Kulldorff and Nagarwalla1995)).
QUANTIFYING CONTINUOUS SPATIAL DEPENDENCE
Spatial dependence refers to the observation that infection indicators (e.g. prevalence of infection or quantitative egg counts) from samples taken in close proximity to each other are more likely to be related than would be expected by chance, either positively or negatively. This is commonly known as Tobler's first law of geography, whereby “everything is related to everything else, but nearby objects are more related than distant objects” (Tobler, Reference Tobler1970). When investigating continuous spatial dependence, we assume that the outcome can be characterized by a mean, a variance and a correlation structure that is a specified function of location. In such instances, assumptions of independence between observations do not hold true and thus any analysis that ignores spatial dependence risks making inaccurate or misleading inferences (Thomson et al. Reference Thomson, Connor, D'Alessandro, Rowlingson, Diggle, Cresswell and Greenwood1999). Quantifying continuous spatial dependence can also provide additional insight into spatial determinants of infection and disease, and thus indicate interesting avenues for investigation. For example, spatial dependence over large spatial scales may suggest the influence of major climatic correlates of infection, whilst spatial dependence existing only between near locations (typical of highly focal infections) might suggest the involvement of local, micro-environmental factors. An understanding of the distance at which spatial dependence occurs can also inform spatial interpolation and prediction and spatial sampling (see below).
When investigating continuous spatial dependence, it is important to distinguish between first order (i.e. generally large-scale, deterministic spatial trends) and second order (i.e. small-scale, stochastic) effects (Pfeiffer et al. Reference Pfeiffer, Robinson, Stevenson, Stevens, Rogers and Clements2008). First order trends, for example a north-south gradient in the prevalence of infection, can be readily modelled and accounted for by standard regression techniques. Second order effects arise from spatial dependence and represent the tendency for neighbouring values to be similar in their deviation from the global mean. It is therefore the presence of second order effects that violates assumptions of independence between observations, and thus should be the main focus of any spatial analysis. The categorisation of first order and second order effects of course will change according to the scale of the analysis – for example, variation that appears as a trend at small spatial scales may be seen as second order variation on a larger scale (Legendre and Fortin, Reference Legendre and Fortin1989; Weins, Reference Weins1989; Levin, Reference Levin1992). Similarly, clear deterministic (first order) relationships between infection prevalence and climatic factors evident at country scales may disappear at a community level, overridden by local environmental and socio-demographic characteristics. Most spatial analyses will first begin with identifying any trends in the global mean, and will then focus on investigating underlying spatial dependency in the residuals (Pfeiffer et al. Reference Pfeiffer, Robinson, Stevenson, Stevens, Rogers and Clements2008). Second order effects are generally assumed to be stationary and isotropic, meaning that correlation between neighbouring observations is independent from absolute location and does not depend on direction. If dependency between observations is defined by either the physical location of the observations, or by direction, the process is respectively known as non-stationary or geometrically anisotropic, which can be considerably harder to analyse and model.
A number of statistics have been developed to better describe second order spatial dependency, including Moran's I and the inversely related Geary's C (Bailey and Gatrell, Reference Bailey and Gatrell1995). These indicators of global spatial association evaluate whether outcome values are clustered, randomly distributed or evenly dispersed in space, and may form a starting point for more detailed spatial analyses. A more widely used descriptive approach however is the semi-variogram – a cornerstone of classical geostatistics (Goovaerts, Reference Goovaerts1997). Semi-variograms define semi-variance (a measure of expected dissimilarity between a given pair of observations) as a function of the distance separating those observations, providing information about the range and rate of decay of spatial autocorrelation, as well as the relative contribution of spatial factors to total variation in the outcome. An empirical semi-variogram can be estimated from survey data by calculating the squared difference between all pairs of observations. For ease of interpretation, semi-variance values are grouped and averaged according to separation distance, termed lags. If spatial autocorrelation is present in the data, semi-variance typically increases to a maximum value, termed the sill, before plateauing (Fig. 2). In some instances, semi-variance may continue to rise (known as an ‘unbounded’ variogram), indicative of first order effects such as directional trends which must be removed from the data, for example by using regression methods.
Once the empirical semi-variogram is estimated, a model semi-variogram can then be fitted as a line through the plotted semi-variance values for each lag. There are a number of permissible model functions that can be used to fit valid semi-variograms, although the most common are the exponential, spherical and Gaussian functions (Cressie, Reference Cressie1991). The modelled value of semi-variance at the intercept (i.e. where points are separated by negligibly small distances) is termed the nugget and represents the stochastic variation between points, measurement error or spatial autocorrelation over distances smaller than those represented in the data. The distance at which the sill is reached is termed the range, and represents the distance over which spatial autocorrelation exists. Points separated by distances larger than the range are therefore equally as dissimilar irrespective of the distance between them. Semi-variograms are a commonly used descriptive tool, and have been used for example to explore spatial heterogeneity of parasite populations within and between communities, and to quantify the spatial scale at which variation occurs (Srividya et al. Reference Srividya, Michael, Palaniyandi, Pani and Das2002; Brooker et al. Reference Brooker, Kabatereine, Tukahebwa and Kazibwe2004b; Sturrock et al. Reference Sturrock, Gething, Clements and Brooker2010).
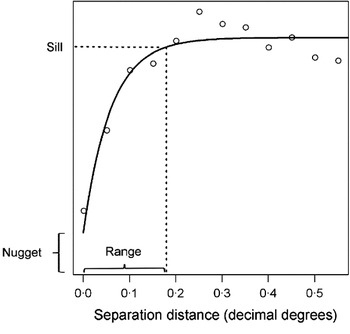
Fig. 2. An example of a semi-variogram, showing its major components. The range represents the separation distance, at which 95% of sill variance is reached, and here is approximately 20 km. The nugget represents the stochastic variation between points, measurement error or spatial autocorrelation over distances smaller than those represented in the data. Data are from a school-based survey of blood in urine indicative of genitourinary schistosomiasis from Coast province, Kenya (Kihara et al. 2011) and were de-trended (i.e. first order spatial structure was removed) using a quadratic trend surface.
A spatial tool that builds upon semi-variogram analysis is kriging, a weighted moving average technique that interpolates or smooths estimates (depending on whether a zero nugget is assumed), based on values at neighbouring locations and parameters from the semi-variogram. It also provides a relative estimate of prediction error (also known as kriging variance) at each prediction location. In parasite epidemiology, kriging has been widely used for predicting spatial patterns (e.g. the prevalence of infection) at unsampled locations. Taking a recent example, Zouré et al. (Reference Zouré, Wanji, Noma, Amazigo, Diggle, Tekle and Remme2011) used this method to produce spatially smoothed contour maps of the interpolated prevalence of eye worm (an indicator for Loa loa infection), based on rapid mapping questionnaire data from a sample of 4,798 villages covering 11 potentially endemic country (Zouré et al. Reference Zouré, Wanji, Noma, Amazigo, Diggle, Tekle and Remme2011). The resulting maps were used to identify zones of hyperendemicity, including several previously unknown foci, and provide critical information for large-scale ivermectin treatment programmes. An extension to ordinary kriging is universal kriging, which includes variation due to both covariates and spatial autocorrelation (Goovaerts, Reference Goovaerts1997), and has for example been used to map malaria risk across Mali (Kleinschmidt et al. Reference Kleinschmidt, Bagayoko, Clarke, Craig and Le Sueur2000). This process considers the variable of interest as a first order large-scale trend determined by covariates and a second order spatially auto-correlated residual. An important feature of universal kriging variance therefore is that it incorporates both the error associated with the trend estimation as well as the error of the spatial interpolation.
Major limitations of a classical geostatistical approach include the inability to account fully for inherent uncertainties, such as those arising from the constraints of finite sampling, imperfect survey measurement, uneven data distribution, or of the fitted semi-variogram parameters themselves. It is also less appropriate when considering non-Gaussian outcomes (e.g. proportions and parasite counts). All of these factors can have considerable implications for risk mapping approaches. This has led spatial epidemiologists to turn towards model-based geostatistics (MBG), in which classical geostatistics is embedded in the (usually Bayesian) framework of a generalised linear model (Diggle et al. Reference Diggle, Moyeed and Tawn1998). This offers a more explicit technical and conceptual framework for capturing the relationship between infection outcomes and covariates, providing a more realistic account of uncertainty in both covariance and mean functions (Diggle et al. Reference Diggle, Moyeed and Tawn1998; Cressie et al. Reference Cressie, Calder, Clark, van Hoes and Wilke2009). Importantly, the model can then be used to generate a distribution of possible values (i.e. a posterior probability distribution) for infection indicators at unsampled locations (interpolation). A rapid expansion of increasingly sophisticated mapping initiatives based upon this method is now being driven by increased computing capacity and the availability of spatially referenced epidemiological data (Soares Magalhães et al. Reference Soares Magalhães, Clements, Patil, Gething and Brooker2011c; Patil et al. Reference Patil, Gething, Piel and Hay2011). Below we discuss some of the more recent advances using the MBG approach, focusing on two key areas of direct relevance to the effective targeting and evaluation of control programmes: predicting spatial distributions and designing sampling strategies.
Quantifying spatial dependence in order to predict spatial distributions
One application for MBG is predicting the spatial distribution of infection and disease, especially in situations where outcome data are geographically sparse. For example, MBG approaches have been used to model prevalence of infection at regional, national and sub-national levels for a variety of human parasitic diseases, including malaria (Clements et al. Reference Clements, Barnett, Cheng, Snow and Zhou2009c; Hay et al. Reference Hay, Guerra, Gething, Patil, Tatem, Noor, Kabaria, Manh, Elyazar, Brooker, Smith, Moyeed and Snow2009; Gosoniu et al. Reference Gosoniu, Veta and Vounatsou2010; Reid et al. Reference Reid, Haque, Clements, Tatem, Vallely, Syed Masud, Islam and Haque2010a, Reference Reid, Vallely, Taleo, Tatem, Kelly, Riley, Harris, Iata, Yama and Clementsb), soil-transmitted helminths (STHs) (Raso et al. Reference Raso, Vounatsou, Gosoniu, Tanner, N'Goran and Utzinger2006a; Pullan et al. Reference Pullan, Gething, Smith, Mwandawiro, Sturrock, Gitonga, Hay and Brooker2011a), schistosomiasis (Clements et al. Reference Clements, Lwambo, Blair, Nyandindi, Kaatano, Kinung'hi, Webster, Fenwick and Brooker2006a, Reference Clements, Moyeed and Brookerb, Reference Clements, Garba, Sacko, Toure, Dembele, Landoure, Bosque-Oliva, Gabrielli and Fenwick2008a, Reference Clements, Bosque-Oliva, Sacko, Landoure, Dembele, Traore, Coulibaly, Gabrielli, Fenwick and Brooker2009a, Reference Clements, Firth, Dembele, Garba, Toure, Sacko, Landoure, Bosque-Oliva, Barnett, Brooker and Fenwickb; Vounatsou et al. Reference Vounatsou, Raso, Tanner, N'Goran and Utzinger2009; Schur et al. Reference Schur, Hürlimann, Garba, Traoré, Ndir, Ratard, Tchuem Tchuenté, Kristensen, Utzinger and Vounatsou2011a), lymphatic filariasis (Stensgaard et al. Reference Stensgaard, Vounatsou, Onapa, Simonsen, Pedersen, Rahbek and Kristensen2011) and trypanosomiasis (Wardrop et al. Reference Wardrop, Atkinson, Gething, Fevre, Picozzi, Kakermo and Welburn2010). Such maps can provide detailed information on the distribution of infection and disease risk, maximising the usefulness of the data that are available whilst best capturing inherent uncertainties, and can be helpful for the monitoring and evaluation of interventions. Overlaying prevalence of infection maps with human population surfaces can present a novel means for burden estimation, as has been done at regional and global scales for schistosomiasis (Clements et al. Reference Clements, Garba, Sacko, Toure, Dembele, Landoure, Bosque-Oliva, Gabrielli and Fenwick2008a; Schur et al. Reference Schur, Hürlimann, Garba, Traoré, Ndir, Ratard, Tchuem Tchuenté, Kristensen, Utzinger and Vounatsou2011a) and malaria (Hay et al. Reference Hay, Okiro, Gething, Patil, Tatem, Guerra and Snow2010).
Nevertheless, despite being statistically appealing, predictive prevalence surfaces (together with their associated uncertainty) still require some degree of interpretation before being useful for practical disease control guidance. One advantage of the Bayesian approach is the ability to produce maps demonstrating the strength of evidence (i.e. the probability) that intervention prevalence thresholds have been exceeded. For example, studies have identified those areas where there is strong evidence that STH, schistosomiasis or Loa loa infection prevalence exceed policy implementation thresholds for mass drug administration, and where high uncertainty warrants further surveys (Diggle et al. Reference Diggle, Thomson, Christensen, Rowlingson, Obsomer, Gardon, Wanji, Takougang, Enyong, Kamgno, Remme, Boussinesq and Molyneux2007; Clements et al. Reference Clements, Garba, Sacko, Toure, Dembele, Landoure, Bosque-Oliva, Gabrielli and Fenwick2008a; Pullan et al. Reference Pullan, Gething, Smith, Mwandawiro, Sturrock, Gitonga, Hay and Brooker2011a). An example of such an approach applied to STH infections, taken from Pullan et al. (Reference Pullan, Gething, Smith, Mwandawiro, Sturrock, Gitonga, Hay and Brooker2011a), is shown in Fig. 3.

Fig. 3. An example of the practical applications of a model-based geostatistical (MBG) predictive mapping of soil-transmitted helminths (STH). (a) Bayesian space-time geostatistical models were developed for each STH species using survey data from 1980–2009, and were used to interpolate the probability that combined infection prevalence exceeded the 20% level defined by the World Health Organisation as a mass drug administration (MDA) threshold in 2009. (b) Population census data were overlaid with the probability models to estimate the proportion of the population at risk (i.e. >50% probability of exceeding 20% prevalence threshold) and requiring treatment in 2009 for each district. Recommended intervention districts (c) are defined as: once yearly mass drug administration (MDA), at least 33% of the district exceeds 20% prevalence threshold, and twice yearly MDA, at least 33% of the district exceeds a 50% prevalence threshold. Continued surveillance is recommended for districts where historically >75% of the district exceeded the 20% prevalence based on predictions for 1999, and areas of high uncertainty are those where we can only be 50–65% certain that prevalence is lower than 20%. Adapted from Pullan et al. 2011.
Although the most common applications of MBG typically use a binomial/logistic regression model (i.e. modelling the prevalence/presence of infection), generalised linear models can handle a variety of data types. For example, density/intensity of infection can provide a more informative indicator of disease burden than simple presence of infection for many parasites. Such data are usually over-dispersed and so better captured using a negative binomial or zero-inflated Poisson distribution. Alexander et al. (Reference Alexander, Moyeed and Stander2000) used a negative binomial MBG to model effectively individual Wuchereria bancrofti parasite count data from communities in Papau New Guinea (Alexander et al. Reference Alexander, Moyeed and Stander2000), whilst Brooker et al. (Reference Brooker, Alexander, Geiger, Moyeed, Stander, Fleming, Hotez, Correa-Oliveira and Bethony2006) adapted this model to investigate the small-scale spatial heterogeneity in STH and schistosome infections in rural and urban environments in Brazil. Spatial negative binomial and zero-inflated Poisson models of faecal egg count data have also been developed for S. mansoni, S. haematobium and hookworm at community and country levels (Vounatsou et al. Reference Vounatsou, Raso, Tanner, N'Goran and Utzinger2009; Pullan et al. Reference Pullan, Kabatereine, Quinnell and Brooker2010; Soares Magalhães et al. Reference Soares Magalhães, Biritwum, Gyapong, Brooker, Zhang, Blair, Fenwick and Clements2011b) and for S. mansoni at regional levels (Clements et al. Reference Clements, Moyeed and Brooker2006b). In addition, multinomial models have been built to stratify areas on the basis of prevalence of high- and low-intensity S. haematobium infections in West Africa (Clements et al. Reference Clements, Firth, Dembele, Garba, Toure, Sacko, Landoure, Bosque-Oliva, Barnett, Brooker and Fenwick2009b), and to model the distribution of malaria-helminth co-infections at country (Raso et al. Reference Raso, Vounatsou, Singer, N'Goran, Tanner and Utzinger2006b) and regional levels (Brooker and Clements, Reference Brooker and Clements2009). Finally, a Bayesian framework allows the inclusion of multiple imputation steps. For example, the Malaria Atlas Project has incorporated a Bayesian model to predict malaria incidence as a function of parasite prevalence directly (Patil et al. Reference Patil, Okiro, Gething, Guerra, Snow and Hay2009) within the geostatistical framework used to model infection prevalence (Hay et al. Reference Hay, Okiro, Gething, Patil, Tatem, Guerra and Snow2010).
Data used for mapping parasitic diseases typically originate from a range of sources using various diagnostics, age groups and sampling methods. A Bayesian inference approach can be adapted to account for these additional sources of uncertainty. For example a number of approaches have been used to adjust for combining data from different age groups, ranging from the inclusion of fixed regression coefficients and random alignment factors (Pullan et al. Reference Pullan, Gething, Smith, Mwandawiro, Sturrock, Gitonga, Hay and Brooker2011a; Schur et al. Reference Schur, Utzinger and Vounatsou2011c) to the incorporation of mathematical age-standardisation algorithms (Hay et al. Reference Hay, Guerra, Gething, Patil, Tatem, Noor, Kabaria, Manh, Elyazar, Brooker, Smith, Moyeed and Snow2009; Gething et al. Reference Gething, Patil, Smith, Guerra, Elyazar, Johnston, Tatem and Hay2011). Diagnostic tests for a large range of parasites typically have poor sensitivity and specificity, at least in part due to significant day-to-day and intra-specimen variation (Utzinger et al. Reference Utzinger, Booth, N'Goran, Muller, Tanner and Lengeler2001; Booth et al. Reference Booth, Vounatsou, N'Goran, Tanner and Utzinger2003; Engels and Savioli, Reference Engels and Savioli2006; Farnert, Reference Farnert2008; Leonardo et al. Reference Leonardo, Rivera, Saniel, Villacorte, Crisostomo, Hernandez, Baquilod, Erce, Martinez and Velayudhan2008; Tarafder et al. Reference Tarafder, Carabin, Joseph, Balolong, Olveda and McGarvey2010). In response, in addition to simply adjusting for the type of diagnostic method used (Pullan et al. Reference Pullan, Gething, Smith, Mwandawiro, Sturrock, Gitonga, Hay and Brooker2011a), authors have explored bivariate outcome spatial models that allow for calibration of spatially correlated data series (Crainiceanu et al. Reference Crainiceanu, Diggle and Rowlingson2008), and models that include outcomes as random variables with ‘informative’ priors defined by observed diagnostic uncertainties (Wang et al. Reference Wang, Zhou, Vounatsou, Chen, Utzinger, Yang, Steinmann and Wu2008).
Another recent extension includes adding a temporal dimension. For example, temporal effects have been handled as random coefficients when modelling STH prevalence across Kenya (Pullan et al. Reference Pullan, Gething, Smith, Mwandawiro, Sturrock, Gitonga, Hay and Brooker2011a) and malaria across Vietnam (Manh et al. Reference Manh, Clements, Thieu, Hung, Hung, Hay, Hien, Wertheim, Snow and Horby2010), explicitly allowing dependency between observations within years. This approach has been extended for mapping malaria at global scales using a sophisticated two-dimensional space-time random coefficient (Hay et al. Reference Hay, Okiro, Gething, Patil, Tatem, Guerra and Snow2010), thus simultaneously modelling correlation between data points in both space and time. Such models can provide more accurate predictions when data are distributed through time as well as space, providing a better understanding of both the contemporary distribution of infection as well as changing risks since the launch of large-scale control. Spatially explicit approaches can also help better capture environmental contexts when investigating co-occurrence of parasite species. For example, studies have used MBG approaches to investigate the geographical distribution of multiple species infection with helminths and malaria at differing spatial scales (Raso et al. Reference Raso, Vounatsou, Singer, N'Goran, Tanner and Utzinger2006b; Brooker and Clements, Reference Brooker and Clements2009; Pullan et al. Reference Pullan, Kabatereine, Bukirwa, Staedke and Brooker2011b; Soares Magalhaes et al. Reference Soares Magalhães, Biritwum, Gyapong, Brooker, Zhang, Blair, Fenwick and Clements2011b; Brooker et al. Reference Brooker, Pullan, Gitonga, Ashton, Kolaczinski, Kabatereine and Snow2012), facilitating more detailed investigation of associations between species. Lastly, MBG models have been adapted to better capture complex, non-linear relationships with covariates thus providing a deeper understanding of the determinants of infection. For example, authors have used methods such as penalised spline regression (Crainiceanu et al. Reference Crainiceanu, Ruppert and Wand2005; Gosoniu et al. Reference Gosoniu, Vounatsou, Sogoba, Maire and Smith2009; Soares Magalhaes et al. Reference Soares Magalhães, Barnett and Clements2011a).
Despite their utility, considerable caution must be used when building and interpreting complex MBG models. For example, careful consideration of appropriate model specifications and priors are essential to prevent invalid or inefficient inferences. Systematic changes in diagnostic or sampling methods over time or space can also be misinterpreted as genuine change in disease status. Most MBG models reported in the literature also assume that spatial autocorrelation does not vary with location (so-called stationary models). Whilst such an assumption may be valid across small scales, this may not be true when considering spatial processes over large geographical areas where variation in geography, control, vectors and even parasite strains can cause spatial variation in autocorrelation. To tackle this problem, a number of approaches have been developed (Gemperli, Reference Gemperli2003; Kim et al. Reference Kim, Mallick and Holmes2005; Raso et al. Reference Raso, Vounatsou, Gosoniu, Tanner, N'Goran and Utzinger2006a, Beck-Worner et al. Reference Beck-Worner, Raso, Vounatsou, N'Goran, Rigo, Parlow and Utzinger2007; Gosoniu et al. Reference Gosoniu, Vounatsou, Sogoba, Maire and Smith2009) although application at large spatial scales is still hindered by practical and computational constraints. To our knowledge, few groups have yet to tackle the issue of geographical anisotropy in parasite epidemiological analyses, although direction is likely to play an important role in observations of spatial dependency for focally transmitted infections such as schistosomiasis and trypanasomiasis (Vounatsou et al. Reference Vounatsou, Raso, Tanner, N'Goran and Utzinger2009). Stein (Reference Stein2005) however has proposed a geographically anisotropic version of the space-time covariance matrix used spatio-temporal MBG, that has since been adapted by Gething et al. (Reference Gething, Patil, Smith, Guerra, Elyazar, Johnston, Tatem and Hay2011) to model the global distribution of malaria (Stein, Reference Stein2005; Gething et al. Reference Gething, Patil, Smith, Guerra, Elyazar, Johnston, Tatem and Hay2011).
Due to the computational burden required to generate predictions at each individual prediction location, most applications of MBG models tend to be via a ‘per prediction point’ approach, yielding marginal prediction intervals that realistically capture appropriate measures of ‘local’ uncertainty. However, failing to account for spatial or temporal correlation between prediction locations can lead to gross underestimation of uncertainty when aggregating prediction estimates across regions, for example when producing country-level credible intervals (Goovaerts, Reference Goovaerts2001). A solution is to use joint or simultaneous simulation, which recreates appropriate spatial and temporal correlation in the predictive surface (Goovaerts, Reference Goovaerts2001), but which can be prohibitively intensive computationally, especially over large areas. Recently however, Gething et al. (Reference Gething, Patil and Hay2010) proposed an approximate algorithm for joint simulation, which they applied to a global scale MBG predictive model for malaria. Importantly, this approach ensured that aggregated estimates of national and regional burdens taken from continuous disease maps still maintained appropriate credible intervals.
Final predictive surfaces are also very dependent upon available data, a problem which becomes more pronounced as spatial heterogeneity increases. For example, a comparison of predictive risk maps of S. haematobium in West Africa generated using similarly robust MBG approaches but different datasets gives rise to maps which, whilst having similar regional trends, exhibit large differences in within-country distributions (Clements et al. Reference Clements, Firth, Dembele, Garba, Toure, Sacko, Landoure, Bosque-Oliva, Barnett, Brooker and Fenwick2009b; Schur et al. Reference Schur, Hürlimann, Garba, Traoré, Ndir, Ratard, Tchuem Tchuenté, Kristensen, Utzinger and Vounatsou2011a; Soares Magalhaes et al. Reference Soares Magalhães, Barnett and Clements2011a). This point is clearly illustrated in Fig. 4. Similar differences are seen for different maps of S. mansoni in East Africa (Clements et al. Reference Clements, Deville, Ndayishimiye, Brooker and Fenwick2010; Schur et al. Reference Schur, Hurlimann, Stensgaard, Chimfwembe, Mushinge, Simoonga, Kabatereine, Kristensen, Utzinger and Vounatsou2011b). Such differences can have important implications for the planning of control activities and estimations of populations at risk, and more generally highlight difficulties in interpreting models from highly spatially heterogeneous data, no matter how sophisticated the underlying model.

Fig. 4. Contrasting predictions of the distribution of Schistosomiasis haematobium generated using similarly robust MBG regression models, but different data. Model 1: Predicted prevalence of S. haematobium among individuals aged ⩽20 years during the period of 2000–2009, based on survey data from 16 West African countries. Model 2: Predicted prevalence of S. haematobium infection in boys aged 10–15 years in Burkina Faso, Mali and Ghana in 2004–2006. Inset maps show the location of survey data used in each model. Although overall trends are similar, these models show considerable differences in within country distributions, particularly in northern Burkina Faso, central Mali and much of Ghana. Figures are adapted from Schur et al. 2011 and Soares et al. 2011.
Quantifying spatial dependency in order to undertake spatial sampling
Data available to the disease mapping community have usually been collected for other purposes, such as to investigate a specific research question or to determine national or sub-national prevalence estimates, using traditional, probability-based sampling methods (Levy and Lemeshow, Reference Levy and Lemeshow2008). Such design-based sampling forms the basis of most prevalence surveys for parasitic infections, including those for Plasmodium infection (Roll Back Malaria Monitoring and Evaluation Reference Group, 2005), STHs (World Health Organization, 2006) and schistosomiasis (World Health Organization, 2006). We now know from other disciplines, such as geology and environmental sciences, that where MBG mapping is the eventual goal, such design-based sampling may be suboptimal and instead purposive (non-probability-based) sampling is generally more efficient (Brus and de Gruijter, Reference Brus and de Gruijter1997; de Gruijter et al. Reference de Gruijter, Brus, Bierkens and Knotters2006). Such purposive sampling does not involve a random selection of sites, rather sites are selected based on their location or characteristics (i.e. selected to represent a particular altitude or ecological zone). The majority of early applications of spatial sampling came from ecological or soil science, but there are now an increasing number of applications in infectious disease epidemiology, which we review here.
Recent surveys of schistosome infection have adopted a stratified cluster random sampling design in order to obtain a spatially representative sample for subsequent risk mapping (Clements et al. Reference Clements, Lwambo, Blair, Nyandindi, Kaatano, Kinung'hi, Webster, Fenwick and Brooker2006a, Reference Clements, Moyeed and Brookerb, Reference Clements, Firth, Dembele, Garba, Toure, Sacko, Landoure, Bosque-Oliva, Barnett, Brooker and Fenwick2009b). A qualitative approach to selecting survey locations was adopted in a recent nationwide school survey of Plasmodium infection in Kenya (Gitonga et al. Reference Gitonga, Karanja, Kihara, Mwanje, Juma, Snow, Noor and Brooker2010), whereby the selection of schools in each district was made with a non-probability-based method to ensure a representative spatial spread of points. Furthermore, sites were over-sampled in sparsely populated districts to allow efficient spatial interpolation in these areas. An alternative approach is spatial coverage sampling, whereby survey sites are selected to ensure maximum coverage over a given survey region, accounting for its shape and previously collected data (de Gruijter et al. Reference de Gruijter, Brus, Bierkens and Knotters2006). Van Groenigen et al. (Reference Van Groenigen, Gandah and Bouma2000) have, for example, used an iterative process to determine the configuration of sites for soil sampling that minimises the distance between any point in an area to its nearest survey site, such that an uniform distribution of sites over areas of any shape or size is obtained.
The selection of survey sites can also be informed by an understanding of the spatial structure of the outcome to be surveyed. For example, if the spatial structure of the data is known (based on a semi-variogram), it is possible to estimate the kriging variance of any configuration of survey sites a priori. This feature makes it possible to optimise the locations of surveys for spatial prediction before data are gathered (Van Groenigen et al. Reference Van Groenigen, Siderius and Stein1999; Brus et al. Reference Brus, de Gruijter, van Groenigen, Lagacherie, McBratney and Voltz2006). Where the autocorrelation structure is unknown or uncertain, pilot surveys can be conducted to quantify the spatial characteristics, which can then be used to optimize secondary data collection (Stein and Ettema, Reference Stein and Ettema2003). Alternatively, Diggle and Lophaven (Reference Diggle and Lophaven2006) propose the use of a lattice plus close pairs design which is formed of a regular grid of points with some additional sites clustered around a selected number of grid sites. Fig. 5 provides an illustration of the lattice plus close pairs design for the selection of schools in a survey of S. mansoni in Ethiopia. First, a grid of a predefined size is placed over the survey region and those schools lying closest to the interstices of the grid are selected. Second, at some of these schools, the five closest neighbouring schools are selected. This stepwise selection ensures both a good spread of sample sites which are efficient for spatial interpolation and some closely located sites which are important for quantifying the spatial structure of the outcome. Recent work by Sturrock et al. (Reference Sturrock, Gething, Ashton, Kolaczinski, Kabatereine and Brooker2011) demonstrates that use of a lattice plus close pairs design followed by kriging provided a more cost-effective approach to identify schools with high prevalence of S. mansoni compared to sampling a small number of children in every school using lot quality assurance sampling (LQAS). This work shows that, whilst LQAS performed better than spatial sampling in identifying schools with a high prevalence, its cost-effectiveness in identifying such schools was lower.

Fig. 5. (a) Illustrative example of the lattice plus close pairs design using a grid size of 50 km to select schools for surveys of S. mansoni in Oromia Regional State, Ethiopia. Dark points refer to selected schools and gray points to unselected schools. (b) A close-up of a region (black box in a) showing the locations of some of the clusters of closely located schools. Adapted from Sturrock et al. (Reference Sturrock, Gething, Ashton, Kolaczinski, Kabatereine and Brooker2011).
Researchers have recently begun to investigate optimal survey designs that also incorporate covariate information (such as environmental and climatic factors) when collecting data for mapping based on MBG techniques. Unlike optimizing sampling for spatial interpolation alone, optimizing sampling for mapping using MBG with covariates requires a spread of points in so-called feature space (i.e. across the full range of included covariates) as well as across geographic space. To find a balance between these differing requirements, Hengl et al. (Reference Hengl, Rossiter and Stein2003) propose an ‘equal-range strategy’ which ensures that equal numbers of sites are randomly selected in areas stratified by relevant covariates. By repeating this process multiple times, the sampling design with the most comprehensive spatial coverage can be chosen. Researchers have also used universal kriging variance to optimize surveys for soil, groundwater dynamics and radioactive releases (Heuvelink et al. Reference Heuvelink, Brus, de Gruijter, Lagacherie, McBratney and Voltz2006; Brus and Heuvelink, Reference Brus and Heuvelink2007; Melles et al. Reference Melles, Heuvelink, Twenhofel, van Dijk, Hiemstra, Baume and Stohlker2011). By finding the configuration of sites that minimises the universal kriging variance, a balance is struck between optimizing sampling across feature and geographic space. An appeal of this approach is that any number of covariates can be included, making it theoretically plausible to optimise surveys for multiple species with differing environmental niches. Such stratified sampling designs do however come with an important caveat: over-sampling in areas with particular characteristics (such as known higher infection prevalence) does risk invalidating standard geostatistical inference, as the implicit assumption of this approach is of non-preferential sampling. Nevertheless, given the recent increase in advocacy for integrated control of multiple parasite species, an investigation into optimal survey methods that consider both environmental correlates and spatial dependency for multiple species is clearly warranted.
DISCRETE SPATIAL VARIATION: UNDERSTANDING SPATIAL NEIGHBOURHOOD STRUCTURE
The methods described above depend on two major assumptions: that the underlying spatial process is continuous and that sufficiently detailed point-level data are available to capture this process. Certain data may only be available at a small-area level (for example, routine health surveillance data, access to water and sanitation, quality of local health services), and as such autocorrelation may only be apparent between immediate neighbours (i.e. based upon proximity rather than actual location). Alternatively, it may be difficult to obtain sufficient point-level data to model spatial variation in infection risk effectively, due to financial or practical constraints. In such instances, it may be more appropriate to make best use of spatially discrete data using hierarchical techniques. Whilst the primary focus of authors developing such techniques has often been in improving demographic and sociological data (Hentschel et al. Reference Hentschel, Lanjouw, Peter and Poggi2000), or in modelling the distribution of non-communicable disease (Jackson et al. Reference Jackson, Richardson and Best2008b; Yiannakoulias et al. Reference Yiannakoulias, Svenson and Schopflocher2009; Danaei et al. Reference Danaei, Finucane, Lin, Singh, Paciorek, Cowan, Farzadfar, Stevens, Lim, Riley and Ezzati2011), many of these methods are also applicable to parasitological and related data only available at an area level, for example the number of malaria cases or intervention population coverage. In the next section we discuss some of these applications, drawing on examples from beyond the infectious disease literature where necessary.
Discrete spatial variation: modelling discrete outcome data
A major objective when modelling discrete disease data is obtaining statistically precise local estimates of the outcome of interest, whilst maintaining fine-scale geographic resolution. This can be a considerable challenge when outcomes are rare or sample sizes are small, as small stochastic differences between areas in the number of cases can result in large apparent differences in the distribution of the outcome. By smoothing high-resolution variability, model-based approaches can compromise between (overly) uncertain within-area estimates and (overly) simplified aggregated higher level estimates, thus stabilising estimation from areas with small populations or sample sizes (Goldstein, Reference Goldstein1995). Such approaches, based upon the use of generalised linear mixed effect models, form the basis of small area estimation, with wide application in the analysis of health and social survey data (Ghosh and Rao, Reference Ghosh and Rao1994; Ghosh et al. Reference Ghosh, Natarajan, Stroud and Carlin1998; Richardson and Best, Reference Richardson and Best2003; Asiimwea et al. Reference Asiimwea, Jehopioa, Atuhairea and Mbonye2011). They are inherently non-spatial, borrowing information across all areas without considering spatial location, and smoothing to the global mean. However, they can easily be extended to include additional model complexity such as spatial dependence using discrete spatial smoothing models based on proximity. Such models, which assume positive spatial correlation between observations, essentially borrow more information from close neighbours than those further away, and so smooth local rates towards local, neighbouring values (Waller and Carlin, Reference Waller, Carlin, Gelfand, Diggle, Fuentes and Guttorp2010).
One of the first examples of spatial discrete modelling is provided by Clayton and Kaldor (Reference Clayton and Kaldor1987), who developed a Poisson regression model with area-specific random intercepts defined using a conditional autoregressive (CAR) structure to model standardised mortality ratios (in this case, cancer rates). By this approach, the area-specific random effect is generated using a simple adjacency weights matrix, such that for each observation the associated random parameter has a weighted mean given by a simple average of its defined neighbours and a conditional variance inversely proportion to the number of neighbours. This model has since been extended to a fully Bayesian formulation (Besag et al. Reference Besag, York and Mollie1991) and can be readily implemented in standard Bayesian inference software. Via this flexible inference platform, spatial CAR models can be structured to allow autocorrelation between adjacent neighbours only, or to allow spatial smoothing to extend to more distant neighbours (Wakefield, Reference Wakefield2004; MacNab, Reference MacNab2010), and can be extended to allow for: estimation of spatially varying covariates; prediction of missing data; inclusion of both spatial and non-spatial dependency; and inclusion of spatio-temporal and multivariate outcome covariance structures (Mollie, Reference Mollie, Richardson and Spiegelhalter1996; Waller and Carlin, Reference Waller, Carlin, Gelfand, Diggle, Fuentes and Guttorp2010).
A similar but less commonly used class of models are the spatial multiple membership (MM) models, which examine to what extent a latent spatially distributed variable can explain the outcomes of interest (Breslow and Clayton, Reference Breslow and Clayton1993; Goldstein, Reference Goldstein1995; Langford et al. Reference Langford, Leyland, Rasbash and Goldstein1999; Browne et al. Reference Browne, Goldstein and Rasbash2001). In contrast to CAR models, the spatial dependence here is modelled through the multiple membership relationship, with an independent area-level random effect.
CAR and MM approaches have most widely been applied to modelling rates of rare non-communicable diseases, such as cancer and heart disease (Lawson, Reference Lawson2006), usually in a developed country setting where comprehensive disease registry data are available. However in tropical epidemiology, analyses of routinely collected surveillance data have used spatial CAR and MM models on varying scales to investigate incidence of malaria in Zimbabwe, South Africa and China (Kleinschmidt et al. Reference Kleinschmidt, Sharp, Mueller and Vounatsou2002; Mabaso et al. Reference Mabaso, Vounatsou, Midzi, Da Silva and Smith2006; Clements et al. Reference Clements, Barnett, Cheng, Snow and Zhou2009c) and dengue in Rio de Janeiro, Brazil (Teixeria and Cruz, Reference Teixeria and Cruz2011) in addition to assisting in the geographical targeting of schistosomiasis control in Tanzania using collated questionnaire data (Clements et al. Reference Clements, Brooker, Nyandindi, Fenwick and Blair2008b).
There are a number of substantial methodological challenges when modelling spatially discrete data. The first of these concerns assumptions made regarding the underlying spatial process. Discrete spatial variation models consider the location of data points in terms of proximity only, rather than as literal positions, and as such the model is valid only for included data; validity is not necessarily preserved if further locations are added to the data (Diggle, Reference Diggle, Durr and Gatrell2004). For this reason, these models are not appropriate for spatial prediction in new locations (interpolation). As for methods quantifying continuous spatial dependency, discrete spatial approaches also model global spatial structure and thus assume that the degree of correlation between neighbouring units is consistent across the study area, and in all directions. This issue was recently tackled in part by Reich and colleagues (2007), who developed a 2NRCAR (CAR prior with two neighbour relations) model that is able to accommodate two difference classes of neighbour relations (e.g. east-west and north-south) (Reich et al. Reference Reich, Hodges and Carlin2007), although to our knowledge this has yet to be applied in an epidemiological context. A third issue concerns the often arbitrarily defined units of representation available for geographical analysis. This is known as the modifiable areal unit problem, by which for any specified number of spatial units, there are many ways of defining the boundaries of these units, which can produce very different results (Openshaw and Taylor, Reference Openshaw, Taylor and Wrigley1979). For example, spatial anomalies may go undetected if the scale of the underlying spatial heterogeneity is smaller than the area unit available. Although this cannot be completely overcome, careful consideration of CAR and MM models does allow smoothing between units, thus blurring the concept of a discrete unit of analysis.
Discrete spatial variation: combining point and area level data
In many instances, disease data may be available at a point level (e.g. survey or sentinel site data), although covariate information may be available only at an area level. For example, although recognised as important factors influencing the distribution of parasitic diseases at varying spatial scales, data on factors such as water supply, sanitation and hygiene (WASH), ownership and use of bednets, coverage of interventions such as mass drug administration, and poverty and deprivation indicators may only be available at district and regional levels (Esrey et al. Reference Esrey, Potash, Roberts and Shiff1991; Kazembe et al. Reference Kazembe, Appleton and Kleinschmidt2007; Soares Magalhaes et al. Reference Soares Magalhães, Barnett and Clements2011a). Alternatively, disease information may only be available aggregated at area-levels for rare outcomes, although individual-level survey data describing the distribution of explanatory factors may be readily available. Despite the aggregated nature of such data, careful analysis can provide information about the relationships between area-level risks and point-level outcomes. This process is known as ecological inference (Richardson and Monfort, Reference Richardson and Monfort2000; Jackson et al. Reference Jackson, Best and Richardson2006, Reference Clements, Garba, Sacko, Toure, Dembele, Landoure, Bosque-Oliva, Gabrielli and Fenwick2008a), and can be valuable when the effect of a variable is believed to operate through its area-level average (sometimes termed a contextual effect) (Begg and Parides, Reference Begg and Parides2003). For instance, control policies for many parasitic infections implemented at the district level have been shown to benefit indirectly those individuals who have not participated. Helminth infection prevalence in non-compliant or non-targeted individuals, for example, is typically seen to reduce after the administration of community or school-based mass chemotherapy (Bundy et al. Reference Bundy, Wong, Lewis and Horton1990; Chan et al. Reference Chan, Bradley and Bundy1997; Vanamail et al. Reference Vanamail, Ramaiah, Subramanian, Pani, Yuvaraj and Das2005; Mathieu et al. Reference Mathieu, Direny, de Rochars, Streit, Addis and Lammie2006; El-Setouhy et al. Reference El-Setouhy, Abd Elaziz, Helmy, Farid, Kamal, Ramzy, Shannon and Weil2007). This is primarily due to a reduction in the force of transmission, analogous to the ‘herd immunity effect’ seen for vaccines. However, in many instances area-level exposure-response relationships may not accurately reflect associations at the community or household level, a process known as the ecological fallacy or ecological bias (Morgenstern, Reference Morgenstern, Rothman, Greenland and Lash2008). For example, an individual-level association between individual socio-economic indicators and regional rates of disease does not necessarily imply an effect of socio-economic status on individual infection status. It can equally be caused by other confounding factors.
The magnitude of ecological bias depends upon the degree of within-area variability in exposures and confounders – if there is no variability, all individuals will experience the same degree of exposure, and so there will be no ecological bias (Wakefield and Lyons, Reference Wakefield, Lyons, Gelfand, Diggle, Fuentes and Guttorp2010). The only way to truly overcome the problem of ecological bias therefore is to supplement aggregate data with samples of data at the individual level, which on their own may be too sparse to accurately capture geographic variation but can provide an indication of intra-unit variation. Several theoretical methods have been proposed to do this, which can be used to address bias and separate individual and contextual effects when either the outcome or the exposure measure is available at an ecological level (Prentice and Sheppard, Reference Prentice and Sheppard1995; Steel and Holt, Reference Steel and Holt1996; Lasserre et al. Reference Lasserre, Guihenneuc-Jouyauc and Richardson2000; Best et al. Reference Best, Cockings, Bennett, Wakefield and Elliott2001; Wakefield and Salway, Reference Wakefield and Salway2001; Glynn et al. Reference Glynn, Wakefield, Handcock and Richardson2008). The so-called aggregate data method, for example, estimates individual-level exposure effects by regressing population-based disease rates on covariate data from survey samples in each population group (Prentice and Sheppard, Reference Prentice and Sheppard1995). An alternative approach, termed hierarchical related regression, assumes a distribution for within-area variability in exposure, and fits the implied model to aggregate data combined with small samples of individual-level exposure and outcome data (Jackson et al. Reference Jackson, Best and Richardson2006, Reference Jackson, Best and Richardson2008a).
Both of these approaches however are not inherently spatial, although the generalised linear model frameworks upon which they are based can in theory be adapted to include multiple levels of aggregation and spatial dependency between baseline risks. For example, spatial CAR models have been combined with aggregate data methods to account better for exposure effect when modelling spatially heterogeneous breast cancer rates (Guthrie et al. Reference Guthrie, Sheppard and Wakefield2002), and with hierarchical related regression when investigating sensitivity of environmental exposure and childhood leukaemia data to ecological bias (Best et al. Reference Best, Cockings, Bennett, Wakefield and Elliott2001). These approaches have yet to be applied within an infectious disease context, but they do have great potential for application in spatial parasite epidemiology, for example, to improve evaluation of intervention programmes using implementation-level, sentinel site and cluster-level data. This may be problematic in practice, as obtaining data on the same population from different sources may lead to considerable inconsistencies, such as differences in variable definition and reporting, timing, and even geographical boundaries between levels, which may in turn lead to unreliable conclusions (Jackson et al. Reference Jackson, Best and Richardson2008a).
SPATIAL POINT PROCESSES: INVESTIGATING SPATIAL CLUSTERING
The global spatial statistics described above provide an important set of epidemiological tools to inform whether spatial heterogeneity is present throughout spatially sampled measurement data. This in turn informs optimal model building and can be used to conduct spatial interpolation and prediction. These methods cannot be used to delineate explicitly the locations of individual clusters and typically make the assumption that the magnitude and scale of clustering is equal throughout the study region. Identifying the propensity for spatial clustering to occur, or the physical locations of individual clusters, is vital for both identifying areas with higher than expected underlying risk and detecting outbreaks, as well as determining the optimal spatial location and scale of interventions. It is also important to emphasise that, whilst identifying the presence of spatial clusters may be useful, it is perhaps more important epidemiologically also to gain a deeper understanding of the determinants of this clustering (Rothman, Reference Rothman1990; Alexander and Boyle, Reference Alexander, Boyle, Elliott, Wakefield, Best and Briggs2001).
Point process statistics aims to analyse the explicit location of events distributed in space under an assumption that the spatial pattern is random (i.e. the locations and numbers of points are not fixed). In parasite epidemiology and ecology, such data typically present either as point locations within a given study area (for example, residence of incident cases or location of vector breeding sites) or as counts of cases from administrative districts partitioning the study area (Waller, Reference Waller, Gelfand, Diggle, Fuentes and Guttorp2010). Point process approaches typically play two distinct roles in the analysis of such data. First, they can be used to investigate the general tendency of points to exist near points, providing a global measure of clustering averaged across the observed point locations. For example, we may be interested in whether summary global measures of clustering for disease cases differ significantly from those for the general at-risk population, and thus whether there is an overall tendency for cases to occur near other cases rather than to occur homogeneously among the population at risk. Secondly, they can be used to delineate explicitly the locations of individual clusters, or anomalous collections of points. Such clusters might be assumed to occur anywhere within the study area, or may be focused, centred around predefined foci of putatively increased risk (e.g. vector or intermediate host breeding sites) (Besag and Newell, Reference Besag and Newell1991). In both scenarios, analysis strategies usually build upon ideas of testing the hypothesis of complete spatial randomness (CSR), such as the realisation of a homogeneous Poisson process (Isham, Reference Isham, Gelfand, Diggle, Fuentes and Guttorp2010). In epidemiology, this is often complicated by the heterogeneous distribution of the at-risk population, with the null model of interest no longer being CSR, but one of spatially constant risk, and thus knowledge of the underlying distribution of the population at-risk, or of appropriate non-infected controls, is essential (Waller, Reference Waller, Gelfand, Diggle, Fuentes and Guttorp2010).
There is a rich body of literature addressing various approaches for spatial point processes, although their existing application to the ecology and epidemiology of parasitic diseases has to date been somewhat limited in scope. This is partly due to the fact that model fitting is not straightforward and often computationally complex. In addition, many approaches have been derived from a rather mathematical perspective and are not necessarily appropriate in an ecological or epidemiological context. We do not therefore provide a comprehensive review of all available methods here, but instead compare and illustrate some of the most popular contemporary approaches for detecting clustering and clusters in parasite epidemiology. More complete general reviews of methods and applications appear elsewhere (Diggle, Reference Diggle2003; Waller and Gotway, Reference Waller and Gotway2004; Gelfand et al. Reference Gelfand, Diggle, Fuentes and Guttorp2010).
Detecting global clustering in point pattern data
Investigations of global clustering usually start by testing benchmark hypotheses regarding the underlying process – i.e. is a point or case equally likely to occur at any location? Such hypothesis testing approaches include Ripley's K function (Ripley, Reference Ripley1976) and the related L function (Besag, Reference Besag1977), which provide a measure of the (scaled) number of additional events expected within distance h of a randomly selected point. Plotting K as a function of h can thus be used to describe characteristics of the point process at many different spatial scales. More recent application of these methods to infectious disease epidemiology includes investigation of urban dynamics of dengue epidemics in the Brazilian city of Belo Horizone (Almeida et al. Reference Almeida, Assuncao, Proietti and Caiaffa2008), identification of epidemic hotspots for malaria in the Kenyan western highlands (Wanjala et al. Reference Wanjala, Waitumbi, Zhou and Githeko2011), and investigation of spatial clustering of households with seropositive children during evaluation of targeted screening strategies to detect Trypanasoma cruzi infection in Peru (Levy et al. Reference Levy, Kawai, Bowman, Waller, Cabrera, Pinedo-Cancino, Seitz, Steurer, Cornejo del Carpio, Cordova-Benzaquen, Maguire, Gilman and Bern2007).
In recent years, summary test-based measures for spatial point processes have been joined by model-based approaches, using both frequentist and Bayesian inference platforms. As with models of continuous and discrete spatial variation, spatial point process models provide an objective and efficient statistical framework for investigating spatial heterogeneity, whilst adjusting for spatially varying risk factors. The more fundamental of these models are based upon the non-homogeneous Poisson process, which assumes a lack of interaction between points (i.e. complete spatial randomness) but still allows point intensity to vary over space. This assumption of independence between points may be appropriate if all spatial variation can be explained by observed or unobserved risk factors, such as climate, topography and inherited genetic risk, which are themselves spatially correlated, an assumption often fitting for non-infectious diseases (Diggle, Reference Diggle, Elliot, Wakefield, Best and Briggs2001). For infectious diseases however, stochastic spatial dependence may still remain between points even after accounting for covariates. For example, foci of parasite transmission can perpetuate and amplify spatial heterogeneity, with heavily infected individuals shedding large numbers of parasites into the environment, increasing risk for those living in close proximity. This can be modelled by hierarchical processes derived from the above non-homogeneous Poisson process, including Poisson cluster and Cox processes. These flexible models are ‘doubly stochastic’ in that they also include a random intensity function, which may be taken to be any random spatial process. As such, they are very effective for describing residual positive association between points. For example, sophisticated log-Gaussian Cox process models, which assume a Gaussian random field for the logarithm of the density function (analogous to the Gaussian geostatistical models detailed above), have been applied to investigations of tick-borne encephalitis in the Czech Republic (Benes et al. Reference Benes, Bodlak, Moller and Waagepetersen2011), and spatio-temporal surveillance of non-specific gastroenteric disease in the UK (Diggle et al. Reference Diggle, Rowlingson and Su2005). However, despite increased application in other areas of spatial epidemiology (Lawson, Reference Lawson2006) to our knowledge we have yet to see these potentially exciting methods being applied to parasite ecology.
Detecting local clusters in point pattern data
Although restricted to hypothesis testing, methods for detecting local clusters in point pattern data are perhaps the most popular point process statistical techniques currently used by parasite epidemiologists, with a variety of methods available for exploring and identifying clusters in both point and aggregated data (for an excellent review see Pfeiffer et al. Reference Pfeiffer, Robinson, Stevenson, Stevens, Rogers and Clements2008). The more popular approaches involve spatial scan statistics, the most developed of these being Kulldorff's spatial scan statistic (Kulldorff and Nagarwalla, Reference Kulldorff and Nagarwalla1995). This method constructs a series of circles of increasing size around each data location and compares the level of risk within each circle to that outside using a likelihood ratio test. A computationally convenient Monte Carlo simulation is then used to generate permutations of the observed number of cases across the entire set of data locations, allowing for testing of the null hypothesis of complete spatial randomness. Other tests that are specifically designed to detect clusters around a source, so called focused tests, include Stone's test and Diggle's test, which have been used to explore clustering of cancers around industrial plants (Stone, Reference Stone1988; Diggle, Reference Diggle1990). Results for all spatial scanning statistics are conditional only over the discrete set of data locations available, an important factor to bear in mind when data locations are based on only a sample of all potential locations (Waller and Gotway, Reference Waller and Gotway2004).
Kulldorff's spatial scan statistic was first used to explore clustering of leukaemia cases in New York (Kulldorff and Nagarwalla, Reference Kulldorff and Nagarwalla1995) and has since been used to investigate clustering for a variety of parasitic diseases, including leishmaniasis (Ryan et al. Reference Ryan, Mbui, Rashid, Wasunna, Kirigi, Marigi, Kinoti, Ngumbi, Martin, Odera, Hochberg, Bautista and Chan2006; Schriefer et al. Reference Schriefer, Guimarães, Machado, Lessa, Lessa, Lago, Ritt, Góes-Neto, Schriefer, Riley and Carvalho2009), lymphatic filariasis (Washington et al. Reference Washington, Radday, Streit, Boyd, Beach, Addiss, Lovince, Lovegrove, Lafontant, Lammie and Hightower2004) schistosomiasis (Peng et al. Reference Peng, Tao, Clements, Jiang, Zhang, Zhou and Jiang2010), and trypanosomiasis (Fèvre et al. Reference Fèvre, Coleman, Odiit, Magona, Welburn and Woolhouse2001; Gorla et al. Reference Gorla, Porcasi, Hrellac and Catala2009). The parasitic disease for which spatial scan statistics have been most widely used is malaria. Brooker et al. (Reference Brooker, Clarke, Njagi, Polack, Mugo, Estambale, Muchiri, Magnussen and Cox2004a) used spatial scan statistics to identify clusters of malaria cases during an epidemic in the highlands of Kenya. More recently, Bousema et al. (Reference Bousema, Drakeley, Gesase, Hashim, Magesa, Mosha, Otieno, Carneiro, Cox, Msuya, Kleinschmidt, Maxwell, Greenwood, Riley, Sauerwein, Chandramohan and Gosling2010) used cluster statistics to illustrate that clustering of seropositive individuals can be used to identify ‘hot spots’ of high malaria disease incidence in Tanzania. Similarly, Cook et al. (Reference Cook, Kleinschmidt, Schwabe, Nseng, Bousema, Corran, Riley and Drakeley2011) used spatial scan statistics to explore clustering of infection and seroprevalence in different age-groups to illustrate spatial heterogeneities in effectiveness of malaria control on Bioko Island in Equatorial Guinea. In a slightly different use of the test, Fevre et al. (Reference Fèvre, Coleman, Odiit, Magona, Welburn and Woolhouse2001) used spatial scan statistics to show that a cattle market was the likely source of an outbreak of Trypanosoma brucei rhodesiense sleeping sickness in Uganda.
Over the last two decades there have been several developments in spatial scan statistics allowing an exploration of clustering in a variety of different data types including multinomial (Jung et al. Reference Jung, Kulldorff and Richard2010) and ordinal (Jung et al. Reference Jung, Kulldorff and Klassen2007) data as well as detection of non-spherical clusters (Tango and Takahashi, Reference Tango and Takahashi2005; Kulldorff et al. Reference Kulldorff, Huang, Pickle and Duczmal2006; Cançado et al. Reference Cançado, Duarte, Duczmal, Ferreira, Fonseca and Gontijo2010). Where data allow, it is also possible to explore clustering through time as well as space, either by exploring years separately (Bejon et al. Reference Bejon, Williams, Liljander, Noor, Wambua, Ogada, Olotu, Osier, Hay, Farnert and Marsh2010) or by considering circular clusters as cylinders that span time (Kulldorff, Reference Kulldorff2001; Kulldorff et al. Reference Kulldorff, Heffernan, Hartman, Assuncao and Mostashari2005). Such spatio-temporal cluster analyses have been used to explore space-time clustering in diarrhoea surveillance data from emergency departments in New York (Kulldorff, Reference Kulldorff2001) and malaria in highland Kenya (Ernst et al. Reference Ernst, Adoka, Kowuor, Wilson and John2006) and South Africa (Coleman et al. Reference Coleman, Coleman, Mabuza, Kok, Coetzee and Durrheim2009). Recent advances in the use of space-time cluster detection analyses additionally include the use of statistical models to better define underlying risk (Robertson et al. Reference Robertson, Nelson, MacNab and Lawson2010a). For example, Kleinman et al. (Reference Kleinman, Abrams, Kulldorff and Platt2005) use a generalized linear mixed model, which uses information on census tract, day of the week, month of the year, holiday status and secular time, to describe the underlying spatio-temporal distribution of reported lower respiratory tract infections in Eastern Massachusetts. Spatial scan statistics are then applied to the data to detect anomalies from model-predicted risk, thus helping to avoid false alarms in areas of explained high incidence.
Other current areas of research include the incorporation of human movement data (Tatem et al. Reference Tatem, Qiu, Smith, Sabot, Ali and Moonen2009; Robertson et al. Reference Robertson, Sawford, Daniel, Nelson and Stephen2010b), which allows researchers to account for the fact that detection of risk in one area does not necessarily correspond with the initial location of infection. With the increasing availability of data from mobile phones and other technological devices with inbuilt GPS devices, such analyses will no doubt become progressively incorporated into disease surveillance systems.
Despite increasingly sophisticated cluster detection methods, a couple of important limitations should be borne in mind when embarking on disease cluster detection. First, systematic bias in study design – including inaccurate and non-standardised case definition, error in exposure measurement or inadequate control of confounding variables – can all lead to high possibility of false-positive clusters (Rothman, Reference Rothman1990). Second, such analyses can be very sensitive to the rather arbitrary assumptions required, such as selection of the scanning window shape and size and upper cluster size threshold, which in turn can lead to different results.
CONCLUSION
With the widespread use of GPS and GIS, and the availability of high resolution environmental data, spatial aspects of parasites and their vectors and intermediate hosts are becoming increasingly well understood. Such an understanding has been facilitated by the development of a wealth of statistical methods that have improved our ability both to describe and to predict parasite distributions over varying spatial scales. A growing number of these methods sit within a Bayesian framework, providing a more flexible approach to modelling that is able to account for both spatial and non-spatial uncertainty effectively. The choice of statistical method and approach used however should be guided both by the type of data available and the scientific questions of interest. A central tenet of statistics that still holds true for spatial analyses should always be borne in mind: that there is no such thing as a “correct” model, and that instead the best model is one that provides a good fit of the data as economically as possible (Bailey and Gatrell, Reference Bailey and Gatrell1995; Pfeiffer, Reference Pfeiffer and McKenzie1996; Diggle, Reference Diggle, Durr and Gatrell2004). Judgement is required to reach the correct balance between an over-simplistic model, which may risk invalid inferences, and an over-elaborate model, which may be inefficient and difficult to validate (Altham, Reference Altham1984). Nevertheless, applied spatial statistics remains an active area of research, continually providing parasitologists, ecologists and epidemiologists with novel approaches. As such, careful consideration of spatial location is rapidly becoming a routine component of parasite ecology and epidemiology.
ACKNOWLEDGEMENTS
We are grateful to the reviewers for their expert comments which greatly improved the quality of this review. RLP and HJWS are supported by grants from the Bill & Melinda Gates Foundation and GlaxoSmithKline, respectively. RJSM is funded by a Post-doctoral Research Fellowship from the University of Queensland (41795457). ACAC is funded by an Australian National Health and Medical Research Council Career Development Award (631619). SJB is funded by a Research Career Development Fellowship (081673) from the Wellcome Trust.