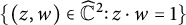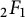1 Introduction
Let
![]() $\widehat {{\mathbb C}}:={\mathbb C} \cup \{\infty \}$
denote the Riemann sphere. The purpose of this paper is to explore the spectral theory of the complex invariant Laplace operator
$\widehat {{\mathbb C}}:={\mathbb C} \cup \{\infty \}$
denote the Riemann sphere. The purpose of this paper is to explore the spectral theory of the complex invariant Laplace operator
of the complement of the complexified unit circle,
by function-theoreticFootnote 1 methods. This approach allows a unified study of the real-analytic spectral theories of the hyperbolic Laplacian
on the open unit disk
![]() ${\mathbb D}:=\{z \in {\mathbb C} \, : \, |z|<1\}$
and the spherical Laplacian
${\mathbb D}:=\{z \in {\mathbb C} \, : \, |z|<1\}$
and the spherical Laplacian
on the Riemann sphere
![]() $\widehat {{\mathbb C}}$
from a complex analytic point of view and, in addition, it also shows how they are interrelated to one another. Beyond that, the complex point of view taken in this paper offers several other useful advantages. In particular, it connects in a natural way the fine structure of the eigenspaces of the hyperbolic and spherical Laplacians as described by Helgason [Reference Helgason21] and Rudin [Reference Rudin37] with the maximal domain of existence of the corresponding holomorphic eigenfunctions of the invariant Laplacian
$\widehat {{\mathbb C}}$
from a complex analytic point of view and, in addition, it also shows how they are interrelated to one another. Beyond that, the complex point of view taken in this paper offers several other useful advantages. In particular, it connects in a natural way the fine structure of the eigenspaces of the hyperbolic and spherical Laplacians as described by Helgason [Reference Helgason21] and Rudin [Reference Rudin37] with the maximal domain of existence of the corresponding holomorphic eigenfunctions of the invariant Laplacian
![]() $\Delta _{zw}$
.
$\Delta _{zw}$
.
As one instance, we analyze from a complex analysis point of view the building blocks of each
![]() $\lambda $
-eigenspace of the hyperbolic Laplacian
$\lambda $
-eigenspace of the hyperbolic Laplacian
![]() $\Delta _{\mathbb D}$
, which have previously been identified, e.g., by Helgason in [Reference Helgason21] using real-variable methods. It turns out that these so-called Poisson–Fourier modes naturally extend to holomorphic eigenfunctions of
$\Delta _{\mathbb D}$
, which have previously been identified, e.g., by Helgason in [Reference Helgason21] using real-variable methods. It turns out that these so-called Poisson–Fourier modes naturally extend to holomorphic eigenfunctions of
![]() $\Delta _{zw}$
which are (maximally) defined either on
$\Delta _{zw}$
which are (maximally) defined either on
![]() $\Omega $
or on one of three distinguished subdomains of
$\Omega $
or on one of three distinguished subdomains of
![]() $\Omega $
depending on the choice of the eigenvalue
$\Omega $
depending on the choice of the eigenvalue
![]() $\lambda $
. This then allows a transparent proof that each holomorphic eigenfunction of
$\lambda $
. This then allows a transparent proof that each holomorphic eigenfunction of
![]() $\Delta _{zw}$
defined on any rotationally invariant subdomain of
$\Delta _{zw}$
defined on any rotationally invariant subdomain of
![]() $\Omega $
has a unique spectral decomposition in form of a locally uniformly and absolutely convergent infinite series composed of Poisson–Fourier modes. In the special case of the bidisk
$\Omega $
has a unique spectral decomposition in form of a locally uniformly and absolutely convergent infinite series composed of Poisson–Fourier modes. In the special case of the bidisk
![]() ${\mathbb D}^2$
and further restriction to the “diagonal”
${\mathbb D}^2$
and further restriction to the “diagonal”
![]() $\{(z,\overline {z}) \, : \, z \in {\mathbb D}\},$
we recover the spectral decomposition of the smooth eigenfunctions of
$\{(z,\overline {z}) \, : \, z \in {\mathbb D}\},$
we recover the spectral decomposition of the smooth eigenfunctions of
![]() $\Delta _{{\mathbb D}}$
on the unit disk
$\Delta _{{\mathbb D}}$
on the unit disk
![]() ${\mathbb D}$
as described, e.g., in [Reference Helgason21] or [Reference Berenstein and Gay8].
${\mathbb D}$
as described, e.g., in [Reference Helgason21] or [Reference Berenstein and Gay8].
As a second instance, we investigate the structure of the closed “Möbius invariant” subspaces of any fixed eigenspace
![]() $X_\lambda ({\mathbb D})$
of
$X_\lambda ({\mathbb D})$
of
![]() $\Delta _{{\mathbb D}}$
from a complex analysis point of view. This topic has been investigated in detail by Rudin in [Reference Rudin37] using purely “real” methods. We shall see that the distinguished subdomains of
$\Delta _{{\mathbb D}}$
from a complex analysis point of view. This topic has been investigated in detail by Rudin in [Reference Rudin37] using purely “real” methods. We shall see that the distinguished subdomains of
![]() $\Omega $
mentioned above naturally lead to the same distinction between exceptional and non-exceptional eigenvalues which has been found by Rudin. In Rudin’s work, the exceptional cases correspond to the eigenvalues
$\Omega $
mentioned above naturally lead to the same distinction between exceptional and non-exceptional eigenvalues which has been found by Rudin. In Rudin’s work, the exceptional cases correspond to the eigenvalues
![]() $\lambda =4m(m+1)$
,
$\lambda =4m(m+1)$
,
![]() $m=0,1,2\ldots $
, and they are characterized by the existence of three nontrivial Möbius invariant closed subspaces of
$m=0,1,2\ldots $
, and they are characterized by the existence of three nontrivial Möbius invariant closed subspaces of
![]() $X_{\lambda }({\mathbb D})$
, exactly one of which,
$X_{\lambda }({\mathbb D})$
, exactly one of which,
![]() $X^0_\lambda ({\mathbb D})$
say, is finite dimensional. It turns out that a complex number
$X^0_\lambda ({\mathbb D})$
say, is finite dimensional. It turns out that a complex number
![]() $\lambda \in {\mathbb C}$
is an exceptional eigenvalue in the sense of Rudin if and only if the invariant Laplacian
$\lambda \in {\mathbb C}$
is an exceptional eigenvalue in the sense of Rudin if and only if the invariant Laplacian
![]() $\Delta _{zw}$
has a globally defined (that is, defined on
$\Delta _{zw}$
has a globally defined (that is, defined on
![]() $\Omega $
) holomorphic
$\Omega $
) holomorphic
![]() $\lambda $
-eigenfunction. Moreover, in this case, the unique finite-dimensional invariant subspace
$\lambda $
-eigenfunction. Moreover, in this case, the unique finite-dimensional invariant subspace
![]() $X^0_{\lambda }({\mathbb D})$
corresponds precisely to the full
$X^0_{\lambda }({\mathbb D})$
corresponds precisely to the full
![]() $\lambda $
-eigenspace of all globally defined
$\lambda $
-eigenspace of all globally defined
![]() $\lambda $
-eigenfunctions of the invariant Laplacian
$\lambda $
-eigenfunctions of the invariant Laplacian
![]() $\Delta _{zw}$
, which then, in fact, is invariant under the full group of all Möbius transformations. For the other two nontrivial invariant subspaces of the exceptional
$\Delta _{zw}$
, which then, in fact, is invariant under the full group of all Möbius transformations. For the other two nontrivial invariant subspaces of the exceptional
![]() $\Delta _{\mathbb D}$
-eigenspace
$\Delta _{\mathbb D}$
-eigenspace
![]() $X_\lambda ({\mathbb D})$
discovered by Rudin as well as the full eigenspace
$X_\lambda ({\mathbb D})$
discovered by Rudin as well as the full eigenspace
![]() $X_{\lambda }({\mathbb D})$
itself, we give a similar but more intricate description in form of Runge-type approximation results in terms of holomorphic
$X_{\lambda }({\mathbb D})$
itself, we give a similar but more intricate description in form of Runge-type approximation results in terms of holomorphic
![]() $\lambda $
-eigenfunctions defined precisely on one of the distinguished three subdomains of
$\lambda $
-eigenfunctions defined precisely on one of the distinguished three subdomains of
![]() $\Omega $
, see Theorem 2.10.
$\Omega $
, see Theorem 2.10.
In the next section, we give an account of the main results of this work and their ramifications for the spectral theory of the hyperbolic and spherical Laplacian as well as an outline of the structure of the remaining sections. The accompanying papers [Reference Heins, Moucha and Roth18, Reference Heins, Moucha, Roth and Sugawa19, Reference Kraus, Roth, Schleißinger and Waldmann27, Reference Moucha32] are related to other aspects of the function theory of the set
![]() $\Omega $
, the complement of the complexified unit circle, and its applications. Our interest in this set and its inhabitants, the holomorphic functions on
$\Omega $
, the complement of the complexified unit circle, and its applications. Our interest in this set and its inhabitants, the holomorphic functions on
![]() $\Omega $
, first arose in connection with previous work [Reference Beiser and Waldmann7, Reference Cahen, Gutt and Rawnsley10, Reference Esposito, Schmitt and Waldmann12, Reference Kraus, Roth, Schötz and Waldmann28, Reference Schmitt and Schötz41, Reference Waldmann43] on canonical Wick-type star products in strict deformation quantization of the unit disk and the Riemann sphere, and from our desire to understand the somehow mysterious role played by
$\Omega $
, first arose in connection with previous work [Reference Beiser and Waldmann7, Reference Cahen, Gutt and Rawnsley10, Reference Esposito, Schmitt and Waldmann12, Reference Kraus, Roth, Schötz and Waldmann28, Reference Schmitt and Schötz41, Reference Waldmann43] on canonical Wick-type star products in strict deformation quantization of the unit disk and the Riemann sphere, and from our desire to understand the somehow mysterious role played by
![]() $\Omega $
and, in particular, by its function-theoretic properties in this regard. A partial explanation was given in [Reference Heins, Moucha, Roth and Sugawa19], where it was indicated that invariant differential operators of Peschl–Minda type, on the one hand, effectively facilitate and unify the study of the star products on the disk and the sphere, and on the other hand, are perhaps best understood as operators acting on the spaces of holomorphic functions on
$\Omega $
and, in particular, by its function-theoretic properties in this regard. A partial explanation was given in [Reference Heins, Moucha, Roth and Sugawa19], where it was indicated that invariant differential operators of Peschl–Minda type, on the one hand, effectively facilitate and unify the study of the star products on the disk and the sphere, and on the other hand, are perhaps best understood as operators acting on the spaces of holomorphic functions on
![]() $\Omega $
and its three distinguished subdomains. We started wondering whether and how the most basic differential operator acting on
$\Omega $
and its three distinguished subdomains. We started wondering whether and how the most basic differential operator acting on
![]() $\Omega $
, the invariant Laplacian
$\Omega $
, the invariant Laplacian
![]() $\Delta _{zw}$
, and its spectral theory possibly fit into this emerging picture. This paper describes what we have found. In the forthcoming paper [Reference Moucha32] of the second-named author, these endeavours will come to full circle: it is shown that there are globally defined eigenfunctions of the Laplacian
$\Delta _{zw}$
, and its spectral theory possibly fit into this emerging picture. This paper describes what we have found. In the forthcoming paper [Reference Moucha32] of the second-named author, these endeavours will come to full circle: it is shown that there are globally defined eigenfunctions of the Laplacian
![]() $\Delta _{zw}$
which form a Schauder basis of the Fréchet space
$\Delta _{zw}$
which form a Schauder basis of the Fréchet space
![]() $\mathcal {H}(\Omega )$
of all holomorphic functions on
$\mathcal {H}(\Omega )$
of all holomorphic functions on
![]() $\Omega $
. The results of the present paper then imply that the algebra
$\Omega $
. The results of the present paper then imply that the algebra
for which the Wick-star product on
![]() ${\mathbb D}$
in [Reference Kraus, Roth, Schötz and Waldmann28] is constructed, admits a spectral decomposition precisely into the finite-dimensional invariant subspaces of the exceptional eigenspaces of the hyperbolic Laplace operator
${\mathbb D}$
in [Reference Kraus, Roth, Schötz and Waldmann28] is constructed, admits a spectral decomposition precisely into the finite-dimensional invariant subspaces of the exceptional eigenspaces of the hyperbolic Laplace operator
![]() $\Delta _{{\mathbb D}}$
on
$\Delta _{{\mathbb D}}$
on
![]() ${\mathbb D}$
discovered by Rudin [Reference Rudin37] many years ago. This provides an intrinsic characterization of the algebra
${\mathbb D}$
discovered by Rudin [Reference Rudin37] many years ago. This provides an intrinsic characterization of the algebra
![]() $\mathcal {A}({\mathbb D})$
in terms of the natural hyperbolic geometry of the unit disk and its canonical invariant Laplacian
$\mathcal {A}({\mathbb D})$
in terms of the natural hyperbolic geometry of the unit disk and its canonical invariant Laplacian
![]() $\Delta _{\mathbb D}$
.
$\Delta _{\mathbb D}$
.
2 Overview and main results
In order to place the results of this paper into a broader context, we begin by recalling in greater detail, the striking distinction between exceptional and non-exceptional eigenvalues of the hyperbolic Laplace operator
![]() $\Delta _{{\mathbb D}}$
and its relevance for the study of the invariant subspaces of the
$\Delta _{{\mathbb D}}$
and its relevance for the study of the invariant subspaces of the
![]() $\Delta _{{\mathbb D}}$
-eigenspaces which has been discovered by Rudin [Reference Rudin37]. The Fréchet space of all twice continuously (real) differentiable functions
$\Delta _{{\mathbb D}}$
-eigenspaces which has been discovered by Rudin [Reference Rudin37]. The Fréchet space of all twice continuously (real) differentiable functions
![]() $f : {\mathbb D} \to {\mathbb C}$
equipped with the standard compact-open topology is denoted by
$f : {\mathbb D} \to {\mathbb C}$
equipped with the standard compact-open topology is denoted by
![]() $C^2({\mathbb D})$
. For each
$C^2({\mathbb D})$
. For each
![]() $\lambda \in {\mathbb C}$
, we denote by
$\lambda \in {\mathbb C}$
, we denote by
![]() $X_{\lambda }({\mathbb D}),$
the vector space of all
$X_{\lambda }({\mathbb D}),$
the vector space of all
![]() $\lambda $
-eigenfunctions
$\lambda $
-eigenfunctions
![]() $f \in C^2({\mathbb D})$
of the hyperbolic Laplacian, that is,
$f \in C^2({\mathbb D})$
of the hyperbolic Laplacian, that is,
It is known that each such
![]() $\Delta _{{\mathbb D}}$
-eigenspace
$\Delta _{{\mathbb D}}$
-eigenspace
![]() $X_{\lambda }({\mathbb D})$
is a closed infinite-dimensional subspace of
$X_{\lambda }({\mathbb D})$
is a closed infinite-dimensional subspace of
![]() $C^2({\mathbb D})$
. The hyperbolic Laplacian
$C^2({\mathbb D})$
. The hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
is invariant under the full group of all conformal automorphisms (biholomorphic maps) T of the unit disk
$\Delta _{{\mathbb D}}$
is invariant under the full group of all conformal automorphisms (biholomorphic maps) T of the unit disk
![]() ${\mathbb D}$
in the sense that
${\mathbb D}$
in the sense that
In order to emphasize that this group consists entirely of Möbius transformations, we call it the Möbius group of
![]() ${\mathbb D}$
and denote it by
${\mathbb D}$
and denote it by
![]() $\mathcal {M}({\mathbb D})$
. A closed subspace Y of
$\mathcal {M}({\mathbb D})$
. A closed subspace Y of
![]() $C^2({\mathbb D})$
is called Möbius invariant if
$C^2({\mathbb D})$
is called Möbius invariant if
![]() $f \circ \psi \in Y$
for all
$f \circ \psi \in Y$
for all
![]() $f \in Y$
and all
$f \in Y$
and all
![]() $\psi \in \mathcal {M}({\mathbb D})$
.Footnote
2
It is called nontrivial if
$\psi \in \mathcal {M}({\mathbb D})$
.Footnote
2
It is called nontrivial if
![]() $Y\not =\{0\}$
and
$Y\not =\{0\}$
and
![]() $Y\not =X$
.
$Y\not =X$
.
Theorem 2.1 (Rudin [Reference Rudin37])
Let
![]() $\lambda \in {\mathbb C}$
.
$\lambda \in {\mathbb C}$
.
-
(NE) If
 $\lambda \not =4m(m+1)$
for
$\lambda \not =4m(m+1)$
for
 $m=0,1,2,\ldots $
, then
$m=0,1,2,\ldots $
, then
 $X_{\lambda }({\mathbb D})$
has no nontrivial Möbius invariant subspaces.
$X_{\lambda }({\mathbb D})$
has no nontrivial Möbius invariant subspaces. -
(E) If
 $\lambda =4m(m+1)$
for some
$\lambda =4m(m+1)$
for some
 $m=0,1,2,\ldots $
, then
$m=0,1,2,\ldots $
, then
 $X_{\lambda }({\mathbb D})$
has precisely three distinct nontrivial Möbius invariant subspaces. There is exactly one nontrivial Möbius invariant subspace of
$X_{\lambda }({\mathbb D})$
has precisely three distinct nontrivial Möbius invariant subspaces. There is exactly one nontrivial Möbius invariant subspace of
 $X_{\lambda }({\mathbb D})$
which is finite dimensional; its dimension is
$X_{\lambda }({\mathbb D})$
which is finite dimensional; its dimension is
 $2m+1$
.
$2m+1$
.
The alternative (E) in Theorem 2.1 will be called the exceptional case and the unique finite-dimensional Möbius invariant subspace of
![]() $X_{\lambda }({\mathbb D})$
will be denoted by
$X_{\lambda }({\mathbb D})$
will be denoted by
![]() $X^0_\lambda ({\mathbb D})$
. The alternative (NE) will be referred to as the non-exceptional case.
$X^0_\lambda ({\mathbb D})$
. The alternative (NE) will be referred to as the non-exceptional case.
One of the main results of the present paper is a complete analog of Theorem 2.1 with
![]() $\Delta _{{\mathbb D}}$
replaced by the differential operator
$\Delta _{{\mathbb D}}$
replaced by the differential operator
![]() $\Delta _{zw}$
(see Theorem 2.6). Apart from being potentially interesting in its own right, it provides a concrete function-theoretic description of the exceptional eigenspaces in Theorem 2.1. This also adds a conceptual component to Rudin’s handling of the invariant eigenspaces of the hyperbolic Laplace operator
$\Delta _{zw}$
(see Theorem 2.6). Apart from being potentially interesting in its own right, it provides a concrete function-theoretic description of the exceptional eigenspaces in Theorem 2.1. This also adds a conceptual component to Rudin’s handling of the invariant eigenspaces of the hyperbolic Laplace operator
![]() $\Delta _{\mathbb D}$
.
$\Delta _{\mathbb D}$
.
The characteristic feature of our approach is to look for holomorphic solutions F of the eigenvalue equation
defined on a subdomain D of
![]() $\Omega $
which we wish to choose as large as possible depending on the eigenvalue
$\Omega $
which we wish to choose as large as possible depending on the eigenvalue
![]() $\lambda $
. These maximal domains of existence (see Definition 2.5) of the
$\lambda $
. These maximal domains of existence (see Definition 2.5) of the
![]() $\lambda $
-eigenfunctions turn out to be the only essential ingredients which are needed to give a complete description of the (invariant)
$\lambda $
-eigenfunctions turn out to be the only essential ingredients which are needed to give a complete description of the (invariant)
![]() $\lambda $
-eigenspaces of the operator
$\lambda $
-eigenspaces of the operator
![]() $\Delta _{zw}$
and its offsprings
$\Delta _{zw}$
and its offsprings
![]() $\Delta _{{\mathbb D}}$
and
$\Delta _{{\mathbb D}}$
and
![]() $\Delta _{\widehat {{\mathbb C}}}$
.
$\Delta _{\widehat {{\mathbb C}}}$
.
In order to state our main results, we have to adapt the notation which we have introduced above for the hyperbolic Laplacian to the case of the differential operator
![]() $\Delta _{zw}=4(1-zw)^2 \partial _z\partial _w$
. Instead of working in the Fréchet space
$\Delta _{zw}=4(1-zw)^2 \partial _z\partial _w$
. Instead of working in the Fréchet space
![]() $C^2({\mathbb D}),$
we now fix a subdomain D of the set
$C^2({\mathbb D}),$
we now fix a subdomain D of the set
![]() $\Omega = \{(z,w) \in \widehat {{\mathbb C}} \, : \, z \cdot w\not =1\}$
, and work in the Fréchet space
$\Omega = \{(z,w) \in \widehat {{\mathbb C}} \, : \, z \cdot w\not =1\}$
, and work in the Fréchet space
![]() $\mathcal {H}(D)$
of all complex-valued holomorphic functions defined on D (again equipped with the topology of locally uniform convergence, this time on D). Our goal is to determine the holomorphic solutions
$\mathcal {H}(D)$
of all complex-valued holomorphic functions defined on D (again equipped with the topology of locally uniform convergence, this time on D). Our goal is to determine the holomorphic solutions
![]() $F : D \to {\mathbb C}$
of the eigenvalue equation (2.1), i.e., we are interested in the
$F : D \to {\mathbb C}$
of the eigenvalue equation (2.1), i.e., we are interested in the
![]() $\Delta _{zw}$
-eigenspaces
$\Delta _{zw}$
-eigenspaces
With regard to Rudin’s theorem (Theorem 2.1), a particularly natural choice for the domain D is the bidisk
![]() ${\mathbb D}^2:={\mathbb D} \times {\mathbb D}$
since it is easy to see that for every
${\mathbb D}^2:={\mathbb D} \times {\mathbb D}$
since it is easy to see that for every
![]() $F \in X_{\lambda }({\mathbb D}^2),$
the “restriction” of F to the “diagonal”
$F \in X_{\lambda }({\mathbb D}^2),$
the “restriction” of F to the “diagonal”
![]() $\{(z,\overline {z}) \, : \, z \in {\mathbb D}\}$
, that is,
$\{(z,\overline {z}) \, : \, z \in {\mathbb D}\}$
, that is,
![]() $f(z):=F(z,\overline {z})$
,
$f(z):=F(z,\overline {z})$
,
![]() $z \in {\mathbb D}$
, yields an eigenfunction
$z \in {\mathbb D}$
, yields an eigenfunction
![]() $f \in C^2({\mathbb D})$
of the hyperbolic Laplacian
$f \in C^2({\mathbb D})$
of the hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
for the eigenvalue
$\Delta _{{\mathbb D}}$
for the eigenvalue
![]() $\lambda $
. In fact, the following result shows that every
$\lambda $
. In fact, the following result shows that every
![]() $f \in X_{\lambda }({\mathbb D})$
arises in this fashion, that is, it has an “extension” to an eigenfunction F of
$f \in X_{\lambda }({\mathbb D})$
arises in this fashion, that is, it has an “extension” to an eigenfunction F of
![]() $\Delta _{zw}$
which is holomorphic on the bidisk
$\Delta _{zw}$
which is holomorphic on the bidisk
![]() ${\mathbb D}^2$
.
${\mathbb D}^2$
.
Theorem 2.2 (Smooth eigenfunctions of
 $\Delta _{{\mathbb D}}$
on
$\Delta _{{\mathbb D}}$
on
 ${\mathbb D}$
vs. holomorphic eigenfunctions of
${\mathbb D}$
vs. holomorphic eigenfunctions of
 $\Delta _{zw}$
on
$\Delta _{zw}$
on
 ${\mathbb D}^2$
)
${\mathbb D}^2$
)
Let
![]() $\lambda \in {\mathbb C}$
and
$\lambda \in {\mathbb C}$
and
![]() $f \in C^{2}({\mathbb D})$
such that
$f \in C^{2}({\mathbb D})$
such that
![]() $\Delta _{{\mathbb D}} f=\lambda f$
on
$\Delta _{{\mathbb D}} f=\lambda f$
on
![]() ${\mathbb D}$
. Then there is a uniquely determined function
${\mathbb D}$
. Then there is a uniquely determined function
![]() $F \in \mathcal {H}({\mathbb D}^2)$
such that
$F \in \mathcal {H}({\mathbb D}^2)$
such that
![]() $\Delta _{zw}F=\lambda F$
on
$\Delta _{zw}F=\lambda F$
on
![]() ${\mathbb D}^2$
and
${\mathbb D}^2$
and
![]() $f(z)=F(z,\overline {z})$
for all
$f(z)=F(z,\overline {z})$
for all
![]() $z \in {\mathbb D}$
. Moreover, the induced bijective linear map
$z \in {\mathbb D}$
. Moreover, the induced bijective linear map
is continuous.
Remark 2.3 If
![]() $f \in C^2({\mathbb D})$
solves
$f \in C^2({\mathbb D})$
solves
![]() $\Delta _{{\mathbb D}} f=\lambda f$
on
$\Delta _{{\mathbb D}} f=\lambda f$
on
![]() ${\mathbb D}$
, then f is real-analytic (see [Reference Rudin38, Theorem 4.2.5]), so there is trivially a holomorphic function
${\mathbb D}$
, then f is real-analytic (see [Reference Rudin38, Theorem 4.2.5]), so there is trivially a holomorphic function
![]() $\tilde {F}$
defined on some open neighborhood
$\tilde {F}$
defined on some open neighborhood
![]() $U \subseteq {\mathbb D}^2$
of the diagonal
$U \subseteq {\mathbb D}^2$
of the diagonal
![]() $((z,\overline {z}) \in {\mathbb D}^2 \, : \, z \in {\mathbb D})$
such that
$((z,\overline {z}) \in {\mathbb D}^2 \, : \, z \in {\mathbb D})$
such that
![]() $\tilde {F}(z,\overline {z})=f(z)$
for all
$\tilde {F}(z,\overline {z})=f(z)$
for all
![]() $z \in {\mathbb D}$
satisfying
$z \in {\mathbb D}$
satisfying
![]() $(z,\overline {z}) \in U$
. In view of a well-known variant of the identity principle (see Lemma 3.1) there is only one such holomorphic extension
$(z,\overline {z}) \in U$
. In view of a well-known variant of the identity principle (see Lemma 3.1) there is only one such holomorphic extension
![]() $\tilde {F} : U \to {\mathbb C}$
of
$\tilde {F} : U \to {\mathbb C}$
of
![]() $f \in C^2({\mathbb D})$
to U. The point of Theorem 2.2 is that
$f \in C^2({\mathbb D})$
to U. The point of Theorem 2.2 is that
![]() $\tilde {F}$
has a holomorphic extension (at least) to the bidisk
$\tilde {F}$
has a holomorphic extension (at least) to the bidisk
![]() ${\mathbb D}^2$
.
${\mathbb D}^2$
.
Theorem 2.2 gives rise to the following definition.
Definition 2.4 Let
![]() $\lambda \in {\mathbb D}$
. Then the continuous bijective linear mapping
$\lambda \in {\mathbb D}$
. Then the continuous bijective linear mapping
is called the hyperbolic restriction map. Its continuous inverse
is called the hyperbolic extension map from
![]() $X_{\lambda }({\mathbb D})$
to
$X_{\lambda }({\mathbb D})$
to
![]() $X_{\lambda }({\mathbb D}^2)$
.
$X_{\lambda }({\mathbb D}^2)$
.
The hyperbolic restriction and extension mappings provide the bridge between the holomorphic spectral theory of the invariant Laplacian
![]() $\Delta _{zw}$
and the smooth spectral theory of the hyperbolic Laplacian
$\Delta _{zw}$
and the smooth spectral theory of the hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
. In particular, one can study the spectral properties of
$\Delta _{{\mathbb D}}$
. In particular, one can study the spectral properties of
![]() $\Delta _{{\mathbb D}}$
on
$\Delta _{{\mathbb D}}$
on
![]() ${\mathbb D}$
from the viewpoint of complex analysis on the bidisk
${\mathbb D}$
from the viewpoint of complex analysis on the bidisk
![]() ${\mathbb D}^2$
. Based on Theorem 2.2, we can now proceed to associate the fine structure of the eigenspaces
${\mathbb D}^2$
. Based on Theorem 2.2, we can now proceed to associate the fine structure of the eigenspaces
![]() $X_{\lambda }({\mathbb D})$
with the maximal domains of existence of holomorphic eigenfunctions in
$X_{\lambda }({\mathbb D})$
with the maximal domains of existence of holomorphic eigenfunctions in
![]() $X_{\lambda }({\mathbb D}^2)$
, a concept which is defined as follows (cf. [Reference Fritzsche and Grauert14, p. 97]).
$X_{\lambda }({\mathbb D}^2)$
, a concept which is defined as follows (cf. [Reference Fritzsche and Grauert14, p. 97]).
Definition 2.5 Let F be a holomorphic function on the bidisk
![]() ${\mathbb D}^2$
. A subdomain
${\mathbb D}^2$
. A subdomain
![]() ${D \subseteq \Omega }$
that contains the bidisk
${D \subseteq \Omega }$
that contains the bidisk
![]() ${\mathbb D}^2$
is called a maximal domain of existence of F if the function F has a holomorphic extension to D but to no strictly larger subdomain of
${\mathbb D}^2$
is called a maximal domain of existence of F if the function F has a holomorphic extension to D but to no strictly larger subdomain of
![]() $\Omega $
.
$\Omega $
.
For our purposes, this definition is natural in several respects. First, the condition
![]() $D \supseteq {\mathbb D}^2$
obviously comes from Theorem 2.2. Second, the condition
$D \supseteq {\mathbb D}^2$
obviously comes from Theorem 2.2. Second, the condition
![]() $D \subseteq \Omega $
is natural in view of the fact that every function which is holomorphic on a subdomain of
$D \subseteq \Omega $
is natural in view of the fact that every function which is holomorphic on a subdomain of
![]() $\widehat {{\mathbb C}}^2$
that is strictly larger than
$\widehat {{\mathbb C}}^2$
that is strictly larger than
![]() $\Omega $
is necessarily constant (see Theorem 5.3 in [Reference Heins, Moucha and Roth18]). In particular, the largest possible maximal domain of existence of any eigenfunction of
$\Omega $
is necessarily constant (see Theorem 5.3 in [Reference Heins, Moucha and Roth18]). In particular, the largest possible maximal domain of existence of any eigenfunction of
![]() $\Delta _{zw}$
in
$\Delta _{zw}$
in
![]() $\mathcal {H}({\mathbb D}^2)$
is
$\mathcal {H}({\mathbb D}^2)$
is
![]() $\Omega $
. Note, this also means that the maximal domain of existence for the constant eigenfunctions is
$\Omega $
. Note, this also means that the maximal domain of existence for the constant eigenfunctions is
![]() $\Omega $
.
$\Omega $
.
With this concept at hand, we can now give a function-theoretic characterization of the exceptional eigenvalues of the hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
and the corresponding unique finite-dimensional nontrivial Möbius invariant subspaces
$\Delta _{{\mathbb D}}$
and the corresponding unique finite-dimensional nontrivial Möbius invariant subspaces
![]() $X_\lambda ^0({\mathbb D})$
of the
$X_\lambda ^0({\mathbb D})$
of the
![]() $\Delta _{{\mathbb D}}$
-eigenspaces
$\Delta _{{\mathbb D}}$
-eigenspaces
![]() $X_{\lambda }({\mathbb D})$
. In addition, the following theorem provides an equivalent condition in terms of existence of globally defined eigenfunctions of the spherical Laplacian
$X_{\lambda }({\mathbb D})$
. In addition, the following theorem provides an equivalent condition in terms of existence of globally defined eigenfunctions of the spherical Laplacian
![]() $\Delta _{\widehat {{\mathbb C}}}$
.
$\Delta _{\widehat {{\mathbb C}}}$
.
Theorem 2.6 (Exceptional smooth eigenfunctions
 $\Delta _{{\mathbb D}}$
on
$\Delta _{{\mathbb D}}$
on
 ${\mathbb D}$
vs. holomorphic eigenfunctions of
${\mathbb D}$
vs. holomorphic eigenfunctions of
 $\Delta _{zw}$
on
$\Delta _{zw}$
on
 $\Omega $
vs. smooth eigenfunctions of
$\Omega $
vs. smooth eigenfunctions of
 $\Delta _{\widehat {{\mathbb C}}}$
on
$\Delta _{\widehat {{\mathbb C}}}$
on
 $\widehat {{\mathbb C}}$
)
$\widehat {{\mathbb C}}$
)
Let
![]() $\lambda \in {\mathbb C}$
. Then the following conditions are pairwise equivalent:
$\lambda \in {\mathbb C}$
. Then the following conditions are pairwise equivalent:
-
(i) There exists a function
 $F \in X_{\lambda }({\mathbb D}^2)$
with
$F \in X_{\lambda }({\mathbb D}^2)$
with
 $\Omega $
as maximal domain of existence.
$\Omega $
as maximal domain of existence. -
(ii) There exists a function
 $g \in C^{2}(\widehat {{\mathbb C}})$
such that
$g \in C^{2}(\widehat {{\mathbb C}})$
such that
 $\Delta _{\widehat {{\mathbb C}}} g=\lambda g$
on
$\Delta _{\widehat {{\mathbb C}}} g=\lambda g$
on
 $\widehat {{\mathbb C}}$
.
$\widehat {{\mathbb C}}$
. -
(iii)
 $\lambda $
is an exceptional eigenvalue of
$\lambda $
is an exceptional eigenvalue of
 $\Delta _{{\mathbb D}}$
, i.e.,
$\Delta _{{\mathbb D}}$
, i.e.,
 $\lambda =4 m (m+1)$
for some nonnegative integer m.
$\lambda =4 m (m+1)$
for some nonnegative integer m.
If one of these conditions is in place and
![]() $\lambda =4m(m+1)$
, then
$\lambda =4m(m+1)$
, then
![]() $\dim X_{\lambda }(\Omega )=2m+1$
and the following statements hold:
$\dim X_{\lambda }(\Omega )=2m+1$
and the following statements hold:
-
(a) (Function-theoretic description of
 $X_\lambda ^0({\mathbb D})$
)
$X_\lambda ^0({\mathbb D})$
)The domain
 $\Omega $
is the maximal domain of existence for every
$\Omega $
is the maximal domain of existence for every
 $F \in X_\lambda ^0({\mathbb D}^2)$
, i.e.,
$F \in X_\lambda ^0({\mathbb D}^2)$
, i.e.,  $$ \begin{align*}X^0_{\lambda}({\mathbb D})=\mathcal{R}_h\left(X_{\lambda}(\Omega)\right) .\end{align*} $$
$$ \begin{align*}X^0_{\lambda}({\mathbb D})=\mathcal{R}_h\left(X_{\lambda}(\Omega)\right) .\end{align*} $$
-
(b) (Function-theoretic description of the smooth eigenfunctions of
 $\Delta _{\widehat {{\mathbb C}}}$
on
$\Delta _{\widehat {{\mathbb C}}}$
on
 $\widehat {{\mathbb C}}$
) (2.2)
$\widehat {{\mathbb C}}$
) (2.2) $$ \begin{align} \big\{ g \in C^2(\widehat{{\mathbb C}}) \, : \, \Delta_{\widehat{{\mathbb C}}} g=\lambda g \text{ on } \widehat{{\mathbb C}}\big\}=\big\{\widehat{{\mathbb C}} \ni z \mapsto F(z,-\overline{z}) \, : \, F \in X_{\lambda}(\Omega) \big\} . \end{align} $$
$$ \begin{align} \big\{ g \in C^2(\widehat{{\mathbb C}}) \, : \, \Delta_{\widehat{{\mathbb C}}} g=\lambda g \text{ on } \widehat{{\mathbb C}}\big\}=\big\{\widehat{{\mathbb C}} \ni z \mapsto F(z,-\overline{z}) \, : \, F \in X_{\lambda}(\Omega) \big\} . \end{align} $$
Remark 2.7
-
(a) Note that
 $X_0^0({\mathbb D}^2)$
and
$X_0^0({\mathbb D}^2)$
and
 $X_0(\Omega )$
consist precisely of the constant functions.
$X_0(\Omega )$
consist precisely of the constant functions. -
(b) In view of Theorem 2.6, an eigenvalue
 $\lambda $
of
$\lambda $
of
 $\Delta _{{\mathbb D}}$
is exceptional if and only if there exists a holomorphic eigenfunction of
$\Delta _{{\mathbb D}}$
is exceptional if and only if there exists a holomorphic eigenfunction of
 $\Delta _{zw}$
on
$\Delta _{zw}$
on
 ${\mathbb D}^2$
with the largest possible maximal domain of existence, the set
${\mathbb D}^2$
with the largest possible maximal domain of existence, the set
 $\Omega $
.
$\Omega $
. -
(c) In Theorem 2.6(a), we think of
 $X_{\lambda }(\Omega )$
as a subspace of
$X_{\lambda }(\Omega )$
as a subspace of
 $X_{\lambda }({\mathbb D}^2)$
. It is a closed subspace of
$X_{\lambda }({\mathbb D}^2)$
. It is a closed subspace of
 $X_{\lambda }({\mathbb D}^2)$
(in the topology of
$X_{\lambda }({\mathbb D}^2)$
(in the topology of
 $\mathcal {H}({\mathbb D}^2)$
) because it is finite dimensional.
$\mathcal {H}({\mathbb D}^2)$
) because it is finite dimensional. -
(d) (Spherical restriction map)
If
 $\lambda \in {\mathbb C}$
is an exceptional eigenvalue, then the spherical restriction map is well-defined. By Theorem 2.6(b),
$\lambda \in {\mathbb C}$
is an exceptional eigenvalue, then the spherical restriction map is well-defined. By Theorem 2.6(b), $$ \begin{align*}\mathcal{R}_s : X_{\lambda}(\Omega) \to C^2(\widehat{{\mathbb C}}) , \qquad \mathcal{R}_s(F)(z):=F(z,-\overline{z}) \qquad (z \in \widehat{{\mathbb C}})\end{align*} $$
$$ \begin{align*}\mathcal{R}_s : X_{\lambda}(\Omega) \to C^2(\widehat{{\mathbb C}}) , \qquad \mathcal{R}_s(F)(z):=F(z,-\overline{z}) \qquad (z \in \widehat{{\mathbb C}})\end{align*} $$
 $\mathcal {R}_s$
is a bijection from
$\mathcal {R}_s$
is a bijection from
 $X_{\lambda }(\Omega )$
onto the
$X_{\lambda }(\Omega )$
onto the
 $\lambda $
-eigenspace
$\lambda $
-eigenspace
 $\big \{ g \in C^2(\widehat {{\mathbb C}}) \, : \, \Delta _{\widehat {{\mathbb C}}} g=\lambda g \text { on } \widehat {{\mathbb C}}\big \}$
of
$\big \{ g \in C^2(\widehat {{\mathbb C}}) \, : \, \Delta _{\widehat {{\mathbb C}}} g=\lambda g \text { on } \widehat {{\mathbb C}}\big \}$
of
 $\Delta _{\widehat {{\mathbb C}}}$
, which is clearly continuous.
$\Delta _{\widehat {{\mathbb C}}}$
, which is clearly continuous.
With Theorem 2.6, we have reached two of our goals, a conceptual characterization of exceptional eigenvalues and the finite-dimensional nontrivial Möbius invariant subspaces of the eigenspaces
![]() $X_{\lambda }({\mathbb D})$
of the hyperbolic Laplacian
$X_{\lambda }({\mathbb D})$
of the hyperbolic Laplacian
![]() $\Delta _{\mathbb D}$
. Next, we address the infinite-dimensional nontrivial Möbius invariant subspaces of the
$\Delta _{\mathbb D}$
. Next, we address the infinite-dimensional nontrivial Möbius invariant subspaces of the
![]() $\Delta _{{\mathbb D}}$
-eigenspaces
$\Delta _{{\mathbb D}}$
-eigenspaces
![]() $X_{\lambda }({\mathbb D})$
. This turns out to be more difficult, and first requires clarification of the invariance properties of the Laplacian
$X_{\lambda }({\mathbb D})$
. This turns out to be more difficult, and first requires clarification of the invariance properties of the Laplacian
![]() $\Delta _{zw}$
. Implicitly, the underlying difficulty is already present in Theorem 2.6, and can be seen as follows. Let
$\Delta _{zw}$
. Implicitly, the underlying difficulty is already present in Theorem 2.6, and can be seen as follows. Let
![]() $\lambda \in {\mathbb C}$
be an exceptional eigenvalue of
$\lambda \in {\mathbb C}$
be an exceptional eigenvalue of
![]() $\Delta _{{\mathbb D}}$
. Then the finite-dimensional Möbius invariant subspace
$\Delta _{{\mathbb D}}$
. Then the finite-dimensional Möbius invariant subspace
![]() $X^0_\lambda ({\mathbb D})$
is invariant under all automorphisms of
$X^0_\lambda ({\mathbb D})$
is invariant under all automorphisms of
![]() ${\mathbb D}$
. However, the corresponding eigenspace
${\mathbb D}$
. However, the corresponding eigenspace
![]() $X_{\lambda }(\Omega )$
for
$X_{\lambda }(\Omega )$
for
![]() $\Delta _{zw}$
, which consists of functions holomorphic on
$\Delta _{zw}$
, which consists of functions holomorphic on
![]() $\Omega $
is, loosely speaking, invariant under a much larger group of automorphisms. In fact, we first note that the invariant Laplacian
$\Omega $
is, loosely speaking, invariant under a much larger group of automorphisms. In fact, we first note that the invariant Laplacian
![]() $\Delta _{zw}$
of
$\Delta _{zw}$
of
![]() $\Omega $
is not invariant under all biholomorphic automorphisms of
$\Omega $
is not invariant under all biholomorphic automorphisms of
![]() $\Omega $
in the sense that the invariance condition
$\Omega $
in the sense that the invariance condition
holds for all
![]() $T \in {\textsf {Aut}}(\Omega )$
. The reason is simply that the automorphism group
$T \in {\textsf {Aut}}(\Omega )$
. The reason is simply that the automorphism group
![]() ${\textsf {Aut}}(\Omega )$
is much too large (see [Reference Heins, Moucha and Roth18]). However,
${\textsf {Aut}}(\Omega )$
is much too large (see [Reference Heins, Moucha and Roth18]). However,
![]() $\Delta _{zw}$
is invariant under the subgroup
$\Delta _{zw}$
is invariant under the subgroup
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() ${\textsf {Aut}}(\Omega )$
defined by
${\textsf {Aut}}(\Omega )$
defined by
 $$ \begin{align} \mathcal{M} := \bigcup \limits_{ \psi \in \mathcal{M}(\widehat{{\mathbb C}})} \left\{ (z,w) \mapsto \left( \psi(z),\frac{1}{\psi(1/w)} \right), \, (z,w) \mapsto \left( \psi(w),\frac{1}{\psi(1/z)} \right) \right\}, \end{align} $$
$$ \begin{align} \mathcal{M} := \bigcup \limits_{ \psi \in \mathcal{M}(\widehat{{\mathbb C}})} \left\{ (z,w) \mapsto \left( \psi(z),\frac{1}{\psi(1/w)} \right), \, (z,w) \mapsto \left( \psi(w),\frac{1}{\psi(1/z)} \right) \right\}, \end{align} $$
where we write
![]() $\mathcal {M}(\widehat {{\mathbb C}})$
for the group of all Möbius transformations
$\mathcal {M}(\widehat {{\mathbb C}})$
for the group of all Möbius transformations
![]() $\psi :\widehat {{\mathbb C}}\to \widehat {{\mathbb C}}$
. This is easy to prove by direct verification. (Conversely, one can show that every
$\psi :\widehat {{\mathbb C}}\to \widehat {{\mathbb C}}$
. This is easy to prove by direct verification. (Conversely, one can show that every
![]() $T \in {\textsf {Aut}}(\Omega )$
for which the invariance property (2.3) holds does necessarily belong to the subgroup
$T \in {\textsf {Aut}}(\Omega )$
for which the invariance property (2.3) holds does necessarily belong to the subgroup
![]() $\mathcal {M}$
, see [Reference Heins, Moucha and Roth18, Theorem 5.2], but we do not need such a result in this paper.) Since
$\mathcal {M}$
, see [Reference Heins, Moucha and Roth18, Theorem 5.2], but we do not need such a result in this paper.) Since
![]() $\mathcal {M}$
is “induced” by the set
$\mathcal {M}$
is “induced” by the set
![]() $\mathcal {M}(\widehat {{\mathbb C}})$
of all Möbius transformations, we call
$\mathcal {M}(\widehat {{\mathbb C}})$
of all Möbius transformations, we call
![]() $\mathcal {M}$
the Möbius group of
$\mathcal {M}$
the Möbius group of
![]() $\Omega $
. Note that
$\Omega $
. Note that
![]() $\mathcal {M}(\widehat {{\mathbb C}})$
is strictly bigger than
$\mathcal {M}(\widehat {{\mathbb C}})$
is strictly bigger than
![]() $\mathcal {M}({\mathbb D})$
,Footnote
3
so the Möbius group
$\mathcal {M}({\mathbb D})$
,Footnote
3
so the Möbius group
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\Omega $
is strictly larger than the Möbius group
$\Omega $
is strictly larger than the Möbius group
![]() $\mathcal {M}({\mathbb D})$
of
$\mathcal {M}({\mathbb D})$
of
![]() ${\mathbb D}$
. Now, while
${\mathbb D}$
. Now, while
![]() $X^0_\lambda ({\mathbb D})$
is invariant under each element of
$X^0_\lambda ({\mathbb D})$
is invariant under each element of
![]() $\mathcal {M}({\mathbb D})$
, the set
$\mathcal {M}({\mathbb D})$
, the set
![]() $X_{\lambda }(\Omega )$
is invariant under each element of
$X_{\lambda }(\Omega )$
is invariant under each element of
![]() $\mathcal {M}$
, simply because
$\mathcal {M}$
, simply because
![]() $X_{\lambda }(\Omega )$
is the entire
$X_{\lambda }(\Omega )$
is the entire
![]() $\lambda $
-eigenspace of the Laplacian
$\lambda $
-eigenspace of the Laplacian
![]() $\Delta _{zw}$
on
$\Delta _{zw}$
on
![]() $\Omega $
and
$\Omega $
and
![]() $\Delta _{zw}$
is invariant with respect to the Möbius group
$\Delta _{zw}$
is invariant with respect to the Möbius group
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
In view of this discussion, it is now clear that a suitable concept of invariance for the eigenspaces
![]() $X_{\lambda }({\mathbb D}^2)$
of
$X_{\lambda }({\mathbb D}^2)$
of
![]() $\Delta _{zw}$
on the bidisk
$\Delta _{zw}$
on the bidisk
![]() ${\mathbb D}^2$
has to be based on the group
${\mathbb D}^2$
has to be based on the group
which we call the Möbius group of the bidisk
![]() ${\mathbb D}^2$
. It consists precisely of all automorphisms of the bidisk
${\mathbb D}^2$
. It consists precisely of all automorphisms of the bidisk
![]() ${\mathbb D}^2$
which have the invariance property (2.3). In fact, it is not difficult to show that
${\mathbb D}^2$
which have the invariance property (2.3). In fact, it is not difficult to show that
 $$ \begin{align} \mathcal{M}({\mathbb D}^2) = \!\!\! \bigcup \limits_{ \psi \in \mathcal{M}({\mathbb D})} \! \left\{ (z,w) \mapsto \left( \psi(z),\frac{1}{\psi(1/w)} \right) , \, (z,w) \mapsto \left( \psi(w),\frac{1}{\psi(1/z)} \right) \right\}. \end{align} $$
$$ \begin{align} \mathcal{M}({\mathbb D}^2) = \!\!\! \bigcup \limits_{ \psi \in \mathcal{M}({\mathbb D})} \! \left\{ (z,w) \mapsto \left( \psi(z),\frac{1}{\psi(1/w)} \right) , \, (z,w) \mapsto \left( \psi(w),\frac{1}{\psi(1/z)} \right) \right\}. \end{align} $$
Clearly, each
![]() $\Delta _{zw}$
-eigenspace
$\Delta _{zw}$
-eigenspace
![]() $X_{\lambda }({\mathbb D}^2)$
is invariant with respect to
$X_{\lambda }({\mathbb D}^2)$
is invariant with respect to
![]() $\mathcal {M}({\mathbb D}^2)$
, that is, whenever
$\mathcal {M}({\mathbb D}^2)$
, that is, whenever
![]() ${F \in X_{\lambda }({\mathbb D}^2)}$
and
${F \in X_{\lambda }({\mathbb D}^2)}$
and
![]() $T \in \mathcal {M}({\mathbb D}^2)$
, then
$T \in \mathcal {M}({\mathbb D}^2)$
, then
![]() $F \circ T \in X_{\lambda }({\mathbb D}^2)$
. Each closed subspace of
$F \circ T \in X_{\lambda }({\mathbb D}^2)$
. Each closed subspace of
![]() $\mathcal {H}({\mathbb D}^2)$
which is invariant under the Möbius group
$\mathcal {H}({\mathbb D}^2)$
which is invariant under the Möbius group
![]() $\mathcal {M}({\mathbb D}^2)$
will be called a Möbius invariant subspace. Theorem 2.2 implies immediately the following result.
$\mathcal {M}({\mathbb D}^2)$
will be called a Möbius invariant subspace. Theorem 2.2 implies immediately the following result.
Corollary 2.8 Let
![]() $\lambda \in {\mathbb C}$
and Y be a subspace of
$\lambda \in {\mathbb C}$
and Y be a subspace of
![]() $X_{\lambda }({\mathbb D})$
. Then Y is Möbius invariant if and only if
$X_{\lambda }({\mathbb D})$
. Then Y is Möbius invariant if and only if
![]() $\mathcal {E}_h(Y)$
is a Möbius invariant subspace of
$\mathcal {E}_h(Y)$
is a Möbius invariant subspace of
![]() $X_{\lambda }({\mathbb D}^2)$
.
$X_{\lambda }({\mathbb D}^2)$
.
We can now give a function-theoretic characterization of the Möbius invariant subspaces of
![]() $X_{\lambda }({\mathbb D}^2)$
and thereby, in view of Corollary 2.8, the Möbius invariant subspaces of
$X_{\lambda }({\mathbb D}^2)$
and thereby, in view of Corollary 2.8, the Möbius invariant subspaces of
![]() $X_{\lambda }({\mathbb D})$
. The following subdomains of
$X_{\lambda }({\mathbb D})$
. The following subdomains of
![]() $\Omega $
play the essential role for this purpose:
$\Omega $
play the essential role for this purpose:

Note that each of these three subdomains of
![]() $\Omega $
contains the bidisk
$\Omega $
contains the bidisk
![]() ${\mathbb D}^2$
. Moreover,
${\mathbb D}^2$
. Moreover,
and
Figure 1 provides a schematic view of
![]() $\Omega $
and its distinguished subsets.
$\Omega $
and its distinguished subsets.

Figure 1: Schematic picture of the sets
![]() $\Omega _*$
,
$\Omega _*$
,
![]() $\Omega _+$
,
$\Omega _+$
,
![]() $\Omega _-$
, and
$\Omega _-$
, and
![]() $\Omega $
(from left to right) with points at infinity. Here,
$\Omega $
(from left to right) with points at infinity. Here,
![]() ${\mathbb D}$
is identified with the diagonal
${\mathbb D}$
is identified with the diagonal
![]() $\{(z,\overline {z}) \, : \, z \in {\mathbb D}\}$
and
$\{(z,\overline {z}) \, : \, z \in {\mathbb D}\}$
and
![]() $\widehat {{\mathbb C}}$
with the rotated diagonal
$\widehat {{\mathbb C}}$
with the rotated diagonal
![]() $\{(z,-\overline {z}) \, : \, z \in \widehat {{\mathbb C}}\}$
.
$\{(z,-\overline {z}) \, : \, z \in \widehat {{\mathbb C}}\}$
.
We note in passing that the subdomains
![]() $\Omega _+$
and
$\Omega _+$
and
![]() $\Omega _-$
arise naturally in the study of the Fréchet space structure of
$\Omega _-$
arise naturally in the study of the Fréchet space structure of
![]() $\mathcal {H}(\Omega )$
(see [Reference Heins, Moucha and Roth18]) and also for studying invariant differential operators of Peschl–Minda type acting on
$\mathcal {H}(\Omega )$
(see [Reference Heins, Moucha and Roth18]) and also for studying invariant differential operators of Peschl–Minda type acting on
![]() $\mathcal {H}(\Omega )$
(see [Reference Heins, Moucha, Roth and Sugawa19]). The following result shows that they are also useful for describing the Möbius invariant subspaces of the eigenspaces of the invariant Laplacian
$\mathcal {H}(\Omega )$
(see [Reference Heins, Moucha, Roth and Sugawa19]). The following result shows that they are also useful for describing the Möbius invariant subspaces of the eigenspaces of the invariant Laplacian
![]() $\Delta _{zw}$
. We use the following terminology.
$\Delta _{zw}$
. We use the following terminology.
Definition 2.9 Let
![]() $U \subseteq V$
be subdomains of some complex manifold, and let
$U \subseteq V$
be subdomains of some complex manifold, and let
![]() $Y \subseteq X$
be subsets of
$Y \subseteq X$
be subsets of
![]() $\mathcal {H}(U)$
. We say that “
$\mathcal {H}(U)$
. We say that “
![]() $X \cap \mathcal {H}(V)$
is dense in Y” if
$X \cap \mathcal {H}(V)$
is dense in Y” if
![]() $X \cap \mathcal {H}(V) \subseteq Y$
and if every function in Y can be approximated locally uniformly on U by functions in X which have a holomorphic extension to V.
$X \cap \mathcal {H}(V) \subseteq Y$
and if every function in Y can be approximated locally uniformly on U by functions in X which have a holomorphic extension to V.
We are now, finally, in a position to formulate the main result of this paper.
Theorem 2.10 Let
![]() $\lambda \in {\mathbb C}$
, and let Y be a nontrivial Möbius invariant subspace of
$\lambda \in {\mathbb C}$
, and let Y be a nontrivial Möbius invariant subspace of
![]() $X_{\lambda }({\mathbb D}^2)$
. Then one and only one of the following four alternatives holds.
$X_{\lambda }({\mathbb D}^2)$
. Then one and only one of the following four alternatives holds.
-
(E0)
 $Y=X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega )$
and
$Y=X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega )$
and
 $\dim Y<\infty $
.
$\dim Y<\infty $
. -
(E+)
 $X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega _+)$
is dense in Y.
$X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega _+)$
is dense in Y. -
(E_)
 $X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega _-)$
is dense in Y.
$X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega _-)$
is dense in Y. -
(NE)
 $X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega _*)$
is dense in Y. In this case
$X_{\lambda }({\mathbb D}^2) \cap \mathcal {H}(\Omega _*)$
is dense in Y. In this case
 $Y=X_{\lambda }({\mathbb D}^2)$
.
$Y=X_{\lambda }({\mathbb D}^2)$
.
In addition,
-
(i) (
 $\textrm {E}_0$
), (
$\textrm {E}_0$
), (
 $\textrm {E}_+$
), and (
$\textrm {E}_+$
), and (
 $\textrm {E}_-$
) cannot occur if
$\textrm {E}_-$
) cannot occur if
 $\lambda \not =4m(m+1)$
for every nonnegative integer m.
$\lambda \not =4m(m+1)$
for every nonnegative integer m. -
(ii) (
 $\textrm {E}_0$
) holds if and only if
$\textrm {E}_0$
) holds if and only if
 $\dim Y<\infty $
. In this case,
$\dim Y<\infty $
. In this case,
 $\dim Y=2m+1$
and
$\dim Y=2m+1$
and
 $\lambda =4m(m+1)$
for some nonnegative integer m.
$\lambda =4m(m+1)$
for some nonnegative integer m. -
(iii) None of the density statements (
 $\textrm {NE}$
), (
$\textrm {NE}$
), (
 $\textrm {E}_+$
), and (
$\textrm {E}_+$
), and (
 $\textrm {E}_-$
) may be improved to equalities.
$\textrm {E}_-$
) may be improved to equalities.
Remark 2.11 Recall that two domains
![]() $U \subseteq V$
in
$U \subseteq V$
in
![]() ${\mathbb C}^n$
form a Runge pair
${\mathbb C}^n$
form a Runge pair
![]() $(U,V)$
if every function in
$(U,V)$
if every function in
![]() $\mathcal {H}(U)$
can be approximated locally uniformly in U by functions in
$\mathcal {H}(U)$
can be approximated locally uniformly in U by functions in
![]() $\mathcal {H}(V)$
. Identifying domains
$\mathcal {H}(V)$
. Identifying domains
![]() $U\subseteq V$
as Runge pairs is a fundamental and, in many cases, challenging problem in complex analysis. Note that in our terminology,
$U\subseteq V$
as Runge pairs is a fundamental and, in many cases, challenging problem in complex analysis. Note that in our terminology,
![]() $(U,V)$
is a Runge pair if and only if
$(U,V)$
is a Runge pair if and only if
![]() $\mathcal {H}(U) \cap \mathcal {H}(V)$
is dense in
$\mathcal {H}(U) \cap \mathcal {H}(V)$
is dense in
![]() $\mathcal {H}(U)$
. For subspaces
$\mathcal {H}(U)$
. For subspaces
![]() $Y \subseteq X$
of
$Y \subseteq X$
of
![]() $\mathcal {H}(U),$
it is tempting to call
$\mathcal {H}(U),$
it is tempting to call
![]() $(Y,X,\mathcal {H}(V))$
a Runge triple, if
$(Y,X,\mathcal {H}(V))$
a Runge triple, if
![]() $X \cap \mathcal {H}(V)$
is dense in Y. Then for every nontrivial infinite-dimensional Möbius invariant subspace Y of
$X \cap \mathcal {H}(V)$
is dense in Y. Then for every nontrivial infinite-dimensional Möbius invariant subspace Y of
![]() $X_{\lambda }({\mathbb D}^2)$
exactly one of the triples
$X_{\lambda }({\mathbb D}^2)$
exactly one of the triples
is a Runge triple. Theorem 2.10 can therefore be regarded as a Runge-type approximation theorem for the Möbius invariant spaces of eigenfunctions of the invariant Laplacian
![]() $\Delta _{zw}$
.
$\Delta _{zw}$
.
The plan of the paper is as follows. We introduce some basic concepts and notation in a preliminary Section 3. In Sections 4 and 5, we develop the general spectral theory of the invariant Laplacian
![]() $\Delta _{zw}$
on
$\Delta _{zw}$
on
![]() $\Omega $
in analogy to the well-established spectral theory of the hyperbolic Laplacian
$\Omega $
in analogy to the well-established spectral theory of the hyperbolic Laplacian
![]() $\Delta _{\mathbb D}$
on
$\Delta _{\mathbb D}$
on
![]() ${\mathbb D}$
. In a sense, we rather closely follow the presentation Berenstein and Gay [Reference Berenstein and Gay8, Section 1.6] have given for the spectral theory of the hyperbolic Laplacian, but we have made an effort either to provide even more rigorous proofs or to give precise references to the literature for all auxiliary results which are needed. In contrast to [Reference Berenstein and Gay8], we completely work in the holomorphic setting. On the one hand, this makes it possible to take advantage of many efficient tools from complex analysis which are not available otherwise. On the other hand, we need to incorporate from the beginning the maximal domain of existence of eigenfunctions; an issue which does not even show up when working “only” on the unit disk. Here, our approach requires some finer analysis of the building blocks of the eigenfunctions, namely, certain hypergeometric functions and their integral representations in terms of Poisson–Fourier modes.
${\mathbb D}$
. In a sense, we rather closely follow the presentation Berenstein and Gay [Reference Berenstein and Gay8, Section 1.6] have given for the spectral theory of the hyperbolic Laplacian, but we have made an effort either to provide even more rigorous proofs or to give precise references to the literature for all auxiliary results which are needed. In contrast to [Reference Berenstein and Gay8], we completely work in the holomorphic setting. On the one hand, this makes it possible to take advantage of many efficient tools from complex analysis which are not available otherwise. On the other hand, we need to incorporate from the beginning the maximal domain of existence of eigenfunctions; an issue which does not even show up when working “only” on the unit disk. Here, our approach requires some finer analysis of the building blocks of the eigenfunctions, namely, certain hypergeometric functions and their integral representations in terms of Poisson–Fourier modes.
In Section 6, we prove Theorem 2.2 and show that it is in some sense best possible by providing an explicit example. This implies that the smooth spectral theory of the hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
on the disk
$\Delta _{{\mathbb D}}$
on the disk
![]() ${\mathbb D}$
and the holomorphic spectral theory of the Laplacian
${\mathbb D}$
and the holomorphic spectral theory of the Laplacian
![]() $\Delta _{zw}$
on the bidisk
$\Delta _{zw}$
on the bidisk
![]() ${\mathbb D}^2$
are essentially equivalent. In the same spirit, we relate the smooth spectral theory of the spherical Laplacian
${\mathbb D}^2$
are essentially equivalent. In the same spirit, we relate the smooth spectral theory of the spherical Laplacian
![]() $\Delta _{\widehat {{\mathbb C}}}$
with the holomorphic spectral theory of the Laplacian
$\Delta _{\widehat {{\mathbb C}}}$
with the holomorphic spectral theory of the Laplacian
![]() $\Delta _{zw}$
on
$\Delta _{zw}$
on
![]() $\Omega $
as well as the exceptional eigenvalues of the hyperbolic Laplacian
$\Omega $
as well as the exceptional eigenvalues of the hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
(see Theorem 6.2). Section 7 is devoted to a study of the transformation behavior of the Poisson–Fourier modes under precompositions with elements of the Möbius group
$\Delta _{{\mathbb D}}$
(see Theorem 6.2). Section 7 is devoted to a study of the transformation behavior of the Poisson–Fourier modes under precompositions with elements of the Möbius group
![]() $\mathcal {M}$
. These results are needed for Section 8, where we prove our main results, Theorems 2.6 and 2.10. By and large, we follow Rudin’s [Reference Rudin37] treatment of invariant subspaces of eigenfunctions of the hyperbolic Laplacian, but again completely working in the holomorphic setting; we briefly comment on the similarities and differences between our and Rudin’s approach in Remark 8.5. We close the paper with Section 9, which connects the Poisson–Fourier modes to the invariant differential operators of Peschl–Minda type studied in [Reference Heins, Moucha, Roth and Sugawa19].
$\mathcal {M}$
. These results are needed for Section 8, where we prove our main results, Theorems 2.6 and 2.10. By and large, we follow Rudin’s [Reference Rudin37] treatment of invariant subspaces of eigenfunctions of the hyperbolic Laplacian, but again completely working in the holomorphic setting; we briefly comment on the similarities and differences between our and Rudin’s approach in Remark 8.5. We close the paper with Section 9, which connects the Poisson–Fourier modes to the invariant differential operators of Peschl–Minda type studied in [Reference Heins, Moucha, Roth and Sugawa19].
Four final preliminary remarks are in order. First, treating the hyperbolic eigenvalue equation
![]() $\Delta _{{\mathbb D}}f=\lambda f$
and the spherical eigenvalue equation
$\Delta _{{\mathbb D}}f=\lambda f$
and the spherical eigenvalue equation
![]() $\Delta _{\widehat {{\mathbb C}}} f=\lambda f$
as special cases of the more general complex eigenvalue equation
$\Delta _{\widehat {{\mathbb C}}} f=\lambda f$
as special cases of the more general complex eigenvalue equation
![]() $\Delta _{zw} F=\lambda F$
has been a recurrent theme in the literature for a long time. To mention but a few of the many references, we refer for instance to the papers [Reference Bauer4–Reference Bauer and Ruscheweyh6] and their bibliographies. What seems to be new is the systematic study of the maximal domains of existence of the holomorphic solutions of
$\Delta _{zw} F=\lambda F$
has been a recurrent theme in the literature for a long time. To mention but a few of the many references, we refer for instance to the papers [Reference Bauer4–Reference Bauer and Ruscheweyh6] and their bibliographies. What seems to be new is the systematic study of the maximal domains of existence of the holomorphic solutions of
![]() $\Delta _{zw} F=\lambda F$
and its ramifications for the study of the invariant subspaces of the
$\Delta _{zw} F=\lambda F$
and its ramifications for the study of the invariant subspaces of the
![]() $\Delta _{{\mathbb D}}$
-eigenspaces. As a second remark, we should point out that Rudin’s work [Reference Rudin37] is in fact concerned with the invariant Laplace operator on the unit ball of
$\Delta _{{\mathbb D}}$
-eigenspaces. As a second remark, we should point out that Rudin’s work [Reference Rudin37] is in fact concerned with the invariant Laplace operator on the unit ball of
![]() ${\mathbb C}^n$
, while our focus is exclusively on the complex one-dimensional case
${\mathbb C}^n$
, while our focus is exclusively on the complex one-dimensional case
![]() $n=1$
. Third, even though we are superficially dealing with holomorphic functions of two complex variables, we only need very few and only elementary facts from the theory of several complex variables. Finally, Helgason [Reference Helgason20–Reference Helgason22] has systematically studied invariant differential operators and their eigenvalue problem in the setting of homogeneous spaces. In contrast to our holomorphic approach, he used entirely real methods. This Lie theoretic approach has since been generalized significantly. While providing a comprehensive list of references would go beyond what we can achieve here, we would like to mention [Reference Kashiwara, Kowata, Minemura, Okamoto, Oshima and Tanaka23, Reference Koryani26], who generalized the theory to higher-dimensional symmetric spaces, and Maass [Reference Maass29], who initiated the vast and fruitful research of Maass wave forms.
$n=1$
. Third, even though we are superficially dealing with holomorphic functions of two complex variables, we only need very few and only elementary facts from the theory of several complex variables. Finally, Helgason [Reference Helgason20–Reference Helgason22] has systematically studied invariant differential operators and their eigenvalue problem in the setting of homogeneous spaces. In contrast to our holomorphic approach, he used entirely real methods. This Lie theoretic approach has since been generalized significantly. While providing a comprehensive list of references would go beyond what we can achieve here, we would like to mention [Reference Kashiwara, Kowata, Minemura, Okamoto, Oshima and Tanaka23, Reference Koryani26], who generalized the theory to higher-dimensional symmetric spaces, and Maass [Reference Maass29], who initiated the vast and fruitful research of Maass wave forms.
3 Notation and preliminaries
We denote the open unit disk in
![]() ${\mathbb C}$
by
${\mathbb C}$
by
![]() ${\mathbb D}$
, the bidisk
${\mathbb D}$
, the bidisk
![]() ${\mathbb D}\times {\mathbb D}$
by
${\mathbb D}\times {\mathbb D}$
by
![]() ${\mathbb D}^2$
and the Riemann sphere by
${\mathbb D}^2$
and the Riemann sphere by
![]() $\widehat {{\mathbb C}}$
. The open disk of radius
$\widehat {{\mathbb C}}$
. The open disk of radius
![]() $r>0$
centered at the origin is denoted by
$r>0$
centered at the origin is denoted by
![]() ${\mathbb D}_r$
. Moreover, we write
${\mathbb D}_r$
. Moreover, we write ![]() for the set of positive integers,
for the set of positive integers, ![]() and
and
![]() ${\mathbb Z}$
for the set of all integers. For an open subset U of
${\mathbb Z}$
for the set of all integers. For an open subset U of
![]() $\widehat {{\mathbb C}}$
or
$\widehat {{\mathbb C}}$
or
![]() $\widehat {{\mathbb C}}^2$
, we write
$\widehat {{\mathbb C}}^2$
, we write
![]() $\partial U$
for its boundary and
$\partial U$
for its boundary and
![]() $\overline {{U}}$
for its closure. The set of all twice resp. infinitely (real) differentiable functions
$\overline {{U}}$
for its closure. The set of all twice resp. infinitely (real) differentiable functions
![]() $f:U\to {\mathbb C}$
is denoted
$f:U\to {\mathbb C}$
is denoted
![]() $C^2(U)$
resp.
$C^2(U)$
resp.
![]() $C^\infty (U)$
, and we write
$C^\infty (U)$
, and we write
![]() $\mathcal {H}(U)$
for set of all holomorphic functions
$\mathcal {H}(U)$
for set of all holomorphic functions
![]() $f:U\to {\mathbb C}$
.
$f:U\to {\mathbb C}$
.
The set
![]() $\Omega =\widehat {{\mathbb C}}^2 \setminus \{(z,w) \in \widehat {{\mathbb C}}^2 \, : \, z \cdot w \not =1\}$
is a complex manifold of complex dimension
$\Omega =\widehat {{\mathbb C}}^2 \setminus \{(z,w) \in \widehat {{\mathbb C}}^2 \, : \, z \cdot w \not =1\}$
is a complex manifold of complex dimension
![]() $2$
and an open submanifold of
$2$
and an open submanifold of
![]() $\widehat {{\mathbb C}}^2$
. In order to describe the complex structure of
$\widehat {{\mathbb C}}^2$
. In order to describe the complex structure of
![]() $\Omega $
only two charts are necessary, the standard chart
$\Omega $
only two charts are necessary, the standard chart
and the flip chart
In these local coordinates, the invariant Laplace operator
![]() $\Delta _{zw}$
of the complex manifold
$\Delta _{zw}$
of the complex manifold
![]() $\Omega $
is then given by
$\Omega $
is then given by
and it is easily seen that
![]() $\Delta _{zw}$
is a well-defined object. Here,
$\Delta _{zw}$
is a well-defined object. Here,
![]() $\partial _z$
and
$\partial _z$
and
![]() $\partial _w$
denote the Wirtinger derivatives with respect to z and w, respectively.
$\partial _w$
denote the Wirtinger derivatives with respect to z and w, respectively.
One of the few elementary results from the theory of functions of several complex variables we need in this paper is the following simple lemma.
Lemma 3.1 (“Two variable identity principle” (p. 18 in [Reference Range35]))
Let U be a subdomain of
![]() ${\mathbb C}^2$
which contains a point of the form
${\mathbb C}^2$
which contains a point of the form
![]() $(z,\overline {{z}})$
resp.
$(z,\overline {{z}})$
resp.
![]() $(z,-\overline {{z}})$
. Let
$(z,-\overline {{z}})$
. Let
![]() $f : U \to {\mathbb C}$
be a holomorphic function such that
$f : U \to {\mathbb C}$
be a holomorphic function such that
Then
![]() $f \equiv 0$
.
$f \equiv 0$
.
Finally, we briefly recall some standard terminology from linear algebra. We denote by
![]() $\mathrm {span}\,\,M$
the collection of all finite linear combinations of elements of a subset M of a given vector space X. The vector spaces that occur in this paper are spaces of smooth or holomorphic functions defined on some open subset U of
$\mathrm {span}\,\,M$
the collection of all finite linear combinations of elements of a subset M of a given vector space X. The vector spaces that occur in this paper are spaces of smooth or holomorphic functions defined on some open subset U of
![]() $\Omega $
, which we equip with the standard topology of uniform convergence on compact subsets of U. If M denotes a set of smooth or holomorphic functions on U, we denote by
$\Omega $
, which we equip with the standard topology of uniform convergence on compact subsets of U. If M denotes a set of smooth or holomorphic functions on U, we denote by
![]() $\operatorname {clos}_{U}M$
the closure of M with respect to locally uniform convergence on U.
$\operatorname {clos}_{U}M$
the closure of M with respect to locally uniform convergence on U.
4 Homogeneous eigenfunctions and Poisson–Fourier modes
By making a separation of variables approach, Rudin [Reference Rudin37] showed that every
![]() $\lambda \in {\mathbb C}$
is an eigenvalue of
$\lambda \in {\mathbb C}$
is an eigenvalue of
![]() $\Delta _{\mathbb D}$
. The analogous result is true for
$\Delta _{\mathbb D}$
. The analogous result is true for
![]() $\Delta _{zw}$
: let
$\Delta _{zw}$
: let
![]() $n \in {\mathbb Z}$
and suppose
$n \in {\mathbb Z}$
and suppose
![]() $f_n : D \to {\mathbb C}$
is a holomorphic function defined on a domain
$f_n : D \to {\mathbb C}$
is a holomorphic function defined on a domain
![]() $D \subseteq {\mathbb C}^2$
containing the origin
$D \subseteq {\mathbb C}^2$
containing the origin
![]() $(0,0)$
. Further, assume that
$(0,0)$
. Further, assume that
![]() $f_n$
is n-homogeneous, i.e.,
$f_n$
is n-homogeneous, i.e.,
and for all
![]() $(z,w) \in {\mathbb C}^2$
belonging to the bidisk
$(z,w) \in {\mathbb C}^2$
belonging to the bidisk
![]() ${\mathbb D}_r^2={\mathbb D}_r \times {\mathbb D}_r$
for some (and hence all)
${\mathbb D}_r^2={\mathbb D}_r \times {\mathbb D}_r$
for some (and hence all)
![]() $r>0$
such that
$r>0$
such that
![]() ${\mathbb D}_{r}^2\subseteq D$
. A consideration of the power series expansion of
${\mathbb D}_{r}^2\subseteq D$
. A consideration of the power series expansion of
![]() $f_n$
at
$f_n$
at
![]() $(0,0)$
in
$(0,0)$
in
![]() ${\mathbb D}_r^2$
implies in a straightforward way that there is a holomorphic function
${\mathbb D}_r^2$
implies in a straightforward way that there is a holomorphic function
![]() $y_n : {\mathbb D}_{r^2} \to {\mathbb C}$
such that
$y_n : {\mathbb D}_{r^2} \to {\mathbb C}$
such that
for all
![]() $(z,w) \in {\mathbb D}_r^2$
. It is, then, easy to see that
$(z,w) \in {\mathbb D}_r^2$
. It is, then, easy to see that
![]() $\Delta _{zw} f_n=\lambda f_n$
on U if and only if
$\Delta _{zw} f_n=\lambda f_n$
on U if and only if
for all
![]() $t\in {\mathbb D}_{r^2}$
. A power series ansatz shows that there is at most one solution
$t\in {\mathbb D}_{r^2}$
. A power series ansatz shows that there is at most one solution
![]() $y_n$
of (4.3) which is holomorphic in a neighborhood of
$y_n$
of (4.3) which is holomorphic in a neighborhood of
![]() $t=0$
and normalized such that
$t=0$
and normalized such that
![]() $y_n(0)=1$
. In order to find this solution, we convert (4.3) into a hypergeometric differential equation as follows. We choose
$y_n(0)=1$
. In order to find this solution, we convert (4.3) into a hypergeometric differential equation as follows. We choose
![]() $\mu \in {\mathbb C}$
such that
$\mu \in {\mathbb C}$
such that
![]() $\lambda =4 \mu (\mu -1),$
and let
$\lambda =4 \mu (\mu -1),$
and let
![]() $\hat {y}_n(t):=(1-t)^{-\mu } y_n(t)$
. Then (4.3) is equivalent to
$\hat {y}_n(t):=(1-t)^{-\mu } y_n(t)$
. Then (4.3) is equivalent to
with
It is well-known (see [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClain33, Section 15.10]) that the only solution
![]() $\hat {y}_n$
of (4.4) which is holomorphic at
$\hat {y}_n$
of (4.4) which is holomorphic at
![]() $t=0$
and normalized at
$t=0$
and normalized at
![]() $t=0$
by
$t=0$
by
![]() $\hat {y}_n(0)=1$
is the hypergeometric series
$\hat {y}_n(0)=1$
is the hypergeometric series
 $$ \begin{align*} {}_2F_1\left(a,b;c;t\right):=\sum_{k=0}^\infty\frac{(a)_k(b)_k}{(c)_k}\frac{t^k}{k!},\quad |t|<1, \end{align*} $$
$$ \begin{align*} {}_2F_1\left(a,b;c;t\right):=\sum_{k=0}^\infty\frac{(a)_k(b)_k}{(c)_k}\frac{t^k}{k!},\quad |t|<1, \end{align*} $$
where
 $$ \begin{align} (\alpha)_k:=\prod\limits_{j=0}^{k-1}(\alpha+j), \, \qquad \alpha\in{\mathbb C}, \, k\in{\mathbb N}_0 \end{align} $$
$$ \begin{align} (\alpha)_k:=\prod\limits_{j=0}^{k-1}(\alpha+j), \, \qquad \alpha\in{\mathbb C}, \, k\in{\mathbb N}_0 \end{align} $$
denotes the (rising) Pochhammer symbol. This procedure leads to the conclusion that
is the unique solution of (4.3) which is holomorphic in
![]() $t=0$
and normalized by
$t=0$
and normalized by
![]() $y_n(0)=1$
. Note that there are, in fact, two complex numbers
$y_n(0)=1$
. Note that there are, in fact, two complex numbers
![]() $\mu \in {\mathbb C}$
such that
$\mu \in {\mathbb C}$
such that
![]() $\lambda =4 \mu (\mu -1)$
. However, as we have seen, both necessarily lead to the same holomorphic solution
$\lambda =4 \mu (\mu -1)$
. However, as we have seen, both necessarily lead to the same holomorphic solution
![]() $y_n$
of (4.3) with
$y_n$
of (4.3) with
![]() $y_n(0)=1$
.
$y_n(0)=1$
.
Remark 4.1 Note that if
![]() $\mu \in {\mathbb C}$
is one solution to
$\mu \in {\mathbb C}$
is one solution to
![]() $\lambda =4\mu (\mu -1)$
, then
$\lambda =4\mu (\mu -1)$
, then
![]() $1-\mu $
is the other one. As we have seen, both numbers induce the same function (4.6). This also follows from the transformation formula (see [Reference Abramowitz, Stegun, Danos and Rafelski1, Equation (15.3.3)])
$1-\mu $
is the other one. As we have seen, both numbers induce the same function (4.6). This also follows from the transformation formula (see [Reference Abramowitz, Stegun, Danos and Rafelski1, Equation (15.3.3)])
In the following, it will often be convenient to choose
![]() $\mu $
such that
$\mu $
such that
![]() $\textsf {Re}\,\mu \geq 1/2$
.
$\textsf {Re}\,\mu \geq 1/2$
.
By a standard fact about hypergeometric functions (see [Reference Abramowitz, Stegun, Danos and Rafelski1, 15.3.1]), the function
![]() $y_n$
has a holomorphic extension at least to the slit plane
$y_n$
has a holomorphic extension at least to the slit plane
Returning to (4.2) with this choice of
![]() $y_n$
, we therefore see that
$y_n$
, we therefore see that
 $$ \begin{align} F^{\mu}_n(z,w):= (1-zw)^\mu {}_2F_1\left(\mu,\mu+|n|;|n|+1;zw\right) \cdot \begin{cases} z^n, & \text{ if } n \ge 0 , \\ w^{|n|}, & \text{ if } n \le 0 ,\end{cases} \end{align} $$
$$ \begin{align} F^{\mu}_n(z,w):= (1-zw)^\mu {}_2F_1\left(\mu,\mu+|n|;|n|+1;zw\right) \cdot \begin{cases} z^n, & \text{ if } n \ge 0 , \\ w^{|n|}, & \text{ if } n \le 0 ,\end{cases} \end{align} $$
is holomorphic at least on the domain
and provides the unique n-homogeneous solution of
![]() $\Delta _{zw} f=\lambda f$
on
$\Delta _{zw} f=\lambda f$
on
![]() $\Omega _*$
up to a multiplicative constant.
$\Omega _*$
up to a multiplicative constant.
Next, we relate the n-homogeneous eigenfunction
![]() $F^{\mu }_n$
of
$F^{\mu }_n$
of
![]() $\Delta _{zw}$
to a complexified version of the Poisson kernel of the unit disk. This slight change of perspective will turn out to be important in the sequel. In fact, a well-known integral representation formula for the hypergeometric function
$\Delta _{zw}$
to a complexified version of the Poisson kernel of the unit disk. This slight change of perspective will turn out to be important in the sequel. In fact, a well-known integral representation formula for the hypergeometric function
![]() ${}_2F_1\left (\mu ,\mu +|n|;|n|+1;zw\right )$
(see [Reference Erdelyi11, Section 2.5.1, Formula (10), p. 81]) shows that for every
${}_2F_1\left (\mu ,\mu +|n|;|n|+1;zw\right )$
(see [Reference Erdelyi11, Section 2.5.1, Formula (10), p. 81]) shows that for every
![]() $n \in {\mathbb Z}$
,
$n \in {\mathbb Z}$
,
 $$ \begin{align} \binom{\mu+|n|-1}{|n|} F^\mu_n(z,w)=\frac{(1-z w)^{\mu}}{2\pi} \int \limits_{0}^{2\pi} \frac{e^{in t}}{\left( 1-z e^{-it} \right)^{\mu} \left(1-w e^{it} \right)^{\mu}} \, dt , \end{align} $$
$$ \begin{align} \binom{\mu+|n|-1}{|n|} F^\mu_n(z,w)=\frac{(1-z w)^{\mu}}{2\pi} \int \limits_{0}^{2\pi} \frac{e^{in t}}{\left( 1-z e^{-it} \right)^{\mu} \left(1-w e^{it} \right)^{\mu}} \, dt , \end{align} $$
with the generalized binomial coefficients
![]() $ \binom {\mu }{n} := \frac {(\mu - n +1)_n}{n!} $
for
$ \binom {\mu }{n} := \frac {(\mu - n +1)_n}{n!} $
for
![]() $\mu \in {\mathbb C}$
,
$\mu \in {\mathbb C}$
,
![]() $ n \in {\mathbb N}_0$
. On the right-hand side of this identity, one can recognize the
$ n \in {\mathbb N}_0$
. On the right-hand side of this identity, one can recognize the
![]() $(-n)$
th Fourier coefficient of (a suitably defined power of order
$(-n)$
th Fourier coefficient of (a suitably defined power of order
![]() $\mu $
of) the function
$\mu $
of) the function
Note that if
![]() $w=\overline {{z}}\in {\mathbb D}$
, then
$w=\overline {{z}}\in {\mathbb D}$
, then
![]() $P(z,\overline {z};\xi )$
is the standard Poisson kernel of the unit disk.
$P(z,\overline {z};\xi )$
is the standard Poisson kernel of the unit disk.
Definition 4.2 (Generalized Poisson kernel, Poisson–Fourier mode, PFM)
-
(a) The function
 $P \colon {\mathbb D}^2 \times \partial {\mathbb D} \longrightarrow {\mathbb C}$
defined by (4.9) is called generalized Poisson kernel.
$P \colon {\mathbb D}^2 \times \partial {\mathbb D} \longrightarrow {\mathbb C}$
defined by (4.9) is called generalized Poisson kernel. -
(b) Let
 $\mu \in {\mathbb C}$
and
$\mu \in {\mathbb C}$
and
 $n\in {\mathbb Z}$
. Then the function
$n\in {\mathbb Z}$
. Then the function
 $P_n^{\mu }: {\mathbb D}^2\rightarrow {\mathbb C}$
, (4.10)is called the nth Poisson–Fourier mode (PFM) of order
$P_n^{\mu }: {\mathbb D}^2\rightarrow {\mathbb C}$
, (4.10)is called the nth Poisson–Fourier mode (PFM) of order $$ \begin{align} P_n^\mu(z,w) := \frac{\left(1-zw\right)^{\mu}}{2\pi }\int\limits_{0}^{2\pi} \frac{e^{-int}}{\left(1-z e^{-it}\right)^\mu \left(1-w e^{it} \right)^\mu} \, dt\, \end{align} $$
$$ \begin{align} P_n^\mu(z,w) := \frac{\left(1-zw\right)^{\mu}}{2\pi }\int\limits_{0}^{2\pi} \frac{e^{-int}}{\left(1-z e^{-it}\right)^\mu \left(1-w e^{it} \right)^\mu} \, dt\, \end{align} $$
 $\mu $
.
$\mu $
.
Here,
 $a^\mu $
is defined for
$a^\mu $
is defined for
 $a \in {\mathbb C} \setminus\, (-\infty ,0]$
as
$a \in {\mathbb C} \setminus\, (-\infty ,0]$
as
 $\exp \left ( \mu \log a\right )$
, where
$\exp \left ( \mu \log a\right )$
, where
 $\log $
denotes the principal branch of the logarithm.
$\log $
denotes the principal branch of the logarithm.
Remark 4.3 If
![]() $w=\overline {z} \in {\mathbb D}$
, then
$w=\overline {z} \in {\mathbb D}$
, then
![]() $P^\mu _n(z,\overline {z})$
is the nth Fourier coefficient of the
$P^\mu _n(z,\overline {z})$
is the nth Fourier coefficient of the
![]() $\mu $
-power of the (real-valued and, in fact, nonnegative) Poisson kernel of the unit disk
$\mu $
-power of the (real-valued and, in fact, nonnegative) Poisson kernel of the unit disk
![]() ${\mathbb D}$
. Further, if
${\mathbb D}$
. Further, if
![]() $\mu =m\in {\mathbb Z}$
, then
$\mu =m\in {\mathbb Z}$
, then
![]() $P^m_n(z,w)$
also is the nth Fourier coefficient of the m-power of the generalized Poisson kernel from (4.9).
$P^m_n(z,w)$
also is the nth Fourier coefficient of the m-power of the generalized Poisson kernel from (4.9).
We can now reformulate (4.8) in terms of PFMs as follows:
 $$ \begin{align} P^\mu_n=(-1)^n \binom{-\mu}{|n|} F^\mu_{-n} =\binom{\mu+|n|-1}{|n|} F^\mu_{-n}. \end{align} $$
$$ \begin{align} P^\mu_n=(-1)^n \binom{-\mu}{|n|} F^\mu_{-n} =\binom{\mu+|n|-1}{|n|} F^\mu_{-n}. \end{align} $$
In particular,
![]() $P^\mu _{n}$
has a holomorphic extension from
$P^\mu _{n}$
has a holomorphic extension from
![]() ${\mathbb D}^2$
to
${\mathbb D}^2$
to
![]() $\Omega _*$
, which we continue to denote by
$\Omega _*$
, which we continue to denote by
![]() $P^{\mu }_n$
.
$P^{\mu }_n$
.
In analogy with (4.1), we call a domain
![]() $D \subseteq \Omega $
rotationally invariant if
$D \subseteq \Omega $
rotationally invariant if
![]() ${(\eta z, w/\eta ) \in D}$
for all
${(\eta z, w/\eta ) \in D}$
for all
![]() $(z,w) \in D$
and all
$(z,w) \in D$
and all
![]() $\eta \in \partial {\mathbb D}$
. Summarizing our considerations leads to the following complete description of the n-homogeneous eigenfunctions of
$\eta \in \partial {\mathbb D}$
. Summarizing our considerations leads to the following complete description of the n-homogeneous eigenfunctions of
![]() $\Delta _{zw}$
.
$\Delta _{zw}$
.
Theorem 4.4 Let D be a rotationally invariant subdomain of
![]() $\Omega $
containing the origin and
$\Omega $
containing the origin and
![]() $n\in {\mathbb Z}$
. Suppose that
$n\in {\mathbb Z}$
. Suppose that
![]() $f \in \mathcal {H}(D)$
is an n-homogeneous solution to
$f \in \mathcal {H}(D)$
is an n-homogeneous solution to
![]() $\Delta _{zw}f=\lambda f$
for some
$\Delta _{zw}f=\lambda f$
for some
![]() $\lambda \in {\mathbb C}$
of the form
$\lambda \in {\mathbb C}$
of the form
![]() $\lambda =4\mu (\mu -1)$
with
$\lambda =4\mu (\mu -1)$
with
![]() $\textsf {Re}\, \mu \ge 1/2$
. Then there is a constant
$\textsf {Re}\, \mu \ge 1/2$
. Then there is a constant
![]() $c \in {\mathbb C}$
such that
$c \in {\mathbb C}$
such that
In particular, f has a holomorphic extension to
![]() $D \cup \Omega _*$
. Moreover, the following dichotomy holds:
$D \cup \Omega _*$
. Moreover, the following dichotomy holds:
-
(NE) (Non-exceptional case)
If
 $\lambda \not =4m (m+1)$
for all
$\lambda \not =4m (m+1)$
for all
 $m \in {\mathbb N}_0$
, then
$m \in {\mathbb N}_0$
, then
 $\Omega _*$
is the maximal domain of existence of f.
$\Omega _*$
is the maximal domain of existence of f. -
(E) (Exceptional case)
If
 $\lambda =4m(m+1)$
for some
$\lambda =4m(m+1)$
for some
 $m \in {\mathbb N}_0$
, then the maximal domain of existence of f is
$m \in {\mathbb N}_0$
, then the maximal domain of existence of f is  $$ \begin{align*}\begin{array}{lcl} \Omega_+ & & n < -m\,; \\[2mm] \Omega_- & \text{ if }\quad & n>m \,; \\[2mm] \Omega & & \! |n|\le m. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{lcl} \Omega_+ & & n < -m\,; \\[2mm] \Omega_- & \text{ if }\quad & n>m \,; \\[2mm] \Omega & & \! |n|\le m. \end{array}\end{align*} $$
Proof It remains to prove that for any nonconstant n-homogeneous eigenfunction
![]() $F^{\mu }_n$
of
$F^{\mu }_n$
of
![]() $\Delta _{zw}$
in
$\Delta _{zw}$
in
![]() $\mathcal {H}(\Omega _*)$
the dichotomy “(NE) vs. (E)” holds.
$\mathcal {H}(\Omega _*)$
the dichotomy “(NE) vs. (E)” holds.
(i) Let
![]() $\mu \not \in {\mathbb N}$
and assume that
$\mu \not \in {\mathbb N}$
and assume that
![]() $\Omega _*$
is not the maximal domain of existence of
$\Omega _*$
is not the maximal domain of existence of
![]() $F^\mu _n$
which is contained in
$F^\mu _n$
which is contained in
![]() $\Omega $
(see Definition 2.5). Then
$\Omega $
(see Definition 2.5). Then
![]() $F^\mu _n$
has a holomorphic extension to some point
$F^\mu _n$
has a holomorphic extension to some point
![]() $(z_0,w_0) \in \Omega $
such that
$(z_0,w_0) \in \Omega $
such that
![]() $z_0w_0 \in {\mathbb R} \cup \{\infty \}$
and
$z_0w_0 \in {\mathbb R} \cup \{\infty \}$
and
![]() $z_0w_0> 1$
. We first consider the case
$z_0w_0> 1$
. We first consider the case
![]() $n \ge 0$
. By definition of
$n \ge 0$
. By definition of
![]() $F^\mu _n$
, see (4.7), and in view of [Reference Abramowitz, Stegun, Danos and Rafelski1, Eq. 15.3.4], we have
$F^\mu _n$
, see (4.7), and in view of [Reference Abramowitz, Stegun, Danos and Rafelski1, Eq. 15.3.4], we have
 $$ \begin{align} \nonumber F^{\mu}_n(z,w) &= (1-zw)^{\mu}{}_2F_1\left(\mu,\mu+n;|n|+1;zw\right)z^n \\ &= {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{zw}{zw-1}\right) z^n, \end{align} $$
$$ \begin{align} \nonumber F^{\mu}_n(z,w) &= (1-zw)^{\mu}{}_2F_1\left(\mu,\mu+n;|n|+1;zw\right)z^n \\ &= {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{zw}{zw-1}\right) z^n, \end{align} $$
from which we infer that
is holomorphic in a neighborhood of the point
![]() $x_0:=z_0w_0/(z_0w_0-1) \ge 1 $
. However, see [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClain33, 15.2.3],
$x_0:=z_0w_0/(z_0w_0-1) \ge 1 $
. However, see [Reference Olver, Olde Daalhuis, Lozier, Schneider, Boisvert, Clark, Miller, Saunders, Cohl and McClain33, 15.2.3],
 $$ \begin{align} \nonumber\lim \limits_{y \to 0^+} & \big[ {}_2F_1\left(\mu,1-\mu;|n|+1;x+i y\right) -{}_2F_1\left(\mu,1-\mu;|n|+1;x-i y\right)\big]\\ & \quad =\frac{2\pi i}{\Gamma(\mu) \Gamma(1-\mu)} \left(x-1 \right)^{|n|} {}_2F_1\left(|n|+1-\mu,|n|+\mu;|n|+1;1-x\right) \end{align} $$
$$ \begin{align} \nonumber\lim \limits_{y \to 0^+} & \big[ {}_2F_1\left(\mu,1-\mu;|n|+1;x+i y\right) -{}_2F_1\left(\mu,1-\mu;|n|+1;x-i y\right)\big]\\ & \quad =\frac{2\pi i}{\Gamma(\mu) \Gamma(1-\mu)} \left(x-1 \right)^{|n|} {}_2F_1\left(|n|+1-\mu,|n|+\mu;|n|+1;1-x\right) \end{align} $$
for all
![]() $x>1$
. By our assumption, the left-hand side of (4.13) has to vanish for all
$x>1$
. By our assumption, the left-hand side of (4.13) has to vanish for all
![]() $x \in {\mathbb R}$
in some open interval
$x \in {\mathbb R}$
in some open interval
![]() $(x_0,x_0+\varepsilon )$
with
$(x_0,x_0+\varepsilon )$
with
![]() $\varepsilon>0$
and hence the same is true for the right-hand side. Since the right-hand side is a holomorphic function of x on the domain
$\varepsilon>0$
and hence the same is true for the right-hand side. Since the right-hand side is a holomorphic function of x on the domain
![]() ${\mathbb C} \setminus\, (-\infty ,0]$
this is clearly only possible if
${\mathbb C} \setminus\, (-\infty ,0]$
this is clearly only possible if
![]() $\mu \in {\mathbb N}$
. The remaining case
$\mu \in {\mathbb N}$
. The remaining case
![]() $n \le 0$
follows from the case
$n \le 0$
follows from the case
![]() $n \ge 0$
and
$n \ge 0$
and
![]() $F^\mu _{-n}(z,w)=F^{\mu }_n(w,z)$
.
$F^\mu _{-n}(z,w)=F^{\mu }_n(w,z)$
.
(ii) Let
![]() $\mu \in {\mathbb N}$
and
$\mu \in {\mathbb N}$
and
![]() $|n| \le \mu -1$
. If
$|n| \le \mu -1$
. If
![]() $n \ge 0$
, then
$n \ge 0$
, then
 $$ \begin{align*}F^\mu_n(z,w)=\frac{G^\mu_n(zw)}{(1-zw)^{\mu-1}} z^{n} ,\end{align*} $$
$$ \begin{align*}F^\mu_n(z,w)=\frac{G^\mu_n(zw)}{(1-zw)^{\mu-1}} z^{n} ,\end{align*} $$
where
 $$ \begin{align} \nonumber G^{\mu}_n(zw)&:= (1-zw)^{2 \mu-1} {}_2F_1\left(\mu,\mu+|n|;|n|+1;zw\right)\\ &\hspace{0.11cm}={}_2F_1\left(1-\mu,|n|+1-\mu;|n|+1;zw\right) \end{align} $$
$$ \begin{align} \nonumber G^{\mu}_n(zw)&:= (1-zw)^{2 \mu-1} {}_2F_1\left(\mu,\mu+|n|;|n|+1;zw\right)\\ &\hspace{0.11cm}={}_2F_1\left(1-\mu,|n|+1-\mu;|n|+1;zw\right) \end{align} $$
is a polynomial in
![]() $zw$
of degree
$zw$
of degree
![]() $\mu -n-1 \ge 0$
(see [Reference Abramowitz, Stegun, Danos and Rafelski1, 15.3.3 and 15.1.1]). Hence,
$\mu -n-1 \ge 0$
(see [Reference Abramowitz, Stegun, Danos and Rafelski1, 15.3.3 and 15.1.1]). Hence,
![]() $F^\mu _n$
is the product of
$F^\mu _n$
is the product of
![]() $z^n$
and a rational function in
$z^n$
and a rational function in
![]() $zw$
of numerator degree
$zw$
of numerator degree
![]() $\mu -n-1$
and of denominator degree
$\mu -n-1$
and of denominator degree
![]() $\mu -1$
with pole only at the point
$\mu -1$
with pole only at the point
![]() $1$
. Therefore,
$1$
. Therefore,
![]() $F^\mu _n \in \mathcal {H}(\Omega )$
. Since
$F^\mu _n \in \mathcal {H}(\Omega )$
. Since
![]() $F^{\mu }_n(z,w)=F^{\mu }_{-n}(w,z)$
, this implies
$F^{\mu }_n(z,w)=F^{\mu }_{-n}(w,z)$
, this implies
![]() $F^{\mu }_n \in \mathcal {H}(\Omega )$
also for
$F^{\mu }_n \in \mathcal {H}(\Omega )$
also for
![]() $1-\mu \le n \le 0$
.
$1-\mu \le n \le 0$
.
(iii) Let
![]() $\mu \in {\mathbb N}$
and
$\mu \in {\mathbb N}$
and
![]() $|n| \ge \mu $
. Since
$|n| \ge \mu $
. Since
![]() $F^{\mu }_n(z,w)=F^{\mu }_{-n}(w,z)$
and
$F^{\mu }_n(z,w)=F^{\mu }_{-n}(w,z)$
and
![]() $\mathcal {H}(\Omega _+) \cap \mathcal {H}(\Omega _-)=\mathcal {H}(\Omega )$
we may assume
$\mathcal {H}(\Omega _+) \cap \mathcal {H}(\Omega _-)=\mathcal {H}(\Omega )$
we may assume
![]() $n \ge \mu $
. In this case, the function
$n \ge \mu $
. In this case, the function
![]() $G^\mu _n$
in (4.14) is a polynomial in
$G^\mu _n$
in (4.14) is a polynomial in
![]() $zw$
of degree
$zw$
of degree
![]() $\mu -1$
, and thus
$\mu -1$
, and thus
![]() $F^\mu _n$
is the product of
$F^\mu _n$
is the product of
![]() $z^{n}$
times a rational function in
$z^{n}$
times a rational function in
![]() $zw$
of numerator degree
$zw$
of numerator degree
![]() $ \mu -1$
and of denominator degree
$ \mu -1$
and of denominator degree
![]() $\mu -1$
, and is therefore holomorphic on
$\mu -1$
, and is therefore holomorphic on
![]() $\Omega _-$
. Moreover,
$\Omega _-$
. Moreover,
![]() $F^\mu _n$
has no holomorphic extension to a point
$F^\mu _n$
has no holomorphic extension to a point
![]() $(\infty ,w_0)$
with
$(\infty ,w_0)$
with
![]() ${w_0 \in \widehat {{\mathbb C}}\setminus \{0\}}$
since in view of (4.14) and (4.12)
${w_0 \in \widehat {{\mathbb C}}\setminus \{0\}}$
since in view of (4.14) and (4.12)
 $$ \begin{align*} \lim \limits_{z \to \infty} \frac{G^\mu_n(zw_0)}{(1-zw_0)^{\mu-1}} & =\lim \limits_{z \to \infty} {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{zw_0}{z w_0-1}\right)={}_2F_1\left(\mu,1-\mu;|n|+1;1\right)\\ &= \frac{\Gamma(n+1) \Gamma(n)}{\Gamma(n+1-\mu) \Gamma(n+\mu)} \in (0,\infty), \end{align*} $$
$$ \begin{align*} \lim \limits_{z \to \infty} \frac{G^\mu_n(zw_0)}{(1-zw_0)^{\mu-1}} & =\lim \limits_{z \to \infty} {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{zw_0}{z w_0-1}\right)={}_2F_1\left(\mu,1-\mu;|n|+1;1\right)\\ &= \frac{\Gamma(n+1) \Gamma(n)}{\Gamma(n+1-\mu) \Gamma(n+\mu)} \in (0,\infty), \end{align*} $$
by [Reference Abramowitz, Stegun, Danos and Rafelski1, Eq. 15.1.20], so
![]() $|F^\mu _n(z,w_0)| \to \infty $
as
$|F^\mu _n(z,w_0)| \to \infty $
as
![]() $z \to \infty $
. This implies that
$z \to \infty $
. This implies that
![]() $\Omega _-$
is the maximal domain of existence of
$\Omega _-$
is the maximal domain of existence of
![]() $F^\mu _n$
.
$F^\mu _n$
.
Corollary 4.5 For every
![]() $\lambda \in {\mathbb C}$
and each
$\lambda \in {\mathbb C}$
and each
![]() $n \in {\mathbb Z}$
, there is an n-homogeneous holomorphic solution of
$n \in {\mathbb Z}$
, there is an n-homogeneous holomorphic solution of
![]() $\Delta _{zw}f =\lambda f$
on the domain
$\Delta _{zw}f =\lambda f$
on the domain
![]() $\Omega _*$
. More precisely, if
$\Omega _*$
. More precisely, if
![]() $\lambda =4\mu (\mu -1) \in {\mathbb C}$
with
$\lambda =4\mu (\mu -1) \in {\mathbb C}$
with
![]() $\textsf {Re}\, \mu \ge 1/2$
, then every such solution has the form
$\textsf {Re}\, \mu \ge 1/2$
, then every such solution has the form
![]() $c P^{\mu }_{-n}$
for some
$c P^{\mu }_{-n}$
for some
![]() $c \in {\mathbb C}$
.
$c \in {\mathbb C}$
.
We close this section by collecting some elementary properties of the PFM
![]() $P^\mu _n$
which will be needed in the sequel.
$P^\mu _n$
which will be needed in the sequel.
Remark 4.6 (Elementary properties of Poisson–Fourier modes)
Let
![]() $\mu \in {\mathbb C}$
,
$\mu \in {\mathbb C}$
,
![]() $n \in {\mathbb N}_0$
and
$n \in {\mathbb N}_0$
and
![]() $z,w \in {\mathbb D}$
.
$z,w \in {\mathbb D}$
.
-
(a) The Poisson–Fourier modes are related to the hypergeometric function
 ${}_2F_1$
via (4.15)This is (4.7) together with (4.11) resp. (4.12).
${}_2F_1$
via (4.15)This is (4.7) together with (4.11) resp. (4.12). $$ \begin{align} \nonumber P_{n}^{\mu}(z,w) &= (-1)^n\binom{-\mu}{n} (1-zw)^\mu w^n {}_2F_1\left(\mu,\mu+n;n+1;zw\right)\\ &= (-1)^n\binom{-\mu}{n} w^n {}_2F_1\left(\mu,1-\mu;n+1;\frac{zw}{zw-1}\right). \end{align} $$
$$ \begin{align} \nonumber P_{n}^{\mu}(z,w) &= (-1)^n\binom{-\mu}{n} (1-zw)^\mu w^n {}_2F_1\left(\mu,\mu+n;n+1;zw\right)\\ &= (-1)^n\binom{-\mu}{n} w^n {}_2F_1\left(\mu,1-\mu;n+1;\frac{zw}{zw-1}\right). \end{align} $$
-
(b) Using the series representation of
 ${}_2F_1$
functions, we see that (4.16)If
${}_2F_1$
functions, we see that (4.16)If $$ \begin{align} P_{n}^{\mu}(z,w) = (-1)^n(1 - zw)^\mu \sum_{k=0}^{\infty} \binom{-\mu}{k + n} \binom{-\mu}{k} z^{k} w^{k+n} . \end{align} $$
$$ \begin{align} P_{n}^{\mu}(z,w) = (-1)^n(1 - zw)^\mu \sum_{k=0}^{\infty} \binom{-\mu}{k + n} \binom{-\mu}{k} z^{k} w^{k+n} . \end{align} $$
 $-\mu =m \in {\mathbb N}_0$
, then
$-\mu =m \in {\mathbb N}_0$
, then
 $P_{\pm n}^{-m} = 0$
, whenever
$P_{\pm n}^{-m} = 0$
, whenever
 $n> m$
. Otherwise, (4.17)
$n> m$
. Otherwise, (4.17) $$ \begin{align} P_{n}^{-m}(z,w) = (-1)^n \sum_{k=0}^{m-n} \binom{m}{k + n} \binom{m}{k} \frac{z^{k} w^{k+n}}{(1 - z w)^m} . \end{align} $$
$$ \begin{align} P_{n}^{-m}(z,w) = (-1)^n \sum_{k=0}^{m-n} \binom{m}{k + n} \binom{m}{k} \frac{z^{k} w^{k+n}}{(1 - z w)^m} . \end{align} $$
-
(c) The PFM are symmetric in the sense that
 $P_{n}^{\mu }(z,w)=P_{-n}^{\mu }(w,z)$
. This allows us to simplify our proofs in the following: we will often prove identities for
$P_{n}^{\mu }(z,w)=P_{-n}^{\mu }(w,z)$
. This allows us to simplify our proofs in the following: we will often prove identities for
 $P^{\mu }_{n}$
only which then implies the corresponding result for
$P^{\mu }_{n}$
only which then implies the corresponding result for
 $P^{\mu }_{-n}$
.
$P^{\mu }_{-n}$
. -
(d) Remark 4.1 implies
(4.18) $$ \begin{align} \binom{\mu-1}{n}P_{\pm n}^{\mu}=\binom{-\mu}{n}P_{\pm n}^{1-\mu}. \end{align} $$
$$ \begin{align} \binom{\mu-1}{n}P_{\pm n}^{\mu}=\binom{-\mu}{n}P_{\pm n}^{1-\mu}. \end{align} $$
Remark 4.7 (Invariant representative functions and the finite-dimensional invariant eigenspaces)
We consider
![]() ${\mathbb D}$
as a symmetric space
${\mathbb D}$
as a symmetric space
![]() $\mathcal {M}({\mathbb D}) / \partial {\mathbb D}$
over its automorphism group
$\mathcal {M}({\mathbb D}) / \partial {\mathbb D}$
over its automorphism group
![]() $\mathcal {M}({\mathbb D})$
with
$\mathcal {M}({\mathbb D})$
with
![]() $\partial {\mathbb D} \cong \operatorname {U}(1)$
acting by rotations. This yields an alternative way of deriving the restrictions to
$\partial {\mathbb D} \cong \operatorname {U}(1)$
acting by rotations. This yields an alternative way of deriving the restrictions to
![]() ${\mathbb D}$
of those Poisson–Fourier modes from (4.17) which are defined on all of
${\mathbb D}$
of those Poisson–Fourier modes from (4.17) which are defined on all of
![]() $\Omega $
, using finite-dimensional representation theory. Such considerations are very much in the spirit of [Reference Helgason21]. The group
$\Omega $
, using finite-dimensional representation theory. Such considerations are very much in the spirit of [Reference Helgason21]. The group
![]() $\mathcal {M}({\mathbb D})$
is isomorphic to the projective split unitary group
$\mathcal {M}({\mathbb D})$
is isomorphic to the projective split unitary group
 $$ \begin{align*}\operatorname{PSU}(1,1) = \bigg\{ {\scriptsize \begin{pmatrix} a & b \\ \overline{{b}} & \overline{{a}} \end{pmatrix}} \colon |a|^2-|b|^2=1 \bigg\} \Big/ \Big\{ \pm {\scriptsize \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}} \Big\}\end{align*} $$
$$ \begin{align*}\operatorname{PSU}(1,1) = \bigg\{ {\scriptsize \begin{pmatrix} a & b \\ \overline{{b}} & \overline{{a}} \end{pmatrix}} \colon |a|^2-|b|^2=1 \bigg\} \Big/ \Big\{ \pm {\scriptsize \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}} \Big\}\end{align*} $$
as a real Lie group. By Schur’s lemma, every irreducible representation
![]() $\pi \colon \mathcal {M}({\mathbb D}) \longrightarrow \operatorname {GL}_n({\mathbb C})$
as invertible
$\pi \colon \mathcal {M}({\mathbb D}) \longrightarrow \operatorname {GL}_n({\mathbb C})$
as invertible
![]() $(n\times n)$
-matrices induces eigenfunctions of the Laplacian on
$(n\times n)$
-matrices induces eigenfunctions of the Laplacian on
![]() $\operatorname {PSU}(1,1)$
via
$\operatorname {PSU}(1,1)$
via
which are known as representative functions or matrix elements. For a systematic discussion, we refer to the textbook [Reference Bröcker and Dieck9, Chapter III]. The corresponding eigenvalues may be computed from representation-theoretic data (see, e.g., [Reference Hall16, Proposition 10.6]). Note that in the literature, many results are formulated for general invariant differential operators or the corresponding Casimir elements and joint eigenfunctions thereof instead of the Laplacian, which is always invariant and thus constitutes a special case. However, the disk
![]() ${\mathbb D}$
is a two-point homogeneous space, so all
${\mathbb D}$
is a two-point homogeneous space, so all
![]() $\mathcal {M}({\mathbb D})$
-invariant differential operators are polynomials in the Laplacian (see [Reference Helgason20, Theorem 11]). Adapting [Reference Hall16, Example 4.10], one may parameterize the irreducible representations of
$\mathcal {M}({\mathbb D})$
-invariant differential operators are polynomials in the Laplacian (see [Reference Helgason20, Theorem 11]). Adapting [Reference Hall16, Example 4.10], one may parameterize the irreducible representations of
![]() $\operatorname {PSU}(1,1)$
as follows: let
$\operatorname {PSU}(1,1)$
as follows: let
![]() $m \in {\mathbb N}_0$
and
$m \in {\mathbb N}_0$
and
the vector space of polynomials of total degree m with
![]() $\dim (V_m) = m+1$
. Then
$\dim (V_m) = m+1$
. Then
for
![]() $m \in {\mathbb N}$
constitutes a complete list of the irreducible finite-dimensional representations of
$m \in {\mathbb N}$
constitutes a complete list of the irreducible finite-dimensional representations of
![]() $\operatorname {SU}(1,1)$
(see also [Reference Hall16, Proposition 4.11 and Section 4.6]). Moreover,
$\operatorname {SU}(1,1)$
(see also [Reference Hall16, Proposition 4.11 and Section 4.6]). Moreover,
![]() $\pi _m$
descends to the quotient
$\pi _m$
descends to the quotient
![]() $\operatorname {PSU}(1,1)$
if and only if m is even, providing a description of all irreducible finite-dimensional representations of
$\operatorname {PSU}(1,1)$
if and only if m is even, providing a description of all irreducible finite-dimensional representations of
![]() $\operatorname {PSU}(1,1)$
. A computation then yields explicit formulas for (4.19), which completes the eigenvalue theory of the Laplacian on
$\operatorname {PSU}(1,1)$
. A computation then yields explicit formulas for (4.19), which completes the eigenvalue theory of the Laplacian on
![]() $\operatorname {PSU}(1,1)$
. Finally, parameterizing a copy of the rotation group
$\operatorname {PSU}(1,1)$
. Finally, parameterizing a copy of the rotation group
![]() $\operatorname {U}(1) \subseteq \operatorname {PSU}(1,1)$
by
$\operatorname {U}(1) \subseteq \operatorname {PSU}(1,1)$
by
![]() $\big (\begin {smallmatrix} i \eta & 0 \\ 0 & - i \overline {{\eta }} \end {smallmatrix}\big )$
with
$\big (\begin {smallmatrix} i \eta & 0 \\ 0 & - i \overline {{\eta }} \end {smallmatrix}\big )$
with
![]() $\eta \in \partial {\mathbb D}$
yields that exactly the representative functions
$\eta \in \partial {\mathbb D}$
yields that exactly the representative functions
![]() $(\pi _{2m})_{m,d}$
with
$(\pi _{2m})_{m,d}$
with
![]() $1 \le d \le 2m+1$
are invariant under the action of
$1 \le d \le 2m+1$
are invariant under the action of
![]() $\operatorname {U}(1)$
and thus pass to the quotient
$\operatorname {U}(1)$
and thus pass to the quotient
![]() ${\mathbb D} \cong \operatorname {PSU}(1,1) / \operatorname {U}(1)$
. By a computation,
${\mathbb D} \cong \operatorname {PSU}(1,1) / \operatorname {U}(1)$
. By a computation,
![]() $(\pi _{2m})_{m,d} = P_{m-d}^{-m}$
with the exceptional Poisson–Fourier modes from (4.17).
$(\pi _{2m})_{m,d} = P_{m-d}^{-m}$
with the exceptional Poisson–Fourier modes from (4.17).
Note that these considerations only recover the finite-dimensional invariant eigenspace, i.e., the case
![]() $(E_0)$
in Theorem 2.10. It would be interesting to study whether this approach generalizes to the other invariant subspaces by incorporating suitable representations on infinite-dimensional spaces.
$(E_0)$
in Theorem 2.10. It would be interesting to study whether this approach generalizes to the other invariant subspaces by incorporating suitable representations on infinite-dimensional spaces.
5 Spectral decomposition of eigenspaces
In this section, we show that for every rotationally invariant domain
![]() $D\subseteq \Omega $
containing the origin each holomorphic eigenfunction of the invariant Laplacian
$D\subseteq \Omega $
containing the origin each holomorphic eigenfunction of the invariant Laplacian
![]() $\Delta _{zw}$
on D has a unique representation as a Poisson–Fourier series, a doubly infinite series with Poisson–Fourier modes as building blocks. We shall also see that if
$\Delta _{zw}$
on D has a unique representation as a Poisson–Fourier series, a doubly infinite series with Poisson–Fourier modes as building blocks. We shall also see that if
![]() $D=\Omega $
this series corresponds to a finite sum, and when D is one of the distinguished domains
$D=\Omega $
this series corresponds to a finite sum, and when D is one of the distinguished domains
![]() $\Omega _+$
or
$\Omega _+$
or
![]() $\Omega _-$
, then the series is one-sided infinite.
$\Omega _-$
, then the series is one-sided infinite.
Theorem 5.1 Let D be a rotationally invariant subdomain of
![]() $\Omega $
containing the origin, and let
$\Omega $
containing the origin, and let
![]() $f \in \mathcal {H}(D)$
be such that
$f \in \mathcal {H}(D)$
be such that
![]() $\Delta _{zw} f=\lambda f$
for some
$\Delta _{zw} f=\lambda f$
for some
![]() $\lambda \in {\mathbb C}$
of the form
$\lambda \in {\mathbb C}$
of the form
![]() $\lambda =4\mu (\mu -1)$
with
$\lambda =4\mu (\mu -1)$
with
![]() $\textsf {Re}\, \mu \ge 1/2$
. Then there are uniquely determined coefficients
$\textsf {Re}\, \mu \ge 1/2$
. Then there are uniquely determined coefficients
![]() $c_n \in {\mathbb C}$
such that
$c_n \in {\mathbb C}$
such that
Here, both series converge absolutely and locally uniformly in D.
Proof (i) For each
![]() $n \in {\mathbb Z}$
and all
$n \in {\mathbb Z}$
and all
![]() $(z,w) \in D$
, we consider
$(z,w) \in D$
, we consider
 $$ \begin{align*}f_n(z,w):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f \left( \eta z,\frac{w}{\eta} \right) \eta^{-(n+1)} \, d\eta .\end{align*} $$
$$ \begin{align*}f_n(z,w):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f \left( \eta z,\frac{w}{\eta} \right) \eta^{-(n+1)} \, d\eta .\end{align*} $$
Since D is rotationally invariant,
![]() $f_n$
is well-defined. Clearly,
$f_n$
is well-defined. Clearly,
![]() $f_n$
is holomorphic on D and n-homogeneous. By Theorem 4.4, there are complex numbers
$f_n$
is holomorphic on D and n-homogeneous. By Theorem 4.4, there are complex numbers
![]() $c_n \in {\mathbb C}$
such that
$c_n \in {\mathbb C}$
such that
(ii) We fix
![]() $(z,w) \in D$
and positive constants
$(z,w) \in D$
and positive constants
![]() $r<1<R$
such that
$r<1<R$
such that
![]() ${(\eta z,w/\eta ) \in D}$
for all
${(\eta z,w/\eta ) \in D}$
for all
![]() $r<|\eta |<R$
. This is possible as D is a rotationally invariant domain. Then
$r<|\eta |<R$
. This is possible as D is a rotationally invariant domain. Then
![]() $\eta \mapsto f(\eta z,w/\eta )$
is holomorphic in the annulus
$\eta \mapsto f(\eta z,w/\eta )$
is holomorphic in the annulus
![]() $r<|\eta |<R$
and therefore has a representation as the Laurent series
$r<|\eta |<R$
and therefore has a representation as the Laurent series
 $$ \begin{align*}f\left(\eta z,\frac{w}{\eta} \right)=\sum \limits_{n=-\infty}^{\infty} f_n(z,w) \eta^n ,\end{align*} $$
$$ \begin{align*}f\left(\eta z,\frac{w}{\eta} \right)=\sum \limits_{n=-\infty}^{\infty} f_n(z,w) \eta^n ,\end{align*} $$
which converges locally uniformly in
![]() $r<|\eta |<R$
. In particular,
$r<|\eta |<R$
. In particular,
This series converges, in fact, uniformly on each compact set
![]() $K\subseteq D$
. In order to see this, let K be such a compact subset of D. We can then choose positive constants
$K\subseteq D$
. In order to see this, let K be such a compact subset of D. We can then choose positive constants
![]() $r_1<1<R_1$
such that
$r_1<1<R_1$
such that
![]() ${K_1:=\{(\eta z,w/\eta ) \, : \, (z,w) \in K, \, r_1 \le |\eta | \le R_1\}}$
is a compact subset of D, and we let
${K_1:=\{(\eta z,w/\eta ) \, : \, (z,w) \in K, \, r_1 \le |\eta | \le R_1\}}$
is a compact subset of D, and we let
![]() ${M_1:=\max \{ |f(z,w)| \, : (z,w) \in K_1\}}$
. Note that
${M_1:=\max \{ |f(z,w)| \, : (z,w) \in K_1\}}$
. Note that
 $$ \begin{align*}f_n(z,w)=\frac{1}{2\pi i} \int \limits_{\partial{\mathbb D}_{\rho}} f\left(\eta z,\frac{w}{\eta} \right) \, \eta^{-(n+1)} \, d \eta \,\end{align*} $$
$$ \begin{align*}f_n(z,w)=\frac{1}{2\pi i} \int \limits_{\partial{\mathbb D}_{\rho}} f\left(\eta z,\frac{w}{\eta} \right) \, \eta^{-(n+1)} \, d \eta \,\end{align*} $$
for all
![]() $n \in {\mathbb Z}$
, all
$n \in {\mathbb Z}$
, all
![]() $(z,w) \in K$
and every
$(z,w) \in K$
and every
![]() $\rho \in [r,R]$
. We therefore get
$\rho \in [r,R]$
. We therefore get
In particular,
![]() $|f_n(z,w)| \le M_1 r_1^{-n}$
for all
$|f_n(z,w)| \le M_1 r_1^{-n}$
for all
![]() $n < 0$
and
$n < 0$
and
![]() $|f_n(z,w)| \le M_1 R_1^{-n}$
for all
$|f_n(z,w)| \le M_1 R_1^{-n}$
for all
![]() $n \ge 0$
, and this ensures the absolute and uniform convergence of the two series
$n \ge 0$
, and this ensures the absolute and uniform convergence of the two series
 $$ \begin{align*}\sum \limits_{n=-\infty}^{-1} f_n(z,w) \quad \text{ and } \quad \sum \limits_{n=0}^{\infty} f_n(z,w)\end{align*} $$
$$ \begin{align*}\sum \limits_{n=-\infty}^{-1} f_n(z,w) \quad \text{ and } \quad \sum \limits_{n=0}^{\infty} f_n(z,w)\end{align*} $$
on the compact set K.
(iii) In view of Step (ii), the coefficients
![]() $f_n(z,w)$
are exactly the Laurent coefficients of
$f_n(z,w)$
are exactly the Laurent coefficients of
![]() ${\eta \mapsto f(\eta z,w/\eta )}$
in an annulus containing the unit circle and are thus uniquely determined by f. Hence,
${\eta \mapsto f(\eta z,w/\eta )}$
in an annulus containing the unit circle and are thus uniquely determined by f. Hence,
![]() $f_n(z,w)=c_n P_{-n}^{\mu }(z,w)$
shows that the coefficients
$f_n(z,w)=c_n P_{-n}^{\mu }(z,w)$
shows that the coefficients
![]() $c_n$
are uniquely determined by f.
$c_n$
are uniquely determined by f.
In fact, the previous proof provides the following more precise information.
Corollary 5.2 Let D be a subdomain of
![]() $\Omega $
containing the origin, and let
$\Omega $
containing the origin, and let
![]() $f \in \mathcal {H}(D)$
be such that
$f \in \mathcal {H}(D)$
be such that
![]() $\Delta _{zw} f=\lambda f$
for some
$\Delta _{zw} f=\lambda f$
for some
![]() $\lambda \in {\mathbb C}$
.
$\lambda \in {\mathbb C}$
.
-
(i) If
 $D=\Omega $
, then
$D=\Omega $
, then
 $\lambda =4m (m+1)$
for some
$\lambda =4m (m+1)$
for some
 $m\in {\mathbb N}_0$
and there are uniquely determined coefficients
$m\in {\mathbb N}_0$
and there are uniquely determined coefficients
 $c_n\in {\mathbb C}$
such that
$c_n\in {\mathbb C}$
such that  $$ \begin{align*}f=\sum \limits_{n=-m}^m c_n P^{m+1}_n .\end{align*} $$
$$ \begin{align*}f=\sum \limits_{n=-m}^m c_n P^{m+1}_n .\end{align*} $$
-
(ii) If
 $D=\Omega _+$
, then
$D=\Omega _+$
, then
 $\lambda =4m (m+1)$
for some
$\lambda =4m (m+1)$
for some
 $m\in {\mathbb N}_0$
and there are uniquely determined coefficients
$m\in {\mathbb N}_0$
and there are uniquely determined coefficients
 $c_n \in {\mathbb C}$
such that
$c_n \in {\mathbb C}$
such that  $$ \begin{align*}f=\sum \limits_{n=-\infty}^m c_n P^{m+1}_n .\end{align*} $$
$$ \begin{align*}f=\sum \limits_{n=-\infty}^m c_n P^{m+1}_n .\end{align*} $$
-
(iii) If
 $D=\Omega _-$
, then
$D=\Omega _-$
, then
 $\lambda =4m (m+1)$
for some
$\lambda =4m (m+1)$
for some
 $m\in {\mathbb N}_0$
and there are uniquely determined coefficients
$m\in {\mathbb N}_0$
and there are uniquely determined coefficients
 $c_n \in {\mathbb C}$
such that
$c_n \in {\mathbb C}$
such that  $$ \begin{align*}f=\sum \limits_{n=-m}^{\infty} c_n P^{m+1}_n .\end{align*} $$
$$ \begin{align*}f=\sum \limits_{n=-m}^{\infty} c_n P^{m+1}_n .\end{align*} $$
Proof (i) If
![]() $f\in \mathcal {H}(\Omega )$
, then the functions
$f\in \mathcal {H}(\Omega )$
, then the functions
 $$ \begin{align*}f_n(z,w):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f \left( \eta z,\frac{w}{\eta} \right) \eta^{-(n+1)} \, d\eta \,\end{align*} $$
$$ \begin{align*}f_n(z,w):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f \left( \eta z,\frac{w}{\eta} \right) \eta^{-(n+1)} \, d\eta \,\end{align*} $$
are holomorphic and n-homogeneous on
![]() $\Omega $
and
$\Omega $
and
with
![]() $\mu \in {\mathbb C}$
such that
$\mu \in {\mathbb C}$
such that
![]() $\lambda =4\mu (\mu -1)$
and
$\lambda =4\mu (\mu -1)$
and
![]() $\textsf {Re}\,\mu \ge 1/2$
. Hence,
$\textsf {Re}\,\mu \ge 1/2$
. Hence,
![]() $\lambda = 4 m (m+1)$
for some
$\lambda = 4 m (m+1)$
for some
![]() $m \in {\mathbb N}_0$
since otherwise
$m \in {\mathbb N}_0$
since otherwise
![]() $P^{\mu }_{-n}$
is not holomorphic on
$P^{\mu }_{-n}$
is not holomorphic on
![]() $\Omega $
by Theorem 4.4. If
$\Omega $
by Theorem 4.4. If
![]() $\lambda =4m(m+1)$
, then for each
$\lambda =4m(m+1)$
, then for each
![]() $|n|> m$
, the function
$|n|> m$
, the function
![]() $P^{m+1}_{-n}$
is not holomorphic on
$P^{m+1}_{-n}$
is not holomorphic on
![]() $\Omega $
again by Theorem 4.4, which forces
$\Omega $
again by Theorem 4.4, which forces
![]() $c_n=0$
for those n. Parts (ii) and (iii) follow in the same way.
$c_n=0$
for those n. Parts (ii) and (iii) follow in the same way.
Since all PFM
![]() $P^{\mu }_n$
are holomorphic on
$P^{\mu }_n$
are holomorphic on
![]() $\Omega _*$
, it is natural to inquire whether the series (5.1) in Theorem 5.1 converges on some bigger domain than D. In Section 6, we shall see that, in general, this is not the case.
$\Omega _*$
, it is natural to inquire whether the series (5.1) in Theorem 5.1 converges on some bigger domain than D. In Section 6, we shall see that, in general, this is not the case.
6 Comparison with the eigenvalue equation of the Laplacian on the unit disk and the Riemann sphere
In this section, we relate the spectral theory of the Laplacian on the unit disk
![]() ${\mathbb D}$
resp. the Riemann sphere
${\mathbb D}$
resp. the Riemann sphere
![]() $\widehat {{\mathbb C}}$
with the spectral theory of the invariant Laplacian on
$\widehat {{\mathbb C}}$
with the spectral theory of the invariant Laplacian on
![]() $\Omega $
which we have developed so far. In particular, we show that all eigenfunctions of
$\Omega $
which we have developed so far. In particular, we show that all eigenfunctions of
![]() $\Delta _{{\mathbb D}}$
on
$\Delta _{{\mathbb D}}$
on
![]() ${\mathbb D}$
resp.
${\mathbb D}$
resp.
![]() $\Delta _{\widehat {{\mathbb C}}}$
on
$\Delta _{\widehat {{\mathbb C}}}$
on
![]() $\widehat {{\mathbb C}}$
do have holomorphic extensions to eigenfunctions of
$\widehat {{\mathbb C}}$
do have holomorphic extensions to eigenfunctions of
![]() $\Delta _{zw}$
on the bidisk
$\Delta _{zw}$
on the bidisk
![]() ${\mathbb D}^2$
resp.
${\mathbb D}^2$
resp.
![]() $\Omega $
. Our approach is similar to the one employed in [Reference Berenstein and Gay8, Section 1.6], which deals exclusively with the hyperbolic Laplacian
$\Omega $
. Our approach is similar to the one employed in [Reference Berenstein and Gay8, Section 1.6], which deals exclusively with the hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
on the unit disk
$\Delta _{{\mathbb D}}$
on the unit disk
![]() ${\mathbb D}$
. However, we need some fine properties of hypergeometric functions, in addition to those which have been employed in [Reference Berenstein and Gay8]. We begin with the following lemma which is crucial for our approach.
${\mathbb D}$
. However, we need some fine properties of hypergeometric functions, in addition to those which have been employed in [Reference Berenstein and Gay8]. We begin with the following lemma which is crucial for our approach.
Lemma 6.1 Let
![]() $\mu \in {\mathbb C}$
with
$\mu \in {\mathbb C}$
with
![]() $\textsf {Re}\, \mu>0$
. Then
$\textsf {Re}\, \mu>0$
. Then
locally uniformly for
![]() $\omega \in {\mathbb C} \setminus [1,\infty )$
.
$\omega \in {\mathbb C} \setminus [1,\infty )$
.
Proof Fix
![]() $m \in {\mathbb N}_0$
such that
$m \in {\mathbb N}_0$
such that
![]() $m> \textsf {Re}\, \mu -2$
, and let
$m> \textsf {Re}\, \mu -2$
, and let
![]() $n \in {\mathbb N}_0$
. Then by [Reference Erdelyi11, Formula (11), p. 76] or [Reference MacRobert30, p. 84] there are complex numbers
$n \in {\mathbb N}_0$
. Then by [Reference Erdelyi11, Formula (11), p. 76] or [Reference MacRobert30, p. 84] there are complex numbers
![]() $A_k$
,
$A_k$
,
![]() $k=1, \ldots , m$
, such that
$k=1, \ldots , m$
, such that
 $$ \begin{align*} {}_2F_1\left(\mu,1-\mu;n+1;\omega\right) = 1+\sum \limits_{k=1}^m \frac{A_k}{\left( n+1 \right) \ldots \left(n+k \right)} \frac{\omega^k}{k!}+\rho_{m+1}(n,\omega) , \end{align*} $$
$$ \begin{align*} {}_2F_1\left(\mu,1-\mu;n+1;\omega\right) = 1+\sum \limits_{k=1}^m \frac{A_k}{\left( n+1 \right) \ldots \left(n+k \right)} \frac{\omega^k}{k!}+\rho_{m+1}(n,\omega) , \end{align*} $$
where
 $$ \begin{align} \rho_{m+1}(n,\omega):=\tilde{\gamma}_n \int \limits_{0}^1 \int \limits_0^1 t^{1-\mu+m} (1-t)^{n+\mu-1} \left( 1- s t \omega\right)^{-\mu-1-m} (1-s)^m \, ds \, dt \, \cdot \, \omega^{m+1} \end{align} $$
$$ \begin{align} \rho_{m+1}(n,\omega):=\tilde{\gamma}_n \int \limits_{0}^1 \int \limits_0^1 t^{1-\mu+m} (1-t)^{n+\mu-1} \left( 1- s t \omega\right)^{-\mu-1-m} (1-s)^m \, ds \, dt \, \cdot \, \omega^{m+1} \end{align} $$
and
 $$ \begin{align*} \tilde{\gamma}_n:=\frac{\Gamma(n+1) \Gamma(\mu+m)}{\Gamma(1-\mu) \Gamma(\mu+n) \Gamma(\mu) \, m!} . \end{align*} $$
$$ \begin{align*} \tilde{\gamma}_n:=\frac{\Gamma(n+1) \Gamma(\mu+m)}{\Gamma(1-\mu) \Gamma(\mu+n) \Gamma(\mu) \, m!} . \end{align*} $$
Note that our choice of the nonnegative integer m guarantees that the integral in (6.2) converges. To prove (6.1), it therefore suffices to show that
![]() $\rho _{m+1}(n,\omega ) \to 0$
uniformly on every compact subset K of
$\rho _{m+1}(n,\omega ) \to 0$
uniformly on every compact subset K of
![]() ${\mathbb C} \setminus [1,\infty )$
as
${\mathbb C} \setminus [1,\infty )$
as
![]() $n \to \infty $
. Fix such a compact set K. Obviously,
$n \to \infty $
. Fix such a compact set K. Obviously,
and since
![]() $-\textsf {Re}\,\mu -1-m<0$
, we have
$-\textsf {Re}\,\mu -1-m<0$
, we have
 $$ \begin{align} \nonumber |\rho_{m+1}(n,\omega)| & \le |\tilde{\gamma}_{n}| \int \limits_{0}^1 t^{1-\textsf{Re}\,\mu+m} (1-t)^{n+\textsf{Re}\,\mu-1} \, dt \frac{|\omega|^{m+1}}{M_K^{m+1+\textsf{Re}\,\mu}} \\ & \nonumber = |\tilde{\gamma}_n| \frac{\Gamma(2+m-\textsf{Re}\,\mu) \, \Gamma(n+\textsf{Re}\,\mu)}{\Gamma(2+m+n)} \frac{|\omega|^{m+1}}{M_K^{m+1+\textsf{Re}\,\mu}} \\ &= \gamma^* \frac{\Gamma(n+\textsf{Re}\,\mu)}{\Gamma(n+1)} \frac{\Gamma(n+1)}{|\Gamma(n+\mu)|} \frac{\Gamma(n+1)}{\Gamma(2+m+n)} \frac{|\omega|^{m+1}}{M_K^{m+1+\textsf{Re}\,\mu}}, \end{align} $$
$$ \begin{align} \nonumber |\rho_{m+1}(n,\omega)| & \le |\tilde{\gamma}_{n}| \int \limits_{0}^1 t^{1-\textsf{Re}\,\mu+m} (1-t)^{n+\textsf{Re}\,\mu-1} \, dt \frac{|\omega|^{m+1}}{M_K^{m+1+\textsf{Re}\,\mu}} \\ & \nonumber = |\tilde{\gamma}_n| \frac{\Gamma(2+m-\textsf{Re}\,\mu) \, \Gamma(n+\textsf{Re}\,\mu)}{\Gamma(2+m+n)} \frac{|\omega|^{m+1}}{M_K^{m+1+\textsf{Re}\,\mu}} \\ &= \gamma^* \frac{\Gamma(n+\textsf{Re}\,\mu)}{\Gamma(n+1)} \frac{\Gamma(n+1)}{|\Gamma(n+\mu)|} \frac{\Gamma(n+1)}{\Gamma(2+m+n)} \frac{|\omega|^{m+1}}{M_K^{m+1+\textsf{Re}\,\mu}}, \end{align} $$
where
 $$ \begin{align*}\gamma^*:= \frac{|\Gamma(\mu+m)| \, \Gamma(2+m-\textsf{Re}\,\mu)}{|\Gamma(1-\mu)| \, |\Gamma(\mu)| \, m!} .\end{align*} $$
$$ \begin{align*}\gamma^*:= \frac{|\Gamma(\mu+m)| \, \Gamma(2+m-\textsf{Re}\,\mu)}{|\Gamma(1-\mu)| \, |\Gamma(\mu)| \, m!} .\end{align*} $$
An application of Stirling’s formula
 $$ \begin{align} \lim \limits_{n \to \infty} \frac{\Gamma(\alpha+n)}{\Gamma(n+1)} e^{-(\alpha-1) \log(n+1)} \to 1 , \quad \alpha \in {\mathbb C} , \end{align} $$
$$ \begin{align} \lim \limits_{n \to \infty} \frac{\Gamma(\alpha+n)}{\Gamma(n+1)} e^{-(\alpha-1) \log(n+1)} \to 1 , \quad \alpha \in {\mathbb C} , \end{align} $$
to each of the first three quotients in (6.3) shows that there is a constant
![]() $\gamma>0$
depending only on
$\gamma>0$
depending only on
![]() $\mu $
, m and K such that
$\mu $
, m and K such that
 $$ \begin{align*}|\rho_{m+1}(n,\omega)| \le \gamma \cdot \left(n+1 \right)^{\textsf{Re}\,\mu-1} \left(n+1 \right)^{1-\textsf{Re}\,\mu} \left(n+1 \right)^{-m-1} |\omega|^{m+1} =\gamma \cdot \left( \frac{|\omega|}{n+1} \right)^{m+1} .\end{align*} $$
$$ \begin{align*}|\rho_{m+1}(n,\omega)| \le \gamma \cdot \left(n+1 \right)^{\textsf{Re}\,\mu-1} \left(n+1 \right)^{1-\textsf{Re}\,\mu} \left(n+1 \right)^{-m-1} |\omega|^{m+1} =\gamma \cdot \left( \frac{|\omega|}{n+1} \right)^{m+1} .\end{align*} $$
In particular,
![]() $\rho _{m+1}(n,\omega ) \to 0$
as
$\rho _{m+1}(n,\omega ) \to 0$
as
![]() $n \to \infty $
uniformly for
$n \to \infty $
uniformly for
![]() $\omega \in K$
. This completes the proof of (6.1).
$\omega \in K$
. This completes the proof of (6.1).
We are now in a position to prove Theorem 2.2.
Proof of Theorem 2.2
Let
![]() $f \in X_\lambda ({\mathbb D})$
, and write
$f \in X_\lambda ({\mathbb D})$
, and write
![]() $\lambda =4 \mu (\mu -1)$
for some complex number
$\lambda =4 \mu (\mu -1)$
for some complex number
![]() $\mu \in {\mathbb C}$
with
$\mu \in {\mathbb C}$
with
![]() $\textsf {Re}\,\mu \ge 1/2$
. By [Reference Berenstein and Gay8, Theorem 16.18], there are uniquely determined coefficients
$\textsf {Re}\,\mu \ge 1/2$
. By [Reference Berenstein and Gay8, Theorem 16.18], there are uniquely determined coefficients
![]() $c_n \in {\mathbb C}$
such that
$c_n \in {\mathbb C}$
such that
the series converges absolutely and pointwise for each
![]() $z \in {\mathbb D}$
. As it is shown in the proof of [Reference Berenstein and Gay8, Theorem 1.6.18], the coefficients
$z \in {\mathbb D}$
. As it is shown in the proof of [Reference Berenstein and Gay8, Theorem 1.6.18], the coefficients
![]() $c_n$
do have the additional property that
$c_n$
do have the additional property that
We proceed to show that (6.5) and Lemma 6.1 together guarantee that the series
converges locally uniformly for
![]() $(z,w) \in {\mathbb D}^2$
, and hence defines a function
$(z,w) \in {\mathbb D}^2$
, and hence defines a function
![]() ${F \in \mathcal {H}({\mathbb D}^2)}$
with the required properties. The identity principle shows further that F is then uniquely determined.
${F \in \mathcal {H}({\mathbb D}^2)}$
with the required properties. The identity principle shows further that F is then uniquely determined.
It remains to prove the local uniform convergence of the series (6.6) in
![]() ${\mathbb D}^2$
. Fix
${\mathbb D}^2$
. Fix
![]() $r \in (0,1)$
. We begin by noting that (4.11) and (4.7) lead to
$r \in (0,1)$
. We begin by noting that (4.11) and (4.7) lead to
 $$ \begin{align} \nonumber \left| P^{\mu}_n(z,w) \right| & = \left| \binom{\mu}{|n|} \right| \, \left|F^{\mu}_{-n}(z,w) \right| \\ &\le \frac{|\Gamma(\mu +|n|)|}{|\Gamma(\mu)| \, \Gamma(|n|+1)} \left| {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{zw}{zw-1}\right) \right|\, r^{|n|} \end{align} $$
$$ \begin{align} \nonumber \left| P^{\mu}_n(z,w) \right| & = \left| \binom{\mu}{|n|} \right| \, \left|F^{\mu}_{-n}(z,w) \right| \\ &\le \frac{|\Gamma(\mu +|n|)|}{|\Gamma(\mu)| \, \Gamma(|n|+1)} \left| {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{zw}{zw-1}\right) \right|\, r^{|n|} \end{align} $$
for all
![]() $ |z|,|w| \le r$
. Since the Möbius transformation
$ |z|,|w| \le r$
. Since the Möbius transformation
maps the unit disk
![]() ${\mathbb D}$
conformally onto the half-plane
${\mathbb D}$
conformally onto the half-plane
![]() $\{\zeta \in {\mathbb C} \, : \, \textsf {Re}\, \zeta <1/2\}$
, the set
$\{\zeta \in {\mathbb C} \, : \, \textsf {Re}\, \zeta <1/2\}$
, the set
is a compact subset of
![]() ${\mathbb C} \setminus [1,\infty )$
. Thus, Lemma 6.1 implies
${\mathbb C} \setminus [1,\infty )$
. Thus, Lemma 6.1 implies
as
![]() $|n| \to \infty $
. Combining this with Stirling’s formula (6.4) we see from inequality (6.7) that there is a constant
$|n| \to \infty $
. Combining this with Stirling’s formula (6.4) we see from inequality (6.7) that there is a constant
![]() $\gamma>0$
such that
$\gamma>0$
such that
for all
![]() $|z| \le r$
,
$|z| \le r$
,
![]() $|w| \le r$
and every
$|w| \le r$
and every
![]() $n \in {\mathbb Z}$
. This estimate together with (6.5) implies that the series (6.6) converges uniformly for
$n \in {\mathbb Z}$
. This estimate together with (6.5) implies that the series (6.6) converges uniformly for
![]() $|z|,|w| \le r$
, as required. In particular, we have shown that the restriction map
$|z|,|w| \le r$
, as required. In particular, we have shown that the restriction map
is bijective. Since
![]() $X_{\lambda }({\mathbb D}^2)$
and
$X_{\lambda }({\mathbb D}^2)$
and
![]() $X_\lambda ({\mathbb D})$
are both Fréchet spaces with respect to the topology of locally uniform convergence on
$X_\lambda ({\mathbb D})$
are both Fréchet spaces with respect to the topology of locally uniform convergence on
![]() ${\mathbb D}^2$
resp.
${\mathbb D}^2$
resp.
![]() ${\mathbb D}$
(see [Reference Rudin38, Corollary 1 to Theorem 4.2.4] for the fact that
${\mathbb D}$
(see [Reference Rudin38, Corollary 1 to Theorem 4.2.4] for the fact that
![]() $X_{\lambda }({\mathbb D})$
is a Fréchet space) and the restriction map
$X_{\lambda }({\mathbb D})$
is a Fréchet space) and the restriction map
![]() $\mathcal {R}_h$
is obviously continuous, its inverse is continuous as well by the Open Mapping Theorem. This completes the proof of Theorem 2.2.
$\mathcal {R}_h$
is obviously continuous, its inverse is continuous as well by the Open Mapping Theorem. This completes the proof of Theorem 2.2.
Theorem 6.2 (
 $C^2$
-eigenfunctions of
$C^2$
-eigenfunctions of
 $\Delta _{\widehat {{\mathbb C}}}$
on
$\Delta _{\widehat {{\mathbb C}}}$
on
 $\widehat {{\mathbb C}}$
vs. holomorphic eigenfunctions of
$\widehat {{\mathbb C}}$
vs. holomorphic eigenfunctions of
 $\Delta _{zw}$
on
$\Delta _{zw}$
on
 $\Omega $
)
$\Omega $
)
Let
![]() $\lambda \in {\mathbb C} $
. Then the following are equivalent:
$\lambda \in {\mathbb C} $
. Then the following are equivalent:
-
(i) There is a function
 $f \in C^{2}(\widehat {{\mathbb C}})$
such that
$f \in C^{2}(\widehat {{\mathbb C}})$
such that
 $\Delta _{\widehat {{\mathbb C}}} f=\lambda f$
on
$\Delta _{\widehat {{\mathbb C}}} f=\lambda f$
on
 $\widehat {{\mathbb C}}$
.
$\widehat {{\mathbb C}}$
. -
(ii) There is a function
 $F \in \mathcal {H}(\Omega )$
such that
$F \in \mathcal {H}(\Omega )$
such that
 $\Delta _{zw} F=\lambda F$
on
$\Delta _{zw} F=\lambda F$
on
 $\Omega $
.
$\Omega $
. -
(iii)
 $\lambda =4 m (m+1)$
for some
$\lambda =4 m (m+1)$
for some
 $m \in {\mathbb N}_0$
.
$m \in {\mathbb N}_0$
.
Theorem 6.2 is a special case of Theorem 2.6.
Proof The implication (ii)
![]() $\Rightarrow $
(iii) is Corollary 5.2, and (iii)
$\Rightarrow $
(iii) is Corollary 5.2, and (iii)
![]() $\Rightarrow $
(ii) is Theorem 4.4. Clearly, (ii) implies (i), so we only need to prove that (i) implies (ii). Accordingly, we write
$\Rightarrow $
(ii) is Theorem 4.4. Clearly, (ii) implies (i), so we only need to prove that (i) implies (ii). Accordingly, we write
![]() $\lambda =4 \mu (\mu -1)$
with
$\lambda =4 \mu (\mu -1)$
with
![]() $\mu \in {\mathbb C}$
and
$\mu \in {\mathbb C}$
and
![]() $\textsf {Re}\,\mu \ge 1/2$
. For
$\textsf {Re}\,\mu \ge 1/2$
. For
![]() $n \in {\mathbb Z}$
, consider
$n \in {\mathbb Z}$
, consider
 $$ \begin{align*}f_n(z):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f (\eta z) \, \eta^{-(n+1)} \, d \eta=\frac{1}{2\pi} \int \limits_{0}^{2\pi} f(e^{it} z) e^{-i n t} \, dt .\end{align*} $$
$$ \begin{align*}f_n(z):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f (\eta z) \, \eta^{-(n+1)} \, d \eta=\frac{1}{2\pi} \int \limits_{0}^{2\pi} f(e^{it} z) e^{-i n t} \, dt .\end{align*} $$
Then
![]() $f_n \in C^{2}(\widehat {{\mathbb C}})$
is n-homogeneous and
$f_n \in C^{2}(\widehat {{\mathbb C}})$
is n-homogeneous and
![]() $\Delta _{\widehat {{\mathbb C}}} f_n=4 \mu (\mu -1) f_n$
on
$\Delta _{\widehat {{\mathbb C}}} f_n=4 \mu (\mu -1) f_n$
on
![]() $\widehat {{\mathbb C}}$
. Arguing in a similar way as in the proof of Theorem 4.4, we see that there is a constant
$\widehat {{\mathbb C}}$
. Arguing in a similar way as in the proof of Theorem 4.4, we see that there is a constant
![]() $c_n \in {\mathbb C}$
such that
$c_n \in {\mathbb C}$
such that
 $$ \begin{align*}f_n(z)=c_n \binom{-\mu}{|n|} {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{|z|^2}{1+|z|^2}\right) \cdot \begin{cases} \overline{z}^{|n|}, & \text{ if } n \ge 0, \\ (-z)^{|n|}, & \text{ if } n \le 0.\end{cases}\end{align*} $$
$$ \begin{align*}f_n(z)=c_n \binom{-\mu}{|n|} {}_2F_1\left(\mu,1-\mu;|n|+1;\frac{|z|^2}{1+|z|^2}\right) \cdot \begin{cases} \overline{z}^{|n|}, & \text{ if } n \ge 0, \\ (-z)^{|n|}, & \text{ if } n \le 0.\end{cases}\end{align*} $$
Therefore, the behavior of
![]() $f_n$
as
$f_n$
as
![]() $z \to \infty $
depends essentially on the value
$z \to \infty $
depends essentially on the value
![]() ${}_2F_1\left (\mu ;1-\mu ;|n|+1\right ){1}$
. It is well-known, see [Reference Andrews, Askey and Roy3, Theorem 2.1.3], that
${}_2F_1\left (\mu ;1-\mu ;|n|+1\right ){1}$
. It is well-known, see [Reference Andrews, Askey and Roy3, Theorem 2.1.3], that
 $$ \begin{align*}\lim \limits_{x \to 1-} \frac{{}_2F_1\left(\mu,1-\mu;|n|+1;1\right)}{-\log (1-x)}=\frac{1}{\Gamma(\mu) \Gamma(1-\mu)} \, \quad \text{ if } n=0 \; ,\end{align*} $$
$$ \begin{align*}\lim \limits_{x \to 1-} \frac{{}_2F_1\left(\mu,1-\mu;|n|+1;1\right)}{-\log (1-x)}=\frac{1}{\Gamma(\mu) \Gamma(1-\mu)} \, \quad \text{ if } n=0 \; ,\end{align*} $$
and, see [Reference Andrews, Askey and Roy3, Theorem 2.2.2],
 $$ \begin{align*}{}_2F_1\left(\mu,1-\mu;|n|+1;1\right) =\frac{\Gamma(|n|+1) \Gamma(|n|)}{\Gamma(|n|+1-\mu) \Gamma(|n|+\mu)} \, \quad \text{ if } n\not=0 .\end{align*} $$
$$ \begin{align*}{}_2F_1\left(\mu,1-\mu;|n|+1;1\right) =\frac{\Gamma(|n|+1) \Gamma(|n|)}{\Gamma(|n|+1-\mu) \Gamma(|n|+\mu)} \, \quad \text{ if } n\not=0 .\end{align*} $$
Hence, if
![]() $n=0$
, then
$n=0$
, then
![]() $f_n$
is defined at the point
$f_n$
is defined at the point
![]() $\infty $
only if
$\infty $
only if
![]() $c_0=0$
or
$c_0=0$
or
![]() $\mu \in {\mathbb N}$
. If
$\mu \in {\mathbb N}$
. If
![]() $n\not =0$
, then
$n\not =0$
, then
![]() ${}_2F_1\left (\mu ,1-\mu ;|n|+1;1\right ) =0 $
if and only if
${}_2F_1\left (\mu ,1-\mu ;|n|+1;1\right ) =0 $
if and only if
![]() $\mu =|n|+1+k$
for some
$\mu =|n|+1+k$
for some
![]() $k \in {\mathbb N}_0$
. Thus,
$k \in {\mathbb N}_0$
. Thus,
![]() $f_n :\widehat {{\mathbb C}} \to {\mathbb C}$
is defined at the point
$f_n :\widehat {{\mathbb C}} \to {\mathbb C}$
is defined at the point
![]() $\infty $
only if
$\infty $
only if
![]() $c_n=0$
or
$c_n=0$
or
![]() $\mu \in {\mathbb N}$
,
$\mu \in {\mathbb N}$
,
![]() $\mu> |n|$
. We conclude that either
$\mu> |n|$
. We conclude that either
![]() $c_n=0$
for every
$c_n=0$
for every
![]() $n \in {\mathbb Z}$
and then
$n \in {\mathbb Z}$
and then
![]() $f \equiv 0$
, or
$f \equiv 0$
, or
![]() $c_n\not =0$
for at least one
$c_n\not =0$
for at least one
![]() $n \in {\mathbb Z}$
and then
$n \in {\mathbb Z}$
and then
![]() $\lambda =4 m(m+1)$
for some
$\lambda =4 m(m+1)$
for some
![]() $m \in {\mathbb N}_0$
. In the latter case, we see that
$m \in {\mathbb N}_0$
. In the latter case, we see that
![]() $c_n\not =0$
forces
$c_n\not =0$
forces
![]() $m+1=\mu =|n|+1+k$
for some
$m+1=\mu =|n|+1+k$
for some
![]() $k \in {\mathbb N}_0$
, so
$k \in {\mathbb N}_0$
, so
![]() $m=|n|+k$
. In particular,
$m=|n|+k$
. In particular,
![]() $c_n=0$
for all
$c_n=0$
for all
![]() $|n|>m$
, so
$|n|>m$
, so
![]() $f(z)=F(z,-\overline {z})$
for
$f(z)=F(z,-\overline {z})$
for
Remark 6.3 We see that the spectrum of the hyperbolic Laplacian
![]() $\Delta _{{\mathbb D}}$
is
$\Delta _{{\mathbb D}}$
is
![]() ${\mathbb C}$
whereas the spectrum of the spherical Laplacian
${\mathbb C}$
whereas the spectrum of the spherical Laplacian
![]() $\Delta _{\widehat {{\mathbb C}}}$
is notably smaller as it only consists of the scalars
$\Delta _{\widehat {{\mathbb C}}}$
is notably smaller as it only consists of the scalars
![]() $4m(m+1)$
for
$4m(m+1)$
for
![]() $m\in {\mathbb N}_0$
. Furthermore, by Theorem 6.2, every eigenfunction of the spherical Laplacian can be extended to the whole domain
$m\in {\mathbb N}_0$
. Furthermore, by Theorem 6.2, every eigenfunction of the spherical Laplacian can be extended to the whole domain
![]() $\Omega $
. This is different from the hyperbolic case where the extension to
$\Omega $
. This is different from the hyperbolic case where the extension to
![]() ${\mathbb D}^2$
provided by Theorem 2.2 is maximal at least for the category of rotationally invariant domains as the following example shows.
${\mathbb D}^2$
provided by Theorem 2.2 is maximal at least for the category of rotationally invariant domains as the following example shows.
Example 6.4 Fix
![]() $\mu \in {\mathbb C}$
with
$\mu \in {\mathbb C}$
with
![]() $\textsf {Re}\,\mu \geq \frac {1}{2}$
, let
$\textsf {Re}\,\mu \geq \frac {1}{2}$
, let
![]() $(z_0,w_0)\in \Omega \setminus {\mathbb D}^2$
with
$(z_0,w_0)\in \Omega \setminus {\mathbb D}^2$
with
![]() $z_0 w_0 \not \in [1,\infty )$
, and define
$z_0 w_0 \not \in [1,\infty )$
, and define
 $$\begin{align*}b_n :=\left(\frac{\Gamma(\mu+|n|)}{\Gamma(\mu)|n|!}{}_2F_1\left(\mu;1-\mu;|n|+1\right){\frac{z_0w_0}{z_0w_0-1}}\right)^{-1}.\end{align*}$$
$$\begin{align*}b_n :=\left(\frac{\Gamma(\mu+|n|)}{\Gamma(\mu)|n|!}{}_2F_1\left(\mu;1-\mu;|n|+1\right){\frac{z_0w_0}{z_0w_0-1}}\right)^{-1}.\end{align*}$$
Note that asymptotically
This follows from Lemma 6.1 and Stirling’s formula (6.4). In view of (6.8), this shows that the series
converges locally uniformly in
![]() ${\mathbb D}^2$
. Hence,
${\mathbb D}^2$
. Hence,
![]() $F \in \mathcal {H}({\mathbb D}^2)$
and, since every function
$F \in \mathcal {H}({\mathbb D}^2)$
and, since every function
![]() $P^\mu _n$
is an eigenfunction of
$P^\mu _n$
is an eigenfunction of
![]() $\Delta _{zw}$
, we have
$\Delta _{zw}$
, we have
![]() $\Delta _{zw} F=4 \mu (\mu -1) F$
in
$\Delta _{zw} F=4 \mu (\mu -1) F$
in
![]() ${\mathbb D}^2$
. In particular,
${\mathbb D}^2$
. In particular,
is of class
![]() $C^{2}({\mathbb D})$
and an eigenfunction of
$C^{2}({\mathbb D})$
and an eigenfunction of
![]() $\Delta _{{\mathbb D}}$
. By Theorem 2.2,
$\Delta _{{\mathbb D}}$
. By Theorem 2.2,
![]() $F \in \mathcal {H}({\mathbb D}^2)$
is the uniquely determined function in
$F \in \mathcal {H}({\mathbb D}^2)$
is the uniquely determined function in
![]() $\mathcal {H}({\mathbb D}^2)$
such that
$\mathcal {H}({\mathbb D}^2)$
such that
![]() $F(z,\overline {z})=f(z)$
in
$F(z,\overline {z})=f(z)$
in
![]() ${\mathbb D}$
. Now assume
${\mathbb D}$
. Now assume
![]() $F\in \mathcal {H}(D)$
, where D is a rotationally invariant domain such that
$F\in \mathcal {H}(D)$
, where D is a rotationally invariant domain such that
![]() ${\mathbb D}^2\subsetneq D \subseteq \Omega $
and
${\mathbb D}^2\subsetneq D \subseteq \Omega $
and
![]() $(z_0,w_0) \in D \setminus {\mathbb D}^2$
. By Theorem 5.1, there are coefficients
$(z_0,w_0) \in D \setminus {\mathbb D}^2$
. By Theorem 5.1, there are coefficients
![]() $(\tilde {b}_n)_{n\in {\mathbb Z}}\subseteq {\mathbb C}$
such that
$(\tilde {b}_n)_{n\in {\mathbb Z}}\subseteq {\mathbb C}$
such that
for all
![]() $(z,w)\in D$
. Since the coefficients are uniquely determined, we conclude
$(z,w)\in D$
. Since the coefficients are uniquely determined, we conclude
![]() $\tilde {b}_n=b_n$
. This is a contradiction because
$\tilde {b}_n=b_n$
. This is a contradiction because
is a divergent series since
![]() $|z_0|\geq 1$
or
$|z_0|\geq 1$
or
![]() $|w_0|\geq 1$
.
$|w_0|\geq 1$
.
Corollary 6.5 Let
![]() $\lambda \in {\mathbb C}$
and D be a rotationally invariant subdomain of
$\lambda \in {\mathbb C}$
and D be a rotationally invariant subdomain of
![]() $\Omega $
such that
$\Omega $
such that
![]() ${\mathbb D}^2\subsetneq D$
. Then there exists a function
${\mathbb D}^2\subsetneq D$
. Then there exists a function
![]() $f \in X_\lambda ({\mathbb D}^2)$
that cannot be analytically continued to D.
$f \in X_\lambda ({\mathbb D}^2)$
that cannot be analytically continued to D.
7 Poisson–Fourier modes and the Möbius group
Recall the Möbius group
![]() $\mathcal {M}({\mathbb D}^2)$
of the bidisk from (2.5). In order to give a characterization of the Möbius invariant eigenspaces of
$\mathcal {M}({\mathbb D}^2)$
of the bidisk from (2.5). In order to give a characterization of the Möbius invariant eigenspaces of
![]() $\Delta _{zw}$
(e.g., proving Theorem 2.10), it will turn out that all we need to understand are precompositions of PFM with automorphisms in
$\Delta _{zw}$
(e.g., proving Theorem 2.10), it will turn out that all we need to understand are precompositions of PFM with automorphisms in
![]() $\mathcal {M}({\mathbb D}^2)$
, that is,
$\mathcal {M}({\mathbb D}^2)$
, that is,
Moreover, since
![]() $\mathcal {M}({\mathbb D}^2)$
is closely related to the Möbius group
$\mathcal {M}({\mathbb D}^2)$
is closely related to the Möbius group
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\Omega $
from (2.4), we can use the following description of
$\Omega $
from (2.4), we can use the following description of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Lemma 7.1 The group
![]() $\mathcal {M}$
is generated by the flip map
$\mathcal {M}$
is generated by the flip map ![]() and the mappings
and the mappings

with
![]() $(z,w) \in \Omega \cap {\mathbb C}^2$
and
$(z,w) \in \Omega \cap {\mathbb C}^2$
and
![]() $\gamma \in {\mathbb C}^*$
. More precisely, for every
$\gamma \in {\mathbb C}^*$
. More precisely, for every
![]() $T \in \mathcal {M}$
, there exist
$T \in \mathcal {M}$
, there exist
![]() $z,w \in {\mathbb C}$
and
$z,w \in {\mathbb C}$
and
![]() $\gamma \in {\mathbb C}^*$
such that
$\gamma \in {\mathbb C}^*$
such that
Remark 7.2 Lemma 7.1 is exactly Lemma 2.2 in [Reference Heins, Moucha, Roth and Sugawa19] where we have replaced the automorphisms
![]() $\Phi _{z,w}$
by the
$\Phi _{z,w}$
by the
![]() $T_{z,w} = \Phi _{z,w} \circ \varrho _{-1}$
automorphisms in (7.1). The reason will become apparent in (7.3) and (7.4). Essentially, the automorphisms
$T_{z,w} = \Phi _{z,w} \circ \varrho _{-1}$
automorphisms in (7.1). The reason will become apparent in (7.3) and (7.4). Essentially, the automorphisms
![]() $T_{z,w}$
in (7.1) are precisely the automorphisms of
$T_{z,w}$
in (7.1) are precisely the automorphisms of
![]() $\Omega $
interchanging a given point
$\Omega $
interchanging a given point
![]() $(z,w)\in \Omega \cap ({\mathbb C}\times {\mathbb C})$
with
$(z,w)\in \Omega \cap ({\mathbb C}\times {\mathbb C})$
with
![]() $(0,0)$
– instead of only sending
$(0,0)$
– instead of only sending
![]() $(0,0)$
to
$(0,0)$
to
![]() $(z,w)$
(see [Reference Moucha32, Section 2.3] for more details on this).
$(z,w)$
(see [Reference Moucha32, Section 2.3] for more details on this).
Therefore, understanding precompositions of a PFM
![]() $P_n^{\mu }$
with elements
$P_n^{\mu }$
with elements
![]() ${T\in \mathcal {M}({\mathbb D}^2)}$
breaks down to understanding precompositions with the above generators. Note that the mappings
${T\in \mathcal {M}({\mathbb D}^2)}$
breaks down to understanding precompositions with the above generators. Note that the mappings
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $T_{z,w}$
for
$T_{z,w}$
for
![]() $w\neq \overline {{z}}$
are not elements of
$w\neq \overline {{z}}$
are not elements of
![]() $\mathcal {M}({\mathbb D}^2)$
. However, the precompositions with these mappings still make sense for those PFM defined on all of
$\mathcal {M}({\mathbb D}^2)$
. However, the precompositions with these mappings still make sense for those PFM defined on all of
![]() $\Omega $
, that is, in view of Theorem 4.4, the precompositions
$\Omega $
, that is, in view of Theorem 4.4, the precompositions
are well-defined. In the case that
![]() $T=\varrho _\gamma $
, we have
$T=\varrho _\gamma $
, we have
![]() ${P_n^{\mu }\circ T=\gamma ^{-n}P_n^{\mu }}$
by the
${P_n^{\mu }\circ T=\gamma ^{-n}P_n^{\mu }}$
by the
![]() $(-n)$
-homogeneity of the PFM for all
$(-n)$
-homogeneity of the PFM for all
![]() $\mu \in {\mathbb C}$
. Next, if
$\mu \in {\mathbb C}$
. Next, if
![]() $T=\mathcal {F}$
, it is easily seen by direct verification based on (4.17) that
$T=\mathcal {F}$
, it is easily seen by direct verification based on (4.17) that
for
![]() $m\in {\mathbb N}_0$
and
$m\in {\mathbb N}_0$
and
![]() $|n|\leq m$
. In order to treat the case that
$|n|\leq m$
. In order to treat the case that
![]() $T=T_{z,w}$
resp.
$T=T_{z,w}$
resp.
![]() $T=T_{z,\overline {{z}}}$
, some preliminary observations are useful. First, every automorphism
$T=T_{z,\overline {{z}}}$
, some preliminary observations are useful. First, every automorphism
![]() $T_{z,w}$
is induced by a Möbius transformation
$T_{z,w}$
is induced by a Möbius transformation
![]() $\psi _{z,w}$
of the form
$\psi _{z,w}$
of the form
in the sense that
![]() $T_{z,w}(u,v) = (\psi _{z,w}(u), 1/\psi _{z,w}(1/v))$
.
$T_{z,w}(u,v) = (\psi _{z,w}(u), 1/\psi _{z,w}(1/v))$
.
Remark 7.3 Choosing
![]() $w=\overline {z}$
in (7.2) yields all self-inverse automorphisms of
$w=\overline {z}$
in (7.2) yields all self-inverse automorphisms of
![]() ${\mathbb D}$
except for the identity, and, similarly, the choice
${\mathbb D}$
except for the identity, and, similarly, the choice
![]() $w=-\overline {z}\in {\mathbb D}$
yields all self-inverse rigid motions of
$w=-\overline {z}\in {\mathbb D}$
yields all self-inverse rigid motions of
![]() $\widehat {{\mathbb C}}$
.
$\widehat {{\mathbb C}}$
.
Further, we will employ the definition of the PFM via integrals from (4.10). By Remark 4.3, when considering points
![]() $(z,\overline {{z}})\in {\mathbb D}^2$
, this definition coincides with the nth Fourier mode of the
$(z,\overline {{z}})\in {\mathbb D}^2$
, this definition coincides with the nth Fourier mode of the
![]() $\mu $
-power of the Poisson kernel on the unit disk. The Poisson kernel on
$\mu $
-power of the Poisson kernel on the unit disk. The Poisson kernel on
![]() ${\mathbb D}$
satisfies the well-known properties
${\mathbb D}$
satisfies the well-known properties
 $$ \begin{align} P\left(z,\overline{{z}};\xi\right)=\frac{\psi_{z,\overline{{z}}}'(\xi)}{\psi_{z,\overline{{z}}}(\xi)}\xi \end{align} $$
$$ \begin{align} P\left(z,\overline{{z}};\xi\right)=\frac{\psi_{z,\overline{{z}}}'(\xi)}{\psi_{z,\overline{{z}}}(\xi)}\xi \end{align} $$
and
 $$ \begin{align} P\left(\psi_{z,\overline{{z}}}(u), \overline{{\psi_{z,\overline{{z}}}(u)}}; \psi_{z,\overline{{z}}}(\xi)\right) = \frac{P(u,\overline{{u}}; \xi)}{P(z,\overline{{z}};\xi)}, \end{align} $$
$$ \begin{align} P\left(\psi_{z,\overline{{z}}}(u), \overline{{\psi_{z,\overline{{z}}}(u)}}; \psi_{z,\overline{{z}}}(\xi)\right) = \frac{P(u,\overline{{u}}; \xi)}{P(z,\overline{{z}};\xi)}, \end{align} $$
where
![]() $z,u\in {\mathbb D}$
,
$z,u\in {\mathbb D}$
,
![]() $\xi \in \partial {\mathbb D}$
, and
$\xi \in \partial {\mathbb D}$
, and
![]() $\psi _{z,\overline {{z}}}\in \mathcal {M}({\mathbb D})$
(see [Reference Rudin38, Theorem 3.3.5]).
$\psi _{z,\overline {{z}}}\in \mathcal {M}({\mathbb D})$
(see [Reference Rudin38, Theorem 3.3.5]).
Remark 7.4 One can define the generalized Poisson kernel P even on
![]() $\Omega \times \partial {\mathbb D}$
. Then P is never zero, and for each
$\Omega \times \partial {\mathbb D}$
. Then P is never zero, and for each
![]() $\xi \in \partial {\mathbb D}$
, the function
$\xi \in \partial {\mathbb D}$
, the function
![]() $P(\cdot ;\xi )$
is meromorphic in the sense of [Reference Fischer and Lieb13, Chapter VI.2]. The identities (7.3) and (7.4) then take the form
$P(\cdot ;\xi )$
is meromorphic in the sense of [Reference Fischer and Lieb13, Chapter VI.2]. The identities (7.3) and (7.4) then take the form
 $$ \begin{align*} P\left(\psi_{z,w}^{-1}(0),1/\psi_{z,w}^{-1}(\infty);\xi\right)&=\frac{\psi_{z,w}'(\xi)}{\psi_{z,w}(\xi)}\xi =P\left(z,w;\xi\right),\\ P\left(\psi_{z,w}(u),\frac{1}{\psi_{z,w}\left(1/v\right)};\psi_{z,w}(\xi)\right)&=\frac{P(u,v;\xi)}{P\left(\psi_{z,w}^{-1}(0),1/\psi_{z,w}^{-1}(\infty);\xi\right)}=\frac{P(u,v;\xi)}{P\left(z,w;\xi\right)} , \end{align*} $$
$$ \begin{align*} P\left(\psi_{z,w}^{-1}(0),1/\psi_{z,w}^{-1}(\infty);\xi\right)&=\frac{\psi_{z,w}'(\xi)}{\psi_{z,w}(\xi)}\xi =P\left(z,w;\xi\right),\\ P\left(\psi_{z,w}(u),\frac{1}{\psi_{z,w}\left(1/v\right)};\psi_{z,w}(\xi)\right)&=\frac{P(u,v;\xi)}{P\left(\psi_{z,w}^{-1}(0),1/\psi_{z,w}^{-1}(\infty);\xi\right)}=\frac{P(u,v;\xi)}{P\left(z,w;\xi\right)} , \end{align*} $$
where
![]() $(z,w)\in \Omega \cap {\mathbb C}^2$
,
$(z,w)\in \Omega \cap {\mathbb C}^2$
,
![]() $(u,v)\in \Omega $
, and
$(u,v)\in \Omega $
, and
![]() $\xi \in \partial {\mathbb D}$
.
$\xi \in \partial {\mathbb D}$
.
With these preparations, we are now in a position to analyze the precompositions of
![]() $P^{\mu }_n$
with elements of
$P^{\mu }_n$
with elements of
![]() $\mathcal {M}({\mathbb D}^2)$
resp.
$\mathcal {M}({\mathbb D}^2)$
resp.
![]() $\mathcal {M}$
. We start with the simplest case,
$\mathcal {M}$
. We start with the simplest case,
![]() $P^{m+1}_0 \circ T_{u,v}$
.
$P^{m+1}_0 \circ T_{u,v}$
.
Proposition 7.5 Let
![]() $m\in {\mathbb N}_0$
,
$m\in {\mathbb N}_0$
,
![]() $(z,w)\in \Omega $
, and
$(z,w)\in \Omega $
, and
![]() $(u,v) \in \Omega \cap {\mathbb C}^2$
. Then
$(u,v) \in \Omega \cap {\mathbb C}^2$
. Then
 $$ \begin{align} \big( P_0^{m+1} \circ T_{u,v} \big)(z,w)=\big( P_0^{-m} \circ T_{u,v} \big)(z,w)=\sum_{j=-m}^{m} P^{m+1}_{-j}\left(u,v\right) P^{-m}_{j}(z,w). \end{align} $$
$$ \begin{align} \big( P_0^{m+1} \circ T_{u,v} \big)(z,w)=\big( P_0^{-m} \circ T_{u,v} \big)(z,w)=\sum_{j=-m}^{m} P^{m+1}_{-j}\left(u,v\right) P^{-m}_{j}(z,w). \end{align} $$
Proof The way of reasoning is as follows: first, fix
![]() $z, u\in {\mathbb D}$
, and let
$z, u\in {\mathbb D}$
, and let
![]() $v:=\overline {u}$
. Then
$v:=\overline {u}$
. Then
![]() $\psi _{u,\overline {{u}}}\in \mathcal {M}({\mathbb D})$
which means, in particular, that
$\psi _{u,\overline {{u}}}\in \mathcal {M}({\mathbb D})$
which means, in particular, that
![]() $T_{u,\overline {{u}}}(z,\overline {{z}})\in \{(t,\overline {{t}})\,:\,t\in {\mathbb D}\}$
. By the two variable identity principle, Lemma 3.1, if we can show (7.5) in this special case, then, keeping
$T_{u,\overline {{u}}}(z,\overline {{z}})\in \{(t,\overline {{t}})\,:\,t\in {\mathbb D}\}$
. By the two variable identity principle, Lemma 3.1, if we can show (7.5) in this special case, then, keeping
![]() $u\in {\mathbb D}$
fixed, (7.5) also holds for points
$u\in {\mathbb D}$
fixed, (7.5) also holds for points
![]() $(z,w)\in \Omega $
since both sides of the equation are holomorphic functions in
$(z,w)\in \Omega $
since both sides of the equation are holomorphic functions in
![]() $\Omega $
. Next, fix
$\Omega $
. Next, fix
![]() $(z,w)\in \Omega $
and note that both sides of (7.5) are holomorphic as functions of
$(z,w)\in \Omega $
and note that both sides of (7.5) are holomorphic as functions of
![]() $(u,v)\in \Omega \cap {\mathbb C}^2$
. Assuming (7.5) for
$(u,v)\in \Omega \cap {\mathbb C}^2$
. Assuming (7.5) for
![]() $v=\overline {{u}}\in {\mathbb D}$
then implies the claim, again by Lemma 3.1.
$v=\overline {{u}}\in {\mathbb D}$
then implies the claim, again by Lemma 3.1.
It remains to show (7.5) for
![]() $w=\overline {{z}}$
and
$w=\overline {{z}}$
and
![]() $v=\overline {{u}}$
with
$v=\overline {{u}}$
with
![]() $z,u\in {\mathbb D}$
. For this purpose, we compute
$z,u\in {\mathbb D}$
. For this purpose, we compute
 $$ \begin{align*} \big( P_0^{m+1} \circ T_{u,\overline{{u}}} \big)(z,\overline{{z}}) &\overset{({4.18})}{=}\big( P_0^{-m} \circ T_{u,\overline{{u}}} \big)(z,\overline{{z}}) \\ &= \frac{1}{2\pi} \int\limits_{0}^{2\pi} P\left(\psi_{u,\overline{{u}}}(z),\frac{1}{\psi_{u,\overline{{u}}}\left(1/\overline{{z}}\right)};e^{it}\right)^{-m}\,dt\\ &\overset{({7.4})}{=} \frac{1}{2\pi} \int\limits_{0}^{2\pi} P\big(z,\overline{{z}}; \psi_{u,\overline{{u}}}^{-1}(e^{it})\big)^{-m} P\big(u,\overline{{u}};\psi_{u,\overline{{u}}}^{-1}(e^{it})\big)^{m}\,dt\\ &\overset{\psi_{u,\overline{{u}}}(e^{is})=e^{it}}{=}\frac{1}{2\pi} \int\limits_{0}^{2\pi} P\big(z,\overline{{z}}; e^{is}\big)^{-m} P\big(u,\overline{{u}};e^{is}\big)^{m+1}\,ds. \end{align*} $$
$$ \begin{align*} \big( P_0^{m+1} \circ T_{u,\overline{{u}}} \big)(z,\overline{{z}}) &\overset{({4.18})}{=}\big( P_0^{-m} \circ T_{u,\overline{{u}}} \big)(z,\overline{{z}}) \\ &= \frac{1}{2\pi} \int\limits_{0}^{2\pi} P\left(\psi_{u,\overline{{u}}}(z),\frac{1}{\psi_{u,\overline{{u}}}\left(1/\overline{{z}}\right)};e^{it}\right)^{-m}\,dt\\ &\overset{({7.4})}{=} \frac{1}{2\pi} \int\limits_{0}^{2\pi} P\big(z,\overline{{z}}; \psi_{u,\overline{{u}}}^{-1}(e^{it})\big)^{-m} P\big(u,\overline{{u}};\psi_{u,\overline{{u}}}^{-1}(e^{it})\big)^{m}\,dt\\ &\overset{\psi_{u,\overline{{u}}}(e^{is})=e^{it}}{=}\frac{1}{2\pi} \int\limits_{0}^{2\pi} P\big(z,\overline{{z}}; e^{is}\big)^{-m} P\big(u,\overline{{u}};e^{is}\big)^{m+1}\,ds. \end{align*} $$
In the last step, we used (7.3). Now, we can interpret the resulting integral as the inner product
![]() $\langle \,\cdot , \,\cdot \,\rangle $
on
$\langle \,\cdot , \,\cdot \,\rangle $
on
![]() $L^2([0,2\pi ],{\mathbb C})$
, the space of square integrable functions
$L^2([0,2\pi ],{\mathbb C})$
, the space of square integrable functions
![]() $f:[0,2\pi ]\to {\mathbb C}$
. Using Parseval’s identity in (P), we obtain
$f:[0,2\pi ]\to {\mathbb C}$
. Using Parseval’s identity in (P), we obtain
 $$ \begin{align*} \big(P_0^{-m} \circ T_{u,\overline{{u}}}\big)(z,\overline{{z}}) &=\left\langle P\left(u,\overline{{u}};e^{is}\right)^{m+1}, \overline{{P(z,\overline{{z}};e^{is})^{-m}}}\right\rangle\\ &\overset{\mathrm{(P)}}{=}\sum_{j=-\infty}^{\infty}\left\langle P\left(u,\overline{{u}};e^{it}\right)^{m+1},e^{-ijt}\right\rangle \left\langle e^{-ijs},\overline{{P(z,\overline{{z}};e^{is})^{-m}}}\right\rangle\\ &=\sum_{j=-\infty}^{\infty}\frac{1}{(2\pi)^2}\int\limits_0^{2\pi} P\left(u,\overline{{u}};e^{it}\right)^{m+1}e^{ijt}\,dt \int\limits_0^{2\pi}P(z,\overline{{z}};e^{is})^{-m}e^{-ijs}\,ds\\ &=\sum_{j=-m}^{m}P_{-j}^{m+1}(u,\overline{{u}})P_j^{-m}(z,\overline{{z}}) , \end{align*} $$
$$ \begin{align*} \big(P_0^{-m} \circ T_{u,\overline{{u}}}\big)(z,\overline{{z}}) &=\left\langle P\left(u,\overline{{u}};e^{is}\right)^{m+1}, \overline{{P(z,\overline{{z}};e^{is})^{-m}}}\right\rangle\\ &\overset{\mathrm{(P)}}{=}\sum_{j=-\infty}^{\infty}\left\langle P\left(u,\overline{{u}};e^{it}\right)^{m+1},e^{-ijt}\right\rangle \left\langle e^{-ijs},\overline{{P(z,\overline{{z}};e^{is})^{-m}}}\right\rangle\\ &=\sum_{j=-\infty}^{\infty}\frac{1}{(2\pi)^2}\int\limits_0^{2\pi} P\left(u,\overline{{u}};e^{it}\right)^{m+1}e^{ijt}\,dt \int\limits_0^{2\pi}P(z,\overline{{z}};e^{is})^{-m}e^{-ijs}\,ds\\ &=\sum_{j=-m}^{m}P_{-j}^{m+1}(u,\overline{{u}})P_j^{-m}(z,\overline{{z}}) , \end{align*} $$
where the series reduces to a finite sum because
![]() $P_j^{-m}$
vanishes for
$P_j^{-m}$
vanishes for
![]() $|j|>m$
(see Remark 4.6(b)).
$|j|>m$
(see Remark 4.6(b)).
The previous proof can be modified to establish the following result.
Theorem 7.6 Let
![]() $\mu \in {\mathbb C}$
,
$\mu \in {\mathbb C}$
,
![]() $\textsf {Re}\,\mu \geq 1/2$
,
$\textsf {Re}\,\mu \geq 1/2$
,
![]() $n\in {\mathbb N}_0$
, and
$n\in {\mathbb N}_0$
, and
![]() $u\in {\mathbb D}$
. Then
$u\in {\mathbb D}$
. Then
 $$ \begin{align} \nonumber &\big( P_{n}^{\mu} \circ T_{u,\overline{{u}}} \big)(z,w) \\ & \quad = \sum \limits_{j=-\infty}^{\infty} \left( \sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{k-n-\ell} \binom{n}{k} \binom{-n}{\ell} u^\ell \overline{{u}}^k P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right) P^{\mu}_{-j}(z,w) \end{align} $$
$$ \begin{align} \nonumber &\big( P_{n}^{\mu} \circ T_{u,\overline{{u}}} \big)(z,w) \\ & \quad = \sum \limits_{j=-\infty}^{\infty} \left( \sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{k-n-\ell} \binom{n}{k} \binom{-n}{\ell} u^\ell \overline{{u}}^k P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right) P^{\mu}_{-j}(z,w) \end{align} $$
and
 $$ \begin{align} \nonumber &\big( P_{-n}^{\mu} \circ T_{u,\overline{{u}}} \big)(z,w) \\ &\quad =\sum\limits_{j=-\infty}^{\infty}\left(\sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{n-k+\ell} \binom{n}{k} \binom{-n}{\ell} u^k \overline{{u}}^{\ell} P^{1-\mu}_{j+k-n-\ell}(u,\overline{{u}}) \right)P^{\mu}_{-j}(z,w) \, \end{align} $$
$$ \begin{align} \nonumber &\big( P_{-n}^{\mu} \circ T_{u,\overline{{u}}} \big)(z,w) \\ &\quad =\sum\limits_{j=-\infty}^{\infty}\left(\sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{n-k+\ell} \binom{n}{k} \binom{-n}{\ell} u^k \overline{{u}}^{\ell} P^{1-\mu}_{j+k-n-\ell}(u,\overline{{u}}) \right)P^{\mu}_{-j}(z,w) \, \end{align} $$
for all
![]() $(z,w) \in {\mathbb D}^2$
. Moreover, both series converge locally uniformly and absolutely w.r.t.
$(z,w) \in {\mathbb D}^2$
. Moreover, both series converge locally uniformly and absolutely w.r.t.
![]() $(z,w)$
in
$(z,w)$
in
![]() ${\mathbb D}^2$
.
${\mathbb D}^2$
.
Proof Using (7.3) and (7.4), we compute
 $$ \begin{align*} \big( P_n^{\mu} \circ T_{u,\overline{{u}}} \big)(z,\overline{{z}}) &=\frac{1}{2\pi} \int\limits_0^{2\pi} P\big(z,\overline{{z}}; e^{is}\big)^{\mu} P\big(u,\overline{{u}};e^{is}\big)^{1-\mu}\psi_{u,\overline{{u}}}(e^{is})^{-n}\,ds\\ &= \nonumber \frac{1}{2\pi } \int\limits_0^{2\pi} P\big(z,\overline{{z}}; e^{is}\big)^{\mu} P\big(u,\overline{{u}};e^{is}\big)^{1-\mu}(1-\overline{{u}}e^{is})^n(u-e^{is})^{-n}\,ds. \end{align*} $$
$$ \begin{align*} \big( P_n^{\mu} \circ T_{u,\overline{{u}}} \big)(z,\overline{{z}}) &=\frac{1}{2\pi} \int\limits_0^{2\pi} P\big(z,\overline{{z}}; e^{is}\big)^{\mu} P\big(u,\overline{{u}};e^{is}\big)^{1-\mu}\psi_{u,\overline{{u}}}(e^{is})^{-n}\,ds\\ &= \nonumber \frac{1}{2\pi } \int\limits_0^{2\pi} P\big(z,\overline{{z}}; e^{is}\big)^{\mu} P\big(u,\overline{{u}};e^{is}\big)^{1-\mu}(1-\overline{{u}}e^{is})^n(u-e^{is})^{-n}\,ds. \end{align*} $$
Note that taking complex powers is unproblematic since the appearing Poisson kernels are positive real quantities. Applying Lemma 3.1 and, additionally, the generalized binomial theorem leads to
 $$ \begin{align*} &\big( P_n^{\mu} \circ T_{u,\overline{{u}}} \big)(z,w)\nonumber\\ & \quad = \sum_{k=0}^n \sum_{\ell=0}^\infty \binom{n}{k} \binom{-n}{\ell} (-1)^{k-n+\ell}\overline{{u}}^ku^\ell \frac{1}{2\pi } \int\limits_0^{2\pi} P\big(z,w; e^{is}\big)^{\mu} P\big(u,\overline{{u}};e^{is}\big)^{1-\mu}e^{is(k-n-\ell)}\, ds. \end{align*} $$
$$ \begin{align*} &\big( P_n^{\mu} \circ T_{u,\overline{{u}}} \big)(z,w)\nonumber\\ & \quad = \sum_{k=0}^n \sum_{\ell=0}^\infty \binom{n}{k} \binom{-n}{\ell} (-1)^{k-n+\ell}\overline{{u}}^ku^\ell \frac{1}{2\pi } \int\limits_0^{2\pi} P\big(z,w; e^{is}\big)^{\mu} P\big(u,\overline{{u}};e^{is}\big)^{1-\mu}e^{is(k-n-\ell)}\, ds. \end{align*} $$
Interpreting the above integral as a
![]() $L^2([0,2\pi ],{\mathbb C})$
inner product as it was done in the proof of Proposition 7.5 shows (7.6a). A similar computation yields (7.6b).
$L^2([0,2\pi ],{\mathbb C})$
inner product as it was done in the proof of Proposition 7.5 shows (7.6a). A similar computation yields (7.6b).
Let
![]() $K\subseteq {\mathbb D}^2$
be compact. It remains to prove that
$K\subseteq {\mathbb D}^2$
be compact. It remains to prove that
 $$ \begin{align*} \sum_{k=0}^n\sum_{\ell=0}^\infty \left\vert\binom{n}{k}\binom{-n}{\ell}\overline{u}^ku^\ell\right\vert \sum_{j=-\infty}^{\infty} \left\vert P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right\vert \sup_{(z,w)\in K}\left\vert P^{\mu}_{-j}(z,w)\right\vert<\infty. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^n\sum_{\ell=0}^\infty \left\vert\binom{n}{k}\binom{-n}{\ell}\overline{u}^ku^\ell\right\vert \sum_{j=-\infty}^{\infty} \left\vert P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right\vert \sup_{(z,w)\in K}\left\vert P^{\mu}_{-j}(z,w)\right\vert<\infty. \end{align*} $$
We have
 $$ \begin{align*} \left\vert P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right\vert\leq\frac{1}{2\pi}\int\limits_0^{2\pi}\left\vert P(u,\overline{{u}};e^{it})^{1-\mu}\right\vert\, dt:=M_u<\infty \end{align*} $$
$$ \begin{align*} \left\vert P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right\vert\leq\frac{1}{2\pi}\int\limits_0^{2\pi}\left\vert P(u,\overline{{u}};e^{it})^{1-\mu}\right\vert\, dt:=M_u<\infty \end{align*} $$
as
![]() $u\in {\mathbb D}$
is fixed. Since K is compact, we find a nonnegative real number
$u\in {\mathbb D}$
is fixed. Since K is compact, we find a nonnegative real number
![]() $r<1$
such that
$r<1$
such that
![]() $|z|,|w|\leq r$
for all
$|z|,|w|\leq r$
for all
![]() $(z,w)\in K$
. Hence, using (6.8), we can ensure that
$(z,w)\in K$
. Hence, using (6.8), we can ensure that
 $$ \begin{align*} \sum_{j=-\infty}^{\infty}\sup_{(z,w)\in K}\left\vert P^{\mu}_{-j}(z,w)\right\vert&\leq\sum_{j=-\infty}^{\infty}\gamma_r \cdot \left(|j|+1 \right)^{\textsf{Re}\,\mu-1} \, r^{|j|}:=N_{r,\mu}<\infty, \end{align*} $$
$$ \begin{align*} \sum_{j=-\infty}^{\infty}\sup_{(z,w)\in K}\left\vert P^{\mu}_{-j}(z,w)\right\vert&\leq\sum_{j=-\infty}^{\infty}\gamma_r \cdot \left(|j|+1 \right)^{\textsf{Re}\,\mu-1} \, r^{|j|}:=N_{r,\mu}<\infty, \end{align*} $$
where
![]() $\gamma _r>0$
depends on r (and
$\gamma _r>0$
depends on r (and
![]() $\mu $
). Thus,
$\mu $
). Thus,
 $$ \begin{align*} \sum_{k=0}^n\sum_{\ell=0}^\infty &\left\vert\binom{n}{k}\binom{-n}{\ell}\overline{u}^ku^\ell\right\vert \sum_{j=-\infty}^{\infty} \left\vert P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right\vert \sup_{(z,w)\in K}\left\vert P^{\mu}_{-j}(z,w)\right\vert\\ &\leq\sum_{k=0}^n\sum_{\ell=0}^\infty \left\vert\binom{n}{k}\binom{-n}{\ell}\overline{u}^ku^\ell\right\vert \cdot M_u\cdot N_{r,\mu}<\infty \end{align*} $$
$$ \begin{align*} \sum_{k=0}^n\sum_{\ell=0}^\infty &\left\vert\binom{n}{k}\binom{-n}{\ell}\overline{u}^ku^\ell\right\vert \sum_{j=-\infty}^{\infty} \left\vert P^{1-\mu}_{j-k+n+\ell}(u,\overline{{u}})\right\vert \sup_{(z,w)\in K}\left\vert P^{\mu}_{-j}(z,w)\right\vert\\ &\leq\sum_{k=0}^n\sum_{\ell=0}^\infty \left\vert\binom{n}{k}\binom{-n}{\ell}\overline{u}^ku^\ell\right\vert \cdot M_u\cdot N_{r,\mu}<\infty \end{align*} $$
since the binomial series over k and
![]() $\ell $
converge absolutely.
$\ell $
converge absolutely.
Let
![]() $m,n\in {\mathbb N}_0$
,
$m,n\in {\mathbb N}_0$
,
![]() $n\leq m$
. For
$n\leq m$
. For
![]() $\mu =-m$
, the j-series in (7.6) terminate. Moreover, in this case, when replacing
$\mu =-m$
, the j-series in (7.6) terminate. Moreover, in this case, when replacing
![]() $(u,\overline {{u}})$
by
$(u,\overline {{u}})$
by
![]() $(u,v)\in {\mathbb D}^2$
in (7.6), a similar argument as in the proof of Theorem 7.6 shows that the series in (7.6) are absolutely and locally uniformly convergent with respect to
$(u,v)\in {\mathbb D}^2$
in (7.6), a similar argument as in the proof of Theorem 7.6 shows that the series in (7.6) are absolutely and locally uniformly convergent with respect to
![]() $(u,v)$
in
$(u,v)$
in
![]() ${\mathbb D}^2$
, too. Further, we know that
${\mathbb D}^2$
, too. Further, we know that
![]() $P_{\pm n}^{-m}\circ T_{u,v}\in \mathcal {H}(\Omega )$
. Thus, both sides of (7.6a) resp. (7.6b) (with
$P_{\pm n}^{-m}\circ T_{u,v}\in \mathcal {H}(\Omega )$
. Thus, both sides of (7.6a) resp. (7.6b) (with
![]() $(u,\overline {u})$
replaced by
$(u,\overline {u})$
replaced by
![]() $(u,v)$
) define holomorphic functions w.r.t.
$(u,v)$
) define holomorphic functions w.r.t.
![]() $(u,v)\in {\mathbb D}^2$
, which allows us to apply the two variable identity principle, Lemma 3.1. We obtain the following.
$(u,v)\in {\mathbb D}^2$
, which allows us to apply the two variable identity principle, Lemma 3.1. We obtain the following.
Corollary 7.7 Let
![]() $m,n\in {\mathbb N}_0$
,
$m,n\in {\mathbb N}_0$
,
![]() $n\leq m$
,
$n\leq m$
,
![]() $(z,w)\in \Omega $
and
$(z,w)\in \Omega $
and
![]() $(u,v)\in {\mathbb D}^2$
. Then
$(u,v)\in {\mathbb D}^2$
. Then
 $$ \begin{align*} &\big( P_{n}^{-m} \circ T_{u,v} \big)(z,w) \\ & \quad = \sum_{j=-m}^m \left( \sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{k-n-\ell} \binom{n}{k} \binom{-n}{\ell} u^\ell v^k P^{m+1}_{j-k+n+\ell}(u,v) \right) P^{-m}_{-j}(z,w) \end{align*} $$
$$ \begin{align*} &\big( P_{n}^{-m} \circ T_{u,v} \big)(z,w) \\ & \quad = \sum_{j=-m}^m \left( \sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{k-n-\ell} \binom{n}{k} \binom{-n}{\ell} u^\ell v^k P^{m+1}_{j-k+n+\ell}(u,v) \right) P^{-m}_{-j}(z,w) \end{align*} $$
and
 $$ \begin{align*} &\big( P_{-n}^{-m}\circ T_{u,v} \big)(z,w) \\ & \quad =\sum\limits_{j=-m}^m \left( \sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{n-k+\ell} \binom{n}{k} \binom{-n}{\ell} u^k v^{\ell} P^{m+1}_{j+k-n-\ell}(u,\overline{{u}}) \right)P^{-m}_{-j}(z,w). \end{align*} $$
$$ \begin{align*} &\big( P_{-n}^{-m}\circ T_{u,v} \big)(z,w) \\ & \quad =\sum\limits_{j=-m}^m \left( \sum_{k=0}^n \sum_{\ell=0}^\infty (-1)^{n-k+\ell} \binom{n}{k} \binom{-n}{\ell} u^k v^{\ell} P^{m+1}_{j+k-n-\ell}(u,\overline{{u}}) \right)P^{-m}_{-j}(z,w). \end{align*} $$
In particular,
![]() $P^{-m}_n \circ T_{u,v} \in \mathrm {span}\{P^{-m}_{j} \, : \, j=-m, \ldots , m\} \subseteq \mathcal {H}(\Omega )$
.
$P^{-m}_n \circ T_{u,v} \in \mathrm {span}\{P^{-m}_{j} \, : \, j=-m, \ldots , m\} \subseteq \mathcal {H}(\Omega )$
.
8 Proof of Theorems 2.6 and 2.10: invariant eigenspaces
Using the theory we have developed so far, we are now able to give an explicit description of the eigenspaces of the Laplace operator
![]() $\Delta _{zw}$
on
$\Delta _{zw}$
on
![]() ${\mathbb D}^2$
resp. on
${\mathbb D}^2$
resp. on
![]() $\Omega $
. This will allow us to conclude Theorems 2.6 and 2.10 afterwards.
$\Omega $
. This will allow us to conclude Theorems 2.6 and 2.10 afterwards.
Theorem 8.1 (Möbius invariant subspaces of
 $X_\lambda ({\mathbb D}^2)$
)
$X_\lambda ({\mathbb D}^2)$
)
Let
![]() $\lambda \in {\mathbb C}$
.
$\lambda \in {\mathbb C}$
.
-
(NE) If
 $\lambda \neq 4m(m+1)$
for all
$\lambda \neq 4m(m+1)$
for all
 $m\in {\mathbb N}_0$
, then
$m\in {\mathbb N}_0$
, then
 $X_\lambda ({\mathbb D}^2)$
has no nontrivial Möbius invariant subspaces.
$X_\lambda ({\mathbb D}^2)$
has no nontrivial Möbius invariant subspaces. -
(E) If
 $\lambda =4m(m+1)$
for some
$\lambda =4m(m+1)$
for some
 $m\in {\mathbb N}_0$
, then
$m\in {\mathbb N}_0$
, then
 $X_\lambda ({\mathbb D}^2)$
has precisely three nontrivial Möbius invariant subspaces
$X_\lambda ({\mathbb D}^2)$
has precisely three nontrivial Möbius invariant subspaces
 $X_{\lambda }^{+}({\mathbb D}^2),X_{\lambda }^{-}({\mathbb D}^2),X_{\lambda }^{0}({\mathbb D}^2)$
of which exactly one, say
$X_{\lambda }^{+}({\mathbb D}^2),X_{\lambda }^{-}({\mathbb D}^2),X_{\lambda }^{0}({\mathbb D}^2)$
of which exactly one, say
 $X_{\lambda }^{0}({\mathbb D}^2)$
, is finite dimensional of dimension
$X_{\lambda }^{0}({\mathbb D}^2)$
, is finite dimensional of dimension
 $2m+1$
. Explicitly, these spaces are given by (8.1a)
$2m+1$
. Explicitly, these spaces are given by (8.1a) $$ \begin{align} X_{\lambda}^{+}({\mathbb D}^2)&=\operatorname{clos}_{{\mathbb D}^2} \left(\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n< \infty\}\right) ,\end{align} $$
(8.1b)
$$ \begin{align} X_{\lambda}^{+}({\mathbb D}^2)&=\operatorname{clos}_{{\mathbb D}^2} \left(\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n< \infty\}\right) ,\end{align} $$
(8.1b) $$ \begin{align} X_{\lambda}^{-}({\mathbb D}^2)&=\operatorname{clos}_{{\mathbb D}^2}\left(\mathrm{span}\{P_n^{m+1} \, : \, -\infty< n\leq m\}\right) , \end{align} $$
(8.1c)where
$$ \begin{align} X_{\lambda}^{-}({\mathbb D}^2)&=\operatorname{clos}_{{\mathbb D}^2}\left(\mathrm{span}\{P_n^{m+1} \, : \, -\infty< n\leq m\}\right) , \end{align} $$
(8.1c)where $$ \begin{align} X_{\lambda}^{0}({\mathbb D}^2)&=\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n\leq m\} , \end{align} $$
$$ \begin{align} X_{\lambda}^{0}({\mathbb D}^2)&=\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n\leq m\} , \end{align} $$
 $\operatorname {clos}_{{\mathbb D}^2}$
denotes the closure with respect to the topology of locally uniform convergence on
$\operatorname {clos}_{{\mathbb D}^2}$
denotes the closure with respect to the topology of locally uniform convergence on
 ${\mathbb D}^2$
.
${\mathbb D}^2$
.
Note that Rudin [Reference Rudin37] gives an explicit characterization of the three nontrivial subspaces in the second case of his theorem (see Theorem 2.1) too. We will discuss the similarities and the differences between Rudin’s and our approach in Remark 8.5.
Three crucial ingredients that we will use for the proof of Theorem 8.1 are the representation of eigenfunctions in terms of PFM from Theorem 5.1, the pullback formula for PFM from Theorem 7.6 and the differential operators
![]() $D^{+}$
and
$D^{+}$
and
![]() $D^{-}$
defined by
$D^{-}$
defined by

for
![]() $f \in \mathcal {H}(D)$
and any subdomain
$f \in \mathcal {H}(D)$
and any subdomain
![]() $D \subseteq {\mathbb C}^2$
. We note an alternative description of these operators based on the automorphisms from (7.1).
$D \subseteq {\mathbb C}^2$
. We note an alternative description of these operators based on the automorphisms from (7.1).
Lemma 8.2 Let
![]() $D \subseteq {\mathbb C}^2$
be a subdomain,
$D \subseteq {\mathbb C}^2$
be a subdomain,
![]() $f \in \mathcal {H}(D)$
. For all
$f \in \mathcal {H}(D)$
. For all
![]() $(z,w) \in D$
, it then holds that
$(z,w) \in D$
, it then holds that
 $$ \begin{align} \nonumber D^{+} f(z,w) = \partial_u \left( f \circ T_{u,0} \circ {\varrho}_{-1} \right) \Big|_{u=0} (z,w) , \\ D^{-} f(z,w) = \partial_v \left( f \circ T_{0,v} \circ \varrho_{-1} \right) \Big|_{v=0} (z,w) . \end{align} $$
$$ \begin{align} \nonumber D^{+} f(z,w) = \partial_u \left( f \circ T_{u,0} \circ {\varrho}_{-1} \right) \Big|_{u=0} (z,w) , \\ D^{-} f(z,w) = \partial_v \left( f \circ T_{0,v} \circ \varrho_{-1} \right) \Big|_{v=0} (z,w) . \end{align} $$
What makes these operators useful is that they act by shifts of the Fourier index on the PFM.
Lemma 8.3 The operators
![]() $D^+$
and
$D^+$
and
![]() $D^-$
commute with
$D^-$
commute with
![]() $\Delta _{zw}$
. Furthermore, for
$\Delta _{zw}$
. Furthermore, for
![]() $\mu \in {\mathbb C}$
and
$\mu \in {\mathbb C}$
and
![]() $n\in {\mathbb Z}$
, it holds that
$n\in {\mathbb Z}$
, it holds that
Proof The operator
![]() $D^+$
commutes with
$D^+$
commutes with
![]() $\Delta _{zw}$
in view of the latter’s
$\Delta _{zw}$
in view of the latter’s
![]() $\mathcal {M}$
-invariance, (8.3) and commutativity of partial derivatives. Moreover,
$\mathcal {M}$
-invariance, (8.3) and commutativity of partial derivatives. Moreover,
![]() $D^+$
lowers homogeneity in the sense of (4.1) by one degree. Since
$D^+$
lowers homogeneity in the sense of (4.1) by one degree. Since
![]() $P_n^{\mu }$
is a
$P_n^{\mu }$
is a
![]() $(-n)$
-homogeneous eigenfunction of
$(-n)$
-homogeneous eigenfunction of
![]() $\Delta _{zw}$
to the eigenvalue
$\Delta _{zw}$
to the eigenvalue
![]() ${4\mu (\mu -1)}$
, this implies that
${4\mu (\mu -1)}$
, this implies that
![]() $D^+ P_n^{\mu }$
is a
$D^+ P_n^{\mu }$
is a
![]() ${-(n+1)}$
-homogeneous eigenfunction of
${-(n+1)}$
-homogeneous eigenfunction of
![]() $\Delta _{zw}$
to the same eigenvalue. Hence, Theorem 4.4 yields
$\Delta _{zw}$
to the same eigenvalue. Hence, Theorem 4.4 yields
![]() ${D^+ P_n^{\mu } = c P_{n+1}^{\mu }}$
for some
${D^+ P_n^{\mu } = c P_{n+1}^{\mu }}$
for some
![]() ${c \in {\mathbb C}}$
. Applying (8.2) and evaluating (4.16) in
${c \in {\mathbb C}}$
. Applying (8.2) and evaluating (4.16) in
![]() $(z,w)=(0,1)$
yields
$(z,w)=(0,1)$
yields
![]() $c = \mu - n - 1$
. Note that one has to distinguish the cases
$c = \mu - n - 1$
. Note that one has to distinguish the cases
![]() $n \ge 0$
and
$n \ge 0$
and
![]() $n < 0$
. The second equality in (8.3) may be derived analogously.
$n < 0$
. The second equality in (8.3) may be derived analogously.
Remark 8.4 One may thus regard the operators
![]() $D^+$
and
$D^+$
and
![]() $D^-$
as ladder operators and together with their commutator
$D^-$
as ladder operators and together with their commutator
which is the Euler vector field corresponding to the homogeneity (4.1), they generate the Lie algebra of
![]() $\mathcal {M}$
. By (8.3), all three operators may, moreover, be regarded as fundamental vector fields of the natural action of
$\mathcal {M}$
. By (8.3), all three operators may, moreover, be regarded as fundamental vector fields of the natural action of
![]() $\mathcal {M}$
as automorphisms of
$\mathcal {M}$
as automorphisms of
![]() $\Omega $
.
$\Omega $
.
Proof (of Theorem 8.1)
Write
![]() $\lambda =4\mu (\mu -1)$
for
$\lambda =4\mu (\mu -1)$
for
![]() $\mu \in {\mathbb C}$
,
$\mu \in {\mathbb C}$
,
![]() $\textsf {Re}\,\mu \geq 1/2$
, and let Y be a nontrivial Möbius invariant subspace of
$\textsf {Re}\,\mu \geq 1/2$
, and let Y be a nontrivial Möbius invariant subspace of
![]() $X_\lambda ({\mathbb D}^2)$
. Our approach is as follows: we first show that Y contains a PFM
$X_\lambda ({\mathbb D}^2)$
. Our approach is as follows: we first show that Y contains a PFM
![]() $P_n^{\mu }$
for some
$P_n^{\mu }$
for some
![]() $n\in {\mathbb Z}$
. If the assumption of (NE) holds, then this will imply that
$n\in {\mathbb Z}$
. If the assumption of (NE) holds, then this will imply that
![]() $P_n^{\mu }\in Y$
for all
$P_n^{\mu }\in Y$
for all
![]() $n\in {\mathbb Z}$
. Conversely, if the assumption of (E) holds for
$n\in {\mathbb Z}$
. Conversely, if the assumption of (E) holds for
![]() $m\in {\mathbb N}_0$
, the existence of
$m\in {\mathbb N}_0$
, the existence of
![]() $P_n^{-m}$
for some
$P_n^{-m}$
for some
![]() $n\in {\mathbb Z}$
will imply that certain other PFM need to be contained in Y, too. Here, we will need to distinguish three cases which will lead to the three specific spaces described on the right-hand side of (8.1). This shows that there are at most three possible choices for Y. Then, in a second step, we show that the three spaces found in the first step are in fact Möbius invariant, which then proves the existence of exactly three nontrivial proper Möbius invariant subspaces.
$n\in {\mathbb Z}$
will imply that certain other PFM need to be contained in Y, too. Here, we will need to distinguish three cases which will lead to the three specific spaces described on the right-hand side of (8.1). This shows that there are at most three possible choices for Y. Then, in a second step, we show that the three spaces found in the first step are in fact Möbius invariant, which then proves the existence of exactly three nontrivial proper Möbius invariant subspaces.
Step 1:
-
(i) Using (8.2), it follows from Y being closed and Möbius invariant that the differential quotients
 $D^+ f, D^- f\in Y$
. Therefore, Y is invariant with respect to
$D^+ f, D^- f\in Y$
. Therefore, Y is invariant with respect to
 $D^+$
and
$D^+$
and
 $D^-$
, and, by iteration,
$D^-$
, and, by iteration,
 $(D^+)^kf,(D^-)^kf\in Y$
for every
$(D^+)^kf,(D^-)^kf\in Y$
for every
 $k\in {\mathbb N}$
.
$k\in {\mathbb N}$
. -
(ii) Since Y is Möbius invariant, Y is, in particular, rotationally invariant. Thus, for every
 $n\in {\mathbb Z}$
, we have
$n\in {\mathbb Z}$
, we have
 $f_n\in Y$
, where
$f_n\in Y$
, where
 $f_n$
is defined by By Theorem 4.4,
$f_n$
is defined by By Theorem 4.4, $$ \begin{align*}f_n(z,w):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f \left( \eta z,\frac{w}{\eta} \right) \eta^{-(n+1)} \, d\eta .\end{align*} $$
$$ \begin{align*}f_n(z,w):=\frac{1}{2\pi i} \int \limits_{\partial {\mathbb D}} f \left( \eta z,\frac{w}{\eta} \right) \eta^{-(n+1)} \, d\eta .\end{align*} $$
 $f_n$
is a multiple of the PFM
$f_n$
is a multiple of the PFM
 $P_{n}^{\mu }$
. Moreover, by Theorem 5.1, there are
$P_{n}^{\mu }$
. Moreover, by Theorem 5.1, there are
 $c_n \in {\mathbb C}$
for all
$c_n \in {\mathbb C}$
for all
 $n \in {\mathbb Z}$
depending on f such that f has the representation Since
$n \in {\mathbb Z}$
depending on f such that f has the representation Since $$ \begin{align*}f=\sum_{n=-\infty}^\infty c_nP_n^{\mu} .\end{align*} $$
$$ \begin{align*}f=\sum_{n=-\infty}^\infty c_nP_n^{\mu} .\end{align*} $$
 $Y\neq \{0\}$
, we may assume
$Y\neq \{0\}$
, we may assume
 $f\not \equiv 0$
, i.e.
$f\not \equiv 0$
, i.e.
 $c_n \neq 0$
for some
$c_n \neq 0$
for some
 $n \in {\mathbb Z}$
. Thus, the above observations imply
$n \in {\mathbb Z}$
. Thus, the above observations imply
 $P_n^{\mu }\in Y$
for some
$P_n^{\mu }\in Y$
for some
 $n\in {\mathbb Z}$
.
$n\in {\mathbb Z}$
.
-
(iii) By Part (ii), there exists
 $P_n^{\mu }\in Y$
for some
$P_n^{\mu }\in Y$
for some
 $n \in {\mathbb Z}$
, and by Part (i), we conclude
$n \in {\mathbb Z}$
, and by Part (i), we conclude
 ${(D^+)^kP_n^{\mu },(D^-)^kP_n^{\mu }\in Y}$
for every
${(D^+)^kP_n^{\mu },(D^-)^kP_n^{\mu }\in Y}$
for every
 $k\in {\mathbb N}$
. Lemma 8.3 shows that these functions are multiples of PFM again, so
$k\in {\mathbb N}$
. Lemma 8.3 shows that these functions are multiples of PFM again, so
 ${(\mu -n-k)_k P_{n+k}^{\mu }}$
,
${(\mu -n-k)_k P_{n+k}^{\mu }}$
,
 $ (\mu +n-k)_k P_{n-k}^{\mu }\in Y$
for every
$ (\mu +n-k)_k P_{n-k}^{\mu }\in Y$
for every
 $k\in {\mathbb N}$
. Recall that the prefactors denote (rising) Pochhammer symbols (see (4.5)).
$k\in {\mathbb N}$
. Recall that the prefactors denote (rising) Pochhammer symbols (see (4.5)).For
 $\mu \not \in {\mathbb Z}$
, the factors
$\mu \not \in {\mathbb Z}$
, the factors
 $(\mu \pm n-k)_k$
never vanish. In this case,
$(\mu \pm n-k)_k$
never vanish. In this case,
 $P_n^{\mu }\in Y$
for every
$P_n^{\mu }\in Y$
for every
 $n\in {\mathbb Z}$
. Using Theorem 5.1 again, this implies
$n\in {\mathbb Z}$
. Using Theorem 5.1 again, this implies
 $Y=X_\lambda ({\mathbb D}^2)$
which proves (NE).
$Y=X_\lambda ({\mathbb D}^2)$
which proves (NE).For
 $\mu \in {\mathbb N}$
, the factors
$\mu \in {\mathbb N}$
, the factors
 $(\mu \pm n-k)_k$
vanish for appropriate
$(\mu \pm n-k)_k$
vanish for appropriate
 $k \in {\mathbb N}$
. This leads to the dichotomy in case (E): assume
$k \in {\mathbb N}$
. This leads to the dichotomy in case (E): assume
 $\mu = m+1\in {\mathbb N}$
, and
$\mu = m+1\in {\mathbb N}$
, and
 $P_n^{m+1}\in Y$
. Then necessarily
$P_n^{m+1}\in Y$
. Then necessarily
 $P_{k}^{m+1}\in Y$
for
$P_{k}^{m+1}\in Y$
for
 $-m\leq k\leq m$
. Since shifting
$-m\leq k\leq m$
. Since shifting
 $P_{k}^{m+1}$
with
$P_{k}^{m+1}$
with
 $D^\pm $
eventually produces the zero function, for
$D^\pm $
eventually produces the zero function, for
 $q < -m$
or
$q < -m$
or
 $q> m$
the function
$q> m$
the function
 $P_q^{m+1}$
does not necessarily need to be contained in Y. However, if
$P_q^{m+1}$
does not necessarily need to be contained in Y. However, if
 $P_q^{m+1} \in Y$
for some
$P_q^{m+1} \in Y$
for some
 $q < -m$
, then since
$q < -m$
, then since
 $P_q^{m+1}$
can be shifted to each of these functions without producing the zero function, it must hold that
$P_q^{m+1}$
can be shifted to each of these functions without producing the zero function, it must hold that
 $P_p^{m+1} \in Y$
for
$P_p^{m+1} \in Y$
for
 $-\infty < p \le m$
. The same argument works for
$-\infty < p \le m$
. The same argument works for
 $q>m$
. In summary, these considerations show that every nontrivial closed Möbius invariant subspace of
$q>m$
. In summary, these considerations show that every nontrivial closed Möbius invariant subspace of
 $X_{\lambda }({\mathbb D}^2)$
contains one of the three spaces:
$X_{\lambda }({\mathbb D}^2)$
contains one of the three spaces:  $$ \begin{align*} Y_{+}&:=\operatorname{clos}_{{\mathbb D}^2}\left(\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n< \infty\}\right) ,\\ Y_{-}&:=\operatorname{clos}_{{\mathbb D}^2}\left(\mathrm{span}\{P_n^{m+1} \, : \, -\infty< n\leq m\}\right) \, \text{ and}\\ Y_{0}\,&:=\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n\leq m\}. \end{align*} $$
$$ \begin{align*} Y_{+}&:=\operatorname{clos}_{{\mathbb D}^2}\left(\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n< \infty\}\right) ,\\ Y_{-}&:=\operatorname{clos}_{{\mathbb D}^2}\left(\mathrm{span}\{P_n^{m+1} \, : \, -\infty< n\leq m\}\right) \, \text{ and}\\ Y_{0}\,&:=\mathrm{span}\{P_n^{m+1} \, : \, -m\leq n\leq m\}. \end{align*} $$
Step 2: It remains to show that
![]() $ Y_{+},Y_-$
, and
$ Y_{+},Y_-$
, and
![]() $Y_0$
are in fact Möbius invariant. Let
$Y_0$
are in fact Möbius invariant. Let
![]() $\mu -1=m\in {\mathbb N}_0$
,
$\mu -1=m\in {\mathbb N}_0$
,
![]() $n\in {\mathbb Z}$
, and
$n\in {\mathbb Z}$
, and
![]() $z,w,u\in {\mathbb D}$
.
$z,w,u\in {\mathbb D}$
.
-
(iv) Assume
 $n\geq 0$
. Theorem 7.6 shows that
$n\geq 0$
. Theorem 7.6 shows that
 $(P_{n}^{m+1} \circ T_{u,\overline {{u}}})(z,w)$
is a series of scalar multiples of
$(P_{n}^{m+1} \circ T_{u,\overline {{u}}})(z,w)$
is a series of scalar multiples of
 $P_{k}^{m+1}(z,w)$
with
$P_{k}^{m+1}(z,w)$
with
 $-m\leq k<\infty $
. To see this recall that by Remark 4.6, we have
$-m\leq k<\infty $
. To see this recall that by Remark 4.6, we have
 $P_n^{-m}\equiv 0$
if
$P_n^{-m}\equiv 0$
if
 $|n|>m$
. Moreover, Theorem 7.6 also implies that this series converges locally uniformly with respect to
$|n|>m$
. Moreover, Theorem 7.6 also implies that this series converges locally uniformly with respect to
 $(z,w)$
on
$(z,w)$
on
 ${\mathbb D}^2$
. Thus,
${\mathbb D}^2$
. Thus,
 $P_{n}^{m+1} \circ T_{u,\overline {{u}}} \in Y_{+}$
. The same argument applies to
$P_{n}^{m+1} \circ T_{u,\overline {{u}}} \in Y_{+}$
. The same argument applies to
 $P_{-n}^{m+1} \circ T_{u,\overline {{u}}}$
.
$P_{-n}^{m+1} \circ T_{u,\overline {{u}}}$
. -
(v) Part (iv) implies that every linear combination
belongs to $$ \begin{align*}\sum_{n=-m}^N c_n P_n^{m+1}\circ T_{u,\overline{{u}}} \,\end{align*} $$
$$ \begin{align*}\sum_{n=-m}^N c_n P_n^{m+1}\circ T_{u,\overline{{u}}} \,\end{align*} $$
 $Y_{+}$
. Since, by definition, every element in
$Y_{+}$
. Since, by definition, every element in
 $Y_{+}$
is a series of the form
$Y_{+}$
is a series of the form
 $\sum _{n=-m}^{\infty } c_n P^{m+1}_n$
, Möbius invariance of
$\sum _{n=-m}^{\infty } c_n P^{m+1}_n$
, Möbius invariance of
 $Y_{+}$
follows. The same argument applies to
$Y_{+}$
follows. The same argument applies to
 $Y_{-}$
.
$Y_{-}$
.
-
(vi) Now, consider
 $-m\leq n\leq m$
. In this case,
$-m\leq n\leq m$
. In this case,
 $P_{ n}^{m+1}$
is a multiple of
$P_{ n}^{m+1}$
is a multiple of
 $P_{n}^{-m}$
by (4.18), and Corollary 7.7 shows that
$P_{n}^{-m}$
by (4.18), and Corollary 7.7 shows that
 $(P_{n}^{m+1}\circ T_{u,\overline {{u}}})(z,w)$
can be expressed as linear combination of
$(P_{n}^{m+1}\circ T_{u,\overline {{u}}})(z,w)$
can be expressed as linear combination of
 $P_{k}^{-m}(z,w)$
with
$P_{k}^{-m}(z,w)$
with
 $-m\leq k\leq m$
. This shows Möbius invariance of
$-m\leq k\leq m$
. This shows Möbius invariance of
 $Y_{0}$
.
$Y_{0}$
.
Remark 8.5
-
(a) In his proof of Theorem 2.1, Rudin employs exclusively a specific differential operator A (see [Reference Rudin37, Formula (5), p. 143]), which in our terminology can be defined by
The operator $$ \begin{align*}A:=D^+ + D^-.\end{align*} $$
$$ \begin{align*}A:=D^+ + D^-.\end{align*} $$
 ${A^{\sharp }:=i \left (D^+ - D^- \right )}$
is “conjugate” to A in the sense that Note the analogy with the Wirtinger derivatives
${A^{\sharp }:=i \left (D^+ - D^- \right )}$
is “conjugate” to A in the sense that Note the analogy with the Wirtinger derivatives $$ \begin{align*}A-i A^{\sharp}=2D^+ \quad \text{ and } \quad A+i A^{\sharp}=2 D^- .\end{align*} $$
$$ \begin{align*}A-i A^{\sharp}=2D^+ \quad \text{ and } \quad A+i A^{\sharp}=2 D^- .\end{align*} $$
 $\partial _z$
and
$\partial _z$
and
 $\partial _{\bar {z}}$
, which satisfy We note that in a related, but different context, namely in [Reference Rudin36], Rudin also considers the operators
$\partial _{\bar {z}}$
, which satisfy We note that in a related, but different context, namely in [Reference Rudin36], Rudin also considers the operators $$ \begin{align*}\partial_x -i \partial_y=2 \partial_z \quad \text{ and } \quad \partial_x+i \partial_y=2 \partial_{\bar{z}} .\end{align*} $$
$$ \begin{align*}\partial_x -i \partial_y=2 \partial_z \quad \text{ and } \quad \partial_x+i \partial_y=2 \partial_{\bar{z}} .\end{align*} $$
 $D^+$
and
$D^+$
and
 $D^-$
. He denotes them by Q and
$D^-$
. He denotes them by Q and
 $\overline {Q}$
(see [Reference Rudin36, Section 4.1, Formula (1)]).
$\overline {Q}$
(see [Reference Rudin36, Section 4.1, Formula (1)]).
-
(b) Step 1 of our proof closely follows the argumentation of Rudin’s proof (Steps 1–3 in his labeling). However, because of the usage of his A-operator (see Part (a)), which does not respect homogeneity when applied to a PFM, Rudin additionally needs to consider the projections on n-homogeneous components in his proof. In our approach based on the
 $D^{\pm }$
-operators, this issue does not arise, since these operators lower resp. raise the degree of homogeneity by exactly one.
$D^{\pm }$
-operators, this issue does not arise, since these operators lower resp. raise the degree of homogeneity by exactly one. -
(c) Step 2 of our proof, where we made heavy use of Proposition 7.5 resp. Theorem 7.6, is different from Rudin’s approach (Step 4 in his labeling). In short, Rudin makes a series expansion in the disk automorphism parameter and uses again that Möbius invariant subspaces are invariant under repeated application of A (see Part (a)).
-
(d) The proof of Theorem 8.1 heavily relies on the PFM. In fact, the usage of n-homogeneous functions is also crucial in the original proof of Theorem 2.1 in [Reference Rudin37], although Rudin does not explicitly define these functions but works with projections on the subspaces of n-homogeneous eigenfunctions.
We are now in a position to prove Theorems 2.6 and 2.10.
Proof
(of Theorem 2.10) Let
![]() $\lambda \in {\mathbb C}$
and
$\lambda \in {\mathbb C}$
and
![]() $Y \subseteq \mathcal {H}({\mathbb D}^2)$
be a nontrivial Möbius invariant subspace of
$Y \subseteq \mathcal {H}({\mathbb D}^2)$
be a nontrivial Möbius invariant subspace of
![]() $X_\lambda ({\mathbb D}^2)$
. Let, first,
$X_\lambda ({\mathbb D}^2)$
. Let, first,
![]() $Y = X_\lambda ({\mathbb D}^2)$
be the full eigenspace. Every PFM is holomorphic at least on
$Y = X_\lambda ({\mathbb D}^2)$
be the full eigenspace. Every PFM is holomorphic at least on
![]() $\Omega _*$
. By rotational invariance of
$\Omega _*$
. By rotational invariance of
![]() ${\mathbb D}^2$
and Theorem 5.1, this implies that
${\mathbb D}^2$
and Theorem 5.1, this implies that
![]() $Y \cap \mathcal {H}(\Omega _*)$
is dense in Y, i.e., (NE) holds. Assume now that Y is a proper subspace of
$Y \cap \mathcal {H}(\Omega _*)$
is dense in Y, i.e., (NE) holds. Assume now that Y is a proper subspace of
![]() $X_\lambda ({\mathbb D}^2)$
. By Theorem 8.1, this is only possible if
$X_\lambda ({\mathbb D}^2)$
. By Theorem 8.1, this is only possible if
![]() $\lambda $
is an exceptional eigenvalue. Furthermore,
$\lambda $
is an exceptional eigenvalue. Furthermore,
Combining (8.1a), (8.1b), resp. (8.1c) with Corollary 5.2 yields (
![]() $\text {E}_+$
), (
$\text {E}_+$
), (
![]() $\text {E}_-$
) resp. (
$\text {E}_-$
) resp. (
![]() $\text {E}_0$
). We have already discussed the additional statements in the latter case in Theorem 8.1.
$\text {E}_0$
). We have already discussed the additional statements in the latter case in Theorem 8.1.
Finally, Corollary 6.5 shows that none of the density statements (
![]() $\text {E}_+$
), (
$\text {E}_+$
), (
![]() $\text {E}_-$
), and (NE) may be improved to holomorphic extensibility of every element.
$\text {E}_-$
), and (NE) may be improved to holomorphic extensibility of every element.
Proof
(of Theorem 2.6) The equivalence of (i), (ii), and (iii) was already established in Theorem 6.2. Let
![]() $\lambda = 4m(m+1)$
for some
$\lambda = 4m(m+1)$
for some
![]() $m \in {\mathbb N}_0$
. By (8.1c), we then have
$m \in {\mathbb N}_0$
. By (8.1c), we then have
![]() $\dim (X_\lambda (\Omega )) = 2m+1$
. Investing moreover Theorem 4.4 yields (a). Remark 6.3 proves the inclusion “
$\dim (X_\lambda (\Omega )) = 2m+1$
. Investing moreover Theorem 4.4 yields (a). Remark 6.3 proves the inclusion “
![]() $\subseteq $
” in (2.2). Conversely, restricting an eigenfunction
$\subseteq $
” in (2.2). Conversely, restricting an eigenfunction
![]() $F \in X_\lambda (\Omega )$
to the rotated diagonal
$F \in X_\lambda (\Omega )$
to the rotated diagonal
![]() $\{(z,-\overline {{z}}) \colon z \in \widehat {{\mathbb C}}\}$
yields an eigenfunction of
$\{(z,-\overline {{z}}) \colon z \in \widehat {{\mathbb C}}\}$
yields an eigenfunction of
![]() $\Delta _{\widehat {{\mathbb C}}}$
. This completes the proof.
$\Delta _{\widehat {{\mathbb C}}}$
. This completes the proof.
The finite-dimensional spaces
![]() $X_{4m(m+1)}(\Omega )$
can also be characterized in terms of the PFM
$X_{4m(m+1)}(\Omega )$
can also be characterized in terms of the PFM
![]() $P_0^{-m}$
only.
$P_0^{-m}$
only.
Corollary 8.6 Let
![]() $m\in {\mathbb N}_0$
. The function
$m\in {\mathbb N}_0$
. The function
![]() $P_0^{-m}$
is cyclic in
$P_0^{-m}$
is cyclic in
![]() $X_{4m(m+1)}(\Omega )$
with respect to the natural action of
$X_{4m(m+1)}(\Omega )$
with respect to the natural action of
![]() $\mathcal {M}$
by pullbacks. That is,
$\mathcal {M}$
by pullbacks. That is,
In addition,
Proof We begin by showing the first equality in (8.5), which implies (8.4). Recall that, by (8.1c), the set
![]() $\{P^{-m}_j \colon -m \le j \le m\}$
constitutes a basis of
$\{P^{-m}_j \colon -m \le j \le m\}$
constitutes a basis of
![]() $X_{4m(m+1)}(\Omega )$
. By (7.5),
$X_{4m(m+1)}(\Omega )$
. By (7.5),
 $$ \begin{align*} P_0^{-m} \circ T_{u,\overline{{u}}} = \sum_{j=-m}^{m} P^{m+1}_{-j}(u,\overline{{u}}) P^{-m}_{j} \end{align*} $$
$$ \begin{align*} P_0^{-m} \circ T_{u,\overline{{u}}} = \sum_{j=-m}^{m} P^{m+1}_{-j}(u,\overline{{u}}) P^{-m}_{j} \end{align*} $$
for every
![]() $u \in {\mathbb D}$
. We interpret the claim as a change of basis from
$u \in {\mathbb D}$
. We interpret the claim as a change of basis from
![]() ${\{P^{-m}_{j} \;|\; -m \le j \le m\}}$
to
${\{P^{-m}_{j} \;|\; -m \le j \le m\}}$
to
![]() ${\{P_0^{-m} \circ T_{u_k,\overline {{u}}_k} \;|\; -m \le k \le m\}}$
. Therefore, we have to find suitable points
${\{P_0^{-m} \circ T_{u_k,\overline {{u}}_k} \;|\; -m \le k \le m\}}$
. Therefore, we have to find suitable points
![]() ${u_{-m}, \ldots , u_m \in {\mathbb D}}$
such that the coefficient matrix
${u_{-m}, \ldots , u_m \in {\mathbb D}}$
such that the coefficient matrix
is invertible. However, it is true in general that given linearly independent complex valued functions
![]() $F_1,\dots , F_M$
for some
$F_1,\dots , F_M$
for some
![]() $M\in {\mathbb N}$
on a set containing at least M elements, it is possible to find the same number of points
$M\in {\mathbb N}$
on a set containing at least M elements, it is possible to find the same number of points
![]() $x_1,\dots , x_M$
in the same set such that the matrix
$x_1,\dots , x_M$
in the same set such that the matrix
![]() $(F_j(x_k))_{1\leq j,k\leq M}$
is invertible (see [Reference Gallier and Quaintance15, Proof of Proposition 7.28]). The second equality in (8.5) follows similarly.
$(F_j(x_k))_{1\leq j,k\leq M}$
is invertible (see [Reference Gallier and Quaintance15, Proof of Proposition 7.28]). The second equality in (8.5) follows similarly.
9 Poisson–Fourier modes and Peschl–Minda operators
In [Reference Heins, Moucha, Roth and Sugawa19], the classical Peschl–Minda differential operators, which were introduced by Peschl [Reference Peschl34] and studied, e.g., by [Reference Aharonov2, Reference Harmelin17, Reference Kim and Sugawa24, Reference Kim and Sugawa25, Reference Minda31, Reference Schippers39, Reference Schippers40, Reference Sugawa, Begehr, Gilbert and Kajiwara42], have been extended to differential operators acting on holomorphic functions defined on subdomains of
![]() $\Omega \cap {\mathbb C}^2$
. It is the purpose of this section to put these (generalized) Peschl–Minda operators into the context of the present paper. In particular, we relate the Poisson–Fourier modes with the Peschl–Minda operators.
$\Omega \cap {\mathbb C}^2$
. It is the purpose of this section to put these (generalized) Peschl–Minda operators into the context of the present paper. In particular, we relate the Poisson–Fourier modes with the Peschl–Minda operators.
We first briefly recall the definition from [Reference Heins, Moucha, Roth and Sugawa19]. Let U be an open subset of
![]() $\Omega \cap {\mathbb C}^2$
and
$\Omega \cap {\mathbb C}^2$
and
![]() ${f \in C^{\infty }(U)}$
. The Peschl–Minda derivative
${f \in C^{\infty }(U)}$
. The Peschl–Minda derivative
![]() $D^{m,n}f$
at the point
$D^{m,n}f$
at the point
![]() $(z,w) \in U$
is defined by
$(z,w) \in U$
is defined by
 $$ \begin{align*}D^{m,n} f(z,w):=\frac{\partial^{m+n}}{\partial u^m \partial v^n} \left( f \circ {T}_{z,w} \circ \varrho_{-1} \right)(u,v) \bigg|_{(u,v)=(0,0)} .\end{align*} $$
$$ \begin{align*}D^{m,n} f(z,w):=\frac{\partial^{m+n}}{\partial u^m \partial v^n} \left( f \circ {T}_{z,w} \circ \varrho_{-1} \right)(u,v) \bigg|_{(u,v)=(0,0)} .\end{align*} $$
We write ![]() and
and ![]() and refer to these operators as pure Peschl–Minda operators. Comparing with (8.3), we note that the roles of
and refer to these operators as pure Peschl–Minda operators. Comparing with (8.3), we note that the roles of
![]() $(z,w)$
and
$(z,w)$
and
![]() $(u,v)$
have been swapped, which yields the operators
$(u,v)$
have been swapped, which yields the operators
![]() $D^1_z$
and
$D^1_z$
and
![]() $D^1_w$
instead of
$D^1_w$
instead of
![]() $D^+$
and
$D^+$
and
![]() $D^-$
, respectively.
$D^-$
, respectively.
Given a linear mapping
![]() $T \colon V \longrightarrow W$
we write
$T \colon V \longrightarrow W$
we write ![]() for its kernel. We observe that the pure Peschl–Minda operators reproduce the generalized Poisson kernel from (4.9) in the following way.
for its kernel. We observe that the pure Peschl–Minda operators reproduce the generalized Poisson kernel from (4.9) in the following way.
Lemma 9.1 Let
![]() $\mu \in {\mathbb C}$
,
$\mu \in {\mathbb C}$
,
![]() $(z,w)\in {\mathbb D}^2$
,
$(z,w)\in {\mathbb D}^2$
,
![]() $\xi \in \partial {\mathbb D}$
, and
$\xi \in \partial {\mathbb D}$
, and
![]() $k \in {\mathbb N}_0$
. Then
$k \in {\mathbb N}_0$
. Then
with
![]() $\psi _{z,w}$
from (7.2). In particular, if
$\psi _{z,w}$
from (7.2). In particular, if
![]() $\mu =-m\in (-{\mathbb N}_0)$
, then
$\mu =-m\in (-{\mathbb N}_0)$
, then
Proof If
![]() $w=\overline {{z}}$
, this is most easily proved by an induction on k and the help of Proposition 3.8 in [Reference Heins, Moucha, Roth and Sugawa19]. Then, the general result follows from Lemma 3.1.
$w=\overline {{z}}$
, this is most easily proved by an induction on k and the help of Proposition 3.8 in [Reference Heins, Moucha, Roth and Sugawa19]. Then, the general result follows from Lemma 3.1.
We note in passing that Lemma 9.1 for
![]() $w=\overline {{z}}$
says that up to multiplication with a unimodular constant the (classical) Poisson kernel
$w=\overline {{z}}$
says that up to multiplication with a unimodular constant the (classical) Poisson kernel
![]() $z \mapsto P(z,\overline {z};\xi )$
is a joint eigenfunction of the (classical) Peschl–Minda operators studied, e.g., in [Reference Kim and Sugawa24]. Remarkably, the Peschl–Minda operators also act as weighted shifts when applied to the zeroth PFM.
$z \mapsto P(z,\overline {z};\xi )$
is a joint eigenfunction of the (classical) Peschl–Minda operators studied, e.g., in [Reference Kim and Sugawa24]. Remarkably, the Peschl–Minda operators also act as weighted shifts when applied to the zeroth PFM.
Proposition 9.2 For
![]() $\mu \in {\mathbb C}$
and
$\mu \in {\mathbb C}$
and
![]() $n \in {\mathbb N}_0$
, we have
$n \in {\mathbb N}_0$
, we have
Proof Let
![]() $z \in {\mathbb D}$
. We prove the claim for points
$z \in {\mathbb D}$
. We prove the claim for points
![]() $(z,\overline {{z}})$
first from which then follows the result by the identity principle (Lemma 3.1). We compute
$(z,\overline {{z}})$
first from which then follows the result by the identity principle (Lemma 3.1). We compute
 $$ \begin{align*} D^{n,0}P_0^{\mu}(z,\overline{{z}})&=\frac{ 1}{2\pi} \int\limits_{0}^{2\pi} D^{n,0}P\big(z,\overline{{z}};e^{it}\big)^{\mu}\, dt \\ &\overset{({9.1a})}{=}\frac{1}{2\pi} \int\limits_{0}^{2\pi}(\mu)_n P\big(z,\overline{{z}};e^{it}\big)^{\mu}\left(\psi_{z,\overline{{z}}}(e^{it})\right)^{-n}\, dt\\ &\overset{({7.4})}{=}\frac{(\mu)_n }{2\pi} \int\limits_{0}^{2\pi}P\big(z,\overline{{z}};\psi_{z,\overline{{z}}}(e^{it})\big)^{-\mu}\left(\psi_{z,\overline{{z}}}(e^{it})\right)^{-n}\, dt\\ &\overset{{7.3}}{=}\frac{(\mu)_n }{2\pi} \int\limits_{0}^{2\pi}P\big(z,\overline{{z}};e^{it}\big)^{1-\mu}e^{-int}\, dt\\ &=(\mu)_nP^{1-\mu}_n(z,\overline{{z}}) \overset{({4.18})}{=}(-\mu+1)_n P^{\mu}_n(z,\overline{{z}}) . \end{align*} $$
$$ \begin{align*} D^{n,0}P_0^{\mu}(z,\overline{{z}})&=\frac{ 1}{2\pi} \int\limits_{0}^{2\pi} D^{n,0}P\big(z,\overline{{z}};e^{it}\big)^{\mu}\, dt \\ &\overset{({9.1a})}{=}\frac{1}{2\pi} \int\limits_{0}^{2\pi}(\mu)_n P\big(z,\overline{{z}};e^{it}\big)^{\mu}\left(\psi_{z,\overline{{z}}}(e^{it})\right)^{-n}\, dt\\ &\overset{({7.4})}{=}\frac{(\mu)_n }{2\pi} \int\limits_{0}^{2\pi}P\big(z,\overline{{z}};\psi_{z,\overline{{z}}}(e^{it})\big)^{-\mu}\left(\psi_{z,\overline{{z}}}(e^{it})\right)^{-n}\, dt\\ &\overset{{7.3}}{=}\frac{(\mu)_n }{2\pi} \int\limits_{0}^{2\pi}P\big(z,\overline{{z}};e^{it}\big)^{1-\mu}e^{-int}\, dt\\ &=(\mu)_nP^{1-\mu}_n(z,\overline{{z}}) \overset{({4.18})}{=}(-\mu+1)_n P^{\mu}_n(z,\overline{{z}}) . \end{align*} $$
The computation for
![]() $D^{0,n}$
and
$D^{0,n}$
and
![]() $P_{-n}^{\mu }$
is analogous.
$P_{-n}^{\mu }$
is analogous.
Remark 9.3 Since Poisson–Fourier modes are closely related to hypergeometric functions, see (4.15), an alternative proof can be given by induction using Gauss’ contiguous identities, more precisely with equation 15.2.24 and with a combination of equations 15.2.1 and 15.2.6 in [Reference Abramowitz, Stegun, Danos and Rafelski1].
In view of [Reference Heins, Moucha, Roth and Sugawa19, Corollary 4.4], we find another connection between the PFM and the pure Peschl–Minda derivatives. Let
![]() $\lambda =4m(m+1)$
,
$\lambda =4m(m+1)$
,
![]() $m,n\in {\mathbb N}_0$
. It is true that
$m,n\in {\mathbb N}_0$
. It is true that
Proposition 9.4 Let
![]() $M\in {\mathbb N}_0$
. Then
$M\in {\mathbb N}_0$
. Then
Proof Denote the left-hand side of (9.2) by
![]() $X_M$
. Note that
$X_M$
. Note that
![]() $\ker (D^{M+1}_z)\cap \ker (D^{M+1}_w)$
and
$\ker (D^{M+1}_z)\cap \ker (D^{M+1}_w)$
and
![]() $X_M$
are finite-dimensional spaces. Moreover,
$X_M$
are finite-dimensional spaces. Moreover,
![]() $X_M$
is the direct sum
$X_M$
is the direct sum
 $$\begin{align*}X_M=\bigoplus_{m=0}^M X_{4m(m+1)}^0({\mathbb D}^2)\end{align*}$$
$$\begin{align*}X_M=\bigoplus_{m=0}^M X_{4m(m+1)}^0({\mathbb D}^2)\end{align*}$$
and
![]() $\dim X_{4m(m+1)}^0({\mathbb D}^2)=2m+1$
by Theorem 8.1. Therefore, we compute on the one hand
$\dim X_{4m(m+1)}^0({\mathbb D}^2)=2m+1$
by Theorem 8.1. Therefore, we compute on the one hand
 $$ \begin{align*}\dim X_M = \sum_{m=0}^M (2m+1) = (M+1)^2 .\end{align*} $$
$$ \begin{align*}\dim X_M = \sum_{m=0}^M (2m+1) = (M+1)^2 .\end{align*} $$
On the other hand, by [Reference Heins, Moucha, Roth and Sugawa19, Corollary 4.4], we have
 $$ \begin{align} \ker(D^{M+1}_z) \cap \ker(D^{M+1}_w) = \mathrm{span} \bigg\{ \frac{z^j w^k}{(1-zw)^M} \colon 0 \le j,k \le M \bigg\} . \end{align} $$
$$ \begin{align} \ker(D^{M+1}_z) \cap \ker(D^{M+1}_w) = \mathrm{span} \bigg\{ \frac{z^j w^k}{(1-zw)^M} \colon 0 \le j,k \le M \bigg\} . \end{align} $$
Consequently,
![]() $\dim (\ker (D^{M+1}_z){\kern-1pt}\cap{\kern-1pt} \ker (D^{M+1}_w)) {\kern-1pt}={\kern-1pt} (M{\kern-1pt}+{\kern-1pt}1)^2$
. Moreover, combining (4.17) with (9.3) yields
$\dim (\ker (D^{M+1}_z){\kern-1pt}\cap{\kern-1pt} \ker (D^{M+1}_w)) {\kern-1pt}={\kern-1pt} (M{\kern-1pt}+{\kern-1pt}1)^2$
. Moreover, combining (4.17) with (9.3) yields
![]() $X_M\subseteq (\ker (D^M_z)\cap \ker (D^M_w))$
. This proves (9.2) by linear algebra.
$X_M\subseteq (\ker (D^M_z)\cap \ker (D^M_w))$
. This proves (9.2) by linear algebra.
Remark 9.5 Note that both the PFM
![]() $P_n^{-m}$
and the generators from (9.3) may be understood as holomorphic functions on all of
$P_n^{-m}$
and the generators from (9.3) may be understood as holomorphic functions on all of
![]() $\Omega $
. It thus makes sense to speak of
$\Omega $
. It thus makes sense to speak of
as the subspace of
![]() $\mathcal {H}(\Omega )$
consisting of all finite linear combinations of elements in the kernels of the Peschl–Minda differential operators. We can even go one step further than Proposition 9.4 and conclude that as sets
$\mathcal {H}(\Omega )$
consisting of all finite linear combinations of elements in the kernels of the Peschl–Minda differential operators. We can even go one step further than Proposition 9.4 and conclude that as sets
 $$ \begin{align*} &\operatorname{clos}_{\Omega}\left( \mathrm{span}\{P_n^{-m}\,:\, m\in{\mathbb N}_0,\,n\in{\mathbb Z},\, |n|\leq m\}\right) \\ & =\operatorname{clos}_{\Omega}\left(\bigoplus_{M\in{\mathbb N}_0}\big(\ker(D_{z}^{M+1})\cap\ker(D_w^{M+1})\big)\right) \\ & =\mathcal{H}(\Omega) ,\end{align*} $$
$$ \begin{align*} &\operatorname{clos}_{\Omega}\left( \mathrm{span}\{P_n^{-m}\,:\, m\in{\mathbb N}_0,\,n\in{\mathbb Z},\, |n|\leq m\}\right) \\ & =\operatorname{clos}_{\Omega}\left(\bigoplus_{M\in{\mathbb N}_0}\big(\ker(D_{z}^{M+1})\cap\ker(D_w^{M+1})\big)\right) \\ & =\mathcal{H}(\Omega) ,\end{align*} $$
where the last equality follows from a combination of (9.3) with [Reference Heins, Moucha and Roth18, Eq. (4.1) and Corollary 4.8]. This observation leads to the question whether the PFM form a Schauder basis of
![]() $\mathcal {H}(\Omega )$
. The second author answers this question affirmatively in [Reference Moucha32]. Perhaps similar results hold for
$\mathcal {H}(\Omega )$
. The second author answers this question affirmatively in [Reference Moucha32]. Perhaps similar results hold for
![]() $\mathcal {H}(\Omega _\pm )$
and the corresponding Poisson–Fourier modes from Theorem 4.4.
$\mathcal {H}(\Omega _\pm )$
and the corresponding Poisson–Fourier modes from Theorem 4.4.
Acknowledgment
The authors wish to thank an anonymous referee for a careful reading of the original manuscript and many helpful suggestions.




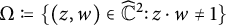 of the “complexified unit circle”
of the “complexified unit circle”