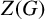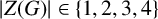1 Introduction
Throughout this paper, all groups are finite and G always denotes a finite group;
![]() $G^{\mathfrak {N}}$
is the nilpotent residual of G, that is, the intersection of all normal subgroups N of G with nilpotent quotient
$G^{\mathfrak {N}}$
is the nilpotent residual of G, that is, the intersection of all normal subgroups N of G with nilpotent quotient
![]() $G/N$
; and
$G/N$
; and
![]() $Z_{\infty }(G)$
is the hypercentre of G, that is, the largest normal subgroup of G such that
$Z_{\infty }(G)$
is the hypercentre of G, that is, the largest normal subgroup of G such that
![]() $C_{G}(H/K)=G$
for every chief factor
$C_{G}(H/K)=G$
for every chief factor
![]() $H/K$
of G below
$H/K$
of G below
![]() $Z_{\infty }(G)$
. A nonnilpotent group G is called minimal nonnilpotent or a Schmidt group if every proper subgroup of G is nilpotent.
$Z_{\infty }(G)$
. A nonnilpotent group G is called minimal nonnilpotent or a Schmidt group if every proper subgroup of G is nilpotent.
The structure of Schmidt groups is well known (see [Reference Huppert10, III, Satz 5.2] and [Reference Ballester-Bolinches, Esteban-Romero and Robinson2]) and such groups have deep applications in the theory of the classes of groups [Reference Ballester-Bolinches and Ezquerro3, Reference Guo8]. Groups in which the condition of subnormality or generalised subnormality is satisfied for all or selected Schmidt subgroups are studied in [Reference Monakhov and Knyagina12, Reference Vedernikov17] and the recent papers [Reference Al-Sharo and Skiba1, Reference Hu and Huang9, Reference Liu, Guo, Safonova and Skiba11, Reference Monakhov and Knyagina13, Reference Sun, Yi and Kamornikov15, Reference Yi and Kamornikov19]. In this article, we consider, in a certain sense, the opposite situation.
A subgroup H of G is said to be abnormal in G if
![]() $x\in \langle H, H^{x} \rangle $
for all
$x\in \langle H, H^{x} \rangle $
for all
![]() $x\in G$
. From the results in [Reference Al-Sharo and Skiba1, Reference Hu and Huang9, Reference Liu, Guo, Safonova and Skiba11, Reference Monakhov and Knyagina13, Reference Sun, Yi and Kamornikov15, Reference Yi and Kamornikov19], it is natural to ask: What is the structure of a group in which all Schmidt subgroups are abnormal? We provide an answer to this question.
$x\in G$
. From the results in [Reference Al-Sharo and Skiba1, Reference Hu and Huang9, Reference Liu, Guo, Safonova and Skiba11, Reference Monakhov and Knyagina13, Reference Sun, Yi and Kamornikov15, Reference Yi and Kamornikov19], it is natural to ask: What is the structure of a group in which all Schmidt subgroups are abnormal? We provide an answer to this question.
We say that G is an
SA-group if G is not nilpotent and every Schmidt subgroup of G is abnormal, and an
SSA-group if G is a nonabelian simple SA-group and for every Schmidt subgroup H of G, we have
![]() $\pi (H)\cap \{2, 3\}\ne \emptyset .$
The usefulness of the concept of an SSA-group is due to the fact that in any SA-group, any of its nonsoluble local subgroups is an SSA-group (see [Reference Gorenstein6, page 444] and Theorem 1.2 below).
$\pi (H)\cap \{2, 3\}\ne \emptyset .$
The usefulness of the concept of an SSA-group is due to the fact that in any SA-group, any of its nonsoluble local subgroups is an SSA-group (see [Reference Gorenstein6, page 444] and Theorem 1.2 below).
Our first result shows that the class of all soluble SA-groups is rather narrow.
Theorem 1.1. The group G is a soluble SA-group if and only if the following conditions hold.
-
(i)
 $G=D\rtimes Q$
, where
$G=D\rtimes Q$
, where
 $D=G^{\mathfrak {N}}\ne 1$
is nilpotent,
$D=G^{\mathfrak {N}}\ne 1$
is nilpotent,
 $Q=\langle x \rangle $
is a cyclic Sylow q-subgroup of G for some prime q dividing
$Q=\langle x \rangle $
is a cyclic Sylow q-subgroup of G for some prime q dividing
 $|G|$
and
$|G|$
and
 $F(G )=D\langle x^{q} \rangle $
. In particular,
$F(G )=D\langle x^{q} \rangle $
. In particular,
 $\langle x^{q} \rangle \leq Z(G)$
.
$\langle x^{q} \rangle \leq Z(G)$
. -
(ii)
 $Z:=Z_{\infty }(G)\cap D\leq \Phi (O_{p}(D))$
for some prime p and, if
$Z:=Z_{\infty }(G)\cap D\leq \Phi (O_{p}(D))$
for some prime p and, if
 $Z\ne 1$
, then
$Z\ne 1$
, then
 $D=O_{p}(D)$
is a Sylow p-subgroup of G.
$D=O_{p}(D)$
is a Sylow p-subgroup of G. -
(iii) For every prime r dividing
 $|D|$
and for the Sylow r-subgroup
$|D|$
and for the Sylow r-subgroup
 $D_{r}$
of D:
$D_{r}$
of D:-
(a)
 $R=(RQ)^{\mathfrak {N}}$
for every normal r-subgroup R of G with
$R=(RQ)^{\mathfrak {N}}$
for every normal r-subgroup R of G with
 $Z < R$
; in particular,
$Z < R$
; in particular,
 $D_{r}=(D_{r}Q)^{\mathfrak {N}}$
;
$D_{r}=(D_{r}Q)^{\mathfrak {N}}$
; -
(b) if
 $H/K$
is any chief factor of G between Z and
$H/K$
is any chief factor of G between Z and
 $D_{r}$
, then
$D_{r}$
, then
 $C_{G}(H/K)=F(G)$
and
$C_{G}(H/K)=F(G)$
and
 $|H/K|=r^{n}$
, where n is the smallest integer such that q divides
$|H/K|=r^{n}$
, where n is the smallest integer such that q divides
 $r^{n}-1$
.
$r^{n}-1$
.
-
-
(iv)
 $ZQ=N_{G}(Q)$
is a Carter subgroup of G and the set of all Carter subgroups of G coincides with the set of all its system normalisers. Moreover, a subgroup C of G is a Carter subgroup if and only if C is a maximal abnormal subgroup of a Schmidt subgroup of G.
$ZQ=N_{G}(Q)$
is a Carter subgroup of G and the set of all Carter subgroups of G coincides with the set of all its system normalisers. Moreover, a subgroup C of G is a Carter subgroup if and only if C is a maximal abnormal subgroup of a Schmidt subgroup of G.
We do not know how wide the class of all nonsoluble SA-groups is (see Section 4). Nevertheless, using Theorem 1.1, we prove the following theorem which partially describes such groups.
Theorem 1.2. If G is a nonsoluble SA-group, then the following conditions hold.
-
(i) G is quasisimple and
 $Z(G)$
is cyclic of order
$Z(G)$
is cyclic of order
 $|Z(G)|\in \{1, 2, 3, 4\}$
. In particular,
$|Z(G)|\in \{1, 2, 3, 4\}$
. In particular,
 $Z(G)\leq \Phi (H)$
for every Schmidt subgroup H of G and
$Z(G)\leq \Phi (H)$
for every Schmidt subgroup H of G and
 $U/Z(G)$
is a Schmidt subgroup of
$U/Z(G)$
is a Schmidt subgroup of
 $G/Z(G)$
if and only if U is a Schmidt subgroup of G.
$G/Z(G)$
if and only if U is a Schmidt subgroup of G. -
(ii)
 $G/Z(G)$
is an SSA-group.
$G/Z(G)$
is an SSA-group. -
(iii) If
 $N=N_{G}(P)$
for some nonnormal p-subgroup P of G, then either N is a group of type (i) with
$N=N_{G}(P)$
for some nonnormal p-subgroup P of G, then either N is a group of type (i) with
 $|Z(G)|\in \{2, 3, 4\}$
, or N is nilpotent or
$|Z(G)|\in \{2, 3, 4\}$
, or N is nilpotent or
 $|N/F(N)|$
is a prime.
$|N/F(N)|$
is a prime.
2 Proof of Theorem 1.1
The first lemma is a corollary of the definition of abnormal subgroups.
Lemma 2.1. Let
![]() $H\leq E$
and
$H\leq E$
and
![]() $N\trianglelefteq G$
, where H is abnormal in G. Then H is abnormal in E, E is abnormal in G and
$N\trianglelefteq G$
, where H is abnormal in G. Then H is abnormal in E, E is abnormal in G and
![]() $HN/N$
is abnormal in
$HN/N$
is abnormal in
![]() $G/N$
.
$G/N$
.
Lemma 2.2. Let
![]() $N, H\leq G$
, where
$N, H\leq G$
, where
![]() $N\trianglelefteq G$
and
$N\trianglelefteq G$
and
![]() $N\leq Z_{\infty }(G)$
. Then H is subnormal in
$N\leq Z_{\infty }(G)$
. Then H is subnormal in
![]() $HN$
and if H is abnormal in G, then
$HN$
and if H is abnormal in G, then
![]() $N\leq H$
.
$N\leq H$
.
Proof. First we show that H is subnormal in
![]() $E=HN$
. Assume this is false and let G be a counterexample of minimal order. Then
$E=HN$
. Assume this is false and let G be a counterexample of minimal order. Then
![]() $H\ne G$
. Since
$H\ne G$
. Since
![]() $N\leq Z_{\infty }(G)\cap E\leq Z_{\infty }(E)$
, the hypothesis holds for
$N\leq Z_{\infty }(G)\cap E\leq Z_{\infty }(E)$
, the hypothesis holds for
![]() $(E, H, N)$
. If
$(E, H, N)$
. If
![]() $E < G$
, then H is subnormal in E by the choice of G, and this contradicts the hypothesis. Therefore,
$E < G$
, then H is subnormal in E by the choice of G, and this contradicts the hypothesis. Therefore,
![]() $G=E=HN$
. Let M be a maximal subgroup of G such that
$G=E=HN$
. Let M be a maximal subgroup of G such that
![]() $H\leq M$
. Then
$H\leq M$
. Then
![]() $M=H(M\cap N)$
, where
$M=H(M\cap N)$
, where
![]() $M\cap N\leq Z_{\infty }(M)$
, so the hypothesis holds for
$M\cap N\leq Z_{\infty }(M)$
, so the hypothesis holds for
![]() $(M, H, M\cap N)$
and hence H is subnormal in M and M is not normal in G. However, the hypothesis holds also for
$(M, H, M\cap N)$
and hence H is subnormal in M and M is not normal in G. However, the hypothesis holds also for
![]() $(G/M_{G}, M/M_{G}, NM_{G}/M_{G})$
, so
$(G/M_{G}, M/M_{G}, NM_{G}/M_{G})$
, so
![]() $M_{G}=1$
. Note also that
$M_{G}=1$
. Note also that
![]() $M\cap N < N_{N}(M\cap N)$
since
$M\cap N < N_{N}(M\cap N)$
since
![]() $ Z_{\infty }(G)$
is nilpotent and so
$ Z_{\infty }(G)$
is nilpotent and so
![]() $M\cap N$
is normal in G. Therefore, from
$M\cap N$
is normal in G. Therefore, from
![]() $G=NM$
and
$G=NM$
and
![]() $M_{G}=1$
, it follows that
$M_{G}=1$
, it follows that
![]() $M\cap N=1$
and so N is a minimal normal subgroup of G contained in
$M\cap N=1$
and so N is a minimal normal subgroup of G contained in
![]() $ Z_{\infty }(G)$
. Hence
$ Z_{\infty }(G)$
. Hence
![]() $N\leq Z(G)$
, so
$N\leq Z(G)$
, so
![]() $G=MN\leq N_{G}(M)$
and this contradicts the hypothesis. Therefore, H is subnormal in
$G=MN\leq N_{G}(M)$
and this contradicts the hypothesis. Therefore, H is subnormal in
![]() $E=NH$
. Finally, if H is abnormal in G, then H is abnormal in E by Lemma 2.1 and so
$E=NH$
. Finally, if H is abnormal in G, then H is abnormal in E by Lemma 2.1 and so
![]() $H=E$
by [Reference Doerk and Hawkes5, I, Illustrations 6.19(b)]. The lemma is proved.
$H=E$
by [Reference Doerk and Hawkes5, I, Illustrations 6.19(b)]. The lemma is proved.
The following lemma is well known (see, for example, [Reference Shemetkov14, I, Lemma 4.1]).
Lemma 2.3. Let A be an abelian irreducible automorphism group of a p-group P of order
![]() $|P|=p^{n}$
. Then A is a cyclic group and n is the smallest integer such that
$|P|=p^{n}$
. Then A is a cyclic group and n is the smallest integer such that
![]() $|A|$
divides
$|A|$
divides
![]() $p^{n}-1$
.
$p^{n}-1$
.
Proof of Theorem 1.1
First we show that if G is a soluble SA-group, then Conditions (i), (ii), (iii) and (iv) hold for G. Assume that this is false and let G be a counterexample of minimal order. Then G is not a Schmidt group since Conditions (i), (ii), (iii) and (iv) hold for every Schmidt group G by Proposition 1.9 in [Reference Guo8, Ch. 1] and the results in [Reference Ballester-Bolinches, Esteban-Romero and Robinson2]. Let
![]() $D=G^{\mathfrak {N}}$
by the nilpotent residual of G. Then
$D=G^{\mathfrak {N}}$
by the nilpotent residual of G. Then
![]() $D\ne 1$
.
$D\ne 1$
.
-
(1) If
 $L\trianglelefteq T\leq G$
, where
$L\trianglelefteq T\leq G$
, where
 $T/L$
is nonnilpotent and either
$T/L$
is nonnilpotent and either
 $L\ne 1$
or
$L\ne 1$
or
 $T\ne G$
, then Conditions (i), (ii), (iii) and (iv) hold for
$T\ne G$
, then Conditions (i), (ii), (iii) and (iv) hold for
 $T/L$
.
$T/L$
.
Let
![]() $E/L$
be a Schmidt subgroup of
$E/L$
be a Schmidt subgroup of
![]() $T/L$
. Then E is not nilpotent, so it contains a Schmidt subgroup, A say, and A is abnormal in G by hypothesis. Then E is abnormal in T and so
$T/L$
. Then E is not nilpotent, so it contains a Schmidt subgroup, A say, and A is abnormal in G by hypothesis. Then E is abnormal in T and so
![]() $E/L$
is abnormal in
$E/L$
is abnormal in
![]() $T/L$
by Lemma 2.1. Therefore, the hypothesis holds for
$T/L$
by Lemma 2.1. Therefore, the hypothesis holds for
![]() $T/L$
, so we have (1) by the choice of G.
$T/L$
, so we have (1) by the choice of G.
-
(2) Every nonabnormal subgroup E of G is nilpotent.
Since every nonnilpotent group possesses a Schmidt subgroup, this follows from Lemma 2.1 and the hypothesis.
-
(3)
 $D < G$
and if
$D < G$
and if
 $D\leq V < G$
, where V is a maximal subgroup of G, then
$D\leq V < G$
, where V is a maximal subgroup of G, then
 $V=F(G)$
is the largest normal nilpotent subgroup of G and
$V=F(G)$
is the largest normal nilpotent subgroup of G and
 $G/D$
is a cyclic group of order
$G/D$
is a cyclic group of order
 $q^{r}$
for some prime q.
$q^{r}$
for some prime q.
Since G is soluble,
![]() $D \ne G$
. However,
$D \ne G$
. However,
![]() $G/D$
is nilpotent, so each maximal subgroup V of G containing D is subnormal in G. Assume that V is not nilpotent. Then V is abnormal in G by (2), so
$G/D$
is nilpotent, so each maximal subgroup V of G containing D is subnormal in G. Assume that V is not nilpotent. Then V is abnormal in G by (2), so
![]() $V/D$
is abnormal in
$V/D$
is abnormal in
![]() $G/D=Z_{\infty }(G/D)$
and hence
$G/D=Z_{\infty }(G/D)$
and hence
![]() $V/D=G/D$
by Lemma 2.2. This contradiction shows that V is nilpotent. If
$V/D=G/D$
by Lemma 2.2. This contradiction shows that V is nilpotent. If
![]() $G/D$
has at least two distinct maximal subgroups
$G/D$
has at least two distinct maximal subgroups
![]() $V/D$
and
$V/D$
and
![]() $W/D$
, then
$W/D$
, then
![]() $G=\langle V, W \rangle $
is nilpotent since the subgroup generated by any two subnormal nilpotent subgroups of the group is nilpotent by [Reference Ballester-Bolinches and Ezquerro3, Theorem 6.3.3]. Therefore,
$G=\langle V, W \rangle $
is nilpotent since the subgroup generated by any two subnormal nilpotent subgroups of the group is nilpotent by [Reference Ballester-Bolinches and Ezquerro3, Theorem 6.3.3]. Therefore,
![]() $G/D $
is a cyclic q-group for some prime q and
$G/D $
is a cyclic q-group for some prime q and
![]() $V=V^{G}$
is the largest normal nilpotent subgroup of G. Hence, we have (3).
$V=V^{G}$
is the largest normal nilpotent subgroup of G. Hence, we have (3).
-
(4) Condition (i) holds for G.
Let Q be a Sylow q-subgroup of G. Then
![]() $Q\cap D$
is a Sylow q-subgroup of D and D has a normal Hall
$Q\cap D$
is a Sylow q-subgroup of D and D has a normal Hall
![]() $q'$
-subgroup V since D is nilpotent by (3). The subgroup V is characteristic in D, so it is normal in G. Moreover,
$q'$
-subgroup V since D is nilpotent by (3). The subgroup V is characteristic in D, so it is normal in G. Moreover,
is nilpotent, so
![]() $D\leq V$
and hence
$D\leq V$
and hence
![]() $Q\cap D= 1$
. Therefore,
$Q\cap D= 1$
. Therefore,
![]() $G=D\rtimes Q$
, where
$G=D\rtimes Q$
, where
![]() $G/D\simeq Q=\langle x \rangle $
is a cyclic q-group and
$G/D\simeq Q=\langle x \rangle $
is a cyclic q-group and
![]() $F(G )=D\langle x^{q} \rangle $
, again by (3). It follows that
$F(G )=D\langle x^{q} \rangle $
, again by (3). It follows that
![]() $\langle x^{q} \rangle \leq Z(G)$
.
$\langle x^{q} \rangle \leq Z(G)$
.
-
(5) Condition (ii) holds for G.
Assume that
![]() $Z\ne 1$
and let L be a minimal normal subgroup of G contained in Z. Then
$Z\ne 1$
and let L be a minimal normal subgroup of G contained in Z. Then
![]() $L\leq Z(G)$
. Let p be any prime dividing
$L\leq Z(G)$
. Let p be any prime dividing
![]() $|Z|$
and let
$|Z|$
and let
![]() $Z_{p}$
be the Sylow p-subgroup of Z. We show that D is a Sylow p-subgroup of G. Assume that
$Z_{p}$
be the Sylow p-subgroup of Z. We show that D is a Sylow p-subgroup of G. Assume that
![]() $D\ne D_{p}:=O_{p}(D)$
. Then for the p-complement V of D, we have
$D\ne D_{p}:=O_{p}(D)$
. Then for the p-complement V of D, we have
![]() $Z_{p}\leq C_{G}(VQ)$
since
$Z_{p}\leq C_{G}(VQ)$
since
![]() $[Q, Z]=1$
by [Reference Weinstein18, Appendixes, Theorem 6.2]. If
$[Q, Z]=1$
by [Reference Weinstein18, Appendixes, Theorem 6.2]. If
![]() $VQ$
is not nilpotent and H is a Schmidt subgroup of
$VQ$
is not nilpotent and H is a Schmidt subgroup of
![]() $VQ$
, then
$VQ$
, then
![]() $Z_{p}\leq H\leq VQ$
by Lemma 2.2. However,
$Z_{p}\leq H\leq VQ$
by Lemma 2.2. However,
![]() $Z_{p}\cap VQ=1$
and so
$Z_{p}\cap VQ=1$
and so
![]() $Z_{p}=1$
, and this contradicts the hypothesis. Hence,
$Z_{p}=1$
, and this contradicts the hypothesis. Hence,
![]() $G/D_{p}\simeq VQ$
is nilpotent, so
$G/D_{p}\simeq VQ$
is nilpotent, so
![]() $D_{p}\leq D\leq D_{p}$
. Thus,
$D_{p}\leq D\leq D_{p}$
. Thus,
![]() $D=D_{p}$
.
$D=D_{p}$
.
Now we show that
![]() $Z\leq \Phi (D)=\Phi (D_{p})$
. Let
$Z\leq \Phi (D)=\Phi (D_{p})$
. Let
![]() $\Phi =\Phi (D)$
. Then
$\Phi =\Phi (D)$
. Then
![]() $ \Phi \leq \Phi (G)$
and so
$ \Phi \leq \Phi (G)$
and so
![]() $G/\Phi $
is not nilpotent. First assume that
$G/\Phi $
is not nilpotent. First assume that
![]() $ \Phi \ne 1$
. Then Condition (ii) holds for
$ \Phi \ne 1$
. Then Condition (ii) holds for
![]() $G/\Phi $
by (1). Hence,
$G/\Phi $
by (1). Hence,
 $$ \begin{align*} Z\Phi/\Phi =(Z_{\infty}(G)\cap D)\Phi/\Phi & \leq Z_{\infty}(G/\Phi)\cap (D/\Phi) = Z_{\infty}(G/\Phi)\cap (G^{\mathfrak{N}}/\Phi) \\ & =Z_{\infty}(G/\Phi)\cap (G/\Phi)^{\mathfrak{N}} \leq \Phi (D/ \Phi)=\Phi/ \Phi, \end{align*} $$
$$ \begin{align*} Z\Phi/\Phi =(Z_{\infty}(G)\cap D)\Phi/\Phi & \leq Z_{\infty}(G/\Phi)\cap (D/\Phi) = Z_{\infty}(G/\Phi)\cap (G^{\mathfrak{N}}/\Phi) \\ & =Z_{\infty}(G/\Phi)\cap (G/\Phi)^{\mathfrak{N}} \leq \Phi (D/ \Phi)=\Phi/ \Phi, \end{align*} $$
so
![]() $Z\leq \Phi =\Phi (D)$
. Finally, assume that
$Z\leq \Phi =\Phi (D)$
. Finally, assume that
![]() $ \Phi =1$
, that is,
$ \Phi =1$
, that is,
![]() $D=D_{p}$
is an elementary abelian p-group. Then
$D=D_{p}$
is an elementary abelian p-group. Then
![]() $D=N_{1}\times \cdots \times N_{t}$
, where
$D=N_{1}\times \cdots \times N_{t}$
, where
![]() $N_{1}, \ldots , N_{t}$
are minimal normal subgroups of G by Maschke’s theorem. It is clear also that for some i, for
$N_{1}, \ldots , N_{t}$
are minimal normal subgroups of G by Maschke’s theorem. It is clear also that for some i, for
![]() $i=1$
say, we have
$i=1$
say, we have
![]() $N_{1}=L\leq Z(G)$
. However, then
$N_{1}=L\leq Z(G)$
. However, then
![]() $G/N_{2}\times \cdots \times N_{t}\simeq N_{1}Q$
is nilpotent and so
$G/N_{2}\times \cdots \times N_{t}\simeq N_{1}Q$
is nilpotent and so
![]() $D\leq N_{2}\times \cdots \times N_{t}$
. This contradiction completes the proof that
$D\leq N_{2}\times \cdots \times N_{t}$
. This contradiction completes the proof that
![]() $Z\leq \Phi =\Phi (D)$
. Therefore, (5) holds.
$Z\leq \Phi =\Phi (D)$
. Therefore, (5) holds.
-
(6) Condition (iii) holds for G.
Let
![]() $E=RQ$
. If E is nilpotent, then
$E=RQ$
. If E is nilpotent, then
![]() $E < G$
and
$E < G$
and
![]() $G/C_{G}(R)$
is an r-group by (4), so
$G/C_{G}(R)$
is an r-group by (4), so
![]() $R\leq Z=Z_{\infty }(G)\cap D$
by [Reference Weinstein18, Appendixes, Theorem 6.3] and this contradicts the hypothesis. Therefore, E is not nilpotent, so
$R\leq Z=Z_{\infty }(G)\cap D$
by [Reference Weinstein18, Appendixes, Theorem 6.3] and this contradicts the hypothesis. Therefore, E is not nilpotent, so
![]() $E^{\mathfrak {N}}=R$
by (1). Finally, if
$E^{\mathfrak {N}}=R$
by (1). Finally, if
![]() $E=G$
, then
$E=G$
, then
![]() $R=D=E^{{\mathfrak {N}}}$
by (4). Hence, Condition (a) holds.
$R=D=E^{{\mathfrak {N}}}$
by (4). Hence, Condition (a) holds.
Now, let
![]() $H/K$
be any chief factor of G between Z and
$H/K$
be any chief factor of G between Z and
![]() $D_{r}$
. First we show that
$D_{r}$
. First we show that
![]() $C_{G}(H/K)=F(G)=D\langle x^{q} \rangle $
. By [Reference Doerk and Hawkes5, Ch. A, Theorem 13.8(b)], we have
$C_{G}(H/K)=F(G)=D\langle x^{q} \rangle $
. By [Reference Doerk and Hawkes5, Ch. A, Theorem 13.8(b)], we have
![]() $F(G)\leq C_{G}(H/K)$
. Assume that
$F(G)\leq C_{G}(H/K)$
. Assume that
![]() $F(G) < C_{G}(H/K)$
. Then
$F(G) < C_{G}(H/K)$
. Then
![]() $C_{G}(H/K)=G,$
so
$C_{G}(H/K)=G,$
so
![]() $Q\leq C_{G}(H/K)$
. Let
$Q\leq C_{G}(H/K)$
. Let
![]() $E=HQ$
. Then
$E=HQ$
. Then
![]() $H=E^{\mathfrak {N}}$
by (a), so
$H=E^{\mathfrak {N}}$
by (a), so
![]() $E/K$
is not nilpotent. However,
$E/K$
is not nilpotent. However,
![]() $Q\leq C_{G}(H/K)$
, so
$Q\leq C_{G}(H/K)$
, so
![]() $QK/K\leq C_{E/K}(H/K)$
and then
$QK/K\leq C_{E/K}(H/K)$
and then
![]() $E/K=(H/K)\times (QK/K)$
is nilpotent, and this contradicts the hypothesis. Hence,
$E/K=(H/K)\times (QK/K)$
is nilpotent, and this contradicts the hypothesis. Hence,
![]() $C_{G}(H/K)=F(G)=D\langle x^{q} \rangle $
.
$C_{G}(H/K)=F(G)=D\langle x^{q} \rangle $
.
From
![]() $G=D\rtimes Q$
, it follows that for every element
$G=D\rtimes Q$
, it follows that for every element
![]() $g\in G$
, we have
$g\in G$
, we have
![]() $g=dy$
for some
$g=dy$
for some
![]() $d\in D$
and
$d\in D$
and
![]() $y\in Q$
, where
$y\in Q$
, where
![]() $d\in C_{G}(H/K)$
, so
$d\in C_{G}(H/K)$
, so
![]() $(hK)^{g}=(hK)^{y}$
. Hence, Q acts irreducibly on
$(hK)^{g}=(hK)^{y}$
. Hence, Q acts irreducibly on
![]() $H/K$
. Therefore,
$H/K$
. Therefore,
![]() $Q/C_{Q}(H/K)=Q/\langle x^{q} \rangle $
is an abelian irreducible automorphim group for
$Q/C_{Q}(H/K)=Q/\langle x^{q} \rangle $
is an abelian irreducible automorphim group for
![]() $H/K$
. Hence,
$H/K$
. Hence,
![]() $|H/K|=r^{n}$
, where n is the smallest integer such that q divides
$|H/K|=r^{n}$
, where n is the smallest integer such that q divides
![]() $r^{n}-1$
by Lemma 2.3. Therefore, Condition (b) holds. Therefore, Condition (iii) holds for G.
$r^{n}-1$
by Lemma 2.3. Therefore, Condition (b) holds. Therefore, Condition (iii) holds for G.
-
(7) Condition (iv) holds for G.
Let
![]() $N=N_{G}(Q)$
and
$N=N_{G}(Q)$
and
![]() $D_{0}=D\cap N$
. Then
$D_{0}=D\cap N$
. Then
![]() $N=N\cap DQ=(N\cap D)Q= D_{0}\times Q $
is nilpotent. However,
$N=N\cap DQ=(N\cap D)Q= D_{0}\times Q $
is nilpotent. However,
Hence,
![]() $D_{0}Q$
is a Carter subgroup of G. In view of (4),
$D_{0}Q$
is a Carter subgroup of G. In view of (4),
![]() $N=D_{0}Q$
is a system normaliser of G. Hence, N covers all central chief factors of G and N avoids all noncentral chief factors of G by [Reference Doerk and Hawkes5, I, Theorem 5.6]. Therefore,
$N=D_{0}Q$
is a system normaliser of G. Hence, N covers all central chief factors of G and N avoids all noncentral chief factors of G by [Reference Doerk and Hawkes5, I, Theorem 5.6]. Therefore,
![]() $|N|$
is the product of the orders of all central factors of a chief series of G by [Reference Doerk and Hawkes5, I, Theorem 5.7]. In view of (5) and (6), the product of the orders of all central factors of a chief series of G is
$|N|$
is the product of the orders of all central factors of a chief series of G by [Reference Doerk and Hawkes5, I, Theorem 5.7]. In view of (5) and (6), the product of the orders of all central factors of a chief series of G is
![]() $|Z||Q|$
. However,
$|Z||Q|$
. However,
![]() $ZQ\leq N$
, so
$ZQ\leq N$
, so
![]() $Z\times Q= D_{0}\times Q$
and hence
$Z\times Q= D_{0}\times Q$
and hence
![]() $Z=D_{0}$
. Therefore,
$Z=D_{0}$
. Therefore,
![]() $ZQ=N_{G}(Q)$
is a Carter subgroup of G and the set of all Carter subgroups of G coincides with the set of all its system normalisers since in a soluble group, every two Carter subgroups and every two system normalisers are conjugate.
$ZQ=N_{G}(Q)$
is a Carter subgroup of G and the set of all Carter subgroups of G coincides with the set of all its system normalisers since in a soluble group, every two Carter subgroups and every two system normalisers are conjugate.
Now, let C be any Carter subgroup of G. Then
![]() $C=(ZQ)^{a}=ZQ^{a}$
for some
$C=(ZQ)^{a}=ZQ^{a}$
for some
![]() $a\in G$
since any two Carter subgroups of a soluble group are conjugate. Let
$a\in G$
since any two Carter subgroups of a soluble group are conjugate. Let
![]() $N/Z$
be a chief factor of G, where
$N/Z$
be a chief factor of G, where
![]() $N\leq D_{r}$
. Then
$N\leq D_{r}$
. Then
![]() $NQ^{a}$
is not nilpotent by (4). Hence, this subgroup contains a Schmidt subgroup H. Moreover,
$NQ^{a}$
is not nilpotent by (4). Hence, this subgroup contains a Schmidt subgroup H. Moreover,
![]() $Z\leq H$
by Lemma 2.2 since H is abnormal in G by hypothesis. Also we have
$Z\leq H$
by Lemma 2.2 since H is abnormal in G by hypothesis. Also we have
![]() $Q^{b}\leq H$
for some
$Q^{b}\leq H$
for some
![]() $b\in G$
since every subgroup of G not containing a conjugate of Q is nilpotent by (6). Therefore, H contains a Carter subgroup
$b\in G$
since every subgroup of G not containing a conjugate of Q is nilpotent by (6). Therefore, H contains a Carter subgroup
![]() $ZQ^{b}=(ZQ)^{b}$
and so C is contained in some conjugate
$ZQ^{b}=(ZQ)^{b}$
and so C is contained in some conjugate
![]() $H^{y}$
of H. Hence, C is a maximal abnormal subgroup of
$H^{y}$
of H. Hence, C is a maximal abnormal subgroup of
![]() $H^{y}$
since
$H^{y}$
since
![]() $H^{y}$
is not nilpotent but each of its maximal subgroups is nilpotent. Similarly, it can be proved that if H is a Schmidt subgroup of G, then each maximal abnormal subgroup of H is a Carter subgroup of G. Hence, we have (7).
$H^{y}$
is not nilpotent but each of its maximal subgroups is nilpotent. Similarly, it can be proved that if H is a Schmidt subgroup of G, then each maximal abnormal subgroup of H is a Carter subgroup of G. Hence, we have (7).
From (3)–(7), it follows that Conditions (i), (ii), (iii) and (iv) hold for G, contrary to the choice of G. This contradiction completes the proof of the necessity of the condition of the theorem.
Conversely, assume that Conditions (i), (ii), (iii) and (iv) hold for G. Then G is a nonnilpotent soluble group. Let H be any Schmidt subgroup of G. Then for some Carter subgroup C of G, we have
![]() $C\leq H$
by Condition (iv), so H is abnormal in G by Lemma 2.1 since every Carter subgroup of G is abnormal by [Reference Huppert10, VI, Satz 12.2(c)]. Therefore, every Schmidt subgroup of G is abnormal in G.
$C\leq H$
by Condition (iv), so H is abnormal in G by Lemma 2.1 since every Carter subgroup of G is abnormal by [Reference Huppert10, VI, Satz 12.2(c)]. Therefore, every Schmidt subgroup of G is abnormal in G.
The theorem is proved.
3 Proof of Theorem 1.2
The following lemma can be proved similarly to Lemma 6.3 in [Reference Huppert10, VI].
Lemma 3.1. Let p be a prime and
![]() $K\leq H$
normal subgroups of G, where
$K\leq H$
normal subgroups of G, where
![]() $K\leq \Phi (G)$
. If
$K\leq \Phi (G)$
. If
![]() $H/K$
is p-closed, then H is p-closed.
$H/K$
is p-closed, then H is p-closed.
Proof of Theorem 1.2
Assume that this theorem is false and let G be a counterexample of minimal order.
-
(1) If
 $L\trianglelefteq T\leq G$
, where
$L\trianglelefteq T\leq G$
, where
 $T/L$
is nonsoluble and either
$T/L$
is nonsoluble and either
 $L\ne 1$
or
$L\ne 1$
or
 $T\ne G$
, then Conditions (i) and (ii) hold for
$T\ne G$
, then Conditions (i) and (ii) hold for
 $T/L$
.
$T/L$
.
Since every Schmidt subgroup of
![]() $T/L$
is abnormal in
$T/L$
is abnormal in
![]() $T/L$
(see (1) in the proof of Theorem 1.1), this follows from the choice of G.
$T/L$
(see (1) in the proof of Theorem 1.1), this follows from the choice of G.
-
(2) If
 $H/K$
is a nonabelian chief factor of G such that K is soluble, then
$H/K$
is a nonabelian chief factor of G such that K is soluble, then
 $H/K=G/K$
is a nonabelian simple group and K is the soluble radical of G (that is, every normal soluble subgroup of G is contained in K). Hence,
$H/K=G/K$
is a nonabelian simple group and K is the soluble radical of G (that is, every normal soluble subgroup of G is contained in K). Hence,
 $G'=G$
and a Sylow
$G'=G$
and a Sylow
 $2$
-subgroup
$2$
-subgroup
 $G_{2}$
of G is not cyclic.
$G_{2}$
of G is not cyclic.
Let
![]() $L/K$
be a minimal normal subgroup of
$L/K$
be a minimal normal subgroup of
![]() $H/K$
. Then
$H/K$
. Then
![]() $L/K$
is a nonabelian simple group. Let A be a Schmidt subgroup of L. Then A is abnormal in G, so
$L/K$
is a nonabelian simple group. Let A be a Schmidt subgroup of L. Then A is abnormal in G, so
![]() $L=H=G$
. Hence,
$L=H=G$
. Hence,
![]() $G/K$
is a nonabelian simple group. Assume that
$G/K$
is a nonabelian simple group. Assume that
![]() $G' < G$
. Then
$G' < G$
. Then
![]() $G'K=G$
, hence
$G'K=G$
, hence
![]() $G'/(G'\cap K)\simeq G/K$
is a nonabelian chief factor of G such that
$G'/(G'\cap K)\simeq G/K$
is a nonabelian chief factor of G such that
![]() $G'\cap K$
is soluble and so
$G'\cap K$
is soluble and so
![]() $G'=G$
, and this contradicts the hypothesis. Hence,
$G'=G$
, and this contradicts the hypothesis. Hence,
![]() $G' = G$
, so
$G' = G$
, so
![]() $G_{2}$
is not cyclic by [Reference Huppert10, IV, Satz 2.8].
$G_{2}$
is not cyclic by [Reference Huppert10, IV, Satz 2.8].
-
(3) K is nilpotent.
Assume that this is false and let R be a minimal normal subgroup of G contained in K. Then
![]() $R\leq O_{p}(G)$
for some prime p since K is soluble. Moreover,
$R\leq O_{p}(G)$
for some prime p since K is soluble. Moreover,
![]() $G/R$
is quasisimple by (1), where
$G/R$
is quasisimple by (1), where
![]() $(G/R)/(K/R)\simeq G/K$
, so
$(G/R)/(K/R)\simeq G/K$
, so
![]() $K/R\leq Z(G/R)$
and hence
$K/R\leq Z(G/R)$
and hence
![]() $K/R$
is nilpotent. If G has a minimal normal subgroup
$K/R$
is nilpotent. If G has a minimal normal subgroup
![]() $N\ne R$
, then
$N\ne R$
, then
![]() $K/1=K/(R\cap N)$
is nilpotent. Hence, R is the unique minimal normal subgroup of G and, by Lemma 3.1,
$K/1=K/(R\cap N)$
is nilpotent. Hence, R is the unique minimal normal subgroup of G and, by Lemma 3.1,
![]() $R\nleq \Phi (G)$
since K is not nilpotent. Let M be a maximal subgroup of G such that
$R\nleq \Phi (G)$
since K is not nilpotent. Let M be a maximal subgroup of G such that
![]() $G=RM$
. Then M is not nilpotent since
$G=RM$
. Then M is not nilpotent since
![]() $G'=G$
and
$G'=G$
and
![]() $R\cap M=1=C_{G}(R)\cap M$
since both these intersections are normal in G, so
$R\cap M=1=C_{G}(R)\cap M$
since both these intersections are normal in G, so
![]() $C_{G}(R)=R(C_{G}(R)\cap M)=R$
and so
$C_{G}(R)=R(C_{G}(R)\cap M)=R$
and so
![]() $|O_{p}(G/R)|=1=|O_{p}(M)|$
by [Reference Doerk and Hawkes5, Ch. A, Lemma 13.6(b)]. It follows that for some prime
$|O_{p}(G/R)|=1=|O_{p}(M)|$
by [Reference Doerk and Hawkes5, Ch. A, Lemma 13.6(b)]. It follows that for some prime
![]() $q\ne p$
, the group M is not q-nilpotent and hence M possesses a q-closed Schmidt subgroup A of the form
$q\ne p$
, the group M is not q-nilpotent and hence M possesses a q-closed Schmidt subgroup A of the form
![]() $A=A_{q}\rtimes A_{r}$
for some prime
$A=A_{q}\rtimes A_{r}$
for some prime
![]() $r\ne q$
by [Reference Huppert10, IV, Satz 5.4]. Let
$r\ne q$
by [Reference Huppert10, IV, Satz 5.4]. Let
![]() $E=RA$
. Then E is a soluble nonnilpotent group with abnormal Schmidt subgroups by Lemma 2.1. Therefore, from Theorem 1.1, it follows that
$E=RA$
. Then E is a soluble nonnilpotent group with abnormal Schmidt subgroups by Lemma 2.1. Therefore, from Theorem 1.1, it follows that
![]() $E=D\rtimes V$
, where
$E=D\rtimes V$
, where
![]() $D=E^{\mathfrak {N}}$
is a nilpotent Hall subgroup of E and V is a cyclic Sylow t-subgroup of E for some prime
$D=E^{\mathfrak {N}}$
is a nilpotent Hall subgroup of E and V is a cyclic Sylow t-subgroup of E for some prime
![]() $t\in \{p, q, r\}$
. However,
$t\in \{p, q, r\}$
. However,
![]() $E/RA_{q}$
is nilpotent, so
$E/RA_{q}$
is nilpotent, so
![]() $D= RA_{q}$
and
$D= RA_{q}$
and
![]() $V\simeq A_{r}$
. Therefore,
$V\simeq A_{r}$
. Therefore,
![]() $ A_{q}\leq C_{G}(R)=R$
. This contradiction completes the proof of (3).
$ A_{q}\leq C_{G}(R)=R$
. This contradiction completes the proof of (3).
-
(4) G has a p-closed Schmidt subgroup
 $A=A_{p}\rtimes A_{q}$
, where
$A=A_{p}\rtimes A_{q}$
, where
 $p\in \pi (A)$
, for every prime p dividing
$p\in \pi (A)$
, for every prime p dividing
 $|G/K|$
.
$|G/K|$
.
From (2), it follows that
![]() $G/K$
is not p-nilpotent, so some subgroup
$G/K$
is not p-nilpotent, so some subgroup
![]() $E/K$
of
$E/K$
of
![]() $G/K$
is a p-closed Schmidt group with
$G/K$
is a p-closed Schmidt group with
![]() $\pi (E/K)=\{p, q\}$
. Let U be a minimal supplement to K in E. Then
$\pi (E/K)=\{p, q\}$
. Let U be a minimal supplement to K in E. Then
![]() $U\cap K\leq \Phi (U)$
, so U is a p-closed nonnilpotent group by Lemma 3.1 with
$U\cap K\leq \Phi (U)$
, so U is a p-closed nonnilpotent group by Lemma 3.1 with
![]() $\pi (U)=\{p, q\}$
. Then U has a p-closed Schmidt subgroup A with
$\pi (U)=\{p, q\}$
. Then U has a p-closed Schmidt subgroup A with
![]() $p\in \pi (A)$
.
$p\in \pi (A)$
.
-
(5)
 $K\leq Z_{\infty }(G)$
.
$K\leq Z_{\infty }(G)$
.
Assume that
![]() $K\nleq Z_{\infty }(G)$
and let
$K\nleq Z_{\infty }(G)$
and let
![]() $C=C_{G}(K)$
. Then
$C=C_{G}(K)$
. Then
![]() $C\ne G$
. If
$C\ne G$
. If
![]() $C\nleq K$
, then
$C\nleq K$
, then
![]() $G=KC$
by (2) and so from the isomorphism
$G=KC$
by (2) and so from the isomorphism
![]() $G/K\simeq C/(C\cap K)$
and (2), it follows that
$G/K\simeq C/(C\cap K)$
and (2), it follows that
![]() $C=G$
and this contradicts the hypothesis. Hence,
$C=G$
and this contradicts the hypothesis. Hence,
![]() $C\leq K$
.
$C\leq K$
.
Let V be the Hall
![]() $2'$
-subgroup of K. The subgroup V is characteristic in K, so it is normal in G. Assume that
$2'$
-subgroup of K. The subgroup V is characteristic in K, so it is normal in G. Assume that
![]() $V\nleq Z_{\infty }(G)$
. Then
$V\nleq Z_{\infty }(G)$
. Then
![]() $V\ne 1$
, so
$V\ne 1$
, so
![]() $K/V\leq Z(G/V)$
by (1) and (2). If
$K/V\leq Z(G/V)$
by (1) and (2). If
![]() $G_{2}V$
is nilpotent, then
$G_{2}V$
is nilpotent, then
![]() $G_{2}\leq C_{G}(V)$
. Since
$G_{2}\leq C_{G}(V)$
. Since
![]() $G/K$
is a nonabelian simple group,
$G/K$
is a nonabelian simple group,
![]() $G_{2}\nleq K$
by the Feit–Thompson theorem. Hence,
$G_{2}\nleq K$
by the Feit–Thompson theorem. Hence,
![]() $C_{G}(V)\nleq K$
, which implies that
$C_{G}(V)\nleq K$
, which implies that
![]() $G=C_{G}(V)K$
and so
$G=C_{G}(V)K$
and so
![]() $G=C_{G}(V)$
by (2). Therefore,
$G=C_{G}(V)$
by (2). Therefore,
![]() $V\leq Z(G)$
and this contradicts the hypothesis. Hence,
$V\leq Z(G)$
and this contradicts the hypothesis. Hence,
![]() $G_{2}V$
is a soluble nonnilpotent group and every Schmidt subgroup of
$G_{2}V$
is a soluble nonnilpotent group and every Schmidt subgroup of
![]() $G_{2}V$
is abnormal in
$G_{2}V$
is abnormal in
![]() $G_{2}V$
, so
$G_{2}V$
, so
![]() $G_{2}$
is cyclic by Theorem 1.1, contrary to (2). Therefore,
$G_{2}$
is cyclic by Theorem 1.1, contrary to (2). Therefore,
![]() $V\leq Z_{\infty }(G)$
. Since also we have
$V\leq Z_{\infty }(G)$
. Since also we have
![]() $K/V\leq Z(G/V)$
, it follows that
$K/V\leq Z(G/V)$
, it follows that
![]() $K\leq Z_{\infty }(G)$
by the Jordan–Hölder theorem for the chief series, contrary to our assumption on K. Hence,
$K\leq Z_{\infty }(G)$
by the Jordan–Hölder theorem for the chief series, contrary to our assumption on K. Hence,
![]() $K\leq G_{2}$
.
$K\leq G_{2}$
.
Finally, G has a p-closed Schmidt subgroup
![]() $A=A_{p}\rtimes A_{q}$
, where
$A=A_{p}\rtimes A_{q}$
, where
![]() $p\in \pi (A)$
, for every prime
$p\in \pi (A)$
, for every prime
![]() $p\ne 2$
dividing
$p\ne 2$
dividing
![]() $|G/K|$
by (4). Then
$|G/K|$
by (4). Then
![]() $(KA)^{^{\mathfrak {N}}}=KA_{p}=K\times A_{p}$
is nilpotent by Theorem 1.1. Therefore,
$(KA)^{^{\mathfrak {N}}}=KA_{p}=K\times A_{p}$
is nilpotent by Theorem 1.1. Therefore,
![]() $ A_{p}\leq C_{G}(K)=K$
. This contradiction completes the proof of (5).
$ A_{p}\leq C_{G}(K)=K$
. This contradiction completes the proof of (5).
-
(6) G is quasisimple. Hence,
 $K=Z(G)\leq \Phi (G)$
.
$K=Z(G)\leq \Phi (G)$
.
Since
![]() $G/C_{G}(K)$
is nilpotent by [Reference Doerk and Hawkes5, IV, Theorem 6.10] and (5),
$G/C_{G}(K)$
is nilpotent by [Reference Doerk and Hawkes5, IV, Theorem 6.10] and (5),
![]() $K=Z(G)\leq \Phi (G)$
by (2). Hence, we have (6).
$K=Z(G)\leq \Phi (G)$
by (2). Hence, we have (6).
-
(7)
 $K\leq \Phi (H)$
for every Schmidt subgroup H of G. Hence, K is a cyclic p-group for some prime p.
$K\leq \Phi (H)$
for every Schmidt subgroup H of G. Hence, K is a cyclic p-group for some prime p.
Let H be a Schmidt subgroup of G. Then
![]() $K\leq H$
by (5) and Lemma 2.2. Moreover, if V is a maximal subgroup of H, then V is nilpotent and so, in fact,
$K\leq H$
by (5) and Lemma 2.2. Moreover, if V is a maximal subgroup of H, then V is nilpotent and so, in fact,
![]() $K\leq V$
. Hence,
$K\leq V$
. Hence,
![]() $K\leq \Phi (H)$
.
$K\leq \Phi (H)$
.
Now observe that
![]() $\pi (K)\subseteq \{2, p\}$
for some prime
$\pi (K)\subseteq \{2, p\}$
for some prime
![]() $p\ne 2$
since G has a Schmidt subgroup A with
$p\ne 2$
since G has a Schmidt subgroup A with
![]() $2\in \pi (A)$
by (2) and (4). From (2) and Burnside’s
$2\in \pi (A)$
by (2) and (4). From (2) and Burnside’s
![]() $p^{a}q^{b}$
-theorem, it follows that for some prime q dividing
$p^{a}q^{b}$
-theorem, it follows that for some prime q dividing
![]() $|G/K|$
, we have
$|G/K|$
, we have
![]() $2\ne q\ne p$
. However, G has a q-closed Schmidt subgroup
$2\ne q\ne p$
. However, G has a q-closed Schmidt subgroup
![]() $A=A_{q}\rtimes A_{r}$
by (4) and we also have
$A=A_{q}\rtimes A_{r}$
by (4) and we also have
![]() $K\leq A$
. Hence,
$K\leq A$
. Hence,
![]() $K\leq A_{r}$
is a cyclic r-group and so we have (7).
$K\leq A_{r}$
is a cyclic r-group and so we have (7).
-
(8) Condition (i) holds for G.
From (6) and (7), we have
![]() $K=Z(G)\leq H$
for every Schmidt subgroup H of G. Now we show that
$K=Z(G)\leq H$
for every Schmidt subgroup H of G. Now we show that
![]() $|K|\in \{1, 2, 3, 4\}$
. Assume that
$|K|\in \{1, 2, 3, 4\}$
. Assume that
![]() $K\ne 1$
. From (6) and (7), it follows that K is cyclic and
$K\ne 1$
. From (6) and (7), it follows that K is cyclic and
![]() $|K|$
divides the order of the Schur multiplier
$|K|$
divides the order of the Schur multiplier
![]() $M(G/K)$
of
$M(G/K)$
of
![]() $G/K$
. Hence,
$G/K$
. Hence,
![]() $|K| \in \{2, 3, 4\}$
(see Section 4.15(A) in [Reference Gorenstein7, Ch. 4]).
$|K| \in \{2, 3, 4\}$
(see Section 4.15(A) in [Reference Gorenstein7, Ch. 4]).
Next assume that
![]() $H/K$
is a Schmidt subgroup of
$H/K$
is a Schmidt subgroup of
![]() $G/K$
. Then H is not nilpotent, so it has a Schmidt subgroup U and we have
$G/K$
. Then H is not nilpotent, so it has a Schmidt subgroup U and we have
![]() $K\leq U$
. Moreover,
$K\leq U$
. Moreover,
![]() $U/K$
is not nilpotent since
$U/K$
is not nilpotent since
![]() $K\leq Z(U)$
and so
$K\leq Z(U)$
and so
![]() $U=H$
since every proper subgroup of
$U=H$
since every proper subgroup of
![]() $H/K$
is nilpotent. Similarly, it can be proved that if H is a Schmidt subgroup of G, then
$H/K$
is nilpotent. Similarly, it can be proved that if H is a Schmidt subgroup of G, then
![]() $K < H$
and
$K < H$
and
![]() $H/K$
is a Schmidt subgroup of
$H/K$
is a Schmidt subgroup of
![]() $G/K$
. Therefore, (8) holds.
$G/K$
. Therefore, (8) holds.
-
(9) Condition (ii) holds for G.
This follows from Condition (i).
-
(10) Condition (iii) holds for G.
If N is soluble and N is not nilpotent, then
![]() $|N/F(N)|$
is a prime by Theorem 1.1. Finally, suppose that
$|N/F(N)|$
is a prime by Theorem 1.1. Finally, suppose that
![]() $N=N_{G}(P)$
is not soluble. Then N is a group of type (i) with
$N=N_{G}(P)$
is not soluble. Then N is a group of type (i) with
![]() $|Z(G)|\in \{2, 3, 4\}$
. Indeed, this follows from (1), if
$|Z(G)|\in \{2, 3, 4\}$
. Indeed, this follows from (1), if
![]() $N < G$
and from (8), in the case when
$N < G$
and from (8), in the case when
![]() $N=G$
.
$N=G$
.
The theorem is proved.
4 Final remarks, examples and open questions
Example 4.1.
-
(1) Let E be an extraspecial group of order
 $3^{7}$
and exponent
$3^{7}$
and exponent
 $3$
. Then
$3$
. Then
 $\text {Aut}(E)$
contains an element
$\text {Aut}(E)$
contains an element
 $\alpha $
of order
$\alpha $
of order
 $7$
which operates irreducibly on
$7$
which operates irreducibly on
 $E/Z_{E}$
and centralises
$E/Z_{E}$
and centralises
 $Z(E)$
by Lemma 20.13 in [Reference Doerk and Hawkes5, Ch. A]. Let
$Z(E)$
by Lemma 20.13 in [Reference Doerk and Hawkes5, Ch. A]. Let
 $E_{1}$
and
$E_{1}$
and
 $E_{2}$
be two copies of the group E and let
$E_{2}$
be two copies of the group E and let
 , where
, where
 $D=\{(a, a^{-1})\mid a\in Z(E)\}$
is the direct product of the groups
$D=\{(a, a^{-1})\mid a\in Z(E)\}$
is the direct product of the groups
 $E_{1}$
and
$E_{1}$
and
 $E_{2}$
with joint centre (see [Reference Huppert10, page 49]). Then
$E_{2}$
with joint centre (see [Reference Huppert10, page 49]). Then
 $\alpha $
induces an automorphism of order
$\alpha $
induces an automorphism of order
 $7$
on P and for the group
$7$
on P and for the group
 $G_{1}=P\rtimes \langle \alpha \rangle $
, all Conditions (i), (ii), (iii) and (iv) are fulfilled for
$G_{1}=P\rtimes \langle \alpha \rangle $
, all Conditions (i), (ii), (iii) and (iv) are fulfilled for
 $G_{1}$
with
$G_{1}$
with
 $Z=Z(E)$
.
$Z=Z(E)$
.Now let
 $G_{2}=C_{57}\rtimes \langle \alpha \rangle $
, where
$G_{2}=C_{57}\rtimes \langle \alpha \rangle $
, where
 $\alpha $
is an element of order
$\alpha $
is an element of order
 $7$
in
$7$
in
 $\text {Aut}(C_{57})$
. Let
$\text {Aut}(C_{57})$
. Let
 $\phi _{i}: G_{i}\to \langle \alpha \rangle $
be an epimorphism of
$\phi _{i}: G_{i}\to \langle \alpha \rangle $
be an epimorphism of
 $G_{i}$
onto
$G_{i}$
onto
 $ \langle \alpha \rangle $
and let be the direct product of the groups
$ \langle \alpha \rangle $
and let be the direct product of the groups
 $G_{1}$
and
$G_{1}$
and
 $G_{2}$
with joint factor group
$G_{2}$
with joint factor group
 $\langle \alpha \rangle $
(see [Reference Huppert10, page 50]). Then Conditions (i), (iii) and (iv) are fulfilled for G.
$\langle \alpha \rangle $
(see [Reference Huppert10, page 50]). Then Conditions (i), (iii) and (iv) are fulfilled for G.
-
(2) The alternating group
 $A_{5}$
of degree 5 is an SA-group and an SSA-group.
$A_{5}$
of degree 5 is an SA-group and an SSA-group. -
(3) It is well known that the alternating group
 $A_{13}$
possesses a Frobenius subgroup
$A_{13}$
possesses a Frobenius subgroup
 $C_{13}\rtimes C_{6}=(C_{13}\rtimes C_{3})\times C_{2}$
(see [Reference Conway, Curtis, Norton, Parker and Wilson4, page 104]), where
$C_{13}\rtimes C_{6}=(C_{13}\rtimes C_{3})\times C_{2}$
(see [Reference Conway, Curtis, Norton, Parker and Wilson4, page 104]), where
 $C_{13}\rtimes C_{3}$
is a Schmidt subgroup of
$C_{13}\rtimes C_{3}$
is a Schmidt subgroup of
 $A_{13}$
. Hence,
$A_{13}$
. Hence,
 $A_{13}$
is neither an SA-group nor an SSA-group.
$A_{13}$
is neither an SA-group nor an SSA-group.
Remark 4.2
-
(1) If G is a soluble SA-group and
 $D_{r}$
a Sylow r-subgroup of G for some prime r dividing
$D_{r}$
a Sylow r-subgroup of G for some prime r dividing
 $G^{\mathfrak {N}}$
, then (using Theorem 1.1) it can be proved by direct verification that all chief factors of G between Z and
$G^{\mathfrak {N}}$
, then (using Theorem 1.1) it can be proved by direct verification that all chief factors of G between Z and
 $D_{r}$
are G-isomorphic.
$D_{r}$
are G-isomorphic. -
(2) In fact, Theorem 1.2 reduces the problem of classification of all nonsoluble SA-groups to the classification of all nonabelian simple SA-groups.
Remark 4.2(2) is a motivation for the following natural questions.
Question 4.3. Classify all nonabelian simple
![]() $SA$
-groups.
$SA$
-groups.
Question 4.4. Classify all nonabelian simple groups in which every nonsoluble local subgroup is an SSA-group.
Question 4.5. Classify all nonabelian simple groups in which every Schmidt subgroup is self-normalising.
In Ref. [Reference Thompson16], Thompson classified nonsoluble groups all of whose local subgroups are soluble. This classical result makes it natural to ask: What is the structure of a nonsoluble group in which every nonsoluble local subgroup is quasisimple?
Acknowledgement
The authors are deeply grateful for the helpful suggestions and remarks of the referee.