Introduction
Constrictions in the solid framework of a porous material are in general points of relative weakness. Because the bonds between snow particles represent the majority of the constrictions in a snow mass, it is reasonable that the strength of snow is determined very largely by the number and size of the intergranular bonds.
Reference Ballard and McGawBallard and McGaw (1965) assume that the external stress σ on a snow mass produces a uniform stress condition in the constrictions and that failure occurs when these internal constrictions are stressed to the ultimate strength of ice, σ i. The failure surface thus generated has an effective porosity n f and the general equation for the failure strength σ f is
Considering n f to be a linear function of porosity n provided a theoretical strength envelope which agrees well with experimental data for porosities less than 50 per cent. However, a more general formulation is needed which expresses the effective porosity as a function of bulk porosity and time over the entire porosity range. It should be possible to develop such a general expression by considering the number and cross-sectional area of the intersected constrictions.
The total cross-sectional area of the constrictions intersected by a failure surface of unit area is 1−n f. The number of constrictions intersected by this unit area, designated as q, is a function of porosity, n; the cross-sectional area of each constriction, designated as A i , is a function of time t. Expressed mathematically,

The functions q(n) and A i (t) which appear in equation (2) must indeed be very complex; but the construction of hypothetical models that approximate actual conditions allows one to derive approximations to these functions, and to write a general strength equation which can be compared with experimental data.
Evaluation of the Porosity Dependence
Snow is conceived to consist of a mass of particles connected by bonds at every interparticle contact. For simplicity all constrictions are considered to originate from bonding even though a small fraction of the constrictions of a natural snow mass are intraparticulate; also, for the purpose of this discussion, it is assumed that the same general particle size distribution and shape are maintained throughout the history of the snow.
Consider a unit volume of this snow in which there is a very large number, N, of particles. Associated with these N particles is a total number of bonds, Q, and each of the Q bonds is shared by two particles. There is then a mean number of bonds, Q/N, associated with each particle. If each particle has p particles bonded to it, then the number of bonds per particle equals one half p:

Since the volume of the solid material, 1−n, in the unit volume is directly proportional to N, the dependence of Q on n may be investigated by cocin Q as N is varied. One should arrive at the same function of N regardless of whether N is continuously increased or decreased, but it is perhaps easier to visualize a hypothetical process in which N decreases. Therefore, imagine the removal of dN particles such that the number dN is small with respect to N but still represents a large number of nonadjacent particles which are uniformly distributed throughout the unit volume. If each of the dN particles has (Q/N)R bonds associated with it, then, since a bond is a junction of two particles, the removal of the dN particles removes dQ bonds, where
In an actual process where N is increasing due to consolidation the force of consolidation produces higher strain-rates in zones of relatively few constrictions; hence there is a tendency for the particles with the least number of bonds to acquire more bonds first, effecting a more uniform stress condition throughout the mass. In order to simulate this tendency to a uniform distribution of constrictions in the model it is necessary that (Q/N)R be the maximum number of bonds per particle that exist for a particular N.
The functional relationship defining (Q/N)max cannot be readily deduced; however, assuming this tendency to a uniform distribution of (Q/N) persists throughout the entire consolidation process then as n approaches zero, (Q/N)max approaches (Q/N). If N m represents the maximum number of particles that can be contained in a unit volume, it then appears reasonable to assume that in the neighborhood of N m, (Q/N)R in equation (4) may be replaced by the mean value Q/N i.e.

Integration of equation (5) from N m to N and from the corresponding Q m to Q produces Q as a function of N,

From equation (6) one has the expression relating (Q/N)max to (Q/N) and N for N close to N m, viz.

Inasmuch as (Q/N) (N m/N) deviates increasingly from (Q/N) as N decreases and satisfies equation (7) at the boundary N = N m, equation (7) will be used as an estimate of (Q/N)max for the larger range of N.
Replacing (Q/N)R in equation (4) by QN m/N 2 yields

Integration of equation (8) from Q ⋆ to Q and from N ⋆ to N yields

where N ⋆ represents the minimum number of particles necessary to produce a naturally occurring structure, and Q ⋆ is the corresponding number of bonds.
Since the particle size distribution has been specified to be invariant with n then N ∝ (1−n),

and

Figure I shows the value of (Q/N), (Q/N)max and [(Q/N max)−(Q/N)] in units of (Q ⋆/N ⋆) as a function of n according to equation (11) and (7) for n m = 0 and n ⋆ = 0.6.

Fig. 1. Mean and maximum number of bonds per particle in terms of the mean number of bonds per particle at n⋆ = 0.6
Defining N 0 as the number of particles in a unit volume at time t 0 with porosity n 0, then

From equation (10) the total number of bonds in a unit volume at time t 0 is

and the number of bonds per particle at time t 0 is

At some time t greater than t 0 with porosity n less than n 0 two groups of bonds will exist in the unit volume of snow and are designated as Q′ and Q″, such that
The first group, Q′, will be composed of all initial bonds in the unit volume (i.e. bonds which were formed at time t 0), and will include bonds which originated in the unit volume at time t 0 plus the net increase of initial bonds in the unit volume due to consolidation of the snow mass. Since Q′ is equal to the number of bonds per particle at time t 0 (equation (14)) multiplied by the number of particles in the unit volume at some subsequent time t (equation 12)), then

The second group of bonds, Q″, consists of those bonds in a unit volume at porosity n which are formed subsequent to the initial bonds at times greater than t 0 as consolidation brings the discrete particles into more intimate contact. From equations (11), (15) and (16).

Now with respect to the failure surface of unit area which intersects a total of q bonds, let q′ and q″ represent the total number of initial bonds and the total number of bonds developed after t 0 respectively which are intersected by such a failure surface. The variables q, q′ and q″ are related to Q, Q′ and Q″ respectively by a proportionality constant k, i.e.
(The factor k is related to the geometry of the system of particles and will be discussed later.)
Designating the product of the parameters k and




Equations (21) through (23) or equations (10), (16) and (17) can be used to calculate the percentages of initial bonds and subsequent bonds that exist at porosity n for a snow mass which originated at porosity n 0. Figure 2 shows the results of these calculations for different values of n 0, assuming that n m = 0.

Fig. 2. Relative number of initial and subsequent bonds at porosity n for a snow mass originating at porosity n0
Although the number of subsequent bonds may be very large they may not contribute significantly to the strength unless the time and temperature are such that the subsequent bonds are relatively well developed.
Evaluation of the Time Dependence
The function A i (t) which appears in equation (2) will now be considered. Specifically, A i is some unknown function, ψ i , of t f−t i , where t f is the time at failure and t i is the time at which the bond originated, i.e.
A considerable knowledge of this function has been gained by the work of Reference KingeryKingery (1960), Reference KuroiwaKuroiwa (1961), and Reference Hobbs and MasonHobbs and Mason (1964). The results of their experiments show that if small ice spheres are brought into contact at time zero, the ratio of the bond neck radius X and the sphere radius R at any time t may be expressed as follows:

where f(T) is some function of temperature, T, and the value of the parameter c lies in the range 4 < c < 7. This indicates that the cross-sectional area of the bond neck should vary as t 2/c . Equation (25), based upon experiments where t is small, does not explicitly show X/R approaching a limiting value for large t; however, there is some indication that X/R does actually approach a quasi limit in sintered powder compacts. According to Reference CobleCoble (1961) the initial stage of the sintering process for crystalline solids is characterized by an increase in the bond cross-sectional area from zero to approximately 0.2 of the particle cross-sectional area, at which point grain growth begins. Since the rate of bond growth is very slow after the incipience of grain growth the bond cross-sectional area which exists at the incipience of grain growth may be considered to represent a limit. In the case of snow, the end of this initial stage of sintering will be defined as the condition for complete age-hardening. The studies by Jellinek (1957), Reference Gow and RamseierGow and Ramseier (1963) and Ramseier and Sander (unpublished) on the strength of age-hardened snow show that when snow is sintered at almost constant porosity, the strength approaches a limiting value for large t, which is further indication that the interparticle contact area approaches a limit.
In order to deduce a satisfactory expression for ψ i (t f−t i ) in equation (24), the right side of equation (25) will be replaced by a function which has a limit as t becomes very large. The following function is somewhat arbitrarily chosen from a family of possible functions:

where X′/R′ is the limiting value for X/R at the completion of age hardening. X′/R′ is dependent on particle size and ω(T) is a temperature-dependent parameter. For small values of t equation (26) becomes

which is of the same form as equation (25). The function ψ i (t f−t i ) may now be written as
where A Li represents the limiting bond cross-sectional area at the termination of the initial stage of sintering and α is approximately 2/c.
The General form of (1−n f)
Now that expressions for the porosity and time function have been derived, one may write the equation for (1−n f) from equation (2).

By defining a mean limiting cross-sectional area A, equation (29) can be written, using equations (22) and (28),

where

Partitioning the interval (t o , t f) into sub-intervals and considering n (and hence q) as a function of t allows one to develop the integral expression for J,

When dn/dt is continuous, equation (31) may be rewritten as

Calculating dq″/dn from equation (23) and replacing J in equation (30) according to equation (32) produces the general expression for 1−n f

The integral in equation (33) can be evaluated numerically for any fixed t f if the parameters ω and α are accurately known and if one has a satisfactory expression for n(t).
Certain situations arise in engineering for which dn/dt in equation (33) is zero, causing the integral to vanish leaving a more easily manageable form of (1−n f).
Age Hardening at Constant Porosity
The time-dependent strength of reworked or processed snow is often considered to be a constant-porosity phenomenon. Specifically, dn/dt in equation (33) is zero, n = n 0, and t 0 = 0. The strength relationship from equation (1) becomes

Choosing the value of σ i to be that of fine-grained polycrystalline bubble-free ice requires that n m = 0. It should be noted that ai can correspond to any fine-grained polycrystalline ice with uniformly distributed voids if n m is chosen accordingly. The boundary condition σ f = σ i at t→∞ and n→0 requires that
and

Equation (36) was compared with data of Reference JellinekJellinek (1959) (Fig. 3), and Reference ButkovichButkovich (1962) (Fig. 4), by using the linearized form
where

Fig. 3. Comparison of theoretical relationship


Fig. 4. Comparison of theoretical relationship

A least squares analysis of Jellinek’s data for a series of values of ω produced a maximum coefficient of correlation for ω = 0.001, and predicted the values of α = 0.22 and σ i = 55 kg./cm2. Using these values of the parameters, equation (36) predicts the ultimate strength of this snow to be 14.5 kg./cm2, and 95 per cent of this strength should be reached after 45 days of age hardening at −10° C.
A similar analysis of Butkovich’s data required ω = 0.0002 and predicted values of α = 0.26 and σ i = 88 kg./cm2. The predicted ultimate strength of this snow is 16.4 kg./cm2 and 95 per cent of this value should be reached after 8 months of age hardening at −20° C.
The Strength Envelope
Since the conditions for fully age-hardened snow are t→∞ and dn/dt = 0, then from equation (36) the maximum strength at any porosity is

The theoretical relative strength envelope

is shown in Figure 5. For comparison the relative strength envelope of Reference Mellor and SmithMellor and Smith (unpublished)


Fig. 5. Comparison of theoretical relative strength envelope



and the linear relative strength envelope of Reference Ballard and McGawBallard and McGaw (1965)

are also shown.
The linearized form of equation (40)
where

was compared with the compressive strength data of ButkovichFootnote * Reference Butkovich(1956) (Fig. 6), by regressing σ f on X. The analysis predicted a value of σ i of 58.8 kg./cm2 for ice at −10° C.
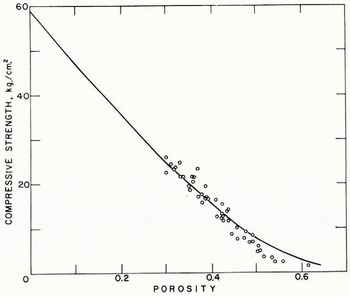
Fig. 6. Comparison of the theoretical strength envelope

Discussion of Constants
It is of interest to examine the reasonableness of equation (35) by considering the magnitude of the various constants contained in the equation. Since by definition

then equation (35) requires that

The mean limiting cross-sectional area, A, of the bonds is associated with some mean particle radius r, and according to Reference CobleCoble (1960, A ~ 0.2πr 2. k introduced in equation (18), may be considered to represent the fraction of the total bonds in a cube of unit volume intersected by a failure surface which is parallel to the face of the cube. If the failure surface does not deviate from a plane by more than r/2 then the size of the volume containing the intersected bonds is approximately r/2; hence, k ~ r/2. The porosity n ⋆ is the maximum which can be naturally obtained with granular particles such as those produced in processed snow. A reasonable value of n ⋆ is in the neighborhood of 0.6. The mean number of bonds per particle (Q⋆/N⋆) which exists at n ⋆ should be very close to 2. This would allow each particle to be touched by an average of four particles. Since N ⋆ is the number of particles that exists in a unit volume at a porosity of n ⋆ ~ 0.6, then

Using these estimated values in calculating the left side of equation (45) one has

which is approximately equal to I as required by equation (45).
Conclusion
The method used to incorporate the porosity-dependent strength of snow into the theory has resulted in a limiting strength relationship, Figure 5, which in general represents the observed strength of age-hardened snow; however, it appears from Figure 6 that this limiting curve still does not satisfactorily agree with the strength data at higher porosities. Since Butkovich used samples from a naturally consolidating snow mass, the higher porosity samples selected from shallow depths where dn/dt is relatively large may not represent an age-hardened snow because of the presence of a significant number of incomplete bonds. On the other hand, it is quite possible that the assumed distribution of the maximum number of bonds per particle made in equation (7) is not valid for this higher porosity range.
Analysis of strength data for age-hardening at constant porosity predicted values of the parameter α which result in values of c > 7 in the ice sphere sintering equation. This may be an indication that the phenomenon of bond growth for an aggregation of irregularly shaped ice particles, such as is visualized for snow, cannot be satisfactorily idealized by the sintering equation for a pair of perfect spheres.
The assumption of uniform stress distribution in the constricted areas of an externally stressed snow mass may be a fallacious one. Indeed, if significant stress concentration can develop just prior to failure, then the magnitudes of these concentrated stresses will be greatly affected by the geometry of the particles and bonds, i.e. they will be a function of porosity and time.
Comparison of the theory with experimental data has predicted values for the strength of ice which are considerably larger than the published values for ice (Reference ButkovichButkovich, 1954). At −10°C. both the porosity-dependent data of Butkovich and the time-dependent data of Jellinek predict consistent values for the strength of ice, 58 and 55 kg./cm2 respectively. That snow should predict a strength of ice that is greater than what direct experimentation on ice indicates is not surprising when one considers that at temperatures near the melting point the surface activity should anneal and repair to such an extent that more of the true molecular strength should be realized. The great number of individual bonds that must be broken in order for the mass to fail precludes the possibility of one surface flaw precipitating failure.