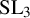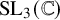1. Introduction
For a finitely generated group
![]() $\Gamma $
and a suitable Lie group G, a primary object of study in low-dimensional geometry and topology is the character variety
$\Gamma $
and a suitable Lie group G, a primary object of study in low-dimensional geometry and topology is the character variety
consisting of group homomorphisms
![]() $\rho $
from
$\rho $
from
![]() $\Gamma $
to G, considered up to conjugation. Here, the quotient is taken in the algebraic geometric sense of geometric invariant theory [Reference Mumford, Fogarty and KirwanMFK94]. Character varieties can be explored using a wide variety of mathematical skill sets. Some examples include the Higgs bundle approach of Hitchin [Reference HitchinHit92], the dynamics approach of Labourie [Reference LabourieLab06] and the representation theory approach of Fock–Goncharov [Reference Fock and GoncharovFG06].
$\Gamma $
to G, considered up to conjugation. Here, the quotient is taken in the algebraic geometric sense of geometric invariant theory [Reference Mumford, Fogarty and KirwanMFK94]. Character varieties can be explored using a wide variety of mathematical skill sets. Some examples include the Higgs bundle approach of Hitchin [Reference HitchinHit92], the dynamics approach of Labourie [Reference LabourieLab06] and the representation theory approach of Fock–Goncharov [Reference Fock and GoncharovFG06].
We are interested in the case where the group G is the special linear group
![]() $\mathrm {SL}_n(\mathbb {C})$
. Adopting the viewpoint of algebraic geometry, one can study the
$\mathrm {SL}_n(\mathbb {C})$
. Adopting the viewpoint of algebraic geometry, one can study the
![]() $\mathrm {SL}_n(\mathbb {C})$
-character variety
$\mathrm {SL}_n(\mathbb {C})$
-character variety
![]() $\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma )$
by means of its commutative algebra of regular functions
$\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma )$
by means of its commutative algebra of regular functions
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma )]$
. An example of a regular function is the trace function
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma )]$
. An example of a regular function is the trace function
![]() $\mathrm {Tr}_\gamma : \mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma ) \to \mathbb {C}$
associated to an element
$\mathrm {Tr}_\gamma : \mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma ) \to \mathbb {C}$
associated to an element
![]() $\gamma \in \Gamma $
, sending a representation
$\gamma \in \Gamma $
, sending a representation
![]() $\rho $
to the trace
$\rho $
to the trace
![]() $\mathrm {Tr}(\rho (\gamma )) \in \mathbb {C}$
of the matrix
$\mathrm {Tr}(\rho (\gamma )) \in \mathbb {C}$
of the matrix
![]() $\rho (\gamma ) \in \mathrm {SL}_n(\mathbb {C})$
. A theorem of Procesi [Reference ProcesiPro76] implies that the trace functions
$\rho (\gamma ) \in \mathrm {SL}_n(\mathbb {C})$
. A theorem of Procesi [Reference ProcesiPro76] implies that the trace functions
![]() $\mathrm {Tr}_\gamma $
generate the algebra of functions
$\mathrm {Tr}_\gamma $
generate the algebra of functions
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma )]$
as an algebra and also identifies all of the relations.
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\Gamma )]$
as an algebra and also identifies all of the relations.
Sikora [Reference SikoraSik01] provided a more refined description of Procesi’s result in the case where
![]() $\Gamma = \pi _1(\mathfrak {X})$
is the fundamental group of a topological space
$\Gamma = \pi _1(\mathfrak {X})$
is the fundamental group of a topological space
![]() $\mathfrak {X}$
; see also the earlier work of Bullock [Reference BullockBul97] for the case
$\mathfrak {X}$
; see also the earlier work of Bullock [Reference BullockBul97] for the case
![]() $G=\mathrm {SL}_2(\mathbb {C})$
. Sikora extended the notion of a trace function to include functions
$G=\mathrm {SL}_2(\mathbb {C})$
. Sikora extended the notion of a trace function to include functions
![]() $\mathrm {Tr}_W \in \mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\mathfrak {X})]$
on the character variety
$\mathrm {Tr}_W \in \mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\mathfrak {X})]$
on the character variety
![]() $\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\mathfrak {X}) := \mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\pi _1(\mathfrak {X}))$
that are associated to homotopy classes of certain (ciliated) oriented n-valent graphs W, called webs, in the space
$\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\mathfrak {X}) := \mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\pi _1(\mathfrak {X}))$
that are associated to homotopy classes of certain (ciliated) oriented n-valent graphs W, called webs, in the space
![]() $\mathfrak {X}$
. The trace functions
$\mathfrak {X}$
. The trace functions
![]() $\mathrm {Tr}_W$
span the algebra of functions
$\mathrm {Tr}_W$
span the algebra of functions
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\mathfrak {X})]$
as a vector space, and the relations are described pictorially in terms of the associated graphs.
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\mathfrak {X})]$
as a vector space, and the relations are described pictorially in terms of the associated graphs.
In this article, we restrict attention to the case where the Lie group is
![]() $\mathrm {SL}_3(\mathbb {C})$
and the space
$\mathrm {SL}_3(\mathbb {C})$
and the space
![]() $\mathfrak {X}=\mathfrak {S}$
is a punctured finite-type surface. Sikora–Westbury [Reference Sikora and WestburySW07] proved that the collection of trace functions
$\mathfrak {X}=\mathfrak {S}$
is a punctured finite-type surface. Sikora–Westbury [Reference Sikora and WestburySW07] proved that the collection of trace functions
![]() $\mathrm {Tr}_W$
associated to nonelliptic webs W, which are certain webs embedded in the surface
$\mathrm {Tr}_W$
associated to nonelliptic webs W, which are certain webs embedded in the surface
![]() $\mathfrak {S} $
, forms a linear basis for the algebra of functions
$\mathfrak {S} $
, forms a linear basis for the algebra of functions
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})]$
.
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})]$
.
An analogous result [Reference Hoste and PrzytyckiHP93] in the case of
![]() $\mathrm {SL}_2(\mathbb {C})$
says that the collection of trace functions
$\mathrm {SL}_2(\mathbb {C})$
says that the collection of trace functions
![]() $\mathrm {Tr}_\gamma $
associated to essential multicurves
$\mathrm {Tr}_\gamma $
associated to essential multicurves
![]() $\gamma $
embedded in the surface
$\gamma $
embedded in the surface
![]() $\mathfrak {S} $
forms a linear basis for the algebra of functions
$\mathfrak {S} $
forms a linear basis for the algebra of functions
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_2(\mathbb {C})}(\mathfrak {S})]$
. A well-known topological-combinatorial fact says that if the punctured surface
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_2(\mathbb {C})}(\mathfrak {S})]$
. A well-known topological-combinatorial fact says that if the punctured surface
![]() $\mathfrak {S}$
is equipped with an ideal triangulation
$\mathfrak {S}$
is equipped with an ideal triangulation
![]() $\lambda $
, then the geometric intersection numbers
$\lambda $
, then the geometric intersection numbers
![]() $\iota (\gamma , E)$
of a curve
$\iota (\gamma , E)$
of a curve
![]() $\gamma $
with the edges E of
$\gamma $
with the edges E of
![]() $\lambda $
furnish an explicit system of nonnegative integer coordinates on the collection of essential multicurves
$\lambda $
furnish an explicit system of nonnegative integer coordinates on the collection of essential multicurves
![]() $\gamma $
. These coordinates can be characterized by finitely many triangle inequalities and parity conditions.
$\gamma $
. These coordinates can be characterized by finitely many triangle inequalities and parity conditions.
The present work is part of a series of two papers, whose goal is to generalize these
![]() $\mathrm {SL}_2$
-properties to the case
$\mathrm {SL}_2$
-properties to the case
![]() $n=3$
. The main result of the current paper is the following.
$n=3$
. The main result of the current paper is the following.
Theorem 1.1. For a punctured finite-type surface
![]() $\mathfrak {S}$
equipped with an ideal triangulation
$\mathfrak {S}$
equipped with an ideal triangulation
![]() $\lambda $
, the Sikora–Westbury
$\lambda $
, the Sikora–Westbury
![]() $\mathrm {SL}_3$
-web basis for the algebra of functions
$\mathrm {SL}_3$
-web basis for the algebra of functions
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})]$
admits an explicit system of nonnegative integer coordinates, which can be characterized by finitely many Knutson–Tao rhombus inequalities [Reference Knutson and TaoKT99] and modulo
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})]$
admits an explicit system of nonnegative integer coordinates, which can be characterized by finitely many Knutson–Tao rhombus inequalities [Reference Knutson and TaoKT99] and modulo
![]() $3$
congruence conditions.
$3$
congruence conditions.
In the companion article [Reference Douglas and SunDS20b], we prove that the web coordinates from Theorem 1.1 are natural with respect to the action of the mapping class group of the surface
![]() $\mathfrak {S}$
.
$\mathfrak {S}$
.
Theorem 1.2. [Reference Douglas and SunDS20b]
If another ideal triangulation
![]() $\lambda ^\prime $
of
$\lambda ^\prime $
of
![]() $\mathfrak {S}$
is chosen, then the induced coordinate transformation takes the form of a tropicalized
$\mathfrak {S}$
is chosen, then the induced coordinate transformation takes the form of a tropicalized
![]() $\mathcal {A}$
-coordinate cluster transformation (as opposed to
$\mathcal {A}$
-coordinate cluster transformation (as opposed to
![]() $\mathcal {X}$
-coordinate) in the language of Fock–Goncharov [Reference Fock and GoncharovFG06, Reference Fomin and ZelevinskyFZ02].
$\mathcal {X}$
-coordinate) in the language of Fock–Goncharov [Reference Fock and GoncharovFG06, Reference Fomin and ZelevinskyFZ02].
Strictly speaking, Theorems 1.1 and 1.2 have been stated assuming that the punctured surface
![]() $\mathfrak {S}$
has empty boundary. In §9, we give two different, but related, generalizations (Theorems 9.1 and 9.8) of Theorem 1.1 valid in the boundary setting,
$\mathfrak {S}$
has empty boundary. In §9, we give two different, but related, generalizations (Theorems 9.1 and 9.8) of Theorem 1.1 valid in the boundary setting,
![]() $\partial \mathfrak {S} \neq \varnothing $
; see also [Reference KimKim20]. There, we also provide applications to the geometry and topology of
$\partial \mathfrak {S} \neq \varnothing $
; see also [Reference KimKim20]. There, we also provide applications to the geometry and topology of
![]() $\mathrm {SL}_3(\mathbb {C})$
-character varieties, as well as to the representation theory of the Lie group
$\mathrm {SL}_3(\mathbb {C})$
-character varieties, as well as to the representation theory of the Lie group
![]() $\mathrm {SL}_3(\mathbb {C})$
. In the companion article [Reference Douglas and SunDS20b], we likewise provide a version of Theorem 1.2 valid in the boundary setting.
$\mathrm {SL}_3(\mathbb {C})$
. In the companion article [Reference Douglas and SunDS20b], we likewise provide a version of Theorem 1.2 valid in the boundary setting.
This work drew much inspiration from papers of Xie [Reference XieXie13], Kuperberg [Reference KuperbergKup96] and Goncharov–Shen [Reference Goncharov and ShenGS15].
At its heart, Theorem 1.1 simply describes how to assign tuples of numbers to pictures. We have motivated these web pictures W by their association with trace functions
![]() $\mathrm {Tr}_W$
. As such, it is desirable to tie directly the coordinates to the trace functions. Such a relationship is well known for
$\mathrm {Tr}_W$
. As such, it is desirable to tie directly the coordinates to the trace functions. Such a relationship is well known for
![]() $\mathrm {SL}_2(\mathbb {C})$
; see [Reference Fock and GoncharovFG07a], for instance. In that case, the trace functions
$\mathrm {SL}_2(\mathbb {C})$
; see [Reference Fock and GoncharovFG07a], for instance. In that case, the trace functions
![]() $\mathrm {Tr}_\gamma $
for curves
$\mathrm {Tr}_\gamma $
for curves
![]() $\gamma $
can be expressed as Laurent polynomials
$\gamma $
can be expressed as Laurent polynomials
![]() $\mathrm {Tr}_\gamma = \mathrm {Tr}_\gamma (X_i)$
in variables
$\mathrm {Tr}_\gamma = \mathrm {Tr}_\gamma (X_i)$
in variables
![]() $X_i$
where there is one variable per coordinate (that is, per edge
$X_i$
where there is one variable per coordinate (that is, per edge
![]() $E_i$
of
$E_i$
of
![]() $\lambda $
). Moreover, the coordinates of a curve
$\lambda $
). Moreover, the coordinates of a curve
![]() $\gamma $
can be read off as the exponents of the highest term of the trace polynomial
$\gamma $
can be read off as the exponents of the highest term of the trace polynomial
![]() $\mathrm {Tr}_\gamma (X_i)$
, demonstrating the tropical geometric nature of these coordinates.
$\mathrm {Tr}_\gamma (X_i)$
, demonstrating the tropical geometric nature of these coordinates.
There is a similar story for
![]() $\mathrm {SL}_3(\mathbb {C})$
and conjecturally for
$\mathrm {SL}_3(\mathbb {C})$
and conjecturally for
![]() $\mathrm {SL}_n(\mathbb {C})$
. The Fock–Goncharov theory tells us how to express the trace functions
$\mathrm {SL}_n(\mathbb {C})$
. The Fock–Goncharov theory tells us how to express the trace functions
![]() $\mathrm {Tr}_W$
for webs W as Laurent polynomials
$\mathrm {Tr}_W$
for webs W as Laurent polynomials
![]() $\mathrm {Tr}_W(X_i)$
. Here, the number of variables
$\mathrm {Tr}_W(X_i)$
. Here, the number of variables
![]() $X_i$
(called Fock–Goncharov coordinates) increases with n. In the case
$X_i$
(called Fock–Goncharov coordinates) increases with n. In the case
![]() $n=3$
, Kim [Reference KimKim20], building on [Reference DouglasDou20], showed that the tropical coordinates of Theorem 1.1 appear as the exponents of the highest term of the Fock–Goncharov trace polynomial
$n=3$
, Kim [Reference KimKim20], building on [Reference DouglasDou20], showed that the tropical coordinates of Theorem 1.1 appear as the exponents of the highest term of the Fock–Goncharov trace polynomial
![]() $\mathrm {Tr}_W(X_i)$
. This idea was Xie’s [Reference XieXie13] point of departure, and these coordinates were constructed following his lead.
$\mathrm {Tr}_W(X_i)$
. This idea was Xie’s [Reference XieXie13] point of departure, and these coordinates were constructed following his lead.
Kuperberg’s landmark paper [Reference KuperbergKup96] influenced [Reference Sikora and WestburySW07] and laid the topological foundation for the present work as well. He proved that a certain collection of web pictures drawn on an ideal polygon
![]() $\mathfrak {D}_k$
indexes a linear basis for the subspace of
$\mathfrak {D}_k$
indexes a linear basis for the subspace of
![]() $\mathrm {SL}_3(\mathbb {C})$
-invariant tensors in a k-fold tensor product of finite-dimensional irreducible representations of
$\mathrm {SL}_3(\mathbb {C})$
-invariant tensors in a k-fold tensor product of finite-dimensional irreducible representations of
![]() $\mathrm {SL}_3(\mathbb {C})$
. Along the way, he showed how the pictures for the ideal polygon
$\mathrm {SL}_3(\mathbb {C})$
. Along the way, he showed how the pictures for the ideal polygon
![]() $\mathfrak {D}_k$
can be obtained by gluing together the more basic pictures for an ideal triangle
$\mathfrak {D}_k$
can be obtained by gluing together the more basic pictures for an ideal triangle
![]() $\mathfrak {D}_3$
. We apply Kuperberg’s local pictorial ideas in order to analyze global web pictures drawn on a triangulated surface
$\mathfrak {D}_3$
. We apply Kuperberg’s local pictorial ideas in order to analyze global web pictures drawn on a triangulated surface
![]() $(\mathfrak {S}, \lambda )$
.
$(\mathfrak {S}, \lambda )$
.
Motivated by the Fock–Goncharov duality conjecture [Reference Fock and GoncharovFG06] (see also [Reference Gross, Hacking, Keel and KontsevichGHKK18, Reference Goncharov and ShenGS18]), Goncharov–Shen [Reference Goncharov and ShenGS15] developed a theory by which bases of algebras of functions on moduli spaces, defined abstractly via the geometric Satake correspondence, can be indexed by positive integral tropical points, namely the preimage points mapping to
![]() $\mathbb {Z}_{\geqslant 0}$
under a tropicalized potential function. They showed that, for an ideal triangle
$\mathbb {Z}_{\geqslant 0}$
under a tropicalized potential function. They showed that, for an ideal triangle
![]() $\mathfrak {D}_3$
equipped with a general linear symmetry group, the positive integral tropical points correspond to solutions of the Knutson–Tao rhombus inequalities. In the
$\mathfrak {D}_3$
equipped with a general linear symmetry group, the positive integral tropical points correspond to solutions of the Knutson–Tao rhombus inequalities. In the
![]() $\mathrm {SL}_3$
-setting of this article, Theorem 1.1 also makes use of these inequalities in order to assign positive integer coordinates to webs. We think of this result as a manifestation of Goncharov–Shen’s ideas about duality; see [Reference Douglas and SunDS20b] for a further discussion. (For another geometric application of the Goncharov–Shen potential function, see [Reference Huang and SunHS23].)
$\mathrm {SL}_3$
-setting of this article, Theorem 1.1 also makes use of these inequalities in order to assign positive integer coordinates to webs. We think of this result as a manifestation of Goncharov–Shen’s ideas about duality; see [Reference Douglas and SunDS20b] for a further discussion. (For another geometric application of the Goncharov–Shen potential function, see [Reference Huang and SunHS23].)
Frohman–Sikora [Reference Frohman and SikoraFS22] independently constructed coordinates for the same
![]() $\mathrm {SL}_3$
-web basis as that appearing in Theorem 1.1. While their topological strategy is the same, their coordinates are different from ours. They do not characterize by inequalities the values taken by their coordinates, and they do not address the question of naturality under changing the triangulation. Their proof is algebraic, as it uses the Sikora–Westbury theorem (discussed above) saying that the nonelliptic webs are linearly independent, which ultimately relies on the diamond lemma from noncommutative algebra. On the other hand, we give a purely topological-combinatorial proof of Theorem 1.1, which does not require using this linear independence. Moreover, we give an alternative geometric proof of this Sikora–Westbury theorem, by using Theorem 1.1 together with the
$\mathrm {SL}_3$
-web basis as that appearing in Theorem 1.1. While their topological strategy is the same, their coordinates are different from ours. They do not characterize by inequalities the values taken by their coordinates, and they do not address the question of naturality under changing the triangulation. Their proof is algebraic, as it uses the Sikora–Westbury theorem (discussed above) saying that the nonelliptic webs are linearly independent, which ultimately relies on the diamond lemma from noncommutative algebra. On the other hand, we give a purely topological-combinatorial proof of Theorem 1.1, which does not require using this linear independence. Moreover, we give an alternative geometric proof of this Sikora–Westbury theorem, by using Theorem 1.1 together with the
![]() $\mathrm {SL}_3$
-quantum trace map [Reference DouglasDou20, Reference KimKim20]. (Ishibashi–Kano [Reference Ishibashi and KanoIK22] mimicked the construction and proof strategy of Theorem 1.1 to define shearing coordinates for unbounded
$\mathrm {SL}_3$
-quantum trace map [Reference DouglasDou20, Reference KimKim20]. (Ishibashi–Kano [Reference Ishibashi and KanoIK22] mimicked the construction and proof strategy of Theorem 1.1 to define shearing coordinates for unbounded
![]() $\mathrm {SL}_3$
-laminations.)
$\mathrm {SL}_3$
-laminations.)
As another application, Kim [Reference KimKim20, Reference KimKim21] used Theorems 1.1 and 1.2 to study a classical and quantum
![]() $\mathrm {SL}_3$
-version of Fock–Goncharov duality, generalizing the
$\mathrm {SL}_3$
-version of Fock–Goncharov duality, generalizing the
![]() $\mathrm {SL}_2$
-case [Reference Fock and GoncharovFG06, Reference Allegretti and KimAK17].
$\mathrm {SL}_2$
-case [Reference Fock and GoncharovFG06, Reference Allegretti and KimAK17].
For the underlying
![]() $\mathrm {SL}_3$
-geometry, see [Reference Fock and GoncharovFG07b, Reference Casella, Tate and TillmannCTT20].
$\mathrm {SL}_3$
-geometry, see [Reference Fock and GoncharovFG07b, Reference Casella, Tate and TillmannCTT20].
We are also interested in comparing our methods to other approaches to studying webs and related objects, falling under the umbrella of so-called ‘higher laminations’. In addition to webs [Reference SikoraSik05, Reference FontaineFon12, Reference Cautis, Kamnitzer and MorrisonCKM14], this includes cluster algebras [Reference Fomin and PylyavskyyFP16, Reference Ishibashi and YuasaIY23], buildings [Reference Fontaine, Kamnitzer and KuperbergFKK13, Reference LeLe16, Reference MartoneMar19] and spectral networks [Reference Gaiotto, Moore and NeitzkeGMN13, Reference Neitzke and YanNY22].
2. Global webs
We introduce the primary topological objects of study.
2.1. Topological setting
Let
![]() $\mathfrak {S}$
be an oriented punctured surface of finite topological type, namely
$\mathfrak {S}$
be an oriented punctured surface of finite topological type, namely
![]() $\mathfrak {S}$
is diffeomorphic to the space obtained by removing a finite subset P, called the set of punctures, from a closed oriented surface
$\mathfrak {S}$
is diffeomorphic to the space obtained by removing a finite subset P, called the set of punctures, from a closed oriented surface
![]() $\overline {\mathfrak {S}}$
. In particular, note that
$\overline {\mathfrak {S}}$
. In particular, note that
![]() $\mathfrak {S}$
has empty boundary,
$\mathfrak {S}$
has empty boundary,
![]() $\partial \mathfrak {S} = \varnothing $
. We require that there is at least one puncture and that the Euler characteristic
$\partial \mathfrak {S} = \varnothing $
. We require that there is at least one puncture and that the Euler characteristic
![]() $\chi (\mathfrak {S})$
of the punctured surface
$\chi (\mathfrak {S})$
of the punctured surface
![]() $\mathfrak {S}$
is strictly less than zero,
$\mathfrak {S}$
is strictly less than zero,
![]() $\chi (\mathfrak {S}) < 0$
. These topological conditions guarantee the existence of an ideal triangulation
$\chi (\mathfrak {S}) < 0$
. These topological conditions guarantee the existence of an ideal triangulation
![]() $\lambda $
of the punctured surface
$\lambda $
of the punctured surface
![]() $\mathfrak {S}$
, namely a triangulation
$\mathfrak {S}$
, namely a triangulation
![]() $\overline {\lambda }$
of the closed surface
$\overline {\lambda }$
of the closed surface
![]() $\overline {\mathfrak {S}}$
whose vertex set is equal to the set of punctures P. See Figure 1 for some examples of ideal triangulations.
$\overline {\mathfrak {S}}$
whose vertex set is equal to the set of punctures P. See Figure 1 for some examples of ideal triangulations.

Figure 1 Ideal triangulations.
To simplify the exposition, we always assume that
![]() $\lambda $
does not contain any self-folded triangles, meaning that each triangle
$\lambda $
does not contain any self-folded triangles, meaning that each triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\lambda $
has three distinct edges. Such a
$\lambda $
has three distinct edges. Such a
![]() $\lambda $
always exists. Our results should generalize, essentially without change, to allow for self-folded triangles.
$\lambda $
always exists. Our results should generalize, essentially without change, to allow for self-folded triangles.
2.2. Webs
Definition 2.1. An immersed curve, or just curve,
![]() $\gamma $
in any surface (possibly with boundary)
$\gamma $
in any surface (possibly with boundary)
![]() $\widehat {\mathfrak {S}}$
is an immersion into
$\widehat {\mathfrak {S}}$
is an immersion into
![]() $\widehat {\mathfrak {S}}$
of the circle
$\widehat {\mathfrak {S}}$
of the circle
![]() $S^1$
or the compact interval I. In other words, a curve is either an oriented loop (that is, a closed curve) or an oriented arc, possibly with self-intersections.
$S^1$
or the compact interval I. In other words, a curve is either an oriented loop (that is, a closed curve) or an oriented arc, possibly with self-intersections.
We will often be working with embedded curves, where there are no self-intersections.
Definition 2.2. An embedded global web, or just global web or web,
![]() $W = \{ w_i \}_i$
on the surface
$W = \{ w_i \}_i$
on the surface
![]() $\mathfrak {S}$
is a finite collection of closed connected oriented trivalent (finite) graphs or closed curves
$\mathfrak {S}$
is a finite collection of closed connected oriented trivalent (finite) graphs or closed curves
![]() $w_i$
embedded in
$w_i$
embedded in
![]() $\mathfrak {S}$
such that the (images of the) components
$\mathfrak {S}$
such that the (images of the) components
![]() $w_i$
are mutually disjoint and such that each vertex of
$w_i$
are mutually disjoint and such that each vertex of
![]() $w_i$
is either a source or a sink, namely the orientations either go all in or all out, respectively. Note that the web W has empty boundary,
$w_i$
is either a source or a sink, namely the orientations either go all in or all out, respectively. Note that the web W has empty boundary,
![]() $\partial W = \varnothing $
.
$\partial W = \varnothing $
.

Figure 2 Web.
For an example, in Figure 2 we show a web on the once punctured torus, which has four components consisting of two trivalent graphs and two curves.
Definition 2.3. Two webs W and
![]() $W^\prime $
on the surface
$W^\prime $
on the surface
![]() $\mathfrak {S}$
are parallel equivalent if W can be taken to
$\mathfrak {S}$
are parallel equivalent if W can be taken to
![]() $W^\prime $
, preserving orientation, by a sequence of moves of the following two types:
$W^\prime $
, preserving orientation, by a sequence of moves of the following two types:
-
1. an isotopy of the web, namely a smoothly varying family of webs;
-
2. a global parallel-move, exchanging two loops that together form the boundary of an embedded annulus A in the surface
 $\mathfrak {S}$
; see Figure 3.
$\mathfrak {S}$
; see Figure 3.
In this case, we say that W and
![]() $W^\prime $
belong to the same parallel equivalence class
$W^\prime $
belong to the same parallel equivalence class
![]() $[W] = [W^\prime ]$
.
$[W] = [W^\prime ]$
.

Figure 3 Global parallel-move.
Intuitively, we think of parallel equivalent as meaning homotopic on the surface.
2.3. Faces
Definition 2.4. A face D of a web W on the surface
![]() $\mathfrak {S}$
is a contractible component of the complement
$\mathfrak {S}$
is a contractible component of the complement
![]() $W^c \subseteq \mathfrak {S}$
of the web. A n-face
$W^c \subseteq \mathfrak {S}$
of the web. A n-face
![]() $D_n$
is a face with n sides, counted with multiplicity. An alternative name for a zero-face
$D_n$
is a face with n sides, counted with multiplicity. An alternative name for a zero-face
![]() $D_0$
, two-face
$D_0$
, two-face
![]() $D_2$
, four-face
$D_2$
, four-face
![]() $D_4$
and six-face
$D_4$
and six-face
![]() $D_6$
is a disk-, bigon-, square- and hexagon-face, respectively.
$D_6$
is a disk-, bigon-, square- and hexagon-face, respectively.
For an example, the web shown in Figure 2 above has one disk-face, one bigon-face, two square-faces and two hexagon-faces; these faces are shaded in the figure. Notice that one of the hexagon-faces consists of five edges of the web, one edge being counted twice.
By orientation considerations, faces must have an even number of sides.
Bigon- and square-faces always consist of exactly two and four edges, respectively, of W. See Figure 4.

Figure 4 Prohibited square-face.
In figures, we often omit the web orientations, as in Figure 5.

Figure 5 Local webs.
2.4. Nonelliptic webs
Definition 2.5. A web W on the surface
![]() $\mathfrak {S}$
is called nonelliptic if it has no disk-, bigon- or square-faces. Otherwise, W is called elliptic.
$\mathfrak {S}$
is called nonelliptic if it has no disk-, bigon- or square-faces. Otherwise, W is called elliptic.
If W is nonelliptic and if
![]() $W^\prime $
is parallel equivalent to W, then
$W^\prime $
is parallel equivalent to W, then
![]() $W^\prime $
is nonelliptic. Denote the set of nonelliptic webs by
$W^\prime $
is nonelliptic. Denote the set of nonelliptic webs by
![]() $\mathscr {W}_{\mathfrak {S}}$
, and the set of parallel equivalence classes of nonelliptic webs by
$\mathscr {W}_{\mathfrak {S}}$
, and the set of parallel equivalence classes of nonelliptic webs by
![]() $[\mathscr {W}_{\mathfrak {S}}]$
. The empty web
$[\mathscr {W}_{\mathfrak {S}}]$
. The empty web
![]() $W = \varnothing $
represents a class with one element in
$W = \varnothing $
represents a class with one element in
![]() $[\mathscr {W}_{\mathfrak {S}}]$
.
$[\mathscr {W}_{\mathfrak {S}}]$
.
3. Local webs
As a technical device, we study webs-with-boundary in the disk.
3.1. Ideal polygons
For a nonnegative integer
![]() $k \geqslant 0$
, an ideal k-polygon
$k \geqslant 0$
, an ideal k-polygon
![]() $\mathfrak {D}_k$
is the surface
$\mathfrak {D}_k$
is the surface
![]() $\mathfrak {D}_0 - P$
obtained by removing k punctures
$\mathfrak {D}_0 - P$
obtained by removing k punctures
![]() $P \subseteq \partial \mathfrak {D}_0$
from the boundary of the closed disk
$P \subseteq \partial \mathfrak {D}_0$
from the boundary of the closed disk
![]() $\mathfrak {D}_0$
.
$\mathfrak {D}_0$
.
Observe that, when
![]() $k> 0$
, the boundary
$k> 0$
, the boundary
![]() $\partial \mathfrak {D}_k$
of the ideal polygon consists of k ideal arcs.
$\partial \mathfrak {D}_k$
of the ideal polygon consists of k ideal arcs.
3.2. Local webs
Recall the notion of a curve (Definition 2.1).
Definition 3.1. An embedded local web, or just local web,
![]() $W = \{ w_i \}_i$
in an ideal polygon
$W = \{ w_i \}_i$
in an ideal polygon
![]() $\mathfrak {D}_k$
is a finite collection of connected oriented trivalent graphs or curves
$\mathfrak {D}_k$
is a finite collection of connected oriented trivalent graphs or curves
![]() $w_i$
embedded in
$w_i$
embedded in
![]() $\mathfrak {D}_k$
such that the components
$\mathfrak {D}_k$
such that the components
![]() $w_i$
are mutually disjoint and such that each vertex of
$w_i$
are mutually disjoint and such that each vertex of
![]() $w_i$
is either a source or sink. Note that the local web W may have boundary, in which case we require
$w_i$
is either a source or sink. Note that the local web W may have boundary, in which case we require
![]() $\partial W = W \cap \partial \mathfrak {D}_k$
and we consider each point
$\partial W = W \cap \partial \mathfrak {D}_k$
and we consider each point
![]() $v \in \partial W$
to be a monovalent vertex.
$v \in \partial W$
to be a monovalent vertex.
For some examples of local webs, see Figure 5. There,
![]() $k=4$
.
$k=4$
.
3.3. External faces
Definition 3.2. A face D of a local web W in an ideal polygon
![]() $\mathfrak {D}_k$
(
$\mathfrak {D}_k$
(
![]() $k \geqslant 0$
) is a contractible component of the complement
$k \geqslant 0$
) is a contractible component of the complement
![]() $W^c \subseteq \mathfrak {D}_k$
of W that is puncture-free, meaning that D does not limit to any punctures
$W^c \subseteq \mathfrak {D}_k$
of W that is puncture-free, meaning that D does not limit to any punctures
![]() $p \in P$
. A n-face
$p \in P$
. A n-face
![]() $D_n$
is a face with n sides. Here, a maximal segment
$D_n$
is a face with n sides. Here, a maximal segment
![]() $\alpha \subseteq (\partial \mathfrak {D}_k) \cap D_n$
of the boundary
$\alpha \subseteq (\partial \mathfrak {D}_k) \cap D_n$
of the boundary
![]() $\partial \mathfrak {D}_k$
contained in the face
$\partial \mathfrak {D}_k$
contained in the face
![]() $D_n$
is counted as a side, called a boundary side. An external face
$D_n$
is counted as a side, called a boundary side. An external face
![]() $D^{\mathrm {ext}}$
(resp. internal face
$D^{\mathrm {ext}}$
(resp. internal face
![]() $D^{\mathrm {int}}$
) of the local web W is a face having at least one (resp. no) boundary side.
$D^{\mathrm {int}}$
) of the local web W is a face having at least one (resp. no) boundary side.
In contrast to internal faces, external faces can have an odd number of sides. An alternative name for an external two-face
![]() $D^{\mathrm {ext}}_2$
, three-face
$D^{\mathrm {ext}}_2$
, three-face
![]() $D^{\mathrm {ext}}_3$
, four-face
$D^{\mathrm {ext}}_3$
, four-face
![]() $D^{\mathrm {ext}}_4$
with one boundary side and five-face
$D^{\mathrm {ext}}_4$
with one boundary side and five-face
![]() $D^{\mathrm {ext}}_5$
with one boundary side is a cap-, fork-, H- and half-hexagon-face, respectively; see Figure 6. Also, as for global webs (see Definition 2.4), an alternative name for an internal zero-face
$D^{\mathrm {ext}}_5$
with one boundary side is a cap-, fork-, H- and half-hexagon-face, respectively; see Figure 6. Also, as for global webs (see Definition 2.4), an alternative name for an internal zero-face
![]() $D^{\mathrm {int}}_0$
, two-face
$D^{\mathrm {int}}_0$
, two-face
![]() $D^{\mathrm {int}}_2$
, four-face
$D^{\mathrm {int}}_2$
, four-face
![]() $D^{\mathrm {int}}_4$
and six-face
$D^{\mathrm {int}}_4$
and six-face
![]() $D^{\mathrm {int}}_2$
is a disk-, bigon-, square- and hexagon-face.
$D^{\mathrm {int}}_2$
is a disk-, bigon-, square- and hexagon-face.

Figure 6 Cap-, fork-, H-, external four-, and half-hexagon-face.
For example, the connected local web in Figure 5a has one fork-face, two H-faces, one half-hexagon-face, one external six-face, one bigon-face, one square-face and one internal eight-face. Also, the disconnected local web in Figure 5b has one cap-face, one fork-face, one H-face, one half-hexagon-face, one external six-face, two disk-faces, one bigon-face and one square-face.
3.4. Combinatorial identity
Proposition 3.3. (compare [Reference KuperbergKup96, §6.1])
Let W be a connected local web in the closed disk
![]() $\mathfrak {D}_0$
with nonempty boundary
$\mathfrak {D}_0$
with nonempty boundary
![]() $\partial W \neq \varnothing $
. Then,
$\partial W \neq \varnothing $
. Then,

Proof. Since W is connected, its complement
![]() $W^c \subseteq \mathfrak {D}_0$
contains at most one annulus, which faces the boundary
$W^c \subseteq \mathfrak {D}_0$
contains at most one annulus, which faces the boundary
![]() $\partial \mathfrak {D}_0$
. Such an annulus does not exist, since
$\partial \mathfrak {D}_0$
. Such an annulus does not exist, since
![]() $\partial W \neq \varnothing $
. Thus, every component D of
$\partial W \neq \varnothing $
. Thus, every component D of
![]() $W^c$
is contractible, and of course puncture-free, so D is a face.
$W^c$
is contractible, and of course puncture-free, so D is a face.
It follows that the closed disk
![]() $\mathfrak {D}_0$
can be tiled by the dual graph of W. More precisely, the vertices of the dual graph are the faces of W, and the complement of the dual graph consists of triangles. In Figure 7, we demonstrate this tiling procedure for the local web W that we saw in Figure 5a above (after forgetting the punctures).
$\mathfrak {D}_0$
can be tiled by the dual graph of W. More precisely, the vertices of the dual graph are the faces of W, and the complement of the dual graph consists of triangles. In Figure 7, we demonstrate this tiling procedure for the local web W that we saw in Figure 5a above (after forgetting the punctures).

Figure 7 Tiling the closed disk with the dual graph of a local web.
This triangular tiling gives rise to a flat Riemannian metric with conical singularities and piecewise-geodesic boundary on the closed disk
![]() $\mathfrak {D}_0$
, by requiring that each triangle is Euclidean equilateral. Apply the Gauss–Bonnet theorem to this singular flat surface.
$\mathfrak {D}_0$
, by requiring that each triangle is Euclidean equilateral. Apply the Gauss–Bonnet theorem to this singular flat surface.
3.5. Nonellipticity
Definition 3.4. As for global webs, a local web W in an ideal polygon
![]() $\mathfrak {D}_k$
is nonelliptic if W has no disk-, bigon-, or square-faces. Otherwise, W is called elliptic; see Figure 8.
$\mathfrak {D}_k$
is nonelliptic if W has no disk-, bigon-, or square-faces. Otherwise, W is called elliptic; see Figure 8.

Figure 8 Nonelliptic local webs in the closed disk.
Lemma 3.5. Let W be a nonelliptic local web in the closed disk
![]() $\mathfrak {D}_0$
such that W is connected, has nonempty boundary
$\mathfrak {D}_0$
such that W is connected, has nonempty boundary
![]() $\partial W \neq \varnothing $
and has at least one trivalent vertex. Then W has at least three fork- and/or H-faces.
$\partial W \neq \varnothing $
and has at least one trivalent vertex. Then W has at least three fork- and/or H-faces.
Proof. We apply the formula of Proposition 3.3. For each internal face
![]() $D_n^{\mathrm {int}}$
of W, the internal angle
$D_n^{\mathrm {int}}$
of W, the internal angle
![]() $2\pi - (\pi /3) n \leqslant 0$
is nonpositive since
$2\pi - (\pi /3) n \leqslant 0$
is nonpositive since
![]() $n \geqslant 6$
by nonellipticity. For each external face
$n \geqslant 6$
by nonellipticity. For each external face
![]() $D_n^{\mathrm {ext}}$
, necessarily
$D_n^{\mathrm {ext}}$
, necessarily
![]() $n \geqslant 2$
, and the external angle
$n \geqslant 2$
, and the external angle
![]() $\pi - (\pi /3)(n-2)$
is
$\pi - (\pi /3)(n-2)$
is
![]() $\leqslant 0$
is nonpositive if and only if
$\leqslant 0$
is nonpositive if and only if
![]() $n \geqslant 5$
. By hypothesis, W has no cap-faces (else W would be an arc). So, those external faces
$n \geqslant 5$
. By hypothesis, W has no cap-faces (else W would be an arc). So, those external faces
![]() $D^{\mathrm {ext}}_n$
with a positive contribution satisfy
$D^{\mathrm {ext}}_n$
with a positive contribution satisfy
![]() $n =3,4$
. The result follows since fork- and H-faces contribute
$n =3,4$
. The result follows since fork- and H-faces contribute
![]() $2 \pi /3$
and
$2 \pi /3$
and
![]() $\pi /3$
, respectively, in the formula.
$\pi /3$
, respectively, in the formula.
Lemma 3.6. Nonelliptic local webs W (
![]() $\neq \varnothing $
) in an ideal polygon
$\neq \varnothing $
) in an ideal polygon
![]() $\mathfrak {D}_k$
(
$\mathfrak {D}_k$
(
![]() $k \geqslant 0$
) having empty boundary
$k \geqslant 0$
) having empty boundary
![]() $\partial W = \varnothing $
do not exist.
$\partial W = \varnothing $
do not exist.
Proof. Suppose otherwise. We may assume W is connected. Since W is nonelliptic, W is not a loop (this uses that
![]() $\mathfrak {D}_k$
is contractible). Then, the outer rim of W forms the boundary of a smaller closed disk
$\mathfrak {D}_k$
is contractible). Then, the outer rim of W forms the boundary of a smaller closed disk
![]() $\mathfrak {D}_0^\prime \subseteq \mathfrak {D}_k$
containing a subweb
$\mathfrak {D}_0^\prime \subseteq \mathfrak {D}_k$
containing a subweb
![]() $W^\prime \subseteq W$
that has nonempty boundary
$W^\prime \subseteq W$
that has nonempty boundary
![]() $\partial W^\prime \neq \varnothing $
. By nonellipticity,
$\partial W^\prime \neq \varnothing $
. By nonellipticity,
![]() $W^\prime $
does not have a cap-face, so
$W^\prime $
does not have a cap-face, so
![]() $W^\prime $
has a trivalent vertex. Applying Lemma 3.5 to connected components of
$W^\prime $
has a trivalent vertex. Applying Lemma 3.5 to connected components of
![]() $W^\prime $
, an analysis of innermost components leads to the fact that
$W^\prime $
, an analysis of innermost components leads to the fact that
![]() $W^\prime $
has at least one fork- or H-face. By nonellipticity,
$W^\prime $
has at least one fork- or H-face. By nonellipticity,
![]() $W^\prime $
does not have an H-face, and it does not have a fork-face by orientation considerations applied to W.
$W^\prime $
does not have an H-face, and it does not have a fork-face by orientation considerations applied to W.
Lemma 3.6 plus a small argument allows us to relax the hypotheses of Lemma 3.5 as follows.
Proposition 3.7. Let W be a nonelliptic local web in the closed disk
![]() $\mathfrak {D}_0$
such that W is connected and has at least one trivalent vertex. Then W has at least three fork- and/or H-faces. If, in addition, W is assumed not to have any cap-faces, then the connectedness hypothesis above is superfluous.
$\mathfrak {D}_0$
such that W is connected and has at least one trivalent vertex. Then W has at least three fork- and/or H-faces. If, in addition, W is assumed not to have any cap-faces, then the connectedness hypothesis above is superfluous.
3.6. Essential and rungless local webs
Definition 3.8. A local web W in an ideal polygon
![]() $\mathfrak {D}_k$
(
$\mathfrak {D}_k$
(
![]() $k \geqslant 0$
) is essential if:
$k \geqslant 0$
) is essential if:
-
1. the local web W is nonelliptic;
-
2. the web W is taut: for any compact arc
 $\alpha $
embedded in
$\alpha $
embedded in
 $\mathfrak {D}_k$
whose boundary
$\mathfrak {D}_k$
whose boundary
 $\partial \alpha $
lies in a component E of the boundary
$\partial \alpha $
lies in a component E of the boundary
 $\partial \mathfrak {D}_k$
(and is disjoint from W), the number of intersection points
$\partial \mathfrak {D}_k$
(and is disjoint from W), the number of intersection points
 $\iota (W, \overline {E})$
of W with the segment
$\iota (W, \overline {E})$
of W with the segment
 $\overline {E} \subseteq E$
delimited by
$\overline {E} \subseteq E$
delimited by
 $\partial \alpha $
does not exceed the number of intersection points
$\partial \alpha $
does not exceed the number of intersection points
 $\iota (W, \alpha )$
of W with
$\iota (W, \alpha )$
of W with
 $\alpha $
, that is
$\alpha $
, that is
 $\iota (W, \overline {E}) \leqslant \iota (W, \alpha )$
; see Figures 9 and 10.
$\iota (W, \overline {E}) \leqslant \iota (W, \alpha )$
; see Figures 9 and 10.
Figure 9 Tautness condition for an essential local web.

Figure 10 More nonelliptic webs.
Note that essential local webs cannot have any cap- or fork-faces but can have H-faces. Later, we will need the operation of adding or removing an H-face, depicted in Figure 11.
Definition 3.9. A local web W in an ideal polygon
![]() $\mathfrak {D}_k$
(
$\mathfrak {D}_k$
(
![]() $k \geqslant 0$
) is rungless if it does not have any H-faces; see Figure 12.
$k \geqslant 0$
) is rungless if it does not have any H-faces; see Figure 12.
Remark 3.10.
-
1. A consequence of Proposition 3.7, which we will not use, is that (nonempty) essential local webs in the closed disk
 $\mathfrak {D}_0$
or ideal monoangle
$\mathfrak {D}_0$
or ideal monoangle
 $\mathfrak {D}_1$
do not exist.
$\mathfrak {D}_1$
do not exist. -
2. Kuperberg [Reference KuperbergKup96, §4, 6.1] says ‘(core of a) nonconvex nonelliptic web in the k-clasped web space’ for our ‘(rungless) essential local web in the ideal k-polygon’.

Figure 11 Adding or removing an H-face.

Figure 12 More essential webs.
3.7. Ladder-webs in ideal biangles
Another name for an ideal two-polygon
![]() $\mathfrak {D}_2$
is an ideal biangle or just biangle, denoted by
$\mathfrak {D}_2$
is an ideal biangle or just biangle, denoted by
![]() $\mathfrak {B}$
. The boundary
$\mathfrak {B}$
. The boundary
![]() $\partial \mathfrak {B}$
consists of two ideal arcs
$\partial \mathfrak {B}$
consists of two ideal arcs
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
, called the boundary edges of the biangle. We want to characterize essential local webs W in the biangle
$E^{\prime \prime }$
, called the boundary edges of the biangle. We want to characterize essential local webs W in the biangle
![]() $\mathfrak {B}$
; compare (1) in Remark 3.10.
$\mathfrak {B}$
; compare (1) in Remark 3.10.
Definition 3.11. For any surface
![]() $\widehat {\mathfrak {S}}$
, possibly with boundary, an immersed multicurve, or just multicurve,
$\widehat {\mathfrak {S}}$
, possibly with boundary, an immersed multicurve, or just multicurve,
![]() $\Gamma = \{ \gamma _i \}$
on
$\Gamma = \{ \gamma _i \}$
on
![]() $\widehat {\mathfrak {S}}$
is a finite collection of connected oriented curves (Definition 2.1)
$\widehat {\mathfrak {S}}$
is a finite collection of connected oriented curves (Definition 2.1)
![]() $\gamma _i$
immersed in
$\gamma _i$
immersed in
![]() $\widehat {\mathfrak {S}}$
such that
$\widehat {\mathfrak {S}}$
such that
![]() $\partial \gamma _i = \gamma _i \cap \partial \widehat {\mathfrak {S}}$
. Note that
$\partial \gamma _i = \gamma _i \cap \partial \widehat {\mathfrak {S}}$
. Note that
![]() $\gamma _i$
and
$\gamma _i$
and
![]() $\gamma _j$
might intersect in
$\gamma _j$
might intersect in
![]() $\widehat {\mathfrak {S}}$
for any i and j. Note also that a component
$\widehat {\mathfrak {S}}$
for any i and j. Note also that a component
![]() $\gamma _i$
may be either a loop or an arc.
$\gamma _i$
may be either a loop or an arc.
In the current section, components
![]() $\gamma _i$
of a multicurve
$\gamma _i$
of a multicurve
![]() $\Gamma $
will always be embedded, but different components might intersect. This will not be the case later on in §8.
$\Gamma $
will always be embedded, but different components might intersect. This will not be the case later on in §8.
A pair of arcs
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
each intersecting both boundary edges in
$\gamma _2$
each intersecting both boundary edges in
![]() $\mathfrak {B}$
are oppositely oriented if
$\mathfrak {B}$
are oppositely oriented if
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
go into (resp. out of) and out of (resp. into)
$\gamma _2$
go into (resp. out of) and out of (resp. into)
![]() $E^\prime $
, respectively. Similarly, the arcs
$E^\prime $
, respectively. Similarly, the arcs
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
are same-oriented if
$\gamma _2$
are same-oriented if
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
both go into (resp. out of)
$\gamma _2$
both go into (resp. out of)
![]() $E^\prime $
, respectively.
$E^\prime $
, respectively.
Definition 3.12. A symmetric strand-set pair
![]() $S = (S^\prime , S^{\prime \prime })$
for the biangle
$S = (S^\prime , S^{\prime \prime })$
for the biangle
![]() $\mathfrak {B}$
is a pair of finite collections
$\mathfrak {B}$
is a pair of finite collections
![]() $S = (S^\prime , S^{\prime \prime }) = ( \{s^\prime \}, \{s^{\prime \prime }\})$
of disjoint oriented strands located on the boundary
$S = (S^\prime , S^{\prime \prime }) = ( \{s^\prime \}, \{s^{\prime \prime }\})$
of disjoint oriented strands located on the boundary
![]() $\partial \mathfrak {B} = E^\prime \cup E^{\prime \prime }$
such that the strands
$\partial \mathfrak {B} = E^\prime \cup E^{\prime \prime }$
such that the strands
![]() $s^\prime $
(resp.
$s^\prime $
(resp.
![]() $s^{\prime \prime }$
) lie on the boundary edge
$s^{\prime \prime }$
) lie on the boundary edge
![]() $E^\prime $
(resp.
$E^\prime $
(resp.
![]() $E^{\prime \prime }$
) and such that the number of in-strands (resp. out-strands) on
$E^{\prime \prime }$
) and such that the number of in-strands (resp. out-strands) on
![]() $E^\prime $
is equal to the number of out-strands (resp. in-strands) on
$E^\prime $
is equal to the number of out-strands (resp. in-strands) on
![]() $E^{\prime \prime }$
; see the leftmost picture in Figure 13.
$E^{\prime \prime }$
; see the leftmost picture in Figure 13.

Figure 13 Construction of a ladder-web.
Given a symmetric strand-set pair
![]() $S = (S^\prime , S^{\prime \prime })$
, in the following definition we associate to S a multicurve in the biangle
$S = (S^\prime , S^{\prime \prime })$
, in the following definition we associate to S a multicurve in the biangle
![]() $\mathfrak {B}$
, denoted
$\mathfrak {B}$
, denoted
![]() $\left< W(S) \right>$
.
$\left< W(S) \right>$
.
Definition 3.13. The local picture
![]() $\left< W(S) \right>$
associated to a symmetric strand-set pair
$\left< W(S) \right>$
associated to a symmetric strand-set pair
![]() $S= (S^\prime , S^{\prime \prime })$
is the multicurve in the biangle
$S= (S^\prime , S^{\prime \prime })$
is the multicurve in the biangle
![]() $\mathfrak {B}$
obtained by connecting the strands on
$\mathfrak {B}$
obtained by connecting the strands on
![]() $E^\prime $
to the strands on
$E^\prime $
to the strands on
![]() $E^{\prime \prime }$
with arcs, in an order preserving and minimally intersecting way, loosely speaking, as illustrated in the middle picture in Figure 13. Here, order preserving means in a way such that no same-oriented arcs intersect.
$E^{\prime \prime }$
with arcs, in an order preserving and minimally intersecting way, loosely speaking, as illustrated in the middle picture in Figure 13. Here, order preserving means in a way such that no same-oriented arcs intersect.
Observe, in the local picture
![]() $\left< W(S) \right>$
, that
$\left< W(S) \right>$
, that
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
intersect if and only if (1) they are oppositely oriented, and (2) they intersect exactly once. We denote by
$\gamma _2$
intersect if and only if (1) they are oppositely oriented, and (2) they intersect exactly once. We denote by
![]() $\mathscr {P}(S) \subseteq \mathfrak {B}$
the set of intersection points p of pairs of oppositely oriented arcs in the local picture
$\mathscr {P}(S) \subseteq \mathfrak {B}$
the set of intersection points p of pairs of oppositely oriented arcs in the local picture
![]() $\left< W(S) \right>$
.
$\left< W(S) \right>$
.
Finally, we say how to associate a local web
![]() $W(S)$
in
$W(S)$
in
![]() $\mathfrak {B}$
to a symmetric pair
$\mathfrak {B}$
to a symmetric pair
![]() $S=(S^\prime , S^{\prime \prime })$
.
$S=(S^\prime , S^{\prime \prime })$
.
Definition 3.14. The ladder-web
![]() $W(S)$
in the biangle
$W(S)$
in the biangle
![]() $\mathfrak {B}$
obtained from a symmetric strand-set pair
$\mathfrak {B}$
obtained from a symmetric strand-set pair
![]() $S= (S^\prime , S^{\prime \prime })$
is the unique (up to ambient isotopy of
$S= (S^\prime , S^{\prime \prime })$
is the unique (up to ambient isotopy of
![]() $\mathfrak {B}$
) local web obtained by resolving each intersection point
$\mathfrak {B}$
) local web obtained by resolving each intersection point
![]() $p \in \mathscr {P}(S)$
into two vertices connected by a horizontal edge, relative to the biangle, called a rung; see Figures 13 and 14.
$p \in \mathscr {P}(S)$
into two vertices connected by a horizontal edge, relative to the biangle, called a rung; see Figures 13 and 14.

Figure 14 Replacing a local crossing with an H (also called a rung).
The following statement is implicit in [Reference KuperbergKup96, Lemma 6.7] and also appears in [Reference Frohman and SikoraFS22, §8].
Proposition 3.15. The ladder-web
![]() $W(S)$
is essential. Conversely, given an essential local web W in the biangle
$W(S)$
is essential. Conversely, given an essential local web W in the biangle
![]() $\mathfrak {B}$
, there exists a unique symmetric strand-set pair
$\mathfrak {B}$
, there exists a unique symmetric strand-set pair
![]() $S= (S^\prime , S^{\prime \prime })$
such that
$S= (S^\prime , S^{\prime \prime })$
such that
![]() $W = W(S)$
. Thus, W is a ladder-web.
$W = W(S)$
. Thus, W is a ladder-web.
Proof. For the first statement, the nonellipticity of
![]() $W(S)$
follows because two oppositely oriented curves in the local picture
$W(S)$
follows because two oppositely oriented curves in the local picture
![]() $\left< W(S) \right>$
do not cross more than once (if there were a square-face, a pair of curves would cross twice), and the tautness of
$\left< W(S) \right>$
do not cross more than once (if there were a square-face, a pair of curves would cross twice), and the tautness of
![]() $W(S)$
is immediate.
$W(S)$
is immediate.
Conversely, let W be an essential local web in
![]() $\mathfrak {B}$
. The collection of ends of W located on the boundary edges
$\mathfrak {B}$
. The collection of ends of W located on the boundary edges
![]() $E^\prime \cup E^{\prime \prime }$
determines a strand-set pair
$E^\prime \cup E^{\prime \prime }$
determines a strand-set pair
![]() $S= (S^\prime , S^{\prime \prime })$
. We show that S is symmetric and
$S= (S^\prime , S^{\prime \prime })$
. We show that S is symmetric and
![]() $W = W(S)$
. In particular, S is uniquely determined.
$W = W(S)$
. In particular, S is uniquely determined.
If W has a trivalent vertex, let
![]() $\overline {W}$
denote the induced local web in the closed disk
$\overline {W}$
denote the induced local web in the closed disk
![]() $\mathfrak {D}_0$
underlying
$\mathfrak {D}_0$
underlying
![]() $\mathfrak {B}$
, obtained by filling in the two punctures of
$\mathfrak {B}$
, obtained by filling in the two punctures of
![]() $\mathfrak {B}$
. Applying Proposition 3.7 to
$\mathfrak {B}$
. Applying Proposition 3.7 to
![]() $\overline {W}$
guarantees that
$\overline {W}$
guarantees that
![]() $\overline {W}$
(possibly minus some arc components) has at least three fork- and/or H-faces. At most two of these faces can straddle the two punctures of
$\overline {W}$
(possibly minus some arc components) has at least three fork- and/or H-faces. At most two of these faces can straddle the two punctures of
![]() $\mathfrak {B}$
, so we gather W has one fork- or H-face
$\mathfrak {B}$
, so we gather W has one fork- or H-face
![]() $D^{\mathrm {ext}}$
lying on
$D^{\mathrm {ext}}$
lying on
![]() $E^\prime $
or
$E^\prime $
or
![]() $E^{\prime \prime }$
. Since W is taut,
$E^{\prime \prime }$
. Since W is taut,
![]() $D^{\mathrm {ext}}$
is an H-face.
$D^{\mathrm {ext}}$
is an H-face.
We can then remove this H-face from
![]() $\mathfrak {B}$
(recall Figure 11), obtaining a local web
$\mathfrak {B}$
(recall Figure 11), obtaining a local web
![]() $W_1$
that is essential and has strictly fewer trivalent vertices than W. Repeating this process, we obtain a sequence of essential local webs
$W_1$
that is essential and has strictly fewer trivalent vertices than W. Repeating this process, we obtain a sequence of essential local webs
![]() $W=W_0, W_1, \dots , W_n$
such that
$W=W_0, W_1, \dots , W_n$
such that
![]() $W_n$
has no trivalent vertices and is obtained from W by removing finitely many H-faces. By nonellipticity,
$W_n$
has no trivalent vertices and is obtained from W by removing finitely many H-faces. By nonellipticity,
![]() $W_n$
consists of a collection of arcs
$W_n$
consists of a collection of arcs
![]() $\gamma _i^{(n)}$
(as opposed to loops), and since
$\gamma _i^{(n)}$
(as opposed to loops), and since
![]() $W_n$
is taut, each arc
$W_n$
is taut, each arc
![]() $\gamma _i^{(n)}$
connects to both boundary edges
$\gamma _i^{(n)}$
connects to both boundary edges
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
of the biangle
$E^{\prime \prime }$
of the biangle
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
Replacing the removed H-faces with local crossings (Figure 14), we obtain a multicurve
![]() $\Gamma $
in
$\Gamma $
in
![]() $\mathfrak {B}$
consisting of arcs
$\mathfrak {B}$
consisting of arcs
![]() $\gamma _i^{(0)}$
, each intersecting both edges
$\gamma _i^{(0)}$
, each intersecting both edges
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
, such that only oppositely oriented arcs
$E^{\prime \prime }$
, such that only oppositely oriented arcs
![]() $\gamma _i^{(0)}$
intersect; see Figure 15. In particular, the pair
$\gamma _i^{(0)}$
intersect; see Figure 15. In particular, the pair
![]() $(S^\prime , S^{\prime \prime })$
is symmetric.
$(S^\prime , S^{\prime \prime })$
is symmetric.

Figure 15 Essential local web
![]() $W_{\mathfrak {B}}$
in the biangle, and its corresponding local picture
$W_{\mathfrak {B}}$
in the biangle, and its corresponding local picture
![]() $ \langle W_{\mathfrak {B}}\rangle $
.
$ \langle W_{\mathfrak {B}}\rangle $
.
We claim
![]() $\Gamma $
is the local picture
$\Gamma $
is the local picture
![]() $\left< W(S) \right>$
. Since only oppositely oriented arcs intersect,
$\left< W(S) \right>$
. Since only oppositely oriented arcs intersect,
![]() $\Gamma $
is order preserving (Definition 3.13). It remains to show
$\Gamma $
is order preserving (Definition 3.13). It remains to show
![]() $\Gamma $
is minimally intersecting, namely that no arcs intersect more than once. Suppose they did. Then, because only oppositely oriented arcs intersect, there would be an embedded bigon B in the complement
$\Gamma $
is minimally intersecting, namely that no arcs intersect more than once. Suppose they did. Then, because only oppositely oriented arcs intersect, there would be an embedded bigon B in the complement
![]() $\Gamma ^c \subseteq \mathfrak {B}$
; see the right side of Figure 16. Such an embedded bigon B corresponds in the local web W to a square-face, violating the nonellipticity of W. We gather
$\Gamma ^c \subseteq \mathfrak {B}$
; see the right side of Figure 16. Such an embedded bigon B corresponds in the local web W to a square-face, violating the nonellipticity of W. We gather
![]() $\Gamma = \left< W(S) \right>$
, as claimed.
$\Gamma = \left< W(S) \right>$
, as claimed.

Figure 16 Prohibited ladder-webs and local pictures.
By definition of the multicurve
![]() $\Gamma $
and the local web
$\Gamma $
and the local web
![]() $W(S)$
, it follows that
$W(S)$
, it follows that
![]() $W = W(S)$
.
$W = W(S)$
.
For technical reasons, in §8 we will need the following concept.
Definition 3.16. The local picture
![]() $ \langle W_{\mathfrak {B}} \rangle$
associated to an essential local web
$ \langle W_{\mathfrak {B}} \rangle$
associated to an essential local web
![]() $W_{\mathfrak {B}}$
in the biangle
$W_{\mathfrak {B}}$
in the biangle
![]() $\mathfrak {B}$
is the local picture
$\mathfrak {B}$
is the local picture
![]() $\left< W(S) \right>$
(Definition 3.13) corresponding to the unique symmetric strand-set pair
$\left< W(S) \right>$
(Definition 3.13) corresponding to the unique symmetric strand-set pair
![]() $S= (S^\prime , S^{\prime \prime })$
such that
$S= (S^\prime , S^{\prime \prime })$
such that
![]() $W_{\mathfrak {B}} = W(S)$
; see Figure 15.
$W_{\mathfrak {B}} = W(S)$
; see Figure 15.
3.8. Honeycomb-webs in ideal triangles
Another name for an ideal three-polygon
![]() $\mathfrak {D}_3$
is an ideal triangle
$\mathfrak {D}_3$
is an ideal triangle
![]() $\mathfrak {T}$
. We want to characterize rungless essential local webs W in triangles
$\mathfrak {T}$
. We want to characterize rungless essential local webs W in triangles
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
Definition 3.17. For a positive integer
![]() $n> 0$
, the n-out-honeycomb-web
$n> 0$
, the n-out-honeycomb-web
![]() $H^{\mathrm {out}}_n$
(resp. n-in-honeycomb-web
$H^{\mathrm {out}}_n$
(resp. n-in-honeycomb-web
![]() $H_n^{\mathrm {in}}$
) in the triangle
$H_n^{\mathrm {in}}$
) in the triangle
![]() $\mathfrak {T}$
is the local web
$\mathfrak {T}$
is the local web
![]() $H_n$
dual to the n-triangulation of
$H_n$
dual to the n-triangulation of
![]() $\mathfrak {T}$
, where the orientation of
$\mathfrak {T}$
, where the orientation of
![]() $H_n$
is such that all the arrows go out of (resp. into) the triangle
$H_n$
is such that all the arrows go out of (resp. into) the triangle
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
For example, in Figure 17 we show the five-out-honeycomb-web
![]() $H_5^{\mathrm {out}}$
.
$H_5^{\mathrm {out}}$
.

Figure 17 Honeycomb-web.
The following statement is implicit in [Reference KuperbergKup96, Lemma 6.8] and also appears in [Reference Frohman and SikoraFS22, §9].
Proposition 3.18. A honeycomb-web
![]() $H_n$
in the triangle
$H_n$
in the triangle
![]() $\mathfrak {T}$
is rungless and essential. Conversely, given a connected rungless essential local web W in
$\mathfrak {T}$
is rungless and essential. Conversely, given a connected rungless essential local web W in
![]() $\mathfrak {T}$
having at least one trivalent vertex, there exists a unique honeycomb-web
$\mathfrak {T}$
having at least one trivalent vertex, there exists a unique honeycomb-web
![]() $H_n = H_n^{\mathrm {out}}$
or
$H_n = H_n^{\mathrm {out}}$
or
![]() $=H_n^{\mathrm {in}}$
such that
$=H_n^{\mathrm {in}}$
such that
![]() $W = H_n$
. Consequently, a (possibly disconnected) rungless essential local web W in
$W = H_n$
. Consequently, a (possibly disconnected) rungless essential local web W in
![]() $\mathfrak {T}$
consists of a unique (possibly empty) honeycomb
$\mathfrak {T}$
consists of a unique (possibly empty) honeycomb
![]() $H_n$
together with a collection of disjoint oriented arcs located on the corners of
$H_n$
together with a collection of disjoint oriented arcs located on the corners of
![]() $\mathfrak {T}$
; see the left-hand side of Figure 18.
$\mathfrak {T}$
; see the left-hand side of Figure 18.

Figure 18 Rungless essential local web
![]() $W_{\mathfrak {T}}$
in the triangle and its corresponding local picture
$W_{\mathfrak {T}}$
in the triangle and its corresponding local picture
![]() $\left < W_{\mathfrak {T}} \right>$
in the holed triangle.
$\left < W_{\mathfrak {T}} \right>$
in the holed triangle.
Proof. The first statement is immediate.
Step 1. Let W be as in the second statement. Just like the proof of Proposition 3.15, applying Proposition 3.7 to the induced web
![]() $\overline {W}$
in the underlying closed disk
$\overline {W}$
in the underlying closed disk
![]() $\mathfrak {D}_0$
guarantees that
$\mathfrak {D}_0$
guarantees that
![]() $\overline {W}$
has at least three fork- and/or H-faces, at most three of which can straddle the three punctures of
$\overline {W}$
has at least three fork- and/or H-faces, at most three of which can straddle the three punctures of
![]() $\mathfrak {T}$
. Since W is taut and rungless, W has no fork- or H-faces. Thus,
$\mathfrak {T}$
. Since W is taut and rungless, W has no fork- or H-faces. Thus,
![]() $\overline {W}$
has exactly three fork- and/or H-faces, each of which straddles a puncture. Since these three faces are the only ones with a positive contribution in the formula of Proposition 3.3, they must be fork-faces. Moreover, since the total contribution of these three fork-faces is
$\overline {W}$
has exactly three fork- and/or H-faces, each of which straddles a puncture. Since these three faces are the only ones with a positive contribution in the formula of Proposition 3.3, they must be fork-faces. Moreover, since the total contribution of these three fork-faces is
![]() $2 \pi $
, every other face has exactly zero contribution. We gather that each interior face of W is a hexagon-face and each external face of W is a half-hexagon-face.
$2 \pi $
, every other face has exactly zero contribution. We gather that each interior face of W is a hexagon-face and each external face of W is a half-hexagon-face.
Step 2. To prove that W is a honeycomb-web
![]() $H_n$
, we argue by induction on n, showing that the triangle
$H_n$
, we argue by induction on n, showing that the triangle
![]() $\mathfrak {T}$
can be tiled by W face-by-face, starting from a corner of
$\mathfrak {T}$
can be tiled by W face-by-face, starting from a corner of
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
(2.a) Assume inductively that some number of half-hexagon-faces have been laid down as part of the bottom layer of faces sitting on the bottom edge E, illustrated in Figure 19.

Figure 19 Laying down a honeycomb: 1 of 2.
The strand labeled s either: (1) ends on the right edge
![]() $E^\prime $
of the triangle
$E^\prime $
of the triangle
![]() $\mathfrak {T}$
, thereby creating a fork straddling the rightmost puncture and completing the bottom layer of faces; (2) ends at a vertex disjoint from the vertices previously laid, hence the strand s is part of the boundary of the next half-hexagon-face; (3) ends at one of the vertices previously laid.
$\mathfrak {T}$
, thereby creating a fork straddling the rightmost puncture and completing the bottom layer of faces; (2) ends at a vertex disjoint from the vertices previously laid, hence the strand s is part of the boundary of the next half-hexagon-face; (3) ends at one of the vertices previously laid.
If (1), we continue to the next step of the induction, which deals with laying down the middle layers. If (2), we repeat the current step. Lastly, we argue (3) cannot occur. Indeed, suppose it did. The strand s is part of the boundary of the next half-hexagon-face
![]() $D_5^{\mathrm {ext}}$
. But, as can be seen from the figure, the external face
$D_5^{\mathrm {ext}}$
. But, as can be seen from the figure, the external face
![]() $D_5^{\mathrm {ext}}$
has
$D_5^{\mathrm {ext}}$
has
![]() $\geqslant $
six sides, which is a contradiction.
$\geqslant $
six sides, which is a contradiction.
(2.b) Assume inductively that the bottom layer and some number of middle layers have been laid down and moreover that some number of faces have been laid down as part of the current layer, illustrated in Figure 20. Consider the next face D shown in the figure.

Figure 20 Laying down a honeycomb: 2 of 2.
The face D is either external or internal. If it is internal, then D is a hexagon-face. In this case, the strands s and
![]() $s^\prime $
end at the fifth and sixth vertices of the hexagon-face, and we repeat the current step. Otherwise, D is external, so it is a half-hexagon-face,
$s^\prime $
end at the fifth and sixth vertices of the hexagon-face, and we repeat the current step. Otherwise, D is external, so it is a half-hexagon-face,
![]() $D = D_{5}^{\mathrm {ext}}$
. However, we see from the figure that in this case
$D = D_{5}^{\mathrm {ext}}$
. However, we see from the figure that in this case
![]() $D_5^{\mathrm {ext}}$
has
$D_5^{\mathrm {ext}}$
has
![]() $\geqslant $
six sides, which is a contradiction.
$\geqslant $
six sides, which is a contradiction.
To finish the induction, we repeat this step until the strand
![]() $s^\prime $
does not exist, in which case the strand s is part of a nonexternal side of a half-hexagon-face lying on the boundary edge
$s^\prime $
does not exist, in which case the strand s is part of a nonexternal side of a half-hexagon-face lying on the boundary edge
![]() $E^\prime $
.
$E^\prime $
.
Step 3. The last statement of the proposition follows since each honeycomb-web
![]() $H_n$
attaches to all three boundary edges of the triangle
$H_n$
attaches to all three boundary edges of the triangle
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
Later, in order to assign coordinates to webs, we will need to consider rungless essential local webs
![]() $W_{\mathfrak {T}}$
in a triangle
$W_{\mathfrak {T}}$
in a triangle
![]() $\mathfrak {T}$
up to a certain equivalence relation. Say that a local parallel-move applied to
$\mathfrak {T}$
up to a certain equivalence relation. Say that a local parallel-move applied to
![]() $W_{\mathfrak {T}}$
is a move swapping two arcs on the same corner of
$W_{\mathfrak {T}}$
is a move swapping two arcs on the same corner of
![]() $\mathfrak {T}$
; see Figure 21.
$\mathfrak {T}$
; see Figure 21.
Definition 3.19. Let
![]() $\mathscr {W}_{\mathfrak {T}}$
denote the collection of rungless essential local webs in the triangle
$\mathscr {W}_{\mathfrak {T}}$
denote the collection of rungless essential local webs in the triangle
![]() $\mathfrak {T}$
. We say that two local webs
$\mathfrak {T}$
. We say that two local webs
![]() $W_{\mathfrak {T}} $
and
$W_{\mathfrak {T}} $
and
![]() $W^\prime _{\mathfrak {T}} $
in
$W^\prime _{\mathfrak {T}} $
in
![]() $\mathscr {W}_{\mathfrak {T}}$
are equivalent up to corner-ambiguity if they are related by local parallel-moves. The corner-ambiguity equivalence class of a local web
$\mathscr {W}_{\mathfrak {T}}$
are equivalent up to corner-ambiguity if they are related by local parallel-moves. The corner-ambiguity equivalence class of a local web
![]() $W_{\mathfrak {T}} \in \mathscr {W}_{\mathfrak {T}}$
is denoted by
$W_{\mathfrak {T}} \in \mathscr {W}_{\mathfrak {T}}$
is denoted by
![]() $[ W_{\mathfrak {T}} ]$
, and the set of corner-ambiguity classes is denoted
$[ W_{\mathfrak {T}} ]$
, and the set of corner-ambiguity classes is denoted
![]() $[ \mathscr {W}_{\mathfrak {T}} ]$
.
$[ \mathscr {W}_{\mathfrak {T}} ]$
.

Figure 21 Local parallel-move.
For technical reasons, in §8 we will need the following concept.
Definition 3.20. Given a triangle
![]() $\mathfrak {T}$
, a holed triangle
$\mathfrak {T}$
, a holed triangle
![]() $\mathfrak {T}^0$
is the triangle minus an open disk
$\mathfrak {T}^0$
is the triangle minus an open disk
![]() $\mathfrak {T}^0 = \mathfrak {T} - \mathrm {Int}(\mathfrak {D}_0)$
; see the right-hand side of Figure 18 above. Let
$\mathfrak {T}^0 = \mathfrak {T} - \mathrm {Int}(\mathfrak {D}_0)$
; see the right-hand side of Figure 18 above. Let
![]() $W_{\mathfrak {T}}$
be a rungless essential local web in
$W_{\mathfrak {T}}$
be a rungless essential local web in
![]() $\mathfrak {T}$
, which by Proposition 3.18 consists of a honeycomb-web
$\mathfrak {T}$
, which by Proposition 3.18 consists of a honeycomb-web
![]() $H_n$
together with a collection of disjoint oriented corner arcs
$H_n$
together with a collection of disjoint oriented corner arcs
![]() $\{ \gamma _i \}$
. The local picture
$\{ \gamma _i \}$
. The local picture
![]() $\left < W_{\mathfrak {T}} \right>$
associated to
$\left < W_{\mathfrak {T}} \right>$
associated to
![]() $W_{\mathfrak {T}}$
is the multicurve (Definition 3.11) in the holed triangle
$W_{\mathfrak {T}}$
is the multicurve (Definition 3.11) in the holed triangle
![]() $\mathfrak {T}^0$
consisting of the corner arcs
$\mathfrak {T}^0$
consisting of the corner arcs
![]() $\gamma _i$
together with
$\gamma _i$
together with
![]() $3n$
oriented arcs
$3n$
oriented arcs
![]() $\{ \gamma ^\prime _j \}$
disjoint from each other and from the
$\{ \gamma ^\prime _j \}$
disjoint from each other and from the
![]() $\gamma _i$
and going either all out of or all into the boundary
$\gamma _i$
and going either all out of or all into the boundary
![]() $\partial \mathfrak {D}_0$
of the removed disk, such that for each boundary edge E of the triangle
$\partial \mathfrak {D}_0$
of the removed disk, such that for each boundary edge E of the triangle
![]() $\mathfrak {T}$
there are n arcs
$\mathfrak {T}$
there are n arcs
![]() $\gamma ^\prime _j$
ending on E; see again Figure 18.
$\gamma ^\prime _j$
ending on E; see again Figure 18.
4. Good position of a global web
Using the technical results about local webs from §3, we continue studying global webs W on the surface
![]() $\mathfrak {S}$
. We assume
$\mathfrak {S}$
. We assume
![]() $\mathfrak {S}$
is equipped with an ideal triangulation
$\mathfrak {S}$
is equipped with an ideal triangulation
![]() $\lambda $
; see §2.1.
$\lambda $
; see §2.1.
4.1. Generic isotopies
Definition 4.1. A web W on
![]() $\mathfrak {S}$
is generic with respect to the ideal triangulation
$\mathfrak {S}$
is generic with respect to the ideal triangulation
![]() $\lambda $
if none of its vertices intersect the edges E of
$\lambda $
if none of its vertices intersect the edges E of
![]() $\lambda $
, and if in addition W intersects
$\lambda $
, and if in addition W intersects
![]() $\lambda $
transversally.
$\lambda $
transversally.
Two generic webs W and
![]() $W^\prime $
are generically isotopic if they are isotopic through generic webs; see Definition 2.3.
$W^\prime $
are generically isotopic if they are isotopic through generic webs; see Definition 2.3.
Whenever there is an ideal triangulation
![]() $\lambda $
present, we always assume that ‘web’ means ‘generic web’. However, we distinguish between isotopies and generic isotopies.
$\lambda $
present, we always assume that ‘web’ means ‘generic web’. However, we distinguish between isotopies and generic isotopies.
4.2. Minimal position
Recall the notion of two parallel equivalent webs; see Definition 2.3.
Definition 4.2. Given a web W on the surface
![]() $\mathfrak {S}$
and given an edge E of the ideal triangulation
$\mathfrak {S}$
and given an edge E of the ideal triangulation
![]() $\lambda $
, the local geometric intersection number of the web W with the edge E is
$\lambda $
, the local geometric intersection number of the web W with the edge E is
where
![]() $\iota (W^\prime , E)$
is the number of intersection points of
$\iota (W^\prime , E)$
is the number of intersection points of
![]() $W^\prime $
with E.
$W^\prime $
with E.
The web W is in minimal position with respect to the ideal triangulation
![]() $\lambda $
if
$\lambda $
if
(If this is the case, W minimizes the intersection number
![]() $\iota (W, \lambda )$
with the ideal triangulation
$\iota (W, \lambda )$
with the ideal triangulation
![]() $\lambda $
.)
$\lambda $
.)
Let
![]() $W^\prime $
be a web, let
$W^\prime $
be a web, let
![]() $\mathfrak {T}$
be a triangle in the ideal triangulation
$\mathfrak {T}$
be a triangle in the ideal triangulation
![]() $\lambda $
, and let
$\lambda $
, and let
![]() $W^\prime _{\mathfrak {T}} = W^\prime \cap \mathfrak {T}$
be the restriction of
$W^\prime _{\mathfrak {T}} = W^\prime \cap \mathfrak {T}$
be the restriction of
![]() $W^\prime $
to
$W^\prime $
to
![]() $\mathfrak {T}$
. Suppose that the local web
$\mathfrak {T}$
. Suppose that the local web
![]() $W^\prime _{\mathfrak {T}}$
is not taut; see Definition 3.8. Then there is an edge E of
$W^\prime _{\mathfrak {T}}$
is not taut; see Definition 3.8. Then there is an edge E of
![]() $\lambda $
and a compact arc
$\lambda $
and a compact arc
![]() $\alpha $
ending on E such that
$\alpha $
ending on E such that
![]() $\iota (W^\prime , E)> \iota (W^\prime , \alpha )$
; see Figure 22. We can then isotope the part of
$\iota (W^\prime , E)> \iota (W^\prime , \alpha )$
; see Figure 22. We can then isotope the part of
![]() $W^\prime $
that is inside the bigon B, which is bounded by
$W^\prime $
that is inside the bigon B, which is bounded by
![]() $\alpha $
and the segment
$\alpha $
and the segment
![]() $\overline {E}$
of E delimited by
$\overline {E}$
of E delimited by
![]() $\partial \alpha $
, into the adjacent triangle, resulting in a new web W. This is called a tightening-move. Similarly, if the restriction
$\partial \alpha $
, into the adjacent triangle, resulting in a new web W. This is called a tightening-move. Similarly, if the restriction
![]() $W^\prime _{\mathfrak {T}}$
has an H-face, then we may apply an H-move to push the H into the adjacent triangle; see again Figure 22.
$W^\prime _{\mathfrak {T}}$
has an H-face, then we may apply an H-move to push the H into the adjacent triangle; see again Figure 22.

Figure 22 Tightening- and H-moves.
Note that tightening- and H-moves can be achieved with an isotopy of the web but not a generic isotopy. Also, by definition, in order to apply an H-move, we assume that the shaded region shown at the bottom of Figure 22 is empty, namely it does not intersect the web.
We borrow the following result from [Reference Frohman and SikoraFS22, §6] (and give essentially the same proof in the arXiv version [Reference Douglas and SunDS20a] of this article).
Proposition 4.3. If
![]() $W^\prime $
is a nonelliptic web on the surface
$W^\prime $
is a nonelliptic web on the surface
![]() $\mathfrak {S}$
, then (by applying tightening-moves) there exists a nonelliptic web W that is isotopic (in particular, parallel equivalent) to
$\mathfrak {S}$
, then (by applying tightening-moves) there exists a nonelliptic web W that is isotopic (in particular, parallel equivalent) to
![]() $W^\prime $
and that is in minimal position with respect to the ideal triangulation
$W^\prime $
and that is in minimal position with respect to the ideal triangulation
![]() $\lambda $
; see Definition 2.5.
$\lambda $
; see Definition 2.5.
Moreover, given any two parallel equivalent nonelliptic webs W and
![]() $W^\prime $
in minimal position, then W can be taken to
$W^\prime $
in minimal position, then W can be taken to
![]() $W^\prime $
by a sequence of H-moves, global parallel-moves and generic isotopies; see Definition 2.3.
$W^\prime $
by a sequence of H-moves, global parallel-moves and generic isotopies; see Definition 2.3.
4.3. Split ideal triangulations
A split ideal triangulation
![]() $\widehat {\lambda }$
with respect to the ideal triangulation
$\widehat {\lambda }$
with respect to the ideal triangulation
![]() $\lambda $
is a collection of bi-infinite arcs obtained by doubling every edge E of
$\lambda $
is a collection of bi-infinite arcs obtained by doubling every edge E of
![]() $\lambda $
. In other words, we fatten each edge E into a biangle
$\lambda $
. In other words, we fatten each edge E into a biangle
![]() $\mathfrak {B}$
; see Figure 23.
$\mathfrak {B}$
; see Figure 23.

Figure 23 Split ideal triangulation.
The notions of generic web and generic isotopy for webs with respect to the split ideal triangulation
![]() $\widehat {\lambda }$
are the same as those for webs with respect to the ideal triangulation
$\widehat {\lambda }$
are the same as those for webs with respect to the ideal triangulation
![]() $\lambda $
. We always assume that webs are generic with respect to
$\lambda $
. We always assume that webs are generic with respect to
![]() $\widehat {\lambda }$
.
$\widehat {\lambda }$
.
To avoid cumbersome notation, we identify the triangles
![]() $\mathfrak {T}$
of the ideal triangulation
$\mathfrak {T}$
of the ideal triangulation
![]() $\lambda $
to the triangles
$\lambda $
to the triangles
![]() $\mathfrak {T}$
of the split ideal triangulation
$\mathfrak {T}$
of the split ideal triangulation
![]() $\widehat {\lambda }$
.
$\widehat {\lambda }$
.
Remark 4.4. For a related usage of split ideal triangulations, in the
![]() $\mathrm {SL}_2$
-case, see [Reference Bonahon and WongBW11].
$\mathrm {SL}_2$
-case, see [Reference Bonahon and WongBW11].
4.4. Good position
Definition 4.5. For a fixed split ideal triangulation
![]() $\widehat {\lambda }$
, a web W on
$\widehat {\lambda }$
, a web W on
![]() $\mathfrak {S}$
is in good position with respect to
$\mathfrak {S}$
is in good position with respect to
![]() $\widehat {\lambda }$
if the restriction
$\widehat {\lambda }$
if the restriction
![]() $W_{\mathfrak {B}} = W \cap \mathfrak {B}$
(resp.
$W_{\mathfrak {B}} = W \cap \mathfrak {B}$
(resp.
![]() $W_{\mathfrak {T}} = W \cap {\mathfrak {T}}$
) of W to each biangle
$W_{\mathfrak {T}} = W \cap {\mathfrak {T}}$
) of W to each biangle
![]() $\mathfrak {B}$
(resp. triangle
$\mathfrak {B}$
(resp. triangle
![]() $\mathfrak {T}$
) of
$\mathfrak {T}$
) of
![]() $\widehat {\lambda }$
is an essential (resp. rungless essential) local web; see Figure 24.
$\widehat {\lambda }$
is an essential (resp. rungless essential) local web; see Figure 24.

Figure 24 (Part of) a web in good position.
Note that for a web W in good position, each restriction
![]() $W_{\mathfrak {B}}$
to a biangle
$W_{\mathfrak {B}}$
to a biangle
![]() $\mathfrak {B}$
of
$\mathfrak {B}$
of
![]() $\widehat {\lambda }$
is a ladder-web; see Definition 3.14, Proposition 3.15 and Figures 13 and 15. Also, each restriction
$\widehat {\lambda }$
is a ladder-web; see Definition 3.14, Proposition 3.15 and Figures 13 and 15. Also, each restriction
![]() $W_{\mathfrak {T}}$
to a triangle
$W_{\mathfrak {T}}$
to a triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
is a (possibly empty) honeycomb-web
$\widehat {\lambda }$
is a (possibly empty) honeycomb-web
![]() $H_n$
together with a collection of disjoint oriented corner arcs; see Definition 3.17, Proposition 3.18 and Figures 17 and 18.
$H_n$
together with a collection of disjoint oriented corner arcs; see Definition 3.17, Proposition 3.18 and Figures 17 and 18.
If W is a web in good position, then a modified H-move carries an H-face in a biangle
![]() $\mathfrak {B}$
to an H-face in an adjacent biangle
$\mathfrak {B}$
to an H-face in an adjacent biangle
![]() $\mathfrak {B}^\prime $
, thereby replacing W with a new web
$\mathfrak {B}^\prime $
, thereby replacing W with a new web
![]() $W^\prime $
; see Figure 25. If, in addition, W is nonelliptic, then
$W^\prime $
; see Figure 25. If, in addition, W is nonelliptic, then
![]() $W^\prime $
is also in good position. The nonelliptic condition for W is required to ensure that the new local web restriction
$W^\prime $
is also in good position. The nonelliptic condition for W is required to ensure that the new local web restriction
![]() $W^\prime _{\mathfrak {B}^\prime }$
is nonelliptic.
$W^\prime _{\mathfrak {B}^\prime }$
is nonelliptic.
Remark 4.6. Of importance will be that the effect in the intermediate triangle
![]() $\mathfrak {T}$
of a modified H-move is to swap two parallel oppositely oriented corner arcs; see again Figure 25.
$\mathfrak {T}$
of a modified H-move is to swap two parallel oppositely oriented corner arcs; see again Figure 25.

Figure 25 Modified H-move.
Once more, the following result is implicit in [Reference KuperbergKup96, Lemma 6.5 and the proof of Theorem 6.2, pp. 139-140] (in the setting of an ideal k-polygon
![]() $\mathfrak {D}_k$
) and also appears in [Reference Frohman and SikoraFS22, §10].
$\mathfrak {D}_k$
) and also appears in [Reference Frohman and SikoraFS22, §10].
Proposition 4.7. If
![]() $W^\prime $
is a nonelliptic web on the surface
$W^\prime $
is a nonelliptic web on the surface
![]() $\mathfrak {S}$
, then there exists a nonelliptic web W that is isotopic (in particular, parallel equivalent) to
$\mathfrak {S}$
, then there exists a nonelliptic web W that is isotopic (in particular, parallel equivalent) to
![]() $W^\prime $
and that is in good position with respect to the split ideal triangulation
$W^\prime $
and that is in good position with respect to the split ideal triangulation
![]() $\widehat {\lambda }$
.
$\widehat {\lambda }$
.
Moreover, given any two parallel equivalent nonelliptic webs W and
![]() $W^\prime $
in good position, then W can be taken to
$W^\prime $
in good position, then W can be taken to
![]() $W^\prime $
by a sequence of modified H-moves, global parallel-moves and generic isotopies.
$W^\prime $
by a sequence of modified H-moves, global parallel-moves and generic isotopies.
Proof. We will keep track of isotopies by moving the split triangulation
![]() $\widehat {\lambda }$
instead of webs.
$\widehat {\lambda }$
instead of webs.
By Proposition 4.3, we can replace
![]() $W^\prime $
with a nonelliptic web W that is isotopic to
$W^\prime $
with a nonelliptic web W that is isotopic to
![]() $W^\prime $
and that is in minimal position with respect to the ideal triangulation
$W^\prime $
and that is in minimal position with respect to the ideal triangulation
![]() $\lambda $
. We proceed to construct the split ideal triangulation
$\lambda $
. We proceed to construct the split ideal triangulation
![]() $\widehat {\lambda }$
.
$\widehat {\lambda }$
.
Let us begin by splitting each edge E of
![]() $\lambda $
into two edges
$\lambda $
into two edges
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
that are very close to E. These split edges form a preliminary split ideal triangulation
$E^{\prime \prime }$
that are very close to E. These split edges form a preliminary split ideal triangulation
![]() $\widehat {\lambda }$
, whose triangles (resp. biangles) are denoted by
$\widehat {\lambda }$
, whose triangles (resp. biangles) are denoted by
![]() $\widehat {\mathfrak {T}}$
(resp.
$\widehat {\mathfrak {T}}$
(resp.
![]() $\mathfrak {B}_E$
); see the left-hand side of Figure 26.
$\mathfrak {B}_E$
); see the left-hand side of Figure 26.

Figure 26 Enlarging a biangle.
By definition of minimal position, the restriction
![]() $W_{\mathfrak {T}}$
of W to a triangle
$W_{\mathfrak {T}}$
of W to a triangle
![]() $\mathfrak {T}$
of the ideal triangulation
$\mathfrak {T}$
of the ideal triangulation
![]() $\lambda $
is taut. Since, in addition, W is nonelliptic, we have that
$\lambda $
is taut. Since, in addition, W is nonelliptic, we have that
![]() $W_{\mathfrak {T}}$
is essential. If the preliminary split ideal triangulation
$W_{\mathfrak {T}}$
is essential. If the preliminary split ideal triangulation
![]() $\widehat {\lambda }$
is sufficiently close to
$\widehat {\lambda }$
is sufficiently close to
![]() $\lambda $
, then the restriction
$\lambda $
, then the restriction
![]() $W_{\widehat {\mathfrak {T}}}$
of W to the triangle
$W_{\widehat {\mathfrak {T}}}$
of W to the triangle
![]() $\widehat {\mathfrak {T}} \subseteq \mathfrak {T}$
associated to
$\widehat {\mathfrak {T}} \subseteq \mathfrak {T}$
associated to
![]() $\mathfrak {T}$
is also an essential local web. If all of the local webs
$\mathfrak {T}$
is also an essential local web. If all of the local webs
![]() $W_{\widehat {\mathfrak {T}}}$
are rungless, then W is in good position with respect to
$W_{\widehat {\mathfrak {T}}}$
are rungless, then W is in good position with respect to
![]() $\widehat {\lambda }$
.
$\widehat {\lambda }$
.
Otherwise, assume
![]() $W_{\widehat {\mathfrak {T}}}$
has an H-face on an edge of
$W_{\widehat {\mathfrak {T}}}$
has an H-face on an edge of
![]() $\widehat {\lambda }$
, say the edge
$\widehat {\lambda }$
, say the edge
![]() $E^\prime $
. Then by isotopy we can enlarge the biangle
$E^\prime $
. Then by isotopy we can enlarge the biangle
![]() $\mathfrak {B}_E$
until it just envelops this H-face. In other words, we can isotope the edge
$\mathfrak {B}_E$
until it just envelops this H-face. In other words, we can isotope the edge
![]() $E^\prime $
so that it cuts out this H-face from the triangle
$E^\prime $
so that it cuts out this H-face from the triangle
![]() $\widehat {\mathfrak {T}}$
; see Figure 26. The result of this step is a new split ideal triangulation
$\widehat {\mathfrak {T}}$
; see Figure 26. The result of this step is a new split ideal triangulation
![]() $\widehat {\lambda }$
, retaining the property that the local web restrictions
$\widehat {\lambda }$
, retaining the property that the local web restrictions
![]() $W_{\widehat {\mathfrak {T}}}$
are essential. Repeating this process until all of the local webs
$W_{\widehat {\mathfrak {T}}}$
are essential. Repeating this process until all of the local webs
![]() $W_{\widehat {\mathfrak {T}}}$
are rungless, we obtain the desired split ideal triangulation
$W_{\widehat {\mathfrak {T}}}$
are rungless, we obtain the desired split ideal triangulation
![]() $\widehat {\lambda }$
. Notice it might be the case that there is more than one biangle into which an H-face can be moved; see again Figure 26.
$\widehat {\lambda }$
. Notice it might be the case that there is more than one biangle into which an H-face can be moved; see again Figure 26.
For the second statement of the proposition, note that if a nonelliptic web W is in good position with respect to
![]() $\widehat {\lambda }$
, then W is minimal with respect to the ideal triangulation
$\widehat {\lambda }$
, then W is minimal with respect to the ideal triangulation
![]() $\lambda $
(which, for the sake of argument, we can take to be contained in
$\lambda $
(which, for the sake of argument, we can take to be contained in
![]() $\widehat {\lambda }$
, that is
$\widehat {\lambda }$
, that is
![]() $\lambda \subseteq \widehat {\lambda }$
). (Indeed, this follows by the proof of the first part of Proposition 4.3, provided in [Reference Frohman and SikoraFS22, Reference Douglas and SunDS20a], and uses the fact that adding a ladder web
$\lambda \subseteq \widehat {\lambda }$
). (Indeed, this follows by the proof of the first part of Proposition 4.3, provided in [Reference Frohman and SikoraFS22, Reference Douglas and SunDS20a], and uses the fact that adding a ladder web
![]() $W_{\mathfrak {B}}$
to a rungless essential web
$W_{\mathfrak {B}}$
to a rungless essential web
![]() $W_{\mathfrak {T}}$
preserves the tautness property.) Similarly,
$W_{\mathfrak {T}}$
preserves the tautness property.) Similarly,
![]() $W^\prime $
is in minimal position. Thus, applying the second part of Proposition 4.3, we gather that W can be taken to
$W^\prime $
is in minimal position. Thus, applying the second part of Proposition 4.3, we gather that W can be taken to
![]() $W^\prime $
by a finite sequence of H-moves, global parallel-moves and generic isotopies. The result follows by the definition of good position and modified H-moves.
$W^\prime $
by a finite sequence of H-moves, global parallel-moves and generic isotopies. The result follows by the definition of good position and modified H-moves.
5. Global coordinates for nonelliptic webs
Recall that
![]() $[\mathscr {W}_{\mathfrak {S}}]$
denotes the collection of parallel equivalence classes of nonelliptic webs on the surface
$[\mathscr {W}_{\mathfrak {S}}]$
denotes the collection of parallel equivalence classes of nonelliptic webs on the surface
![]() $\mathfrak {S}$
; see just below Definition 2.5. Our goal in this section is to define a function
$\mathfrak {S}$
; see just below Definition 2.5. Our goal in this section is to define a function
![]() $\Phi _{\lambda }^{\mathrm {FG}}: [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
depending on the ideal triangulation
$\Phi _{\lambda }^{\mathrm {FG}}: [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
depending on the ideal triangulation
![]() $\lambda $
, where
$\lambda $
, where
![]() $N = -8\chi (\mathfrak {S})> 0$
is a positive integer depending only on the topology of
$N = -8\chi (\mathfrak {S})> 0$
is a positive integer depending only on the topology of
![]() $\mathfrak {S}$
. In §6-8, we characterize the image of
$\mathfrak {S}$
. In §6-8, we characterize the image of
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
and prove that it is injective. We think of
$\Phi _{\lambda }^{\mathrm {FG}}$
and prove that it is injective. We think of
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
as putting global coordinates on
$\Phi _{\lambda }^{\mathrm {FG}}$
as putting global coordinates on
![]() $[\mathscr {W}_{\mathfrak {S}}]$
.
$[\mathscr {W}_{\mathfrak {S}}]$
.
5.1. Dotted ideal triangulations
Consider a surface
![]() $\widehat {\mathfrak {S}} = \mathfrak {S}$
or
$\widehat {\mathfrak {S}} = \mathfrak {S}$
or
![]() $= \mathfrak {T}$
equipped with an ideal triangulation
$= \mathfrak {T}$
equipped with an ideal triangulation
![]() $\lambda $
, where, in this subsection,
$\lambda $
, where, in this subsection,
![]() $\lambda = \mathfrak {T}$
when
$\lambda = \mathfrak {T}$
when
![]() $\widehat {\mathfrak {S}} = \mathfrak {T}$
. The associated dotted ideal triangulation is the pair consisting of
$\widehat {\mathfrak {S}} = \mathfrak {T}$
. The associated dotted ideal triangulation is the pair consisting of
![]() $\lambda $
together with
$\lambda $
together with
![]() $N^\prime =N$
or
$N^\prime =N$
or
![]() $=7$
distinct dots attached to the one- and two-cells of
$=7$
distinct dots attached to the one- and two-cells of
![]() $\lambda $
, where there are two edge-dots attached to each one-cell and there is one triangle-dot attached to each two-cell; see Figure 27. Given a triangle
$\lambda $
, where there are two edge-dots attached to each one-cell and there is one triangle-dot attached to each two-cell; see Figure 27. Given a triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\lambda $
and an edge E of
$\lambda $
and an edge E of
![]() $\mathfrak {T}$
, it makes sense to talk about the left-edge-dot and right-edge-dot as viewed from
$\mathfrak {T}$
, it makes sense to talk about the left-edge-dot and right-edge-dot as viewed from
![]() $\mathfrak {T}$
; see Figure 27b. Choosing an ordering for the
$\mathfrak {T}$
; see Figure 27b. Choosing an ordering for the
![]() $N^\prime $
dots lying on the dotted ideal triangulation
$N^\prime $
dots lying on the dotted ideal triangulation
![]() $\lambda $
defines a one-to-one correspondence between functions
$\lambda $
defines a one-to-one correspondence between functions
![]() $\{ \text {dots} \} \to \mathbb {Z}$
and elements of
$\{ \text {dots} \} \to \mathbb {Z}$
and elements of
![]() $\mathbb {Z}^{N^\prime }$
. We always assume that such an ordering has been chosen.
$\mathbb {Z}^{N^\prime }$
. We always assume that such an ordering has been chosen.

Figure 27 Dotted ideal triangulations.
5.2. Local coordinate functions
Consider a dotted ideal triangle
![]() $\mathfrak {T}$
; see Figure 27b. Recall (Definition 3.19) that
$\mathfrak {T}$
; see Figure 27b. Recall (Definition 3.19) that
![]() $\mathscr {W}_{\mathfrak {T}}$
denotes the collection of rungless essential local webs
$\mathscr {W}_{\mathfrak {T}}$
denotes the collection of rungless essential local webs
![]() $W_{\mathfrak {T}}$
in
$W_{\mathfrak {T}}$
in
![]() $\mathfrak {T}$
and that
$\mathfrak {T}$
and that
![]() $[\mathscr {W}_{\mathfrak {T}}]$
denotes the set of corner-ambiguity classes
$[\mathscr {W}_{\mathfrak {T}}]$
denotes the set of corner-ambiguity classes
![]() $[ W_{\mathfrak {T}} ]$
of local webs
$[ W_{\mathfrak {T}} ]$
of local webs
![]() $W_{\mathfrak {T}}$
in
$W_{\mathfrak {T}}$
in
![]() $\mathscr {W}_{\mathfrak {T}}$
.
$\mathscr {W}_{\mathfrak {T}}$
.
Definition 5.1. An integer local coordinate function or just local coordinate function,
is a function assigning to each local web
![]() $W_{\mathfrak {T}}$
in
$W_{\mathfrak {T}}$
in
![]() $\mathscr {W}_{\mathfrak {T}}$
one integer coordinate per dot lying on the dotted triangle
$\mathscr {W}_{\mathfrak {T}}$
one integer coordinate per dot lying on the dotted triangle
![]() $\mathfrak {T}$
, satisfying the following properties:
$\mathfrak {T}$
, satisfying the following properties:
-
1. if a local web
 $W_{\mathfrak {T}}$
in
$W_{\mathfrak {T}}$
in
 $\mathscr {W}_{\mathfrak {T}}$
can be written
$\mathscr {W}_{\mathfrak {T}}$
can be written
 $W_{\mathfrak {T}} = W^\prime _{\mathfrak {T}} \sqcup W^{\prime \prime }_{\mathfrak {T}}$
as the disjoint union of two local webs, each in
$W_{\mathfrak {T}} = W^\prime _{\mathfrak {T}} \sqcup W^{\prime \prime }_{\mathfrak {T}}$
as the disjoint union of two local webs, each in
 $\mathscr {W}_{\mathfrak {T}}$
, then
$\mathscr {W}_{\mathfrak {T}}$
, then  $$ \begin{align*} \Phi_{\mathfrak{T}}(W_{\mathfrak{T}}) = \Phi_{\mathfrak{T}}(W^\prime_{\mathfrak{T}}) + \Phi_{\mathfrak{T}}(W^{\prime\prime}_{\mathfrak{T}}) \quad \in \mathbb{Z}^7; \end{align*} $$
$$ \begin{align*} \Phi_{\mathfrak{T}}(W_{\mathfrak{T}}) = \Phi_{\mathfrak{T}}(W^\prime_{\mathfrak{T}}) + \Phi_{\mathfrak{T}}(W^{\prime\prime}_{\mathfrak{T}}) \quad \in \mathbb{Z}^7; \end{align*} $$
-
2. for an edge E of
 $\mathfrak {T}$
, the ordered pair of coordinates
$\mathfrak {T}$
, the ordered pair of coordinates
 $(a^L_E, a^R_E)$
of the function
$(a^L_E, a^R_E)$
of the function
 $\Phi _{\mathfrak {T}}$
assigned to the left- and right-edge-dots lying on E, respectively, depends only on the pair
$\Phi _{\mathfrak {T}}$
assigned to the left- and right-edge-dots lying on E, respectively, depends only on the pair
 $(n^{\text {in}}_E, n^{\text {out}}_E)$
of numbers of in- and out-strands of the local web
$(n^{\text {in}}_E, n^{\text {out}}_E)$
of numbers of in- and out-strands of the local web
 $ W_{\mathfrak {T}}$
on the edge E; moreover, different pairs
$ W_{\mathfrak {T}}$
on the edge E; moreover, different pairs
 $(n_E^{\mathrm {in}}, n_E^{\mathrm {out}})$
yield different pairs of coordinates
$(n_E^{\mathrm {in}}, n_E^{\mathrm {out}})$
yield different pairs of coordinates
 $(a^L_E, a^R_E)$
;
$(a^L_E, a^R_E)$
; -
3. there are two symmetries; the first is that
 $\Phi _{\mathfrak {T}}$
respects the rotational symmetry of the triangle (see Remark 5.2 below for a more precise statement), and the second is that if the numbers
$\Phi _{\mathfrak {T}}$
respects the rotational symmetry of the triangle (see Remark 5.2 below for a more precise statement), and the second is that if the numbers
 $n^{\text {in}}_E$
and
$n^{\text {in}}_E$
and
 $n^{\text {out}}_E$
of in- and out-strands on an edge E are exchanged, then the coordinates
$n^{\text {out}}_E$
of in- and out-strands on an edge E are exchanged, then the coordinates
 $a^L_E$
and
$a^L_E$
and
 $a^R_E$
are exchanged as well;
$a^R_E$
are exchanged as well; -
4. observe, by property (1), the function
 $\Phi _{\mathfrak {T}}(W_{\mathfrak {T}}) = \Phi _{\mathfrak {T}}(W^\prime _{\mathfrak {T}})$
agrees on local webs
$\Phi _{\mathfrak {T}}(W_{\mathfrak {T}}) = \Phi _{\mathfrak {T}}(W^\prime _{\mathfrak {T}})$
agrees on local webs
 $W_{\mathfrak {T}}$
and
$W_{\mathfrak {T}}$
and
 $W^\prime _{\mathfrak {T}}$
in
$W^\prime _{\mathfrak {T}}$
in
 $\mathscr {W}_{\mathfrak {T}}$
representing the same corner-ambiguity class
$\mathscr {W}_{\mathfrak {T}}$
representing the same corner-ambiguity class
 $[W_{\mathfrak {T}}] = [W^\prime _{\mathfrak {T}}]$
in
$[W_{\mathfrak {T}}] = [W^\prime _{\mathfrak {T}}]$
in
 $[ \mathscr {W}_{\mathfrak {T}} ]$
(because
$[ \mathscr {W}_{\mathfrak {T}} ]$
(because
 $W_{\mathfrak {T}}$
and
$W_{\mathfrak {T}}$
and
 $W^\prime _{\mathfrak {T}}$
differ only by permutations of oriented corner arcs), thus inducing also called
$W^\prime _{\mathfrak {T}}$
differ only by permutations of oriented corner arcs), thus inducing also called $$ \begin{align*} \Phi_{\mathfrak{T}} : [\mathscr{W}_{\mathfrak{T}}] \longrightarrow \mathbb{Z}^7, \end{align*} $$
$$ \begin{align*} \Phi_{\mathfrak{T}} : [\mathscr{W}_{\mathfrak{T}}] \longrightarrow \mathbb{Z}^7, \end{align*} $$
 $\Phi _{\mathfrak {T}}$
; we require that this induced function
$\Phi _{\mathfrak {T}}$
; we require that this induced function
 $\Phi _{\mathfrak {T}}$
is an injection.
$\Phi _{\mathfrak {T}}$
is an injection.
The coordinates assigned by
![]() $\Phi _{\mathfrak {T}}$
to edge-dots (resp. triangle-dots) are called edge-coordinates (resp. triangle-coordinates).
$\Phi _{\mathfrak {T}}$
to edge-dots (resp. triangle-dots) are called edge-coordinates (resp. triangle-coordinates).

Figure 28 Property (1):
![]() $a_i = a_i^\prime + a_i^{\prime \prime }$
.
$a_i = a_i^\prime + a_i^{\prime \prime }$
.

Figure 29 Properties (2) and (3).
We illustrate properties (1), (2), (3) in Figures 28 and 29.
Remark 5.2. (from pictures to coordinates)
Let us be more precise about what we mean by the first symmetry of property (3), which will also allow us the opportunity to give a clearer explanation of the meaning of pictures such as those shown in the figures below. We will use the picture displayed on the left-hand side of Figure 28 as a reference. When we draw such a picture, we have implicitly selected a preferred vertex of the triangle
![]() $\mathfrak {T}$
, say the vertex appearing at the top of the picture; write
$\mathfrak {T}$
, say the vertex appearing at the top of the picture; write
![]() $\mathfrak {T}_0$
to indicate this extra data. A tuple
$\mathfrak {T}_0$
to indicate this extra data. A tuple
![]() $(a_1, a_2, \dots , a_7)\in \mathbb {Z}^7$
defines a function
$(a_1, a_2, \dots , a_7)\in \mathbb {Z}^7$
defines a function
![]() $\{\text {dots of }\mathfrak {T}_0\}\to \mathbb {Z}$
by sending the i-th dot to
$\{\text {dots of }\mathfrak {T}_0\}\to \mathbb {Z}$
by sending the i-th dot to
![]() $a_i$
, as indicated in the picture. If this tuple is associated to a local web
$a_i$
, as indicated in the picture. If this tuple is associated to a local web
![]() $W_{\mathfrak {T}_0}$
, then we say this tuple is the value
$W_{\mathfrak {T}_0}$
, then we say this tuple is the value
![]() $\Phi _{\mathfrak {T}_0}(W_{\mathfrak {T}_0})$
of the local coordinate function evaluated on the web
$\Phi _{\mathfrak {T}_0}(W_{\mathfrak {T}_0})$
of the local coordinate function evaluated on the web
![]() $W_{\mathfrak {T}_0}$
. The rotational symmetry of property (3) says that if
$W_{\mathfrak {T}_0}$
. The rotational symmetry of property (3) says that if
![]() $W^\prime _{\mathfrak {T}_0}$
is the different local web obtained by rotating
$W^\prime _{\mathfrak {T}_0}$
is the different local web obtained by rotating
![]() $W_{\mathfrak {T}_0}$
by
$W_{\mathfrak {T}_0}$
by
![]() $2\pi /3$
radians clockwise, with coordinates
$2\pi /3$
radians clockwise, with coordinates
![]() $\Phi _{\mathfrak {T}_0}(W^\prime _{\mathfrak {T}_0})=(a^\prime _1, a^\prime _2, \dots , a^\prime _7)$
, then
$\Phi _{\mathfrak {T}_0}(W^\prime _{\mathfrak {T}_0})=(a^\prime _1, a^\prime _2, \dots , a^\prime _7)$
, then
![]() $a^\prime _1=a_5$
,
$a^\prime _1=a_5$
,
![]() $a^\prime _2=a_6$
,
$a^\prime _2=a_6$
,
![]() $a^\prime _3=a_1$
,
$a^\prime _3=a_1$
,
![]() $a^\prime _4=a_2$
,
$a^\prime _4=a_2$
,
![]() $a^\prime _5=a_3$
,
$a^\prime _5=a_3$
,
![]() $a^\prime _6=a_4$
and
$a^\prime _6=a_4$
and
![]() $a^\prime _7=a_7$
. Lastly, we define
$a^\prime _7=a_7$
. Lastly, we define
![]() $\Phi _{\mathfrak {T}}(W_{\mathfrak {T}})=\Phi _{\mathfrak {T}_0}(W_{\mathfrak {T}_0})$
, and the rotational symmetry implies that this is independent of the choice of preferred vertex.
$\Phi _{\mathfrak {T}}(W_{\mathfrak {T}})=\Phi _{\mathfrak {T}_0}(W_{\mathfrak {T}_0})$
, and the rotational symmetry implies that this is independent of the choice of preferred vertex.
5.3. Local coordinates from Fock–Goncharov theory
We define an explicit Fock–Goncharov local coordinate function
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}: \mathscr {W}_{\mathfrak {T}} \to \mathbb {Z}_{\geqslant 0}^7$
valued in nonnegative integers.
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}: \mathscr {W}_{\mathfrak {T}} \to \mathbb {Z}_{\geqslant 0}^7$
valued in nonnegative integers.
By property (1) in Definition 5.1, it suffices to define
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
on connected local webs in
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
on connected local webs in
![]() $\mathscr {W}_{\mathfrak {T}}$
. By Proposition 3.18, these come in one of exactly eight types
$\mathscr {W}_{\mathfrak {T}}$
. By Proposition 3.18, these come in one of exactly eight types
![]() $H_n^{\text {out}}$
,
$H_n^{\text {out}}$
,
![]() $H_n^{\text {in}}$
,
$H_n^{\text {in}}$
,
![]() $R_1$
,
$R_1$
,
![]() $L_1$
,
$L_1$
,
![]() $R_2$
,
$R_2$
,
![]() $L_2$
,
$L_2$
,
![]() $R_3$
,
$R_3$
,
![]() $L_3$
illustrated in Figure 30. In the figure, note that in the two top left triangles we have, for visibility, drawn the local pictures
$L_3$
illustrated in Figure 30. In the figure, note that in the two top left triangles we have, for visibility, drawn the local pictures
![]() $\left < H_n^{\text {out}} \right>$
and
$\left < H_n^{\text {out}} \right>$
and
![]() $\left < H_n^{\text {in}} \right>$
as a shorthand for the actual n-out-honeycomb-web
$\left < H_n^{\text {in}} \right>$
as a shorthand for the actual n-out-honeycomb-web
![]() $H_n^{\text {out}}$
and n-in-honeycomb-web
$H_n^{\text {out}}$
and n-in-honeycomb-web
![]() $H_n^{\text {in}}$
, respectively; see Definition 3.20. It is immediate that
$H_n^{\text {in}}$
, respectively; see Definition 3.20. It is immediate that
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
satisfies property (3) and the first part of (2). The second part of (2) follows by the invertibility of the matrix
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
satisfies property (3) and the first part of (2). The second part of (2) follows by the invertibility of the matrix
![]() $\left ( \begin {smallmatrix} 2 & 1 \\ 1 & 2 \end {smallmatrix} \right )$
. We will check property (4) in §6.
$\left ( \begin {smallmatrix} 2 & 1 \\ 1 & 2 \end {smallmatrix} \right )$
. We will check property (4) in §6.
Remark 5.3.
-
1. Xie [Reference XieXie13] writes down the same local coordinates (up to a multiplicative factor of 3) for
 $R_1$
,
$R_1$
,
 $L_1$
,
$L_1$
,
 $R_2$
,
$R_2$
,
 $L_2$
,
$L_2$
,
 $R_3$
,
$R_3$
,
 $L_3$
as well as the one-honeycomb-webs
$L_3$
as well as the one-honeycomb-webs
 $H_1^{\text {out}}$
and
$H_1^{\text {out}}$
and
 $H_1^{\text {in}}$
.
$H_1^{\text {in}}$
. -
2. The definition of these local coordinates can be checked experimentally by studying the highest terms of the Fock–Goncharov
 $\mathrm {SL}_3$
-trace polynomials; see the introduction as well as [Reference KimKim20, Proposition 5.80] (and [Reference KimKim21, Proposition 3.15]). Moreover, it appears that these coordinates fit into a broader geometric context [Reference Sun, Wienhard and ZhangSWZ20, Theorem 8.22(2)].
$\mathrm {SL}_3$
-trace polynomials; see the introduction as well as [Reference KimKim20, Proposition 5.80] (and [Reference KimKim21, Proposition 3.15]). Moreover, it appears that these coordinates fit into a broader geometric context [Reference Sun, Wienhard and ZhangSWZ20, Theorem 8.22(2)]. -
3. The coordinates in the
 $\mathrm {SL}_2$
-setting are geometric intersection numbers; see the introduction. In contrast, the
$\mathrm {SL}_2$
-setting are geometric intersection numbers; see the introduction. In contrast, the
 $\mathrm {SL}_3$
-coordinates depend on the choice of orientation of
$\mathrm {SL}_3$
-coordinates depend on the choice of orientation of
 $\mathfrak {S}$
.
$\mathfrak {S}$
.

Figure 30 Fock–Goncharov local coordinate function
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
.
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
.
5.4. Global coordinates from local coordinate functions
Assume that, for an abstract dotted triangle
![]() $\mathfrak {T}$
, we have chosen an arbitrary local coordinate function
$\mathfrak {T}$
, we have chosen an arbitrary local coordinate function
![]() $\Phi _{\mathfrak {T}}: \mathscr {W}_{\mathfrak {T}} \to \mathbb {Z}^7$
. We show that this induces a global coordinate function
$\Phi _{\mathfrak {T}}: \mathscr {W}_{\mathfrak {T}} \to \mathbb {Z}^7$
. We show that this induces a global coordinate function
![]() $\Phi _{\lambda } : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}^N$
that is well adapted to the choice of
$\Phi _{\lambda } : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}^N$
that is well adapted to the choice of
![]() $\Phi _{\mathfrak {T}}$
. The argument uses only properties (1), the first part of (2) and (3) of
$\Phi _{\mathfrak {T}}$
. The argument uses only properties (1), the first part of (2) and (3) of
![]() $\Phi _{\mathfrak {T}}$
.
$\Phi _{\mathfrak {T}}$
.
As a guiding example of the construction to come, reference Figure 33, which uses the Fock–Goncharov local coordinate function
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
. This is an example on the once punctured torus
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
. This is an example on the once punctured torus
![]() $\mathfrak {S}$
. Note that the web W in the example has one hexagon-face. All of the other components of
$\mathfrak {S}$
. Note that the web W in the example has one hexagon-face. All of the other components of
![]() $W^c$
are not contractible. So W is nonelliptic.
$W^c$
are not contractible. So W is nonelliptic.
Step 1. Consider the split ideal triangulation
![]() $\widehat {\lambda }$
(§4.3). We put dots on each triangle
$\widehat {\lambda }$
(§4.3). We put dots on each triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
. The chosen local coordinate function
$\widehat {\lambda }$
. The chosen local coordinate function
![]() $\Phi _{\mathfrak {T}}$
can be associated to each of these dotted triangles
$\Phi _{\mathfrak {T}}$
can be associated to each of these dotted triangles
![]() $\mathfrak {T}$
; see the left-hand side of Figure 31.
$\mathfrak {T}$
; see the left-hand side of Figure 31.

Figure 31 Local coordinates
![]() $\Phi _{\mathfrak {T}}$
attached to the triangles
$\Phi _{\mathfrak {T}}$
attached to the triangles
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
(left), and the corresponding global coordinates
$\widehat {\lambda }$
(left), and the corresponding global coordinates
![]() $\Phi _{\lambda }$
attached to
$\Phi _{\lambda }$
attached to
![]() $\lambda $
(right).
$\lambda $
(right).
Step 2. Fix a nonelliptic web W on
![]() $\mathfrak {S}$
that is in good position (Definition 4.5) with respect to the split ideal triangulation
$\mathfrak {S}$
that is in good position (Definition 4.5) with respect to the split ideal triangulation
![]() $\widehat {\lambda }$
. We assign to W one integer coordinate per dot lying on the dotted ideal triangulation
$\widehat {\lambda }$
. We assign to W one integer coordinate per dot lying on the dotted ideal triangulation
![]() $\lambda $
, namely an element
$\lambda $
, namely an element
![]() $\Phi _{\lambda }(W)$
in
$\Phi _{\lambda }(W)$
in
![]() $\mathbb {Z}^N$
.
$\mathbb {Z}^N$
.
By good position, the local web restriction
![]() $W_{\mathfrak {T}} = W \cap \mathfrak {T}$
is in
$W_{\mathfrak {T}} = W \cap \mathfrak {T}$
is in
![]() $\mathscr {W}_{\mathfrak {T}}$
for each triangle
$\mathscr {W}_{\mathfrak {T}}$
for each triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
. So, we may evaluate the local coordinate function
$\widehat {\lambda }$
. So, we may evaluate the local coordinate function
![]() $\Phi _{\mathfrak {T}}$
on
$\Phi _{\mathfrak {T}}$
on
![]() $W_{\mathfrak {T}}$
, obtaining coordinates for each of the seven dots lying on the dotted triangle
$W_{\mathfrak {T}}$
, obtaining coordinates for each of the seven dots lying on the dotted triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
. For instance, in this way we assign coordinates to all of the dots shown on the left-hand side of Figure 31 above. We claim that these coordinates glue together along each biangle
$\widehat {\lambda }$
. For instance, in this way we assign coordinates to all of the dots shown on the left-hand side of Figure 31 above. We claim that these coordinates glue together along each biangle
![]() $\mathfrak {B}$
of
$\mathfrak {B}$
of
![]() $\widehat {\lambda }$
in such a way that we obtain one coordinate per dot lying on the dotted ideal triangulation
$\widehat {\lambda }$
in such a way that we obtain one coordinate per dot lying on the dotted ideal triangulation
![]() $\lambda $
; see Figure 31.
$\lambda $
; see Figure 31.
Indeed, suppose
![]() $\mathfrak {B}$
is a biangle between two triangles
$\mathfrak {B}$
is a biangle between two triangles
![]() $\mathfrak {T}^\prime $
and
$\mathfrak {T}^\prime $
and
![]() $\mathfrak {T}^{\prime \prime }$
of
$\mathfrak {T}^{\prime \prime }$
of
![]() $\widehat {\lambda }$
. Let
$\widehat {\lambda }$
. Let
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
be the corresponding boundary edges of
$E^{\prime \prime }$
be the corresponding boundary edges of
![]() $\mathfrak {B}$
, and let
$\mathfrak {B}$
, and let
![]() $a^{ L}_{E^\prime }$
and
$a^{ L}_{E^\prime }$
and
![]() $a^{ R}_{E^\prime }$
(resp.
$a^{ R}_{E^\prime }$
(resp.
![]() $a^{ L}_{E^{\prime \prime }}$
and
$a^{ L}_{E^{\prime \prime }}$
and
![]() $a^{ R}_{E^{\prime \prime }}$
) be the coordinates assigned by
$a^{ R}_{E^{\prime \prime }}$
) be the coordinates assigned by
![]() $\Phi _{\mathfrak {T}^\prime }$
(resp.
$\Phi _{\mathfrak {T}^\prime }$
(resp.
![]() $\Phi _{\mathfrak {T}^{\prime \prime }}$
) to the left- and right-edge-dots, respectively, lying on
$\Phi _{\mathfrak {T}^{\prime \prime }}$
) to the left- and right-edge-dots, respectively, lying on
![]() $E^\prime $
(resp.
$E^\prime $
(resp.
![]() $E^{\prime \prime }$
) as viewed from
$E^{\prime \prime }$
) as viewed from
![]() $\mathfrak {T}^\prime $
(resp.
$\mathfrak {T}^\prime $
(resp.
![]() $\mathfrak {T}^{\prime \prime }$
). Also, denote by
$\mathfrak {T}^{\prime \prime }$
). Also, denote by
![]() $n^{\text {in}}_{E^\prime }$
and
$n^{\text {in}}_{E^\prime }$
and
![]() $n^{\text {out}}_{E^\prime }$
(resp.
$n^{\text {out}}_{E^\prime }$
(resp.
![]() $n^{\text {in}}_{E^{\prime \prime }}$
and
$n^{\text {in}}_{E^{\prime \prime }}$
and
![]() $n^{\text {out}}_{E^{\prime \prime }}$
) the numbers of in- and out-strands of the local web restriction
$n^{\text {out}}_{E^{\prime \prime }}$
) the numbers of in- and out-strands of the local web restriction
![]() $W_{\mathfrak {T}^\prime }$
(resp.
$W_{\mathfrak {T}^\prime }$
(resp.
![]() $W_{\mathfrak {T}^{\prime \prime }}$
) lying on the edge
$W_{\mathfrak {T}^{\prime \prime }}$
) lying on the edge
![]() $E^\prime $
(resp.
$E^\prime $
(resp.
![]() $E^{\prime \prime }$
); see Figure 32.
$E^{\prime \prime }$
); see Figure 32.

Figure 32 Local coordinates attached to a biangle:
![]() $a^L_{E^\prime } = a^R_{E^{\prime \prime }}$
and
$a^L_{E^\prime } = a^R_{E^{\prime \prime }}$
and
![]() $a^R_{E^\prime } = a^L_{E^{\prime \prime }}$
.
$a^R_{E^\prime } = a^L_{E^{\prime \prime }}$
.

Figure 33 Tropical Fock–Goncharov
![]() $\mathcal {A}$
-coordinates for a nonelliptic web.
$\mathcal {A}$
-coordinates for a nonelliptic web.
Since, by good position, the restriction
![]() $W_{\mathfrak {B}} = W \cap \mathfrak {B}$
is a ladder-web, we have
$W_{\mathfrak {B}} = W \cap \mathfrak {B}$
is a ladder-web, we have
![]() $n^{\text {out}}_{E^\prime } = n^{\text {in}}_{E^{\prime \prime }}$
and
$n^{\text {out}}_{E^\prime } = n^{\text {in}}_{E^{\prime \prime }}$
and
![]() $ n^{\text {in}}_{E^{\prime }} = n^{\text {out}}_{E^{\prime \prime }}$
. It follows immediately from properties (3) and the first part of (2) that the coordinates across from each other agree
$ n^{\text {in}}_{E^{\prime }} = n^{\text {out}}_{E^{\prime \prime }}$
. It follows immediately from properties (3) and the first part of (2) that the coordinates across from each other agree
![]() $a^L_{E^\prime } = a^R_{E^{\prime \prime }}$
and
$a^L_{E^\prime } = a^R_{E^{\prime \prime }}$
and
![]() $a^R_{E^\prime } = a^L_{E^{\prime \prime }}$
. So, we may glue together the two pairs of coordinates into two coordinates lying on the edge E of
$a^R_{E^\prime } = a^L_{E^{\prime \prime }}$
. So, we may glue together the two pairs of coordinates into two coordinates lying on the edge E of
![]() $\lambda $
, as desired.
$\lambda $
, as desired.
Step 3. For a general nonelliptic web
![]() $W^\prime $
on
$W^\prime $
on
![]() $\mathfrak {S}$
, by the first part of Proposition 4.7 there exists a nonelliptic web W that is parallel equivalent to
$\mathfrak {S}$
, by the first part of Proposition 4.7 there exists a nonelliptic web W that is parallel equivalent to
![]() $W^\prime $
and that is in good position with respect to the split ideal triangulation
$W^\prime $
and that is in good position with respect to the split ideal triangulation
![]() $\widehat {\lambda }$
. Define
$\widehat {\lambda }$
. Define
![]() $\Phi _{\lambda }(W^\prime ) = \Phi _{\lambda }(W)$
in
$\Phi _{\lambda }(W^\prime ) = \Phi _{\lambda }(W)$
in
![]() $\mathbb {Z}^N$
.
$\mathbb {Z}^N$
.
To show
![]() $\Phi _{\lambda }(W^\prime )$
is well defined, suppose
$\Phi _{\lambda }(W^\prime )$
is well defined, suppose
![]() $W_2$
is another web as W. By the second part of Proposition 4.7, the nonelliptic webs W and
$W_2$
is another web as W. By the second part of Proposition 4.7, the nonelliptic webs W and
![]() $W_2$
are related by a sequence of modified H-moves and global parallel-moves. The effect of either of these moves on a web in good position is to swap, possibly many, parallel oppositely oriented corner arcs in the triangles
$W_2$
are related by a sequence of modified H-moves and global parallel-moves. The effect of either of these moves on a web in good position is to swap, possibly many, parallel oppositely oriented corner arcs in the triangles
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
; recall Figures 25 and 3 above, respectively. By property (1) of
$\widehat {\lambda }$
; recall Figures 25 and 3 above, respectively. By property (1) of
![]() $\Phi _{\mathfrak {T}}$
, we have
$\Phi _{\mathfrak {T}}$
, we have
![]() $\Phi _{\lambda }(W) = \Phi _{\lambda }(W_2)$
.
$\Phi _{\lambda }(W) = \Phi _{\lambda }(W_2)$
.
From this point on, our approach diverges from that in [Reference Frohman and SikoraFS22]. In particular, our coordinates are different from theirs.
Definition 5.4. The Fock–Goncharov global coordinate function
is the well defined global coordinate function on
![]() $[\mathscr {W}_{\mathfrak {S}}]$
, valued in nonnegative integers, induced by the Fock–Goncharov local coordinate function
$[\mathscr {W}_{\mathfrak {S}}]$
, valued in nonnegative integers, induced by the Fock–Goncharov local coordinate function
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
. In §7-8, we prove:
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}$
. In §7-8, we prove:
Proposition 5.5. The Fock–Goncharov global coordinate function
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
is an injection of sets.
$\Phi _{\lambda }^{\mathrm {FG}}$
is an injection of sets.
Remark 5.6. Proposition 5.5 is valid for any global coordinate function
![]() $\Phi _{\lambda } : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}^N$
induced by a local coordinate function
$\Phi _{\lambda } : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}^N$
induced by a local coordinate function
![]() $\Phi _{\mathfrak {T}} : [\mathscr {W}_{\mathfrak {T}}] \to \mathbb {Z}^7$
. The proof is the same as the one we will give for
$\Phi _{\mathfrak {T}} : [\mathscr {W}_{\mathfrak {T}}] \to \mathbb {Z}^7$
. The proof is the same as the one we will give for
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
and uses properties (4) and the second part of (2) in Definition 5.1.
$\Phi _{\lambda }^{\mathrm {FG}}$
and uses properties (4) and the second part of (2) in Definition 5.1.
Remark 5.7. (relation to Fock–Goncharov theory; see [Reference Douglas and SunDS20b] for a more detailed discussion)
To a surface-with-boundary
![]() $\widehat {\mathfrak {S}}$
(see §9 below), Fock–Goncharov/Goncharov–Shen [Reference Fock and GoncharovFG06, Reference Goncharov and ShenGS15] associated two dual moduli spaces
$\widehat {\mathfrak {S}}$
(see §9 below), Fock–Goncharov/Goncharov–Shen [Reference Fock and GoncharovFG06, Reference Goncharov and ShenGS15] associated two dual moduli spaces
![]() $\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}$
and
$\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}$
and
![]() $\mathscr {R}_{\mathrm {SL}_n,\widehat {\mathfrak {S}}}$
, both of which are certain generalizations of the character variety. They are dual in the sense of Fock–Goncharov–Shen duality, which in particular says that the positive tropical integer points
$\mathscr {R}_{\mathrm {SL}_n,\widehat {\mathfrak {S}}}$
, both of which are certain generalizations of the character variety. They are dual in the sense of Fock–Goncharov–Shen duality, which in particular says that the positive tropical integer points
![]() $\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)$
of the
$\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)$
of the
![]() $\mathcal {A}$
-moduli space index a natural linear basis for the ring
$\mathcal {A}$
-moduli space index a natural linear basis for the ring
![]() $\mathscr {O}(\mathscr {R}_{\mathrm {SL}_n,\widehat {\mathfrak {S}}})$
of regular functions on the generalized character variety. Here, the positivity is taken with respect to the tropicalized Goncharov–Shen potential.
$\mathscr {O}(\mathscr {R}_{\mathrm {SL}_n,\widehat {\mathfrak {S}}})$
of regular functions on the generalized character variety. Here, the positivity is taken with respect to the tropicalized Goncharov–Shen potential.
An ideal triangulation
![]() $\lambda $
determines a coordinate chart
$\lambda $
determines a coordinate chart
![]() $\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_\lambda $
of
$\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_\lambda $
of
![]() $\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)$
. More concretely, in coordinates the positivity condition with respect to the tropicalized Goncharov–Shen potential translates to the Knutson–Tao rhombus inequalities (see §6 below), and in this way the coordinate chart
$\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)$
. More concretely, in coordinates the positivity condition with respect to the tropicalized Goncharov–Shen potential translates to the Knutson–Tao rhombus inequalities (see §6 below), and in this way the coordinate chart
![]() $\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_\lambda \cong \mathscr {C}^+_{\lambda }$
becomes identified with the Knutson–Tao cone
$\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_\lambda \cong \mathscr {C}^+_{\lambda }$
becomes identified with the Knutson–Tao cone
![]() $\mathscr {C}^+_{\lambda }$
. If
$\mathscr {C}^+_{\lambda }$
. If
![]() $\lambda ^\prime $
is another ideal triangulation, the coordinate change map
$\lambda ^\prime $
is another ideal triangulation, the coordinate change map
![]() $\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_\lambda \to \mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_{\lambda ^\prime }$
takes the form of a tropicalized
$\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_\lambda \to \mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)_{\lambda ^\prime }$
takes the form of a tropicalized
![]() $\mathcal {A}$
-coordinate cluster transformation. For these reasons, Theorems 1.1 and 1.2 can be interpreted as saying that the web coordinates constructed above provide a natural identification between the set
$\mathcal {A}$
-coordinate cluster transformation. For these reasons, Theorems 1.1 and 1.2 can be interpreted as saying that the web coordinates constructed above provide a natural identification between the set
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
of parallel equivalence classes of rungless essential webs (see §9 below) and the positive tropical integer points
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
of parallel equivalence classes of rungless essential webs (see §9 below) and the positive tropical integer points
![]() $\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)$
.
$\mathcal {A}_{\mathrm {PGL}_3,\widehat {\mathfrak {S}}}^+(\mathbb {Z}^t)$
.
As another concrete manifestation of Fock–Goncharov duality, when the trace function
![]() $\mathrm {Tr}_W$
on the
$\mathrm {Tr}_W$
on the
![]() $\mathrm {SL}_3$
-character variety associated to a basis web W is written as a polynomial in the Fock–Goncharov
$\mathrm {SL}_3$
-character variety associated to a basis web W is written as a polynomial in the Fock–Goncharov
![]() $\mathcal {X}$
-coordinates, then this polynomial has a unique highest term, whose exponents are precisely the tropical
$\mathcal {X}$
-coordinates, then this polynomial has a unique highest term, whose exponents are precisely the tropical
![]() $\mathcal {A}$
-coordinates assigned to the web W; see §9.3 below for more precise statements.
$\mathcal {A}$
-coordinates assigned to the web W; see §9.3 below for more precise statements.
For a discussion of previous works motivating our construction, see the introduction as well as Remarks 3.10(2), 4.4, 5.3(1, 2), 6.5(1), 9.2, 9.12(2).
6. Knutson–Tao cone
For
![]() $N = - 8 \chi (\mathfrak {S})> 0$
, we construct a subset
$N = - 8 \chi (\mathfrak {S})> 0$
, we construct a subset
![]() $\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
that we will show, in §7-8, is the image
$\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
that we will show, in §7-8, is the image
![]() $\mathscr {C}^+_{\lambda }=\Phi _{\lambda }^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {S}}])$
of the mapping
$\mathscr {C}^+_{\lambda }=\Phi _{\lambda }^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {S}}])$
of the mapping
![]() $\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
constructed in §5. The subset
$\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
constructed in §5. The subset
![]() $\mathscr {C}^+_{\lambda }$
is called the Knutson–Tao cone associated to the ideal triangulation
$\mathscr {C}^+_{\lambda }$
is called the Knutson–Tao cone associated to the ideal triangulation
![]() $\lambda $
, and is defined by finitely many Knutson–Tao rhombus inequalities and modulo 3 congruence conditions.
$\lambda $
, and is defined by finitely many Knutson–Tao rhombus inequalities and modulo 3 congruence conditions.
6.1. Integer cones
Definition 6.1. An integer cone, or just cone,
![]() $\mathscr {C}$
is a submonoid of
$\mathscr {C}$
is a submonoid of
![]() $\mathbb {Z}^n$
for some positive integer n. In other words,
$\mathbb {Z}^n$
for some positive integer n. In other words,
![]() $\mathscr {C} \subseteq \mathbb {Z}^n$
is a subset that contains 0 and is closed under addition.
$\mathscr {C} \subseteq \mathbb {Z}^n$
is a subset that contains 0 and is closed under addition.
A partition of
![]() $\mathscr {C}$
is a decomposition
$\mathscr {C}$
is a decomposition
![]() $\mathscr {C} = \mathscr {C}_1 \sqcup \mathscr {C}_2 \sqcup \dots \sqcup \mathscr {C}_k$
as a disjoint union of subsets.
$\mathscr {C} = \mathscr {C}_1 \sqcup \mathscr {C}_2 \sqcup \dots \sqcup \mathscr {C}_k$
as a disjoint union of subsets.
A positive integer cone, or just positive cone,
![]() $\mathscr {C}^+$
is a cone that is contained in
$\mathscr {C}^+$
is a cone that is contained in
![]() $\mathbb {Z}_{\geqslant 0}^n$
.
$\mathbb {Z}_{\geqslant 0}^n$
.
We define notions of independence for cones.
Definition 6.2. Let
![]() $\mathscr {C} \subseteq \mathbb {Z}^n \subseteq \mathbb {Q}^n$
be a cone, and let
$\mathscr {C} \subseteq \mathbb {Z}^n \subseteq \mathbb {Q}^n$
be a cone, and let
![]() $\Omega \subseteq \mathbb {Q}$
be a subset such that
$\Omega \subseteq \mathbb {Q}$
be a subset such that
![]() $0 \in \Omega $
. Let
$0 \in \Omega $
. Let
![]() $c_1, c_2, \dots , c_k$
be a collection of cone points in
$c_1, c_2, \dots , c_k$
be a collection of cone points in
![]() $\mathscr {C}$
. We say that the cone points
$\mathscr {C}$
. We say that the cone points
![]() $\{ c_i \}$
$\{ c_i \}$
-
1. span the cone
 $\mathscr {C}$
if every cone point
$\mathscr {C}$
if every cone point
 $c \in \mathscr {C}$
can be written as a
$c \in \mathscr {C}$
can be written as a
 $\mathbb {Z}_{\geqslant 0}$
-linear combination of the cone points
$\mathbb {Z}_{\geqslant 0}$
-linear combination of the cone points
 $\{ c_i \}$
;
$\{ c_i \}$
; -
2. are weakly independent over
 $\Omega $
if
$\Omega $
if  $$ \begin{align*} \omega_1 c_1 + \cdots + \omega_k c_k = 0 \in \mathbb{Q}^n \quad \Longrightarrow \quad \omega_1 = \cdots = \omega_k = 0 \quad\quad \left( \omega_1, \dots, \omega_k \in \Omega \right); \end{align*} $$
$$ \begin{align*} \omega_1 c_1 + \cdots + \omega_k c_k = 0 \in \mathbb{Q}^n \quad \Longrightarrow \quad \omega_1 = \cdots = \omega_k = 0 \quad\quad \left( \omega_1, \dots, \omega_k \in \Omega \right); \end{align*} $$
-
3. form a weak basis of
 $\mathscr {C}$
if they span
$\mathscr {C}$
if they span
 $\mathscr {C}$
and are weakly independent over
$\mathscr {C}$
and are weakly independent over
 $\Omega =\mathbb {Z}_{\geqslant 0} \subseteq \mathbb {Q}$
;
$\Omega =\mathbb {Z}_{\geqslant 0} \subseteq \mathbb {Q}$
; -
4. are strongly independent over
 $\Omega $
if
$\Omega $
if  $$ \begin{align*} \omega_1 c_1 + \cdots + \omega_k c_k = \omega^\prime_1 c_1 + \cdots + \omega^\prime_k c_k \in \mathbb{Q}^n \quad \Longrightarrow \quad \omega_1 = \omega^\prime_1, \dots, \omega_k = \omega^\prime_k \quad\quad ( \omega_i, \omega^\prime_j \in \Omega ). \end{align*} $$
$$ \begin{align*} \omega_1 c_1 + \cdots + \omega_k c_k = \omega^\prime_1 c_1 + \cdots + \omega^\prime_k c_k \in \mathbb{Q}^n \quad \Longrightarrow \quad \omega_1 = \omega^\prime_1, \dots, \omega_k = \omega^\prime_k \quad\quad ( \omega_i, \omega^\prime_j \in \Omega ). \end{align*} $$
Note:
-
• strongly independent over
 $\Omega \Longrightarrow $
weakly independent over
$\Omega \Longrightarrow $
weakly independent over
 $\Omega $
;
$\Omega $
; -
• strongly independent over
 $\mathbb {Z}_{\geqslant 0}$
$\mathbb {Z}_{\geqslant 0}$
 $\Longleftrightarrow $
weakly independent over
$\Longleftrightarrow $
weakly independent over
 $\mathbb {Z}$
$\mathbb {Z}$
 $\Longleftrightarrow $
linearly independent over
$\Longleftrightarrow $
linearly independent over
 $\mathbb {Q}$
(the usual definition from linear algebra).
$\mathbb {Q}$
(the usual definition from linear algebra).
The following technical fact is immediate from the definitions.
Lemma 6.3. Let
![]() $\mathscr {C}, \mathscr {C}^\prime \subseteq \mathbb {Z}^n$
be two cones. Consider a
$\mathscr {C}, \mathscr {C}^\prime \subseteq \mathbb {Z}^n$
be two cones. Consider a
![]() $\mathbb {Z}_{\geqslant 0}$
-linear bijection
$\mathbb {Z}_{\geqslant 0}$
-linear bijection
![]() $\psi \colon \mathscr {C}^\prime \to \mathscr {C}$
that extends to a
$\psi \colon \mathscr {C}^\prime \to \mathscr {C}$
that extends to a
![]() $\mathbb {Q}$
-linear isomorphism
$\mathbb {Q}$
-linear isomorphism
![]() $\widetilde {\psi } : \mathbb {Q}^n \to \mathbb {Q}^n$
. Let
$\widetilde {\psi } : \mathbb {Q}^n \to \mathbb {Q}^n$
. Let
![]() $\{ c_i \}$
be cone points of
$\{ c_i \}$
be cone points of
![]() $\mathscr {C}$
, and let
$\mathscr {C}$
, and let
![]() $\{ c^\prime _i\}$
be cone points of
$\{ c^\prime _i\}$
be cone points of
![]() $\mathscr {C}^\prime $
, such that
$\mathscr {C}^\prime $
, such that
![]() $\psi (c_i^\prime ) = c_i$
. Then,
$\psi (c_i^\prime ) = c_i$
. Then,
-
1. if the cone points
 $\{ c^\prime _i \}$
span
$\{ c^\prime _i \}$
span
 $\mathscr {C}^\prime $
, then the cone points
$\mathscr {C}^\prime $
, then the cone points
 $\{ c_i \}$
span
$\{ c_i \}$
span
 $\mathscr {C}$
;
$\mathscr {C}$
; -
2. if the
 $\{ c^\prime _i \}$
are weakly independent over
$\{ c^\prime _i \}$
are weakly independent over
 $\mathbb {Z}_{\geqslant 0}$
, then so are the
$\mathbb {Z}_{\geqslant 0}$
, then so are the
 $\{ c_i \}$
;
$\{ c_i \}$
; -
3. therefore, if the
 $\{ c^\prime _i \}$
form a weak basis of
$\{ c^\prime _i \}$
form a weak basis of
 $\mathscr {C}^\prime $
, then the
$\mathscr {C}^\prime $
, then the
 $\{ c_i \}$
form a weak basis of
$\{ c_i \}$
form a weak basis of
 $\mathscr {C}$
;
$\mathscr {C}$
; -
4. if the
 $\{ c^\prime _i \}$
are strongly independent over
$\{ c^\prime _i \}$
are strongly independent over
 $\mathbb {Z}_{\geqslant 0}$
, then so are the
$\mathbb {Z}_{\geqslant 0}$
, then so are the
 $\{ c_i \}$
;
$\{ c_i \}$
; -
5. the function
 $\psi $
sends partitions of
$\psi $
sends partitions of
 $\mathscr {C}^\prime $
to partitions of
$\mathscr {C}^\prime $
to partitions of
 $\mathscr {C}$
.
$\mathscr {C}$
.
6.2. Local Knutson–Tao cone
Let
![]() $\mathfrak {T}$
be a dotted ideal triangle (§5.1); recall Figure 27b above. In this section, we are going to order the dots on
$\mathfrak {T}$
be a dotted ideal triangle (§5.1); recall Figure 27b above. In this section, we are going to order the dots on
![]() $\mathfrak {T}$
so that if the dots are labeled as in the left-hand side of Figure 34, then a point
$\mathfrak {T}$
so that if the dots are labeled as in the left-hand side of Figure 34, then a point
![]() $c \in \mathbb {Z}^7$
will be written
$c \in \mathbb {Z}^7$
will be written

Figure 34 Rhombus numbers.
Let
![]() $\mathbb {Z}/3 \subseteq \mathbb {Q}$
denote the set of integer thirds within the rational numbers, namely
$\mathbb {Z}/3 \subseteq \mathbb {Q}$
denote the set of integer thirds within the rational numbers, namely
![]() $\mathbb {Z}/3$
is the image of the map
$\mathbb {Z}/3$
is the image of the map
![]() $\mathbb {Z} \to \mathbb {Q}$
sending
$\mathbb {Z} \to \mathbb {Q}$
sending
![]() $n \mapsto n/3$
. Note that
$n \mapsto n/3$
. Note that
![]() $\mathbb {Z} \subseteq \mathbb {Z}/3$
.
$\mathbb {Z} \subseteq \mathbb {Z}/3$
.
To each point
![]() $c \in \mathbb {Z}^7$
, as in Equation (*), associate a nine-tuple of rhombus numbers
$c \in \mathbb {Z}^7$
, as in Equation (*), associate a nine-tuple of rhombus numbers
by the linear equations (see Figure 34 above)
Definition 6.4. The local Knutson–Tao positive cone, or just local Knutson–Tao cone or local cone,
![]() $\mathscr {C}^+_{\mathfrak {T}}$
associated to the dotted ideal triangle
$\mathscr {C}^+_{\mathfrak {T}}$
associated to the dotted ideal triangle
![]() $\mathfrak {T}$
is defined by
$\mathfrak {T}$
is defined by
By linearity, this indeed defines a cone contained in
![]() $\mathbb {Z}^7$
. We will prove below in this subsection that
$\mathbb {Z}^7$
. We will prove below in this subsection that
![]() $\mathscr {C}^+_{\mathfrak {T}} \subseteq \mathbb {Z}_{\geqslant 0}^7$
is, in fact, a positive cone.
$\mathscr {C}^+_{\mathfrak {T}} \subseteq \mathbb {Z}_{\geqslant 0}^7$
is, in fact, a positive cone.
Remark 6.5.
-
1. The inequalities
 $3 r_{ij} \geqslant 0$
are known as the Knutson–Tao rhombus inequalities; see [Reference Knutson and TaoKT99, Appendix 2] and [Reference Goncharov and ShenGS15, §3.1]. Note that
$3 r_{ij} \geqslant 0$
are known as the Knutson–Tao rhombus inequalities; see [Reference Knutson and TaoKT99, Appendix 2] and [Reference Goncharov and ShenGS15, §3.1]. Note that
 $3 r_{ij}$
is always in
$3 r_{ij}$
is always in
 $\mathbb {Z}$
by definition. We impose the additional modulo 3 congruence condition that the
$\mathbb {Z}$
by definition. We impose the additional modulo 3 congruence condition that the
 $r_{ij}$
are integers. This is analogous to the parity condition imposed in [Reference FockFoc97, §3.1] in the case of
$r_{ij}$
are integers. This is analogous to the parity condition imposed in [Reference FockFoc97, §3.1] in the case of
 $\mathrm {SL}_2$
.
$\mathrm {SL}_2$
. -
2. By the proof of Proposition 6.6 below, we could just as well have taken rational coefficients
 $c \in \mathbb {Q}^7$
in Definition 6.4 without changing the resulting cone
$c \in \mathbb {Q}^7$
in Definition 6.4 without changing the resulting cone
 $\mathscr {C}^+_{\mathfrak {T}} \subseteq \mathbb {Z}_{\geqslant 0}^7 \subseteq \mathbb {Q}^7$
. That is, any rational solution to
$\mathscr {C}^+_{\mathfrak {T}} \subseteq \mathbb {Z}_{\geqslant 0}^7 \subseteq \mathbb {Q}^7$
. That is, any rational solution to
 $r(c) \in \mathbb {Z}_{\geqslant 0}^9$
is, in fact, a nonnegative integer solution.
$r(c) \in \mathbb {Z}_{\geqslant 0}^9$
is, in fact, a nonnegative integer solution.
To see that
![]() $\mathscr {C}^+_{\mathfrak {T}}$
is nontrivial, one checks that the image
$\mathscr {C}^+_{\mathfrak {T}}$
is nontrivial, one checks that the image
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}(\mathscr {W}_{\mathfrak {T}})$
of the Fock-Goncharov local coordinate function
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}(\mathscr {W}_{\mathfrak {T}})$
of the Fock-Goncharov local coordinate function
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}} : \mathscr {W}_{\mathfrak {T}} \to \mathbb {Z}_{\geqslant 0}^7$
(§5.3) lies in the local cone
$\Phi _{\mathfrak {T}}^{\mathrm {FG}} : \mathscr {W}_{\mathfrak {T}} \to \mathbb {Z}_{\geqslant 0}^7$
(§5.3) lies in the local cone
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}(\mathscr {W}_{\mathfrak {T}}) \subseteq \mathscr {C}^+_{\mathfrak {T}}$
. By property (1) in Definition 5.1, it suffices to check this on the connected local webs in
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}(\mathscr {W}_{\mathfrak {T}}) \subseteq \mathscr {C}^+_{\mathfrak {T}}$
. By property (1) in Definition 5.1, it suffices to check this on the connected local webs in
![]() $\mathscr {W}_{\mathfrak {T}}$
; recall Figure 30 above. Specifically, using the convention in Equation (*), we have
$\mathscr {W}_{\mathfrak {T}}$
; recall Figure 30 above. Specifically, using the convention in Equation (*), we have
 $$ \begin{align*} c(R_1) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(R_1) = \left(0, 0, 1, 2, 2, 1, 1\right), \quad\quad\quad\quad\quad c(L_1) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_1) = \left(0, 0, 2, 1, 1, 2, 2\right),\\c(R_2) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(R_2) = \left(2, 1, 0, 0, 1, 2, 1\right), \quad\quad\quad\quad\quad c(L_2) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_2) =\left(1, 2, 0, 0, 2, 1, 2\right),\\c(R_3) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(R_3) =\left(1, 2, 2, 1, 0, 0, 1\right), \quad\quad\quad\quad\quad c(L_3) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_3) =\left(2, 1, 1, 2, 0, 0, 2\right),\\c(H_n^{\mathrm{in}}) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(H_n^{\mathrm{in}}) =\left(2n, n, 2n, n, 2n, n, 3n\right), \hphantom{\quad\quad\quad\quad\quad c(L_1) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_1) = \left(0, 0, 2, 1, 1, 2, 2\right),}\\c(H_n^{\mathrm{out}}) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(H_n^{\mathrm{out}}) =\left(n, 2n, n, 2n, n, 2n, 3n\right). \hphantom{\quad\quad\quad\quad\quad c(L_1) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_1) = \left(0, 0, 2, 1, 1, 2, 2\right),}\end{align*} $$
$$ \begin{align*} c(R_1) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(R_1) = \left(0, 0, 1, 2, 2, 1, 1\right), \quad\quad\quad\quad\quad c(L_1) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_1) = \left(0, 0, 2, 1, 1, 2, 2\right),\\c(R_2) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(R_2) = \left(2, 1, 0, 0, 1, 2, 1\right), \quad\quad\quad\quad\quad c(L_2) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_2) =\left(1, 2, 0, 0, 2, 1, 2\right),\\c(R_3) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(R_3) =\left(1, 2, 2, 1, 0, 0, 1\right), \quad\quad\quad\quad\quad c(L_3) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_3) =\left(2, 1, 1, 2, 0, 0, 2\right),\\c(H_n^{\mathrm{in}}) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(H_n^{\mathrm{in}}) =\left(2n, n, 2n, n, 2n, n, 3n\right), \hphantom{\quad\quad\quad\quad\quad c(L_1) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_1) = \left(0, 0, 2, 1, 1, 2, 2\right),}\\c(H_n^{\mathrm{out}}) &= \Phi_{\mathfrak{T}}^{\mathrm{FG}}(H_n^{\mathrm{out}}) =\left(n, 2n, n, 2n, n, 2n, 3n\right). \hphantom{\quad\quad\quad\quad\quad c(L_1) = \Phi_{\mathfrak{T}}^{\mathrm{FG}}(L_1) = \left(0, 0, 2, 1, 1, 2, 2\right),}\end{align*} $$
The associated nine-tuples of rhombus numbers are
 $$ \begin{align*} r(c(R_1)) &= \left(1, 0, 0, 0, 0, 0, 0, 0, 0\right), \quad\quad r(c(L_1)) = \left(0, 1, 1, 0, 0, 0, 0, 0, 0\right),\\r(c(R_2)) &= \left(0, 0, 0, 1, 0, 0, 0, 0, 0\right), \quad\quad r(c(L_2)) = \left(0, 0, 0, 0, 1, 1, 0, 0, 0\right),\\r(c(R_3)) &= \left(0, 0, 0, 0, 0, 0, 1, 0, 0\right), \quad\quad r(c(L_3)) = \left(0, 0, 0, 0, 0, 0, 0, 1, 1\right), \\r(c(H_n^{\mathrm{in}})) &= \left(0, 0, n, 0, 0, n, 0, 0, n\right), \hphantom{\quad\quad r(c(L_1)) = \left(0, 1, 1, 0, 0, 0, 0, 0, 0\right),}\\r(c(H_n^{\mathrm{out}})) &= \left(0, n, 0, 0, n, 0, 0, n, 0\right). \hphantom{\quad\quad r(c(L_1)) = \left(0, 1, 1, 0, 0, 0, 0, 0, 0\right),} \end{align*} $$
$$ \begin{align*} r(c(R_1)) &= \left(1, 0, 0, 0, 0, 0, 0, 0, 0\right), \quad\quad r(c(L_1)) = \left(0, 1, 1, 0, 0, 0, 0, 0, 0\right),\\r(c(R_2)) &= \left(0, 0, 0, 1, 0, 0, 0, 0, 0\right), \quad\quad r(c(L_2)) = \left(0, 0, 0, 0, 1, 1, 0, 0, 0\right),\\r(c(R_3)) &= \left(0, 0, 0, 0, 0, 0, 1, 0, 0\right), \quad\quad r(c(L_3)) = \left(0, 0, 0, 0, 0, 0, 0, 1, 1\right), \\r(c(H_n^{\mathrm{in}})) &= \left(0, 0, n, 0, 0, n, 0, 0, n\right), \hphantom{\quad\quad r(c(L_1)) = \left(0, 1, 1, 0, 0, 0, 0, 0, 0\right),}\\r(c(H_n^{\mathrm{out}})) &= \left(0, n, 0, 0, n, 0, 0, n, 0\right). \hphantom{\quad\quad r(c(L_1)) = \left(0, 1, 1, 0, 0, 0, 0, 0, 0\right),} \end{align*} $$
By rank considerations, the eight cone points
![]() $c(R_1)$
,
$c(R_1)$
,
![]() $c(L_1)$
,
$c(L_1)$
,
![]() $c(R_2)$
,
$c(R_2)$
,
![]() $c(L_2)$
,
$c(L_2)$
,
![]() $c(R_3)$
,
$c(R_3)$
,
![]() $c(L_3)$
,
$c(L_3)$
,
![]() $c(H_n^{\mathrm {in}})$
,
$c(H_n^{\mathrm {in}})$
,
![]() $c(H_n^{\mathrm {out}})$
have a linear dependence relation over
$c(H_n^{\mathrm {out}})$
have a linear dependence relation over
![]() $\mathbb {Z}$
. For instance (see Figure 35),
$\mathbb {Z}$
. For instance (see Figure 35),

Figure 35 Linear dependence relation over
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Nevertheless, we can say the following:
Proposition 6.6. The collection of eight cone points
forms a weak basis of the Knutson–Tao local cone
![]() $\mathscr {C}^+_{\mathfrak {T}}$
.
$\mathscr {C}^+_{\mathfrak {T}}$
.
Among these eight cone points, the seven points
are strongly independent over
![]() $\mathbb {Z}_{\geqslant 0}$
, and the seven points
$\mathbb {Z}_{\geqslant 0}$
, and the seven points
are strongly independent over
![]() $\mathbb {Z}_{\geqslant 0}$
. Moreover, each cone point c in
$\mathbb {Z}_{\geqslant 0}$
. Moreover, each cone point c in
![]() $\mathscr {C}^+_{\mathfrak {T}}$
can be uniquely expressed in exactly one of the following three forms:
$\mathscr {C}^+_{\mathfrak {T}}$
can be uniquely expressed in exactly one of the following three forms:
 $$ \begin{align*} c &= n_1 c(R_1) + n_2 c(L_1) + \cdots + n_6 c(L_3), \\ c &= n_1 c(R_1) + n_2 c(L_1) + \cdots + n_6 c(L_3) + n c(H_1^{\mathrm{in}}), \\ c &= n_1 c(R_1) + n_2 c(L_1) + \cdots + n_6 c(L_3) + n c(H_1^{\mathrm{out}}), \quad\quad\left(n_i \in \mathbb{Z}_{\geqslant 0}, \quad n \in \mathbb{Z}_{>0}\right). \end{align*} $$
$$ \begin{align*} c &= n_1 c(R_1) + n_2 c(L_1) + \cdots + n_6 c(L_3), \\ c &= n_1 c(R_1) + n_2 c(L_1) + \cdots + n_6 c(L_3) + n c(H_1^{\mathrm{in}}), \\ c &= n_1 c(R_1) + n_2 c(L_1) + \cdots + n_6 c(L_3) + n c(H_1^{\mathrm{out}}), \quad\quad\left(n_i \in \mathbb{Z}_{\geqslant 0}, \quad n \in \mathbb{Z}_{>0}\right). \end{align*} $$
Because the spanning set
![]() $c(R_1), c(L_1), c(R_2), c(L_2), c(R_3), c(L_3), c(H_1^{\mathrm {in}}), c(H_1^{\mathrm {out}})$
consists of positive points, we immediately obtain:
$c(R_1), c(L_1), c(R_2), c(L_2), c(R_3), c(L_3), c(H_1^{\mathrm {in}}), c(H_1^{\mathrm {out}})$
consists of positive points, we immediately obtain:
Corollary 6.7. The local Knutson–Tao cone satisfies the property that
![]() $\mathscr {C}^+_{\mathfrak {T}} = \Phi _{\mathfrak {T}}^{\mathrm {FG}}(\mathscr {W}_{\mathfrak {T}}) \subseteq \mathbb {Z}_{\geqslant 0}^7$
. In particular,
$\mathscr {C}^+_{\mathfrak {T}} = \Phi _{\mathfrak {T}}^{\mathrm {FG}}(\mathscr {W}_{\mathfrak {T}}) \subseteq \mathbb {Z}_{\geqslant 0}^7$
. In particular,
![]() $\mathscr {C}^+_{\mathfrak {T}}$
is a positive cone.
$\mathscr {C}^+_{\mathfrak {T}}$
is a positive cone.
Corollary 6.8. The Fock–Goncharov local coordinate function
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}: \mathscr {W}_{\mathfrak {T}} \to \mathscr {C}^+_{\mathfrak {T}}$
satisfies property (4) in Definition 5.1, namely, the induced function
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}: \mathscr {W}_{\mathfrak {T}} \to \mathscr {C}^+_{\mathfrak {T}}$
satisfies property (4) in Definition 5.1, namely, the induced function
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}: [\mathscr {W}_{\mathfrak {T}}] \hookrightarrow \mathscr {C}^+_{\mathfrak {T}}$
, defined on the collection of corner-ambiguity classes
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}: [\mathscr {W}_{\mathfrak {T}}] \hookrightarrow \mathscr {C}^+_{\mathfrak {T}}$
, defined on the collection of corner-ambiguity classes
![]() $[W_{\mathfrak {T}}]$
of local webs
$[W_{\mathfrak {T}}]$
of local webs
![]() $W_{\mathfrak {T}}$
in
$W_{\mathfrak {T}}$
in
![]() $\mathscr {W}_{\mathfrak {T}}$
, is an injection.
$\mathscr {W}_{\mathfrak {T}}$
, is an injection.
Proof. Assume
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}(W_{\mathfrak {T}}) = \Phi _{\mathfrak {T}}^{\mathrm {FG}}(W^\prime _{\mathfrak {T}}) \in \mathscr {C}^+_{\mathfrak {T}}$
. This cone point falls into one of the three families in Proposition 6.6. For the sake of argument, suppose
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}(W_{\mathfrak {T}}) = \Phi _{\mathfrak {T}}^{\mathrm {FG}}(W^\prime _{\mathfrak {T}}) \in \mathscr {C}^+_{\mathfrak {T}}$
. This cone point falls into one of the three families in Proposition 6.6. For the sake of argument, suppose
Note that
![]() $n c(H_1^{\mathrm {in}}) = c(H_n^{\mathrm {in}})$
in
$n c(H_1^{\mathrm {in}}) = c(H_n^{\mathrm {in}})$
in
![]() $\mathscr {C}^+_{\mathfrak {T}}$
; see Figure 30. By the uniqueness property in Proposition 6.6 together with property (1) in Definition 5.1, we gather that
$\mathscr {C}^+_{\mathfrak {T}}$
; see Figure 30. By the uniqueness property in Proposition 6.6 together with property (1) in Definition 5.1, we gather that
![]() $W_{\mathfrak {T}}$
and
$W_{\mathfrak {T}}$
and
![]() $W^\prime _{\mathfrak {T}}$
have
$W^\prime _{\mathfrak {T}}$
have
![]() $1 + \sum _{i=1}^6 n_i$
connected components, one of which is a n-in-honeycomb
$1 + \sum _{i=1}^6 n_i$
connected components, one of which is a n-in-honeycomb
![]() $H_n^{\mathrm {in}}$
, and
$H_n^{\mathrm {in}}$
, and
![]() $n_1$
(resp.
$n_1$
(resp.
![]() $n_2$
,
$n_2$
,
![]() $n_3$
,
$n_3$
,
![]() $n_4$
,
$n_4$
,
![]() $n_5$
,
$n_5$
,
![]() $n_6$
) of which are corner arcs
$n_6$
) of which are corner arcs
![]() $R_1$
(resp.
$R_1$
(resp.
![]() $L_1$
,
$L_1$
,
![]() $R_2$
,
$R_2$
,
![]() $L_2$
,
$L_2$
,
![]() $R_3$
,
$R_3$
,
![]() $L_3$
). The only ambiguity is how these corner arcs are permuted on their respective corners, that is
$L_3$
). The only ambiguity is how these corner arcs are permuted on their respective corners, that is
![]() $[W_{\mathfrak {T}}] = [W^\prime _{\mathfrak {T}}]$
in
$[W_{\mathfrak {T}}] = [W^\prime _{\mathfrak {T}}]$
in
![]() $[\mathscr {W}_{\mathfrak {T}}]$
.
$[\mathscr {W}_{\mathfrak {T}}]$
.
Proof of Proposition 6.6
Define two subsets
![]() $\overline {(\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {in}}}$
and
$\overline {(\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {in}}}$
and
![]() $(\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {out}}$
of
$(\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {out}}$
of
![]() $\mathscr {C}^+_{\mathfrak {T}}$
by
$\mathscr {C}^+_{\mathfrak {T}}$
by
(Here,
![]() $A+B = \{ a+b; \quad a \in A \text { and } b \in B \}$
.) Put
$A+B = \{ a+b; \quad a \in A \text { and } b \in B \}$
.) Put
By Lemma 6.3, with
![]() $\mathscr {C} = \mathscr {C}^+_{\mathfrak {T}}$
, in order to prove Proposition 6.6 it suffices to establish:
$\mathscr {C} = \mathscr {C}^+_{\mathfrak {T}}$
, in order to prove Proposition 6.6 it suffices to establish:
Claim 6.9. There exists
-
1. a cone
 $\mathscr {C}^\prime \subseteq \mathbb {Z}^7$
;
$\mathscr {C}^\prime \subseteq \mathbb {Z}^7$
; -
2. a collection of cone points
 $c^{\prime }_1, \dots , c^{\prime }_8$
in
$c^{\prime }_1, \dots , c^{\prime }_8$
in
 $\mathscr {C}^\prime $
;
$\mathscr {C}^\prime $
; -
3. a partition
 $\mathscr {C}^\prime = \overline {(\mathscr {C}^\prime )^{>0}} \sqcup (\mathscr {C}^\prime )^{< 0}$
;
$\mathscr {C}^\prime = \overline {(\mathscr {C}^\prime )^{>0}} \sqcup (\mathscr {C}^\prime )^{< 0}$
; -
4. a
 $\mathbb {Z}_{\geqslant 0}$
-linear bijection
$\mathbb {Z}_{\geqslant 0}$
-linear bijection
 $\psi \colon \mathscr {C}^\prime \to \mathscr {C}^+_{\mathfrak {T}}$
;
$\psi \colon \mathscr {C}^\prime \to \mathscr {C}^+_{\mathfrak {T}}$
; -
5. an extension
 $\widetilde {\psi }$
of
$\widetilde {\psi }$
of
 $\psi $
to a
$\psi $
to a
 $\mathbb {Q}$
-linear isomorphism
$\mathbb {Q}$
-linear isomorphism
 $\widetilde {\psi } \colon \mathbb {Q}^7 \to \mathbb {Q}^7$
;
$\widetilde {\psi } \colon \mathbb {Q}^7 \to \mathbb {Q}^7$
;
such that
-
1. we have
 $\psi (c^{\prime }_i) = c_i$
;
$\psi (c^{\prime }_i) = c_i$
; -
2. we have
 $\psi (\overline {(\mathscr {C}^\prime )^{>0}}) = \overline {(\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {in}}}$
and
$\psi (\overline {(\mathscr {C}^\prime )^{>0}}) = \overline {(\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {in}}}$
and
 $\psi ((\mathscr {C}^\prime )^{<0}) = (\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {out}}$
;
$\psi ((\mathscr {C}^\prime )^{<0}) = (\mathscr {C}^+_{\mathfrak {T}})^{\mathrm {out}}$
; -
3. the eight cone points
 $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
form a weak basis of the cone
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
form a weak basis of the cone
 $\mathscr {C}^\prime $
;
$\mathscr {C}^\prime $
; -
4. the seven cone points
 $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7$
are strongly independent over
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7$
are strongly independent over
 $\mathbb {Z}_{\geqslant 0}$
;
$\mathbb {Z}_{\geqslant 0}$
; -
5. the seven cone points
 $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_8$
are strongly independent over
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_8$
are strongly independent over
 $\mathbb {Z}_{\geqslant 0}$
.
$\mathbb {Z}_{\geqslant 0}$
.
We prove the claim. Define
![]() $\mathscr {C}^\prime \subseteq \mathbb {Z}_{\geqslant 0}^6 \times \mathbb {Z} \subseteq \mathbb {Z}^7$
by
$\mathscr {C}^\prime \subseteq \mathbb {Z}_{\geqslant 0}^6 \times \mathbb {Z} \subseteq \mathbb {Z}^7$
by
It follows from the definition that
![]() $\mathscr {C}^\prime $
is a cone. Put
$\mathscr {C}^\prime $
is a cone. Put
 $$ \begin{align*} c^{\prime}_1 &= \left(1, 0, 0, 0, 0, 0, 0\right), & c^{\prime}_2 &= \left(0, 1, 0, 0, 0, 0, 0\right), \\ c^{\prime}_3 &= \left(0, 0, 1, 0, 0, 0, 0\right), & c^{\prime}_4 &= \left(0, 0, 0, 1, 0, 0, 0\right), \\ c^{\prime}_5 &= \left(0, 0, 0, 0, 1, 0, 0\right), & c^{\prime}_6 &= \left(0, 0, 0, 0, 0, 1, 0\right), \\ c^{\prime}_7 &= \left(0, 0, 0, 0, 0, 0, 1\right), & c^{\prime}_8 &= \left(0,1,0,1,0,1,-1\right). \end{align*} $$
$$ \begin{align*} c^{\prime}_1 &= \left(1, 0, 0, 0, 0, 0, 0\right), & c^{\prime}_2 &= \left(0, 1, 0, 0, 0, 0, 0\right), \\ c^{\prime}_3 &= \left(0, 0, 1, 0, 0, 0, 0\right), & c^{\prime}_4 &= \left(0, 0, 0, 1, 0, 0, 0\right), \\ c^{\prime}_5 &= \left(0, 0, 0, 0, 1, 0, 0\right), & c^{\prime}_6 &= \left(0, 0, 0, 0, 0, 1, 0\right), \\ c^{\prime}_7 &= \left(0, 0, 0, 0, 0, 0, 1\right), & c^{\prime}_8 &= \left(0,1,0,1,0,1,-1\right). \end{align*} $$
One checks that
![]() $c^{\prime }_1, \dots , c^{\prime }_8$
are in
$c^{\prime }_1, \dots , c^{\prime }_8$
are in
![]() $\mathscr {C}^\prime $
. Define
$\mathscr {C}^\prime $
. Define
Then
![]() $\mathscr {C}^\prime = \overline {(\mathscr {C}^\prime )^{>0}} \sqcup (\mathscr {C}^\prime )^{<0}$
is a partition.
$\mathscr {C}^\prime = \overline {(\mathscr {C}^\prime )^{>0}} \sqcup (\mathscr {C}^\prime )^{<0}$
is a partition.
First, we show
![]() $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
spans
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
spans
![]() $\mathscr {C}^\prime $
. We see that
$\mathscr {C}^\prime $
. We see that
If
![]() $c' \in (\mathscr {C}^\prime )^{<0}$
, then its last coordinate is
$c' \in (\mathscr {C}^\prime )^{<0}$
, then its last coordinate is
![]() $x \leqslant -1$
. Since
$x \leqslant -1$
. Since
![]() $-x> 0$
and
$-x> 0$
and
![]() $-x \leqslant \mathrm {min}(r_{12}, r_{22}, r_{32})$
,
$-x \leqslant \mathrm {min}(r_{12}, r_{22}, r_{32})$
,
for some
![]() $r_{11}, r^{\prime }_{12}, r_{21}, r^{\prime }_{22}, r_{31}, r^{\prime }_{32} \in \mathbb {Z}_{\geqslant 0}$
and
$r_{11}, r^{\prime }_{12}, r_{21}, r^{\prime }_{22}, r_{31}, r^{\prime }_{32} \in \mathbb {Z}_{\geqslant 0}$
and
![]() $-x \in \mathbb {Z}_{>0}$
. That is,
$-x \in \mathbb {Z}_{>0}$
. That is,
Thus,
where the
![]() $\supseteq $
containment follows since
$\supseteq $
containment follows since
![]() $\mathrm {Span}_{\mathbb {Z}_{\geqslant 0}} (c^{\prime }_1, \dots , c^{\prime }_6 ) + \mathbb {Z}_{>0} \cdot c^{\prime }_8 \subseteq \mathbb {Z}_{\geqslant 0}^6 \times \mathbb {Z}_{<0}$
.
$\mathrm {Span}_{\mathbb {Z}_{\geqslant 0}} (c^{\prime }_1, \dots , c^{\prime }_6 ) + \mathbb {Z}_{>0} \cdot c^{\prime }_8 \subseteq \mathbb {Z}_{\geqslant 0}^6 \times \mathbb {Z}_{<0}$
.
Next, we show
![]() $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
are weakly independent over
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
are weakly independent over
![]() $\mathbb {Z}_{\geqslant 0}$
. Indeed, if
$\mathbb {Z}_{\geqslant 0}$
. Indeed, if
![]() $n_1 c^{\prime }_1 + \cdots + n_7 c^{\prime }_7 + n_8 c^{\prime }_8 = 0$
, then
$n_1 c^{\prime }_1 + \cdots + n_7 c^{\prime }_7 + n_8 c^{\prime }_8 = 0$
, then
![]() $n_1 = n_3 = n_5 = 0$
and
$n_1 = n_3 = n_5 = 0$
and
![]() $n_2 + n_8, n_4 + n_8, n_6 + n_8, n_7 - n_8 = 0$
. Since all
$n_2 + n_8, n_4 + n_8, n_6 + n_8, n_7 - n_8 = 0$
. Since all
![]() $n_i \in \mathbb {Z}_{\geqslant 0}$
, it follows that
$n_i \in \mathbb {Z}_{\geqslant 0}$
, it follows that
![]() $n_2 = n_4 = n_6 = n_8 = 0$
, and so
$n_2 = n_4 = n_6 = n_8 = 0$
, and so
![]() $n_7 = n_8 = 0$
, as desired.
$n_7 = n_8 = 0$
, as desired.
We gather that
![]() $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
form a weak basis of
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7, c^{\prime }_8$
form a weak basis of
![]() $\mathscr {C}^\prime $
.
$\mathscr {C}^\prime $
.
Next, we show
![]() $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7$
are strongly independent over
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_7$
are strongly independent over
![]() $\mathbb {Z}_{\geqslant 0}$
. This is equivalent to being linearly independent over
$\mathbb {Z}_{\geqslant 0}$
. This is equivalent to being linearly independent over
![]() $\mathbb {Q}$
, which follows from the definitions. Similarly, it follows from the definitions that
$\mathbb {Q}$
, which follows from the definitions. Similarly, it follows from the definitions that
![]() $c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_8$
are strongly independent over
$c^{\prime }_1, \dots , c^{\prime }_6, c^{\prime }_8$
are strongly independent over
![]() $\mathbb {Z}_{\geqslant 0}$
.
$\mathbb {Z}_{\geqslant 0}$
.
We now define a
![]() $\mathbb {Z}_{\geqslant 0}$
-linear bijection
$\mathbb {Z}_{\geqslant 0}$
-linear bijection
![]() $\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
. Its inverse will be the desired
$\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
. Its inverse will be the desired
![]() $\mathbb {Z}_{\geqslant 0}$
-linear bijection
$\mathbb {Z}_{\geqslant 0}$
-linear bijection
![]() $\psi = \varphi ^{-1} \colon \mathscr {C}^\prime \to \mathscr {C}^+_{\mathfrak {T}}$
. Let c be a cone point in
$\psi = \varphi ^{-1} \colon \mathscr {C}^\prime \to \mathscr {C}^+_{\mathfrak {T}}$
. Let c be a cone point in
![]() $\mathscr {C}^+_{\mathfrak {T}}$
, written as in Equation (*). Put
$\mathscr {C}^+_{\mathfrak {T}}$
, written as in Equation (*). Put
where the rhombus numbers
![]() $r_{ij}$
are in
$r_{ij}$
are in
![]() $\mathbb {Z}_{\geqslant 0}$
since
$\mathbb {Z}_{\geqslant 0}$
since
![]() $c \in \mathscr {C}^+_{\mathfrak {T}}$
; see Figure 36 (we think of x as the tropical Fock–Goncharov
$c \in \mathscr {C}^+_{\mathfrak {T}}$
; see Figure 36 (we think of x as the tropical Fock–Goncharov
![]() $\mathcal {X}$
-coordinate for the triangle). Thus,
$\mathcal {X}$
-coordinate for the triangle). Thus,
Therefore, recalling
![]() $\mathscr {C}^\prime \subseteq \mathbb {Z}_{\geqslant 0}^6 \times \mathbb {Z}$
(Equation (**)), we may define the function
$\mathscr {C}^\prime \subseteq \mathbb {Z}_{\geqslant 0}^6 \times \mathbb {Z}$
(Equation (**)), we may define the function
![]() $\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
by
$\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
by

Figure 36 Four ways to view the tropical Fock–Goncharov
![]() $\mathcal {X}$
-coordinate.
$\mathcal {X}$
-coordinate.
It follows from the definition that
![]() $\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
is
$\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
is
![]() $\mathbb {Z}_{\geqslant 0}$
-linear. One checks that
$\mathbb {Z}_{\geqslant 0}$
-linear. One checks that
![]() $\varphi (c_i) = c^{\prime }_i$
. Since the
$\varphi (c_i) = c^{\prime }_i$
. Since the
![]() $c^{\prime }_i$
span
$c^{\prime }_i$
span
![]() $\mathscr {C}^\prime $
, we have
$\mathscr {C}^\prime $
, we have
![]() $\varphi $
is surjective. In particular, by Equations (#),(##),(†),(††),
$\varphi $
is surjective. In particular, by Equations (#),(##),(†),(††),
The formula for
![]() $\varphi $
extends to define a
$\varphi $
extends to define a
![]() $\mathbb {Q}$
-linear isomorphism
$\mathbb {Q}$
-linear isomorphism
![]() $\widetilde {\varphi } \colon \mathbb {Q}^7 \to \mathbb {Q}^7$
, and its inverse is the desired
$\widetilde {\varphi } \colon \mathbb {Q}^7 \to \mathbb {Q}^7$
, and its inverse is the desired
![]() $\mathbb {Q}$
-linear isomorphism
$\mathbb {Q}$
-linear isomorphism
![]() $\widetilde {\psi } = (\widetilde {\varphi })^{-1} \colon \mathbb {Q}^7 \to \mathbb {Q}^7$
. Indeed, the bijectivity of
$\widetilde {\psi } = (\widetilde {\varphi })^{-1} \colon \mathbb {Q}^7 \to \mathbb {Q}^7$
. Indeed, the bijectivity of
![]() $\widetilde {\varphi }$
follows by computing the values on the standard column basis of
$\widetilde {\varphi }$
follows by computing the values on the standard column basis of
![]() $\mathbb {Q}^7$
, giving the invertible matrix
$\mathbb {Q}^7$
, giving the invertible matrix
 $$ \begin{align*} \widetilde{\varphi}(\vec{e}_1, \vec{e}_2, \vec{e}_3, \vec{e}_4, \vec{e}_5, \vec{e}_6, \vec{e}_7) = \frac{1}{3} \left( \begin{smallmatrix} 0&0&0&1&1&0&-1 \\ -1&0&0&0&-1&1&1 \\ 1&0&0&0&0&1&-1 \\ -1&1&-1&0&0&0&1 \\ 0&1&1&0&0&0&-1 \\ 0&0&-1&1&-1&0&1 \\ 1&-1&1&-1&1&-1&0 \\ \end{smallmatrix} \right). \end{align*} $$
$$ \begin{align*} \widetilde{\varphi}(\vec{e}_1, \vec{e}_2, \vec{e}_3, \vec{e}_4, \vec{e}_5, \vec{e}_6, \vec{e}_7) = \frac{1}{3} \left( \begin{smallmatrix} 0&0&0&1&1&0&-1 \\ -1&0&0&0&-1&1&1 \\ 1&0&0&0&0&1&-1 \\ -1&1&-1&0&0&0&1 \\ 0&1&1&0&0&0&-1 \\ 0&0&-1&1&-1&0&1 \\ 1&-1&1&-1&1&-1&0 \\ \end{smallmatrix} \right). \end{align*} $$
So
![]() $\widetilde {\psi } = (\widetilde {\varphi })^{-1}$
is defined. Since
$\widetilde {\psi } = (\widetilde {\varphi })^{-1}$
is defined. Since
![]() $\widetilde {\varphi }$
is an injection so is its restriction
$\widetilde {\varphi }$
is an injection so is its restriction
![]() $\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
. Also, since, as we argued above,
$\varphi \colon \mathscr {C}^+_{\mathfrak {T}} \to \mathscr {C}^\prime $
. Also, since, as we argued above,
![]() $\varphi $
is a surjection, we gather
$\varphi $
is a surjection, we gather
![]() $\varphi $
is a bijection. Thus,
$\varphi $
is a bijection. Thus,
![]() $\psi = \varphi ^{-1} : \mathscr {C}^\prime \to \mathscr {C}^+_{\mathfrak {T}}$
is defined. This completes the proof of the claim, thereby establishing the proposition.
$\psi = \varphi ^{-1} : \mathscr {C}^\prime \to \mathscr {C}^+_{\mathfrak {T}}$
is defined. This completes the proof of the claim, thereby establishing the proposition.
6.3. Global Knutson–Tao cone
Given the dotted ideal triangulation
![]() $\lambda $
on the surface
$\lambda $
on the surface
![]() $\mathfrak {S}$
, an element c of
$\mathfrak {S}$
, an element c of
![]() $\mathbb {Z}^N$
corresponds to a function
$\mathbb {Z}^N$
corresponds to a function
![]() $\{\text {dots on } \lambda \} \to \mathbb {Z}$
; see §5.1. If
$\{\text {dots on } \lambda \} \to \mathbb {Z}$
; see §5.1. If
![]() $\mathfrak {T}$
is a dotted triangle of
$\mathfrak {T}$
is a dotted triangle of
![]() $\lambda $
, then an element c of
$\lambda $
, then an element c of
![]() $\mathbb {Z}^N$
induces a function
$\mathbb {Z}^N$
induces a function
![]() $\{ \text {dots on } \mathfrak {T} \} \to \mathbb {Z}$
, which likewise corresponds to an element
$\{ \text {dots on } \mathfrak {T} \} \to \mathbb {Z}$
, which likewise corresponds to an element
![]() $c_{\mathfrak {T}}$
of
$c_{\mathfrak {T}}$
of
![]() $\mathbb {Z}^7$
.
$\mathbb {Z}^7$
.
Definition 6.10. The global Knutson–Tao positive cone, or just Knutson–Tao cone or global cone,
![]() $\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
is defined by
$\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
is defined by
It follows from Corollary 6.7 that
![]() $\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
is indeed a positive cone.
$\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
is indeed a positive cone.
In §5, we defined the global coordinate function
![]() $\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
; see Definition 5.4. Since the image
$\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
; see Definition 5.4. Since the image
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {T}}]) \subseteq \mathscr {C}^+_{\mathfrak {T}}$
(which is, in fact, an equality by Corollary 6.7), it follows by the construction of
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {T}}]) \subseteq \mathscr {C}^+_{\mathfrak {T}}$
(which is, in fact, an equality by Corollary 6.7), it follows by the construction of
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
that the image
$\Phi _{\lambda }^{\mathrm {FG}}$
that the image
![]() $\Phi _{\lambda }^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {S}}]) \subseteq \mathscr {C}^+_{\lambda }$
; recall, for instance, Figure 33.
$\Phi _{\lambda }^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {S}}]) \subseteq \mathscr {C}^+_{\lambda }$
; recall, for instance, Figure 33.
7. Main result: global coordinates
We summarize what we have done so far. Consider a punctured surface
![]() $\mathfrak {S}$
with empty boundary; see §2. Let
$\mathfrak {S}$
with empty boundary; see §2. Let
![]() $[\mathscr {W}_{\mathfrak {S}}]$
denote the collection of parallel equivalence classes of global nonelliptic webs on
$[\mathscr {W}_{\mathfrak {S}}]$
denote the collection of parallel equivalence classes of global nonelliptic webs on
![]() $\mathfrak {S}$
. Assume that
$\mathfrak {S}$
. Assume that
![]() $\mathfrak {S}$
is equipped with an ideal triangulation
$\mathfrak {S}$
is equipped with an ideal triangulation
![]() $\lambda $
. For
$\lambda $
. For
![]() $N = - 8 \chi (\mathfrak {S})$
, in §5 we defined the Fock–Goncharov global coordinate function
$N = - 8 \chi (\mathfrak {S})$
, in §5 we defined the Fock–Goncharov global coordinate function
![]() $\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
, depending on the choice of the ideal triangulation
$\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathbb {Z}_{\geqslant 0}^N$
, depending on the choice of the ideal triangulation
![]() $\lambda $
. Proposition 5.5, which still needs to be proved, says that the mapping
$\lambda $
. Proposition 5.5, which still needs to be proved, says that the mapping
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
is injective. In §6, we defined the global Knutson–Tao positive cone
$\Phi _{\lambda }^{\mathrm {FG}}$
is injective. In §6, we defined the global Knutson–Tao positive cone
![]() $\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
, which also depends on the ideal triangulation
$\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
, which also depends on the ideal triangulation
![]() $\lambda $
. By construction, the image
$\lambda $
. By construction, the image
![]() $\Phi _{\lambda }^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {S}}]) \subseteq \mathscr {C}^+_{\lambda }$
. According to Proposition 6.11, which also still needs to be proved,
$\Phi _{\lambda }^{\mathrm {FG}}([\mathscr {W}_{\mathfrak {S}}]) \subseteq \mathscr {C}^+_{\lambda }$
. According to Proposition 6.11, which also still needs to be proved,
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
maps
$\Phi _{\lambda }^{\mathrm {FG}}$
maps
![]() $[\mathscr {W}_{\mathfrak {S}}]$
onto
$[\mathscr {W}_{\mathfrak {S}}]$
onto
![]() $\mathscr {C}^+_{\lambda }$
. Therefore, assuming Propositions 5.5 and 6.11, we have proved:
$\mathscr {C}^+_{\lambda }$
. Therefore, assuming Propositions 5.5 and 6.11, we have proved:
Theorem 7.1. The Fock–Goncharov global coordinate function
is a bijection of sets.
Remark 7.2. In §9, we generalize Theorem 7.1 to the setting of surfaces-with-boundary
![]() $\widehat {\mathfrak {S}}$
.
$\widehat {\mathfrak {S}}$
.
7.1. Inverse mapping
Our strategy for proving Propositions 5.5 and 6.11 (equivalently, Theorem 7.1) is to construct an explicit inverse mapping
namely a function that is both a left and a right inverse for the function
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
. The definition of the mapping
$\Phi _{\lambda }^{\mathrm {FG}}$
. The definition of the mapping
![]() $\Psi _{\lambda }^{\mathrm {FG}}$
is relatively straightforward, and it will be automatic that it is an inverse for
$\Psi _{\lambda }^{\mathrm {FG}}$
is relatively straightforward, and it will be automatic that it is an inverse for
![]() $\Phi _{\lambda }^{\mathrm {FG}}$
. The more challenging part will be to show that
$\Phi _{\lambda }^{\mathrm {FG}}$
. The more challenging part will be to show that
![]() $\Psi _{\lambda }^{\mathrm {FG}}$
is well defined.
$\Psi _{\lambda }^{\mathrm {FG}}$
is well defined.
7.2. Inverse mapping: ladder gluing construction
Recall that for a triangle
![]() $\mathfrak {T}$
we denote by
$\mathfrak {T}$
we denote by
![]() $\mathscr {W}_{\mathfrak {T}}$
the collection of rungless essential local webs
$\mathscr {W}_{\mathfrak {T}}$
the collection of rungless essential local webs
![]() $W_{\mathfrak {T}}$
in
$W_{\mathfrak {T}}$
in
![]() $\mathfrak {T}$
; see Definition 3.19. We will once again make use of the split ideal triangulation
$\mathfrak {T}$
; see Definition 3.19. We will once again make use of the split ideal triangulation
![]() $\widehat {\lambda }$
; see §4.3.
$\widehat {\lambda }$
; see §4.3.
Definition 7.3. A collection
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda } }$
of local webs
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda } }$
of local webs
![]() $W_{\mathfrak {T}} \in \mathscr {W}_{\mathfrak {T}}$
, varying over the triangles
$W_{\mathfrak {T}} \in \mathscr {W}_{\mathfrak {T}}$
, varying over the triangles
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
, is compatible if for each biangle
$\widehat {\lambda }$
, is compatible if for each biangle
![]() $\mathfrak {B}$
, with boundary edges
$\mathfrak {B}$
, with boundary edges
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
, sitting between two triangles
$E^{\prime \prime }$
, sitting between two triangles
![]() $\mathfrak {T}^\prime $
and
$\mathfrak {T}^\prime $
and
![]() $\mathfrak {T}^{\prime \prime }$
, respectively, the number of out-strands (resp. in-strands) of
$\mathfrak {T}^{\prime \prime }$
, respectively, the number of out-strands (resp. in-strands) of
![]() $W_{\mathfrak {T}^\prime }$
on
$W_{\mathfrak {T}^\prime }$
on
![]() $E^\prime $
is equal to the number of in-strands (resp. out-strands) of
$E^\prime $
is equal to the number of in-strands (resp. out-strands) of
![]() $W_{\mathfrak {T}^{\prime \prime }}$
on
$W_{\mathfrak {T}^{\prime \prime }}$
on
![]() $E^{\prime \prime }$
.
$E^{\prime \prime }$
.
For example, see the third row of Figure 37, an example on a once-punctured torus.

Figure 37 Ladder gluing construction (on the once-punctured torus). Shown are two different ways of assigning the local webs, differing by permutations of corner arcs. On the left, the result of the gluing is a nonelliptic web. On the right, the result is an elliptic web, which has to be resolved by removing a square before becoming a nonelliptic web. The two nonelliptic webs obtained in this way are equivalent.
To a compatible collection
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda } }$
of local webs, we will associate a global web W on
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda } }$
of local webs, we will associate a global web W on
![]() $\mathfrak {S}$
that need not be nonelliptic and that is in good position with respect to
$\mathfrak {S}$
that need not be nonelliptic and that is in good position with respect to
![]() $\widehat {\lambda }$
; recall Definition 4.5. The global web W is well defined up to ambient isotopy of
$\widehat {\lambda }$
; recall Definition 4.5. The global web W is well defined up to ambient isotopy of
![]() $\mathfrak {S}$
respecting
$\mathfrak {S}$
respecting
![]() $\widehat {\lambda }$
.
$\widehat {\lambda }$
.
Construction of W. Consider a biangle
![]() $\mathfrak {B}$
sitting between two triangles
$\mathfrak {B}$
sitting between two triangles
![]() $\mathfrak {T}^\prime $
and
$\mathfrak {T}^\prime $
and
![]() $\mathfrak {T}^{\prime \prime }$
. The local webs
$\mathfrak {T}^{\prime \prime }$
. The local webs
![]() $W_{\mathfrak {T}^\prime }$
and
$W_{\mathfrak {T}^\prime }$
and
![]() $W_{\mathfrak {T}^{\prime \prime }}$
determine strand sets
$W_{\mathfrak {T}^{\prime \prime }}$
determine strand sets
![]() $S^\prime $
and
$S^\prime $
and
![]() $S^{\prime \prime }$
on the boundary edges
$S^{\prime \prime }$
on the boundary edges
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
, respectively. By the compatibility property, the strand-set pair
$E^{\prime \prime }$
, respectively. By the compatibility property, the strand-set pair
![]() $S = (S^\prime , S^{\prime \prime })$
is symmetric; see Definition 3.12. Let
$S = (S^\prime , S^{\prime \prime })$
is symmetric; see Definition 3.12. Let
![]() $W_{\mathfrak {B}} = W_{\mathfrak {B}}(S)$
be the induced ladder-web in
$W_{\mathfrak {B}} = W_{\mathfrak {B}}(S)$
be the induced ladder-web in
![]() $\mathfrak {B}$
; see Definition 3.14.
$\mathfrak {B}$
; see Definition 3.14.
Define W to be the global web obtained by gluing together the local webs
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
![]() $\{ W_{\mathfrak {B}} \}_{\mathfrak {B} \in \widehat {\lambda }}$
in the obvious way; see the fourth row and the left side of the fifth row of Figure 37.
$\{ W_{\mathfrak {B}} \}_{\mathfrak {B} \in \widehat {\lambda }}$
in the obvious way; see the fourth row and the left side of the fifth row of Figure 37.
Definition 7.4. We say that the global web W has been obtained from the compatible collection
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda } }$
of local webs by applying the ladder gluing construction.
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda } }$
of local webs by applying the ladder gluing construction.
The following statement is immediate.
Lemma 7.5. A global web W obtained via the ladder gluing construction is in good position with respect to
![]() $\widehat {\lambda }$
. Conversely, if W is a global web in good position, then W can be recovered as the result of applying the ladder gluing construction to
$\widehat {\lambda }$
. Conversely, if W is a global web in good position, then W can be recovered as the result of applying the ladder gluing construction to
![]() $\{ W_{\mathfrak {T}} = W \cap \mathfrak {T} \}_{\mathfrak {T} \in \widehat {\lambda }}$
.
$\{ W_{\mathfrak {T}} = W \cap \mathfrak {T} \}_{\mathfrak {T} \in \widehat {\lambda }}$
.
If the global web W is obtained via the ladder gluing construction, then W could be (1) nonelliptic, for example, see the left side of the fifth row of Figure 37, or (2) elliptic, for example, see the fourth row of Figure 37.
7.3. Inverse mapping: resolving an elliptic web
Recall the notion of a local parallel-move; see Figure 21. Note that if
![]() $\{ W_{\mathfrak {T}}^\prime \}_{\mathfrak {T} \in \widehat {\lambda }}$
is a compatible collection of local webs and if
$\{ W_{\mathfrak {T}}^\prime \}_{\mathfrak {T} \in \widehat {\lambda }}$
is a compatible collection of local webs and if
![]() $W_{\mathfrak {T}}$
is related to
$W_{\mathfrak {T}}$
is related to
![]() $W^\prime _{\mathfrak {T}}$
by a sequence of local parallel-moves, then
$W^\prime _{\mathfrak {T}}$
by a sequence of local parallel-moves, then
![]() $\{ W_{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
is also compatible.
$\{ W_{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
is also compatible.
Lemma 7.6. Given a compatible collection
![]() $\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
of local webs, there exist local webs
$\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
of local webs, there exist local webs
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
such that
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
such that
![]() $W_{\mathfrak {T}}$
is related to
$W_{\mathfrak {T}}$
is related to
![]() $W^\prime _{\mathfrak {T}}$
by a sequence of local parallel-moves and the global web W obtained by applying the ladder gluing construction to
$W^\prime _{\mathfrak {T}}$
by a sequence of local parallel-moves and the global web W obtained by applying the ladder gluing construction to
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is nonelliptic.
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is nonelliptic.
Proof. Suppose that the global web
![]() $W^\prime $
obtained by applying the ladder gluing construction to the local webs
$W^\prime $
obtained by applying the ladder gluing construction to the local webs
![]() $\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is elliptic.
$\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is elliptic.
Step 1. We show that the elliptic global web
![]() $W^\prime $
has no disk- or bigon-faces. If there were a disk- or bigon-face, then it could not lie completely in a triangle
$W^\prime $
has no disk- or bigon-faces. If there were a disk- or bigon-face, then it could not lie completely in a triangle
![]() $\mathfrak {T}$
or biangle
$\mathfrak {T}$
or biangle
![]() $\mathfrak {B}$
of
$\mathfrak {B}$
of
![]() $\widehat {\lambda }$
, for this would violate that the local web restriction
$\widehat {\lambda }$
, for this would violate that the local web restriction
![]() $W^\prime _{\mathfrak {T}}$
or
$W^\prime _{\mathfrak {T}}$
or
![]() $W^\prime _{\mathfrak {B}}$
is essential (in particular, nonelliptic) by Lemma 7.5. Consequently, there is a cap- or fork-face lying in some
$W^\prime _{\mathfrak {B}}$
is essential (in particular, nonelliptic) by Lemma 7.5. Consequently, there is a cap- or fork-face lying in some
![]() $\mathfrak {T}$
or
$\mathfrak {T}$
or
![]() $\mathfrak {B}$
, contradicting that the local web restriction
$\mathfrak {B}$
, contradicting that the local web restriction
![]() $W^\prime _{\mathfrak {T}}$
or
$W^\prime _{\mathfrak {T}}$
or
![]() $W^\prime _{\mathfrak {B}}$
is essential (in particular, taut).
$W^\prime _{\mathfrak {B}}$
is essential (in particular, taut).
Step 2. We consider the possible positions of square-faces relative to the split ideal triangulation
![]() $\widehat {\lambda }$
. We claim that a square-face can only appear as demonstrated at the top of Figure 38, namely having two H-faces in two (possibly identical) biangles
$\widehat {\lambda }$
. We claim that a square-face can only appear as demonstrated at the top of Figure 38, namely having two H-faces in two (possibly identical) biangles
![]() $\mathfrak {B}$
and, in between, having opposite sides traveling parallel through the intermediate triangles
$\mathfrak {B}$
and, in between, having opposite sides traveling parallel through the intermediate triangles
![]() $\mathfrak {T}$
and biangles
$\mathfrak {T}$
and biangles
![]() $\mathfrak {B}$
. Indeed, otherwise there would be a square-, cap-, or fork-face, similar to Step 1.
$\mathfrak {B}$
. Indeed, otherwise there would be a square-, cap-, or fork-face, similar to Step 1.

Figure 38 Resolving a square-face.
Step 3. We remove a square-face. Since the square-faces are positioned in this way, given a fixed square-face there is a well defined state into which the square-face can be resolved, illustrated in Figure 38. The resulting global web
![]() $W_1$
is in good position with respect to
$W_1$
is in good position with respect to
![]() $\widehat {\lambda }$
. Also,
$\widehat {\lambda }$
. Also,
![]() $W_1$
is less complex than
$W_1$
is less complex than
![]() $W^\prime $
, where the complexity of a global web in good position is measured by the total number of vertices lying in the union
$W^\prime $
, where the complexity of a global web in good position is measured by the total number of vertices lying in the union
![]() $\cup _{\mathfrak {B}} \mathfrak {B}$
of all of the biangles
$\cup _{\mathfrak {B}} \mathfrak {B}$
of all of the biangles
![]() $\mathfrak {B}$
. Note that resolving a square-face decreases the complexity by four.
$\mathfrak {B}$
. Note that resolving a square-face decreases the complexity by four.
The effect of resolving a square-face is to perform, in each triangle
![]() $\mathfrak {T}$
, some number (possibly zero) of local parallel-moves, replacing the original local webs
$\mathfrak {T}$
, some number (possibly zero) of local parallel-moves, replacing the original local webs
![]() $\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
with new local webs
$\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
with new local webs
![]() $\{ (W_1)_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
such that
$\{ (W_1)_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
such that
![]() $(W_1)_{\mathfrak {T}}$
is equivalent to
$(W_1)_{\mathfrak {T}}$
is equivalent to
![]() $W^\prime _{\mathfrak {T}}$
up to corner-ambiguity; see Figure 38.
$W^\prime _{\mathfrak {T}}$
up to corner-ambiguity; see Figure 38.
Step 4. By a complexity argument, we can repeat the previous step until we obtain a sequence
![]() $W^\prime = W_0, W_1, W_2, \dots , W_n = W$
of global webs in good position such that
$W^\prime = W_0, W_1, W_2, \dots , W_n = W$
of global webs in good position such that
![]() $\{ (W_{i+1})_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is related to
$\{ (W_{i+1})_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is related to
![]() $\{ (W_{i})_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
by a sequence of local parallel-moves and such that W has no square-faces. By Lemma 7.5, W is recovered by applying the ladder gluing construction to
$\{ (W_{i})_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
by a sequence of local parallel-moves and such that W has no square-faces. By Lemma 7.5, W is recovered by applying the ladder gluing construction to
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
. By Step 1, W has no disk- or bigon-faces. Thus, W is nonelliptic.
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
. By Step 1, W has no disk- or bigon-faces. Thus, W is nonelliptic.
We refer to the algorithm used in the proof of Lemma 7.6 as the square removing algorithm. For example, see the fourth row and the right side of the fifth row of Figure 37.
Note that the algorithm removes the square-faces at random, thus the local webs
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
satisfying the conclusion of Lemma 7.6 are not necessarily unique. For example, see Figure 39.
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
satisfying the conclusion of Lemma 7.6 are not necessarily unique. For example, see Figure 39.

Figure 39 Elliptic web resulting from the ladder gluing construction (top) and two different applications of the square removing algorithm, yielding different, but parallel equivalent, nonelliptic webs (bottom).
7.4. Inverse mapping: definition
Let c be a point in the global cone
![]() $\mathscr {C}^+_{\lambda }$
; see Definition 6.10. Our goal is to associate to c a parallel equivalence class
$\mathscr {C}^+_{\lambda }$
; see Definition 6.10. Our goal is to associate to c a parallel equivalence class
![]() $\Psi _{\lambda }^{\mathrm {FG}}(c) \in [\mathscr {W}_{\mathfrak {S}}]$
of global nonelliptic webs on
$\Psi _{\lambda }^{\mathrm {FG}}(c) \in [\mathscr {W}_{\mathfrak {S}}]$
of global nonelliptic webs on
![]() $\mathfrak {S}$
. Equivalently, we want to associate to c a nonelliptic web
$\mathfrak {S}$
. Equivalently, we want to associate to c a nonelliptic web
![]() $\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
on
$\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
on
![]() $\mathfrak {S}$
well defined up to parallel equivalence; see Definition 2.3. Recall that we identify the triangles
$\mathfrak {S}$
well defined up to parallel equivalence; see Definition 2.3. Recall that we identify the triangles
![]() $\mathfrak {T}$
of the ideal triangulation
$\mathfrak {T}$
of the ideal triangulation
![]() $\lambda $
with the triangles
$\lambda $
with the triangles
![]() $\mathfrak {T}$
of the split ideal triangulation
$\mathfrak {T}$
of the split ideal triangulation
![]() $\widehat {\lambda }$
.
$\widehat {\lambda }$
.
Construction of
![]() $\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
. The global cone point c determines a local cone point
$\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
. The global cone point c determines a local cone point
![]() $c_{\mathfrak {T}}$
in the local cone
$c_{\mathfrak {T}}$
in the local cone
![]() $\mathscr {C}^+_{\mathfrak {T}}$
for each triangle
$\mathscr {C}^+_{\mathfrak {T}}$
for each triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\lambda $
; see just before Definition 6.10. By the triangle identifications between
$\lambda $
; see just before Definition 6.10. By the triangle identifications between
![]() $\lambda $
and
$\lambda $
and
![]() $\widehat {\lambda }$
, the local cone point
$\widehat {\lambda }$
, the local cone point
![]() $c_{\mathfrak {T}} \in \mathscr {C}^+_{\mathfrak {T}}$
is assigned to each triangle
$c_{\mathfrak {T}} \in \mathscr {C}^+_{\mathfrak {T}}$
is assigned to each triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
; see the first and second rows of Figure 37.
$\widehat {\lambda }$
; see the first and second rows of Figure 37.
Note, by construction, corresponding edge-coordinates located across a biangle
![]() $\mathfrak {B}$
take the same value. More precisely, if
$\mathfrak {B}$
take the same value. More precisely, if
![]() $\mathfrak {B}$
sits between two triangles
$\mathfrak {B}$
sits between two triangles
![]() $\mathfrak {T}^\prime $
and
$\mathfrak {T}^\prime $
and
![]() $\mathfrak {T}^{\prime \prime }$
and if the boundary edges of
$\mathfrak {T}^{\prime \prime }$
and if the boundary edges of
![]() $\mathfrak {B}$
are
$\mathfrak {B}$
are
![]() $E^\prime $
and
$E^\prime $
and
![]() $E^{\prime \prime }$
, respectively, then the coordinate
$E^{\prime \prime }$
, respectively, then the coordinate
![]() $a^L_{E^\prime }$
(resp.
$a^L_{E^\prime }$
(resp.
![]() $a^R_{E^\prime }$
) lying on the left-edge-dot (resp. right-edge-dot) as viewed from
$a^R_{E^\prime }$
) lying on the left-edge-dot (resp. right-edge-dot) as viewed from
![]() $\mathfrak {T}^\prime $
agrees with the coordinate
$\mathfrak {T}^\prime $
agrees with the coordinate
![]() $a^R_{E^{\prime \prime }}$
(resp.
$a^R_{E^{\prime \prime }}$
(resp.
![]() $a^L_{E^{\prime \prime }}$
) lying on the right-edge-dot (resp. left-edge-dot) as viewed from
$a^L_{E^{\prime \prime }}$
) lying on the right-edge-dot (resp. left-edge-dot) as viewed from
![]() $\mathfrak {T}^{\prime \prime }$
; see Figure 37.
$\mathfrak {T}^{\prime \prime }$
; see Figure 37.
By Corollaries 6.7 and 6.8, for each local cone point
![]() $c_{\mathfrak {T}} \in \mathscr {C}^+_{\mathfrak {T}}$
assigned to a triangle
$c_{\mathfrak {T}} \in \mathscr {C}^+_{\mathfrak {T}}$
assigned to a triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
, there exists a unique corner-ambiguity class
$\widehat {\lambda }$
, there exists a unique corner-ambiguity class
![]() $[W_{\mathfrak {T}}]$
of local webs
$[W_{\mathfrak {T}}]$
of local webs
![]() $W_{\mathfrak {T}}$
in
$W_{\mathfrak {T}}$
in
![]() $\mathscr {W}_{\mathfrak {T}}$
such that
$\mathscr {W}_{\mathfrak {T}}$
such that
![]() $\Phi _{\mathfrak {T}}^{\mathrm {FG}}(W_{\mathfrak {T}}) = c_{\mathfrak {T}}$
for any representative
$\Phi _{\mathfrak {T}}^{\mathrm {FG}}(W_{\mathfrak {T}}) = c_{\mathfrak {T}}$
for any representative
![]() $W_{\mathfrak {T}}$
of
$W_{\mathfrak {T}}$
of
![]() $[W_{\mathfrak {T}}]$
.
$[W_{\mathfrak {T}}]$
.
We now make a choice of such a representative
![]() $W_{\mathfrak {T}}$
for each
$W_{\mathfrak {T}}$
for each
![]() $\mathfrak {T}$
. Two different choices
$\mathfrak {T}$
. Two different choices
![]() $W_{\mathfrak {T}}$
and
$W_{\mathfrak {T}}$
and
![]() $W^\prime _{\mathfrak {T}}$
of local webs representing
$W^\prime _{\mathfrak {T}}$
of local webs representing
![]() $[W_{\mathfrak {T}}] = [W^\prime _{\mathfrak {T}}]$
are, by definition, related by local parallel-moves; see the third row of Figure 37.
$[W_{\mathfrak {T}}] = [W^\prime _{\mathfrak {T}}]$
are, by definition, related by local parallel-moves; see the third row of Figure 37.
Since corresponding edge-coordinates across biangles agree, the collection
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
of local webs is compatible (Definition 7.3). This follows by Figure 30. (There is also a general argument, by properties (2) and (3) in Definition 5.1, which uses the fact that if
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
of local webs is compatible (Definition 7.3). This follows by Figure 30. (There is also a general argument, by properties (2) and (3) in Definition 5.1, which uses the fact that if
![]() $W_{\mathfrak {T}} \in \mathscr {W}_{\mathfrak {T}}$
, then the opposite web
$W_{\mathfrak {T}} \in \mathscr {W}_{\mathfrak {T}}$
, then the opposite web
![]() $W^{\mathrm {op}}_{\mathfrak {T}}$
obtained by reversing all of the orientations of
$W^{\mathrm {op}}_{\mathfrak {T}}$
obtained by reversing all of the orientations of
![]() $W_{\mathfrak {T}}$
is also in
$W_{\mathfrak {T}}$
is also in
![]() $\mathscr {W}_{\mathfrak {T}}$
).
$\mathscr {W}_{\mathfrak {T}}$
).
By Lemma 7.6, this choice of a compatible collection
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
of local webs can be made (in a nonunique way) such that the global web W on
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
of local webs can be made (in a nonunique way) such that the global web W on
![]() $\mathfrak {S}$
obtained by applying the ladder gluing construction to
$\mathfrak {S}$
obtained by applying the ladder gluing construction to
![]() $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is nonelliptic. Finally, we define
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
is nonelliptic. Finally, we define
![]() $\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c) = W$
. In order for the global web
$\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c) = W$
. In order for the global web
![]() $\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
to be well defined up to parallel equivalence, we require:
$\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
to be well defined up to parallel equivalence, we require:
Main Lemma 7.7. Assume that each of
![]() $\{W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
$\{W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
![]() $\{W^\prime _{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
is a compatible collection of rungless essential webs in the
$\{W^\prime _{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
is a compatible collection of rungless essential webs in the
![]() $\mathscr {W}_{\mathfrak {T}}$
, satisfying
$\mathscr {W}_{\mathfrak {T}}$
, satisfying
-
1. for each triangle
 $\mathfrak {T}$
, the local webs
$\mathfrak {T}$
, the local webs
 $W_{\mathfrak {T}}$
and
$W_{\mathfrak {T}}$
and
 $W^\prime _{\mathfrak {T}}$
are equivalent up to corner-ambiguity;
$W^\prime _{\mathfrak {T}}$
are equivalent up to corner-ambiguity; -
2. both global webs W and
 $W^\prime $
, obtained from the compatible collections
$W^\prime $
, obtained from the compatible collections
 $\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
$\{ W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
 $\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
, respectively, by applying the ladder gluing construction, are nonelliptic.
$\{ W^\prime _{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
, respectively, by applying the ladder gluing construction, are nonelliptic.
Then, the nonelliptic webs W and
![]() $W^\prime $
represent the same parallel equivalence class in
$W^\prime $
represent the same parallel equivalence class in
![]() $[\mathscr {W}_{\mathfrak {S}}]$
.
$[\mathscr {W}_{\mathfrak {S}}]$
.
Definition 7.8. The inverse mapping
is defined by sending a cone point c in the global Knutson–Tao cone
![]() $\mathscr {C}^+_{\lambda }$
to the parallel equivalence class in
$\mathscr {C}^+_{\lambda }$
to the parallel equivalence class in
![]() $[\mathscr {W}_{\mathfrak {S}}]$
of the global nonelliptic web
$[\mathscr {W}_{\mathfrak {S}}]$
of the global nonelliptic web
![]() $\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
on
$\widetilde {\Psi }_{\lambda }^{\mathrm {FG}}(c)$
on
![]() $\mathfrak {S}$
.
$\mathfrak {S}$
.
Proof of Propositions 5.5 and 6.11
Assuming Main Lemma 7.7 to be true, it follows immediately from the constructions that the well defined mapping
![]() $\Psi _{\lambda }^{\mathrm {FG}} : \mathscr {C}^+_{\lambda } \to [\mathscr {W}_{\mathfrak {S}}]$
is the set-functional inverse of the Fock–Goncharov global coordinate function
$\Psi _{\lambda }^{\mathrm {FG}} : \mathscr {C}^+_{\lambda } \to [\mathscr {W}_{\mathfrak {S}}]$
is the set-functional inverse of the Fock–Goncharov global coordinate function
![]() $\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathscr {C}^+_{\lambda }$
.
$\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\mathfrak {S}}] \to \mathscr {C}^+_{\lambda }$
.
In summary, we have reduced the proof of Theorem 7.1 to proving the main lemma.
8. Proof of the main lemma
In this section, we prove the main Lemma 7.7. In particular, we provide an explicit algorithm taking one web to the other by a sequence of modified H-moves and global parallel-moves.
The strategy of the proof is simple, whereas its implementation is more complicated due to the combinatorics. The key idea is to think of a web W not as a graph, but as a multicurve
![]() $\left < W \right>$
, which we call a web picture; see Figure 40. We have already previewed web pictures at the local level, in Definitions 3.16 and 3.20 (see also the second paragraph of §5.3).
$\left < W \right>$
, which we call a web picture; see Figure 40. We have already previewed web pictures at the local level, in Definitions 3.16 and 3.20 (see also the second paragraph of §5.3).

Figure 40 (Parts of) two webs W and
![]() $W^\prime $
in good position on the surface, and their corresponding global pictures
$W^\prime $
in good position on the surface, and their corresponding global pictures
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\left < W^\prime \right>$
on the holed surface. Note that, over triangles, W and
$\left < W^\prime \right>$
on the holed surface. Note that, over triangles, W and
![]() $W^\prime $
differ by a permutation of corner arcs.
$W^\prime $
differ by a permutation of corner arcs.
If W and
![]() $W^\prime $
are two nonelliptic webs as in the main Lemma 7.7, we show that their associated multicurves
$W^\prime $
are two nonelliptic webs as in the main Lemma 7.7, we show that their associated multicurves
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\left < W^\prime \right>$
satisfy a fellow traveler property; see Lemma 8.3. As a consequence of this fellow traveler lemma, the intersection points
$\left < W^\prime \right>$
satisfy a fellow traveler property; see Lemma 8.3. As a consequence of this fellow traveler lemma, the intersection points
![]() $\mathscr {P} \subseteq \left < W \right>$
are in natural bijection with those
$\mathscr {P} \subseteq \left < W \right>$
are in natural bijection with those
![]() $\mathscr {P}^\prime \subseteq \left < W^\prime \right>$
; here, the nonelliptic hypothesis is necessary. To finish, we can use modified H-moves (Figures 25 and 41) to push around these intersection points in both webs until they are in the same configuration, establishing that W and
$\mathscr {P}^\prime \subseteq \left < W^\prime \right>$
; here, the nonelliptic hypothesis is necessary. To finish, we can use modified H-moves (Figures 25 and 41) to push around these intersection points in both webs until they are in the same configuration, establishing that W and
![]() $W^\prime $
are equivalent.
$W^\prime $
are equivalent.

Figure 41 Modified H-move from the perspective of web pictures.
8.1. Preparation: web pictures on the surface
For a web W on
![]() $\mathfrak {S}$
in good position with respect to the split ideal triangulation
$\mathfrak {S}$
in good position with respect to the split ideal triangulation
![]() $\widehat {\lambda }$
, the restrictions
$\widehat {\lambda }$
, the restrictions
![]() $W_{\mathfrak {B}} = W \cap \mathfrak {B}$
and
$W_{\mathfrak {B}} = W \cap \mathfrak {B}$
and
![]() $W_{\mathfrak {T}} = W \cap \mathfrak {T}$
in the biangles
$W_{\mathfrak {T}} = W \cap \mathfrak {T}$
in the biangles
![]() $\mathfrak {B}$
and triangles
$\mathfrak {B}$
and triangles
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
are essential and rungless essential local webs, respectively. By Definitions 3.16 and 3.20, we may consider the corresponding local pictures
$\widehat {\lambda }$
are essential and rungless essential local webs, respectively. By Definitions 3.16 and 3.20, we may consider the corresponding local pictures
![]() $ \langle W_{\mathfrak {B}} \rangle$
and
$ \langle W_{\mathfrak {B}} \rangle$
and
![]() $\left < W_{\mathfrak {T}} \right>$
, which are in particular immersed multicurves in the biangle
$\left < W_{\mathfrak {T}} \right>$
, which are in particular immersed multicurves in the biangle
![]() $\mathfrak {B}$
and the holed triangle
$\mathfrak {B}$
and the holed triangle
![]() $\mathfrak {T}^0$
, respectively; see Definition 3.11 and Figures 15 and 18.
$\mathfrak {T}^0$
, respectively; see Definition 3.11 and Figures 15 and 18.
Definition 8.1. The holed surface
![]() $\mathfrak {S}^0$
is the surface
$\mathfrak {S}^0$
is the surface
![]() $\mathfrak {S}$
minus one open disk per triangle
$\mathfrak {S}$
minus one open disk per triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
. The global picture
$\widehat {\lambda }$
. The global picture
![]() $\left < W \right>$
corresponding to a web W in good position with respect to
$\left < W \right>$
corresponding to a web W in good position with respect to
![]() $\widehat {\lambda }$
is the multicurve on the holed surface
$\widehat {\lambda }$
is the multicurve on the holed surface
![]() $\mathfrak {S}^0$
obtained by gluing together in the obvious way the collection of local pictures
$\mathfrak {S}^0$
obtained by gluing together in the obvious way the collection of local pictures
![]() $\{ \langle W_{\mathfrak {B}} \rangle \}_{\mathfrak {B} \in \widehat {\lambda }}$
and
$\{ \langle W_{\mathfrak {B}} \rangle \}_{\mathfrak {B} \in \widehat {\lambda }}$
and
![]() $\{ \left < W_{\mathfrak {T}} \right> \}_{\mathfrak {T} \in \widehat {\lambda }}$
associated to the biangles
$\{ \left < W_{\mathfrak {T}} \right> \}_{\mathfrak {T} \in \widehat {\lambda }}$
associated to the biangles
![]() $\mathfrak {B}$
and triangles
$\mathfrak {B}$
and triangles
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
, well defined up to ambient isotopy of
$\widehat {\lambda }$
, well defined up to ambient isotopy of
![]() $\mathfrak {S}^0$
respecting
$\mathfrak {S}^0$
respecting
![]() $\widehat {\lambda }$
. See Figure 40.
$\widehat {\lambda }$
. See Figure 40.
Figure 41 depicts how a modified H-move between webs W and
![]() $W^\prime $
in good position looks when viewed from the perspective of the global pictures
$W^\prime $
in good position looks when viewed from the perspective of the global pictures
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\left < W^\prime \right>$
; see Figure 25.
$\left < W^\prime \right>$
; see Figure 25.
Note the global picture
![]() $\left < W \right>$
has no U-turns on any edge of
$\left < W \right>$
has no U-turns on any edge of
![]() $\widehat {\lambda }$
, meaning there are no bigons formed between a component
$\widehat {\lambda }$
, meaning there are no bigons formed between a component
![]() $\gamma $
of
$\gamma $
of
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\widehat {\lambda }$
. We call this the no-switchbacks property.
$\widehat {\lambda }$
. We call this the no-switchbacks property.
Definition 8.2. A based multicurve
![]() $(\Gamma , \{ x_0^j \})$
on the holed surface
$(\Gamma , \{ x_0^j \})$
on the holed surface
![]() $\mathfrak {S}^0$
is a multicurve
$\mathfrak {S}^0$
is a multicurve
![]() $\Gamma = \{ \gamma _i \}$
equipped with a base point
$\Gamma = \{ \gamma _i \}$
equipped with a base point
![]() $x_0^j \in \gamma _j$
for each loop component
$x_0^j \in \gamma _j$
for each loop component
![]() $\gamma _j$
of
$\gamma _j$
of
![]() $\Gamma $
such that the base points
$\Gamma $
such that the base points
![]() $x_0^j$
do not lie on any edges of the split ideal triangulation
$x_0^j$
do not lie on any edges of the split ideal triangulation
![]() $\widehat {\lambda }$
; see Definition 3.11.
$\widehat {\lambda }$
; see Definition 3.11.
8.2. Preparation: sequences
A convex subset
![]() $I \subseteq \mathbb {Z}$
of the integers is a subset such that if
$I \subseteq \mathbb {Z}$
of the integers is a subset such that if
![]() $n, m \in I$
are integers, then all the integers between n and m are in I.
$n, m \in I$
are integers, then all the integers between n and m are in I.
A sequence
![]() $(a_i)_{i \in I}$
valued in a set
$(a_i)_{i \in I}$
valued in a set
![]() $\mathscr {A}$
is a function
$\mathscr {A}$
is a function
![]() $I \to \mathscr {A}$
,
$I \to \mathscr {A}$
,
![]() $i \mapsto a_i$
, where
$i \mapsto a_i$
, where
![]() $I \subseteq \mathbb {Z}$
is a convex subset of the integers.
$I \subseteq \mathbb {Z}$
is a convex subset of the integers.
Given a sequence
![]() $(a_i)_{i \in I}$
, a subsequence
$(a_i)_{i \in I}$
, a subsequence
![]() $(a_{i_k})_{k \in K}$
is the sequence
$(a_{i_k})_{k \in K}$
is the sequence
![]() $K \to \mathscr {A}$
determined by a convex subset
$K \to \mathscr {A}$
determined by a convex subset
![]() $K \subseteq \mathbb {Z}$
together with an order-preserving injective function
$K \subseteq \mathbb {Z}$
together with an order-preserving injective function
![]() $K \to I$
,
$K \to I$
,
![]() $k \mapsto i_k$
.
$k \mapsto i_k$
.
Given a sequence
![]() $(a_i)_{i \in I}$
, a convex subsequence
$(a_i)_{i \in I}$
, a convex subsequence
![]() $(a_{i_k})_{k \in K}$
is a subsequence such that the image
$(a_{i_k})_{k \in K}$
is a subsequence such that the image
![]() $I^\prime $
of K in I under the function
$I^\prime $
of K in I under the function
![]() $K \to I$
is a convex subset of
$K \to I$
is a convex subset of
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Given two sequences
![]() $(a_i)_{i \in I}$
and
$(a_i)_{i \in I}$
and
![]() $(b_j)_{j \in J}$
taking values in the same set, a common subsequence
$(b_j)_{j \in J}$
taking values in the same set, a common subsequence
![]() $\{ (a_{i_k})_{k \in K}, (b_{j_k})_{k \in K} \}$
is a pair of subsequences having the same indexing set K such that
$\{ (a_{i_k})_{k \in K}, (b_{j_k})_{k \in K} \}$
is a pair of subsequences having the same indexing set K such that
![]() $a_{i_k} = b_{j_k}$
for all
$a_{i_k} = b_{j_k}$
for all
![]() $k \in K$
.
$k \in K$
.
A convex common subsequence
![]() $\{ (a_{i_k})_{k \in K}, (b_{j_k})_{k \in K} \}$
is a common subsequence such that both subsequences
$\{ (a_{i_k})_{k \in K}, (b_{j_k})_{k \in K} \}$
is a common subsequence such that both subsequences
![]() $(a_{i_k})_{k \in K}$
and
$(a_{i_k})_{k \in K}$
and
![]() $(b_{j_k})_{k \in K}$
are convex.
$(b_{j_k})_{k \in K}$
are convex.
A maximal convex common subsequence
![]() $\{ (a_{i_k})_{k \in K}, (b_{j_k})_{k \in K} \}$
is a convex common subsequence such that there does not exist:
$\{ (a_{i_k})_{k \in K}, (b_{j_k})_{k \in K} \}$
is a convex common subsequence such that there does not exist:
![]() $K \subsetneq K^\prime $
and a convex common subsequence
$K \subsetneq K^\prime $
and a convex common subsequence
![]() $\{ (a_{i^\prime _k})_{k \in K^\prime }, (b_{j^\prime _k})_{k \in K^\prime } \}$
, satisfying
$\{ (a_{i^\prime _k})_{k \in K^\prime }, (b_{j^\prime _k})_{k \in K^\prime } \}$
, satisfying
![]() $i^\prime _k = i_k$
and
$i^\prime _k = i_k$
and
![]() $j^\prime _k = j_k$
for all
$j^\prime _k = j_k$
for all
![]() $k \in K$
.
$k \in K$
.
8.3. Preparation: edge-sequences and the fellow traveler lemma
Let W be a web on
![]() $\mathfrak {S}$
in good position with respect to
$\mathfrak {S}$
in good position with respect to
![]() $\widehat {\lambda }$
such that its global picture
$\widehat {\lambda }$
such that its global picture
![]() $(\left < W \right>, \{x_0^j\})$
is based.
$(\left < W \right>, \{x_0^j\})$
is based.
Let
![]() $\gamma $
be a loop or arc in
$\gamma $
be a loop or arc in
![]() $\left < W \right>$
. Associated to the component
$\left < W \right>$
. Associated to the component
![]() $\gamma $
is an edge-sequence
$\gamma $
is an edge-sequence
![]() $(E_i)_{i \in I}$
, where
$(E_i)_{i \in I}$
, where
![]() $E_i$
is an edge of the split ideal triangulation
$E_i$
is an edge of the split ideal triangulation
![]() $\widehat {\lambda }$
. More precisely, the sequence
$\widehat {\lambda }$
. More precisely, the sequence
![]() $(E_i)_{i \in I}$
describes the i-th edge crossed by
$(E_i)_{i \in I}$
describes the i-th edge crossed by
![]() $\gamma $
listed in order according to
$\gamma $
listed in order according to
![]() $\gamma $
’s orientation. In the case where
$\gamma $
’s orientation. In the case where
![]() $\gamma $
is an arc, we put
$\gamma $
is an arc, we put
![]() $I=\{0,1,\dots ,n\} \subseteq \mathbb {Z}$
, and the edge-sequence is well defined. In the case where
$I=\{0,1,\dots ,n\} \subseteq \mathbb {Z}$
, and the edge-sequence is well defined. In the case where
![]() $\gamma $
is a loop with base point
$\gamma $
is a loop with base point
![]() $x_0$
, we put
$x_0$
, we put
![]() $I = \mathbb {Z}$
, and the edge-sequence is well defined by sending
$I = \mathbb {Z}$
, and the edge-sequence is well defined by sending
![]() $0$
to the first edge
$0$
to the first edge
![]() $E_0$
encountered by
$E_0$
encountered by
![]() $\gamma $
after passing
$\gamma $
after passing
![]() $x_0$
.
$x_0$
.
We also associate an inverse edge-sequence
![]() $(E^{-1}_i)_{i \in I^{-1}}$
to the inverse curve
$(E^{-1}_i)_{i \in I^{-1}}$
to the inverse curve
![]() $\gamma ^{-1}$
, defined as follows. In the case of an arc put
$\gamma ^{-1}$
, defined as follows. In the case of an arc put
![]() $I^{-1} = \{-n, \dots , 1, 0\}$
, and in the case of a loop put
$I^{-1} = \{-n, \dots , 1, 0\}$
, and in the case of a loop put
![]() $I^{-1} = \mathbb {Z}$
. Then the inverse edge-sequence is defined by
$I^{-1} = \mathbb {Z}$
. Then the inverse edge-sequence is defined by
![]() $E^{-1}_{i} = E_{-i}$
for all
$E^{-1}_{i} = E_{-i}$
for all
![]() $i \in I^{-1}$
.
$i \in I^{-1}$
.
Another name for a loop or arc
![]() $\gamma $
in the global picture
$\gamma $
in the global picture
![]() $\left < W \right>$
is a traveler. Another name for an inverse curve
$\left < W \right>$
is a traveler. Another name for an inverse curve
![]() $\gamma ^{-1}$
is a past-traveler. The edge-sequence
$\gamma ^{-1}$
is a past-traveler. The edge-sequence
![]() $( E_i)_{i \in I}$
associated to a traveler
$( E_i)_{i \in I}$
associated to a traveler
![]() $\gamma $
is called its route, and the edge-sequence
$\gamma $
is called its route, and the edge-sequence
![]() $( E^{-1}_i)_{i \in I^{-1}}$
associated to a past-traveler
$( E^{-1}_i)_{i \in I^{-1}}$
associated to a past-traveler
![]() $\gamma ^{-1}$
is called its past-route; see Figure 42. Two travelers
$\gamma ^{-1}$
is called its past-route; see Figure 42. Two travelers
![]() $\gamma $
in
$\gamma $
in
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\gamma ^\prime $
in
$\gamma ^\prime $
in
![]() $\left < W^\prime \right>$
are called fellow travelers if they have the same routes
$\left < W^\prime \right>$
are called fellow travelers if they have the same routes
![]() $(E_i)_{i \in I} = (E^\prime _i)_{i \in I^\prime }$
,
$(E_i)_{i \in I} = (E^\prime _i)_{i \in I^\prime }$
,
![]() $I = I^\prime $
. In particular, if
$I = I^\prime $
. In particular, if
![]() $\gamma $
is a loop (resp. arc), then
$\gamma $
is a loop (resp. arc), then
![]() $\gamma ^\prime $
is also a loop (resp. arc of the same length).
$\gamma ^\prime $
is also a loop (resp. arc of the same length).

Figure 42 Route and past-route.
The following statement is the key to proving the main lemma.
Lemma 8.3. (Fellow traveler lemma)
Fix compatible local webs
![]() $\{W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
$\{W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
![]() $\{W^\prime _{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
in the
$\{W^\prime _{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
in the
![]() $\mathscr {W}_{\mathfrak {T}}$
satisfying hypothesis (1) of the main Lemma 7.7, and let W and
$\mathscr {W}_{\mathfrak {T}}$
satisfying hypothesis (1) of the main Lemma 7.7, and let W and
![]() $W^\prime $
be the induced global webs obtained by the ladder gluing construction. Then, there exists a natural one-to-one correspondence
$W^\prime $
be the induced global webs obtained by the ladder gluing construction. Then, there exists a natural one-to-one correspondence
between the collection of travelers
![]() $\gamma $
in the global picture
$\gamma $
in the global picture
![]() $\left < W \right>$
and the collection of travelers
$\left < W \right>$
and the collection of travelers
![]() $\gamma ^\prime = \varphi (\gamma )$
in
$\gamma ^\prime = \varphi (\gamma )$
in
![]() $\left < W^\prime \right>$
, and there exists a choice of base points
$\left < W^\prime \right>$
, and there exists a choice of base points
![]() $ x_0$
and
$ x_0$
and
![]() $x^{\prime }_0$
for the loops
$x^{\prime }_0$
for the loops
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^\prime $
in
$\gamma ^\prime $
in
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\left < W^\prime \right>$
, respectively, such that
$\left < W^\prime \right>$
, respectively, such that
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^\prime =\varphi (\gamma )$
are fellow travelers for all travelers
$\gamma ^\prime =\varphi (\gamma )$
are fellow travelers for all travelers
![]() $\gamma $
.
$\gamma $
.
For an example of the fellow traveler lemma on the once punctured torus, see Figure 43.
Proof of Lemma 8.3
Let E be an edge of
![]() $\widehat {\lambda }$
. This is associated to a unique triangle
$\widehat {\lambda }$
. This is associated to a unique triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
containing E in its boundary. Let
$\widehat {\lambda }$
containing E in its boundary. Let
![]() $S^{(E)\mathrm {out}}=(s_i^{(E)\mathrm {out}})_{i=1,\dots ,n_E^{\mathrm {out}}}$
(resp.
$S^{(E)\mathrm {out}}=(s_i^{(E)\mathrm {out}})_{i=1,\dots ,n_E^{\mathrm {out}}}$
(resp.
![]() $S^{\prime (E)\mathrm {out}}=(s_i^{\prime (E)\mathrm {out}})_{i=1,\dots ,n_E^{\prime \mathrm {out}}}$
) denote the sequence of out-strands of the global picture
$S^{\prime (E)\mathrm {out}}=(s_i^{\prime (E)\mathrm {out}})_{i=1,\dots ,n_E^{\prime \mathrm {out}}}$
) denote the sequence of out-strands of the global picture
![]() $\left < W \right>$
(resp.
$\left < W \right>$
(resp.
![]() $\left < W^\prime \right>$
) lying on the edge E, ordered, say, from left to right as viewed from
$\left < W^\prime \right>$
) lying on the edge E, ordered, say, from left to right as viewed from
![]() $\mathfrak {T}$
. By hypothesis (1) of the main lemma,
$\mathfrak {T}$
. By hypothesis (1) of the main lemma,
![]() $n_E^{\mathrm {out}}=n_E^{\prime \mathrm {out}}$
. Let
$n_E^{\mathrm {out}}=n_E^{\prime \mathrm {out}}$
. Let
![]() $\gamma _i^{(E)}$
denote the unique traveler in
$\gamma _i^{(E)}$
denote the unique traveler in
![]() $\left < W \right>$
containing the strand
$\left < W \right>$
containing the strand
![]() $s_i^{(E)\mathrm {out}}$
. Similarly, define travelers
$s_i^{(E)\mathrm {out}}$
. Similarly, define travelers
![]() $\gamma _i^{\prime (E)}$
with respect to
$\gamma _i^{\prime (E)}$
with respect to
![]() $\left < W^\prime \right>$
. The mapping
$\left < W^\prime \right>$
. The mapping
![]() $\varphi $
is defined by
$\varphi $
is defined by
Note every traveler
![]() $\gamma $
in
$\gamma $
in
![]() $\left < W \right>$
(resp.
$\left < W \right>$
(resp.
![]() $\gamma ^\prime $
in
$\gamma ^\prime $
in
![]() $\left < W^\prime \right>$
) is of the form
$\left < W^\prime \right>$
) is of the form
![]() $\gamma _i^{(E)}$
(resp.
$\gamma _i^{(E)}$
(resp.
![]() $\gamma _i^{\prime (E)}$
) for some E.
$\gamma _i^{\prime (E)}$
) for some E.
To establish that
![]() $\varphi $
is well defined, we show that
$\varphi $
is well defined, we show that
![]() $\gamma _{i_1}^{(E_1)} = \gamma _{i_2}^{(E_2)}$
implies
$\gamma _{i_1}^{(E_1)} = \gamma _{i_2}^{(E_2)}$
implies
![]() $\gamma _{i_1}^{\prime (E_1)} = \gamma _{i_2}^{\prime (E_2)}$
. This property follows immediately from:
$\gamma _{i_1}^{\prime (E_1)} = \gamma _{i_2}^{\prime (E_2)}$
. This property follows immediately from:
Claim 8.4. For some
![]() $k \in \{ 1, 2, \dots , n_E^{\mathrm {out}}=n_E^{\prime \mathrm {out}} \}$
, let
$k \in \{ 1, 2, \dots , n_E^{\mathrm {out}}=n_E^{\prime \mathrm {out}} \}$
, let
![]() $s_k^{(E)\mathrm {out}} \in S^{(E)\mathrm {out}}$
and
$s_k^{(E)\mathrm {out}} \in S^{(E)\mathrm {out}}$
and
![]() $s_k^{\prime (E)\mathrm {out}} \in S^{\prime (E)\mathrm {out}}$
be out-strands of
$s_k^{\prime (E)\mathrm {out}} \in S^{\prime (E)\mathrm {out}}$
be out-strands of
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\left < W^\prime \right>$
, respectively, lying on an edge E of a triangle
$\left < W^\prime \right>$
, respectively, lying on an edge E of a triangle
![]() $\mathfrak {T}$
of
$\mathfrak {T}$
of
![]() $\widehat {\lambda }$
. Note that each of these strands, according to its orientation, enters via the edge E into a biangle
$\widehat {\lambda }$
. Note that each of these strands, according to its orientation, enters via the edge E into a biangle
![]() $\mathfrak {B}$
, exits via an edge
$\mathfrak {B}$
, exits via an edge
![]() $E_2$
into a triangle
$E_2$
into a triangle
![]() $\mathfrak {T}_2$
and then either
$\mathfrak {T}_2$
and then either
-
1. turns left in
 $\mathfrak {T}_2$
, ending as a strand s or
$\mathfrak {T}_2$
, ending as a strand s or
 $s^\prime $
, respectively, lying on an edge
$s^\prime $
, respectively, lying on an edge
 $E_3$
;
$E_3$
; -
2. turns right in
 $\mathfrak {T}_2$
, ending as a strand s or
$\mathfrak {T}_2$
, ending as a strand s or
 $s^\prime $
, respectively, lying on an edge
$s^\prime $
, respectively, lying on an edge
 $E_3$
;
$E_3$
; -
3. terminates in a honeycomb
 $H_n$
.
$H_n$
.
The claim is that if the forward motion of the strand
![]() $s_k^{(E)\mathrm {out}}$
is described by item
$s_k^{(E)\mathrm {out}}$
is described by item
![]() $(i)$
above for
$(i)$
above for
![]() $i \in \{ 1, 2, 3 \}$
, then the forward motion of the strand
$i \in \{ 1, 2, 3 \}$
, then the forward motion of the strand
![]() $s_k^{\prime (E)\mathrm {out}}$
is also described by item
$s_k^{\prime (E)\mathrm {out}}$
is also described by item
![]() $(i)$
. Consequently, in cases (1) or (2), there exists some
$(i)$
. Consequently, in cases (1) or (2), there exists some
![]() $k_3 \in \{ 1, 2, \dots , n_{E_3}^{\mathrm {out}}=n_{E_3}^{\prime \mathrm {out}} \}$
such that
$k_3 \in \{ 1, 2, \dots , n_{E_3}^{\mathrm {out}}=n_{E_3}^{\prime \mathrm {out}} \}$
such that
The claim is true since, by hypothesis, on each corner of each triangle,
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\left < W^\prime \right>$
have the same number of clockwise-oriented (resp. counterclockwise-oriented) corner arcs, together with the fact that only oppositely oriented arcs cross in the biangles; see Figure 44.
$\left < W^\prime \right>$
have the same number of clockwise-oriented (resp. counterclockwise-oriented) corner arcs, together with the fact that only oppositely oriented arcs cross in the biangles; see Figure 44.
Having established that
![]() $\varphi $
is well defined, it follows by the definition that
$\varphi $
is well defined, it follows by the definition that
![]() $\varphi $
is a bijection. Another consequence of Claim 8.4 is that if
$\varphi $
is a bijection. Another consequence of Claim 8.4 is that if
![]() $\gamma $
is an arc, then
$\gamma $
is an arc, then
![]() $\gamma ^\prime = \varphi (\gamma )$
is an arc such that
$\gamma ^\prime = \varphi (\gamma )$
is an arc such that
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^\prime $
are fellow travelers. Also, if
$\gamma ^\prime $
are fellow travelers. Also, if
![]() $\gamma =\gamma _i^{(E)}$
is a loop, then
$\gamma =\gamma _i^{(E)}$
is a loop, then
![]() $\gamma ^\prime = \varphi (\gamma )=\gamma _i^{\prime (E)}$
is a loop. Choosing base points
$\gamma ^\prime = \varphi (\gamma )=\gamma _i^{\prime (E)}$
is a loop. Choosing base points
![]() $x_0$
and
$x_0$
and
![]() $x_0^\prime $
on the out-strands
$x_0^\prime $
on the out-strands
![]() $s_i^{(E)\mathrm {out}}$
and
$s_i^{(E)\mathrm {out}}$
and
![]() $s_i^{\prime (E)\mathrm {out}}$
, respectively, just before, say, the strands cross the edge E makes the loops
$s_i^{\prime (E)\mathrm {out}}$
, respectively, just before, say, the strands cross the edge E makes the loops
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^\prime $
into fellow travelers.
$\gamma ^\prime $
into fellow travelers.

Figure 43 Fellow traveler lemma.

Figure 44 Cases (1) (top) and (3) (bottom) in Claim 8.4.
8.4. Preparation: shared-routes
As in the previous subsection, let W be a web on
![]() $\mathfrak {S}$
in good position with respect to
$\mathfrak {S}$
in good position with respect to
![]() $\widehat {\lambda }$
such that its global picture
$\widehat {\lambda }$
such that its global picture
![]() $(\left < W \right>, \{x_0^j\})$
is based.
$(\left < W \right>, \{x_0^j\})$
is based.
Let
![]() $\gamma $
be a traveler in
$\gamma $
be a traveler in
![]() $\left < W \right>$
having route
$\left < W \right>$
having route
![]() $(E_i)_{i \in I}$
. For some
$(E_i)_{i \in I}$
. For some
![]() $i \in I$
indexing an edge
$i \in I$
indexing an edge
![]() $E_i$
, by definition of the route there is a corresponding point
$E_i$
, by definition of the route there is a corresponding point
![]() $y_i$
of
$y_i$
of
![]() $\gamma $
lying on
$\gamma $
lying on
![]() $E_i$
. Consider the associated segment
$E_i$
. Consider the associated segment
![]() $\overline {\gamma }_{i}$
of
$\overline {\gamma }_{i}$
of
![]() $\gamma $
lying between the points
$\gamma $
lying between the points
![]() $y_i$
and
$y_i$
and
![]() $y_{i+1}$
. Similarly, define segments
$y_{i+1}$
. Similarly, define segments
![]() $\overline {(\gamma ^{-1})}_i$
associated to the past-traveler
$\overline {(\gamma ^{-1})}_i$
associated to the past-traveler
![]() $\gamma ^{-1}$
with respect to its past-route
$\gamma ^{-1}$
with respect to its past-route
![]() $(E^{-1}_i)_{i \in I^{-1}}$
.
$(E^{-1}_i)_{i \in I^{-1}}$
.
Definition 8.5. Let
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $\gamma _2$
be travelers in
$\gamma _2$
be travelers in
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\gamma _1^{-1}$
,
$\gamma _1^{-1}$
,
![]() $\gamma _2^{-1}$
the corresponding past travelers, with routes
$\gamma _2^{-1}$
the corresponding past travelers, with routes
![]() $(E^1_i)_{i \in I}$
and
$(E^1_i)_{i \in I}$
and
![]() $(E^2_j)_{j \in J}$
and past routes
$(E^2_j)_{j \in J}$
and past routes
![]() $((E^1)^{-1}_i)_{ \in I^{-1}}$
and
$((E^1)^{-1}_i)_{ \in I^{-1}}$
and
![]() $((E^2)^{-1}_j)_{ \in J^{-1}}$
.
$((E^2)^{-1}_j)_{ \in J^{-1}}$
.
An oppositely oriented shared-route, or just shared-route,
![]() $SR$
for the ordered pair
$SR$
for the ordered pair
![]() $(\gamma _1, \gamma _2)$
of travelers is a maximal convex common subsequence (§8.2)
$(\gamma _1, \gamma _2)$
of travelers is a maximal convex common subsequence (§8.2)
![]() $SR= \{ (E^1_{i_k})_{k \in K}, ((E^2)^{-1}_{j_k})_{k \in K} \}$
for the route
$SR= \{ (E^1_{i_k})_{k \in K}, ((E^2)^{-1}_{j_k})_{k \in K} \}$
for the route
![]() $(E^1_i)_{i \in I}$
of
$(E^1_i)_{i \in I}$
of
![]() $\gamma _1$
and the past-route
$\gamma _1$
and the past-route
![]() $((E^2)^{-1}_j)_{ \in J^{-1}}$
of
$((E^2)^{-1}_j)_{ \in J^{-1}}$
of
![]() $\gamma _2^{-1}$
.
$\gamma _2^{-1}$
.
A shared-route is open (resp. closed) if its domain K is not equal to (resp. equal to)
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
A shared-route is crossing if there exists an index
![]() $k \in K$
such that the associated segments
$k \in K$
such that the associated segments
![]() $\overline {(\gamma _1)}_{i_k}$
and
$\overline {(\gamma _1)}_{i_k}$
and
![]() $\overline {(\gamma _2)^{-1}_{j_k}}$
intersect, say at a point
$\overline {(\gamma _2)^{-1}_{j_k}}$
intersect, say at a point
![]() $p_k$
. We call
$p_k$
. We call
![]() $p_k$
an intersection point of the crossing shared-route. Note that an intersection point must lie inside a biangle
$p_k$
an intersection point of the crossing shared-route. Note that an intersection point must lie inside a biangle
![]() $\mathfrak {B}$
of
$\mathfrak {B}$
of
![]() $\widehat {\lambda }$
. A shared-route is noncrossing if it has no intersection points.
$\widehat {\lambda }$
. A shared-route is noncrossing if it has no intersection points.

Figure 45 Crossing shared-route.

Figure 46 Noncrossing shared-routes.
For some examples, see Figures 45 and 46. Our pictures for shared-routes are only schematics, since the actual shared-routes on
![]() $\mathfrak {S}^0$
might cross the same edge multiple times. That is, there might exist
$\mathfrak {S}^0$
might cross the same edge multiple times. That is, there might exist
![]() $k \neq k^\prime $
such that
$k \neq k^\prime $
such that
![]() $E^1_{i_k} = (E^2)^{-1}_{j_k} = E^1_{i_{k^\prime }} = (E^2)^{-1}_{j_{k^\prime }}$
. Alternatively, one could think of these pictures at the level of the universal cover
$E^1_{i_k} = (E^2)^{-1}_{j_k} = E^1_{i_{k^\prime }} = (E^2)^{-1}_{j_{k^\prime }}$
. Alternatively, one could think of these pictures at the level of the universal cover
![]() $\widetilde {\mathfrak {S}^0}$
. Note that travelers in open shared-routes may end in honeycombs (Figure 44), but this will not affect our arguments.
$\widetilde {\mathfrak {S}^0}$
. Note that travelers in open shared-routes may end in honeycombs (Figure 44), but this will not affect our arguments.
Lemma 8.6. Assume in addition that W is nonelliptic. Then any shared-route
![]() $SR$
has at most one intersection point p. In particular, a crossing shared-route is necessarily open.
$SR$
has at most one intersection point p. In particular, a crossing shared-route is necessarily open.
Proof. The second statement follows from the first since otherwise the oriented holed surface
![]() $\mathfrak {S}^0$
would contain a Möbius strip.
$\mathfrak {S}^0$
would contain a Möbius strip.
Suppose, for an ordered pair
![]() $(\gamma _1, \gamma _2)$
of travelers, there were a crossing shared-route
$(\gamma _1, \gamma _2)$
of travelers, there were a crossing shared-route
![]() $ \{ (E^1_{i_k})_{k \in K}, ((E^2)^{-1}_{j_k})_{k \in K} \}$
that has more than one intersection point. There are only finitely many intersection points, denoted
$ \{ (E^1_{i_k})_{k \in K}, ((E^2)^{-1}_{j_k})_{k \in K} \}$
that has more than one intersection point. There are only finitely many intersection points, denoted
![]() $p_{k_1}, p_{k_2}, \dots , p_{k_m}$
with
$p_{k_1}, p_{k_2}, \dots , p_{k_m}$
with
![]() $k_i < k_{i+1}$
. The intersection points
$k_i < k_{i+1}$
. The intersection points
![]() $p_{k_1}$
and
$p_{k_1}$
and
![]() $p_{k_{2}}$
form the tips of an immersed bigon B, which we formalize as the convex common subsequence
$p_{k_{2}}$
form the tips of an immersed bigon B, which we formalize as the convex common subsequence
![]() $ B = \{ (E^1_{i_k})_{k_1 \leqslant k \leqslant k_2+1}, ((E^2)^{-1}_{j_k})_{k_1 \leqslant k \leqslant k_2+1} \}$
; see the bottom of Figure 47. Alternatively, we think of B as bounded by the segments of
$ B = \{ (E^1_{i_k})_{k_1 \leqslant k \leqslant k_2+1}, ((E^2)^{-1}_{j_k})_{k_1 \leqslant k \leqslant k_2+1} \}$
; see the bottom of Figure 47. Alternatively, we think of B as bounded by the segments of
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
between
$\gamma _2$
between
![]() $p_{k_1}$
and
$p_{k_1}$
and
![]() $p_{k_2}$
.
$p_{k_2}$
.

Figure 47 Immersed bigons do not exist: 1 of 2.
Let
![]() $\pi $
be the projection map from the universal cover
$\pi $
be the projection map from the universal cover
![]() $\widetilde {\mathfrak {S}^0}$
to the holed surface
$\widetilde {\mathfrak {S}^0}$
to the holed surface
![]() $\mathfrak {S}^0$
. Equip
$\mathfrak {S}^0$
. Equip
![]() $\widetilde {\mathfrak {S}^0}$
with the lifted split ideal triangulation
$\widetilde {\mathfrak {S}^0}$
with the lifted split ideal triangulation
![]() $\widetilde {\widehat {\lambda }} = \pi ^{-1}(\widehat {\lambda })$
. For a traveler
$\widetilde {\widehat {\lambda }} = \pi ^{-1}(\widehat {\lambda })$
. For a traveler
![]() $\gamma $
, consider one of its lifts
$\gamma $
, consider one of its lifts
![]() $\widetilde {\gamma }$
in
$\widetilde {\gamma }$
in
![]() $\widetilde {\mathfrak {S}^0}$
. By the no-switchbacks property (§8.1), and the fact that the dual graph of
$\widetilde {\mathfrak {S}^0}$
. By the no-switchbacks property (§8.1), and the fact that the dual graph of
![]() $\widetilde {\widehat {\lambda }}$
in
$\widetilde {\widehat {\lambda }}$
in
![]() $\widetilde {\mathfrak {S}^0}$
is a tree, the lifted curve
$\widetilde {\mathfrak {S}^0}$
is a tree, the lifted curve
![]() $\widetilde {\gamma }$
does not cross the same edge
$\widetilde {\gamma }$
does not cross the same edge
![]() $\widetilde {E}$
in the universal cover
$\widetilde {E}$
in the universal cover
![]() $\widetilde {\mathfrak {S}^0}$
more than once. Therefore, the immersed bigon B lifts to an embedded topological bigon
$\widetilde {\mathfrak {S}^0}$
more than once. Therefore, the immersed bigon B lifts to an embedded topological bigon
![]() $\widetilde {B}$
in
$\widetilde {B}$
in
![]() $\widetilde {\mathfrak {S}^0}$
, bounded by segments of lifts
$\widetilde {\mathfrak {S}^0}$
, bounded by segments of lifts
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma _2}$
of the curves
$\widetilde {\gamma _2}$
of the curves
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
; see Figure 47.
$\gamma _2$
; see Figure 47.
The preimage
![]() $\widetilde {W} = \pi ^{-1}(W)$
of the web W is an (infinite) web in
$\widetilde {W} = \pi ^{-1}(W)$
of the web W is an (infinite) web in
![]() $\widetilde {\mathfrak {S}^0}$
. Moreover,
$\widetilde {\mathfrak {S}^0}$
. Moreover,
![]() $\widetilde {W}$
is in good position with respect to
$\widetilde {W}$
is in good position with respect to
![]() $\widetilde {\widehat {\lambda }}$
. Since W is nonelliptic, so is
$\widetilde {\widehat {\lambda }}$
. Since W is nonelliptic, so is
![]() $\widetilde {W}$
(compare the proof of Lemma 7.6). Let
$\widetilde {W}$
(compare the proof of Lemma 7.6). Let
![]() $\big< \widetilde {W} \big>$
be the global picture associated to
$\big< \widetilde {W} \big>$
be the global picture associated to
![]() $\widetilde {W}$
. Note that the lifted curves
$\widetilde {W}$
. Note that the lifted curves
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma }_2$
are in
$\widetilde {\gamma }_2$
are in
![]() $\big< \widetilde {W} \big>$
. Observe that it is possible for
$\big< \widetilde {W} \big>$
. Observe that it is possible for
![]() $\mathrm {int}(\widetilde {B}) \cap \big< \widetilde {W} \big> \neq \varnothing $
to be nonempty; see Figure 48. However, by the no-switchbacks property, there are no closed curves of
$\mathrm {int}(\widetilde {B}) \cap \big< \widetilde {W} \big> \neq \varnothing $
to be nonempty; see Figure 48. However, by the no-switchbacks property, there are no closed curves of
![]() $\big< \widetilde {W} \big>$
in this interior.
$\big< \widetilde {W} \big>$
in this interior.

Figure 48 Immersed bigons do not exist: 2 of 2.
The rest of the proof is similar to the proof of Proposition 3.15; see Figure 16. Here, the web orientation is important. Specifically, since only (locally) oppositely oriented (with respect to biangles) curves in the global picture
![]() $\big< \widetilde {W} \big>$
can intersect, it follows by the no-switchbacks property that if a curve
$\big< \widetilde {W} \big>$
can intersect, it follows by the no-switchbacks property that if a curve
![]() $\widetilde {\gamma }$
enters the embedded bigon
$\widetilde {\gamma }$
enters the embedded bigon
![]() $\widetilde {B}$
via a boundary edge
$\widetilde {B}$
via a boundary edge
![]() $\widetilde {E}$
, then
$\widetilde {E}$
, then
![]() $\widetilde {\gamma }$
must leave through
$\widetilde {\gamma }$
must leave through
![]() $\widetilde {E}$
as well. Consequently, there exists an innermost embedded bigon
$\widetilde {E}$
as well. Consequently, there exists an innermost embedded bigon
![]() $\widetilde {B}^\prime \subseteq \widetilde {B}$
whose interior does not intersect
$\widetilde {B}^\prime \subseteq \widetilde {B}$
whose interior does not intersect
![]() $\big< \widetilde {W} \big>$
; see Figure 48. But then
$\big< \widetilde {W} \big>$
; see Figure 48. But then
![]() $\widetilde {B}^\prime $
corresponds to a square-face
$\widetilde {B}^\prime $
corresponds to a square-face
![]() $\widetilde {D}$
in the lifted nonelliptic web
$\widetilde {D}$
in the lifted nonelliptic web
![]() $\widetilde {W}$
, which is a contradiction.
$\widetilde {W}$
, which is a contradiction.
Lemma 8.7. If the web W is nonelliptic, then there are no intersection points of
![]() $\left < W \right>$
along any closed noncrossing shared-route (as opposed to open noncrossing shared-routes). In particular, each closed noncrossing shared-route
$\left < W \right>$
along any closed noncrossing shared-route (as opposed to open noncrossing shared-routes). In particular, each closed noncrossing shared-route
![]() $SR$
is embedded, namely its travelers
$SR$
is embedded, namely its travelers
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
bound an embedded annulus
$\gamma _2$
bound an embedded annulus
![]() $A \subseteq \mathfrak {S}$
; see Figure 46b.
$A \subseteq \mathfrak {S}$
; see Figure 46b.
Proof. If there were an intersection point of
![]() $\left < W \right>$
along either traveler, then an argument similar to that depicted in Figure 48 implies there would exist an immersed bigon in
$\left < W \right>$
along either traveler, then an argument similar to that depicted in Figure 48 implies there would exist an immersed bigon in
![]() $\left < W \right>$
.
$\left < W \right>$
.
Definition 8.8. Consider an open shared-route
![]() $SR$
for an ordered pair
$SR$
for an ordered pair
![]() $(\gamma _1, \gamma _2)$
of travelers in
$(\gamma _1, \gamma _2)$
of travelers in
![]() $\left < W \right>$
. We say that the source-end
$\left < W \right>$
. We say that the source-end
![]() $\mathscr {E}$
of the open shared-route
$\mathscr {E}$
of the open shared-route
![]() $SR$
is the unique end
$SR$
is the unique end
![]() $\mathscr {E}$
of
$\mathscr {E}$
of
![]() $SR$
such that the traveler
$SR$
such that the traveler
![]() $\gamma _1$
enters the shared-route
$\gamma _1$
enters the shared-route
![]() $SR$
through the end
$SR$
through the end
![]() $\mathscr {E}$
.
$\mathscr {E}$
.
Assuming W is nonelliptic, we say that the unique intersection point p in a crossing shared-route
![]() $SR$
, which is necessarily open by Lemma 8.6, lies in the i-th shared-route-biangle
$SR$
, which is necessarily open by Lemma 8.6, lies in the i-th shared-route-biangle
![]() $\mathfrak {B}_i$
, denoted
$\mathfrak {B}_i$
, denoted
![]() $p \in _{SR} \mathfrak {B}_i$
,
$p \in _{SR} \mathfrak {B}_i$
,
![]() $i \geqslant 0$
, if
$i \geqslant 0$
, if
![]() $\gamma _1$
crosses
$\gamma _1$
crosses
![]() $\gamma _2^{-1}$
(at the point p) inside the i-th biangle through which
$\gamma _2^{-1}$
(at the point p) inside the i-th biangle through which
![]() $\gamma _1$
travels after entering
$\gamma _1$
travels after entering
![]() $SR$
through the source-end
$SR$
through the source-end
![]() $\mathscr {E}$
.
$\mathscr {E}$
.
For example, in Figure 45, the source-end
![]() $\mathscr {E}$
of
$\mathscr {E}$
of
![]() $SR$
is the end labeled L.
$SR$
is the end labeled L.
Also, in Figure 45, p is in the shared-route-biangle
![]() $p \in _{SR} \mathfrak {B}_2$
. Note that there is a unique index i such that
$p \in _{SR} \mathfrak {B}_2$
. Note that there is a unique index i such that
![]() $p \in _{SR} \mathfrak {B}_i$
. This definition is specially designed to circumvent the situation where
$p \in _{SR} \mathfrak {B}_i$
. This definition is specially designed to circumvent the situation where
![]() $\mathfrak {B}_i$
and
$\mathfrak {B}_i$
and
![]() $\mathfrak {B}_j$
represent the same biangle
$\mathfrak {B}_j$
represent the same biangle
![]() $\mathfrak {B}$
on the surface for different indices
$\mathfrak {B}$
on the surface for different indices
![]() $i \neq j$
. For example, in Figure 45, even if, say,
$i \neq j$
. For example, in Figure 45, even if, say,
![]() $\mathfrak {B}_5$
represented the same biangle
$\mathfrak {B}_5$
represented the same biangle
![]() $\mathfrak {B}$
as
$\mathfrak {B}$
as
![]() $\mathfrak {B}_2$
, we would say
$\mathfrak {B}_2$
, we would say
![]() $p \in _{SR} \mathfrak {B}_2$
and
$p \in _{SR} \mathfrak {B}_2$
and
![]() $p \notin _{SR} \mathfrak {B}_5$
. Alternatively, one could think of this distinction at the level of the universal cover.
$p \notin _{SR} \mathfrak {B}_5$
. Alternatively, one could think of this distinction at the level of the universal cover.
8.5. Preparation: oriented shared-routes
As previously, let W be a web on
![]() $\mathfrak {S}$
in good position with respect to
$\mathfrak {S}$
in good position with respect to
![]() $\widehat {\lambda }$
such that its global picture
$\widehat {\lambda }$
such that its global picture
![]() $(\left < W \right>, \{x_0^j\})$
is based.
$(\left < W \right>, \{x_0^j\})$
is based.
Definition 8.9. We say that a noncrossing shared-route
![]() $SR$
for an ordered pair
$SR$
for an ordered pair
![]() $(\gamma _1, \gamma _2)$
of travelers in
$(\gamma _1, \gamma _2)$
of travelers in
![]() $\left < W \right>$
is left-oriented (resp. right-oriented) if for either of the travelers
$\left < W \right>$
is left-oriented (resp. right-oriented) if for either of the travelers
![]() $\gamma _1$
or
$\gamma _1$
or
![]() $\gamma _2$
, call it
$\gamma _2$
, call it
![]() $\gamma $
, the other traveler appears on the left (resp. right) of
$\gamma $
, the other traveler appears on the left (resp. right) of
![]() $\gamma $
with respect to
$\gamma $
with respect to
![]() $\gamma $
’s orientation; see Figure 46.
$\gamma $
’s orientation; see Figure 46.
The web W is closed-left-oriented (resp. closed-right-oriented) if all of
![]() $\left < W \right>$
’s closed noncrossing shared-routes are left-oriented (resp. right-oriented); see Figure 46b.
$\left < W \right>$
’s closed noncrossing shared-routes are left-oriented (resp. right-oriented); see Figure 46b.
Note, by Lemma 8.7, a nonelliptic web W can always be replaced with a closed-left-oriented or closed-right-oriented nonelliptic web by performing global parallel-moves (Definition 2.3); see Figure 3.
We also want to define a notion of orientation for crossing shared-routes. Unlike for noncrossing shared-routes, this will depend on the ordering of the pair
![]() $(\gamma _1, \gamma _2)$
. Since we will be dealing with nonelliptic webs, by Lemma 8.6 it suffices to think about open shared-routes.
$(\gamma _1, \gamma _2)$
. Since we will be dealing with nonelliptic webs, by Lemma 8.6 it suffices to think about open shared-routes.
Definition 8.10. We say that an end
![]() $\mathscr {E}$
of an open shared-route
$\mathscr {E}$
of an open shared-route
![]() $SR$
is left-oriented or right-oriented in the same way as in Definition 8.9 for noncrossing shared routes.
$SR$
is left-oriented or right-oriented in the same way as in Definition 8.9 for noncrossing shared routes.
Assuming W is nonelliptic, a crossing shared-route
![]() $SR$
for an ordered pair
$SR$
for an ordered pair
![]() $(\gamma _1, \gamma _2)$
of travelers in
$(\gamma _1, \gamma _2)$
of travelers in
![]() $\left < W \right>$
, which is necessarily open by Lemma 8.6, is left-oriented (resp. right-oriented) if its source-end
$\left < W \right>$
, which is necessarily open by Lemma 8.6, is left-oriented (resp. right-oriented) if its source-end
![]() $\mathscr {E}$
(Definition 8.8) is left-oriented (resp. right-oriented).
$\mathscr {E}$
(Definition 8.8) is left-oriented (resp. right-oriented).
For example, the crossing shared-route shown in Figure 45 is left-oriented.
8.6. Proof of the main lemma: intersection points
We now begin the formal proof of the main Lemma 7.7. Fix local webs
![]() $\{W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
$\{W_{\mathfrak {T}} \}_{\mathfrak {T} \in \widehat {\lambda }}$
and
![]() $\{W^\prime _{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
in the
$\{W^\prime _{\mathfrak {T}}\}_{\mathfrak {T} \in \widehat {\lambda }}$
in the
![]() $\mathscr {W}_{\mathfrak {T}}$
satisfying the hypotheses of the main lemma, and let W and
$\mathscr {W}_{\mathfrak {T}}$
satisfying the hypotheses of the main lemma, and let W and
![]() $W^\prime $
be the induced nonelliptic global webs obtained by the ladder gluing construction. By applying global parallel-moves, we may assume that both W and
$W^\prime $
be the induced nonelliptic global webs obtained by the ladder gluing construction. By applying global parallel-moves, we may assume that both W and
![]() $W^\prime $
are closed-left-oriented, say (Definition 8.9). Assume that the global pictures
$W^\prime $
are closed-left-oriented, say (Definition 8.9). Assume that the global pictures
![]() $(\left <W\right>, \{x_0^j\})$
and
$(\left <W\right>, \{x_0^j\})$
and
![]() $(\left <W^\prime \right>, \{ x_0^{\prime j} \})$
are based and that the base points
$(\left <W^\prime \right>, \{ x_0^{\prime j} \})$
are based and that the base points
![]() $x_0^j$
and
$x_0^j$
and
![]() $x_0^{\prime j}$
satisfy the conclusion of the fellow traveler Lemma 8.3. Throughout, for each traveler
$x_0^{\prime j}$
satisfy the conclusion of the fellow traveler Lemma 8.3. Throughout, for each traveler
![]() $\gamma $
in
$\gamma $
in
![]() $\left < W \right>$
we denote by
$\left < W \right>$
we denote by
![]() $\gamma ^\prime $
the corresponding traveler in
$\gamma ^\prime $
the corresponding traveler in
![]() $\left < W^\prime \right>$
as provided by the fellow traveler lemma.
$\left < W^\prime \right>$
as provided by the fellow traveler lemma.
Let
![]() $\mathscr {P}$
(resp.
$\mathscr {P}$
(resp.
![]() $\mathscr {P}^\prime $
) denote the set of intersection points p of all travelers in
$\mathscr {P}^\prime $
) denote the set of intersection points p of all travelers in
![]() $\left < W \right>$
(resp.
$\left < W \right>$
(resp.
![]() $\left < W^\prime \right>$
).
$\left < W^\prime \right>$
).
Corollary 8.11. There is a natural bijection
![]() $\varphi : \mathscr {P} \overset {\sim }{\to } \mathscr {P}^\prime $
. We write
$\varphi : \mathscr {P} \overset {\sim }{\to } \mathscr {P}^\prime $
. We write
![]() $p^\prime = \varphi (p)$
.
$p^\prime = \varphi (p)$
.

Figure 49 Natural one-to-one correspondence between intersection points.
For the proof, we will need the following notion.
Definition 8.12. Let
![]() $p \in \mathscr {P}$
. We define the left-oriented crossing shared-route generated by p, denoted
$p \in \mathscr {P}$
. We define the left-oriented crossing shared-route generated by p, denoted
![]() $SR(p)$
, to be the unique left-oriented crossing shared-route (Definition 8.10) in
$SR(p)$
, to be the unique left-oriented crossing shared-route (Definition 8.10) in
![]() $\left < W \right>$
whose intersection point is p. Note, in particular, that the left-orientation condition determines the order
$\left < W \right>$
whose intersection point is p. Note, in particular, that the left-orientation condition determines the order
![]() $(\gamma _1, \gamma _2)$
of the involved travelers. (Technically speaking, we choose K starting at
$(\gamma _1, \gamma _2)$
of the involved travelers. (Technically speaking, we choose K starting at
![]() $0$
, and then the shared-route
$0$
, and then the shared-route
![]() $SR(p) = \{ (E^1_{i_k})_{k \in K}, ((E^2)^{-1}_{j_k})_{k \in K} \}$
is only uniquely determined after choosing the two indices
$SR(p) = \{ (E^1_{i_k})_{k \in K}, ((E^2)^{-1}_{j_k})_{k \in K} \}$
is only uniquely determined after choosing the two indices
![]() $i_0$
and
$i_0$
and
![]() $j_0$
assigned by
$j_0$
assigned by
![]() $0 \in K$
; this ambiguity only occurs when the shared-route has – part of – a loop traveler.)
$0 \in K$
; this ambiguity only occurs when the shared-route has – part of – a loop traveler.)
Proof of Corollary 8.11
Consider the left-oriented crossing shared-route
![]() $SR(p)$
in
$SR(p)$
in
![]() $\left < W \right>$
with travelers
$\left < W \right>$
with travelers
![]() $(\gamma _1, \gamma _2)$
generated by the intersection point p. By the fellow traveler lemma, there is a corresponding shared-route
$(\gamma _1, \gamma _2)$
generated by the intersection point p. By the fellow traveler lemma, there is a corresponding shared-route
![]() $SR^\prime $
in
$SR^\prime $
in
![]() $\left < W^\prime \right>$
with the travelers
$\left < W^\prime \right>$
with the travelers
![]() $(\gamma ^\prime _1, \gamma ^\prime _2)$
, which must also be open; see Figures 45 and 46a. Moreover, the ends
$(\gamma ^\prime _1, \gamma ^\prime _2)$
, which must also be open; see Figures 45 and 46a. Moreover, the ends
![]() $\mathscr {E}^\prime $
of
$\mathscr {E}^\prime $
of
![]() $SR^\prime $
have orientations (Definition 8.10) matching those of the ends
$SR^\prime $
have orientations (Definition 8.10) matching those of the ends
![]() $\mathscr {E}$
of
$\mathscr {E}$
of
![]() $SR(p)$
. It follows that
$SR(p)$
. It follows that
![]() $SR^\prime $
is crossing. Its unique intersection point
$SR^\prime $
is crossing. Its unique intersection point
![]() $p^\prime $
is the desired image of p; see Figure 49. (Note for later that since
$p^\prime $
is the desired image of p; see Figure 49. (Note for later that since
![]() $SR(p)$
is left-oriented, so is
$SR(p)$
is left-oriented, so is
![]() $SR^\prime $
, thus
$SR^\prime $
, thus
![]() $SR^\prime = SR^\prime (p^\prime )$
.)
$SR^\prime = SR^\prime (p^\prime )$
.)
Recall that a crossing shared-route
![]() $SR$
for the ordered pair
$SR$
for the ordered pair
![]() $(\gamma _1, \gamma _2)$
comes with an ordering of the shared-route-biangles
$(\gamma _1, \gamma _2)$
comes with an ordering of the shared-route-biangles
![]() $\mathfrak {B}_i$
appearing along
$\mathfrak {B}_i$
appearing along
![]() $\gamma _1$
’s route, starting from the source-end
$\gamma _1$
’s route, starting from the source-end
![]() $\mathscr {E}$
; see Definition 8.8. If p and
$\mathscr {E}$
; see Definition 8.8. If p and
![]() $p^\prime $
are intersection points as in Corollary 8.11 and its proof, then the left-oriented crossing shared-routes
$p^\prime $
are intersection points as in Corollary 8.11 and its proof, then the left-oriented crossing shared-routes
![]() $SR(p)$
and
$SR(p)$
and
![]() $SR^\prime (p^\prime )$
have the same associated sequence of shared-route-biangles
$SR^\prime (p^\prime )$
have the same associated sequence of shared-route-biangles
![]() $\mathfrak {B}_i$
. However, if
$\mathfrak {B}_i$
. However, if
![]() $p \in _{SR(p)} \mathfrak {B}_i$
and
$p \in _{SR(p)} \mathfrak {B}_i$
and
![]() $p^\prime \in _{SR^\prime (p^\prime )} \mathfrak {B}_j$
(see again Definition 8.8), it need not be true that
$p^\prime \in _{SR^\prime (p^\prime )} \mathfrak {B}_j$
(see again Definition 8.8), it need not be true that
![]() $i = j$
; see Figure 49.
$i = j$
; see Figure 49.
Definition 8.13. We say that two corresponding intersection points p and
![]() $p^\prime $
, as in Corollary 8.11, lie in the same shared-route-biangle if there is an index i such that
$p^\prime $
, as in Corollary 8.11, lie in the same shared-route-biangle if there is an index i such that
![]() $p \in _{SR(p)} \mathfrak {B}_i \ni _{SR^\prime (p^\prime )} p^\prime $
, where the sequence of shared-route-biangles
$p \in _{SR(p)} \mathfrak {B}_i \ni _{SR^\prime (p^\prime )} p^\prime $
, where the sequence of shared-route-biangles
![]() $\{ \mathfrak {B}_i \}$
is defined with respect to the left-oriented crossing shared-routes
$\{ \mathfrak {B}_i \}$
is defined with respect to the left-oriented crossing shared-routes
![]() $SR(p)$
and
$SR(p)$
and
![]() $SR^\prime (p^\prime )$
generated by p and
$SR^\prime (p^\prime )$
generated by p and
![]() $p^\prime $
, respectively.
$p^\prime $
, respectively.
For example, in Figure 49, even if it were true that
![]() $\mathfrak {B}_0$
and
$\mathfrak {B}_0$
and
![]() $\mathfrak {B}_2$
represented the same biangle
$\mathfrak {B}_2$
represented the same biangle
![]() $\mathfrak {B}$
on the surface, we would not say that p and
$\mathfrak {B}$
on the surface, we would not say that p and
![]() $p^\prime $
lie in the same shared-route-biangle.
$p^\prime $
lie in the same shared-route-biangle.
Lemma 8.14. There is a sequence of modified H-moves (Figure 41) applicable to the web W and a sequence of modified H-moves applicable to
![]() $W^\prime $
, after which the bijection
$W^\prime $
, after which the bijection
![]() $\mathscr {P} \leftrightarrow \mathscr {P}^\prime $
from Corollary 8.11 satisfies the property that each intersection point p in the global picture
$\mathscr {P} \leftrightarrow \mathscr {P}^\prime $
from Corollary 8.11 satisfies the property that each intersection point p in the global picture
![]() $\left < W \right>$
and its corresponding intersection point
$\left < W \right>$
and its corresponding intersection point
![]() $p^\prime $
in
$p^\prime $
in
![]() $\left < W^\prime \right>$
lie in the same shared-route-biangle
$\left < W^\prime \right>$
lie in the same shared-route-biangle
![]() $\mathfrak {B}_i$
.
$\mathfrak {B}_i$
.
Before giving a proof (§8.8), we reduce the proof of the main lemma to that of Lemma 8.14.
8.7. Proof of the main lemma: finishing the argument
Assuming corresponding intersection points lie in the same shared-route-biangle, we claim that we are done,
![]() $W = W^\prime $
.
$W = W^\prime $
.
By the proof of the fellow traveler lemma, not only is there a natural bijection of travelers
![]() $\gamma \leftrightarrow \gamma ^\prime $
, moreover for each edge E of
$\gamma \leftrightarrow \gamma ^\prime $
, moreover for each edge E of
![]() $\widehat {\lambda }$
there is a natural bijection of oriented strands
$\widehat {\lambda }$
there is a natural bijection of oriented strands
![]() $s \leftrightarrow s^\prime $
of
$s \leftrightarrow s^\prime $
of
![]() $\left < W \right>$
and
$\left < W \right>$
and
![]() $\left < W^\prime \right>$
, respectively, on E. Namely, the k-th out-strand (resp. in-strand) s, measured from left to right, say, with respect to
$\left < W^\prime \right>$
, respectively, on E. Namely, the k-th out-strand (resp. in-strand) s, measured from left to right, say, with respect to
![]() $\mathfrak {T}$
, is matched with the k-th out-strand (resp. in-strand)
$\mathfrak {T}$
, is matched with the k-th out-strand (resp. in-strand)
![]() $s^\prime $
. This satisfies that s lies in
$s^\prime $
. This satisfies that s lies in
![]() $\gamma $
if and only if
$\gamma $
if and only if
![]() $s^\prime $
lies in
$s^\prime $
lies in
![]() $\gamma ^\prime $
.
$\gamma ^\prime $
.
Fix an edge E adjacent to a triangle
![]() $\mathfrak {T}$
. Let
$\mathfrak {T}$
. Let
![]() $S = (s_i)$
(resp.
$S = (s_i)$
(resp.
![]() $S^\prime =(s^*_i)$
) be the full sequence of oriented strands for
$S^\prime =(s^*_i)$
) be the full sequence of oriented strands for
![]() $\left < W \right>$
(resp.
$\left < W \right>$
(resp.
![]() $\left < W^\prime \right>$
) on the edge E, measured from left to right. In particular, both in- and out-strands occur in S (resp.
$\left < W^\prime \right>$
) on the edge E, measured from left to right. In particular, both in- and out-strands occur in S (resp.
![]() $S^\prime $
).
$S^\prime $
).
Lemma 8.15. Assuming corresponding intersection points lie in the same shared-route-biangle, we have that
![]() $S = S^\prime $
, for every edge E of
$S = S^\prime $
, for every edge E of
![]() $\widehat {\lambda }$
; see Definition 8.13. (That is,
$\widehat {\lambda }$
; see Definition 8.13. (That is,
![]() $s^*_i=s^\prime _i$
for all i.)
$s^*_i=s^\prime _i$
for all i.)
Proof. It suffices to prove the following statement.
Claim 8.16. If
![]() $s^{\mathrm {out}}$
is an out-strand of S and if
$s^{\mathrm {out}}$
is an out-strand of S and if
![]() $s^{\mathrm {in}}$
is an in-strand of S, then
$s^{\mathrm {in}}$
is an in-strand of S, then
See Figure 50. To prove the forward direction of the claim, suppose otherwise, that is suppose
![]() $s^{\prime \mathrm {out}}$
lies to the right of
$s^{\prime \mathrm {out}}$
lies to the right of
![]() $s^{\prime \mathrm {in}}$
. Let
$s^{\prime \mathrm {in}}$
. Let
![]() $SR$
(resp.
$SR$
(resp.
![]() $SR^\prime $
) be a shared-route containing
$SR^\prime $
) be a shared-route containing
![]() $s^{\mathrm {out}}$
and
$s^{\mathrm {out}}$
and
![]() $s^{\mathrm {in}}$
(resp.
$s^{\mathrm {in}}$
(resp.
![]() $s^{\prime \mathrm {out}}$
and
$s^{\prime \mathrm {out}}$
and
![]() $s^{\prime \mathrm {in}}$
) (there are two possibilities for each, determined by the order of the pair of involved travelers). By the fellow traveler lemma,
$s^{\prime \mathrm {in}}$
) (there are two possibilities for each, determined by the order of the pair of involved travelers). By the fellow traveler lemma,
![]() $SR$
is crossing (resp. open/closed noncrossing) if and only if
$SR$
is crossing (resp. open/closed noncrossing) if and only if
![]() $SR^\prime $
is crossing (resp. open/closed noncrossing).
$SR^\prime $
is crossing (resp. open/closed noncrossing).

Figure 50 Identical oriented strand-sequences on each edge E.
Suppose
![]() $SR$
and
$SR$
and
![]() $SR^\prime $
are crossing. Then we may assume that
$SR^\prime $
are crossing. Then we may assume that
![]() $SR=SR(p)$
and
$SR=SR(p)$
and
![]() $SR^\prime =SR^\prime (p^\prime )$
have been chosen as the left-oriented crossing shared-routes generated by their unique intersection points p and
$SR^\prime =SR^\prime (p^\prime )$
have been chosen as the left-oriented crossing shared-routes generated by their unique intersection points p and
![]() $p^\prime $
, respectively; see Definition 8.12. By hypothesis, p and
$p^\prime $
, respectively; see Definition 8.12. By hypothesis, p and
![]() $p^\prime $
lie in the same shared-route-biangle, call it
$p^\prime $
lie in the same shared-route-biangle, call it
![]() $\mathfrak {B}_i$
, that is
$\mathfrak {B}_i$
, that is
![]() $p \in _{SR(p)} \mathfrak {B}_i \ni _{SR^\prime (p^\prime )} p^\prime $
. Letting
$p \in _{SR(p)} \mathfrak {B}_i \ni _{SR^\prime (p^\prime )} p^\prime $
. Letting
![]() $\mathfrak {B}_j$
denote the shared-route-biangle containing the edge E with the strands
$\mathfrak {B}_j$
denote the shared-route-biangle containing the edge E with the strands
![]() $s^{\mathrm {out}}$
and
$s^{\mathrm {out}}$
and
![]() $s^{\mathrm {in}}$
(and
$s^{\mathrm {in}}$
(and
![]() $s^{\prime \mathrm {in}}$
and
$s^{\prime \mathrm {in}}$
and
![]() $s^{\prime \mathrm {out}}$
), let us say that the strands are on the close (resp. far) side if they are on the first (resp. last) edge of
$s^{\prime \mathrm {out}}$
), let us say that the strands are on the close (resp. far) side if they are on the first (resp. last) edge of
![]() $\mathfrak {B}_j$
hit while traveling from the source-end of the shared-route. Similarly, it makes sense to say that the crossing comes before (resp. after) the strands with respect to the source-end. Our first observation is that since the source-end is left-oriented, and since
$\mathfrak {B}_j$
hit while traveling from the source-end of the shared-route. Similarly, it makes sense to say that the crossing comes before (resp. after) the strands with respect to the source-end. Our first observation is that since the source-end is left-oriented, and since
![]() $s^{\mathrm {out}}$
lies to the left of
$s^{\mathrm {out}}$
lies to the left of
![]() $s^{\mathrm {in}}$
, it cannot be true that the crossing comes after the strands. So let Case 1 (resp. Case 2) be the case that the crossing comes before the strands and that the strands are on the close (resp. far) side. Since
$s^{\mathrm {in}}$
, it cannot be true that the crossing comes after the strands. So let Case 1 (resp. Case 2) be the case that the crossing comes before the strands and that the strands are on the close (resp. far) side. Since
![]() $s^{\prime \mathrm {in}}$
lies to the left of
$s^{\prime \mathrm {in}}$
lies to the left of
![]() $s^{\prime \mathrm {out}}$
(by contradiction hypothesis), both Case 1 and Case 2 lead to a contradiction, namely that both ends of the crossing shared-route
$s^{\prime \mathrm {out}}$
(by contradiction hypothesis), both Case 1 and Case 2 lead to a contradiction, namely that both ends of the crossing shared-route
![]() $SR^\prime $
are left-oriented (Definition 8.10); see Figure 51.
$SR^\prime $
are left-oriented (Definition 8.10); see Figure 51.

Figure 51 Proof of Claim 8.16, by contradiction.
Similarly, if
![]() $SR$
and
$SR$
and
![]() $SR^\prime $
are noncrossing, the contradiction is that one of the shared-routes is left-oriented, and the other is right-oriented; see Definition 8.9. Indeed, in the open case (Figure 46a), this violates their matching end orientations (by the fellow traveler lemma), and in the closed case (Figure 46b), this violates that both W and
$SR^\prime $
are noncrossing, the contradiction is that one of the shared-routes is left-oriented, and the other is right-oriented; see Definition 8.9. Indeed, in the open case (Figure 46a), this violates their matching end orientations (by the fellow traveler lemma), and in the closed case (Figure 46b), this violates that both W and
![]() $W^\prime $
are closed-left-oriented; see the beginning of §8.6.
$W^\prime $
are closed-left-oriented; see the beginning of §8.6.
The backward direction of the claim is proved by symmetry.
Proof of main Lemma 7.7
By Lemma 8.14, we may assume that corresponding intersection points lie in the same shared-route-biangle. By hypothesis, the webs W and
![]() $W^\prime $
may differ over triangles
$W^\prime $
may differ over triangles
![]() $\mathfrak {T}$
by permutations of corner arcs. However, we gather from Lemma 8.15 that they in fact have the same orderings of corner arcs in each triangle
$\mathfrak {T}$
by permutations of corner arcs. However, we gather from Lemma 8.15 that they in fact have the same orderings of corner arcs in each triangle
![]() $\mathfrak {T}$
. Also, since the ladder-webs in the biangles
$\mathfrak {T}$
. Also, since the ladder-webs in the biangles
![]() $\mathfrak {B}$
are uniquely determined by their boundary-edge sequences, it follows that W and
$\mathfrak {B}$
are uniquely determined by their boundary-edge sequences, it follows that W and
![]() $W^\prime $
have the same ladder-web in each biangle
$W^\prime $
have the same ladder-web in each biangle
![]() $\mathfrak {B}$
; see Proposition 3.15.
$\mathfrak {B}$
; see Proposition 3.15.
8.8. Proof of the main lemma: proof of Lemma 8.14
We have reduced the proof of the main lemma to proving Lemma 8.14. We begin by laying some groundwork.
Let
![]() $\mathfrak {B}$
be a biangle, and let
$\mathfrak {B}$
be a biangle, and let
![]() $\mathscr {P}_{\mathfrak {B}} = \mathscr {P} \cap \mathfrak {B}$
be the set of intersection points of
$\mathscr {P}_{\mathfrak {B}} = \mathscr {P} \cap \mathfrak {B}$
be the set of intersection points of
![]() $\left < W \right>$
in
$\left < W \right>$
in
![]() $\mathfrak {B}$
. Let E be a boundary edge of the biangle
$\mathfrak {B}$
. Let E be a boundary edge of the biangle
![]() $\mathfrak {B}$
, and let
$\mathfrak {B}$
, and let
![]() $\mathfrak {B}_1$
and
$\mathfrak {B}_1$
and
![]() $\mathfrak {B}_2$
be the two biangles opposite
$\mathfrak {B}_2$
be the two biangles opposite
![]() $\mathfrak {B}$
across the triangle
$\mathfrak {B}$
across the triangle
![]() $\mathfrak {T}$
adjacent to the edge E; see Figure 52.
$\mathfrak {T}$
adjacent to the edge E; see Figure 52.
Definition 8.17. Let
![]() $p \in \mathscr {P}_{\mathfrak {B}}$
be an intersection point in
$p \in \mathscr {P}_{\mathfrak {B}}$
be an intersection point in
![]() $\mathfrak {B}$
of two travelers
$\mathfrak {B}$
of two travelers
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
in
$\gamma _2$
in
![]() $\left < W \right>$
. We denote by
$\left < W \right>$
. We denote by
![]() $\overline {\gamma }_1(p, E)$
the half-segment of
$\overline {\gamma }_1(p, E)$
the half-segment of
![]() $\gamma _1$
connecting p to E. Define similarly
$\gamma _1$
connecting p to E. Define similarly
![]() $\overline {\gamma }_2(p, E)$
. The pyramid
$\overline {\gamma }_2(p, E)$
. The pyramid
![]() $\Delta (p, E)$
bounded by p and E is the triangular subset of the biangle
$\Delta (p, E)$
bounded by p and E is the triangular subset of the biangle
![]() $\mathfrak {B}$
bordered by the boundary edge E and the two half-segments
$\mathfrak {B}$
bordered by the boundary edge E and the two half-segments
![]() $\overline {\gamma }_1(p, E)$
and
$\overline {\gamma }_1(p, E)$
and
![]() $\overline {\gamma }_2(p, E)$
; see Figure 52.
$\overline {\gamma }_2(p, E)$
; see Figure 52.
Let
![]() $P \subseteq \mathscr {P}_{\mathfrak {B}}$
be a subset of intersection points. We call P saturated with respect to E if
$P \subseteq \mathscr {P}_{\mathfrak {B}}$
be a subset of intersection points. We call P saturated with respect to E if
 $$ \begin{align*} \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{p \in P} \Delta(p, E) \right) = P. \end{align*} $$
$$ \begin{align*} \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{p \in P} \Delta(p, E) \right) = P. \end{align*} $$
In other words, there are no intersection points in the pyramids
![]() $\Delta (p, E)$
,
$\Delta (p, E)$
,
![]() $p\in P$
, that are not already in P.
$p\in P$
, that are not already in P.
An intersection point
![]() $p \in \mathscr {P}_{\mathfrak {B}}$
is movable with respect to E if, after crossing E, the half-segments
$p \in \mathscr {P}_{\mathfrak {B}}$
is movable with respect to E if, after crossing E, the half-segments
![]() $\overline {\gamma }_1(p, E)$
and
$\overline {\gamma }_1(p, E)$
and
![]() $\overline {\gamma }_2(p, E)$
extend parallel to each other across the adjacent triangle
$\overline {\gamma }_2(p, E)$
extend parallel to each other across the adjacent triangle
![]() $\mathfrak {T}$
, thus landing in the same opposite biangle, either
$\mathfrak {T}$
, thus landing in the same opposite biangle, either
![]() $\mathfrak {B}_1$
or
$\mathfrak {B}_1$
or
![]() $\mathfrak {B}_2$
; see Figure 52, where on the left, six points are movable; in the middle, four points are movable and on the right, none are movable. We say a subset
$\mathfrak {B}_2$
; see Figure 52, where on the left, six points are movable; in the middle, four points are movable and on the right, none are movable. We say a subset
![]() $P \subseteq \mathscr {P}_{\mathfrak {B}}$
is movable with respect to E if each
$P \subseteq \mathscr {P}_{\mathfrak {B}}$
is movable with respect to E if each
![]() $p \in P$
is movable.
$p \in P$
is movable.
Claim 8.18. Let
![]() $P \subseteq \mathscr {P}_{\mathfrak {B}}$
be a subset of intersection points that is saturated and movable with respect to E. Then, there exists a sequence
$P \subseteq \mathscr {P}_{\mathfrak {B}}$
be a subset of intersection points that is saturated and movable with respect to E. Then, there exists a sequence
![]() $W = W_0$
,
$W = W_0$
,
![]() $W_1$
,
$W_1$
,
![]() $\dots , W_n$
of webs and a sequence
$\dots , W_n$
of webs and a sequence
![]() $P_{-1} = \varnothing \subsetneq P_0 \subsetneq P_1 \subsetneq \dots \subsetneq P_{n-1}=P \subseteq \mathscr {P}_{\mathfrak {B}}$
of intersection points of
$P_{-1} = \varnothing \subsetneq P_0 \subsetneq P_1 \subsetneq \dots \subsetneq P_{n-1}=P \subseteq \mathscr {P}_{\mathfrak {B}}$
of intersection points of
![]() $\left < W \right>$
in the biangle
$\left < W \right>$
in the biangle
![]() $\mathfrak {B}$
, such that
$\mathfrak {B}$
, such that
![]() $W_{i+1}$
is obtained from
$W_{i+1}$
is obtained from
![]() $W_i$
by a finite number of modified H-moves (Figure 41) in such a way that the points
$W_i$
by a finite number of modified H-moves (Figure 41) in such a way that the points
![]() $P_i - P_{i-1}$
are carried into the two biangles
$P_i - P_{i-1}$
are carried into the two biangles
![]() $\mathfrak {B}_1 \cup \mathfrak {B}_2$
and no other intersection points are moved. After this process is complete, P has been moved into
$\mathfrak {B}_1 \cup \mathfrak {B}_2$
and no other intersection points are moved. After this process is complete, P has been moved into
![]() $\mathfrak {B}_1 \cup \mathfrak {B}_2$
and all the other intersection points
$\mathfrak {B}_1 \cup \mathfrak {B}_2$
and all the other intersection points
![]() $\mathscr {P} - P$
remain unmoved in their original biangles.
$\mathscr {P} - P$
remain unmoved in their original biangles.

Figure 52 Pushing a saturated movable subset P into adjacent biangles. (Two rounds of pushes are required to go from the second to third picture.).
Claim 8.18 will first be used in the proof of Claim 8.22. We now prepare to prove Claim 8.18.
We say that
![]() $p \in \mathscr {P}_{\mathfrak {B}}$
is immediately movable with respect to E if it is movable and there are no other intersection points in the pyramid
$p \in \mathscr {P}_{\mathfrak {B}}$
is immediately movable with respect to E if it is movable and there are no other intersection points in the pyramid
![]() $\Delta (p, E)$
, that is
$\Delta (p, E)$
, that is
![]() $\Delta (p, E) \cap \mathscr {P}_{\mathfrak {B}} = \{ p \}$
. Equivalently,
$\Delta (p, E) \cap \mathscr {P}_{\mathfrak {B}} = \{ p \}$
. Equivalently,
![]() $\mathrm {Int}(\Delta (p, E)) \cap \left < W \right> = \varnothing $
, hence a modified H-move can be applied to carry p across the edge E, across the adjacent triangle
$\mathrm {Int}(\Delta (p, E)) \cap \left < W \right> = \varnothing $
, hence a modified H-move can be applied to carry p across the edge E, across the adjacent triangle
![]() $\mathfrak {T}$
and into one of the opposite biangles
$\mathfrak {T}$
and into one of the opposite biangles
![]() $\mathfrak {B}_1$
or
$\mathfrak {B}_1$
or
![]() $\mathfrak {B}_2$
; see Figure 52, where on the left and in the middle, two and three points are immediately movable.
$\mathfrak {B}_2$
; see Figure 52, where on the left and in the middle, two and three points are immediately movable.
The following statement is evident from the ladder-web structure in the biangle
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
Fact 8.19. (Nested pyramids)
If
![]() $q \in \mathscr {P}_{\mathfrak {B}} \cap \Delta (p, E)$
is an intersection point in the pyramid
$q \in \mathscr {P}_{\mathfrak {B}} \cap \Delta (p, E)$
is an intersection point in the pyramid
![]() $\Delta (p, E)$
, then
$\Delta (p, E)$
, then
![]() $\Delta (q, E) \subseteq \Delta (p, E)$
. Consequently, if p is movable, then so is q. Therefore, if p is movable, then there exists an innermost q in
$\Delta (q, E) \subseteq \Delta (p, E)$
. Consequently, if p is movable, then so is q. Therefore, if p is movable, then there exists an innermost q in
![]() $\Delta (p, E)$
that is immediately movable.
$\Delta (p, E)$
that is immediately movable.
Proof of Claim 8.18
By induction, assume
![]() $W_i$
and
$W_i$
and
![]() $P_{i-1}$
are given. At this stage, the intersection points
$P_{i-1}$
are given. At this stage, the intersection points
![]() $P_{i-1}$
have been moved into
$P_{i-1}$
have been moved into
![]() $\mathfrak {B}_1 \cup \mathfrak {B}_2$
, and the intersection points
$\mathfrak {B}_1 \cup \mathfrak {B}_2$
, and the intersection points
![]() $P - P_{i-1} \neq \varnothing $
are still in
$P - P_{i-1} \neq \varnothing $
are still in
![]() $\mathfrak {B}$
. Note that, since P is saturated in
$\mathfrak {B}$
. Note that, since P is saturated in
![]() $\left < W \right>$
,
$\left < W \right>$
,
![]() $P - P_{i-1}$
is saturated in
$P - P_{i-1}$
is saturated in
![]() $\left < W_i \right>$
, that is,
$\left < W_i \right>$
, that is,
Since by hypothesis each
![]() $p \in P - P_{i-1}$
is movable, by Fact 8.19 the subset
$p \in P - P_{i-1}$
is movable, by Fact 8.19 the subset
is nonempty. In particular,
![]() $Q_i \subseteq P - P_{i-1}$
. We can thus apply modified H-moves to
$Q_i \subseteq P - P_{i-1}$
. We can thus apply modified H-moves to
![]() $W_i$
to move the intersection points
$W_i$
to move the intersection points
![]() $Q_i$
from the biangle
$Q_i$
from the biangle
![]() $\mathfrak {B}$
into the two biangles
$\mathfrak {B}$
into the two biangles
![]() $\mathfrak {B}_1 \cup \mathfrak {B}_2$
, yielding the new web
$\mathfrak {B}_1 \cup \mathfrak {B}_2$
, yielding the new web
![]() $W_{i+1}$
. Putting
$W_{i+1}$
. Putting
![]() $P_{i} = P_{i-1} \cup Q_i$
finishes the induction step; see Figure 52, where
$P_{i} = P_{i-1} \cup Q_i$
finishes the induction step; see Figure 52, where
![]() $n=3$
.
$n=3$
.
The following statement is immediate from Fact 8.19.
Fact 8.20. (Saturation of a subset of intersection points)
For any subset
![]() $Q \subseteq \mathscr {P}_{\mathfrak {B}}$
, the set
$Q \subseteq \mathscr {P}_{\mathfrak {B}}$
, the set
 $$ \begin{align*} P = \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{q \in Q} \Delta(q, E) \right) \quad \subseteq \mathscr{P}_{\mathfrak{B}} \end{align*} $$
$$ \begin{align*} P = \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{q \in Q} \Delta(q, E) \right) \quad \subseteq \mathscr{P}_{\mathfrak{B}} \end{align*} $$
is saturated with respect to E.
We continue moving toward the proof of Lemma 8.14. We are now dealing with two webs W and
![]() $W^\prime $
. Let E,
$W^\prime $
. Let E,
![]() $\mathfrak {T}$
,
$\mathfrak {T}$
,
![]() $\mathfrak {B}$
,
$\mathfrak {B}$
,
![]() $\mathfrak {B}_1$
,
$\mathfrak {B}_1$
,
![]() $\mathfrak {B}_2$
be as before. We begin by setting some notation.
$\mathfrak {B}_2$
be as before. We begin by setting some notation.
Given a subset
![]() $P \subseteq \mathscr {P}_{\mathfrak {B}}$
, put
$P \subseteq \mathscr {P}_{\mathfrak {B}}$
, put
 $$ \begin{align*} P^\prime(P, E) = \mathscr{P}^\prime_{\mathfrak{B}} \cap \left( \bigcup_{ \{ p \in P; \quad p \text{ and } p^\prime \text{ lie in the same shared-route-biangle} \} } \Delta(p^\prime, E) \right) \quad \subseteq \mathscr{P}^\prime_{\mathfrak{B}}. \end{align*} $$
$$ \begin{align*} P^\prime(P, E) = \mathscr{P}^\prime_{\mathfrak{B}} \cap \left( \bigcup_{ \{ p \in P; \quad p \text{ and } p^\prime \text{ lie in the same shared-route-biangle} \} } \Delta(p^\prime, E) \right) \quad \subseteq \mathscr{P}^\prime_{\mathfrak{B}}. \end{align*} $$
In other words,
![]() $P^\prime (P, E)$
consists of the points in
$P^\prime (P, E)$
consists of the points in
![]() $\mathscr {P}^\prime _{\mathfrak {B}}$
lying in the pyramids
$\mathscr {P}^\prime _{\mathfrak {B}}$
lying in the pyramids
![]() $\Delta (p^\prime , E)$
generated by those intersection points
$\Delta (p^\prime , E)$
generated by those intersection points
![]() $p^\prime $
in
$p^\prime $
in
![]() $\mathscr {P}^\prime _{\mathfrak {B}}$
whose corresponding intersection point p lies in the same shared-route-biangle as
$\mathscr {P}^\prime _{\mathfrak {B}}$
whose corresponding intersection point p lies in the same shared-route-biangle as
![]() $p^\prime $
and satisfies
$p^\prime $
and satisfies
![]() $p \in P$
. Symmetrically, given a subset
$p \in P$
. Symmetrically, given a subset
![]() $P^\prime \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
, put
$P^\prime \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
, put
 $$ \begin{align*} P(P^\prime, E) = \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{ \{ p^\prime \in P^\prime; \quad p^\prime \text{ and } p \text{ lie in the same shared-route-biangle} \} } \Delta(p, E) \right) \quad \subseteq \mathscr{P}_{\mathfrak{B}}. \end{align*} $$
$$ \begin{align*} P(P^\prime, E) = \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{ \{ p^\prime \in P^\prime; \quad p^\prime \text{ and } p \text{ lie in the same shared-route-biangle} \} } \Delta(p, E) \right) \quad \subseteq \mathscr{P}_{\mathfrak{B}}. \end{align*} $$
Note that (1) the above shared-route-biangles necessarily coincide with the biangle
![]() $\mathfrak {B}$
, and (2) generally, either of the sets
$\mathfrak {B}$
, and (2) generally, either of the sets
![]() $P^\prime (P, E)$
or
$P^\prime (P, E)$
or
![]() $P(P^\prime , E)$
may be empty.
$P(P^\prime , E)$
may be empty.
Fact 8.21. The union of movable sets is movable. Let
![]() $P \subseteq \mathscr {P}_{\mathfrak {B}}$
(resp.
$P \subseteq \mathscr {P}_{\mathfrak {B}}$
(resp.
![]() $P^\prime \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
) be movable with respect to E. Then
$P^\prime \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
) be movable with respect to E. Then
![]() $P^\prime (P, E) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
(resp.
$P^\prime (P, E) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
(resp.
![]() $P(P^\prime , E) \subseteq \mathscr {P}_{\mathfrak {B}}$
) is movable with respect to E.
$P(P^\prime , E) \subseteq \mathscr {P}_{\mathfrak {B}}$
) is movable with respect to E.
Proof. The first statement is obvious. For the second, if
![]() $p \in P$
is movable and if
$p \in P$
is movable and if
![]() $p^\prime $
lies in the same shared-route-biangle as p, then, by the fellow traveler Lemma 8.3,
$p^\prime $
lies in the same shared-route-biangle as p, then, by the fellow traveler Lemma 8.3,
![]() $p^\prime $
is movable. By Fact 8.19,
$p^\prime $
is movable. By Fact 8.19,
![]() $\mathscr {P}^\prime _{\mathfrak {B}} \cap \Delta (p^\prime , E) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
is movable. By the first statement,
$\mathscr {P}^\prime _{\mathfrak {B}} \cap \Delta (p^\prime , E) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
is movable. By the first statement,
![]() $P^\prime (P, E)$
is movable.
$P^\prime (P, E)$
is movable.
We are now prepared to prove Lemma 8.14, which we restate here for convenience.
Lemma 8.14. There is a sequence of modified H-moves (Figure 41) applicable to the web W and a sequence of modified H-moves applicable to
![]() $W^\prime $
, after which the bijection
$W^\prime $
, after which the bijection
![]() $\mathscr {P} \leftrightarrow \mathscr {P}^\prime $
from Corollary 8.11 satisfies the property that each intersection point p in the global picture
$\mathscr {P} \leftrightarrow \mathscr {P}^\prime $
from Corollary 8.11 satisfies the property that each intersection point p in the global picture
![]() $\left < W \right>$
and its corresponding intersection point
$\left < W \right>$
and its corresponding intersection point
![]() $p^\prime $
in
$p^\prime $
in
![]() $\left < W^\prime \right>$
lie in the same shared-route-biangle.
$\left < W^\prime \right>$
lie in the same shared-route-biangle.
Proof.
Step 1. Let N equal the cardinality
![]() $N = |\mathscr {P}| = |\mathscr {P}^\prime |$
. Define
$N = |\mathscr {P}| = |\mathscr {P}^\prime |$
. Define
If
![]() $N(W, W^\prime ) = N$
, then we are done. So assume
$N(W, W^\prime ) = N$
, then we are done. So assume
![]() $N(W, W^\prime ) < N$
.
$N(W, W^\prime ) < N$
.
The strategy is simple. If two intersection points
![]() $p \in \mathscr {P}_{\mathfrak {B}}$
and
$p \in \mathscr {P}_{\mathfrak {B}}$
and
![]() $p^\prime \in \mathscr {P}_{\mathfrak {B}^\prime }$
do not lie in the same shared-route-biangle, then we choose sufficiently large saturated movable sets
$p^\prime \in \mathscr {P}_{\mathfrak {B}^\prime }$
do not lie in the same shared-route-biangle, then we choose sufficiently large saturated movable sets
![]() $p \in P \subseteq \mathscr {P}_{\mathfrak {B}}$
and
$p \in P \subseteq \mathscr {P}_{\mathfrak {B}}$
and
![]() $p^\prime \in P^\prime \subseteq \mathscr {P}_{\mathfrak {B}^\prime }$
such that pushing P and
$p^\prime \in P^\prime \subseteq \mathscr {P}_{\mathfrak {B}^\prime }$
such that pushing P and
![]() $P^\prime $
into adjacent biangles via Claim 8.18 does not decrease
$P^\prime $
into adjacent biangles via Claim 8.18 does not decrease
![]() $N(W, W^\prime )$
. This can be done in a controlled way so that eventually
$N(W, W^\prime )$
. This can be done in a controlled way so that eventually
![]() $N(W, W^\prime )$
increases.
$N(W, W^\prime )$
increases.
Step 2. Let E,
![]() $\mathfrak {T}$
,
$\mathfrak {T}$
,
![]() $\mathfrak {B}$
,
$\mathfrak {B}$
,
![]() $\mathfrak {B}_1$
,
$\mathfrak {B}_1$
,
![]() $\mathfrak {B}_2$
be as above.
$\mathfrak {B}_2$
be as above.
Claim 8.22. Let
![]() $p_0 \in \mathscr {P}_{\mathfrak {B}}$
be movable with respect to E. Then, there exist subsets
$p_0 \in \mathscr {P}_{\mathfrak {B}}$
be movable with respect to E. Then, there exist subsets
![]() $p_0 \in P(p_0) \subseteq \mathscr {P}_{\mathfrak {B}}$
and
$p_0 \in P(p_0) \subseteq \mathscr {P}_{\mathfrak {B}}$
and
![]() $P^\prime (p_0) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
, and webs
$P^\prime (p_0) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
, and webs
![]() $W_1$
and
$W_1$
and
![]() $W^\prime _1$
obtained by applying finitely many modified H-moves to W and
$W^\prime _1$
obtained by applying finitely many modified H-moves to W and
![]() $W^\prime $
, respectively, such that: in
$W^\prime $
, respectively, such that: in
![]() $\left < W_1 \right>$
and
$\left < W_1 \right>$
and
![]() $\left < W_1^\prime \right>$
the subsets
$\left < W_1^\prime \right>$
the subsets
![]() $P(p_0)$
and
$P(p_0)$
and
![]() $P^\prime (p_0)$
have been moved into
$P^\prime (p_0)$
have been moved into
![]() $\mathfrak {B}_1 \cup \mathfrak {B}_2$
; also
$\mathfrak {B}_1 \cup \mathfrak {B}_2$
; also
![]() $\mathscr {P} - P(p_0)$
and
$\mathscr {P} - P(p_0)$
and
![]() $\mathscr {P}^\prime - P^\prime (p_0)$
are unmoved; and
$\mathscr {P}^\prime - P^\prime (p_0)$
are unmoved; and
We prove the claim. Our main task is to define two subsets
![]() $p_0 \in P(p_0) \subseteq \mathscr {P}_{\mathfrak {B}}$
and
$p_0 \in P(p_0) \subseteq \mathscr {P}_{\mathfrak {B}}$
and
![]() $P^\prime (p_0) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
that are saturated and movable with respect to E, satisfying the property that
$P^\prime (p_0) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
that are saturated and movable with respect to E, satisfying the property that
We do this simultaneously by a ping-pong procedure.
Put
![]() $P_1 = \mathscr {P}_{\mathfrak {B}} \cap \Delta (p_0, E)$
and
$P_1 = \mathscr {P}_{\mathfrak {B}} \cap \Delta (p_0, E)$
and
![]() $P^\prime _1 = P^\prime (P_1, E) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
. Having defined
$P^\prime _1 = P^\prime (P_1, E) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
. Having defined
![]() $P_i \subseteq \mathscr {P}_{\mathfrak {B}}$
and
$P_i \subseteq \mathscr {P}_{\mathfrak {B}}$
and
![]() $P^\prime _i \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
, put
$P^\prime _i \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
, put
![]() $P_{i+1} = P_i \cup P(P^\prime _i, E)$
and
$P_{i+1} = P_i \cup P(P^\prime _i, E)$
and
![]() $P^\prime _{i+1} = P^\prime _i \cup P^\prime (P_{i+1}, E)$
. This defines two nested infinite sequences
$P^\prime _{i+1} = P^\prime _i \cup P^\prime (P_{i+1}, E)$
. This defines two nested infinite sequences
![]() $P_1 \subseteq P_2 \subseteq \cdots \subseteq \mathscr {P}_{\mathfrak {B}}$
and
$P_1 \subseteq P_2 \subseteq \cdots \subseteq \mathscr {P}_{\mathfrak {B}}$
and
![]() $P^\prime _1 \subseteq P^\prime _2 \subseteq \cdots \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
. Since
$P^\prime _1 \subseteq P^\prime _2 \subseteq \cdots \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
. Since
![]() $\mathscr {P}_{\mathfrak {B}}$
and
$\mathscr {P}_{\mathfrak {B}}$
and
![]() $\mathscr {P}^\prime _{\mathfrak {B}}$
are finite, these sequences stabilize:
$\mathscr {P}^\prime _{\mathfrak {B}}$
are finite, these sequences stabilize:
![]() $P_i = P_{i+1}$
and
$P_i = P_{i+1}$
and
![]() $P^\prime _i = P^\prime _{i+1}$
for all
$P^\prime _i = P^\prime _{i+1}$
for all
![]() $i \geqslant i_0$
. Set
$i \geqslant i_0$
. Set
![]() $P(p_0) = P_{i_0} \ni p_0$
and
$P(p_0) = P_{i_0} \ni p_0$
and
![]() $P^\prime (p_0) = P^\prime _{i_0}$
.
$P^\prime (p_0) = P^\prime _{i_0}$
.
Note that, by construction, there exists
![]() $Q \subseteq \mathscr {P}_{\mathfrak {B}}$
and
$Q \subseteq \mathscr {P}_{\mathfrak {B}}$
and
![]() $Q^\prime \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
such that
$Q^\prime \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
such that
 $$ \begin{align*} P(p_0) = \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{q \in Q} \Delta(q, E) \right) \quad \text{and} \quad P^\prime(p_0) = \mathscr{P}^\prime_{\mathfrak{B}} \cap \left( \bigcup_{q^\prime \in Q^\prime} \Delta(q^\prime, E) \right). \end{align*} $$
$$ \begin{align*} P(p_0) = \mathscr{P}_{\mathfrak{B}} \cap \left( \bigcup_{q \in Q} \Delta(q, E) \right) \quad \text{and} \quad P^\prime(p_0) = \mathscr{P}^\prime_{\mathfrak{B}} \cap \left( \bigcup_{q^\prime \in Q^\prime} \Delta(q^\prime, E) \right). \end{align*} $$
By Fact 8.20,
![]() $P(p_0)$
and
$P(p_0)$
and
![]() $P^\prime (p_0)$
are saturated with respect to E.
$P^\prime (p_0)$
are saturated with respect to E.
Observe also that since
![]() $p_0 \in \mathscr {P}_{\mathfrak {B}}$
is movable by hypothesis,
$p_0 \in \mathscr {P}_{\mathfrak {B}}$
is movable by hypothesis,
![]() $P_1 = \mathscr {P}_{\mathfrak {B}} \cap \Delta (p_0, E)$
is movable by Fact 8.19, hence
$P_1 = \mathscr {P}_{\mathfrak {B}} \cap \Delta (p_0, E)$
is movable by Fact 8.19, hence
![]() $P(p_0) \subseteq \mathscr {P}_{\mathfrak {B}}$
and
$P(p_0) \subseteq \mathscr {P}_{\mathfrak {B}}$
and
![]() $P^\prime (p_0) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
are movable by Fact 8.21.
$P^\prime (p_0) \subseteq \mathscr {P}^\prime _{\mathfrak {B}}$
are movable by Fact 8.21.
To check Equation (**), by symmetry it suffices to check one direction. Assume
![]() $p \in P(p_0)$
and that p and
$p \in P(p_0)$
and that p and
![]() $p^\prime $
lie in the same shared-route-biangle. Let i be such that
$p^\prime $
lie in the same shared-route-biangle. Let i be such that
![]() $p \in P_i$
. Then
$p \in P_i$
. Then
To prove Equation (*), we use Claim 8.18 to move the saturated and movable sets
![]() $P(p_0)$
and
$P(p_0)$
and
![]() $P^\prime (p_0)$
, and only these sets, into the opposite biangles
$P^\prime (p_0)$
, and only these sets, into the opposite biangles
![]() $\mathfrak {B}_1 \cup \mathfrak {B}_2$
via finitely many modified H-moves applied to W and
$\mathfrak {B}_1 \cup \mathfrak {B}_2$
via finitely many modified H-moves applied to W and
![]() $W^\prime $
, yielding the desired webs
$W^\prime $
, yielding the desired webs
![]() $W_1$
and
$W_1$
and
![]() $W^\prime _1$
(note what we are here calling
$W^\prime _1$
(note what we are here calling
![]() $W_1$
was called
$W_1$
was called
![]() $W_n$
in the statement of Claim 8.18). If
$W_n$
in the statement of Claim 8.18). If
![]() $p \in P(p_0)$
moves into the biangle
$p \in P(p_0)$
moves into the biangle
![]() $\mathfrak {B}_1$
(resp.
$\mathfrak {B}_1$
(resp.
![]() $\mathfrak {B}_2$
), and if
$\mathfrak {B}_2$
), and if
![]() $p^\prime $
lies in the same shared-route-biangle as p so that
$p^\prime $
lies in the same shared-route-biangle as p so that
![]() $p^\prime \in P^\prime (p_0)$
by Equation (**), then by the fellow traveler Lemma 8.3
$p^\prime \in P^\prime (p_0)$
by Equation (**), then by the fellow traveler Lemma 8.3
![]() $p^\prime $
also moves into the biangle
$p^\prime $
also moves into the biangle
![]() $\mathfrak {B}_1$
(resp.
$\mathfrak {B}_1$
(resp.
![]() $\mathfrak {B}_2$
) and similarly if the roles of p and
$\mathfrak {B}_2$
) and similarly if the roles of p and
![]() $p^\prime $
are reversed.
$p^\prime $
are reversed.
Step 3. To finish the proof, assume that p and
![]() $p^\prime $
do not lie in the same shared-route-biangle. Then it makes sense to talk about which of p or
$p^\prime $
do not lie in the same shared-route-biangle. Then it makes sense to talk about which of p or
![]() $p^\prime $
is farther away from the source-end
$p^\prime $
is farther away from the source-end
![]() $\mathscr {E}$
or
$\mathscr {E}$
or
![]() $\mathscr {E}^\prime $
of the left-oriented crossing shared-route
$\mathscr {E}^\prime $
of the left-oriented crossing shared-route
![]() $SR(p)$
or
$SR(p)$
or
![]() $SR^\prime (p^\prime )$
which it generates, respectively. More precisely, if
$SR^\prime (p^\prime )$
which it generates, respectively. More precisely, if
![]() $p \in _{SR(p)} \mathfrak {B}_i$
and
$p \in _{SR(p)} \mathfrak {B}_i$
and
![]() $p^\prime \in _{SR^\prime (p^\prime )} \mathfrak {B}_j$
,
$p^\prime \in _{SR^\prime (p^\prime )} \mathfrak {B}_j$
,
![]() $i, j \geqslant 0$
, then
$i, j \geqslant 0$
, then
![]() $i \neq j$
and p being farther away is equivalent to
$i \neq j$
and p being farther away is equivalent to
![]() $i> j$
.
$i> j$
.
Assume p is farther away, so
![]() $i> j$
. By Claim 8.22, we can push p one step closer to the source-end
$i> j$
. By Claim 8.22, we can push p one step closer to the source-end
![]() $\mathscr {E}$
, that is we can push p into
$\mathscr {E}$
, that is we can push p into
![]() $\mathfrak {B}_{i-1}$
. For this step,
$\mathfrak {B}_{i-1}$
. For this step,
![]() $p^\prime $
either (1) stays in
$p^\prime $
either (1) stays in
![]() $\mathfrak {B}_j$
, (2) is pushed into
$\mathfrak {B}_j$
, (2) is pushed into
![]() $\mathfrak {B}_{j-1}$
, or (3) is pushed into
$\mathfrak {B}_{j-1}$
, or (3) is pushed into
![]() $\mathfrak {B}_{j+1}$
; see Figure 53. Notice since no two adjacent edges in a shared-route can represent the same edge in the split ideal triangulation
$\mathfrak {B}_{j+1}$
; see Figure 53. Notice since no two adjacent edges in a shared-route can represent the same edge in the split ideal triangulation
![]() $\widehat {\lambda }$
(by the no-switchbacks property), case (3) can only happen if
$\widehat {\lambda }$
(by the no-switchbacks property), case (3) can only happen if
![]() $j < i-1$
. Also, again by Claim 8.22, as a result of this step the number
$j < i-1$
. Also, again by Claim 8.22, as a result of this step the number
![]() $N(W, W^\prime )$
only increases or stays the same.
$N(W, W^\prime )$
only increases or stays the same.

Figure 53 Moving intersection points into the same shared-route-biangle.
Since the indices i,j are bounded below, after multiple applications of this step eventually p and
![]() $p^\prime $
fall into the same shared-route-biangle, at which point
$p^\prime $
fall into the same shared-route-biangle, at which point
![]() $N(W, W^\prime )$
strictly increases. Repeating this procedure for each pair p and
$N(W, W^\prime )$
strictly increases. Repeating this procedure for each pair p and
![]() $p^\prime $
completes the proof of Lemma 8.14.
$p^\prime $
completes the proof of Lemma 8.14.
9. Webs on surfaces-with-boundary
We generalize Theorem 7.1 to the case of surfaces-with-boundary
![]() $\widehat {\mathfrak {S}}$
. More precisely, we give two distinct, but complementary, versions of the result. The first version, where we think of the surface
$\widehat {\mathfrak {S}}$
. More precisely, we give two distinct, but complementary, versions of the result. The first version, where we think of the surface
![]() $\widehat {\mathfrak {S}}$
as generalizing punctured surfaces
$\widehat {\mathfrak {S}}$
as generalizing punctured surfaces
![]() $\mathfrak {S}$
, originates in the geometry and topology of
$\mathfrak {S}$
, originates in the geometry and topology of
![]() $\mathrm {SL}_3(\mathbb {C})$
-character varieties. The second version, where we think of the surface
$\mathrm {SL}_3(\mathbb {C})$
-character varieties. The second version, where we think of the surface
![]() $\widehat {\mathfrak {S}}$
as generalizing ideal polygons
$\widehat {\mathfrak {S}}$
as generalizing ideal polygons
![]() $\mathfrak {D}_k$
, originates in the representation theory of the Lie group
$\mathfrak {D}_k$
, originates in the representation theory of the Lie group
![]() $\mathrm {SL}_3(\mathbb {C})$
. The proof of either statement is essentially the same as in the empty boundary case.
$\mathrm {SL}_3(\mathbb {C})$
. The proof of either statement is essentially the same as in the empty boundary case.
9.1. Essential webs
9.1.1. Surfaces-with-boundary
Our surfaces, now denoted
![]() $\widehat {\mathfrak {S}}=\overline {\mathfrak {S}}-P$
, are obtained by removing a finite set P of punctures from a compact oriented surface
$\widehat {\mathfrak {S}}=\overline {\mathfrak {S}}-P$
, are obtained by removing a finite set P of punctures from a compact oriented surface
![]() $\overline {\mathfrak {S}}$
. We require that there is at least one puncture, that each boundary component of
$\overline {\mathfrak {S}}$
. We require that there is at least one puncture, that each boundary component of
![]() $\overline {\mathfrak {S}}$
contains a puncture, and that the resulting punctured surface
$\overline {\mathfrak {S}}$
contains a puncture, and that the resulting punctured surface
![]() $\widehat {\mathfrak {S}}$
admits an ideal triangulation
$\widehat {\mathfrak {S}}$
admits an ideal triangulation
![]() $\lambda $
; this last property is equivalent to the Euler characteristic condition
$\lambda $
; this last property is equivalent to the Euler characteristic condition
![]() $\chi (\widehat {\mathfrak {S}}) < d/2$
, where d is the number of components of
$\chi (\widehat {\mathfrak {S}}) < d/2$
, where d is the number of components of
![]() $\partial \widehat {\mathfrak {S}}$
. The boundary edges of
$\partial \widehat {\mathfrak {S}}$
. The boundary edges of
![]() $\widehat {\mathfrak {S}}$
count as edges in an ideal triangulation
$\widehat {\mathfrak {S}}$
count as edges in an ideal triangulation
![]() $\lambda $
.
$\lambda $
.
Once again, for simplicity, we assume that
![]() $\lambda $
does not contain any self-folded triangles; however, our results should extend to this setting essentially without change.
$\lambda $
does not contain any self-folded triangles; however, our results should extend to this setting essentially without change.
The split ideal triangulation
![]() $\widehat {\lambda }$
associated to an ideal triangulation
$\widehat {\lambda }$
associated to an ideal triangulation
![]() $\lambda $
is defined as in §4.3. In particular, the boundary edges of
$\lambda $
is defined as in §4.3. In particular, the boundary edges of
![]() $\widehat {\mathfrak {S}}$
are split as well.
$\widehat {\mathfrak {S}}$
are split as well.
9.1.2. Essential webs
A global web, or just web, W on the surface
![]() $\widehat {\mathfrak {S}}$
is defined as in Definition 3.1, except ‘
$\widehat {\mathfrak {S}}$
is defined as in Definition 3.1, except ‘
![]() $\mathfrak {D}_k$
’ is replaced by ‘
$\mathfrak {D}_k$
’ is replaced by ‘
![]() $\widehat {\mathfrak {S}}$
’ and ‘local’ is replaced by ‘global’.
$\widehat {\mathfrak {S}}$
’ and ‘local’ is replaced by ‘global’.
The internal and external faces of a web W on
![]() $\widehat {\mathfrak {S}}$
are defined as in Definition 3.2, except with the appropriate replacements as above. As usual, a web W on
$\widehat {\mathfrak {S}}$
are defined as in Definition 3.2, except with the appropriate replacements as above. As usual, a web W on
![]() $\widehat {\mathfrak {S}}$
is nonelliptic if all of its internal faces have at least six sides; compare Definition 3.4.
$\widehat {\mathfrak {S}}$
is nonelliptic if all of its internal faces have at least six sides; compare Definition 3.4.
An essential web W on
![]() $\widehat {\mathfrak {S}}$
is defined as in Definition 3.8, where in addition the arc
$\widehat {\mathfrak {S}}$
is defined as in Definition 3.8, where in addition the arc
![]() $\alpha $
needs to be isotopic (respecting boundary) in
$\alpha $
needs to be isotopic (respecting boundary) in
![]() $\widehat {\mathfrak {S}}$
to the segment
$\widehat {\mathfrak {S}}$
to the segment
![]() $\overline {E}$
.
$\overline {E}$
.
The good position of a web W with respect to a split ideal triangulation
![]() $\widehat {\lambda }$
is defined exactly as in Definition 4.5, without change.
$\widehat {\lambda }$
is defined exactly as in Definition 4.5, without change.
9.2. Rungless essential webs; first version of the boundary result
9.2.1. Rungless essential webs
As usual, a rungless web W on the surface
![]() $\widehat {\mathfrak {S}}$
is a web that does not have any H-faces; compare Definition 3.9.
$\widehat {\mathfrak {S}}$
is a web that does not have any H-faces; compare Definition 3.9.
The parallel equivalence class of a rungless web W is defined as in Definition 2.3, except we have to include another global parallel-move exchanging two arcs that together with segments in
![]() $\partial \widehat {\mathfrak {S}}$
form the boundary of an embedded rectangle R in the surface
$\partial \widehat {\mathfrak {S}}$
form the boundary of an embedded rectangle R in the surface
![]() $\widehat {\mathfrak {S}}$
; for instance, this would be the case in Figure 3 had we not identified the top and bottom edges of the surface.
$\widehat {\mathfrak {S}}$
; for instance, this would be the case in Figure 3 had we not identified the top and bottom edges of the surface.
The property of being essential is preserved by parallel equivalence. The collection of parallel equivalence classes of rungless essential webs is denoted by
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
. (Note, by definition, the empty class
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
. (Note, by definition, the empty class
![]() $[W]=[\varnothing ]$
is in
$[W]=[\varnothing ]$
is in
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
.)
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
.)
9.2.2. Knutson–Tao cone associated to an ideal triangulation
To an ideal triangulation
![]() $\lambda $
of the surface
$\lambda $
of the surface
![]() $\widehat {\mathfrak {S}}$
we associate a dotted ideal triangulation, also denoted
$\widehat {\mathfrak {S}}$
we associate a dotted ideal triangulation, also denoted
![]() $\lambda $
, as in §5.1. In particular, there are dots located on the boundary edges of
$\lambda $
, as in §5.1. In particular, there are dots located on the boundary edges of
![]() $\widehat {\mathfrak {S}}$
, as, for example, in Figure 27b, where
$\widehat {\mathfrak {S}}$
, as, for example, in Figure 27b, where
![]() $\widehat {\mathfrak {S}} = \mathfrak {T}$
is an ideal triangle. The number N of dots in the dotted triangulation
$\widehat {\mathfrak {S}} = \mathfrak {T}$
is an ideal triangle. The number N of dots in the dotted triangulation
![]() $\lambda $
can be computed as
$\lambda $
can be computed as
![]() $N = 2 * \#\left \{\text {edges } E \text { of } \lambda \right \} + \#\left \{\text {triangles } \mathfrak {T} \text { of } \lambda \right \}$
. (Since each ideal triangulation
$N = 2 * \#\left \{\text {edges } E \text { of } \lambda \right \} + \#\left \{\text {triangles } \mathfrak {T} \text { of } \lambda \right \}$
. (Since each ideal triangulation
![]() $\lambda $
has
$\lambda $
has
![]() $-3\chi (\widehat {\mathfrak {S}})+2d$
edges and
$-3\chi (\widehat {\mathfrak {S}})+2d$
edges and
![]() $-2\chi (\widehat {\mathfrak {S}})+d$
triangles, note N is independent of
$-2\chi (\widehat {\mathfrak {S}})+d$
triangles, note N is independent of
![]() $\lambda $
.)
$\lambda $
.)
To the dotted triangulation
![]() $\lambda $
we associate the Knutson–Tao cone
$\lambda $
we associate the Knutson–Tao cone
![]() $\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
, as in §6.3.
$\mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
, as in §6.3.
9.2.3. Coordinates for rungless essential webs
The minimal position of a rungless web W with respect to an ideal triangulation
![]() $\lambda $
is defined as in Definition 4.2. Then, Proposition 4.3 holds word for word, except ‘nonelliptic’ is replaced by ‘rungless essential’.
$\lambda $
is defined as in Definition 4.2. Then, Proposition 4.3 holds word for word, except ‘nonelliptic’ is replaced by ‘rungless essential’.
Modified H-moves take rungless essential webs in good position to webs of the same type. Proposition 4.7 holds verbatim, except ‘nonelliptic’ is replaced by ‘rungless essential’.
Given an ideal triangulation
![]() $\lambda $
, we define the Fock–Goncharov global coordinate function
$\lambda $
, we define the Fock–Goncharov global coordinate function
![]() $\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\widehat {\mathfrak {S}}}] \to \mathscr {C}^+_{\lambda }$
as in §5.4; see Definition 5.4.
$\Phi _{\lambda }^{\mathrm {FG}} : [\mathscr {W}_{\widehat {\mathfrak {S}}}] \to \mathscr {C}^+_{\lambda }$
as in §5.4; see Definition 5.4.
Theorem 9.1. (First boundary result)
The Fock–Goncharov global coordinate function
is a bijection of sets, identifying parallel equivalence classes of rungless essential webs on the surface
![]() $\widehat {\mathfrak {S}}$
with points of the Knutson–Tao cone associated to the ideal triangulation
$\widehat {\mathfrak {S}}$
with points of the Knutson–Tao cone associated to the ideal triangulation
![]() $\lambda $
.
$\lambda $
.
Proof. As in the proof of Theorem 7.1, the strategy is to construct an explicit inverse
The mapping
![]() $\Psi _{\lambda }^{\mathrm {FG}}$
is defined via the ladder gluing construction followed by removing internal elliptic faces, as explained in §7.2-7.3. Because of the rungless condition, we also need to remove external H-faces, which can be done at the cost of swapping two strands of the web lying on the boundary
$\Psi _{\lambda }^{\mathrm {FG}}$
is defined via the ladder gluing construction followed by removing internal elliptic faces, as explained in §7.2-7.3. Because of the rungless condition, we also need to remove external H-faces, which can be done at the cost of swapping two strands of the web lying on the boundary
![]() $\partial \widehat {\mathfrak {S}}$
. For two examples of this procedure, see Figures 54 and 55 (compare Figures 37 and 39). As before, the resulting rungless essential web is not unique in general.
$\partial \widehat {\mathfrak {S}}$
. For two examples of this procedure, see Figures 54 and 55 (compare Figures 37 and 39). As before, the resulting rungless essential web is not unique in general.

Figure 54 Ladder gluing construction for rungless essential webs: 1 of 2 (on the ideal square).

Figure 55 Ladder gluing construction for rungless essential webs: 2 of 2.
In order to deal with this ambiguity, we need the analogue of the main Lemma 7.7, saying that two rungless essential webs resulting from the ladder gluing construction are parallel equivalent. The proof of the main lemma is essentially unchanged from §8. To say a word about it, the proof of Corollary 8.11 requires the fact that there are no crossing shared-routes terminating on the boundary
![]() $\partial \widehat {\mathfrak {S}}$
. This follows from the rungless condition.
$\partial \widehat {\mathfrak {S}}$
. This follows from the rungless condition.
Remark 9.2. Theorem 9.1 is closely related to [Reference KimKim20, Proposition 1.12].
9.3. Application: geometry and topology of
 $\mathrm {SL}_3(\mathbb {C})$
-character varieties
$\mathrm {SL}_3(\mathbb {C})$
-character varieties
As a consequence of the first version of the result, Theorem 9.1, we give an alternative geometric proof of the Sikora–Westbury theorem [Reference Sikora and WestburySW07, Theorem 9.5] (see also [Reference Frohman and SikoraFS22, Proposition 4]), whose original proof in [Reference Sikora and WestburySW07] assumes the diamond lemma from noncommutative algebra.
Corollary 9.3. (Application of the first boundary result)
The collection
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
of parallel equivalence classes of rungless essential webs on the surface
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
of parallel equivalence classes of rungless essential webs on the surface
![]() $\widehat {\mathfrak {S}}$
indexes a natural linear basis for the algebra
$\widehat {\mathfrak {S}}$
indexes a natural linear basis for the algebra
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\widehat {\mathfrak {S}})]$
of regular functions on the
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\widehat {\mathfrak {S}})]$
of regular functions on the
![]() $\mathrm {SL}_3(\mathbb {C})$
-character variety.
$\mathrm {SL}_3(\mathbb {C})$
-character variety.
Here, the character variety
![]() $\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\widehat {\mathfrak {S}})$
, for general n, was discussed in the introduction for surfaces
$\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\widehat {\mathfrak {S}})$
, for general n, was discussed in the introduction for surfaces
![]() $\widehat {\mathfrak {S}} = \mathfrak {S}$
with empty boundary. When
$\widehat {\mathfrak {S}} = \mathfrak {S}$
with empty boundary. When
![]() $\partial \widehat {\mathfrak {S}} \neq \varnothing $
, there is not a mainstream definition for
$\partial \widehat {\mathfrak {S}} \neq \varnothing $
, there is not a mainstream definition for
![]() $\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\widehat {\mathfrak {S}})$
. Possible models may be found in [Reference Fomin and PylyavskyyFP14, Reference Goncharov and ShenGS15, Reference Costantino and LêCL22, Reference Korinman and QuesneyKQ19, Reference Frohman and SikoraFS22, Reference HigginsHig23]. In order for Corollary 9.3 to be well posed, we make use of a purely topological model, via skein algebras, which has the advantage of admitting a natural deformation quantization.
$\mathscr {R}_{\mathrm {SL}_n(\mathbb {C})}(\widehat {\mathfrak {S}})$
. Possible models may be found in [Reference Fomin and PylyavskyyFP14, Reference Goncharov and ShenGS15, Reference Costantino and LêCL22, Reference Korinman and QuesneyKQ19, Reference Frohman and SikoraFS22, Reference HigginsHig23]. In order for Corollary 9.3 to be well posed, we make use of a purely topological model, via skein algebras, which has the advantage of admitting a natural deformation quantization.
Definition 9.4. Following Frohman–Sikora [Reference Frohman and SikoraFS22, §1,12], for a surface-with-boundary
![]() $\widehat {\mathfrak {S}}$
we define the algebra
$\widehat {\mathfrak {S}}$
we define the algebra
![]() $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\widehat {\mathfrak {S}})]$
of regular functions on the
$\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\widehat {\mathfrak {S}})]$
of regular functions on the
![]() $\mathrm {SL}_3(\mathbb {C})$
-character variety to be the commutative (reduced skein) algebra
$\mathrm {SL}_3(\mathbb {C})$
-character variety to be the commutative (reduced skein) algebra
![]() $\mathscr {S}^{1}(\widehat {\mathfrak {S}})$
of [Reference Frohman and SikoraFS22, §3], where we have taken the specialization
$\mathscr {S}^{1}(\widehat {\mathfrak {S}})$
of [Reference Frohman and SikoraFS22, §3], where we have taken the specialization
![]() $q=a=1$
of their deformation parameters.
$q=a=1$
of their deformation parameters.
In particular, a web W on
![]() $\widehat {\mathfrak {S}}$
represents an element of
$\widehat {\mathfrak {S}}$
represents an element of
![]() $\mathscr {S}^1(\widehat {\mathfrak {S}})$
.
$\mathscr {S}^1(\widehat {\mathfrak {S}})$
.
Remark 9.5. When
![]() $\widehat {\mathfrak {S}} = \mathfrak {S}$
, Sikora [Reference SikoraSik01] proved that the trace functions
$\widehat {\mathfrak {S}} = \mathfrak {S}$
, Sikora [Reference SikoraSik01] proved that the trace functions
![]() $\mathrm {Tr}_W$
on the character variety
$\mathrm {Tr}_W$
on the character variety
![]() $\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})$
furnish a natural isomorphism
$\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})$
furnish a natural isomorphism
![]() $\mathscr {S}^1(\mathfrak {S}) \cong \mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})]$
.
$\mathscr {S}^1(\mathfrak {S}) \cong \mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})]$
.
Proof of Corollary 9.3
We prove a more general statement. Let
![]() $\mathscr {S}^{q,a}(\widehat {\mathfrak {S}})$
be the reduced
$\mathscr {S}^{q,a}(\widehat {\mathfrak {S}})$
be the reduced
![]() $\mathrm {SL}_3$
-skein algebra of [Reference Frohman and SikoraFS22, §3] for deformation parameters
$\mathrm {SL}_3$
-skein algebra of [Reference Frohman and SikoraFS22, §3] for deformation parameters
![]() $q, a \in \mathbb {C} - \left \{ 0 \right \}$
. So,
$q, a \in \mathbb {C} - \left \{ 0 \right \}$
. So,
![]() $\mathscr {S}^1(\widehat {\mathfrak {S}}) = \mathscr {S}^{1,1}(\widehat {\mathfrak {S}})$
.
$\mathscr {S}^1(\widehat {\mathfrak {S}}) = \mathscr {S}^{1,1}(\widehat {\mathfrak {S}})$
.
Higgins [Reference HigginsHig23] defined a
![]() $\mathrm {SL}_3$
-stated skein algebra
$\mathrm {SL}_3$
-stated skein algebra
![]() $\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
generalizing the
$\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
generalizing the
![]() $\mathrm {SL}_2$
-stated skein algebra of [Reference Costantino and LêCL22]. More precisely, we define
$\mathrm {SL}_2$
-stated skein algebra of [Reference Costantino and LêCL22]. More precisely, we define
![]() $\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
to be Kim’s [Reference KimKim20, §5] adaptation of Higgins’ stated skein algebra.
$\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
to be Kim’s [Reference KimKim20, §5] adaptation of Higgins’ stated skein algebra.
When
![]() $a = 1$
, inclusion provides a natural algebra homomorphism
$a = 1$
, inclusion provides a natural algebra homomorphism
![]() $\iota : \mathscr {S}^{q, 1}(\widehat {\mathfrak {S}}) \to \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
from the Frohman–Sikora reduced skein algebra to the Higgins stated skein algebra; in fact, the mapping
$\iota : \mathscr {S}^{q, 1}(\widehat {\mathfrak {S}}) \to \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
from the Frohman–Sikora reduced skein algebra to the Higgins stated skein algebra; in fact, the mapping
![]() $\iota $
is onto the subalgebra
$\iota $
is onto the subalgebra
![]() $\mathscr {S}^q_{\mathrm {st}=\mathrm {top}}(\widehat {\mathfrak {S}})$
generated by webs with all-top-states on the boundary
$\mathscr {S}^q_{\mathrm {st}=\mathrm {top}}(\widehat {\mathfrak {S}})$
generated by webs with all-top-states on the boundary
![]() $\partial \widehat {\mathfrak {S}}$
. Put
$\partial \widehat {\mathfrak {S}}$
. Put
![]() $\mathscr {S}^q(\widehat {\mathfrak {S}}) := \mathscr {S}^{q, 1}(\widehat {\mathfrak {S}})$
. In summary,
$\mathscr {S}^q(\widehat {\mathfrak {S}}) := \mathscr {S}^{q, 1}(\widehat {\mathfrak {S}})$
. In summary,
![]() $\iota : \mathscr {S}^q(\widehat {\mathfrak {S}}) \twoheadrightarrow \mathscr {S}^q_{\mathrm {st}=\mathrm {top}}(\widehat {\mathfrak {S}}) \subseteq \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
.
$\iota : \mathscr {S}^q(\widehat {\mathfrak {S}}) \twoheadrightarrow \mathscr {S}^q_{\mathrm {st}=\mathrm {top}}(\widehat {\mathfrak {S}}) \subseteq \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
.
Using the boundary orientation of
![]() $\partial \widehat {\mathfrak {S}}$
induced by the orientation of
$\partial \widehat {\mathfrak {S}}$
induced by the orientation of
![]() $\widehat {\mathfrak {S}}$
, a web W on
$\widehat {\mathfrak {S}}$
, a web W on
![]() $\widehat {\mathfrak {S}}$
lifts to an element of the skein algebra
$\widehat {\mathfrak {S}}$
lifts to an element of the skein algebra
![]() $\mathscr {S}^q(\widehat {\mathfrak {S}})$
. Moreover, parallel equivalent rungless webs
$\mathscr {S}^q(\widehat {\mathfrak {S}})$
. Moreover, parallel equivalent rungless webs
![]() $W \sim W^\prime $
determine the same element of
$W \sim W^\prime $
determine the same element of
![]() $\mathscr {S}^q(\widehat {\mathfrak {S}})$
(by [Reference Frohman and SikoraFS22, Figure 6] since
$\mathscr {S}^q(\widehat {\mathfrak {S}})$
(by [Reference Frohman and SikoraFS22, Figure 6] since
![]() $a=1$
). We prove
$a=1$
). We prove
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
forms a basis for
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
forms a basis for
![]() $\mathscr {S}^q(\widehat {\mathfrak {S}})$
. It is immediate by construction that
$\mathscr {S}^q(\widehat {\mathfrak {S}})$
. It is immediate by construction that
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
is spanning.
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
is spanning.
We mimic the strategy of [Reference Bonahon and WongBW11, §8] in the
![]() $\mathrm {SL}_2$
-case. Fix an ideal triangulation
$\mathrm {SL}_2$
-case. Fix an ideal triangulation
![]() $\lambda $
of
$\lambda $
of
![]() $\widehat {\mathfrak {S}}$
. Building on [Reference DouglasDou20, Reference DouglasDou21a, Reference DouglasDou21b], Kim [Reference KimKim20] defined a
$\widehat {\mathfrak {S}}$
. Building on [Reference DouglasDou20, Reference DouglasDou21a, Reference DouglasDou21b], Kim [Reference KimKim20] defined a
![]() $\mathrm {SL}_3$
-quantum trace map, which in particular is an algebra homomorphism
$\mathrm {SL}_3$
-quantum trace map, which in particular is an algebra homomorphism
![]() $\mathrm {Tr}^q_\lambda : \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}}) \to \mathscr {T}^q_\lambda $
from the stated skein algebra
$\mathrm {Tr}^q_\lambda : \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}}) \to \mathscr {T}^q_\lambda $
from the stated skein algebra
![]() $\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
to a quantum torus
$\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
to a quantum torus
![]() $\mathscr {T}^q_\lambda $
depending on
$\mathscr {T}^q_\lambda $
depending on
![]() $\lambda $
. More precisely,
$\lambda $
. More precisely,
![]() $\mathscr {T}^q_\lambda = \mathbb {C}[Z_1^{\pm 1},Z_2^{\pm 1}, \dots , Z_N^{\pm 1}]^q$
is a noncommutative q-deformation of the algebra of Laurent polynomials in variables
$\mathscr {T}^q_\lambda = \mathbb {C}[Z_1^{\pm 1},Z_2^{\pm 1}, \dots , Z_N^{\pm 1}]^q$
is a noncommutative q-deformation of the algebra of Laurent polynomials in variables
![]() $Z_i$
, which no longer commute but q-commute (according to a quiver drawn on the triangulated surface). Here, N is the number of coordinates in Theorem 9.1. (When
$Z_i$
, which no longer commute but q-commute (according to a quiver drawn on the triangulated surface). Here, N is the number of coordinates in Theorem 9.1. (When
![]() $q=1$
, the variables
$q=1$
, the variables
![]() $Z_i=X_i^{1/3}$
can be thought of as formal cube roots of the Fock–Goncharov coordinates
$Z_i=X_i^{1/3}$
can be thought of as formal cube roots of the Fock–Goncharov coordinates
![]() $X_i$
.)
$X_i$
.)
By [Reference KimKim20, Proposition 5.80] (and [Reference KimKim21, Proposition 3.15]), the quantum trace map
![]() $\mathrm {Tr}^q_\lambda $
satisfies the property that the polynomial
$\mathrm {Tr}^q_\lambda $
satisfies the property that the polynomial
![]() $\mathrm {Tr}^q_\lambda (\iota (W))$
, obtained by evaluating a rungless essential web W in
$\mathrm {Tr}^q_\lambda (\iota (W))$
, obtained by evaluating a rungless essential web W in
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
, has a highest term
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
, has a highest term
![]() $ Z_1^{a_1} Z_2^{a_2} \cdots Z_N^{a_N}$
(omitting the power of q coefficient) whose exponents are the coordinates
$ Z_1^{a_1} Z_2^{a_2} \cdots Z_N^{a_N}$
(omitting the power of q coefficient) whose exponents are the coordinates
![]() $(a_1, a_2, \dots , a_N) = \Phi _{\lambda }^{\mathrm {FG}}(W) \in \mathbb {Z}_{\geqslant 0}^N$
of Theorem 9.1. (Here, by highest term, we mean that if a monomial
$(a_1, a_2, \dots , a_N) = \Phi _{\lambda }^{\mathrm {FG}}(W) \in \mathbb {Z}_{\geqslant 0}^N$
of Theorem 9.1. (Here, by highest term, we mean that if a monomial
![]() $Z_1^{a^\prime _1} Z_2^{a^\prime _2} \cdots Z_N^{a^\prime _N}$
also appears in
$Z_1^{a^\prime _1} Z_2^{a^\prime _2} \cdots Z_N^{a^\prime _N}$
also appears in
![]() $\mathrm {Tr}^q_\lambda (\iota (W))$
, then
$\mathrm {Tr}^q_\lambda (\iota (W))$
, then
![]() $a^\prime _i \leqslant a_i$
for all
$a^\prime _i \leqslant a_i$
for all
![]() $i = 1, 2, \dots , N$
.)
$i = 1, 2, \dots , N$
.)
It follows that each W is nonzero in
![]() $\mathscr {S}^q(\widehat {\mathfrak {S}})$
, that
$\mathscr {S}^q(\widehat {\mathfrak {S}})$
, that
![]() $\iota $
is injective on
$\iota $
is injective on
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
, that
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
, that
![]() $\iota ([\mathscr {W}_{\widehat {\mathfrak {S}}}])$
is linearly independent in
$\iota ([\mathscr {W}_{\widehat {\mathfrak {S}}}])$
is linearly independent in
![]() $\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
, and lastly that
$\mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
, and lastly that
![]() $\iota : \mathscr {S}^q(\widehat {\mathfrak {S}}) \overset {\sim }{\to } \mathscr {S}^q_{\mathrm {st}=\mathrm {top}}(\widehat {\mathfrak {S}}) \subseteq \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
is an isomorphism. In particular, we gather
$\iota : \mathscr {S}^q(\widehat {\mathfrak {S}}) \overset {\sim }{\to } \mathscr {S}^q_{\mathrm {st}=\mathrm {top}}(\widehat {\mathfrak {S}}) \subseteq \mathscr {S}^q_{\mathrm {st}}(\widehat {\mathfrak {S}})$
is an isomorphism. In particular, we gather
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
is independent, hence a basis of
$[\mathscr {W}_{\widehat {\mathfrak {S}}}]$
is independent, hence a basis of
![]() $\mathscr {S}^q(\widehat {\mathfrak {S}})$
.
$\mathscr {S}^q(\widehat {\mathfrak {S}})$
.
9.4. Boundary-fixed essential webs; second version of the boundary result
9.4.1. Boundary-fixed essential webs
For a boundary edge E of the surface
![]() $\widehat {\mathfrak {S}}$
, a strand-set
$\widehat {\mathfrak {S}}$
, a strand-set
![]() $S_E$
is a (possibly empty) set
$S_E$
is a (possibly empty) set
![]() $S_E = \{ s \}$
of disjoint oriented strands s located on E (compare Definition 3.12); see Figures 56 and 57, where the strands are indicated by white-headed arrows. A strand-set
$S_E = \{ s \}$
of disjoint oriented strands s located on E (compare Definition 3.12); see Figures 56 and 57, where the strands are indicated by white-headed arrows. A strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}} = \{ S_E \}$
for
$S_{\partial \widehat {\mathfrak {S}}} = \{ S_E \}$
for
![]() $\widehat {\mathfrak {S}}$
is a collection of strand-sets
$\widehat {\mathfrak {S}}$
is a collection of strand-sets
![]() $S_E$
varying over all
$S_E$
varying over all
![]() $E \subseteq \partial \widehat {\mathfrak {S}}$
.
$E \subseteq \partial \widehat {\mathfrak {S}}$
.
Definition 9.6. A boundary-fixed web W with respect to a strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
for the surface
$S_{\partial \widehat {\mathfrak {S}}}$
for the surface
![]() $\widehat {\mathfrak {S}}$
is a web W whose end-strands match the strand-set
$\widehat {\mathfrak {S}}$
is a web W whose end-strands match the strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
; see Figures 56 and 57.
$S_{\partial \widehat {\mathfrak {S}}}$
; see Figures 56 and 57.

Figure 56 Ladder construction for boundary-fixed essential webs: 1 of 2 (on the ideal square).

Figure 57 Ladder construction for boundary-fixed essential webs: 2 of 2.
If W is boundary-fixed for a strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
, then W is not boundary-fixed for any strand-set
$S_{\partial \widehat {\mathfrak {S}}}$
, then W is not boundary-fixed for any strand-set
![]() $S^\prime _{\partial \widehat {\mathfrak {S}}}$
obtained by swapping two oppositely oriented strands of
$S^\prime _{\partial \widehat {\mathfrak {S}}}$
obtained by swapping two oppositely oriented strands of
![]() $S_{\partial \widehat {\mathfrak {S}}}$
on a boundary edge.
$S_{\partial \widehat {\mathfrak {S}}}$
on a boundary edge.
For boundary-fixed webs, global parallel-moves can only be performed across embedded annuli, in contrast to rungless webs (§9.2.1). Global parallel-moves preserve the property of being essential. We denote by
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}})$
the collection of parallel equivalence classes of boundary-fixed essential webs for the strand-set
$[\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}})$
the collection of parallel equivalence classes of boundary-fixed essential webs for the strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
. (Note, by definition,
$S_{\partial \widehat {\mathfrak {S}}}$
. (Note, by definition,
![]() $[W] = [\varnothing ] \in [\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}})$
if and only if
$[W] = [\varnothing ] \in [\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}})$
if and only if
![]() $S_{\partial \widehat {\mathfrak {S}}} = \varnothing $
.)
$S_{\partial \widehat {\mathfrak {S}}} = \varnothing $
.)
9.4.2. Boundary-fixed Knutson–Tao cone
By Figure 30 (recall also property (2) of Definition 5.1), a strand-set
![]() $S_E$
determines two local coordinates on a boundary edge E of
$S_E$
determines two local coordinates on a boundary edge E of
![]() $\widehat {\mathfrak {S}}$
. More generally, a strand-set
$\widehat {\mathfrak {S}}$
. More generally, a strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
for the surface fixes
$S_{\partial \widehat {\mathfrak {S}}}$
for the surface fixes
![]() $2 * \#\{\text {boundary edges }E\}$
coordinates on the boundary
$2 * \#\{\text {boundary edges }E\}$
coordinates on the boundary
![]() $\partial \widehat {\mathfrak {S}}$
. See Figure 56, for an example, where the fixed coordinates are colored red.
$\partial \widehat {\mathfrak {S}}$
. See Figure 56, for an example, where the fixed coordinates are colored red.
Definition 9.7. The boundary-fixed Knutson–Tao cone
![]() ${\mathscr {C}}^+_{\lambda }(S_{\partial \widehat {\mathfrak {S}}}) \subseteq {\mathscr {C}}^+_{\lambda } \subseteq {\mathbb {Z}}_{\geqslant 0}^N$
with respect to a strand-set
${\mathscr {C}}^+_{\lambda }(S_{\partial \widehat {\mathfrak {S}}}) \subseteq {\mathscr {C}}^+_{\lambda } \subseteq {\mathbb {Z}}_{\geqslant 0}^N$
with respect to a strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
is the subset of
$S_{\partial \widehat {\mathfrak {S}}}$
is the subset of
![]() ${\mathscr {C}}^+_{\lambda }$
(as defined in §9.2.2) consisting of points whose boundary coordinates agree with those determined by
${\mathscr {C}}^+_{\lambda }$
(as defined in §9.2.2) consisting of points whose boundary coordinates agree with those determined by
![]() $S_{\partial \widehat {\mathfrak {S}}}$
.
$S_{\partial \widehat {\mathfrak {S}}}$
.
Note that, in contrast to boundary-fixed webs (§9.4.1), the boundary-fixed Knutson–Tao cone
![]() $\mathscr {C}^+_{\lambda }(S_{\partial \widehat {\mathfrak {S}}}) \subseteq \mathscr {C}^+_{\lambda }$
is independent of permuting the boundary strands of
$\mathscr {C}^+_{\lambda }(S_{\partial \widehat {\mathfrak {S}}}) \subseteq \mathscr {C}^+_{\lambda }$
is independent of permuting the boundary strands of
![]() $S_{\partial \widehat {\mathfrak {S}}}$
. This is because the coordinates on a boundary component only depend on the number of in- and out-strands, not on their ordering along the edge (see property (2) in Definition 5.1).
$S_{\partial \widehat {\mathfrak {S}}}$
. This is because the coordinates on a boundary component only depend on the number of in- and out-strands, not on their ordering along the edge (see property (2) in Definition 5.1).
9.4.3. Coordinates for boundary-fixed essential webs
The minimal position of a boundary-fixed web W with respect to an ideal triangulation
![]() $\lambda $
is defined as in Definition 4.2. Proposition 4.3 holds word for word, except ‘nonelliptic’ is replaced by ‘boundary-fixed essential’.
$\lambda $
is defined as in Definition 4.2. Proposition 4.3 holds word for word, except ‘nonelliptic’ is replaced by ‘boundary-fixed essential’.
Modified H-moves take boundary-fixed essential webs in good position to webs of the same type. Proposition 4.7 holds, except ‘nonelliptic’ is replaced by ‘boundary-fixed essential’.
Given a strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
and an ideal triangulation
$S_{\partial \widehat {\mathfrak {S}}}$
and an ideal triangulation
![]() $\lambda $
, we define the Fock–Goncharov global coordinate function
$\lambda $
, we define the Fock–Goncharov global coordinate function
![]() $\Phi _{\lambda }^{\mathrm {FG}}(S_{\partial \widehat {\mathfrak {S}}}) : [\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}}) \to \mathscr {C}^+_{\lambda }(S_{\partial \widehat {\mathfrak {S}}}) \subseteq \mathscr {C}^+_{\lambda }$
as in §5.4; see Definition 5.4.
$\Phi _{\lambda }^{\mathrm {FG}}(S_{\partial \widehat {\mathfrak {S}}}) : [\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}}) \to \mathscr {C}^+_{\lambda }(S_{\partial \widehat {\mathfrak {S}}}) \subseteq \mathscr {C}^+_{\lambda }$
as in §5.4; see Definition 5.4.
Theorem 9.8. (Second boundary result)
The Fock–Goncharov global coordinate function
with respect to the strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
is a bijection of sets, identifying parallel equivalence classes of boundary-fixed essential webs with points of the boundary-fixed Knutson–Tao cone.
$S_{\partial \widehat {\mathfrak {S}}}$
is a bijection of sets, identifying parallel equivalence classes of boundary-fixed essential webs with points of the boundary-fixed Knutson–Tao cone.
Proof. As in the proof of Theorem 7.1, the strategy is to construct an explicit inverse
The mapping
![]() $\Psi _{\lambda }^{\mathrm {FG}}(S_{\partial \widehat {\mathfrak {S}}})$
is defined via the ladder gluing construction followed by removing internal elliptic faces, as explained in §7.2-7.3. In contrast to the rungless setting (§9.2.3), no new reductions are required. For examples, see Figures 56 and 57; compare the empty-boundary case, Figures 37 and 39, and the rungless boundary case, Figures 54 and 55.
$\Psi _{\lambda }^{\mathrm {FG}}(S_{\partial \widehat {\mathfrak {S}}})$
is defined via the ladder gluing construction followed by removing internal elliptic faces, as explained in §7.2-7.3. In contrast to the rungless setting (§9.2.3), no new reductions are required. For examples, see Figures 56 and 57; compare the empty-boundary case, Figures 37 and 39, and the rungless boundary case, Figures 54 and 55.
We also need the analogue of the main Lemma 7.7, saying that two boundary-fixed essential webs resulting from the ladder gluing construction are parallel equivalent. The proof of the main lemma is essentially unchanged from §8. To say a word about it, for the proof of Corollary 8.11, if a shared-route for W ending on the boundary
![]() $\partial \widehat {\mathfrak {S}}$
is crossing, then the corresponding shared-route for
$\partial \widehat {\mathfrak {S}}$
is crossing, then the corresponding shared-route for
![]() $W^\prime $
is also crossing, by the boundary-fixed condition.
$W^\prime $
is also crossing, by the boundary-fixed condition.
Corollary 9.9. Let two strand-sets
![]() $S_{\partial \widehat {\mathfrak {S}}}$
and
$S_{\partial \widehat {\mathfrak {S}}}$
and
![]() $S^\prime _{\partial \widehat {\mathfrak {S}}}$
be the same up to permuting strands lying on the same boundary edge. Then, there is a natural one-to-one correspondence
$S^\prime _{\partial \widehat {\mathfrak {S}}}$
be the same up to permuting strands lying on the same boundary edge. Then, there is a natural one-to-one correspondence
sending parallel equivalence classes of boundary-fixed essential webs W for
![]() $S_{\partial \widehat {\mathfrak {S}}}$
to parallel equivalence classes of boundary-fixed essential webs
$S_{\partial \widehat {\mathfrak {S}}}$
to parallel equivalence classes of boundary-fixed essential webs
![]() $W^\prime $
for
$W^\prime $
for
![]() $S^\prime _{\partial \widehat {\mathfrak {S}}}$
. Here, natural means that the resulting bijection
$S^\prime _{\partial \widehat {\mathfrak {S}}}$
. Here, natural means that the resulting bijection
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}}) \to [\mathscr {W}_{\widehat {\mathfrak {S}}}](S^\prime _{\partial \widehat {\mathfrak {S}}})$
is independent of the choice of triangulation
$[\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}}) \to [\mathscr {W}_{\widehat {\mathfrak {S}}}](S^\prime _{\partial \widehat {\mathfrak {S}}})$
is independent of the choice of triangulation
![]() $\lambda $
.
$\lambda $
.
Proof. Let W be a boundary-fixed essential web for
![]() $S_{\partial \widehat {\mathfrak {S}}}$
, and let
$S_{\partial \widehat {\mathfrak {S}}}$
, and let
![]() ${\lambda _1}$
and
${\lambda _1}$
and
![]() ${\lambda _2}$
be two ideal triangulations. We claim that there are webs
${\lambda _2}$
be two ideal triangulations. We claim that there are webs
![]() $W_{\lambda _1}$
and
$W_{\lambda _1}$
and
![]() $W_{{\lambda _2}}$
isotopic to W and in good position for the split ideal triangulation
$W_{{\lambda _2}}$
isotopic to W and in good position for the split ideal triangulation
![]() $\widehat {\lambda }_1$
and
$\widehat {\lambda }_1$
and
![]() $\widehat {\lambda }_2$
, respectively, such that
$\widehat {\lambda }_2$
, respectively, such that
![]() $W_{\lambda _1}$
and
$W_{\lambda _1}$
and
![]() $W_{{\lambda _2}}$
have the same ladders in the boundary biangles
$W_{{\lambda _2}}$
have the same ladders in the boundary biangles
![]() $\mathfrak {B}$
facing
$\mathfrak {B}$
facing
![]() $\partial \widehat {\mathfrak {S}}$
.
$\partial \widehat {\mathfrak {S}}$
.
Indeed, by pushing as many H’s of W as possible into the boundary biangles
![]() $\mathfrak {B}$
, we may assume that the web
$\mathfrak {B}$
, we may assume that the web
![]() $\widetilde {W}$
obtained from W by chopping off the boundary biangles
$\widetilde {W}$
obtained from W by chopping off the boundary biangles
![]() $\mathfrak {B}$
is rungless essential. By §9.2.3 there exist webs
$\mathfrak {B}$
is rungless essential. By §9.2.3 there exist webs
![]() $\widetilde {W}_{\lambda _1}$
and
$\widetilde {W}_{\lambda _1}$
and
![]() $\widetilde {W}_{{\lambda _2}}$
isotopic to
$\widetilde {W}_{{\lambda _2}}$
isotopic to
![]() $\widetilde {W}$
that are in good position for
$\widetilde {W}$
that are in good position for
![]() $\widehat {\lambda }_1$
and
$\widehat {\lambda }_1$
and
![]() $\widehat {\lambda }_2$
, respectively. Let
$\widehat {\lambda }_2$
, respectively. Let
![]() $W_{\lambda _1}$
and
$W_{\lambda _1}$
and
![]() $W_{{\lambda _2}}$
be obtained by reattaching the ladders from the cut-off boundary biangles
$W_{{\lambda _2}}$
be obtained by reattaching the ladders from the cut-off boundary biangles
![]() $\mathfrak {B}$
to
$\mathfrak {B}$
to
![]() $\widetilde {W}_{\lambda _1}$
and
$\widetilde {W}_{\lambda _1}$
and
![]() $\widetilde {W}_{{\lambda _2}}$
, respectively. This proves the claim.
$\widetilde {W}_{{\lambda _2}}$
, respectively. This proves the claim.
To finish, the map
![]() $[\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}}) \to [\mathscr {W}_{\widehat {\mathfrak {S}}}](S^\prime _{\partial \widehat {\mathfrak {S}}})$
for
$[\mathscr {W}_{\widehat {\mathfrak {S}}}](S_{\partial \widehat {\mathfrak {S}}}) \to [\mathscr {W}_{\widehat {\mathfrak {S}}}](S^\prime _{\partial \widehat {\mathfrak {S}}})$
for
![]() ${\lambda _1}$
is computed via the following steps: (1) erase the ladders of
${\lambda _1}$
is computed via the following steps: (1) erase the ladders of
![]() $W_{\lambda _1}$
from the boundary biangles
$W_{\lambda _1}$
from the boundary biangles
![]() $\mathfrak {B}$
; (2) replace
$\mathfrak {B}$
; (2) replace
![]() $S_{\partial \widehat {\mathfrak {S}}}$
with
$S_{\partial \widehat {\mathfrak {S}}}$
with
![]() $S^\prime _{\partial \widehat {\mathfrak {S}}}$
by permuting boundary strands; (3) insert the unique ladders into the boundary biangles
$S^\prime _{\partial \widehat {\mathfrak {S}}}$
by permuting boundary strands; (3) insert the unique ladders into the boundary biangles
![]() $\mathfrak {B}$
matching this new boundary data; (4) eliminate elliptic faces. A similar computation holds for the map with respect to
$\mathfrak {B}$
matching this new boundary data; (4) eliminate elliptic faces. A similar computation holds for the map with respect to
![]() ${\lambda _2}$
. By the claim, the webs for
${\lambda _2}$
. By the claim, the webs for
![]() ${\lambda _1}$
and
${\lambda _1}$
and
![]() ${\lambda _2}$
resulting after step (3) are isotopic.
${\lambda _2}$
resulting after step (3) are isotopic.
9.5. Application: representation theory of the Lie group
 $\mathrm {SL}_3(\mathbb {C})$
$\mathrm {SL}_3(\mathbb {C})$
As a consequence of the second version of the result, Theorem 9.8, we make a connection to Kuperberg’s famous theorem relating webs in the disk to the representation theory of
![]() $\mathrm {SL}_3(\mathbb {C})$
.
$\mathrm {SL}_3(\mathbb {C})$
.
The finite-dimensional irreducible representations of
![]() $\mathrm {SL}_3(\mathbb {C})$
are in one-to-one correspondence with ordered pairs
$\mathrm {SL}_3(\mathbb {C})$
are in one-to-one correspondence with ordered pairs
![]() $(n^{\mathrm {in}}, n^{\mathrm {out}}) \in \mathbb {Z}_{\geqslant 0}^2$
. For example, we may say that
$(n^{\mathrm {in}}, n^{\mathrm {out}}) \in \mathbb {Z}_{\geqslant 0}^2$
. For example, we may say that
![]() $(1, 0)$
corresponds to the defining vector representation V and
$(1, 0)$
corresponds to the defining vector representation V and
![]() $(0, 1)$
corresponds to its dual representation
$(0, 1)$
corresponds to its dual representation
![]() $V^*$
.
$V^*$
.
We assign to each strand-set
![]() $S_{\partial \widehat {\mathfrak {S}}}$
a tensor product
$S_{\partial \widehat {\mathfrak {S}}}$
a tensor product
![]() $V(S_{\partial \widehat {\mathfrak {S}}}) = \otimes _E V_E$
of finite-dimensional irreducible representations
$V(S_{\partial \widehat {\mathfrak {S}}}) = \otimes _E V_E$
of finite-dimensional irreducible representations
![]() $V_E$
of
$V_E$
of
![]() $\mathrm {SL}_3(\mathbb {C})$
, varying over boundary edges E of
$\mathrm {SL}_3(\mathbb {C})$
, varying over boundary edges E of
![]() $\widehat {\mathfrak {S}}$
, as follows. If
$\widehat {\mathfrak {S}}$
, as follows. If
![]() $n^{\mathrm {in}}_E$
(resp.
$n^{\mathrm {in}}_E$
(resp.
![]() $n^{\mathrm {out}}_E$
) is the number of in-strands (resp. out-strands) of
$n^{\mathrm {out}}_E$
) is the number of in-strands (resp. out-strands) of
![]() $S_E$
, where
$S_E$
, where
![]() $S_{\partial \widehat {\mathfrak {S}}} = \{ S_E \}_E$
, then we define
$S_{\partial \widehat {\mathfrak {S}}} = \{ S_E \}_E$
, then we define
![]() $V_E$
to be the irreducible representation corresponding to
$V_E$
to be the irreducible representation corresponding to
![]() $(n^{\mathrm {in}}_E, n^{\mathrm {out}}_E)$
.
$(n^{\mathrm {in}}_E, n^{\mathrm {out}}_E)$
.
Note
![]() $V(S_{\partial \widehat {\mathfrak {S}}}) = V(S^\prime _{\partial \widehat {\mathfrak {S}}})$
if
$V(S_{\partial \widehat {\mathfrak {S}}}) = V(S^\prime _{\partial \widehat {\mathfrak {S}}})$
if
![]() $S_{\partial \widehat {\mathfrak {S}}}$
and
$S_{\partial \widehat {\mathfrak {S}}}$
and
![]() $S^\prime _{\partial \widehat {\mathfrak {S}}}$
are the same up to permuting strands on an E.
$S^\prime _{\partial \widehat {\mathfrak {S}}}$
are the same up to permuting strands on an E.
For a representation V of
![]() $\mathrm {SL}_3(\mathbb {C})$
, let
$\mathrm {SL}_3(\mathbb {C})$
, let
![]() $V^{\mathrm {SL}_3(\mathbb {C})} \subseteq V$
be the subspace of invariant vectors.
$V^{\mathrm {SL}_3(\mathbb {C})} \subseteq V$
be the subspace of invariant vectors.
Theorem 9.10. [Reference KuperbergKup96, Theorem 6.1]
For
![]() $\widehat {\mathfrak {S}} = \mathfrak {D}_k$
(
$\widehat {\mathfrak {S}} = \mathfrak {D}_k$
(
![]() $k \geqslant 1$
) the ideal polygon with k boundary edges (§3.1), the collection
$k \geqslant 1$
) the ideal polygon with k boundary edges (§3.1), the collection
![]() $[\mathscr {W}_{\mathfrak {D}_k}](S_{\partial \mathfrak {D}_k})$
of classes
$[\mathscr {W}_{\mathfrak {D}_k}](S_{\partial \mathfrak {D}_k})$
of classes
![]() $[W]$
of boundary-fixed essential webs with respect to a strand-set
$[W]$
of boundary-fixed essential webs with respect to a strand-set
![]() $S_{\partial \mathfrak {D}_k}$
indexes a linear basis for the invariant space
$S_{\partial \mathfrak {D}_k}$
indexes a linear basis for the invariant space
![]() $V(S_{\partial \mathfrak {D}_k})^{\mathrm {SL}_3(\mathbb {C})}$
.
$V(S_{\partial \mathfrak {D}_k})^{\mathrm {SL}_3(\mathbb {C})}$
.
Note that, for
![]() $\widehat {\mathfrak {S}} = \mathfrak {D}_k$
, a parallel equivalence class
$\widehat {\mathfrak {S}} = \mathfrak {D}_k$
, a parallel equivalence class
![]() $[W] \in [\mathscr {W}_{\mathfrak {D}_k}](S_{\partial \mathfrak {D}_k})$
is an isotopy class.
$[W] \in [\mathscr {W}_{\mathfrak {D}_k}](S_{\partial \mathfrak {D}_k})$
is an isotopy class.
From Kuperberg’s theorem, together with Theorem 9.8, we immediately obtain:
Corollary 9.11. (Application of the second boundary result)
For
![]() $\widehat {\mathfrak {S}} = \mathfrak {D}_k$
(
$\widehat {\mathfrak {S}} = \mathfrak {D}_k$
(
![]() $k \geqslant 3$
), a strand-set
$k \geqslant 3$
), a strand-set
![]() $S_{\partial \mathfrak {D}_k}$
, and an ideal triangulation
$S_{\partial \mathfrak {D}_k}$
, and an ideal triangulation
![]() $\lambda $
of
$\lambda $
of
![]() $\mathfrak {D}_k$
, the boundary-fixed Knutson–Tao cone
$\mathfrak {D}_k$
, the boundary-fixed Knutson–Tao cone
![]() $\mathscr {C}^+_{\lambda }(S_{\partial \mathfrak {D}_k}) \subseteq \mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
indexes a linear basis for the invariant space
$\mathscr {C}^+_{\lambda }(S_{\partial \mathfrak {D}_k}) \subseteq \mathscr {C}^+_{\lambda } \subseteq \mathbb {Z}_{\geqslant 0}^N$
indexes a linear basis for the invariant space
![]() $V(S_{\partial \mathfrak {D}_k})^{\mathrm {SL}_3(\mathbb {C})}$
.
$V(S_{\partial \mathfrak {D}_k})^{\mathrm {SL}_3(\mathbb {C})}$
.
Remark 9.12.
-
1. This corollary is reminiscent of results about the Knutson–Tao hive model [Reference Knutson and TaoKT99, Reference BuchBuc00] for the general linear group
 $\mathrm {GL}_n(\mathbb {C})$
, where the Littlewood–Richardson coefficients
$\mathrm {GL}_n(\mathbb {C})$
, where the Littlewood–Richardson coefficients
 $c_{\lambda \mu }^\nu $
associated to highest weights
$c_{\lambda \mu }^\nu $
associated to highest weights
 $\lambda , \mu , \nu $
provide the multiplicities of irreducible representations
$\lambda , \mu , \nu $
provide the multiplicities of irreducible representations
 $V_\nu $
in
$V_\nu $
in
 $V_\lambda \otimes V_\mu $
. Certain multiplicities
$V_\lambda \otimes V_\mu $
. Certain multiplicities
 $c_{\lambda \mu }^\nu $
can be computed as the number of solutions of the Knutson–Tao rhombus inequalities, without n-congruence conditions (see Remark 6.5(1)), on the dotted n-triangle matching certain fixed boundary conditions determined by the weights
$c_{\lambda \mu }^\nu $
can be computed as the number of solutions of the Knutson–Tao rhombus inequalities, without n-congruence conditions (see Remark 6.5(1)), on the dotted n-triangle matching certain fixed boundary conditions determined by the weights
 $\lambda , \mu , \nu $
. (Possibly related, see [Reference MageeMag20].)
$\lambda , \mu , \nu $
. (Possibly related, see [Reference MageeMag20].) -
2. Corollary 9.11 was the result of Kuperberg’s theorem combined with Theorem 9.8. We would like to have gone in the other direction. That is, we would like to give an alternative geometric proof of Kuperberg’s theorem, as a consequence of Theorem 9.8 and Corollary 9.11. Indeed, this was the spirit of Kuperberg’s proof for the
 $\mathrm {SL}_2(\mathbb {C})$
-version of his result [Reference KuperbergKup96, Theorem 2.4], where the
$\mathrm {SL}_2(\mathbb {C})$
-version of his result [Reference KuperbergKup96, Theorem 2.4], where the
 $\mathrm {SL}_2(\mathbb {C})$
-analogue of Corollary 9.11 is a simple consequence of the Clebsch–Gordan theorem. It is natural then to ask:
$\mathrm {SL}_2(\mathbb {C})$
-analogue of Corollary 9.11 is a simple consequence of the Clebsch–Gordan theorem. It is natural then to ask:
Question 9.13. Is there an alternative purely representation theoretic proof of Corollary 9.11?
Question 9.14. Is there a representation theoretic interpretation of Theorem 9.8 for any surface-with-boundary
![]() $\widehat {\mathfrak {S}}$
, generalizing Kuperberg’s theorem in the case
$\widehat {\mathfrak {S}}$
, generalizing Kuperberg’s theorem in the case
![]() $\widehat {\mathfrak {S}} = \mathfrak {D}_k$
? (We ask this question also for
$\widehat {\mathfrak {S}} = \mathfrak {D}_k$
? (We ask this question also for
![]() $\mathrm {SL}_2(\mathbb {C})$
.) Possible clues may lie in [Reference Fomin and PylyavskyyFP14, Reference Costantino and LêCL22, Reference Goncharov and ShenGS19].
$\mathrm {SL}_2(\mathbb {C})$
.) Possible clues may lie in [Reference Fomin and PylyavskyyFP14, Reference Costantino and LêCL22, Reference Goncharov and ShenGS19].
Acknowledgements
This research would not have been possible without the help and support of many people, whose time and patience often seem limitless. In particular, we are profoundly grateful to Dylan Allegretti for his involvement during the early stages of this project; Charlie Frohman for his guidance from the very beginning; Francis Bonahon and Viktor Kleen for helping us refine our ideas and for technical assistance; Tommaso Cremaschi for his invaluable feedback after reading way too many drafts; as well as Vijay Higgins, Hyun Kyu Kim, Linhui Shen and Adam Sikora for helpful conversations. Much of this work was completed during very enjoyable visits to Tsinghua University in Beijing (supported by a GEAR graduate internship grant) and the University of Southern California in Los Angeles. We would like to take this opportunity to extend our enormous gratitude to these institutions for their warm hospitality and many tasty dinners (the first author was especially fond of the sōngshǔ guìyú).
Competing interest
The authors have no competing interests to declare.
Funding statement
This work was partially supported by the U.S. National Science Foundation grants DMS-1107452, 1107263, 1107367 ‘RNMS: GEometric structures And Representation varieties’ (the GEAR Network). The first author was also partially supported by the U.S. National Science Foundation grants DMS-1406559 and 1711297, and the second author by the China Postdoctoral Science Foundation grant 2018T110084, the FNR AFR Bilateral grant COALAS 11802479-2, and the Huawei Young Talents Program at IHES.