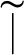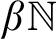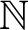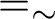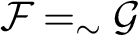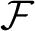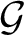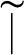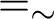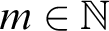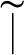1 Introduction
Let
![]() $\mathbb {N}$
be the set of natural numbers. The relation
$\mathbb {N}$
be the set of natural numbers. The relation
![]() $\hspace {1mm}\widetilde {\mid }$
, an extension of the divisibility relation
$\hspace {1mm}\widetilde {\mid }$
, an extension of the divisibility relation
![]() $\mid $
on
$\mid $
on
![]() $\mathbb {N}$
to the set
$\mathbb {N}$
to the set
![]() $\beta \mathbb {N}$
of ultrafilters on
$\beta \mathbb {N}$
of ultrafilters on
![]() $\mathbb {N}$
, was introduced in [Reference Šobot11] and further investigated in [12–15]. The main idea was to understand the impact of various properties of
$\mathbb {N}$
, was introduced in [Reference Šobot11] and further investigated in [12–15]. The main idea was to understand the impact of various properties of
![]() $\mid $
to
$\mid $
to
![]() $\hspace {1mm}\widetilde {\mid }\hspace {1mm}$
and possibly, learning about the
$\hspace {1mm}\widetilde {\mid }\hspace {1mm}$
and possibly, learning about the
![]() $\hspace {1mm}\widetilde {\mid }$
-hierarchy, to acquire better understanding of
$\hspace {1mm}\widetilde {\mid }$
-hierarchy, to acquire better understanding of
![]() $\mid $
. In this paper we will make another step in that direction, considering possible extensions of the congruence relation to
$\mid $
. In this paper we will make another step in that direction, considering possible extensions of the congruence relation to
![]() $\beta \mathbb {N}$
and their relation to
$\beta \mathbb {N}$
and their relation to
![]() $\hspace {1mm}\widetilde {\mid }$
, as well as to the operations of addition and multiplication on
$\hspace {1mm}\widetilde {\mid }$
, as well as to the operations of addition and multiplication on
![]() $\beta \mathbb {N}$
.
$\beta \mathbb {N}$
.
When working with the set of ultrafilters
![]() $\beta S$
on a set S it is common to identify each element
$\beta S$
on a set S it is common to identify each element
![]() $s\in S$
with the principal ultrafilter
$s\in S$
with the principal ultrafilter
![]() $\{A\subseteq S:s\in A\}$
. Having that in mind, any binary operation
$\{A\subseteq S:s\in A\}$
. Having that in mind, any binary operation
![]() $\star $
on S can be extended to
$\star $
on S can be extended to
![]() $\beta S$
as follows: for
$\beta S$
as follows: for
![]() $A\subseteq S$
,
$A\subseteq S$
,
 $$ \begin{align} A\in\mathcal{F}\star\mathcal{G}\Leftrightarrow\{s\in S:s^{-1}A\in\mathcal{G}\}\in\mathcal{F}, \end{align} $$
$$ \begin{align} A\in\mathcal{F}\star\mathcal{G}\Leftrightarrow\{s\in S:s^{-1}A\in\mathcal{G}\}\in\mathcal{F}, \end{align} $$
where
![]() $s^{-1}A=\{t\in S:s\star t\in A\}$
. If
$s^{-1}A=\{t\in S:s\star t\in A\}$
. If
![]() $(S,\star )$
is a semigroup equiped with the discrete topology,
$(S,\star )$
is a semigroup equiped with the discrete topology,
![]() $(\beta S,\star )$
becomes a compact Hausdorff right-topological semigroup. The base sets for the topology are (clopen) sets
$(\beta S,\star )$
becomes a compact Hausdorff right-topological semigroup. The base sets for the topology are (clopen) sets
![]() $\overline {A}=\{\mathcal {F}\in \beta S:A\in \mathcal {F}\}$
. Many aspects of structures obtained in this way were examined in [Reference Hindman and Strauss6].
$\overline {A}=\{\mathcal {F}\in \beta S:A\in \mathcal {F}\}$
. Many aspects of structures obtained in this way were examined in [Reference Hindman and Strauss6].
Every function
![]() $f:\mathbb {N}\rightarrow \mathbb {N}$
can be extended uniquely to a continuous
$f:\mathbb {N}\rightarrow \mathbb {N}$
can be extended uniquely to a continuous
 $\widetilde {f}:\beta \mathbb {N}\rightarrow \beta \mathbb {N}$
: the ultrafilter
$\widetilde {f}:\beta \mathbb {N}\rightarrow \beta \mathbb {N}$
: the ultrafilter
 $\widetilde {f}(\mathcal {F})$
is generated by
$\widetilde {f}(\mathcal {F})$
is generated by
![]() $\{f[A]:A\in \mathcal {F}\}$
. This was used in [Reference Šobot11] to define analogously an extension of a binary relation
$\{f[A]:A\in \mathcal {F}\}$
. This was used in [Reference Šobot11] to define analogously an extension of a binary relation
![]() $\rho $
on
$\rho $
on
![]() $\mathbb {N}$
to a relation
$\mathbb {N}$
to a relation
![]() $\widetilde {\rho }$
on
$\widetilde {\rho }$
on
![]() $\beta \mathbb {N}$
:
$\beta \mathbb {N}$
:
![]() $\mathcal {F}\widetilde {\rho }\mathcal {G}$
if and only if for every
$\mathcal {F}\widetilde {\rho }\mathcal {G}$
if and only if for every
![]() $A\in \mathcal {F}$
the set
$A\in \mathcal {F}$
the set
![]() $\rho [A]:=\{n\in \mathbb {N}:(\exists a\in A)a\rho n\}$
is in
$\rho [A]:=\{n\in \mathbb {N}:(\exists a\in A)a\rho n\}$
is in
![]() $\mathcal {G}$
. This coincides with the so-called canonical way of extending relations from
$\mathcal {G}$
. This coincides with the so-called canonical way of extending relations from
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $\beta \mathbb {N}$
described in [Reference Goranko5]. It turned out that the extension
$\beta \mathbb {N}$
described in [Reference Goranko5]. It turned out that the extension
![]() $\hspace {1mm}\widetilde {\mid }\hspace {1mm}$
of the divisibility relation
$\hspace {1mm}\widetilde {\mid }\hspace {1mm}$
of the divisibility relation
![]() $\mid $
has a simple equivalent definition, more convenient for practical use:
$\mid $
has a simple equivalent definition, more convenient for practical use:
 $$ \begin{align*}\mathcal{F}\hspace{1mm}\widetilde{\mid}\hspace{1mm}\mathcal{G}\Leftrightarrow\mathcal{F}\cap\mathcal{U}\subseteq\mathcal{G},\end{align*} $$
$$ \begin{align*}\mathcal{F}\hspace{1mm}\widetilde{\mid}\hspace{1mm}\mathcal{G}\Leftrightarrow\mathcal{F}\cap\mathcal{U}\subseteq\mathcal{G},\end{align*} $$
where
![]() $\mathcal {U}=\{A\in P(\mathbb {N})\setminus \{\emptyset \}:A\hspace {-0.1cm}\uparrow =A\}$
is the family of sets upward closed for
$\mathcal {U}=\{A\in P(\mathbb {N})\setminus \{\emptyset \}:A\hspace {-0.1cm}\uparrow =A\}$
is the family of sets upward closed for
![]() $\mid $
.
$\mid $
.
![]() $\hspace {1mm}\widetilde {\mid }$
is a quasiorder, so we think of it as an order on the set of
$\hspace {1mm}\widetilde {\mid }$
is a quasiorder, so we think of it as an order on the set of
![]() $=_{\sim }$
-equivalence classes, where
$=_{\sim }$
-equivalence classes, where
![]() $\mathcal {F}=_{\sim }\mathcal {G}$
if and only if
$\mathcal {F}=_{\sim }\mathcal {G}$
if and only if
 $\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
and
$\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
and
 $\mathcal {G}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}$
. We say that
$\mathcal {G}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}$
. We say that
![]() $C\subseteq \mathbb {N}$
is convex if for all
$C\subseteq \mathbb {N}$
is convex if for all
![]() $x,y\in C$
and all z such that
$x,y\in C$
and all z such that
![]() $x\mid z$
and
$x\mid z$
and
![]() $z\mid y$
holds
$z\mid y$
holds
![]() $z\in C$
. All ultrafilters from the same
$z\in C$
. All ultrafilters from the same
![]() $=_{\sim }$
-equivalence class
$=_{\sim }$
-equivalence class
![]() $\mathcal {C}$
have the same convex sets. Clearly, each equivalence class
$\mathcal {C}$
have the same convex sets. Clearly, each equivalence class
![]() $\mathcal {C}$
is determined by
$\mathcal {C}$
is determined by
![]() $\mathcal {F}\cap \mathcal {U}$
(for any
$\mathcal {F}\cap \mathcal {U}$
(for any
![]() $\mathcal {F}\in \mathcal {C}$
), or by the family of convex sets belonging to any
$\mathcal {F}\in \mathcal {C}$
), or by the family of convex sets belonging to any
![]() $\mathcal {F}\in \mathcal {C}$
.
$\mathcal {F}\in \mathcal {C}$
.
An ultrafilter
![]() $\mathcal {F}$
is divisible by some
$\mathcal {F}$
is divisible by some
![]() $n\in \mathbb {N}$
if and only if
$n\in \mathbb {N}$
if and only if
![]() $n\mathbb {N}:=\{nk:k\in \mathbb {N}\}\in \mathcal {F}$
. If
$n\mathbb {N}:=\{nk:k\in \mathbb {N}\}\in \mathcal {F}$
. If
![]() $\mathcal {F}\in \mathbb {N}$
as well,
$\mathcal {F}\in \mathbb {N}$
as well,
 $n\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}$
holds if and only if
$n\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}$
holds if and only if
![]() $n\mid \mathcal {F}$
. Hence, we can write just
$n\mid \mathcal {F}$
. Hence, we can write just
![]() $n\mid \mathcal {F}$
in case
$n\mid \mathcal {F}$
in case
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Especially useful are prime ultrafilters
![]() $\mathcal {P}$
: those
$\mathcal {P}$
: those
![]() $\hspace {1mm}\widetilde {\mid }$
-divisible only by 1 and themselves. This is equivalent to
$\hspace {1mm}\widetilde {\mid }$
-divisible only by 1 and themselves. This is equivalent to
![]() $P\in \mathcal {P}$
, where P is the set of prime numbers.
$P\in \mathcal {P}$
, where P is the set of prime numbers.
The
![]() $\hspace {1mm}\widetilde {\mid }$
-hierarchy can be naturally divided into two parts. The “lower” part, L, can be divided into levels:
$\hspace {1mm}\widetilde {\mid }$
-hierarchy can be naturally divided into two parts. The “lower” part, L, can be divided into levels:
 $L=\bigcup _{l<\omega }\overline {L_{l}}$
, where
$L=\bigcup _{l<\omega }\overline {L_{l}}$
, where
is the set of natural numbers having exactly l (not necessarily distinct) prime factors. Some nice properties of L were established in [Reference Šobot15]; for example every ultrafilter in
![]() $\overline {L_{l}}$
has exactly l prime ingredients (but being divisible by the n-th power of a prime
$\overline {L_{l}}$
has exactly l prime ingredients (but being divisible by the n-th power of a prime
![]() $\mathcal {P}$
is not the same as being divisible by
$\mathcal {P}$
is not the same as being divisible by
![]() $\mathcal {P}\, n$
times). The “upper” part, however, is much more complicated. It contains the maximal
$\mathcal {P}\, n$
times). The “upper” part, however, is much more complicated. It contains the maximal
![]() $=_{\sim }$
-class,
$=_{\sim }$
-class,
![]() $MAX$
, consisting of ultrafilters divisible by all
$MAX$
, consisting of ultrafilters divisible by all
![]() $n\in \mathbb {N}$
, and consequently by all
$n\in \mathbb {N}$
, and consequently by all
![]() $\mathcal {F}\in \beta \mathbb {N}$
([Reference Šobot12], Lemma 4.6). Another interesting class is
$\mathcal {F}\in \beta \mathbb {N}$
([Reference Šobot12], Lemma 4.6). Another interesting class is
![]() $NMAX$
, maximal among
$NMAX$
, maximal among
![]() $\mathbb {N}$
-free ultrafiters (those that are not divisible by any
$\mathbb {N}$
-free ultrafiters (those that are not divisible by any
![]() $n\in \mathbb {N}$
), see [Reference Šobot14], Theorem 5.4. A set belonging to an
$n\in \mathbb {N}$
), see [Reference Šobot14], Theorem 5.4. A set belonging to an
![]() $\mathbb {N}$
-free ultrafilter is called an
$\mathbb {N}$
-free ultrafilter is called an
![]() $\mathbb {N}$
-free set.
$\mathbb {N}$
-free set.
The paper is organized as follows. In §2 several well-known results of elementary number theory are employed to obtain results about the congruence of ultrafilters modulo an integer in connection with the divisibility relation
![]() $\hspace {1mm}\widetilde {\mid }$
. In §3 we recapitulate basic definitions about
$\hspace {1mm}\widetilde {\mid }$
. In §3 we recapitulate basic definitions about
![]() $\omega $
-hyperextensions, obtained by iterating nonstandard extensions of the set
$\omega $
-hyperextensions, obtained by iterating nonstandard extensions of the set
![]() $\mathbb {Z}$
. Tensor pairs play an important role here. They were first considered by Puritz in [Reference Puritz10]; Di Nasso proved several useful characterizations and coined the term (see [Reference Di Nasso3]). Most of the results in §3 are taken from Luperi Baglini’s thesis [Reference Luperi Baglini7], where the concept of a tensor pair is implemented in the surrounding of
$\mathbb {Z}$
. Tensor pairs play an important role here. They were first considered by Puritz in [Reference Puritz10]; Di Nasso proved several useful characterizations and coined the term (see [Reference Di Nasso3]). Most of the results in §3 are taken from Luperi Baglini’s thesis [Reference Luperi Baglini7], where the concept of a tensor pair is implemented in the surrounding of
![]() $\omega $
-hyperextensions. In §4 we define congruence modulo an ultrafilter and find several conditions equivalent to this definition. The next section deals with a stronger relation, and we prove some results connecting it to
$\omega $
-hyperextensions. In §4 we define congruence modulo an ultrafilter and find several conditions equivalent to this definition. The next section deals with a stronger relation, and we prove some results connecting it to
![]() $\hspace {1mm}\widetilde {\mid }\hspace {1mm}$
and operations of addition and multiplication of ultrafilters. In §6 we define another version of divisibility, obtained in a natural way from the strong congruence relation, and get some basic results about it. The last section contains several remarks and open questions.
$\hspace {1mm}\widetilde {\mid }\hspace {1mm}$
and operations of addition and multiplication of ultrafilters. In §6 we define another version of divisibility, obtained in a natural way from the strong congruence relation, and get some basic results about it. The last section contains several remarks and open questions.
Notation.
![]() $\mathbb {N}$
is the set of natural numbers (without zero),
$\mathbb {N}$
is the set of natural numbers (without zero),
![]() $\omega =\mathbb {N}\cup \{0\}$
, P is the set of prime numbers and
$\omega =\mathbb {N}\cup \{0\}$
, P is the set of prime numbers and
![]() $\mathbb {Z}$
the set of integers. The calligraphic letters
$\mathbb {Z}$
the set of integers. The calligraphic letters
![]() $\mathcal {F},\mathcal {G},\mathcal {H},\dots $
are mostly reserved for ultrafilters, and small letters
$\mathcal {F},\mathcal {G},\mathcal {H},\dots $
are mostly reserved for ultrafilters, and small letters
![]() $x,y,z,\dots $
for integers (both standard and nonstandard). For
$x,y,z,\dots $
for integers (both standard and nonstandard). For
![]() $A\subseteq \mathbb {N}$
,
$A\subseteq \mathbb {N}$
,
![]() $A\hspace {-0.1cm}\uparrow =\{n\in \mathbb {N}:(\exists a\in A)a\mid n\}$
and
$A\hspace {-0.1cm}\uparrow =\{n\in \mathbb {N}:(\exists a\in A)a\mid n\}$
and
![]() $A\hspace {-0.1cm}\downarrow =\{n\in \mathbb {N}:(\exists a\in A)n\mid a\}$
. If
$A\hspace {-0.1cm}\downarrow =\{n\in \mathbb {N}:(\exists a\in A)n\mid a\}$
. If
![]() $m,r\in \mathbb {N}$
, then
$m,r\in \mathbb {N}$
, then
![]() $\mathbb {Z}_{m}=\{0,1,\dots ,m-1\}$
and
$\mathbb {Z}_{m}=\{0,1,\dots ,m-1\}$
and
![]() $mA+r=\{mn+r:n\in A\}$
. Finally,
$mA+r=\{mn+r:n\in A\}$
. Finally,
![]() $\mathcal {U}=\{A\in P(\mathbb {N})\setminus \{\emptyset \}:A\hspace {-0.1cm}\uparrow =A\}$
and
$\mathcal {U}=\{A\in P(\mathbb {N})\setminus \{\emptyset \}:A\hspace {-0.1cm}\uparrow =A\}$
and
![]() $\mathcal {V}=\{A\in P(\mathbb {N})\setminus \{\mathbb {N}\}:A\hspace {-0.1cm}\downarrow =A\}$
.
$\mathcal {V}=\{A\in P(\mathbb {N})\setminus \{\mathbb {N}\}:A\hspace {-0.1cm}\downarrow =A\}$
.
Because we use
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
for a nonstandard extension of
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
for a nonstandard extension of
![]() $\mathbb {N}$
, to avoid confusion we will not denote
$\mathbb {N}$
, to avoid confusion we will not denote
![]() $\beta \mathbb {N}\setminus \mathbb {N}$
with
$\beta \mathbb {N}\setminus \mathbb {N}$
with
![]() $\mathbb {N}^{*}$
. Likewise, we will avoid writing
$\mathbb {N}^{*}$
. Likewise, we will avoid writing
![]() $A^{2}$
for
$A^{2}$
for
![]() $A\times A$
, since this notation had another meaning in papers preceding this one.
$A\times A$
, since this notation had another meaning in papers preceding this one.
2 Congruence modulo integer
Let
![]() $m\in \mathbb {N}$
and let
$m\in \mathbb {N}$
and let
![]() $\mathbb {Z}_{m}$
be given the discrete topology. The homomorphism
$\mathbb {Z}_{m}$
be given the discrete topology. The homomorphism
![]() $h_{m}:\mathbb {N}\rightarrow \mathbb {Z}_{m}$
is defined as follows:
$h_{m}:\mathbb {N}\rightarrow \mathbb {Z}_{m}$
is defined as follows:
![]() $h_{m}(n)$
is the residue of n modulo m.
$h_{m}(n)$
is the residue of n modulo m.
![]() $h_{m}$
extends uniquely to a continuous function
$h_{m}$
extends uniquely to a continuous function
 $\widetilde {h_{m}}:\beta \mathbb {N}\rightarrow \mathbb {Z}_{m}$
. The next results follows directly from [Reference Hindman and Strauss6], Corollary 4.22.
$\widetilde {h_{m}}:\beta \mathbb {N}\rightarrow \mathbb {Z}_{m}$
. The next results follows directly from [Reference Hindman and Strauss6], Corollary 4.22.
Proposition 2.1.
![]() $\widetilde {h_{m}}$
is a homomorphism, both for addition and multiplication of ultrafilters.
$\widetilde {h_{m}}$
is a homomorphism, both for addition and multiplication of ultrafilters.
As described in §1, the relation
![]() $\equiv _{m}$
of congruence modulo m can be extended to a relation
$\equiv _{m}$
of congruence modulo m can be extended to a relation
![]() $\widetilde {\equiv _{m}}$
on
$\widetilde {\equiv _{m}}$
on
![]() $\beta \mathbb {N}$
:
$\beta \mathbb {N}$
:
![]() $\mathcal {F}\widetilde {\equiv _{m}}\mathcal {G}$
if and only if, for every
$\mathcal {F}\widetilde {\equiv _{m}}\mathcal {G}$
if and only if, for every
![]() $A\in \mathcal {F}$
,
$A\in \mathcal {F}$
,
![]() $\{n\in \mathbb {N}:(\exists a\in A)n\equiv _{m}a\}\in \mathcal {G}$
. Recall that the kernel of a function
$\{n\in \mathbb {N}:(\exists a\in A)n\equiv _{m}a\}\in \mathcal {G}$
. Recall that the kernel of a function
![]() $h:X\rightarrow Y$
is the relation
$h:X\rightarrow Y$
is the relation
![]() $\text {ker}h=\{(x,y)\in X\times X:h(x)=h(y)\}$
.
$\text {ker}h=\{(x,y)\in X\times X:h(x)=h(y)\}$
.
Proposition 2.2 ([Reference Šobot11], Theorem 2.13)
If
![]() $h:\mathbb {N}\rightarrow \mathbb {N}$
and
$h:\mathbb {N}\rightarrow \mathbb {N}$
and
![]() $\rho =\ker h$
, then
$\rho =\ker h$
, then
 $\widetilde {\rho }=\ker \widetilde {h}$
.
$\widetilde {\rho }=\ker \widetilde {h}$
.
Thus, for
![]() $m\in \mathbb {N}$
the extension of
$m\in \mathbb {N}$
the extension of
![]() $\equiv _{m}$
to
$\equiv _{m}$
to
![]() $\beta \mathbb {N}$
coincides with the definition found in [Reference Hindman and Strauss6]:
$\beta \mathbb {N}$
coincides with the definition found in [Reference Hindman and Strauss6]:
![]() $\mathcal {F}\widetilde {\equiv _{m}}\mathcal {G}$
if and only if
$\mathcal {F}\widetilde {\equiv _{m}}\mathcal {G}$
if and only if
 $\widetilde {h_{m}}(\mathcal {F})=\widetilde {h_{m}}(\mathcal {G})$
. In particular,
$\widetilde {h_{m}}(\mathcal {F})=\widetilde {h_{m}}(\mathcal {G})$
. In particular,
![]() $r<m$
is the residue of
$r<m$
is the residue of
![]() $\mathcal {F}\in \beta \mathbb {N}$
modulo m (
$\mathcal {F}\in \beta \mathbb {N}$
modulo m (
![]() $\mathcal {F}\widetilde {\equiv _{m}}r$
) if and only if
$\mathcal {F}\widetilde {\equiv _{m}}r$
) if and only if
![]() $m\mathbb {N}+r\in \mathcal {F}$
. For practical reasons, we will denote the extension of
$m\mathbb {N}+r\in \mathcal {F}$
. For practical reasons, we will denote the extension of
![]() $\equiv _{m}$
to
$\equiv _{m}$
to
![]() $\beta \mathbb {N}$
also by
$\beta \mathbb {N}$
also by
![]() $\equiv _{m}$
from now on.
$\equiv _{m}$
from now on.
The congruence of ultrafilters modulo integer is not new, but it was mostly marginally mentioned; for example the following interesting result has only the status of a comment in [Reference Hindman and Strauss6].
Proposition 2.3 ([Reference Hindman and Strauss6], Comment 11.20)
For every
![]() $\mathcal {F}\in \beta \mathbb {N}$
and every
$\mathcal {F}\in \beta \mathbb {N}$
and every
![]() $U\in \mathcal {F}$
there is a neighborhood
$U\in \mathcal {F}$
there is a neighborhood
![]() $\overline{A}$
of
$\overline{A}$
of
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $A\subseteq U$
and for all
$A\subseteq U$
and for all
![]() $\mathcal {G}\in {\overline{A}}\setminus A$
and all
$\mathcal {G}\in {\overline{A}}\setminus A$
and all
![]() $m\in \mathbb {N}$
holds
$m\in \mathbb {N}$
holds
![]() $\mathcal {G}\equiv _{m}\mathcal {F}$
.
$\mathcal {G}\equiv _{m}\mathcal {F}$
.
We begin with a simple result about the solvability of a system of congruences in
![]() $\beta \mathbb {N}$
. A system such that its every finite subsystem has a solution in
$\beta \mathbb {N}$
. A system such that its every finite subsystem has a solution in
![]() $\beta \mathbb {N}$
will be called feasible.
$\beta \mathbb {N}$
will be called feasible.
-
(a) Let
 $x\equiv _{m_{i}}a_{i}$
(for
$x\equiv _{m_{i}}a_{i}$
(for
 $i=0,1,\dots ,k$
,
$i=0,1,\dots ,k$
,
 $a_{i}\in \mathbb {Z}$
and
$a_{i}\in \mathbb {Z}$
and
 $m_{i}\in \mathbb {N}$
) be a finite system of congruences. It has a solution in
$m_{i}\in \mathbb {N}$
) be a finite system of congruences. It has a solution in
 $\beta \mathbb {N}\setminus \mathbb {N}$
if and only if it has a solution in
$\beta \mathbb {N}\setminus \mathbb {N}$
if and only if it has a solution in
 $\mathbb {N}$
.
$\mathbb {N}$
. -
(b) The system
 $x\equiv _{m_{i}}a_{i}$
(for
$x\equiv _{m_{i}}a_{i}$
(for
 $i\in \omega $
,
$i\in \omega $
,
 $a_{i}\in \mathbb {Z}$
and
$a_{i}\in \mathbb {Z}$
and
 $m_{i}\in \mathbb {N}$
) of congruences has a solution in
$m_{i}\in \mathbb {N}$
) of congruences has a solution in
 $\beta \mathbb {N}$
if and only if it is feasible.
$\beta \mathbb {N}$
if and only if it is feasible.
-
(a) Let
 $\mathcal {F}\in \beta \mathbb {N}\setminus \mathbb {N}$
be a solution of the given system. Then
$\mathcal {F}\in \beta \mathbb {N}\setminus \mathbb {N}$
be a solution of the given system. Then
 $A_{i}:=\{x\in \mathbb {N}:x\equiv _{m_{i}}a_{i}\}\in \mathcal {F}$
for each
$A_{i}:=\{x\in \mathbb {N}:x\equiv _{m_{i}}a_{i}\}\in \mathcal {F}$
for each
 $i=0,1,\dots ,k$
. Hence
$i=0,1,\dots ,k$
. Hence
 $A:=\bigcap _{i=0}^{k}A_{i}\in \mathcal {F}$
, and any
$A:=\bigcap _{i=0}^{k}A_{i}\in \mathcal {F}$
, and any
 $x\in A$
is a solution of the given system.
$x\in A$
is a solution of the given system.On the other hand, if
 $s\in \mathbb {N}$
is a solution and
$s\in \mathbb {N}$
is a solution and
 $u=lcm(m_{0},m_{1},\dots ,m_{k})$
(the least common multiplier of
$u=lcm(m_{0},m_{1},\dots ,m_{k})$
(the least common multiplier of
 $m_{0},m_{1},\dots ,m_{k}$
), then all the elements of the set
$m_{0},m_{1},\dots ,m_{k}$
), then all the elements of the set
 $B=\{x\in \mathbb {N}:x\equiv _{u}s\}$
are also solutions. Thus every
$B=\{x\in \mathbb {N}:x\equiv _{u}s\}$
are also solutions. Thus every
 $\mathcal {F}\in \overline {B}\setminus B$
is a solution of the system in
$\mathcal {F}\in \overline {B}\setminus B$
is a solution of the system in
 $\beta \mathbb {N}\setminus \mathbb {N}$
.
$\beta \mathbb {N}\setminus \mathbb {N}$
. -
(b) One direction is trivial, so assume the given system to be feasible. Let
 $A_{i}=\{x\in \mathbb {N}:x\equiv _{m_{i}}a_{i}\}$
. By the assumption, every finite subsystem of the given system has a solution, so the family
$A_{i}=\{x\in \mathbb {N}:x\equiv _{m_{i}}a_{i}\}$
. By the assumption, every finite subsystem of the given system has a solution, so the family
 $\{\overline {A_{i}}:i<\omega \}$
has the finite intersection property. Since all the sets
$\{\overline {A_{i}}:i<\omega \}$
has the finite intersection property. Since all the sets
 $\overline {A_{i}}$
are closed, it follows that
$\overline {A_{i}}$
are closed, it follows that
 $A=\bigcap _{i<\omega }\overline {A_{i}}$
is nonempty, and any
$A=\bigcap _{i<\omega }\overline {A_{i}}$
is nonempty, and any
 $\mathcal {F}\in A$
is a solution of the given system.⊣
$\mathcal {F}\in A$
is a solution of the given system.⊣
Since
![]() $=_{\sim }$
-equivalence classes within L are singletons ([Reference Šobot15], Corollary 5.10), each class in L trivially contains ultrafilters congruent only to one residue modulo m. We want to investigate for which systems of congruences there is a
$=_{\sim }$
-equivalence classes within L are singletons ([Reference Šobot15], Corollary 5.10), each class in L trivially contains ultrafilters congruent only to one residue modulo m. We want to investigate for which systems of congruences there is a
![]() $=_{\sim }$
-class such that all its ultrafilters satisfy it. Clearly, such a system must be feasible. On the other hand, by Lemma 2.4 a feasible system S has a solution
$=_{\sim }$
-class such that all its ultrafilters satisfy it. Clearly, such a system must be feasible. On the other hand, by Lemma 2.4 a feasible system S has a solution
![]() $\mathcal {G}\in \beta \mathbb {N}$
so we can assume that it is a system of all congruences satisfied by
$\mathcal {G}\in \beta \mathbb {N}$
so we can assume that it is a system of all congruences satisfied by
![]() $\mathcal {G}$
(we will call such a system maximal). Also, every congruence
$\mathcal {G}$
(we will call such a system maximal). Also, every congruence
![]() $x\equiv _{m_{i}}r_{i}$
is equivalent to a system of congruences modulo mutually prime factors of
$x\equiv _{m_{i}}r_{i}$
is equivalent to a system of congruences modulo mutually prime factors of
![]() $m_{i}$
, so we can assume that all
$m_{i}$
, so we can assume that all
![]() $m_{i}$
are powers of primes themselves. Let
$m_{i}$
are powers of primes themselves. Let
![]() $Q_{S}=\{p\in P:\mathcal {G}\equiv _{p^{n}}0\mbox { for all }n\in \mathbb {N}\}$
and
$Q_{S}=\{p\in P:\mathcal {G}\equiv _{p^{n}}0\mbox { for all }n\in \mathbb {N}\}$
and
![]() $T_{S}=P\setminus Q_{S}$
. As a special case, if
$T_{S}=P\setminus Q_{S}$
. As a special case, if
![]() $T_{S}=\emptyset $
, all ultrafilters from the class
$T_{S}=\emptyset $
, all ultrafilters from the class
![]() $MAX$
satisfy S.
$MAX$
satisfy S.
![]() $A\subset \mathbb {N}$
is an antichain if there are no distinct
$A\subset \mathbb {N}$
is an antichain if there are no distinct
![]() $a,b\in A$
such that
$a,b\in A$
such that
![]() $a\mid b$
.
$a\mid b$
.
Theorem 2.5. For every maximal feasible system S of congruences
![]() $x\equiv _{p^{n}}r_{p,n}$
(for
$x\equiv _{p^{n}}r_{p,n}$
(for
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $p\in P$
and
$p\in P$
and
![]() $r_{p,n}<p^{n}$
) such that
$r_{p,n}<p^{n}$
) such that
![]() $T_{S}$
is infinite there is an
$T_{S}$
is infinite there is an
![]() $=_{\sim }$
-equivalence class
$=_{\sim }$
-equivalence class
![]() $\mathcal {C}\not \subseteq L$
such that
$\mathcal {C}\not \subseteq L$
such that
![]() $\mathcal {F}\equiv _{p^{n}}r_{p,n}$
for all
$\mathcal {F}\equiv _{p^{n}}r_{p,n}$
for all
![]() $\mathcal {F}\in \mathcal {C}$
.
$\mathcal {F}\in \mathcal {C}$
.
Proof We consider two cases.
![]() $1^{\circ } Q_{S}$
is infinite. Let
$1^{\circ } Q_{S}$
is infinite. Let
![]() $\{q_{i}:i\in \omega \}$
and
$\{q_{i}:i\in \omega \}$
and
![]() $\{t_{i}:i\in \omega \}$
be enumerations of
$\{t_{i}:i\in \omega \}$
be enumerations of
![]() $Q_{S}$
and
$Q_{S}$
and
![]() $T_{S}$
respectively. For
$T_{S}$
respectively. For
![]() $i\in \omega $
let
$i\in \omega $
let
 $s_{i}=\min \{n\in \mathbb {N}:\mathcal {G}\not \equiv _{t_{i}^{n}}0\}$
. We construct, by recursion on n, a set
$s_{i}=\min \{n\in \mathbb {N}:\mathcal {G}\not \equiv _{t_{i}^{n}}0\}$
. We construct, by recursion on n, a set
![]() $A=\{a_{n}:n\in \omega \}$
such that
$A=\{a_{n}:n\in \omega \}$
such that
![]() $a_{n}<a_{n+1}$
and:
$a_{n}<a_{n+1}$
and:
-
(1)
 $a_{n}\in t_{i}^{s_{i}+n}\mathbb {N}+r_{t_{i},s_{i}+n}$
for
$a_{n}\in t_{i}^{s_{i}+n}\mathbb {N}+r_{t_{i},s_{i}+n}$
for
 $i<n$
;
$i<n$
; -
(2)
 $t_{n}^{s_{n}}\mid a_{n}$
; and
$t_{n}^{s_{n}}\mid a_{n}$
; and -
(3)
 $q_{j}^{n}\mid a_{n}$
for every
$q_{j}^{n}\mid a_{n}$
for every
 $j<n$
.
$j<n$
.
Start with choosing any
 $a_{0}\in t_{0}^{s_{0}}\mathbb {N}$
. Assume that
$a_{0}\in t_{0}^{s_{0}}\mathbb {N}$
. Assume that
![]() $a_{n}$
is constructed. We want to choose
$a_{n}$
is constructed. We want to choose
![]() $a_{n+1}$
satisfying the system
$a_{n+1}$
satisfying the system
 $x\equiv _{t_{i}^{s_{i}+n+1}}r_{t_{i},s_{i}+n+1}$
for
$x\equiv _{t_{i}^{s_{i}+n+1}}r_{t_{i},s_{i}+n+1}$
for
![]() $i\leq n$
,
$i\leq n$
,
 $x\equiv _{t_{n+1}^{s_{n+1}}}0$
and
$x\equiv _{t_{n+1}^{s_{n+1}}}0$
and
 $x\equiv_{q_j^{n+1}}0$
for
$x\equiv_{q_j^{n+1}}0$
for
![]() $j\leq n$
. By the Chinese remainder theorem this system has a solution in
$j\leq n$
. By the Chinese remainder theorem this system has a solution in
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
![]() $a_{n+1}>a_{n}$
. Clearly, obtained
$a_{n+1}>a_{n}$
. Clearly, obtained
![]() $a_{n+1}$
satisfies conditions (1)–(3).
$a_{n+1}$
satisfies conditions (1)–(3).
A is an antichain: for all
![]() $m<n$
,
$m<n$
,
![]() $a_{m}<a_{n}$
implies that
$a_{m}<a_{n}$
implies that
![]() $a_{n}\nmid a_{m}$
, and
$a_{n}\nmid a_{m}$
, and
![]() $t_{m}^{s_{m}}\mid a_{m}$
and (1) imply that
$t_{m}^{s_{m}}\mid a_{m}$
and (1) imply that
![]() $a_{m}\nmid a_{n}$
. Let
$a_{m}\nmid a_{n}$
. Let
![]() $\mathcal {C}$
be the
$\mathcal {C}$
be the
![]() $=_{\sim }$
-equivalence class of any ultrafilter containing A. Every ultrafilter
$=_{\sim }$
-equivalence class of any ultrafilter containing A. Every ultrafilter
![]() $\mathcal {F}\in \mathcal {C}$
contains
$\mathcal {F}\in \mathcal {C}$
contains
![]() $A\hspace {-0.1cm}\uparrow $
and
$A\hspace {-0.1cm}\uparrow $
and
![]() $A\hspace {-0.1cm}\downarrow $
, so it contains
$A\hspace {-0.1cm}\downarrow $
, so it contains
![]() $A=A\hspace {-0.1cm}\uparrow \cap A\hspace {-0.1cm}\downarrow $
as well. Condition (3) clearly implies that A intersects each level
$A=A\hspace {-0.1cm}\uparrow \cap A\hspace {-0.1cm}\downarrow $
as well. Condition (3) clearly implies that A intersects each level
![]() $L_{l}$
only in finitely many elements, so
$L_{l}$
only in finitely many elements, so
![]() $\mathcal {F}\notin L$
, and in particular
$\mathcal {F}\notin L$
, and in particular
![]() $\mathcal {F}$
is nonprincipal. By (1),
$\mathcal {F}$
is nonprincipal. By (1),
![]() $A\setminus (t_{i}^{m}\mathbb {N}+r_{t_{i},m})$
is finite for all i and all m, hence
$A\setminus (t_{i}^{m}\mathbb {N}+r_{t_{i},m})$
is finite for all i and all m, hence
 $\mathcal {F}\equiv _{t_{i}^{m}}r_{t_{i},m}$
. By (3),
$\mathcal {F}\equiv _{t_{i}^{m}}r_{t_{i},m}$
. By (3),
![]() $\mathcal {F}\equiv _{q_{i}^{n}}0$
for all
$\mathcal {F}\equiv _{q_{i}^{n}}0$
for all
![]() $i\in \omega $
and
$i\in \omega $
and
![]() $n\in \mathbb {N}$
. Thus
$n\in \mathbb {N}$
. Thus
![]() $\mathcal {F}$
satisfies all congruences of the given system.
$\mathcal {F}$
satisfies all congruences of the given system.
![]() $2^{\circ } Q_{S}$
is finite. We repeat the construction from case
$2^{\circ } Q_{S}$
is finite. We repeat the construction from case
![]() $1^{\circ }$
, but for
$1^{\circ }$
, but for
![]() $j\geq |Q_{S}|$
(when we “run out” of elements from
$j\geq |Q_{S}|$
(when we “run out” of elements from
![]() $Q_{S}$
) instead of
$Q_{S}$
) instead of
![]() $q_{j}$
in condition (3) we use some elements
$q_{j}$
in condition (3) we use some elements
![]() $t_{i}\in T$
for
$t_{i}\in T$
for
![]() $i>n$
. (This condition is needed here only to ensure that
$i>n$
. (This condition is needed here only to ensure that
![]() $\mathcal {F}\notin L$
.)⊣
$\mathcal {F}\notin L$
.)⊣
Proposition 2.6 ([Reference Šobot14], Lemma 5.2)
If A is an
![]() $\mathbb {N}$
-free set, then
$\mathbb {N}$
-free set, then
![]() $A\not \subseteq n_{1}\mathbb {N}\cup n_{2}\mathbb {N}\cup \dots \cup n_{k}\mathbb {N}$
for any
$A\not \subseteq n_{1}\mathbb {N}\cup n_{2}\mathbb {N}\cup \dots \cup n_{k}\mathbb {N}$
for any
![]() $n_{1},n_{2},\dots ,n_{k}\in \mathbb {N}\setminus \{1\}$
.
$n_{1},n_{2},\dots ,n_{k}\in \mathbb {N}\setminus \{1\}$
.
Example 2.7.
-
(1) Let us show that the condition of
 $T_{S}$
being infinite in the theorem above is necessary. Consider a system S consisting of
$T_{S}$
being infinite in the theorem above is necessary. Consider a system S consisting of
 $x\equiv _{t_{i}}r_{i}$
(for some primes
$x\equiv _{t_{i}}r_{i}$
(for some primes
 $t_{0},t_{1},\dots ,t_{l-1}$
and some nonzero
$t_{0},t_{1},\dots ,t_{l-1}$
and some nonzero
 $r_{i}<t_{i}$
) and
$r_{i}<t_{i}$
) and
 $x\equiv _{p^{n}}0$
for all
$x\equiv _{p^{n}}0$
for all
 $p\in P\setminus \{t_{0},t_{1},\dots ,t_{l-1}\}$
and all
$p\in P\setminus \{t_{0},t_{1},\dots ,t_{l-1}\}$
and all
 $n\in \mathbb {N}$
. Let us show that there can be no
$n\in \mathbb {N}$
. Let us show that there can be no
 $=_{\sim }$
-class
$=_{\sim }$
-class
 $\mathcal {C}$
such that all
$\mathcal {C}$
such that all
 $\mathcal {F}\in \mathcal {C}$
satisfy S. Assume the opposite. Then every such
$\mathcal {F}\in \mathcal {C}$
satisfy S. Assume the opposite. Then every such
 $\mathcal {F}$
contains all sets in
$\mathcal {F}$
contains all sets in
 $\mathcal {U}_{N}:=\{A\in \mathcal {U}:A\mbox { is }\mathbb {N}\mbox {-free}\}$
: by Proposition 2.6 each
$\mathcal {U}_{N}:=\{A\in \mathcal {U}:A\mbox { is }\mathbb {N}\mbox {-free}\}$
: by Proposition 2.6 each
 $A\in \mathcal {U}_{N}$
must contain an element a mutually prime to all
$A\in \mathcal {U}_{N}$
must contain an element a mutually prime to all
 $t_{0},t_{1},\dots ,t_{l-1}$
; hence
$t_{0},t_{1},\dots ,t_{l-1}$
; hence
 $a\mid \mathcal {F}$
implies
$a\mid \mathcal {F}$
implies
 $a\mathbb {N}\in \mathcal {F}$
, and therefore
$a\mathbb {N}\in \mathcal {F}$
, and therefore
 $A\in \mathcal {F}$
. This means that
$A\in \mathcal {F}$
. This means that
 $\mathcal {F}\cap \mathcal {U}=\mathcal {U}_{N}\cup \{A\in \mathcal {U}:n\mathbb {N}\subseteq A\mbox { for some }n\in \mathbb {N}\mbox { such that }t_{i}\nmid n\mbox { for all }i=0,1,\dots ,l-1\}$
. But now, if we change any of the
$\mathcal {F}\cap \mathcal {U}=\mathcal {U}_{N}\cup \{A\in \mathcal {U}:n\mathbb {N}\subseteq A\mbox { for some }n\in \mathbb {N}\mbox { such that }t_{i}\nmid n\mbox { for all }i=0,1,\dots ,l-1\}$
. But now, if we change any of the
 $r_{i}$
s into another nonzero value we stay inside the same class
$r_{i}$
s into another nonzero value we stay inside the same class
 $\mathcal {C}$
.
$\mathcal {C}$
. -
(2) In the class
 $NMAX$
of
$NMAX$
of
 $\hspace {1mm}\widetilde {\mid }$
-maximal
$\hspace {1mm}\widetilde {\mid }$
-maximal
 $\mathbb {N}$
-free ultrafilters one can find an ultrafilter congruent to r modulo m for any
$\mathbb {N}$
-free ultrafilters one can find an ultrafilter congruent to r modulo m for any
 $0<r<m$
such that
$0<r<m$
such that
 $gcd(m,r)=1$
. Namely, the family
$gcd(m,r)=1$
. Namely, the family
 $\mathcal {U}_{N}\cup \{\mathbb {N}\setminus n\mathbb {N}:n>1\}\cup \{m\mathbb {N}+r\}$
has the finite intersection property: for any given
$\mathcal {U}_{N}\cup \{\mathbb {N}\setminus n\mathbb {N}:n>1\}\cup \{m\mathbb {N}+r\}$
has the finite intersection property: for any given
 $A\in \mathcal {U}_{N}$
and
$A\in \mathcal {U}_{N}$
and
 $n_{0},n_{1},\dots ,n_{k}\in \mathbb {N}\setminus \{1\}$
, since A is
$n_{0},n_{1},\dots ,n_{k}\in \mathbb {N}\setminus \{1\}$
, since A is
 $\mathbb {N}$
-free, Proposition 2.6 says that there is
$\mathbb {N}$
-free, Proposition 2.6 says that there is
 $a\in A$
mutually prime to all of
$a\in A$
mutually prime to all of
 $m,n_{0},\dots ,n_{k}$
. By the Chinese remainder theorem the system
$m,n_{0},\dots ,n_{k}$
. By the Chinese remainder theorem the system
 $x\equiv _{m}r$
,
$x\equiv _{m}r$
,
 $x\not \equiv _{n_{i}}0$
,
$x\not \equiv _{n_{i}}0$
,
 $x\equiv _{a}0$
has a solution, and it belongs to
$x\equiv _{a}0$
has a solution, and it belongs to
 $A\cap (m\mathbb {N}+r)\cap \bigcap _{0\leq i\leq k}(\mathbb {N}\setminus n_{i}\mathbb {N})$
.
$A\cap (m\mathbb {N}+r)\cap \bigcap _{0\leq i\leq k}(\mathbb {N}\setminus n_{i}\mathbb {N})$
.
Now we will prove a result describing which residues modulo a given prime can appear in the same
![]() $=_{\sim }$
-class; first we need the following definition. A set S of residues modulo
$=_{\sim }$
-class; first we need the following definition. A set S of residues modulo
![]() $p\in P$
is a geometric set of residues if there are s and r such that
$p\in P$
is a geometric set of residues if there are s and r such that
![]() $0\leq s<p$
,
$0\leq s<p$
,
![]() $0<r<p$
and
$0<r<p$
and
![]() $S=\{rest(sr^{k},p):k\in \omega \}$
, where
$S=\{rest(sr^{k},p):k\in \omega \}$
, where
![]() $rest(x,p)$
is the residue of x modulo p.
$rest(x,p)$
is the residue of x modulo p.
Theorem 2.8. Let
![]() $p\in P$
and let
$p\in P$
and let
![]() $S\subseteq \{0,1,\dots ,p-1\}$
. There is an
$S\subseteq \{0,1,\dots ,p-1\}$
. There is an
![]() $=_{\sim }$
-equivalence class
$=_{\sim }$
-equivalence class
![]() $\mathcal {C}$
such that the set of residues of ultrafilters
$\mathcal {C}$
such that the set of residues of ultrafilters
![]() $\mathcal {F}\in \mathcal {C}$
modulo p is exactly S if and only if S is a geometric set of residues.
$\mathcal {F}\in \mathcal {C}$
modulo p is exactly S if and only if S is a geometric set of residues.
Proof (
![]() $\Leftarrow $
) First assume that
$\Leftarrow $
) First assume that
![]() $S=\{s_{0},\dots ,s_{l-1}\}$
is a geometric set of residues, where
$S=\{s_{0},\dots ,s_{l-1}\}$
is a geometric set of residues, where
![]() $s_{i}=rest(s_{0}r^{i},p)$
(for
$s_{i}=rest(s_{0}r^{i},p)$
(for
![]() $i=0,1,\dots ,l-1$
) are exactly all distinct residues of numbers
$i=0,1,\dots ,l-1$
) are exactly all distinct residues of numbers
![]() $s_{0}r^{k}$
modulo p. If
$s_{0}r^{k}$
modulo p. If
![]() $S=\{0\}$
, which happens for
$S=\{0\}$
, which happens for
![]() $s_{0}=0$
, any
$s_{0}=0$
, any
![]() $=_{\sim }$
-class of ultrafilters divisible by p (i.e., containg the set
$=_{\sim }$
-class of ultrafilters divisible by p (i.e., containg the set
![]() $p\mathbb {N}$
) will do. Otherwise, by Dirichlet’s prime number theorem, there are primes
$p\mathbb {N}$
) will do. Otherwise, by Dirichlet’s prime number theorem, there are primes
![]() $s\equiv _{p}s_{0}$
and
$s\equiv _{p}s_{0}$
and
![]() $b\equiv _{p}r$
. Let
$b\equiv _{p}r$
. Let
![]() $B=\{sb^{k}:k\in \omega \}$
,
$B=\{sb^{k}:k\in \omega \}$
,
![]() $\mathcal {U}^{\prime }=\{U\in \mathcal {U}:U\cap B\neq \emptyset \}$
and
$\mathcal {U}^{\prime }=\{U\in \mathcal {U}:U\cap B\neq \emptyset \}$
and
![]() $\mathcal {V}^{\prime }=\{V\in \mathcal {V}:\mathbb {N}\setminus V\notin \mathcal {U}^{\prime }\}$
. Then the family
$\mathcal {V}^{\prime }=\{V\in \mathcal {V}:\mathbb {N}\setminus V\notin \mathcal {U}^{\prime }\}$
. Then the family
![]() $\mathcal {U}^{\prime \prime }=\mathcal {U}^{\prime }\cup \mathcal {V}^{\prime }$
has the finite intersection property:
$\mathcal {U}^{\prime \prime }=\mathcal {U}^{\prime }\cup \mathcal {V}^{\prime }$
has the finite intersection property:
![]() $\mathcal {U}^{\prime }$
is closed for finite intersections, and every
$\mathcal {U}^{\prime }$
is closed for finite intersections, and every
![]() $V\in \mathcal {V}^{\prime }$
contains B. Let
$V\in \mathcal {V}^{\prime }$
contains B. Let
![]() $\mathcal {C}$
be the
$\mathcal {C}$
be the
![]() $=_{\sim }$
-equivalence class determined by
$=_{\sim }$
-equivalence class determined by
![]() $\mathcal {U}^{\prime \prime }$
. For every
$\mathcal {U}^{\prime \prime }$
. For every
![]() $\mathcal {F}\in \mathcal {C}$
we have
$\mathcal {F}\in \mathcal {C}$
we have
![]() $B\in \mathcal {F}$
(since
$B\in \mathcal {F}$
(since
![]() $B\cup \{b^{k}:k\in \omega \}\in \mathcal {V}^{\prime }$
and
$B\cup \{b^{k}:k\in \omega \}\in \mathcal {V}^{\prime }$
and
![]() $\mathbb {N}\setminus \{b^{k}:k\in \omega \}\in \mathcal {U}^{\prime }$
) and
$\mathbb {N}\setminus \{b^{k}:k\in \omega \}\in \mathcal {U}^{\prime }$
) and
 $B\subseteq \bigcup _{i=0}^{l-1}(p\mathbb {N}+s_{i})$
, so every such
$B\subseteq \bigcup _{i=0}^{l-1}(p\mathbb {N}+s_{i})$
, so every such
![]() $\mathcal {F}$
is congruent to some
$\mathcal {F}$
is congruent to some
![]() $s_{i}$
modulo p. On the other hand, for each
$s_{i}$
modulo p. On the other hand, for each
![]() $i\in \{0,1,\dots ,l-1\}$
the family
$i\in \{0,1,\dots ,l-1\}$
the family
![]() $\mathcal {U}^{\prime \prime }\cup \{p\mathbb {N}+s_{i}\}$
has the finite intersection property: B contains infinitely many elements from each of the sets
$\mathcal {U}^{\prime \prime }\cup \{p\mathbb {N}+s_{i}\}$
has the finite intersection property: B contains infinitely many elements from each of the sets
![]() $p\mathbb {N}+s_{i}$
, and finite intersections of sets from
$p\mathbb {N}+s_{i}$
, and finite intersections of sets from
![]() $\mathcal {U}^{\prime \prime }$
contain all but finitely many elements from B, so they also intersect
$\mathcal {U}^{\prime \prime }$
contain all but finitely many elements from B, so they also intersect
![]() $p\mathbb {N}+s_{i}$
. Hence there is an ultrafilter
$p\mathbb {N}+s_{i}$
. Hence there is an ultrafilter
![]() $\mathcal {F}\in \mathcal {C}$
such that
$\mathcal {F}\in \mathcal {C}$
such that
![]() $\mathcal {F}\equiv _{p} s_{i}$
.
$\mathcal {F}\equiv _{p} s_{i}$
.
(
![]() $\Rightarrow $
) Now assume S is the set of residues modulo p of ultrafilters
$\Rightarrow $
) Now assume S is the set of residues modulo p of ultrafilters
![]() $\mathcal {F}\in \mathcal {C}$
for some
$\mathcal {F}\in \mathcal {C}$
for some
![]() $=_{\sim }$
-equivalence class
$=_{\sim }$
-equivalence class
![]() $\mathcal {C}$
. Every singleton is clearly a geometric set of residues (obtained by choosing the quotient
$\mathcal {C}$
. Every singleton is clearly a geometric set of residues (obtained by choosing the quotient
![]() $r=1$
), so we will assume
$r=1$
), so we will assume
![]() $|S|>1$
. Let
$|S|>1$
. Let
![]() $\mathcal {W}$
be the family of all convex sets belonging to all
$\mathcal {W}$
be the family of all convex sets belonging to all
![]() $\mathcal {F}\in \mathcal {C}$
. Since the elements of S are all possible residues of ultrafilters
$\mathcal {F}\in \mathcal {C}$
. Since the elements of S are all possible residues of ultrafilters
![]() $\mathcal {F}\in \mathcal {C}$
, there is
$\mathcal {F}\in \mathcal {C}$
, there is
![]() $C\in \mathcal {W}$
(a finite intersection of sets from
$C\in \mathcal {W}$
(a finite intersection of sets from
![]() $(\mathcal {U}\cup \mathcal {V})\cap \mathcal {F}$
) such that
$(\mathcal {U}\cup \mathcal {V})\cap \mathcal {F}$
) such that
 $C\subseteq \bigcup _{k=0}^{l-1}(p\mathbb {N}+s_{k})$
(otherwise
$C\subseteq \bigcup _{k=0}^{l-1}(p\mathbb {N}+s_{k})$
(otherwise
 $\mathcal {W}\cup \{\mathbb {N}\setminus \bigcup _{k=0}^{l-1}(p\mathbb {N}+s_{k})\}$
would have the finite intersection property).
$\mathcal {W}\cup \{\mathbb {N}\setminus \bigcup _{k=0}^{l-1}(p\mathbb {N}+s_{k})\}$
would have the finite intersection property).
Let q be a primitive root modulo p (this means that for every
![]() $0<r<p$
there is
$0<r<p$
there is
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $q^{k}\equiv _{p}r$
; see [Reference Burton2] for more details). Let
$q^{k}\equiv _{p}r$
; see [Reference Burton2] for more details). Let
![]() $S=\{s_{0},\dots ,s_{l-1}\}$
, where
$S=\{s_{0},\dots ,s_{l-1}\}$
, where
![]() $s_{i}=rest(q^{k_{i}},p)$
,
$s_{i}=rest(q^{k_{i}},p)$
,
![]() $k_{0}<k_{1}<\dots <k_{l-1}$
and for each
$k_{0}<k_{1}<\dots <k_{l-1}$
and for each
![]() $s_{i}$
the smallest
$s_{i}$
the smallest
![]() $k_{i}$
is chosen. If we denote
$k_{i}$
is chosen. If we denote
![]() $r_{i}=k_{i}-k_{0}$
for
$r_{i}=k_{i}-k_{0}$
for
![]() $0<i<l$
, then
$0<i<l$
, then
![]() $s_{i}=rest(s_{0}q^{r_{i}},p)$
.
$s_{i}=rest(s_{0}q^{r_{i}},p)$
.
Claim 1. The set
![]() $R:=\{r_{i}:0<i<l\}$
is closed for the
$R:=\{r_{i}:0<i<l\}$
is closed for the
![]() $gcd$
(greatest common divisor) operation.
$gcd$
(greatest common divisor) operation.
Proof of Claim 1 Let
![]() $0<i<j<l$
. Take
$0<i<j<l$
. Take
![]() $A_{0}$
to be the set of
$A_{0}$
to be the set of
![]() $\mid $
-minimal elements of
$\mid $
-minimal elements of
![]() $C\cap (p\mathbb {N}+s_{0})$
. By recursion on k, let
$C\cap (p\mathbb {N}+s_{0})$
. By recursion on k, let
![]() $A_{3k+1}$
be the set of
$A_{3k+1}$
be the set of
![]() $\mid $
-minimal elements of
$\mid $
-minimal elements of
![]() $C\cap A_{3k}\hspace {-0.1cm}\uparrow \cap (p\mathbb {N}+s_{i})$
,
$C\cap A_{3k}\hspace {-0.1cm}\uparrow \cap (p\mathbb {N}+s_{i})$
,
![]() $A_{3k+2}$
the set of
$A_{3k+2}$
the set of
![]() $\mid $
-minimal elements of
$\mid $
-minimal elements of
![]() $C\cap A_{3k+1}\hspace {-0.1cm}\uparrow \cap (p\mathbb {N}+s_{j})$
and
$C\cap A_{3k+1}\hspace {-0.1cm}\uparrow \cap (p\mathbb {N}+s_{j})$
and
![]() $A_{3k+3}$
the set of
$A_{3k+3}$
the set of
![]() $\mid $
-minimal elements of
$\mid $
-minimal elements of
![]() $C\cap A_{3k+2}\hspace {-0.1cm}\uparrow \cap (p\mathbb {N}+s_{0})$
. Each of the sets
$C\cap A_{3k+2}\hspace {-0.1cm}\uparrow \cap (p\mathbb {N}+s_{0})$
. Each of the sets
![]() $A_{m}$
(for
$A_{m}$
(for
![]() $m\in \omega $
) must be nonempty, since otherwise
$m\in \omega $
) must be nonempty, since otherwise
and each of the (convex) sets on the right would miss one of the sets
![]() $p\mathbb {N}+s_{0}$
,
$p\mathbb {N}+s_{0}$
,
![]() $p\mathbb {N}+s_{i}$
or
$p\mathbb {N}+s_{i}$
or
![]() $p\mathbb {N}+s_{j}$
, so it could not belong to all ultrafilters in
$p\mathbb {N}+s_{j}$
, so it could not belong to all ultrafilters in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Now let
![]() $d=gcd(r_{i},r_{j})$
. By Bézout’s lemma there are
$d=gcd(r_{i},r_{j})$
. By Bézout’s lemma there are
![]() $a^{\prime },b^{\prime }\in \mathbb {Z}$
such that
$a^{\prime },b^{\prime }\in \mathbb {Z}$
such that
![]() $a^{\prime }r_{i}+b^{\prime }r_{j}=d$
. By replacing
$a^{\prime }r_{i}+b^{\prime }r_{j}=d$
. By replacing
![]() $a^{\prime },b^{\prime }$
with their residues modulo
$a^{\prime },b^{\prime }$
with their residues modulo
![]() $p-1$
we get
$p-1$
we get
![]() $a,b\in \mathbb {Z}_{p-1}$
such that
$a,b\in \mathbb {Z}_{p-1}$
such that
![]() $ar_{i}+br_{j}\equiv _{p-1}d$
. Let
$ar_{i}+br_{j}\equiv _{p-1}d$
. Let
![]() $m=3(a+b)$
and let
$m=3(a+b)$
and let
![]() $\langle c_{i}:0\leq i<m\rangle $
be a
$\langle c_{i}:0\leq i<m\rangle $
be a
![]() $\mid $
-chain in C of length m such that
$\mid $
-chain in C of length m such that
![]() $c_{i}\in A_{i}$
(it exists since
$c_{i}\in A_{i}$
(it exists since
![]() $A_{m-1}\neq \emptyset $
). Let
$A_{m-1}\neq \emptyset $
). Let
![]() $c_{i+1}=c_{i}d_{i}$
; then
$c_{i+1}=c_{i}d_{i}$
; then
![]() $d_{3k}\equiv _{p} q^{r_{i}}$
and
$d_{3k}\equiv _{p} q^{r_{i}}$
and
![]() $d_{3k}d_{3k+1}\equiv _{p} q^{r_{j}}$
for all k. Hence
$d_{3k}d_{3k+1}\equiv _{p} q^{r_{j}}$
for all k. Hence
 $$ \begin{align*} e &:= d_{0}d_{3}\dots d_{3(a-1)}d_{3a}d_{3a+1}d_{3(a+1)}d_{3(a+1)+1}\dots d_{3(a+b-1)}d_{3(a+b-1)+1}\\ &\equiv_{p} (q^{r_{i}})^{a}(q^{r_{j}})^{b}=q^{ar_{i}+br_{j}}\equiv_{p} q^{d} \end{align*} $$
$$ \begin{align*} e &:= d_{0}d_{3}\dots d_{3(a-1)}d_{3a}d_{3a+1}d_{3(a+1)}d_{3(a+1)+1}\dots d_{3(a+b-1)}d_{3(a+b-1)+1}\\ &\equiv_{p} (q^{r_{i}})^{a}(q^{r_{j}})^{b}=q^{ar_{i}+br_{j}}\equiv_{p} q^{d} \end{align*} $$
(in the last equality we used Fermat’s little theorem). But
![]() $c_{0}e$
is divisible by
$c_{0}e$
is divisible by
![]() $c_{0}$
and divides
$c_{0}$
and divides
![]() $c_{m}$
; since C is convex,
$c_{m}$
; since C is convex,
![]() $c_{0}e\in C$
and hence
$c_{0}e\in C$
and hence
![]() $d\in R$
.⊣
$d\in R$
.⊣
Claim 2.
![]() $rest(tr_{1},p-1)\in R$
for all
$rest(tr_{1},p-1)\in R$
for all
![]() $t\in \mathbb {N}$
.
$t\in \mathbb {N}$
.
Proof of Claim 2 is similar to (though simpler than) the proof of Claim 1. We construct a
![]() $\mid $
-chain
$\mid $
-chain
![]() $\langle c_{i}:0\leq i\leq 2t-2\rangle $
such that
$\langle c_{i}:0\leq i\leq 2t-2\rangle $
such that
![]() $c_{i}\in p\mathbb {N}+s_{0}$
for odd i and
$c_{i}\in p\mathbb {N}+s_{0}$
for odd i and
![]() $c_{i}\in p\mathbb {N}+s_{1}$
for even i. If
$c_{i}\in p\mathbb {N}+s_{1}$
for even i. If
![]() $c_{i+1}=c_{i}d_{i}$
, we get
$c_{i+1}=c_{i}d_{i}$
, we get
![]() $c_{0}d_{1}d_{3}\dots d_{2t-3}\equiv _{p} q^{tr_{1}}$
, so
$c_{0}d_{1}d_{3}\dots d_{2t-3}\equiv _{p} q^{tr_{1}}$
, so
![]() $tr_{1}\equiv _{p-1}r_{j}$
for some
$tr_{1}\equiv _{p-1}r_{j}$
for some
![]() $r_{j}\in R$
.⊣
$r_{j}\in R$
.⊣
Now, since
![]() $r_{1}<r_{2}<\dots <r_{l-1}$
, the two Claims show that R must have the form
$r_{1}<r_{2}<\dots <r_{l-1}$
, the two Claims show that R must have the form
![]() $R=\{ir_{1}:0<i<l\}$
. But then
$R=\{ir_{1}:0<i<l\}$
. But then
![]() $s_{i}\equiv _{p} s_{0}(q^{r_{1}})^{i}$
, which is what we wanted to prove.⊣
$s_{i}\equiv _{p} s_{0}(q^{r_{1}})^{i}$
, which is what we wanted to prove.⊣
3
 $\omega $
-hyperextensions of
$\omega $
-hyperextensions of
 $\mathbb {Z}$
$\mathbb {Z}$
In the previous two papers, [Reference Šobot12] and [Reference Šobot14], we employed nonstandard methods (more precisely, the superstructure approach) to get more information on the relation
![]() $\hspace {1mm}\widetilde {\mid }$
. We will continue that practice here. However, now we turn to extensions of the set
$\hspace {1mm}\widetilde {\mid }$
. We will continue that practice here. However, now we turn to extensions of the set
![]() $\mathbb {Z}$
of all integers instead of
$\mathbb {Z}$
of all integers instead of
![]() $\mathbb {N}$
. The reason is, of course, that we want to use the operation of subtraction. Let X be a set containing a copy of
$\mathbb {N}$
. The reason is, of course, that we want to use the operation of subtraction. Let X be a set containing a copy of
![]() $\mathbb {Z}$
consisting of atoms: none of the elements of X contains as an element any of the other relevant sets. Let
$\mathbb {Z}$
consisting of atoms: none of the elements of X contains as an element any of the other relevant sets. Let
![]() $V_{0}(X)=X$
,
$V_{0}(X)=X$
,
![]() $V_{n+1}(X)=V_{n}(X)\cup P(V_{n}(X))$
for
$V_{n+1}(X)=V_{n}(X)\cup P(V_{n}(X))$
for
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $V(X)=\bigcup _{n<\omega }V_{n}(X)$
.
$V(X)=\bigcup _{n<\omega }V_{n}(X)$
.
![]() $V(X)$
is then called a superstructure. The rank of an element
$V(X)$
is then called a superstructure. The rank of an element
![]() $x\in V(X)$
is the smallest
$x\in V(X)$
is the smallest
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $x\in V_{n}(X)$
.
$x\in V_{n}(X)$
.
If
![]() $V(X)$
is a superstructure, its nonstandard extension is a pair
$V(X)$
is a superstructure, its nonstandard extension is a pair
![]() $(V(Y),*)$
, where
$(V(Y),*)$
, where
![]() $V(Y)$
is a superstructure with the set of atoms Y and
$V(Y)$
is a superstructure with the set of atoms Y and
![]() $*:V(X)\rightarrow V(Y)$
is a rank-preserving function such that
$*:V(X)\rightarrow V(Y)$
is a rank-preserving function such that
![]() $A\subseteq {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}$
for
$A\subseteq {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}$
for
![]() $A\subseteq X$
,
$A\subseteq X$
,
![]() $\mathbb {Z}\subset {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
,
$\mathbb {Z}\subset {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
,
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}X}=Y$
and satisfying the Transfer principle (we delay the formulation of Transfer until later, since we will need a more general version).
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}X}=Y$
and satisfying the Transfer principle (we delay the formulation of Transfer until later, since we will need a more general version).
A nonstandard extension
![]() $(V(Y),*)$
of
$(V(Y),*)$
of
![]() $V(X)$
is a
$V(X)$
is a
![]() $\kappa $
- enlargement if for every family F of subsets of some set in
$\kappa $
- enlargement if for every family F of subsets of some set in
![]() $V(X)$
with the finite intersection property such that
$V(X)$
with the finite intersection property such that
![]() $|F|<\kappa $
there is an element in
$|F|<\kappa $
there is an element in
![]() $\bigcap _{A\in F}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}$
.
$\bigcap _{A\in F}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}$
.
![]() $\kappa $
-enlargements are known to exist in ZFC.
$\kappa $
-enlargements are known to exist in ZFC.
For an excellent introduction to nonstandard methods we refer the reader to [Reference Goldblatt4].
The connection between a nonstandard extension and
![]() $\beta \mathbb {Z}$
is given by the function
$\beta \mathbb {Z}$
is given by the function
![]() $v:{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\rightarrow \beta \mathbb {Z}$
, defined by
$v:{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\rightarrow \beta \mathbb {Z}$
, defined by
![]() $v(x)=\{A\subseteq \mathbb {Z}:x\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}\}$
. v is onto whenever
$v(x)=\{A\subseteq \mathbb {Z}:x\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}\}$
. v is onto whenever
![]() $(V(Y),*)$
is a
$(V(Y),*)$
is a
![]() $\mathfrak{c}^+$
-enlargement.
$\mathfrak{c}^+$
-enlargement.
Proposition 3.1 ([Reference Ng and Render8], Lemma 1)
For every
![]() $x\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb{Z}}$
and every
$x\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb{Z}}$
and every
![]() $f:\mathbb {Z}\rightarrow \mathbb {Z}$
,
$f:\mathbb {Z}\rightarrow \mathbb {Z}$
,
 $v({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(x))=\widetilde {f}(v(x))$
.
$v({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(x))=\widetilde {f}(v(x))$
.
More information about v can be found in [Reference Ng and Render8] and [Reference Luperi Baglini7]. The following proposition is Theorem 3.1 of [Reference Šobot12], adjusted for extensions of
![]() $\mathbb {Z}$
(instead of
$\mathbb {Z}$
(instead of
![]() $\mathbb {N}$
).
$\mathbb {N}$
).
Proposition 3.2. The following conditions are equivalent for every two ultrafilters
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
:
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
:
-
(i)
 $\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
;
$\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
; -
(ii) in every
 $\mathfrak{c}^+$
-enlargement
$\mathfrak{c}^+$
-enlargement
 $V(Y)$
, there are
$V(Y)$
, there are
 $x,y\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
such that
$x,y\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
such that
 $v(x)=\mathcal {F}$
,
$v(x)=\mathcal {F}$
,
 $v(y)=\mathcal {G}$
and
$v(y)=\mathcal {G}$
and
 $x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
; and
$x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
; and -
(iii) in some
 $\mathfrak{c}^+$
-enlargement
$\mathfrak{c}^+$
-enlargement
 $V(Y)$
, there are
$V(Y)$
, there are
 $x,y\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
such that
$x,y\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
such that
 $v(x)=\mathcal {F}$
,
$v(x)=\mathcal {F}$
,
 $v(y)=\mathcal {G}$
and
$v(y)=\mathcal {G}$
and
 $x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
.
$x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
.
First, let us establish that we can use all previously obtained results about
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
while working with
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
while working with
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
. In every extension
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
. In every extension
![]() $V(Y)$
the nonstandard set
$V(Y)$
the nonstandard set
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
consists of
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
consists of
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
, another (“inverted”) copy of
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
, another (“inverted”) copy of
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
(containing negative nonstandard numbers) and zero. For
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
(containing negative nonstandard numbers) and zero. For
![]() $x,y\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
,
$x,y\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
,
![]() $x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
holds if and only if
$x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
holds if and only if
![]() $|x|\;{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid }\;|y|$
.
$|x|\;{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid }\;|y|$
.
The situation with
![]() $\beta \mathbb {Z}$
is similar. Let, for
$\beta \mathbb {Z}$
is similar. Let, for
![]() $A\subseteq \mathbb {Z}$
,
$A\subseteq \mathbb {Z}$
,
![]() $-A:=\{-a:a\in A\}$
; likewise, for
$-A:=\{-a:a\in A\}$
; likewise, for
![]() $\mathcal {F}\in \beta \mathbb {N}$
let
$\mathcal {F}\in \beta \mathbb {N}$
let
![]() $-\mathcal {F}:=\{-A:A\in \mathcal {F}\}$
. Then every ultrafilter in
$-\mathcal {F}:=\{-A:A\in \mathcal {F}\}$
. Then every ultrafilter in
![]() $\beta \mathbb {Z}$
(except the principal ultrafilter identified with zero) contains either
$\beta \mathbb {Z}$
(except the principal ultrafilter identified with zero) contains either
![]() $\mathbb {N}$
or
$\mathbb {N}$
or
![]() $-\mathbb {N}$
, so
$-\mathbb {N}$
, so
![]() $\beta \mathbb {Z}=\beta \mathbb {N}\cup \{-\mathcal {F}:\mathcal {F}\in \beta \mathbb {N}\}\cup \{0\}$
. The family
$\beta \mathbb {Z}=\beta \mathbb {N}\cup \{-\mathcal {F}:\mathcal {F}\in \beta \mathbb {N}\}\cup \{0\}$
. The family
![]() $\mathcal {U}_{Z}:=\{U\in P(\mathbb {Z})\setminus \{\emptyset \}:U\hspace {-0.1cm}\uparrow =U\}$
of upward closed subsets of
$\mathcal {U}_{Z}:=\{U\in P(\mathbb {Z})\setminus \{\emptyset \}:U\hspace {-0.1cm}\uparrow =U\}$
of upward closed subsets of
![]() $\mathbb {Z}$
consists of sets
$\mathbb {Z}$
consists of sets
![]() $V\cup -V\cup \{0\}$
for
$V\cup -V\cup \{0\}$
for
![]() $V\in \mathcal {U}$
, and divisibility in
$V\in \mathcal {U}$
, and divisibility in
![]() $\beta \mathbb {Z}$
is naturally defined as:
$\beta \mathbb {Z}$
is naturally defined as:
 $\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
if and only if
$\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
if and only if
![]() $\mathcal {F}\cap \mathcal {U}_{Z}\subseteq \mathcal {G}$
. Thus,
$\mathcal {F}\cap \mathcal {U}_{Z}\subseteq \mathcal {G}$
. Thus,
 $\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
if and only if
$\mathcal {F}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {G}$
if and only if
 $|\mathcal {F}|\hspace {1mm}\widetilde {\mid }\hspace {1mm}|\mathcal {G}|$
(for absolute values of ultrafilters defined in the obvious way).
$|\mathcal {F}|\hspace {1mm}\widetilde {\mid }\hspace {1mm}|\mathcal {G}|$
(for absolute values of ultrafilters defined in the obvious way).
We will write
![]() $\mathcal {F}-\mathcal {G}$
instead of
$\mathcal {F}-\mathcal {G}$
instead of
![]() $\mathcal {F}+(-\mathcal {G})$
. So
$\mathcal {F}+(-\mathcal {G})$
. So
![]() $A\in \mathcal {F}-\mathcal {G}$
if and only if
$A\in \mathcal {F}-\mathcal {G}$
if and only if
![]() $\{n\in \mathbb {Z}:n-A\in \mathcal {G}\}\in \mathcal {F}$
, where
$\{n\in \mathbb {Z}:n-A\in \mathcal {G}\}\in \mathcal {F}$
, where
![]() $n-A=\{n-a:a\in A\}$
. Note that there can be no confusion with this notation, since
$n-A=\{n-a:a\in A\}$
. Note that there can be no confusion with this notation, since
![]() $\mathcal {F}-\mathcal {G}$
is exactly the ultrafilter obtained by extending the subtraction operation from
$\mathcal {F}-\mathcal {G}$
is exactly the ultrafilter obtained by extending the subtraction operation from
![]() $\mathbb {Z}$
to
$\mathbb {Z}$
to
![]() $\beta \mathbb {Z}$
, as defined in (1).
$\beta \mathbb {Z}$
, as defined in (1).
A nonstandard extension
![]() $(V(Y),*)$
of
$(V(Y),*)$
of
![]() $V(X)$
is called a single superstructure model if
$V(X)$
is called a single superstructure model if
![]() $Y=X$
. The existence of such a model was proved in [Reference Benci1]. In a single superstructure model it is possible to iterate the star-function, since it is defined for all elements in the range of
$Y=X$
. The existence of such a model was proved in [Reference Benci1]. In a single superstructure model it is possible to iterate the star-function, since it is defined for all elements in the range of
![]() $*$
.
$*$
.
Definition 3.3. Let
![]() $(V(X),*)$
be a single superstructure model with
$(V(X),*)$
be a single superstructure model with
![]() $\mathbb {Z}\subseteq X$
. Define recursively, for
$\mathbb {Z}\subseteq X$
. Define recursively, for
![]() $x\in V(X)$
,
$x\in V(X)$
,
![]() $S_{0}(x)=x$
and
$S_{0}(x)=x$
and
![]() $S_{k+1}(x)={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}S_{k}(x))$
for all
$S_{k+1}(x)={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}S_{k}(x))$
for all
![]() $k\in \omega $
. For
$k\in \omega $
. For
![]() $A\subseteq X$
the set
$A\subseteq X$
the set
![]() ${{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}A}=\bigcup _{k<\omega }S_{k}(A)$
is called an
${{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}A}=\bigcup _{k<\omega }S_{k}(A)$
is called an
![]() $\omega $
-hyperextension of A.
$\omega $
-hyperextension of A.
Now, any
![]() $(V(X),S_{k})$
is a nonstandard extension. Moreover, we have the following.
$(V(X),S_{k})$
is a nonstandard extension. Moreover, we have the following.
Proposition 3.4 ([Reference Luperi Baglini7], Proposition 2.5.7)
If
![]() $(V(X),*)$
is a single superstructure model which is a
$(V(X),*)$
is a single superstructure model which is a
![]() $\mathfrak{c}^+$
-enlargement, then
$\mathfrak{c}^+$
-enlargement, then
![]() $(V(X),S_{k})$
for every
$(V(X),S_{k})$
for every
![]() $k\in \omega $
are also
$k\in \omega $
are also
![]() $\mathfrak{c}^+$
-enlargements.
$\mathfrak{c}^+$
-enlargements.
We will call a single superstructure model
![]() $(V(X),*)$
which is a
$(V(X),*)$
which is a
![]() $\mathfrak{c}^+$
-enlargement an
$\mathfrak{c}^+$
-enlargement an
![]() $\omega $
-hyperenlargement.
$\omega $
-hyperenlargement.
Now we can use the Transfer principle within any of the mentioned extensions. Recall that a first-order formula
![]() $\varphi (x_{1},x_{2},\dots ,x_{n})$
is bounded if all its quantifiers are bounded, i.e., of the form
$\varphi (x_{1},x_{2},\dots ,x_{n})$
is bounded if all its quantifiers are bounded, i.e., of the form
![]() $(\forall x\in y)$
or
$(\forall x\in y)$
or
![]() $(\exists x\in y)$
. In the Transfer principle the free variables
$(\exists x\in y)$
. In the Transfer principle the free variables
![]() $x_{1},x_{2},\dots ,x_{n}$
that appear in
$x_{1},x_{2},\dots ,x_{n}$
that appear in
![]() $\varphi (x_{1},x_{2},\dots ,x_{n})$
can take values of elements
$\varphi (x_{1},x_{2},\dots ,x_{n})$
can take values of elements
![]() $a_{1},a_{2},\dots ,a_{n}\in V(X)$
and in
$a_{1},a_{2},\dots ,a_{n}\in V(X)$
and in
![]() $\varphi ({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}a}_{1},{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}a}_{2},\dots ,{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}a}_{n})$
they are replaced with their star-counterparts. Any k-ary relation
$\varphi ({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}a}_{1},{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}a}_{2},\dots ,{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}a}_{n})$
they are replaced with their star-counterparts. Any k-ary relation
![]() $A\in V(X)$
appearing as an atomic subformula in
$A\in V(X)$
appearing as an atomic subformula in
![]() $\varphi $
is also considered like a free variable and gets replaced with
$\varphi $
is also considered like a free variable and gets replaced with
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}$
.
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}A}$
.
The Transfer principle. For every bounded formula
![]() $\varphi $
and every
$\varphi $
and every
![]() $a_{1},a_{2},\dots $
,
$a_{1},a_{2},\dots $
,
![]() $a_{n}\in V(X)$
, in
$a_{n}\in V(X)$
, in
![]() $V(X)\, \varphi (a_{1},a_{2},\dots ,a_{n})$
holds if and only if
$V(X)\, \varphi (a_{1},a_{2},\dots ,a_{n})$
holds if and only if
![]() $\varphi (S_{k}(a_{1}),S_{k}(a_{2}),\dots $
,
$\varphi (S_{k}(a_{1}),S_{k}(a_{2}),\dots $
,
![]() $S_{k}(a_{n}))$
holds (for any
$S_{k}(a_{n}))$
holds (for any
![]() $k\in \mathbb {N}$
).
$k\in \mathbb {N}$
).
As a simple application of Transfer notice that
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x+y)={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
for
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x+y)={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
for
![]() $x,y\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}Z}$
, a fact that we will need later: if
$x,y\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}Z}$
, a fact that we will need later: if
![]() $z=x+y$
, Transfer implies that
$z=x+y$
, Transfer implies that
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
. Likewise,
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
. Likewise,
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x\cdot y)={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
.
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x\cdot y)={{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
.
Proposition 3.5 ([Reference Luperi Baglini7], Proposition 2.5.3)
-
(a) For
 $k\leq l$
and
$k\leq l$
and
 $A\subseteq \mathbb {Z}$
,
$A\subseteq \mathbb {Z}$
,
 $S_{k}(A)=S_{l}(A)\cap S_{k}(\mathbb {Z})$
. Consequently,
$S_{k}(A)=S_{l}(A)\cap S_{k}(\mathbb {Z})$
. Consequently,
 $S_{k}(A)={{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}A}\cap S_{k}(\mathbb {Z})$
.
$S_{k}(A)={{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}A}\cap S_{k}(\mathbb {Z})$
. -
(b) For
 $k\leq l$
,
$k\leq l$
,
 $h:\mathbb {Z}\rightarrow \mathbb {Z}$
and
$h:\mathbb {Z}\rightarrow \mathbb {Z}$
and
 $x\in S_{k}(\mathbb {Z})$
,
$x\in S_{k}(\mathbb {Z})$
,
 $S_l(h)(x)=S_k(h)(x)$
.
$S_l(h)(x)=S_k(h)(x)$
.
Therefore we can write
![]() ${}^\bullet h:{}^\bullet\mathbb{N}\rightarrow{}^\bullet\mathbb{N}$
for the function defined by
${}^\bullet h:{}^\bullet\mathbb{N}\rightarrow{}^\bullet\mathbb{N}$
for the function defined by
![]() ${}^\bullet h(x)=S_k(h)$
for
${}^\bullet h(x)=S_k(h)$
for
![]() $x\in S_k(\mathbb{Z})$
.
$x\in S_k(\mathbb{Z})$
.
Let us comment on the iterated version of the divisibility relation. It is common to omit
![]() $*$
(or, more generally,
$*$
(or, more generally,
![]() $S_{k}$
) in formulas in front of the relations
$S_{k}$
) in formulas in front of the relations
![]() $=$
and
$=$
and
![]() $\in $
and arithmetical operations, in order to simplify notation. Let us show that it is justified to do the same with the divisibility relation, even when working in an
$\in $
and arithmetical operations, in order to simplify notation. Let us show that it is justified to do the same with the divisibility relation, even when working in an
![]() $\omega $
-hyperextension. Firstly,
$\omega $
-hyperextension. Firstly,
![]() $(x,y)\in S_{k}(\mid )$
can hold only if
$(x,y)\in S_{k}(\mid )$
can hold only if
![]() $x,y\in S_{k}(\mathbb {Z})$
. On the other hand, for
$x,y\in S_{k}(\mathbb {Z})$
. On the other hand, for
![]() $x\in S_{k}(\mathbb {N})$
,
$x\in S_{k}(\mathbb {N})$
,
![]() $y\in S_{k}(\mathbb {Z})$
and
$y\in S_{k}(\mathbb {Z})$
and
![]() $l>k$
, we will show that
$l>k$
, we will show that
![]() $(x,y)\in S_{k}(\mid )$
if and only if
$(x,y)\in S_{k}(\mid )$
if and only if
![]() $(x,y)\in S_{l}(\mid )$
.
$(x,y)\in S_{l}(\mid )$
.
![]() $(x,y)\in S_{k}(\mid )$
means that there is
$(x,y)\in S_{k}(\mid )$
means that there is
![]() $z\in S_{k}(\mathbb {Z})$
such that
$z\in S_{k}(\mathbb {Z})$
such that
![]() $y=xz$
. But
$y=xz$
. But
![]() $S_{k}(\mathbb {Z})\subseteq S_{l}(\mathbb {Z})$
, so
$S_{k}(\mathbb {Z})\subseteq S_{l}(\mathbb {Z})$
, so
![]() $(x,y)\in S_{l}(\mid )$
follows. In the other direction, if
$(x,y)\in S_{l}(\mid )$
follows. In the other direction, if
![]() $(x,y)\in S_{l}(\mid )$
for some
$(x,y)\in S_{l}(\mid )$
for some
![]() $l>k$
, and
$l>k$
, and
![]() $y=xz$
, then
$y=xz$
, then
![]() $z\in S_{k}(\mathbb {Z})$
so
$z\in S_{k}(\mathbb {Z})$
so
![]() $(x,y)\in S_{k}(\mid )$
as well. Thus, there will be no ambiguity if we drop the stars and write simply
$(x,y)\in S_{k}(\mid )$
as well. Thus, there will be no ambiguity if we drop the stars and write simply
![]() $x\mid y$
instead of
$x\mid y$
instead of
![]() $(x,y)\in S_{k}(\mid )$
.
$(x,y)\in S_{k}(\mid )$
.
Definition 3.6. For
![]() $\mathcal {F}\in \beta \mathbb {Z}$
,
$\mathcal {F}\in \beta \mathbb {Z}$
,
![]() $\mu _{n}(\mathcal {F})=\{x\in S_{n}(\mathbb {Z}):(\forall A\in \mathcal {F})x\in S_{n}(A)\}$
.
$\mu _{n}(\mathcal {F})=\{x\in S_{n}(\mathbb {Z}):(\forall A\in \mathcal {F})x\in S_{n}(A)\}$
.
The monad of
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\mu (\mathcal {F})=\bigcup _{n<\omega }\mu _{n}(\mathcal {F})=\{x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}:(\forall A\in \mathcal {F})x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}A}\}$
.
$\mu (\mathcal {F})=\bigcup _{n<\omega }\mu _{n}(\mathcal {F})=\{x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}:(\forall A\in \mathcal {F})x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}A}\}$
.
For
![]() $x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
,
$x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
,
![]() $v(x)$
is the unique
$v(x)$
is the unique
![]() $\mathcal {F}\in \beta \mathbb {Z}$
such that
$\mathcal {F}\in \beta \mathbb {Z}$
such that
![]() $x\in \mu (\mathcal {F})$
.
$x\in \mu (\mathcal {F})$
.
Note that this definition of
![]() $v(x)$
agrees with the previous one (for
$v(x)$
agrees with the previous one (for
![]() $x\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
).
$x\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
).
Proposition 3.7 ([Reference Luperi Baglini7], Proposition 2.5.11)
For every
![]() $x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
and every
$x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
and every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $v(S_{n}(x))=v(x)$
.
$v(S_{n}(x))=v(x)$
.
Let us recall the tensor (or Fubini) product of ultrafilters: for
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
![]() $\mathcal {F}\otimes \mathcal {G}$
is the ultrafilter on
$\mathcal {F}\otimes \mathcal {G}$
is the ultrafilter on
![]() $\mathbb {Z}\times \mathbb {Z}$
defined by
$\mathbb {Z}\times \mathbb {Z}$
defined by
The definitions of monads of ultrafilters of the form
![]() $\mathcal {F}\otimes \mathcal {G}$
and the corresponding function v are analogous as above. For ultrafilters
$\mathcal {F}\otimes \mathcal {G}$
and the corresponding function v are analogous as above. For ultrafilters
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
and nonstandard numbers
$\mathcal {G}$
and nonstandard numbers
![]() $x\in \mu (\mathcal {F})$
and
$x\in \mu (\mathcal {F})$
and
![]() $y\in \mu (\mathcal {G})$
,
$y\in \mu (\mathcal {G})$
,
![]() $(x,y)$
is a tensor pair if
$(x,y)$
is a tensor pair if
![]() $(x,y)\in \mu (\mathcal {F}\otimes \mathcal {G})$
.
$(x,y)\in \mu (\mathcal {F}\otimes \mathcal {G})$
.
Lemma 3.8. If
![]() $(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\times {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
is a tensor pair, then so are
$(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\times {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
is a tensor pair, then so are
![]() $(x,-y)$
and
$(x,-y)$
and
![]() $(-x,y)$
.
$(-x,y)$
.
Proof Let
![]() $\mathcal {F}=v(x)$
and
$\mathcal {F}=v(x)$
and
![]() $\mathcal {G}=v(y)$
; then
$\mathcal {G}=v(y)$
; then
![]() $v(-y)=-\mathcal {G}$
and
$v(-y)=-\mathcal {G}$
and
![]() $v((x,y))=\mathcal {F}\otimes \mathcal {G}$
. We need to prove that
$v((x,y))=\mathcal {F}\otimes \mathcal {G}$
. We need to prove that
![]() $v((x,-y))=\mathcal {F}\otimes (-\mathcal {G})$
. But whenever
$v((x,-y))=\mathcal {F}\otimes (-\mathcal {G})$
. But whenever
![]() $(x,-y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}S}$
for some
$(x,-y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}S}$
for some
![]() $S\subseteq \mathbb {Z}\times \mathbb {Z}$
, we have
$S\subseteq \mathbb {Z}\times \mathbb {Z}$
, we have
![]() $(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}S}^{\prime }$
, where
$(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}S}^{\prime }$
, where
![]() $S^{\prime }:=\{(m,-n):(m,n)\in S\}$
. By the assumptions
$S^{\prime }:=\{(m,-n):(m,n)\in S\}$
. By the assumptions
![]() $S^{\prime }\in \mathcal {F}\otimes \mathcal {G}$
, so
$S^{\prime }\in \mathcal {F}\otimes \mathcal {G}$
, so
 $\{x\in \mathbb {Z}:\{y\in \mathbb {Z}:(x,y)\in S\}\in (-\mathcal {G})\}=\{x\in \mathbb {Z}:-\{y\in \mathbb {Z}:(x,y)\in S\}\in \mathcal {G}\}=\{x\in \mathbb {Z}:\{y\in \mathbb {Z}:(x,y)\in S^{\prime }\}\in \mathcal {G}\}\in \mathcal {F}$
, and
$\{x\in \mathbb {Z}:\{y\in \mathbb {Z}:(x,y)\in S\}\in (-\mathcal {G})\}=\{x\in \mathbb {Z}:-\{y\in \mathbb {Z}:(x,y)\in S\}\in \mathcal {G}\}=\{x\in \mathbb {Z}:\{y\in \mathbb {Z}:(x,y)\in S^{\prime }\}\in \mathcal {G}\}\in \mathcal {F}$
, and
![]() $S\in \mathcal {F}\otimes (-\mathcal {G})$
.
$S\in \mathcal {F}\otimes (-\mathcal {G})$
.
The proof for
![]() $(-x,y)$
is analogous. ⊣
$(-x,y)$
is analogous. ⊣
By [Reference Di Nasso3], Proposition 11.7.2, for any tensor pair
![]() $(x,y)$
we have
$(x,y)$
we have
![]() $x+y\in \mu (\mathcal {F}+\mathcal {G})$
and
$x+y\in \mu (\mathcal {F}+\mathcal {G})$
and
![]() $x\cdot y\in \mu (\mathcal {F}\cdot \mathcal {G})$
. An important feature of
$x\cdot y\in \mu (\mathcal {F}\cdot \mathcal {G})$
. An important feature of
![]() $\omega $
-hyperextensions is that they provide a canonical way to obtain tensor pairs.
$\omega $
-hyperextensions is that they provide a canonical way to obtain tensor pairs.
Proposition 3.9 ([Reference Luperi Baglini7], Theorem 2.5.27)
If
![]() $x\in \mu (\mathcal {F})$
and
$x\in \mu (\mathcal {F})$
and
![]() $y\in \mu (\mathcal {G})$
, then the pair
$y\in \mu (\mathcal {G})$
, then the pair
![]() $(x,{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
is a tensor pair. Hence,
$(x,{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
is a tensor pair. Hence,
![]() $x+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\in \mu (\mathcal {F}+\mathcal {G})$
and
$x+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\in \mu (\mathcal {F}+\mathcal {G})$
and
![]() $x\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\in \mu (\mathcal {F}\cdot \mathcal {G})$
.
$x\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\in \mu (\mathcal {F}\cdot \mathcal {G})$
.
4 Congruence modulo ultrafilter
A natural way to define the congruence relation modulo an ultrafilter would be to imitate again the construction of an extension
![]() $\widetilde {\rho }$
, as described in §1.
$\widetilde {\rho }$
, as described in §1.
Definition 4.1. For
![]() $\mathcal {M}\in \beta \mathbb {N}$
and
$\mathcal {M}\in \beta \mathbb {N}$
and
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
![]() $\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
if and only if for every
$\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
if and only if for every
![]() $A\in \mathcal {M}$
the set
$A\in \mathcal {M}$
the set
![]() $\{(x,y)\in \mathbb {Z}\times \mathbb {Z}:(\exists m\in A)x\equiv _{m}y\}$
belongs to the ultrafilter
$\{(x,y)\in \mathbb {Z}\times \mathbb {Z}:(\exists m\in A)x\equiv _{m}y\}$
belongs to the ultrafilter
![]() $\mathcal {F}\otimes \mathcal {G}$
.
$\mathcal {F}\otimes \mathcal {G}$
.
This definition has a nice equivalent formulation via divisibility of ultrafilters.
Lemma 4.2. For
![]() $\mathcal {M}\in \beta \mathbb {N}$
and
$\mathcal {M}\in \beta \mathbb {N}$
and
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
![]() $\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
if and only if
$\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
if and only if
 $\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
.
$\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
.
 $$ \begin{align*} \mathcal{F}\equiv_{\mathcal{M}}\mathcal{G} &\Leftrightarrow (\forall A\in\mathcal{M})\{x\in \mathbb{Z}:\{y\in \mathbb{Z}:(\exists m\in A)x\equiv_{m}y\}\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M})\{x\in \mathbb{Z}:\{y\in \mathbb{Z}:x-y\in A\hspace{-0.1cm}\uparrow\}\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M}\cap\mathcal{U})\{x\in \mathbb{Z}:\{y\in \mathbb{Z}:x-y\in A\}\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M}\cap\mathcal{U})\{x\in \mathbb{Z}:x-A\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M}\cap\mathcal{U})A\in\mathcal{F}-\mathcal{G}, \end{align*} $$
$$ \begin{align*} \mathcal{F}\equiv_{\mathcal{M}}\mathcal{G} &\Leftrightarrow (\forall A\in\mathcal{M})\{x\in \mathbb{Z}:\{y\in \mathbb{Z}:(\exists m\in A)x\equiv_{m}y\}\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M})\{x\in \mathbb{Z}:\{y\in \mathbb{Z}:x-y\in A\hspace{-0.1cm}\uparrow\}\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M}\cap\mathcal{U})\{x\in \mathbb{Z}:\{y\in \mathbb{Z}:x-y\in A\}\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M}\cap\mathcal{U})\{x\in \mathbb{Z}:x-A\in\mathcal{G}\}\in\mathcal{F}\\ &\Leftrightarrow (\forall A\in\mathcal{M}\cap\mathcal{U})A\in\mathcal{F}-\mathcal{G}, \end{align*} $$
which is equivalent to
 $\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
.⊣
$\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
.⊣
The following lemma justifies our using the same notation as for the relation from §2.
Lemma 4.3. If
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
,
![]() $\mathcal {F}\equiv _{m}\mathcal {G}$
as defined in §2 is equivalent to
$\mathcal {F}\equiv _{m}\mathcal {G}$
as defined in §2 is equivalent to
![]() $\mathcal {F}\equiv _{m}\mathcal {G}$
from Definition 4.1.
$\mathcal {F}\equiv _{m}\mathcal {G}$
from Definition 4.1.
Proof By Proposition 2.1
![]() $\widetilde {h_{m}}$
is a homomorphism, so
$\widetilde {h_{m}}$
is a homomorphism, so
 $\widetilde {h_{m}}(\mathcal {F}-\mathcal {G})=\widetilde {h_{m}}(\mathcal {F})-\widetilde {h_{m}}(\mathcal {G})$
. It follows that
$\widetilde {h_{m}}(\mathcal {F}-\mathcal {G})=\widetilde {h_{m}}(\mathcal {F})-\widetilde {h_{m}}(\mathcal {G})$
. It follows that
![]() $m\mid \mathcal {F}-\mathcal {G}$
if and only if
$m\mid \mathcal {F}-\mathcal {G}$
if and only if
 $\widetilde {h_{m}}(\mathcal {F}-\mathcal {G})=0$
, if and only if
$\widetilde {h_{m}}(\mathcal {F}-\mathcal {G})=0$
, if and only if
 $\widetilde {h_{m}}(\mathcal {F})=\widetilde {h_{m}}(\mathcal {G})$
. ⊣
$\widetilde {h_{m}}(\mathcal {F})=\widetilde {h_{m}}(\mathcal {G})$
. ⊣
![]() $\equiv _{\mathcal {M}}$
also has a nonstandard characterization. First we recall Puritz’s result that
$\equiv _{\mathcal {M}}$
also has a nonstandard characterization. First we recall Puritz’s result that
![]() $(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}\times {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
is a tensor pair if and only if
$(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}\times {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}$
is a tensor pair if and only if
![]() $x<{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)$
for every
$x<{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)$
for every
![]() $f:\mathbb {N}\rightarrow \mathbb {N}$
such that
$f:\mathbb {N}\rightarrow \mathbb {N}$
such that
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}\setminus \mathbb {N}$
([Reference Puritz10], Theorem 3.4). Taking into account Lemma 3.8, we get the following version of this result.
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}}\setminus \mathbb {N}$
([Reference Puritz10], Theorem 3.4). Taking into account Lemma 3.8, we get the following version of this result.
Proposition 4.4.
![]() $(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\times {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
is a tensor pair if and only if
$(x,y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\times {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}$
is a tensor pair if and only if
![]() $|x|<|{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)|$
for every
$|x|<|{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)|$
for every
![]() $f:\mathbb {Z}\rightarrow \mathbb {Z}$
such that
$f:\mathbb {Z}\rightarrow \mathbb {Z}$
such that
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\setminus \mathbb {Z}$
.
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {Z}}\setminus \mathbb {Z}$
.
If we denote
![]() $\mathcal {G}=v(y)$
, the condition
$\mathcal {G}=v(y)$
, the condition
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)\notin \mathbb {Z}$
is equivalent to
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)\notin \mathbb {Z}$
is equivalent to
![]() $f\upharpoonright B$
not being constant for any
$f\upharpoonright B$
not being constant for any
![]() $B\in \mathcal {G}$
. Let us call
$B\in \mathcal {G}$
. Let us call
![]() $f:\mathbb {Z}\rightarrow \mathbb {Z}$
non-
$f:\mathbb {Z}\rightarrow \mathbb {Z}$
non-
![]() $\mathcal {G}$
-constant in that case.
$\mathcal {G}$
-constant in that case.
Note that we are still working in any
![]() $\mathfrak{c}^+$
-enlargement (we do not need an
$\mathfrak{c}^+$
-enlargement (we do not need an
![]() $\omega $
-hyperextension), so
$\omega $
-hyperextension), so
![]() $\mu (\mathcal {F})$
here actually means
$\mu (\mathcal {F})$
here actually means
![]() $\mu _{1}(\mathcal {F})$
.
$\mu _{1}(\mathcal {F})$
.
Theorem 4.5. Let
![]() $\mathcal {M}\in \beta \mathbb {N}$
and
$\mathcal {M}\in \beta \mathbb {N}$
and
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
. The following conditions are equivalent:
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
. The following conditions are equivalent:
-
(i)
 $\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
$\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
-
(ii) in some
 $\mathfrak{c}^+$
-enlargement holds (2)
$\mathfrak{c}^+$
-enlargement holds (2) $$ \begin{align} (\forall m\in\mu(\mathcal{M}))(\exists x\in\mu(\mathcal{F}))(\exists y\in\mu(\mathcal{G}))((x,y)\mbox{ is a tensor pair }\land m\mid x-y) \end{align} $$
$$ \begin{align} (\forall m\in\mu(\mathcal{M}))(\exists x\in\mu(\mathcal{F}))(\exists y\in\mu(\mathcal{G}))((x,y)\mbox{ is a tensor pair }\land m\mid x-y) \end{align} $$
-
(iii) in every
 $\mathfrak{c}^+$
-enlargement holds (2).
$\mathfrak{c}^+$
-enlargement holds (2).
Proof (ii)
![]() $\Rightarrow $
(i) Let (2) hold in some
$\Rightarrow $
(i) Let (2) hold in some
![]() $\mathfrak{c}^+$
-enlargement. If
$\mathfrak{c}^+$
-enlargement. If
![]() $y\in \mu (\mathcal {G})$
then
$y\in \mu (\mathcal {G})$
then
![]() $-y\in \mu (-\mathcal {G})$
. Since for a tensor pair
$-y\in \mu (-\mathcal {G})$
. Since for a tensor pair
![]() $(x,y)$
we have, by Lemma 3.8,
$(x,y)$
we have, by Lemma 3.8,
![]() $x-y=x+ (-y)\in \mu (\mathcal {F}-\mathcal {G})$
, the result follows directly from Proposition 3.2 and Lemma 4.2.
$x-y=x+ (-y)\in \mu (\mathcal {F}-\mathcal {G})$
, the result follows directly from Proposition 3.2 and Lemma 4.2.
(i)
![]() $\Rightarrow $
(iii) Assume
$\Rightarrow $
(iii) Assume
 $\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
; we work in arbitrary
$\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
; we work in arbitrary
![]() $\mathfrak{c}^+$
-enlargement. We define, for
$\mathfrak{c}^+$
-enlargement. We define, for
![]() $A,B\subseteq \mathbb {Z}$
,
$A,B\subseteq \mathbb {Z}$
,
![]() $M\subseteq \mathbb {N}$
and
$M\subseteq \mathbb {N}$
and
![]() $f:\mathbb {Z}\rightarrow \mathbb {Z}$
:
$f:\mathbb {Z}\rightarrow \mathbb {Z}$
:
 $$ \begin{align*} & E_{A,B,M}=\{(m,a,b)\in\mathbb{N}\times\mathbb{Z}\times\mathbb{Z}:a\in A\land b\in B\land m\in M\land m\mid a-b\}\\ & F_{f}=\{(m,a,b)\in\mathbb{N}\times\mathbb{Z}\times\mathbb{Z}:|a|<|f(b)|\}. \end{align*} $$
$$ \begin{align*} & E_{A,B,M}=\{(m,a,b)\in\mathbb{N}\times\mathbb{Z}\times\mathbb{Z}:a\in A\land b\in B\land m\in M\land m\mid a-b\}\\ & F_{f}=\{(m,a,b)\in\mathbb{N}\times\mathbb{Z}\times\mathbb{Z}:|a|<|f(b)|\}. \end{align*} $$
We prove that the family
![]() $\{E_{A,B,M}:A\in \mathcal {F},B\in \mathcal {G},M\in \mathcal {M}\}\cup \{F_{f}:f:\mathbb {Z}\rightarrow \mathbb {Z}\mbox { is non-}\mathcal {G}\mbox {-constant}\}$
has the finite intersection property.
$\{E_{A,B,M}:A\in \mathcal {F},B\in \mathcal {G},M\in \mathcal {M}\}\cup \{F_{f}:f:\mathbb {Z}\rightarrow \mathbb {Z}\mbox { is non-}\mathcal {G}\mbox {-constant}\}$
has the finite intersection property.
![]() $\{E_{A,B,M}:A\in \mathcal {F},B\in \mathcal {G},M\in \mathcal {M}\}$
is closed for finite intersections. So let
$\{E_{A,B,M}:A\in \mathcal {F},B\in \mathcal {G},M\in \mathcal {M}\}$
is closed for finite intersections. So let
![]() $A\in \mathcal {F}$
,
$A\in \mathcal {F}$
,
![]() $B\in \mathcal {G}$
,
$B\in \mathcal {G}$
,
![]() $M\in \mathcal {M}$
and let
$M\in \mathcal {M}$
and let
![]() $f_{1},f_{2},\dots ,f_{k}:\mathbb {Z}\rightarrow \mathbb {Z}$
be non-
$f_{1},f_{2},\dots ,f_{k}:\mathbb {Z}\rightarrow \mathbb {Z}$
be non-
![]() $\mathcal {G}$
-constant. Since
$\mathcal {G}$
-constant. Since
![]() $M\hspace {-0.1cm}\uparrow \in \mathcal {M}\cap \mathcal {U}$
,
$M\hspace {-0.1cm}\uparrow \in \mathcal {M}\cap \mathcal {U}$
,
 $\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
implies
$\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}-\mathcal {G}$
implies
![]() $M\hspace {-0.1cm}\uparrow \in \mathcal {F}-\mathcal {G}$
. Hence
$M\hspace {-0.1cm}\uparrow \in \mathcal {F}-\mathcal {G}$
. Hence
![]() $\{n\in \mathbb {Z}:n-M\hspace {-0.1cm}\uparrow \in \mathcal {G}\}\in \mathcal {F}$
. Let
$\{n\in \mathbb {Z}:n-M\hspace {-0.1cm}\uparrow \in \mathcal {G}\}\in \mathcal {F}$
. Let
![]() $a\in A\cap \{n\in \mathbb {Z}:n-M\hspace {-0.1cm}\uparrow \in \mathcal {G}\}$
. This means that
$a\in A\cap \{n\in \mathbb {Z}:n-M\hspace {-0.1cm}\uparrow \in \mathcal {G}\}$
. This means that
![]() $B_{1}:=B\cap (a-M\hspace {-0.1cm}\uparrow )\in \mathcal {G}$
. Hence there is
$B_{1}:=B\cap (a-M\hspace {-0.1cm}\uparrow )\in \mathcal {G}$
. Hence there is
![]() $b\in B_{1}$
such that
$b\in B_{1}$
such that
![]() $|f_{i}(b)|>|a|$
for all
$|f_{i}(b)|>|a|$
for all
![]() $i\leq k$
(otherwise
$i\leq k$
(otherwise
![]() $\{b\in B_{1}:f_{i}(b)=j\}\in \mathcal {G}$
for some
$\{b\in B_{1}:f_{i}(b)=j\}\in \mathcal {G}$
for some
![]() $i\leq k$
and some
$i\leq k$
and some
![]() $-a\leq j\leq a$
, a contradiction with the assumption that
$-a\leq j\leq a$
, a contradiction with the assumption that
![]() $f_{i}$
is non-
$f_{i}$
is non-
![]() $\mathcal {G}$
-constant). Since
$\mathcal {G}$
-constant). Since
![]() $b\in a-M\hspace {-0.1cm}\uparrow $
, there is
$b\in a-M\hspace {-0.1cm}\uparrow $
, there is
![]() $m\in M$
such that
$m\in M$
such that
![]() $m\mid a-b$
, so
$m\mid a-b$
, so
 $(m,a,b)\in E_{A,B,M}\cap F_{f_{1}}\cap F_{f_{2}}\cap \dots \cap F_{f_{k}}$
.
$(m,a,b)\in E_{A,B,M}\cap F_{f_{1}}\cap F_{f_{2}}\cap \dots \cap F_{f_{k}}$
.
Now, since we are working with a
![]() $\mathfrak{c}^+$
-enlargement, there is
$\mathfrak{c}^+$
-enlargement, there is
 $$ \begin{align*}(m,x,y)\in\bigcap_{A\in\mathcal{F},B\in\mathcal{G},M\in\mathcal{M}}{{{\hspace{-0.0001pt}}}^{*}\hspace{-0.5mm}E}_{A,B,M}\;\;\cap\bigcap_{f\mbox{ non-}\mathcal{G}\mbox{-constant}}{{{\hspace{-0.0001pt}}}^{*}\hspace{-0.5mm}F}_{f}.\end{align*} $$
$$ \begin{align*}(m,x,y)\in\bigcap_{A\in\mathcal{F},B\in\mathcal{G},M\in\mathcal{M}}{{{\hspace{-0.0001pt}}}^{*}\hspace{-0.5mm}E}_{A,B,M}\;\;\cap\bigcap_{f\mbox{ non-}\mathcal{G}\mbox{-constant}}{{{\hspace{-0.0001pt}}}^{*}\hspace{-0.5mm}F}_{f}.\end{align*} $$
This means that
![]() $m\in \mu (\mathcal {M})$
,
$m\in \mu (\mathcal {M})$
,
![]() $x\in \mu (\mathcal {F})$
,
$x\in \mu (\mathcal {F})$
,
![]() $y\in \mu (\mathcal {G})$
and
$y\in \mu (\mathcal {G})$
and
![]() $m\mid x-y$
. Also, for every non-
$m\mid x-y$
. Also, for every non-
![]() $\mathcal {G}$
-constant
$\mathcal {G}$
-constant
![]() $f:\mathbb {Z}\rightarrow \mathbb {Z}$
,
$f:\mathbb {Z}\rightarrow \mathbb {Z}$
,
![]() $|{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)|>|x|$
, so
$|{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}f}(y)|>|x|$
, so
![]() $(x,y)$
is a tensor pair. ⊣
$(x,y)$
is a tensor pair. ⊣
Unfortunately, we do not even know whether
![]() $\equiv _{\mathcal {M}}$
is an equivalence relation on
$\equiv _{\mathcal {M}}$
is an equivalence relation on
![]() $\beta \mathbb {Z}$
, which makes it unconvenient to work with. Therefore in the next section we introduce a stronger relation with much nicer properties.
$\beta \mathbb {Z}$
, which makes it unconvenient to work with. Therefore in the next section we introduce a stronger relation with much nicer properties.
5 Strong congruence
To better explain the forthcoming definition of congruence, we begin with a few simple lemmas. Recall that
![]() $MAX$
is the class of ultrafilters
$MAX$
is the class of ultrafilters
![]() $\hspace {1mm}\widetilde {\mid }$
-divisible by all others.
$\hspace {1mm}\widetilde {\mid }$
-divisible by all others.
Lemma 5.1. Let
![]() $x,y\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
and
$x,y\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
and
![]() $v(x)=v(y)$
. Then
$v(x)=v(y)$
. Then
![]() $m\mid x-y$
for all
$m\mid x-y$
for all
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $x-y\in \mu (MAX)$
.
$x-y\in \mu (MAX)$
.
Proof For each
![]() $m\in \mathbb {N}$
, let
$m\in \mathbb {N}$
, let
![]() $h_{m}$
be the function defined in §2. Then
$h_{m}$
be the function defined in §2. Then
![]() ${{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}(x)\in \mathbb {Z}_{m}$
for all
${{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}(x)\in \mathbb {Z}_{m}$
for all
![]() $x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
. By Proposition 3.1,
$x\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
. By Proposition 3.1,
 $v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}(x))=\widetilde {h_{m}}(v(x))=\widetilde {h_{m}}(v(y))=v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}(y))$
, so x and y have the same residue modulo m.
$v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}(x))=\widetilde {h_{m}}(v(x))=\widetilde {h_{m}}(v(y))=v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}(y))$
, so x and y have the same residue modulo m.
Ultrafilters from
![]() $MAX$
are those divisible by all
$MAX$
are those divisible by all
![]() $m\in \mathbb {N}$
. Hence
$m\in \mathbb {N}$
. Hence
![]() $\mu (MAX)$
consists exactly of nonstandard numbers divisible by all
$\mu (MAX)$
consists exactly of nonstandard numbers divisible by all
![]() $m\in \mathbb {N}$
, so the second statement follows directly from the first. ⊣
$m\in \mathbb {N}$
, so the second statement follows directly from the first. ⊣
By Theorem 2.8, the assumption of Lemma 5.1 can not be relaxed to
![]() $v(x)=_{\sim } v(y)$
: there are
$v(x)=_{\sim } v(y)$
: there are
![]() $=_{\sim }$
-equivalent ultrafilters giving different residues modulo some
$=_{\sim }$
-equivalent ultrafilters giving different residues modulo some
![]() $m\in \mathbb {N}$
.
$m\in \mathbb {N}$
.
Lemma 5.2. Let
![]() $x,y\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
,
$x,y\in {{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}$
,
![]() $v(x)=v(y)$
and
$v(x)=v(y)$
and
![]() $m\in S_{k}(\mathbb {N})$
. Then
$m\in S_{k}(\mathbb {N})$
. Then
![]() $m\mid S_{k}(x)-S_{k}(y)$
.
$m\mid S_{k}(x)-S_{k}(y)$
.
Proof By Lemma 5.1,
![]() $(\forall m\in \mathbb {N})m\mid x-y$
. By Transfer,
$(\forall m\in \mathbb {N})m\mid x-y$
. By Transfer,
![]() $(\forall m\in S_{k}(\mathbb {N}))m\mid S_{k}(x)-S_{k}(y)$
. ⊣
$(\forall m\in S_{k}(\mathbb {N}))m\mid S_{k}(x)-S_{k}(y)$
. ⊣
Thus, for every
![]() $m\in S_{k}(\mathbb {N})$
, all the numbers from
$m\in S_{k}(\mathbb {N})$
, all the numbers from
![]() $\mu (\mathcal {F})\cap S_{k}[{{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}]$
have the same residue modulo m. We will use this to establish a strengthening of congruence modulo
$\mu (\mathcal {F})\cap S_{k}[{{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}\mathbb {Z}}]$
have the same residue modulo m. We will use this to establish a strengthening of congruence modulo
![]() $\mathcal {M}\in \beta \mathbb {N}$
.
$\mathcal {M}\in \beta \mathbb {N}$
.
Definition 5.3. Ultrafilters
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
are strongly congruent modulo
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
are strongly congruent modulo
![]() $\mathcal {M}\in \beta \mathbb {N}$
if, in every
$\mathcal {M}\in \beta \mathbb {N}$
if, in every
![]() $\omega $
-hyperenlargement,
$\omega $
-hyperenlargement,
We write
![]() $\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
.
$\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
.
We easily get the following equivalent condition.
Lemma 5.4.
![]() $\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
implies that in every
$\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
implies that in every
![]() $\omega $
-hyperenlargement
$\omega $
-hyperenlargement
Proof Let
![]() $x_{0}\in \mu (\mathcal {F})$
and
$x_{0}\in \mu (\mathcal {F})$
and
![]() $y_{0}\in \mu (\mathcal {G})$
be such that
$y_{0}\in \mu (\mathcal {G})$
be such that
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{0}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{0}$
, and let
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{0}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{0}$
, and let
![]() $x\in \mu (\mathcal {F})$
and
$x\in \mu (\mathcal {F})$
and
![]() $y\in \mu (\mathcal {G})$
be arbitrary. By Lemma 5.2,
$y\in \mu (\mathcal {G})$
be arbitrary. By Lemma 5.2,
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{0}$
and
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{0}$
and
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{0}$
, so
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{0}$
, so
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
as well. ⊣
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
as well. ⊣
To avoid constant repetition, in each of the proofs in the rest of the paper it will be understood that we are working in an
![]() $\omega $
-hyperenlargement (a single superstructure extension which is a
$\omega $
-hyperenlargement (a single superstructure extension which is a
![]() $\mathfrak{c}^+$
-enlargement).
$\mathfrak{c}^+$
-enlargement).
It will follow from Lemmas 6.5, 6.3, and 4.2 that
![]() $\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
implies
$\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
implies
![]() $\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
. For now we prove that
$\mathcal {F}\equiv _{\mathcal {M}}\mathcal {G}$
. For now we prove that
![]() $\equiv _{m}^{s}$
for
$\equiv _{m}^{s}$
for
![]() $m\in \mathbb {N}$
also coincides with the congruence relation modulo integer (from §2).
$m\in \mathbb {N}$
also coincides with the congruence relation modulo integer (from §2).
Lemma 5.5. If
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $\mathcal {F},\ \mathcal {G}\in \beta \mathbb {Z}$
,
$\mathcal {F},\ \mathcal {G}\in \beta \mathbb {Z}$
,
![]() $\mathcal {F}\equiv _{m}^{s}\mathcal {G}$
holds if and only if
$\mathcal {F}\equiv _{m}^{s}\mathcal {G}$
holds if and only if
![]() $\mathcal {F}\equiv _{m}\mathcal {G}$
.
$\mathcal {F}\equiv _{m}\mathcal {G}$
.
Proof The only element of
![]() $\mu _{1}(m)$
is m itself. Let
$\mu _{1}(m)$
is m itself. Let
![]() $x\in \mu (\mathcal {F})$
and
$x\in \mu (\mathcal {F})$
and
![]() $y\in \mu (\mathcal {G})$
be such that
$y\in \mu (\mathcal {G})$
be such that
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
; then
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
; then
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
and
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
and
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
have the same residue modulo m:
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
have the same residue modulo m:
![]() ${{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x})={{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
. Then, by Propositions 3.1 and 3.7,
${{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x})={{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
. Then, by Propositions 3.1 and 3.7,
 $\widetilde {h_{m}}(\mathcal {F})=v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}))=v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}))=\widetilde {h_{m}}(\mathcal {G})$
, so
$\widetilde {h_{m}}(\mathcal {F})=v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}))=v({{{\hspace {-0.0001pt}}}^{\bullet }\hspace {-0.5mm}h}_{m}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}))=\widetilde {h_{m}}(\mathcal {G})$
, so
![]() $\mathcal {F}\equiv _{m}\mathcal {G}$
. The other implication is proved similarly, using Lemma 5.4. ⊣
$\mathcal {F}\equiv _{m}\mathcal {G}$
. The other implication is proved similarly, using Lemma 5.4. ⊣
Lemma 5.6.
![]() $\equiv _{\mathcal {M}}^{s}$
is an equivalence relation on the set
$\equiv _{\mathcal {M}}^{s}$
is an equivalence relation on the set
![]() $\beta \mathbb {Z}$
.
$\beta \mathbb {Z}$
.
Proof Reflexivity and symmetry are obvious from the definition. So let
![]() $\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
and
$\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
and
![]() $\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {H}$
. By Lemma 5.4, for any
$\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {H}$
. By Lemma 5.4, for any
![]() $m\in \mu _{1}(\mathcal {M})$
,
$m\in \mu _{1}(\mathcal {M})$
,
![]() $x\in \mu (\mathcal {F})$
,
$x\in \mu (\mathcal {F})$
,
![]() $y\in \mu (\mathcal {G})$
and
$y\in \mu (\mathcal {G})$
and
![]() $z\in \mu (\mathcal {H})$
holds
$z\in \mu (\mathcal {H})$
holds
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
and
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
and
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}$
. Then
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}$
. Then
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}$
, so
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}$
, so
![]() $\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {H}$
. ⊣
$\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {H}$
. ⊣
Theorem 5.7. Let
![]() $\mathcal {M}\in \beta \mathbb {N}$
.
$\mathcal {M}\in \beta \mathbb {N}$
.
![]() $\equiv _{\mathcal {M}}^{s}$
is compatible with operations
$\equiv _{\mathcal {M}}^{s}$
is compatible with operations
![]() $+$
and
$+$
and
![]() $\cdot $
in
$\cdot $
in
![]() $\beta \mathbb {Z}$
:
$\beta \mathbb {Z}$
:
-
(a)
 $\mathcal {F}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}$
and
$\mathcal {F}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}$
and
 $\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {G}_{2}$
imply
$\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {G}_{2}$
imply
 $\mathcal {F}_{1}+\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}+\mathcal {G}_{2}$
and
$\mathcal {F}_{1}+\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}+\mathcal {G}_{2}$
and -
(b)
 $\mathcal {F}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}$
and
$\mathcal {F}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}$
and
 $\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {G}_{2}$
imply
$\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {G}_{2}$
imply
 $\mathcal {F}_{1}\cdot \mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}\cdot \mathcal {G}_{2}$
.
$\mathcal {F}_{1}\cdot \mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}\cdot \mathcal {G}_{2}$
.
Proof Let
![]() $m\in \mu _{1}(\mathcal {M})$
,
$m\in \mu _{1}(\mathcal {M})$
,
![]() $x_{1}\in \mu _{1}(\mathcal {F}_{1})$
,
$x_{1}\in \mu _{1}(\mathcal {F}_{1})$
,
![]() $x_{2}\in \mu _{1}(\mathcal {F}_{2})$
,
$x_{2}\in \mu _{1}(\mathcal {F}_{2})$
,
![]() $y_{1}\in \mu _{1}(\mathcal {G}_{1})$
and
$y_{1}\in \mu _{1}(\mathcal {G}_{1})$
and
![]() $y_{2}\in \mu _{1}(\mathcal {G}_{2})$
. It follows from Proposition 3.7 that
$y_{2}\in \mu _{1}(\mathcal {G}_{2})$
. It follows from Proposition 3.7 that
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}\in \mu (\mathcal {G}_{1})$
and
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}\in \mu (\mathcal {G}_{1})$
and
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}\in \mu (\mathcal {G}_{2})$
. By the assumptions we have
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}\in \mu (\mathcal {G}_{2})$
. By the assumptions we have
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}$
and
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}$
and
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}}$
.
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}}$
.
-
(a) By Proposition 3.9
 $x_{1}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}\in \mu (\mathcal {F}_{1}+\mathcal {G}_{1})$
and
$x_{1}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}\in \mu (\mathcal {F}_{1}+\mathcal {G}_{1})$
and
 $x_{2}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}\in \mu (\mathcal {F}_{2}+\mathcal {G}_{2})$
. From the above conclusions follows
$x_{2}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}\in \mu (\mathcal {F}_{2}+\mathcal {G}_{2})$
. From the above conclusions follows
 $m\mid ({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}})-({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}})$
, i.e.,
$m\mid ({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}})-({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}})$
, i.e.,
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{1}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1})-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{2}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2})$
. Since we started with arbitrary
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{1}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1})-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{2}+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2})$
. Since we started with arbitrary
 $m\in \mu _{1}(\mathcal {M})$
, this means that
$m\in \mu _{1}(\mathcal {M})$
, this means that
 $\mathcal {F}_{1}+\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}+\mathcal {G}_{2}$
.
$\mathcal {F}_{1}+\mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}+\mathcal {G}_{2}$
. -
(b) By Proposition 3.9
 $x_{1}\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}\in \mu (\mathcal {F}_{1}\cdot \mathcal {G}_{1})$
and
$x_{1}\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}\in \mu (\mathcal {F}_{1}\cdot \mathcal {G}_{1})$
and
 $x_{2}\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}\in \mu (\mathcal {F}_{2}\cdot \mathcal {G}_{2})$
. We have
$x_{2}\cdot {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}\in \mu (\mathcal {F}_{2}\cdot \mathcal {G}_{2})$
. We have
 $m\mid ({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}){{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}$
and
$m\mid ({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}){{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}$
and
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}})$
. Hence
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}})$
. Hence
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}}$
, i.e.,
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{1}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1}}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}_{2}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2}}$
, i.e.,
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{1}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1})-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{2}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2})$
, so
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{1}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{1})-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x_{2}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}_{2})$
, so
 $\mathcal {F}_{1}\cdot \mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}\cdot \mathcal {G}_{2}$
.⊣
$\mathcal {F}_{1}\cdot \mathcal {G}_{1}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{2}\cdot \mathcal {G}_{2}$
.⊣
The following simple result is a version of a well-known fact ([Reference Puritz9], Corollary 8.3).
Lemma 5.8.
-
(a) Every
 $\mathcal {F}\in MAX$
is strongly congruent to zero modulo any ultrafilter and
$\mathcal {F}\in MAX$
is strongly congruent to zero modulo any ultrafilter and -
(b) for every
 $\mathcal {F}\in \beta \mathbb {Z}\setminus \mathbb {Z}$
,
$\mathcal {F}\in \beta \mathbb {Z}\setminus \mathbb {Z}$
,
 $\mathcal {F}-\mathcal {F}\in MAX$
.
$\mathcal {F}-\mathcal {F}\in MAX$
.
Proof
-
(a) For any
 $\mathcal {F}\in MAX$
and any
$\mathcal {F}\in MAX$
and any
 $x\in \mu (\mathcal {F})$
,
$x\in \mu (\mathcal {F})$
,
 $(\forall m\in \mathbb {N})m\mid x$
implies by Transfer
$(\forall m\in \mathbb {N})m\mid x$
implies by Transfer
 $(\forall m\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}})m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
, which gives us
$(\forall m\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}})m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
, which gives us
 $\mathcal {F}\equiv _{\mathcal {M}} 0$
for any
$\mathcal {F}\equiv _{\mathcal {M}} 0$
for any
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(b) We will show that
 $A\in \mathcal {F}-\mathcal {F}$
for all
$A\in \mathcal {F}-\mathcal {F}$
for all
 $A\in \mathcal {U}_{Z}$
(see the two paragraphs following Proposition 3.2). Let
$A\in \mathcal {U}_{Z}$
(see the two paragraphs following Proposition 3.2). Let
 $m\in A$
be arbitrary. Then there is
$m\in A$
be arbitrary. Then there is
 $r\in \mathbb {Z}_{m}$
such that
$r\in \mathbb {Z}_{m}$
such that
 $m\mathbb {Z}+r\in \mathcal {F}$
, so since
$m\mathbb {Z}+r\in \mathcal {F}$
, so since
 $m\mathbb {Z}\subseteq -A$
, it follows that
$m\mathbb {Z}\subseteq -A$
, it follows that
 $n-A\in \mathcal {F}$
for all
$n-A\in \mathcal {F}$
for all
 $n\in m\mathbb {Z}+r$
. Thus
$n\in m\mathbb {Z}+r$
. Thus
 $m\mathbb {Z}+r\subseteq \{n\in \mathbb {Z}:n-A\in \mathcal {F}\}$
, so
$m\mathbb {Z}+r\subseteq \{n\in \mathbb {Z}:n-A\in \mathcal {F}\}$
, so
 $\{n\in \mathbb {Z}:n-A\in \mathcal {F}\}\in \mathcal {F}$
, which means that
$\{n\in \mathbb {Z}:n-A\in \mathcal {F}\}\in \mathcal {F}$
, which means that
 $A\in \mathcal {F}-\mathcal {F}$
.⊣
$A\in \mathcal {F}-\mathcal {F}$
.⊣
Let us also note, regarding the lemma above, that
![]() $\mathcal {F}=_{\sim }\mathcal {G}$
is not enough to conclude that
$\mathcal {F}=_{\sim }\mathcal {G}$
is not enough to conclude that
![]() $\mathcal {F}-\mathcal {G}\in MAX$
. By Theorem 2.8 there are
$\mathcal {F}-\mathcal {G}\in MAX$
. By Theorem 2.8 there are
![]() $\mathcal {F},\ \mathcal {G}\in \beta \mathbb {N}$
and
$\mathcal {F},\ \mathcal {G}\in \beta \mathbb {N}$
and
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $\mathcal {F}=_{\sim }\mathcal {G}$
but
$\mathcal {F}=_{\sim }\mathcal {G}$
but
![]() $\mathcal {F}\not \equiv _{m}\mathcal {G}$
, say
$\mathcal {F}\not \equiv _{m}\mathcal {G}$
, say
![]() $\mathcal {F}\equiv _{m}r_{1}$
and
$\mathcal {F}\equiv _{m}r_{1}$
and
![]() $\mathcal {G}\equiv _{m}r_{2}$
for some
$\mathcal {G}\equiv _{m}r_{2}$
for some
![]() $r_{1}<m$
and
$r_{1}<m$
and
![]() $r_{2}<m$
. From Proposition 2.1 we get
$r_{2}<m$
. From Proposition 2.1 we get
![]() $\mathcal {F}-\mathcal {G}\equiv _{m} r_{1}-r_{2}\neq 0$
, so
$\mathcal {F}-\mathcal {G}\equiv _{m} r_{1}-r_{2}\neq 0$
, so
![]() $m\nmid \mathcal {F}-\mathcal {G}$
.
$m\nmid \mathcal {F}-\mathcal {G}$
.
Definition 5.9. A family
![]() $\{\mathcal {F}_{i}:i\in I\}$
of ultrafilters is a complete residue system modulo
$\{\mathcal {F}_{i}:i\in I\}$
of ultrafilters is a complete residue system modulo
![]() $\mathcal {M}\in \beta \mathbb {N}$
if it contains exactly one element of every equivalence class of strong congruence modulo
$\mathcal {M}\in \beta \mathbb {N}$
if it contains exactly one element of every equivalence class of strong congruence modulo
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
As an application of the above results, we have an ultrafilter version of a well-known theorem on complete residue systems in
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Theorem 5.10. If
![]() $\{\mathcal {F}_{i}:i\in I\}$
is a complete residue system modulo
$\{\mathcal {F}_{i}:i\in I\}$
is a complete residue system modulo
![]() $\mathcal {M}\in \beta \mathbb {N}$
then, for every
$\mathcal {M}\in \beta \mathbb {N}$
then, for every
![]() $\mathcal {G}\in \beta \mathbb {N}$
,
$\mathcal {G}\in \beta \mathbb {N}$
,
![]() $\{\mathcal {F}_{i}+\mathcal {G}:i\in I\}$
and
$\{\mathcal {F}_{i}+\mathcal {G}:i\in I\}$
and
![]() $\{\mathcal {G}+\mathcal {F}_{i}:i\in I\}$
are complete residue systems modulo
$\{\mathcal {G}+\mathcal {F}_{i}:i\in I\}$
are complete residue systems modulo
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof We need to show that in
![]() $\mathcal {R}=\{\mathcal {F}_{i}+\mathcal {G}:i\in I\}$
no two ultrafilters are congruent modulo
$\mathcal {R}=\{\mathcal {F}_{i}+\mathcal {G}:i\in I\}$
no two ultrafilters are congruent modulo
![]() $\mathcal {M}$
, and that each congruence class has a representative in
$\mathcal {M}$
, and that each congruence class has a representative in
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
First assume
![]() $\mathcal {F}_{i}+\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}+\mathcal {G}$
for some
$\mathcal {F}_{i}+\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}+\mathcal {G}$
for some
![]() $i,j\in I$
,
$i,j\in I$
,
![]() $i\neq j$
. By Theorem 5.7
$i\neq j$
. By Theorem 5.7
![]() $\mathcal {F}_{i}+\mathcal {G}-\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}+\mathcal {G}-\mathcal {G}$
. By Lemma 5.8
$\mathcal {F}_{i}+\mathcal {G}-\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}+\mathcal {G}-\mathcal {G}$
. By Lemma 5.8
![]() $\mathcal {F}_{i}=\mathcal {F}_{i}+0\equiv _{\mathcal {M}}^{s}\mathcal {F}_{i}+\mathcal {G}-\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}+\mathcal {G}-\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}$
, a contradiction.
$\mathcal {F}_{i}=\mathcal {F}_{i}+0\equiv _{\mathcal {M}}^{s}\mathcal {F}_{i}+\mathcal {G}-\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}+\mathcal {G}-\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {F}_{j}$
, a contradiction.
Now let
![]() $\mathcal {H}\in \beta \mathbb {N}$
be arbitrary. There is
$\mathcal {H}\in \beta \mathbb {N}$
be arbitrary. There is
![]() $i\in I$
such that
$i\in I$
such that
![]() $\mathcal {F}_{i}\equiv _{\mathcal {M}}^{s}\mathcal {H}-\mathcal {G}$
. Using Theorem 5.7 and Lemma 5.8 again we get
$\mathcal {F}_{i}\equiv _{\mathcal {M}}^{s}\mathcal {H}-\mathcal {G}$
. Using Theorem 5.7 and Lemma 5.8 again we get
![]() $\mathcal {F}_{i}+\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {H}-\mathcal {G}+\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {H}$
.
$\mathcal {F}_{i}+\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {H}-\mathcal {G}+\mathcal {G}\equiv _{\mathcal {M}}^{s}\mathcal {H}$
.
The proof that
![]() $\{\mathcal {G}+\mathcal {F}_{i}:i\in I\}$
is a complete residue system modulo
$\{\mathcal {G}+\mathcal {F}_{i}:i\in I\}$
is a complete residue system modulo
![]() $\mathcal {M}\in \beta \mathbb {N}$
is analogous. ⊣
$\mathcal {M}\in \beta \mathbb {N}$
is analogous. ⊣
6 Strong divisibility
It is natural to ask: which ultrafilters are strongly congruent to zero modulo some
![]() $\mathcal {M}\in \beta \mathbb {N}$
? Are those exactly the ultrafilters divisible by
$\mathcal {M}\in \beta \mathbb {N}$
? Are those exactly the ultrafilters divisible by
![]() $\mathcal {M}$
? For example, we saw in Lemma 5.8 that
$\mathcal {M}$
? For example, we saw in Lemma 5.8 that
![]() $\hspace {1mm}\widetilde {\mid }$
-maximal ultrafilters are always strongly congruent to zero. In general, the above question leads us to the following definition.
$\hspace {1mm}\widetilde {\mid }$
-maximal ultrafilters are always strongly congruent to zero. In general, the above question leads us to the following definition.
Definition 6.1. Let
![]() $\mathcal {M}\in \beta \mathbb {N}$
and
$\mathcal {M}\in \beta \mathbb {N}$
and
![]() $\mathcal {F}\in \beta \mathbb {Z}$
.
$\mathcal {F}\in \beta \mathbb {Z}$
.
![]() $\mathcal {F}$
is strongly divisible by
$\mathcal {F}$
is strongly divisible by
![]() $\mathcal {M}$
if, in every
$\mathcal {M}$
if, in every
![]() $\omega $
-hyperenlargement,
$\omega $
-hyperenlargement,
We write
![]() $\mathcal {M}\mid ^{s}\mathcal {F}$
.
$\mathcal {M}\mid ^{s}\mathcal {F}$
.
In the same way as Lemma 5.4, we get a seemingly stronger condition.
Lemma 6.2.
![]() $\mathcal {M}\mid ^{s}\mathcal {F}$
implies that in every
$\mathcal {M}\mid ^{s}\mathcal {F}$
implies that in every
![]() $\omega $
-hyperenlargement
$\omega $
-hyperenlargement
Proposition 3.2 easily implies the following.
Lemma 6.3. For all
![]() $\mathcal {M}\in \beta \mathbb {N}$
and
$\mathcal {M}\in \beta \mathbb {N}$
and
![]() $\mathcal {F}\in \beta \mathbb {Z}$
,
$\mathcal {F}\in \beta \mathbb {Z}$
,
![]() $\mathcal {M}\mid ^{s}\mathcal {F}$
implies
$\mathcal {M}\mid ^{s}\mathcal {F}$
implies
 $\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}$
.
$\mathcal {M}\hspace {1mm}\widetilde {\mid }\hspace {1mm}\mathcal {F}$
.
It is tempting to try to prove the reverse implication; unfortunately this is not true, as we will now see.
Lemma 6.4. No
![]() $\mathbb {N}$
-free ultrafilter has any
$\mathbb {N}$
-free ultrafilter has any
![]() $\mid ^{s}$
-divisors.
$\mid ^{s}$
-divisors.
Proof Assume the opposite, that an
![]() $\mathbb {N}$
-free ultrafilter
$\mathbb {N}$
-free ultrafilter
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\mid ^{s}$
-divisible by some
$\mid ^{s}$
-divisible by some
![]() $\mathcal {G}$
. Then
$\mathcal {G}$
. Then
![]() $\mathcal {G}$
is also
$\mathcal {G}$
is also
![]() $\mathbb {N}$
-free, and for any
$\mathbb {N}$
-free, and for any
![]() $x\in \mu (\mathcal {F})$
holds
$x\in \mu (\mathcal {F})$
holds
![]() $(\forall m\in \mathbb {N})m\nmid x$
. By Transfer
$(\forall m\in \mathbb {N})m\nmid x$
. By Transfer
![]() $(\forall m\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}})m\nmid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
, a contradiction with
$(\forall m\in {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}\mathbb {N}})m\nmid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
, a contradiction with
![]() $\mathcal {G}\mid ^{s}\mathcal {F}$
. ⊣
$\mathcal {G}\mid ^{s}\mathcal {F}$
. ⊣
Thus, this notion of divisibility is too strong to be our main divisibility relation, but it has some properties that are in good accordance with the strong congruence relation and operations on
![]() $\beta \mathbb {N}$
.
$\beta \mathbb {N}$
.
Lemma 6.4 also says that
![]() $\mid ^{s}$
is not reflexive:
$\mid ^{s}$
is not reflexive:
![]() $\mathbb {N}$
-free ultrafilters are not divisible by themselves. It is, however, transitive: let
$\mathbb {N}$
-free ultrafilters are not divisible by themselves. It is, however, transitive: let
![]() $\mathcal {F}\mid ^{s}\mathcal {G}$
and
$\mathcal {F}\mid ^{s}\mathcal {G}$
and
![]() $\mathcal {G}\mid ^{s}\mathcal {H}$
. Let
$\mathcal {G}\mid ^{s}\mathcal {H}$
. Let
![]() $x\in \mu _{1}(\mathcal {F})$
,
$x\in \mu _{1}(\mathcal {F})$
,
![]() $y\in \mu _{1}(\mathcal {G})$
and
$y\in \mu _{1}(\mathcal {G})$
and
![]() $z\in \mu _{1}(\mathcal {H})$
be arbitrary. Then
$z\in \mu _{1}(\mathcal {H})$
be arbitrary. Then
![]() $x\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
and
$x\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
and
![]() $y\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}$
. Hence
$y\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}$
. Hence
![]() ${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}}$
, so
${{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}}$
, so
![]() $x\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}}$
, which suffices for
$x\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}z}}$
, which suffices for
![]() $\mathcal {F}\mid ^{s}\mathcal {H}$
.
$\mathcal {F}\mid ^{s}\mathcal {H}$
.
Lemma 6.5.
![]() $\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
if and only if
$\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
if and only if
![]() $\mathcal {M}\mid ^{s}\mathcal {F}-\mathcal {G}$
.
$\mathcal {M}\mid ^{s}\mathcal {F}-\mathcal {G}$
.
Proof (
![]() $\Rightarrow $
) Let
$\Rightarrow $
) Let
![]() $m\in \mu _{1}(\mathcal {M})$
be arbitrary and let
$m\in \mu _{1}(\mathcal {M})$
be arbitrary and let
![]() $x\in \mu _{1}(\mathcal {F})$
and
$x\in \mu _{1}(\mathcal {F})$
and
![]() $y\in \mu _{1}(\mathcal {G})$
be such that
$y\in \mu _{1}(\mathcal {G})$
be such that
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
. By Proposition 3.7,
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
. By Proposition 3.7,
![]() $v(y)=v({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
so, by Lemma 5.2,
$v(y)=v({{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
so, by Lemma 5.2,
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
. It follows that
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
. It follows that
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
, i.e.,
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
, i.e.,
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
. On the other hand, since
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
. On the other hand, since
![]() $-y\in \mu (-\mathcal {G})$
, by Lemma 3.8 and Proposition 3.9,
$-y\in \mu (-\mathcal {G})$
, by Lemma 3.8 and Proposition 3.9,
![]() $x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}=x+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}-y)\in \mu (\mathcal {F}-\mathcal {G})$
, so
$x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}=x+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}-y)\in \mu (\mathcal {F}-\mathcal {G})$
, so
![]() $\mathcal {M}\mid ^{s}\mathcal {F}-\mathcal {G}$
.
$\mathcal {M}\mid ^{s}\mathcal {F}-\mathcal {G}$
.
(
![]() $\Leftarrow $
) Let
$\Leftarrow $
) Let
![]() $m\in \mu _{1}(\mathcal {M})$
,
$m\in \mu _{1}(\mathcal {M})$
,
![]() $x\in \mu _{1}(\mathcal {F})$
and
$x\in \mu _{1}(\mathcal {F})$
and
![]() $y\in \mu _{1}(\mathcal {G})$
be arbitrary. Then
$y\in \mu _{1}(\mathcal {G})$
be arbitrary. Then
![]() $x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\in \mu (\mathcal {F}-\mathcal {G})$
so, by Lemma 6.2,
$x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}\in \mu (\mathcal {F}-\mathcal {G})$
so, by Lemma 6.2,
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
. By Lemma 5.2 again we have
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
. By Lemma 5.2 again we have
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
, so
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
, so
![]() $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
, meaning that
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}-{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}$
, meaning that
![]() $\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
. ⊣
$\mathcal {F}\equiv _{\mathcal {M}}^{s}\mathcal {G}$
. ⊣
Theorem 6.6. Let
![]() $\mathcal {M}\in \beta \mathbb {N}$
and
$\mathcal {M}\in \beta \mathbb {N}$
and
![]() $\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
.
$\mathcal {F},\mathcal {G}\in \beta \mathbb {Z}$
.
-
(a)
 $\mathcal {M}\mid ^{s}\mathcal {F}$
and
$\mathcal {M}\mid ^{s}\mathcal {F}$
and
 $\mathcal {M}\mid ^{s}\mathcal {G}$
imply
$\mathcal {M}\mid ^{s}\mathcal {G}$
imply
 $\mathcal {M}\mid ^{s}\mathcal {F}+\mathcal {G}$
;
$\mathcal {M}\mid ^{s}\mathcal {F}+\mathcal {G}$
; -
(b)
 $\mathcal {M}\mid ^{s}\mathcal {F}$
implies
$\mathcal {M}\mid ^{s}\mathcal {F}$
implies
 $\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
; and
$\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
; and -
(c)
 $\mathcal {M}\mid ^{s}\mathcal {G}$
implies
$\mathcal {M}\mid ^{s}\mathcal {G}$
implies
 $\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
.
$\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
.
Proof Let
![]() $m\in \mu _{1}(\mathcal {M})$
,
$m\in \mu _{1}(\mathcal {M})$
,
![]() $x\in \mu _{1}(\mathcal {F})$
and
$x\in \mu _{1}(\mathcal {F})$
and
![]() $y\in \mu _{1}(\mathcal {G})$
.
$y\in \mu _{1}(\mathcal {G})$
.
-
(a) By assumptions
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
and
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
and
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
. Hence
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
. Hence
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
, and therefore
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x+{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
, and therefore
 $\mathcal {M}\mid ^{s}\mathcal {F}+\mathcal {G}$
.
$\mathcal {M}\mid ^{s}\mathcal {F}+\mathcal {G}$
. -
(b) Now we have
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
, which suffices for
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}$
, which suffices for
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
i.e.
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
i.e.
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
, so
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}(}x{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y})$
, so
 $\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
.
$\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
. -
(c) By Lemma 6.2
 $\mathcal {M}\mid ^{s}\mathcal {G}$
implies
$\mathcal {M}\mid ^{s}\mathcal {G}$
implies
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
, so again
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
, so again
 $m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
and
$m\mid {{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}x}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}{{{\hspace {-0.0001pt}}}^{*}\hspace {-0.5mm}y}}$
and
 $\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
.⊣
$\mathcal {M}\mid ^{s}\mathcal {F}\cdot \mathcal {G}$
.⊣
Let us remind ourselves of the definitions of other three divisibility relations from [Reference Šobot11]:
 $$ \begin{align*} \mathcal{G}\mid_{L}\mathcal{F} &\ \mbox{iff}\ (\exists\mathcal{H}\in\beta \mathbb{N})\mathcal{F}=\mathcal{H}\cdot\mathcal{G},\\ \mathcal{G}\mid_{R}\mathcal{F} &\ \mbox{iff}\ (\exists\mathcal{H}\in\beta \mathbb{N})\mathcal{F}=\mathcal{G}\cdot\mathcal{H},\\ \mathcal{G}\mid_{M}\mathcal{F} &\ \mbox{iff}\ (\exists\mathcal{H}_{1},\mathcal{H}_{2}\in\beta \mathbb{N})\mathcal{F}=\mathcal{H}_{1}\cdot\mathcal{G}\cdot\mathcal{H}_{2}. \end{align*} $$
$$ \begin{align*} \mathcal{G}\mid_{L}\mathcal{F} &\ \mbox{iff}\ (\exists\mathcal{H}\in\beta \mathbb{N})\mathcal{F}=\mathcal{H}\cdot\mathcal{G},\\ \mathcal{G}\mid_{R}\mathcal{F} &\ \mbox{iff}\ (\exists\mathcal{H}\in\beta \mathbb{N})\mathcal{F}=\mathcal{G}\cdot\mathcal{H},\\ \mathcal{G}\mid_{M}\mathcal{F} &\ \mbox{iff}\ (\exists\mathcal{H}_{1},\mathcal{H}_{2}\in\beta \mathbb{N})\mathcal{F}=\mathcal{H}_{1}\cdot\mathcal{G}\cdot\mathcal{H}_{2}. \end{align*} $$
What is the place of
![]() $\mid ^{s}$
(restricted to
$\mid ^{s}$
(restricted to
![]() $\beta \mathbb {N}\times \beta \mathbb {N}$
) among these relations? Like all the others, its restriction to
$\beta \mathbb {N}\times \beta \mathbb {N}$
) among these relations? Like all the others, its restriction to
![]() $\mathbb {N}\times \mathbb {N}$
is just the usual divisibility relation (Lemma 5.5). We already saw that
$\mathbb {N}\times \mathbb {N}$
is just the usual divisibility relation (Lemma 5.5). We already saw that
 $\mid ^{s}\subset \hspace {1mm}\widetilde {\mid }$
. We will show that this is the only inclusion that can be established:
$\mid ^{s}\subset \hspace {1mm}\widetilde {\mid }$
. We will show that this is the only inclusion that can be established:

First, why
![]() $\mid _{L}\not \subseteq \mid ^{s}$
? Let
$\mid _{L}\not \subseteq \mid ^{s}$
? Let
![]() $\mathcal {P},\mathcal {Q}\in \beta \mathbb {N}\setminus \mathbb {N}$
be
$\mathcal {P},\mathcal {Q}\in \beta \mathbb {N}\setminus \mathbb {N}$
be
![]() $\hspace {1mm}\widetilde {\mid }$
-prime and let
$\hspace {1mm}\widetilde {\mid }$
-prime and let
![]() $\mathcal {F}=\mathcal {P}\cdot \mathcal {Q}$
. Then
$\mathcal {F}=\mathcal {P}\cdot \mathcal {Q}$
. Then
![]() $\mathcal {Q}\mid _{L}\mathcal {F}$
but, by Lemma 6.4,
$\mathcal {Q}\mid _{L}\mathcal {F}$
but, by Lemma 6.4,
![]() $\mathcal {Q}\nmid^{\hspace{1pt}s}\mathcal {F}$
. Analogously we conclude that
$\mathcal {Q}\nmid^{\hspace{1pt}s}\mathcal {F}$
. Analogously we conclude that
![]() $\mid _{R}\not \subseteq \mid ^{s}$
.
$\mid _{R}\not \subseteq \mid ^{s}$
.
That
![]() $\mid ^{s}\subseteq \mid _{M}$
does not hold either can be seen by considering maximal classes of these two orders. By [Reference Šobot13], Theorem 4.1, the
$\mid ^{s}\subseteq \mid _{M}$
does not hold either can be seen by considering maximal classes of these two orders. By [Reference Šobot13], Theorem 4.1, the
![]() $\mid _{M}$
-maximal ultrafilters are exactly those in the smallest ideal
$\mid _{M}$
-maximal ultrafilters are exactly those in the smallest ideal
![]() $K(\beta \mathbb {N},\cdot )$
. On the other hand, the class of
$K(\beta \mathbb {N},\cdot )$
. On the other hand, the class of
![]() $\mid ^{s}$
-maximal ultrafilters is exactly
$\mid ^{s}$
-maximal ultrafilters is exactly
![]() $MAX$
by Lemmas 5.8 and 6.3. But
$MAX$
by Lemmas 5.8 and 6.3. But
![]() $MAX$
is a proper superset of
$MAX$
is a proper superset of
![]() $K(\beta \mathbb {N},\cdot )$
; we postpone the detailed examination of this and other aspects of maximal ultrafilters until a projected sequel to this paper.
$K(\beta \mathbb {N},\cdot )$
; we postpone the detailed examination of this and other aspects of maximal ultrafilters until a projected sequel to this paper.
7 Final remarks and questions
Even after finding, in §4, several equivalent conditions for
![]() $\equiv _{\mathcal {M}}$
, we were not able to answer the following.
$\equiv _{\mathcal {M}}$
, we were not able to answer the following.
Question 7.1. Is
![]() $\equiv _{\mathcal {M}}$
an equivalence relation?
$\equiv _{\mathcal {M}}$
an equivalence relation?
Not being able to prove that it is presents a big drawback for using this relation, which seems to be the most natural extension of the congruence relation to
![]() $\beta \mathbb {N}$
.
$\beta \mathbb {N}$
.
Some more properties of our relations could be proved if we worked with
![]() $\mathfrak{c}^+$
-saturated nonstandard extensions. This is a stronger condition than being a
$\mathfrak{c}^+$
-saturated nonstandard extensions. This is a stronger condition than being a
![]() $\mathfrak{c}^+$
-enlargement:
$\mathfrak{c}^+$
-enlargement:
![]() $(V(Y),*)$
is
$(V(Y),*)$
is
![]() $\kappa $
-saturated if every family F of internal sets in
$\kappa $
-saturated if every family F of internal sets in
![]() $V(Y)$
with the finite intersection property such that
$V(Y)$
with the finite intersection property such that
![]() $|F|<\kappa $
has nonempty intersection. To Proposition 3.2 one can add two more equivalent conditions (see [Reference Šobot14], Theorem 3.4):
$|F|<\kappa $
has nonempty intersection. To Proposition 3.2 one can add two more equivalent conditions (see [Reference Šobot14], Theorem 3.4):
-
(i) In every
 $\mathfrak{c}^+$
-saturated extension
$\mathfrak{c}^+$
-saturated extension
 $V(Y)$
, for every
$V(Y)$
, for every
 $x\in \mu (\mathcal {F})$
there is
$x\in \mu (\mathcal {F})$
there is
 $y\in \mu (\mathcal {G})$
such that
$y\in \mu (\mathcal {G})$
such that
 $x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
;
$x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
; -
(ii) In every
 $\mathfrak{c}^+$
-saturated extension
$\mathfrak{c}^+$
-saturated extension
 $V(Y)$
, for every
$V(Y)$
, for every
 $y\in \mu (\mathcal {G})$
there is
$y\in \mu (\mathcal {G})$
there is
 $x\in \mu (\mathcal {F})$
such that
$x\in \mu (\mathcal {F})$
such that
 $x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
.
$x{{{\hspace {-0.0001pt}}}^{*}\hspace {-1mm}\mid } y$
.
However, Proposition 3.4 does not hold for
![]() $\mathfrak{c}^+$
-saturation in place of
$\mathfrak{c}^+$
-saturation in place of
![]() $\mathfrak{c}^+$
-enlargement: see [Reference Luperi Baglini7], page 74. So to use the equivalents (iv) and (v) we would have to answer the following question.
$\mathfrak{c}^+$
-enlargement: see [Reference Luperi Baglini7], page 74. So to use the equivalents (iv) and (v) we would have to answer the following question.
Question 7.2. Is it possible to construct a
![]() $\mathfrak{c}^+$
-saturated
$\mathfrak{c}^+$
-saturated
![]() $\omega $
-hyperextension of
$\omega $
-hyperextension of
![]() $\mathbb {Z}$
?
$\mathbb {Z}$
?
Acknowledgments
The author acknowledges financial support of the Science Fund of the Republic of Serbia (call PROMIS, project CLOUDS, grant no. 6062228) and Ministry of Education, Science and Technological Development of the Republic of Serbia (grant no. 451-03-68/2020-14/200125).
The author wishes to thank the referee for careful reading of the manuscript.