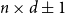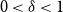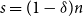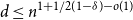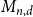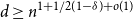1. Introduction
Compressed sensing is a modern technique of data acquisition, which is at the intersection of mathematics, electrical engineering, computer science, and physics, and has grown tremendously in recent years. Mathematically, we define an unknown signal as a vector
![]() $\boldsymbol{{x}}\in \mathbb{R}^d$
, and we have access to linear measurements: that is, for any vector
$\boldsymbol{{x}}\in \mathbb{R}^d$
, and we have access to linear measurements: that is, for any vector
![]() $\boldsymbol{{a}}\in \mathbb{R}^d$
, we have access to
$\boldsymbol{{a}}\in \mathbb{R}^d$
, we have access to
![]() $\boldsymbol{{a}}\cdot \boldsymbol{{x}}=\sum _{i=1}^da_ix_i$
. In particular, if
$\boldsymbol{{a}}\cdot \boldsymbol{{x}}=\sum _{i=1}^da_ix_i$
. In particular, if
![]() $\boldsymbol{{a}}^{(1)},\ldots \boldsymbol{{a}}^{(n)}\in \mathbb{R}^d$
are the measurements we make, then we have an access to the vector
$\boldsymbol{{a}}^{(1)},\ldots \boldsymbol{{a}}^{(n)}\in \mathbb{R}^d$
are the measurements we make, then we have an access to the vector
![]() $\boldsymbol{{b}}\;:\!=\;A\boldsymbol{{x}}$
, where
$\boldsymbol{{b}}\;:\!=\;A\boldsymbol{{x}}$
, where
 \begin{equation*} A\;:\!=\;\begin {pmatrix} - & \quad\boldsymbol{{a}}^{(1)} & \quad-\\ & \;\;\;\vdots & \\ -& \quad\boldsymbol{{a}}^{(n)} & \quad-\\ \end {pmatrix}. \end{equation*}
\begin{equation*} A\;:\!=\;\begin {pmatrix} - & \quad\boldsymbol{{a}}^{(1)} & \quad-\\ & \;\;\;\vdots & \\ -& \quad\boldsymbol{{a}}^{(n)} & \quad-\\ \end {pmatrix}. \end{equation*}
The tasks of compressed sensing are:
![]() $(i)$
to recover
$(i)$
to recover
![]() $\boldsymbol{{x}}$
from
$\boldsymbol{{x}}$
from
![]() $A$
and
$A$
and
![]() $\boldsymbol{{b}}$
as accurately as possible, and
$\boldsymbol{{b}}$
as accurately as possible, and
![]() $(ii)$
doing so in an efficient way. In practice, one would like to recover a high dimensional signal (that is,
$(ii)$
doing so in an efficient way. In practice, one would like to recover a high dimensional signal (that is,
![]() $d$
is large) from as few measurements as possible (that is,
$d$
is large) from as few measurements as possible (that is,
![]() $n$
is small). In this regime, for an arbitrary vector
$n$
is small). In this regime, for an arbitrary vector
![]() $x\in \mathbb{R}^d$
the problem is ill-posed: for any given
$x\in \mathbb{R}^d$
the problem is ill-posed: for any given
![]() $\boldsymbol{{b}}$
, the solution of
$\boldsymbol{{b}}$
, the solution of
![]() $\boldsymbol{{b}}=A\boldsymbol{{x}}$
, if it exists, forms a (translation of) linear subspace of dimension at least
$\boldsymbol{{b}}=A\boldsymbol{{x}}$
, if it exists, forms a (translation of) linear subspace of dimension at least
![]() $d-n$
, and therefore there is no way to uniquely recover the original
$d-n$
, and therefore there is no way to uniquely recover the original
![]() $\boldsymbol{{x}}$
.
$\boldsymbol{{x}}$
.
A key quantity to look at to guarantee the success of (unique) recovery is the sparsity of the vector
![]() $\boldsymbol{{x}}$
, and we say that a vector is
$\boldsymbol{{x}}$
, and we say that a vector is
![]() $s$
-sparse if its support is of size at most
$s$
-sparse if its support is of size at most
![]() $s$
. That is, if
$s$
. That is, if
A neat observation is that having at most one
![]() $s$
-sparse solution to
$s$
-sparse solution to
![]() $A\boldsymbol{{x}}=\boldsymbol{{b}}$
for every
$A\boldsymbol{{x}}=\boldsymbol{{b}}$
for every
![]() $\boldsymbol{{b}}$
is equivalent to saying that
$\boldsymbol{{b}}$
is equivalent to saying that
![]() $A$
is
$A$
is
![]() $2s$
-robust (that is, every
$2s$
-robust (that is, every
![]() $2s$
columns of
$2s$
columns of
![]() $A$
are linearly independent). Indeed, if we have two
$A$
are linearly independent). Indeed, if we have two
![]() $s$
-sparse vectors
$s$
-sparse vectors
![]() $\boldsymbol{{x}}\neq \boldsymbol{{y}}$
such that
$\boldsymbol{{x}}\neq \boldsymbol{{y}}$
such that
![]() $A\boldsymbol{{x}}=A\boldsymbol{{y}}$
then
$A\boldsymbol{{x}}=A\boldsymbol{{y}}$
then
![]() $\boldsymbol{{x}}-\boldsymbol{{y}}$
is a nonzero
$\boldsymbol{{x}}-\boldsymbol{{y}}$
is a nonzero
![]() $2s$
-sparse vector in the kernel of
$2s$
-sparse vector in the kernel of
![]() $A$
. For the other direction, if there is a nonzero
$A$
. For the other direction, if there is a nonzero
![]() $2s$
-sparse vector in the kernel of
$2s$
-sparse vector in the kernel of
![]() $A$
, one can split its support into two disjoint sets of size at most
$A$
, one can split its support into two disjoint sets of size at most
![]() $s$
each and consider the vectors restricted to these sets, one of which is multiplied by
$s$
each and consider the vectors restricted to these sets, one of which is multiplied by
![]() $-1$
.
$-1$
.
If we take
![]() $A$
to be a random Gaussian matrix
$A$
to be a random Gaussian matrix
![]() $A$
(or any other matrix drawn from some ‘nice’ continuous distribution), then we clearly have that with probability one
$A$
(or any other matrix drawn from some ‘nice’ continuous distribution), then we clearly have that with probability one
![]() $A$
is
$A$
is
![]() $s$
-robust for
$s$
-robust for
![]() $n=s$
and any
$n=s$
and any
![]() $d\in \mathbb{N}$
(and in particular, one can uniquely recover
$d\in \mathbb{N}$
(and in particular, one can uniquely recover
![]() $s/2$
-sparse vectors). Moreover, in their seminal work, Candes and Tao [Reference Candes and Tao3] showed that it is possible to efficiently reconstruct
$s/2$
-sparse vectors). Moreover, in their seminal work, Candes and Tao [Reference Candes and Tao3] showed that it is possible to efficiently reconstruct
![]() $\boldsymbol{{x}}$
with very high accuracy by solving a simple linear programme if we take
$\boldsymbol{{x}}$
with very high accuracy by solving a simple linear programme if we take
![]() $n=O(s\log\!(d/s))$
.
$n=O(s\log\!(d/s))$
.
In this paper, we are interested in the compressed sensing problem with integer-valued measurement matrices and with entries of magnitude at most
![]() $k$
. Integer-valued measurement matrices have found applications in measuring gene regulatory expressions, wireless communications, and natural images [Reference Abdi, Fekri and Zhang1, Reference Eldar, Haimovich and Rossi4, Reference Haseyama, He and Ogawa12], and they are quick to generate and easy to store in practice [Reference Iwen13, Reference Jiang, Liu, Xia and Zheng14]. Under this setting, for integer-valued signal
$k$
. Integer-valued measurement matrices have found applications in measuring gene regulatory expressions, wireless communications, and natural images [Reference Abdi, Fekri and Zhang1, Reference Eldar, Haimovich and Rossi4, Reference Haseyama, He and Ogawa12], and they are quick to generate and easy to store in practice [Reference Iwen13, Reference Jiang, Liu, Xia and Zheng14]. Under this setting, for integer-valued signal
![]() $\boldsymbol{{x}}$
, we can have exact recovery even if we allow some noise
$\boldsymbol{{x}}$
, we can have exact recovery even if we allow some noise
![]() $\boldsymbol{{e}}$
with
$\boldsymbol{{e}}$
with
![]() $\|\boldsymbol{{e}}\|_{\infty }\lt 1/2$
(for more details, see [Reference Fukshansky, Needell and Sudakov10]).
$\|\boldsymbol{{e}}\|_{\infty }\lt 1/2$
(for more details, see [Reference Fukshansky, Needell and Sudakov10]).
The first step is to understand when the compressed sensing problem is well-posed for given
![]() $s,n, k$
, and
$s,n, k$
, and
![]() $d$
. Namely, for which values of
$d$
. Namely, for which values of
![]() $s,n,k$
and
$s,n,k$
and
![]() $d$
does an
$d$
does an
![]() $s$
-robust
$s$
-robust
![]() $n\times d$
integer-valued matrix with entries in
$n\times d$
integer-valued matrix with entries in
![]() $\{-k,\ldots, k\}$
exist? For
$\{-k,\ldots, k\}$
exist? For
![]() $s=n$
, observe that if
$s=n$
, observe that if
![]() $d\geq (2k+1)^2n$
, then by the pigeonhole principle, one can find
$d\geq (2k+1)^2n$
, then by the pigeonhole principle, one can find
![]() $n$
columns for which their first two rows are proportional and therefore are not linearly independent. In particular, we have
$n$
columns for which their first two rows are proportional and therefore are not linearly independent. In particular, we have
![]() $d=O_k(n)$
. In [Reference Fukshansky, Needell and Sudakov10], Fukshansky, Needell, and Sudakov showed that there exists an
$d=O_k(n)$
. In [Reference Fukshansky, Needell and Sudakov10], Fukshansky, Needell, and Sudakov showed that there exists an
![]() $s$
-robust
$s$
-robust
![]() $A$
with
$A$
with
![]() $d=\Omega (\sqrt{k} n)$
, using the result of Bourgain, Vu and Wood [Reference Bourgain, Vu and Wood2] on the singularity of discrete random matrices (in fact, the more recent result by Tikhomirov [Reference Tikhomirov17] gives a better bound for
$d=\Omega (\sqrt{k} n)$
, using the result of Bourgain, Vu and Wood [Reference Bourgain, Vu and Wood2] on the singularity of discrete random matrices (in fact, the more recent result by Tikhomirov [Reference Tikhomirov17] gives a better bound for
![]() $k=1$
). Konyagin and Sudakov [Reference Konyagin and Sudakov15] improved the upper bound to
$k=1$
). Konyagin and Sudakov [Reference Konyagin and Sudakov15] improved the upper bound to
![]() $d=O(k\sqrt{\log k}n)$
, and they gave a deterministic construction of
$d=O(k\sqrt{\log k}n)$
, and they gave a deterministic construction of
![]() $A$
when
$A$
when
![]() $d\geq \frac{1}{2} k^{n/(n-1)}\gt n$
.
$d\geq \frac{1}{2} k^{n/(n-1)}\gt n$
.
When
![]() $1\leq s\leq n-1$
and
$1\leq s\leq n-1$
and
![]() $k=2$
, Fukshansky and Hsu [Reference Fukshansky and Hsu9] gave a deterministic construction such that
$k=2$
, Fukshansky and Hsu [Reference Fukshansky and Hsu9] gave a deterministic construction such that
![]() $d\geq \left (\frac{n+2}{2}\right )^{1+\frac{2}{3s-2}}$
. When
$d\geq \left (\frac{n+2}{2}\right )^{1+\frac{2}{3s-2}}$
. When
![]() $s=o(\!\log n)$
, this implies we can take
$s=o(\!\log n)$
, this implies we can take
![]() $d=\omega (n)$
. This result hints that if we allow
$d=\omega (n)$
. This result hints that if we allow
![]() $s$
to be ‘separated away’ from
$s$
to be ‘separated away’ from
![]() $n$
, then one could take
$n$
, then one could take
![]() $d$
to be ‘very large’. A natural and nontrivial step to understanding the
$d$
to be ‘very large’. A natural and nontrivial step to understanding the
![]() $s$
-robustness property of matrices is to investigate the typical behaviour. For convenience, we will focus on the case
$s$
-robustness property of matrices is to investigate the typical behaviour. For convenience, we will focus on the case
![]() $k=1$
(even though our argument can be generalized to all fixed
$k=1$
(even though our argument can be generalized to all fixed
![]() $k$
), and we define, for all
$k$
), and we define, for all
![]() $n,d\in \mathbb{N}$
, the random variable
$n,d\in \mathbb{N}$
, the random variable
![]() $M_{n,d}$
which corresponds to an
$M_{n,d}$
which corresponds to an
![]() $n\times d$
matrix with independent entries chosen uniformly from
$n\times d$
matrix with independent entries chosen uniformly from
![]() $\{\pm 1\}$
. For
$\{\pm 1\}$
. For
![]() $1\leq s\leq n$
, we would like to investigate the threshold behaviour of
$1\leq s\leq n$
, we would like to investigate the threshold behaviour of
![]() $M\;:\!=\;M_{n,d}$
with respect to being
$M\;:\!=\;M_{n,d}$
with respect to being
![]() $s$
-robust. That is, we wish to find some
$s$
-robust. That is, we wish to find some
![]() $d^*\;:\!=\;d(s,n)$
such that
$d^*\;:\!=\;d(s,n)$
such that
 \begin{equation*} \lim _{n\to \infty }\mathbb {P}[M \textrm { is }s\textrm {-robust}]= \begin {cases} 0 & d/d^*\rightarrow \infty \\ 1 & d/d^*\rightarrow 0. \end {cases} \end{equation*}
\begin{equation*} \lim _{n\to \infty }\mathbb {P}[M \textrm { is }s\textrm {-robust}]= \begin {cases} 0 & d/d^*\rightarrow \infty \\ 1 & d/d^*\rightarrow 0. \end {cases} \end{equation*}
It is trivial to show (deterministically) that if
![]() $s=n$
and
$s=n$
and
![]() $M$
is
$M$
is
![]() $s$
-robust, then
$s$
-robust, then
![]() $d\leq 2n$
. What if we allow
$d\leq 2n$
. What if we allow
![]() $s$
to be ‘separated away’ from
$s$
to be ‘separated away’ from
![]() $n$
? That is, what if
$n$
? That is, what if
![]() $s=(1-\delta )n$
for some
$s=(1-\delta )n$
for some
![]() $0\lt \delta \lt 1$
? It is not hard to show (and it follows from the proof of Lemma 3.3) that the probability for a random
$0\lt \delta \lt 1$
? It is not hard to show (and it follows from the proof of Lemma 3.3) that the probability for a random
![]() $n\times n$
matrix to have rank at least
$n\times n$
matrix to have rank at least
![]() $(1-\delta )n$
is at least
$(1-\delta )n$
is at least
![]() $1-2^{-\Omega (\delta ^2n^2)}$
. Therefore, one could think that a typical
$1-2^{-\Omega (\delta ^2n^2)}$
. Therefore, one could think that a typical
![]() $M_{n,d}$
might be
$M_{n,d}$
might be
![]() $(1-\delta )n$
-robust for some
$(1-\delta )n$
-robust for some
![]() $d=2^{n^{1-o(1)}}$
. This turns out to be wrong as we show in the following simple theorem:
$d=2^{n^{1-o(1)}}$
. This turns out to be wrong as we show in the following simple theorem:
Theorem 1.1.
For any fixed
![]() $0\lt \delta \lt 1$
there exists
$0\lt \delta \lt 1$
there exists
![]() $C\gt 0$
such that for sufficiently large
$C\gt 0$
such that for sufficiently large
![]() $n\in \mathbb{N}$
the following holds. If
$n\in \mathbb{N}$
the following holds. If
![]() $s= (1-\delta )n$
and
$s= (1-\delta )n$
and
![]() $d\ge Cn^{1+1/(1-\delta )}$
, then every
$d\ge Cn^{1+1/(1-\delta )}$
, then every
![]() $\pm 1$
$\pm 1$
![]() $n\times d$
matrix
$n\times d$
matrix
![]() $M$
is not
$M$
is not
![]() $s$
-robust.
$s$
-robust.
Proof. Given any
![]() $s/2$
-subset of column vectors
$s/2$
-subset of column vectors
![]() $\boldsymbol{{v}}_1,\ldots,\boldsymbol{{v}}_{s/2}\in \{\pm 1\}^n$
of
$\boldsymbol{{v}}_1,\ldots,\boldsymbol{{v}}_{s/2}\in \{\pm 1\}^n$
of
![]() $M$
, by Spencer’s ‘six standard deviations suffice’ [Reference Spencer16], there exist some
$M$
, by Spencer’s ‘six standard deviations suffice’ [Reference Spencer16], there exist some
![]() $x_1,\ldots,x_{s/2} \in \{\pm 1\}$
for which
$x_1,\ldots,x_{s/2} \in \{\pm 1\}$
for which
![]() $\|\sum _{i=1}^{s/2}x_i\boldsymbol{{v}}_i\|_{\infty }\leq C'\sqrt{n}$
for a universal constant
$\|\sum _{i=1}^{s/2}x_i\boldsymbol{{v}}_i\|_{\infty }\leq C'\sqrt{n}$
for a universal constant
![]() $C'\gt 0$
(a simple Chernoff bound suffices if one is willing to lose a
$C'\gt 0$
(a simple Chernoff bound suffices if one is willing to lose a
![]() $\sqrt{\log n}$
factor). Fix such a combination
$\sqrt{\log n}$
factor). Fix such a combination
![]() $\sum _{i=1}^{s/2}x_i\boldsymbol{{v}}_i$
for each
$\sum _{i=1}^{s/2}x_i\boldsymbol{{v}}_i$
for each
![]() $s/2$
-subset of column vectors. Since there are at most
$s/2$
-subset of column vectors. Since there are at most
![]() $\left (3C'\sqrt{n}\right )^{n}$
integer-valued vectors in the box
$\left (3C'\sqrt{n}\right )^{n}$
integer-valued vectors in the box
![]() $[\!-\!C'\sqrt{n},C'\sqrt{n}]^n$
, and since
$[\!-\!C'\sqrt{n},C'\sqrt{n}]^n$
, and since
 \begin{equation*}\binom {d}{s/2}\geq \left (\frac {d}{s}\right )^{s/2} = \left (\frac {Cn^{1/(1-\delta )}}{1-\delta }\right )^{(1-\delta )n/2} \gt \left (3C'\sqrt {n}\right )^{n},\end{equation*}
\begin{equation*}\binom {d}{s/2}\geq \left (\frac {d}{s}\right )^{s/2} = \left (\frac {Cn^{1/(1-\delta )}}{1-\delta }\right )^{(1-\delta )n/2} \gt \left (3C'\sqrt {n}\right )^{n},\end{equation*}
by the pigeonhole principle, as long as
![]() $C$
is large enough, there are two
$C$
is large enough, there are two
![]() $s/2$
-subsets whose corresponding combination of column vectors are the same. Subtracting the corresponding combination of column vectors leads to a nonzero
$s/2$
-subsets whose corresponding combination of column vectors are the same. Subtracting the corresponding combination of column vectors leads to a nonzero
![]() $s$
-sparse kernel vector of
$s$
-sparse kernel vector of
![]() $M$
(since the indices of two
$M$
(since the indices of two
![]() $s/2$
-subsets are not the same), proving the result.
$s/2$
-subsets are not the same), proving the result.![]()
In our main result, we determine the (typical) asymptotic behaviour up to a window of
![]() $(\!\log n)^{\omega (1)}$
.
$(\!\log n)^{\omega (1)}$
.
Theorem 1.2.
For any fixed
![]() $0\lt \delta \lt 1$
, let
$0\lt \delta \lt 1$
, let
![]() $n\in \mathbb{N}$
be sufficiently large, let
$n\in \mathbb{N}$
be sufficiently large, let
![]() $s= (1-\delta )n$
, and let
$s= (1-\delta )n$
, and let
![]() $\varepsilon =\omega (\!\log \log n/\log n)$
. We have that:
$\varepsilon =\omega (\!\log \log n/\log n)$
. We have that:
-
(1) If
 $d\leq n^{1+1/(2-2\delta )-\varepsilon }$
then with high probability
$d\leq n^{1+1/(2-2\delta )-\varepsilon }$
then with high probability
 $M_{n,d}$
is
$M_{n,d}$
is
 $s$
-robust.
$s$
-robust. -
(2) If
 $d\geq n^{1+1/(2-2\delta )+\varepsilon }$
then with high probability
$d\geq n^{1+1/(2-2\delta )+\varepsilon }$
then with high probability
 $M_{n,d}$
is not
$M_{n,d}$
is not
 $s$
-robust.
$s$
-robust.
We believe that by optimizing our bounds/similar methods, one would be able to push the bounds in Theorem 1.2 up to a constant factor of
![]() $n^{1+1/(2-2\delta )}$
(though we did not focus on this aspect). It would be interesting to obtain the
$n^{1+1/(2-2\delta )}$
(though we did not focus on this aspect). It would be interesting to obtain the
![]() $1+o(1)$
multiplicative threshold behaviour.
$1+o(1)$
multiplicative threshold behaviour.
2. Proof outline
We first outline the proof of Theorem 1.2. We will prove part (1) of Theorem 1.2 over
![]() $\mathbb{F}_p$
for some prime
$\mathbb{F}_p$
for some prime
![]() $p=e^{\omega (\!\log ^2 n)}$
to be chosen later (a stronger statement). Our strategy, at large, is to generate
$p=e^{\omega (\!\log ^2 n)}$
to be chosen later (a stronger statement). Our strategy, at large, is to generate
![]() $M$
as
$M$
as
 \begin{equation*}M=\begin {pmatrix} M_1 \\ M_2\end {pmatrix}\end{equation*}
\begin{equation*}M=\begin {pmatrix} M_1 \\ M_2\end {pmatrix}\end{equation*}
where
![]() $M_1=M_{n_1,d}$
and
$M_1=M_{n_1,d}$
and
![]() $M_2=M_{n_2,d}$
, with
$M_2=M_{n_2,d}$
, with
![]() $n_1\approx n$
and
$n_1\approx n$
and
![]() $n_2=o(n)$
. The proof consists of the following two phases:
$n_2=o(n)$
. The proof consists of the following two phases:
-
(1) Phase 1: Given any nonzero vector
 $\boldsymbol{{a}}\in \mathbb{F}_p^d$
, we let(2.1)where the
$\boldsymbol{{a}}\in \mathbb{F}_p^d$
, we let(2.1)where the \begin{equation} \rho _{\mathbb{F}_p}(\boldsymbol{{a}})=\max _{x\in \mathbb{F}_p}\mathbb{P}\left [\sum _{i=1}^da_i\xi _i=x\right ], \end{equation}
\begin{equation} \rho _{\mathbb{F}_p}(\boldsymbol{{a}})=\max _{x\in \mathbb{F}_p}\mathbb{P}\left [\sum _{i=1}^da_i\xi _i=x\right ], \end{equation}
 $\xi _i$
s are i.i.d. Rademacher random variables. In this phase, we will show that
$\xi _i$
s are i.i.d. Rademacher random variables. In this phase, we will show that-
(a)
 $M_1$
is with high probability such that for all nonzero
$M_1$
is with high probability such that for all nonzero
 $\boldsymbol{{a}}\in \mathbb{F}_p^d$
, if
$\boldsymbol{{a}}\in \mathbb{F}_p^d$
, if
 $|\textrm{supp}\,{\boldsymbol{{a}}}|\leq s\;:\!=\;(1-\delta )n$
and
$|\textrm{supp}\,{\boldsymbol{{a}}}|\leq s\;:\!=\;(1-\delta )n$
and
 $M_1\boldsymbol{{a}}=\textbf{0}$
, then
$M_1\boldsymbol{{a}}=\textbf{0}$
, then
 $\rho _{\mathbb{F}_p}(\boldsymbol{{a}})=e^{-\omega (\!\log ^2 n)}$
, and
$\rho _{\mathbb{F}_p}(\boldsymbol{{a}})=e^{-\omega (\!\log ^2 n)}$
, and -
(b)
 $M_1$
is with high probability such that every
$M_1$
is with high probability such that every
 $s$
-subset of its columns has rank
$s$
-subset of its columns has rank
 $s-o(s)$
.
$s-o(s)$
.
-
-
(2) Phase 2: Conditioned on the above properties, we will use the extra randomness of
 $M_2$
to show that for a specific set of
$M_2$
to show that for a specific set of
 $s$
columns, after exposing
$s$
columns, after exposing
 $M_2$
, the probability that it does not have full rank is
$M_2$
, the probability that it does not have full rank is
 $o\left (1/\binom{d}{s}\right )$
, and hence a simple union bound will give us the desired result.
$o\left (1/\binom{d}{s}\right )$
, and hence a simple union bound will give us the desired result.
In this strategy, it turns out that Phase 1(a) is the limiting factor, that is, ruling out structured kernel vectors.
For the proof of the upper bound in Theorem 1.2, we exploit this observation. We show using the second-moment method that it is highly likely that some
![]() $2\lfloor (1-\delta )n/2\rfloor$
columns sum to the zero vector (corresponding to an all
$2\lfloor (1-\delta )n/2\rfloor$
columns sum to the zero vector (corresponding to an all
![]() $1$
s, highly structured kernel vector).
$1$
s, highly structured kernel vector).
3. Proof of the lower bound in Theorem 1.2
In this section we prove Theorem 1.2. Let (say)
![]() $p\approx e^{\log ^3 n}$
be a prime, let
$p\approx e^{\log ^3 n}$
be a prime, let
![]() $d=n^{1+1/(2-2\delta )-\varepsilon }$
and
$d=n^{1+1/(2-2\delta )-\varepsilon }$
and
![]() $s=(1-\delta )n$
as given, and
$s=(1-\delta )n$
as given, and
![]() $n_1=(1-\beta )n$
where
$n_1=(1-\beta )n$
where
![]() $\beta =\omega (1/\log n)$
and
$\beta =\omega (1/\log n)$
and
![]() $\beta =o(\!\log \log n/\log n)$
. As described in Section 2, our proof consists of two phases, each of which will be handled separately.
$\beta =o(\!\log \log n/\log n)$
. As described in Section 2, our proof consists of two phases, each of which will be handled separately.
3.1 Phase 1: no sparse structured vectors in the kernel of
 $M_1$
$M_1$
Our first goal is to prove the following proposition.
Proposition 3.1.
![]() $M_{n_1,d}$
is with high probability such that for every
$M_{n_1,d}$
is with high probability such that for every
![]() $(1-\delta )n$
-sparse vector
$(1-\delta )n$
-sparse vector
![]() $\boldsymbol{{a}}\in \mathbb{F}_p^d\setminus \{\textbf{0}\}$
, if
$\boldsymbol{{a}}\in \mathbb{F}_p^d\setminus \{\textbf{0}\}$
, if
![]() $M_1\boldsymbol{{a}}=\textbf{0}$
then
$M_1\boldsymbol{{a}}=\textbf{0}$
then
![]() $\rho _{\mathbb{F}_p}(\boldsymbol{{a}})=e^{-\omega (\!\log ^2 n)}.$
$\rho _{\mathbb{F}_p}(\boldsymbol{{a}})=e^{-\omega (\!\log ^2 n)}.$
In order to prove the above proposition, we need some auxiliary results.
Lemma 3.2.
![]() $M_{n_1,d}$
is with high probability
$M_{n_1,d}$
is with high probability
![]() $n/\log ^4n$
-robust over
$n/\log ^4n$
-robust over
![]() $\mathbb{F}_p$
.
$\mathbb{F}_p$
.
Proof. Observe that for any
![]() $\boldsymbol{{a}}\in \mathbb{F}_p^d\setminus \{\textbf{0}\}$
we trivially have that
$\boldsymbol{{a}}\in \mathbb{F}_p^d\setminus \{\textbf{0}\}$
we trivially have that
![]() $\mathbb{P}[M_1\boldsymbol{{a}}=\textbf{0}]\leq 2^{-n_1}=2^{-\Theta (n)}$
. Since there are at most
$\mathbb{P}[M_1\boldsymbol{{a}}=\textbf{0}]\leq 2^{-n_1}=2^{-\Theta (n)}$
. Since there are at most
 \begin{equation*}\binom {d}{n/\log ^4n}p^{n/\log ^4n}\leq \left (\frac {edp\log ^4 n}{n}\right )^{n/\log ^4n}=2^{o(n)} \end{equation*}
\begin{equation*}\binom {d}{n/\log ^4n}p^{n/\log ^4n}\leq \left (\frac {edp\log ^4 n}{n}\right )^{n/\log ^4n}=2^{o(n)} \end{equation*}
![]() $n/\log ^4n$
-sparse vectors
$n/\log ^4n$
-sparse vectors
![]() $\boldsymbol{{a}}\in \mathbb{F}_p^d$
, by a simple union bound we obtain that the probability for such an
$\boldsymbol{{a}}\in \mathbb{F}_p^d$
, by a simple union bound we obtain that the probability for such an
![]() $\boldsymbol{{a}}$
to satisfy
$\boldsymbol{{a}}$
to satisfy
![]() $M_1\boldsymbol{{a}}=\textbf{0}$
is
$M_1\boldsymbol{{a}}=\textbf{0}$
is
![]() $o(1)$
. This completes the proof.
$o(1)$
. This completes the proof.![]()
In particular, by combining the above lemma with the Erdős-Littlewood-Offord inequality [Reference Erdös5], we conclude that if
![]() $\boldsymbol{{a}}\in \mathbb{F}_p^d$
is
$\boldsymbol{{a}}\in \mathbb{F}_p^d$
is
![]() $(1-\delta )n$
-sparse and
$(1-\delta )n$
-sparse and
![]() $M_1\boldsymbol{{a}}=\textbf{0}$
, then
$M_1\boldsymbol{{a}}=\textbf{0}$
, then
![]() $\rho _{\mathbb{F}_p}(\boldsymbol{{a}})=O(\!\log ^2 n/n^{1/2})$
. However, to prove Proposition 3.1, we need a stronger estimate.
$\rho _{\mathbb{F}_p}(\boldsymbol{{a}})=O(\!\log ^2 n/n^{1/2})$
. However, to prove Proposition 3.1, we need a stronger estimate.
The following lemma asserts that every subset of
![]() $s$
columns in
$s$
columns in
![]() $M_1$
has large rank. It will be crucial in Phase 2.
$M_1$
has large rank. It will be crucial in Phase 2.
Lemma 3.3.
Let
![]() $t = \omega (\!\log n)$
. Then, with high probability
$t = \omega (\!\log n)$
. Then, with high probability
![]() $M_1=M_{n_1,d}$
is such that every subset of
$M_1=M_{n_1,d}$
is such that every subset of
![]() $s$
columns contains at least
$s$
columns contains at least
![]() $s-t$
linearly independent columns.
$s-t$
linearly independent columns.
Proof. Consider the event that one such subset has rank at most
![]() $s-t$
. There are
$s-t$
. There are
![]() $\binom{d}{s}\le d^s\le n^n$
possible choices of columns. For each such choice, there are at most
$\binom{d}{s}\le d^s\le n^n$
possible choices of columns. For each such choice, there are at most
![]() $2^s\le 2^n$
ways to choose a spanning set of
$2^s\le 2^n$
ways to choose a spanning set of
![]() $r\le s-t$
columns. Such a subset has span containing at most
$r\le s-t$
columns. Such a subset has span containing at most
![]() $2^s$
many
$2^s$
many
![]() $\{\pm 1\}$
vectors (indeed, consider a full-rank
$\{\pm 1\}$
vectors (indeed, consider a full-rank
![]() $r\times r$
sub-block; any
$r\times r$
sub-block; any
![]() $\{\pm 1\}$
vector in the span of the columns is determined by its value on these
$\{\pm 1\}$
vector in the span of the columns is determined by its value on these
![]() $r$
coordinates), so the probability that the remaining at least
$r$
coordinates), so the probability that the remaining at least
![]() $t = \omega (\!\log n)$
columns are in the span is at most
$t = \omega (\!\log n)$
columns are in the span is at most
![]() $(2^s/2^{n_1})^t\le (2^{-(\delta -\beta )n})^t = o(n^{-n})$
. Taking a union bound, the result follows.
$(2^s/2^{n_1})^t\le (2^{-(\delta -\beta )n})^t = o(n^{-n})$
. Taking a union bound, the result follows.![]()
Next, we state a version of Halász’s inequality [Reference Halász11, Theorem 3] as well as a ‘counting inverse Littlewood-Offord theorem’ as was developed in [Reference Ferber, Jain, Luh and Samotij7].
Definition 3.4. Let
![]() $\boldsymbol{{a}}\in \mathbb{F}_p^n$
and
$\boldsymbol{{a}}\in \mathbb{F}_p^n$
and
![]() $k\in \mathbb{N}$
. We define
$k\in \mathbb{N}$
. We define
![]() $R_k^{\ast }(\boldsymbol{{a}})$
to be the number of solutions to
$R_k^{\ast }(\boldsymbol{{a}})$
to be the number of solutions to
with
![]() $|\{i_1,\ldots,i_{2k}\}|\gt 1.01k$
.
$|\{i_1,\ldots,i_{2k}\}|\gt 1.01k$
.
Theorem 3.5. ([Reference Ferber, Jain, Luh and Samotij7, Theorem 1.4]). Given an odd prime
![]() $p$
, integer
$p$
, integer
![]() $n$
, and vector a = (a 1, … , an) ∈
$n$
, and vector a = (a 1, … , an) ∈
![]() $\mathbb{F}_p^{n}\setminus \{\textbf{0}\}$
, suppose that an integer
$\mathbb{F}_p^{n}\setminus \{\textbf{0}\}$
, suppose that an integer
![]() $0\le k \le n/2$
and positive real
$0\le k \le n/2$
and positive real
![]() $L$
satisfy
$L$
satisfy
![]() $30L \le |\textrm{supp}{(\boldsymbol{{a}})}|$
and
$30L \le |\textrm{supp}{(\boldsymbol{{a}})}|$
and
![]() $80kL \le n$
. Then
$80kL \le n$
. Then
We denote
![]() $\boldsymbol{{b}} \subset \boldsymbol{{a}}$
if
$\boldsymbol{{b}} \subset \boldsymbol{{a}}$
if
![]() $\boldsymbol{{b}}$
is a subvector of
$\boldsymbol{{b}}$
is a subvector of
![]() $\boldsymbol{{a}}$
and let
$\boldsymbol{{a}}$
and let
![]() $| \boldsymbol{{b}}|$
be the size of the support of a vector
$| \boldsymbol{{b}}|$
be the size of the support of a vector
![]() $\boldsymbol{{b}}$
.
$\boldsymbol{{b}}$
.
Theorem 3.6. ([Reference Ferber, Jain, Luh and Samotij7, Theorem 1.7]). Let
![]() $p$
be a prime, let
$p$
be a prime, let
![]() $k, n \in \mathbb{N}$
,
$k, n \in \mathbb{N}$
,
![]() $s\in [n]$
and
$s\in [n]$
and
![]() $t\in [p]$
. Define
$t\in [p]$
. Define
![]() ${\boldsymbol{{B}}}_{k,m,\geq t}(s,d)$
as the following set:
${\boldsymbol{{B}}}_{k,m,\geq t}(s,d)$
as the following set:
 \begin{align*} \left \{\boldsymbol{{a}} \in \mathbb{F}_{p}^{d} \;:\; |\boldsymbol{{a}}|\leq s, \textrm{ and }R_k^{\ast }(\boldsymbol{{b}})\geq t\cdot \frac{2^{2k} \cdot |\boldsymbol{{b}}|^{2k}}{p} \text{ for every } \boldsymbol{{b}}\subseteq \boldsymbol{{a}} \text{ with } |\boldsymbol{{b}}|\geq m\right \}, \end{align*}
\begin{align*} \left \{\boldsymbol{{a}} \in \mathbb{F}_{p}^{d} \;:\; |\boldsymbol{{a}}|\leq s, \textrm{ and }R_k^{\ast }(\boldsymbol{{b}})\geq t\cdot \frac{2^{2k} \cdot |\boldsymbol{{b}}|^{2k}}{p} \text{ for every } \boldsymbol{{b}}\subseteq \boldsymbol{{a}} \text{ with } |\boldsymbol{{b}}|\geq m\right \}, \end{align*}
We have
We now are in position to prove Proposition 3.1. The proof is quite similar to the proofs in [Reference Ferber and Jain6–Reference Ferber, Luh and McKinley8].
Proof of Proposition
3.1. Let
![]() $k = \log ^3 n$
and
$k = \log ^3 n$
and
![]() $m = n/\log ^4 n, p\approx e^{\log ^3 n}$
.
$m = n/\log ^4 n, p\approx e^{\log ^3 n}$
.
First we use Lemma 3.2 to rule out vectors
![]() $\boldsymbol{{a}}$
with a support of size less than
$\boldsymbol{{a}}$
with a support of size less than
![]() $n/\log ^4n$
. Next, let (say)
$n/\log ^4n$
. Next, let (say)
![]() $L = n/\log ^{10}n$
and let
$L = n/\log ^{10}n$
and let
![]() $\sqrt{L}\leq t\leq p$
.
$\sqrt{L}\leq t\leq p$
.
Consider a fixed
![]() $\boldsymbol{{a}}\in{\boldsymbol{{B}}}_{k,m,\geq t}(s,d)\setminus{\boldsymbol{{B}}}_{k,m,\geq 2t}(s,d)$
and we wish to bound the probability that
$\boldsymbol{{a}}\in{\boldsymbol{{B}}}_{k,m,\geq t}(s,d)\setminus{\boldsymbol{{B}}}_{k,m,\geq 2t}(s,d)$
and we wish to bound the probability that
![]() $M_1\boldsymbol{{a}}=\textbf{0}$
. By definition, there is a set
$M_1\boldsymbol{{a}}=\textbf{0}$
. By definition, there is a set
![]() $S\subseteq \operatorname{supp}\!(\boldsymbol{{a}})$
of size at least
$S\subseteq \operatorname{supp}\!(\boldsymbol{{a}})$
of size at least
![]() $m$
such that
$m$
such that
Since the rows are independent and since
![]() $\rho _{\mathbb{F}_p}\!(\boldsymbol{{a}})\leq \rho _{\mathbb{F}_p}\!(\boldsymbol{{a}}|_S)$
, the probability that
$\rho _{\mathbb{F}_p}\!(\boldsymbol{{a}})\leq \rho _{\mathbb{F}_p}\!(\boldsymbol{{a}}|_S)$
, the probability that
![]() $M_1\boldsymbol{{a}}=\textbf{0}$
is at most
$M_1\boldsymbol{{a}}=\textbf{0}$
is at most
![]() $\rho _{\mathbb{F}_p}(\boldsymbol{{a}}|_S)^{n_1}$
. Furthermore, by Theorem 3.5 and the given conditions, which guarantee
$\rho _{\mathbb{F}_p}(\boldsymbol{{a}}|_S)^{n_1}$
. Furthermore, by Theorem 3.5 and the given conditions, which guarantee
![]() $30L\le m\le |\operatorname{supp}\!(\boldsymbol{{a}}|_S)|$
and
$30L\le m\le |\operatorname{supp}\!(\boldsymbol{{a}}|_S)|$
and
![]() $80kL\le m\le |S|$
, and by
$80kL\le m\le |S|$
, and by
![]() $\sqrt{L}\le t\le p$
, we have
$\sqrt{L}\le t\le p$
, we have
 \begin{align} \rho _{\mathbb{F}_p}(\boldsymbol{{a}}|_S)&\le \frac{1}{p}+C_{3.5}\frac{R_k^\ast (\boldsymbol{{a}}|_S) + ((40k)^{0.99}|S|^{1.01})^k}{2^{2k} |S|^{2k} L^{1/2}} + e^{-L}\notag \\ &\le \frac{1}{p} + \frac{2C_{3.5}t}{p\sqrt{L}} + \frac{10^k C_{3.5}}{L^{1/2}}\bigg (\frac{k}{|S|}\bigg )^{0.99k} + e^{-L}\notag \\ &\le \frac{Ct}{p\sqrt{L}} \end{align}
\begin{align} \rho _{\mathbb{F}_p}(\boldsymbol{{a}}|_S)&\le \frac{1}{p}+C_{3.5}\frac{R_k^\ast (\boldsymbol{{a}}|_S) + ((40k)^{0.99}|S|^{1.01})^k}{2^{2k} |S|^{2k} L^{1/2}} + e^{-L}\notag \\ &\le \frac{1}{p} + \frac{2C_{3.5}t}{p\sqrt{L}} + \frac{10^k C_{3.5}}{L^{1/2}}\bigg (\frac{k}{|S|}\bigg )^{0.99k} + e^{-L}\notag \\ &\le \frac{Ct}{p\sqrt{L}} \end{align}
for all sufficiently large
![]() $n$
by equation (3.1). All in all, taking a union bound over all the possible choices of
$n$
by equation (3.1). All in all, taking a union bound over all the possible choices of
![]() $\boldsymbol{{a}}$
(Theorem 3.6), and using the fact that
$\boldsymbol{{a}}$
(Theorem 3.6), and using the fact that
![]() $s= (1-\delta )n$
and
$s= (1-\delta )n$
and
![]() $n_1=(1-\beta )n$
with
$n_1=(1-\beta )n$
with
![]() $\beta =\omega (1/\log n)$
, we obtain the bound
$\beta =\omega (1/\log n)$
, we obtain the bound
 \begin{align*} \binom{d}{s}\left (\frac{m}{s}\right )^{\!2k-1} (1.01t)^{m-s}p^{s}\bigg (\frac{Ct}{p\sqrt{L}}\bigg )^{n_1} & \leq \left (\frac{ed}{s}\right )^{s}(1.01t)^{m}\left (\frac{p}{1.01t}\right )^{s}\bigg (\frac{Ct}{p\sqrt{L}}\bigg )^{(1-\beta )n}\\ & \leq \left (\frac{ed}{(1-\delta )n}\right )^{\!(1-\delta )n}\!2^{o(n)}\bigg (\frac{1.01 t}{p}\bigg )^{\!(\delta -\beta ) n}\!\left (\frac{C(\!\log n)^5}{\sqrt{n}}\right )^{\!(1-\beta )n}\\ &= o(1/p) \end{align*}
\begin{align*} \binom{d}{s}\left (\frac{m}{s}\right )^{\!2k-1} (1.01t)^{m-s}p^{s}\bigg (\frac{Ct}{p\sqrt{L}}\bigg )^{n_1} & \leq \left (\frac{ed}{s}\right )^{s}(1.01t)^{m}\left (\frac{p}{1.01t}\right )^{s}\bigg (\frac{Ct}{p\sqrt{L}}\bigg )^{(1-\beta )n}\\ & \leq \left (\frac{ed}{(1-\delta )n}\right )^{\!(1-\delta )n}\!2^{o(n)}\bigg (\frac{1.01 t}{p}\bigg )^{\!(\delta -\beta ) n}\!\left (\frac{C(\!\log n)^5}{\sqrt{n}}\right )^{\!(1-\beta )n}\\ &= o(1/p) \end{align*}
on the probability
![]() $M_1$
has such a kernel vector for sufficiently large
$M_1$
has such a kernel vector for sufficiently large
![]() $n$
. Here we used the bounds
$n$
. Here we used the bounds
![]() $d\leq n^{1+1/(2-2\delta )-\varepsilon }$
,
$d\leq n^{1+1/(2-2\delta )-\varepsilon }$
,
![]() $\varepsilon =\omega (\!\log \log n/\log n)$
and
$\varepsilon =\omega (\!\log \log n/\log n)$
and
![]() $\beta =o(\varepsilon )$
. Union bounding over all possible values of
$\beta =o(\varepsilon )$
. Union bounding over all possible values of
![]() $t$
shows that there is an appropriately small chance of having such a vector for any
$t$
shows that there is an appropriately small chance of having such a vector for any
![]() $t\ge \sqrt{L}$
.
$t\ge \sqrt{L}$
.
Finally, note that
![]() $B_{k,m,\ge p}(s,d)$
is empty and thus the above shows that kernel vectors
$B_{k,m,\ge p}(s,d)$
is empty and thus the above shows that kernel vectors
![]() $\boldsymbol{{a}}$
cannot be in
$\boldsymbol{{a}}$
cannot be in
![]() $\boldsymbol{{B}}_{k,m,\ge \sqrt{L}}(s,d)$
. A similar argument as in equations (3.1) and (3.2) shows that
$\boldsymbol{{B}}_{k,m,\ge \sqrt{L}}(s,d)$
. A similar argument as in equations (3.1) and (3.2) shows that
and the result follows.![]()
3.2 Phase 2: boosting the rank using
 $M_2$
$M_2$
Here we show that, conditioned on the conclusions of Proposition 3.1 and Lemma 3.3, after exposing
![]() $M_2$
with high probability
$M_2$
with high probability
 $M=\begin{pmatrix} M_1\\ M_2 \end{pmatrix}$
is
$M=\begin{pmatrix} M_1\\ M_2 \end{pmatrix}$
is
![]() $s$
-robust.
$s$
-robust.
To analyse the probability that a given subset of
![]() $s$
columns is not of full rank, we will use the following procedure:
$s$
columns is not of full rank, we will use the following procedure:
Fix any subset of
![]() $s$
columns in
$s$
columns in
![]() $M_1$
, and let
$M_1$
, and let
![]() $C\;:\!=\;(\boldsymbol{{c}}_1,\ldots,\boldsymbol{{c}}_{s})$
be the submatrix in
$C\;:\!=\;(\boldsymbol{{c}}_1,\ldots,\boldsymbol{{c}}_{s})$
be the submatrix in
![]() $M_1$
that consists of those columns. We reveal
$M_1$
that consists of those columns. We reveal
![]() $M_2$
according to the following steps:
$M_2$
according to the following steps:
-
(1) Let
 $I\subseteq [s]$
be the largest subset of indices such that the columns
$I\subseteq [s]$
be the largest subset of indices such that the columns
 $\{\boldsymbol{{c}}_i \mid i\in I\}$
are linearly independent. By Lemma 3.3 we have that
$\{\boldsymbol{{c}}_i \mid i\in I\}$
are linearly independent. By Lemma 3.3 we have that
 $T\;:\!=\;|I|\geq s-t= (1-\delta )n-t$
, where
$T\;:\!=\;|I|\geq s-t= (1-\delta )n-t$
, where
 $t=\omega (\!\log n)$
. Without loss of generality we may assume that
$t=\omega (\!\log n)$
. Without loss of generality we may assume that
 $I\;:\!=\;\{\boldsymbol{{c}}_1,\ldots,\boldsymbol{{c}}_T\}$
and
$I\;:\!=\;\{\boldsymbol{{c}}_1,\ldots,\boldsymbol{{c}}_T\}$
and
 $T\leq s-1$
(otherwise we have already found
$T\leq s-1$
(otherwise we have already found
 $s$
independent columns of
$s$
independent columns of
 $M$
). By maximality, we know that
$M$
). By maximality, we know that
 $\boldsymbol{{c}}_{T+1}$
can be written (uniquely) as a linear combination of
$\boldsymbol{{c}}_{T+1}$
can be written (uniquely) as a linear combination of
 $\boldsymbol{{c}}_1,\ldots, \boldsymbol{{c}}_{T}$
. That is, there exists a unique combination for which
$\boldsymbol{{c}}_1,\ldots, \boldsymbol{{c}}_{T}$
. That is, there exists a unique combination for which
 $\sum ^{T}_{i=1} x_i \boldsymbol{{c}}_i= \boldsymbol{{c}}_{T+1}$
. In particular, this means thatand hence the vector
$\sum ^{T}_{i=1} x_i \boldsymbol{{c}}_i= \boldsymbol{{c}}_{T+1}$
. In particular, this means thatand hence the vector \begin{align*} \sum _{i=1}^Tx_i \boldsymbol{{c}}_i-\boldsymbol{{c}}_{T+1}=0, \end{align*}
\begin{align*} \sum _{i=1}^Tx_i \boldsymbol{{c}}_i-\boldsymbol{{c}}_{T+1}=0, \end{align*}
 $\boldsymbol{{x}}=(0,\ldots, x_1,\ldots,x_{T}, -1, \ldots,0)\in \mathbb{F}_{q}^d$
is
$\boldsymbol{{x}}=(0,\ldots, x_1,\ldots,x_{T}, -1, \ldots,0)\in \mathbb{F}_{q}^d$
is
 $(T+1)$
-sparse and satisfies
$(T+1)$
-sparse and satisfies
 $M_1\boldsymbol{{x}}=0$
. Since
$M_1\boldsymbol{{x}}=0$
. Since
 $T+1\leq s$
, by Proposition 3.1 we know that
$T+1\leq s$
, by Proposition 3.1 we know that
 $\rho _{\mathbb{F}_p}(\boldsymbol{{x}})=2^{-\omega (\!\log ^2 n)}$
.
$\rho _{\mathbb{F}_p}(\boldsymbol{{x}})=2^{-\omega (\!\log ^2 n)}$
.
-
(2) Expose the row vector of dimension
 $T+1$
from
$T+1$
from
 $M_2$
below the matrix
$M_2$
below the matrix
 $(\boldsymbol{{c}}_1,\ldots, \boldsymbol{{c}}_{T+1})$
. We obtain a matrix of size
$(\boldsymbol{{c}}_1,\ldots, \boldsymbol{{c}}_{T+1})$
. We obtain a matrix of size
 $(n_1+1)\times (T+1)$
. Denote the new row as
$(n_1+1)\times (T+1)$
. Denote the new row as
 $(y_1,\ldots,y_{T+1})$
.
$(y_1,\ldots,y_{T+1})$
. -
(3) If the new matrix is of rank
 $T+1$
, then consider this step as a ‘success’, expose the entire row and start over from
$T+1$
, then consider this step as a ‘success’, expose the entire row and start over from
 $(1)$
. Otherwise, consider this step as a ‘failure’ (As we failed to increase the rank) and observe that if
$(1)$
. Otherwise, consider this step as a ‘failure’ (As we failed to increase the rank) and observe that if
 $\begin{bmatrix} \boldsymbol{{c}}_1 &\ldots & \boldsymbol{{c}}_{T+1}\\ y_1 &\ldots &y_{T+1} \end{bmatrix}$
is not of full rank, then we must haveThe probability to expose such a vector
$\begin{bmatrix} \boldsymbol{{c}}_1 &\ldots & \boldsymbol{{c}}_{T+1}\\ y_1 &\ldots &y_{T+1} \end{bmatrix}$
is not of full rank, then we must haveThe probability to expose such a vector \begin{equation*} x_1y_1+x_2y_2+\ldots -y_{T+1}=0. \end{equation*}
\begin{equation*} x_1y_1+x_2y_2+\ldots -y_{T+1}=0. \end{equation*}
 $y$
is at most
$y$
is at most
 $\rho _{\mathbb{F}_p}(\boldsymbol{{x}})=e^{-\omega (\!\log ^2 n)}$
.
$\rho _{\mathbb{F}_p}(\boldsymbol{{x}})=e^{-\omega (\!\log ^2 n)}$
.
-
(4) All in all, the probability for more than
 $\beta n-t$
failures is at most
$\beta n-t$
failures is at most
 $\binom{\beta n}{t}\left (e^{-\omega (\!\log ^2 n)}\right )^{\beta n-t}=e^{-\omega (n\log n)}=o\left (\binom{d}{s}^{-1}\right )$
. Therefore, by the union bound we obtain that with high probability
$\binom{\beta n}{t}\left (e^{-\omega (\!\log ^2 n)}\right )^{\beta n-t}=e^{-\omega (n\log n)}=o\left (\binom{d}{s}^{-1}\right )$
. Therefore, by the union bound we obtain that with high probability
 $M$
is
$M$
is
 $s$
-robust.
$s$
-robust.
This completes the proof.
4. Proof of the upper bound in Theorem 1.2
We first perform preliminary computations to compute a certain correlation. This boils down to estimating binomial sums. Let
![]() $\xi _i,\xi' _{\!\!i}$
be independent Rademacher variables and define
$\xi _i,\xi' _{\!\!i}$
be independent Rademacher variables and define
Clearly
![]() $\alpha (n,m)\le \alpha (n,n)\le 10\sqrt{n}$
by [Reference Erdös5].
$\alpha (n,m)\le \alpha (n,n)\le 10\sqrt{n}$
by [Reference Erdös5].
Lemma 4.1.
Fix
![]() $\lambda \gt 0$
. If
$\lambda \gt 0$
. If
![]() $n$
is even and
$n$
is even and
![]() $0\le m\le (1-\varepsilon )n$
we have
$0\le m\le (1-\varepsilon )n$
we have
Proof. We have
 \begin{equation*}\alpha (n,m)\le \frac {\sup _k\mathbb {P}[\xi _1+\cdots +\xi _{n-m}=k]}{\mathbb {P}[\xi _1+\cdots +\xi _n=0]^2}\le \frac {2^{-(n-m)}\binom {n-m}{\lfloor (n-m)/2\rfloor }}{2^{-n}\binom {n}{n/2}}= 1 + O(m/(n-m)).\end{equation*}
\begin{equation*}\alpha (n,m)\le \frac {\sup _k\mathbb {P}[\xi _1+\cdots +\xi _{n-m}=k]}{\mathbb {P}[\xi _1+\cdots +\xi _n=0]^2}\le \frac {2^{-(n-m)}\binom {n-m}{\lfloor (n-m)/2\rfloor }}{2^{-n}\binom {n}{n/2}}= 1 + O(m/(n-m)).\end{equation*}
We will also need a more refined bound when
![]() $m$
is small.
$m$
is small.
Lemma 4.2.
If
![]() $n$
is even and
$n$
is even and
![]() $0\le m\le n^{1/2}$
, we have
$0\le m\le n^{1/2}$
, we have
Proof. Using the approximation
![]() $1-x=\exp\!(\!-x-x^2/2+O(x^3))$
for
$1-x=\exp\!(\!-x-x^2/2+O(x^3))$
for
![]() $|x|\le 1/2$
we see that if
$|x|\le 1/2$
we see that if
![]() $y$
is an integer satisfying
$y$
is an integer satisfying
![]() $1\le y\le x/2$
then
$1\le y\le x/2$
then
 \begin{align} x(x-1)\cdots (x-y+1) &= x^y\exp \bigg (\!-\sum _{i=0}^{y-1}\frac{i}{x}-\sum _{i=0}^{y-1}\frac{i^2}{2x^2}+O\Big (\frac{y^4}{x^3}\Big )\bigg )\notag \\ &= x^y\exp \bigg (\!-\frac{y(y-1)}{2x}-\frac{y(y-1)(2y-1)}{12x^2} + O\Big (\frac{y^4}{x^3}\Big )\bigg ). \end{align}
\begin{align} x(x-1)\cdots (x-y+1) &= x^y\exp \bigg (\!-\sum _{i=0}^{y-1}\frac{i}{x}-\sum _{i=0}^{y-1}\frac{i^2}{2x^2}+O\Big (\frac{y^4}{x^3}\Big )\bigg )\notag \\ &= x^y\exp \bigg (\!-\frac{y(y-1)}{2x}-\frac{y(y-1)(2y-1)}{12x^2} + O\Big (\frac{y^4}{x^3}\Big )\bigg ). \end{align}
We now apply this to the situation at hand. We see
![]() $\alpha (n,m)$
is equal to
$\alpha (n,m)$
is equal to
 \begin{align*} & \frac{2^{-(2n-m)}\sum _{k=0}^m\!\binom{m}{k}\binom{n-m}{n/2-k}^2}{2^{-2n}\binom{n}{n/2}^2}\\ & = 2^m\sum _{k=0}^m\binom{m}{k}\bigg (\frac{(n/2)(n/2-1)\cdots (n/2-k+1)\times (n/2)(n/2-1)\cdots (n/2-(m-k)+1)}{n(n-1)\cdots (n-m+1)}\bigg )^2\\ & = 2^m\sum _{k=0}^m\binom{m}{k}\bigg (\frac{(n/2)^me^{-\frac{k(k-1)}{n}-\frac{k(k-1)(2k-1)}{3n^2}-\frac{(m-k)(m-k-1)}{n}-\frac{(m-k)(m-k-1)(2m-2k-1)}{3n^2}+O(m^4/n^3)}}{n^me^{-\frac{m(m-1)}{2n}-\frac{m(m-1)(2m-1)}{12n^2}+O(m^4/n^3)}}\bigg )^2\\ & =2^{-m}\sum _{k=0}^m\binom{m}{k}\exp \bigg (\!-\frac{m^3-4mk(m-k)+n(2k-m)^2-nm}{2n^2}+O(m^2/n^2)\bigg )\\ & = 2^{-m}\sum _{k=0}^m\binom{m}{k}\bigg (\!1-\frac{m^3-4mk(m-k)-nm}{2n^2}+O(m^2/n^2)\bigg )\!\bigg (\!1-\frac{(2k-m)^2}{2n}+O\bigg (\frac{(2k-m)^4}{n^2}\bigg )\!\bigg )\\ & = 2^{-m}\sum _{k=0}^m\binom{m}{k}\bigg (\!1-\frac{m^3-4mk(m-k)-nm}{2n^2}\bigg )\!\bigg (\!1-\frac{(2k-m)^2}{2n}\bigg )+O(m^2/n^2). \end{align*}
\begin{align*} & \frac{2^{-(2n-m)}\sum _{k=0}^m\!\binom{m}{k}\binom{n-m}{n/2-k}^2}{2^{-2n}\binom{n}{n/2}^2}\\ & = 2^m\sum _{k=0}^m\binom{m}{k}\bigg (\frac{(n/2)(n/2-1)\cdots (n/2-k+1)\times (n/2)(n/2-1)\cdots (n/2-(m-k)+1)}{n(n-1)\cdots (n-m+1)}\bigg )^2\\ & = 2^m\sum _{k=0}^m\binom{m}{k}\bigg (\frac{(n/2)^me^{-\frac{k(k-1)}{n}-\frac{k(k-1)(2k-1)}{3n^2}-\frac{(m-k)(m-k-1)}{n}-\frac{(m-k)(m-k-1)(2m-2k-1)}{3n^2}+O(m^4/n^3)}}{n^me^{-\frac{m(m-1)}{2n}-\frac{m(m-1)(2m-1)}{12n^2}+O(m^4/n^3)}}\bigg )^2\\ & =2^{-m}\sum _{k=0}^m\binom{m}{k}\exp \bigg (\!-\frac{m^3-4mk(m-k)+n(2k-m)^2-nm}{2n^2}+O(m^2/n^2)\bigg )\\ & = 2^{-m}\sum _{k=0}^m\binom{m}{k}\bigg (\!1-\frac{m^3-4mk(m-k)-nm}{2n^2}+O(m^2/n^2)\bigg )\!\bigg (\!1-\frac{(2k-m)^2}{2n}+O\bigg (\frac{(2k-m)^4}{n^2}\bigg )\!\bigg )\\ & = 2^{-m}\sum _{k=0}^m\binom{m}{k}\bigg (\!1-\frac{m^3-4mk(m-k)-nm}{2n^2}\bigg )\!\bigg (\!1-\frac{(2k-m)^2}{2n}\bigg )+O(m^2/n^2). \end{align*}
In the third line, we used equation (4.1) and in the fourth line, we simplified the expression and used
![]() $k\le m\le n^{1/2}$
to subsume many terms into an error of size
$k\le m\le n^{1/2}$
to subsume many terms into an error of size
![]() $O(m^2/n^2)$
. The fifth line used
$O(m^2/n^2)$
. The fifth line used
![]() $\exp\!(x)=1+x+O(x^2)$
for
$\exp\!(x)=1+x+O(x^2)$
for
![]() $|x|\le 1$
and the sixth line uses
$|x|\le 1$
and the sixth line uses
![]() $2^{-m}\binom{m}{k}(2k-m)^4\le 2m^2\exp\!(\!-(2k-m)^2/100)$
. Finally, this sum equals
$2^{-m}\binom{m}{k}(2k-m)^4\le 2m^2\exp\!(\!-(2k-m)^2/100)$
. Finally, this sum equals
We are ready to prove the upper bound in Theorem 1.2.
Proof of the upper bound in Theorem
1.2. We are given
![]() $\delta \in (0,1)$
and
$\delta \in (0,1)$
and
![]() $\varepsilon = \omega (\!\log \log n/\log n)$
, with
$\varepsilon = \omega (\!\log \log n/\log n)$
, with
![]() $d = n^{1+1/(2-2\delta )+\varepsilon }$
. Let
$d = n^{1+1/(2-2\delta )+\varepsilon }$
. Let
![]() $s = 2\lfloor (1-\delta )n/2\rfloor$
. We consider an
$s = 2\lfloor (1-\delta )n/2\rfloor$
. We consider an
![]() $n\times d$
random matrix with independent Rademacher entries and wish to show it is not
$n\times d$
random matrix with independent Rademacher entries and wish to show it is not
![]() $s$
-robust with high probability. We may assume
$s$
-robust with high probability. We may assume
![]() $\varepsilon \lt 1/2$
as increasing
$\varepsilon \lt 1/2$
as increasing
![]() $d$
makes the desired statement strictly easier.
$d$
makes the desired statement strictly easier.
For an
![]() $s$
-tuple of columns labelled by the index set
$s$
-tuple of columns labelled by the index set
![]() $S\subseteq [d]$
, let
$S\subseteq [d]$
, let
![]() $X_S$
be the indicator of the event that these columns sum to the zero vector. Let
$X_S$
be the indicator of the event that these columns sum to the zero vector. Let
![]() $X = \sum _{S\in \binom{[d]}{s}}X_S$
, and let
$X = \sum _{S\in \binom{[d]}{s}}X_S$
, and let
![]() $(\xi _1,\ldots,\xi _d)$
be a vector of independent Rademachers. We have
$(\xi _1,\ldots,\xi _d)$
be a vector of independent Rademachers. We have
and
 \begin{align*} \operatorname{Var}X &= \mathbb{E}X^2-(\mathbb{E}X)^2 = \sum _{S,T\in \binom{[d]}{s}}\Big (\mathbb{P}\Big [\sum _{i\in S}\xi _i=\sum _{j\in T}\xi _j=0\Big ]^n-\mathbb{P}[\xi _1+\cdots +\xi _s=0]^{2n}\Big )\\ &= (\mathbb{E}X)^2\cdot \frac{1}{\binom{d}{s}^2}\sum _{S,T\in \binom{[d]}{s}}\Bigg (\frac{\mathbb{P}\Big [\sum _{i\in S}\xi _i=\sum _{j\in T}\xi _j=0\Big ]^n}{\mathbb{P}[\xi _1+\cdots +\xi _s=0]^{2n}}-1\Bigg )\\ &= (\mathbb{E}X)^2\sum _{m=0}^s\frac{\binom{s}{m}\binom{d-s}{s-m}}{\binom{d}{s}}\cdot (\alpha (s,m)^n-1). \end{align*}
\begin{align*} \operatorname{Var}X &= \mathbb{E}X^2-(\mathbb{E}X)^2 = \sum _{S,T\in \binom{[d]}{s}}\Big (\mathbb{P}\Big [\sum _{i\in S}\xi _i=\sum _{j\in T}\xi _j=0\Big ]^n-\mathbb{P}[\xi _1+\cdots +\xi _s=0]^{2n}\Big )\\ &= (\mathbb{E}X)^2\cdot \frac{1}{\binom{d}{s}^2}\sum _{S,T\in \binom{[d]}{s}}\Bigg (\frac{\mathbb{P}\Big [\sum _{i\in S}\xi _i=\sum _{j\in T}\xi _j=0\Big ]^n}{\mathbb{P}[\xi _1+\cdots +\xi _s=0]^{2n}}-1\Bigg )\\ &= (\mathbb{E}X)^2\sum _{m=0}^s\frac{\binom{s}{m}\binom{d-s}{s-m}}{\binom{d}{s}}\cdot (\alpha (s,m)^n-1). \end{align*}
For every
![]() $\eta \gt 0$
and
$\eta \gt 0$
and
![]() $m\le c_\eta n^{1/2}$
, where
$m\le c_\eta n^{1/2}$
, where
![]() $c_\eta$
is a sufficiently small absolute constant in terms of
$c_\eta$
is a sufficiently small absolute constant in terms of
![]() $\eta$
, we see
$\eta$
, we see
![]() $|\alpha (s,m)^n-1|\le \eta$
by Lemma 4.2. For
$|\alpha (s,m)^n-1|\le \eta$
by Lemma 4.2. For
![]() $c_\eta n^{1/2} \lt m\le (1-\varepsilon/8)s$
we have
$c_\eta n^{1/2} \lt m\le (1-\varepsilon/8)s$
we have
![]() $\alpha (s,m)^n\le \exp\!(O(m/\varepsilon ))$
by Lemma 4.1. For this range we have, since
$\alpha (s,m)^n\le \exp\!(O(m/\varepsilon ))$
by Lemma 4.1. For this range we have, since
![]() $m/s\ge n^{\delta/2}s/d$
,
$m/s\ge n^{\delta/2}s/d$
,
 \begin{equation*}\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\le (s+1)\mathbb {P}[\mathrm {Bin}(s,s/d)\ge m]\le \exp\!(\!-s D(m/(2s)||s/d))\le \exp\!(\!-m(\delta/4)\log n)\end{equation*}
\begin{equation*}\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\le (s+1)\mathbb {P}[\mathrm {Bin}(s,s/d)\ge m]\le \exp\!(\!-s D(m/(2s)||s/d))\le \exp\!(\!-m(\delta/4)\log n)\end{equation*}
by Chernoff–Hoeffding (the fact that
![]() $\mathrm{Bin}(n,p)$
exceeds
$\mathrm{Bin}(n,p)$
exceeds
![]() $nq$
for
$nq$
for
![]() $q\ge p$
with probability at most
$q\ge p$
with probability at most
![]() $\exp\!(\!-nD(q||p))$
, where this is the KL-divergence). Thus
$\exp\!(\!-nD(q||p))$
, where this is the KL-divergence). Thus
 \begin{equation*}\sum _{m=c\sqrt {n}}^{(1-\varepsilon )s}\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\cdot (\alpha (s,m)^n-1)\le \sum _{m=c\sqrt {n}}^{(1-\varepsilon )s}\exp\!(O(m/\varepsilon ))\cdot \exp\!(\!-m(\delta/4)\log n) = o(1)\end{equation*}
\begin{equation*}\sum _{m=c\sqrt {n}}^{(1-\varepsilon )s}\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\cdot (\alpha (s,m)^n-1)\le \sum _{m=c\sqrt {n}}^{(1-\varepsilon )s}\exp\!(O(m/\varepsilon ))\cdot \exp\!(\!-m(\delta/4)\log n) = o(1)\end{equation*}
as
![]() $\varepsilon = \omega (\!\log \log n/\log n)$
.
$\varepsilon = \omega (\!\log \log n/\log n)$
.
Finally for
![]() $(1-\varepsilon/8)s\le m\le s$
we have
$(1-\varepsilon/8)s\le m\le s$
we have
 \begin{equation*}\sum _{m=(1-\varepsilon )s}^s\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\cdot (\alpha (s,m)^n-1)\le \sum _{m=(1-\varepsilon )s}^s\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}(10\sqrt {n})^n\le 2^{s}\frac {\binom {d}{\varepsilon s/8}}{\binom {d}{s}}(10\sqrt {n})^n.\end{equation*}
\begin{equation*}\sum _{m=(1-\varepsilon )s}^s\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\cdot (\alpha (s,m)^n-1)\le \sum _{m=(1-\varepsilon )s}^s\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}(10\sqrt {n})^n\le 2^{s}\frac {\binom {d}{\varepsilon s/8}}{\binom {d}{s}}(10\sqrt {n})^n.\end{equation*}
Thus
 \begin{equation*}\sum _{m=(1-\varepsilon )s}^s\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\cdot (\alpha (s,m)^n-1)\le \bigg (\frac {10s}{\varepsilon d}\bigg )^{(1-\varepsilon/8)s}(10\sqrt {n})^n\le (n^{-\frac {1}{2-2\delta }-\varepsilon/2})^{(1-\varepsilon/8)(1-\delta )n}(10\sqrt {n})^n,\end{equation*}
\begin{equation*}\sum _{m=(1-\varepsilon )s}^s\frac {\binom {s}{m}\binom {d-s}{s-m}}{\binom {d}{s}}\cdot (\alpha (s,m)^n-1)\le \bigg (\frac {10s}{\varepsilon d}\bigg )^{(1-\varepsilon/8)s}(10\sqrt {n})^n\le (n^{-\frac {1}{2-2\delta }-\varepsilon/2})^{(1-\varepsilon/8)(1-\delta )n}(10\sqrt {n})^n,\end{equation*}
since
![]() $d = n^{1+1/(2-2\delta )+\varepsilon }$
and
$d = n^{1+1/(2-2\delta )+\varepsilon }$
and
![]() $s = 2\lfloor (1-\delta )n/2\rfloor$
along with
$s = 2\lfloor (1-\delta )n/2\rfloor$
along with
![]() $\varepsilon = \omega (\!\log \log n/\log n)$
. We see that this is
$\varepsilon = \omega (\!\log \log n/\log n)$
. We see that this is
![]() $o(1)$
. Thus
$o(1)$
. Thus
for
![]() $n$
sufficiently large, and thus
$n$
sufficiently large, and thus
![]() $X\gt 0$
with probability at least
$X\gt 0$
with probability at least
![]() $1-2\eta$
.
$1-2\eta$
.![]()