In sports, body composition analysis is utilised in evaluating body hydration with the intention to balance fluid loss with fluid intake, and in monitoring the efficacy of physical training on the resulting soft tissue mass adaptation.
Bioelectrical impedance analysis (BIA) is a non-invasive and portable method of body composition analysis. Impedance is represented with a complex number (a point) in the real–imaginary plane (Z vector) that is a combination of resistance, R (i.e. the opposition to flow of an alternating current through intra- and extracellular ionic solutions, representing the real part of Z) and reactance, Xc (i.e. the capacitative component of cell membranes and organelles, and tissue interfaces, representing the imaginary part of Z) (Foster & Lukaski, Reference Foster and Lukaski1996; Grimnes & Martinsen, Reference Grimnes and Martinsen2000).
Although impedance is an electrical property of tissues that can be directly utilised in body composition analysis, it is commonly embedded in predictive equations that are derived by correlation with criterion measures of body compartments. Total body water (TBW) and its compartments intracellular water (ICW) and extracellular water (ECW) are estimated through regression equations with isotope dilution methods. ICW is also considered an estimate of body cell mass (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998; Ellis, Reference Ellis2000). Many equations are available in the literature for the estimation of fluid compartments, fat and fat-free mass in healthy subjects. The validity of these equations is not established in sports inducing heavy changes in body composition.
Literature is divided along four methods of body composition analysis based on impedance. The first and the most validated is prediction of TBW with functions of 50 kHz single-frequency impedance (either series measures or their parallel equivalents, mostly neglecting the Xc component) (Lukaski & Bolonchuck, Reference Lukaski and Bolonchuck1988; Sun et al. Reference Sun, Chumlea, Heymsfield, Lukaski, Schoeller, Friedl, Kuczmarski, Flegal, Johnson and Hubbard Van2003). The second is prediction of ECW and TBW with functions of low (1–5 kHz)- and high (100–500 kHz)-frequency impedance (dual- or multiple-frequency BIA), with the ICW calculated by difference (Steijaert et al. Reference Steijaert, Deurenberg, Van Gaal and De Leeuw1997). The third is use of many impedance measurements at 1–1000 kHz through bioelectrical impedance spectroscopy (BIS) following the Cole's model approach (i.e. extrapolating R values at limit frequencies) for prediction of TBW, ECW, and ICW (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998) (Fig. 1; Appendix 1). The fourth, and more recent, method is use of the direct impedance vector measurement (both R and Xc component) at 50 kHz in a probabilistic graph (vector BIA with the RXc graph). Vector BIA is a stand-alone method of body composition analysis, where the continuous, bivariate, random vector of impedance at 50 kHz is evaluated through an ordinal scale of the deviation from a reference population (tolerance interval percentiles). Body composition is then evaluated through patterns of vector distribution with respect to the reference percentiles (Piccoli, Reference Piccoli2002; Piccoli et al. Reference Piccoli, Rossi, Pillon and Bucciante1994, Reference Piccoli, Nigrelli, Caberlotto, Bottazzo, Rossi, Pillon and Maggiore1995, Reference Piccoli, Pillon and Dumler2002).

Fig. 1 The arc of the Cole's model for cell suspension is utilised in body composition analysis. The curve formed by Z vectors on the resistance–reactance (R–Xc) plane (impedance locus) is a semicircle with a depressed centre (see Fig. 2). At the extrapolated zero frequency limit resistance, R0, current would only flow through the extracellular water (ECW) solution. The current frequency at which Xc reaches the maximum is the characteristic frequency (Fc). At the extrapolated infinite frequency limit resistance, R∞, the current would flow through both intracellular water (ICW) and ECW solution (total body water (TBW) compartment). The model is not appropriate for human tissues due to their anisotropy (longitudinal conduction of part of low-frequency current through muscle cells) which transforms R0 into a random sum of extra- plus intracellular resistance. Ri, intracellular R.
We recently provided evidence that single-frequency 50 kHz impedance measurements yield the same information as BIS and multiple-frequency BIA in dynamic conditions of ECW overload and removal with haemodialysis, which could be accounted for by current conduction through cells also at low frequencies (see Appendix 1) (Piccoli et al. Reference Piccoli, Pastori, Guizzo, Rebeschini, Naso and Cascone2005).
In the present study we sought to prove equivalence of information between bioimpedance analysis conducted at 50 kHz and with BIS in the extreme increase in lean soft tissue mass, as is observed in ‘professional’ bodybuilders, in whom ICW is out of the normal range due to muscle cell hypertrophy.
Experimental methods
Hypothesis
Tissue anisotropy leads to equivalence between information provided by single-frequency 50 kHz impedance measurements v. other frequencies because part of the current at any frequency flows through extra- and intracellular ionic solutions of soft tissues. We tested this hypothesis of equivalence by assessing measurement validity (construct and content validity) of BIS v. 50 kHz frequency impedance in healthy males with normal soft tissue mass (ideal BMI) and in bodybuilders with an extreme increase in lean soft tissue.
Construct validity of BIS (the measurement corresponds to theoretical expectations) was checked by looking at the distribution of Xc at the lowest frequencies, where Xc values were expected to approach zero because current flow would be mainly extracellular.
Content validity (the measurement incorporates the domain of the phenomenon under study) was checked by comparing the amount of information provided by BIS with respect to 50 kHz measurements (correlation between R and Xc measurements at extreme frequencies v. R and Xc measurements at 50 kHz).
Study design
This was a cross-sectional, observational study in a group of male bodybuilders and a group of healthy males of comparable age. All subjects gave their written informed consent to the study following approval of the University of Padova ethical committee.
The study design considered two groups, each of thirty Caucasian adult males, in the age range 18–45 years. The control group included healthy subjects with a BMI in the range 19–25 kg/m2 who were undergoing regular physical activity while the other group included professional registered bodybuilders, with no limitation to their BMI.
Bioimpedance measurements
Body weight, height and bioimpedance measurements were obtained in the morning in a resting condition and without physical activity in the previous 12 h. Whole-body (hand–foot) impedance was measured on right limbs following the standard tetrapolar method described elsewhere (Lukaski & Bolonchuck, Reference Lukaski and Bolonchuck1988; Sun et al. Reference Sun, Chumlea, Heymsfield, Lukaski, Schoeller, Friedl, Kuczmarski, Flegal, Johnson and Hubbard Van2003). Adhesive, pre-gelled electrodes (Q-trace 5400; Kendall-LTP, Chicopee, MA, USA) were used.
Multiple-frequency and spectral impedance measurements were obtained with SEAC SFB3 multiple-frequency bioimpedance meter (UniQuest-SEAC, Brisbane, Australia) operating with an alternate current of 0·190 mA, and performing measurements on 496 frequencies in the range 4–1024 kHz, including a measurement at 50 kHz. Two runs of measurements were performed and recorded for BIS in 30 s. The software provided by the manufacturer allowed data transfer to computer, raw data presentation by frequency (R and Xc, or Z magnitude and phase angle at each frequency, including 50 kHz).
An independent measurement of impedance at 50 kHz was obtained with an RJL Systems single-frequency bioimpedance meter (BIA-101; RJL Systems, Clinton Township, MI, USA).
Bioimpedance data analysis
Bioelectrical impedance spectroscopy and multiple-frequency bioelectrical impedance analysis
The SEAC software allowed the impedance spectrum fit according to the Cole model (semicircular locus in the R–Xc plane with suppressed centre) (Figs. 1 and 2). The impedance semicircle was fitted according to non-linear least-squares fitting procedures (root mean square error of predicted v. observed Xc, as an indicator of goodness of fit) (Stroud et al. Reference Stroud, Cornish, Thomas and Ward1995; De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998).

Fig. 2 The mean Cole's arc with radius (vertical bar) is depicted for both study groups. In bodybuilders, the increase in soft tissue mass is associated with a smaller circle and with a migration from the right to the left. R, resistance; Xc, reactance. Mean Z vectors (95 % CI in Table 2) are represented (Δ, 5 kHz; ○, characteristic frequency, ●, 50 kHz; X, 100 kHz; □, 300 kHz).
One operator (G. P.) performed visual checks of goodness of fit of the impedance semicircle through the 496 point vectors recorded at different frequencies in every set of measures. Two runs of 496 frequencies were available in all sixty subjects. We considered sixty semicircles for the statistical analysis, using either the first of the two available runs with a comparable goodness of fit, or the run with the better fitting.
For the statistical analysis, in addition to the extrapolated, limit R values of BIS, R0 and R∞, we also considered the measured vector components R and Xc at 5, 50, 100 and 300 kHz, and at the characteristic frequency (Fc; i.e. the frequency where Xc reaches the maximum) for each of the sixty data sets. Ri was calculated as 1/Ri = 1/R∞ – 1/R0 (see Appendix 1). Valid Xc values >0 were recorded in the range of frequencies between 5 and 300 kHz which then were considered the lowest and highest frequencies to be utilised for statistical analysis of individual frequencies before the limit frequencies of zero and infinity, respectively.
BIS estimates of TBW, ECW, and ICW were provided by the SEAC software according to the Cole and Hanai models, whose equations are described and justified elsewhere (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998; Ellis, Reference Ellis2000).
Single-frequency bioelectrical impedance analysis at 50 kHz: conventional bioelectrical impedance analysis
TBW estimate (litres) using the impedance measurement at the fixed frequency of 50 kHz was calculated with the sex-specific regression equation that has been recently validated (multicomponent model) in a large population by Sun et al. (Reference Sun, Chumlea, Heymsfield, Lukaski, Schoeller, Friedl, Kuczmarski, Flegal, Johnson and Hubbard Van2003) with a standard error of estimate of 3·8 litres (bias 0·5) for healthy males:
TBW (litres) in males = 1·203+0·449 height2/R+0·176 weight.
In this equation we used R measurements that were obtained at 50 kHz with the SEAC SFB3 multiple-frequency bioimpedance meter. As Sun's equation was derived using R measurements obtained with an RJL Systems single-frequency bioimpedance meter (BIA-101; RJL Systems) (Sun et al. Reference Sun, Chumlea, Heymsfield, Lukaski, Schoeller, Friedl, Kuczmarski, Flegal, Johnson and Hubbard Van2003) we evaluated the agreement of R measurements at 50 kHz between the two analysers according to the Bland & Altman (Reference Bland and Altman1986) method. We found a tight correlation (r 0·99) between measurements with a bias of 4 Ω (greater with the RJL System v. SEAC device) and 95 % limits of agreement between − 9 and 17 Ω.
Single-frequency bioelectrical impedance analysis at 50 kHz: vector bioelectrical impedance analysis
Bioelectrical impedance vector analysis (BIVA or vector BIA) was performed with the RXc graph method (Piccoli, Reference Piccoli2002; Piccoli et al. Reference Piccoli, Rossi, Pillon and Bucciante1994, Reference Piccoli, Nigrelli, Caberlotto, Bottazzo, Rossi, Pillon and Maggiore1995, Reference Piccoli, Pillon and Dumler2002). An impedance measurement made at 50 kHz is considered a bivariate, normal, random vector with two correlated components, R and Xc (a point in the R–Xc plane). In an RXc graph, point vectors are plotted on the reference, sex-specific, bivariate, 50, 75 and 95 % tolerance intervals of the impedance vector indexed by the subject's height (Z/height = (R/height, Xc/height), in Ω/m). These intervals are the ellipses within which the vector of an individual subject falls with a probability of 50, 75 and 95 %, respectively. We utilised the reference ellipses derived from the healthy Italian population that are available in the literature (Piccoli et al. Reference Piccoli, Nigrelli, Caberlotto, Bottazzo, Rossi, Pillon and Maggiore1995).
The bivariate 95 % CI were calculated for the mean impedance vectors of groups (i.e. the ellipses containing the means of both R and Xc with 95 % probability). Separate 95 % confidence ellipses of mean vectors indicate a statistically significant difference in vector position on the R–Xc plane, which is equivalent to a significant (P < 0·05) Hotelling's T2 test for unpaired data (Piccoli et al. Reference Piccoli, Rossi, Pillon and Bucciante1994, Reference Piccoli, Pillon and Dumler2002; Jolicouer, Reference Jolicouer1999).
Statistical methods
The programs of the statistical package SPSS (version 13; SPSS Inc., Chicago, IL, USA) were used for standard calculations, including the Hotelling's T2 test for mean vector comparison (Reliability procedure), and the linear correlation coefficient r. A test P level of less than 0·05 was considered as statistically significant. Confidence and tolerance ellipses were drawn using the BIVA software (version 2002; free software available from the corresponding author).
Results
Bodybuilders (age 32·1 (sd 5·7) years, range 23–45 years; height 175 (sd 8) cm, range 160–194 cm) and control subjects (age 25·2 (sd 5·3) years, range 18–38 years; height 179 (sd 6) cm, range 165–190 cm) were of similar age range and stature. Body weight (88·2 (sd 12·7) kg, range 61–118 kg v. 71·4 (sd 6·6) kg, range 61–88 kg) and BMI (28·9 (sd 3·6) kg/m2, range 19·5–39·1 kg/m2v. 22·3 (sd 1·4) kg/m2, range 19·5–25·0 kg/m2) were definitely greater in bodybuilders than in control subjects (P < 0·001).
Vector displacement and soft tissue mass
Parameters of Cole's arc and mean impedance vectors at middle and extreme frequencies are reported in Table 1.
Table 1 Measured impedance vector components of Cole's semicircle parameters (centre, radius, characteristic frequency (Fc)) at different frequencies, and of extrapolated resistance (R) values (Mean values and standard deviations)

Xc, reactance; R0, R at zero frequency; R∞, R at infinity frequency; Ri, intracellular R.
* Student's t test for unpaired data.
† R at the Fc is the same as the centre's R.
The average arc of the Cole's model in bodybuilders was significantly smaller (radius; P < 0·0019) and shifted to the left on the R–Xc plane (centre's R; P < 0·001) compared with control subjects (Fig. 2). Hence, in bodybuilders both R and Xc values were significantly (P < 0·001) decreased at any individual frequency with the exception of Xc at 5 kHz (Table 1).
The Fc decreased in bodybuilders by 3 kHz (32 to 29 kHz), indicating a very small counter-clockwise rotation of impedance spectra with an increased soft tissue mass. As this rotation was associated with a decreasing circle diameter, the difference between Xc at Fc and Xc at 50 kHz was negligible, between 2·4 to 3·2 Ω (Table 1; Fig. 2).
Inequalities among reactance values by current frequency
Low frequencies
Xc measurements at 5 kHz were expected to be close to zero due to the postulated, negligible capacitative component of cell membranes (current path only extracellular in the Cole's model) (Fig. 1). In contrast, Xc values at 5 kHz were not only greater than zero (lower 95 % confidence limit higher than 36 Ω) but they also were as high as 64 to 70 % of the maximum Xc that was reached at the Fc (29 to 32 kHz frequency) (Tables 1 and 2; Fig. 2).
Table 2 Measured and extrapolated impedance vector components at extreme current frequencies (Mean values and 95 % CI)

R, resistance; R0, R at zero frequency; R∞, R at infinity frequency; Xc, reactance; Fc, characteristic frequency.
High frequencies
Xc measurements at 5 kHz were expected to be smaller than Xc values at 300 kHz, where the capacitative component of cell membranes is predicted by the Cole's model to be progressively decreasing (Figs. 1 and 2). In contrast, Xc values at 5 kHz were greater than Xc at 300 kHz (by 1·35 to 1·54 times), with a separate 95 % CI in either group as indicated by the lower 95 % confidence limit of 36–38 Ω at 5 kHz, v. upper 95 % confidence limit of 27–32 Ω at 300 kHz (Table 2; Fig. 2).
Evidence for anisotropy
Contrary to the null Xc expectation of the Cole's model, the observed profile of Xc values at 5 kHz indicated a huge contribution of dielectric properties of cells, consistent with tissue anisotropy which caused a definite contribution of intracellular current flows at low frequencies (Tables 1 and 2; Fig. 2).
Inequalities of resistance values by current frequency
Correlation of impedance measurements at different frequencies
The matrix of simple, linear correlation coefficients (r) between individual vector components, R and Xc, measured at 50 kHz v. the components measured at 5 kHz, Fc (29 to 32 kHz), 100 kHz, and 300 kHz is reported in Table 3.
Table 3 Matrix of simple, linear correlation coefficients (r ) between impedance vector components, resistance (R) and reactance (Xc), measured at 50 kHz v. other frequencies

R0, R at zero frequency; R∞, R at infinity frequency; Fc, characteristic frequency.
The correlation coefficient between R at 50 kHz and R at other frequencies ranged from 0·943 (r 2 89 %) with R0 to 0·998 (r 2 99·6 %) with R at 100 kHz. Geometrically, as expected by circle properties, there was a clockwise rotation of regression lines from the left to the right of the identity line (regressions with frequencies < Fc lay on the left of the identity line), indicating that different, proportional levels of the same physical phenomenon were measured at different frequencies (Figs. 3, 4 and 5) (Bland & Altman, Reference Bland and Altman1986). In other words, statements on body composition based on functions of R measurements made at 50 kHz are equivalent to those based on other frequencies because they are tightly correlated with each other along straight lines (property of linear transformation of random variables).

Fig. 3 Scattergram of resistance (R) values at the limit 0 kHz frequency (○, Δ) and at 5 kHz (●, ▲) (ordinate) with R values at 50 kHz (abscissa) in bodybuilders (○, ●) and control subjects (Δ, ▲).

Fig. 4 Scattergram of resistance (R) values at the characteristic frequency (○, Δ) and at 100 kHz (●, ▲) (ordinate) with R values at 50 kHz (abscissa) in bodybuilders (○, ●) and control subjects (Δ, ▲).

Fig. 5 Scattergram of resistance (R) values at the limit infinity frequency (●, ▲) and at 300 kHz (○, Δ) (ordinate) with R values at 50 kHz (abscissa) in bodybuilders (○, ●) and control subjects (Δ, ▲).
The correlation coefficient between Xc at 50 kHz and Xc at other frequencies (5 kHz, Fc, 100 kHz and 300 kHz, whereas Xc values at zero and infinity are zero) ranged from 0·702 (r 2 49 %) to 0·993 (r 2 99 %) (Figs. 6 and 7), with a higher degree of correlation in control subjects. In bodybuilders, the moderate correlation between Xc at 50 kHz and Xc measurements at the extreme frequencies (5 and 300 kHz) might be due to a larger Xc measurement error, to a greater tissue anisotropy effect, or to their combination.

Fig. 6 Scattergram of reactance (Xc) values at the characteristic frequency (○, Δ) and at 100 kHz (●, ▲) (ordinate) with resistance (R) values at 50 kHz (abscissa) in bodybuilders (○, ●) and control subjects (Δ, ▲).

Fig. 7 Scattergram of reactance (Xc) values at 5 kHz frequency (○, Δ) and at 300 kHz (●, ▲) (ordinate) with Xc values at 50 kHz (abscissa) in bodybuilders (○, ●) and control subjects (Δ, ▲).
Body fluid volume
Following the traditional approach of BIS literature we calculated body fluid volumes in both groups. TBW was estimated using BIS methodology (Appendix 1) and using the prediction equation by Sun et al. (Reference Sun, Chumlea, Heymsfield, Lukaski, Schoeller, Friedl, Kuczmarski, Flegal, Johnson and Hubbard Van2003) based on R readings at 50 kHz.
As a consequence of decreasing R∞ and R0 values, TBW and both ECW and ICW significantly increased in bodybuilders by 16·9 litres for the TBW, 4·5 litres for the ECW and 12·4 litres for the ICW. Fractional hydration increased or decreased in bodybuilders when expressed as ICW (62·3 v. 58·4 %, or 3·9 % of the TBW) or as ECW (37·7 v. 41·6 %, or − 3·9 % of the TBW) (Table 4).
Table 4 Body fluid estimates obtained with bioelectrical impedance spectroscopy (BIS) and estimate of total body water (TBW) with single-frequency bioelectrical impedance analysis (50 kHz, with Sun's formula) (Mean values and standard deviations)

R, resistance; ECW, extracellular water; ICW, intracellular water.
The correlation between TBW estimates with BIS v. Sun's formula (R at 50 kHz) was high, with r 0·98 (P < 0·001) (Fig. 8). Correlation coefficients of a same degree were found between TBW with Sun's formula and both ECW and ICW (r 0·99 and r 0·94, respectively; scattergrams not reported).

Fig. 8 Relationship (y = − 9·1+1·24x ; r 0·98) between total body water (TBW) estimated with bioimpedance spectroscopy (BIS) and TBW estimated with Sun's formula (50 kHz) for bodybuilders (●) and control subjects (Δ).
Vector bioelectrical impedance analysis
Mean impedance vectors of bodybuilders and control subjects were drawn with their 95 % confidence ellipses as an RXc graph on the reference 50, 75 and 95 % tolerance ellipses of the Italian adult male population (Fig. 9) (Piccoli et al. Reference Piccoli, Nigrelli, Caberlotto, Bottazzo, Rossi, Pillon and Maggiore1995). Separate 95 % confidence ellipses indicated a significant mean vector displacement (P < 0·05, meaning a significant Hotelling's T2). The distance from the centre of the tolerance ellipses (reference mean) was greater for the mean vector of bodybuilders, in the direction of the ellipses' minor axis indicating an increased soft tissue mass (Piccoli et al. Reference Piccoli, Pillon and Dumler2002). Indeed, both vector components decreased in bodybuilders compared with control subjects, but with an increased Xc:R ratio (i.e. a greater phase angle), indicating that the electric current flowed through more body fluids with more cells per unit volume (intracellular fluid volume) (Fig. 9).
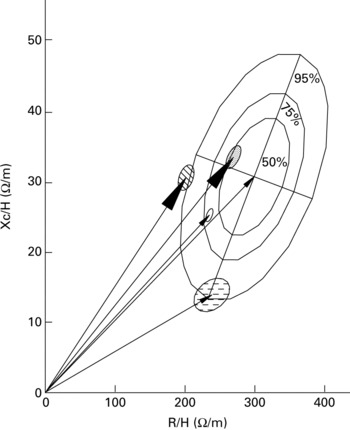
Fig. 9 Mean impedance vectors at 50 kHz (–▸, –▸) are represented as an RXc graph with the reference 50, 75 and 95 % tolerance ellipses of the adult healthy male population (age 15–85 years; BMI 17–31 kg/m2; Piccoli et al. Reference Piccoli, Nigrelli, Caberlotto, Bottazzo, Rossi, Pillon and Maggiore1995). Mean vectors from bodybuilders and control subjects (–▸) correspond to those in the Cole's arcs in Fig. 2. The small ellipses are the 95 % confidence ellipses of the mean vectors of bodybuilders (BMI 20–39 kg/m2; ![]() ), control subjects (BMI 20–25 kg/m2;
), control subjects (BMI 20–25 kg/m2; ![]() ), obese subjects (BMI 31–67 kg/m2; □) and nephrotic patients with oedema (BMI 17–34 kg/m2;
), obese subjects (BMI 31–67 kg/m2; □) and nephrotic patients with oedema (BMI 17–34 kg/m2; ![]() ). The obese and oedematous patients participated in a previous study (Piccoli et al. Reference Piccoli, Brunani, Savia, Pillon, Favaro, Berselli and Cavagnini1998). Bodybuilders are characterised by a pattern with decreased resistance/height (R/H) component (increased body fluid volume) and by an increased phase angle (more cell membranes per fluid volume unit, i.e. increased intracellular fluid). In obese subjects, who also have a decreased R/H component, the phase angle is the same as the reference population (increased body fluid volume with a normal extracellular:intracellular fluid ratio).
). The obese and oedematous patients participated in a previous study (Piccoli et al. Reference Piccoli, Brunani, Savia, Pillon, Favaro, Berselli and Cavagnini1998). Bodybuilders are characterised by a pattern with decreased resistance/height (R/H) component (increased body fluid volume) and by an increased phase angle (more cell membranes per fluid volume unit, i.e. increased intracellular fluid). In obese subjects, who also have a decreased R/H component, the phase angle is the same as the reference population (increased body fluid volume with a normal extracellular:intracellular fluid ratio).
The mean vector position in the RXc graph was consistent with spectroscopy analysis where the Cole's arc was smaller (smaller Xc value) and more shifted to the left (smaller R value) in bodybuilders (Figs. 2 and 10; 50 kHz point vector). The additional information provided by vector BIA is the direct assessment of the distance of mean vectors from the reference mean with the metrics of bivariate percentiles.

Fig. 10 The mean Cole's arc is depicted for four groups. Diameter is smaller in bodybuilders compared with control subjects, and in haemodialysis patients from a previous study (Piccoli et al. Reference Piccoli, Pastori, Guizzo, Rebeschini, Naso and Cascone2005) before the session (HDo) compared with after 180 min fluid removal (HD180 min). In bodybuilders, compared with control subjects, the increase in lean soft tissue mass is associated with a smaller circle and with a migration from the right to the left. Extracellular fluid removal with dialysis is associated with arc enlargment and migration from the left to the right. Both size and migration of the arcs can be tracked by any vector at a single frequency (for example, 50 kHz). Mean vectors are represented (Δ, 5 kHz; ○, characteristic frequency, ●, 50 kHz; X, 100 kHz; □, 300 kHz). R, resistance, Xc, reactance.
Discussion
The bodybuilder is a good experimental model of increased intracellular volume due to hypertrophy of muscle fibres. Bodybuilders achieve their target body structure after a strong training aimed to increase the muscle mass with a decrease in fat mass. It has been proved with muscle biopsy in bodybuilders that muscle fibres undergo mainly hypertrophy with a little contribution of hyperplasia (MacDougall et al. Reference MacDougall, Sale, Elder and Sutton1982, Reference MacDougall, Sale, Alway and Sutton1984).
In BIS methodology, TBW, ECW, and ICW volumes are estimated assuming that the current path is only extracellular at the lowest frequencies and that it is both extra- and intracellular at the highest frequencies, with ICW as the difference between them (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998). Most authors agree that at the lowest frequencies, part of the current still passes through cells and that at the highest frequencies, part of the current still cannot fully penetrate all cells (Foster & Lukaski, Reference Foster and Lukaski1996; De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998; Gudivaka et al. Reference Gudivaka, Schoeller, Kushner and Bolt1999; Faes et al. Reference Faes, van der Meij, de Munck and Heethaar1999; Grimnes & Martinsen, Reference Grimnes and Martinsen2000; Ellis, Reference Ellis2000). The obvious conclusion would be that body impedance, which is the unique non-invasive technique specifically measuring the electric volume of intra- and extracellular ionic solutions of tissues (90 % from limbs) yields a direct assessment of soft tissue hydration status, which can be reasonably considered a proxy of TBW volume. Nevertheless, in BIS methodology, the extrapolation from measured to the limit, zero and infinity frequencies is utilised in the hope to overcome the technical problem. This point is a matter of assumptions because measurement errors diverge at the extreme frequencies (Stroud et al. Reference Stroud, Cornish, Thomas and Ward1995; Faes et al. Reference Faes, van der Meij, de Munck and Heethaar1999; Grimnes & Martinsen, Reference Grimnes and Martinsen2000). But, as outlined in Appendix 1, intracellular current flow due to tissue anisotropy prevents a reliable determination of the extracellular electric volume, hence of the intracellular volume, which impairs both construct and content validity of BIS methodology.
We previously demonstrated that in monitoring tissue hydration during extracellular fluid removal with haemodialysis, no loss of information occurred when only considering single-frequency (50 kHz) impedance vector displacement because no additional information was provided by other measured frequencies or by limit frequencies at zero and infinity. Moreover, estimates of ECW and ICW provided by BIS equations were apparently the yield of model assumptions and numeric handling of R0 and R∞. In other words, the content validity of BIS methodology was impaired in conditions of extracellular fluid overload and removal. Also, the construct validity of BIS methodology was impaired in conditions of extracellular fluid changes because the Xc at 5 kHz:Xc at the Fc ratio was higher than 65 %, due to an important intracellular current path, instead of the expected value close to 0 % if the current path was only extracellular (Piccoli et al. Reference Piccoli, Pastori, Guizzo, Rebeschini, Naso and Cascone2005).
In the present study we wanted to test content and construct validity of BIS methodology in the condition of increased intracellular volume that is achieved in bodybuilders. Again, we proved that no loss of information occurred when only considering single-frequency (50 kHz) impedance vector displacement in the study groups because the arc fitting the impedance spectrum was smaller in bodybuilders than in control subjects and moved to the left on the R–Xc plane. As a geometrical consequence, both R and Xc values were lower in bodybuilders than in control subjects at any measured and extrapolated frequency (Figs. 2 and 10). As a statistical consequence, impedance vector components at 50 kHz were correlated with other frequencies, including limit frequencies (Reference De Lorenzo, Andreoli, Matthie and Withers3–Reference Grimnes and Martinsen8). If information from BIS was different from that at 50 kHz, the correlation with extreme frequencies should have been poor. The moderate correlation between Xc at 50 kHz and Xc measurements at the extreme frequencies (5 and 300 kHz; Fig. 7) might be due to a larger measurement error (critical signal:noise ratio) (Van Marken Lichtenbelt et al. Reference Van Marken Lichtenbelt, Westerterp, Wouters and Luijendijk1994; Stroud et al. Reference Stroud, Cornish, Thomas and Ward1995; Grimnes & Martinsen, Reference Grimnes and Martinsen2000), to a variable tissue anisotropy between subjects, or to their combination.
Also the construct validity of BIS methodology was impaired in conditions of intracellular fluid increase because the Xc at 5 kHz:Xc at the Fc ratio was as high as 70 %, due to a substantial intracellular current path, contrary to the expected value close to 0 % if the current path was only extracellular.
In practice, both centre migration and diameter changes can be directly tracked by vector BIA considering both R and Xc vector components at 50 kHz as an RXc graph (Fig. 2) (Piccoli et al. Reference Piccoli, Rossi, Pillon and Bucciante1994, Reference Piccoli, Nigrelli, Caberlotto, Bottazzo, Rossi, Pillon and Maggiore1995). Impedance measurements at 50 kHz, which is close to the Fc, provide the best information at the body level, as the signal:noise ratio is maximised (maximal Xc values in the order of 1/10 of R values), and both frequency-dependent errors and variability of electric flow paths are minimised (Grimnes & Martinsen, Reference Grimnes and Martinsen2000). In addition, the individual variability is directly compared with the between-subject variability that is represented by the tolerance ellipses of the reference population, which is not possible to do with BIS methodology.
Prediction equations based on impedance may be flawed in extremes of body composition, particularly if tissue hydration is abnormal (Piccoli et al. Reference Piccoli, Brunani, Savia, Pillon, Favaro, Berselli and Cavagnini1998; Ellis, Reference Ellis2000; Sun et al. Reference Sun, Chumlea, Heymsfield, Lukaski, Schoeller, Friedl, Kuczmarski, Flegal, Johnson and Hubbard Van2003; Piccoli, Reference Piccoli2004). Accuracy and precision of prediction equations for fat and fat-free mass have been recently evaluated in bodybuilders using as the reference method the four-component model which is the function of body density (underwater weighing), TBW (2H dilution) and bone mineral content (dual X-ray absorptiometry). Accuracy of BIA prediction equations was good (–0·94 % for fat mass and 0·76 kg for fat-free mass), but precision was unsatisfactory ( ± 8·1 % for fat mass and ± 6·6 kg for fat-free mass). Individual prediction errors were attributed to the great variability in body fat content (BMI 21–32 kg/m2) and in fat-free mass hydration (71–76 %) that is commonplace during strength training (Van Marken Lichtenbelt et al. Reference Van Marken Lichtenbelt, Hartgens, Vollaard, Ebbing and Kuipers2004). This could be an explanation of the doubling of the standard deviation we documented in bodybuilders compared with control subjects (Table 4). Nevertheless, we have no explanation for the greater ECW volume in bodybuilders. Estimation of the ECW volume could have been more sensitive to anisotropy. Finally, using equations that were based on calibration data from individuals who are not bodybuilders may have decreased accuracy and precision of TBW, ECW and ICW estimates.
Implications in practice
Utility of BIA in subjects with an abnormal body composition can be achieved by using vector BIA as a stand-alone procedure based on patterns of direct impedance measurements (impedance random vectors) without knowledge of body weight and without a priori assumptions on body composition. Evaluation in real time is based on R and Xc readings at 50 kHz, which are available in a few seconds and can be plotted on the RXc graph (Piccoli, Reference Piccoli2002; Piccoli et al. Reference Piccoli, Rossi, Pillon and Bucciante1994, Reference Piccoli, Nigrelli, Caberlotto, Bottazzo, Rossi, Pillon and Maggiore1995, Reference Piccoli, Pillon and Dumler2002).
As with laboratory tests, the individual minimal detectable change of an impedance vector can be calculated from the analytical error, namely minimal detectable change = 2·8 precision, where precision is the CV in repeated measurement (Ellis, Reference Ellis2000). Short- and long-term CV for impedance measurements range between 1·8 and 2·9 % respectively (Houtkooper et al. Reference Houtkooper, Lohman, Going and Howell1996). Hence an impedance vector displacement greater than the minimal detectable change of 5 to 8 Ω can be attributed to the biological or clinical variability which can be ranked and interpreted with respect to the reference vector distribution (50, 75 and 95 % tolerance ellipses) (Piccoli, Reference Piccoli2002).
From clinical validation studies of vector BIA in adults (Piccoli, Reference Piccoli1998, Reference Piccoli2002, Reference Piccoli2004; Toso et al. Reference Toso, Piccoli, Gusella, Menon, Bononi, Crepaldi and Ferrazzi2000; Piccoli et al. Reference Piccoli, Pittoni, Facco, Favaro and Pillon2000, Reference Piccoli, Pillon and Dumler2002; Bosy-Westphal et al. Reference Bosy-Westphal, Danielzik, Doerhoefer, Piccoli and Mueller2005), vector displacements parallel to the major axis of tolerance ellipses indicate progressive changes in tissue hydration (dehydration with long vectors, and hyperhydration with short vectors).
In the present study, vector displacements in the direction of the minor axis and with phase angles greater than normal were associated with an increase in lean soft tissue mass. The 75 and 95 % tolerance ellipses can be used to rank the distance of vectors from the norm (Fig. 9). Both vector components decreased in bodybuilders compared with control subjects, but with an increased Xc:R ratio (i.e. a greater phase angle), indicating that the electric current flowed through more body fluids with more cells per unit volume (intracellular fluid volume). In obese subjects a comparable decrease in the R component is associated with a proportional decrease in the Xc component (normal phase angle) indicating that current flows through more body fluids but with a normal proportion in the number of cells per unit volume (Piccoli, Reference Piccoli1998; Piccoli et al. Reference Piccoli, Brunani, Savia, Pillon, Favaro, Berselli and Cavagnini1998, Reference Piccoli, Pillon and Dumler2002; Bosy-Westphal et al. Reference Bosy-Westphal, Danielzik, Doerhoefer, Piccoli and Mueller2005). Also, in extracellular fluid overload (for example, pitting oedema) both components decrease, but with a fall in the Xc component indicating that current flows through more body fluids with fewer cells per unit volume (Piccoli, Reference Piccoli1998, Reference Piccoli2004; Piccoli et al. Reference Piccoli, Rossi, Pillon and Bucciante1994, Reference Piccoli, Brunani, Savia, Pillon, Favaro, Berselli and Cavagnini1998) (Fig. 9).
However, we lack direct evidence to support the present study hypothesis because we did not perform independent measurements of body composition.
Conclusions
No information was lost when only considering the displacement of the impedance vector at 50 kHz, nor was additional information provided by prediction equations of fluid compartments of BIS methodology. The increased lean soft tissue mass in bodybuilders was detectable through a specific pattern of vector BIA at 50 kHz. The comparison of vector position with reference intervals represents an additional advantage of vector BIA, which is not allowed with BIS.
Acknowledgements
A. Piccoli was responsible for the study design and writing of the manuscript; G. P. was responsible for measurements, BIS analysis and data collection; M. C. was responsible for the study design, data analysis and discussion of results; A. Paoli was responsible for the selection of subjects and discussion of results. None of the authors had a conflict of interest.
Appendix 1
Bioelectrical impedance spectroscopy models and the Cole's arc
Different methods of obtaining body impedance measurements (single or multiple current frequency; distal, proximal or segmental measures) aim to provide quantitative estimates of body compartments and are supported by electric models of the human body and tissues (Foster & Lukaski, Reference Foster and Lukaski1996; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998; Grimnes & Martinsen, Reference Grimnes and Martinsen2000; Ellis, Reference Ellis2000). An electrical model (for example, series, parallel, Cole's, Hanai's model, etc) is used as an electrical equivalent (Grimnes & Martinsen, Reference Grimnes and Martinsen2000) that is a circuit that behaves electrically like the original, is expressed through mathematical equations, and aims to represent anatomical structures or physical processes (for example, sketches of 75 trillion cells of the human body, three to six body compartments, cellular and vascular fluid shifts, etc) (Ellis, Reference Ellis2000).
Since the 1950s, the β-relaxation theory (or Maxwell–Wagner dispersion theory) (Grimnes & Martinsen, Reference Grimnes and Martinsen2000) has been successfully applied to cellular suspension analysis to obtain membrane capacity and intracellular resistivity, allowing the accurate measurement of living cell volume by biomass transducers (for example, industrial fermentation process, blood cell counter). In bioelectrical impedance spectroscopy (BIS), parameters of Cole's model are estimated through non-linear curve fitting in the resistance–reactance (R–Xc) plane of a number of Z vectors that are measured by BIS in a cell suspension (Grimnes & Martinsen, Reference Grimnes and Martinsen2000) (Fig. 1). The curve formed by Z vectors (impedance locus) on the R–Xc plane is a semicircle with a depressed centre (Cole's arc, with a negative Xc coordinate) (Fig. 2). At very low frequencies, extrapolated to zero frequency limit, R0, current only flows through the extracellular water (ECW) solution because the cell membrane would act as a capacitor and the impedance would become ECW resistance. The current frequency at which Xc reaches the maximum is the characteristic frequency (Fc). At very high frequencies, extrapolated to infinite frequency limit, R∞, the current also penetrates cells such that the impedance becomes total body water (TBW) resistance. The intracellular water (ICW) resistance, Ri, is then derived as 1/Ri = 1/R∞ – 1/R0. ICW and ECW volumes of a suspension containing non-conducting spheres (Hanai's mixture theory) can be estimated introducing in the model two constants, that are the resistivity of the conducting medium and the concentration of non-conducting spheres (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Grimnes & Martinsen, Reference Grimnes and Martinsen2000; Ellis, Reference Ellis2000).
In human subjects, ECW and ICW volumes are calculated from the extrapolated values of R0 and R∞, according to Hanai's mixture–volume equation for non-conducting spheres. Three arbitrary constants are needed in the prediction equations, namely a dimensionless shape factor Kb (4·3 for either sex) accounting for body geometry (arms, legs, and trunk as five cylinders), a resistivity constant of the ECW solution kECW (0·306 in men and 0·316 in women, as a powered ratio of ECW resistivity and body density), and the ratio of ICW:ECW resistivities kρ (3·82 in men and 3·40 in women) (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997). As demanded by the model, we used these coefficients as constants in the equations, although they are population specific (by age and sex in healthy subjects) with a very high CV, in the order of 19 to 29 % (Ellis & Wong, Reference Ellis and Wong1998; Ellis, Reference Ellis2000). We did not use the correction for time delay of the electric signal which is recommended for Xitron devices (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997; Matthie et al. Reference Matthie, Zarowitz, De Lorenzo, Andreoli, Katzarski, Pan and Whiters1998), but not for SEAC devices (Stroud et al. Reference Stroud, Cornish, Thomas and Ward1995).
ECW, ICW, and TBW (in litres) were calculated according to equations 1, 2 and 3, respectively (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997):
In the literature, the standard error of estimate (or root mean square error) of TBW, ECW and ICW prediction equations compared with dilution methods is 1·33 (bias − 4·46), 0·90 (bias 2·69) and 1·69 (bias − 7·14) litres in healthy subjects (De Lorenzo et al. Reference De Lorenzo, Andreoli, Matthie and Withers1997).
Tissue anisotropy and bioelectrical impedance spectroscopy models
Impedance models that work well in suspensions of spherical cells, where Xc is close to 0 Ω at low frequencies, are flawed in determining intra- and extracellular electrical volumes of cells in tissues because human tissues are anisotropic conductors (Foster & Lukaski, Reference Foster and Lukaski1996; Faes et al. Reference Faes, van der Meij, de Munck and Heethaar1999; Grimnes & Martinsen, Reference Grimnes and Martinsen2000; Ellis, Reference Ellis2000). Anisotropy means that current conduction is not constant in different directions. Anisotropy is small in suspensions of non-spherical cells (for example, erythrocytes) but is large in tissues because of the orientation of cells, tissue interfaces, macromembranes, and organs which leads to a progressive increase in Xc values above the expected value of 0 Ω (only extracellular current path) (Faes et al. Reference Faes, van der Meij, de Munck and Heethaar1999; Grimnes & Martinsen, Reference Grimnes and Martinsen2000). Muscle tissue is strongly anisotropic with a low-frequency conductance ratio of 1:8 between transversal and longitudinal directions (Foster & Lukaski, Reference Foster and Lukaski1996; Grimnes & Martinsen, Reference Grimnes and Martinsen2000). This means that a low frequency current (up to 10 kHz) in the longitudinal direction also flows through muscle cells, leading to a biased estimation of the ECW volume (R0 becomes the sum of the extra- plus a variable intracellular R). Comparable volumes of lean soft tissues generate different impedance vector components than fat soft tissues because adipocyte droplets (anhydrous triacylglycerols) are poor conductors. Contribution of bone to body impedance is negligible in the current range of biomedical analysers (Foster & Lukaski, Reference Foster and Lukaski1996; Faes et al. Reference Faes, van der Meij, de Munck and Heethaar1999; Ellis, Reference Ellis2000; Grimnes & Martinsen, Reference Grimnes and Martinsen2000).
















