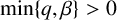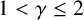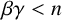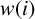1. Introduction
The Wolff potential of a nonnegative function
$f \in L_{loc}^1(\mathbb {R}^n)$
is defined as in [Reference Hedberg and Wolff10] by
$$ \begin{align*} W_{\beta,\gamma}(f)(x)=\int_0^{\infty} \bigg[\int_{B_t(x)} \frac{f(y)}{t^{n-\beta\gamma}} \,dy\bigg]^{{1}/{(\gamma-1)}} \,\frac{dt}{t}, \end{align*} $$
where
$1<\gamma <\infty $
,
$\beta>0$
,
$\beta \gamma <n$
and
$B_t(x)$
is a ball of radius t centred at x. It is not difficult to see that
$W_{1,2}(f)$
is the Newton potential and
$W_{{\alpha }/{2},2}(f)$
is the Reisz potential.
The Wolff potentials are helpful for understanding nonlinear partial differential equations (see [Reference Kilpelaiinen and Maly15, Reference Labutin16, Reference Phuc and Verbitsky23]). For example, if
$\mu $
is a positive Borel measure,
$W_{1,\gamma }(\mu )$
can be used to estimate positive solutions of the
$\gamma $
-Laplace equation
$$ \begin{align} {-}\mbox{div}(|\nabla u|^{\gamma-2}\nabla u)=\mu. \end{align} $$
If
$\inf _{R^n}u=0$
, then there exist positive constants
$C_1$
and
$C_2$
such that (see [Reference Kilpelaiinen and Maly15, Reference Phuc and Verbitsky23])
$$ \begin{align} C_1W_{1,\gamma}(\mu)(x) \leq u(x) \leq C_2W_{1,\gamma}(\mu)(x), \quad x \in \mathbb{R}^n. \end{align} $$
Set
$R(x)=u(x)[W_{1,\gamma }(\mu )(x)]^{-1}$
. Then u solves the integral equation
$$ \begin{align} u(x)=R(x)W_{\beta,\gamma}(\mu)(x) \quad\mbox{and}\quad u>0, \quad x\in\mathbb{R}^n, \end{align} $$
with
$\beta =1$
, where
$R(x)$
is a double-bounded function (in view of (1.2)). When
${\mu =u^q}$
, the qualitative properties of positive solutions of (1.3) are well studied. Existence results can be seen in [Reference Lei and Li17] and the radial symmetry of positive solutions can be seen in [Reference Chen and Li4, Reference Liu21]. See also [Reference Ma, Chen and Li22] for the integrability of finite energy solutions and [Reference Sun and Lei25] for the asymptotic behaviour of those solutions at infinity which shows that the decay rate of those positive solutions of (1.1) with
$\mu =u^q$
is the same as the fast decay rate in [Reference Franca8, Reference Kawano, Yanagida and Yotsutani14].
Equation (1.3) with
$R(x) \equiv 1$
and
$\mu \!=\!u^q$
is a generalisation of the Hardy–Littlewood– Sobolev integral equation. Namely, when
$\gamma =2$
and
$\beta =\alpha /2$
, (1.3) reduces to
$$ \begin{align} u(x) = \int_{\mathbb{R}^{n}} \frac{u^{q}(y)}{|x-y|^{n-\alpha}}\,dy \quad\mbox{and}\quad u>0, \quad x\in \mathbb{R}^n. \end{align} $$
This equation is associated with the extremal functions of the Hardy–Littlewood– Sobolev inequality (see [Reference Lieb20]):
$$ \begin{align} \int_{\mathbb{R}^n}\int_{\mathbb{R}^n}\frac{f(x)g(y)}{|x-y|^{n-\alpha}}\,dx\,dy \leq C(n,s,\alpha)\|f\|_{L^r(\mathbb{R}^n)}\|g\|_{L^s(\mathbb{R}^n)}, \end{align} $$
where
$\min \{s,r\}>1$
,
${1}/{r}+{1}/{s}={(n+\alpha )}/{n}$
,
$f \in L^r(\mathbb {R}^n)$
,
$g \in L^s(\mathbb {R}^n)$
. Positive solutions of (1.4) and the corresponding partial differential equations of the Lane–Emden type are well studied. In particular, see [Reference Chen, Jin, Li and Lim2, Reference Jin and Li13] for the integrability of positive finite energy solutions of the corresponding system. Based on this result, [Reference Lei, Li and Ma18] gives the asymptotic behaviour of those positive solutions.
In 2015, Huang et al. [Reference Huang, Li and Yin12] used (1.5) to prove a discrete Hardy–Littlewood–Sobolev inequality and deduce the Euler–Lagrange system satisfied by the extremal sequences. When
$f \equiv g$
, such a system can be seen as the discrete form of (1.4). Chen and Zheng [Reference Chen and Zheng6] obtained the summability of some positive solutions and their asymptotic behaviour is obtained in [Reference Lei, Li and Tang19].
The discrete Wolff potential is used to study some nonlinear problems in [Reference Cascante, Ortega and Verbitsky1, Reference Hedberg and Wolff10, Reference Phuc and Verbitsky23]. Let
$f=f(i)$
,
$i \in \mathbb {Z}^n$
, be a nonnegative sequence. Define a discrete form of the Wolff potential by
$$ \begin{align*} W_{\beta,\gamma}(f)(i)=\int_0^{\infty} \bigg[\sum_{j \in Z^n,|j-i|<t} \frac{f(j)}{t^{n-\beta\gamma}}\bigg]^{{1}/{(\gamma-1)}} \,\frac{dt}{t}. \end{align*} $$
The discrete form of (1.3) is
$$ \begin{align} w(i)=R(i)W_{\beta,\gamma}(w^{q})(i), \quad i\in \mathbb{Z}^n, \end{align} $$
where
$$ \begin{align} n \geq 1, \ \beta>0, \ \gamma \in (1,2], \ \beta\gamma<n, \ q>0, \ C^{-1} \leq R(i) \leq C. \end{align} $$
Here,
$C>1$
is an absolute constant and such an
$R(i)$
is called a double-bounded sequence. This equation appears in the study of crystal physics, neural networks and other nonlinear problems (see [Reference Li7, Reference Gassner, Probst, Lauenstein and Hermansson9, Reference Hua and Li11]). We investigate the summability and the asymptotic behaviour of positive solutions of (1.6). We use a regularity lifting lemma (Lemma 2.2) to obtain an initial summability interval of positive solutions. We then extend the interval to an optimal one by means of a Wolff-type inequality (Lemma 2.1).
We now state the main results in this paper. Write
$$ \begin{align*} s_0:=\frac{n(q-\gamma+1)}{\beta\gamma}. \end{align*} $$
Theorem 1.1. Assume
$w \in l^{s_0}(\mathbb {Z}^n)$
solves (1.6) with (1.7). If
$$ \begin{align} q \geq \frac{n(\gamma-1)}{n-\beta\gamma}, \end{align} $$
we have the following summability and asymptotic behaviour results:
-
(i) w belongs to
$l^s(\mathbb {Z}^n)$
for any
$s \in ({n(\gamma -1)}/{(n-\beta \gamma )},\infty ]$
and the left end point
${n(\gamma -1)}/{(n-\beta \gamma )}$
is optimal; -
(ii) if
$w(i)$
belongs to a radially symmetric and decreasing surface, then the sequence
$w(i) |i|^{{(n-\beta \gamma )}/{(\gamma -1)}}$
is double-bounded.
Remark 1.2. Condition (1.8) in Theorem 1.1 is not essential. In fact, by a similar argument to that in [Reference Lei and Li17], (1.6) has no positive solution when
$0<q \leq {n(\gamma -1)}/{(n-\beta \gamma )}$
. An analogous nonexistence result for another discrete Wolff-type equation can be seen in [Reference Phuc and Verbitsky23].
Remark 1.3. The assumption ‘the deceasing surface’ in Theorem 1.1(ii) is not essential. In fact, for bounded i, it is easy to see that
$w(i) |i|^{{(n-\beta \gamma )}/{(\gamma -1)}}$
is double-bounded. Therefore, we only consider the case when
$|i|$
is sufficiently large. By the ideas in Step 1 of the proof of [Reference Chen and Li4, Theorem 1], and by the same argument in [Reference Lei, Li and Tang19, Section 2.1], we also deduce that
$w(i)$
is decreasing about some
$i_0 \in \mathbb {Z}^n$
when
$|i|$
is large.
Remark 1.4. When
$\beta =\alpha /2$
,
$\gamma =2$
, Theorem 1.1(i) and (ii) are consistent with the results in [Reference Chen and Zheng6, Reference Lei, Li and Tang19], respectively. The initial summability condition
$w \in l^{s_0}(\mathbb {Z}^n)$
appears in [Reference Chen, Li and Ou5], but is different to the initial integrability condition in [Reference Ma, Chen and Li22, Reference Sun and Lei25]. In fact,
$s_0$
can take all the values mentioned in these papers for the different critical exponents q which determine the existence of positive solutions (see [Reference Serrin and Zou24]).
2. Preliminaries
2.1. Wolff-type inequality
In 2008, Phuc and Verbitsky [Reference Phuc and Verbitsky23] gave the following relation between the Wolff potential and the Riesz potential. If
$q>\gamma -1>0$
, there exists
${C>1}$
such that
$$ \begin{align*} C^{-1}\|W_{\beta,\gamma}(\mu)\|_{L^q(\mathbb{R}^n)}^q \leq \|I_{\beta\gamma}(\mu)\|_{L^{q/(\gamma-1)}(\mathbb{R}^n)}^{q/(\gamma-1)} \leq C\|W_{\beta,\gamma}(\mu)\|_{L^q(\mathbb{R}^n)}^q. \end{align*} $$
Combining this with the Hardy–Littlewood–Sobolev inequality, one can obtain the Wolff-type inequality (see [Reference Ma, Chen and Li22, Corollary 2.1]):
$$ \begin{align} \|W_{\beta,\gamma}(f)\|_{L^q(\mathbb{R}^n)} \leq C \|f\|_{L^{qn/[n(\gamma-1)+q\beta\gamma]}(\mathbb{R}^n)}^{1/(\gamma-1)}. \end{align} $$
For the discrete sequence
$f(i)$
, we have the same kind of inequality.
Lemma 2.1. When
$q>\gamma -1>0$
,
$$ \begin{align} \|W_{\beta,\gamma}(f)(i)\|_{l^q(\mathbb{Z}^n)} \leq C \|f(i)\|_{l^{qn/[n(\gamma-1)+q\beta\gamma]}(\mathbb{Z}^n)}^{1/(\gamma-1)}. \end{align} $$
Proof. Let
$\epsilon \in (0, 1/3)$
be sufficiently small and in (2.1), take
$$ \begin{align*}f(x) = \begin{cases} f(i) &\mbox{for}\ |x-i|<\epsilon \mbox{ and all } i \in \mathbb{Z}^n, \\ 0 &\mbox{otherwise}. \end{cases} \end{align*} $$
We claim that
$$ \begin{align} \|f\|_{L^{qn/[n(\gamma-1)+q\beta\gamma]}(\mathbb{R}^n)} \leq C \|f(i)\|_{l^{qn/[n(\gamma-1)+q\beta\gamma]}(\mathbb{Z}^n)}. \end{align} $$
In fact, since
$B_{\epsilon }(i) \cap B_{\epsilon }(j) =\emptyset $
for
$i \neq j$
,
$$ \begin{align*}\begin{aligned} \int_{\mathbb{R}^n} f^{qn/[n(\gamma-1)+q\beta\gamma]}(y)\,dy & =\sum_{i \in \mathbb{Z}^n} \int_{B_\epsilon(i)}f^{qn/[n(\gamma-1)+q\beta\gamma]}(i)\,dy \\ & =|B_1(0)|\epsilon^n \sum_{i \in \mathbb{Z}^n} f^{qn/[n(\gamma-1)+q\beta\gamma]}(i). \end{aligned} \end{align*} $$
This implies (2.3).
However, when
$t>2\epsilon $
, we have
$\bigcup _{|j-i|<t-2\epsilon }B_{\epsilon }(j) \subset B_{t-\epsilon }(i) \subset B_t(x)$
. Therefore,
$$ \begin{align} \int_{B_t(x)}f(y)\,dy \geq c\sum_{j \in \mathbb{Z}^n,|j-i|<t-2\epsilon}f(j)\int_{B_\epsilon(j)}dy \geq c|B_1(0)|\epsilon^{n}\sum_{j \in \mathbb{Z}^n,|j-i|<t-2\epsilon}f(j). \end{align} $$
Since
$i,j \in \mathbb {Z}^n$
, when
$\epsilon $
is sufficiently small,
$|j-i| \geq 2\epsilon $
for
$i \neq j,$
and when
$t>2\epsilon $
,
$$ \begin{align*} \{j \in \mathbb{Z}^n : |j-i|<t-2\epsilon\}=\{j \in \mathbb{Z}^n : |j-i|<t\} \quad \mbox{for all } i \in \mathbb{Z}^n. \end{align*} $$
Therefore,
$$ \begin{align*} \sum_{j \in \mathbb{Z}^n,|j-i|<2\epsilon}f(j)=0 \quad \mbox{and} \quad \sum_{j \in \mathbb{Z}^n,|j-i|<t-2\epsilon}f(j)=\sum_{j \in \mathbb{Z}^n,|j-i|<t}f(j), \end{align*} $$
when
$\epsilon $
is sufficiently small. Thus, from (2.4),
$$ \begin{align*} W_{\beta,\gamma}(f)(i) =0+\int_{2\epsilon}^\infty \bigg[\sum_{j \in \mathbb{Z}^n,|j-i|<t}f(j)\bigg]^{{1}/{(\gamma-1)}} t^{{(\beta\gamma-n)}{(\gamma-1)}}\,\frac{dt}{t} \leq C W_{\beta,\gamma}(f)(x). \end{align*} $$
Inserting this result and (2.3) into (2.1), we obtain (2.2).
2.2. Regularity lifting lemma
Let V be a topological vector space. Suppose there are two extended norms,
$\|\cdot \|_X, \|\cdot \|_Y :V \to [0,\infty ]$
, defined on V (that is, allowing that the norm of an element in V might be infinity). Let
$$ \begin{align*} X := \{ v \in V : \|v\|_X < \infty\} \quad \mbox{and} \quad Y := \{ v \in V : \|v\|_Y < \infty\}. \end{align*} $$
Lemma 2.2 [Reference Chen and Li3, Theorem 3.3.1].
Let T be a contraction map from X into itself and from Y into itself. Assume that
$f \in X$
and that there exists a function
$g \in Z := X \cap Y$
such that
$f = Tf + g$
in X. Then f also belongs to Z.
This regularity lifting lemma can be used to study integral equations involving the Riesz potentials and the Wolff potentials. It was used in [Reference Chen, Jin, Li and Lim2, Reference Chen, Li and Ou5, Reference Chen and Zheng6, Reference Jin and Li13, Reference Ma, Chen and Li22] to obtain better integrability results for positive solutions of Hardy–Littlewood–Sobolev-type equations, Stein–Weiss-type equations, discrete Stein–Weiss-type equations and Wolff-type equations.
3. Summability
Theorem 3.1. Assume
$w \in l^{s_0}(\mathbb {Z}^n)$
solves (1.6) with (1.7) and (1.8). Then,
$$ \begin{align} w \in l^s(\mathbb{Z}^n) \quad \mbox{for all } {s} \in \bigg(\frac{n(\gamma-1)}{n-\beta\gamma},\infty \bigg]. \end{align} $$
Proof. By [Reference Chen and Zheng6, Lemma 2.2] or [Reference Huang, Li and Yin12, Lemma 2.1],
$w \in l^{s_0}(\mathbb {Z}^n)$
implies
$w \in l^{\infty }(\mathbb {Z}^n)$
, and hence
$$ \begin{align} w \in l^{s}(\mathbb{Z}^n) \quad \mbox{for all } s \in [s_0,\infty]. \end{align} $$
From (1.8), it follows that
$s_0 \geq {n((\gamma -1))}/{(n-\beta \gamma )}$
. We lift the summability from (3.2) to (3.1).
Step 1. Establish an operator equation. For
$A>0$
, set
$$ \begin{align*}w_A(i) = \begin{cases} w(i) & \mbox{if } |i|>A, \\ 0 & \mbox{otherwise}, \end{cases} \end{align*} $$
and
$w_B(i)=w(i)-w_A(i)$
. Let
$\sigma $
satisfy
$$ \begin{align} \frac{2-\gamma}{s_0}<\frac{1}{\sigma}<\frac{2-\gamma}{s_0} +\frac{n-\beta\gamma}{n}. \end{align} $$
For
$g \in l^\sigma (\mathbb {Z}^n)$
, define operators T and S by
$$ \begin{align*} Tg:=R(i)\int_0^\infty \bigg(\frac{\sum_{|j-i|<t}w^{q}(j)} {t^{n-\beta\gamma}}\bigg)^{{(2-\gamma)}/{(\gamma-1)}} \frac{\sum_{|j-i|<t}w_A^{q-1}(j)g(j)}{t^{n-\beta\gamma}} \,\frac{dt}{t}, \end{align*} $$
$$ \begin{align*} Sg:=\int_0^\infty \bigg(\frac{\sum_{|j-i|<t}w_A^{q-1}(j)g(j)} {t^{n-\beta\gamma}}\bigg)^{{1}/{(\gamma-1)}} \,\frac{dt}{t} \end{align*} $$
and write
$$ \begin{align*} F:=R(x)\int_0^\infty \bigg(\frac{\sum_{|j-i|<t}w^{q}(j)} {t^{n-\beta\gamma}}\bigg)^{{(2-\gamma)}/{(\gamma-1)}} \frac{\sum_{|j-i|<t}w_B^{q}(j)}{t^{n-\beta\gamma}} \,\frac{dt}{t}. \end{align*} $$
Clearly, w is a solution of the operator equation
$g=Tg+F$
.
Step 2. T is a contraction map from
$l^\sigma (\mathbb {Z}^n)$
into itself. In fact, the Hölder inequality and (1.7) imply
$|Tg| \leq Cw^{2-\gamma } |Sg|^{\gamma -1}$
. Using the Hölder inequality again yields
$$ \begin{align} \|Tg\|_\sigma \leq C\|w\|_{s_0}^{2-\gamma} \|Sg\|_t^{\gamma-1}, \end{align} $$
where
$t>0$
satisfies
$$ \begin{align} \frac{1}{\sigma}=\frac{2-\gamma}{s_0}+\frac{\gamma-1}{t}. \end{align} $$
Hereafter, for simplicity, we denote
$\|\cdot \|_{l^s(\mathbb {Z}^n)}$
by
$\|\cdot \|_s$
.
$$ \begin{align} 0<\frac{\gamma-1}{t}<1-\frac{\beta\gamma}{n}. \end{align} $$
Therefore, we can use Lemma 2.1 to obtain
$$ \begin{align} \|Sg\|_t \leq C\|w_A^{q-1} g\|_{{nt}/{(n(\gamma-1)+t\beta\gamma)}}^{{1}/{(\gamma-1)}}. \end{align} $$
Since (3.5) leads to
$$ \begin{align*} \frac{\gamma-1}{t}-\frac{1}{\sigma} =\frac{q-1}{s_0}-\frac{\beta\gamma}{n}, \end{align*} $$
it follows from (3.7) and the Hölder inequality that
$\|Sg\|_t^{\gamma -1} \leq C\|w_A\|_{s_0}^{q-1} \|g\|_\sigma $
. Inserting this into (3.4) yields
$$ \begin{align*} \|Tg\|_\sigma \leq C\|w\|_{s_0}^{2-\gamma} \|w_A\|_{s_0}^{q-1} \|g\|_\sigma. \end{align*} $$
Since
$w \in l^{s_0}(\mathbb {Z}^n)$
,
$$ \begin{align*} C\|w\|_{s_0}^{2-\gamma} \|w_A\|_{s_0}^{q-1} \leq \tfrac{1}{2} \end{align*} $$
when A is sufficiently large. Thus, T is a shrinking operator. Since T is linear, it follows that T is a contraction map from
$l^{\sigma }(\mathbb {Z}^n)$
to itself as long as
$\sigma $
satisfies (3.3).
Step 3. Estimating F to lift the regularity. Similar to the derivation of (3.4) and (3.7), for all
$\sigma $
satisfying (3.3), we also deduce that
$$ \begin{align*} \|F\|_\sigma \leq C\|w\|_{s_0}^{2-\gamma} \|w_B^{q}\|_{{nt}/{(n(\gamma-1)+t\beta\gamma)}}, \end{align*} $$
where t satisfies (3.6). Noting
$w\in l^{s_0}(\mathbb {Z}^n)$
and the definition of
$w_B$
, we have
$F \in l^{\sigma }(\mathbb {Z}^n)$
as long as
$\sigma $
satisfies (3.3). Taking
$X=l^{s_0}(\mathbb {Z}^n)$
,
$Y=l^{\sigma }(\mathbb {Z}^n)$
and
$Z=l^{s_0}(\mathbb {Z}^n) \cap l^{\sigma }(\mathbb {Z}^n)$
in Lemma 2.2, yields
$w \in l^{\sigma }(\mathbb {Z}^n)$
for all
$\sigma $
satisfying (3.3).
Step 4. Extend the interval from (3.3) to that in (3.1). Let
$$ \begin{align} \frac{1}{s} \in \bigg(0,\frac{n-\beta\gamma}{n(\gamma-1)}\bigg). \end{align} $$
Then we can use Lemma 2.1 to deduce that
$$ \begin{align} \|w\|_s \leq C\|w^{q}\|_{{ns}/{(n(\gamma-1)+s\beta\gamma)}}^{{1}/{(\gamma-1)}} = C\|w\|_{{nsq}/{(n(\gamma-1)+s\beta\gamma)}}^{{q}/{(\gamma-1)}}. \end{align} $$
Noting (3.3), from (3.9), we see that
$\|w\|_s <\infty $
as long as s satisfies
$$ \begin{align} \frac{2-\gamma}{s_0}< \frac{n(\gamma-1)+s\beta\gamma}{nsq} <\frac{2-\gamma}{s_0}+\frac{n-\beta\gamma}{n}. \end{align} $$
Next, we will prove that (3.10) is true as long as (3.8) holds. We only need to verify
$$ \begin{align} \frac{n-\beta\gamma}{n(\gamma-1)} \leq \frac{q}{\gamma-1}\bigg[\frac{2-\gamma}{s_0}+\frac{n-\beta\gamma}{n}\bigg] -\frac{\beta\gamma}{n(\gamma-1)}. \end{align} $$
In fact,
$$ \begin{align*}\begin{aligned} \frac{n-\beta\gamma}{n(\gamma-1)} &\leq \frac{q}{\gamma-1}\bigg[\frac{\beta\gamma(2-\gamma)}{n(q-\gamma+1)} +\frac{n-\beta\gamma}{n}\bigg]-\frac{\beta\gamma}{n(\gamma-1)}\\ &\Longleftrightarrow 1 \leq q\bigg[\frac{\beta\gamma}{n}\bigg(\frac{2-\gamma}{q-\gamma+1}-1\bigg)+1\bigg] =q\bigg[\frac{\beta\gamma}{n}\frac{1-q}{q-\gamma+1}+1\bigg]\\ &\Longleftrightarrow \beta\gamma q(q-1) \leq n(q-\gamma+1)(q-1)\\ &\Longleftrightarrow q \geq \frac{n(\gamma-1)}{n-\beta\gamma}. \end{aligned} \end{align*} $$
Thus, (3.11) is true, and hence
$w \in l^s(\mathbb {Z}^n)$
for all s satisfying (3.8). Combining this with (3.2), we see that (3.1) is true.
Step 5. If
$$ \begin{align} 1/s \geq (n-\beta\gamma)/[n(\gamma-1)], \end{align} $$
we claim
$w \not \in l^s(\mathbb {Z}^n)$
. In fact, when
$|i|$
is suitably large,
$$ \begin{align*} w(i) \geq c\int_{2|i|}^\infty \bigg[\frac{\sum_{|j| \leq 1}w^q(j)}{t^{n-\beta\gamma}}\bigg]^{{1}/{\gamma}} \geq c|i|^{{(\beta\gamma-n)}/{(\gamma-1)}}. \end{align*} $$
Therefore, by (3.12), for suitably large
$M>0$
,
$$ \begin{align*} \sum_{|i| \geq M} w^s(i) \geq c\sum_{|i| \geq M} |i|^{{s(\beta\gamma-n)}/{(\gamma-1)}}=\infty. \end{align*} $$
The claim is proved.
Steps 4 and 5 show that the integrability interval is the one in (3.1). The proof of Theorem 3.1 is complete.
4. Decay rates
Proposition 4.1. Assume
$w \in l^{s_0}(\mathbb {Z}^n)$
solves (1.6) with (1.7) and (1.8). If
$w(i)$
belongs to a radially symmetric and decreasing surface, we can find
$C>1$
such that for large
$|i|$
,
$$ \begin{align*} C^{-1} |i|^{{(\beta\gamma-n)}/{(\gamma-1)}} \leq w(i) \leq C |i|^{{(\beta\gamma-n)}/{(\gamma-1)}}. \end{align*} $$
Proof. Without loss of generality, we assume
$w(i)$
is radially symmetric about
$i_0$
. Write
$$ \begin{align*} \omega(r)=w(i) \quad with \quad r=|i-i_0|. \end{align*} $$
Step 1. For any
$s>{(n-\beta \gamma )}/{n(\gamma -1)}$
, we can find
$C>0$
such that for large
$R>0$
,
$$ \begin{align} \omega(R) \leq CR^{-n/s}. \end{align} $$
In fact, from Theorem 3.1,
$w \in l^s(\mathbb {Z}^n)$
when s belongs to the interval of (3.1). Thus, we can denote
$\sum _{i \in \mathbb {Z}^n}w^s(i)$
by a constant
$C_s$
. In view of the monotonicity of
$\omega (R)$
, we deduce that
$$ \begin{align*} c \ \omega^s(R) R^n \leq \sum_{R/2<|j-i_0|<R} w^s(j) \leq C_s. \end{align*} $$
Thus, (4.1) is verified.
Step 2. There exists
$c>0$
such that
$w(i) \geq c|i|^{-{(n-\beta \gamma )}/{(\gamma -1)}}$
for large
$|i|$
. In fact, if
${|j-i_0|<2}$
, then for large
$|i|$
and
$t \in (2|i|,4|i|)$
,
$$ \begin{align*} |j-i| \leq |j-i_0|+|i-i_0| <2+|i_0|+|i|<t. \end{align*} $$
This means
$\{j : |j-i_0|<2\} \subset \{j : |j-i|<t\}$
. Therefore, by the monotonicity of
$\omega (r)$
,
$$ \begin{align*} \sum_{|j-i|<t}w^{q}(j) \geq \sum_{|j-i_0|<2}w^{q}(j) \geq \omega^q(2)\bigg(\sum_{|j-i_0|<2}1\bigg)=c, \end{align*} $$
when
$t \in (2|i|,4|i|)$
. Thus,
$$ \begin{align*} w(i) \geq \int_{2|i|}^{4|i|} \bigg[\frac{\sum_{|j-i|<t}w^{q}(j)}{t^{n-\beta\gamma}}\bigg]^{{1}/{(\gamma-1)}} \,\frac{dt}{t} \geq c \int_{2|i|}^{4|i|} \frac{1}{t^{{(n-\beta\gamma)}/({\gamma-1)}}} \,\frac{dt}{t} \geq \frac{c}{|i|^{{(n-\beta\gamma)}/{(\gamma-1)}}}. \end{align*} $$
Step 3. Estimate the upper bound of
$w(i)$
for large
$|i|$
. Clearly,
$$ \begin{align*}\begin{array}{ll} w(i) & \leq C\displaystyle\int_0^{{|i|}/{2}} \bigg[\frac{\sum_{|j-i|<t}w^{q}(j)}{t^{n-\beta\gamma}}\bigg]^{{1}/{(\gamma-1)}} \,\frac{dt}{t} +C\displaystyle\int_{{|i|}/{2}}^{\infty} \bigg[\frac{\sum_{|j-i|<t}w^{q}(j)}{t^{n-\beta\gamma}}\bigg]^{{1}/{(\gamma-1)}} \,\frac{dt}{t} \\ &:=C(I_1+I_2). \end{array} \end{align*} $$
Claim 1. There exists
$C>0$
such that
$ I_1 \leq C|i|^{-{(n-\beta \gamma )}/{(\gamma -1)}} $
for large
$|i|$
. In fact, we have
${|i|}/{2} \leq |j| \leq {3|i|}/{2}$
when
$|j-i|<t$
and
$t<{|i|}/{2}$
. By virtue of the monotonicity of
$\omega (r)$
, for large
$|i|$
,
$$ \begin{align*} w(j)=\omega(|j-i_0|) \leq C \omega\bigg(\frac{|j|}{3}\bigg) \leq C \omega\bigg(\frac{|i|}{6}\bigg) \end{align*} $$
when
$|j-i|<t$
and
$t<{|i|}/{2}$
. Therefore, by (4.1),
$$ \begin{align} |i|^{{(n-\beta\gamma)}/{(\gamma-1)}}I_1 & \leq C|i|^{{(n-\beta\gamma)}/{(\gamma-1)}} \displaystyle\int_0^{{|i|}/{2}} \bigg[\frac{\omega^q(|i|/6)t^n }{t^{n-\beta\gamma}}\bigg]^{{1}/{(\gamma-1)}}\,\frac{dt}{t} \notag\\ & \leq C|i|^{{(n-\beta\gamma)}/{(\gamma-1)} -{nq}/{s(\gamma-1)}} \displaystyle\int_0^{{|i|}/{2}} t^{{\beta\gamma}/{(\gamma-1)}} \,\frac{dt}{t} \leq C|i|^{{n}/{(\gamma-1)} -{nq}/{s(\gamma-1)}}. \end{align} $$
We choose s approaching the left end point of the interval of (3.1) such that
$$ \begin{align} 1-\frac{q}{s}<0. \end{align} $$
Inserting this in (4.2) proves the claim.
Claim 2. There exists
$C>0$
such that
$ I_2 \leq C|i|^{-{(n-\beta \gamma )}/{(\gamma -1)}} $
for large
$|i|$
. In fact, since
$(\gamma -1)^{-1} \geq 1$
, Jensen’s inequality gives
$$ \begin{align*} I_2 &\leq C\displaystyle\int_{{|i|}/{2}}^{\infty} \bigg[\frac{\sum_{|j| \leq 2|i_0|,|j-i|<t}w^q(j)}{t^{n-\beta\gamma}}\bigg]^{{1}/{(\gamma-1)}} \,\frac{dt}{t} +C\displaystyle\int_{{|x|}/{2}}^{\infty} \bigg[\frac{\sum_{|j|>2|i_0|,|j-i|<t}w^q(j)}{t^{n-\beta\gamma}}\bigg]^{{1}/{(\gamma-1)}} \,\frac{dt}{t}\\ &:=C(I_{21}+I_{22}). \end{align*} $$
Since
$\sum _{|j| \leq 2|i_0|}w^q(j) \leq C$
,
$$ \begin{align*} |i|^{{(n-\beta\gamma)}/{(\gamma-1)}}I_{21} \leq C|i|^{{(n-\beta\gamma)}/{(\gamma-1)}} \int_{{|i|}/{2}}^{\infty} t^{{(\beta\gamma-n)}/{(\gamma-1)}} \,\frac{dt}{t} \leq C. \end{align*} $$
However, when
$|j|> 2|i_0|$
, we have
$|j-i_0| \geq |j|-|i_0|> {|j|}/{2}$
. Applying the monotonicity of
$\omega (r)$
and (4.1),
$$ \begin{align*} w^q(j)=\omega^q(|j-i_0|) \leq \omega^q\bigg(\frac{|j|}{2}\bigg) \leq C\bigg(\frac{|j|}{2}\bigg)^{-nq/s}. \end{align*} $$
By this result and (4.3),
$$ \begin{align*} \sum_{|j|> 2|i_0|,|j-i|<t}w^q(j) \leq C\sum_{2|i_0|<|j|<|i|+t} |j|^{-{nq}/{s}} \leq C. \end{align*} $$
Inserting this into
$I_{22}$
yields
$$ \begin{align*} |i|^{{(n-\beta\gamma)}/{(\gamma-1)}}I_{22} \leq C|i|^{{(n-\beta\gamma)}/{(\gamma-1)}} \int_{{|i|}/{2}}^{\infty} t^{-{(n-\beta\gamma)}/{(\gamma-1)}} \,\frac{dt}{t} \leq C. \end{align*} $$
Claim 2 is proved and the proof of Proposition 4.1 is complete.
Acknowledgement
The authors thank the unknown referees very much for their helpful suggestions.
