Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-01T14:17:47.963Z Has data issue: false hasContentIssue false
  • English
  • Français

A NONCOMMUTATIVE ANALOGUE OF CLAUSEN’S VIEW ON THE IDÈLE CLASS GROUP

Part of: Locally compact abelian groups Abelian categories $K$-theory in number theory Whitehead groups and $K_1$

Published online by Cambridge University Press:  02 April 2024

Oliver Braunling Open the ORCID record for Oliver Braunling [Opens in a new window] ,
Ruben Henrard  and
Adam-Christiaan van Roosmalen
Oliver Braunling*
Affiliation:
Universidad Autónoma de Madrid, Mathematics, Ciudad Universitaria de Cantoblanco, 28049 Madrid, Spain
Ruben Henrard
Affiliation:
Universiteit Hasselt, Campus Diepenbeek, Dept. WNI, 3590 Diepenbeek, Belgium (ruben.henrard@uhasselt.be)
Adam-Christiaan van Roosmalen
Affiliation:
Xi’an Jiaotong-Liverpool University, Dept. of Pure Mathematics, Suzhou 215123, P.R. China (ac.vanroosmalen@xjtlu.edu.cn)
*
oliver.braunling@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Clausen a prédit que le groupe des classes d’idèles de Chevalley d’un corps de nombres F apparaît comme le premier K-groupe de la catégorie des F-espaces vectoriels localement compacts. Cela s’est avéré vrai, et se généralise même aux groupes K supérieurs dans un sens approprié. Nous remplaçons F par une 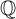$\mathbb {Q}$-algèbre semi-simple, et obtenons le groupe des classes d’idèles noncommutatif de Fröhlich de manière analogue, modulo les éléments de norme réduite une. Même dans le cas du corps de nombres, notre preuve est plus simple que celle existante, et repose sur le théorème de localisation pour des sous-catégories percolées. Enfin, en utilisant la théorie des corps de classes, nous interprétons la loi de réciprocité d’Hilbert (ainsi qu’une variante noncommutative) en termes de nos résultats.

Clausen predicted that Chevalley’s idèle class group of a number field F appears as the first K-group of the category of locally compact F-vector spaces. This has turned out to be true and even generalizes to the higher K-groups in a suitable sense. We replace F by a semisimple 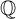$\mathbb {Q}$-algebra and obtain Fröhlich’s noncommutative idèle class group in an analogous fashion, modulo the reduced norm one elements. Even in the number field case, our proof is simpler than the existing one and based on the localization theorem for percolating subcategories. Finally, using class field theory as input, we interpret Hilbert’s reciprocity law (as well as a noncommutative variant) in terms of our results.

Keywords

Locally compact modulesK-theoryexact categoryidèle class groupHilbert symbol

MSC classification

Primary: 19B28: $K_1$ of group rings and orders 19F05: Generalized class field theory 18E35: Localization of categories
Secondary: 22B05: General properties and structure of LCA groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , First View , pp. 1 - 48
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by DFG GK1821 “Cohomological Methods in Geometry”. The third author was supported by FWO (12.M33.16N)

References

Arndt, P. and Braunling, O., ‘On the automorphic side of the $\mathrm{K}$ -theoretic Artin symbol’, Selecta Math. (N.S.) 25(3) (2019), Art. 38, 47. MR 3954369CrossRefGoogle Scholar
Auslander, M. and Goldman, O., ‘Maximal orders’, Trans. Amer. Math. Soc. 97 (1960), 1–24. MR 117252CrossRefGoogle Scholar
Armacost, D., The Structure of Locally Compact Abelian Groups, Monographs and Textbooks in Pure and Applied Mathematics, vol. 68 (Marcel Dekker, Inc., New York, 1981). MR 637201Google Scholar
Borceux, F. and Bourn, D., Mal’cev, Protomodular, Homological and Semi-Abelian Categories, vol. 566 (Kluwer Academic Publishers, Dordrecht, 2004). MR 2044291CrossRefGoogle Scholar
Bazzoni, S. and Crivei, S., ‘One-sided exact categories’, J. Pure Appl. Algebra 217(2) (2013), 377–391. MR 2969259CrossRefGoogle Scholar
Burns, D. and Flach, M., ‘Tamagawa numbers for motives with (non-commutative) coefficients’, Doc. Math. 6 (2001), 501–570. MR 1884523CrossRefGoogle Scholar
Blumberg, A., Gepner, D. and Tabuada, G., ‘A universal characterization of higher algebraic $\mathrm{K}$ -theory’, Geom. Topol. 17(2) (2013), 733–838. MR 3070515CrossRefGoogle Scholar
Barr, M., Grillet, P. A. and van Osdol, D. H., Exact Categories and Categories of Sheaves, vol. 236 (Springer, Cham, 1971). MR 3727441CrossRefGoogle Scholar
Braunling, O., Henrard, R. and van Roosmalen, A.-C., ‘ $\mathrm{K}$ -theory of locally compact modules over orders’, Israel Journal of Mathematics 246 (2021) 315–333. MR 4358282CrossRefGoogle Scholar
Bak, A. and Rehmann, U., ‘ ${K}_2$ -analogs of Hasse’s norm theorems’, Comment. Math. Helv. 59(1) (1984), 1–11. MR 743941CrossRefGoogle Scholar
Braunling, O., ‘On the relative $\mathrm{K}$ -group in the $\mathrm{ETNC}$ ’, New York J. Math. 25 (2019), 1112–1177. MR 4028830Google Scholar
Bühler, T., ‘Exact categories’, Expo. Math. 28(1) (2010), 1–69. MR 2606234CrossRefGoogle Scholar
Carlsson, G., ‘On the algebraic $\mathrm{K}$ -theory of infinite product categories’, $K$ -Theory 9(4) (1995), 305–322. MR 1351941Google Scholar
Clausen, D., ‘A $\mathrm{K}$ -theoretic approach to Artin maps’, unpublished, arXiv:1703.07842 [math.KT], (2017).Google Scholar
Curtis, C. and Reiner, I., Methods of Representation Theory. Vol. II, Pure and Applied Mathematics (New York) (John Wiley & Sons, Inc., New York, 1987). With applications to finite groups and orders, A Wiley-Interscience Publication. MR 892316Google Scholar
Curtis, C. and Reiner, I., Methods of Representation Theory. Vol. I, Wiley Classics Library (John Wiley & Sons, Inc., New York, 1990). With applications to finite groups and orders, Reprint of the 1981 original, A Wiley-Interscience Publication. MR 1038525Google Scholar
Chase, S. and Waterhouse, W., ‘Moore’s theorem on uniqueness of reciprocity laws’, Invent. Math. 16 (1972), 267–270. MR 311623CrossRefGoogle Scholar
Fröhlich, A., ‘Locally free modules over arithmetic orders’, J. Reine Angew. Math. 274/275 (1975), 112–124. Collection of articles dedicated to Helmut Hasse on his seventy-fifth birthday, III. MR 0376619Google Scholar
Fesenko, I. and Vostokov, S., Local Fields and Their Extensions, second edn., Translations of Mathematical Monographs, vol. 121 (American Mathematical Society, Providence, RI, 2002). With a foreword by I. R. Shafarevich. MR 1915966Google Scholar
Gras, G., Class Field Theory, Springer Monographs in Mathematics (Springer-Verlag, Berlin, 2003). From theory to practice, Translated from the French manuscript by Henri Cohen. MR 1941965CrossRefGoogle Scholar
Harari, D., Galois Cohomology and Class Field Theory, Universitext (Springer, Cham, 2020). Translated from the 2017 French original by Andrei Yafaev. MR 4174395CrossRefGoogle Scholar
Henrard, R., Kvamme, S., van Roosmalen, A.-C. and Wegner, S.-A., ‘The left heart and exact hull of an additive regular category’, Rev. Mat. Iberoam. 39(2) (2023), 439–494. MR 4575371CrossRefGoogle Scholar
Hewitt, E. and Ross, K., Abstract Harmonic Analysis. Vol. I, second edn., Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 115 (Springer-Verlag, Berlin-New York, 1979). Structure of topological groups, integration theory, group representations. MR 551496CrossRefGoogle Scholar
Hoffmann, N. and Spitzweck, M., ‘Homological algebra with locally compact abelian groups’, Adv. Math. 212(2) (2007), 504–524. MR 2329311CrossRefGoogle Scholar
Hutchinson, K., ‘The 2-Sylow subgroup of the wild kernel of exceptional number fields’, J. Number Theory 87(2) (2001), 222–238. MR 1824144CrossRefGoogle Scholar
Hutchinson, K., ‘On tame and wild kernels of special number fields’, J. Number Theory 107(2) (2004), 368–391. MR 2072396CrossRefGoogle Scholar
Henrard, R. and van Roosmalen, A.-C., ‘Derived categories of (one-sided) exact categories and their localizations’, Preprint, 2019, arxiv:1903.12647 [math.CT].Google Scholar
Henrard, R. and van Roosmalen, A.-C., ‘Localizations of (one-sided) exact categories’, Preprint, 2019, arxiv:1903.10861 [math.CT].Google Scholar
Henrard, R. and van Roosmalen, A.-C., ‘On the obscure axiom for one-sided exact categories’, Journal of Pure and Applied Algebra, 228(7) (2024), p. 107635.Google Scholar
Henrard, R. and van Roosmalen, A.-C., ‘Preresolving categories and derived equivalences’, Preprint, 2020, arxiv:2010.13208 [math.CT].Google Scholar
Keller, B., ‘Chain complexes and stable categories’, Manuscripta Math. 67(4) (1990), 379–417. MR 1052551CrossRefGoogle Scholar
Kahn, B. and Levine, M., ‘Motives of Azumaya algebras’, J. Inst. Math. Jussieu 9(3) (2010), 481–599. MR 2650808CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Categories and Sheaves, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 332 (Springer-Verlag, Berlin, 2006). MR 2182076CrossRefGoogle Scholar
Kasprowski, D. and Winges, C., ‘Algebraic $\mathrm{K}$ -theory of stable $\infty$ -categories via binary complexes’, J. Topol. 12(2) (2019), 442–462. MR 4072172CrossRefGoogle Scholar
Lang, S., Cyclotomic Fields I and II, second edn., Graduate Texts in Mathematics, vol. 121 (Springer-Verlag, New York, 1990). With an appendix by Karl Rubin. MR 1029028CrossRefGoogle Scholar
Lurie, J., ‘Higher algebra’, unpublished (2017).Google Scholar
Merkurjev, A., ‘On the torsion in ${\mathrm{K}}_2$ of local fields’, Ann. of Math. (2) 118(2) (1983), 375–381. MR 717828CrossRefGoogle Scholar
Moore, C. C., ‘Group extensions of $\mathrm{p}$ -adic and adelic linear groups’, Inst. Hautes Études Sci. Publ. Math. (35) (1968), 157–222. MR 244258CrossRefGoogle Scholar
Merkurjev, A. and Suslin, A., ‘ $K$ -cohomology of Severi–Brauer varieties and the norm residue homomorphism’, Izv. Akad. Nauk SSSR Ser. Mat. 46(5) (1982), 1011–1046, 1135–1136. MR 675529Google Scholar
Merkurjev, A. and Suslin, A., ‘Motivic cohomology of the simplicial motive of a Rost variety’, J. Pure Appl. Algebra 214(11) (2010), 2017–2026. MR 2645334CrossRefGoogle Scholar
Nikolaus, T. and Scholze, P., ‘On topological cyclic homology’, Acta Math. 221(2) (2018), 203–409. MR 3904731CrossRefGoogle Scholar
Reiner, I., Maximal Orders, London Mathematical Society Monographs. New Series, vol. 28 (The Clarendon Press, Oxford University Press, Oxford, 2003). Corrected reprint of the 1975 original, with a foreword by M. J. Taylor. MR 1972204CrossRefGoogle Scholar
Rosenberg, A., ‘Homological algebra of noncommutative spaces, I’, preprint, 2011, Max Planck, Bonn: MPIM 11-69.Google Scholar
Schlichting, M., ‘Negative $\mathrm{K}$ -theory of derived categories’, Math. Z. 253(1) (2006), 97–134. MR 2206639CrossRefGoogle Scholar
Shastri, P., ‘ Reciprocity laws: Artin–Hilbert, Cyclotomic fields and related topics ’, in Proceedings of the Summer School, Pune, India, June 7–30, 1999 (Bhaskaracharya Pratishthana, Pune, 2000), 175–183. MR 1802370Google Scholar
Srinivas, V., Algebraic $K$ -Theory (Birkhäuser, Boston, MA, 2008). MR 1382659Google Scholar
Wilson, S. M. J., ‘Reduced norms in the $\mathrm{K}$ -theory of orders’, J. Algebra 46(1) (1977), 1–11. MR 0447211CrossRefGoogle Scholar