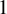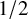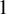1 Introduction
Throughout the article, the ground field is assumed to be the complex number field
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
1.1 K-stability, birational superrigidity and a conjecture
The notion of K-stability was introduced by Tian [Reference TianTia97] as an attempt to characterize the existence of Kähler–Einstein metrics (KE metrics, for short) on Fano manifolds. Later, K-stability was extended and reformulated by Donaldson [Reference DonaldsonDon02] in algebraic terms. The notion of K-stability emerged in the study of KE metrics (see [Reference DonaldsonDon02], [Reference TianTia97]), and it gives a characterization of the existence of a KE metric for smooth Fano manifolds (see [Reference Chen, Donaldson and SunCDS15], [Reference TianTia15]).
Birational (super)rigidity means the uniqueness of a Mori fiber space in the birational equivalence class (see Definition 2.2), and this notion has its origin in the rationality problem of Fano varieties. Specifically, it grew out of the study of birational self-maps of smooth quartic 3-folds by Iskovskikh and Manin [Reference Iskovskikh and ManinIM71] (see [Reference PukhlikovPuk13] and [Reference CheltsovChe05] for surveys).
K-stability and birational superrigidity have completely different origins, and we are unable to find a similarity in their definitions. However, both of them are closely related to some mildness of singularities of pluri-anticanonical divisors (or linear systems). For example, it is proved by Odaka and Sano [Reference Odaka and SanoOS12] (see also [Reference TianTia87]) that a Fano variety X of dimension n is K-stable if
![]() $\alpha (X)> n/(n+1)$
. Here,
$\alpha (X)> n/(n+1)$
. Here,
is called the alpha invariant of X and it measures singularities of pluri-anticanonical divisors. We refer readers to [Reference FujitaFuj19b], [Reference LiLi17], [Reference Fujita and OdakaFO18] and [Reference Blum and JonssonBJ20] for criteria for K-stability in terms of beta and delta invariants which are more or less related to singularities of pluri-anticanonical divisors. On the other hand, it is known that a Fano variety of Picard number one is birationally superrigid if and only if the pair
![]() $(X, \lambda \mathcal {M})$
is canonical for any
$(X, \lambda \mathcal {M})$
is canonical for any
![]() $\lambda \in \mathbb {Q}_{> 0}$
and any movable linear system
$\lambda \in \mathbb {Q}_{> 0}$
and any movable linear system
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\lambda \mathcal {M} \sim _{\mathbb {Q}} - K_X$
(see Theorem 2.4). With these relations in mind, one may expect a positive answer to the following.
$\lambda \mathcal {M} \sim _{\mathbb {Q}} - K_X$
(see Theorem 2.4). With these relations in mind, one may expect a positive answer to the following.
Conjecture 1.1. A birationally superrigid Fano variety is K-stable.
Actually, we expect stronger conjectures to hold (see Section 7.4 for discussions). The main aim of this article is to verify Conjecture 1.1 for quasi-smooth Fano 3-fold weighted hypersurfaces.
1.2 Evidences for the conjecture
1.2.a Smooth Fano manifolds
Smooth quartic
![]() $3$
-folds and double covers of
$3$
-folds and double covers of
![]() $\mathbb {P}^3$
branched along a smooth hypersurface of degree
$\mathbb {P}^3$
branched along a smooth hypersurface of degree
![]() $6$
(or equivalently smooth weighted hypersurfaces of degree
$6$
(or equivalently smooth weighted hypersurfaces of degree
![]() $6$
in
$6$
in
![]() $\mathbb {P} (1, 1, 1, 1, 3)$
) are the only smooth Fano 3-fold that are birationally superrigid (see [Reference Iskovskikh and ManinIM71], [Reference IskovskikhIsk80], [Reference CheltsovChe05]). K-stability (and hence the existence of a KE metric) is proved for smooth quartic 3-folds ([Reference FujitaFuj19a, Corollary 1.4]) and for smooth weighted hypersurfaces of degree
$\mathbb {P} (1, 1, 1, 1, 3)$
) are the only smooth Fano 3-fold that are birationally superrigid (see [Reference Iskovskikh and ManinIM71], [Reference IskovskikhIsk80], [Reference CheltsovChe05]). K-stability (and hence the existence of a KE metric) is proved for smooth quartic 3-folds ([Reference FujitaFuj19a, Corollary 1.4]) and for smooth weighted hypersurfaces of degree
![]() $6$
in
$6$
in
![]() $\mathbb {P} (1, 1, 1, 1, 3)$
([Reference Cheltsov, Park and WonCPW14, Corollary 3.4]).
$\mathbb {P} (1, 1, 1, 1, 3)$
([Reference Cheltsov, Park and WonCPW14, Corollary 3.4]).
We have evidences in arbitrary dimension
![]() $n \ge 3$
. After the results established in low-dimensional cases in [Reference Iskovskikh and ManinIM71], [Reference PukhlikovPuk87] and [Reference de Fernex, Ein and MustaţădFEM03], it is finally proved by de Fernex [Reference de FernexdF13] that any smooth hypersurface of degree
$n \ge 3$
. After the results established in low-dimensional cases in [Reference Iskovskikh and ManinIM71], [Reference PukhlikovPuk87] and [Reference de Fernex, Ein and MustaţădFEM03], it is finally proved by de Fernex [Reference de FernexdF13] that any smooth hypersurface of degree
![]() $n+1$
in
$n+1$
in
![]() $\mathbb {P}^{n+1}$
is birationally superrigid for
$\mathbb {P}^{n+1}$
is birationally superrigid for
![]() $n \ge 3$
. On the other hand, it is proved by Fujita [Reference FujitaFuj19a] that any such hypersurface is K-stable (hence admits a KE metric). It is also proved in [Reference ZhuangZhu20b] that a smooth Fano complete intersection
$n \ge 3$
. On the other hand, it is proved by Fujita [Reference FujitaFuj19a] that any such hypersurface is K-stable (hence admits a KE metric). It is also proved in [Reference ZhuangZhu20b] that a smooth Fano complete intersection
![]() $X \subset \mathbb {P}^{n+r}$
of Fano index
$X \subset \mathbb {P}^{n+r}$
of Fano index
![]() $1$
, codimension r and dimension
$1$
, codimension r and dimension
![]() $n \ge 10 r$
is birationally superrigid and K-stable.
$n \ge 10 r$
is birationally superrigid and K-stable.
1.2.b Fano 3-fold weighted hypersurfaces
By a quasi-smooth Fano
![]() $3$
-fold weighted hypersurface, we mean a Fano 3-fold (with only terminal singularities) embedded as a quasi-smooth hypersurface in a well-formed weighted projective 4-space
$3$
-fold weighted hypersurface, we mean a Fano 3-fold (with only terminal singularities) embedded as a quasi-smooth hypersurface in a well-formed weighted projective 4-space
![]() $\mathbb {P} (a_0, \dots , a_4)$
(see Section 2.2.b for quasi-smoothness and well-formedness). Let
$\mathbb {P} (a_0, \dots , a_4)$
(see Section 2.2.b for quasi-smoothness and well-formedness). Let
![]() $X = X_d \subset \mathbb {P} (a_0, \dots , a_4)$
be a quasi-smooth Fano 3-fold weighted hypersurface of degree d. Then the class group
$X = X_d \subset \mathbb {P} (a_0, \dots , a_4)$
be a quasi-smooth Fano 3-fold weighted hypersurface of degree d. Then the class group
![]() $\operatorname {Cl} (X)$
is isomorphic to
$\operatorname {Cl} (X)$
is isomorphic to
![]() $\mathbb {Z}$
and is generated by
$\mathbb {Z}$
and is generated by
![]() $\mathcal {O}_X (1)$
(see, for example, [Reference OkadaOka19, Remark 4.2]). By adjunction, we have
$\mathcal {O}_X (1)$
(see, for example, [Reference OkadaOka19, Remark 4.2]). By adjunction, we have
![]() $\mathcal {O}_X (-K_X) \cong \mathcal {O}_X (\iota _X)$
, where
$\mathcal {O}_X (-K_X) \cong \mathcal {O}_X (\iota _X)$
, where
 $$\begin{align*}\iota_X := \sum_{i=0}^4 a_i - d \in \mathbb{Z}_{> 0}. \end{align*}$$
$$\begin{align*}\iota_X := \sum_{i=0}^4 a_i - d \in \mathbb{Z}_{> 0}. \end{align*}$$
We call
![]() $\iota _X$
the Fano index (or simply index) of X.
$\iota _X$
the Fano index (or simply index) of X.
By [Reference Iano-FletcherIF00] and [Reference Chen, Chen and ChenCCC11], quasi-smooth Fano 3-fold weighted hypersurfaces of index
![]() $1$
are classified and they consist of 95 families. Among them, quartic 3-folds and weighted hypersurfaces of degree
$1$
are classified and they consist of 95 families. Among them, quartic 3-folds and weighted hypersurfaces of degree
![]() $6$
in
$6$
in
![]() $\mathbb {P} (1, 1, 1, 1, 3)$
are smooth and the remaining 93 families consist of singular Fano 3-folds (with terminal quotient singularities). The descriptions of these 93 families are given in Table 7.
$\mathbb {P} (1, 1, 1, 1, 3)$
are smooth and the remaining 93 families consist of singular Fano 3-folds (with terminal quotient singularities). The descriptions of these 93 families are given in Table 7.
Theorem 1.2 [Reference Cheltsov and ParkCP17], [Reference Corti, Pukhlikhov and ReidCPR00].
Any quasi-smooth Fano
![]() $3$
-fold weighted hypersurface of index
$3$
-fold weighted hypersurface of index
![]() $1$
is birationally rigid.
$1$
is birationally rigid.
Among the 95 families, any quasi-smooth member of each of specific 50 families is birationally superrigid. The 50 families consist of 48 families in Table 7 which do not admit singularity with ‘quadratic involution (QI)’ or ‘elliptic involution (EI)’ in the fourth column plus the two families of smooth Fano weighted hypersurfaces. For each of the remaining 45 families, a general quasi-smooth member is strictly birationally rigid (meaning that it is not birationally superrigid) but some special quasi-smooth members are birationally superrigid (see Section 2.3 for details).
Theorem 1.3 [Reference CheltsovChe09, Corollary 1.45].
A general quasi-smooth member of each of the 95 families is K-stable and admits a KE metric.
The generality assumption is crucial in Theorem 1.3. In particular, it is highly likely that birationally superrigid special members of each of the above mentioned 45 families are not treated in Theorem 1.3. Note that openness of K-stability is known (see [Reference OdakaOda13], [Reference DonaldsonDon15] and [Reference Belousov and LoginovBL22]), and this implies the difficulty in determining which Fano varieties (in a given family) are K-stable. Although Theorems 1.2 and 1.3 give strong evidence for Conjecture 1.1, it is very important to consider special (quasi-smooth) members for Conjecture 1.1.
1.2.c Conceptual evidences
Apart from evidences by concrete examples given in Sections 1.2.a and 1.2.b, we have conceptual results supporting Conjecture 1.1.
The notion of slope stability for polarized varieties was introduced by Ross and Thomas (cf. [Reference Ross and ThomasRT07]). For a Fano variety X, slope stability of
![]() $(X, -K_X)$
is a weaker version of K-stability.
$(X, -K_X)$
is a weaker version of K-stability.
Theorem 1.4 [Reference Odaka and OkadaOO13, Theorem 1.1].
Let X be a birationally superrigid Fano manifold of Fano index
![]() $1$
. If
$1$
. If
![]() $\left | -K_X \right |$
is base point free, then
$\left | -K_X \right |$
is base point free, then
![]() $(X, -K_X)$
is slope stable.
$(X, -K_X)$
is slope stable.
As it is explained in Section 1.1, K-stability of a Fano variety X of dimension n follows from the inequality
![]() $\alpha (X)> n/(n+1)$
. In practice, the computations of alpha invariants are very difficult and hence it is not easy to prove the inequality
$\alpha (X)> n/(n+1)$
. In practice, the computations of alpha invariants are very difficult and hence it is not easy to prove the inequality
![]() $\alpha (X)> n/(n+1)$
.
$\alpha (X)> n/(n+1)$
.
Remark 1.5. In fact, our results show that there exists a birationally superrigid Fano 3-fold X such that
![]() $\alpha (X) < 3/4$
(see Example 5.17).
$\alpha (X) < 3/4$
(see Example 5.17).
Recently, Stibitz and Zhuang relaxed the assumption on the alpha invariants significantly under the assumption of birational superrigidity and obtained the following.
Theorem 1.6 [Reference Stibitz and ZhuangSZ19, Theorem 1.2, Corollary 3.1].
Let X be a birationally superrigid Fano variety. If
![]() $\alpha (X) \ge 1/2$
, then X is K-stable.
$\alpha (X) \ge 1/2$
, then X is K-stable.
Note that the assumption on the alpha invariant is
![]() $\alpha (X)> 1/2$
in [Reference Stibitz and ZhuangSZ19, Theorem 1.2], but the equality is allowed by [Reference Stibitz and ZhuangSZ19, Corollary 3.1]. It is informed by C. Xu and Z. Zhuang that one can even conclude the uniform K-stability of X in Theorem 1.6 under the same assumption. The notion of uniform K-stability is originally introduced in [Reference DerbanDer16b] and [Reference Boucksom, Hisamoto and JonssonBHJ17] (see also [Reference FujitaFuj19b] and [Reference Blum and JonssonBJ20]) and it is stronger than K-stabilityFootnote
1
. Moreover, it is very important to mention that uniform K-stability implies the existence of a KE metric ([Reference Li, Tian and WangLTW19]). Combining these results, we have the following.
$\alpha (X)> 1/2$
in [Reference Stibitz and ZhuangSZ19, Theorem 1.2], but the equality is allowed by [Reference Stibitz and ZhuangSZ19, Corollary 3.1]. It is informed by C. Xu and Z. Zhuang that one can even conclude the uniform K-stability of X in Theorem 1.6 under the same assumption. The notion of uniform K-stability is originally introduced in [Reference DerbanDer16b] and [Reference Boucksom, Hisamoto and JonssonBHJ17] (see also [Reference FujitaFuj19b] and [Reference Blum and JonssonBJ20]) and it is stronger than K-stabilityFootnote
1
. Moreover, it is very important to mention that uniform K-stability implies the existence of a KE metric ([Reference Li, Tian and WangLTW19]). Combining these results, we have the following.
Theorem 1.7 [Reference XuXu21, Theorem 9.6], [Reference Stibitz and ZhuangSZ19], [Reference Li, Tian and WangLTW19].
Let X be a birationally superrigid Fano variety, and assume that
![]() $\alpha (X) \ge 1/2$
. Then X is uniformly K-stable. In particular, X is K-stable and it admits a KE metric.
$\alpha (X) \ge 1/2$
. Then X is uniformly K-stable. In particular, X is K-stable and it admits a KE metric.
1.3 Main results
We state main theorem of this article.
Theorem 1.8 (Main theorem).
Let X be a quasi-smooth Fano
![]() $3$
-fold weighted hypersurface of index
$3$
-fold weighted hypersurface of index
![]() $1$
. Then
$1$
. Then
![]() $\alpha (X) \ge 1/2$
.
$\alpha (X) \ge 1/2$
.
The following is a direct consequence of Theorems 1.8 and 1.7.
Corollary 1.9. Any birationally superrigid quasi-smooth Fano
![]() $3$
-fold weighted hypersurface of index
$3$
-fold weighted hypersurface of index
![]() $1$
is K-stable and admits a KE metric.
$1$
is K-stable and admits a KE metric.
By [Reference Abban, Cheltsov and ParkACP20, Corollary 1.3], a birationally superrigid quasi-smooth Fano 3-fold weighted hypersurface necessarily has Fano index
![]() $1$
. Thus, we obtain the following.
$1$
. Thus, we obtain the following.
Corollary 1.10. Conjecture 1.1 is true for quasi-smooth Fano 3-fold weighted hypersurfaces.
It is natural to consider a generalization of Conjecture 1.1 by relaxing the assumption of birational superrigidity to birational rigidity (see Section 7.4) or to expect that the conclusion of Corollary 1.9 holds without the assumption of birational superrigidity. We are unable to relax the assumption of birational superrigidity to birational rigidity in Theorem 1.6 or 1.7, and thus we cannot conclude K-stability for strictly birationally rigid members as a direct consequence of Theorem 1.8. By the arguments delivered in this article, we are able to prove
![]() $\alpha (X)> 3/4$
for any quasi-smooth member X of suitable families. As a consequence, we have the following (see Section 7.3 for details).
$\alpha (X)> 3/4$
for any quasi-smooth member X of suitable families. As a consequence, we have the following (see Section 7.3 for details).
Theorem 1.11 (= Theorem 7.7).
Let X be any quasi-smooth member of a family which is given ‘KE’ in the right-most column of Table 7. Then X is K-stable and admits a KE metric.
We can also prove K-stability for any quasi-smooth member (which is not necessarily birationally superrigid) of suitable families.
Theorem 1.12 (= Corollary 7.13).
Let X be any quasi-smooth member of a family which is given ‘K’ or ‘KE’ in the right-most column of Table 7. Then X is K-stable.
We explain the organization of this article. In Section 2, we recall definitions and basic properties of relevant notions such as birational (super)rigidity, log canonical thresholds, alpha invariants and weighted projective varieties. In Section 3, we explain methods of computing log canonical thresholds and alpha invariants. By applying these methods, we compute local alpha invariants
![]() $\alpha _{\mathsf {p}} (X)$
for any point
$\alpha _{\mathsf {p}} (X)$
for any point
![]() $\mathsf {p}$
on a quasi-smooth Fano 3-fold weighted hypersurface X of index
$\mathsf {p}$
on a quasi-smooth Fano 3-fold weighted hypersurface X of index
![]() $1$
. In Sections 4 and 5, we compute local alpha invariants at smooth and singular points, respectively. At this stage, Theorem 1.8 is proved except for seven specific families. These exceptional families are families No. 2, 4, 5, 6, 8, 10 and 14, and we need extra arguments to prove
$1$
. In Sections 4 and 5, we compute local alpha invariants at smooth and singular points, respectively. At this stage, Theorem 1.8 is proved except for seven specific families. These exceptional families are families No. 2, 4, 5, 6, 8, 10 and 14, and we need extra arguments to prove
![]() $\alpha (X) \ge 1/2$
, which will be done in Section 6. In Section 7, we will consider and prove further results such as Theorems 1.11 and 1.12. We will also discuss related problems that arise naturally through the experience of huge amount of computations. Finally, in Section 8, various information on the families of quasi-smooth Fano 3-fold weighted hypersurfaces of index
$\alpha (X) \ge 1/2$
, which will be done in Section 6. In Section 7, we will consider and prove further results such as Theorems 1.11 and 1.12. We will also discuss related problems that arise naturally through the experience of huge amount of computations. Finally, in Section 8, various information on the families of quasi-smooth Fano 3-fold weighted hypersurfaces of index
![]() $1$
are summarized, and we also make it clear in Remark 8.1 what is left about K-stability for quasi-smooth Fano
$1$
are summarized, and we also make it clear in Remark 8.1 what is left about K-stability for quasi-smooth Fano
![]() $3$
-fold weighted hypersurfaces of index
$3$
-fold weighted hypersurfaces of index
![]() $1$
.
$1$
.
1.4 Relevant results in K-stability
Recently both theoretical and explicit studies of K-stability of Fano varieties have been developed drastically. We refer readers to [Reference XuXu21] for up-to-date surveys. Following the suggestion from the referee, we add Section 1.4 to explain some of them that are developed during the preparation or after the completion of this article.
One of the most striking one is the equivalence of the notions of K-stability and uniform K-stability for klt Fano varieties that is proved in [Reference Liu, Xu and ZhuangLXZ22]. It in particular follows that the K-stability implies the existence of KE metric for klt Fano varieties. As a consequence, we are now able to conclude in Theorem 1.12 not only the K-stability of X but also the existence of a KE metric on X.
It should be mentioned that currently there are various methods in hand to check K-stability: The most powerful methods at present are the induction method of Abban and Zhuang [Reference Abban and ZhuangAZ22] computing (local) delta invariants or the moduli method of Liu et al. (see, e.g., [Reference LiuLiu22], [Reference Liu and XuLX19]). These methods are developed parallel to the preparation of this article, and we do not use them. As it is explained in Section 1.3, the proofs of the main results of this article rely on the computation of (local) alpha invariants.
This article aims the systematic study of singular Fano
![]() $3$
-folds. There are on-going work by Cheltsov and collaborators on smooth Fano
$3$
-folds. There are on-going work by Cheltsov and collaborators on smooth Fano
![]() $3$
-folds. In the book [Ara+23], it is completely determined whether the general member of each of the 105 irreducible families of smooth Fano 3-folds admits a KE metric or not. Very recently, there have been a lot of works aiming to drop the generality assumption in the above result and to classify K-(poly)stable smooth Fano 3-folds in each family completely (see [Reference LiuLiu23], [Reference Cheltsov and ParkCP22], [Reference Cheltsov, Fujita, Kishimoto and OkadaCFKO22], [Reference Cheltsov, Fujita, Kishimoto and PrakCFKP23], [Reference Belousov and LoginovBL22], [Reference DenisovaDen22], [Reference Cheltsov, Denisova and FujitaCDF22], [Reference MalbonMal23]).
$3$
-folds. In the book [Ara+23], it is completely determined whether the general member of each of the 105 irreducible families of smooth Fano 3-folds admits a KE metric or not. Very recently, there have been a lot of works aiming to drop the generality assumption in the above result and to classify K-(poly)stable smooth Fano 3-folds in each family completely (see [Reference LiuLiu23], [Reference Cheltsov and ParkCP22], [Reference Cheltsov, Fujita, Kishimoto and OkadaCFKO22], [Reference Cheltsov, Fujita, Kishimoto and PrakCFKP23], [Reference Belousov and LoginovBL22], [Reference DenisovaDen22], [Reference Cheltsov, Denisova and FujitaCDF22], [Reference MalbonMal23]).
2 Preliminaries
2.1 Basic definitions and properties
We refer readers’ to [Reference Kollär, Mori, Clemens and CortiKM98] for standard notions of birational geometry which are not explained in this article.
Definition 2.1. By a Fano variety, we mean a normal projective
![]() $\mathbb {Q}$
-factorial variety with at most terminal singularities whose anticanonical divisor is ample.
$\mathbb {Q}$
-factorial variety with at most terminal singularities whose anticanonical divisor is ample.
For a variety X, we denote by
![]() $\operatorname {Sm} (X)$
the smooth locus of X and
$\operatorname {Sm} (X)$
the smooth locus of X and
![]() $\operatorname {Sing} (X) = X \setminus \operatorname {Sm} (X)$
the singular locus of X. For a subset
$\operatorname {Sing} (X) = X \setminus \operatorname {Sm} (X)$
the singular locus of X. For a subset
![]() $\Gamma \subset X$
, we define
$\Gamma \subset X$
, we define
![]() $\operatorname {Sing}_{\Gamma } (X) := \operatorname {Sing} (X) \cap \Gamma $
. Let X be a normal variety and D a Weil divisor (class) on X. We denote by
$\operatorname {Sing}_{\Gamma } (X) := \operatorname {Sing} (X) \cap \Gamma $
. Let X be a normal variety and D a Weil divisor (class) on X. We denote by
![]() $|D|_{\mathbb {Q}}$
the set of effective
$|D|_{\mathbb {Q}}$
the set of effective
![]() $\mathbb {Q}$
-divisors on X which are
$\mathbb {Q}$
-divisors on X which are
![]() $\mathbb {Q}$
-linearly equivalent to D. For a smooth point
$\mathbb {Q}$
-linearly equivalent to D. For a smooth point
![]() $\mathsf {p} \in X$
, we define
$\mathsf {p} \in X$
, we define
![]() $|\mathcal {I}_{\mathsf {p}} (D)|$
to be the linear subspace of
$|\mathcal {I}_{\mathsf {p}} (D)|$
to be the linear subspace of
![]() $|D|$
consisting of members of
$|D|$
consisting of members of
![]() $|D|$
passing through
$|D|$
passing through
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
2.1.a Birational (super)rigidity of Fano varieties
Let X be a normal
![]() $\mathbb {Q}$
-factorial variety, D a
$\mathbb {Q}$
-factorial variety, D a
![]() $\mathbb {Q}$
-divisor on X and
$\mathbb {Q}$
-divisor on X and
![]() $\mathcal {M}$
a movable linear system on X. For a prime divisor E over X, we define
$\mathcal {M}$
a movable linear system on X. For a prime divisor E over X, we define
![]() $\operatorname {ord}_E (D)$
to be the coefficient of E in
$\operatorname {ord}_E (D)$
to be the coefficient of E in
![]() $\varphi ^*D$
, where
$\varphi ^*D$
, where
![]() $\varphi \colon Y \to X$
is a birational morphism such that
$\varphi \colon Y \to X$
is a birational morphism such that
![]() $E \subset Y$
, and we set
$E \subset Y$
, and we set
![]() $m_E (\mathcal {M}) := \operatorname {ord}_E (M)$
, where M is a general member of
$m_E (\mathcal {M}) := \operatorname {ord}_E (M)$
, where M is a general member of
![]() $\mathcal {M}$
. For a positive rational number
$\mathcal {M}$
. For a positive rational number
![]() $\lambda $
, we say that a pair
$\lambda $
, we say that a pair
![]() $(X, \lambda \mathcal {M})$
is canonical if
$(X, \lambda \mathcal {M})$
is canonical if
for any exceptional prime divisor E over X.
Let X be a Fano variety of Picard number one. Note that we can view X (or more precisely the structure morphism
![]() $X \to \operatorname {Spec} \mathbb {C}$
) as a Mori fiber space.
$X \to \operatorname {Spec} \mathbb {C}$
) as a Mori fiber space.
Definition 2.2. We say that X is birationally rigid if the existence of a Mori fiber space
![]() $Y \to T$
such that Y is birational to X implies that Y is isomorphic to X (and
$Y \to T$
such that Y is birational to X implies that Y is isomorphic to X (and
![]() $T = \operatorname {Spec} \mathbb {C}$
). We say that X is birationally superrigid if X is birationally rigid and
$T = \operatorname {Spec} \mathbb {C}$
). We say that X is birationally superrigid if X is birationally rigid and
![]() $\operatorname {Bir} (X) = \operatorname {Aut} (X)$
.
$\operatorname {Bir} (X) = \operatorname {Aut} (X)$
.
Definition 2.3. A closed subvariety
![]() $\Gamma \subset X$
is called a maximal center if there exists a movable linear system
$\Gamma \subset X$
is called a maximal center if there exists a movable linear system
![]() $\mathcal {M} \sim _{\mathbb {Q}} - n K_X$
and an exceptional prime divisor E over X such that
$\mathcal {M} \sim _{\mathbb {Q}} - n K_X$
and an exceptional prime divisor E over X such that
![]() $m_E (\mathcal {M})> n a_E (K_X)$
.
$m_E (\mathcal {M})> n a_E (K_X)$
.
Theorem 2.4 [Reference Cheltsov and ShramovCS08, Theorem 1.26].
A Fano variety X of Picard number
![]() $1$
is birationally superrigid if and only if the pair
$1$
is birationally superrigid if and only if the pair
![]() $(X, \frac {1}{n} \mathcal {M})$
is canonical for any movable linear system
$(X, \frac {1}{n} \mathcal {M})$
is canonical for any movable linear system
![]() $\mathcal {M}$
on X, where
$\mathcal {M}$
on X, where
![]() $n \in \mathbb {Q}_{> 0}$
is such that
$n \in \mathbb {Q}_{> 0}$
is such that
![]() $\mathcal {M} \sim _{\mathbb {Q}} - n K_X$
, or equivalently if and only if there is no maximal center on X.
$\mathcal {M} \sim _{\mathbb {Q}} - n K_X$
, or equivalently if and only if there is no maximal center on X.
2.1.b Log canonical thresholds and alpha invariants
Definition 2.5. Let
![]() $(X, \Delta )$
be a pair, D an effective
$(X, \Delta )$
be a pair, D an effective
![]() $\mathbb {Q}$
-divisor on X, and let
$\mathbb {Q}$
-divisor on X, and let
![]() $\mathsf {p} \in X$
be a point. Assume that
$\mathsf {p} \in X$
be a point. Assume that
![]() $(X, \Delta )$
has at most log canonical singularities. We define the log canonical threshold (abbreviated as LCT) of
$(X, \Delta )$
has at most log canonical singularities. We define the log canonical threshold (abbreviated as LCT) of
![]() $(X, \Delta; D)$
at
$(X, \Delta; D)$
at
![]() $\mathsf {p}$
and the log canonical threshold of
$\mathsf {p}$
and the log canonical threshold of
![]() $(X, \Delta; D)$
to be the numbers
$(X, \Delta; D)$
to be the numbers
 $$ \begin{align*} \operatorname{lct}_{\mathsf{p}} (X, \Delta; D) &= \sup \{\, c \in \mathbb{Q}_{\ge 0} \mid (X, \Delta + c D)\ \text{is log canonical at}\ \mathsf{p} \,\}, \\ \operatorname{lct} (X, \Delta; D) &= \sup \{\, c \in \mathbb{Q}_{\ge 0} \mid (X, \Delta + c D)\ \text{is log canonical} \,\}, \end{align*} $$
$$ \begin{align*} \operatorname{lct}_{\mathsf{p}} (X, \Delta; D) &= \sup \{\, c \in \mathbb{Q}_{\ge 0} \mid (X, \Delta + c D)\ \text{is log canonical at}\ \mathsf{p} \,\}, \\ \operatorname{lct} (X, \Delta; D) &= \sup \{\, c \in \mathbb{Q}_{\ge 0} \mid (X, \Delta + c D)\ \text{is log canonical} \,\}, \end{align*} $$
respectively. We set
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) = \operatorname {lct}_{\mathsf {p}} (X, 0; D)$
and
$\operatorname {lct}_{\mathsf {p}} (X; D) = \operatorname {lct}_{\mathsf {p}} (X, 0; D)$
and
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) = \operatorname {lct} (X, \Delta; D)$
when
$\operatorname {lct}_{\mathsf {p}} (X; D) = \operatorname {lct} (X, \Delta; D)$
when
![]() $\Delta = 0$
. Assume that
$\Delta = 0$
. Assume that
![]() $\left | -K_X \right |{}_{\mathbb {Q}} \ne \emptyset $
. Then we define the alpha invariant of X at
$\left | -K_X \right |{}_{\mathbb {Q}} \ne \emptyset $
. Then we define the alpha invariant of X at
![]() $\mathsf {p}$
and the alpha invariant of X to be the numbers
$\mathsf {p}$
and the alpha invariant of X to be the numbers
 $$ \begin{align*} \alpha_{\mathsf{p}} (X) &= \inf \{\, \operatorname{lct}_{\mathsf{p}} (X, D) \mid D \in \left| -K_X \right|{}_{\mathbb{Q}} \,\}, \\ \alpha (X) &= \inf \{\, \alpha_{\mathsf{p}} (X) \mid \mathsf{p} \in X \, \}, \end{align*} $$
$$ \begin{align*} \alpha_{\mathsf{p}} (X) &= \inf \{\, \operatorname{lct}_{\mathsf{p}} (X, D) \mid D \in \left| -K_X \right|{}_{\mathbb{Q}} \,\}, \\ \alpha (X) &= \inf \{\, \alpha_{\mathsf{p}} (X) \mid \mathsf{p} \in X \, \}, \end{align*} $$
respectively.
The following fact is frequently used.
Remark 2.6. Let
![]() $\mathsf {p}$
be a point on X, and let
$\mathsf {p}$
be a point on X, and let
![]() $D_1, D_2$
be effective
$D_1, D_2$
be effective
![]() $\mathbb {Q}$
-divisors on X. If both
$\mathbb {Q}$
-divisors on X. If both
![]() $(X, D_1)$
and
$(X, D_1)$
and
![]() $(X, D_2)$
are log canonical at
$(X, D_2)$
are log canonical at
![]() $\mathsf {p}$
, then the pair
$\mathsf {p}$
, then the pair
is log canonical at
![]() $\mathsf {p}$
for any
$\mathsf {p}$
for any
![]() $\lambda \in \mathbb {Q}$
such that
$\lambda \in \mathbb {Q}$
such that
![]() $0 \le \lambda \le 1$
. In particular, if
$0 \le \lambda \le 1$
. In particular, if
![]() $\alpha _{\mathsf {p}} (X) < c$
for some number
$\alpha _{\mathsf {p}} (X) < c$
for some number
![]() $c> 0$
, then there exists an irreducible
$c> 0$
, then there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in \left |-K_X \right |{}_{\mathbb {Q}}$
such that
$D \in \left |-K_X \right |{}_{\mathbb {Q}}$
such that
![]() $(X, c D)$
is not log canonical at
$(X, c D)$
is not log canonical at
![]() $\mathsf {p}$
. Here, a
$\mathsf {p}$
. Here, a
![]() $\mathbb {Q}$
-divisor is irreducible if its support
$\mathbb {Q}$
-divisor is irreducible if its support
![]() $\operatorname {Supp} (D)$
is irreducible.
$\operatorname {Supp} (D)$
is irreducible.
2.1.c Cyclic quotient singularities and orbifold multiplicities
Definition 2.7. Let
![]() $r> 0$
and
$r> 0$
and
![]() $a_1, \dots , a_n$
be integers. Suppose that the cyclic group
$a_1, \dots , a_n$
be integers. Suppose that the cyclic group
![]() ${\boldsymbol {\mu }}_r$
of rth roots of unity in
${\boldsymbol {\mu }}_r$
of rth roots of unity in
![]() $\mathbb {C}$
acts on the affine n-space
$\mathbb {C}$
acts on the affine n-space
![]() $\mathbb {A}^n$
with affine coordinates
$\mathbb {A}^n$
with affine coordinates
![]() $x_1, \dots , x_n$
via
$x_1, \dots , x_n$
via
where
![]() $\zeta \in {\boldsymbol {\mu }}_r$
is a fixed primitive rth root of unity. We denote by
$\zeta \in {\boldsymbol {\mu }}_r$
is a fixed primitive rth root of unity. We denote by
![]() $\bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
the image of the origin
$\bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
the image of the origin
![]() $o \in \mathbb {A}^n$
under the quotient morphism
$o \in \mathbb {A}^n$
under the quotient morphism
![]() $\mathbb {A}^n \to \mathbb {A}^n/{\boldsymbol {\mu }}_r$
. A singularity
$\mathbb {A}^n \to \mathbb {A}^n/{\boldsymbol {\mu }}_r$
. A singularity
![]() $\mathsf {p} \in X$
is a cyclic quotient singularity of type
$\mathsf {p} \in X$
is a cyclic quotient singularity of type
![]() $\frac {1}{r} (a_1, \dots , a_n)$
if
$\frac {1}{r} (a_1, \dots , a_n)$
if
![]() $\mathsf {p} \in X$
is analytically isomorphic to an analytic germ
$\mathsf {p} \in X$
is analytically isomorphic to an analytic germ
![]() $\bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
. In this case, r is called the index of the cyclic quotient singularity
$\bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
. In this case, r is called the index of the cyclic quotient singularity
![]() $\mathsf {p} \in X$
.
$\mathsf {p} \in X$
.
Remark 2.8. Let
![]() $\mathsf {p} \in X$
be an n-dimensional cyclic quotient singular point. Then we have a suitable action of
$\mathsf {p} \in X$
be an n-dimensional cyclic quotient singular point. Then we have a suitable action of
![]() ${\boldsymbol {\mu }}_r$
on
${\boldsymbol {\mu }}_r$
on
![]() $\mathbb {A}^n$
such that there is an analytic isomorphism
$\mathbb {A}^n$
such that there is an analytic isomorphism
![]() $\bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r \cong \mathsf {p} \in X$
of (analytic) germs. In the following, the germ
$\bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r \cong \mathsf {p} \in X$
of (analytic) germs. In the following, the germ
![]() $o \in \mathbb {A}^n$
is often denoted by
$o \in \mathbb {A}^n$
is often denoted by
![]() $\check {\mathsf {p}} \in \check {X}$
. By identifying
$\check {\mathsf {p}} \in \check {X}$
. By identifying
![]() $\mathsf {p} \in X \cong \bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
, the quotient morphism
$\mathsf {p} \in X \cong \bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
, the quotient morphism
![]() $o \in \mathbb {A}^n \to \bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
is denoted by
$o \in \mathbb {A}^n \to \bar {o} \in \mathbb {A}^n/{\boldsymbol {\mu }}_r$
is denoted by
![]() $q_{\mathsf {p}} \colon \check {X} \to X$
and is called the quotient morphism of
$q_{\mathsf {p}} \colon \check {X} \to X$
and is called the quotient morphism of
![]() $\mathsf {p} \in X$
.
$\mathsf {p} \in X$
.
Note that, by convention, the case
![]() $r = 1$
is allowed in the definition of cyclic quotient singularity. A cyclic quotient singularity
$r = 1$
is allowed in the definition of cyclic quotient singularity. A cyclic quotient singularity
![]() $\mathsf {p} \in X$
of index
$\mathsf {p} \in X$
of index
![]() $1$
is nothing but a smooth point
$1$
is nothing but a smooth point
![]() $\mathsf {p} \in X$
and in that case the quotient morphism
$\mathsf {p} \in X$
and in that case the quotient morphism
![]() $q_{\mathsf {p}} \colon \check {X} \to X$
is simply an isomorphism.
$q_{\mathsf {p}} \colon \check {X} \to X$
is simply an isomorphism.
Definition 2.9. Let
![]() $\mathsf {p} \in X$
be a cyclic quotient singularity, and let
$\mathsf {p} \in X$
be a cyclic quotient singularity, and let
![]() $q_{\mathsf {p}} \colon \check {X} \to X$
be its quotient morphism with
$q_{\mathsf {p}} \colon \check {X} \to X$
be its quotient morphism with
![]() $\check {\mathsf {p}} \in \check {X}$
the preimage of
$\check {\mathsf {p}} \in \check {X}$
the preimage of
![]() $\mathsf {p}$
. For an effective
$\mathsf {p}$
. For an effective
![]() $\mathbb {Q}$
-divisor D on X, we define
$\mathbb {Q}$
-divisor D on X, we define
and call it the orbifold multiplicity of D at
![]() $\mathsf {p}$
. By convention, we set
$\mathsf {p}$
. By convention, we set
![]() $\operatorname {omult}_{\mathsf {p}} (D) = \operatorname {mult}_{\mathsf {p}} (D)$
when
$\operatorname {omult}_{\mathsf {p}} (D) = \operatorname {mult}_{\mathsf {p}} (D)$
when
![]() $\mathsf {p} \in X$
is a smooth point.
$\mathsf {p} \in X$
is a smooth point.
2.1.d Kawamata blowup
Let
![]() $\mathsf {p} \in V$
be a three-dimensional terminal quotient singularity. Then it is of type
$\mathsf {p} \in V$
be a three-dimensional terminal quotient singularity. Then it is of type
![]() $\frac {1}{r} (1, a, r-a)$
, where r and a are coprime positive integers with
$\frac {1}{r} (1, a, r-a)$
, where r and a are coprime positive integers with
![]() $r> a$
(see [Reference Morrison and StevensMS84]). Let
$r> a$
(see [Reference Morrison and StevensMS84]). Let
![]() $\varphi \colon W \to V$
be the weighted blowup of V at
$\varphi \colon W \to V$
be the weighted blowup of V at
![]() $\mathsf {p}$
with weight
$\mathsf {p}$
with weight
![]() $\frac {1}{r} (1,a,r-a)$
. By [Reference KawamataKaw96],
$\frac {1}{r} (1,a,r-a)$
. By [Reference KawamataKaw96],
![]() $\varphi $
is the unique divisorial contraction centered at
$\varphi $
is the unique divisorial contraction centered at
![]() $\mathsf {p}$
and we call
$\mathsf {p}$
and we call
![]() $\varphi $
the Kawamata blowup of V at
$\varphi $
the Kawamata blowup of V at
![]() $\mathsf {p}$
. If we denote by E the
$\mathsf {p}$
. If we denote by E the
![]() $\varphi $
-exceptional divisor, then
$\varphi $
-exceptional divisor, then
![]() $E \cong \mathbb {P} (1,a,r-a)$
and we have
$E \cong \mathbb {P} (1,a,r-a)$
and we have
and
 $$\begin{align*}(E^3) = \frac{r^2}{a (r-a)}. \end{align*}$$
$$\begin{align*}(E^3) = \frac{r^2}{a (r-a)}. \end{align*}$$
2.2 Weighted projective varieties
We recall basic definitions of various notions concerning weighted projective spaces and their subvarieties. We refer readers to [Reference Iano-FletcherIF00] for details.
2.2.a Weighted projective space
Let N be a positive integer. For positive integers
![]() $a_0, \dots , a_N$
, let
$a_0, \dots , a_N$
, let
be the graded ring whose grading is given by
![]() $\deg x_i = a_i$
. We define
$\deg x_i = a_i$
. We define
and call it the weighted projective space with homogeneous coordinates
![]() $x_0, \dots , x_N$
(of degree
$x_0, \dots , x_N$
(of degree
![]() $\deg x_i = a_i$
). We sometimes denote
$\deg x_i = a_i$
). We sometimes denote
in order to make it clear the homogeneous coordinates
![]() $x_0, \dots , x_N$
. For
$x_0, \dots , x_N$
. For
![]() $i = 0, \dots , N$
, we denote by
$i = 0, \dots , N$
, we denote by
the coordinate point at which only the coordinate
![]() $x_i$
does not vanish. Let
$x_i$
does not vanish. Let
![]() $f \in R := R (a_0, \dots , a_N) = \mathbb {C} [x_0, \dots , x_N]$
be a polynomial. We say that f is quasi-homogeneous (resp. homogeneous) if it is homogeneous with respect to the grading
$f \in R := R (a_0, \dots , a_N) = \mathbb {C} [x_0, \dots , x_N]$
be a polynomial. We say that f is quasi-homogeneous (resp. homogeneous) if it is homogeneous with respect to the grading
![]() $\deg x_i = a_i$
(resp.
$\deg x_i = a_i$
(resp.
![]() $\deg x_i = 1$
) for
$\deg x_i = 1$
) for
![]() $i = 0, 1, \dots , N$
. For a polynomial
$i = 0, 1, \dots , N$
. For a polynomial
![]() $f \in \mathbb {C} [x_0, \dots , x_N]$
and a monomial
$f \in \mathbb {C} [x_0, \dots , x_N]$
and a monomial
![]() $M = x_0^{m_0} \cdots x_N^{m_N}$
, we denote by
$M = x_0^{m_0} \cdots x_N^{m_N}$
, we denote by
the coefficient of M in f, and, by a slight abuse of notation, we write
![]() $M \in f$
if
$M \in f$
if
![]() $\operatorname {coeff}_f (M) \ne 0$
. For quasi-homogeneous polynomials
$\operatorname {coeff}_f (M) \ne 0$
. For quasi-homogeneous polynomials
![]() $f_1, \dots , f_k \in R$
, we denote by
$f_1, \dots , f_k \in R$
, we denote by
the closed subscheme defined by the quasi-homogeneous ideal
![]() $(f_1, \dots , f_k) \subset R$
. Moreover, for a closed subscheme
$(f_1, \dots , f_k) \subset R$
. Moreover, for a closed subscheme
![]() $X \subset \mathbb {P} (a_0, \dots , a_N)$
and quasi-homogeneous polynomials
$X \subset \mathbb {P} (a_0, \dots , a_N)$
and quasi-homogeneous polynomials
![]() $g_1, \dots , g_l \in R$
, we define
$g_1, \dots , g_l \in R$
, we define
which is a closed subscheme of X. For
![]() $i = 0, \dots , N$
, we define
$i = 0, \dots , N$
, we define
 $$ \begin{align} \mathcal{H}_{x_i} &:= (x_i = 0) \subset \mathbb{P} (a_0, \dots, a_N), \nonumber\\ \mathcal{U}_{x_i} &:= \mathbb{P} (a_0, \dots, a_N) \setminus \mathcal{H}_{x_i}. \end{align} $$
$$ \begin{align} \mathcal{H}_{x_i} &:= (x_i = 0) \subset \mathbb{P} (a_0, \dots, a_N), \nonumber\\ \mathcal{U}_{x_i} &:= \mathbb{P} (a_0, \dots, a_N) \setminus \mathcal{H}_{x_i}. \end{align} $$
Remark 2.10. The weighted projective space
![]() $\mathbb {P} (a, b, c, d, e)$
with homogeneous coordinates x, y, z, t, w of degrees a, b, c, d, e, respectively, is sometimes denoted by
$\mathbb {P} (a, b, c, d, e)$
with homogeneous coordinates x, y, z, t, w of degrees a, b, c, d, e, respectively, is sometimes denoted by
in order to emphasize the homogeneous coordinates. For a coordinate
![]() $v \in \{x, \dots , w\}$
, the point
$v \in \{x, \dots , w\}$
, the point
![]() $\mathsf {p}_v \in \mathbb {P} (a, b, c, d, e)$
, the quasi-hyperplane
$\mathsf {p}_v \in \mathbb {P} (a, b, c, d, e)$
, the quasi-hyperplane
![]() $\mathcal {H}_v = (v = 0) \subset \mathbb {P} (a, b, c, d, e)$
and the open set
$\mathcal {H}_v = (v = 0) \subset \mathbb {P} (a, b, c, d, e)$
and the open set
![]() $\mathcal {U}_v = \mathbb {P} (a, b, c, d, e) \setminus \mathcal {H}_v$
are similarly defined as in equations (2.1) and (2.2).
$\mathcal {U}_v = \mathbb {P} (a, b, c, d, e) \setminus \mathcal {H}_v$
are similarly defined as in equations (2.1) and (2.2).
2.2.b Well-formedness and quasi-smoothness
Definition 2.11. We say that a weighted projective space
![]() $\mathbb {P} (a_0, \dots , a_N)$
is well-formed if
$\mathbb {P} (a_0, \dots , a_N)$
is well-formed if
for any
![]() $i = 0, 1, \dots , N$
.
$i = 0, 1, \dots , N$
.
Definition 2.12. Let
![]() $\mathbb {P} (a_0, \dots , a_N)$
be a weighted projective space such that
$\mathbb {P} (a_0, \dots , a_N)$
be a weighted projective space such that
![]() $\gcd \{a_0, \dots , a_N\} = 1$
. For
$\gcd \{a_0, \dots , a_N\} = 1$
. For
![]() $j = 0, 1, \dots , N$
, we set
$j = 0, 1, \dots , N$
, we set
 $$ \begin{align*} l_j &:= \gcd \{ a_0, a_1, \dots, \hat{a}_j, \dots, a_N\}, \\ m_j &:= l_0 l_1 \cdots \hat{l}_j \cdots l_N, \\ b_j &:= \frac{a_j}{m_j}. \end{align*} $$
$$ \begin{align*} l_j &:= \gcd \{ a_0, a_1, \dots, \hat{a}_j, \dots, a_N\}, \\ m_j &:= l_0 l_1 \cdots \hat{l}_j \cdots l_N, \\ b_j &:= \frac{a_j}{m_j}. \end{align*} $$
We then define
and call it the well-formed model of
![]() $\mathbb {P} (a_0, \dots , a_N)$
.
$\mathbb {P} (a_0, \dots , a_N)$
.
Remark 2.13. Any weighted projective space is isomorphic to a well-formed one (see, e.g., [Reference Iano-FletcherIF00, Lemma 5.7]). More precisely, for a weighted projective space
![]() $\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)$
with
$\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)$
with
![]() $\gcd \{a_0, \dots , a_N\} = 1$
, there exists an isomorphism
$\gcd \{a_0, \dots , a_N\} = 1$
, there exists an isomorphism
such that
![]() $\phi ^* \mathcal {H}_{y_i} = m_i \mathcal {H}_{x_i}$
for
$\phi ^* \mathcal {H}_{y_i} = m_i \mathcal {H}_{x_i}$
for
![]() $i = 0, 1, \dots , N$
, where
$i = 0, 1, \dots , N$
, where
![]() $\mathcal {H}_{x_i} = (x_i = 0) \subset \mathbb {P}$
and
$\mathcal {H}_{x_i} = (x_i = 0) \subset \mathbb {P}$
and
![]() $\mathcal {H}_{y_i} = (y_i = 0) \subset \mathbb {P}^{\operatorname {wf}}$
.
$\mathcal {H}_{y_i} = (y_i = 0) \subset \mathbb {P}^{\operatorname {wf}}$
.
In the following, we set
![]() $\mathbb {P} := \mathbb {P} (a_0, \dots , a_N)$
and we denote by
$\mathbb {P} := \mathbb {P} (a_0, \dots , a_N)$
and we denote by
the canonical projection. Let
![]() $X \subset \mathbb {P}$
be a closed subscheme. We set
$X \subset \mathbb {P}$
be a closed subscheme. We set
![]() $C_X^* := \Pi ^{-1} (X)$
and call it the punctured affine quasi-cone over X. The affine quasi-cone
$C_X^* := \Pi ^{-1} (X)$
and call it the punctured affine quasi-cone over X. The affine quasi-cone
![]() $C_X$
over X is the closure of
$C_X$
over X is the closure of
![]() $C_X^*$
in
$C_X^*$
in
![]() $\mathbb {A}^{N+1}$
. We set
$\mathbb {A}^{N+1}$
. We set
![]() $\pi := \Pi |_{C_X^*} \colon C_X^* \to X$
.
$\pi := \Pi |_{C_X^*} \colon C_X^* \to X$
.
Definition 2.14. We say that a closed subscheme
![]() $X \subset \mathbb {P}$
is well-formed if
$X \subset \mathbb {P}$
is well-formed if
![]() $\mathbb {P}$
is well-formed and
$\mathbb {P}$
is well-formed and
![]() $\operatorname {codim}_X (X \cap \operatorname {Sing} (\mathbb {P})) \ge 2$
.
$\operatorname {codim}_X (X \cap \operatorname {Sing} (\mathbb {P})) \ge 2$
.
Definition 2.15. Let
![]() $X \subset \mathbb {P}$
be a closed subscheme as above. We define the quasi-smooth locus of X as
$X \subset \mathbb {P}$
be a closed subscheme as above. We define the quasi-smooth locus of X as
Let S be a subset of X. We say that X is quasi-smooth along S if
![]() $S \subset \operatorname {QSm} (X)$
. We simply say that X is quasi-smooth when
$S \subset \operatorname {QSm} (X)$
. We simply say that X is quasi-smooth when
![]() $X = \operatorname {QSm} (X)$
.
$X = \operatorname {QSm} (X)$
.
2.2.c Orbifold charts
Let
![]() $\mathcal {U}_{x_i}$
be the open subset of
$\mathcal {U}_{x_i}$
be the open subset of
![]() $\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)_{x_0, \dots , x_N}$
as in equation (2.2), where
$\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)_{x_0, \dots , x_N}$
as in equation (2.2), where
![]() $i \in \{0, 1, \dots , N\}$
. We call
$i \in \{0, 1, \dots , N\}$
. We call
![]() $\mathcal {U}_{x_i}$
the standard affine open subset of
$\mathcal {U}_{x_i}$
the standard affine open subset of
![]() $\mathbb {P}$
containing
$\mathbb {P}$
containing
![]() $\mathsf {p}_{x_i}$
. We denote by
$\mathsf {p}_{x_i}$
. We denote by
![]() $\breve {\mathcal {U}}_{x_i}$
the affine N-space
$\breve {\mathcal {U}}_{x_i}$
the affine N-space
![]() $\mathbb {A}^N$
with affine coordinates
$\mathbb {A}^N$
with affine coordinates
![]() $\breve {x}_0, \dots , \widehat {\breve {x}_i}, \dots , \breve {x}_N$
. Consider the
$\breve {x}_0, \dots , \widehat {\breve {x}_i}, \dots , \breve {x}_N$
. Consider the
![]() ${\boldsymbol {\mu }}_{a_i}$
-action on
${\boldsymbol {\mu }}_{a_i}$
-action on
![]() $\breve {\mathcal {U}}_i$
defined by
$\breve {\mathcal {U}}_i$
defined by
where
![]() $\zeta \in {\boldsymbol {\mu }}_{a_i}$
is a primitive
$\zeta \in {\boldsymbol {\mu }}_{a_i}$
is a primitive
![]() $a_i$
th root of unity. Then the open set
$a_i$
th root of unity. Then the open set
![]() $\mathcal {U}_i$
can be naturally identified with the quotient
$\mathcal {U}_i$
can be naturally identified with the quotient
![]() $\breve {\mathcal {U}}_{x_i}/{\boldsymbol {\mu }}_{a_i}$
. In fact, this can be seen by the identification
$\breve {\mathcal {U}}_{x_i}/{\boldsymbol {\mu }}_{a_i}$
. In fact, this can be seen by the identification
 $$\begin{align*}\breve{x}_j = \frac{x_j}{x_i^{a_j/a_i}}, \quad \text{for}\ j = 0, \dots, \hat{i}, \dots, N. \end{align*}$$
$$\begin{align*}\breve{x}_j = \frac{x_j}{x_i^{a_j/a_i}}, \quad \text{for}\ j = 0, \dots, \hat{i}, \dots, N. \end{align*}$$
The quotient morphism
![]() $\breve {\mathcal {U}}_{x_i} \to \breve {\mathcal {U}}_{x_i}/{\boldsymbol {\mu }}_{a_i} = \mathcal {U}_{x_i}$
is denoted by
$\breve {\mathcal {U}}_{x_i} \to \breve {\mathcal {U}}_{x_i}/{\boldsymbol {\mu }}_{a_i} = \mathcal {U}_{x_i}$
is denoted by
and is called the orbifold chart of
![]() $\mathbb {P}$
containing
$\mathbb {P}$
containing
![]() $\mathsf {p}_{x_i}$
.
$\mathsf {p}_{x_i}$
.
Let
![]() $X \subset \mathbb {P}$
be a subscheme. Usually, we denote by
$X \subset \mathbb {P}$
be a subscheme. Usually, we denote by
![]() $U_{x_i} \subset X$
the open set
$U_{x_i} \subset X$
the open set
![]() $\mathcal {U}_{x_i} \cap X$
, and we call
$\mathcal {U}_{x_i} \cap X$
, and we call
![]() $U_{x_i}$
the standard affine open subset of X containing
$U_{x_i}$
the standard affine open subset of X containing
![]() $\mathsf {p}_{x_i}$
. In this case, we set
$\mathsf {p}_{x_i}$
. In this case, we set
![]() $\breve {U}_{x_i} = \rho _{x_i}^{-1} (U_{x_i}) \subset \breve {\mathcal {U}}_{x_i}$
. By a slight abuse of notation, the morphism
$\breve {U}_{x_i} = \rho _{x_i}^{-1} (U_{x_i}) \subset \breve {\mathcal {U}}_{x_i}$
. By a slight abuse of notation, the morphism
![]() $\rho _{x_i}|_{U_i} \colon \breve {U}_{x_i} \to U_{x_i}$
is also denote by
$\rho _{x_i}|_{U_i} \colon \breve {U}_{x_i} \to U_{x_i}$
is also denote by
and is called the orbifold chart of X containing
![]() $\mathsf {p}_{x_i}$
. When we are using the notation
$\mathsf {p}_{x_i}$
. When we are using the notation
![]() $\mathsf {p} = \mathsf {p}_{x_i}$
, the morphism
$\mathsf {p} = \mathsf {p}_{x_i}$
, the morphism
![]() $\rho _{x_i}$
is sometimes denoted by
$\rho _{x_i}$
is sometimes denoted by
![]() $\rho _{\mathsf {p}}$
. Note that
$\rho _{\mathsf {p}}$
. Note that
![]() $\breve {U}_{x_i}$
is not necessary smooth in general.
$\breve {U}_{x_i}$
is not necessary smooth in general.
Suppose that
![]() $X \subset \mathbb {P}$
is a closed subvariety containing the point
$X \subset \mathbb {P}$
is a closed subvariety containing the point
![]() $\mathsf {p} = \mathsf {p}_{x_i}$
. The preimage
$\mathsf {p} = \mathsf {p}_{x_i}$
. The preimage
![]() $\breve {\mathsf {p}}$
of
$\breve {\mathsf {p}}$
of
![]() $\mathsf {p}$
is the origin of
$\mathsf {p}$
is the origin of
![]() $\breve {U}_{x_i} \subset \breve {\mathcal {U}}_{x_i} = \mathbb {A}^N$
. It is straightforward to see that X is quasi-smooth at
$\breve {U}_{x_i} \subset \breve {\mathcal {U}}_{x_i} = \mathbb {A}^N$
. It is straightforward to see that X is quasi-smooth at
![]() $\mathsf {p}$
if and only if
$\mathsf {p}$
if and only if
![]() $\breve {U}_{x_i}$
is smooth at
$\breve {U}_{x_i}$
is smooth at
![]() $\breve {\mathsf {p}}$
. Suppose that X is quasi-smooth at
$\breve {\mathsf {p}}$
. Suppose that X is quasi-smooth at
![]() $\mathsf {p}$
. A system of local coordinates of
$\mathsf {p}$
. A system of local coordinates of
![]() $U_{x_i}$
at
$U_{x_i}$
at
![]() $\breve {\mathsf {p}}$
is called a system of local orbifold coordinates of X at
$\breve {\mathsf {p}}$
is called a system of local orbifold coordinates of X at
![]() $\mathsf {p}$
. In this case,
$\mathsf {p}$
. In this case,
![]() $\mathsf {p} \in X$
is a cyclic quotient singularity of index
$\mathsf {p} \in X$
is a cyclic quotient singularity of index
![]() $a_i$
and
$a_i$
and
![]() $\rho _{x_i} \colon \breve {U}_{x_i} \to U_{x_i}$
can be identified with (or analytically equivalent to) the quotient morphism
$\rho _{x_i} \colon \breve {U}_{x_i} \to U_{x_i}$
can be identified with (or analytically equivalent to) the quotient morphism
![]() $q_{\mathsf {p}}$
of
$q_{\mathsf {p}}$
of
![]() $\mathsf {p} \in X$
after shrinking
$\mathsf {p} \in X$
after shrinking
![]() $U_{x_i}$
and then
$U_{x_i}$
and then
![]() $\breve {U}_{x_i}$
. Moreover, if X is quasi-smooth, then
$\breve {U}_{x_i}$
. Moreover, if X is quasi-smooth, then
![]() $\breve {U}_i$
is smooth for any i.
$\breve {U}_i$
is smooth for any i.
Remark 2.16. When we work with
![]() $\mathbb {P} = \mathbb {P} (a, b, c, d, e)_{x, y, z, t, w}$
and its closed subscheme
$\mathbb {P} = \mathbb {P} (a, b, c, d, e)_{x, y, z, t, w}$
and its closed subscheme
![]() $X \subset \mathbb {P}$
, then
$X \subset \mathbb {P}$
, then
![]() $\mathcal {U}_{v} = \mathbb {A}^5_{\breve {x}, \dots , \hat {\breve {v}}, \dots , \breve {w}}$
,
$\mathcal {U}_{v} = \mathbb {A}^5_{\breve {x}, \dots , \hat {\breve {v}}, \dots , \breve {w}}$
,
![]() $\rho _v \colon \breve {\mathcal {U}}_v \to \mathcal {U}_v$
,
$\rho _v \colon \breve {\mathcal {U}}_v \to \mathcal {U}_v$
,
![]() $\breve {U}_{v} = \rho _v^{-1} (U_v) \subset \mathcal {U}_v$
and
$\breve {U}_{v} = \rho _v^{-1} (U_v) \subset \mathcal {U}_v$
and
![]() $\rho _v \colon \breve {U}_v \to U_v$
are similarly defined.
$\rho _v \colon \breve {U}_v \to U_v$
are similarly defined.
2.2.d Weighted hypersurfaces and quasi-tangent divisors
As in the previous subsections, we work with
![]() $\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)_{x_0, \dots , x_N}$
.
$\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)_{x_0, \dots , x_N}$
.
Definition 2.17. A quasi-linear polynomial (or a quasi-linear form) in variables
![]() $x_0, \dots , x_{n+1}$
is a quasi-homogeneous polynomial
$x_0, \dots , x_{n+1}$
is a quasi-homogeneous polynomial
![]() $f = f (x_0,\dots , x_{n+1})$
such that
$f = f (x_0,\dots , x_{n+1})$
such that
![]() $x_i \in f$
for some
$x_i \in f$
for some
![]() $i = 0, \dots , n+1$
.
$i = 0, \dots , n+1$
.
Definition 2.18. We say that a subvariety
![]() $S \subset \mathbb {P}$
is a quasi-linear subspace of
$S \subset \mathbb {P}$
is a quasi-linear subspace of
![]() $\mathbb {P}$
if it is a complete intersection in
$\mathbb {P}$
if it is a complete intersection in
![]() $\mathbb {P}$
defined by quasi-linear equations of the form
$\mathbb {P}$
defined by quasi-linear equations of the form
where
![]() $\ell _1, \ell _2, \dots , \ell _k$
are linearly independent linear forms in variables
$\ell _1, \ell _2, \dots , \ell _k$
are linearly independent linear forms in variables
![]() $x_0, \dots , x_{n+1}$
and
$x_0, \dots , x_{n+1}$
and
![]() $f_1, \dots , f_k \in \mathbb {C} [x_0, \dots , x_{n+1}]$
are quasi-homogeneous polynomials which are not quasi-linear. A quasi-linear subspace of
$f_1, \dots , f_k \in \mathbb {C} [x_0, \dots , x_{n+1}]$
are quasi-homogeneous polynomials which are not quasi-linear. A quasi-linear subspace of
![]() $\mathbb {P}$
of codimension
$\mathbb {P}$
of codimension
![]() $1$
(resp. dimension
$1$
(resp. dimension
![]() $1$
) is called a quasi-hyperplane (resp. quasi-line) of
$1$
) is called a quasi-hyperplane (resp. quasi-line) of
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
It is clear that a quasi-linear subspace of
![]() $\mathbb {P}$
is isomorphic to a weighted projective space. In particular, a quasi-line is isomorphic to
$\mathbb {P}$
is isomorphic to a weighted projective space. In particular, a quasi-line is isomorphic to
![]() $\mathbb {P}^1$
.
$\mathbb {P}^1$
.
Let X be a hypersurface in
![]() $\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)$
defined by a quasi-homogeneous polynomial of degree d. We often denote it as
$\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)$
defined by a quasi-homogeneous polynomial of degree d. We often denote it as
![]() $X = X_d \subset \mathbb {P} (a_0, \dots , a_N)$
. Suppose that X is quasi-smooth at a point
$X = X_d \subset \mathbb {P} (a_0, \dots , a_N)$
. Suppose that X is quasi-smooth at a point
![]() $\mathsf {p} = \mathsf {p}_{x_i}$
. Then the defining polynomial
$\mathsf {p} = \mathsf {p}_{x_i}$
. Then the defining polynomial
![]() $F = F (x_0, \dots , x_N)$
of X can be written as
$F = F (x_0, \dots , x_N)$
of X can be written as
where
![]() $m \ge 0$
,
$m \ge 0$
,
![]() $f = f (x_0, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
$f = f (x_0, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
![]() $d - m a_i$
which is quasi-linear and
$d - m a_i$
which is quasi-linear and
![]() $g_k = g_k (x_0, \dots ,\hat {x}_i, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
$g_k = g_k (x_0, \dots ,\hat {x}_i, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
![]() $d - k a_i$
which is not quasi-linear for
$d - k a_i$
which is not quasi-linear for
![]() $0 \le k \le m - 1$
. Note that the expression (2.3) is uniquely determined once the homogeneous coordinates of
$0 \le k \le m - 1$
. Note that the expression (2.3) is uniquely determined once the homogeneous coordinates of
![]() $\mathbb {P}$
are fixed.
$\mathbb {P}$
are fixed.
Definition 2.19. Under the notation and assumptions as above, we call f the quasi-tangent polynomial of X at
![]() $\mathsf {p}$
and the divisor
$\mathsf {p}$
and the divisor
![]() $(f = 0)_X$
on X is called the quasi-tangent divisor of X at
$(f = 0)_X$
on X is called the quasi-tangent divisor of X at
![]() $\mathsf {p}$
. When
$\mathsf {p}$
. When
![]() $f = x_j$
for some j, then we also call
$f = x_j$
for some j, then we also call
![]() $x_j$
as the quasi-tangent coordinate of X at
$x_j$
as the quasi-tangent coordinate of X at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Remark 2.20. Let
![]() $X = X_7 \subset \mathbb {P} (1, 1, 1, 2, 3)_{x, y, z, t, w}$
be a weighted hypersurface of degree
$X = X_7 \subset \mathbb {P} (1, 1, 1, 2, 3)_{x, y, z, t, w}$
be a weighted hypersurface of degree
![]() $7$
. Suppose that its defining polynomial is of the form
$7$
. Suppose that its defining polynomial is of the form
where
![]() $g_5, g_7 \in \mathbb {C} [x, y, z, w]$
are quasi-homogeneous polynomials of degree
$g_5, g_7 \in \mathbb {C} [x, y, z, w]$
are quasi-homogeneous polynomials of degree
![]() $5, 7$
, respectively. In this case X is quasi-smooth at
$5, 7$
, respectively. In this case X is quasi-smooth at
![]() $\mathsf {p} = \mathsf {p}_t$
. The quasi-tangent polynomial of X at
$\mathsf {p} = \mathsf {p}_t$
. The quasi-tangent polynomial of X at
![]() $\mathsf {p}$
is
$\mathsf {p}$
is
![]() $t x + w$
. Note that x is not a quasi-tangent coordinate of X at
$t x + w$
. Note that x is not a quasi-tangent coordinate of X at
![]() $\mathsf {p}$
because of the presence of
$\mathsf {p}$
because of the presence of
![]() $t^2 w \in F$
.
$t^2 w \in F$
.
Lemma 2.21. Let
![]() $X \subset \mathbb {P}$
be a weighted hypersurface of degree d. Assume that X is quasi-smooth at a point
$X \subset \mathbb {P}$
be a weighted hypersurface of degree d. Assume that X is quasi-smooth at a point
![]() $\mathsf {p} = \mathsf {p}_{x_i}$
for some
$\mathsf {p} = \mathsf {p}_{x_i}$
for some
![]() $i = 0, 1, \dots , N$
, and let
$i = 0, 1, \dots , N$
, and let
![]() $x_j$
be a homogeneous coordinate such that
$x_j$
be a homogeneous coordinate such that
![]() $x_j \in f$
, where f is the quasi-tangent polynomial of X at
$x_j \in f$
, where f is the quasi-tangent polynomial of X at
![]() $\mathsf {p}$
. Then, after a suitable choice of homogeneous coordinates
$\mathsf {p}$
. Then, after a suitable choice of homogeneous coordinates
![]() $x_0, \dots , x_N$
, the defining polynomial F of X can be written as
$x_0, \dots , x_N$
, the defining polynomial F of X can be written as
where
![]() $g_k = g_k (x_0, \dots , \hat {x}_i, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
$g_k = g_k (x_0, \dots , \hat {x}_i, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
![]() $d - k a_i$
which is not quasi-linear.
$d - k a_i$
which is not quasi-linear.
Proof. We can write
![]() $F = x_i^m f + g$
, where
$F = x_i^m f + g$
, where
![]() $m \ge 0$
,
$m \ge 0$
,
![]() $f = f (x_0, \dots , x_N) \ni x_j$
is the quasi-tangent polynomial and g is a quasi-homogeneous polynomial of degree d which does not involve a monomial divisible by
$f = f (x_0, \dots , x_N) \ni x_j$
is the quasi-tangent polynomial and g is a quasi-homogeneous polynomial of degree d which does not involve a monomial divisible by
![]() $x_i^m$
and which is contained in the ideal
$x_i^m$
and which is contained in the ideal
![]() $(x_0, \dots , \hat {x}_i, \dots , x_N)^2$
. We write
$(x_0, \dots , \hat {x}_i, \dots , x_N)^2$
. We write
![]() $g = x_j^e h_{e} + \cdots + x_j h_1 + h_0$
, where
$g = x_j^e h_{e} + \cdots + x_j h_1 + h_0$
, where
![]() $e \ge 0$
and
$e \ge 0$
and
![]() $h_k$
is a quasi-homogeneous polynomial of degree
$h_k$
is a quasi-homogeneous polynomial of degree
![]() $d - k a_j$
which does not involve the variables
$d - k a_j$
which does not involve the variables
![]() $x_j$
. By rescaling
$x_j$
. By rescaling
![]() $x_j$
, we may assume
$x_j$
, we may assume
![]() $f = x_j - \tilde {f}$
, where
$f = x_j - \tilde {f}$
, where
![]() $x_j \notin \tilde {f}$
, and we write
$x_j \notin \tilde {f}$
, and we write
![]() $\tilde {f} = x_i^n \tilde {f}_n + \cdots + x_i \tilde {f}_1 + \tilde {f}_0$
, where
$\tilde {f} = x_i^n \tilde {f}_n + \cdots + x_i \tilde {f}_1 + \tilde {f}_0$
, where
![]() $\tilde {f}_k$
is a quasi-homogeneous polynomial of degree
$\tilde {f}_k$
is a quasi-homogeneous polynomial of degree
![]() $d - (m + k) a_i$
which does not involve the variable
$d - (m + k) a_i$
which does not involve the variable
![]() $x_i$
. We consider the coordinate change
$x_i$
. We consider the coordinate change
![]() $x_j \mapsto x_j + \tilde {f}$
. Then the new defining polynomial can be written as
$x_j \mapsto x_j + \tilde {f}$
. Then the new defining polynomial can be written as
 $$ \begin{align*} F &= x_i^m x_j + (x_j + x_i^n \tilde{f}_n + \cdots)^e h_{e} + \cdots + (x_j + x_i^n \tilde{f}_n + \cdots) h_1 + h_0 \\ &= (x_i^{n e - m} \tilde{f}_n^e + \cdots + x_j) x_i^m + \cdots \end{align*} $$
$$ \begin{align*} F &= x_i^m x_j + (x_j + x_i^n \tilde{f}_n + \cdots)^e h_{e} + \cdots + (x_j + x_i^n \tilde{f}_n + \cdots) h_1 + h_0 \\ &= (x_i^{n e - m} \tilde{f}_n^e + \cdots + x_j) x_i^m + \cdots \end{align*} $$
It follows that the new quasi-tangent polynomial is
![]() $x_i^{n e - m} \tilde {f}_n^e + \cdots + x_j$
. We claim that
$x_i^{n e - m} \tilde {f}_n^e + \cdots + x_j$
. We claim that
![]() $n e - m< n$
. We have
$n e - m< n$
. We have
![]() $d = m a_i + a_j$
,
$d = m a_i + a_j$
,
![]() $d = e a_j + \deg h_e \ge e a_j$
and
$d = e a_j + \deg h_e \ge e a_j$
and
![]() $a_j = n a_i + \deg \tilde {f}_n> n a_i$
, which implies
$a_j = n a_i + \deg \tilde {f}_n> n a_i$
, which implies
![]() $n e - m < n$
. Thus, repeating the above coordinate change, we can drop the degree of the quasi-tangent coordinate with respect to
$n e - m < n$
. Thus, repeating the above coordinate change, we can drop the degree of the quasi-tangent coordinate with respect to
![]() $x_i$
, and we may assume
$x_i$
, and we may assume
![]() $F = x_i^m f + x_i^{m-1} g_{m-1} + \cdots + x_i g + g_0$
, where
$F = x_i^m f + x_i^{m-1} g_{m-1} + \cdots + x_i g + g_0$
, where
![]() $f \ni x_j$
and
$f \ni x_j$
and
![]() $g_k$
are quasi-homogeneous polynomials of degree
$g_k$
are quasi-homogeneous polynomials of degree
![]() $a_j$
and
$a_j$
and
![]() $d - k a_i$
, respectively, which do not involve the variable
$d - k a_i$
, respectively, which do not involve the variable
![]() $x_i$
. Moreover,
$x_i$
. Moreover,
![]() $g_k$
is not quasi-linear for
$g_k$
is not quasi-linear for
![]() $0 \le k \le m-1$
. Finally, replacing
$0 \le k \le m-1$
. Finally, replacing
![]() $x_j$
, we may assume
$x_j$
, we may assume
![]() $f = x_j$
and this completes the proof.
$f = x_j$
and this completes the proof.
Remark 2.22. Suppose that a weighted hypersurface
![]() $X \subset \mathbb {P}$
is quasi-smooth at
$X \subset \mathbb {P}$
is quasi-smooth at
![]() $\mathsf {p} = \mathsf {p}_{x_i}$
. Then
$\mathsf {p} = \mathsf {p}_{x_i}$
. Then
![]() $\operatorname {omult}_{\mathsf {p}} ((f = 0)_X)> 1$
for the quasi-tangent polynomial f of X at
$\operatorname {omult}_{\mathsf {p}} ((f = 0)_X)> 1$
for the quasi-tangent polynomial f of X at
![]() $\mathsf {p}$
. Moreover,
$\mathsf {p}$
. Moreover,
![]() $x_j$
is a quasi-tangent coordinate of X at
$x_j$
is a quasi-tangent coordinate of X at
![]() $\mathsf {p}$
if and only if
$\mathsf {p}$
if and only if
![]() $\operatorname {omult}_{\mathsf {p}} (H_{x_j})> 1$
.
$\operatorname {omult}_{\mathsf {p}} (H_{x_j})> 1$
.
2.3 The 95 families
2.3.a Definition of the families
As it is explained in Section 1.2.b, quasi-smooth Fano 3-fold weighted hypersurfaces of index 1 are classified and they form 95 families. According to the classification, the minimum of the weights of an ambient space is
![]() $1$
. Hence a family is determined by a quadruple
$1$
. Hence a family is determined by a quadruple
![]() $(a_1, a_2, a_3, a_4)$
, which means that the family corresponding to a quadruple
$(a_1, a_2, a_3, a_4)$
, which means that the family corresponding to a quadruple
![]() $(a_1, a_2, a_3, a_4)$
is the family of weighted hypersurfaces of degree
$(a_1, a_2, a_3, a_4)$
is the family of weighted hypersurfaces of degree
![]() $d = a_1 + a_2 + a_3 + a_4$
in
$d = a_1 + a_2 + a_3 + a_4$
in
![]() $\mathbb {P} (1, a_1, a_2, a_3, a_4)$
. The 95 families are numbered in the lexicographical order on
$\mathbb {P} (1, a_1, a_2, a_3, a_4)$
. The 95 families are numbered in the lexicographical order on
![]() $(d, a_1, a_2, a_3, a_4)$
, and each family is referred to as family No.
$(d, a_1, a_2, a_3, a_4)$
, and each family is referred to as family No.
![]() $\mathsf {i}$
for
$\mathsf {i}$
for
![]() $\mathsf {i} \in \{1, 2, \dots , 95\}$
. Families No.
$\mathsf {i} \in \{1, 2, \dots , 95\}$
. Families No.
![]() $1$
and
$1$
and
![]() $3$
are the families consisting of quartic 3-folds and degree
$3$
are the families consisting of quartic 3-folds and degree
![]() $6$
hypersurfaces in
$6$
hypersurfaces in
![]() $\mathbb {P} (1, 1, 1, 1, 3)$
, respectively, and for any smooth member of these two families, K-stability (and hence the existence of KE metrics) is known.
$\mathbb {P} (1, 1, 1, 1, 3)$
, respectively, and for any smooth member of these two families, K-stability (and hence the existence of KE metrics) is known.
Definition 2.23. We set
and, for
![]() $\mathsf {i} \in \mathsf {I}$
, we denote by
$\mathsf {i} \in \mathsf {I}$
, we denote by
![]() $\mathcal {F}_{\mathsf {i}}$
the family consisting of the quasi-smooth members of family No.
$\mathcal {F}_{\mathsf {i}}$
the family consisting of the quasi-smooth members of family No.
![]() $\mathsf {i}$
.
$\mathsf {i}$
.
The main objects of this article is thus the members of
![]() $\mathcal {F}_{\mathsf {i}}$
for
$\mathcal {F}_{\mathsf {i}}$
for
![]() $\mathsf {i} \in \mathsf {I}$
.
$\mathsf {i} \in \mathsf {I}$
.
We set
The set
![]() $\mathsf {I}_1$
is characterized as follows: Let
$\mathsf {I}_1$
is characterized as follows: Let
![]() $X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4)$
,
$X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4)$
,
![]() $a_1 \le a_2 \le a_3 \le a_4$
, be a member of a family
$a_1 \le a_2 \le a_3 \le a_4$
, be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
. Then
$\mathsf {i} \in \mathsf {I}$
. Then
![]() $\mathsf {i} \in \mathsf {I}_1$
if and only if
$\mathsf {i} \in \mathsf {I}_1$
if and only if
![]() $a_2 = 1$
. The computations of alpha invariants will be done in a relatively systematic way for families
$a_2 = 1$
. The computations of alpha invariants will be done in a relatively systematic way for families
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
(see Sections 4 and 5), while the computations will be done separately for families
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
(see Sections 4 and 5), while the computations will be done separately for families
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}_1$
(see Section 6).
$\mathsf {i} \in \mathsf {I}_1$
(see Section 6).
We explain notation and conventions concerning the main objects of this article. Let
![]() $X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4) =: \mathbb {P}$
be a member of a family
$X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4) =: \mathbb {P}$
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
.
$\mathsf {i} \in \mathsf {I}$
.
-
• Unless otherwise specified, we assume
 $a_1 \le a_2 \le a_3 \le a_4$
.
$a_1 \le a_2 \le a_3 \le a_4$
. -
• In many situations (especially when we treat a specific family), we denote by
 $x, y, z, t, w$
the homogeneous coordinates of
$x, y, z, t, w$
the homogeneous coordinates of
 $\mathbb {P}$
of degree, respectively,
$\mathbb {P}$
of degree, respectively,
 $1, a_1, a_2, a_3, a_4$
.
$1, a_1, a_2, a_3, a_4$
. -
• We denote by F the polynomial defining X in
 $\mathbb {P}$
, which is quasi-homogeneous of degree
$\mathbb {P}$
, which is quasi-homogeneous of degree
 $d = a_1 + a_2 + a_3 + a_4$
.
$d = a_1 + a_2 + a_3 + a_4$
. -
• We set
 $A = -K_X$
, which is the positive generator of of
$A = -K_X$
, which is the positive generator of of
 $\operatorname {Cl} (X) \cong \mathbb {Z}$
. Note that we have
$\operatorname {Cl} (X) \cong \mathbb {Z}$
. Note that we have  $$\begin{align*}(-K_X)^3 = (A^3) = \frac{d}{a_1 a_2 a_3 a_4} = \frac{a_1 + a_2 + a_3 + a_4}{a_1 a_2 a_3 a_4}. \end{align*}$$
$$\begin{align*}(-K_X)^3 = (A^3) = \frac{d}{a_1 a_2 a_3 a_4} = \frac{a_1 + a_2 + a_3 + a_4}{a_1 a_2 a_3 a_4}. \end{align*}$$
2.3.b Definitions of QI and EI centers and birational (super)rigidity
In this subsection, let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
, where
$\mathsf {i} \in \mathsf {I}$
, where
![]() $a_1 \le a_2 \le a_3 \le a_4$
. We give definitions of QI and EI centers, which are particular singular points on X and are important for understanding birational (super)rigidity of X. For EI centers, we only give an ad hoc definition (see [Reference Corti, Pukhlikhov and ReidCPR00, Section 4.10] and [Reference Cheltsov and ParkCP17, Section 4.2] for more detailed treatments).
$a_1 \le a_2 \le a_3 \le a_4$
. We give definitions of QI and EI centers, which are particular singular points on X and are important for understanding birational (super)rigidity of X. For EI centers, we only give an ad hoc definition (see [Reference Corti, Pukhlikhov and ReidCPR00, Section 4.10] and [Reference Cheltsov and ParkCP17, Section 4.2] for more detailed treatments).
Definition 2.24. Let
![]() $\mathsf {p} \in X$
be a singular point. We say that
$\mathsf {p} \in X$
be a singular point. We say that
![]() $\mathsf {p} \in X$
is an EI center if the upper script
$\mathsf {p} \in X$
is an EI center if the upper script
![]() $\mathrm {EI}$
is given in the fourth column of Table 7, or equivalently if
$\mathrm {EI}$
is given in the fourth column of Table 7, or equivalently if
![]() $\mathsf {i}$
and
$\mathsf {i}$
and
![]() $\mathsf {p}$
belong to one of the following.
$\mathsf {p}$
belong to one of the following.
-
•
 $\mathsf {i} = 7$
and
$\mathsf {i} = 7$
and
 $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
 $\frac {1}{2} (1, 1, 1)$
.
$\frac {1}{2} (1, 1, 1)$
. -
•
 $\mathsf {i} \in \{23, 40, 44, 61, 76\}$
and
$\mathsf {i} \in \{23, 40, 44, 61, 76\}$
and
 $\mathsf {p} = \mathsf {p}_t$
.
$\mathsf {p} = \mathsf {p}_t$
. -
•
 $\mathsf {i} \in \{20, 36\}$
and
$\mathsf {i} \in \{20, 36\}$
and
 $\mathsf {p} = \mathsf {p}_z$
.
$\mathsf {p} = \mathsf {p}_z$
.
We say that
![]() $\mathsf {p} \in X$
is a QI center if there are distinct j and k such that
$\mathsf {p} \in X$
is a QI center if there are distinct j and k such that
![]() $d = 2 a_k + a_j$
and the index of the cyclic quotient singularity
$d = 2 a_k + a_j$
and the index of the cyclic quotient singularity
![]() $\mathsf {p} \in X$
coincides with
$\mathsf {p} \in X$
coincides with
![]() $a_k$
.
$a_k$
.
We say that
![]() $\mathsf {p} \in X$
is a birational involution (BI) center if it is either an EI center or a QI center.
$\mathsf {p} \in X$
is a birational involution (BI) center if it is either an EI center or a QI center.
Remark 2.25. Let X be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
. Then the following are proved in [Reference Cheltsov and ParkCP17].
$\mathsf {i} \in \mathsf {I}$
. Then the following are proved in [Reference Cheltsov and ParkCP17].
-
1. No smooth point on X is a maximal center.
-
2. A singular point
 $\mathsf {p} \in X$
is a maximal center only if either
$\mathsf {p} \in X$
is a maximal center only if either
 $\mathsf {p}$
is a BI center or X is a member of
$\mathsf {p}$
is a BI center or X is a member of
 $\mathcal {F}_{23}$
and
$\mathcal {F}_{23}$
and
 $\mathsf {p} = \mathsf {p}_z$
is of type
$\mathsf {p} = \mathsf {p}_z$
is of type
 $\frac {1}{3} (1, 1, 2)$
.
$\frac {1}{3} (1, 1, 2)$
.
Note that a BI center
![]() $\mathsf {p} \in X$
is not always a maximal center (see Section 5.3, especially Remark 5.10, for the complete analysis for QI centers). Note also that the
$\mathsf {p} \in X$
is not always a maximal center (see Section 5.3, especially Remark 5.10, for the complete analysis for QI centers). Note also that the
![]() $\frac {1}{3} (1, 1, 2)$
point
$\frac {1}{3} (1, 1, 2)$
point
![]() $\mathsf {p}_z$
on a member X of
$\mathsf {p}_z$
on a member X of
![]() $\mathcal {F}_{23}$
is not a maximal center if X is general. However,
$\mathcal {F}_{23}$
is not a maximal center if X is general. However,
![]() $\mathsf {p}_z \in X$
can be a maximal center and in that case there is a birational involution of X (called an invisible involution) with center
$\mathsf {p}_z \in X$
can be a maximal center and in that case there is a birational involution of X (called an invisible involution) with center
![]() $\mathsf {p}_z$
(see [Reference Cheltsov and ParkCP17, Section 4.3]).
$\mathsf {p}_z$
(see [Reference Cheltsov and ParkCP17, Section 4.3]).
Definition 2.26. We define the subset
![]() $\mathsf {I}_{\mathrm {BSR}} \subset \mathsf {I}$
as follows:
$\mathsf {I}_{\mathrm {BSR}} \subset \mathsf {I}$
as follows:
![]() $\mathsf {i} \in \mathsf {I}_{\mathrm {BSR}}$
if and only if a member X of
$\mathsf {i} \in \mathsf {I}_{\mathrm {BSR}}$
if and only if a member X of
![]() $\mathcal {F}_{\mathsf {i}}$
does not admit a BI center. We then define
$\mathcal {F}_{\mathsf {i}}$
does not admit a BI center. We then define
![]() $\mathsf {I}_{\mathrm {BR}} = \mathsf {I} \setminus \mathsf {I}_{\mathrm {BSR}}$
.
$\mathsf {I}_{\mathrm {BR}} = \mathsf {I} \setminus \mathsf {I}_{\mathrm {BSR}}$
.
Note that
![]() $|\mathsf {I}_{\mathrm {BSR}}| = 48$
and
$|\mathsf {I}_{\mathrm {BSR}}| = 48$
and
![]() $|\mathsf {I}_{\mathrm {BR}}| = 45$
. The following is a more precise version of Theorem 1.2.
$|\mathsf {I}_{\mathrm {BR}}| = 45$
. The following is a more precise version of Theorem 1.2.
Theorem 2.27 [Reference Cheltsov and ParkCP17].
Let X be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
.
$\mathsf {i} \in \mathsf {I}$
.
-
1. If
 $\mathsf {i} \in \mathsf {I}_{\mathrm {BSR}}$
, then any member of
$\mathsf {i} \in \mathsf {I}_{\mathrm {BSR}}$
, then any member of
 $\mathcal {F}_{\mathsf {i}}$
is birationally superrigid.
$\mathcal {F}_{\mathsf {i}}$
is birationally superrigid. -
2. If
 $\mathsf {i} \in \mathsf {I}_{\mathrm {BR}}$
, then any member of
$\mathsf {i} \in \mathsf {I}_{\mathrm {BR}}$
, then any member of
 $\mathcal {F}_{\mathsf {i}}$
is birationally rigid while its general member is not birationally superrigid.
$\mathcal {F}_{\mathsf {i}}$
is birationally rigid while its general member is not birationally superrigid.
We emphasize that a family
![]() $\mathcal {F}_{\mathsf {i}}$
, where
$\mathcal {F}_{\mathsf {i}}$
, where
![]() $\mathsf {i} \in \mathsf {I}_{\mathrm {BR}}$
, can contain (in fact does contain for most of
$\mathsf {i} \in \mathsf {I}_{\mathrm {BR}}$
, can contain (in fact does contain for most of
![]() $\mathsf {i} \in \mathsf {I}_{\mathrm {BR}}$
) birationally superrigid Fano 3-folds as special members.
$\mathsf {i} \in \mathsf {I}_{\mathrm {BR}}$
) birationally superrigid Fano 3-folds as special members.
2.3.c Numerics on weights and degrees
Let
be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
. Throughout the subsection, we assume that
$\mathcal {F}_{\mathsf {i}}$
. Throughout the subsection, we assume that
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
and that
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
and that
![]() $a_1 \le a_2 \le a_3 \le a_4$
. We collect some elementary numerical results on weights
$a_1 \le a_2 \le a_3 \le a_4$
. We collect some elementary numerical results on weights
![]() $a_1, \dots , a_4$
, the degree
$a_1, \dots , a_4$
, the degree
![]() $d = a_1 + a_2 + a_3 + a_4$
of the defining polynomial
$d = a_1 + a_2 + a_3 + a_4$
of the defining polynomial
![]() $F = F (x, y, z, t, w)$
of X, and the anticanonical degree
$F = F (x, y, z, t, w)$
of X, and the anticanonical degree
![]() $(A^3)$
of X which will be repeatedly used in the rest of this article.
$(A^3)$
of X which will be repeatedly used in the rest of this article.
Lemma 2.28. One of the following happens.
-
1.
 $d = 2 a_4$
.
$d = 2 a_4$
. -
2.
 $d = 3 a_4$
.
$d = 3 a_4$
. -
3.
 $d = 2 a_4 + a_j$
for some
$d = 2 a_4 + a_j$
for some
 $j \in \{1, 2, 3\}$
.
$j \in \{1, 2, 3\}$
.
Proof. We see that either
![]() $w^n \in F$
for some
$w^n \in F$
for some
![]() $n \ge 2$
or
$n \ge 2$
or
![]() $x^n v \in F$
for some
$x^n v \in F$
for some
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $v \in \{x, y, z, t\}$
by the quasi-smoothness of X.
$v \in \{x, y, z, t\}$
by the quasi-smoothness of X.
Suppose
![]() $w^n \in F$
for some
$w^n \in F$
for some
![]() $n \ge 2$
. Then we have
$n \ge 2$
. Then we have
Hence,
![]() $n = 2, 3$
and we are in case (1) or (2). Suppose
$n = 2, 3$
and we are in case (1) or (2). Suppose
![]() $w^n v \in F$
for some
$w^n v \in F$
for some
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $v \in \{y, z, t\}$
. Then we have
$v \in \{y, z, t\}$
. Then we have
![]() $d = n a_4 + a_j$
and moreover we have
$d = n a_4 + a_j$
and moreover we have
This shows
![]() $n = 2$
, that is,
$n = 2$
, that is,
![]() $d = 2 a_4 + a_j$
.
$d = 2 a_4 + a_j$
.
If
![]() $a_1 = 1$
, then the proof is completed. It remains to show that the case
$a_1 = 1$
, then the proof is completed. It remains to show that the case
![]() $d = 2 a_4 + 1$
does not take place assuming
$d = 2 a_4 + 1$
does not take place assuming
![]() $a_1 \ge 2$
. Suppose
$a_1 \ge 2$
. Suppose
![]() $d = 2 a_4 + 1$
and
$d = 2 a_4 + 1$
and
![]() $a_1 \ge 2$
. Then
$a_1 \ge 2$
. Then
![]() $w^2 x \in F$
and the singularity of
$w^2 x \in F$
and the singularity of
![]() $\mathsf {p}_w \in X$
is of type
$\mathsf {p}_w \in X$
is of type
![]() $\frac {1}{a_4} (a_1, a_2, a_3)$
. There exist distinct
$\frac {1}{a_4} (a_1, a_2, a_3)$
. There exist distinct
![]() $i, j \in \{1,2,3\}$
such that
$i, j \in \{1,2,3\}$
such that
![]() $a_i + a_j$
is divisible by
$a_i + a_j$
is divisible by
![]() $a_4$
since
$a_4$
since
![]() $\mathsf {p}_w \in X$
is terminal. We have
$\mathsf {p}_w \in X$
is terminal. We have
![]() $a_i + a_j = a_4$
since
$a_i + a_j = a_4$
since
![]() $0 < a_i + a_j < 2 a_4$
. Let
$0 < a_i + a_j < 2 a_4$
. Let
![]() $k \in \{1,2,3\}$
be such that
$k \in \{1,2,3\}$
be such that
![]() $\{i, j, k\} = \{1,2,3\}$
. Then
$\{i, j, k\} = \{1,2,3\}$
. Then
Combining this with
![]() $d = 2 a_4 + 1$
, we have
$d = 2 a_4 + 1$
, we have
![]() $a_k = 1$
. This is a contradiction since
$a_k = 1$
. This is a contradiction since
![]() $a_k \ge a_1 \ge 2$
.
$a_k \ge a_1 \ge 2$
.
Lemma 2.29.
-
1. We have
 $\mathsf {i} \in \{9, 17\}$
if and only if
$\mathsf {i} \in \{9, 17\}$
if and only if
 $d = 3 a_4$
and
$d = 3 a_4$
and
 $a_1 = 1$
.
$a_1 = 1$
. -
2. We have
 $a_1 a_2 a_3 (A^3) \le 3$
and the equality holding if and only if
$a_1 a_2 a_3 (A^3) \le 3$
and the equality holding if and only if
 $d = 3 a_4$
.
$d = 3 a_4$
. -
3. If
 $a_1 < a_2$
, then we have
$a_1 < a_2$
, then we have
 $a_1 (A^3) < 1$
.
$a_1 (A^3) < 1$
. -
4. If
 $1 < a_1 < a_2$
, then
$1 < a_1 < a_2$
, then
 $a_1 a_3 (A^3) \le 1$
.
$a_1 a_3 (A^3) \le 1$
. -
5. If
 $a_1 < a_2$
and
$a_1 < a_2$
and
 $d> 2 a_4$
, then
$d> 2 a_4$
, then
 $a_1 a_4 (A^3) \le 2$
.
$a_1 a_4 (A^3) \le 2$
. -
6. If d is divisible by
 $a_4$
and
$a_4$
and
 $\mathsf {i} \notin \{9, 17\}$
, then
$\mathsf {i} \notin \{9, 17\}$
, then
 $a_2 a_3 (A^3) \le 2$
.
$a_2 a_3 (A^3) \le 2$
. -
7. If d is not divisible by
 $a_4$
and
$a_4$
and
 $a_1 \ge 2$
, then
$a_1 \ge 2$
, then
 $a_2 a_4 (A^3) \le 2$
.
$a_2 a_4 (A^3) \le 2$
.
Proof. We prove (1). The ‘only if’ part is obvious. Suppose
![]() $d = 3 a_4$
and
$d = 3 a_4$
and
![]() $a_1 = 1$
. Then we have
$a_1 = 1$
. Then we have
![]() $2 a_4 = 1 + a_2 + a_3$
. This implies
$2 a_4 = 1 + a_2 + a_3$
. This implies
![]() $a_2 = a_4 - 1$
and
$a_2 = a_4 - 1$
and
![]() $a_3 = a_4$
since
$a_3 = a_4$
since
![]() $a_2 \le a_3 \le a_4$
. Then, by setting
$a_2 \le a_3 \le a_4$
. Then, by setting
![]() $a = a_2 \ge 2$
, X is a weighted hypersurface in
$a = a_2 \ge 2$
, X is a weighted hypersurface in
![]() $\mathbb {P} (1, 1, a, a+1, a+1)$
of degree
$\mathbb {P} (1, 1, a, a+1, a+1)$
of degree
![]() $3 (a+1)$
. Suppose
$3 (a+1)$
. Suppose
![]() $\mathsf {p}_z \notin X$
. Then some power of z is contained in F and this implies that
$\mathsf {p}_z \notin X$
. Then some power of z is contained in F and this implies that
![]() $3 (a+1)$
is divisible by a. In particular, we have
$3 (a+1)$
is divisible by a. In particular, we have
![]() $a = 3$
and this case corresponds to
$a = 3$
and this case corresponds to
![]() $\mathsf {i} = 17$
. Suppose
$\mathsf {i} = 17$
. Suppose
![]() $\mathsf {p}_z \notin X$
, then either
$\mathsf {p}_z \notin X$
, then either
![]() $3 (a+1) \equiv 1 \pmod {a}$
or
$3 (a+1) \equiv 1 \pmod {a}$
or
![]() $3 (a+1) \equiv a+1 \pmod {a}$
by the quasi-smoothness of X. In both cases, we have
$3 (a+1) \equiv a+1 \pmod {a}$
by the quasi-smoothness of X. In both cases, we have
![]() $a = 2$
, ad hence
$a = 2$
, ad hence
![]() $\mathsf {i} = 9$
. Thus, (1) is proved.
$\mathsf {i} = 9$
. Thus, (1) is proved.
The assertion (2) follows immediately since we have
and
![]() $d \le 3 a_4$
by Lemma 2.28.
$d \le 3 a_4$
by Lemma 2.28.
We prove (3). Note that
![]() $2 \le a_2 \le a_3 \le a_4$
. Note also that
$2 \le a_2 \le a_3 \le a_4$
. Note also that
![]() $a_4> a_2$
because otherwise X has nonisolated singularity along
$a_4> a_2$
because otherwise X has nonisolated singularity along
![]() $L_{xy}$
which is impossible. In particular, we have
$L_{xy}$
which is impossible. In particular, we have
![]() $a_1 + \cdots + a_4 < 4 a_4$
and
$a_1 + \cdots + a_4 < 4 a_4$
and
![]() $a_2 a_3 \ge 4$
and we have
$a_2 a_3 \ge 4$
and we have
which proves (3).
We prove (4). We have
![]() $a_2 \ge 3$
since
$a_2 \ge 3$
since
![]() $a_2> a_1 > 1$
and thus
$a_2> a_1 > 1$
and thus
We prove (5). We have
![]() $d> 2 a_4$
by assumption. Then, by Lemma 2.28, we have
$d> 2 a_4$
by assumption. Then, by Lemma 2.28, we have
![]() $d = 2 a_4 + a_j$
for some
$d = 2 a_4 + a_j$
for some
![]() $j \in \{1,2,3,4\}$
, and combining this with
$j \in \{1,2,3,4\}$
, and combining this with
![]() $d = a_1 + a_2 + a_3 + a_4$
, we have
$d = a_1 + a_2 + a_3 + a_4$
, we have
If
![]() $a_1> 1$
, then we have
$a_1> 1$
, then we have
![]() $a_2, a_3 \ge 3$
and thus
$a_2, a_3 \ge 3$
and thus
Suppose
![]() $a_1 = 1$
. In this case
$a_1 = 1$
. In this case
![]() $2 \le a_2 \le a_3$
. If
$2 \le a_2 \le a_3$
. If
![]() $a_3 \ge 3$
, then
$a_3 \ge 3$
, then
Suppose
![]() $a_3 = 2$
, that is,
$a_3 = 2$
, that is,
![]() $a_2 = a_3 = 2$
. Then we have
$a_2 = a_3 = 2$
. Then we have
![]() $a_4 = 3$
and
$a_4 = 3$
and
![]() $d = 8$
since
$d = 8$
since
![]() $d = 5 + a_4> 2 a_4$
and
$d = 5 + a_4> 2 a_4$
and
![]() $a_4$
is odd. In this case, we have
$a_4$
is odd. In this case, we have
![]() $a_4 (A^3) = 2$
. This proves (5).
$a_4 (A^3) = 2$
. This proves (5).
We prove (6). By Lemma 2.28 and (1), either
![]() $d = 2 a_4$
or
$d = 2 a_4$
or
![]() $d = 3 a_4$
and
$d = 3 a_4$
and
![]() $a_1 \ge 2$
. If
$a_1 \ge 2$
. If
![]() $d = 2 a_4$
(resp.
$d = 2 a_4$
(resp.
![]() $d = 3 a_4$
and
$d = 3 a_4$
and
![]() $a_1 \ge 2$
), then
$a_1 \ge 2$
), then
This proves (6).
We prove (7). By Lemma 2.28, we have
![]() $d = 2 a_4 + a_j$
for some
$d = 2 a_4 + a_j$
for some
![]() $j \in \{1, 2, 3\}$
. Then we have
$j \in \{1, 2, 3\}$
. Then we have
![]() $a_4 = a_1 + a_2 + a_3 - a_j \le a_2 + a_3$
. If
$a_4 = a_1 + a_2 + a_3 - a_j \le a_2 + a_3$
. If
![]() $a_1 \ge 3$
, then
$a_1 \ge 3$
, then
We continue the proof assuming
![]() $a_1 = 2$
. If in addition
$a_1 = 2$
. If in addition
![]() $a_2 < a_3$
, then
$a_2 < a_3$
, then
We continue the proof assuming
![]() $a_1 = 2$
and
$a_1 = 2$
and
![]() $a_2 = a_3$
. In this case, by setting
$a_2 = a_3$
. In this case, by setting
![]() $a = a_2 = a_3$
and
$a = a_2 = a_3$
and
![]() $b = a_4$
, X is a weighted hypersurface of degree d in
$b = a_4$
, X is a weighted hypersurface of degree d in
![]() $\mathbb {P} (1, 2, a, a, b)$
and either
$\mathbb {P} (1, 2, a, a, b)$
and either
![]() $d = 2 b + 2$
or
$d = 2 b + 2$
or
![]() $d = 2 b + a$
. If
$d = 2 b + a$
. If
![]() $d = 2 b + 2$
, then
$d = 2 b + 2$
, then
![]() $b = 2 a$
but this is impossible since X has only terminal singularities. Hence,
$b = 2 a$
but this is impossible since X has only terminal singularities. Hence,
![]() $d = 2 b + a$
. In this case
$d = 2 b + a$
. In this case
![]() $b = a + 2$
and
$b = a + 2$
and
![]() $d = 3 a + 4$
. By the quasi-smoothness of X, we see that
$d = 3 a + 4$
. By the quasi-smoothness of X, we see that
![]() $d = 3 a + 4$
is divisible by a. This implies that
$d = 3 a + 4$
is divisible by a. This implies that
![]() $a \in \{2, 4\}$
. This is impossible since X has only terminal singularities. Therefore, (7) is proved.
$a \in \{2, 4\}$
. This is impossible since X has only terminal singularities. Therefore, (7) is proved.
2.3.d How to compute alpha invariants?
Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
. For the proof of Theorem 1.8, it is necessary to show
$\mathsf {i} \in \mathsf {I}$
. For the proof of Theorem 1.8, it is necessary to show
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any point
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any point
![]() $\mathsf {p} \in X$
. Let
$\mathsf {p} \in X$
. Let
![]() $\mathsf {p} \in X$
be a point. We briefly explain the most typical method of bounding
$\mathsf {p} \in X$
be a point. We briefly explain the most typical method of bounding
![]() $\alpha _{\mathsf {p}} (X)$
from below, which goes as follows.
$\alpha _{\mathsf {p}} (X)$
from below, which goes as follows.
-
1. Choose and fix a divisor S on X which vanishes at
 $\mathsf {p}$
to a relatively large (orbifold) multiplicity
$\mathsf {p}$
to a relatively large (orbifold) multiplicity
 $m = \operatorname {omult}_{\mathsf {p}} (S)> 0$
. In some cases,
$m = \operatorname {omult}_{\mathsf {p}} (S)> 0$
. In some cases,
 $S = H_x$
(when
$S = H_x$
(when
 $\mathsf {p} \in H_x$
), and in other cases, S is the quasi-tangent divisor of X at
$\mathsf {p} \in H_x$
), and in other cases, S is the quasi-tangent divisor of X at
 $\mathsf {p}$
. Let a be the positive integer such that
$\mathsf {p}$
. Let a be the positive integer such that
 $S \sim a A$
.
$S \sim a A$
. -
2. Let
 $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
 $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
 $\frac {1}{a} S$
. Then
$\frac {1}{a} S$
. Then
 $D \cdot S$
is an effective
$D \cdot S$
is an effective
 $1$
-cycle on X.
$1$
-cycle on X. -
3. Find a
 $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
 $T \in |e A|_{\mathbb {Q}}$
for some
$T \in |e A|_{\mathbb {Q}}$
for some
 $e \in \mathbb {Z}_{> 0}$
such that
$e \in \mathbb {Z}_{> 0}$
such that
 $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
 $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
 $D \cdot S$
. We will find such a
$D \cdot S$
. We will find such a
 $\mathbb {Q}$
-divisor T by considering
$\mathbb {Q}$
-divisor T by considering
 $\mathsf {p}$
-isolating set or class which will be explained in Section 3.1.c.
$\mathsf {p}$
-isolating set or class which will be explained in Section 3.1.c. -
4. Let
 $q = q_{\mathsf {p}}$
be the quotient morphism of
$q = q_{\mathsf {p}}$
be the quotient morphism of
 $\mathsf {p} \in X$
and
$\mathsf {p} \in X$
and
 $\check {\mathsf {p}}$
be the preimage of
$\check {\mathsf {p}}$
be the preimage of
 $\mathsf {p}$
via q. By the above choices,
$\mathsf {p}$
via q. By the above choices,
 $\operatorname {Supp} (q^*D) \cap \operatorname {Supp} (q^*S) \cap \operatorname {Supp} (q^*T)$
is a finite set of points including
$\operatorname {Supp} (q^*D) \cap \operatorname {Supp} (q^*S) \cap \operatorname {Supp} (q^*T)$
is a finite set of points including
 $\check {\mathsf {p}}$
, and hence the local intersection number
$\check {\mathsf {p}}$
, and hence the local intersection number
 $(q^*D \cdot q^*S \cdot q^*T)_{\check {\mathsf {p}}}$
is defined (see Section 3.1.a). Then we have the inequalities where r is the index of the cyclic quotient singularity
$(q^*D \cdot q^*S \cdot q^*T)_{\check {\mathsf {p}}}$
is defined (see Section 3.1.a). Then we have the inequalities where r is the index of the cyclic quotient singularity $$\begin{align*}m \operatorname{omult}_{\mathsf{p}} (D) \le (q_{\mathsf{p}}^*D \cdot q_{\mathsf{p}}^*S \cdot q_{\mathsf{p}}^*T)_{\check{\mathsf{p}}} \le r (D \cdot S \cdot T) = r a e (A^3), \end{align*}$$
$$\begin{align*}m \operatorname{omult}_{\mathsf{p}} (D) \le (q_{\mathsf{p}}^*D \cdot q_{\mathsf{p}}^*S \cdot q_{\mathsf{p}}^*T)_{\check{\mathsf{p}}} \le r (D \cdot S \cdot T) = r a e (A^3), \end{align*}$$
 $\mathsf {p} \in X$
. Note that q is the identity morphism and
$\mathsf {p} \in X$
. Note that q is the identity morphism and
 $r = 1$
when
$r = 1$
when
 $\mathsf {p} \in X$
is a smooth point. By Lemma 3.2 which will be explained below, we have for any D as in (2).
$\mathsf {p} \in X$
is a smooth point. By Lemma 3.2 which will be explained below, we have for any D as in (2). $$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X;D) \ge \frac{r a e (A^3)}{m} \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X;D) \ge \frac{r a e (A^3)}{m} \end{align*}$$
-
5. As a conclusion, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; S), \ \frac{r a e (A^3)}{m} \right\}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; S), \ \frac{r a e (A^3)}{m} \right\}. \end{align*}$$
-
6. It remains to bound
 $\operatorname {lct}_{\mathsf {p}} (X;S)$
from below. This is easy when S is quasi-smooth at
$\operatorname {lct}_{\mathsf {p}} (X;S)$
from below. This is easy when S is quasi-smooth at
 $\mathsf {p}$
because in that case we have
$\mathsf {p}$
because in that case we have
 $\operatorname {lct}_{\mathsf {p}} (X;S) = 1$
. The computation gets involved when S is the quasi-tangent divisor but will be done by considering suitable weighted blowups which will be explained in Section 3.2.b.
$\operatorname {lct}_{\mathsf {p}} (X;S) = 1$
. The computation gets involved when S is the quasi-tangent divisor but will be done by considering suitable weighted blowups which will be explained in Section 3.2.b.
We need to consider variants of the above explained method or other methods especially for points in special positions. These will be explained in Section 3.
3 Methods of computing log canonical thresholds
3.1 Auxiliary results
3.1.a Some results on multiplicities and log canonicity
Let V be an n-dimensional variety. For effective Cartier divisors
![]() $D_1, \dots , D_n$
on V and a point
$D_1, \dots , D_n$
on V and a point
![]() $\mathsf {p} \in V$
which is an isolated component of
$\mathsf {p} \in V$
which is an isolated component of
![]() $\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_n)$
, the intersection multiplicity
$\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_n)$
, the intersection multiplicity
is defined (see [Reference FultonFul98, Example 7.1.10]). Suppose that V is
![]() $\mathbb {Q}$
-factorial. Then this definition is naturally generalized to effective
$\mathbb {Q}$
-factorial. Then this definition is naturally generalized to effective
![]() $\mathbb {Q}$
-divisors
$\mathbb {Q}$
-divisors
![]() $D_1, \dots , D_n$
as follows:
$D_1, \dots , D_n$
as follows:
where d is a positive integer such that
![]() $d D_i$
is a Cartier divisor for any i. In this paper, we set
$d D_i$
is a Cartier divisor for any i. In this paper, we set
and call it the local intersection number of
![]() $D_1, \dots , D_n$
at
$D_1, \dots , D_n$
at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Remark 3.1. If
![]() $\mathsf {p} \in V$
is a smooth point,
$\mathsf {p} \in V$
is a smooth point,
![]() $D_1, \dots , D_n$
are effective divisors defined by
$D_1, \dots , D_n$
are effective divisors defined by
![]() $f_1, \dots , f_n \in \mathcal {O}_{V, \mathsf {p}}$
around
$f_1, \dots , f_n \in \mathcal {O}_{V, \mathsf {p}}$
around
![]() $\mathsf {p}$
, and
$\mathsf {p}$
, and
![]() $\mathsf {p}$
is an isolated component of
$\mathsf {p}$
is an isolated component of
![]() $\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_n)$
, then
$\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_n)$
, then
If
![]() $X \subset \mathbb {P} (a_0, \dots , a_N)$
is an n-dimensional subvariety which is quasi-smooth at
$X \subset \mathbb {P} (a_0, \dots , a_N)$
is an n-dimensional subvariety which is quasi-smooth at
![]() $\mathsf {p} = \mathsf {p}_{x_i} \in V$
,
$\mathsf {p} = \mathsf {p}_{x_i} \in V$
,
![]() $D_1 = (G_1 = 0)_X, \dots , D_n = (G_n = 0)_X$
are effective Weil divisors such that
$D_1 = (G_1 = 0)_X, \dots , D_n = (G_n = 0)_X$
are effective Weil divisors such that
![]() $\mathsf {p}$
is an isolated component of
$\mathsf {p}$
is an isolated component of
![]() $D_1 \cap \cdots \cap D_n$
, where
$D_1 \cap \cdots \cap D_n$
, where
![]() $G_i = G_i (x_0, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
$G_i = G_i (x_0, \dots , x_N)$
is a quasi-homogeneous polynomial of degree
![]() $d_i$
, then
$d_i$
, then
where
![]() $\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}} := X \cap \mathcal {U}_{\mathsf {p}}$
is the orbifold chart with
$\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}} := X \cap \mathcal {U}_{\mathsf {p}}$
is the orbifold chart with
![]() $\breve {\mathsf {p}} \in \breve {U}_{\mathsf {p}}$
the preimage of
$\breve {\mathsf {p}} \in \breve {U}_{\mathsf {p}}$
the preimage of
![]() $\mathsf {p}$
and
$\mathsf {p}$
and
![]() $g_i = G (\breve {x}_0, \dots , 1, \dots , \breve {x}_N)$
with
$g_i = G (\breve {x}_0, \dots , 1, \dots , \breve {x}_N)$
with
![]() $\breve {x}_j = x_j/x_i^{a_j/a_i}$
for
$\breve {x}_j = x_j/x_i^{a_j/a_i}$
for
![]() $j \ne i$
.
$j \ne i$
.
We will frequently use the following property of local intersection numbers. Let
![]() $D_1, \dots , D_n$
be effective
$D_1, \dots , D_n$
be effective
![]() $\mathbb {Q}$
-divisors on X and
$\mathbb {Q}$
-divisors on X and
![]() $\mathsf {p} \in X$
be a smooth point. If
$\mathsf {p} \in X$
be a smooth point. If
![]() $\mathsf {p}$
is an isolated component of
$\mathsf {p}$
is an isolated component of
![]() $\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_n)$
, then
$\operatorname {Supp} (D_1) \cap \cdots \cap \operatorname {Supp} (D_n)$
, then
 $$\begin{align*}(D_1 \cdot \ldots \cdot D_n)_{\mathsf{p}} \ge \prod_{i=1}^n \operatorname{mult}_{\mathsf{p}} (D_i). \end{align*}$$
$$\begin{align*}(D_1 \cdot \ldots \cdot D_n)_{\mathsf{p}} \ge \prod_{i=1}^n \operatorname{mult}_{\mathsf{p}} (D_i). \end{align*}$$
We refer readers to [Reference FultonFul98, Corollary 12.4] for a proof. Although the following results are well-known to experts, we include their proofs for readers’ convenience.
Lemma 3.2. Let
![]() $\mathsf {p} \in X$
be either a germ of a smooth variety or a germ of a cyclic quotient singular point, and let D be an effective
$\mathsf {p} \in X$
be either a germ of a smooth variety or a germ of a cyclic quotient singular point, and let D be an effective
![]() $\mathbb {Q}$
-divisor on X. Then the inequality
$\mathbb {Q}$
-divisor on X. Then the inequality
holds.
Proof. Let
![]() $q = q_{\mathsf {p}} \colon \check {X} \to X$
be the quotient morphism of
$q = q_{\mathsf {p}} \colon \check {X} \to X$
be the quotient morphism of
![]() $\mathsf {p} \in X$
, which is étale in codimension
$\mathsf {p} \in X$
, which is étale in codimension
![]() $1$
, and let
$1$
, and let
![]() $\check {\mathsf {p}} \in \check {X}$
be the preimage of
$\check {\mathsf {p}} \in \check {X}$
be the preimage of
![]() $\mathsf {p}$
. By [Reference KollárKol+92, 20.4 Corollary], we have
$\mathsf {p}$
. By [Reference KollárKol+92, 20.4 Corollary], we have
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) = \operatorname {lct}_{\check {\mathsf {p}}} (\check {X};q^*D)$
. Note that
$\operatorname {lct}_{\mathsf {p}} (X;D) = \operatorname {lct}_{\check {\mathsf {p}}} (\check {X};q^*D)$
. Note that
![]() $\check {\mathsf {p}} \in \check {X}$
is smooth. Hence, by [Reference KollárKol97, 8.10 Lemma], we have
$\check {\mathsf {p}} \in \check {X}$
is smooth. Hence, by [Reference KollárKol97, 8.10 Lemma], we have
and the proof is completed.
Lemma 3.3 (
 $2n$
-inequality, cf. [Reference CortiCor00, Corollary 3.5]).
$2n$
-inequality, cf. [Reference CortiCor00, Corollary 3.5]).
Let
![]() $\mathsf {p} \in X$
be a germ of a smooth
$\mathsf {p} \in X$
be a germ of a smooth
![]() $3$
-fold, D an effective
$3$
-fold, D an effective
![]() $\mathbb {Q}$
-divisor on X,
$\mathbb {Q}$
-divisor on X,
![]() $n> 0$
a rational number, and let
$n> 0$
a rational number, and let
![]() $\varphi \colon Y \to X$
be the blowup of X at
$\varphi \colon Y \to X$
be the blowup of X at
![]() $\mathsf {p}$
with exceptional divisor E. If
$\mathsf {p}$
with exceptional divisor E. If
![]() $(X, \frac {1}{n} D)$
is not canonical at
$(X, \frac {1}{n} D)$
is not canonical at
![]() $\mathsf {p}$
, then there exists a line
$\mathsf {p}$
, then there exists a line
![]() $L \subset E \cong \mathbb {P}^2$
with the following property.
$L \subset E \cong \mathbb {P}^2$
with the following property.
-
• For any prime divisor T on X such that T is smooth at
 $\mathsf {p}$
and that its proper transform
$\mathsf {p}$
and that its proper transform
 $\tilde {T}$
contains L, we have
$\tilde {T}$
contains L, we have
 $\operatorname {mult}_{\mathsf {p}} (D|_T)> 2 n$
.
$\operatorname {mult}_{\mathsf {p}} (D|_T)> 2 n$
.
Proof. We set
![]() $m = \operatorname {mult}_{\mathsf {p}} (D)$
. By [Reference CortiCor00, Corollary 3.5], one of the following holds.
$m = \operatorname {mult}_{\mathsf {p}} (D)$
. By [Reference CortiCor00, Corollary 3.5], one of the following holds.
-
1.
 $m> 2 n$
.
$m> 2 n$
. -
2. There is a line
 $L \subset E$
such that the pair is not log canonical at the generic point of L.
$L \subset E$
such that the pair is not log canonical at the generic point of L. $$\begin{align*}\left(Y, \left(\frac{m}{n} - 1\right)E + \frac{1}{n} \tilde{D} \right) \end{align*}$$
$$\begin{align*}\left(Y, \left(\frac{m}{n} - 1\right)E + \frac{1}{n} \tilde{D} \right) \end{align*}$$
Note that in [Reference CortiCor00, Corollary 3.5] the boundary is a movable linear system
![]() $\mathcal {H}$
, but the same argument applies if we replace
$\mathcal {H}$
, but the same argument applies if we replace
![]() $\mathcal {H}$
by an effective
$\mathcal {H}$
by an effective
![]() $\mathbb {Q}$
-divisor D. We may assume
$\mathbb {Q}$
-divisor D. We may assume
![]() $m \le 2n$
because otherwise
$m \le 2n$
because otherwise
![]() $\operatorname {mult}_{\mathsf {p}} (D|_T)> 2 n$
for any prime divisor T which is smooth at
$\operatorname {mult}_{\mathsf {p}} (D|_T)> 2 n$
for any prime divisor T which is smooth at
![]() $\mathsf {p}$
and the assertion follows by choosing any line on E. Thus, the option (2) takes place. Let T be a prime divisor on X such that T is smooth at
$\mathsf {p}$
and the assertion follows by choosing any line on E. Thus, the option (2) takes place. Let T be a prime divisor on X such that T is smooth at
![]() $\mathsf {p}$
and
$\mathsf {p}$
and
![]() $\tilde {T} \supset L$
. We have
$\tilde {T} \supset L$
. We have
 $$\begin{align*}K_Y + \left( \frac{m}{n} - 1 \right) E + \frac{1}{n} \tilde{D} + \tilde{T} = \varphi^* \left( K_X + \frac{1}{n} D + T \right). \end{align*}$$
$$\begin{align*}K_Y + \left( \frac{m}{n} - 1 \right) E + \frac{1}{n} \tilde{D} + \tilde{T} = \varphi^* \left( K_X + \frac{1}{n} D + T \right). \end{align*}$$
Note that
![]() $E|_{\tilde {T}} = L$
, and we can write
$E|_{\tilde {T}} = L$
, and we can write
![]() $\tilde {D}|_{\tilde {T}} = \alpha L + G$
, where
$\tilde {D}|_{\tilde {T}} = \alpha L + G$
, where
![]() $\alpha \ge 0$
is a rational number and G is an effective
$\alpha \ge 0$
is a rational number and G is an effective
![]() $\mathbb {Q}$
-divisor on
$\mathbb {Q}$
-divisor on
![]() $\tilde {T}$
. Thus, by restricting the above equation to
$\tilde {T}$
. Thus, by restricting the above equation to
![]() $\tilde {T}$
, we have
$\tilde {T}$
, we have
 $$\begin{align*}K_{\tilde{T}} + \left( \frac{m}{n} - 1 + \alpha \right) L + G = \varphi^* \left(K_T + \frac{1}{n} D|_T \right), \end{align*}$$
$$\begin{align*}K_{\tilde{T}} + \left( \frac{m}{n} - 1 + \alpha \right) L + G = \varphi^* \left(K_T + \frac{1}{n} D|_T \right), \end{align*}$$
and the pair
is not log canonical at the generic point of L. This implies
![]() $\frac {m}{n} - 1 + \alpha> 1$
, and we have
$\frac {m}{n} - 1 + \alpha> 1$
, and we have
Thus,
![]() $\operatorname {mult}_{\mathsf {p}} (D|_T)> 2 n$
and the proof is completed.
$\operatorname {mult}_{\mathsf {p}} (D|_T)> 2 n$
and the proof is completed.
Lemma 3.4. Let
![]() $D \in \left | \mathcal {O}_{\mathbb {P}^2} (3) \right |$
be a divisor on
$D \in \left | \mathcal {O}_{\mathbb {P}^2} (3) \right |$
be a divisor on
![]() $\mathbb {P}^2$
which is not a triple line. Then
$\mathbb {P}^2$
which is not a triple line. Then
![]() $\operatorname {lct} (\mathbb {P}^2; D) \ge 1/2$
.
$\operatorname {lct} (\mathbb {P}^2; D) \ge 1/2$
.
Proof. We have the following possibilities for D.
-
1. D is irreducible and reduced.
-
2.
 $D = Q + L$
, where Q is an irreducible conic and L is a line.
$D = Q + L$
, where Q is an irreducible conic and L is a line. -
3.
 $D = L_1 + 2 L_2$
, where
$D = L_1 + 2 L_2$
, where
 $L_1, L_2$
are distinct lines.
$L_1, L_2$
are distinct lines. -
4.
 $D = L_1 + L_2 + L_3$
, where
$D = L_1 + L_2 + L_3$
, where
 $L_1, L_2, L_3$
are mutually distinct lines.
$L_1, L_2, L_3$
are mutually distinct lines.
If we are in one of the cases (1), (2) and (3), then
![]() $\operatorname {mult}_{\mathsf {p}} (D) \le 2$
for any point
$\operatorname {mult}_{\mathsf {p}} (D) \le 2$
for any point
![]() $\mathsf {p} \in D$
and thus
$\mathsf {p} \in D$
and thus
![]() $(\mathbb {P}^2, \frac {1}{2} D)$
is log canonical. If we are in case (3), then it is obvious that the pair
$(\mathbb {P}^2, \frac {1}{2} D)$
is log canonical. If we are in case (3), then it is obvious that the pair
![]() $(\mathbb {P}^2, \frac {1}{2} D) = (\mathbb {P}^2, \frac {1}{2} L_1 + L_2)$
is log canonical.
$(\mathbb {P}^2, \frac {1}{2} D) = (\mathbb {P}^2, \frac {1}{2} L_1 + L_2)$
is log canonical.
Lemma 3.5. Let X be a Fano
![]() $3$
-fold of Picard number one, and let
$3$
-fold of Picard number one, and let
![]() $\mathsf {p} \in X$
be a cyclic quotient terminal singular point (which is not a smooth point). If
$\mathsf {p} \in X$
be a cyclic quotient terminal singular point (which is not a smooth point). If
![]() $\mathsf {p} \in X$
is not a maximal center, then there is at most one irreducible
$\mathsf {p} \in X$
is not a maximal center, then there is at most one irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in \left | -K_X \right |{}_{\mathbb {Q}}$
such that
$D \in \left | -K_X \right |{}_{\mathbb {Q}}$
such that
![]() $(X, D)$
is not canonical at
$(X, D)$
is not canonical at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Proof. Suppose that there are two distinct irreducible
![]() $\mathbb {Q}$
-divisors
$\mathbb {Q}$
-divisors
![]() $D_i \sim _{\mathbb {Q}} - K_X$
such that
$D_i \sim _{\mathbb {Q}} - K_X$
such that
![]() $(X, D_i)$
is not canonical at
$(X, D_i)$
is not canonical at
![]() $\mathsf {p}$
for
$\mathsf {p}$
for
![]() $i = 1, 2$
. Let
$i = 1, 2$
. Let
![]() $r> 1$
be the index of the singularity
$r> 1$
be the index of the singularity
![]() $\mathsf {p} \in X$
, and let
$\mathsf {p} \in X$
, and let
![]() $\varphi \colon Y \to X$
be the Kawamata blowup at
$\varphi \colon Y \to X$
be the Kawamata blowup at
![]() $\mathsf {p}$
with exceptional divisor E. By [Reference KawamataKaw96], we have
$\mathsf {p}$
with exceptional divisor E. By [Reference KawamataKaw96], we have
![]() $\operatorname {ord}_E (D_i)> 1/r$
. Take a positive integer n such that
$\operatorname {ord}_E (D_i)> 1/r$
. Take a positive integer n such that
![]() $n D_1, n D_2$
are both integral and
$n D_1, n D_2$
are both integral and
![]() $n D_1 \sim n D_2$
. Then the pencil
$n D_1 \sim n D_2$
. Then the pencil
![]() $\mathcal {M} \sim - n K_X$
generated by
$\mathcal {M} \sim - n K_X$
generated by
![]() $n D_1$
and
$n D_1$
and
![]() $n D_2$
is a movable linear system and we have
$n D_2$
is a movable linear system and we have
![]() $\operatorname {ord}_E (\mathcal {M}) \ge n/r$
. It follows that the pair
$\operatorname {ord}_E (\mathcal {M}) \ge n/r$
. It follows that the pair
![]() $(X, \frac {1}{n} \mathcal {M})$
is not canonical at
$(X, \frac {1}{n} \mathcal {M})$
is not canonical at
![]() $\mathsf {p}$
. This is a contradiction since
$\mathsf {p}$
. This is a contradiction since
![]() $\mathsf {p} \in X$
is not a maximal center.
$\mathsf {p} \in X$
is not a maximal center.
Lemma 3.6. Let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
. Let
$\mathsf {i} \in \mathsf {I}$
. Let
![]() $i \in \{1, 2, 3, 4\}$
be such that
$i \in \{1, 2, 3, 4\}$
be such that
![]() $b_i> 1$
and
$b_i> 1$
and
![]() $\mathsf {p} := \mathsf {p}_{y_i} \in X$
. If
$\mathsf {p} := \mathsf {p}_{y_i} \in X$
. If
![]() $H_x$
is the quasi-tangent divisor of X at
$H_x$
is the quasi-tangent divisor of X at
![]() $\mathsf {p}$
, then the pair
$\mathsf {p}$
, then the pair
![]() $(X, H_x)$
is not canonical at
$(X, H_x)$
is not canonical at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Proof. Note that the point
![]() $\mathsf {p} \in X$
is of type
$\mathsf {p} \in X$
is of type
![]() $\frac {1}{b_i} (b_j, b_k, b_l)$
, where
$\frac {1}{b_i} (b_j, b_k, b_l)$
, where
![]() $\{i, j, k, l\} = \{1, 2, 3, 4\}$
, and it is a terminal singularity. Let
$\{i, j, k, l\} = \{1, 2, 3, 4\}$
, and it is a terminal singularity. Let
![]() $\varphi \colon Y \to X$
be the Kawamata blowup with exceptional divisor E. Since
$\varphi \colon Y \to X$
be the Kawamata blowup with exceptional divisor E. Since
![]() $H_x$
is the quasi-tangent divisor of X at
$H_x$
is the quasi-tangent divisor of X at
![]() $\mathsf {p}$
, we have
$\mathsf {p}$
, we have
Combining this with
we see that the discrepancy of the pair
![]() $(X, H_x)$
along E is negative. This completes the proof.
$(X, H_x)$
along E is negative. This completes the proof.
3.1.b Some results on singularities of weighted hypersurfaces
Lemma 3.7. Let X be a quasi-smooth weighted hypersurface in
![]() $\mathbb {P} (b_0, \dots , b_4)$
. Assume that
$\mathbb {P} (b_0, \dots , b_4)$
. Assume that
![]() $\mathbb {P} (b_0, \dots , b_4)$
is well-formed and X has at most isolated singularities. Then any quasi-hyperplane section on X is a normal surface.
$\mathbb {P} (b_0, \dots , b_4)$
is well-formed and X has at most isolated singularities. Then any quasi-hyperplane section on X is a normal surface.
Proof. Let
![]() $x_0, \dots , x_4$
be the homogeneous coordinates of
$x_0, \dots , x_4$
be the homogeneous coordinates of
![]() $\mathbb {P} = \mathbb {P} (b_0, \dots , b_4)$
of degree
$\mathbb {P} = \mathbb {P} (b_0, \dots , b_4)$
of degree
![]() $b_0, \dots , b_4$
, respectively. Let
$b_0, \dots , b_4$
, respectively. Let
![]() $F = F (x_0,\dots ,x_4)$
be the defining polynomial of X, and let S be a quasi-hyperplane section on X. After replacing homogeneous coordinates, we may assume
$F = F (x_0,\dots ,x_4)$
be the defining polynomial of X, and let S be a quasi-hyperplane section on X. After replacing homogeneous coordinates, we may assume
![]() $S = (x_4 = 0)_X = (x_4 = F = 0) \subset \mathbb {P}$
. It is enough to show that the singular locus
$S = (x_4 = 0)_X = (x_4 = F = 0) \subset \mathbb {P}$
. It is enough to show that the singular locus
![]() $\operatorname {Sing} (S)$
of S is a finite set of points.
$\operatorname {Sing} (S)$
of S is a finite set of points.
We write
![]() $F = x_4 G + \bar {F}$
, where
$F = x_4 G + \bar {F}$
, where
![]() $G = G (x_0, \dots , x_4)$
and
$G = G (x_0, \dots , x_4)$
and
![]() $\bar {F} = \bar {F} (x_0, \dots , x_3)$
are quasi-homogeneous polynomials. We set
$\bar {F} = \bar {F} (x_0, \dots , x_3)$
are quasi-homogeneous polynomials. We set
![]() $\bar {\mathbb {P}} = \mathbb {P} (b_0, \dots , b_3)$
. We claim that
$\bar {\mathbb {P}} = \mathbb {P} (b_0, \dots , b_3)$
. We claim that
![]() $\bar {\mathbb {P}}$
is well-formed. Suppose it is not. Then
$\bar {\mathbb {P}}$
is well-formed. Suppose it is not. Then
![]() $\operatorname {Sing} (\mathbb {P})$
contains a two-dimensional stratum. We have
$\operatorname {Sing} (\mathbb {P})$
contains a two-dimensional stratum. We have
![]() $\operatorname {Sing} (X) = \operatorname {Sing} (\mathbb {P}) \cap X$
since a quasi-smooth weighted hypersurface is well-formed ([Reference Iano-FletcherIF00, Theorem 6.17]). It follows that
$\operatorname {Sing} (X) = \operatorname {Sing} (\mathbb {P}) \cap X$
since a quasi-smooth weighted hypersurface is well-formed ([Reference Iano-FletcherIF00, Theorem 6.17]). It follows that
![]() $\operatorname {Sing} (X)$
cannot be a finite set of points. This is a contradiction, and the claim is proved. The surface S is identified with the hypersurface
$\operatorname {Sing} (X)$
cannot be a finite set of points. This is a contradiction, and the claim is proved. The surface S is identified with the hypersurface
![]() $(\bar {F} = 0) \subset \bar {\mathbb {P}}$
, and we have
$(\bar {F} = 0) \subset \bar {\mathbb {P}}$
, and we have
We claim that
![]() $\operatorname {Sing} (\bar {\mathbb {P}}) \cap S$
is a finite set of points. Suppose not. Then
$\operatorname {Sing} (\bar {\mathbb {P}}) \cap S$
is a finite set of points. Suppose not. Then
![]() $\operatorname {Sing} (\bar {\mathbb {P}}) \cap S$
contains a curve and so does
$\operatorname {Sing} (\bar {\mathbb {P}}) \cap S$
contains a curve and so does
![]() $\operatorname {Sing} (\mathbb {P}) \cap S$
. In particular,
$\operatorname {Sing} (\mathbb {P}) \cap S$
. In particular,
![]() $\operatorname {Sing} (X) = \operatorname {Sing} (\mathbb {P}) \cap X$
contains a curve. This is impossible since
$\operatorname {Sing} (X) = \operatorname {Sing} (\mathbb {P}) \cap X$
contains a curve. This is impossible since
![]() $\operatorname {Sing} (X)$
is a finite set of points, and the claim is proved.
$\operatorname {Sing} (X)$
is a finite set of points, and the claim is proved.
It remains to show that the closed subset
![]() $\Sigma := S \setminus \operatorname {QSm} (S) \subset \mathbb {P}$
is a finite set of points. Let
$\Sigma := S \setminus \operatorname {QSm} (S) \subset \mathbb {P}$
is a finite set of points. Let
![]() $\Pi \colon \mathbb {A}^5 \setminus \{o\} \to \mathbb {P}$
be the natural quotient morphism. Then
$\Pi \colon \mathbb {A}^5 \setminus \{o\} \to \mathbb {P}$
be the natural quotient morphism. Then
![]() $\Sigma = \Pi (\operatorname {Sing} (C^*_S))$
, where
$\Sigma = \Pi (\operatorname {Sing} (C^*_S))$
, where
![]() $C^*_S \subset \mathbb {A}^5 \setminus \{o\}$
is the punctured affine quasi-cone of S. We have
$C^*_S \subset \mathbb {A}^5 \setminus \{o\}$
is the punctured affine quasi-cone of S. We have
![]() $\operatorname {Sing} (C_X) \cap C_S = \operatorname {Sing} (C_S) \cap (G = 0)$
. By the quasi-smoothness of X, we have
$\operatorname {Sing} (C_X) \cap C_S = \operatorname {Sing} (C_S) \cap (G = 0)$
. By the quasi-smoothness of X, we have
![]() $\operatorname {Sing} (C_X) = \{o\} \subset \mathbb {A}^5$
. This implies
$\operatorname {Sing} (C_X) = \{o\} \subset \mathbb {A}^5$
. This implies
![]() $\Sigma \cap (G = 0) = \emptyset $
. Since
$\Sigma \cap (G = 0) = \emptyset $
. Since
![]() $(G = 0)$
is an ample divisor on
$(G = 0)$
is an ample divisor on
![]() $\mathbb {P}$
, we see that
$\mathbb {P}$
, we see that
![]() $\Sigma $
is a finite set of points. This completes the proof.
$\Sigma $
is a finite set of points. This completes the proof.
Lemma 3.8. Let S be a weighted hypersurface in
![]() $\mathbb {P} (b_0, b_1, b_2, b_3)$
, and let
$\mathbb {P} (b_0, b_1, b_2, b_3)$
, and let
![]() $T \subset \mathbb {P} (b_0, b_1, b_2, b_3)$
be a quasi-hyperplane. If the scheme-theoretic intersection
$T \subset \mathbb {P} (b_0, b_1, b_2, b_3)$
be a quasi-hyperplane. If the scheme-theoretic intersection
![]() $S \cap T$
is quasi-smooth at a point
$S \cap T$
is quasi-smooth at a point
![]() $\mathsf {p}$
, then S is quasi-smooth at
$\mathsf {p}$
, then S is quasi-smooth at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Proof. Let
![]() $x_0, x_1, x_2, x_3$
be the homogeneous coordinates of
$x_0, x_1, x_2, x_3$
be the homogeneous coordinates of
![]() $\mathbb {P} = \mathbb {P} (b_0, b_1, b_2, b_3)$
of degree
$\mathbb {P} = \mathbb {P} (b_0, b_1, b_2, b_3)$
of degree
![]() $b_0, b_1, b_2, b_3$
, respectively, and let
$b_0, b_1, b_2, b_3$
, respectively, and let
![]() $F= F (x_0, x_1, x_2, x_3)$
be the defining polynomial of S. We may assume
$F= F (x_0, x_1, x_2, x_3)$
be the defining polynomial of S. We may assume
![]() $T = H_{x_3} \subset \mathbb {P}$
, and we write
$T = H_{x_3} \subset \mathbb {P}$
, and we write
![]() $F = x_3 G + \bar {F}$
, where
$F = x_3 G + \bar {F}$
, where
![]() $G = G (x_0, x_1, x_2, x_3)$
and
$G = G (x_0, x_1, x_2, x_3)$
and
![]() $\bar {F} = \bar {F} (x_0, x_1, x_2)$
are quasi-homogeneous polynomials. Then
$\bar {F} = \bar {F} (x_0, x_1, x_2)$
are quasi-homogeneous polynomials. Then
![]() $S \cap T$
is the closed subscheme in
$S \cap T$
is the closed subscheme in
![]() $\mathbb {P} (b_0,b_1,b_2,b_3)$
defined by
$\mathbb {P} (b_0,b_1,b_2,b_3)$
defined by
![]() $x_3 = \bar {F} = 0$
. By the quasi-smoothness of
$x_3 = \bar {F} = 0$
. By the quasi-smoothness of
![]() $S \cap T$
at
$S \cap T$
at
![]() $\mathsf {p}$
, there exists
$\mathsf {p}$
, there exists
![]() $i \in \{0, 1, 2\}$
such that
$i \in \{0, 1, 2\}$
such that
It follows that
since
![]() $\mathsf {p} \in H_{x_3}$
. Thus, S is quasi-smooth at
$\mathsf {p} \in H_{x_3}$
. Thus, S is quasi-smooth at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Lemma 3.9. Let S be a normal weighted hypersurface in a well-formed weighted projective
![]() $3$
-space
$3$
-space
![]() $\mathbb {P} (b_0,\dots , b_3)$
and
$\mathbb {P} (b_0,\dots , b_3)$
and
![]() $T \subset \mathbb {P} (b_0,\dots , b_3)$
a quasi-hyperplane such that
$T \subset \mathbb {P} (b_0,\dots , b_3)$
a quasi-hyperplane such that
![]() $T \ne S$
. Let
$T \ne S$
. Let
![]() $\Gamma $
be an irreducible component of
$\Gamma $
be an irreducible component of
![]() $S \cap T$
, and we assume that
$S \cap T$
, and we assume that
where
![]() $\Delta $
is an effective divisor on S such that
$\Delta $
is an effective divisor on S such that
![]() $\Gamma \not \subset \operatorname {Supp} (\Delta )$
. If
$\Gamma \not \subset \operatorname {Supp} (\Delta )$
. If
![]() $\Gamma $
is a smooth weighted complete intersection curve and S is quasi-smooth at each point of
$\Gamma $
is a smooth weighted complete intersection curve and S is quasi-smooth at each point of
![]() $\Gamma \cap \operatorname {Supp} (\Delta )$
, then S is quasi-smooth along
$\Gamma \cap \operatorname {Supp} (\Delta )$
, then S is quasi-smooth along
![]() $\Gamma $
and the pair
$\Gamma $
and the pair
![]() $(S, \Gamma )$
is purely log terminal (plt) along
$(S, \Gamma )$
is purely log terminal (plt) along
![]() $\Gamma $
.
$\Gamma $
.
Proof. We set
![]() $\Xi = \Gamma \cap \operatorname {Supp} (\Delta )$
. By [Reference Iano-FletcherIF00, Theorem 12.1],
$\Xi = \Gamma \cap \operatorname {Supp} (\Delta )$
. By [Reference Iano-FletcherIF00, Theorem 12.1],
![]() $\Gamma $
is quasi-smooth. We have
$\Gamma $
is quasi-smooth. We have
![]() $(S \cap T) \setminus \Xi = \Gamma \setminus \Xi $
. It follows that
$(S \cap T) \setminus \Xi = \Gamma \setminus \Xi $
. It follows that
![]() $S \cap T$
is quasi-smooth along
$S \cap T$
is quasi-smooth along
![]() $\Gamma \setminus \Xi $
. By Lemma 3.8, S is quasi-smooth along
$\Gamma \setminus \Xi $
. By Lemma 3.8, S is quasi-smooth along
![]() $\Gamma \setminus \Xi $
. Therefore, S is quasi-smooth along
$\Gamma \setminus \Xi $
. Therefore, S is quasi-smooth along
![]() $\Gamma $
.
$\Gamma $
.
For
![]() $i = 0,1,2,3$
, let
$i = 0,1,2,3$
, let
![]() $S_i = (x_i \ne 0) \cap S$
be the standard open set of S and let
$S_i = (x_i \ne 0) \cap S$
be the standard open set of S and let
![]() $\rho _i \colon \breve {S}_i \to S_i$
be the orbifold chart. Note that
$\rho _i \colon \breve {S}_i \to S_i$
be the orbifold chart. Note that
![]() $\rho _i$
is a finite surjective morphism of degree
$\rho _i$
is a finite surjective morphism of degree
![]() $b_i$
which is étale in codimension
$b_i$
which is étale in codimension
![]() $1$
. By the quasi-smoothness of S, the affine varieties
$1$
. By the quasi-smoothness of S, the affine varieties
![]() $\breve {S}_i$
and
$\breve {S}_i$
and
![]() $\rho _i^*(\Gamma \cap S_i)$
are smooth. Hence, the pair
$\rho _i^*(\Gamma \cap S_i)$
are smooth. Hence, the pair
![]() $(\breve {S}_i, \rho _i^*(\Gamma \cap S_i))$
is plt along
$(\breve {S}_i, \rho _i^*(\Gamma \cap S_i))$
is plt along
![]() $\rho _i^*(\Gamma \cap S_i)$
. By [Reference KollárKol+92, Corollary 20.4], the pair
$\rho _i^*(\Gamma \cap S_i)$
. By [Reference KollárKol+92, Corollary 20.4], the pair
![]() $(S_i, \Gamma \cap S_i)$
is plt along
$(S_i, \Gamma \cap S_i)$
is plt along
![]() $\Gamma \cap S_i$
. This completes the proof.
$\Gamma \cap S_i$
. This completes the proof.
Remark 3.10. Let S, T and
![]() $\Gamma $
be as in Lemma 3.9. We assume in addition that
$\Gamma $
be as in Lemma 3.9. We assume in addition that
![]() $\Gamma $
is rational, that is,
$\Gamma $
is rational, that is,
![]() $\Gamma \cong \mathbb {P}^1$
. Let
$\Gamma \cong \mathbb {P}^1$
. Let
![]() $\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_1,\dots ,\mathsf {p}_n\}$
be the set of singular points of S along
$\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_1,\dots ,\mathsf {p}_n\}$
be the set of singular points of S along
![]() $\Gamma $
, and let
$\Gamma $
, and let
![]() $m_i$
be the index of the quotient singular point
$m_i$
be the index of the quotient singular point
![]() $\mathsf {p}_i \in S$
. Then, since the pair
$\mathsf {p}_i \in S$
. Then, since the pair
![]() $(S, \Gamma )$
is plt along
$(S, \Gamma )$
is plt along
![]() $\Gamma $
, we can apply [Reference KollárKol+92, Proposition 16.6] and we have
$\Gamma $
, we can apply [Reference KollárKol+92, Proposition 16.6] and we have
 $$\begin{align*}(K_S + \Gamma)|_{\Gamma} = K_{\Gamma} + \sum_{i=1}^n \frac{m_i-1}{m_i} \mathsf{p}_i. \end{align*}$$
$$\begin{align*}(K_S + \Gamma)|_{\Gamma} = K_{\Gamma} + \sum_{i=1}^n \frac{m_i-1}{m_i} \mathsf{p}_i. \end{align*}$$
Thus, we have
 $$\begin{align*}(\Gamma^2)_S = - (K_S \cdot \Gamma)_S -2 + \sum_{i=1}^n \frac{m_i-1}{m_i}. \end{align*}$$
$$\begin{align*}(\Gamma^2)_S = - (K_S \cdot \Gamma)_S -2 + \sum_{i=1}^n \frac{m_i-1}{m_i}. \end{align*}$$
3.1.c Isolating set and class
We recall the definitions of isolating set and class which are introduced by Corti, Pukhlikov and Reid [Reference Corti, Pukhlikhov and ReidCPR00] as well as their basic properties.
Let V be a normal projective variety embedded in a weighted projective space
![]() $\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)$
with homogeneous coordinates
$\mathbb {P} = \mathbb {P} (a_0, \dots , a_N)$
with homogeneous coordinates
![]() $x_0, \dots , x_N$
with
$x_0, \dots , x_N$
with
![]() $\deg x_i = a_i$
, and let A be a Weil divisor on V such that
$\deg x_i = a_i$
, and let A be a Weil divisor on V such that
![]() $\mathcal {O}_V (A) \cong \mathcal {O}_V (1)$
. We do not assume that
$\mathcal {O}_V (A) \cong \mathcal {O}_V (1)$
. We do not assume that
![]() $a_0 \le \cdots \le a_N$
.
$a_0 \le \cdots \le a_N$
.
Definition 3.11. Let
![]() $\mathsf {p} \in V$
be a point. We say that a set
$\mathsf {p} \in V$
be a point. We say that a set
![]() $\{g_1, \dots , g_m\}$
of quasi-homogeneous polynomials
$\{g_1, \dots , g_m\}$
of quasi-homogeneous polynomials
![]() $g_1, \dots , g_m \in \mathbb {C} [x_0, \dots , x_N]$
isolates
$g_1, \dots , g_m \in \mathbb {C} [x_0, \dots , x_N]$
isolates
![]() $\mathsf {p}$
or is a
$\mathsf {p}$
or is a
![]() $\mathsf {p}$
-isolating set if
$\mathsf {p}$
-isolating set if
![]() $\mathsf {p}$
is an isolated component of the set
$\mathsf {p}$
is an isolated component of the set
Definition 3.12. Let
![]() $\mathsf {p} \in V$
be a smooth point, and let L be a Weil divisor class on V. For positive integers k and l, we define
$\mathsf {p} \in V$
be a smooth point, and let L be a Weil divisor class on V. For positive integers k and l, we define
![]() $|\mathcal {I}_{\mathsf {p}}^k (l L)|$
to be the linear subsystem of
$|\mathcal {I}_{\mathsf {p}}^k (l L)|$
to be the linear subsystem of
![]() $|l L|$
consisting of divisors vanishing at
$|l L|$
consisting of divisors vanishing at
![]() $\mathsf {p}$
with multiplicity at least k. We say that L isolates
$\mathsf {p}$
with multiplicity at least k. We say that L isolates
![]() $\mathsf {p}$
or is a
$\mathsf {p}$
or is a
![]() $\mathsf {p}$
-isolating class if
$\mathsf {p}$
-isolating class if
![]() $\mathsf {p}$
is an isolated component of the base locus of
$\mathsf {p}$
is an isolated component of the base locus of
![]() $|\mathcal {I}^k_{\mathsf {p}} (kL)|$
.
$|\mathcal {I}^k_{\mathsf {p}} (kL)|$
.
Lemma 3.13 [Reference Corti, Pukhlikhov and ReidCPR00, Lemma 5.6.4].
Let
![]() $\mathsf {p} \in V$
be a smooth point. If
$\mathsf {p} \in V$
be a smooth point. If
![]() $\{g_1, \dots , g_m\}$
is a
$\{g_1, \dots , g_m\}$
is a
![]() $\mathsf {p}$
-isolating class, then
$\mathsf {p}$
-isolating class, then
![]() $l A$
is a
$l A$
is a
![]() $\mathsf {p}$
-isolating class, where
$\mathsf {p}$
-isolating class, where
Lemma 3.14. Let
![]() $\mathsf {p} \in V$
be a point,
$\mathsf {p} \in V$
be a point,
![]() $Z_1, \dots , Z_k$
irreducible closed subsets of V such that
$Z_1, \dots , Z_k$
irreducible closed subsets of V such that
![]() $\dim Z_i> 0$
for any i, and let
$\dim Z_i> 0$
for any i, and let
![]() $g_1, \dots , g_n \in \mathbb {C} [x_0, \dots , x_N]$
be quasi-homogeneous polynomials. Suppose that V is quasi-smooth at
$g_1, \dots , g_n \in \mathbb {C} [x_0, \dots , x_N]$
be quasi-homogeneous polynomials. Suppose that V is quasi-smooth at
![]() $\mathsf {p}$
and that
$\mathsf {p}$
and that
![]() $\{g_1, \dots , g_n\}$
isolates
$\{g_1, \dots , g_n\}$
isolates
![]() $\mathsf {p}$
. We set
$\mathsf {p}$
. We set
![]() $G_i = (g_i = 0)_V$
, and we set
$G_i = (g_i = 0)_V$
, and we set
 $$\begin{align*}\mu := \min \left\{\, \frac{\operatorname{omult}_{\mathsf{p}} (G_i)}{\deg g_i} \; \middle| \; i = 1, \dots, n \,\right\}. \end{align*}$$
$$\begin{align*}\mu := \min \left\{\, \frac{\operatorname{omult}_{\mathsf{p}} (G_i)}{\deg g_i} \; \middle| \; i = 1, \dots, n \,\right\}. \end{align*}$$
Then there exists an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \sim _{\mathbb {Q}} A$
such that
$T \sim _{\mathbb {Q}} A$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge \mu $
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge \mu $
and
![]() $\operatorname {Supp} (T)$
does not contain any
$\operatorname {Supp} (T)$
does not contain any
![]() $Z_i$
.
$Z_i$
.
Proof. Let d be the least common multiple of
![]() $\deg g_1, \dots , \deg g_n$
, and we set
$\deg g_1, \dots , \deg g_n$
, and we set
![]() $e_i = d/\deg g_i$
. Consider the linear system
$e_i = d/\deg g_i$
. Consider the linear system
![]() $\Lambda \subset |d A|$
on V generated by
$\Lambda \subset |d A|$
on V generated by
![]() $g_1^{e_1}, \dots , g_n^{e_n}$
. We see that
$g_1^{e_1}, \dots , g_n^{e_n}$
. We see that
![]() $\mathsf {p}$
is an isolating component of
$\mathsf {p}$
is an isolating component of
![]() $\operatorname {Bs} \Lambda $
since
$\operatorname {Bs} \Lambda $
since
![]() $\{g_1, \dots , g_n\}$
isolates
$\{g_1, \dots , g_n\}$
isolates
![]() $\mathsf {p}$
. Hence, a general
$\mathsf {p}$
. Hence, a general
![]() $D \in \Lambda $
does not contain any
$D \in \Lambda $
does not contain any
![]() $Z_i$
in its support. Moreover, for any
$Z_i$
in its support. Moreover, for any
![]() $D \in \Lambda $
, we have
$D \in \Lambda $
, we have
Thus, the assertion follows by setting
![]() $T = \frac {1}{d} D \sim _{\mathbb {Q}} A$
for a general
$T = \frac {1}{d} D \sim _{\mathbb {Q}} A$
for a general
![]() $D \in \Lambda $
.
$D \in \Lambda $
.
Remark 3.15. Lemma 3.14 will be frequently applied in the following way: under the same notation and assumptions as in Lemma 3.14, there exists an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \sim _{\mathbb {Q}} e A$
, where
$T \sim _{\mathbb {Q}} e A$
, where
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any
$\operatorname {Supp} (T)$
does not contain any
![]() $Z_i$
.
$Z_i$
.
Lemma 3.16. Let
![]() $X = X_d \subset \mathbb {P} (1, a_1, \dots , a_4)_{x, y, z, t, w}$
be a member of a family
$X = X_d \subset \mathbb {P} (1, a_1, \dots , a_4)_{x, y, z, t, w}$
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
, where we assume that
$\mathsf {i} \in \mathsf {I}$
, where we assume that
![]() $a_1 \le a_2 \le a_3 \le a_4$
, and let
$a_1 \le a_2 \le a_3 \le a_4$
, and let
![]() $\mathsf {p} \in H_x \setminus L_{xy}$
. Then
$\mathsf {p} \in H_x \setminus L_{xy}$
. Then
![]() $a_1 a_4 A$
isolates
$a_1 a_4 A$
isolates
![]() $\mathsf {p}$
. If
$\mathsf {p}$
. If
![]() $w^k$
appears in the defining polynomial of X with nonzero coefficient, then
$w^k$
appears in the defining polynomial of X with nonzero coefficient, then
![]() $a_1 a_3 A$
isolates
$a_1 a_3 A$
isolates
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Proof. We can write
![]() $\mathsf {p} = (0\!:\!1\!:\!\alpha _2\!:\!\alpha _3\!:\!\alpha _4)$
for some
$\mathsf {p} = (0\!:\!1\!:\!\alpha _2\!:\!\alpha _3\!:\!\alpha _4)$
for some
![]() $\alpha _2, \alpha _3, \alpha _4 \in \mathbb {C}$
. Then it is easy to see that the set
$\alpha _2, \alpha _3, \alpha _4 \in \mathbb {C}$
. Then it is easy to see that the set
isolates
![]() $\mathsf {p}$
, and thus
$\mathsf {p}$
, and thus
![]() $a_1 a_4 A$
isolates
$a_1 a_4 A$
isolates
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Suppose that
![]() $w^k$
appears in the defining polynomial of X. Then the natural projection
$w^k$
appears in the defining polynomial of X. Then the natural projection
![]() $\mathbb {P} (1, a_1, \dots , a_4) \dashrightarrow \mathbb {P} (1, a_1, a_2, a_3)$
restricts to a finite morphism
$\mathbb {P} (1, a_1, \dots , a_4) \dashrightarrow \mathbb {P} (1, a_1, a_2, a_3)$
restricts to a finite morphism
![]() $\pi \colon X \to \mathbb {P} (1, a_1, a_2, a_3)$
. The common zero locus (in X) of the sections contained in the set
$\pi \colon X \to \mathbb {P} (1, a_1, a_2, a_3)$
. The common zero locus (in X) of the sections contained in the set
coincides with the set
![]() $\pi ^{-1} (\mathsf {q})$
, where
$\pi ^{-1} (\mathsf {q})$
, where
![]() $\mathsf {q} = (0\!:\!1\!:\!\alpha _2\!:\!\alpha _3) \in \mathbb {P} (1, a_1, a_2, a_3)$
. It follows that the above set isolates
$\mathsf {q} = (0\!:\!1\!:\!\alpha _2\!:\!\alpha _3) \in \mathbb {P} (1, a_1, a_2, a_3)$
. It follows that the above set isolates
![]() $\mathsf {p}$
since
$\mathsf {p}$
since
![]() $\pi ^{-1} (\mathsf {q})$
is a finite set containing
$\pi ^{-1} (\mathsf {q})$
is a finite set containing
![]() $\mathsf {p}$
. Thus,
$\mathsf {p}$
. Thus,
![]() $a_1 a_3 A$
isolates
$a_1 a_3 A$
isolates
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
3.2 Methods
3.2.a Computations by intersecting two divisors
We recall methods of computing log canonial thresholds (LCTs) and consider their generalizations for some of them.
Lemma 3.17 (cf. [Reference Kim, Okada and WonKOW18, Lemma 2.5]).
Let X be a normal projective
![]() $\mathbb {Q}$
-factorial
$\mathbb {Q}$
-factorial
![]() $3$
-fold with nef and big anticanonical divisor, and let
$3$
-fold with nef and big anticanonical divisor, and let
![]() $\mathsf {p} \in X$
be either a smooth point or a terminal quotient singular point of index r (below we set
$\mathsf {p} \in X$
be either a smooth point or a terminal quotient singular point of index r (below we set
![]() $r = 1$
when
$r = 1$
when
![]() $\mathsf {p} \in X$
is a smooth point). Suppose that there are prime divisors
$\mathsf {p} \in X$
is a smooth point). Suppose that there are prime divisors
![]() $S \sim _{\mathbb {Q}} - a K_X$
and
$S \sim _{\mathbb {Q}} - a K_X$
and
![]() $T \sim _{\mathbb {Q}} - b K_X$
with
$T \sim _{\mathbb {Q}} - b K_X$
with
![]() $a, b \in \mathbb {Q}$
such that
$a, b \in \mathbb {Q}$
such that
![]() $S \cap T$
is irreducible and
$S \cap T$
is irreducible and
![]() $q^* S \cdot q^* T = m \check {\Gamma }$
, where
$q^* S \cdot q^* T = m \check {\Gamma }$
, where
![]() $q = q_{\mathsf {p}} \colon \check {U} \to U$
is the quotient morphism of an analytic neighborhood
$q = q_{\mathsf {p}} \colon \check {U} \to U$
is the quotient morphism of an analytic neighborhood
![]() $\mathsf {p} \in U$
of
$\mathsf {p} \in U$
of
![]() $\mathsf {p} \in X$
,
$\mathsf {p} \in X$
,
![]() $\check {\mathsf {p}}$
is the preimage of
$\check {\mathsf {p}}$
is the preimage of
![]() $\mathsf {p}$
via q, m is a positive integer and
$\mathsf {p}$
via q, m is a positive integer and
![]() $\check {\Gamma }$
is an irreducible and reduced curve on
$\check {\Gamma }$
is an irreducible and reduced curve on
![]() $\check {U}$
. Then we have
$\check {U}$
. Then we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; \tfrac{1}{a} S), \ \frac{b}{m \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma})}, \ \frac{1}{r a b (-K_X)^3} \right\}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; \tfrac{1}{a} S), \ \frac{b}{m \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma})}, \ \frac{1}{r a b (-K_X)^3} \right\}. \end{align*}$$
Proof. We set
 $$\begin{align*}c := \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; \tfrac{1}{a} S), \ \frac{b}{m \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma})}, \ \frac{1}{r a b (-K_X)^3} \right\}. \end{align*}$$
$$\begin{align*}c := \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; \tfrac{1}{a} S), \ \frac{b}{m \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma})}, \ \frac{1}{r a b (-K_X)^3} \right\}. \end{align*}$$
We will derive a contradiction assuming
![]() $\alpha _{\mathsf {p}} (X) < c$
. By the assumption, there is an irreducible
$\alpha _{\mathsf {p}} (X) < c$
. By the assumption, there is an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in \left | - K_X \right |{}_{\mathbb {Q}}$
such that
$D \in \left | - K_X \right |{}_{\mathbb {Q}}$
such that
![]() $(X, c D)$
is not log canonical at
$(X, c D)$
is not log canonical at
![]() $\mathsf {p}$
. Then the pair
$\mathsf {p}$
. Then the pair
![]() $(\check {U}, c \rho ^*D)$
is not log canonical at
$(\check {U}, c \rho ^*D)$
is not log canonical at
![]() $\check {\mathsf {p}}$
and we have
$\check {\mathsf {p}}$
and we have
Since
![]() $q^*S \cdot q^*T = m \check {\Gamma }$
and
$q^*S \cdot q^*T = m \check {\Gamma }$
and
![]() $S \cap T$
is irreducible, we have
$S \cap T$
is irreducible, we have
![]() $S \cdot T = m \Gamma $
, where
$S \cdot T = m \Gamma $
, where
![]() $\Gamma $
is an irreducible and reduced curve such that
$\Gamma $
is an irreducible and reduced curve such that
![]() $\check {\Gamma } = q^*\Gamma $
. We have
$\check {\Gamma } = q^*\Gamma $
. We have
This in particular implies
We have
![]() $\operatorname {Supp} (D) \ne S$
since
$\operatorname {Supp} (D) \ne S$
since
![]() $\operatorname {lct}_{\mathsf {p}} (X;S) \ge c$
, and thus
$\operatorname {lct}_{\mathsf {p}} (X;S) \ge c$
, and thus
![]() $q^*D \cdot q^*S$
is an effective
$q^*D \cdot q^*S$
is an effective
![]() $1$
-cycle on
$1$
-cycle on
![]() $\check {U}$
. We write
$\check {U}$
. We write
![]() $q^*D \cdot q^*S = \gamma \check {\Gamma } + \check {\Delta }$
, where
$q^*D \cdot q^*S = \gamma \check {\Gamma } + \check {\Delta }$
, where
![]() $\gamma \ge 0$
and
$\gamma \ge 0$
and
![]() $\check {\Delta }$
is an effective
$\check {\Delta }$
is an effective
![]() $1$
-cycle on
$1$
-cycle on
![]() $\check {U}$
such that
$\check {U}$
such that
![]() $\check {\Gamma } \not \subset \operatorname {Supp} (\check {\Delta })$
. Then
$\check {\Gamma } \not \subset \operatorname {Supp} (\check {\Delta })$
. Then
![]() $D \cdot S = \gamma \Gamma + \Delta + \Xi $
, where
$D \cdot S = \gamma \Gamma + \Delta + \Xi $
, where
![]() $\Delta = \frac {1}{r} q_*\check {\Delta }$
and
$\Delta = \frac {1}{r} q_*\check {\Delta }$
and
![]() $\Xi $
is an effective
$\Xi $
is an effective
![]() $1$
-cycle such that
$1$
-cycle such that
![]() $\Gamma \not \subset \operatorname {Supp} (\Xi )$
. By equation (3.2), we have
$\Gamma \not \subset \operatorname {Supp} (\Xi )$
. By equation (3.2), we have
where the inequality holds since
![]() $-K_X$
is nef. Note that
$-K_X$
is nef. Note that
![]() $(-K_X)^3> 0$
since
$(-K_X)^3> 0$
since
![]() $-K_X$
is nef and big. Hence,
$-K_X$
is nef and big. Hence,
By equations (3.1) and (3.3), we have
 $$ \begin{align*} r \left(a b (-K_X)^3 - \frac{a b^2 (-K_X)^3}{m} \gamma\right) &= r (T \cdot (D \cdot S - \gamma \Gamma)) \\ &= r (T \cdot (\Delta + \Xi)) \ge r (T \cdot \Delta) \\ &\ge r (T \cdot \Delta)_{\mathsf{p}} = (q^*T \cdot \check{\Delta})_{\check{\mathsf{p}}} \\ &\ge \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Delta}) \\ &> \frac{1}{c} - \gamma \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma}), \end{align*} $$
$$ \begin{align*} r \left(a b (-K_X)^3 - \frac{a b^2 (-K_X)^3}{m} \gamma\right) &= r (T \cdot (D \cdot S - \gamma \Gamma)) \\ &= r (T \cdot (\Delta + \Xi)) \ge r (T \cdot \Delta) \\ &\ge r (T \cdot \Delta)_{\mathsf{p}} = (q^*T \cdot \check{\Delta})_{\check{\mathsf{p}}} \\ &\ge \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Delta}) \\ &> \frac{1}{c} - \gamma \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma}), \end{align*} $$
where
![]() $(\ \cdot \ )_{\mathsf {p}}$
and
$(\ \cdot \ )_{\mathsf {p}}$
and
![]() $(\ \cdot \ )_{\check {\mathsf {p}}}$
denote the local intersection numbers at
$(\ \cdot \ )_{\check {\mathsf {p}}}$
denote the local intersection numbers at
![]() $\mathsf {p}$
and
$\mathsf {p}$
and
![]() $\check {\mathsf {p}}$
, respectively. It follows that
$\check {\mathsf {p}}$
, respectively. It follows that
 $$ \begin{align} \left(\operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma}) - \frac{r a b^2 (-K_X)^3}{m}\right) \gamma> \frac{1}{c} - r a b (-K_X)^3. \end{align} $$
$$ \begin{align} \left(\operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma}) - \frac{r a b^2 (-K_X)^3}{m}\right) \gamma> \frac{1}{c} - r a b (-K_X)^3. \end{align} $$
We have
![]() $\operatorname {mult}_{\check {\mathsf {p}}} (\check {\Gamma }) - r a b^2 (-K_X)^3/m> 0$
since
$\operatorname {mult}_{\check {\mathsf {p}}} (\check {\Gamma }) - r a b^2 (-K_X)^3/m> 0$
since
![]() $1/c - r a b (-K_X)^3 \ge 0$
by the definition of c. Combining equations (3.4) and (3.5), we have
$1/c - r a b (-K_X)^3 \ge 0$
by the definition of c. Combining equations (3.4) and (3.5), we have
 $$\begin{align*}c> \frac{b}{m \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma})}. \end{align*}$$
$$\begin{align*}c> \frac{b}{m \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma})}. \end{align*}$$
This contradicts the definition of c and the proof is completed.
Lemma 3.17 is very useful in computing alpha invariants but works only when
![]() $S \cap T$
is irreducible. We consider its generalization that can be applied when
$S \cap T$
is irreducible. We consider its generalization that can be applied when
![]() $S \cap T$
is reducible.
$S \cap T$
is reducible.
Definition 3.18. Let
![]() $M = (a_{ij})$
be an
$M = (a_{ij})$
be an
![]() $n \times n$
matrix with entries in
$n \times n$
matrix with entries in
![]() $\mathbb {R}$
, where
$\mathbb {R}$
, where
![]() $n \ge 2$
. For a nonempty subset
$n \ge 2$
. For a nonempty subset
![]() $I \subset \{1,2,\dots ,n\}$
, we denote by
$I \subset \{1,2,\dots ,n\}$
, we denote by
![]() $M_I$
the submatrix of M consisting of ith rows and columns for
$M_I$
the submatrix of M consisting of ith rows and columns for
![]() $i \in I$
. We say that M satisfies the condition
$i \in I$
. We say that M satisfies the condition
![]() $(\star )$
if the following are satisfied.
$(\star )$
if the following are satisfied.
-
•
 $(-1)^{|I|} \det M_I \ge 0$
for any nonempty proper subset
$(-1)^{|I|} \det M_I \ge 0$
for any nonempty proper subset
 $I \subset \{1,2,\dots ,n\}$
.
$I \subset \{1,2,\dots ,n\}$
. -
•
 $(-1)^{n-1} \det M> 0$
.
$(-1)^{n-1} \det M> 0$
. -
•
 $a_{ij}> 0$
for any
$a_{ij}> 0$
for any
 $i, j$
with
$i, j$
with
 $i \ne j$
.
$i \ne j$
.
For
![]() $v = {}^t (v_1,\dots ,v_n), w = {}^t (w_1,\dots ,w_n) \in \mathbb {R}^n$
, the expression
$v = {}^t (v_1,\dots ,v_n), w = {}^t (w_1,\dots ,w_n) \in \mathbb {R}^n$
, the expression
![]() $v \le w$
means
$v \le w$
means
![]() $v_i \le w_i$
for any i.
$v_i \le w_i$
for any i.
Lemma 3.19. Let
![]() $M = (a_{i j})$
be an
$M = (a_{i j})$
be an
![]() $n \times n$
matrix with entries in
$n \times n$
matrix with entries in
![]() $\mathbb {R}$
satisfying the condition
$\mathbb {R}$
satisfying the condition
![]() $(\star )$
, and let
$(\star )$
, and let
![]() $v, w \in \mathbb {R}^n$
. Then
$v, w \in \mathbb {R}^n$
. Then
![]() $M v \le M w$
implies
$M v \le M w$
implies
![]() $v \le w$
.
$v \le w$
.
Proof. It is enough to show that
![]() $v \le 0$
assuming
$v \le 0$
assuming
![]() $M v \le 0$
for
$M v \le 0$
for
![]() $v \in \mathbb {R}^n$
. We prove this assertion by induction on
$v \in \mathbb {R}^n$
. We prove this assertion by induction on
![]() $n \ge 2$
. The case
$n \ge 2$
. The case
![]() $n = 2$
is easily done, and we omit it.
$n = 2$
is easily done, and we omit it.
Assume
![]() $n \ge 3$
. Suppose that there is a diagonal entry
$n \ge 3$
. Suppose that there is a diagonal entry
![]() $a_{kk}$
such that
$a_{kk}$
such that
![]() $a_{kk} = 0$
. Then we have
$a_{kk} = 0$
. Then we have
![]() $\det M_{\{k,l\}} < 0$
since
$\det M_{\{k,l\}} < 0$
since
![]() $a_{k l}, a_{l k}> 0$
. By the condition
$a_{k l}, a_{l k}> 0$
. By the condition
![]() $(\star )$
, this is impossible since
$(\star )$
, this is impossible since
![]() $n \ge 3$
.
$n \ge 3$
.
In the following, we may assume that
![]() $a_{ii} \ne 0$
for any i. By the condition
$a_{ii} \ne 0$
for any i. By the condition
![]() $(\star )$
, we have
$(\star )$
, we have
![]() $a_{ii} = \det M_{\{i\}} \le 0$
and hence
$a_{ii} = \det M_{\{i\}} \le 0$
and hence
![]() $a_{ii} < 0$
for any i. Let
$a_{ii} < 0$
for any i. Let
![]() $M'$
be the matrix obtained by adding the first row multiplied by the positive integer
$M'$
be the matrix obtained by adding the first row multiplied by the positive integer
![]() $-a_{i1}/a_{11}$
to the ith row, for
$-a_{i1}/a_{11}$
to the ith row, for
![]() $i = 2,\dots ,n$
. Then we obtain the inequality
$i = 2,\dots ,n$
. Then we obtain the inequality
![]() $M' v \le 0$
and we can write
$M' v \le 0$
and we can write

where
![]() $N'$
is an
$N'$
is an
![]() $(n-1) \times (n-1)$
matrix. It is straightforward to check that N satisfies the condition
$(n-1) \times (n-1)$
matrix. It is straightforward to check that N satisfies the condition
![]() $(\star )$
. Since
$(\star )$
. Since
![]() $N' {}^t (v_2 \ \dots \ v_n) \le 0$
, we have
$N' {}^t (v_2 \ \dots \ v_n) \le 0$
, we have
![]() $v_2, \dots , v_n \le 0$
by induction hypothesis. Next, let
$v_2, \dots , v_n \le 0$
by induction hypothesis. Next, let
![]() $M"$
be the matrix obtained by adding the nth row multiplied by the positive integer
$M"$
be the matrix obtained by adding the nth row multiplied by the positive integer
![]() $- a_{i n}/a_{nn}$
to the ith row, for
$- a_{i n}/a_{nn}$
to the ith row, for
![]() $i = 1, 2, \dots , n-1$
. Then we have
$i = 1, 2, \dots , n-1$
. Then we have
![]() $M" v \le 0$
and, by repeating the similar argument as above, we conclude
$M" v \le 0$
and, by repeating the similar argument as above, we conclude
![]() $v_1, \dots , v_{n-1} \le 0$
by induction. This completes the proof.
$v_1, \dots , v_{n-1} \le 0$
by induction. This completes the proof.
Definition 3.20. Let S be a normal projective surface, and let
![]() $\Gamma _1, \dots , \Gamma _k$
be irreducible and reduced curves on S. Then the
$\Gamma _1, \dots , \Gamma _k$
be irreducible and reduced curves on S. Then the
![]() $k \times k$
matrix
$k \times k$
matrix
is called the intersection matrix of curves
![]() $\Gamma _1, \dots , \Gamma _k$
on S.
$\Gamma _1, \dots , \Gamma _k$
on S.
Lemma 3.21. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
. Let
$\mathsf {i} \in \mathsf {I}$
. Let
![]() $S \in \left | - a K_X \right |$
be a normal surface on X,
$S \in \left | - a K_X \right |$
be a normal surface on X,
![]() $T \in \left | - b K_X \right |$
an effective divisor and
$T \in \left | - b K_X \right |$
an effective divisor and
![]() $\mathsf {p} \in S$
a point, where
$\mathsf {p} \in S$
a point, where
![]() $a, b> 0$
. We set
$a, b> 0$
. We set
![]() $r = 1$
when
$r = 1$
when
![]() $\mathsf {p} \in X$
is a smooth point, and otherwise we denote by r the index of the cyclic quotient singularity
$\mathsf {p} \in X$
is a smooth point, and otherwise we denote by r the index of the cyclic quotient singularity
![]() $\mathsf {p} \in X$
. Suppose that
$\mathsf {p} \in X$
. Suppose that
where
![]() $\Gamma _1, \dots , \Gamma _k$
are distinct irreducible and reduced curves on S and
$\Gamma _1, \dots , \Gamma _k$
are distinct irreducible and reduced curves on S and
![]() $m_1, \dots , m_k$
are positive integers, and the following properties are satisfied.
$m_1, \dots , m_k$
are positive integers, and the following properties are satisfied.
-
•
 $r b \deg \Gamma _1 \le m_1$
.
$r b \deg \Gamma _1 \le m_1$
. -
•
 $\mathsf {p} \in \Gamma _1 \setminus (\cup _{i \ge 2} \Gamma _i)$
, and
$\mathsf {p} \in \Gamma _1 \setminus (\cup _{i \ge 2} \Gamma _i)$
, and
 $S, \Gamma _1$
are both quasi-smooth at
$S, \Gamma _1$
are both quasi-smooth at
 $\mathsf {p}$
.
$\mathsf {p}$
. -
• The intersection matrix
 $M (\Gamma _1, \dots , \Gamma _k)$
satisfies the condition
$M (\Gamma _1, \dots , \Gamma _k)$
satisfies the condition
 $(\star )$
.
$(\star )$
.
Then we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ a, \ \frac{m_1}{r a b (-K_X)^3 + \frac{m_1^2}{b} - r m_1 \deg \Gamma_1} \right\}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ a, \ \frac{m_1}{r a b (-K_X)^3 + \frac{m_1^2}{b} - r m_1 \deg \Gamma_1} \right\}. \end{align*}$$
Proof. Let
![]() $D \in \left | - K_X \right |{}_{\mathbb {Q}}$
be an irreducible
$D \in \left | - K_X \right |{}_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor. If
$\mathbb {Q}$
-divisor. If
![]() $\operatorname {Supp} (D) = S$
, then
$\operatorname {Supp} (D) = S$
, then
![]() $D = \frac {1}{a} S$
and we have
$D = \frac {1}{a} S$
and we have
![]() $\operatorname {lct}_{\mathsf {p}} (X, D) \ge a$
since S is quasi-smooth at
$\operatorname {lct}_{\mathsf {p}} (X, D) \ge a$
since S is quasi-smooth at
![]() $\mathsf {p}$
. We assume
$\mathsf {p}$
. We assume
![]() $\operatorname {Supp} (D) \ne S$
. It is enough to prove the inequality
$\operatorname {Supp} (D) \ne S$
. It is enough to prove the inequality
 $$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X; D) \ge \frac{m_1}{r a b (-K_X)^3 + \frac{m_1^2}{b} - r m_1 \deg \Gamma_1}. \end{align} $$
$$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X; D) \ge \frac{m_1}{r a b (-K_X)^3 + \frac{m_1^2}{b} - r m_1 \deg \Gamma_1}. \end{align} $$
We can write
where
![]() $\gamma _1, \dots , \gamma _k \ge 0$
and
$\gamma _1, \dots , \gamma _k \ge 0$
and
![]() $\Delta $
is an effective
$\Delta $
is an effective
![]() $\mathbb {Q}$
-divisor on S such that
$\mathbb {Q}$
-divisor on S such that
![]() $\Gamma _i \not \subset \operatorname {Supp} (\Delta )$
for
$\Gamma _i \not \subset \operatorname {Supp} (\Delta )$
for
![]() $i = 1, \dots , k$
. We set
$i = 1, \dots , k$
. We set
![]() $\sigma _i = (\Gamma _i^2)_S$
and
$\sigma _i = (\Gamma _i^2)_S$
and
![]() $\chi _{i,j} = (\Gamma _i \cdot \Gamma _j)_S$
. For
$\chi _{i,j} = (\Gamma _i \cdot \Gamma _j)_S$
. For
![]() $i = 1, \dots , k$
, we have
$i = 1, \dots , k$
, we have
 $$ \begin{align} b \deg \Gamma_i &= (T|_S \cdot \Gamma_i)_S \nonumber\\ &= m_1 \chi_{1,i} + \cdots + m_{i-1} \chi_{i - 1, i} + m_i \sigma_i + m_{i+1} \chi_{i+1, i} + \cdots + m_k \chi_{k,i}, \end{align} $$
$$ \begin{align} b \deg \Gamma_i &= (T|_S \cdot \Gamma_i)_S \nonumber\\ &= m_1 \chi_{1,i} + \cdots + m_{i-1} \chi_{i - 1, i} + m_i \sigma_i + m_{i+1} \chi_{i+1, i} + \cdots + m_k \chi_{k,i}, \end{align} $$
and
 $$ \begin{align} \deg \Gamma_i &= (D|_S \cdot \Gamma_i)_S \nonumber\\ &\ge \gamma_1 \chi_{1, i} + \cdots + \gamma_{i-1} \chi_{i-1} + \gamma_i \sigma_i + \gamma_{i+1} \chi_{i+1,i} + \cdots + \gamma_k \chi_{k,i+1}. \end{align} $$
$$ \begin{align} \deg \Gamma_i &= (D|_S \cdot \Gamma_i)_S \nonumber\\ &\ge \gamma_1 \chi_{1, i} + \cdots + \gamma_{i-1} \chi_{i-1} + \gamma_i \sigma_i + \gamma_{i+1} \chi_{i+1,i} + \cdots + \gamma_k \chi_{k,i+1}. \end{align} $$
We set
![]() $M = M (\Gamma _1, \dots , \Gamma _k)$
. Combining inequalities (3.7) and (3.8), we have
$M = M (\Gamma _1, \dots , \Gamma _k)$
. Combining inequalities (3.7) and (3.8), we have
 $$\begin{align*}M \begin{pmatrix} b \gamma_1 \\ \vdots \\ b \gamma_k \end{pmatrix} \le M \begin{pmatrix} m_1 \\ \vdots \\ m_k \end{pmatrix}. \end{align*}$$
$$\begin{align*}M \begin{pmatrix} b \gamma_1 \\ \vdots \\ b \gamma_k \end{pmatrix} \le M \begin{pmatrix} m_1 \\ \vdots \\ m_k \end{pmatrix}. \end{align*}$$
By Lemma 3.19, this implies
![]() $\gamma _i \le m_i/b$
for any i.
$\gamma _i \le m_i/b$
for any i.
When
![]() $\mathsf {p}$
is a singular point, then we set
$\mathsf {p}$
is a singular point, then we set
![]() $\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
, which is the orbifold chart of X containing
$\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
, which is the orbifold chart of X containing
![]() $\mathsf {p}$
. When
$\mathsf {p}$
. When
![]() $\mathsf {p}$
is a smooth point of X, then we set
$\mathsf {p}$
is a smooth point of X, then we set
![]() $\breve {U} = U = X$
and
$\breve {U} = U = X$
and
![]() $\rho \colon \breve {U} \to U$
is assumed to be the identity morphism. Moreover, we set
$\rho \colon \breve {U} \to U$
is assumed to be the identity morphism. Moreover, we set
![]() $\breve {S} := q^*(S \cap U)$
and
$\breve {S} := q^*(S \cap U)$
and
![]() $\rho _S = \rho |_{\breve {S}} \colon \breve {S} \to S \cap U$
. We see that
$\rho _S = \rho |_{\breve {S}} \colon \breve {S} \to S \cap U$
. We see that
![]() $\breve {S}$
is smooth at the preimage
$\breve {S}$
is smooth at the preimage
![]() $\breve {\mathsf {p}}$
of
$\breve {\mathsf {p}}$
of
![]() $\mathsf {p}$
since S is quasi-smooth at
$\mathsf {p}$
since S is quasi-smooth at
![]() $\mathsf {p}$
, and
$\mathsf {p}$
, and
This implies
since
![]() $\rho _S^*\Gamma _i$
does not pass through
$\rho _S^*\Gamma _i$
does not pass through
![]() $\breve {\mathsf {p}}$
for
$\breve {\mathsf {p}}$
for
![]() $i \ge 2$
and
$i \ge 2$
and
![]() $\rho _S^*\Gamma _1$
is smooth at
$\rho _S^*\Gamma _1$
is smooth at
![]() $\breve {\mathsf {p}}$
by the quasi-smoothness of
$\breve {\mathsf {p}}$
by the quasi-smoothness of
![]() $\Gamma _1$
at
$\Gamma _1$
at
![]() $\mathsf {p}$
. We have
$\mathsf {p}$
. We have
 $$ \begin{align*} r (ab (-K_X)^3 - b \gamma_1 \deg \Gamma_1) &\ge r (T|_S \cdot (D|_S - \gamma_1 \Gamma_1 - \cdots - \gamma_k \Gamma_k))_S \\ &= r (T|_S \cdot \Delta)_S \\ &\ge m_1 r (\Gamma_1 \cdot \Delta)_S \\ &\ge m_1 (\rho_S^*\Gamma_1 \cdot \rho_S^*\Delta)_{\breve{\mathsf{p}}} \\ &\ge m_1 \operatorname{mult}_{\breve{\mathsf{p}}} (\rho_S^*\Delta) \\ &\ge m_1 (\operatorname{omult}_{\mathsf{p}} (D) - \gamma_1). \end{align*} $$
$$ \begin{align*} r (ab (-K_X)^3 - b \gamma_1 \deg \Gamma_1) &\ge r (T|_S \cdot (D|_S - \gamma_1 \Gamma_1 - \cdots - \gamma_k \Gamma_k))_S \\ &= r (T|_S \cdot \Delta)_S \\ &\ge m_1 r (\Gamma_1 \cdot \Delta)_S \\ &\ge m_1 (\rho_S^*\Gamma_1 \cdot \rho_S^*\Delta)_{\breve{\mathsf{p}}} \\ &\ge m_1 \operatorname{mult}_{\breve{\mathsf{p}}} (\rho_S^*\Delta) \\ &\ge m_1 (\operatorname{omult}_{\mathsf{p}} (D) - \gamma_1). \end{align*} $$
Since
![]() $m_1 - r b \deg \Gamma _1 \ge 0$
and
$m_1 - r b \deg \Gamma _1 \ge 0$
and
![]() $\gamma _1 \le m_1/b$
, we have
$\gamma _1 \le m_1/b$
, we have
 $$ \begin{align*} \operatorname{omult}_{\mathsf{p}} (D) &\le \frac{1}{m_1} (r a b (-K_X)^3 + (m_1 - r b \deg \Gamma_1) \gamma_1) \\ & \le \frac{1}{m_1} (r a b (-K_X)^3 + \frac{m_1^2}{b}- r m_1 \deg \Gamma_1). \end{align*} $$
$$ \begin{align*} \operatorname{omult}_{\mathsf{p}} (D) &\le \frac{1}{m_1} (r a b (-K_X)^3 + (m_1 - r b \deg \Gamma_1) \gamma_1) \\ & \le \frac{1}{m_1} (r a b (-K_X)^3 + \frac{m_1^2}{b}- r m_1 \deg \Gamma_1). \end{align*} $$
. This implies equation (3.6), and the proof is completed.
The following is a version of Lemma 3.21, which may be effective when S is singular at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Lemma 3.22. Let X be a normal projective
![]() $\mathbb {Q}$
-factorial
$\mathbb {Q}$
-factorial
![]() $3$
-fold. Let
$3$
-fold. Let
![]() $S \sim _{\mathbb {Q}} - a K_X$
be a normal surface on X,
$S \sim _{\mathbb {Q}} - a K_X$
be a normal surface on X,
![]() $T \sim _{\mathbb {Q}} - b K_X$
an effective divisor and
$T \sim _{\mathbb {Q}} - b K_X$
an effective divisor and
![]() $\mathsf {p} \in S$
a point, where
$\mathsf {p} \in S$
a point, where
![]() $a, b$
are positive rational numbers. Suppose that
$a, b$
are positive rational numbers. Suppose that
where
![]() $\Gamma _1, \dots , \Gamma _k$
are distinct irreducible and reduced curves on S and
$\Gamma _1, \dots , \Gamma _k$
are distinct irreducible and reduced curves on S and
![]() $m_1, \dots , m_k$
are positive integers, and the following properties are satisfied.
$m_1, \dots , m_k$
are positive integers, and the following properties are satisfied.
-
•
 $b \deg \Gamma _1 \le \operatorname {mult}_{\mathsf {p}} (\Gamma _1)$
.
$b \deg \Gamma _1 \le \operatorname {mult}_{\mathsf {p}} (\Gamma _1)$
. -
•
 $\mathsf {p} \in \Gamma _1 \setminus (\cup _{i \ge 2} \Gamma _i)$
, and X is smooth at
$\mathsf {p} \in \Gamma _1 \setminus (\cup _{i \ge 2} \Gamma _i)$
, and X is smooth at
 $\mathsf {p}$
.
$\mathsf {p}$
. -
• The intersection matrix
 $M (\Gamma _1, \dots , \Gamma _k)$
satisfies the condition
$M (\Gamma _1, \dots , \Gamma _k)$
satisfies the condition
 $(\star )$
.
$(\star )$
.
Then we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \frac{a}{\operatorname{mult}_{\mathsf{p}} (S)}, \ \frac{\operatorname{mult}_{\mathsf{p}} (S)}{a b (-K_X)^3 + \frac{m_1}{b} \operatorname{mult}_{\mathsf{p}} (\Gamma_1) - m_1 \deg \Gamma_1} \right\}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \frac{a}{\operatorname{mult}_{\mathsf{p}} (S)}, \ \frac{\operatorname{mult}_{\mathsf{p}} (S)}{a b (-K_X)^3 + \frac{m_1}{b} \operatorname{mult}_{\mathsf{p}} (\Gamma_1) - m_1 \deg \Gamma_1} \right\}. \end{align*}$$
Proof. Let
![]() $D \in \left | - K_X \right |{}_{\mathbb {Q}}$
be an irreducible
$D \in \left | - K_X \right |{}_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor. If
$\mathbb {Q}$
-divisor. If
![]() $\operatorname {Supp} (D) = S$
, then
$\operatorname {Supp} (D) = S$
, then
![]() $D = \frac {1}{a} S$
and we have
$D = \frac {1}{a} S$
and we have
![]() $\operatorname {lct}_{\mathsf {p}} (X, D) \ge a/\operatorname {mult}_{\mathsf {p}} (S)$
. We assume
$\operatorname {lct}_{\mathsf {p}} (X, D) \ge a/\operatorname {mult}_{\mathsf {p}} (S)$
. We assume
![]() $\operatorname {Supp} (D) \ne S$
. It is enough to show that
$\operatorname {Supp} (D) \ne S$
. It is enough to show that
 $$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X; D) \ge \frac{\operatorname{mult}_{\mathsf{p}} (S)}{a b (-K_X)^3 + \frac{m_1}{b} \operatorname{mult}_{\mathsf{p}} (\Gamma_1) - m_1 \deg \Gamma_1}. \end{align} $$
$$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X; D) \ge \frac{\operatorname{mult}_{\mathsf{p}} (S)}{a b (-K_X)^3 + \frac{m_1}{b} \operatorname{mult}_{\mathsf{p}} (\Gamma_1) - m_1 \deg \Gamma_1}. \end{align} $$
We write
where
![]() $\gamma _1, \dots , \gamma _k \ge 0$
and
$\gamma _1, \dots , \gamma _k \ge 0$
and
![]() $\Delta $
is an effective divisor on S such that
$\Delta $
is an effective divisor on S such that
![]() $\Gamma _i \not \subset \operatorname {Supp} (\Delta )$
for
$\Gamma _i \not \subset \operatorname {Supp} (\Delta )$
for
![]() $i = 1, \dots , k$
. By the same argument as in the proof of Lemma 3.21, we have
$i = 1, \dots , k$
. By the same argument as in the proof of Lemma 3.21, we have
![]() $\gamma _i \le m_i/b$
for any i. We consider the
$\gamma _i \le m_i/b$
for any i. We consider the
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S = \gamma _1 \Gamma _1 + \cdots + \gamma _k \Gamma _k$
on X, and we have
$D \cdot S = \gamma _1 \Gamma _1 + \cdots + \gamma _k \Gamma _k$
on X, and we have
 $$ \begin{align*} ab (-K_X)^3 - b \gamma_1 \deg \Gamma_1 &\ge (T \cdot (D \cdot S - \gamma_1 \Gamma_1 - \cdots - \gamma_k \Gamma_k))_X \\ & = (T \cdot \Delta)_X \\ &\ge \operatorname{mult}_{\mathsf{p}} (\Delta) \\ &\ge (\operatorname{mult}_{\mathsf{p}} (S)) (\operatorname{mult}_{\mathsf{p}} (D)) - \gamma_1 \operatorname{mult}_{\mathsf{p}} (\Gamma_1). \end{align*} $$
$$ \begin{align*} ab (-K_X)^3 - b \gamma_1 \deg \Gamma_1 &\ge (T \cdot (D \cdot S - \gamma_1 \Gamma_1 - \cdots - \gamma_k \Gamma_k))_X \\ & = (T \cdot \Delta)_X \\ &\ge \operatorname{mult}_{\mathsf{p}} (\Delta) \\ &\ge (\operatorname{mult}_{\mathsf{p}} (S)) (\operatorname{mult}_{\mathsf{p}} (D)) - \gamma_1 \operatorname{mult}_{\mathsf{p}} (\Gamma_1). \end{align*} $$
Since
![]() $\operatorname {mult}_{\mathsf {p}} (\Gamma _1) - b \deg \Gamma _1 \ge 0$
and
$\operatorname {mult}_{\mathsf {p}} (\Gamma _1) - b \deg \Gamma _1 \ge 0$
and
![]() $\gamma _1 \le m_1/b$
, we have
$\gamma _1 \le m_1/b$
, we have
 $$ \begin{align*} \operatorname{mult}_{\mathsf{p}} (D) &\le \frac{1}{\operatorname{mult}_{\mathsf{p}} (S)} (ab (-K_X)^3 + (\operatorname{mult}_{\mathsf{p}} (\Gamma_1) - b \deg \Gamma_1) \gamma_1) \\ & \le \frac{1}{\operatorname{mult}_{\mathsf{p}} (S)} \left( ab (-K_X)^3 + \frac{m_1}{b} \operatorname{mult}_{\mathsf{p}} (\Gamma_1) - m_1 \deg \Gamma_1 \right). \end{align*} $$
$$ \begin{align*} \operatorname{mult}_{\mathsf{p}} (D) &\le \frac{1}{\operatorname{mult}_{\mathsf{p}} (S)} (ab (-K_X)^3 + (\operatorname{mult}_{\mathsf{p}} (\Gamma_1) - b \deg \Gamma_1) \gamma_1) \\ & \le \frac{1}{\operatorname{mult}_{\mathsf{p}} (S)} \left( ab (-K_X)^3 + \frac{m_1}{b} \operatorname{mult}_{\mathsf{p}} (\Gamma_1) - m_1 \deg \Gamma_1 \right). \end{align*} $$
. This implies equation (3.9), and the proof is completed.
Lemma 3.23. Let X be a normal projective
![]() $\mathbb {Q}$
-factorial
$\mathbb {Q}$
-factorial
![]() $3$
-fold. Let
$3$
-fold. Let
![]() $S \sim _{\mathbb {Q}} - a K_X$
be a normal surface on X,
$S \sim _{\mathbb {Q}} - a K_X$
be a normal surface on X,
![]() $T \sim _{\mathbb {Q}} - b K_X$
an effective divisor and
$T \sim _{\mathbb {Q}} - b K_X$
an effective divisor and
![]() $\mathsf {p} \in X$
a point, where
$\mathsf {p} \in X$
a point, where
![]() $a, b$
be positive rational numbers. Suppose that
$a, b$
be positive rational numbers. Suppose that
where
![]() $\Gamma _1, \Gamma _2$
are distinct irreducible and reduced curves on S, and the following properties are satisfied.
$\Gamma _1, \Gamma _2$
are distinct irreducible and reduced curves on S, and the following properties are satisfied.
-
•
 $\deg \Gamma _i \le 2/b$
for
$\deg \Gamma _i \le 2/b$
for
 $i = 1, 2$
.
$i = 1, 2$
. -
•
 $\mathsf {p} \in \Gamma _1 \cap \Gamma _2$
and all the X, S,
$\mathsf {p} \in \Gamma _1 \cap \Gamma _2$
and all the X, S,
 $\Gamma _1$
and
$\Gamma _1$
and
 $\Gamma _2$
are smooth at
$\Gamma _2$
are smooth at
 $\mathsf {p}$
.
$\mathsf {p}$
. -
• The intersection matrix
 $M (\Gamma _1, \Gamma _2)$
satisfies the condition
$M (\Gamma _1, \Gamma _2)$
satisfies the condition
 $(\star )$
.
$(\star )$
.
Then we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ a, \ \frac{b}{2} \right\}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ a, \ \frac{b}{2} \right\}. \end{align*}$$
Proof. We have
![]() $\operatorname {lct}_{\mathsf {p}} (X, \frac {1}{a} S) \ge a$
since S is smooth at
$\operatorname {lct}_{\mathsf {p}} (X, \frac {1}{a} S) \ge a$
since S is smooth at
![]() $\mathsf {p}$
by assumption. Let
$\mathsf {p}$
by assumption. Let
![]() $D \in \left | - K_X \right |{}_{\mathbb {Q}}$
be an irreducible
$D \in \left | - K_X \right |{}_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X such that
$\mathbb {Q}$
-divisor on X such that
![]() $\operatorname {Supp} (D) \ne S$
. It is enough to prove the inequality
$\operatorname {Supp} (D) \ne S$
. It is enough to prove the inequality
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge b/2$
. We write
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge b/2$
. We write
where
![]() $\gamma _1, \gamma _2 \ge 0$
and
$\gamma _1, \gamma _2 \ge 0$
and
![]() $\Delta $
is an effective divisor on S with
$\Delta $
is an effective divisor on S with
![]() $\Gamma _1, \Gamma _2 \not \subset \operatorname {Supp} (\Delta )$
. By the proof of Lemma 3.21, we have
$\Gamma _1, \Gamma _2 \not \subset \operatorname {Supp} (\Delta )$
. By the proof of Lemma 3.21, we have
![]() $\gamma _1, \gamma _2 \le 1/b$
. We have
$\gamma _1, \gamma _2 \le 1/b$
. We have
Since
![]() $\operatorname {mult}_{\mathsf {p}} (T|_S) = 2$
and
$\operatorname {mult}_{\mathsf {p}} (T|_S) = 2$
and
![]() $\operatorname {mult}_{\mathsf {p}} (\Delta ) \ge \operatorname {mult}_{\mathsf {p}} (D) - \gamma _1 - \gamma _2$
, we have
$\operatorname {mult}_{\mathsf {p}} (\Delta ) \ge \operatorname {mult}_{\mathsf {p}} (D) - \gamma _1 - \gamma _2$
, we have
 $$ \begin{align*} ab (-K_X)^3 - b \gamma_1 \deg \Gamma_1 - b \gamma_2 \deg \Gamma_2 &= (T|_S \cdot (D|_S - \gamma_1 \Gamma_1 - \gamma_2 \Gamma_2))_S \\ &= (T|_S \cdot \Delta)_S \\ & \ge 2 (\operatorname{mult}_{\mathsf{p}} (D) - \gamma_1 - \gamma_2). \end{align*} $$
$$ \begin{align*} ab (-K_X)^3 - b \gamma_1 \deg \Gamma_1 - b \gamma_2 \deg \Gamma_2 &= (T|_S \cdot (D|_S - \gamma_1 \Gamma_1 - \gamma_2 \Gamma_2))_S \\ &= (T|_S \cdot \Delta)_S \\ & \ge 2 (\operatorname{mult}_{\mathsf{p}} (D) - \gamma_1 - \gamma_2). \end{align*} $$
By equation (3.10), the assumption
![]() $\deg \Gamma _1, \deg \Gamma _2 \le 2/b$
and
$\deg \Gamma _1, \deg \Gamma _2 \le 2/b$
and
![]() $\gamma _1, \gamma _2 \le 1/b$
, we have
$\gamma _1, \gamma _2 \le 1/b$
, we have
 $$ \begin{align*} \operatorname{mult}_{\mathsf{p}} (D) &\le\frac{1}{2} (ab (-K_X)^3 + (2 - b \deg \Gamma_1) \gamma_1 + (2- b \deg \Gamma_2) \gamma_2) \\ & \le \frac{2}{b}. \end{align*} $$
$$ \begin{align*} \operatorname{mult}_{\mathsf{p}} (D) &\le\frac{1}{2} (ab (-K_X)^3 + (2 - b \deg \Gamma_1) \gamma_1 + (2- b \deg \Gamma_2) \gamma_2) \\ & \le \frac{2}{b}. \end{align*} $$
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge b/2$
and thus
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge b/2$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge \min \{a, b/2\}$
.
$\alpha _{\mathsf {p}} (X) \ge \min \{a, b/2\}$
.
3.2.b Computations by weighted blowups
We explain methods of computing LCTs via suitable weighted blowups.
Let
![]() $\mathsf {p} \in X$
be a germ of a smooth variety of dimension n with a system of local coordinates
$\mathsf {p} \in X$
be a germ of a smooth variety of dimension n with a system of local coordinates
![]() $\{x_1, \dots , x_n\}$
at
$\{x_1, \dots , x_n\}$
at
![]() $\mathsf {p}$
, and let D be an effective
$\mathsf {p}$
, and let D be an effective
![]() $\mathbb {Q}$
-divisor on X. Let
$\mathbb {Q}$
-divisor on X. Let
![]() $\varphi \colon Y \to X$
be the weighted blowup at
$\varphi \colon Y \to X$
be the weighted blowup at
![]() $\mathsf {p}$
with weight
$\mathsf {p}$
with weight
![]() $\operatorname {wt} (x_1, \dots , x_n) = (c_1, \dots , c_n)$
, where
$\operatorname {wt} (x_1, \dots , x_n) = (c_1, \dots , c_n)$
, where
![]() $\underline {c} = (c_1, \dots , c_n)$
is a tuple of positive integers such that
$\underline {c} = (c_1, \dots , c_n)$
is a tuple of positive integers such that
![]() $\gcd \{c_1, \dots , c_n\} = 1$
. Let
$\gcd \{c_1, \dots , c_n\} = 1$
. Let
![]() $E \cong \mathbb {P} (\underline {c}) = \mathbb {P} (c_1, \dots , c_n)$
be the exceptional divisor of
$E \cong \mathbb {P} (\underline {c}) = \mathbb {P} (c_1, \dots , c_n)$
be the exceptional divisor of
![]() $\varphi $
. Note that Y can be singular along a divisor on E (see Remark 3.24 below) so that we cannot expect the usual adjunction
$\varphi $
. Note that Y can be singular along a divisor on E (see Remark 3.24 below) so that we cannot expect the usual adjunction
![]() $(K_Y + E)|_E = K_E$
. In general, we need a correction term and we have
$(K_Y + E)|_E = K_E$
. In general, we need a correction term and we have
where the correction term
![]() $\operatorname {Diff}$
is a
$\operatorname {Diff}$
is a
![]() $\mathbb {Q}$
-divisor on E which is called the different (see [Reference KollárKol+92, Chapter 16]).
$\mathbb {Q}$
-divisor on E which is called the different (see [Reference KollárKol+92, Chapter 16]).
Remark 3.24. We give a concrete description of
![]() $\operatorname {Diff}$
. Let
$\operatorname {Diff}$
. Let
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
be the well-formed model of
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
be the well-formed model of
![]() $\mathbb {P} (\underline {c})$
, and we identify E with
$\mathbb {P} (\underline {c})$
, and we identify E with
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
. For
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
. For
![]() $i = 0, 1, \dots , n$
, let
$i = 0, 1, \dots , n$
, let
be the quasi-hyperplane of
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}_{\tilde {x}_1, \dots , \tilde {x}_n}$
, and we set
$\mathbb {P} (\underline {c})^{\operatorname {wf}}_{\tilde {x}_1, \dots , \tilde {x}_n}$
, and we set
![]() $m_i = \gcd \{c_0, \dots , \hat {c}_i, \dots , c_n\}$
. We see that Y is singular at the generic point of
$m_i = \gcd \{c_0, \dots , \hat {c}_i, \dots , c_n\}$
. We see that Y is singular at the generic point of
![]() $H^{\operatorname {wf}}_i$
if and only if
$H^{\operatorname {wf}}_i$
if and only if
![]() $m_i> 1$
, and if this is the case, then the singularity of Y along
$m_i> 1$
, and if this is the case, then the singularity of Y along
![]() $H^{\operatorname {wf}}_i$
is a cyclic quotient singularity of index
$H^{\operatorname {wf}}_i$
is a cyclic quotient singularity of index
![]() $m_i$
. It follows from [Reference KollárKol+92, Proposition 16.6] that
$m_i$
. It follows from [Reference KollárKol+92, Proposition 16.6] that
 $$\begin{align*}\operatorname{Diff} = \sum_{i=1}^n \frac{m_i-1}{m_i} H^{\operatorname{wf}}_i \end{align*}$$
$$\begin{align*}\operatorname{Diff} = \sum_{i=1}^n \frac{m_i-1}{m_i} H^{\operatorname{wf}}_i \end{align*}$$
under the identification
![]() $E \cong \mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
$E \cong \mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
Lemma 3.25. Let the notation and assumption as above. Then we have
 $$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X;D) \ge \min \left\{ \frac{c_1 + \cdots + c_n}{\operatorname{ord}_E (D)}, \ \operatorname{lct} (E, \operatorname{Diff}; \tilde{D}|_E) \right\}, \end{align} $$
$$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X;D) \ge \min \left\{ \frac{c_1 + \cdots + c_n}{\operatorname{ord}_E (D)}, \ \operatorname{lct} (E, \operatorname{Diff}; \tilde{D}|_E) \right\}, \end{align} $$
where
![]() $\tilde {D}$
is the proper transform of D. If in addition the inequality
$\tilde {D}$
is the proper transform of D. If in addition the inequality
holds, then we have
Proof. We set
![]() $c = c_1 + \cdots + c_n$
and let
$c = c_1 + \cdots + c_n$
and let
![]() $\lambda $
be any rational number such that
$\lambda $
be any rational number such that
 $$\begin{align*}0 < \lambda \le \min \left\{ \frac{c}{\operatorname{ord}_E (D)}, \ \operatorname{lct} (E, \operatorname{Diff}; \tilde{D}|_E) \right\}. \end{align*}$$
$$\begin{align*}0 < \lambda \le \min \left\{ \frac{c}{\operatorname{ord}_E (D)}, \ \operatorname{lct} (E, \operatorname{Diff}; \tilde{D}|_E) \right\}. \end{align*}$$
We will show that the pair
![]() $(X, \lambda D)$
is log canonical at
$(X, \lambda D)$
is log canonical at
![]() $\mathsf {p}$
, which will prove the inequality (3.11).
$\mathsf {p}$
, which will prove the inequality (3.11).
We assume that the pair
![]() $(X, \lambda D)$
is not log canonical at
$(X, \lambda D)$
is not log canonical at
![]() $\mathsf {p}$
. We have
$\mathsf {p}$
. We have
and the pair
![]() $(Y, \lambda \tilde {D} + (\lambda \operatorname {ord}_E (D) - c + 1)E)$
is not log canonical along E. Since
$(Y, \lambda \tilde {D} + (\lambda \operatorname {ord}_E (D) - c + 1)E)$
is not log canonical along E. Since
![]() $\lambda \le c/\operatorname {ord}_E (D)$
, we have
$\lambda \le c/\operatorname {ord}_E (D)$
, we have
which implies that the pair
![]() $(Y, \lambda \tilde {D} + E)$
is not log canonical along E. Thus, the pair
$(Y, \lambda \tilde {D} + E)$
is not log canonical along E. Thus, the pair
![]() $(E, \operatorname {Diff} + \lambda \tilde {D}|_E)$
is not log canonical. This is impossible since
$(E, \operatorname {Diff} + \lambda \tilde {D}|_E)$
is not log canonical. This is impossible since
![]() $\lambda \le \operatorname {lct} (E, \operatorname {Diff};\tilde {D}|_E)$
. Therefore, the pair
$\lambda \le \operatorname {lct} (E, \operatorname {Diff};\tilde {D}|_E)$
. Therefore, the pair
![]() $(X, \lambda D)$
is log canonical at
$(X, \lambda D)$
is log canonical at
![]() $\mathsf {p}$
, and the inequality (3.11) is proved.
$\mathsf {p}$
, and the inequality (3.11) is proved.
By considering the coefficient of E in equation (3.14), it is easy to see that
Under the assumption (3.12), this shows the equality (3.13).
We consider Lemma 3.25 in more details in a concrete setting.
Definition 3.26. Let
![]() $\underline {c} = (c_1, \dots , c_n)$
be an n-tuple of positive integers such that
$\underline {c} = (c_1, \dots , c_n)$
be an n-tuple of positive integers such that
![]() $\gcd \{c_1, \dots , c_n\} = 1$
, and we set
$\gcd \{c_1, \dots , c_n\} = 1$
, and we set
for
![]() $i = 1, \dots , n$
. Let
$i = 1, \dots , n$
. Let
![]() $f = f (x_1, \dots , x_n)$
be a polynomial which is quasi-homogeneous with respect to
$f = f (x_1, \dots , x_n)$
be a polynomial which is quasi-homogeneous with respect to
![]() $\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
.
$\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
.
If f is irreducible and
![]() $f \ne x_i$
for
$f \ne x_i$
for
![]() $i = 1, \dots , n$
, then there exists an irreducible polynomial
$i = 1, \dots , n$
, then there exists an irreducible polynomial
![]() $f^{\operatorname {wf}} = f^{\operatorname {wf}} (\tilde {x}_1, \dots , \tilde {x}_n)$
(in new variables
$f^{\operatorname {wf}} = f^{\operatorname {wf}} (\tilde {x}_1, \dots , \tilde {x}_n)$
(in new variables
![]() $\tilde {x}_1, \dots , \tilde {x}_n$
) such that
$\tilde {x}_1, \dots , \tilde {x}_n$
) such that
We call
![]() $f^{\operatorname {wf}}$
the well-formed model of f (with respect to the weight
$f^{\operatorname {wf}}$
the well-formed model of f (with respect to the weight
![]() $\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
).
$\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
).
In general, we have a decomposition
where
![]() $k, \lambda _1, \dots , \lambda _n, \mu _1, \dots , \mu _k$
are nonnegative integers and
$k, \lambda _1, \dots , \lambda _n, \mu _1, \dots , \mu _k$
are nonnegative integers and
![]() $f_1, \dots , f_k$
are irreducible polynomials in variables
$f_1, \dots , f_k$
are irreducible polynomials in variables
![]() $x_1, \dots , x_n$
which are quasi-homogeneous with respect to
$x_1, \dots , x_n$
which are quasi-homogeneous with respect to
![]() $\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
and which are not
$\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
and which are not
![]() $x_i$
for any i. We define
$x_i$
for any i. We define
and call it the well-formed model of f. Note that
![]() $f^{\operatorname {wf}}$
is in general not a polynomial since
$f^{\operatorname {wf}}$
is in general not a polynomial since
![]() $\lambda _i/m_i$
need not be an integer. In this case, the effective
$\lambda _i/m_i$
need not be an integer. In this case, the effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
 $$\begin{align*}\mathcal{D}^{\operatorname{wf}}_f := \sum_{i=1}^n \frac{\lambda_i}{m_i} H^{\operatorname{wf}}_i + \sum_{j=1}^k \mu_j (f_j^{\operatorname{wf}} = 0) \end{align*}$$
$$\begin{align*}\mathcal{D}^{\operatorname{wf}}_f := \sum_{i=1}^n \frac{\lambda_i}{m_i} H^{\operatorname{wf}}_i + \sum_{j=1}^k \mu_j (f_j^{\operatorname{wf}} = 0) \end{align*}$$
on the well-formed model
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}_{\tilde {x}_1, \dots , \tilde {x}_n}$
of
$\mathbb {P} (\underline {c})^{\operatorname {wf}}_{\tilde {x}_1, \dots , \tilde {x}_n}$
of
![]() $\mathbb {P} (\underline {c})$
is called the effective
$\mathbb {P} (\underline {c})$
is called the effective
![]() $\mathbb {Q}$
-divisor on
$\mathbb {Q}$
-divisor on
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
associated to f, where
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
associated to f, where
![]() $H_i^{\operatorname {wf}}$
is the quasi-hyperplane on
$H_i^{\operatorname {wf}}$
is the quasi-hyperplane on
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
defined by
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
defined by
![]() $\tilde {x}_i = 0$
.
$\tilde {x}_i = 0$
.
Lemma 3.27. Let
![]() $\mathbb {P} (\underline {b}) := \mathbb {P} (b_0, \dots , b_{n+1})_{x_0, \dots , x_{n+1}}$
be a well-formed weighted projective space, and let
$\mathbb {P} (\underline {b}) := \mathbb {P} (b_0, \dots , b_{n+1})_{x_0, \dots , x_{n+1}}$
be a well-formed weighted projective space, and let
![]() $X \subset \mathbb {P} (\underline {b})$
be a normal weighted hypersurface with defining polynomial
$X \subset \mathbb {P} (\underline {b})$
be a normal weighted hypersurface with defining polynomial
![]() $F = F (x_0, \dots , x_{n+1})$
. Let
$F = F (x_0, \dots , x_{n+1})$
. Let
![]() $\underline {c} = (c_1, \dots , c_n)$
be a tuple of positive integers such that
$\underline {c} = (c_1, \dots , c_n)$
be a tuple of positive integers such that
![]() $\gcd \{c_1, \dots , c_n\} = 1$
. Assume that
$\gcd \{c_1, \dots , c_n\} = 1$
. Assume that
 $$\begin{align*}F = x_0^e x_{n+1} + \sum_{i=1}^e x_0^{e-i} f_i, \end{align*}$$
$$\begin{align*}F = x_0^e x_{n+1} + \sum_{i=1}^e x_0^{e-i} f_i, \end{align*}$$
where
![]() $e \in \mathbb {Z}_{> 0}$
and
$e \in \mathbb {Z}_{> 0}$
and
![]() $f_i = f_i (x_1, \dots , x_n, x_{n+1})$
is a quasi-homogeneous polynomial of degree
$f_i = f_i (x_1, \dots , x_n, x_{n+1})$
is a quasi-homogeneous polynomial of degree
![]() $i b_0 + b_{n+1}$
. Let
$i b_0 + b_{n+1}$
. Let
![]() $G = G (x_1, \dots x_n)$
be the lowest weight part of
$G = G (x_1, \dots x_n)$
be the lowest weight part of
![]() $\bar {F} := F (1, x_1, \dots , x_n,0)$
with respect to
$\bar {F} := F (1, x_1, \dots , x_n,0)$
with respect to
![]() $\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
Then, for the point
$\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
Then, for the point
![]() $\mathsf {p} = \mathsf {p}_{x_0} = (1\!:\!0\!:\!\cdots \!:\!0) \in X$
, we have
$\mathsf {p} = \mathsf {p}_{x_0} = (1\!:\!0\!:\!\cdots \!:\!0) \in X$
, we have
 $$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_{x_{n+1}}) \ge \min \left\{ \frac{c_1 + \cdots + c_n}{\operatorname{wt}_{\underline{c}} (\bar{F})}, \ \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}^{\operatorname{wf}}_G) \right\}, \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_{x_{n+1}}) \ge \min \left\{ \frac{c_1 + \cdots + c_n}{\operatorname{wt}_{\underline{c}} (\bar{F})}, \ \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}^{\operatorname{wf}}_G) \right\}, \end{align*}$$
where
![]() $\operatorname {wt}_{\underline {c}} (\bar {F})$
,
$\operatorname {wt}_{\underline {c}} (\bar {F})$
,
![]() $\operatorname {Diff}$
and
$\operatorname {Diff}$
and
![]() $\mathcal {D}^{\operatorname {wf}}_G$
are as follows.
$\mathcal {D}^{\operatorname {wf}}_G$
are as follows.
-
•
 $\operatorname {wt}_{\underline {c}} (\bar {F})$
is the weight of
$\operatorname {wt}_{\underline {c}} (\bar {F})$
is the weight of
 $\bar {F}$
with respect to
$\bar {F}$
with respect to
 $\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
.
$\operatorname {wt} (x_1, \dots , x_n) = \underline {c}$
. -
•
 $\operatorname {Diff} = \sum _{i=1}^n \frac {m_i-1}{m_i} H^{\operatorname {wf}}_i$
, where
$\operatorname {Diff} = \sum _{i=1}^n \frac {m_i-1}{m_i} H^{\operatorname {wf}}_i$
, where
 $H^{\operatorname {wf}}_i = (\tilde {x}_i = 0)$
is the ith coordinate quasi-hyperplane of
$H^{\operatorname {wf}}_i = (\tilde {x}_i = 0)$
is the ith coordinate quasi-hyperplane of
 $\mathbb {P} (\underline {c})^{\operatorname {wf}}_{\tilde {x}_1, \dots , \tilde {x}_n}$
and
$\mathbb {P} (\underline {c})^{\operatorname {wf}}_{\tilde {x}_1, \dots , \tilde {x}_n}$
and
 $m_i = \gcd \{c_1, \dots , \hat {c}_i, \dots , c_n\}$
for
$m_i = \gcd \{c_1, \dots , \hat {c}_i, \dots , c_n\}$
for
 $i = 1, \dots , n$
.
$i = 1, \dots , n$
. -
•
 $\mathcal {D}^{\operatorname {wf}}_G$
is the effective
$\mathcal {D}^{\operatorname {wf}}_G$
is the effective
 $\mathbb {Q}$
-divisor on
$\mathbb {Q}$
-divisor on
 $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
associated to G.
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
associated to G.
If in addition the inequality
holds, then we have
Proof. Let
![]() $\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}} \subset X$
, where
$\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}} \subset X$
, where
![]() $U_{\mathsf {p}} = U_{x_0}$
, be the orbifold chart containing
$U_{\mathsf {p}} = U_{x_0}$
, be the orbifold chart containing
![]() $\mathsf {p}$
, and we set
$\mathsf {p}$
, and we set
![]() $\rho = \rho _{\mathsf {p}}, \breve {U} = \breve {U}_{\mathsf {p}}$
and
$\rho = \rho _{\mathsf {p}}, \breve {U} = \breve {U}_{\mathsf {p}}$
and
![]() $U = U_{\mathsf {p}}$
. We set
$U = U_{\mathsf {p}}$
. We set
![]() $H = H_{x_{n+1}}$
and
$H = H_{x_{n+1}}$
and
![]() $\breve {H} = \rho ^*H$
. We have
$\breve {H} = \rho ^*H$
. We have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H) = \operatorname {lct}_{\check {\mathsf {p}}} (\check {U}; \check {H})$
. The variety
$\operatorname {lct}_{\mathsf {p}} (X; H) = \operatorname {lct}_{\check {\mathsf {p}}} (\check {U}; \check {H})$
. The variety
![]() $\breve {U}$
is the hypersurface in
$\breve {U}$
is the hypersurface in
![]() $\mathcal {U}_{x_0} = \mathbb {A}^{n+1}_{\breve {x}_1, \dots , \breve {x}_{n+1}}$
defined by the equation
$\mathcal {U}_{x_0} = \mathbb {A}^{n+1}_{\breve {x}_1, \dots , \breve {x}_{n+1}}$
defined by the equation
 $$ \begin{align} F (1, \breve{x}_1, \dots, \breve{x}_{n+1}) = \breve{x}_{n+1} + \sum_{i=1}^e \breve{f}_i = 0, \end{align} $$
$$ \begin{align} F (1, \breve{x}_1, \dots, \breve{x}_{n+1}) = \breve{x}_{n+1} + \sum_{i=1}^e \breve{f}_i = 0, \end{align} $$
where
![]() $\breve {f}_i = f_i (\breve {x}_1, \dots , \breve {x}_{n+1})$
, and
$\breve {f}_i = f_i (\breve {x}_1, \dots , \breve {x}_{n+1})$
, and
![]() $\breve {\mathsf {p}}$
corresponds to the origin. We see that
$\breve {\mathsf {p}}$
corresponds to the origin. We see that
![]() $\{\breve {x}_1, \dots , \breve {x}_n\}$
is a system of local coordinates of
$\{\breve {x}_1, \dots , \breve {x}_n\}$
is a system of local coordinates of
![]() $\breve {U}$
at
$\breve {U}$
at
![]() $\breve {\mathsf {p}}$
. Let
$\breve {\mathsf {p}}$
. Let
![]() $\varphi \colon Y \to \breve {U}$
be the weighted blowup at
$\varphi \colon Y \to \breve {U}$
be the weighted blowup at
![]() $\breve {\mathsf {p}}$
with
$\breve {\mathsf {p}}$
with
![]() $\operatorname {wt} (\breve {x}_1, \dots , \breve {x}_n) = (c_1, \dots , c_n)$
. We can identify the
$\operatorname {wt} (\breve {x}_1, \dots , \breve {x}_n) = (c_1, \dots , c_n)$
. We can identify the
![]() $\varphi $
-exceptional divisor E with
$\varphi $
-exceptional divisor E with
![]() $\mathbb {P} (\underline {c})_{\breve {x}_1, \dots , \breve {x}_n}$
. Filtering off terms divisible by
$\mathbb {P} (\underline {c})_{\breve {x}_1, \dots , \breve {x}_n}$
. Filtering off terms divisible by
![]() $\breve {x}_{n+1}$
in equation (3.15), we have
$\breve {x}_{n+1}$
in equation (3.15), we have
on
![]() $\breve {U}$
, where the omitted term in the left-hand side is a polynomial vanishing at
$\breve {U}$
, where the omitted term in the left-hand side is a polynomial vanishing at
![]() $\breve {\mathsf {p}}$
. Since
$\breve {\mathsf {p}}$
. Since
![]() $\breve {H}$
is the divisor on
$\breve {H}$
is the divisor on
![]() $\breve {U}$
defined by
$\breve {U}$
defined by
![]() $\breve {x}_{n+1} = 0$
, we see that
$\breve {x}_{n+1} = 0$
, we see that
![]() $\operatorname {ord}_E (\breve {H}) = \operatorname {wt}_{\underline {c}} (\bar {F})$
and the divisor
$\operatorname {ord}_E (\breve {H}) = \operatorname {wt}_{\underline {c}} (\bar {F})$
and the divisor
![]() $\tilde {H}|_E$
corresponds to the divisor
$\tilde {H}|_E$
corresponds to the divisor
![]() $\mathcal {D}^{\operatorname {wf}}_G$
on
$\mathcal {D}^{\operatorname {wf}}_G$
on
![]() $E \cong \mathbb {P} (\underline {c})^{\operatorname {wf}}$
, where
$E \cong \mathbb {P} (\underline {c})^{\operatorname {wf}}$
, where
![]() $\tilde {H}$
is the proper transform of
$\tilde {H}$
is the proper transform of
![]() $\breve {H}$
on Y. Therefore, the proof is completed by Lemma 3.25 and Remark 3.24.
$\breve {H}$
on Y. Therefore, the proof is completed by Lemma 3.25 and Remark 3.24.
Lemma 3.28. Let
![]() $X \subset \mathbb {P} (a, b_1, b_2, b_3, r)_{x, y_1, y_2, y_3, z}$
be a member of a family
$X \subset \mathbb {P} (a, b_1, b_2, b_3, r)_{x, y_1, y_2, y_3, z}$
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
with defining polynomial
$\mathsf {i} \in \mathsf {I}$
with defining polynomial
![]() $F = F (x, y_1, y_2, y_3, z)$
. Assume that F can be written as
$F = F (x, y_1, y_2, y_3, z)$
. Assume that F can be written as
where
![]() $f_i \in \mathbb {C} [x, y_1, y_2, y_3]$
is a quasi-homogeneous polynomial of degree i, and we set
$f_i \in \mathbb {C} [x, y_1, y_2, y_3]$
is a quasi-homogeneous polynomial of degree i, and we set
If either
![]() $\bar {F} \in (y_1, y_2, y_3)^2 \setminus (y_1, y_2, y_3)^3$
or
$\bar {F} \in (y_1, y_2, y_3)^2 \setminus (y_1, y_2, y_3)^3$
or
![]() $\bar {F} \in (y_1, y_2, y_3)^3$
and the cubic part of
$\bar {F} \in (y_1, y_2, y_3)^3$
and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form in
$\bar {F}$
is not a cube of a linear form in
![]() $y_1, y_2, y_3$
, then for the point
$y_1, y_2, y_3$
, then for the point
![]() $\mathsf {p} := \mathsf {p}_z \in X$
, we have
$\mathsf {p} := \mathsf {p}_z \in X$
, we have
If in addition
![]() $a = 1$
,
$a = 1$
,
![]() $r> 1$
and
$r> 1$
and
![]() $\mathsf {p} \in X$
is not a maximal center, then
$\mathsf {p} \in X$
is not a maximal center, then
Proof. Let
![]() $\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of X containing
$\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of X containing
![]() $\mathsf {p}$
. We see that Let
$\mathsf {p}$
. We see that Let
![]() $\breve {U}_{\mathsf {p}}$
be the hypersurface in
$\breve {U}_{\mathsf {p}}$
be the hypersurface in
![]() $\breve {\mathcal {U}}_{\mathsf {p}} = \mathbb {A}^4_{\breve {x}, \breve {y}_1, \breve {y}_2, \breve {y}_3}$
defined by the equation
$\breve {\mathcal {U}}_{\mathsf {p}} = \mathbb {A}^4_{\breve {x}, \breve {y}_1, \breve {y}_2, \breve {y}_3}$
defined by the equation
We see that
![]() $\breve {U}_{\mathsf {p}}$
is smooth and the morphism
$\breve {U}_{\mathsf {p}}$
is smooth and the morphism
![]() $\rho _{\mathsf {p}}$
can be identified with the quotient morphism of the singularity
$\rho _{\mathsf {p}}$
can be identified with the quotient morphism of the singularity
![]() $\mathsf {p} \in X$
over a suitable analytic neighborhood of
$\mathsf {p} \in X$
over a suitable analytic neighborhood of
![]() $\mathsf {p}$
. We denote by
$\mathsf {p}$
. We denote by
![]() $\breve {\mathsf {p}} \in \breve {U}$
the origin of
$\breve {\mathsf {p}} \in \breve {U}$
the origin of
![]() $\breve {\mathcal {U}}_{\mathsf {p}} = \mathbb {A}^4$
which is the preimage of
$\breve {\mathcal {U}}_{\mathsf {p}} = \mathbb {A}^4$
which is the preimage of
![]() $\mathsf {p}$
via
$\mathsf {p}$
via
![]() $\rho _{\mathsf {p}}$
. Filtering off terms divisible by x in
$\rho _{\mathsf {p}}$
. Filtering off terms divisible by x in
![]() $F (x, y_1, y_2, y_3, 1)$
, we have
$F (x, y_1, y_2, y_3, 1)$
, we have
on
![]() $\breve {U}_{\mathsf {p}}$
. Note that we can choose
$\breve {U}_{\mathsf {p}}$
. Note that we can choose
![]() $\{\breve {y}_1, \breve {y}_2, \breve {y}_3\}$
as a system of local coordinates of
$\{\breve {y}_1, \breve {y}_2, \breve {y}_3\}$
as a system of local coordinates of
![]() $\breve {U}_{\mathsf {p}}$
at
$\breve {U}_{\mathsf {p}}$
at
![]() $\breve {\mathsf {p}}$
. If
$\breve {\mathsf {p}}$
. If
![]() $\bar {F} \in (y_1, y_2, y_3)^2 \setminus (y_1, y_2, y_3)^3$
, then
$\bar {F} \in (y_1, y_2, y_3)^2 \setminus (y_1, y_2, y_3)^3$
, then
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = \operatorname {mult}_{\breve {\mathsf {p}}} (\rho _{\mathsf {p}}^*H_x) = 2$
and hence
$\operatorname {omult}_{\mathsf {p}} (H_x) = \operatorname {mult}_{\breve {\mathsf {p}}} (\rho _{\mathsf {p}}^*H_x) = 2$
and hence
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
Suppose that
![]() $\bar {F} \in (y_1, y_2, y_3)^3$
and the cubic part of
$\bar {F} \in (y_1, y_2, y_3)^3$
and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form in
$\bar {F}$
is not a cube of a linear form in
![]() $y_1, y_2, y_3$
. Let
$y_1, y_2, y_3$
. Let
![]() $\varphi \colon V \to \breve {U}$
be the blowup of
$\varphi \colon V \to \breve {U}$
be the blowup of
![]() $\breve {U}$
at
$\breve {U}$
at
![]() $\breve {\mathsf {p}}$
with exceptional divisor
$\breve {\mathsf {p}}$
with exceptional divisor
![]() $E \cong \mathbb {P}^2$
. We set
$E \cong \mathbb {P}^2$
. We set
![]() $D = \rho _{\mathsf {p}}^*H_x$
. Since
$D = \rho _{\mathsf {p}}^*H_x$
. Since
![]() $\operatorname {mult}_{\breve {\mathsf {p}}} (D) = 3$
, we have
$\operatorname {mult}_{\breve {\mathsf {p}}} (D) = 3$
, we have
 $$\begin{align*}K_V + \frac{1}{2} \tilde{D} = \varphi^* \left(K_{\check{U}} + \frac{1}{2} D \right) + \frac{1}{2} E, \end{align*}$$
$$\begin{align*}K_V + \frac{1}{2} \tilde{D} = \varphi^* \left(K_{\check{U}} + \frac{1}{2} D \right) + \frac{1}{2} E, \end{align*}$$
where
![]() $\tilde {D}$
is the proper transform of D on V. The divisor
$\tilde {D}$
is the proper transform of D on V. The divisor
![]() $\tilde {D}|_E$
on E is isomorphic to the hypersurface in
$\tilde {D}|_E$
on E is isomorphic to the hypersurface in
![]() $\mathbb {P}^2_{\breve {y}_1, \breve {y}_2, \breve {y}_3}$
defined by the cubic part of
$\mathbb {P}^2_{\breve {y}_1, \breve {y}_2, \breve {y}_3}$
defined by the cubic part of
![]() $\bar {F} (\breve {y}_1, \breve {y}_2, \breve {y}_3)$
, and the pair
$\bar {F} (\breve {y}_1, \breve {y}_2, \breve {y}_3)$
, and the pair
![]() $(E, \frac {1}{2} \tilde {D}|_E)$
is log canonical by Lemma 3.4. It then follows that the pair
$(E, \frac {1}{2} \tilde {D}|_E)$
is log canonical by Lemma 3.4. It then follows that the pair
![]() $(V, \frac {1}{2} \tilde {D})$
is log canonical along E. This shows that the pair
$(V, \frac {1}{2} \tilde {D})$
is log canonical along E. This shows that the pair
![]() $(\breve {U}, \frac {1}{2} D)$
is log canonical at
$(\breve {U}, \frac {1}{2} D)$
is log canonical at
![]() $\breve {\mathsf {p}}$
, and hence
$\breve {\mathsf {p}}$
, and hence
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
as desired.
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
as desired.
Suppose in addition that
![]() $r> 1$
and
$r> 1$
and
![]() $\mathsf {p} \in X$
is not a maximal center. By Lemma 3.6, the pair
$\mathsf {p} \in X$
is not a maximal center. By Lemma 3.6, the pair
![]() $(X, H_x)$
is not canonical at
$(X, H_x)$
is not canonical at
![]() $\mathsf {p} = \mathsf {p}_z$
and thus we have
$\mathsf {p} = \mathsf {p}_z$
and thus we have
![]() $\alpha _{\mathsf {p}} (X) = \min \{1, \operatorname {lct}_{\mathsf {p}}; (X;H_x)\}$
by Lemma 3.5. This proves the latter assertion.
$\alpha _{\mathsf {p}} (X) = \min \{1, \operatorname {lct}_{\mathsf {p}}; (X;H_x)\}$
by Lemma 3.5. This proves the latter assertion.
3.2.c Computations by
 $2 n$
-inequality
$2 n$
-inequality
Lemma 3.29. Let
![]() $X \subset \mathbb {P} (b_1, b_2, b_3, c, r)_{x_1, x_2, x_3, y, z}$
be a member of a family
$X \subset \mathbb {P} (b_1, b_2, b_3, c, r)_{x_1, x_2, x_3, y, z}$
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
with defining polynomial
$\mathsf {i} \in \mathsf {I}$
with defining polynomial
![]() $F = F (x_1, x_2, x_3, y, z)$
, and suppose
$F = F (x_1, x_2, x_3, y, z)$
, and suppose
![]() $\mathsf {p} :=\mathsf {p}_z \in X$
. We assume that
$\mathsf {p} :=\mathsf {p}_z \in X$
. We assume that
![]() $b_1 \le b_2 \le b_3$
and that we can choose y as a quasi-tangent coordinate of X at
$b_1 \le b_2 \le b_3$
and that we can choose y as a quasi-tangent coordinate of X at
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
In particular, if
![]() $r b_2 b_3 (A^3) \le 4$
, then
$r b_2 b_3 (A^3) \le 4$
, then
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
Proof. Let
![]() $\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of X containing
$\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of X containing
![]() $\mathsf {p} = \mathsf {p}_z$
. We set
$\mathsf {p} = \mathsf {p}_z$
. We set
![]() $\rho = \rho _{\mathsf {p}}$
,
$\rho = \rho _{\mathsf {p}}$
,
![]() $\breve {U} = \breve {U}_{\mathsf {p}}$
and
$\breve {U} = \breve {U}_{\mathsf {p}}$
and
![]() $U = U_{\mathsf {p}}$
. We see that
$U = U_{\mathsf {p}}$
. We see that
![]() $\breve {U}$
is the hypersurface in
$\breve {U}$
is the hypersurface in
![]() $\breve {\mathcal {U}}_{\mathsf {p}} = \mathbb {A}^4_{\breve {x}_1, \breve {x}_2, \breve {x}_3, \breve {y})}$
defined by the equation
$\breve {\mathcal {U}}_{\mathsf {p}} = \mathbb {A}^4_{\breve {x}_1, \breve {x}_2, \breve {x}_3, \breve {y})}$
defined by the equation
We see that
![]() $\breve {U}$
is smooth, and the morphism
$\breve {U}$
is smooth, and the morphism
![]() $\rho $
can be identified with the quotient morphism of
$\rho $
can be identified with the quotient morphism of
![]() $\mathsf {p} \in X$
over a suitable analytic neighborhood of
$\mathsf {p} \in X$
over a suitable analytic neighborhood of
![]() $\mathsf {p}$
. We denote by
$\mathsf {p}$
. We denote by
![]() $\breve {\mathsf {p}} \in \breve {U}$
the origin which is the preimage of
$\breve {\mathsf {p}} \in \breve {U}$
the origin which is the preimage of
![]() $\mathsf {p}$
via
$\mathsf {p}$
via
![]() $\rho $
. By the assumption, we can choose
$\rho $
. By the assumption, we can choose
![]() $\breve {x}_1, \breve {x}_2, \breve {x}_3$
as a system of local coordinates of
$\breve {x}_1, \breve {x}_2, \breve {x}_3$
as a system of local coordinates of
![]() $\breve {U}$
at
$\breve {U}$
at
![]() $\breve {\mathsf {p}}$
.
$\breve {\mathsf {p}}$
.
We set
and assume that
![]() $\alpha _{\mathsf {p}} (X) < \lambda $
. Then there exists an irreducible
$\alpha _{\mathsf {p}} (X) < \lambda $
. Then there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \sim _{\mathbb {Q}} A$
such that the pair
$D \sim _{\mathbb {Q}} A$
such that the pair
![]() $(X, \lambda D)$
is not log canonical at
$(X, \lambda D)$
is not log canonical at
![]() $\mathsf {p}$
. In particular, the pair
$\mathsf {p}$
. In particular, the pair
![]() $(\breve {U}, \lambda \rho ^*D)$
is not log canonical at
$(\breve {U}, \lambda \rho ^*D)$
is not log canonical at
![]() $\breve {\mathsf {p}}$
. Let
$\breve {\mathsf {p}}$
. Let
![]() $\varphi \colon V \to \breve {U}$
be the blowup of
$\varphi \colon V \to \breve {U}$
be the blowup of
![]() $\breve {U}$
at
$\breve {U}$
at
![]() $\breve {\mathsf {p}}$
with exceptional divisor
$\breve {\mathsf {p}}$
with exceptional divisor
![]() $E \cong \mathbb {P}^2$
. By Lemma 3.3, there exists a line
$E \cong \mathbb {P}^2$
. By Lemma 3.3, there exists a line
![]() $L \subset E$
with the property that for any prime divisor T on
$L \subset E$
with the property that for any prime divisor T on
![]() $\breve {U}$
such that T is smooth at
$\breve {U}$
such that T is smooth at
![]() $\breve {\mathsf {p}}$
and that its proper transform
$\breve {\mathsf {p}}$
and that its proper transform
![]() $\tilde {T}$
contains L, we have
$\tilde {T}$
contains L, we have
![]() $\operatorname {mult}_{\breve {\mathsf {p}}} (D|_T)> 2/\lambda $
. By a slight abuse of notation, we have an isomorphism
$\operatorname {mult}_{\breve {\mathsf {p}}} (D|_T)> 2/\lambda $
. By a slight abuse of notation, we have an isomorphism
![]() $E \cong \mathbb {P}^2_{\breve {x}_1, \breve {x}_2, \breve {x}_3}$
. The line
$E \cong \mathbb {P}^2_{\breve {x}_1, \breve {x}_2, \breve {x}_3}$
. The line
![]() $L \subset E$
is isomorphic to
$L \subset E$
is isomorphic to
![]() $(\alpha _1 \breve {x}_1 + \alpha _2 \breve {x}_2 + \alpha _3 \breve {x}_3 = 0) \subset \mathbb {P}^2$
, for some
$(\alpha _1 \breve {x}_1 + \alpha _2 \breve {x}_2 + \alpha _3 \breve {x}_3 = 0) \subset \mathbb {P}^2$
, for some
![]() $\alpha _1, \alpha _2, \alpha _3 \in \mathbb {C}$
with
$\alpha _1, \alpha _2, \alpha _3 \in \mathbb {C}$
with
![]() $(\alpha _1, \alpha _2, \alpha _3) \ne (0, 0, 0)$
. We set
$(\alpha _1, \alpha _2, \alpha _3) \ne (0, 0, 0)$
. We set
Then
![]() $\breve {T}$
is smooth at
$\breve {T}$
is smooth at
![]() $\breve {\mathsf {p}}$
and its proper transform on V contains L. It follows that
$\breve {\mathsf {p}}$
and its proper transform on V contains L. It follows that
![]() $\operatorname {mult}_{\breve {\mathsf {p}}} (\rho ^*D|_{\breve {T}})> 2/\lambda $
. Set
$\operatorname {mult}_{\breve {\mathsf {p}}} (\rho ^*D|_{\breve {T}})> 2/\lambda $
. Set
![]() $k := \max \{\, i \mid \alpha _i \ne 0 \, \}$
. We have
$k := \max \{\, i \mid \alpha _i \ne 0 \, \}$
. We have
![]() $r \breve {T} = \rho ^*G$
for some effective Weil divisor
$r \breve {T} = \rho ^*G$
for some effective Weil divisor
![]() $G \sim r b_k A$
. Let
$G \sim r b_k A$
. Let
![]() $j \in \{1, 2, 3\}$
be such that
$j \in \{1, 2, 3\}$
be such that
Then, since
![]() $\{x_1, x_2, x_3\}$
isolates
$\{x_1, x_2, x_3\}$
isolates
![]() $\mathsf {p}$
, we can take an effective
$\mathsf {p}$
, we can take an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $S \sim _{\mathbb {Q}} A$
such that
$S \sim _{\mathbb {Q}} A$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (S) \ge 1/b_j$
and
$\operatorname {omult}_{\mathsf {p}} (S) \ge 1/b_j$
and
![]() $\rho ^*S$
does not contain any component of
$\rho ^*S$
does not contain any component of
![]() $\rho ^*D|_{\breve {T}}$
. Hence, we have
$\rho ^*D|_{\breve {T}}$
. Hence, we have
 $$\begin{align*}r b_k (A^3) = (D \cdot G \cdot S) \ge (\rho^*D \cdot \breve{T} \cdot \rho^*S)_{\breve{\mathsf{p}}}> \frac{2}{b_j \lambda} = \frac{r b_2 b_3 (A^3)}{b_j}. \end{align*}$$
$$\begin{align*}r b_k (A^3) = (D \cdot G \cdot S) \ge (\rho^*D \cdot \breve{T} \cdot \rho^*S)_{\breve{\mathsf{p}}}> \frac{2}{b_j \lambda} = \frac{r b_2 b_3 (A^3)}{b_j}. \end{align*}$$
This is a contradiction since
![]() $b_j b_k \le b_2 b_3$
, and the proof is completed.
$b_j b_k \le b_2 b_3$
, and the proof is completed.
3.2.d Computations by
 $\operatorname {\overline {NE}}$
$\operatorname {\overline {NE}}$
Let X be a quasi-smooth Fano 3-fold weighted hypersurface of index
![]() $1$
. Let
$1$
. Let
![]() $\mathsf {p} \in X$
be a singular point, and we denote by
$\mathsf {p} \in X$
be a singular point, and we denote by
![]() $\varphi \colon Y \to X$
the Kawamata blowup at
$\varphi \colon Y \to X$
the Kawamata blowup at
![]() $\mathsf {p}$
. In [Reference Cheltsov and ParkCP17], the assertion
$\mathsf {p}$
. In [Reference Cheltsov and ParkCP17], the assertion
![]() $(-K_Y)^2 \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
is verified in many cases, where
$(-K_Y)^2 \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
is verified in many cases, where
![]() $\operatorname {\overline {NE}} (Y)$
is the cone of effective curves on Y. Thus, the following result is very useful.
$\operatorname {\overline {NE}} (Y)$
is the cone of effective curves on Y. Thus, the following result is very useful.
Lemma 3.30 [Reference Kim, Okada and WonKOW18, Lemma 2.8].
Let
![]() $\mathsf {p} \in X$
be a terminal quotient singular point and
$\mathsf {p} \in X$
be a terminal quotient singular point and
![]() $\varphi \colon Y \to X$
the Kawamata blowup at
$\varphi \colon Y \to X$
the Kawamata blowup at
![]() $\mathsf {p}$
. Suppose that
$\mathsf {p}$
. Suppose that
![]() $(-K_Y)^2 \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
and there exists a prime divisor S on X such that
$(-K_Y)^2 \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
and there exists a prime divisor S on X such that
![]() $\tilde {S} \sim _{\mathbb {Q}} - m K_Y$
for some
$\tilde {S} \sim _{\mathbb {Q}} - m K_Y$
for some
![]() $m> 0$
, where
$m> 0$
, where
![]() $\tilde {S}$
is the proper transform of S on Y. Then
$\tilde {S}$
is the proper transform of S on Y. Then
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
4 Smooth points
The aim of this section is to prove the following.
Theorem 4.1. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then
for any smooth point
![]() $\mathsf {p} \in X$
.
$\mathsf {p} \in X$
.
We explain the organization of this section. Throughout the present section, let
be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, where we assume
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, where we assume
![]() $a_1 \le \cdots \le a_4$
. Note that
$a_1 \le \cdots \le a_4$
. Note that
![]() $a_2 \ge 2$
since
$a_2 \ge 2$
since
![]() $\mathsf {i} \notin \mathsf {I}_1$
. Recall that we denote by
$\mathsf {i} \notin \mathsf {I}_1$
. Recall that we denote by
![]() $F = F (x, y, z, t, w)$
the defining polynomial of X with
$F = F (x, y, z, t, w)$
the defining polynomial of X with
![]() $\deg F = d$
, and we set
$\deg F = d$
, and we set
![]() $A := -K_X$
. We set
$A := -K_X$
. We set
 $$ \begin{align*} U_1 &:= \bigcup_{v \in \{x,y,z,t,w\}, \deg v = 1} (v \ne 0) \cap X, \\ L_{xy} &:= H_x \cap H_y = (x = y = 0) \cap X. \end{align*} $$
$$ \begin{align*} U_1 &:= \bigcup_{v \in \{x,y,z,t,w\}, \deg v = 1} (v \ne 0) \cap X, \\ L_{xy} &:= H_x \cap H_y = (x = y = 0) \cap X. \end{align*} $$
Note that
![]() $U_1$
is an open subset of X contained in
$U_1$
is an open subset of X contained in
![]() $\operatorname {Sm} (X)$
, and
$\operatorname {Sm} (X)$
, and
![]() $L_{xy}$
is a one-dimensional closed subset of X. The proof of the inequality
$L_{xy}$
is a one-dimensional closed subset of X. The proof of the inequality
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
for
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for
![]() $\mathsf {p} \in U_1$
will be done in Section 4.1. The proof for the other smooth points will be done as follows.
$\mathsf {p} \in U_1$
will be done in Section 4.1. The proof for the other smooth points will be done as follows.
-
• If
 $1 < a_1 < a_2$
, then
$1 < a_1 < a_2$
, then
 $\operatorname {Sm} (X) \subset U_1 \sqcup (H_x \setminus L_{xy}) \sqcup L_{xy}$
. In this case, the proof of
$\operatorname {Sm} (X) \subset U_1 \sqcup (H_x \setminus L_{xy}) \sqcup L_{xy}$
. In this case, the proof of
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for smooth point
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for smooth point
 $\mathsf {p}$
of X contained in
$\mathsf {p}$
of X contained in
 $H_x \setminus L_{xy}$
(resp.
$H_x \setminus L_{xy}$
(resp.
 $L_{xy}$
) will be done in Section 4.2 (resp. Sections 4.3 and 4.4), respectively.
$L_{xy}$
) will be done in Section 4.2 (resp. Sections 4.3 and 4.4), respectively. -
• If
 $1 = a_1 < a_2$
, then
$1 = a_1 < a_2$
, then
 $\operatorname {Sm} (X) \subset U_1 \sqcup L_{xy}$
. In this case, the proof of
$\operatorname {Sm} (X) \subset U_1 \sqcup L_{xy}$
. In this case, the proof of
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for smooth point
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for smooth point
 $\mathsf {p}$
of X contained in
$\mathsf {p}$
of X contained in
 $L_{xy}$
will be done in Sections 4.3 and 4.4.
$L_{xy}$
will be done in Sections 4.3 and 4.4. -
• If
 $1 < a_1 = a_2$
, then
$1 < a_1 = a_2$
, then
 $\operatorname {Sm} (X) \subset U_1 \sqcup H_x$
. In this case, the proof of
$\operatorname {Sm} (X) \subset U_1 \sqcup H_x$
. In this case, the proof of
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for smooth point
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for smooth point
 $\mathsf {p}$
of X contained in
$\mathsf {p}$
of X contained in
 $H_x$
will be done in Section 4.5.
$H_x$
will be done in Section 4.5.
Therefore, Theorem 4.7 will follow from Propositions 4.7, 4.8, 4.10, 4.11 and 4.19, which are the main results of Sections 4.1, 4.2, 4.3, 4.4 and 4.5, respectively.
4.1 Smooth points on
 $U_1$
for families indexed by
$U_1$
for families indexed by
 $\mathsf {I} \setminus \mathsf {I}_1$
$\mathsf {I} \setminus \mathsf {I}_1$
Lemma 4.2. We have
for any point
![]() $\mathsf {p} \in U_1$
.
$\mathsf {p} \in U_1$
.
Proof. Let
![]() $\mathsf {p} \in U_1$
be a point. We may assume
$\mathsf {p} \in U_1$
be a point. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
by a change of coordinates. Let
$\mathsf {p} = \mathsf {p}_x$
by a change of coordinates. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor. The linear system
$\mathbb {Q}$
-divisor. The linear system
![]() $|\mathcal {I}_{\mathsf {p}} (a_2 A)|$
is movable, and let
$|\mathcal {I}_{\mathsf {p}} (a_2 A)|$
is movable, and let
![]() $S \in |\mathcal {I}_{\mathsf {p}} (a_2 A)|$
be a general member so that
$S \in |\mathcal {I}_{\mathsf {p}} (a_2 A)|$
be a general member so that
![]() $\operatorname {Supp} (S) \ne \operatorname {Supp} (D)$
. The set
$\operatorname {Supp} (S) \ne \operatorname {Supp} (D)$
. The set
![]() $\{y, z, t, w\}$
isolates
$\{y, z, t, w\}$
isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_4 A|_{\mathbb {Q}}$
such that
$T \in |a_4 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S$
(see Remark 3.15). Then we have
$D \cdot S$
(see Remark 3.15). Then we have
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/a_2 a_4 (A^3)$
, and the proof is completed.
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/a_2 a_4 (A^3)$
, and the proof is completed.
Lemma 4.3. Suppose that d is divisible by
![]() $a_4$
. Then
$a_4$
. Then
for any point
![]() $\mathsf {p} \in U_1$
.
$\mathsf {p} \in U_1$
.
Proof. Let
![]() $\mathsf {p} \in U_1$
be a point. We may assume
$\mathsf {p} \in U_1$
be a point. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
. We can choose coordinates so that
$\mathsf {p} = \mathsf {p}_x$
. We can choose coordinates so that
![]() $w^{d/a_4} \in F$
. Indeed, if
$w^{d/a_4} \in F$
. Indeed, if
![]() $a_4> a_3$
, then
$a_4> a_3$
, then
![]() $w^{d/a_4} \in F$
by the quasi-smoothness of X. If
$w^{d/a_4} \in F$
by the quasi-smoothness of X. If
![]() $a_4 = a_3$
, then there is a monomial of degree d consisting of
$a_4 = a_3$
, then there is a monomial of degree d consisting of
![]() $t, w$
by the quasi-smoothness of X and we can choose coordinates
$t, w$
by the quasi-smoothness of X and we can choose coordinates
![]() $t, w$
so that
$t, w$
so that
![]() $w^{d/a_4} \in F$
. Under the above choice of coordinates, we see that
$w^{d/a_4} \in F$
. Under the above choice of coordinates, we see that
![]() $\{y, z, t\}$
isolates
$\{y, z, t\}$
isolates
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor. Let S be a general member of the movable linear system
$\mathbb {Q}$
-divisor. Let S be a general member of the movable linear system
![]() $|\mathcal {I}_{\mathsf {p}} (a_2 A)|$
so that
$|\mathcal {I}_{\mathsf {p}} (a_2 A)|$
so that
![]() $\operatorname {Supp} (S)$
does not contain
$\operatorname {Supp} (S)$
does not contain
![]() $\operatorname {Supp} (D)$
. We can take a
$\operatorname {Supp} (D)$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_3 A|_{\mathbb {Q}}$
such that
$T \in |a_3 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S$
since
$D \cdot S$
since
![]() $\{y, z, t\}$
isolates
$\{y, z, t\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
This shows
![]() $\alpha _{\mathsf {p}} (D) \ge 1/a_2 a_3 (A^3)$
and the proof is completed.
$\alpha _{\mathsf {p}} (D) \ge 1/a_2 a_3 (A^3)$
and the proof is completed.
Remark 4.4. The objects of Section 4 are members of families
![]() $\mathcal {F}_{\mathsf {i}}$
for
$\mathcal {F}_{\mathsf {i}}$
for
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, and the inequality
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, and the inequality
![]() $a_2 \ge 2$
is assumed throughout the present section. It is, however, noted that in Lemmas 4.2 and 4.3, the assumption
$a_2 \ge 2$
is assumed throughout the present section. It is, however, noted that in Lemmas 4.2 and 4.3, the assumption
![]() $a_2 \ge 2$
is not required, and the statement holds for members of
$a_2 \ge 2$
is not required, and the statement holds for members of
![]() $\mathcal {F}_{\mathsf {i}}$
for any
$\mathcal {F}_{\mathsf {i}}$
for any
![]() $\mathsf {i} \in \mathsf {I}$
.
$\mathsf {i} \in \mathsf {I}$
.
Lemma 4.5. Suppose that d is not divisible by
![]() $a_4$
, and assume
$a_4$
, and assume
![]() $a_1 = 1$
. Then
$a_1 = 1$
. Then
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X;S_{\mathsf{p}}), \ \frac{1}{a_4 (A^3)} \right\} \ge \frac{1}{2} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X;S_{\mathsf{p}}), \ \frac{1}{a_4 (A^3)} \right\} \ge \frac{1}{2} \end{align*}$$
for any
![]() $\mathsf {p} \in U_1$
, where
$\mathsf {p} \in U_1$
, where
![]() $S_{\mathsf {p}}$
is the unique member of
$S_{\mathsf {p}}$
is the unique member of
![]() $|\mathcal {I}_{\mathsf {p}} (A)|$
.
$|\mathcal {I}_{\mathsf {p}} (A)|$
.
Proof. Let
![]() $\mathsf {p} \in U_1$
be a point. We may assume
$\mathsf {p} \in U_1$
be a point. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
. Note that we have
$\mathsf {p} = \mathsf {p}_x$
. Note that we have
![]() $a_2> 1$
and thus the linear system
$a_2> 1$
and thus the linear system
![]() $|\mathcal {I}_{\mathsf {p}} (A)|$
indeed consists of a unique member
$|\mathcal {I}_{\mathsf {p}} (A)|$
indeed consists of a unique member
![]() $S_{\mathsf {p}}$
. In this case,
$S_{\mathsf {p}}$
. In this case,
![]() $S_{\mathsf {p}} = H_y$
.
$S_{\mathsf {p}} = H_y$
.
We first prove
![]() $\operatorname {lct}_{\mathsf {p}} (X;S_{\mathsf {p}}) \ge 1/2$
, that is,
$\operatorname {lct}_{\mathsf {p}} (X;S_{\mathsf {p}}) \ge 1/2$
, that is,
![]() $(X, \frac {1}{2} H_y)$
is log canonical at
$(X, \frac {1}{2} H_y)$
is log canonical at
![]() $\mathsf {p}$
. Assume to the contrary that
$\mathsf {p}$
. Assume to the contrary that
![]() $(X, \frac {1}{2} H_y)$
is not log canonical at
$(X, \frac {1}{2} H_y)$
is not log canonical at
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
. Suppose
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
. Suppose
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) = 3$
. Then, by Lemma 3.4, the degree
$\operatorname {mult}_{\mathsf {p}} (H_y) = 3$
. Then, by Lemma 3.4, the degree
![]() $3$
part of
$3$
part of
![]() $F (1,0,z,t,w)$
with respect to
$F (1,0,z,t,w)$
with respect to
![]() $\deg (z,t,w) = (1,1,1)$
is a cube of a linear form, that is, it can be written as
$\deg (z,t,w) = (1,1,1)$
is a cube of a linear form, that is, it can be written as
![]() $(\alpha z + \beta t + \gamma w)^3$
for some
$(\alpha z + \beta t + \gamma w)^3$
for some
![]() $\alpha , \beta , \gamma \in \mathbb {C}$
. By Lemma 2.28, we have
$\alpha , \beta , \gamma \in \mathbb {C}$
. By Lemma 2.28, we have
![]() $d < 3 a_4$
since d is not divisible by
$d < 3 a_4$
since d is not divisible by
![]() $a_4$
. From this, we deduce
$a_4$
. From this, we deduce
![]() $\gamma = 0$
. Then we can write
$\gamma = 0$
. Then we can write
where
![]() $g = g (x,z,t,w) \in (z,t,w)^4 \subset \mathbb {C} [x,z,t,w]$
and
$g = g (x,z,t,w) \in (z,t,w)^4 \subset \mathbb {C} [x,z,t,w]$
and
![]() $h = h (x,y,z,t,w)$
. By the inequality
$h = h (x,y,z,t,w)$
. By the inequality
![]() $d < 3 a_4$
, no monomial in g can be divisible by
$d < 3 a_4$
, no monomial in g can be divisible by
![]() $w^3$
so that
$w^3$
so that
![]() $g \in (z,t)^2$
. But then X is not quasi-smooth along the nonempty subset
$g \in (z,t)^2$
. But then X is not quasi-smooth along the nonempty subset
This is impossible, and we have
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 4$
. By the same argument as above, we can write
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 4$
. By the same argument as above, we can write
where
![]() $g \in (z,t)^2$
, which implies that X is not quasi-smooth. This is a contradiction and thus
$g \in (z,t)^2$
, which implies that X is not quasi-smooth. This is a contradiction and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X; S_{\mathsf {p}}) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; S_{\mathsf {p}}) \ge 1/2$
.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $S_{\mathsf {p}} = H_y$
. Note that
$S_{\mathsf {p}} = H_y$
. Note that
![]() $D \cdot H_y$
is an effective
$D \cdot H_y$
is an effective
![]() $1$
-cycle. The set
$1$
-cycle. The set
![]() $\{y, z, t, w\}$
isolates
$\{y, z, t, w\}$
isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_4 A|_{\mathbb {Q}}$
such that
$T \in |a_4 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot H_y$
. We have
$D \cdot H_y$
. We have
where the last inequality follows from (5) of Lemma 2.29 since
![]() $a_1 = 1$
. Thus,
$a_1 = 1$
. Thus,
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/a_4 (A^3) \ge 1/2$
, and the proof is completed.
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/a_4 (A^3) \ge 1/2$
, and the proof is completed.
Lemma 4.6. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \{9,17\}$
. Then
$\mathsf {i} \in \{9,17\}$
. Then
for any point
![]() $\mathsf {p} \in U_1$
.
$\mathsf {p} \in U_1$
.
Proof. In this case,
where
![]() $a = 2, 3$
if
$a = 2, 3$
if
![]() $\mathsf {i} = 9, 17$
, respectively. Let
$\mathsf {i} = 9, 17$
, respectively. Let
![]() $\mathsf {p} \in U_1$
be a point. We may assume
$\mathsf {p} \in U_1$
be a point. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
.
$\mathsf {p} = \mathsf {p}_x$
.
We show that
![]() $(X, \frac {1}{2} H_y)$
is log canonical at
$(X, \frac {1}{2} H_y)$
is log canonical at
![]() $\mathsf {p}$
. Assume to the contrary that it is not. Then
$\mathsf {p}$
. Assume to the contrary that it is not. Then
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
and, by Lemma 3.4, we can write
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
and, by Lemma 3.4, we can write
where
![]() $g = g (x,z,t,w) \in (z,t,w)^4 \subset \mathbb {C} [x,y,t,w]$
and
$g = g (x,z,t,w) \in (z,t,w)^4 \subset \mathbb {C} [x,y,t,w]$
and
![]() $h = h (x,y,z,t,w)$
. By degree reason, any monomial in
$h = h (x,y,z,t,w)$
. By degree reason, any monomial in
![]() $g \in (z,t,w)^4$
is divisible by
$g \in (z,t,w)^4$
is divisible by
![]() $z^3$
. It follows that X is not quasi-smooth along the nonempty subset
$z^3$
. It follows that X is not quasi-smooth along the nonempty subset
This is a contradiction, and the pair
![]() $(X, \frac {1}{2} H_y)$
is log canonical at
$(X, \frac {1}{2} H_y)$
is log canonical at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_y$
. The set
$H_y$
. The set
![]() $\{y, z, t, w\}$
clearly isolates
$\{y, z, t, w\}$
clearly isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |(a+1) A|_{\mathbb {Q}}$
such that
$T \in |(a+1) A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_y$
. Then we have
$D \cdot H_y$
. Then we have
since
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 2$
. This shows
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 2$
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X, D) \ge 4/3$
and the proof is completed.
$\operatorname {lct}_{\mathsf {p}} (X, D) \ge 4/3$
and the proof is completed.
Proposition 4.7. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then
for any point
![]() $\mathsf {p} \in U_1$
.
$\mathsf {p} \in U_1$
.
Proof. Let
![]() $X = X_d \subset \mathbb {P} (1,a_1,a_2,a_3,a_4)$
be a member of
$X = X_d \subset \mathbb {P} (1,a_1,a_2,a_3,a_4)$
be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, where we assume
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, where we assume
![]() $a_1 \le \cdots \le a_4$
.
$a_1 \le \cdots \le a_4$
.
-
• If d is not divisible by
 $a_4$
and
$a_4$
and
 $a_1 \ge 2$
, then
$a_1 \ge 2$
, then
 $a_2 a_4 (A^3) \le 2$
and the assertion follows from Lemma 4.2.
$a_2 a_4 (A^3) \le 2$
and the assertion follows from Lemma 4.2. -
• If d is not divisible by
 $a_4$
and
$a_4$
and
 $a_1 = 1$
, then the assertion follows from Lemma 4.5.
$a_1 = 1$
, then the assertion follows from Lemma 4.5. -
• If d is divisible by
 $a_4$
and
$a_4$
and
 $\mathsf {i} \notin \{9, 17\}$
, then
$\mathsf {i} \notin \{9, 17\}$
, then
 $a_2 a_3 (A^3) \le 2$
by Lemma 2.29 and the assertion follows from Lemma 4.3.
$a_2 a_3 (A^3) \le 2$
by Lemma 2.29 and the assertion follows from Lemma 4.3. -
• If
 $\mathsf {i} \in \{9, 17\}$
, then the assertion follows from Lemma 4.6.
$\mathsf {i} \in \{9, 17\}$
, then the assertion follows from Lemma 4.6.
This completes the proof.
4.2 Smooth points on
 $H_x \setminus L_{xy}$
for families with
$H_x \setminus L_{xy}$
for families with
 $1 < a_1 < a_2$
$1 < a_1 < a_2$
Let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
![]() $1 < a_1 < a_2 \le a_3 \le a_4$
. In this section, we set
$1 < a_1 < a_2 \le a_3 \le a_4$
. In this section, we set
![]() $\bar {F} = F (0,y,z,t,w)$
. Then
$\bar {F} = F (0,y,z,t,w)$
. Then
![]() $H_x$
is isomorphic to the weighted hypersurface in
$H_x$
is isomorphic to the weighted hypersurface in
![]() $\mathbb {P} (a_1, \dots , a_4)$
defined by
$\mathbb {P} (a_1, \dots , a_4)$
defined by
![]() $\bar {F} = 0$
. We note that if a smooth point
$\bar {F} = 0$
. We note that if a smooth point
![]() $\mathsf {p} \in X$
contained in
$\mathsf {p} \in X$
contained in
![]() $H_x$
satisfies
$H_x$
satisfies
![]() $\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
, then
$\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
, then
![]() $\mathsf {p}$
belongs to the subset
$\mathsf {p}$
belongs to the subset
 $$\begin{align*}\bigcap_{v_1, v_2 \in \{y,z,t,w\}} \left( \frac{\partial^2 \bar{F}}{\partial v_1 \partial v_2} = 0 \right) \cap X. \end{align*}$$
$$\begin{align*}\bigcap_{v_1, v_2 \in \{y,z,t,w\}} \left( \frac{\partial^2 \bar{F}}{\partial v_1 \partial v_2} = 0 \right) \cap X. \end{align*}$$
The following is the main result of this section.
Proposition 4.8. Let
![]() $X = X_d \subset \mathbb {P} (1, a_1, \dots , a_4)$
,
$X = X_d \subset \mathbb {P} (1, a_1, \dots , a_4)$
,
![]() $a_1 \le \dots \le a_4$
, be a member of a family
$a_1 \le \dots \le a_4$
, be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
![]() $1 < a_1 < a_2$
. Then
$1 < a_1 < a_2$
. Then
for any smooth point
![]() $\mathsf {p}$
of X contained in
$\mathsf {p}$
of X contained in
![]() $H_x \setminus L_{xy}$
.
$H_x \setminus L_{xy}$
.
The rest of this section is entirely devoted to the proof of Proposition 4.8 which will be done by division into several cases.
4.2.a Case:
 $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
 $d = 2 a_4$
$d = 2 a_4$
We will prove Proposition 4.8 under the assumption of
![]() $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
![]() $d = 2 a_4$
.
$d = 2 a_4$
.
Let
![]() $\mathsf {p} \in X$
be a smooth point contained in
$\mathsf {p} \in X$
be a smooth point contained in
![]() $H_x \setminus L_{xy}$
. We have
$H_x \setminus L_{xy}$
. We have
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
since
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
since
![]() $w^2 \in F$
, and thus
$w^2 \in F$
, and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
. Let
$\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_x$
. By Lemma 3.16,
$H_x$
. By Lemma 3.16,
![]() $a_1 a_3 A$
isolates
$a_1 a_3 A$
isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_1 a_3 A|_{\mathbb {Q}}$
such that
$T \in |a_1 a_3 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
. Then we have
$D \cdot H_x$
. Then we have
where the last inequality follows from Lemma 2.29. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and the proof is completed.
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and the proof is completed.
4.2.b Case:
 $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
 $d = 2 a_4 + a_1$
$d = 2 a_4 + a_1$
We will prove Proposition 4.8 under the assumption of
![]() $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
![]() $d = 2 a_4 + a_1$
.
$d = 2 a_4 + a_1$
.
Let
![]() $\mathsf {p} \in X$
be a smooth point contained in
$\mathsf {p} \in X$
be a smooth point contained in
![]() $H_x \setminus L_{xy}$
. We can write
$H_x \setminus L_{xy}$
. We can write
where
![]() $f, g \in \mathbb {C} [x, y, z, t]$
are quasi-homogeneous polynomials of degree
$f, g \in \mathbb {C} [x, y, z, t]$
are quasi-homogeneous polynomials of degree
![]() $d-a_4$
and d, respectively. Since
$d-a_4$
and d, respectively. Since
![]() $\partial ^2 \bar {F}/\partial w^2 = y$
and y does not vanish at
$\partial ^2 \bar {F}/\partial w^2 = y$
and y does not vanish at
![]() $\mathsf {p} \in H_x \setminus L_{xy}$
, we have
$\mathsf {p} \in H_x \setminus L_{xy}$
, we have
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
and thus
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_x$
. By Lemma 3.16,
$H_x$
. By Lemma 3.16,
![]() $a_1 a_4 A$
isolates
$a_1 a_4 A$
isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_1 a_4 A|_{\mathbb {Q}}$
such that
$T \in |a_1 a_4 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
. Then we have
$D \cdot H_x$
. Then we have
where the last inequality from Lemma 2.29. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
and the proof is completed.
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
and the proof is completed.
4.2.c Case:
 $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
 $d = 2 a_4 + a_2$
$d = 2 a_4 + a_2$
We will prove Proposition 4.8 under the assumption of
![]() $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
![]() $d = 2 a_4 + a_2$
.
$d = 2 a_4 + a_2$
.
Let
![]() $\mathsf {p} \in X$
be a smooth point contained in
$\mathsf {p} \in X$
be a smooth point contained in
![]() $H_x \setminus L_{xy}$
. We can write
$H_x \setminus L_{xy}$
. We can write
where
![]() $f, h \in \mathbb {C} [x,y,z,t]$
and
$f, h \in \mathbb {C} [x,y,z,t]$
and
![]() $g \in \mathbb {C} [x,y,t]$
are quasi-homogeneous polynomials of degrees
$g \in \mathbb {C} [x,y,t]$
are quasi-homogeneous polynomials of degrees
![]() $a_4, a_2 + a_4$
and d, respectively.
$a_4, a_2 + a_4$
and d, respectively.
Claim 1.
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
Proof of Claim 1.
We prove
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
. Assume to the contrary that
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
. Assume to the contrary that
![]() $\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
. Since
$\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
. Since
the point
![]() $\mathsf {p}$
is contained in
$\mathsf {p}$
is contained in
![]() $H_x \cap H_z \cap (2 w + f = 0)$
. Suppose in addition that
$H_x \cap H_z \cap (2 w + f = 0)$
. Suppose in addition that
![]() $\mathsf {p} \in H_t$
. Note that we have
$\mathsf {p} \in H_t$
. Note that we have
![]() $a_4 = a_1 + a_3$
since
$a_4 = a_1 + a_3$
since
![]() $d = a_1 + a_2 + a_3 + a_4$
and
$d = a_1 + a_2 + a_3 + a_4$
and
![]() $d = 2 a_4 + a_2$
. We see that
$d = 2 a_4 + a_2$
. We see that
![]() $a_1$
does not divide
$a_1$
does not divide
![]() $a_4 = a_1 + a_3$
because otherwise
$a_4 = a_1 + a_3$
because otherwise
![]() $\gcd \{a_1, a_3, a_4\}> 1$
and X has a nonisolated singularity which is clearly worse than terminal, a contradiction. It follows that f does not contain a power of y, that is,
$\gcd \{a_1, a_3, a_4\}> 1$
and X has a nonisolated singularity which is clearly worse than terminal, a contradiction. It follows that f does not contain a power of y, that is,
![]() $f (0,y,0) = 0$
, and
$f (0,y,0) = 0$
, and
This is impossible since
![]() $\mathsf {p}_y$
is a singular point of X. Thus,
$\mathsf {p}_y$
is a singular point of X. Thus,
![]() $\mathsf {p} \notin H_t$
. Since
$\mathsf {p} \notin H_t$
. Since
![]() $a_4 = a_1 + a_3$
, we may assume that
$a_4 = a_1 + a_3$
, we may assume that
![]() $\mathsf {p} \in H_w$
after replacing w by
$\mathsf {p} \in H_w$
after replacing w by
![]() $w - \xi y t$
for some
$w - \xi y t$
for some
![]() $\xi \in \mathbb {C}$
. We can write
$\xi \in \mathbb {C}$
. We can write
![]() $\mathsf {p} = (0\!:\!1\!:\!0\!:\!\lambda \!:\!0)$
for some nonzero
$\mathsf {p} = (0\!:\!1\!:\!0\!:\!\lambda \!:\!0)$
for some nonzero
![]() $\lambda \in \mathbb {C}$
. The set
$\lambda \in \mathbb {C}$
. The set
![]() $\{x, z, w, t^{a_1} - \lambda ^{a_1} y^{a_3}\}$
isolates
$\{x, z, w, t^{a_1} - \lambda ^{a_1} y^{a_3}\}$
isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_1 a_3 A|_{\mathbb {Q}}$
such that
$T \in |a_1 a_3 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $H_x \cdot H_z$
. Then we have
$H_x \cdot H_z$
. Then we have
where the last inequality follows from Lemma 2.29. This shows
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
, and thus
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
, and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_x$
. By Lemma 3.16,
$H_x$
. By Lemma 3.16,
![]() $a_1 a_4 A$
isolates
$a_1 a_4 A$
isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_1 a_4 A|_{mbQ}$
such that
$T \in |a_1 a_4 A|_{mbQ}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot H_x$
. We have
$D \cdot H_x$
. We have
where the last inequality follows from Lemma 2.29. Thus,
![]() $\operatorname {lct}_{\mathsf {p}} (X; D)> 1/2$
and we conclude
$\operatorname {lct}_{\mathsf {p}} (X; D)> 1/2$
and we conclude
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
4.2.d Case:
 $1 < a_1 < a_2$
,
$1 < a_1 < a_2$
,
 $d = 2 a_4 + a_3$
and
$d = 2 a_4 + a_3$
and
 $a_3 \ne a_4$
$a_3 \ne a_4$
The proof of Proposition 4.8 under the assumption of
![]() $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
![]() $d = 2 a_4 + a_3$
is completely parallel to the one given in Section 4.2.c. Indeed, the same proof applies after interchanging the role of z and t (and hence
$d = 2 a_4 + a_3$
is completely parallel to the one given in Section 4.2.c. Indeed, the same proof applies after interchanging the role of z and t (and hence
![]() $a_2$
and
$a_2$
and
![]() $a_3$
). Thus, we omit the proof.
$a_3$
). Thus, we omit the proof.
4.2.e Case:
 $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
 $d = 3 a_4$
$d = 3 a_4$
We will prove Proposition 4.8 under the assumption of
![]() $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
![]() $d = 3 a_4$
.
$d = 3 a_4$
.
Let
![]() $\mathsf {p} \in X$
be a smooth point contained in
$\mathsf {p} \in X$
be a smooth point contained in
![]() $H_x \setminus L_{xy}$
. We first prove
$H_x \setminus L_{xy}$
. We first prove
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
assuming that the inequality
$\alpha _{\mathsf {p}} (X) \ge 1/2$
assuming that the inequality
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
holds. Let
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
holds. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_x$
. By Lemma 3.16,
$H_x$
. By Lemma 3.16,
![]() $a_1 a_4 A$
isolates
$a_1 a_4 A$
isolates
![]() $\mathsf {p}$
, and hence we can take a
$\mathsf {p}$
, and hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |a_1 a_4 A|_{\mathbb {Q}}$
such that
$T \in |a_1 a_4 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
. Then we have
$D \cdot H_x$
. Then we have
where the last inequality follows from Lemma 2.29. This shows
![]() $\operatorname {mult}_{\mathsf {p}} (D) \le 2$
, and we have
$\operatorname {mult}_{\mathsf {p}} (D) \le 2$
, and we have
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
.
Therefore, the proof of Proposition 4.8 under the assumption of
![]() $1< a_1 < a_2$
and
$1< a_1 < a_2$
and
![]() $d = 3 a_4$
is reduced to the following.
$d = 3 a_4$
is reduced to the following.
Claim 2. We have
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
for any smooth point
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
for any smooth point
![]() $\mathsf {p} \in X$
contained in
$\mathsf {p} \in X$
contained in
![]() $H_x \setminus L_{xy}$
.
$H_x \setminus L_{xy}$
.
The rest of this subsection is devoted to the proof of Claim 2, which will be done by considering each family individually. The families satisfying
![]() $1 < a_1 < a_2$
and
$1 < a_1 < a_2$
and
![]() $d = 3 a_4$
are families
$d = 3 a_4$
are families
![]() $\mathcal {F}_{\mathsf {i}}$
, where
$\mathcal {F}_{\mathsf {i}}$
, where
In the following, for a polynomial
![]() $f (x,y,z,\dots )$
in variables
$f (x,y,z,\dots )$
in variables
![]() $x, y, z, \dots $
, we set
$x, y, z, \dots $
, we set
![]() $\bar {f} = \bar {f} (y,z,\dots ) := f (0,y,z,\dots )$
. We first consider the family
$\bar {f} = \bar {f} (y,z,\dots ) := f (0,y,z,\dots )$
. We first consider the family
![]() $\mathcal {F}_{27}$
, which is the unique family satisfying
$\mathcal {F}_{27}$
, which is the unique family satisfying
![]() $d = 3 a_3 = 3 a_4$
We then consider the rest of the families which satisfy
$d = 3 a_3 = 3 a_4$
We then consider the rest of the families which satisfy
![]() $d = 3 a_4> 3 a_3$
.
$d = 3 a_4> 3 a_3$
.
4.2.e.1 The family
 $\mathcal {F}_{27}$
$\mathcal {F}_{27}$
We can choose w and t so that
where
![]() $b_5, c_{10}, d_{10}, e_{15} \in \mathbb {C} [x,y,z]$
are quasi-homogeneous polynomials of indicated degrees. Let
$b_5, c_{10}, d_{10}, e_{15} \in \mathbb {C} [x,y,z]$
are quasi-homogeneous polynomials of indicated degrees. Let
![]() $\mathsf {p} \in H_x \setminus L_{xy}$
be a smooth point of X, and we assume
$\mathsf {p} \in H_x \setminus L_{xy}$
be a smooth point of X, and we assume
![]() $\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
. Since
$\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
. Since
we have
![]() $\mathsf {p} \in H_t \cap H_w$
. Then we can write
$\mathsf {p} \in H_t \cap H_w$
. Then we can write
![]() $\mathsf {p} = (0\!:\!1\!:\!\lambda \!:\!0\!:\!0)$
for some nonzero
$\mathsf {p} = (0\!:\!1\!:\!\lambda \!:\!0\!:\!0)$
for some nonzero
![]() $\lambda \in \mathbb {C}$
since
$\lambda \in \mathbb {C}$
since
![]() $\mathsf {p} \notin H_y$
and
$\mathsf {p} \notin H_y$
and
![]() $\mathsf {p} \ne \mathsf {p}_y$
. We can write
$\mathsf {p} \ne \mathsf {p}_y$
. We can write
![]() $\bar {e}_{15} = z (z^2 - \lambda ^2 y^3)(z^2 - \mu y^3)$
for some
$\bar {e}_{15} = z (z^2 - \lambda ^2 y^3)(z^2 - \mu y^3)$
for some
![]() $\mu \in \mathbb {C}$
. We have
$\mu \in \mathbb {C}$
. We have
 $$ \begin{align*} \frac{\partial^2 \bar{F}}{\partial z^2} (\mathsf{p}) &= 2 \lambda (7 \lambda^2 - 3 \mu) = 0, \\ \frac{\partial^2 \bar{F}}{\partial z \partial y} (\mathsf{p}) &= - 3 \lambda^2 (3 \lambda^2 + \mu) = 0, \end{align*} $$
$$ \begin{align*} \frac{\partial^2 \bar{F}}{\partial z^2} (\mathsf{p}) &= 2 \lambda (7 \lambda^2 - 3 \mu) = 0, \\ \frac{\partial^2 \bar{F}}{\partial z \partial y} (\mathsf{p}) &= - 3 \lambda^2 (3 \lambda^2 + \mu) = 0, \end{align*} $$
which implies
![]() $\lambda = 0$
. This is a contradiction, and Claim 2 is proved for the family
$\lambda = 0$
. This is a contradiction, and Claim 2 is proved for the family
![]() $\mathcal {F}_{27}$
.
$\mathcal {F}_{27}$
.
We consider the rest of the families, which satisfies
![]() $d = 3 a_4> 3 a_3$
. Replacing w if necessary, we can write
$d = 3 a_4> 3 a_3$
. Replacing w if necessary, we can write
where
![]() $g_{2 a_4}, h_{3 a_4} \in \mathbb {C} [x,y,z,t]$
are quasi-homogeneous polynomials of degree
$g_{2 a_4}, h_{3 a_4} \in \mathbb {C} [x,y,z,t]$
are quasi-homogeneous polynomials of degree
![]() $2 a_4, 3 a_4$
, respectively. Let
$2 a_4, 3 a_4$
, respectively. Let
![]() $\mathsf {p} \in H_x \setminus L_{xy}$
be a smooth point of X, and we assume
$\mathsf {p} \in H_x \setminus L_{xy}$
be a smooth point of X, and we assume
![]() $\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
. Since
$\operatorname {mult}_{\mathsf {p}} (H_x)> 2$
. Since
![]() $\partial ^2 \bar {F}/\partial w^2 = 6 w$
, we have
$\partial ^2 \bar {F}/\partial w^2 = 6 w$
, we have
![]() $\mathsf {p} \in H_w$
so that
$\mathsf {p} \in H_w$
so that
![]() $\mathsf {p} \in H_x \cap H_w$
and
$\mathsf {p} \in H_x \cap H_w$
and
![]() $\mathsf {p} \notin H_y$
. In the following, we will derive a contradiction by considering each family separately.
$\mathsf {p} \notin H_y$
. In the following, we will derive a contradiction by considering each family separately.
4.2.e.2 The family
 $\mathcal {F}_{19}$
$\mathcal {F}_{19}$
Replacing
![]() $t \mapsto t - \xi z$
for a suitable
$t \mapsto t - \xi z$
for a suitable
![]() $\xi \in \mathbb {C}$
, we may assume
$\xi \in \mathbb {C}$
, we may assume
![]() $\mathsf {p} \in H_t$
. Since
$\mathsf {p} \in H_t$
. Since
![]() $\mathsf {p} \in H_x \cap H_t \cap H_w$
,
$\mathsf {p} \in H_x \cap H_t \cap H_w$
,
![]() $\mathsf {p} \notin H_y$
and
$\mathsf {p} \notin H_y$
and
![]() $\mathsf {p} \ne \mathsf {p}_y$
, we have
$\mathsf {p} \ne \mathsf {p}_y$
, we have
![]() $\mathsf {p} = (0\!:\!1\!:\!\lambda \!:\!0\!:\!0)$
for a nonzero
$\mathsf {p} = (0\!:\!1\!:\!\lambda \!:\!0\!:\!0)$
for a nonzero
![]() $\lambda \in \mathbb {C}$
. We can write
$\lambda \in \mathbb {C}$
. We can write
![]() $\bar {h}_{12} = (z^2 - \lambda ^2 y^3)(z^2 - \mu y^3) + t e_9$
for some
$\bar {h}_{12} = (z^2 - \lambda ^2 y^3)(z^2 - \mu y^3) + t e_9$
for some
![]() $\mu \in \mathbb {C}$
and
$\mu \in \mathbb {C}$
and
![]() $e_9 = e_9 (y,z,t)$
. It is then straightforward to check that
$e_9 = e_9 (y,z,t)$
. It is then straightforward to check that
 $$\begin{align*}\frac{\partial^2 \bar{F}}{\partial z^2} (\mathsf{p}) = \frac{\partial^2 \bar{F}}{\partial z \partial y} (\mathsf{p}) = 0 \end{align*}$$
$$\begin{align*}\frac{\partial^2 \bar{F}}{\partial z^2} (\mathsf{p}) = \frac{\partial^2 \bar{F}}{\partial z \partial y} (\mathsf{p}) = 0 \end{align*}$$
is impossible, and this is a contradiction.
4.2.e.3 The family
 $\mathcal {F}_{39}$
$\mathcal {F}_{39}$
We have
![]() $g_{2 a_4} = g_{12}$
,
$g_{2 a_4} = g_{12}$
,
![]() $h_{3 a_4} = h_{18}$
, and we can write
$h_{3 a_4} = h_{18}$
, and we can write
where
![]() $\alpha , \lambda , \mu \in \mathbb {C}$
. By the quasi-smoothness of X, we have
$\alpha , \lambda , \mu \in \mathbb {C}$
. By the quasi-smoothness of X, we have
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
![]() $\mu \ne 0$
. We have
$\mu \ne 0$
. We have
 $$\begin{align*}\frac{\partial^2 \bar{F}}{\partial w \partial t} = \alpha z y, \quad \frac{\partial^2 \bar{F}}{\partial w \partial z} = \alpha t y + 3 \lambda z^2, \quad \frac{\partial^2 \bar{F}}{\partial w \partial y} = \alpha t z + 3 \mu y^2. \end{align*}$$
$$\begin{align*}\frac{\partial^2 \bar{F}}{\partial w \partial t} = \alpha z y, \quad \frac{\partial^2 \bar{F}}{\partial w \partial z} = \alpha t y + 3 \lambda z^2, \quad \frac{\partial^2 \bar{F}}{\partial w \partial y} = \alpha t z + 3 \mu y^2. \end{align*}$$
Suppose that
![]() $\alpha \ne 0$
, then, since both
$\alpha \ne 0$
, then, since both
![]() $\alpha z y$
and
$\alpha z y$
and
![]() $\alpha t y + 3 \lambda z^2$
vanish at
$\alpha t y + 3 \lambda z^2$
vanish at
![]() $\mathsf {p}$
and y does not vanish at
$\mathsf {p}$
and y does not vanish at
![]() $\mathsf {p}$
, we have
$\mathsf {p}$
, we have
![]() $\mathsf {p} \in H_z \cap H_t$
. It follows that
$\mathsf {p} \in H_z \cap H_t$
. It follows that
![]() $\mathsf {p} = \mathsf {p}_y$
. This is impossible since
$\mathsf {p} = \mathsf {p}_y$
. This is impossible since
![]() $\mathsf {p}_y$
is a singular point of X. Thus,
$\mathsf {p}_y$
is a singular point of X. Thus,
![]() $\alpha = 0$
. Then both
$\alpha = 0$
. Then both
![]() $3 \lambda z^2$
and
$3 \lambda z^2$
and
![]() $\alpha t z + 3 \mu y^2$
vanish at
$\alpha t z + 3 \mu y^2$
vanish at
![]() $\mathsf {p}$
, which implies that y vanishes at
$\mathsf {p}$
, which implies that y vanishes at
![]() $\mathsf {p}$
. This is a contradiction.
$\mathsf {p}$
. This is a contradiction.
4.2.e.4 The family
 $\mathcal {F}_{49}$
$\mathcal {F}_{49}$
We have
![]() $g_{2 a_4} = g_{14}, h_{3 a_4} = h_{21}$
, and we can write
$g_{2 a_4} = g_{14}, h_{3 a_4} = h_{21}$
, and we can write
where
![]() $\lambda , \alpha , \beta , \dots , \varepsilon \in \mathbb {C}$
. By the quasi-smoothness of X, we have
$\lambda , \alpha , \beta , \dots , \varepsilon \in \mathbb {C}$
. By the quasi-smoothness of X, we have
![]() $\lambda \ne 0$
, and by replacing t, we can assume that
$\lambda \ne 0$
, and by replacing t, we can assume that
![]() $\alpha = 0$
. Since
$\alpha = 0$
. Since
![]() $\mathsf {p} \in H_w$
,
$\mathsf {p} \in H_w$
,
![]() $\mathsf {p} \notin H_y$
and
$\mathsf {p} \notin H_y$
and
we have
![]() $\mathsf {p} \in H_t$
. Then
$\mathsf {p} \in H_t$
. Then
![]() $\mathsf {p} \notin H_z$
because otherwise
$\mathsf {p} \notin H_z$
because otherwise
![]() $\mathsf {p} = \mathsf {p}_y$
is a singular point and this is impossible. We have
$\mathsf {p} = \mathsf {p}_y$
is a singular point and this is impossible. We have
 $$\begin{align*}\frac{\partial^2 \bar{F}}{\partial z \partial y} = w \frac{\partial g_{14} (0,y,z,t)}{\partial z \partial y} + 6 \delta z^2 y, \end{align*}$$
$$\begin{align*}\frac{\partial^2 \bar{F}}{\partial z \partial y} = w \frac{\partial g_{14} (0,y,z,t)}{\partial z \partial y} + 6 \delta z^2 y, \end{align*}$$
which implies
![]() $\delta = 0$
. Then, by the quasi-smoothness of X, we have
$\delta = 0$
. Then, by the quasi-smoothness of X, we have
![]() $\varepsilon \ne 0$
. But the polynomial
$\varepsilon \ne 0$
. But the polynomial
 $$\begin{align*}\frac{\partial^2 \bar{F}}{\partial y^2} = w \frac{\partial^2 g_{14} (0,y,z,t)}{\partial y^2} + 20 \gamma t y^3 + 42 \varepsilon y^5 \end{align*}$$
$$\begin{align*}\frac{\partial^2 \bar{F}}{\partial y^2} = w \frac{\partial^2 g_{14} (0,y,z,t)}{\partial y^2} + 20 \gamma t y^3 + 42 \varepsilon y^5 \end{align*}$$
does not vanish at
![]() $\mathsf {p}$
. This is a contradiction.
$\mathsf {p}$
. This is a contradiction.
4.2.e.5 The family
 $\mathcal {F}_{59}$
$\mathcal {F}_{59}$
We have
![]() $g_{2 a_4} = g_{16}, h_{3 a_4} = h_{24}$
, and we can write
$g_{2 a_4} = g_{16}, h_{3 a_4} = h_{24}$
, and we can write
where
![]() $\lambda , \mu , \alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X, we have
$\lambda , \mu , \alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X, we have
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
![]() $\mu \ne 0$
. Since
$\mu \ne 0$
. Since
![]() $\mathsf {p} \notin H_y$
,
$\mathsf {p} \notin H_y$
,
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
we have
![]() $\mathsf {p} \in H_t$
. This is a contradiction since
$\mathsf {p} \in H_t$
. This is a contradiction since
![]() $\mathsf {p} \in H_x \cap H_t \cap H_w$
but
$\mathsf {p} \in H_x \cap H_t \cap H_w$
but
![]() $H_x \cap H_t \cap H_w$
consists of singular points.
$H_x \cap H_t \cap H_w$
consists of singular points.
4.2.e.6 The family
 $\mathcal {F}_{66}$
$\mathcal {F}_{66}$
We have
![]() $h_{3 a_4} = h_{27}$
, and we can write
$h_{3 a_4} = h_{27}$
, and we can write
where
![]() $\alpha , \lambda , \mu \in \mathbb {C}$
. By the quasi-smoothness of X, we have
$\alpha , \lambda , \mu \in \mathbb {C}$
. By the quasi-smoothness of X, we have
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
![]() $\mu \ne 0$
. We have
$\mu \ne 0$
. We have
 $$\begin{align*}\frac{\partial^2 \bar{F}}{\partial t \partial y} = w \frac{\partial^2 g_{18} (0,y,z,t)}{\partial t \partial y} + 4 \mu y^3. \end{align*}$$
$$\begin{align*}\frac{\partial^2 \bar{F}}{\partial t \partial y} = w \frac{\partial^2 g_{18} (0,y,z,t)}{\partial t \partial y} + 4 \mu y^3. \end{align*}$$
This is a contradiction since
![]() $\mathsf {p} \in H_w$
,
$\mathsf {p} \in H_w$
,
![]() $\mathsf {p} \notin H_y$
and
$\mathsf {p} \notin H_y$
and
![]() $\mu \ne 0$
.
$\mu \ne 0$
.
4.2.e.7 The family
 $\mathcal {F}_{84}$
$\mathcal {F}_{84}$
We have
where
![]() $\alpha , \beta , \lambda , \mu \in \mathbb {C}$
. By the quasi-smoothness of X, we have
$\alpha , \beta , \lambda , \mu \in \mathbb {C}$
. By the quasi-smoothness of X, we have
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
![]() $\mu \ne 0$
. We have
$\mu \ne 0$
. We have
which implies
![]() $\mathsf {p} \in H_t$
since
$\mathsf {p} \in H_t$
since
![]() $\mathsf {p} \in H_w$
and
$\mathsf {p} \in H_w$
and
![]() $\mu \ne 0$
. We have
$\mu \ne 0$
. We have
which implies
![]() $\mathsf {p} \in H_z$
since
$\mathsf {p} \in H_z$
since
![]() $\mathsf {p} \in H_t$
and
$\mathsf {p} \in H_t$
and
![]() $\lambda \ne 0$
. This shows
$\lambda \ne 0$
. This shows
![]() $\mathsf {p} = \mathsf {p}_y$
, and this is a contradiction since
$\mathsf {p} = \mathsf {p}_y$
, and this is a contradiction since
![]() $\mathsf {p}_y$
is a singular point.
$\mathsf {p}_y$
is a singular point.
Therefore, we derive a contradiction for all families and the proof of Claim 2 is completed.
4.3 Smooth points on
 $L_{xy}$
for families with
$L_{xy}$
for families with
 $a_1 < a_2$
, Part 1
$a_1 < a_2$
, Part 1
In this section and the next sections, we consider a member
of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
![]() $a_1 < a_2 \le a_3 \le a_4$
and prove
$a_1 < a_2 \le a_3 \le a_4$
and prove
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
for a smooth point
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for a smooth point
![]() $\mathsf {p}$
of X contained in the one-dimensional scheme
$\mathsf {p}$
of X contained in the one-dimensional scheme
![]() $L_{xy} := (x = y = 0) \cap X$
. We divide families indexed by
$L_{xy} := (x = y = 0) \cap X$
. We divide families indexed by
![]() $\mathsf {I} \setminus \mathsf {I}_1$
into two types:
$\mathsf {I} \setminus \mathsf {I}_1$
into two types:
-
• Families
 $\mathcal {F}_{\mathsf {i}}$
such that
$\mathcal {F}_{\mathsf {i}}$
such that
 $L_{xy} := (x = y = 0) \cap X$
is irreducible and reduced for any member X. These families are treated in the current Section 4.3.
$L_{xy} := (x = y = 0) \cap X$
is irreducible and reduced for any member X. These families are treated in the current Section 4.3. -
• Families
 $\mathcal {F}_{\mathsf {i}}$
such that
$\mathcal {F}_{\mathsf {i}}$
such that
 $L_{xy}$
is either reducible or nonreduced for some member X (see equation (4.1) for specific families). These families will be treated in Section 4.4.
$L_{xy}$
is either reducible or nonreduced for some member X (see equation (4.1) for specific families). These families will be treated in Section 4.4.
The objects of this section are members X such that the one-dimensional scheme
![]() $L_{xy} = (x = y = 0) \cap X$
is irreducible and reduced.
$L_{xy} = (x = y = 0) \cap X$
is irreducible and reduced.
Lemma 4.9. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
which satisfies
$\mathsf {i} \in \mathsf {I}$
which satisfies
![]() $a_1 < a_2$
and which is listed in Table 1
(resp. Table 2
). Then
$a_1 < a_2$
and which is listed in Table 1
(resp. Table 2
). Then
![]() $L_{xy}$
is an irreducible smooth curve (resp. irreducible and reduced curve which is smooth along
$L_{xy}$
is an irreducible smooth curve (resp. irreducible and reduced curve which is smooth along
![]() $L_{xy} \cap \operatorname {Sm} (X)$
).
$L_{xy} \cap \operatorname {Sm} (X)$
).
Proof. Let F be the defining polynomial of X, and set
![]() $d = \deg F$
. The scheme
$d = \deg F$
. The scheme
![]() $L_{xy}$
is isomorphic to the hypersurface in
$L_{xy}$
is isomorphic to the hypersurface in
![]() $\mathbb {P} (a_2,a_3,a_4)_{z, t, w}$
defined by the polynomial
$\mathbb {P} (a_2,a_3,a_4)_{z, t, w}$
defined by the polynomial
![]() $f := F (0,0,z,t,w)$
. We explain that f can be transformed into the polynomial given in Tables 1 and 2 by a suitable change of homogeneous coordinates.
$f := F (0,0,z,t,w)$
. We explain that f can be transformed into the polynomial given in Tables 1 and 2 by a suitable change of homogeneous coordinates.
Table 1
![]() $L_{xy}$
: Irreducible and smooth case.
$L_{xy}$
: Irreducible and smooth case.

Table 2
![]() $L_{xy}$
: Irreducible and singular case.
$L_{xy}$
: Irreducible and singular case.

Suppose
![]() $\mathsf {i} \notin \{11, 15, 16, 17, 21, 27, 34\}$
. Then there are only a few monomials of degree d in variables
$\mathsf {i} \notin \{11, 15, 16, 17, 21, 27, 34\}$
. Then there are only a few monomials of degree d in variables
![]() $z, t, w$
. We first simply express f as a linear combination of those monomials and then consider the following coordinate change.
$z, t, w$
. We first simply express f as a linear combination of those monomials and then consider the following coordinate change.
-
• Suppose
 $d = 2 a_4$
. In this case, f is quadratic with respect to w and we eliminate the term of the form
$d = 2 a_4$
. In this case, f is quadratic with respect to w and we eliminate the term of the form
 $w g (z, t)$
by replacing w suitably. Then we may assume
$w g (z, t)$
by replacing w suitably. Then we may assume
 $f = w^2 + h (z, t)$
for some quasi-homogeneous polynomial
$f = w^2 + h (z, t)$
for some quasi-homogeneous polynomial
 $h = h (z, t)$
of degree d.
$h = h (z, t)$
of degree d. -
• Suppose
 $d = 3 a_4$
. In this case, f is cubic with respect to w and we eliminate the term of the form
$d = 3 a_4$
. In this case, f is cubic with respect to w and we eliminate the term of the form
 $w^2 g (z, t)$
by replacing w suitably. Then we may assume
$w^2 g (z, t)$
by replacing w suitably. Then we may assume
 $f = w^3 + w h_1 (z, t) + h_2 (z,t)$
for some quasi-homogeneous polynomials
$f = w^3 + w h_1 (z, t) + h_2 (z,t)$
for some quasi-homogeneous polynomials
 $h_1 = h_1 (z, t), h = h_2 (z, t)$
of degrees
$h_1 = h_1 (z, t), h = h_2 (z, t)$
of degrees
 $d - a_4 = 2 a_4$
and
$d - a_4 = 2 a_4$
and
 $d = 3 a_4$
, respectively.
$d = 3 a_4$
, respectively.
After the above coordinate change, we observe that f is a linear combination of at most three distinct monomials and it is possible to make those coefficients
![]() $1$
by rescaling
$1$
by rescaling
![]() $z, t, w$
. The resulting polynomial is the one given in Tables 1 and 2. Once an explicit form of the defining polynomial is given, it is then easy to show that
$z, t, w$
. The resulting polynomial is the one given in Tables 1 and 2. Once an explicit form of the defining polynomial is given, it is then easy to show that
![]() $L_{xy}$
is entirely smooth or is smooth along
$L_{xy}$
is entirely smooth or is smooth along
![]() $L_{xy} \cap \operatorname {Sm} (X)$
.
$L_{xy} \cap \operatorname {Sm} (X)$
.
For
![]() $\mathsf {i} = \{11, 15, 16, 17, 21, 27, 34\}$
, the description of f is explained as follows.
$\mathsf {i} = \{11, 15, 16, 17, 21, 27, 34\}$
, the description of f is explained as follows.
-
• Suppose
 $\mathsf {i} = 11$
. In this case,
$\mathsf {i} = 11$
. In this case,
 $f = w^2 + h (z,t)$
, where h is a quintic form in
$f = w^2 + h (z,t)$
, where h is a quintic form in
 $z, t$
. The solutions of the equation
$z, t$
. The solutions of the equation
 $h = 0$
correspond to the five singular points of type
$h = 0$
correspond to the five singular points of type
 $\frac {1}{2} (1,1,1)$
. Thus, h does not have a multiple component and in particular
$\frac {1}{2} (1,1,1)$
. Thus, h does not have a multiple component and in particular
 $L_{xy}$
is smooth.
$L_{xy}$
is smooth. -
• Suppose
 $\mathsf {i} = 15$
. In this case,
$\mathsf {i} = 15$
. In this case,
 $f = w^2 + \alpha t^4 + \beta t^2 z^3 + \gamma z^6$
for some
$f = w^2 + \alpha t^4 + \beta t^2 z^3 + \gamma z^6$
for some
 $\alpha , \beta , \gamma \in \mathbb {C}$
. We have
$\alpha , \beta , \gamma \in \mathbb {C}$
. We have
 $\alpha \ne 0$
(resp.
$\alpha \ne 0$
(resp.
 $\gamma \ne 0$
) because otherwise X cannot be quasi-smooth at
$\gamma \ne 0$
) because otherwise X cannot be quasi-smooth at
 $\mathsf {p}_t$
(resp.
$\mathsf {p}_t$
(resp.
 $\mathsf {p}_z$
). Replacing t and rescaling z, we may assume
$\mathsf {p}_z$
). Replacing t and rescaling z, we may assume
 $\alpha = 1$
,
$\alpha = 1$
,
 $\beta = 0$
and
$\beta = 0$
and
 $\gamma = 1$
, and we obtain the desired form
$\gamma = 1$
, and we obtain the desired form
 $f = w^2 + t^4 + z^6$
. It is easy to see that
$f = w^2 + t^4 + z^6$
. It is easy to see that
 $L_{xy}$
is smooth.
$L_{xy}$
is smooth. -
• Suppose
 $\mathsf {i} = 16$
. In this case,
$\mathsf {i} = 16$
. In this case,
 $f = w^2 z + h (z, t)$
, where
$f = w^2 z + h (z, t)$
, where
 $h = \alpha t^3 + \beta t^2 z^2 + \gamma t z^4 + \delta z^6$
for some
$h = \alpha t^3 + \beta t^2 z^2 + \gamma t z^4 + \delta z^6$
for some
 $\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X, we have
$\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X, we have
 $\alpha \ne 0$
. Moreover, the solutions of
$\alpha \ne 0$
. Moreover, the solutions of
 $h (z, t) = 0$
correspond to three singular points of type
$h (z, t) = 0$
correspond to three singular points of type
 $\frac {1}{2} (1,1,1)$
. Thus,
$\frac {1}{2} (1,1,1)$
. Thus,
 $h (z, t)$
does not have a multiple component and in particular
$h (z, t)$
does not have a multiple component and in particular
 $L_{xy}$
is smooth.
$L_{xy}$
is smooth. -
• Suppose
 $\mathsf {i} = 17$
. In this case,
$\mathsf {i} = 17$
. In this case,
 $f = c (t, w) + \alpha z^4$
, where
$f = c (t, w) + \alpha z^4$
, where
 $\alpha \in \mathbb {C}$
and
$\alpha \in \mathbb {C}$
and
 $c (t, w)$
is a cubic form in
$c (t, w)$
is a cubic form in
 $t, w$
. By the quasi-smoothness of X, we have
$t, w$
. By the quasi-smoothness of X, we have
 $\alpha \ne 0$
and we may assume
$\alpha \ne 0$
and we may assume
 $\alpha = 1$
by rescaling z. Moreover, the solutions of
$\alpha = 1$
by rescaling z. Moreover, the solutions of
 $c (t, w) = 0$
correspond to three singular points of type
$c (t, w) = 0$
correspond to three singular points of type
 $\frac {1}{4} (1,1,3)$
. Thus,
$\frac {1}{4} (1,1,3)$
. Thus,
 $c (t, w)$
does not have a multiple component and in particular
$c (t, w)$
does not have a multiple component and in particular
 $L_{xy}$
is smooth.
$L_{xy}$
is smooth. -
• Suppose
 $\mathsf {i} = 21$
. In this case,
$\mathsf {i} = 21$
. In this case,
 $f = w^2 + h (z, t)$
, where
$f = w^2 + h (z, t)$
, where
 $h = \alpha t^3 z + \beta t^2 z^3 + \gamma t z^5 + \delta z^7$
for some
$h = \alpha t^3 z + \beta t^2 z^3 + \gamma t z^5 + \delta z^7$
for some
 $\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X at
$\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X at
 $\mathsf {p}_t$
, we have
$\mathsf {p}_t$
, we have
 $t^3 z \in F$
, that is,
$t^3 z \in F$
, that is,
 $\alpha \ne 0$
. Moreover, the solutions of
$\alpha \ne 0$
. Moreover, the solutions of
 $\alpha t^3 + \beta t^2 z^2 + \gamma t z^4 + \delta z^6 = 0$
correspond to the three singular points of type
$\alpha t^3 + \beta t^2 z^2 + \gamma t z^4 + \delta z^6 = 0$
correspond to the three singular points of type
 $\frac {1}{2} (1,1,1)$
. Thus, h does not have a multiple component and in particular
$\frac {1}{2} (1,1,1)$
. Thus, h does not have a multiple component and in particular
 $L_{xy}$
is smooth.
$L_{xy}$
is smooth. -
• Suppose
 $\mathsf {i} = 27$
. In this case,
$\mathsf {i} = 27$
. In this case,
 $f = c (t, w) + \alpha z^5$
, where
$f = c (t, w) + \alpha z^5$
, where
 $\alpha \in \mathbb {C}$
and
$\alpha \in \mathbb {C}$
and
 $c (t, w)$
is a cubic form in
$c (t, w)$
is a cubic form in
 $t, w$
. By the same arguments as in the case of
$t, w$
. By the same arguments as in the case of
 $\mathsf {i} = 17$
,
$\mathsf {i} = 17$
,
 $c (t, w)$
does not have a multiple component and we may assume
$c (t, w)$
does not have a multiple component and we may assume
 $\alpha =1$
. Thus,
$\alpha =1$
. Thus,
 $L_{xy}$
is smooth.
$L_{xy}$
is smooth. -
• Suppose
 $\mathsf {i} = 34$
. In this case,
$\mathsf {i} = 34$
. In this case,
 $f = w^2 + h (z, t)$
, where
$f = w^2 + h (z, t)$
, where
 $h = \alpha t^3 + \beta t^2 z^3 + \gamma t z^6 + \delta z^9$
for some
$h = \alpha t^3 + \beta t^2 z^3 + \gamma t z^6 + \delta z^9$
for some
 $\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X, we have
$\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. By the quasi-smoothness of X, we have
 $t^3 \in F$
, that is,
$t^3 \in F$
, that is,
 $\alpha \ne 0$
. Moreover, the solutions of
$\alpha \ne 0$
. Moreover, the solutions of
 $h = 0$
correspond to three singular points of type
$h = 0$
correspond to three singular points of type
 $\frac {1}{2} (1,1,1)$
. Thus, h does not have a multiple component and in particular
$\frac {1}{2} (1,1,1)$
. Thus, h does not have a multiple component and in particular
 $L_{xy}$
is smooth.
$L_{xy}$
is smooth.
This completes the proof.
Proposition 4.10. Let
![]() $X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4)$
,
$X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4)$
,
![]() $a_1 \le a_2 \le a_3 \le a_4$
be a member of a family
$a_1 \le a_2 \le a_3 \le a_4$
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
which satisfies
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
which satisfies
![]() $a_1 < a_2$
and which is listed in Tables 1 and 2. Then
$a_1 < a_2$
and which is listed in Tables 1 and 2. Then
for any smooth point
![]() $\mathsf {p}$
of X contained in
$\mathsf {p}$
of X contained in
![]() $L_{xy}$
.
$L_{xy}$
.
Proof. Take a point
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. Let
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |a_1 A|$
be general members. By Lemma 4.9,
$T \in |a_1 A|$
be general members. By Lemma 4.9,
![]() $L_{xy}$
is an irreducible and reduced curve, and we have
$L_{xy}$
is an irreducible and reduced curve, and we have
![]() $S \cdot T = L_{xy}$
. Note that
$S \cdot T = L_{xy}$
. Note that
![]() $L_{xy}$
is quasi-smooth at
$L_{xy}$
is quasi-smooth at
![]() $\mathsf {p}$
, and we have
$\mathsf {p}$
, and we have
![]() $\operatorname {mult}_{\mathsf {p}} (L_{xy}) = 1$
. By Lemma 3.8, S is quasi-smooth at
$\operatorname {mult}_{\mathsf {p}} (L_{xy}) = 1$
. By Lemma 3.8, S is quasi-smooth at
![]() $\mathsf {p}$
. It follows that
$\mathsf {p}$
. It follows that
![]() $\operatorname {lct}_{\mathsf {p}} (X;S) = 1$
. By Lemma 3.17, we have
$\operatorname {lct}_{\mathsf {p}} (X;S) = 1$
. By Lemma 3.17, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X;S), \ \frac{a_1}{\operatorname{mult}_{\mathsf{p}} (L_{xy})}, \ \frac{1}{a_1 (A^3)} \right\} = 1 \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X;S), \ \frac{a_1}{\operatorname{mult}_{\mathsf{p}} (L_{xy})}, \ \frac{1}{a_1 (A^3)} \right\} = 1 \end{align*}$$
since
![]() $1/a_1 (A^3)> 1$
by Lemma 2.29.
$1/a_1 (A^3)> 1$
by Lemma 2.29.
4.4 Smooth points on
 $L_{xy}$
for families with
$L_{xy}$
for families with
 $a_1 < a_2$
, Part 2
$a_1 < a_2$
, Part 2
In this section, we consider families
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
such that
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
such that
![]() $L_{xy}$
is either irreducible or reduced for some member X. Specifically, these families consist of families
$L_{xy}$
is either irreducible or reduced for some member X. Specifically, these families consist of families
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
 $$ \begin{align} \mathsf{i} \in \{ & 7, 9, 12, 13, 15, 20, 23, 24, 25, 29, 30, 31, 32, \nonumber\\ & 33, 37, 38, 39, 40, 42, 49, 50, 52, 58, 60, 63, 64\}, \end{align} $$
$$ \begin{align} \mathsf{i} \in \{ & 7, 9, 12, 13, 15, 20, 23, 24, 25, 29, 30, 31, 32, \nonumber\\ & 33, 37, 38, 39, 40, 42, 49, 50, 52, 58, 60, 63, 64\}, \end{align} $$
and the aim of this section is to prove the following.
Proposition 4.11. Let
![]() $X = X_d \subset \mathbb {P} (1,a_1,a_2,a_3,a_4)$
,
$X = X_d \subset \mathbb {P} (1,a_1,a_2,a_3,a_4)$
,
![]() $a_1 \le a_2 \le a_3 \le a_4$
, be a member of a family
$a_1 \le a_2 \le a_3 \le a_4$
, be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
which satisfies
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
which satisfies
![]() $a_1 < a_2$
and which is not listed in Tables 1 and 2. Then
$a_1 < a_2$
and which is not listed in Tables 1 and 2. Then
for any smooth point
![]() $\mathsf {p}$
of X contained in
$\mathsf {p}$
of X contained in
![]() $L_{xy}$
.
$L_{xy}$
.
The proof of Proposition 4.11 will be completed in Section 4.4.b by considering each family separately and by case-by-case arguments. Those arguments form several patterns, and we describe them in Section 4.4.a.
4.4.a General arguments
In this subsection, let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Throughout this subsection, we assume that
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Throughout this subsection, we assume that
![]() $a < b_i$
for
$a < b_i$
for
![]() $i = 1, 2, 3$
. Note that we do not assume
$i = 1, 2, 3$
. Note that we do not assume
![]() $b_1 \le b_2 \le b_3$
. As before, we denote by
$b_1 \le b_2 \le b_3$
. As before, we denote by
![]() $F = F (x, y, z_1, z_2, z_3)$
the defining polynomial of X, and we set
$F = F (x, y, z_1, z_2, z_3)$
the defining polynomial of X, and we set
![]() $A := -K_X$
.
$A := -K_X$
.
The following very elementary lemma will be used several times.
Lemma 4.12. Let
![]() $a, e_1, e_2, e_3$
be positive integers such that
$a, e_1, e_2, e_3$
be positive integers such that
![]() $a < e_i$
for
$a < e_i$
for
![]() $i = 1, 2, 3$
and
$i = 1, 2, 3$
and
![]() $\gcd \{e_1, e_2, e_3\} = 1$
, and let
$\gcd \{e_1, e_2, e_3\} = 1$
, and let
![]() $\lambda \ge 1$
be a number. Then the following inequalities hold.
$\lambda \ge 1$
be a number. Then the following inequalities hold.
-
1.
 $\dfrac {1 + e_2 + e_3}{e_1 e_2 e_3} \le \dfrac {1}{2}$
.
$\dfrac {1 + e_2 + e_3}{e_1 e_2 e_3} \le \dfrac {1}{2}$
. -
2.
 $\dfrac {a + e_2 + e_3}{e_1 e_2 e_3} + \dfrac {\lambda }{a} \le \dfrac {1}{2} + \lambda $
.
$\dfrac {a + e_2 + e_3}{e_1 e_2 e_3} + \dfrac {\lambda }{a} \le \dfrac {1}{2} + \lambda $
. -
3.
 $a (a + e_2 + e_3) < e_1 e_2 e_3$
.
$a (a + e_2 + e_3) < e_1 e_2 e_3$
.
Proof. In view of the assumption
![]() $\gcd \{e_1, e_2, e_3\} = 1$
, it is easy to see that
$\gcd \{e_1, e_2, e_3\} = 1$
, it is easy to see that
attains its maximum when
![]() $(e_1, e_2, e_3) = (2, 2, 3)$
, which implies (1).
$(e_1, e_2, e_3) = (2, 2, 3)$
, which implies (1).
It is also easy to see that
viewed as a function of a, attains its maximum when
![]() $a = 1$
since
$a = 1$
since
![]() $1 \le a \le \sqrt {\lambda e_1 e_2 e_3}$
. Combining this with (1), the inequality (2) follows.
$1 \le a \le \sqrt {\lambda e_1 e_2 e_3}$
. Combining this with (1), the inequality (2) follows.
By the assumption, we have
![]() $e_1 e_2 \ge (a+1)^2$
. Hence, we have
$e_1 e_2 \ge (a+1)^2$
. Hence, we have
 $$ \begin{align*} e_1 e_2 e_3 - a (a + e_2 + e_3) &= e_3 (e_1 e_2 - a) - a^2 - a e_2 \\ & \ge e_3 (a^2 + a + 1) - a^2 - a e_2 \\ &= a^2 (e_3 - 1) + a (e_3 - e_2) + e_3 \\ &> 0. \end{align*} $$
$$ \begin{align*} e_1 e_2 e_3 - a (a + e_2 + e_3) &= e_3 (e_1 e_2 - a) - a^2 - a e_2 \\ & \ge e_3 (a^2 + a + 1) - a^2 - a e_2 \\ &= a^2 (e_3 - 1) + a (e_3 - e_2) + e_3 \\ &> 0. \end{align*} $$
This proves (3).
Lemma 4.13. Suppose that
![]() $L_{xy} := (x = y = 0)_X$
is an irreducible and reduced curve which is smooth along
$L_{xy} := (x = y = 0)_X$
is an irreducible and reduced curve which is smooth along
![]() $L_{xy} \cap \operatorname {Sm} (X)$
. Then
$L_{xy} \cap \operatorname {Sm} (X)$
. Then
for any
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
Proof. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |a A|$
be general members. Then we have
$T \in |a A|$
be general members. Then we have
![]() $S \cap T = L_{xy}$
. Take any point
$S \cap T = L_{xy}$
. Take any point
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. By Lemma 3.8, S is smooth at
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. By Lemma 3.8, S is smooth at
![]() $\mathsf {p}$
. It follows that
$\mathsf {p}$
. It follows that
![]() $\operatorname {mult}_{\mathsf {p}} (L_{xy}) = 1$
and
$\operatorname {mult}_{\mathsf {p}} (L_{xy}) = 1$
and
![]() $\operatorname {lct}_{\mathsf {p}} (X;S) = 1$
. By Lemma 3.17, we have
$\operatorname {lct}_{\mathsf {p}} (X;S) = 1$
. By Lemma 3.17, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X;S), \ \frac{1}{\operatorname{mult}_{\mathsf{p}} (L_{xy})}, \ \frac{1}{a (A^3)} \right\} = 1 \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X;S), \ \frac{1}{\operatorname{mult}_{\mathsf{p}} (L_{xy})}, \ \frac{1}{a (A^3)} \right\} = 1 \end{align*}$$
since
![]() $1/a (A^3)> 1$
by Lemma 2.29.
$1/a (A^3)> 1$
by Lemma 2.29.
Lemma 4.14. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |aA|$
be general members. Suppose that the following assertions are satisfied.
$T \in |aA|$
be general members. Suppose that the following assertions are satisfied.
-
1.
 $T|_S = \Gamma + \Delta $
, where
$T|_S = \Gamma + \Delta $
, where
 $\Gamma = (x = y = z_1 = 0)$
is a quasi-line and
$\Gamma = (x = y = z_1 = 0)$
is a quasi-line and
 $\Delta $
is an irreducible and reduced curve which is quasi-smooth along
$\Delta $
is an irreducible and reduced curve which is quasi-smooth along
 $\Delta \cap \operatorname {Sm} (X)$
.
$\Delta \cap \operatorname {Sm} (X)$
. -
2. S is quasi-smooth along
 $\Gamma \cap \Delta $
.
$\Gamma \cap \Delta $
. -
3.
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_{z_2}, \mathsf {p}_{z_3}\}$
.
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_{z_2}, \mathsf {p}_{z_3}\}$
.
Then
for any point
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
Proof. By assumptions (1), (2) and Lemma 3.9, S is quasi-smooth along
![]() $\Gamma $
.
$\Gamma $
.
Claim 3. The intersection matrix
![]() $M = M (\Gamma , \Delta )$
satisfies the condition
$M = M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 3.
By the assumption (3) and the quasi-smoothness of S, we see that
![]() $\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_{z_2}, \mathsf {p}_{z_3}\}$
and
$\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_{z_2}, \mathsf {p}_{z_3}\}$
and
![]() $\mathsf {p}_{z_i} \in S$
is a cyclic quotient singularity of index
$\mathsf {p}_{z_i} \in S$
is a cyclic quotient singularity of index
![]() $b_i$
for
$b_i$
for
![]() $i = 2, 3$
. By Remark 3.10, we have
$i = 2, 3$
. By Remark 3.10, we have
By taking the intersection number of
![]() $T|_S = \Gamma + \Delta $
and
$T|_S = \Gamma + \Delta $
and
![]() $\Gamma $
, we have
$\Gamma $
, we have
Note that we have
and then by taking the intersection number of
![]() $T|_S = \Gamma + \Delta $
and
$T|_S = \Gamma + \Delta $
and
![]() $\Delta $
, we have
$\Delta $
, we have
Finally, we have
 $$ \begin{align*} \det M &= \frac{b_2 + b_3}{b_2 b_3} \cdot \frac{(b_1-a)(a + b_2 + b_3)}{b_1 b_2 b_3} - \frac{(a + b_2 + b_3)^2}{b_2^2 b_3^2} \\ &= - \frac{a (a + b_2 + b_3)(b_1 + b_2 + b_3)}{b_1 b_2^2 b_3^2} < 0. \end{align*} $$
$$ \begin{align*} \det M &= \frac{b_2 + b_3}{b_2 b_3} \cdot \frac{(b_1-a)(a + b_2 + b_3)}{b_1 b_2 b_3} - \frac{(a + b_2 + b_3)^2}{b_2^2 b_3^2} \\ &= - \frac{a (a + b_2 + b_3)(b_1 + b_2 + b_3)}{b_1 b_2^2 b_3^2} < 0. \end{align*} $$
It follows that M satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Let
![]() $\mathsf {p} \in (\Gamma \setminus \Delta ) \cap \operatorname {Sm} (X)$
be a point. By Lemma 3.7, S is a normal surface. It is easy to check that
$\mathsf {p} \in (\Gamma \setminus \Delta ) \cap \operatorname {Sm} (X)$
be a point. By Lemma 3.7, S is a normal surface. It is easy to check that
![]() $a \deg \Gamma = a/(b_2 b_3) \le 1$
and that X, S and
$a \deg \Gamma = a/(b_2 b_3) \le 1$
and that X, S and
![]() $\Gamma $
are smooth at
$\Gamma $
are smooth at
![]() $\mathsf {p}$
. Thus, we can apply Lemma 3.21 and we conclude
$\mathsf {p}$
. Thus, we can apply Lemma 3.21 and we conclude
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{a (A^3) + \frac{1}{a} - \deg \Gamma} \right\} = \min \left\{ 1, \ \frac{1}{\frac{a + b_2 + b_3}{b_1 b_2 b_3} + \frac{1}{a}} \right\} \ge \frac{2}{3}, \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{a (A^3) + \frac{1}{a} - \deg \Gamma} \right\} = \min \left\{ 1, \ \frac{1}{\frac{a + b_2 + b_3}{b_1 b_2 b_3} + \frac{1}{a}} \right\} \ge \frac{2}{3}, \end{align*}$$
where the last inequality follows from Lemma 4.12.
Let
![]() $\mathsf {p} \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
be a point. Note that
$\mathsf {p} \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
be a point. Note that
![]() $\Delta $
is smooth at
$\Delta $
is smooth at
![]() $\mathsf {p}$
since it is quasi-smooth at
$\mathsf {p}$
since it is quasi-smooth at
![]() $\mathsf {p}$
by the assumption (1). We have
$\mathsf {p}$
by the assumption (1). We have
 $$\begin{align*}a \deg \Delta = a \left( a (A^3) - \frac{1}{b_2 b_3} \right) = \frac{a (a + b_2 + b_3)}{b_1 b_2 b_3} < 1 \end{align*}$$
$$\begin{align*}a \deg \Delta = a \left( a (A^3) - \frac{1}{b_2 b_3} \right) = \frac{a (a + b_2 + b_3)}{b_1 b_2 b_3} < 1 \end{align*}$$
by Lemma 4.12. Note that we have
since
![]() $1 \le a < b_i$
. Thus, we can apply Lemma 3.21 and conclude
$1 \le a < b_i$
. Thus, we can apply Lemma 3.21 and conclude
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{a (A^3) + \frac{1}{a} - \deg \Delta} \right\} \ge \frac{4}{5}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{a (A^3) + \frac{1}{a} - \deg \Delta} \right\} \ge \frac{4}{5}. \end{align*}$$
Finally, let
![]() $\mathsf {p} \in (\Gamma \cap \Delta ) \cap \operatorname {Sm} (X)$
be a point. Note that S is smooth at
$\mathsf {p} \in (\Gamma \cap \Delta ) \cap \operatorname {Sm} (X)$
be a point. Note that S is smooth at
![]() $\mathsf {p}$
by the assumption (2), and we have
$\mathsf {p}$
by the assumption (2), and we have
where the former inequality is obvious and the latter follows from Lemma 4.12. Thus, we can apply Lemma 3.23 and conclude that
Therefore, the proof is completed.
Remark 4.15. Let the notation and assumption as in Lemma 4.14. Assume in addition that
![]() $a \ge 2$
and
$a \ge 2$
and
![]() $\Gamma \cap \Delta \subset \operatorname {Sing} (X)$
. Then
$\Gamma \cap \Delta \subset \operatorname {Sing} (X)$
. Then
for any
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
Indeed, since
![]() $\Gamma \cap \Delta \subset \operatorname {Sing} (X)$
, we have
$\Gamma \cap \Delta \subset \operatorname {Sing} (X)$
, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{1, \ \frac{1}{\frac{a + b_2 + b_3}{b_1 b_2 b_3} + \frac{1}{a}}, \ \frac{4}{5} \right\} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{1, \ \frac{1}{\frac{a + b_2 + b_3}{b_1 b_2 b_3} + \frac{1}{a}}, \ \frac{4}{5} \right\} \end{align*}$$
by the proof of Lemma 4.14. Since
![]() $2 \le a < \sqrt {b_1 b_2 b_3}$
and
$2 \le a < \sqrt {b_1 b_2 b_3}$
and
![]() $a < b_i$
for
$a < b_i$
for
![]() $i = 1, 2, 3$
, we have
$i = 1, 2, 3$
, we have
This proves the desired inequality.
Lemma 4.16. Suppose that
![]() $b_1, b_2, b_3$
are mutually coprime and
$b_1, b_2, b_3$
are mutually coprime and
![]() $a \in \{1, 2\}$
. Suppose in addition that F can be written as
$a \in \{1, 2\}$
. Suppose in addition that F can be written as
where
![]() $m \in \{2, 3\}$
and
$m \in \{2, 3\}$
and
![]() $f_1, f_2 \in \mathbb {C} [z_1, z_2], g \in [x, y, z_1, z_2, z_3]$
are quasi-homogeneous polynomials satisfying the following properties.
$f_1, f_2 \in \mathbb {C} [z_1, z_2], g \in [x, y, z_1, z_2, z_3]$
are quasi-homogeneous polynomials satisfying the following properties.
-
1.
 $\deg F = b_1 b_2 + a$
.
$\deg F = b_1 b_2 + a$
. -
2. g is contained in the ideal
 $(x, y) \cap (x, y, z_3)^2 \subset \mathbb {C} [x, y, z_1, z_2, z_3]$
.
$(x, y) \cap (x, y, z_3)^2 \subset \mathbb {C} [x, y, z_1, z_2, z_3]$
.
Then
for any point
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
Proof. We have
![]() $d = m b_3 + b_2$
since
$d = m b_3 + b_2$
since
![]() $z_3^m z_2 \in F$
, and combining this with
$z_3^m z_2 \in F$
, and combining this with
![]() $d = a + b_1 + b_2 + b_3$
, we have
$d = a + b_1 + b_2 + b_3$
, we have
Claim 4. We can assume
 $$ \begin{align} F = \begin{cases} z_2^{b_1} x - z_1^{b_2} y + z_3^m z_2 + g, & \text{if}\ a = 1, \\ z_1^k z_2^l x + (z_1^{b_2} - z_2^{b_1}) y + z_3^m z_2 + g, & \text{if}\ a = 2 \\ \end{cases} \end{align} $$
$$ \begin{align} F = \begin{cases} z_2^{b_1} x - z_1^{b_2} y + z_3^m z_2 + g, & \text{if}\ a = 1, \\ z_1^k z_2^l x + (z_1^{b_2} - z_2^{b_1}) y + z_3^m z_2 + g, & \text{if}\ a = 2 \\ \end{cases} \end{align} $$
after replacing x and y suitably, where k and l are nonnegative integers.
Proof of Claim 4.
Suppose
![]() $a = 1$
. Then, since
$a = 1$
. Then, since
![]() $\deg f_1 = \deg f_2 = b_1 b_2$
, we can write
$\deg f_1 = \deg f_2 = b_1 b_2$
, we can write
where
![]() $\ell _1, \ell _2$
are linear forms in
$\ell _1, \ell _2$
are linear forms in
![]() $x, y$
. We see that
$x, y$
. We see that
![]() $\ell _1, \ell _2$
are linearly independent because otherwise we can write
$\ell _1, \ell _2$
are linearly independent because otherwise we can write
![]() $\ell _2 = \alpha \ell _1$
for some nonzero
$\ell _2 = \alpha \ell _1$
for some nonzero
![]() $\alpha \in \mathbb {C}$
and X is not quasi-smooth along
$\alpha \in \mathbb {C}$
and X is not quasi-smooth along
This is a contradiction. Thus,
![]() $\ell _1, \ell _2$
are linearly independent and we may assume
$\ell _1, \ell _2$
are linearly independent and we may assume
![]() $\ell _1 = x$
and
$\ell _1 = x$
and
![]() $\ell _2 = y$
, as desired.
$\ell _2 = y$
, as desired.
Suppose
![]() $a = 2$
. We have
$a = 2$
. We have
![]() $f_2 = \alpha z_1^{b_2} + \beta z_2^{b_1}$
for some
$f_2 = \alpha z_1^{b_2} + \beta z_2^{b_1}$
for some
![]() $\alpha , \beta \in \mathbb {C}$
since
$\alpha , \beta \in \mathbb {C}$
since
![]() $\deg f_2 = b_1 b_2$
. By the quasi-smooth of X at
$\deg f_2 = b_1 b_2$
. By the quasi-smooth of X at
![]() $\mathsf {p}_z, \mathsf {p}_t$
, we have
$\mathsf {p}_z, \mathsf {p}_t$
, we have
![]() $\alpha , \beta \ne 0$
, and thus we may assume
$\alpha , \beta \ne 0$
, and thus we may assume
![]() $\alpha =1$
,
$\alpha =1$
,
![]() $\beta = -1$
by rescaling
$\beta = -1$
by rescaling
![]() $z_1, z_2$
. We see that the equation
$z_1, z_2$
. We see that the equation
![]() $f_1 (z_1, z_2) = f_2 (z_1, z_2) = 0$
on variables
$f_1 (z_1, z_2) = f_2 (z_1, z_2) = 0$
on variables
![]() $z_1, z_2$
has only trivial solution because otherwise X is not quasi-smooth along the nonempty set
$z_1, z_2$
has only trivial solution because otherwise X is not quasi-smooth along the nonempty set
which is impossible. This implies that
![]() $f_1 \ne 0$
as a polynomial, and there exists a monomial
$f_1 \ne 0$
as a polynomial, and there exists a monomial
![]() $z_1^k z_2^l$
of degree
$z_1^k z_2^l$
of degree
![]() $b_1 b_2 + 1$
. Since
$b_1 b_2 + 1$
. Since
![]() $b_1$
is coprime to
$b_1$
is coprime to
![]() $b_2$
,
$b_2$
,
![]() $z_1^k z_2^l$
is the unique monomial of degree
$z_1^k z_2^l$
is the unique monomial of degree
![]() $b_1 b_2 + 1$
in variables
$b_1 b_2 + 1$
in variables
![]() $z_1, z_2$
. Thus, we have
$z_1, z_2$
. Thus, we have
![]() $f_2 = \gamma z_1^k z_2^l$
for some nonzero
$f_2 = \gamma z_1^k z_2^l$
for some nonzero
![]() $\gamma \in \mathbb {C}$
. Rescaling x, we may assume
$\gamma \in \mathbb {C}$
. Rescaling x, we may assume
![]() $\gamma = 1$
, and the claim is proved.
$\gamma = 1$
, and the claim is proved.
We continue the proof of Lemma 4.16. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |a A|$
be general members. We have
$T \in |a A|$
be general members. We have
where
since
![]() $F (0,0,z,t,w) = z_3^m z_2$
. We see that
$F (0,0,z,t,w) = z_3^m z_2$
. We see that
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
are quasi-lines of degree
$\Delta $
are quasi-lines of degree
![]() $1/b_1 b_3$
and
$1/b_1 b_3$
and
![]() $1/b_1 b_2$
, respectively, and
$1/b_1 b_2$
, respectively, and
![]() $\Gamma \cap \Delta = \{\mathsf {p}_{z_1}\} \subset \operatorname {Sing} (X)$
. We see that S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_{z_1}\} \subset \operatorname {Sing} (X)$
. We see that S is quasi-smooth at
![]() $\mathsf {p}_{z_1}$
since
$\mathsf {p}_{z_1}$
since
![]() $z_1^{b_2} y \in F$
. By Lemma 3.9, S is quasi-smooth along
$z_1^{b_2} y \in F$
. By Lemma 3.9, S is quasi-smooth along
![]() $\Gamma $
and the pair
$\Gamma $
and the pair
![]() $(S, \Gamma )$
is plt.
$(S, \Gamma )$
is plt.
Claim 5. The intersection matrix
![]() $M = M (\Gamma , \Delta )$
satisfies the condition
$M = M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 5.
We see that d is not divisible by
![]() $b_1$
or
$b_1$
or
![]() $b_3$
since
$b_3$
since
![]() $d = b_1 b_2 + a = m b_3 + b_2$
,
$d = b_1 b_2 + a = m b_3 + b_2$
,
![]() $a < b_1$
and
$a < b_1$
and
![]() $b_2$
is coprime to
$b_2$
is coprime to
![]() $b_3$
. It follows that
$b_3$
. It follows that
![]() $\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_{z_1}, \mathsf {p}_{z_3}\}$
and
$\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_{z_1}, \mathsf {p}_{z_3}\}$
and
![]() $\mathsf {p}_{z_i} \in S$
is a cyclic quotient singularity of index
$\mathsf {p}_{z_i} \in S$
is a cyclic quotient singularity of index
![]() $b_i$
for
$b_i$
for
![]() $i = 1, 3$
. By Remark 3.10, we have
$i = 1, 3$
. By Remark 3.10, we have
By taking intersection number of
![]() $T|_S = \Gamma + m \Delta $
and
$T|_S = \Gamma + m \Delta $
and
![]() $\Gamma $
, we obtain
$\Gamma $
, we obtain
Similarly, by taking intersection number of
![]() $T|_S$
and
$T|_S$
and
![]() $\Delta $
, we obtain
$\Delta $
, we obtain
where the second equality follows from equation (4.2). Finally, we have
 $$\begin{align*}\det M = \frac{b_1 + b_3}{b_1 b_3} \cdot \frac{b_2 - a}{m b_1 b_2} - \frac{1}{b_1^2} = - \frac{a (b_1 + b_2 + b_3)}{b_1^2 b_2 b_3} < 0, \end{align*}$$
$$\begin{align*}\det M = \frac{b_1 + b_3}{b_1 b_3} \cdot \frac{b_2 - a}{m b_1 b_2} - \frac{1}{b_1^2} = - \frac{a (b_1 + b_2 + b_3)}{b_1^2 b_2 b_3} < 0, \end{align*}$$
where the second equality follows from equation (4.2). It follows that M satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Let
![]() $\mathsf {p} \in (\Gamma \setminus \Delta ) \cap \operatorname {Sm} (X)$
. We see that
$\mathsf {p} \in (\Gamma \setminus \Delta ) \cap \operatorname {Sm} (X)$
. We see that
![]() $X, S$
and
$X, S$
and
![]() $\Gamma $
are smooth at
$\Gamma $
are smooth at
![]() $\mathsf {p}$
, and it is easy to see
$\mathsf {p}$
, and it is easy to see
![]() $a \deg \Gamma = a/(b_1 b_3) < 1$
. Hence, we can apply Lemma 3.21 and we have
$a \deg \Gamma = a/(b_1 b_3) < 1$
. Hence, we can apply Lemma 3.21 and we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{a (A^3) + \frac{1}{a} - \deg \Gamma} \right\} = \min \left\{ 1, \ \frac{1}{\frac{a + b_1 + b_3}{b_1 b_2 b_3} + \frac{1}{a}} \right\} \ge \frac{2}{3}, \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{a (A^3) + \frac{1}{a} - \deg \Gamma} \right\} = \min \left\{ 1, \ \frac{1}{\frac{a + b_1 + b_3}{b_1 b_2 b_3} + \frac{1}{a}} \right\} \ge \frac{2}{3}, \end{align*}$$
where the last inequality follows from Lemma 4.12.
It remains to consider
![]() $\mathsf {p} \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
since
$\mathsf {p} \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
since
![]() $\Gamma \cap \Delta = \{\mathsf {p}_{z_1}\} \subset \operatorname {Sing} (X)$
. We first consider the case when
$\Gamma \cap \Delta = \{\mathsf {p}_{z_1}\} \subset \operatorname {Sing} (X)$
. We first consider the case when
![]() $a = 2$
. In this case,
$a = 2$
. In this case,
![]() $S = H_x$
is quasi-smooth along
$S = H_x$
is quasi-smooth along
![]() $\Delta \setminus \{\mathsf {q}\}$
, where
$\Delta \setminus \{\mathsf {q}\}$
, where
![]() $\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
, and S has a double point at
$\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
, and S has a double point at
![]() $\mathsf {q}$
. We have
$\mathsf {q}$
. We have
![]() $\operatorname {mult}_{\mathsf {p}} (\Delta ) = 1$
, and
$\operatorname {mult}_{\mathsf {p}} (\Delta ) = 1$
, and
![]() $a \deg \Delta = a/(b_1 b_2) < 1$
. Thus, we can apply Lemma 3.22 and conclude
$a \deg \Delta = a/(b_1 b_2) < 1$
. Thus, we can apply Lemma 3.22 and conclude
 $$ \begin{align*} \alpha_{\mathsf{p}} (X) &\ge \min \left\{ \frac{2}{\operatorname{mult}_{\mathsf{p}} (S)}, \ \frac{\operatorname{mult}_{\mathsf{p}} (S)}{2 (A^3) + \frac{m}{2} - m \deg \Delta} \right\} \\ &= \min \left\{ \frac{2}{\operatorname{mult}_{\mathsf{p}} (S)}, \ \frac{\operatorname{mult}_{\mathsf{p}} (S)}{\frac{1}{b_1 b_3} + \frac{m}{2}} \right\} \\ &\ge \min \left\{ 1, \ \frac{1}{\frac{1}{12} + \frac{3}{2}} \right\} \\ &= \frac{12}{19} \end{align*} $$
$$ \begin{align*} \alpha_{\mathsf{p}} (X) &\ge \min \left\{ \frac{2}{\operatorname{mult}_{\mathsf{p}} (S)}, \ \frac{\operatorname{mult}_{\mathsf{p}} (S)}{2 (A^3) + \frac{m}{2} - m \deg \Delta} \right\} \\ &= \min \left\{ \frac{2}{\operatorname{mult}_{\mathsf{p}} (S)}, \ \frac{\operatorname{mult}_{\mathsf{p}} (S)}{\frac{1}{b_1 b_3} + \frac{m}{2}} \right\} \\ &\ge \min \left\{ 1, \ \frac{1}{\frac{1}{12} + \frac{3}{2}} \right\} \\ &= \frac{12}{19} \end{align*} $$
since
![]() $1/(b_1 b_3) \le 1/12$
,
$1/(b_1 b_3) \le 1/12$
,
![]() $m \in \{2, 3\}$
and
$m \in \{2, 3\}$
and
![]() $\operatorname {mult}_{\mathsf {p}} (S) \in \{1, 2\}$
.
$\operatorname {mult}_{\mathsf {p}} (S) \in \{1, 2\}$
.
Suppose
![]() $a = 1$
. We set
$a = 1$
. We set
![]() $S' = (z_3 = 0) \cap X \in |b_3 A|$
. For
$S' = (z_3 = 0) \cap X \in |b_3 A|$
. For
![]() $\lambda \in \mathbb {C}$
, we set
$\lambda \in \mathbb {C}$
, we set
![]() $T^{\prime }_{\lambda } = (y - \lambda x = 0) \cap X \in |A|$
. We can write
$T^{\prime }_{\lambda } = (y - \lambda x = 0) \cap X \in |A|$
. We can write
![]() $g (x, \lambda x, z_1, z_2, 0) = x^2 h_{\lambda }$
for some
$g (x, \lambda x, z_1, z_2, 0) = x^2 h_{\lambda }$
for some
![]() $h_{\lambda } = h_{\lambda } (x,z_1,z_2)$
since
$h_{\lambda } = h_{\lambda } (x,z_1,z_2)$
since
![]() $g \in (x,y,z_3)^2$
. In view of equation (4.3), we have
$g \in (x,y,z_3)^2$
. In view of equation (4.3), we have
where
The polynomial
![]() $\phi _{\lambda }$
is irreducible for any nonzero
$\phi _{\lambda }$
is irreducible for any nonzero
![]() $\lambda \in \mathbb {C}$
. We have
$\lambda \in \mathbb {C}$
. We have
where
is an irreducible and reduced curve. We have
![]() $\Delta \cap \Xi _{\lambda } = \{\mathsf {q}_{\lambda }\} \subset \operatorname {Sm} (X)$
, where
$\Delta \cap \Xi _{\lambda } = \{\mathsf {q}_{\lambda }\} \subset \operatorname {Sm} (X)$
, where
![]() $\mathsf {q}_{\lambda } = (0\!:\!0\!:\!\sqrt [b_2]{\lambda }\!:\!1\!:\!0)$
. It is easy to see that
$\mathsf {q}_{\lambda } = (0\!:\!0\!:\!\sqrt [b_2]{\lambda }\!:\!1\!:\!0)$
. It is easy to see that
![]() $S'$
is quasi-smooth at
$S'$
is quasi-smooth at
![]() $\mathsf {q}_{\lambda }$
. Hence,
$\mathsf {q}_{\lambda }$
. Hence,
![]() $S'$
is quasi-smooth along
$S'$
is quasi-smooth along
![]() $\Delta $
by Lemma 3.9.
$\Delta $
by Lemma 3.9.
Claim 6. The intersection matrix
![]() $M' = M (\Delta , \Xi _{\lambda })$
satisfies the condition
$M' = M (\Delta , \Xi _{\lambda })$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 6.
By Remark 3.10, we have
By taking intersection number of
![]() $T^{\prime }_{\lambda }|_{S'} = \Delta + \Xi _{\lambda }$
and
$T^{\prime }_{\lambda }|_{S'} = \Delta + \Xi _{\lambda }$
and
![]() $\Delta $
, we obtain
$\Delta $
, we obtain
By taking intersection number of
![]() $T^{\prime }_{\lambda }|_{S'}$
and
$T^{\prime }_{\lambda }|_{S'}$
and
![]() $\Xi _{\lambda }$
, we obtain
$\Xi _{\lambda }$
, we obtain
It is then obvious that
![]() $\det M' < 0$
and the proof is completed.
$\det M' < 0$
and the proof is completed.
Now, we take any point
![]() $\mathsf {p} \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
, and then we can choose a nonzero
$\mathsf {p} \in (\Delta \setminus \Gamma ) \cap \operatorname {Sm} (X)$
, and then we can choose a nonzero
![]() $\lambda \in \mathbb {C}$
so that
$\lambda \in \mathbb {C}$
so that
![]() $\mathsf {p} \ne \mathsf {q}_{\lambda }$
. By Lemma 3.8,
$\mathsf {p} \ne \mathsf {q}_{\lambda }$
. By Lemma 3.8,
![]() $S'$
is smooth at
$S'$
is smooth at
![]() $\mathsf {p}$
since
$\mathsf {p}$
since
![]() $S' \cap T^{\prime }_{\lambda }$
is smooth at
$S' \cap T^{\prime }_{\lambda }$
is smooth at
![]() $\mathsf {p}$
. It is easy to see that
$\mathsf {p}$
. It is easy to see that
![]() $\deg \Delta = 1/(b_1 b_2) < 1$
. Thus, we can apply Lemma 3.21 and conclude
$\deg \Delta = 1/(b_1 b_2) < 1$
. Thus, we can apply Lemma 3.21 and conclude
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ b_3, \ \frac{1}{b_3 (A^3) + 1 - \deg \Delta} \right\} = \min \left\{ b_3, \ \frac{1}{2} \right\} = \frac{1}{2}, \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ b_3, \ \frac{1}{b_3 (A^3) + 1 - \deg \Delta} \right\} = \min \left\{ b_3, \ \frac{1}{2} \right\} = \frac{1}{2}, \end{align*}$$
where the first equality follows since
This completes the proof.
Lemma 4.17. Suppose that
![]() $b_1, b_2, b_3$
are mutually coprime and
$b_1, b_2, b_3$
are mutually coprime and
![]() $a \in \{1, 2, 3\}$
. Suppose in addition that F can be written as
$a \in \{1, 2, 3\}$
. Suppose in addition that F can be written as
where
![]() $m \ge 2, e_1, e_2$
are positive integers and
$m \ge 2, e_1, e_2$
are positive integers and
![]() $g \in \mathbb {C} [x, y, z_1 z_2, z_3]$
is a homogeneous polynomial satisfying the following properties.
$g \in \mathbb {C} [x, y, z_1 z_2, z_3]$
is a homogeneous polynomial satisfying the following properties.
-
1. If
 $a \ge 2$
, then
$a \ge 2$
, then
 $m \le 2 a$
.
$m \le 2 a$
. -
2. If
 $a = 1$
, then
$a = 1$
, then
 $e_1 \le b_2$
.
$e_1 \le b_2$
. -
3. g is a homogeneous polynomial contained in the ideal
 $(x, y) \cap (x, y, z_3)^2 \subset \mathbb {C} [x, y, z_1, z_2, z_3]$
.
$(x, y) \cap (x, y, z_3)^2 \subset \mathbb {C} [x, y, z_1, z_2, z_3]$
.
Then
for any
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
Proof. We first consider the case where
![]() $a \ge 2$
. Let
$a \ge 2$
. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |a A|$
be general members. We have
$T \in |a A|$
be general members. We have
where
is a quasi-line of degree
![]() $1/(b_1 b_2)$
. Let
$1/(b_1 b_2)$
. Let
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. It is straightforward to check that S is smooth at
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. It is straightforward to check that S is smooth at
![]() $\mathsf {p}$
, which implies
$\mathsf {p}$
, which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{a} S) = a$
. By Lemma 3.17, we have
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{a} S) = a$
. By Lemma 3.17, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ a, \ \frac{a}{m}, \ \frac{1}{a (A^3)} \right\} \ge \frac{1}{2} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ a, \ \frac{a}{m}, \ \frac{1}{a (A^3)} \right\} \ge \frac{1}{2} \end{align*}$$
since
![]() $a/m \ge 1/2$
and
$a/m \ge 1/2$
and
![]() $1/(a (A^3))> 1$
by the assumption (1) and Lemma 2.29, respectively.
$1/(a (A^3))> 1$
by the assumption (1) and Lemma 2.29, respectively.
In the following, we assume
![]() $a = 1$
. We set
$a = 1$
. We set
![]() $S' = (z_3 = 0) \cap X \in |b_3 A|$
and
$S' = (z_3 = 0) \cap X \in |b_3 A|$
and
![]() $\Gamma = (x = y = z_3 = 0) \subset S'$
. We have
$\Gamma = (x = y = z_3 = 0) \subset S'$
. We have
![]() $L_{xy} = \Gamma $
set-theoretically. For
$L_{xy} = \Gamma $
set-theoretically. For
![]() $\lambda \in \mathbb {C}$
, we set
$\lambda \in \mathbb {C}$
, we set
![]() $T^{\prime }_{\lambda } = (y - \lambda x = 0) \cap X \in |aA|$
. We can write
$T^{\prime }_{\lambda } = (y - \lambda x = 0) \cap X \in |aA|$
. We can write
where
![]() $h_{\lambda }$
is a quasi-homogeneous polynomial in variables
$h_{\lambda }$
is a quasi-homogeneous polynomial in variables
![]() $x, z_1, z_2$
since
$x, z_1, z_2$
since
![]() $g \in (x, y, z_3)^2$
. We have
$g \in (x, y, z_3)^2$
. We have
Claim 7. The quasi-homogeneous polynomial
is irreducible for any
![]() $\lambda \in \mathbb {C} \setminus \{0\}$
.
$\lambda \in \mathbb {C} \setminus \{0\}$
.
Proof of Claim 7.
We assume
![]() $\lambda \ne 0$
. If
$\lambda \ne 0$
. If
![]() $\phi _{\lambda }$
is a reducible polynomial, then we can write
$\phi _{\lambda }$
is a reducible polynomial, then we can write
for some
![]() $c_1, c_2 \in \mathbb {Z}_{\ge 0}$
with
$c_1, c_2 \in \mathbb {Z}_{\ge 0}$
with
![]() $c_1 \le e_1$
and
$c_1 \le e_1$
and
![]() $0 < c_2 < e_2$
, and nonzero
$0 < c_2 < e_2$
, and nonzero
![]() $\alpha , \beta \in \mathbb {C}$
such that
$\alpha , \beta \in \mathbb {C}$
such that
![]() $\alpha \beta = \lambda $
. We have
$\alpha \beta = \lambda $
. We have
![]() $c_2 b_2 = c_1 b_1$
. Since
$c_2 b_2 = c_1 b_1$
. Since
![]() $b_1$
is coprime to
$b_1$
is coprime to
![]() $b_2$
, we see that
$b_2$
, we see that
![]() $c_1$
is divisible by
$c_1$
is divisible by
![]() $b_2$
. This implies
$b_2$
. This implies
![]() $c_1 = e_1 = b_2$
since
$c_1 = e_1 = b_2$
since
![]() $c_1 \le e_1 \le b_2$
. By the equality
$c_1 \le e_1 \le b_2$
. By the equality
![]() $e_2 b_2 = e_1 b_1$
, we have
$e_2 b_2 = e_1 b_1$
, we have
![]() $c_2 = e_2 = b_1$
. This is a contradiction since
$c_2 = e_2 = b_1$
. This is a contradiction since
![]() $c_2 < e_2$
. Therefore,
$c_2 < e_2$
. Therefore,
![]() $\phi _{\lambda }$
is irreducible for
$\phi _{\lambda }$
is irreducible for
![]() $\lambda \ne 0$
.
$\lambda \ne 0$
.
We continue the proof of Lemma 4.17. By Claim 7, we have
where
is an irreducible and reduced curve for any
![]() $\lambda \in \mathbb {C} \setminus \{0\}$
. We have
$\lambda \in \mathbb {C} \setminus \{0\}$
. We have
![]() $\Gamma \cap \Delta _{\lambda } = \{\mathsf {q}_{\lambda }\}$
, where
$\Gamma \cap \Delta _{\lambda } = \{\mathsf {q}_{\lambda }\}$
, where
It is easy to check that
![]() $S'$
is quasi-smooth at
$S'$
is quasi-smooth at
![]() $\mathsf {q}_{\lambda }$
. By Lemma 3.9,
$\mathsf {q}_{\lambda }$
. By Lemma 3.9,
![]() $S'$
is quasi-smooth along
$S'$
is quasi-smooth along
![]() $\Gamma $
and the pair
$\Gamma $
and the pair
![]() $(S', \Gamma )$
is plt.
$(S', \Gamma )$
is plt.
Claim 8. The intersection matrix
![]() $M' = M (\Gamma , \Xi ^{\prime }_{\lambda })$
satisfies the condition
$M' = M (\Gamma , \Xi ^{\prime }_{\lambda })$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 8.
We see that
![]() $\operatorname {Sing}_{\Gamma } (S') = \{\mathsf {p}_{z_1}, \mathsf {p}_{z_2}\}$
and
$\operatorname {Sing}_{\Gamma } (S') = \{\mathsf {p}_{z_1}, \mathsf {p}_{z_2}\}$
and
![]() $\mathsf {p}_{z_i} \in S'$
is a cyclic quotient singular point of index
$\mathsf {p}_{z_i} \in S'$
is a cyclic quotient singular point of index
![]() $b_i$
for
$b_i$
for
![]() $i = 1, 2$
. By the same computation as in Claim 6, we have
$i = 1, 2$
. By the same computation as in Claim 6, we have
 $$ \begin{align*} (\Gamma^2)_{S'} &= - \frac{b_1 + b_2 + b_3 -1}{b_1 b_2} < 0, \\ (\Gamma \cdot \Delta_{\lambda})_{S'} &= \frac{b_1 + b_2 + b_3}{b_1 b_2}> 0, \\ (\Delta_{\lambda}^2)_{S'} &= 0. \end{align*} $$
$$ \begin{align*} (\Gamma^2)_{S'} &= - \frac{b_1 + b_2 + b_3 -1}{b_1 b_2} < 0, \\ (\Gamma \cdot \Delta_{\lambda})_{S'} &= \frac{b_1 + b_2 + b_3}{b_1 b_2}> 0, \\ (\Delta_{\lambda}^2)_{S'} &= 0. \end{align*} $$
It is then easy to see that
![]() $\det M' < 0$
, which shows that
$\det M' < 0$
, which shows that
![]() $M'$
satisfies
$M'$
satisfies
![]() $(\star )$
.
$(\star )$
.
Now, take a point
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X) = \Gamma \cap \operatorname {Sm} (X)$
. We choose and fix a general
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X) = \Gamma \cap \operatorname {Sm} (X)$
. We choose and fix a general
![]() $\lambda \in \mathbb {C}$
so that
$\lambda \in \mathbb {C}$
so that
![]() $\Delta _{\lambda }$
is irreducible and
$\Delta _{\lambda }$
is irreducible and
![]() $\mathsf {q}_{\lambda } \ne \mathsf {p}$
. Then
$\mathsf {q}_{\lambda } \ne \mathsf {p}$
. Then
![]() $\mathsf {p} \in (\Gamma \setminus \Xi _{\lambda }) \cap \operatorname {Sm} (X)$
. We see that X,
$\mathsf {p} \in (\Gamma \setminus \Xi _{\lambda }) \cap \operatorname {Sm} (X)$
. We see that X,
![]() $S'$
and
$S'$
and
![]() $\Gamma $
are smooth at
$\Gamma $
are smooth at
![]() $\mathsf {p}$
, and
$\mathsf {p}$
, and
![]() $\deg \Gamma = 1/(b_1 b_2) < 1$
. Thus, we can apply Lemma 3.21 and conclude
$\deg \Gamma = 1/(b_1 b_2) < 1$
. Thus, we can apply Lemma 3.21 and conclude
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ b_3, \ \frac{1}{b_3 (A^3) + 1 - \deg \Gamma} \right\} = \min \left\{ b_3, \ \frac{1}{\frac{e_1}{b_2} + 1} \right\} \ge \frac{1}{2}, \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ b_3, \ \frac{1}{b_3 (A^3) + 1 - \deg \Gamma} \right\} = \min \left\{ b_3, \ \frac{1}{\frac{e_1}{b_2} + 1} \right\} \ge \frac{1}{2}, \end{align*}$$
where the last inequality follows from the assumption (2). This completes the proof.
Lemma 4.18. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |a A|$
be general members. Suppose that
$T \in |a A|$
be general members. Suppose that
where
![]() $\Gamma = (x = y = z_3 = 0)$
. Then
$\Gamma = (x = y = z_3 = 0)$
. Then
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; S), \ \frac{a}{2}, \ \frac{1}{a (A^3)} \right\} \ge \frac{1}{2} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} (X; S), \ \frac{a}{2}, \ \frac{1}{a (A^3)} \right\} \ge \frac{1}{2} \end{align*}$$
for any point
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
Proof. Let
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. We have
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. We have
![]() $\operatorname {mult}_{\mathsf {p}} (\Gamma ) = 1$
, and the first inequality follows from Lemma 3.17. We have
$\operatorname {mult}_{\mathsf {p}} (\Gamma ) = 1$
, and the first inequality follows from Lemma 3.17. We have
![]() $\operatorname {mult}_{\mathsf {p}} (S) \le \operatorname {mult}_{\mathsf {p}} (S \cdot T) = 2$
, which implies
$\operatorname {mult}_{\mathsf {p}} (S) \le \operatorname {mult}_{\mathsf {p}} (S \cdot T) = 2$
, which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X; S) \ge 1/2$
. Thus, the second inequality in the statement follows since
$\operatorname {lct}_{\mathsf {p}} (X; S) \ge 1/2$
. Thus, the second inequality in the statement follows since
![]() $1/(a (A^3))> 1$
by Lemma 2.29.
$1/(a (A^3))> 1$
by Lemma 2.29.
4.4.b Proof of Proposition 4.11
This subsection is entirely devoted to the proof of Proposition 4.11.
Let
![]() $X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4)$
,
$X = X_d \subset \mathbb {P} (1, a_1, a_2, a_3, a_4)$
,
![]() $a_1 \le \cdots \le a_4$
, be a member of a family
$a_1 \le \cdots \le a_4$
, be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfying
![]() $a_1 < a_2$
. Let
$a_1 < a_2$
. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |a_1 A|$
are general members so that their scheme-theoretic intersection
$T \in |a_1 A|$
are general members so that their scheme-theoretic intersection
![]() $S \cap T$
coincides with
$S \cap T$
coincides with
![]() $L_{xy}$
. Note that S is a normal surface by Lemma 3.7 and T is a quasi-hyperplane section on X. We set
$L_{xy}$
. Note that S is a normal surface by Lemma 3.7 and T is a quasi-hyperplane section on X. We set
so that
![]() $L_{xy}$
is isomorphic to the hypersurface in
$L_{xy}$
is isomorphic to the hypersurface in
![]() $\mathbb {P} (a_2, a_3, a_4)_{z, t, w}$
defined by
$\mathbb {P} (a_2, a_3, a_4)_{z, t, w}$
defined by
![]() $f = 0$
.
$f = 0$
.
4.4.b.1 The family
 $\mathcal {F}_7$
$\mathcal {F}_7$
We have
where
![]() $\ell , h$
are linear and quadratic forms in
$\ell , h$
are linear and quadratic forms in
![]() $z, t$
, respectively. By the quasi-smoothness of X, we have
$z, t$
, respectively. By the quasi-smoothness of X, we have
![]() $\ell (z, t) \ne 0$
, and
$\ell (z, t) \ne 0$
, and
![]() $h (z,t)$
does not have a multiple component.
$h (z,t)$
does not have a multiple component.
-
• Case (i): h is not divisible by
 $\ell $
. In this case,
$\ell $
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii): h is divisible by
 $\ell $
. Replacing z and t, we may assume
$\ell $
. Replacing z and t, we may assume
 $\ell (z,t) = z$
. We can write
$\ell (z,t) = z$
. We can write
 $h = z c (z,t)$
, where
$h = z c (z,t)$
, where
 $c (z,t)$
is a cubic form in
$c (z,t)$
is a cubic form in
 $z, t$
. Note that
$z, t$
. Note that
 $c (z,t)$
is not divisible by z since
$c (z,t)$
is not divisible by z since
 $h (z,t) = z c (z,t)$
does not have a multiple component, and we can assume
$h (z,t) = z c (z,t)$
does not have a multiple component, and we can assume
 $c (0,t) = - t^3$
by rescaling t. In this case,
$c (0,t) = - t^3$
by rescaling t. In this case,
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + c (z,t) = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + c (z,t) = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible quasi-smooth curve since
$\Delta $
is an irreducible quasi-smooth curve since
 $c (z, t)$
does not have a multiple component. We have
$c (z, t)$
does not have a multiple component. We have
 $\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
$\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
 $\mathsf {q} = (0\!:\!0\!:\!0\!:\!1\!:\!1) \in \operatorname {Sm} (X)$
. We claim that S is quasi-smooth (and hence smooth) at
$\mathsf {q} = (0\!:\!0\!:\!0\!:\!1\!:\!1) \in \operatorname {Sm} (X)$
. We claim that S is quasi-smooth (and hence smooth) at
 $\mathsf {q}$
. We have
$\mathsf {q}$
. We have
 $(\partial F/\partial z) (\mathsf {q}) = (\partial F/\partial t)(\mathsf {q}) = (\partial F/\partial w) (\mathsf {q}) = 0$
. Hence, at least one of
$(\partial F/\partial z) (\mathsf {q}) = (\partial F/\partial t)(\mathsf {q}) = (\partial F/\partial w) (\mathsf {q}) = 0$
. Hence, at least one of
 $(\partial F/\partial x)(\mathsf {q})$
and
$(\partial F/\partial x)(\mathsf {q})$
and
 $(\partial F/\partial y)(\mathsf {q})$
is nonzero by the quasi-smoothness of X. By choosing x and y, we may assume that
$(\partial F/\partial y)(\mathsf {q})$
is nonzero by the quasi-smoothness of X. By choosing x and y, we may assume that
 $S = H_x$
and
$S = H_x$
and
 $(\partial F/\partial y)(\mathsf {q}) \ne 0$
. It then follows that S is quasi-smooth at
$(\partial F/\partial y)(\mathsf {q}) \ne 0$
. It then follows that S is quasi-smooth at
 $\mathsf {q}$
. Finally, we have
$\mathsf {q}$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Thus, the assumptions of Lemma 4.14 are satisfied and we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Thus, the assumptions of Lemma 4.14 are satisfied and we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $L_{xy} \cap \operatorname {Sm} (X)$
.
$L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.2 The family
 $\mathcal {F}_9$
$\mathcal {F}_9$
We have
where
![]() $\ell = \ell (t,w)$
and
$\ell = \ell (t,w)$
and
![]() $c = c (t,w)$
are linear and cubic forms in
$c = c (t,w)$
are linear and cubic forms in
![]() $t, w$
, respectively. By the quasi-smoothness of X,
$t, w$
, respectively. By the quasi-smoothness of X,
![]() $c (t, w)$
does not have a multiple component.
$c (t, w)$
does not have a multiple component.
-
• Case (i):
 $\ell (t,w) \ne 0$
and
$\ell (t,w) \ne 0$
and
 $c (t,w)$
is not divisible by
$c (t,w)$
is not divisible by
 $\ell (t,w)$
. In this case,
$\ell (t,w)$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\ell (t, w) \ne 0$
and
$\ell (t, w) \ne 0$
and
 $c (t, w)$
is divisible by
$c (t, w)$
is divisible by
 $\ell (t,w)$
. We write
$\ell (t,w)$
. We write
 $c (t,w) = \ell (t, w) q (t, w)$
, where
$c (t,w) = \ell (t, w) q (t, w)$
, where
 $q (t,w)$
is a quadratic form in
$q (t,w)$
is a quadratic form in
 $t, w$
which is not divisible by
$t, w$
which is not divisible by
 $\ell (t,w)$
. Replacing t and w, we may assume
$\ell (t,w)$
. Replacing t and w, we may assume
 $\ell = t$
, that is,
$\ell = t$
, that is,
 $f = w (q (t,w) + z^3)$
. We may also assume
$f = w (q (t,w) + z^3)$
. We may also assume
 $q (0,w) = - w^2$
since
$q (0,w) = - w^2$
since
 $c (t,w)$
does not have a multiple component. In this case,
$c (t,w)$
does not have a multiple component. In this case,
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = q + z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = q + z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible quasi-smooth curve since
$\Delta $
is an irreducible quasi-smooth curve since
 $q (t,w)$
is not a square of a linear form. We have
$q (t,w)$
is not a square of a linear form. We have
 $\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
$\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
 $\mathsf {q} = (0\!:\!0\!:\!1\!:\!0\!:\!1) \in \operatorname {Sm} (X)$
. By the similar argument as in Case (ii) of Section 4.4.b, we can conclude that S is quasi-smooth at
$\mathsf {q} = (0\!:\!0\!:\!1\!:\!0\!:\!1) \in \operatorname {Sm} (X)$
. By the similar argument as in Case (ii) of Section 4.4.b, we can conclude that S is quasi-smooth at
 $\mathsf {q}$
. Finally, we have
$\mathsf {q}$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $L_{xy} \cap \operatorname {Sm} (X)$
.
$L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\ell (t,w) = 0$
. In this case,
$\ell (t,w) = 0$
. In this case,
 $f = \ell _1 \ell _2 \ell _3$
, where
$f = \ell _1 \ell _2 \ell _3$
, where
 $\ell _1, \ell _2, \ell _3$
are linear forms in
$\ell _1, \ell _2, \ell _3$
are linear forms in
 $t, w$
which are not mutually proportional, and
$t, w$
which are not mutually proportional, and
 $T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
, where
$T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
, where
 $\Gamma _1, \Gamma _2, \Gamma _3$
are as follows.
$\Gamma _1, \Gamma _2, \Gamma _3$
are as follows.-
– For
 $i = 1, 2, 3$
,
$i = 1, 2, 3$
,
 $\Gamma _i = (x = y = \ell _i = 0)$
is a quasi-line and
$\Gamma _i = (x = y = \ell _i = 0)$
is a quasi-line and
 $\operatorname {Sing}_{\Gamma _i} = \{1 \times \frac {1}{2} (1, 1), 1 \times \frac {1}{3} (1, 2)\}$
.
$\operatorname {Sing}_{\Gamma _i} = \{1 \times \frac {1}{2} (1, 1), 1 \times \frac {1}{3} (1, 2)\}$
. -
–
 $\Gamma _i \cap \Gamma _j = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
for
$\Gamma _i \cap \Gamma _j = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
for
 $i \ne j$
. Moreover, S is quasi-smooth at
$i \ne j$
. Moreover, S is quasi-smooth at
 $\mathsf {p}_z$
since
$\mathsf {p}_z$
since
 $S \in |A|$
is general.
$S \in |A|$
is general.
We can compute
 $(\Gamma _i^2)_S = -5/6$
by the method explained in Remark 3.10 and then we have
$(\Gamma _i^2)_S = -5/6$
by the method explained in Remark 3.10 and then we have
 $(\Gamma _i \cdot \Gamma _j)_S = 1/2$
for
$(\Gamma _i \cdot \Gamma _j)_S = 1/2$
for
 $i \ne j$
by considering
$i \ne j$
by considering
 $(\Gamma _l \cdot T|_S)_S$
for
$(\Gamma _l \cdot T|_S)_S$
for
 $l = 1, 2, 3$
. Thus, the intersection matrix of
$l = 1, 2, 3$
. Thus, the intersection matrix of
 $\Gamma _1, \Gamma _2, \Gamma _3$
is given by and it satisfies the condition
$\Gamma _1, \Gamma _2, \Gamma _3$
is given by and it satisfies the condition $$\begin{align*}((\Gamma_i \cdot \Gamma_j)_S) = \begin{pmatrix} - \frac{5}{6} & \frac{1}{2} & \frac{1}{2} \\[1mm] \frac{1}{2} & - \frac{5}{6} & \frac{1}{2} \\[1mm] \frac{1}{2} & \frac{1}{2} & - \frac{5}{6} \end{pmatrix} \end{align*}$$
$$\begin{align*}((\Gamma_i \cdot \Gamma_j)_S) = \begin{pmatrix} - \frac{5}{6} & \frac{1}{2} & \frac{1}{2} \\[1mm] \frac{1}{2} & - \frac{5}{6} & \frac{1}{2} \\[1mm] \frac{1}{2} & \frac{1}{2} & - \frac{5}{6} \end{pmatrix} \end{align*}$$
 $(\star )$
. By Lemma 3.21, we have for any
$(\star )$
. By Lemma 3.21, we have for any $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{1, \frac{3}{4} \right\} = \frac{3}{4} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{1, \frac{3}{4} \right\} = \frac{3}{4} \end{align*}$$
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
4.4.b.3 The family
 $\mathcal {F}_{12}$
$\mathcal {F}_{12}$
We have
![]() $w^2 z \in F$
by the quasi-smoothness of X at
$w^2 z \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
. Hence, rescaling w, we can write
$\mathsf {p}_w$
. Hence, rescaling w, we can write
![]() $f = w^2 z + \alpha w t^2 + \lambda w z^3 + \beta t^2 z^2 + \mu z^5$
, where
$f = w^2 z + \alpha w t^2 + \lambda w z^3 + \beta t^2 z^2 + \mu z^5$
, where
![]() $\alpha , \beta , \lambda , \mu \in \mathbb {C}$
. We can eliminate the monomial
$\alpha , \beta , \lambda , \mu \in \mathbb {C}$
. We can eliminate the monomial
![]() $z^5$
by replacing w and hence we assume
$z^5$
by replacing w and hence we assume
![]() $\mu = 0$
. Then, by the quasi-smoothness of X at
$\mu = 0$
. Then, by the quasi-smoothness of X at
![]() $\mathsf {p}_z$
, we have
$\mathsf {p}_z$
, we have
![]() $\lambda \ne 0$
and we may assume
$\lambda \ne 0$
and we may assume
![]() $\lambda = -1$
by rescaling z. Thus, we can write
$\lambda = -1$
by rescaling z. Thus, we can write
-
• Case (i):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $\beta \ne 0$
. In this case,
$\beta \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha \ne 0$
and either
$\alpha \ne 0$
and either
 $\beta = 0$
or
$\beta = 0$
or
 $\beta = \alpha $
. When
$\beta = \alpha $
. When
 $\beta = \alpha $
, we replace
$\beta = \alpha $
, we replace
 $w \mapsto w - z^2$
and
$w \mapsto w - z^2$
and
 $z \mapsto - z$
. After this replacement, we may assume
$z \mapsto - z$
. After this replacement, we may assume
 $\beta = 0$
. Moreover, we may assume
$\beta = 0$
. Moreover, we may assume
 $\alpha = 1$
by rescaling t. Then we have
$\alpha = 1$
by rescaling t. Then we have
 $f = w (w z + t^2 - z^3)$
and
$f = w (w z + t^2 - z^3)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w z + t^2 - z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w z + t^2 - z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible quasi-smooth curve. We have
$\Delta $
is an irreducible quasi-smooth curve. We have
 $\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
$\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
 $\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in \operatorname {Sm} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
$\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in \operatorname {Sm} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
 $\mathsf {q}$
. Finally, we have
$\mathsf {q}$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. Rescaling t, we may assume
$\beta \ne 0$
. Rescaling t, we may assume
 $\beta = 1$
. Then we have
$\beta = 1$
. Then we have
 $f = z (w^2 + w z^2 + t^2 z)$
and
$f = z (w^2 + w z^2 + t^2 z)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + w z^2 + t^2 z = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + w z^2 + t^2 z = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible quasi-smooth curve. We have
$\Delta $
is an irreducible quasi-smooth curve. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. By the similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. By the similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
 $\mathsf {p}_t$
. Finally, we have
$\mathsf {p}_t$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iv):
 $\alpha = \beta = 0$
. In this case,
$\alpha = \beta = 0$
. In this case,
 $f = z w (w + z^2)$
and
$f = z w (w + z^2)$
and
 $T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
, where
$T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
, where
 $\Gamma _1, \Gamma _2, \Gamma _3$
are as follows.
$\Gamma _1, \Gamma _2, \Gamma _3$
are as follows.-
–
 $\Gamma _1 = (x = y = z = 0)$
is a quasi-line of degree
$\Gamma _1 = (x = y = z = 0)$
is a quasi-line of degree
 $1/12$
and
$1/12$
and
 $\operatorname {Sing}_{\Gamma _1} (S) = \{1 \times \frac {1}{3} (1,3), 1 \times \frac {1}{4} (1,3)\}$
.
$\operatorname {Sing}_{\Gamma _1} (S) = \{1 \times \frac {1}{3} (1,3), 1 \times \frac {1}{4} (1,3)\}$
. -
–
 $\Gamma _2 = (x = y = w = 0)$
and
$\Gamma _2 = (x = y = w = 0)$
and
 $\Gamma _3 = (x = y = w + z^2 = 0)$
are quasi-lines of degree
$\Gamma _3 = (x = y = w + z^2 = 0)$
are quasi-lines of degree
 $1/6$
and
$1/6$
and
 $\operatorname {Sing}_{\Gamma _i} (S) = \{1 \times \frac {1}{2} (1,1), \frac {1}{3} (1,2)\}$
for
$\operatorname {Sing}_{\Gamma _i} (S) = \{1 \times \frac {1}{2} (1,1), \frac {1}{3} (1,2)\}$
for
 $i = 2, 3$
.
$i = 2, 3$
. -
– For
 $1 \le i < j \le 3$
, we have
$1 \le i < j \le 3$
, we have
 $\Gamma _i \cap \Gamma _j = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. Moreover, S is quasi-smooth at
$\Gamma _i \cap \Gamma _j = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. Moreover, S is quasi-smooth at
 $\mathsf {p}_t$
since
$\mathsf {p}_t$
since
 $S \in |A|$
is general.
$S \in |A|$
is general.
By the similar computation as in Case (iii) of Section 4.4.b, the intersection matrix of
 $\Gamma _1, \Gamma _2, \Gamma _3$
is given by
$\Gamma _1, \Gamma _2, \Gamma _3$
is given by  $$\begin{align*}\begin{pmatrix} - \frac{7}{12} & \frac{1}{3} & \frac{1}{3} \\[1mm] \frac{1}{3} & - \frac{5}{6} & \frac{2}{3} \\[1mm] \frac{1}{3} & \frac{2}{3} & - \frac{5}{6} \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} - \frac{7}{12} & \frac{1}{3} & \frac{1}{3} \\[1mm] \frac{1}{3} & - \frac{5}{6} & \frac{2}{3} \\[1mm] \frac{1}{3} & \frac{2}{3} & - \frac{5}{6} \end{pmatrix} \end{align*}$$
-
and it satisfies the condition
![]() $(\star )$
. By Lemma 3.21, we have
$(\star )$
. By Lemma 3.21, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} 3/4, & \text{if}\ \mathsf{p} \in \Gamma_1 \cap \operatorname{Sm} (X), \\ 4/5, & \text{if}\ \mathsf{p} \in \Gamma_i \cap \operatorname{Sm} (X)\ \text{for}\ i = 2, 3. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} 3/4, & \text{if}\ \mathsf{p} \in \Gamma_1 \cap \operatorname{Sm} (X), \\ 4/5, & \text{if}\ \mathsf{p} \in \Gamma_i \cap \operatorname{Sm} (X)\ \text{for}\ i = 2, 3. \end{cases} \end{align*}$$
Thus,
![]() $\alpha _{\mathsf {p}} (X) \ge 3/4$
for any
$\alpha _{\mathsf {p}} (X) \ge 3/4$
for any
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.4 The family
 $\mathcal {F}_{13}$
$\mathcal {F}_{13}$
We have
where
![]() $\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. Note that
$\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. Note that
![]() $(\alpha ,\gamma ) \ne (0,0)$
since X is quasi-smooth at
$(\alpha ,\gamma ) \ne (0,0)$
since X is quasi-smooth at
![]() $\mathsf {p}_t$
.
$\mathsf {p}_t$
.
-
• Case (i):
 $\alpha \ne 0$
,
$\alpha \ne 0$
,
 $(\beta , \delta ) \ne (0,0)$
and
$(\beta , \delta ) \ne (0,0)$
and
 $(\alpha ,\gamma )$
is not proportional to
$(\alpha ,\gamma )$
is not proportional to
 $(\beta ,\delta )$
. In this case,
$(\beta ,\delta )$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha \ne 0$
,
$\alpha \ne 0$
,
 $(\beta , \delta ) \ne (0,0)$
and
$(\beta , \delta ) \ne (0,0)$
and
 $(\alpha ,\gamma )$
is proportional to
$(\alpha ,\gamma )$
is proportional to
 $(\beta ,\delta )$
. In this case,
$(\beta ,\delta )$
. In this case,
 $f = (\alpha w + \gamma t z)(t^2 + \varepsilon z^3)$
, where
$f = (\alpha w + \gamma t z)(t^2 + \varepsilon z^3)$
, where
 $\varepsilon := \beta /\alpha \in \mathbb {C}$
is nonzero. Replacing w and z, we may assume
$\varepsilon := \beta /\alpha \in \mathbb {C}$
is nonzero. Replacing w and z, we may assume
 $f = w (t^2 - z^3)$
and
$f = w (t^2 - z^3)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = t^2 - z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = t^2 - z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
$\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
 $\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in \operatorname {Sm} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
$\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in \operatorname {Sm} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
 $\mathsf {q}$
. Finally, we have
$\mathsf {q}$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $(\beta ,\delta ) = (0,0)$
. In this case,
$(\beta ,\delta ) = (0,0)$
. In this case,
 $f = t^2 (\alpha w + \gamma t z)$
and we may assume
$f = t^2 (\alpha w + \gamma t z)$
and we may assume
 $f = t^2 w$
by replacing w. We can write where
$f = t^2 w$
by replacing w. We can write where $$\begin{align*}F = f_1 (z,w) x + f_2 (z,w) y + t^2 w + g (x,y,z,t,w), \end{align*}$$
$$\begin{align*}F = f_1 (z,w) x + f_2 (z,w) y + t^2 w + g (x,y,z,t,w), \end{align*}$$
 $f_1, f_2 \in \mathbb {C} [z,w]$
and
$f_1, f_2 \in \mathbb {C} [z,w]$
and
 $g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
$g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
 $g \in (x, y) \cap (x,y,t)^2$
. By Lemma 4.16, we have
$g \in (x, y) \cap (x,y,t)^2$
. By Lemma 4.16, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iv):
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. Note that
$\beta \ne 0$
. Note that
 $\gamma \ne 0$
. In this case,
$\gamma \ne 0$
. In this case,
 $f = z (\beta w z^2 + \gamma t^3 + \delta t z^3)$
. Then
$f = z (\beta w z^2 + \gamma t^3 + \delta t z^3)$
. Then
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = \beta w z^2 + \gamma t^3 + \delta t z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = \beta w z^2 + \gamma t^3 + \delta t z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_w\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_w\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
 $\mathsf {p}_w$
. Finally, we have
$\mathsf {p}_w$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Then, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Then, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (v):
 $\alpha = \beta = 0$
and
$\alpha = \beta = 0$
and
 $\delta \ne 0$
. Note that
$\delta \ne 0$
. Note that
 $\gamma \ne 0$
. In this case,
$\gamma \ne 0$
. In this case,
 $f = z t (\gamma t^2 + \delta z^3)$
and
$f = z t (\gamma t^2 + \delta z^3)$
and
 $T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
, where
$T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
, where
 $\Gamma _1, \Gamma _2, \Gamma _3$
are as follows.
$\Gamma _1, \Gamma _2, \Gamma _3$
are as follows.-
–
 $\Gamma _1 = (x = y = z = 0)$
is a quasi-line of degree
$\Gamma _1 = (x = y = z = 0)$
is a quasi-line of degree
 $1/15$
and
$1/15$
and
 $\operatorname {Sing}_{\Gamma _1} (S) = \{1 \times \frac {1}{3} (1,2), 1 \times \frac {1}{5} (2,3)\}$
.
$\operatorname {Sing}_{\Gamma _1} (S) = \{1 \times \frac {1}{3} (1,2), 1 \times \frac {1}{5} (2,3)\}$
. -
–
 $\Gamma _2 = (x = y = t = 0)$
is a quasi-line of degree
$\Gamma _2 = (x = y = t = 0)$
is a quasi-line of degree
 $1/10$
and
$1/10$
and
 $\operatorname {Sing}_{\Gamma _2} (S) = \{1 \times \frac {1}{2} (1,1), 1 \times \frac {1}{5} (2,3)\}$
.
$\operatorname {Sing}_{\Gamma _2} (S) = \{1 \times \frac {1}{2} (1,1), 1 \times \frac {1}{5} (2,3)\}$
. -
–
 $\Gamma _3 = (x = y = \gamma t^2 + \delta z^3 = 0)$
is an irreducible smooth curve of degree
$\Gamma _3 = (x = y = \gamma t^2 + \delta z^3 = 0)$
is an irreducible smooth curve of degree
 $1/5$
.
$1/5$
. -
– For
 $ 1 \le i < j \le 3$
, we have
$ 1 \le i < j \le 3$
, we have
 $\Gamma _i \cap \Gamma _j = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
. Moreover, S is quasi-smooth at
$\Gamma _i \cap \Gamma _j = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
. Moreover, S is quasi-smooth at
 $\mathsf {p}_w$
.
$\mathsf {p}_w$
.
We compute
 $(\Gamma _1^2)_S = - 8/15$
and
$(\Gamma _1^2)_S = - 8/15$
and
 $(\Gamma _2^2)_S = - 15/19$
by the method explained in Remark 3.10. We can choose
$(\Gamma _2^2)_S = - 15/19$
by the method explained in Remark 3.10. We can choose
 $z, t$
as orbifold coordinates of S at
$z, t$
as orbifold coordinates of S at
 $\mathsf {p}_w$
. It follows that
$\mathsf {p}_w$
. It follows that
 $\Gamma _1, \Gamma _2$
intersect transversally at the point over
$\Gamma _1, \Gamma _2$
intersect transversally at the point over
 $\mathsf {p}_w$
on the orbifold chart of S at
$\mathsf {p}_w$
on the orbifold chart of S at
 $\mathsf {p}_w$
, and we have
$\mathsf {p}_w$
, and we have
 $(\Gamma _1 \cdot \Gamma _2)_S = 1/5$
. Then, by taking intersections with
$(\Gamma _1 \cdot \Gamma _2)_S = 1/5$
. Then, by taking intersections with
 $T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
with
$T|_S = \Gamma _1 + \Gamma _2 + \Gamma _3$
with
 $\Gamma _i$
for
$\Gamma _i$
for
 $i = 1,2,3$
, we see that the intersection matrix of
$i = 1,2,3$
, we see that the intersection matrix of
 $\Gamma _1, \Gamma _2, \Gamma _3$
is given by and it satisfies the condition
$\Gamma _1, \Gamma _2, \Gamma _3$
is given by and it satisfies the condition $$\begin{align*}\begin{pmatrix} - \frac{8}{15} & \frac{1}{5} & \frac{2}{5} \\[1mm] \frac{1}{5} & - \frac{7}{10} & \frac{3}{5} \\[1mm] \frac{2}{5} & \frac{3}{5} & - 1 \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} - \frac{8}{15} & \frac{1}{5} & \frac{2}{5} \\[1mm] \frac{1}{5} & - \frac{7}{10} & \frac{3}{5} \\[1mm] \frac{2}{5} & \frac{3}{5} & - 1 \end{pmatrix} \end{align*}$$
 $(\star )$
. By Lemma 3.21, Thus, we have
$(\star )$
. By Lemma 3.21, Thus, we have $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} 10/13, & \text{if}\ \mathsf{p} \in \Gamma_1 \cap \operatorname{Sm} (X), \\ 15/19, & \text{if}\ \mathsf{p} \in \Gamma_2 \cap \operatorname{Sm} (X), \\ 6/7, & \text{if}\ \mathsf{p} \in \Gamma_3 \cap \operatorname{Sm}(X). \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} 10/13, & \text{if}\ \mathsf{p} \in \Gamma_1 \cap \operatorname{Sm} (X), \\ 15/19, & \text{if}\ \mathsf{p} \in \Gamma_2 \cap \operatorname{Sm} (X), \\ 6/7, & \text{if}\ \mathsf{p} \in \Gamma_3 \cap \operatorname{Sm}(X). \end{cases} \end{align*}$$
 $\alpha _{\mathsf {p}} (X) \ge 10/13$
for any
$\alpha _{\mathsf {p}} (X) \ge 10/13$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
-
• Case (vi):
 $\alpha = \beta = \delta = 0$
. In this case,
$\alpha = \beta = \delta = 0$
. In this case,
 $\gamma \ne 0$
and we may assume that
$\gamma \ne 0$
and we may assume that
 $f = t^3 z$
by rescaling z. We can write where
$f = t^3 z$
by rescaling z. We can write where $$\begin{align*}F = f_1 (z,w) x + f_2 (z,w) y + t^3 z + g (x,y,z,t,w), \end{align*}$$
$$\begin{align*}F = f_1 (z,w) x + f_2 (z,w) y + t^3 z + g (x,y,z,t,w), \end{align*}$$
 $f_1, f_2 \in \mathbb {C} [z,w]$
and
$f_1, f_2 \in \mathbb {C} [z,w]$
and
 $g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
$g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
 $g \in (x,y) \cap (x,y,t)^2$
. By Lemma 4.16, we have
$g \in (x,y) \cap (x,y,t)^2$
. By Lemma 4.16, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.5 The family
 $\mathcal {F}_{15}$
$\mathcal {F}_{15}$
We have
![]() $w^2 \in f$
. Replacing w, we may assume that the coefficients of
$w^2 \in f$
. Replacing w, we may assume that the coefficients of
![]() $z^6$
and
$z^6$
and
![]() $t^4$
are both
$t^4$
are both
![]() $0$
. Then, by the quasi-smoothness of X at
$0$
. Then, by the quasi-smoothness of X at
![]() $\mathsf {p}_z, \mathsf {p}_t \in X$
, we have
$\mathsf {p}_z, \mathsf {p}_t \in X$
, we have
![]() $t^2 w, z^3 w \in F$
. Hence, by rescaling
$t^2 w, z^3 w \in F$
. Hence, by rescaling
![]() $w, t$
and z, we can write
$w, t$
and z, we can write
for some
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. Replacing w and rescaling z, we may assume
$\alpha = 0$
. Replacing w and rescaling z, we may assume
 $f = w(w + t^2 - z^3)$
and
$f = w(w + t^2 - z^3)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + t^2 - z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + t^2 - z^3 = 0). \end{align*}$$
 $\Gamma $
and
$\Gamma $
and
 $\Delta $
are both quasi-lines. We have
$\Delta $
are both quasi-lines. We have
 $\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
$\Gamma \cap \Delta = \{\mathsf {q}\}$
, where
 $\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in \operatorname {Sm} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
$\mathsf {q} = (0\!:\!0\!:\!1\!:\!1\!:\!0) \in \operatorname {Sm} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
 $\mathsf {q}$
. Finally, we have
$\mathsf {q}$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.6 The family
 $\mathcal {F}_{20}$
$\mathcal {F}_{20}$
We have
![]() $w^2 z \in F$
by the quasi-smoothness of X at
$w^2 z \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
. Hence, we can write
$\mathsf {p}_w$
. Hence, we can write
where
![]() $\alpha , \beta \in \mathbb {C}$
.
$\alpha , \beta \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $\beta \ne 0$
. In this case,
$\beta \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $\beta = 0$
. We have
$\beta = 0$
. We have
 $f = w (w z + \alpha t^2)$
and thus
$f = w (w z + \alpha t^2)$
and thus
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w z + \alpha t^2 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w z + \alpha t^2 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible quasi-smooth curve. We have
$\Delta $
is an irreducible quasi-smooth curve. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
 $\mathsf {p}_z$
. Finally, we have
$\mathsf {p}_z$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. We have
$\beta \ne 0$
. We have
 $f = z (w^2 + \beta t z^2)$
and thus
$f = z (w^2 + \beta t z^2)$
and thus
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + \beta t z^2 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + \beta t z^2 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\}$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\}$
. By a similar argument as in Case (ii) of Section 4.4.b, we conclude that S is quasi-smooth at
 $\mathsf {p}_t$
. Finally, we have
$\mathsf {p}_t$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iv):
 $\alpha = \beta = 0$
. In this case,
$\alpha = \beta = 0$
. In this case,
 $f = w^2 z$
and we can write where
$f = w^2 z$
and we can write where $$\begin{align*}F = f_1 (z,t) x + f_2 (z,t) y + w^2 z + g (x,y,z,t,w), \end{align*}$$
$$\begin{align*}F = f_1 (z,t) x + f_2 (z,t) y + w^2 z + g (x,y,z,t,w), \end{align*}$$
 $f_1, f_2 \in \mathbb {C} [z,t]$
and
$f_1, f_2 \in \mathbb {C} [z,t]$
and
 $g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
$g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
 $g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.16, we have
$g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.16, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.7 The family
 $\mathcal {F}_{23}$
$\mathcal {F}_{23}$
We have
![]() $w^2 t \in F$
by the quasi-smoothness of X at
$w^2 t \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
. Hence, we can write
$\mathsf {p}_w$
. Hence, we can write
where
![]() $\alpha , \beta \in \mathbb {C}$
.
$\alpha , \beta \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $\beta \ne 0$
. In this case,
$\beta \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $\beta = 0$
. We have
$\beta = 0$
. We have
 $f = w (w t + \alpha z^3)$
and thus
$f = w (w t + \alpha z^3)$
and thus
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w t + \alpha z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w t + \alpha z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible quasi-smooth curve. We have
$\Delta $
is an irreducible quasi-smooth curve. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
 $\mathsf {p}_t$
since
$\mathsf {p}_t$
since
 $t^3 y \in F$
and
$t^3 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. We have
$\beta \ne 0$
. We have
 $f = t (w^2 + \beta t z^2)$
and thus
$f = t (w^2 + \beta t z^2)$
and thus
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = w^2 + \beta t z^2 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = w^2 + \beta t z^2 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and S is quasi-smooth at
 $\mathsf {p}_z$
since
$\mathsf {p}_z$
since
 $z^4 y \in F$
and
$z^4 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iv):
 $\alpha = \beta = 0$
. In this case,
$\alpha = \beta = 0$
. In this case,
 $f = w^2 t$
and we can write where
$f = w^2 t$
and we can write where $$\begin{align*}F = f_1 (z,t) x + f_2 (z,t) + w^2 t + g (x,y,z,t,w), \end{align*}$$
$$\begin{align*}F = f_1 (z,t) x + f_2 (z,t) + w^2 t + g (x,y,z,t,w), \end{align*}$$
 $f_1, f_2 \in \mathbb {C} [z,t]$
and
$f_1, f_2 \in \mathbb {C} [z,t]$
and
 $g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
$g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
 $g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.16, we have
$g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.16, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.8 The family
 $\mathcal {F}_{24}$
$\mathcal {F}_{24}$
We have
![]() $t^3 \in F$
and, by rescaling t, we can write
$t^3 \in F$
and, by rescaling t, we can write
where
![]() $\alpha , \beta \in \mathbb {C}$
.
$\alpha , \beta \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. By rescaling z, we may assume
$\beta \ne 0$
. By rescaling z, we may assume
 $f = t (t^2 + z^5)$
. Then
$f = t (t^2 + z^5)$
. Then
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = t^2 + z^5 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = t^2 + z^5 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and S is quasi-smooth at
 $\mathsf {p}_w$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
$\mathsf {p}_w$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\alpha = \beta = 0$
. In this case,
$\alpha = \beta = 0$
. In this case,
 $f = t^3$
and the defining polynomial F of X can be written as where
$f = t^3$
and the defining polynomial F of X can be written as where $$\begin{align*}F = w^2 \ell_1 (x,y) + t^3 + z^7 \ell_2 (x,y) + w h_8 (x,y,z,t) + h_{15} (x,y,z,t), \end{align*}$$
$$\begin{align*}F = w^2 \ell_1 (x,y) + t^3 + z^7 \ell_2 (x,y) + w h_8 (x,y,z,t) + h_{15} (x,y,z,t), \end{align*}$$
 $h_8, h_{15} \in \mathbb {C} [x,y,z,t]$
are homogeneous polynomials of degrees
$h_8, h_{15} \in \mathbb {C} [x,y,z,t]$
are homogeneous polynomials of degrees
 $8, 15$
, respectively, such that
$8, 15$
, respectively, such that
 $z^4 \notin h_8$
and
$z^4 \notin h_8$
and
 $t^3, z^7 x, z^7 y \notin h_{15}$
, and
$t^3, z^7 x, z^7 y \notin h_{15}$
, and
 $\ell _1, \ell _2$
are linear forms in
$\ell _1, \ell _2$
are linear forms in
 $x, y$
. Note that
$x, y$
. Note that
 $h_8, h_{15} \in (x,y) \cap (x,y,t)^2$
. By the quasi-smoothness of X, we see that
$h_8, h_{15} \in (x,y) \cap (x,y,t)^2$
. By the quasi-smoothness of X, we see that
 $\ell _1$
and
$\ell _1$
and
 $\ell _2$
are linearly independent. Replacing
$\ell _2$
are linearly independent. Replacing
 $x, y$
, we can assume that where
$x, y$
, we can assume that where $$\begin{align*}F = w^2 x + t^3 - z^7 y + g, \end{align*}$$
$$\begin{align*}F = w^2 x + t^3 - z^7 y + g, \end{align*}$$
 $h = w h_8 + h_{15} \in (x, y) \cap (x, y, t)^2$
. Thus, by Lemma 4.17, we have
$h = w h_8 + h_{15} \in (x, y) \cap (x, y, t)^2$
. Thus, by Lemma 4.17, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.9 The family
 $\mathcal {F}_{25}$
$\mathcal {F}_{25}$
We have
![]() $z^5 \in F$
and, by rescaling z, we can write
$z^5 \in F$
and, by rescaling z, we can write
where
![]() $\alpha , \beta \in \mathbb {C}$
.
$\alpha , \beta \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. By the quasi-smoothness of X at
$\alpha = 0$
. By the quasi-smoothness of X at
 $\mathsf {p}_t$
, we have
$\mathsf {p}_t$
, we have
 $\beta \ne 0$
, and hence we may assume
$\beta \ne 0$
, and hence we may assume
 $\beta = 1$
. Then
$\beta = 1$
. Then
 $f = z ( t^3 + z^5)$
and we have
$f = z ( t^3 + z^5)$
and we have
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = t^3 + z^5 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = t^3 + z^5 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and S is quasi-smooth at
 $\mathsf {p}_w$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
$\mathsf {p}_w$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.10 The family
 $\mathcal {F}_{29}$
$\mathcal {F}_{29}$
We have
![]() $w^2 \in F$
and, by rescaling w, we can write
$w^2 \in F$
and, by rescaling w, we can write
![]() $f = w^2 + \lambda w z^4 + \alpha t^2 z^3 + \mu z^8$
, where
$f = w^2 + \lambda w z^4 + \alpha t^2 z^3 + \mu z^8$
, where
![]() $\alpha , \lambda , \mu \in \mathbb {C}$
. By replacing w, we can eliminate the term
$\alpha , \lambda , \mu \in \mathbb {C}$
. By replacing w, we can eliminate the term
![]() $\mu z^8$
, that is, we may assume
$\mu z^8$
, that is, we may assume
![]() $\mu = 0$
. Then, by the quasi-smoothness of X at
$\mu = 0$
. Then, by the quasi-smoothness of X at
![]() $\mathsf {p}_z$
, we have
$\mathsf {p}_z$
, we have
![]() $w z^4 \in F$
, that is,
$w z^4 \in F$
, that is,
![]() $\lambda \ne 0$
. Thus, we can write
$\lambda \ne 0$
. Thus, we can write
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. Then we have
$\alpha = 0$
. Then we have
 $f = w(w+z^4)$
and
$f = w(w+z^4)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + z^4). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + z^4). \end{align*}$$
 $\Gamma $
and
$\Gamma $
and
 $\Delta $
are both quasi-lines. We have
$\Delta $
are both quasi-lines. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
 $\mathsf {p}_t$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
$\mathsf {p}_t$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.11 The family
 $\mathcal {F}_{30}$
$\mathcal {F}_{30}$
We have
![]() $w^2 \in F$
and, by rescaling w, we can write
$w^2 \in F$
and, by rescaling w, we can write
![]() $f = w^2 + \lambda w t^2 + \mu t^4 + \alpha t z^4$
, where
$f = w^2 + \lambda w t^2 + \mu t^4 + \alpha t z^4$
, where
![]() $\alpha , \lambda , \mu \in \mathbb {C}$
. We may assume
$\alpha , \lambda , \mu \in \mathbb {C}$
. We may assume
![]() $\mu = 0$
by replacing w, and then we have
$\mu = 0$
by replacing w, and then we have
![]() $w t^2 \in F$
by the quasi-smoothness of X at
$w t^2 \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_t$
. Thus, we can write
$\mathsf {p}_t$
. Thus, we can write
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. Then we have
$\alpha = 0$
. Then we have
 $f = w(w+t^2)$
and
$f = w(w+t^2)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + t^2 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + t^2 = 0). \end{align*}$$
 $\Gamma $
and
$\Gamma $
and
 $\Delta $
are both quasi-lines. We have
$\Delta $
are both quasi-lines. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and S is quasi-smooth at
 $\mathsf {p}_z$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
$\mathsf {p}_z$
by a similar argument as in Case (ii) of Section 4.4.b. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.12 The family
 $\mathcal {F}_{31}$
$\mathcal {F}_{31}$
We have
![]() $w^2 z \in F$
by the quasi-smoothness of X at
$w^2 z \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
, and we have
$\mathsf {p}_w$
, and we have
![]() $z^4 \in F$
. Rescaling w and z, we can write
$z^4 \in F$
. Rescaling w and z, we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = z (w^2 - z^3)$
and
$f = z (w^2 - z^3)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 - z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 - z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
 $\mathsf {p}_t$
by a similar argument as in Case (ii) of Section 4.4.b. Thus, by Lemma 4.14, we have
$\mathsf {p}_t$
by a similar argument as in Case (ii) of Section 4.4.b. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.13 The family
 $\mathcal {F}_{32}$
$\mathcal {F}_{32}$
We have
![]() $t^4 \in F$
, and we can write
$t^4 \in F$
, and we can write
where
![]() $\alpha , \beta \in \mathbb {C}$
.
$\alpha , \beta \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. Rescaling z, we may assume
$\beta \ne 0$
. Rescaling z, we may assume
 $\beta = 1$
and
$\beta = 1$
and
 $f = t (t^3 + z^4)$
. Then
$f = t (t^3 + z^4)$
. Then
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = t^3 + z^4 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = t^3 + z^4 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and S is quasi-smooth at
 $\mathsf {p}_w$
since
$\mathsf {p}_w$
since
 $w^2 y \in F$
and
$w^2 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\alpha = \beta = 0$
. In this case,
$\alpha = \beta = 0$
. In this case,
 $f = t^4$
. Since
$f = t^4$
. Since
 $w z^3, t z^4 \notin F$
, we have
$w z^3, t z^4 \notin F$
, we have
 $z^5 x \in F$
, and we can write where
$z^5 x \in F$
, and we can write where $$\begin{align*}F = w^2 y + t^4 + z^5 x + w h_9 (x,y,z,t) + h_{16} (x,y,z,t), \end{align*}$$
$$\begin{align*}F = w^2 y + t^4 + z^5 x + w h_9 (x,y,z,t) + h_{16} (x,y,z,t), \end{align*}$$
 $g_i \in \mathbb {C} [x,y,z,t]$
is a homogeneous polynomial of degree i such that
$g_i \in \mathbb {C} [x,y,z,t]$
is a homogeneous polynomial of degree i such that
 $z^3 \notin h_9$
and
$z^3 \notin h_9$
and
 $t^4, t z^4, z^5 x \notin h_{16}$
. Note that
$t^4, t z^4, z^5 x \notin h_{16}$
. Note that
 $h_9, h_{16} \in (x, y) \cap (x, y, t)^2$
. Thus, by Lemma 4.17, we have
$h_9, h_{16} \in (x, y) \cap (x, y, t)^2$
. Thus, by Lemma 4.17, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.14 The family
 $\mathcal {F}_{33}$
$\mathcal {F}_{33}$
We have
![]() $w^2 z \in F$
by the quasi-smoothness of X at
$w^2 z \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
, and we can write
$\mathsf {p}_w$
, and we can write
where
![]() $\alpha , \beta \in \mathbb {C}$
.
$\alpha , \beta \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $\beta \ne 0$
. In this case,
$\beta \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha \ne 0$
and
$\alpha \ne 0$
and
 $\beta = 0$
. In this case,
$\beta = 0$
. In this case,
 $f = w (w z + \alpha z^2)$
and
$f = w (w z + \alpha z^2)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w z + \alpha z^2 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w z + \alpha z^2 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible quasi-smooth curve. We have
$\Delta $
is an irreducible quasi-smooth curve. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
 $\mathsf {p}_z$
since
$\mathsf {p}_z$
since
 $z^5 t \in F$
and
$z^5 t \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iii):
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. In this case,
$\beta \ne 0$
. In this case,
 $f = z (w^2 + \beta t z^3)$
and
$f = z (w^2 + \beta t z^3)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + \beta t z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + \beta t z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
 $\mathsf {p}_t$
since
$\mathsf {p}_t$
since
 $t^3 y \in F$
and
$t^3 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
-
• Case (iv):
 $\alpha = \beta = 0$
. In this case,
$\alpha = \beta = 0$
. In this case,
 $f = w^2 z$
and we can write where
$f = w^2 z$
and we can write where $$\begin{align*}F = f_1 (z,t) x + f_2 (z,t) y + w^2 z + g (x,y,z,t,w), \end{align*}$$
$$\begin{align*}F = f_1 (z,t) x + f_2 (z,t) y + w^2 z + g (x,y,z,t,w), \end{align*}$$
 $f_1, f_2 \in ^mbC [z,t]$
and
$f_1, f_2 \in ^mbC [z,t]$
and
 $g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
$g \in \mathbb {C} [x,y,z,t,w]$
are homogeneous polynomials such that
 $g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.16, we have
$g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.16, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.15 The family
 $\mathcal {F}_{37}$
$\mathcal {F}_{37}$
We have
![]() $w^2 \in F$
, and we can write
$w^2 \in F$
, and we can write
![]() $f = w^2 + \lambda w z^3 + \alpha t^3 z^2 + \mu z^6$
, where
$f = w^2 + \lambda w z^3 + \alpha t^3 z^2 + \mu z^6$
, where
![]() $\alpha , \lambda , \mu \in \mathbb {C}$
. Replacing w, we may assume
$\alpha , \lambda , \mu \in \mathbb {C}$
. Replacing w, we may assume
![]() $\mu = 0$
. Then, by the quasi-smoothness of X at
$\mu = 0$
. Then, by the quasi-smoothness of X at
![]() $\mathsf {p}_z$
, we have
$\mathsf {p}_z$
, we have
![]() $\lambda \ne 0$
. Rescaling z, we can write
$\lambda \ne 0$
. Rescaling z, we can write
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = w(w+z^3)$
and
$f = w(w+z^3)$
and
 $T|_S = \Gamma + \Delta $
, where are both quasi-lines. We have
$T|_S = \Gamma + \Delta $
, where are both quasi-lines. We have $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + z^3 = 0) \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + z^3 = 0) \end{align*}$$
 $\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
 $\mathsf {p}_t$
since
$\mathsf {p}_t$
since
 $t^4 y \in F$
and
$t^4 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.16 The family
 $\mathcal {F}_{38}$
$\mathcal {F}_{38}$
We have
![]() $z^6 \in F$
, and we can write
$z^6 \in F$
, and we can write
where
![]() $\alpha , \beta \in \mathbb {C}$
. Note that we have
$\alpha , \beta \in \mathbb {C}$
. Note that we have
![]() $(\alpha ,\beta ) \ne (0,0)$
by the quasi-smoothness of X.
$(\alpha ,\beta ) \ne (0,0)$
by the quasi-smoothness of X.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_w \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap X_{\operatorname {sm}}$
.
$\mathsf {p} \in L_{xy} \cap X_{\operatorname {sm}}$
. -
• Case (ii):
 $\alpha = 0$
. Note that
$\alpha = 0$
. Note that
 $\beta \ne 0$
. In this case,
$\beta \ne 0$
. In this case,
 $f = z (\beta t^3 + z^5)$
and
$f = z (\beta t^3 + z^5)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = \beta t^3 + z^5 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = \beta t^3 + z^5 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_w\} = \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
 $\mathsf {p}_w$
since
$\mathsf {p}_w$
since
 $w^2 y \in F$
and
$w^2 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.17 The family
 $\mathcal {F}_{39}$
$\mathcal {F}_{39}$
We have
![]() $w^3 \in F$
and
$w^3 \in F$
and
![]() $w z^3 \in F$
by the quasi-smoothness of X. Rescaling w and z, we can write
$w z^3 \in F$
by the quasi-smoothness of X. Rescaling w and z, we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = z (w^2 + z^3)$
and we have
$f = z (w^2 + z^3)$
and we have
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + z^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + z^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_t\} = \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_t\} = \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
 $\mathsf {p}_t$
since
$\mathsf {p}_t$
since
 $t^3 y \in F$
and
$t^3 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.18 The family
 $\mathcal {F}_{40}$
$\mathcal {F}_{40}$
We have
![]() $w^2 t \in F$
and
$w^2 t \in F$
and
![]() $t^3 z \in F$
by the quasi-smoothness of X at
$t^3 z \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
and
$\mathsf {p}_w$
and
![]() $\mathsf {p}_t$
. Rescaling w and z, we can write
$\mathsf {p}_t$
. Rescaling w and z, we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = t (w^2 + t^2 z)$
and
$f = t (w^2 + t^2 z)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = w^2 + t^2 z = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = w^2 + t^2 z = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_z\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_z\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and Sbis quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and Sbis quasi-smooth at
 $\mathsf {p}_z$
since
$\mathsf {p}_z$
since
 $z^4 y \in F$
and
$z^4 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.19 The family
 $\mathcal {F}_{42}$
$\mathcal {F}_{42}$
We have
![]() $w^2 \in F$
, and we can write
$w^2 \in F$
, and we can write
![]() $f = w^2 + \lambda w t^2 + \mu t^4 + \alpha t z^5$
, where
$f = w^2 + \lambda w t^2 + \mu t^4 + \alpha t z^5$
, where
![]() $\alpha , \lambda , \mu \in \mathbb {C}$
. Replacing w, we may assume
$\alpha , \lambda , \mu \in \mathbb {C}$
. Replacing w, we may assume
![]() $\mu = 0$
. Then, by the quasi-smoothness of X at
$\mu = 0$
. Then, by the quasi-smoothness of X at
![]() $\mathsf {p}_t$
, we have
$\mathsf {p}_t$
, we have
![]() $\lambda \ne 0$
. Rescaling t, we can write
$\lambda \ne 0$
. Rescaling t, we can write
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = w(w+t^2)$
and
$f = w(w+t^2)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + t^2 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = w = 0), \quad \Delta = (x = y = w + t^2 = 0). \end{align*}$$
 $\Gamma $
and
$\Gamma $
and
 $\Delta $
are both quasi-lines. We have
$\Delta $
are both quasi-lines. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_z\} \subset \operatorname {Sing} (X)$
, and S is quasi-smooth at
 $\mathsf {p}_z$
since
$\mathsf {p}_z$
since
 $z^6 y \in F$
and
$z^6 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z, \mathsf {p}_t\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.20 The family
 $\mathcal {F}_{49}$
$\mathcal {F}_{49}$
We have
![]() $w^3 \in F$
, and we can write
$w^3 \in F$
, and we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = w^3$
and, after replacing
$f = w^3$
and, after replacing
 $x, y$
suitably, the defining polynomial F of X can be written as where
$x, y$
suitably, the defining polynomial F of X can be written as where $$\begin{align*}F = w^3 + t^3 y - z^3 x + g_{21} (x,y,z,t,w), \end{align*}$$
$$\begin{align*}F = w^3 + t^3 y - z^3 x + g_{21} (x,y,z,t,w), \end{align*}$$
 $g_{21} \in \mathbb {C} [x,y,z,t,w]$
is a homogeneous polynomial of degree
$g_{21} \in \mathbb {C} [x,y,z,t,w]$
is a homogeneous polynomial of degree
 $21$
such that
$21$
such that
 $g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.17, we have
$g \in (x,y) \cap (x,y,w)^2$
. By Lemma 4.17, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.21 The family
 $\mathcal {F}_{50}$
$\mathcal {F}_{50}$
We have
![]() $w^2 \in F$
, and we can write
$w^2 \in F$
, and we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. We have
$\alpha = 0$
. We have
 $S \cdot T = 2 \Gamma $
, where
$S \cdot T = 2 \Gamma $
, where
 $\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
$\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.22 The family
 $\mathcal {F}_{52}$
$\mathcal {F}_{52}$
We have
![]() $w^2 \in F$
, and we can write
$w^2 \in F$
, and we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\{\mathsf {p}_z, \mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\{\mathsf {p}_z, \mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. We have
$\alpha = 0$
. We have
 $S \cdot T = 2 \Gamma $
, where
$S \cdot T = 2 \Gamma $
, where
 $\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
$\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.23 The family
 $\mathcal {F}_{58}$
$\mathcal {F}_{58}$
We have
![]() $w^2 z \in F$
by the quasi-smoothness of X at
$w^2 z \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
. Also, we have
$\mathsf {p}_w$
. Also, we have
![]() $z^6 \in F$
. Rescaling w and z, we can write
$z^6 \in F$
. Rescaling w and z, we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = z (w^2 + z^5)$
and
$f = z (w^2 + z^5)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + z^5 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = z = 0), \quad \Delta = (x = y = w^2 + z^5 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_t\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_t\}$
, and S is quasi-smooth at
 $\mathsf {p}_t$
since
$\mathsf {p}_t$
since
 $t^3 y \in F$
and
$t^3 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_t,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.24 The family
 $\mathcal {F}_{60}$
$\mathcal {F}_{60}$
We have
![]() $w^2 t \in F$
by the quasi-smoothness of X at
$w^2 t \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
. Also, we have
$\mathsf {p}_w$
. Also, we have
![]() $t^4 \in F$
. Rescaling w and t, we can write
$t^4 \in F$
. Rescaling w and t, we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
$S \cdot T = L_{xy}$
is irreducible and smooth. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. In this case,
$\alpha = 0$
. In this case,
 $f = t (w^2 + t^3)$
and
$f = t (w^2 + t^3)$
and
 $T|_S = \Gamma + \Delta $
, where We see that
$T|_S = \Gamma + \Delta $
, where We see that $$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = w^2 + t^3 = 0). \end{align*}$$
$$\begin{align*}\Gamma = (x = y = t = 0), \quad \Delta = (x = y = w^2 + t^3 = 0). \end{align*}$$
 $\Gamma $
is a quasi-line and
$\Gamma $
is a quasi-line and
 $\Delta $
is an irreducible curve which is quasi-smooth along
$\Delta $
is an irreducible curve which is quasi-smooth along
 $\Delta \setminus \{\mathsf {p}_z\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
$\Delta \setminus \{\mathsf {p}_z\} \supset \Delta \cap \operatorname {Sm} (X)$
. We have
 $\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_z\}$
, and S is quasi-smooth at
 $\mathsf {p}_z$
since
$\mathsf {p}_z$
since
 $z^4 y \in F$
and
$z^4 y \in F$
and
 $S = H_x$
. Finally, we have
$S = H_x$
. Finally, we have
 $\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
$\operatorname {Sing}_{\Gamma } (X) = \{\mathsf {p}_z,\mathsf {p}_w\}$
. Thus, by Lemma 4.14, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.25 The family
 $\mathcal {F}_{63}$
$\mathcal {F}_{63}$
We have
![]() $w^2 \in F$
, and we can write
$w^2 \in F$
, and we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $ \mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$ \mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. We have
$\alpha = 0$
. We have
 $S \cdot T = 2 \Gamma $
, where
$S \cdot T = 2 \Gamma $
, where
 $\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
$\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.4.b.26 The family
 $\mathcal {F}_{64}$
$\mathcal {F}_{64}$
We have
![]() $w^2 \in F$
, and we can write
$w^2 \in F$
, and we can write
where
![]() $\alpha \in \mathbb {C}$
.
$\alpha \in \mathbb {C}$
.
-
• Case (i):
 $\alpha \ne 0$
. In this case,
$\alpha \ne 0$
. In this case,
 $S \cdot T = L_{xy}$
is irreducible and is smooth outside
$S \cdot T = L_{xy}$
is irreducible and is smooth outside
 $\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
$\mathsf {p}_t \in \operatorname {Sing} (X)$
. By Lemma 4.13, we have
 $\alpha _{\mathsf {p}} (X) = 1$
for any
$\alpha _{\mathsf {p}} (X) = 1$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
. -
• Case (ii):
 $\alpha = 0$
. We have
$\alpha = 0$
. We have
 $S \cdot T = 2 \Gamma $
, where
$S \cdot T = 2 \Gamma $
, where
 $\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
$\Gamma = (x = y = w = 0)$
. By Lemma 4.18, we have
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
$\alpha _{\mathsf {p}} (X) \ge 1/2$
for any
 $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
4.5 Smooth points on
 $H_x$
for families with
$H_x$
for families with
 $1 < a_1 = a_2$
$1 < a_1 = a_2$
The aim of this section is to prove the following.
Proposition 4.19. Let
![]() $X = X_d \subset \mathbb {P} (1, a_1, \dots , a_4)$
,
$X = X_d \subset \mathbb {P} (1, a_1, \dots , a_4)$
,
![]() $a_1 \le \dots \le a_4$
, be a member of a family
$a_1 \le \dots \le a_4$
, be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
such that
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
such that
![]() $1 < a_1 = a_2$
. Then
$1 < a_1 = a_2$
. Then
for any smooth point
![]() $\mathsf {p} \in X$
contained in
$\mathsf {p} \in X$
contained in
![]() $H_x$
.
$H_x$
.
Note that a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfies the assumption of Proposition 4.19 if and only if
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
satisfies the assumption of Proposition 4.19 if and only if
4.5.a The family
 $\mathcal {F}_{18}$
$\mathcal {F}_{18}$
This subsection is devoted to the proof of Proposition 4.19 for the family
![]() $\mathcal {F}_{18}$
. Let
$\mathcal {F}_{18}$
. Let
![]() $X = X_{12} \subset \mathbb {P} (1, 2, 2, 3, 5)$
be a member of
$X = X_{12} \subset \mathbb {P} (1, 2, 2, 3, 5)$
be a member of
![]() $\mathcal {F}_{18}$
.
$\mathcal {F}_{18}$
.
By the quasi-smoothness of X, We have
![]() $t^4 \in F$
and we may assume
$t^4 \in F$
and we may assume
![]() $\operatorname {coeff}_F (t^4) = 1$
by rescaling t. We have
$\operatorname {coeff}_F (t^4) = 1$
by rescaling t. We have
![]() $(x = y = z = 0) \cap X = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
. Hence, we may assume
$(x = y = z = 0) \cap X = \{\mathsf {p}_w\} \subset \operatorname {Sing} (X)$
. Hence, we may assume
![]() $\mathsf {p} \in H_y$
and
$\mathsf {p} \in H_y$
and
![]() $\mathsf {p} \notin H_z$
after possibly replacing y and z, and we can write
$\mathsf {p} \notin H_z$
after possibly replacing y and z, and we can write
![]() $\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!\mu )$
for some
$\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!\mu )$
for some
![]() $\lambda , \mu \in \mathbb {C}$
. We can write
$\lambda , \mu \in \mathbb {C}$
. We can write
where
![]() $\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. We will derive a contradiction by assuming
$\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. We will derive a contradiction by assuming
![]() $\alpha _{\mathsf {p}} (X) < 1/2$
. By the assumption, there exists an irreducible
$\alpha _{\mathsf {p}} (X) < 1/2$
. By the assumption, there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
such that
$D \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) < 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;D) < 1/2$
.
Suppose
![]() $\lambda \ne 0$
. Then, by replacing w by
$\lambda \ne 0$
. Then, by replacing w by
![]() $\lambda w - \mu z t$
, we may assume
$\lambda w - \mu z t$
, we may assume
![]() $\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!0)$
. Let S be a general member of the pencil
$\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!0)$
. Let S be a general member of the pencil
![]() $|\mathcal {I}_{\mathsf {p}} (2 A)|$
so that
$|\mathcal {I}_{\mathsf {p}} (2 A)|$
so that
![]() $\frac {1}{2} S \ne D$
. We can take a
$\frac {1}{2} S \ne D$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |5 A|_{\mathbb {Q}}$
such that
$T \in |5 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S$
since
$D \cdot S$
since
![]() $\{x, y, w\}$
isolates
$\{x, y, w\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
. This is impossible, and we have
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
. This is impossible, and we have
![]() $\lambda = 0$
.
$\lambda = 0$
.
By rescaling w, we may assume
![]() $\mathsf {p} = (0\!:\!0\!:\!1\!:\!0\!:\!1)$
. Suppose
$\mathsf {p} = (0\!:\!0\!:\!1\!:\!0\!:\!1)$
. Suppose
![]() $\alpha \ne 0$
. Then we have
$\alpha \ne 0$
. Then we have
![]() $\delta = - \alpha $
since
$\delta = - \alpha $
since
![]() $F (\mathsf {p}) = 0$
. In this case,
$F (\mathsf {p}) = 0$
. In this case,
![]() $H_x$
is smooth at
$H_x$
is smooth at
![]() $\mathsf {p}$
since
$\mathsf {p}$
since
![]() $(\partial F/\partial z) (\mathsf {p}) = - 5 \alpha \ne 0$
. In particular,
$(\partial F/\partial z) (\mathsf {p}) = - 5 \alpha \ne 0$
. In particular,
![]() $H_x \ne D$
. We can take a
$H_x \ne D$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |3 A|_{\mathbb {Q}}$
such that
$T \in |3 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
since
$D \cdot H_x$
since
![]() $\{x, y, t\}$
isolates
$\{x, y, t\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge 5/3$
. This is impossible, and we have
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge 5/3$
. This is impossible, and we have
![]() $\alpha = 0$
. Note that
$\alpha = 0$
. Note that
![]() $\delta = 0$
since
$\delta = 0$
since
![]() $F (\mathsf {p}) = 0$
, and we have
$F (\mathsf {p}) = 0$
, and we have
We claim
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
. We set
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
. We set
![]() $\zeta := \operatorname {coeff}_F (w^2 y)$
and
$\zeta := \operatorname {coeff}_F (w^2 y)$
and
![]() $\eta := \operatorname {coeff}_F (z^5 y)$
. By the quasi-smoothness of X, we see
$\eta := \operatorname {coeff}_F (z^5 y)$
. By the quasi-smoothness of X, we see
![]() $\zeta , \eta \ne 0$
since
$\zeta , \eta \ne 0$
since
![]() $w^2 y, z^6 \notin F$
. We have
$w^2 y, z^6 \notin F$
. We have
If either
![]() $\zeta + \eta \ne 0$
or
$\zeta + \eta \ne 0$
or
![]() $\beta \ne 0$
, then we have
$\beta \ne 0$
, then we have
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) = 1$
. If
$\operatorname {mult}_{\mathsf {p}} (H_x) = 1$
. If
![]() $\zeta + \eta = \beta = 0$
, then we have
$\zeta + \eta = \beta = 0$
, then we have
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) = 2$
since the term
$\operatorname {mult}_{\mathsf {p}} (H_x) = 2$
since the term
![]() $\zeta y (w^2 - z^5)$
appears in F. Thus, the claim is proved.
$\zeta y (w^2 - z^5)$
appears in F. Thus, the claim is proved.
By the claim, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
and in particular
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
and in particular
![]() $D \ne H_x$
. We can take a
$D \ne H_x$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |10 A|_{\mathbb {Q}}$
such that
$T \in |10 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot H_x$
since
$D \cdot H_x$
since
![]() $\{x, y, t, w^2 - z^5\}$
isolates
$\{x, y, t, w^2 - z^5\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
. This is a contradiction and the proof is completed.
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
. This is a contradiction and the proof is completed.
4.5.b The family
 $\mathcal {F}_{22}$
$\mathcal {F}_{22}$
This subsection is devoted to the proof of Proposition 4.19 for the family
![]() $\mathcal {F}_{22}$
. Let
$\mathcal {F}_{22}$
. Let
![]() $X = X_{14} \subset \mathbb {P} (1, 2, 2, 3, 7)$
be a member of
$X = X_{14} \subset \mathbb {P} (1, 2, 2, 3, 7)$
be a member of
![]() $\mathcal {F}_{22}$
.
$\mathcal {F}_{22}$
.
By the quasi-smoothness of X, we have
![]() $w^2 \in F$
and we may assume
$w^2 \in F$
and we may assume
![]() $\operatorname {coeff}_F (w^2) = 1$
by rescaling w. We see that
$\operatorname {coeff}_F (w^2) = 1$
by rescaling w. We see that
![]() $(x = y = z = 0) \cap X = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. Hence, we may assume
$(x = y = z = 0) \cap X = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. Hence, we may assume
![]() $\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!\mu )$
for some
$\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!\mu )$
for some
![]() $\lambda , \mu \in \mathbb {C}$
after possibly replacing y and z. We can write
$\lambda , \mu \in \mathbb {C}$
after possibly replacing y and z. We can write
where
![]() $\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. We will derive a contradiction by assuming
$\alpha , \beta , \gamma , \delta \in \mathbb {C}$
. We will derive a contradiction by assuming
![]() $\alpha _{\mathsf {p}} (X) < 1/2$
. By the assumption, there exists an irreducible
$\alpha _{\mathsf {p}} (X) < 1/2$
. By the assumption, there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
such that
$D \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) < 1/2$
. Let S be a general member of the pencil
$\operatorname {lct}_{\mathsf {p}} (X;D) < 1/2$
. Let S be a general member of the pencil
![]() $|\mathcal {I}_{\mathsf {p}} (2 A)|$
so that
$|\mathcal {I}_{\mathsf {p}} (2 A)|$
so that
![]() $\frac {1}{2} S \ne D$
.
$\frac {1}{2} S \ne D$
.
Suppose
![]() $\lambda = 0$
. In this case, we can take a
$\lambda = 0$
. In this case, we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |3 A|_{\mathbb {Q}}$
such that
$T \in |3 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S$
since
$D \cdot S$
since
![]() $\{x, y, t\}$
isolates
$\{x, y, t\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
. This is impossible, and we have
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
. This is impossible, and we have
![]() $\lambda \ne 0$
.
$\lambda \ne 0$
.
Replacing w by
![]() $\lambda w - \mu t z^2$
, we may assume
$\lambda w - \mu t z^2$
, we may assume
![]() $\mu = 0$
, that is,
$\mu = 0$
, that is,
![]() $\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!0)$
. We see that the set
$\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!0)$
. We see that the set
![]() $\{x, y, t^2 - \lambda ^2 z^3\}$
isolates
$\{x, y, t^2 - \lambda ^2 z^3\}$
isolates
![]() $\mathsf {p}$
. It follows that we can take a
$\mathsf {p}$
. It follows that we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |6 A|_{\mathbb {Q}}$
such that
$T \in |6 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
which does not contain any component of
$\operatorname {Supp} (T)$
which does not contain any component of
![]() $D \cdot S$
. Then we have
$D \cdot S$
. Then we have
which implies
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
. This is a contradiction, and the proof is completed.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
. This is a contradiction, and the proof is completed.
4.5.c The family
 $\mathcal {F}_{28}$
$\mathcal {F}_{28}$
This subsection is devoted to the proof of Proposition 4.19 for the family
![]() $\mathcal {F}_{28}$
. Let
$\mathcal {F}_{28}$
. Let
![]() $X = X_{15} \subset \mathbb {P} (1, 3, 3, 4, 5)$
be a member of
$X = X_{15} \subset \mathbb {P} (1, 3, 3, 4, 5)$
be a member of
![]() $\mathcal {F}_{28}$
.
$\mathcal {F}_{28}$
.
By the quasi-smoothness of X, we have
![]() $w^3 \in F$
and we may assume
$w^3 \in F$
and we may assume
![]() $\operatorname {coeff}_F (w^3) = 1$
by rescaling w. We see that
$\operatorname {coeff}_F (w^3) = 1$
by rescaling w. We see that
![]() $(x = y = z = 0) \cap X = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. Hence, we may assume
$(x = y = z = 0) \cap X = \{\mathsf {p}_t\} \subset \operatorname {Sing} (X)$
. Hence, we may assume
![]() $\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!\mu )$
for some
$\mathsf {p} = (0\!:\!0\!:\!1\!:\!\lambda \!:\!\mu )$
for some
![]() $\lambda , \mu \in \mathbb {C}$
after possibly replacing y and z. We can write
$\lambda , \mu \in \mathbb {C}$
after possibly replacing y and z. We can write
where
![]() $\alpha , \beta , \gamma \in \mathbb {C}$
. We will derive a contradiction by assuming
$\alpha , \beta , \gamma \in \mathbb {C}$
. We will derive a contradiction by assuming
![]() $\alpha _{\mathsf {p}} (X) < 1/2$
. By the assumption, there exists an irreducible
$\alpha _{\mathsf {p}} (X) < 1/2$
. By the assumption, there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
such that
$D \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) < 1/2$
. Let S be a general member of the pencil
$\operatorname {lct}_{\mathsf {p}} (X;D) < 1/2$
. Let S be a general member of the pencil
![]() $|\mathcal {I}_{\mathsf {p}} (3 A)|$
so that
$|\mathcal {I}_{\mathsf {p}} (3 A)|$
so that
![]() $\operatorname {Supp} (S) \ne \operatorname {Supp} (D)$
.
$\operatorname {Supp} (S) \ne \operatorname {Supp} (D)$
.
Suppose
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
![]() $\mu \ne 0$
. In this case, the set
$\mu \ne 0$
. In this case, the set
![]() $\{x, y, \mu t^2 - \lambda ^2 w z\}$
isolates
$\{x, y, \mu t^2 - \lambda ^2 w z\}$
isolates
![]() $\mathsf {p}$
, and we can take a
$\mathsf {p}$
, and we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |8 A|_{\mathbb {Q}}$
such that
$T \in |8 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S$
. Then we have
$D \cdot S$
. Then we have
which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
. This is impossible, and we have either
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1/2$
. This is impossible, and we have either
![]() $\lambda = 0$
or
$\lambda = 0$
or
![]() $\mu = 0$
.
$\mu = 0$
.
Suppose
![]() $\lambda = 0$
. In this case, we can take a
$\lambda = 0$
. In this case, we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |4 A|_{\mathbb {Q}}$
such that
$T \in |4 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S$
since
$D \cdot S$
since
![]() $\{x, y, t\}$
isolates
$\{x, y, t\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
which implies
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
. This is impossible. We have
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
. This is impossible. We have
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
![]() $\mu = 0$
. In this case, we may assume
$\mu = 0$
. In this case, we may assume
![]() $\lambda = 1$
by rescaling t, that is, we may assume
$\lambda = 1$
by rescaling t, that is, we may assume
![]() $\mathsf {p} = (0\!:\!0\!:\!1\!:\!1\!:\!0)$
.
$\mathsf {p} = (0\!:\!0\!:\!1\!:\!1\!:\!0)$
.
We claim
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
. We set
$\operatorname {mult}_{\mathsf {p}} (H_x) \le 2$
. We set
![]() $\zeta := \operatorname {coeff}_F (t^3 y)$
and
$\zeta := \operatorname {coeff}_F (t^3 y)$
and
![]() $\eta := \operatorname {coeff}_F (z^4 y)$
. We have
$\eta := \operatorname {coeff}_F (z^4 y)$
. We have
![]() $\beta + \gamma = 0$
since
$\beta + \gamma = 0$
since
![]() $F (\mathsf {p}) = 0$
. Then
$F (\mathsf {p}) = 0$
. Then
If either
![]() $\gamma \ne 0$
or
$\gamma \ne 0$
or
![]() $\zeta + \eta \ne 0$
, then we have
$\zeta + \eta \ne 0$
, then we have
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) = 1$
. It remains to consider the case where
$\operatorname {mult}_{\mathsf {p}} (H_x) = 1$
. It remains to consider the case where
![]() $\gamma = \zeta + \eta = 0$
. Note that we have
$\gamma = \zeta + \eta = 0$
. Note that we have
![]() $\beta = 0$
since
$\beta = 0$
since
![]() $\beta + \gamma = 0$
. By the quasi-smoothness of X at
$\beta + \gamma = 0$
. By the quasi-smoothness of X at
![]() $\mathsf {p}_t$
, we have
$\mathsf {p}_t$
, we have
![]() $\zeta \ne 0$
. Then we see that
$\zeta \ne 0$
. Then we see that
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) = 2$
since the term
$\operatorname {mult}_{\mathsf {p}} (H_x) = 2$
since the term
![]() $\zeta y (t^3 - z^4)$
appears in F. Thus, the claim is proved.
$\zeta y (t^3 - z^4)$
appears in F. Thus, the claim is proved.
By the claim, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
and in particular
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
and in particular
![]() $D \ne H_x$
. We can take a
$D \ne H_x$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |12 A|_{\mathbb {Q}}$
such that
$T \in |12 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
since
$D \cdot H_x$
since
![]() $\{x, y, w, t^3 - z^4\}$
isolates
$\{x, y, w, t^3 - z^4\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
which implies
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
. This is a contradiction and the proof is completed.
$\alpha _{\mathsf {p}} (X) \ge 1$
. This is a contradiction and the proof is completed.
5 Singular points
The aim of this section is to prove the following.
Theorem 5.1. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then
for any singular point
![]() $\mathsf {p} \in X$
.
$\mathsf {p} \in X$
.
Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then the inequality
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
. Then the inequality
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
will follow from Propositions 5.2, 5.3, 5.5 for singular points
$\alpha _{\mathsf {p}} (X) \ge 1/2$
will follow from Propositions 5.2, 5.3, 5.5 for singular points
![]() $\mathsf {p} \in X$
which are not BI centers; from Proposition 5.6 for EI centers; and from Propositions 5.15, 5.16 and 5.18 for QI centers. This will complete the proof of Theorem 5.1.
$\mathsf {p} \in X$
which are not BI centers; from Proposition 5.6 for EI centers; and from Propositions 5.15, 5.16 and 5.18 for QI centers. This will complete the proof of Theorem 5.1.
5.1 Non-BI centers
Throughout the present section, let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
.
$\mathsf {i} \in \mathsf {I}$
.
5.1.a Computation by
 $\operatorname {\overline {NE}} (Y)$
$\operatorname {\overline {NE}} (Y)$
Proposition 5.2. Let
![]() $\mathsf {p} \in X$
be a singular point with subscript
$\mathsf {p} \in X$
be a singular point with subscript
![]() $\heartsuit $
in the fifth column of Table 7, and let
$\heartsuit $
in the fifth column of Table 7, and let
![]() $\varphi \colon Y \to X$
be the Kawamata blowup at
$\varphi \colon Y \to X$
be the Kawamata blowup at
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
![]() $(-K_Y)^2 \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
and
$(-K_Y)^2 \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
and
![]() $\tilde {D} \sim -K_Y$
for the proper transform of a general member
$\tilde {D} \sim -K_Y$
for the proper transform of a general member
![]() $D \in |A|$
. In particular, we have
$D \in |A|$
. In particular, we have
Proof. Let
![]() $r> 1$
be the index of the quotient singular point
$r> 1$
be the index of the quotient singular point
![]() $\mathsf {p} \in X$
. For every instance, we have either
$\mathsf {p} \in X$
. For every instance, we have either
![]() $a_1 = 1$
or
$a_1 = 1$
or
![]() $d - 1$
is not divisible by r. This means that we can take x as a part of local orbifold coordinates of X at
$d - 1$
is not divisible by r. This means that we can take x as a part of local orbifold coordinates of X at
![]() $\mathsf {p}$
, and hence
$\mathsf {p}$
, and hence
![]() $\tilde {D} \sim - K_Y$
for a general
$\tilde {D} \sim - K_Y$
for a general
![]() $D \in |A|$
. The point
$D \in |A|$
. The point
![]() $\mathsf {p}$
is excluded as a maximal center by either Lemma 3.2.2 or 3.2.4 of [Reference Cheltsov and ParkCP17].
$\mathsf {p}$
is excluded as a maximal center by either Lemma 3.2.2 or 3.2.4 of [Reference Cheltsov and ParkCP17].
We set
![]() $S := \tilde {D} \sim - K_Y$
, where
$S := \tilde {D} \sim - K_Y$
, where
![]() $D \in |A|$
is a general member. If
$D \in |A|$
is a general member. If
![]() $\mathsf {p}$
is excluded by [Reference Cheltsov and ParkCP17, Lemma 3.2.2], then it follows from its proof that
$\mathsf {p}$
is excluded by [Reference Cheltsov and ParkCP17, Lemma 3.2.2], then it follows from its proof that
![]() $(- K_Y)^2 = (-K_Y) \cdot S \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
. If
$(- K_Y)^2 = (-K_Y) \cdot S \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
. If
![]() $\mathsf {p}$
is excluded by [Reference Cheltsov and ParkCP17, Lemma 3.2.4], then there exists a nef divisor T on Y such that
$\mathsf {p}$
is excluded by [Reference Cheltsov and ParkCP17, Lemma 3.2.4], then there exists a nef divisor T on Y such that
![]() $(T \cdot S \cdot - K_Y) \le 0$
, which implies
$(T \cdot S \cdot - K_Y) \le 0$
, which implies
![]() $(-K_Y)^2 = (-K_Y) \cdot S \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
. The latter assertion follows from Lemma 3.30.
$(-K_Y)^2 = (-K_Y) \cdot S \notin \operatorname {Int} \operatorname {\overline {NE}} (Y)$
. The latter assertion follows from Lemma 3.30.
5.1.b Computation by
 $L_{xy}$
$L_{xy}$
Proposition 5.3. Let
![]() $\mathsf {p} \in X$
be a singular point with the subscript
$\mathsf {p} \in X$
be a singular point with the subscript
![]() $\diamondsuit $
or
$\diamondsuit $
or
![]() $\diamondsuit '$
in the fifth column of Table 7, and let
$\diamondsuit '$
in the fifth column of Table 7, and let
![]() $q = q_{\mathsf {p}}$
be the quotient morphism of
$q = q_{\mathsf {p}}$
be the quotient morphism of
![]() $\mathsf {p} \in X$
. We denote by r the index of the cyclic quotient singularity
$\mathsf {p} \in X$
. We denote by r the index of the cyclic quotient singularity
![]() $\mathsf {p} \in X$
. Let
$\mathsf {p} \in X$
. Let
![]() $S \in |A|$
and
$S \in |A|$
and
![]() $T \in |a_1 A|$
be general members. Then the following assertions hold.
$T \in |a_1 A|$
be general members. Then the following assertions hold.
-
1. The pair
 $(X, S)$
is log canonical at
$(X, S)$
is log canonical at
 $\mathsf {p}$
.
$\mathsf {p}$
. -
2. The intersection
 $S \cap T$
is irreducible, and we have
$S \cap T$
is irreducible, and we have
 $q^*S \cdot q^*T = \check {\Gamma }$
, where
$q^*S \cdot q^*T = \check {\Gamma }$
, where
 $\check {\Gamma }$
is an irreducible and reduced curve such that
$\check {\Gamma }$
is an irreducible and reduced curve such that  $$\begin{align*}0 < \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma}) \le a_1. \end{align*}$$
$$\begin{align*}0 < \operatorname{mult}_{\check{\mathsf{p}}} (\check{\Gamma}) \le a_1. \end{align*}$$
-
3. We have
 $$\begin{align*}r a_1 (A^3) \le \begin{cases} 1, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit, \\ \frac{3}{2}, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit'. \end{cases} \end{align*}$$
$$\begin{align*}r a_1 (A^3) \le \begin{cases} 1, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit, \\ \frac{3}{2}, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit'. \end{cases} \end{align*}$$
In particular,
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} 1, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit, \\ \frac{3}{2}, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit'. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} 1, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit, \\ \frac{3}{2}, & \text{if the subscript of}\ \mathsf{p}\ \text{is}\ \diamondsuit'. \end{cases} \end{align*}$$
Proof. Let
![]() $\mathsf {p} \in X$
be as in the statement. The assertion (3) can be checked individually, and it remains to consider (1) and (2).
$\mathsf {p} \in X$
be as in the statement. The assertion (3) can be checked individually, and it remains to consider (1) and (2).
It is straightforward to check that X is a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
which is listed in one of the Tables 1 and 2. It follows that
$\mathcal {F}_{\mathsf {i}}$
which is listed in one of the Tables 1 and 2. It follows that
![]() $S \cap T = L_{xy}$
is irreducible. It is easy to check that we may assume
$S \cap T = L_{xy}$
is irreducible. It is easy to check that we may assume
![]() $\mathsf {p} = \mathsf {p}_{v}$
for some
$\mathsf {p} = \mathsf {p}_{v}$
for some
![]() $v \in \{z, t, w\}$
after replacing coordinates. Let
$v \in \{z, t, w\}$
after replacing coordinates. Let
![]() $\rho = \rho _v \colon \breve {U}_v \to U_v$
be the orbifold chart. We set
$\rho = \rho _v \colon \breve {U}_v \to U_v$
be the orbifold chart. We set
![]() $\breve {\Gamma } = (\breve {x} = \breve {y} = 0) \subset U_v$
. We see that
$\breve {\Gamma } = (\breve {x} = \breve {y} = 0) \subset U_v$
. We see that
![]() $\breve {\Gamma }$
is an irreducible and reduced curve since so is
$\breve {\Gamma }$
is an irreducible and reduced curve since so is
![]() $L_{xy}$
, and that
$L_{xy}$
, and that
![]() $\rho ^*S \cdot \rho ^*T = \breve {\Gamma }$
. Note that q can be identified with
$\rho ^*S \cdot \rho ^*T = \breve {\Gamma }$
. Note that q can be identified with
![]() $\rho $
over a suitable analytic neighborhood of
$\rho $
over a suitable analytic neighborhood of
![]() $\mathsf {p} \in U_v$
, and hence it is enough to prove the inequality
$\mathsf {p} \in U_v$
, and hence it is enough to prove the inequality
![]() $\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) \le a_1$
for the proof of (2).
$\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) \le a_1$
for the proof of (2).
If X is listed in Table 1, then
![]() $\breve {\Gamma }$
is irreducible and smooth by Lemma 4.9. In this case, S is quasi-smooth at
$\breve {\Gamma }$
is irreducible and smooth by Lemma 4.9. In this case, S is quasi-smooth at
![]() $\mathsf {p}$
and thus both (1) and (2) are clearly satisfied.
$\mathsf {p}$
and thus both (1) and (2) are clearly satisfied.
Suppose that X is listed in Table 2. Then X is a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
, where
$\mathcal {F}_{\mathsf {i}}$
, where
If
![]() $\mathsf {p}$
is not the unique singular point of
$\mathsf {p}$
is not the unique singular point of
![]() $L_{xy}$
which is described in Table 2, then (1) and (2) follow immediately. Suppose that
$L_{xy}$
which is described in Table 2, then (1) and (2) follow immediately. Suppose that
![]() $\mathsf {p}$
is the unique singular point of
$\mathsf {p}$
is the unique singular point of
![]() $L_{xy}$
. Then we have
$L_{xy}$
. Then we have
![]() $\mathsf {i} \in \{44, 61, 83\}$
and
$\mathsf {i} \in \{44, 61, 83\}$
and
![]() $\mathsf {p} = \mathsf {p}_t$
. By the equation given in Table 2, we compute
$\mathsf {p} = \mathsf {p}_t$
. By the equation given in Table 2, we compute
![]() $\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) = 2$
. This shows (2) since
$\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) = 2$
. This shows (2) since
![]() $a_1 \ge 2$
. We see that
$a_1 \ge 2$
. We see that
![]() $r = a_3$
does not divide
$r = a_3$
does not divide
![]() $d-1$
, which implies that S is quasi-smooth at
$d-1$
, which implies that S is quasi-smooth at
![]() $\mathsf {p}$
and hence (1) follows. Therefore, (1), (2) and (3) are verified and the assertion on
$\mathsf {p}$
and hence (1) follows. Therefore, (1), (2) and (3) are verified and the assertion on
![]() $\alpha _{\mathsf {p}} (X)$
follows from Lemma 3.17.
$\alpha _{\mathsf {p}} (X)$
follows from Lemma 3.17.
5.1.c Computation by isolating class
Proposition 5.4. Let
![]() $\mathsf {p} \in X$
be a singular point with subscript
$\mathsf {p} \in X$
be a singular point with subscript
![]() $\clubsuit $
in the fifth column of Table 7 which is also listed in Table 3. Then the set of coordinates given in the fifth column of Table 3 isolates
$\clubsuit $
in the fifth column of Table 7 which is also listed in Table 3. Then the set of coordinates given in the fifth column of Table 3 isolates
![]() $\mathsf {p}$
. In particular, we have
$\mathsf {p}$
. In particular, we have
where c is the number given in the seventh column of Table 3.
Table 3 Isolating set.

Proof. Let
![]() $\mathcal {C}$
be the set of homogeneous coordinates given in the fifth column of Table 3. It is straightforward to check that
$\mathcal {C}$
be the set of homogeneous coordinates given in the fifth column of Table 3. It is straightforward to check that
is a finite set of points including
![]() $\mathsf {p}$
, which shows that
$\mathsf {p}$
, which shows that
![]() $\mathcal {C}$
isolates
$\mathcal {C}$
isolates
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Let c be the number listed in the seventh column of Table 3, and assume that
![]() $\alpha _{\mathsf {p}} (X) < \min \{1, c\}$
. Then there exists an irreducible
$\alpha _{\mathsf {p}} (X) < \min \{1, c\}$
. Then there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \sim _{\mathbb {Q}} A$
such that
$D \sim _{\mathbb {Q}} A$
such that
![]() $(X, c D)$
is not log canonical at
$(X, c D)$
is not log canonical at
![]() $\mathsf {p}$
. In particular, we have
$\mathsf {p}$
. In particular, we have
![]() $\operatorname {omult}_{\mathsf {p}} (D)> 1/c$
. If
$\operatorname {omult}_{\mathsf {p}} (D)> 1/c$
. If
![]() $H_x$
(resp.
$H_x$
(resp.
![]() $|n A|$
for some
$|n A|$
for some
![]() $n> 0$
) is given in the fourth column of Table 3, then we set
$n> 0$
) is given in the fourth column of Table 3, then we set
![]() $S := H_x$
(resp. we define S to be a general member of
$S := H_x$
(resp. we define S to be a general member of
![]() $|n A|$
). We set
$|n A|$
). We set
![]() $n = 1$
if
$n = 1$
if
![]() $S = H_x$
so that
$S = H_x$
so that
![]() $S \sim n A$
in any case. Let r be the index of the cyclic quotient singularity
$S \sim n A$
in any case. Let r be the index of the cyclic quotient singularity
![]() $\mathsf {p} \in X$
. We claim that
$\mathsf {p} \in X$
. We claim that
![]() $\operatorname {Supp} (D)$
is not contained in S. This is clear when
$\operatorname {Supp} (D)$
is not contained in S. This is clear when
![]() $S \in |nA|$
is a general member. Suppose that
$S \in |nA|$
is a general member. Suppose that
![]() $S = H_x$
. Then we see that
$S = H_x$
. Then we see that
![]() $d-1$
is not divisible by r, which implies that
$d-1$
is not divisible by r, which implies that
![]() $S = H_x$
is quasi-smooth at
$S = H_x$
is quasi-smooth at
![]() $\mathsf {p}$
. Hence,
$\mathsf {p}$
. Hence,
![]() $(X, S)$
is log canonical at
$(X, S)$
is log canonical at
![]() $\mathsf {p}$
and we have
$\mathsf {p}$
and we have
![]() $D \ne H_x$
as desired. By the claim,
$D \ne H_x$
as desired. By the claim,
![]() $D \cdot S$
is an effective
$D \cdot S$
is an effective
![]() $1$
-cycle on X. Let e be the integer given in the sixth column of Table 3. Note that
$1$
-cycle on X. Let e be the integer given in the sixth column of Table 3. Note that
![]() $e = \max \{\, \deg v \mid v \in \mathcal {C} \,\}$
and
$e = \max \{\, \deg v \mid v \in \mathcal {C} \,\}$
and
There exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \sim _{\mathbb {Q}} e A$
such that
$T \sim _{\mathbb {Q}} e A$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot S$
since
$D \cdot S$
since
![]() $\mathcal {C}$
isolates
$\mathcal {C}$
isolates
![]() $\mathsf {p}$
. It follows that
$\mathsf {p}$
. It follows that
where
![]() $q = q_{\mathsf {p}}$
is the quotient morphism of
$q = q_{\mathsf {p}}$
is the quotient morphism of
![]() $\mathsf {p} \in X$
and
$\mathsf {p} \in X$
and
![]() $\check {\mathsf {p}}$
is the preimage of
$\check {\mathsf {p}}$
is the preimage of
![]() $\mathsf {p}$
via q. This is a contradiction and the inequality
$\mathsf {p}$
via q. This is a contradiction and the inequality
![]() $\alpha _{\mathsf {p}} (X) \ge \min \{1, c\}$
is proved.
$\alpha _{\mathsf {p}} (X) \ge \min \{1, c\}$
is proved.
5.1.d Remaining non-BI centers
Proposition 5.5. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
, and let
$\mathsf {i} \in \mathsf {I}$
, and let
![]() $\mathsf {p} \in X$
be a singular point with subscript
$\mathsf {p} \in X$
be a singular point with subscript
![]() $\spadesuit $
in the fifth column of Table 7 which is also listed below.
$\spadesuit $
in the fifth column of Table 7 which is also listed below.
-
•
 $\mathsf {i} = 12$
and singular points of type
$\mathsf {i} = 12$
and singular points of type
 $\frac {1}{2} (1,1,1)$
.
$\frac {1}{2} (1,1,1)$
. -
•
 $\mathsf {i} = 13$
and the singular point of type
$\mathsf {i} = 13$
and the singular point of type
 $\frac {1}{2} (1,1,1)$
.
$\frac {1}{2} (1,1,1)$
. -
•
 $\mathsf {i} = 24$
and the singular point of type
$\mathsf {i} = 24$
and the singular point of type
 $\frac {1}{2} (1,1,1)$
.
$\frac {1}{2} (1,1,1)$
. -
•
 $\mathsf {i} = 27$
and the singular point of type
$\mathsf {i} = 27$
and the singular point of type
 $\frac {1}{2} (1,1,1)$
.
$\frac {1}{2} (1,1,1)$
. -
•
 $\mathsf {i} = 32$
and the singular point of type
$\mathsf {i} = 32$
and the singular point of type
 $\frac {1}{3} (1,1,2)$
.
$\frac {1}{3} (1,1,2)$
. -
•
 $\mathsf {i} = 33$
and the singular point of type
$\mathsf {i} = 33$
and the singular point of type
 $\frac {1}{2} (1,1,1)$
.
$\frac {1}{2} (1,1,1)$
. -
•
 $\mathsf {i} = 40$
and the singular point of type
$\mathsf {i} = 40$
and the singular point of type
 $\frac {1}{3} (1,1,2)$
.
$\frac {1}{3} (1,1,2)$
. -
•
 $\mathsf {i} = 47$
and the singular point of type
$\mathsf {i} = 47$
and the singular point of type
 $\frac {1}{5} (1, 2, 3)$
.
$\frac {1}{5} (1, 2, 3)$
. -
•
 $\mathsf {i} = 48$
and the singular point of type
$\mathsf {i} = 48$
and the singular point of type
 $\frac {1}{2} (1,1,1)$
.
$\frac {1}{2} (1,1,1)$
. -
•
 $\mathsf {i} = 49$
and the singular point of type
$\mathsf {i} = 49$
and the singular point of type
 $\frac {1}{5} (1, 2, 3)$
.
$\frac {1}{5} (1, 2, 3)$
. -
•
 $\mathsf {i} = 62$
and the singular point of type
$\mathsf {i} = 62$
and the singular point of type
 $\frac {1}{5} (1, 2, 3)$
.
$\frac {1}{5} (1, 2, 3)$
. -
•
 $\mathsf {i} = 65$
and the singular point of type
$\mathsf {i} = 65$
and the singular point of type
 $\frac {1}{2} (1, 1, 1)$
.
$\frac {1}{2} (1, 1, 1)$
. -
•
 $\mathsf {i} = 67$
and the singular point of type
$\mathsf {i} = 67$
and the singular point of type
 $\frac {1}{9} (1, 4, 5)$
.
$\frac {1}{9} (1, 4, 5)$
. -
•
 $\mathsf {i} = 82$
and the singular point of type
$\mathsf {i} = 82$
and the singular point of type
 $\frac {1}{5} (1, 2, 3)$
.
$\frac {1}{5} (1, 2, 3)$
. -
•
 $\mathsf {i} = 84$
and the singular point of type
$\mathsf {i} = 84$
and the singular point of type
 $\frac {1}{7} (1, 2, 5)$
.
$\frac {1}{7} (1, 2, 5)$
.
Then we have
The rest of this subsection is to prove Proposition 5.5 which will be separately for each family.
5.1.d.1 The family
 $\mathcal {F}_{12}$
, points of type
$\mathcal {F}_{12}$
, points of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $X = X_{10} \subset \mathbb {P} (1, 1, 2, 3, 4)$
be a member of
$X = X_{10} \subset \mathbb {P} (1, 1, 2, 3, 4)$
be a member of
![]() $\mathcal {F}_{12}$
and
$\mathcal {F}_{12}$
and
![]() $\mathsf {p}$
a singular point of type
$\mathsf {p}$
a singular point of type
![]() $\frac {1}{2} (1,1,1)$
. We may assume
$\frac {1}{2} (1,1,1)$
. We may assume
![]() $\mathsf {p} = \mathsf {p}_z$
after replacing w. Then we have
$\mathsf {p} = \mathsf {p}_z$
after replacing w. Then we have
![]() $z^3 w \in F$
by the quasi-smoothness of X at
$z^3 w \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}$
. By Lemma 3.29, we have
$\mathsf {p}$
. By Lemma 3.29, we have
and the proof is completed in this case.
5.1.d.2 The family
 $\mathcal {F}_{13}$
, the singular point of type
$\mathcal {F}_{13}$
, the singular point of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $X = X_{11} \subset \mathbb {P} (1, 1, 2, 3, 5)$
be a member of
$X = X_{11} \subset \mathbb {P} (1, 1, 2, 3, 5)$
be a member of
![]() $\mathcal {F}_{13}$
and
$\mathcal {F}_{13}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
the singular point of type
$\mathsf {p} = \mathsf {p}_z$
the singular point of type
![]() $\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
$\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 1 \cdot 3 \cdot (A^3)} = \frac{10}{11}, & \text{if}\ z^3 w \in F, \\ \frac{2}{2 \cdot 1 \cdot 5 \cdot (A^3)} = \frac{6}{11}, & \text{if}\ z^3 w \notin F\ \text{and}\ z^4 t \in F. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 1 \cdot 3 \cdot (A^3)} = \frac{10}{11}, & \text{if}\ z^3 w \in F, \\ \frac{2}{2 \cdot 1 \cdot 5 \cdot (A^3)} = \frac{6}{11}, & \text{if}\ z^3 w \notin F\ \text{and}\ z^4 t \in F. \end{cases} \end{align*}$$
It remains to consider the case where
![]() $z^3 w, z^4 t \notin F$
. Then, by choosing
$z^3 w, z^4 t \notin F$
. Then, by choosing
![]() $x, y$
suitably, we can write
$x, y$
suitably, we can write
where
![]() $f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t \notin f_3$
and
$t \notin f_3$
and
![]() $w \notin f_5$
.
$w \notin f_5$
.
We claim
![]() $w^2 y \in F$
. Assume
$w^2 y \in F$
. Assume
![]() $w^2 y \notin F$
. Then, by the quasi-smoothness of X at
$w^2 y \notin F$
. Then, by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
, we have
$\mathsf {p}_w$
, we have
![]() $w^2 x \in F$
and we may assume
$w^2 x \in F$
and we may assume
![]() $\operatorname {coeff}_F (w^2 x) = -1$
. We can write
$\operatorname {coeff}_F (w^2 x) = -1$
. We can write
![]() $F = (z^5 - w^2) x + f'$
, where
$F = (z^5 - w^2) x + f'$
, where
![]() $f' = z^4 f_3 + z^3 f_5 + z^2 f_7 + z f_9 + f_{11} + w^2 x$
. It is straightforward to check that
$f' = z^4 f_3 + z^3 f_5 + z^2 f_7 + z f_9 + f_{11} + w^2 x$
. It is straightforward to check that
![]() $f' \in (x, y, t)^2$
and thus X is not quasi-smooth at the point
$f' \in (x, y, t)^2$
and thus X is not quasi-smooth at the point
![]() $(0\!:\!0\!:\!1\!:\!0\!:\!1) \in X$
, which is a contradiction. Thus,
$(0\!:\!0\!:\!1\!:\!0\!:\!1) \in X$
, which is a contradiction. Thus,
![]() $w^2 y \in F$
.
$w^2 y \in F$
.
We see that
![]() $\bar {F} := F (0, y, 1, t, w) \in (y, t, w)^3$
and the cubic part of
$\bar {F} := F (0, y, 1, t, w) \in (y, t, w)^3$
and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form since
$\bar {F}$
is not a cube of a linear form since
![]() $w^2 y \in \bar {F}$
and
$w^2 y \in \bar {F}$
and
![]() $w^3 \notin \bar {F}$
. Thus, we have
$w^3 \notin \bar {F}$
. Thus, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
by Lemma 3.28.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
by Lemma 3.28.
5.1.d.3 The family
 $\mathcal {F}_{24}$
, the point of type
$\mathcal {F}_{24}$
, the point of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $X = X_{15} \subset \mathbb {P} (1, 1, 2, 5, 7)$
be a member of
$X = X_{15} \subset \mathbb {P} (1, 1, 2, 5, 7)$
be a member of
![]() $\mathcal {F}_{24}$
and
$\mathcal {F}_{24}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
the singular point of type
$\mathsf {p} = \mathsf {p}_z$
the singular point of type
![]() $\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
$\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 1 \cdot 5 \cdot (A^3)} = \frac{14}{15}, & \text{if}\ z^4 w \in F, \\ \frac{2}{2 \cdot 1 \cdot 7 \cdot (A^3)} = \frac{2}{3}, & \text{if}\ z^4 w \notin F\ \text{and}\ z^5 t \in F. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 1 \cdot 5 \cdot (A^3)} = \frac{14}{15}, & \text{if}\ z^4 w \in F, \\ \frac{2}{2 \cdot 1 \cdot 7 \cdot (A^3)} = \frac{2}{3}, & \text{if}\ z^4 w \notin F\ \text{and}\ z^5 t \in F. \end{cases} \end{align*}$$
Suppose
![]() $z^4 w, z^5 t \notin F$
. Then we can write
$z^4 w, z^5 t \notin F$
. Then we can write
where
![]() $f_i = f_i (x, y, t, w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x, y, t, w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t \notin f_5$
and
$t \notin f_5$
and
![]() $w \notin f_7$
.
$w \notin f_7$
.
We claim
![]() $w^2 y \in F$
. Assume to the contrary
$w^2 y \in F$
. Assume to the contrary
![]() $w^2 y \notin F$
. Then we can write
$w^2 y \notin F$
. Then we can write
![]() $F = (z^7 + g) x + h$
, where
$F = (z^7 + g) x + h$
, where
![]() $g \in \mathbb {C} [x,y,z,t,w]$
and
$g \in \mathbb {C} [x,y,z,t,w]$
and
![]() $h \in \mathbb {C} [y,z,t,w]$
are quasi-homogeneous polynomials such that
$h \in \mathbb {C} [y,z,t,w]$
are quasi-homogeneous polynomials such that
![]() $h \in (y,t)^2$
. But then X is not quasi-smooth along the nonempty subset
$h \in (y,t)^2$
. But then X is not quasi-smooth along the nonempty subset
This is a contradiction, and the claim is proved.
We see that
![]() $\bar {F} := F (0, y, 1, t, w) \in (y,t,w)^3$
,
$\bar {F} := F (0, y, 1, t, w) \in (y,t,w)^3$
,
![]() $w^2 y \in \bar {F}$
and
$w^2 y \in \bar {F}$
and
![]() $w^3 \notin \bar {F}$
. In particular,
$w^3 \notin \bar {F}$
. In particular,
![]() $\bar {F}$
cannot be a cube of a linear form and thus
$\bar {F}$
cannot be a cube of a linear form and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
by Lemma 3.28.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
by Lemma 3.28.
5.1.d.4 The family
 $\mathcal {F}_{27}$
, the point of type
$\mathcal {F}_{27}$
, the point of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $X = X_{15} \subset \mathbb {P} (1, 2, 3, 5, 5)$
be a member of
$X = X_{15} \subset \mathbb {P} (1, 2, 3, 5, 5)$
be a member of
![]() $\mathcal {F}_{27}$
and
$\mathcal {F}_{27}$
and
![]() $\mathsf {p} = \mathsf {p}_y$
the singular point of type
$\mathsf {p} = \mathsf {p}_y$
the singular point of type
![]() $\frac {1}{2} (1,1,1)$
. If either
$\frac {1}{2} (1,1,1)$
. If either
![]() $y^5 w \in F$
or
$y^5 w \in F$
or
![]() $y^5 t \in F$
, then we have
$y^5 t \in F$
, then we have
by Lemma 3.29.
Suppose
![]() $y^5 w, y^5 t \notin F$
and
$y^5 w, y^5 t \notin F$
and
![]() $y^6 z \in F$
. Then we can write
$y^6 z \in F$
. Then we can write
where
![]() $f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $w, t \notin f_5$
. We see that
$w, t \notin f_5$
. We see that
![]() $\operatorname {omult}_{\mathsf {p}} (H_z) = 3$
and thus
$\operatorname {omult}_{\mathsf {p}} (H_z) = 3$
and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{3} H_z) \ge 1$
. Let
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{3} H_z) \ge 1$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $\frac {1}{3} H_z$
. Then we can take a
$\frac {1}{3} H_z$
. Then we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |5 A|_{\mathbb {Q}}$
such that
$T \in |5 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot H_x$
since
$D \cdot H_x$
since
![]() $\{x, z, t, w\}$
isolates
$\{x, z, t, w\}$
isolates
![]() $\mathsf {p}$
. Since
$\mathsf {p}$
. Since
![]() $\operatorname {omult}_{\mathsf {p}} (H_z) = 3$
, we have
$\operatorname {omult}_{\mathsf {p}} (H_z) = 3$
, we have
where
![]() $q = q_{\mathsf {p}}$
is the quotient morphism of
$q = q_{\mathsf {p}}$
is the quotient morphism of
![]() $\mathsf {p} \in X$
and
$\mathsf {p} \in X$
and
![]() $\check {\mathsf {p}}$
is the preimage of
$\check {\mathsf {p}}$
is the preimage of
![]() $\mathsf {p}$
via q. This shows
$\mathsf {p}$
via q. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge 1$
and thus
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge 1$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
Suppose
![]() $y^5 w, y^5 t, y^6 z \notin F$
. Then we can write
$y^5 w, y^5 t, y^6 z \notin F$
. Then we can write
where
![]() $f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $z \notin f_3$
and
$z \notin f_3$
and
![]() $w, t \notin f_5$
. We see that
$w, t \notin f_5$
. We see that
![]() $\bar {F} = F (0,1,z,t,w) \in (z,t,w)^3$
and the cubic part of
$\bar {F} = F (0,1,z,t,w) \in (z,t,w)^3$
and the cubic part of
![]() $\bar {F}$
cannot be cube of a linear form since
$\bar {F}$
cannot be cube of a linear form since
![]() $F (0,1,0,t,w) = F (0,0,0,t,w)$
is a product of three linearly independent linear forms in
$F (0,1,0,t,w) = F (0,0,0,t,w)$
is a product of three linearly independent linear forms in
![]() $t, w$
by the quasi-smoothness of X. By Lemma 3.28, we have
$t, w$
by the quasi-smoothness of X. By Lemma 3.28, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
.
5.1.d.5 The family
 $\mathcal {F}_{32}$
, the point of type
$\mathcal {F}_{32}$
, the point of type
 $\frac {1}{3} (1,1,2)$
$\frac {1}{3} (1,1,2)$
Let
![]() $X = X_{16} \subset \mathbb {P} (1, 2, 3, 4, 7)$
be a member of
$X = X_{16} \subset \mathbb {P} (1, 2, 3, 4, 7)$
be a member of
![]() $\mathcal {F}_{32}$
and
$\mathcal {F}_{32}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
the singular point of type
$\mathsf {p} = \mathsf {p}_z$
the singular point of type
![]() $\frac {1}{3} (1,1,2)$
. By Lemma 3.29, we have
$\frac {1}{3} (1,1,2)$
. By Lemma 3.29, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{3 \cdot 2 \cdot 4 \cdot (A^3)} = \frac{7}{8}, & \text{if}\ z^3 w \in F, \\ \frac{2}{3 \cdot 2 \cdot 7 \cdot (A^3)} = \frac{1}{2}, & \text{if}\ z^3 w \notin F\ \text{and}\ z^4 t \in F. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{3 \cdot 2 \cdot 4 \cdot (A^3)} = \frac{7}{8}, & \text{if}\ z^3 w \in F, \\ \frac{2}{3 \cdot 2 \cdot 7 \cdot (A^3)} = \frac{1}{2}, & \text{if}\ z^3 w \notin F\ \text{and}\ z^4 t \in F. \end{cases} \end{align*}$$
Suppose
![]() $z^3 w, z^4 t \notin F$
. Then
$z^3 w, z^4 t \notin F$
. Then
![]() $z^5 x \in F$
by the quasi-smoothness of X at
$z^5 x \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}$
and we can write
$\mathsf {p}$
and we can write
where
![]() $f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
$f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
![]() $w^2 y \in F$
by the quasi-smoothness of X at
$w^2 y \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
. It follows that either
$\mathsf {p}_w$
. It follows that either
![]() $\bar {F} = F (0,y,1,t,w) \in (y,t,w)^2 \setminus (y,t,w)^3$
or
$\bar {F} = F (0,y,1,t,w) \in (y,t,w)^2 \setminus (y,t,w)^3$
or
![]() $\bar {F} \in (y,t,w)^3$
and the cubic part of
$\bar {F} \in (y,t,w)^3$
and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form since
$\bar {F}$
is not a cube of a linear form since
![]() $w^3 \notin \bar {F}$
. By Lemma 3.28, we have
$w^3 \notin \bar {F}$
. By Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
5.1.d.6 The family
 $\mathcal {F}_{33}$
, the point of type
$\mathcal {F}_{33}$
, the point of type
 $\frac {1}{2} (1, 1, 1)$
$\frac {1}{2} (1, 1, 1)$
Let
![]() $X = X_{17} \subset \mathbb {P} (1, 2, 3, 5, 7)$
be a member of
$X = X_{17} \subset \mathbb {P} (1, 2, 3, 5, 7)$
be a member of
![]() $\mathcal {F}_{33}$
and
$\mathcal {F}_{33}$
and
![]() $\mathsf {p} = \mathsf {p}_y$
the singular point of type
$\mathsf {p} = \mathsf {p}_y$
the singular point of type
![]() $\frac {1}{2} (1, 1, 1)$
.
$\frac {1}{2} (1, 1, 1)$
.
Suppose that at least one of
![]() $y^5 w$
,
$y^5 w$
,
![]() $y^6 t$
and
$y^6 t$
and
![]() $y^7 z$
appear in F with nonzero coefficient. In this case,
$y^7 z$
appear in F with nonzero coefficient. In this case,
![]() $H_x$
is quasi-smooth at
$H_x$
is quasi-smooth at
![]() $\mathsf {p}$
and we have
$\mathsf {p}$
and we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) = 1$
. Let
$\operatorname {lct}_{\mathsf {p}} (X; H_x) = 1$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_x$
. We can take a
$H_x$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |7 A|_{\mathbb {Q}}$
such that
$T \in |7 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of of the effective
$\operatorname {Supp} (T)$
does not contain any component of of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
since the set
$D \cdot H_x$
since the set
![]() $\{x, z, t, w\}$
isolates
$\{x, z, t, w\}$
isolates
![]() $\mathsf {p}$
. It follows that
$\mathsf {p}$
. It follows that
Thus,
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge 15/17$
and we have
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge 15/17$
and we have
![]() $\alpha _{\mathsf {p}} (X) \ge 15/17$
.
$\alpha _{\mathsf {p}} (X) \ge 15/17$
.
Suppose
![]() $y^5 w, y^6 t, y^7 z \notin F$
. Then
$y^5 w, y^6 t, y^7 z \notin F$
. Then
![]() $y^8 x \in F$
by the quasi-smoothness of X at
$y^8 x \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}$
and we can write
$\mathsf {p}$
and we can write
where
![]() $f_i = f_i (x, z, t, w)$
is a quasi-homogeneous polynomial of degree i. We see that
$f_i = f_i (x, z, t, w)$
is a quasi-homogeneous polynomial of degree i. We see that
![]() $\bar {F} := F (0, 1, z, t, w) \in (z, t, w)^3$
,
$\bar {F} := F (0, 1, z, t, w) \in (z, t, w)^3$
,
![]() $w^3 \notin \bar {F}$
and
$w^3 \notin \bar {F}$
and
![]() $w^2 z \in \bar {F}$
. It follows that
$w^2 z \in \bar {F}$
. It follows that
![]() $\bar {F} \in (z, t, w)^3$
, and it cannot be a cube of a linear form. By Lemma 3.28, we have
$\bar {F} \in (z, t, w)^3$
, and it cannot be a cube of a linear form. By Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
5.1.d.7 The family
 $\mathcal {F}_{40}$
, the point of type
$\mathcal {F}_{40}$
, the point of type
 $\frac {1}{3} (1, 1, 2)$
$\frac {1}{3} (1, 1, 2)$
Let
![]() $X = X_{19} \subset \mathbb {P} (1, 3, 4, 5, 7)$
be a member of
$X = X_{19} \subset \mathbb {P} (1, 3, 4, 5, 7)$
be a member of
![]() $\mathcal {F}_{40}$
and
$\mathcal {F}_{40}$
and
![]() $\mathsf {p} = \mathsf {p}_y$
the singular point of type
$\mathsf {p} = \mathsf {p}_y$
the singular point of type
![]() $\frac {1}{3} (1, 1, 2)$
.
$\frac {1}{3} (1, 1, 2)$
.
Suppose that either
![]() $y^4 w \in F$
or
$y^4 w \in F$
or
![]() $y^5 z \in F$
. In this case,
$y^5 z \in F$
. In this case,
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) = 1$
since
$\operatorname {lct}_{\mathsf {p}} (X; H_x) = 1$
since
![]() $H_x$
is quasi-smooth at
$H_x$
is quasi-smooth at
![]() $\mathsf {p}$
. Let
$\mathsf {p}$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_x$
. We can take a
$H_x$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |7 A|_{\mathbb {Q}}$
such that
$T \in |7 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of of the effective
$\operatorname {Supp} (T)$
does not contain any component of of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
since the set
$D \cdot H_x$
since the set
![]() $\{x, z, t, w\}$
isolates
$\{x, z, t, w\}$
isolates
![]() $\mathsf {p}$
. It follows that
$\mathsf {p}$
. It follows that
Thus,
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge 20/19$
and we have
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge 20/19$
and we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
Suppose
![]() $y^4 w, y^5 z \notin F$
. Then
$y^4 w, y^5 z \notin F$
. Then
![]() $y^6 x \in F$
by the quasi-smoothness of X at
$y^6 x \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}$
and we can write
$\mathsf {p}$
and we can write
where
![]() $f_i = f_i (x, z, t, w)$
is a quasi-homogeneous polynomial of degree i. We set
$f_i = f_i (x, z, t, w)$
is a quasi-homogeneous polynomial of degree i. We set
![]() $\bar {F} := F (0, 1, z, t, w) \in (z, t, w)^3$
. It is easy to see that
$\bar {F} := F (0, 1, z, t, w) \in (z, t, w)^3$
. It is easy to see that
![]() $w^3 \notin \bar {F}$
and
$w^3 \notin \bar {F}$
and
![]() $w^2 z \in \bar {F}$
. It follows that either
$w^2 z \in \bar {F}$
. It follows that either
![]() $\bar {F} \in (z, t, w)^2$
or
$\bar {F} \in (z, t, w)^2$
or
![]() $\bar {F} \in (z, t, w)^3$
, and it cannot be a cube of a linear form. By Lemma 3.28, we have
$\bar {F} \in (z, t, w)^3$
, and it cannot be a cube of a linear form. By Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
5.1.d.8 The family
 $\mathcal {F}_{47}$
, the point of type
$\mathcal {F}_{47}$
, the point of type
 $\frac {1}{5} (1, 2, 3)$
$\frac {1}{5} (1, 2, 3)$
Let
![]() $X = X_{21} \subset \mathbb {P} (1, 1, 5, 7, 8)$
be a member of
$X = X_{21} \subset \mathbb {P} (1, 1, 5, 7, 8)$
be a member of
![]() $\mathcal {F}_{47}$
and
$\mathcal {F}_{47}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
the singular point of type
$\mathsf {p} = \mathsf {p}_z$
the singular point of type
![]() $\frac {1}{5} (1,2,3)$
. We can write
$\frac {1}{5} (1,2,3)$
. We can write
where
![]() $f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i. By the quasi-smoothness of X at
$f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i. By the quasi-smoothness of X at
![]() $\mathsf {p}_w$
, we have
$\mathsf {p}_w$
, we have
![]() $w^2 \in f_{16}$
, which implies
$w^2 \in f_{16}$
, which implies
![]() $\bar {F} = F (0, y, 1, t, w) \in (y, t, w)^2 \setminus (y, t, w)^3$
. Thus, by Lemma 3.28, we have
$\bar {F} = F (0, y, 1, t, w) \in (y, t, w)^2 \setminus (y, t, w)^3$
. Thus, by Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
5.1.d.9 The family
 $\mathcal {F}_{48}$
, the point of type
$\mathcal {F}_{48}$
, the point of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $X = X_{21} \subset \mathbb {P} (1, 2, 3, 7, 9)$
be a member of
$X = X_{21} \subset \mathbb {P} (1, 2, 3, 7, 9)$
be a member of
![]() $\mathcal {F}_{48}$
and
$\mathcal {F}_{48}$
and
![]() $\mathsf {p} = \mathsf {p}_y$
the singular point of type
$\mathsf {p} = \mathsf {p}_y$
the singular point of type
![]() $\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
$\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 3 \cdot 7 \cdot (A^3)} = \frac{6}{7}, & \text{if}\ y^6 w \in F, \\ \frac{2}{2 \cdot 3 \cdot 9 \cdot (A^3)} = \frac{2}{3}, & \text{if}\ y^6 w \notin F\ \text{and}\ y^7 t \in F. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 3 \cdot 7 \cdot (A^3)} = \frac{6}{7}, & \text{if}\ y^6 w \in F, \\ \frac{2}{2 \cdot 3 \cdot 9 \cdot (A^3)} = \frac{2}{3}, & \text{if}\ y^6 w \notin F\ \text{and}\ y^7 t \in F. \end{cases} \end{align*}$$
Suppose
![]() $y^6 w, y^7 t \notin F$
and
$y^6 w, y^7 t \notin F$
and
![]() $y^9 z \in F$
. We can write
$y^9 z \in F$
. We can write
where
![]() $f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t \notin f_7$
and
$t \notin f_7$
and
![]() $w \notin f_9$
. We have
$w \notin f_9$
. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 1$
and thus
$\operatorname {omult}_{\mathsf {p}} (H_x) = 1$
and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) = 1$
. Let
$\operatorname {lct}_{\mathsf {p}} (X;H_x) = 1$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_x$
. We can take a
$H_x$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |9 A|_{\mathbb {Q}}$
with such that
$T \in |9 A|_{\mathbb {Q}}$
with such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot H_x$
since
$D \cdot H_x$
since
![]() $\{x, z, t, w\}$
isolates
$\{x, z, t, w\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
where
![]() $q = q_{\mathsf {p}}$
is the quotient morphism of
$q = q_{\mathsf {p}}$
is the quotient morphism of
![]() $\mathsf {p} \in X$
and
$\mathsf {p} \in X$
and
![]() $\check {\mathsf {p}}$
is the preimage of
$\check {\mathsf {p}}$
is the preimage of
![]() $\mathsf {p}$
via q. This shows
$\mathsf {p}$
via q. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
Suppose
![]() $y^6 w, y^7 t, y^9 z \notin F$
. Then
$y^6 w, y^7 t, y^9 z \notin F$
. Then
![]() $y^{10} x \in F$
and we can write
$y^{10} x \in F$
and we can write
where
![]() $f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $z \notin f_3$
,
$z \notin f_3$
,
![]() $t \notin f_7$
and
$t \notin f_7$
and
![]() $w \notin f_9$
. We see that
$w \notin f_9$
. We see that
![]() $\bar {F} := F (0,1,z,t,w) \in (z,t,w)^3$
, and the cubic part of
$\bar {F} := F (0,1,z,t,w) \in (z,t,w)^3$
, and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form since
$\bar {F}$
is not a cube of a linear form since
![]() $w^2 z \in \bar {F}$
and
$w^2 z \in \bar {F}$
and
![]() $w^3 \notin \bar {F}$
. Thus, by Lemma 3.28, we have
$w^3 \notin \bar {F}$
. Thus, by Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
5.1.d.10 The family
 $\mathcal {F}_{49}$
, the point of type
$\mathcal {F}_{49}$
, the point of type
 $\frac {1}{5} (1,2,3)$
$\frac {1}{5} (1,2,3)$
Let
![]() $X = X_{21} \subset \mathbb {P} (1, 3, 5, 6, 7)$
be a member of
$X = X_{21} \subset \mathbb {P} (1, 3, 5, 6, 7)$
be a member of
![]() $\mathcal {F}_{49}$
and
$\mathcal {F}_{49}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
the singular point of type
$\mathsf {p} = \mathsf {p}_z$
the singular point of type
![]() $\frac {1}{5} (1,2,3)$
. If
$\frac {1}{5} (1,2,3)$
. If
![]() $z^3 t \in F$
, then
$z^3 t \in F$
, then
by Lemma 3.29.
Suppose
![]() $z^3 t \notin F$
. Then
$z^3 t \notin F$
. Then
![]() $z^4 x \in F$
and we can write
$z^4 x \in F$
and we can write
where
![]() $f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t \notin f_6$
. We have
$t \notin f_6$
. We have
![]() $w^3, t^3 y \in F$
, and we may assume
$w^3, t^3 y \in F$
, and we may assume
![]() $\operatorname {coeff}_F (w^3) = \operatorname {coeff}_F (t^3 y) = 1$
.
$\operatorname {coeff}_F (w^3) = \operatorname {coeff}_F (t^3 y) = 1$
.
We claim
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. If
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. If
![]() $y^2 \in f_6$
, then
$y^2 \in f_6$
, then
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
and thus
$\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. We assume
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. We assume
![]() $y^2 \notin f_6$
. Then we can write
$y^2 \notin f_6$
. Then we can write
where
![]() $\alpha , \beta , \gamma , \delta , \varepsilon \in \mathbb {C}$
. We set
$\alpha , \beta , \gamma , \delta , \varepsilon \in \mathbb {C}$
. We set
![]() $\bar {F} := F (0, y, 1, t, w) \in \mathbb {C} [y, t, w]$
.
$\bar {F} := F (0, y, 1, t, w) \in \mathbb {C} [y, t, w]$
.
-
• Suppose
 $\alpha \ne 0$
. Then
$\alpha \ne 0$
. Then
 $\bar {F} \in (y,t,w)^3$
and its cubic part is
$\bar {F} \in (y,t,w)^3$
and its cubic part is
 $\alpha w t y + w^3$
. By Lemma 3.28, we have
$\alpha w t y + w^3$
. By Lemma 3.28, we have
 $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
in this case.
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
in this case. -
• Suppose
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. Then the lowest weight part of
$\beta \ne 0$
. Then the lowest weight part of
 $\bar {F}$
with respect to
$\bar {F}$
with respect to
 $\operatorname {wt} (y,t,w) = (6,7,9)$
is
$\operatorname {wt} (y,t,w) = (6,7,9)$
is
 $\beta w y^3 + w^3 + t^3 y$
. By Lemma 3.27, we have
$\beta w y^3 + w^3 + t^3 y$
. By Lemma 3.27, we have  $$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_x) \ge \min \left\{ \frac{22}{27}, \operatorname{lct} (\tilde{\mathbb{P}}, \operatorname{Diff}; \mathcal{D} ) \right\}, \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_x) \ge \min \left\{ \frac{22}{27}, \operatorname{lct} (\tilde{\mathbb{P}}, \operatorname{Diff}; \mathcal{D} ) \right\}, \end{align*}$$
where
-
–
 $\tilde {\mathbb {P}} = \mathbb {P} (2, 7, 9)_{\tilde {y}, \tilde {t}, \tilde {w}} = \mathbb {P} (6, 7, 9)^{\operatorname {wf}}$
,
$\tilde {\mathbb {P}} = \mathbb {P} (2, 7, 9)_{\tilde {y}, \tilde {t}, \tilde {w}} = \mathbb {P} (6, 7, 9)^{\operatorname {wf}}$
, -
–
 $\operatorname {Diff} = \frac {2}{3} H_{\tilde {t}}$
with
$\operatorname {Diff} = \frac {2}{3} H_{\tilde {t}}$
with
 $H_{\tilde {t}} = (\tilde {t} = 0) \subset \tilde {\mathbb {P}}$
, and
$H_{\tilde {t}} = (\tilde {t} = 0) \subset \tilde {\mathbb {P}}$
, and -
–
 $\mathcal {D}$
is the prime divisor
$\mathcal {D}$
is the prime divisor
 $(\beta \tilde {w} \tilde {y}^3 + \tilde {w}^3 + \tilde {t} \tilde {y} = 0)$
on
$(\beta \tilde {w} \tilde {y}^3 + \tilde {w}^3 + \tilde {t} \tilde {y} = 0)$
on
 $\tilde {\mathbb {P}}$
.
$\tilde {\mathbb {P}}$
.
We see that
 $\mathcal {D}$
is quasi-smooth and it intersects
$\mathcal {D}$
is quasi-smooth and it intersects
 $H_{\tilde {t}}$
transversally. It follows that
$H_{\tilde {t}}$
transversally. It follows that
 $\operatorname {lct} (\tilde {\mathbb {P}}, \operatorname {Diff}; \mathcal {D}) = 1$
and thus
$\operatorname {lct} (\tilde {\mathbb {P}}, \operatorname {Diff}; \mathcal {D}) = 1$
and thus
 $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 22/27$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 22/27$
. -
-
• Suppose
 $\alpha = \beta = 0$
. Then the lowest weight part of
$\alpha = \beta = 0$
. Then the lowest weight part of
 $\bar {F}$
with respect to
$\bar {F}$
with respect to
 $\operatorname {wt} (y,z,t) = (3,6,7)$
is
$\operatorname {wt} (y,z,t) = (3,6,7)$
is
 $w^3 + t^3 y + \gamma t^2 y^3 + \delta t y^5 + \varepsilon y^7$
. By Lemma 3.27, we have where
$w^3 + t^3 y + \gamma t^2 y^3 + \delta t y^5 + \varepsilon y^7$
. By Lemma 3.27, we have where $$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_x) \ge \min \left\{ \frac{16}{21}, \operatorname{lct} (\tilde{\mathbb{P}}, \operatorname{Diff}; \mathcal{D} ) \right\}, \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_x) \ge \min \left\{ \frac{16}{21}, \operatorname{lct} (\tilde{\mathbb{P}}, \operatorname{Diff}; \mathcal{D} ) \right\}, \end{align*}$$
-
–
 $\tilde {\mathbb {P}} = \mathbb {P} (1, 2, 9)_{\tilde {y}, \tilde {t}, \tilde {w}} = \mathbb {P} (3, 6, 7)^{\operatorname {wf}}$
,
$\tilde {\mathbb {P}} = \mathbb {P} (1, 2, 9)_{\tilde {y}, \tilde {t}, \tilde {w}} = \mathbb {P} (3, 6, 7)^{\operatorname {wf}}$
, -
–
 $\operatorname {Diff} = \frac {2}{3} H_{\tilde {w}}$
with
$\operatorname {Diff} = \frac {2}{3} H_{\tilde {w}}$
with
 $H_{\tilde {w}} = (\tilde {w} = 0) \subset \tilde {\mathbb {P}}$
, and
$H_{\tilde {w}} = (\tilde {w} = 0) \subset \tilde {\mathbb {P}}$
, and -
–
 $\mathcal {D}$
is the prime divisor
$\mathcal {D}$
is the prime divisor
 $(\tilde {w} + \tilde {t}^3 \tilde {y} + \gamma \tilde {t}^2 \tilde {y}^3 + \delta \tilde {t} \tilde {y}^5 + \varepsilon \tilde {y}^7 = 0)$
on
$(\tilde {w} + \tilde {t}^3 \tilde {y} + \gamma \tilde {t}^2 \tilde {y}^3 + \delta \tilde {t} \tilde {y}^5 + \varepsilon \tilde {y}^7 = 0)$
on
 $\tilde {\mathbb {P}}$
.
$\tilde {\mathbb {P}}$
.
We see that
 $\mathcal {D}$
is quasi-smooth. The solutions of the equation
$\mathcal {D}$
is quasi-smooth. The solutions of the equation
 $\tilde {t}^3 \tilde {y} + \gamma \tilde {t}^2 \tilde {y}^3 + \delta \tilde {t} \tilde {y}^5 + \varepsilon \tilde {y}^7 = 0$
corresponds to the three points of type
$\tilde {t}^3 \tilde {y} + \gamma \tilde {t}^2 \tilde {y}^3 + \delta \tilde {t} \tilde {y}^5 + \varepsilon \tilde {y}^7 = 0$
corresponds to the three points of type
 $\frac {1}{3} (1, 1, 2)$
on X. In particular, the equation has three distinct solutions. It follows that
$\frac {1}{3} (1, 1, 2)$
on X. In particular, the equation has three distinct solutions. It follows that
 $\mathcal {D}$
intersects
$\mathcal {D}$
intersects
 $H_{\tilde {w}}$
transversally, and we have
$H_{\tilde {w}}$
transversally, and we have
 $\operatorname {lct} (\tilde {\mathbb {P}}, \operatorname {Diff}; \mathcal {D}) = 1$
. Thus,
$\operatorname {lct} (\tilde {\mathbb {P}}, \operatorname {Diff}; \mathcal {D}) = 1$
. Thus,
 $\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 16/21$
.
$\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 16/21$
. -
Thus, the claim is proved.
The point
![]() $\mathsf {p}$
is not a maximal center, and the pair
$\mathsf {p}$
is not a maximal center, and the pair
![]() $(X, H_x)$
is not canonical by Lemma 3.6. Thus,
$(X, H_x)$
is not canonical by Lemma 3.6. Thus,
by Lemma 3.5.
5.1.d.11 The family
 $\mathcal {F}_{62}$
, the point of
$\mathcal {F}_{62}$
, the point of
 $\frac {1}{5} (1,2,3)$
$\frac {1}{5} (1,2,3)$
Let
![]() $X = X_{26} \subset \mathbb {P} (1, 1, 5, 7, 13)$
be a member of
$X = X_{26} \subset \mathbb {P} (1, 1, 5, 7, 13)$
be a member of
![]() $\mathcal {F}_{62}$
and
$\mathcal {F}_{62}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
the singular point of type
$\mathsf {p} = \mathsf {p}_z$
the singular point of type
![]() $\frac {1}{5} (1,2,3)$
. Replacing x and y, we can write
$\frac {1}{5} (1,2,3)$
. Replacing x and y, we can write
where
![]() $f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
$f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
$\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
![]() $w^2 \in F$
. Hence,
$w^2 \in F$
. Hence,
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. The point
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. The point
![]() $\mathsf {p}$
is not a maximal center, and the pair
$\mathsf {p}$
is not a maximal center, and the pair
![]() $(X, H_x)$
is not canonical at
$(X, H_x)$
is not canonical at
![]() $\mathsf {p}$
by Lemma 3.6. Thus,
$\mathsf {p}$
by Lemma 3.6. Thus,
by Lemma 3.5.
5.1.d.12 The family
 $\mathcal {F}_{65}$
, the point of type
$\mathcal {F}_{65}$
, the point of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $X = X_{27} \subset \mathbb {P} (1, 2, 5, 9, 11)$
be a member of
$X = X_{27} \subset \mathbb {P} (1, 2, 5, 9, 11)$
be a member of
![]() $\mathcal {F}_{65}$
and
$\mathcal {F}_{65}$
and
![]() $\mathsf {p} = \mathsf {p}_y$
the singular point of type
$\mathsf {p} = \mathsf {p}_y$
the singular point of type
![]() $\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
$\frac {1}{2} (1,1,1)$
. By Lemma 3.29, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 5 \cdot 9 \cdot (A^3)} = \frac{22}{27}, & \text{if}\ y^8 w \in F, \\ \frac{2}{2 \cdot 5 \cdot 11 \cdot (A^3)} = \frac{2}{3}, & \text{if}\ y^8 w \notin F\ \text{and}\ y^9 t \in F. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{2 \cdot 5 \cdot 9 \cdot (A^3)} = \frac{22}{27}, & \text{if}\ y^8 w \in F, \\ \frac{2}{2 \cdot 5 \cdot 11 \cdot (A^3)} = \frac{2}{3}, & \text{if}\ y^8 w \notin F\ \text{and}\ y^9 t \in F. \end{cases} \end{align*}$$
Suppose
![]() $y^8 w, y^9 t \notin F$
and
$y^8 w, y^9 t \notin F$
and
![]() $y^{11} z \in F$
. Then we can write
$y^{11} z \in F$
. Then we can write
where
![]() $f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t \notin f_9$
and
$t \notin f_9$
and
![]() $w \notin f_{11}$
. We have
$w \notin f_{11}$
. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 1$
and thus
$\operatorname {omult}_{\mathsf {p}} (H_x) = 1$
and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) = 1$
. Let
$\operatorname {lct}_{\mathsf {p}} (X;H_x) = 1$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_x$
. We see that
$H_x$
. We see that
![]() $\{x, z, t, w\}$
isolates
$\{x, z, t, w\}$
isolates
![]() $\mathsf {p}$
, hence we can take a
$\mathsf {p}$
, hence we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |11 A|_{\mathbb {Q}}$
such that
$T \in |11 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot H_x$
. Then we have
$D \cdot H_x$
. Then we have
where
![]() $q_{\mathsf {p}}$
is the quotient morphism of
$q_{\mathsf {p}}$
is the quotient morphism of
![]() $\mathsf {p} \in X$
and
$\mathsf {p} \in X$
and
![]() $\check {\mathsf {p}}$
is the preimage of
$\check {\mathsf {p}}$
is the preimage of
![]() $\mathsf {p}$
via
$\mathsf {p}$
via
![]() $q_{\mathsf {p}}$
. This shows
$q_{\mathsf {p}}$
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
Suppose that
![]() $y^8 w, y^9 t, y^{11} z \notin F$
. Then
$y^8 w, y^9 t, y^{11} z \notin F$
. Then
![]() $y^{13} x \in F$
and we can write
$y^{13} x \in F$
and we can write
where
![]() $f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $z \notin f_5$
,
$z \notin f_5$
,
![]() $t \notin f_9$
and
$t \notin f_9$
and
![]() $w \notin f_{11}$
. We see that
$w \notin f_{11}$
. We see that
![]() $\bar {F} := F (0,1,z,t,w) \in (z,t,w)^3$
, and the cubic part of
$\bar {F} := F (0,1,z,t,w) \in (z,t,w)^3$
, and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form since
$\bar {F}$
is not a cube of a linear form since
![]() $w^2 z \in \bar {F}$
and
$w^2 z \in \bar {F}$
and
![]() $w^3 \notin \bar {F}$
. By Lemma 3.28, we have
$w^3 \notin \bar {F}$
. By Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
5.1.d.13 The family
 $\mathcal {F}_{67}$
, the point of
$\mathcal {F}_{67}$
, the point of
 $\frac {1}{9} (1,4,5)$
$\frac {1}{9} (1,4,5)$
Let
![]() $X = X_{28} \subset \mathbb {P} (1, 1, 4, 9, 14)$
be a member of
$X = X_{28} \subset \mathbb {P} (1, 1, 4, 9, 14)$
be a member of
![]() $\mathcal {F}_{67}$
and
$\mathcal {F}_{67}$
and
![]() $\mathsf {p} = \mathsf {p}_t$
the singular point of type
$\mathsf {p} = \mathsf {p}_t$
the singular point of type
![]() $\frac {1}{9} (1,4,5)$
. Replacing x and y, we can write
$\frac {1}{9} (1,4,5)$
. Replacing x and y, we can write
where
![]() $f_i = f_i (x,y,z,w)$
is a quasi-homogeneous polynomial of degree i. We have
$f_i = f_i (x,y,z,w)$
is a quasi-homogeneous polynomial of degree i. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
$\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
![]() $w^2 \in F$
. Hence,
$w^2 \in F$
. Hence,
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
by Lemma 3.6. Thus,
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
by Lemma 3.6. Thus,
by Lemma 3.5.
5.1.d.14 The family
 $\mathcal {F}_{82}$
, the point of
$\mathcal {F}_{82}$
, the point of
 $\frac {1}{5} (1,2,3)$
$\frac {1}{5} (1,2,3)$
Let
![]() $X = X_{36} \subset \mathbb {P} (1, 1, 5, 12, 18)$
be a member of
$X = X_{36} \subset \mathbb {P} (1, 1, 5, 12, 18)$
be a member of
![]() $\mathcal {F}_{82}$
and
$\mathcal {F}_{82}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
the singular point of type
$\mathsf {p} = \mathsf {p}_z$
the singular point of type
![]() $\frac {1}{5} (1,2,3)$
. Replacing x and y, we can write
$\frac {1}{5} (1,2,3)$
. Replacing x and y, we can write
where
![]() $f_i = f_i (x, y, t, w)$
is a quasi-homogeneous polynomial of degree i. We have
$f_i = f_i (x, y, t, w)$
is a quasi-homogeneous polynomial of degree i. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
$\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
![]() $w^2 \in F$
. Hence,
$w^2 \in F$
. Hence,
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
by Lemma 3.6. Thus,
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
by Lemma 3.6. Thus,
by Lemma 3.5.
5.1.d.15 The family
 $\mathcal {F}_{84}$
, the point of type
$\mathcal {F}_{84}$
, the point of type
 $\frac {1}{7} (1,2,5)$
$\frac {1}{7} (1,2,5)$
Let
![]() $X = X_{36} \subset \mathbb {P} (1, 7, 8, 9, 12)$
be a member of
$X = X_{36} \subset \mathbb {P} (1, 7, 8, 9, 12)$
be a member of
![]() $\mathcal {F}_{84}$
and
$\mathcal {F}_{84}$
and
![]() $\mathsf {p} = \mathsf {p}_y$
the singular point of type
$\mathsf {p} = \mathsf {p}_y$
the singular point of type
![]() $\frac {1}{7} (1,2,5)$
. By the quasi-smoothness of X, either
$\frac {1}{7} (1,2,5)$
. By the quasi-smoothness of X, either
![]() $y^4 z \in F$
or
$y^4 z \in F$
or
![]() $y^5 x \in F$
. Moreover, we have
$y^5 x \in F$
. Moreover, we have
![]() $w^3, t^4, z^3 w \in F$
and we assume
$w^3, t^4, z^3 w \in F$
and we assume
![]() $\operatorname {coeff}_F (w^3) = \operatorname {coeff}_F (t^4) = \operatorname {coeff}_F (z^3 w) = 1$
by rescaling
$\operatorname {coeff}_F (w^3) = \operatorname {coeff}_F (t^4) = \operatorname {coeff}_F (z^3 w) = 1$
by rescaling
![]() $z, t, w$
.
$z, t, w$
.
Suppose
![]() $y^4 z \in F$
. Let
$y^4 z \in F$
. Let
![]() $\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
the orbifold chart of X containing
$\rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
the orbifold chart of X containing
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
![]() $\rho _{\mathsf {p}}^* H_x \cdot \rho ^*_{\mathsf {p}} H_z = \breve {\Gamma }$
, where
$\rho _{\mathsf {p}}^* H_x \cdot \rho ^*_{\mathsf {p}} H_z = \breve {\Gamma }$
, where
is an irreducible and reduced curve with
![]() $\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) = 3$
. We see that
$\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) = 3$
. We see that
![]() $(X, H_x)$
is log canonical at
$(X, H_x)$
is log canonical at
![]() $\mathsf {p}$
since
$\mathsf {p}$
since
![]() $H_x$
is quasi-smooth at
$H_x$
is quasi-smooth at
![]() $\mathsf {p}$
. Thus, by Lemma 3.17, we have
$\mathsf {p}$
. Thus, by Lemma 3.17, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
Suppose
![]() $y^4 z \notin F$
. Then
$y^4 z \notin F$
. Then
![]() $y^5 x \in F$
and we can write
$y^5 x \in F$
and we can write
where
![]() $f_i = f_i (x, z, t, w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x, z, t, w)$
is a quasi-homogeneous polynomial of degree i with
![]() $z \notin f_8$
. By setting
$z \notin f_8$
. By setting
![]() $\alpha := \operatorname {coeff}_F (y w t z)$
, we have
$\alpha := \operatorname {coeff}_F (y w t z)$
, we have
-
• If
 $\alpha \ne 0$
, then
$\alpha \ne 0$
, then
 $\bar {F} \in (z,t,w)^3$
and the cubic part of
$\bar {F} \in (z,t,w)^3$
and the cubic part of
 $\bar {F}$
is not a cube of a linear form. Hence,
$\bar {F}$
is not a cube of a linear form. Hence,
 $\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
by Lemma 3.28.
$\operatorname {lct}_{\mathsf {p}} (X; H_x) \ge 1/2$
by Lemma 3.28. -
• If
 $\alpha = 0$
, then the lowest weight part of
$\alpha = 0$
, then the lowest weight part of
 $\bar {F}$
with respect to
$\bar {F}$
with respect to
 $\operatorname {wt} (z, t, w) = (8,9,12)$
is
$\operatorname {wt} (z, t, w) = (8,9,12)$
is
 $\bar {F} = w^3 + w z^3 + t^4$
. By Lemma 3.27, we have where
$\bar {F} = w^3 + w z^3 + t^4$
. By Lemma 3.27, we have where $$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_x) \ge \min \left\{ \frac{29}{36}, \operatorname{lct} (\tilde{\mathbb{P}}, \operatorname{Diff}; \mathcal{D} ) \right\}, \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_x) \ge \min \left\{ \frac{29}{36}, \operatorname{lct} (\tilde{\mathbb{P}}, \operatorname{Diff}; \mathcal{D} ) \right\}, \end{align*}$$
-
–
 $\tilde {\mathbb {P}} = \mathbb {P} (2, 3, 1)_{\tilde {z}, \tilde {t}, \tilde {w}} = \mathbb {P} (8, 9, 12)^{\operatorname {wf}}$
,
$\tilde {\mathbb {P}} = \mathbb {P} (2, 3, 1)_{\tilde {z}, \tilde {t}, \tilde {w}} = \mathbb {P} (8, 9, 12)^{\operatorname {wf}}$
, -
–
 $\operatorname {Diff} = \frac {2}{3} H_{\tilde {z}} + \frac {3}{4} H_{\tilde {t}}$
with
$\operatorname {Diff} = \frac {2}{3} H_{\tilde {z}} + \frac {3}{4} H_{\tilde {t}}$
with
 $H_{\tilde {z}} = (\tilde {z} = 0) \subset \tilde {\mathbb {P}}$
,
$H_{\tilde {z}} = (\tilde {z} = 0) \subset \tilde {\mathbb {P}}$
,
 $H_{\tilde {t}} = (\tilde {t} = 0) \subset \tilde {\mathbb {P}}$
, and
$H_{\tilde {t}} = (\tilde {t} = 0) \subset \tilde {\mathbb {P}}$
, and -
–
 $\mathcal {D}$
is the prime divisor
$\mathcal {D}$
is the prime divisor
 $(\tilde {w}^3 + \tilde {w} \tilde {z} + \tilde {t} = 0)$
on
$(\tilde {w}^3 + \tilde {w} \tilde {z} + \tilde {t} = 0)$
on
 $\tilde {\mathbb {P}}$
.
$\tilde {\mathbb {P}}$
.
We see that
 $\mathcal {D}$
is quasi-smooth,
$\mathcal {D}$
is quasi-smooth,
 $\mathcal {D} \cap H_{\tilde {z}} \cap H_{\tilde {t}} = \emptyset $
and any two of
$\mathcal {D} \cap H_{\tilde {z}} \cap H_{\tilde {t}} = \emptyset $
and any two of
 $\mathcal {D}, H_{\tilde {z}}, H_{\tilde {t}}$
intersect transversally. It follows that
$\mathcal {D}, H_{\tilde {z}}, H_{\tilde {t}}$
intersect transversally. It follows that
 $\operatorname {lct} (\tilde {\mathbb {P}}, \operatorname {Diff}; \mathcal {D}) = 1$
and thus
$\operatorname {lct} (\tilde {\mathbb {P}}, \operatorname {Diff}; \mathcal {D}) = 1$
and thus
 $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 29/36$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 29/36$
. -
Note that
![]() $\mathsf {p} \in X$
is not a maximal center and the pair
$\mathsf {p} \in X$
is not a maximal center and the pair
![]() $(X, H_x)$
is not canonical at
$(X, H_x)$
is not canonical at
![]() $\mathsf {p}$
by Lemma 3.6. Thus,
$\mathsf {p}$
by Lemma 3.6. Thus,
by Lemma 3.5.
5.2 EI centers
Proposition 5.6. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
and
$\mathsf {i} \in \mathsf {I}$
and
![]() $\mathsf {p} \in X$
an EI center. Then
$\mathsf {p} \in X$
an EI center. Then
Proof. We have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
by Proposition 5.3 for a member X of
$\alpha _{\mathsf {p}} (X) \ge 1$
by Proposition 5.3 for a member X of
![]() $\mathcal {F}_{\mathsf {i}}$
and
$\mathcal {F}_{\mathsf {i}}$
and
![]() $\mathsf {p} \in X$
, where
$\mathsf {p} \in X$
, where
-
•
 $\mathsf {i} = 36$
and
$\mathsf {i} = 36$
and
 $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
 $\frac {1}{4} (1, 1, 3)$
.
$\frac {1}{4} (1, 1, 3)$
. -
•
 $\mathsf {i} = 44$
and
$\mathsf {i} = 44$
and
 $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
 $\frac {1}{6} (1, 1, 5)$
.
$\frac {1}{6} (1, 1, 5)$
. -
•
 $\mathsf {i} = 61$
and
$\mathsf {i} = 61$
and
 $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
 $\frac {1}{7} (1, 2, 5)$
.
$\frac {1}{7} (1, 2, 5)$
. -
•
 $\mathsf {i} = 76$
and
$\mathsf {i} = 76$
and
 $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
 $\frac {1}{8} (1, 3, 5)$
.
$\frac {1}{8} (1, 3, 5)$
.
We have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
by Proposition 5.4 for a member X of
$\alpha _{\mathsf {p}} (X) \ge 1/2$
by Proposition 5.4 for a member X of
![]() $\mathcal {F}_{\mathsf {i}}$
and
$\mathcal {F}_{\mathsf {i}}$
and
![]() $\mathsf {p} \in X$
, where
$\mathsf {p} \in X$
, where
-
•
 $\mathsf {i} = 23$
and
$\mathsf {i} = 23$
and
 $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
 $\frac {1}{4} (1, 1, 3)$
.
$\frac {1}{4} (1, 1, 3)$
. -
•
 $\mathsf {i} = 40$
and
$\mathsf {i} = 40$
and
 $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
 $\frac {1}{5} (1, 2, 3)$
.
$\frac {1}{5} (1, 2, 3)$
.
It remains to consider members of families
![]() $\mathcal {F}_7$
and
$\mathcal {F}_7$
and
![]() $\mathcal {F}_{20}$
, and singular points of types
$\mathcal {F}_{20}$
, and singular points of types
![]() $\frac {1}{2} (1, 1, 1)$
and
$\frac {1}{2} (1, 1, 1)$
and
![]() $\frac {1}{3} (1, 1, 2)$
, respectively.
$\frac {1}{3} (1, 1, 2)$
, respectively.
Let
![]() $X = X_8 \subset \mathbb {P} (1, 1, 2, 2, 3)$
be a member of
$X = X_8 \subset \mathbb {P} (1, 1, 2, 2, 3)$
be a member of
![]() $\mathcal {F}_7$
and
$\mathcal {F}_7$
and
![]() $\mathsf {p}$
a singular point of type
$\mathsf {p}$
a singular point of type
![]() $\frac {1}{2} (1, 1, 1)$
. Replacing homogeneous coordinates, we may assume
$\frac {1}{2} (1, 1, 1)$
. Replacing homogeneous coordinates, we may assume
![]() $\mathsf {p} = \mathsf {p}_t$
and we can write
$\mathsf {p} = \mathsf {p}_t$
and we can write
where
![]() $f_i = f_i (x, y, z, w)$
is a quasi-homogeneous polynomial of degree i. Hence, by Lemma 3.29, we have
$f_i = f_i (x, y, z, w)$
is a quasi-homogeneous polynomial of degree i. Hence, by Lemma 3.29, we have
Let
![]() $X = X_{13} \subset \mathbb {P} (1, 1, 3, 4, 5)$
be a member of
$X = X_{13} \subset \mathbb {P} (1, 1, 3, 4, 5)$
be a member of
![]() $\mathcal {F}_{20}$
and
$\mathcal {F}_{20}$
and
![]() $\mathsf {p} = \mathsf {p}_z$
be the singular point of type
$\mathsf {p} = \mathsf {p}_z$
be the singular point of type
![]() $\frac {1}{3} (1, 1, 2)$
. If
$\frac {1}{3} (1, 1, 2)$
. If
![]() $z^3 t \in F$
, then we have
$z^3 t \in F$
, then we have
by Lemma 3.29. Suppose
![]() $z^3 t \notin F$
. Then we can write that
$z^3 t \notin F$
. Then we can write that
where
![]() $f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x,y,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t \notin f_4$
. We have
$t \notin f_4$
. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
$\operatorname {omult}_{\mathsf {p}} (H_x) = 2$
since
![]() $w^2 z \in F$
by the quasi-smoothness of X at
$w^2 z \in F$
by the quasi-smoothness of X at
![]() $\mathsf {p}_w$
. This shows
$\mathsf {p}_w$
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. The point
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. The point
![]() $\mathsf {p}$
is not a maximal singularity, and the pair
$\mathsf {p}$
is not a maximal singularity, and the pair
![]() $(X, H_x)$
is not canonical at
$(X, H_x)$
is not canonical at
![]() $\mathsf {p}$
by Lemma 3.6. Thus,
$\mathsf {p}$
by Lemma 3.6. Thus,
by Lemma 3.5. This completes the proof.
5.3 Equations for QI centers
Let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
. We set
$\mathsf {i} \in \mathsf {I}$
. We set
![]() $a_0 = 1$
and let
$a_0 = 1$
and let
![]() $F = F (x_0, \dots , x_4)$
be the defining polynomial of X.
$F = F (x_0, \dots , x_4)$
be the defining polynomial of X.
Definition 5.7. Let
![]() $\mathsf {p} \in X$
be a QI center, and let
$\mathsf {p} \in X$
be a QI center, and let
![]() $j, k$
be such that
$j, k$
be such that
![]() $j \ne k$
,
$j \ne k$
,
![]() $d = 2 a_k + a_j$
and the index of
$d = 2 a_k + a_j$
and the index of
![]() $\mathsf {p} \in X$
coincides with
$\mathsf {p} \in X$
coincides with
![]() $a_k$
. Then we can choose coordinates so that
$a_k$
. Then we can choose coordinates so that
![]() $\mathsf {p} = \mathsf {p}_{x_k}$
. We say that
$\mathsf {p} = \mathsf {p}_{x_k}$
. We say that
![]() $\mathsf {p}$
is an exceptional QI center if
$\mathsf {p}$
is an exceptional QI center if
![]() $x_k^2 x_l \notin F$
for any
$x_k^2 x_l \notin F$
for any
![]() $l \in \{0, \dots , 4\}$
.
$l \in \{0, \dots , 4\}$
.
Lemma 5.8. Let
![]() $\mathsf {p} \in X$
be a nonexceptional QI center. Then we can choose homogeneous coordinates
$\mathsf {p} \in X$
be a nonexceptional QI center. Then we can choose homogeneous coordinates
![]() $x_{i_1}, x_{i_2}, x_{i_3}, x_j, x_k$
of
$x_{i_1}, x_{i_2}, x_{i_3}, x_j, x_k$
of
![]() $\mathbb {P}$
, where
$\mathbb {P}$
, where
![]() $\{i_1, i_2, i_3, j, k\} = \{0, 1, 2, 3, 4\}$
, such that
$\{i_1, i_2, i_3, j, k\} = \{0, 1, 2, 3, 4\}$
, such that
![]() $a_{i_1}, a_{i_2}, a_{i_3} < a_k$
,
$a_{i_1}, a_{i_2}, a_{i_3} < a_k$
,
![]() $\mathsf {p} = \mathsf {p}_{x_k}$
and
$\mathsf {p} = \mathsf {p}_{x_k}$
and
for some quasi-homogeneous polynomials
![]() $f, g \in \mathbb {C} [x_{i_1}, x_{i_2}, x_{i_3}, x_j]$
of degree
$f, g \in \mathbb {C} [x_{i_1}, x_{i_2}, x_{i_3}, x_j]$
of degree
![]() $d - a_k$
, d, respectively.
$d - a_k$
, d, respectively.
Proof. Basically, this follows by looking at Table 7. See also [Reference Corti, Pukhlikhov and ReidCPR00, Theorem 4.9].
Let
![]() $\mathsf {p} \in X$
be a nonexceptional QI center, and we choose and fix homogeneous coordinates
$\mathsf {p} \in X$
be a nonexceptional QI center, and we choose and fix homogeneous coordinates
![]() $x_{i_1}, x_{i_2}, x_{i_3}, x_j, x_k$
of
$x_{i_1}, x_{i_2}, x_{i_3}, x_j, x_k$
of
![]() $\mathbb {P}$
as in Lemma 5.8.
$\mathbb {P}$
as in Lemma 5.8.
Definition 5.9. We say that
![]() $\mathsf {p}$
is a degenerate QI center if
$\mathsf {p}$
is a degenerate QI center if
![]() $f (x_{i_1}, x_{i_2}, x_{i_3},0) = 0$
as a polynomial, otherwise we call
$f (x_{i_1}, x_{i_2}, x_{i_3},0) = 0$
as a polynomial, otherwise we call
![]() $\mathsf {p}$
a nondegenerate QI center.
$\mathsf {p}$
a nondegenerate QI center.
Remark 5.10. It is proved in [Reference Cheltsov and ParkCP17, Section 4.1] that a QI center
![]() $\mathsf {p} \in X$
is a maximal center if and only if it is nondegenerate.
$\mathsf {p} \in X$
is a maximal center if and only if it is nondegenerate.
Lemma 5.11. Let
![]() $\mathsf {p}$
be a degenerate QI center. Then we can choose homogeneous coordinates
$\mathsf {p}$
be a degenerate QI center. Then we can choose homogeneous coordinates
![]() $x_{i_1}, x_{i_2}, x_{i_3}, x_j, x_k$
of
$x_{i_1}, x_{i_2}, x_{i_3}, x_j, x_k$
of
![]() $\mathbb {P}$
such that
$\mathbb {P}$
such that
![]() $a_{i_1}, a_{i_2}, a_{i_3} < a_k$
,
$a_{i_1}, a_{i_2}, a_{i_3} < a_k$
,
![]() $\mathsf {p} = \mathsf {p}_{x_k}$
and
$\mathsf {p} = \mathsf {p}_{x_k}$
and
for some quasi-homogeneous polynomial
![]() $g \in \mathbb {C} [x_{i_1},x_{i_2},x_{i_3},x_j]$
of degree d. Moreover, the hypersurface
$g \in \mathbb {C} [x_{i_1},x_{i_2},x_{i_3},x_j]$
of degree d. Moreover, the hypersurface
is quasi-smooth.
Proof. We have
![]() $f = x_j f'$
for some
$f = x_j f'$
for some
![]() $f' \in \mathbb {C} [x_{i_1}, x_{i_2}, x_{i_3}, x_j]$
since
$f' \in \mathbb {C} [x_{i_1}, x_{i_2}, x_{i_3}, x_j]$
since
![]() $\mathsf {p}$
is degenerate. Filtering off terms divisible by
$\mathsf {p}$
is degenerate. Filtering off terms divisible by
![]() $x_j$
in equation (5.1), we have
$x_j$
in equation (5.1), we have
We can eliminate the term
![]() $x_k x_j f'$
by replacing
$x_k x_j f'$
by replacing
![]() $x_k \mapsto x_k - f'/2$
. This shows the first assertion.
$x_k \mapsto x_k - f'/2$
. This shows the first assertion.
We choose and fix homogeneous coordinates so that F is of the form (5.2). We set
![]() $\bar {g} = g (x_{i_1},x_{i_2},x_{i_3},0)$
. Then we can write
$\bar {g} = g (x_{i_1},x_{i_2},x_{i_3},0)$
. Then we can write
![]() $g = \bar {g} + x_j h$
, where
$g = \bar {g} + x_j h$
, where
![]() $h = h (x_{i_1},x_{i_2},x_{i_3},x_j)$
. Suppose to the contrary that
$h = h (x_{i_1},x_{i_2},x_{i_3},x_j)$
. Suppose to the contrary that
![]() $(\bar {g} = 0) \subset \mathbb {P} (a_{i_1},a_{i_2},a_{i_3})$
is not quasi-smooth at a point
$(\bar {g} = 0) \subset \mathbb {P} (a_{i_1},a_{i_2},a_{i_3})$
is not quasi-smooth at a point
![]() $(\alpha _1\!:\!\alpha _2\!:\!\alpha _3)$
. We choose and fix
$(\alpha _1\!:\!\alpha _2\!:\!\alpha _3)$
. We choose and fix
![]() $\beta \in \mathbb {C}$
such that
$\beta \in \mathbb {C}$
such that
![]() $\beta ^2 + h (\alpha _1,\alpha _2,\alpha _3,0) = 0$
and set
$\beta ^2 + h (\alpha _1,\alpha _2,\alpha _3,0) = 0$
and set
It is easy to see that
![]() $(\partial F/\partial v) (\mathsf {q}) = 0$
for any
$(\partial F/\partial v) (\mathsf {q}) = 0$
for any
![]() $v \in \{x_{i_1},x_{i_2},x_{i_3},x_j,x_k\}$
. This is impossible since X is quasi-smooth. Therefore,
$v \in \{x_{i_1},x_{i_2},x_{i_3},x_j,x_k\}$
. This is impossible since X is quasi-smooth. Therefore,
![]() $(\bar {g} = 0) \subset \mathbb {P} (a_{i_1},a_{i_2},a_{i_3})$
is quasi-smooth.
$(\bar {g} = 0) \subset \mathbb {P} (a_{i_1},a_{i_2},a_{i_3})$
is quasi-smooth.
Lemma 5.12. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
. Suppose that X has a QI center. Then one of the following holds.
$\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
. Suppose that X has a QI center. Then one of the following holds.
-
1. X has a unique QI center. In this case, by a choice of homogeneous coordinates, we have
where a is coprime to b, $$\begin{align*}X = X_{2 r + c} \subset \mathbb{P} (1, a, b, c, r)_{x, s, u, v, w}, \end{align*}$$
$$\begin{align*}X = X_{2 r + c} \subset \mathbb{P} (1, a, b, c, r)_{x, s, u, v, w}, \end{align*}$$
 $a < b$
,
$a < b$
,
 $a + b = r$
,
$a + b = r$
,
 $c < r$
, and the unique QI center is the point
$c < r$
, and the unique QI center is the point
 $\mathsf {p} = \mathsf {p}_w$
, which is of type
$\mathsf {p} = \mathsf {p}_w$
, which is of type
 $\frac {1}{r} (1, a, b)$
.
$\frac {1}{r} (1, a, b)$
.
-
2. X has exactly three distinct QI centers. In this case, by a choice of homogeneous coordinates, we have
where a is coprime to b, $$\begin{align*}X = X_{3 r} \subset \mathbb{P} (1, a, b, r, r)_{x, y, z, t, w}, \end{align*}$$
$$\begin{align*}X = X_{3 r} \subset \mathbb{P} (1, a, b, r, r)_{x, y, z, t, w}, \end{align*}$$
 $a \le b$
and
$a \le b$
and
 $a + b = r$
. The three QI centers are the three points in
$a + b = r$
. The three QI centers are the three points in
 $(x = y = z = 0) \cap X$
, and they are all of type
$(x = y = z = 0) \cap X$
, and they are all of type
 $\frac {1}{r} (1, a, b)$
.
$\frac {1}{r} (1, a, b)$
.
-
3. X has exactly two distinct QI centers, and their singularity types are equal. In this case, by a choice of homogeneous coordinates, we have
where a is coprime to b, $$\begin{align*}X = X_{4 r} \subset \mathbb{P} (1, a, b, r, 2 r)_{x, y, z, t, w}, \end{align*}$$
$$\begin{align*}X = X_{4 r} \subset \mathbb{P} (1, a, b, r, 2 r)_{x, y, z, t, w}, \end{align*}$$
 $a \le b$
and
$a \le b$
and
 $a + b = r$
. The QI centers are the two points in
$a + b = r$
. The QI centers are the two points in
 $(x = y = z = 0) \cap X$
, and they are both of type
$(x = y = z = 0) \cap X$
, and they are both of type
 $\frac {1}{r} (1, a, b)$
.
$\frac {1}{r} (1, a, b)$
.
-
4. X has exactly two distinct QI centers, and their singularity types are distinct. In this case, by a choice of homogeneous coordinates, we have
where a is coprime to b, $$\begin{align*}X = X_{4 a + 3 b} \subset \mathbb{P} (1, a, b, r_1, r_2)_{x, u, v, t, w}, \end{align*}$$
$$\begin{align*}X = X_{4 a + 3 b} \subset \mathbb{P} (1, a, b, r_1, r_2)_{x, u, v, t, w}, \end{align*}$$
 $a + b = r_1$
and
$a + b = r_1$
and
 $2 a + b = r_2$
. The QI centers are
$2 a + b = r_2$
. The QI centers are
 $\mathsf {p}_t$
and
$\mathsf {p}_t$
and
 $\mathsf {p}_w$
which are of types
$\mathsf {p}_w$
which are of types
 $\frac {1}{r_1} (1, a, b)$
and
$\frac {1}{r_1} (1, a, b)$
and
 $\frac {1}{r_2} (1, a, a + b)$
, respectively.
$\frac {1}{r_2} (1, a, a + b)$
, respectively.
Proof. Let
be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
. We set
$\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
. We set
![]() $a_0 = 1$
and assume
$a_0 = 1$
and assume
![]() $a_1 \le \dots \le a_4$
. We assume that X has at least one QI center.
$a_1 \le \dots \le a_4$
. We assume that X has at least one QI center.
Suppose
![]() $d = 3 a_4$
. Let
$d = 3 a_4$
. Let
![]() $\mathsf {p} \in X$
be a QI center. Then, after replacing homogeneous coordinates, we may assume
$\mathsf {p} \in X$
be a QI center. Then, after replacing homogeneous coordinates, we may assume
![]() $\mathsf {p} = \mathsf {p}_{x_i}$
and
$\mathsf {p} = \mathsf {p}_{x_i}$
and
![]() $x_i^2 x_j \in F$
for some
$x_i^2 x_j \in F$
for some
![]() $i \in \{0, 1, 2, 3, 4\}$
and
$i \in \{0, 1, 2, 3, 4\}$
and
![]() $j \in \{0, 1, 2, 3, 4\} \setminus \{i\}$
. In particular, we have
$j \in \{0, 1, 2, 3, 4\} \setminus \{i\}$
. In particular, we have
![]() $d = 3 a_4 = 2 a_i + a_j$
, which is possible if and only if
$d = 3 a_4 = 2 a_i + a_j$
, which is possible if and only if
![]() $a_i = a_j = a_4$
. Thus, we have
$a_i = a_j = a_4$
. Thus, we have
![]() $a_3 = a_4$
and we may assume
$a_3 = a_4$
and we may assume
![]() $i = 4, j = 3$
. We see that
$i = 4, j = 3$
. We see that
![]() $\mathsf {p} \in X$
is of type
$\mathsf {p} \in X$
is of type
![]() $\frac {1}{a_4} (1, a_1, a_2)$
and
$\frac {1}{a_4} (1, a_1, a_2)$
and
![]() $\mathsf {p} \in X$
is terminal. It follows that
$\mathsf {p} \in X$
is terminal. It follows that
![]() $a_1 + a_2 = a_4$
and
$a_1 + a_2 = a_4$
and
![]() $a_l$
is coprime to
$a_l$
is coprime to
![]() $a_4$
for
$a_4$
for
![]() $l = 1, 2$
. By setting
$l = 1, 2$
. By setting
![]() $a := a_1$
,
$a := a_1$
,
![]() $b := a_2$
and
$b := a_2$
and
![]() $r := a_3 = a_4$
, this case corresponds to (2). In the following, we assume
$r := a_3 = a_4$
, this case corresponds to (2). In the following, we assume
![]() $d < 3 a_4$
.
$d < 3 a_4$
.
Suppose
![]() $d = 2 a_4$
. We have
$d = 2 a_4$
. We have
![]() $a_4 = a_1 + a_2 + a_3$
since
$a_4 = a_1 + a_2 + a_3$
since
![]() $d = a_1 + a_2 + a_3 + a_4 = 2 a_4$
. Let
$d = a_1 + a_2 + a_3 + a_4 = 2 a_4$
. Let
![]() $\mathsf {p} \in X$
be a QI center. Then we may assume
$\mathsf {p} \in X$
be a QI center. Then we may assume
![]() $\mathsf {p} = \mathsf {p}_{x_i}$
and
$\mathsf {p} = \mathsf {p}_{x_i}$
and
![]() $x_i^2 x_j \in F$
for some
$x_i^2 x_j \in F$
for some
![]() $i \in \{0, 1, 2, 3\}$
and
$i \in \{0, 1, 2, 3\}$
and
![]() $j \in \{0, 1, 2, 3, 4\} \setminus \{i\}$
. In particular, we have
$j \in \{0, 1, 2, 3, 4\} \setminus \{i\}$
. In particular, we have
![]() $d = 2 a_i + a_j$
, and hence
$d = 2 a_i + a_j$
, and hence
which is only possible when
![]() $j = 4$
and
$j = 4$
and
![]() $i = 3$
. Hence,
$i = 3$
. Hence,
![]() $i = 3$
,
$i = 3$
,
![]() $j = 4$
, and we have
$j = 4$
, and we have
![]() $a_4 = 2 a_3$
since
$a_4 = 2 a_3$
since
![]() $d = 2 a_3 + a_4 = 2 a_4$
. We see that
$d = 2 a_3 + a_4 = 2 a_4$
. We see that
![]() $\mathsf {p} \in X$
is of type
$\mathsf {p} \in X$
is of type
![]() $\frac {1}{a_3} (1, a_1, a_2)$
and
$\frac {1}{a_3} (1, a_1, a_2)$
and
![]() $\mathsf {p} \in X$
is terminal. It follows that
$\mathsf {p} \in X$
is terminal. It follows that
![]() $a_3 = a_1 + a_2$
and
$a_3 = a_1 + a_2$
and
![]() $a_l$
is coprime to
$a_l$
is coprime to
![]() $a_3$
for
$a_3$
for
![]() $l = 1, 2$
. By setting
$l = 1, 2$
. By setting
![]() $a:= a_1$
,
$a:= a_1$
,
![]() $b := a_2$
,
$b := a_2$
,
![]() $r := a_3$
, this case corresponds to (3).
$r := a_3$
, this case corresponds to (3).
Suppose
![]() $d = 2 a_4 + a_3$
. We have
$d = 2 a_4 + a_3$
. We have
![]() $a_4 = a_1 + a_2$
since
$a_4 = a_1 + a_2$
since
![]() $d = a_1 + a_2 + a_3 + a_4$
. We see that
$d = a_1 + a_2 + a_3 + a_4$
. We see that
![]() $\mathsf {p}_4 \in X$
is of type
$\mathsf {p}_4 \in X$
is of type
![]() $\frac {1}{a_4} (1, a_1, a_2)$
, and it is a QI center. It follows that
$\frac {1}{a_4} (1, a_1, a_2)$
, and it is a QI center. It follows that
![]() $a_4$
is coprime to
$a_4$
is coprime to
![]() $a_l$
for
$a_l$
for
![]() $l = 1, 2$
since
$l = 1, 2$
since
![]() $\mathsf {p}_4 \in X$
is a terminal singularity. If X admits a QI center other than
$\mathsf {p}_4 \in X$
is a terminal singularity. If X admits a QI center other than
![]() $\mathsf {p}_4$
, then we have
$\mathsf {p}_4$
, then we have
![]() $d = 2 a_i + a_j$
, where
$d = 2 a_i + a_j$
, where
![]() $i \in \{1, 2, 3\}$
and
$i \in \{1, 2, 3\}$
and
![]() $j \in \{0, 1, 2, 3, 4\} \setminus \{ i\}$
which is impossible. Thus,
$j \in \{0, 1, 2, 3, 4\} \setminus \{ i\}$
which is impossible. Thus,
![]() $\mathsf {p}_4 \in X$
is a unique QI center, and we are in case (1) by setting
$\mathsf {p}_4 \in X$
is a unique QI center, and we are in case (1) by setting
![]() $a := a_1$
,
$a := a_1$
,
![]() $b := a_2$
,
$b := a_2$
,
![]() $c := a_3$
and
$c := a_3$
and
![]() $r := a_4$
. Note that we have
$r := a_4$
. Note that we have
![]() $a < b$
because otherwise we have
$a < b$
because otherwise we have
![]() $a_1 = a_2 = 1$
and
$a_1 = a_2 = 1$
and
![]() $a_4 = 2$
and X belongs to a family
$a_4 = 2$
and X belongs to a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \{2, 8\}$
which is impossible.
$\mathsf {i} \in \{2, 8\}$
which is impossible.
Suppose
![]() $d = 2 a_4 + a_2$
. Then
$d = 2 a_4 + a_2$
. Then
![]() $a_4 = a_1 + a_3$
. We see that
$a_4 = a_1 + a_3$
. We see that
![]() $\mathsf {p}_4 \in X$
is of type
$\mathsf {p}_4 \in X$
is of type
![]() $\frac {1}{a_4} (1, a_1, a_3)$
, and it is a QI center. If
$\frac {1}{a_4} (1, a_1, a_3)$
, and it is a QI center. If
![]() $\mathsf {p}_4$
is a unique QI center, then we are in case (1) by setting
$\mathsf {p}_4$
is a unique QI center, then we are in case (1) by setting
![]() $a := a_1$
,
$a := a_1$
,
![]() $b := a_3$
,
$b := a_3$
,
![]() $c := a_2$
and
$c := a_2$
and
![]() $r := a_4$
. We assume that X admits a QI center
$r := a_4$
. We assume that X admits a QI center
![]() $\mathsf {p} \in X$
other than
$\mathsf {p} \in X$
other than
![]() $\mathsf {p}_4$
. We may assume
$\mathsf {p}_4$
. We may assume
![]() $\mathsf {p} = \mathsf {p}_i$
after replacing homogeneous coordinates, and we have
$\mathsf {p} = \mathsf {p}_i$
after replacing homogeneous coordinates, and we have
![]() $d = 2 a_i + a_j$
for some
$d = 2 a_i + a_j$
for some
![]() $i \in \{1, 2, 3\}$
and
$i \in \{1, 2, 3\}$
and
![]() $j \in \{0, 1, 2, 3, 4\} \setminus \{i\}$
. Then we have
$j \in \{0, 1, 2, 3, 4\} \setminus \{i\}$
. Then we have
![]() $a_j = a_4$
and
$a_j = a_4$
and
![]() $a_i = a_3$
. Thus,
$a_i = a_3$
. Thus,
![]() $i = 3$
,
$i = 3$
,
![]() $j = 4$
and we have
$j = 4$
and we have
![]() $a_3 = a_1 + a_2$
. The singularity of
$a_3 = a_1 + a_2$
. The singularity of
![]() $\mathsf {p} = \mathsf {p}_i \in X$
is of type
$\mathsf {p} = \mathsf {p}_i \in X$
is of type
![]() $\frac {1}{a_3} (1, a_1, a_2)$
and it is terminal. It follows that
$\frac {1}{a_3} (1, a_1, a_2)$
and it is terminal. It follows that
![]() $a_1$
is coprime to
$a_1$
is coprime to
![]() $a_2$
. Thus, we are in case (4) by setting
$a_2$
. Thus, we are in case (4) by setting
![]() $a := a_1$
,
$a := a_1$
,
![]() $b := a_2$
,
$b := a_2$
,
![]() $r_1 := a_3$
and
$r_1 := a_3$
and
![]() $r_2 = a_4$
.
$r_2 = a_4$
.
Suppose
![]() $d = 2 a_4 + a_1$
. Then, by interchanging the role of
$d = 2 a_4 + a_1$
. Then, by interchanging the role of
![]() $a_1$
and
$a_1$
and
![]() $a_2$
in the previous arguments, we conclude that this case corresponds to either (1) or (4). This completes the proof.
$a_2$
in the previous arguments, we conclude that this case corresponds to either (1) or (4). This completes the proof.
Lemma 5.13. Let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
with a unique QI center, where a is coprime to b,
$\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
with a unique QI center, where a is coprime to b,
![]() $a < b$
,
$a < b$
,
![]() $r = a + b$
and
$r = a + b$
and
![]() $c < r$
. Then the following assertions hold.
$c < r$
. Then the following assertions hold.
-
1. If
 $c = 1$
, then X belongs to a family
$c = 1$
, then X belongs to a family
 $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
 $\mathsf {i} \in \{24, 46\}$
.
$\mathsf {i} \in \{24, 46\}$
. -
2. If
 $2 r + c$
is not divisible by b, then
$2 r + c$
is not divisible by b, then
 $b = a + 1$
,
$b = a + 1$
,
 $c = a + 2$
,
$c = a + 2$
,
 $r = 2 a + 1$
and
$r = 2 a + 1$
and
 $a \in \{2, 3, 4\}$
.
$a \in \{2, 3, 4\}$
.
Proof. This follows from Table 7.
Lemma 5.14. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
and let
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
and let
![]() $\mathsf {p} \in X$
be an exceptional QI center. Then we are in Case (4) of Lemma 5.12 and
$\mathsf {p} \in X$
be an exceptional QI center. Then we are in Case (4) of Lemma 5.12 and
![]() $\mathsf {p} = \mathsf {p}_t$
. Moreover, we can write
$\mathsf {p} = \mathsf {p}_t$
. Moreover, we can write
where
![]() $f_i \in \mathbb {C} [x, u, v, w]$
is a quasi-homogeneous polynomial of degree i with
$f_i \in \mathbb {C} [x, u, v, w]$
is a quasi-homogeneous polynomial of degree i with
![]() $w \notin f_{2 a + b}$
.
$w \notin f_{2 a + b}$
.
Proof. We are in (1), (2), (3) and (4) of Lemma 5.12. Suppose that we are in (1). Then
![]() $\mathsf {p} = \mathsf {p}_w$
. Since
$\mathsf {p} = \mathsf {p}_w$
. Since
![]() $\mathsf {p} \in X$
is exceptional and X is quasi-smooth at
$\mathsf {p} \in X$
is exceptional and X is quasi-smooth at
![]() $\mathsf {p}$
, we have
$\mathsf {p}$
, we have
![]() $w^m q \in F$
for some
$w^m q \in F$
for some
![]() $m \ge 3$
and a homogeneous coordinate
$m \ge 3$
and a homogeneous coordinate
![]() $q \in \{x, s, u, v\}$
. This implies
$q \in \{x, s, u, v\}$
. This implies
which is impossible since
![]() $c < r$
. By similar arguments we can show that (2) and (3) are both impossible.
$c < r$
. By similar arguments we can show that (2) and (3) are both impossible.
It follows that we are in Case (4). In this case either
![]() $\mathsf {p} = \mathsf {p}_t$
or
$\mathsf {p} = \mathsf {p}_t$
or
![]() $\mathsf {p} = \mathsf {p}_w$
. The latter is impossible since
$\mathsf {p} = \mathsf {p}_w$
. The latter is impossible since
![]() $d = 4 a + 3 b < 3 r_2$
. Hence,
$d = 4 a + 3 b < 3 r_2$
. Hence,
![]() $\mathsf {p} = \mathsf {p}_t$
. We have
$\mathsf {p} = \mathsf {p}_t$
. We have
![]() $t^m q \in F$
for some integer
$t^m q \in F$
for some integer
![]() $m \ge 3$
and a homogeneous coordinate
$m \ge 3$
and a homogeneous coordinate
![]() $q \in \{x, u, v, w\}$
. It is easy to see that this is possible if and only if
$q \in \{x, u, v, w\}$
. It is easy to see that this is possible if and only if
![]() $m = 3$
and
$m = 3$
and
![]() $\deg q = a$
. Possibly replacing coordinates we may assume
$\deg q = a$
. Possibly replacing coordinates we may assume
![]() $q = u$
. Then it is straightforward to see that F can be written as equation (5.3).
$q = u$
. Then it is straightforward to see that F can be written as equation (5.3).
5.4 QI centers: exceptional case
The aim of this section is to prove the following.
Proposition 5.15. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, and let
$\mathsf {i} \in \mathsf {I} \setminus \mathsf {I}_1$
, and let
![]() $\mathsf {p} \in X$
be an exceptional QI center. Then
$\mathsf {p} \in X$
be an exceptional QI center. Then
Let X be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
which admits an exceptional QI center, Then, by Lemma 5.14 and Table 7, we have
$\mathsf {i} \in \mathsf {I} \setminus \{2, 8\}$
which admits an exceptional QI center, Then, by Lemma 5.14 and Table 7, we have
The rest of this section is devoted to the proof of Proposition 5.15 which will be done by division into cases. By Lemma 5.14, we can choose coordinates
![]() $x, u, v, t, w$
of
$x, u, v, t, w$
of
![]() $\mathbb {P} = \mathbb {P} (1, a, b, r_1, r_2)$
as in Case (4) of Lemma 5.12 with
$\mathbb {P} = \mathbb {P} (1, a, b, r_1, r_2)$
as in Case (4) of Lemma 5.12 with
![]() $\mathsf {p} = \mathsf {p}_t$
and the defining polynomial F is as in equation (5.3).
$\mathsf {p} = \mathsf {p}_t$
and the defining polynomial F is as in equation (5.3).
5.4.a Case:
 $a \ge 2$
and
$a \ge 2$
and
 $4 a \le 3 b$
$4 a \le 3 b$
This case corresponds to families
![]() $\mathcal {F}_{33}$
and
$\mathcal {F}_{33}$
and
![]() $\mathcal {F}_{58}$
. We have
$\mathcal {F}_{58}$
. We have
![]() $w^2 v \in f_{4 a + 3 b}$
since X is quasi-smooth at
$w^2 v \in f_{4 a + 3 b}$
since X is quasi-smooth at
![]() $\mathsf {p}_w$
. Moreover, we see that no quadratic monomial in variables
$\mathsf {p}_w$
. Moreover, we see that no quadratic monomial in variables
![]() $x, v, w$
appear in
$x, v, w$
appear in
![]() $f_{2 a + b}, f_{3 a + 2 b}, f _{4 a + 3 b}$
. This implies
$f_{2 a + b}, f_{3 a + 2 b}, f _{4 a + 3 b}$
. This implies
![]() $\operatorname {omult}_{\mathsf {p}} (H_u) = 3$
, and we have
$\operatorname {omult}_{\mathsf {p}} (H_u) = 3$
, and we have
 $$\begin{align*}\alpha_{\mathsf{p}} \left( X; \frac{1}{a} H_u \right) \ge \frac{a}{3} \ge \frac{2}{3}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} \left( X; \frac{1}{a} H_u \right) \ge \frac{a}{3} \ge \frac{2}{3}. \end{align*}$$
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an effective
$D \in |A|_{\mathbb {Q}}$
be an effective
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $\frac {1}{a} H_u$
. We can take a
$\frac {1}{a} H_u$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |r_2 A|_{\mathbb {Q}}$
such that
$T \in |r_2 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_u$
since
$D \cdot H_u$
since
![]() $\{x, u, v, w\}$
isolates
$\{x, u, v, w\}$
isolates
![]() $\mathsf {p}$
. Let
$\mathsf {p}$
. Let
![]() $q = q_{\mathsf {p}}$
be the quotient morphism of
$q = q_{\mathsf {p}}$
be the quotient morphism of
![]() $\mathsf {p} \in X$
, and let
$\mathsf {p} \in X$
, and let
![]() $\check {\mathsf {p}}$
be the preimage of
$\check {\mathsf {p}}$
be the preimage of
![]() $\mathsf {p}$
via q. Then we have
$\mathsf {p}$
via q. Then we have
since
![]() $4 a \le 3 b$
. Thus,
$4 a \le 3 b$
. Thus,
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge 1/2$
and the inequality
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge 1/2$
and the inequality
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved.
5.4.b Case:
 $a = 1$
$a = 1$
This case corresponds to families
![]() $\mathcal {F}_{12}$
,
$\mathcal {F}_{12}$
,
![]() $\mathcal {F}_{20}$
and
$\mathcal {F}_{20}$
and
![]() $\mathcal {F}_{31}$
. We have either
$\mathcal {F}_{31}$
. We have either
![]() $\bar {F} = F (x, 0, v, 1, w) \in (x, v, w)^2 \setminus (x, v, w)^3$
or
$\bar {F} = F (x, 0, v, 1, w) \in (x, v, w)^2 \setminus (x, v, w)^3$
or
![]() $\bar {F} \in (x, v, w) \in (x, v, w)^3$
, and its cubic part is not a cube of a linear form since
$\bar {F} \in (x, v, w) \in (x, v, w)^3$
, and its cubic part is not a cube of a linear form since
![]() $w^2 v \in F$
and
$w^2 v \in F$
and
![]() $w^3 \notin F$
. By Lemma 3.28, we have
$w^3 \notin F$
. By Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
since
$\alpha _{\mathsf {p}} (X) \ge 1/2$
since
![]() $a = 1$
.
$a = 1$
.
5.4.c Case: X is a member of the family
 $\mathcal {F}_{13}$
$\mathcal {F}_{13}$
Let
be a member of
![]() $\mathcal {F}_{13}$
and
$\mathcal {F}_{13}$
and
![]() $\mathsf {p} \in X$
an exceptional QI center. Then we have
$\mathsf {p} \in X$
an exceptional QI center. Then we have
where
![]() $f_i \in \mathbb {C} [x, y, z, w]$
is a quasi-homogeneous polynomial of degree i with
$f_i \in \mathbb {C} [x, y, z, w]$
is a quasi-homogeneous polynomial of degree i with
![]() $w \notin f_5$
, and
$w \notin f_5$
, and
![]() $\mathsf {p} = \mathsf {p}_t$
. Let
$\mathsf {p} = \mathsf {p}_t$
. Let
![]() $S, T \in |A|$
be general members. We have
$S, T \in |A|$
be general members. We have
where
![]() $\alpha , \beta \in \mathbb {C}$
. We set
$\alpha , \beta \in \mathbb {C}$
. We set
![]() $\Gamma = (x = y = z = 0)$
, which is a quasi-line of degree
$\Gamma = (x = y = z = 0)$
, which is a quasi-line of degree
![]() $1/15$
. If
$1/15$
. If
![]() $\beta \ne 0$
, then we set
$\beta \ne 0$
, then we set
which is clearly an irreducible and reduced curve of degree
![]() $3/10$
and does not pass through
$3/10$
and does not pass through
![]() $\mathsf {p}$
. Moreover, we have
$\mathsf {p}$
. Moreover, we have
Claim 9. If
![]() $\beta \ne 0$
, then the intersection matrix
$\beta \ne 0$
, then the intersection matrix
![]() $M (\Gamma , \Delta )$
satisfies the condition
$M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 9.
We have
![]() $\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and it is easy to see that S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_w\}$
, and it is easy to see that S is quasi-smooth at
![]() $\mathsf {p}_w$
since
$\mathsf {p}_w$
since
![]() $S \in |A|$
is general. By Lemma 3.9, S is quasi-smooth along
$S \in |A|$
is general. By Lemma 3.9, S is quasi-smooth along
![]() $\Gamma $
and we have
$\Gamma $
and we have
![]() $\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_t, \mathsf {p}_w\}$
, where
$\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_t, \mathsf {p}_w\}$
, where
![]() $\mathsf {p}_t, \mathsf {p}_w \in S$
are of types
$\mathsf {p}_t, \mathsf {p}_w \in S$
are of types
![]() $\frac {1}{3} (1, 2)$
,
$\frac {1}{3} (1, 2)$
,
![]() $\frac {1}{5} (2, 3)$
, respectively. By Remark 3.10, we have
$\frac {1}{5} (2, 3)$
, respectively. By Remark 3.10, we have
By taking intersection numbers of
![]() $T|_S = \Gamma + \Delta $
and
$T|_S = \Gamma + \Delta $
and
![]() $\Gamma , \Delta $
, we have
$\Gamma , \Delta $
, we have
Thus,
![]() $M (\Gamma , \Delta )$
satisfies the condition
$M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Suppose
![]() $\beta = 0$
and
$\beta = 0$
and
![]() $\alpha \ne 0$
. We set
$\alpha \ne 0$
. We set
which are irreducible and reduced curves of degrees
![]() $1/10$
,
$1/10$
,
![]() $1/5$
, respectively, which do not pass through
$1/5$
, respectively, which do not pass through
![]() $\mathsf {p}$
. We have
$\mathsf {p}$
. We have
Claim 10. If
![]() $\beta = 0$
and
$\beta = 0$
and
![]() $\alpha \ne 0$
, then the intersection matrix
$\alpha \ne 0$
, then the intersection matrix
![]() $M (\Gamma , \Xi , \Theta )$
satisfies the condition
$M (\Gamma , \Xi , \Theta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 10.
We have
![]() $(\Gamma ^2)_S = - 8/15$
by the proof of Claim 9. We see that
$(\Gamma ^2)_S = - 8/15$
by the proof of Claim 9. We see that
![]() $\Xi \cap (\Gamma \cup \Theta ) = \{\mathsf {p}_w\}$
and S is quasi-smooth at
$\Xi \cap (\Gamma \cup \Theta ) = \{\mathsf {p}_w\}$
and S is quasi-smooth at
![]() $\mathsf {p}_w$
. By Lemma 3.9, S is quasi-smooth along
$\mathsf {p}_w$
. By Lemma 3.9, S is quasi-smooth along
![]() $\Xi $
and we have
$\Xi $
and we have
![]() $\operatorname {Sing}_{\Xi } (S) = \{\mathsf {p}_z, \mathsf {p}_w\}$
, where
$\operatorname {Sing}_{\Xi } (S) = \{\mathsf {p}_z, \mathsf {p}_w\}$
, where
![]() $\mathsf {p}_z, \mathsf {p}_w \in S$
are of types
$\mathsf {p}_z, \mathsf {p}_w \in S$
are of types
![]() $\frac {1}{2} (1, 1)$
,
$\frac {1}{2} (1, 1)$
,
![]() $\frac {1}{5} (2, 3)$
, respectively. By Remark 3.10, we have
$\frac {1}{5} (2, 3)$
, respectively. By Remark 3.10, we have
We compute the intersection number
![]() $(\Gamma \cdot \Xi )_S$
. We have
$(\Gamma \cdot \Xi )_S$
. We have
![]() $\Gamma \cap \Xi = \{\mathsf {p}_w\}$
, and the germ
$\Gamma \cap \Xi = \{\mathsf {p}_w\}$
, and the germ
![]() $\mathsf {p}_w \in S$
is analytically isomorphic to
$\mathsf {p}_w \in S$
is analytically isomorphic to
![]() $\bar {o} \in \mathbb {A}^2_{z, t}/{\boldsymbol {\mu }}_5$
, where the
$\bar {o} \in \mathbb {A}^2_{z, t}/{\boldsymbol {\mu }}_5$
, where the
![]() ${\boldsymbol {\mu }}_5$
-action on
${\boldsymbol {\mu }}_5$
-action on
![]() $\mathbb {A}^2_{z, t}$
is given by
$\mathbb {A}^2_{z, t}$
is given by
and
![]() $\bar {o}$
is the image of the origin
$\bar {o}$
is the image of the origin
![]() $o \in \mathbb {A}^2_{z, t}$
. Under the isomorphism,
$o \in \mathbb {A}^2_{z, t}$
. Under the isomorphism,
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Xi $
corresponds to the quotient of
$\Xi $
corresponds to the quotient of
![]() $(z = 0)$
and
$(z = 0)$
and
![]() $(t = 0)$
. It follows that
$(t = 0)$
. It follows that
Then, by taking intersection numbers of
![]() $T|_S = \Gamma + \Xi + \Theta $
and
$T|_S = \Gamma + \Xi + \Theta $
and
![]() $\Gamma , \Xi , \Theta $
, we have
$\Gamma , \Xi , \Theta $
, we have
Thus,
![]() $M (\Gamma , \Xi , \Theta )$
satisfies the condition
$M (\Gamma , \Xi , \Theta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Suppose
![]() $\beta = \alpha = 0$
. Then
$\beta = \alpha = 0$
. Then
where
![]() $\Xi = (x = y = t = 0)$
.
$\Xi = (x = y = t = 0)$
.
Claim 11. If
![]() $\beta = \alpha = 0$
, then the intersection matrix
$\beta = \alpha = 0$
, then the intersection matrix
![]() $M (\Gamma , \Xi )$
satisfies the condition
$M (\Gamma , \Xi )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 11.
We have
![]() $(\Gamma ^2)_S = - 8/15$
by the proof of Claim 9. By taking intersection numbers of
$(\Gamma ^2)_S = - 8/15$
by the proof of Claim 9. By taking intersection numbers of
![]() $T|_S = \Gamma + 3 \Xi $
and
$T|_S = \Gamma + 3 \Xi $
and
![]() $\Gamma , \Xi $
, we have
$\Gamma , \Xi $
, we have
Thus,
![]() $M (\Gamma , \Xi )$
satisfies the condition
$M (\Gamma , \Xi )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
By Claims 9, 10, 11 and Lemma 3.21, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{3 (A^3) + 1 - 3 \deg \Gamma} \right\} = \frac{10}{19}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{3 (A^3) + 1 - 3 \deg \Gamma} \right\} = \frac{10}{19}. \end{align*}$$
5.4.d Case: X is a member of the family
 $\mathcal {F}_{25}$
$\mathcal {F}_{25}$
Let
be a member of
![]() $\mathcal {F}_{25}$
, and let
$\mathcal {F}_{25}$
, and let
![]() $\mathsf {p}$
be an exceptional QI center. Then we have
$\mathsf {p}$
be an exceptional QI center. Then we have
where
![]() $f_i \in \mathbb {C} [x, y, z, w]$
is a quasi-homogeneous polynomial of degree i with
$f_i \in \mathbb {C} [x, y, z, w]$
is a quasi-homogeneous polynomial of degree i with
![]() $w \notin f_7$
, and we have
$w \notin f_7$
, and we have
![]() $\mathsf {p} = \mathsf {p}_t$
. By the quasi-smoothness we have
$\mathsf {p} = \mathsf {p}_t$
. By the quasi-smoothness we have
![]() $z^5 \in f_{15}$
and we may assume
$z^5 \in f_{15}$
and we may assume
![]() $\operatorname {coeff}_{f_{15}} (z^5) = 1$
. Then we have
$\operatorname {coeff}_{f_{15}} (z^5) = 1$
. Then we have
Let
![]() $S, T \in |A|$
be general members. Then we have
$S, T \in |A|$
be general members. Then we have
where
![]() $\Gamma = (x = y = z = 0)$
is a quasi-line of degree
$\Gamma = (x = y = z = 0)$
is a quasi-line of degree
![]() $1/28$
and
$1/28$
and
![]() $\Delta = (x = y = t^3 + z^4)$
is an irreducible and reduced curve of degree
$\Delta = (x = y = t^3 + z^4)$
is an irreducible and reduced curve of degree
![]() $1/7$
that does not pass through
$1/7$
that does not pass through
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Claim 12. The intersection matrix
![]() $M (\Gamma , \Delta )$
satisfies the condition
$M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 12.
We have
![]() $\Gamma \cap \Delta = \{\mathsf {p}_w\}$
and S is quasi-smooth at
$\Gamma \cap \Delta = \{\mathsf {p}_w\}$
and S is quasi-smooth at
![]() $\mathsf {p}_w$
. Hence, S is quasi-smooth along
$\mathsf {p}_w$
. Hence, S is quasi-smooth along
![]() $\Gamma $
by Lemma 3.9, and we have
$\Gamma $
by Lemma 3.9, and we have
![]() $\operatorname {Sing}_{\Gamma } (S) = \{ \mathsf {p}_t, \mathsf {p}_w\}$
, where
$\operatorname {Sing}_{\Gamma } (S) = \{ \mathsf {p}_t, \mathsf {p}_w\}$
, where
![]() $\mathsf {p}_t, \mathsf {p}_w \in S$
are of types
$\mathsf {p}_t, \mathsf {p}_w \in S$
are of types
![]() $\frac {1}{4} (1, 3), \frac {1}{7} (3, 4)$
, respectively. By Remark 3.10, we have
$\frac {1}{4} (1, 3), \frac {1}{7} (3, 4)$
, respectively. By Remark 3.10, we have
By taking intersection numbers of
![]() $T|_S = \Gamma + \Delta $
and
$T|_S = \Gamma + \Delta $
and
![]() $\Gamma , \Delta $
, we have
$\Gamma , \Delta $
, we have
It follows that
![]() $M (\Gamma , \Delta )$
satisfies the condition
$M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
By Claim 12 and Lemma 3.21, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{4 (A^3) + 1 - 4 \deg \Gamma} \right\} = \frac{7}{11}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{4 (A^3) + 1 - 4 \deg \Gamma} \right\} = \frac{7}{11}. \end{align*}$$
5.4.e Case: X is a member of the family
 $\mathcal {F}_{38}$
$\mathcal {F}_{38}$
Let
be a member of
![]() $\mathcal {F}_{38}$
and
$\mathcal {F}_{38}$
and
![]() $\mathsf {p} \in X$
an exceptional QI center. Then we have
$\mathsf {p} \in X$
an exceptional QI center. Then we have
where
![]() $f_i \in \mathbb {C} [x, y, z, w]$
is a quasi-homogeneous polynomial of degree i with
$f_i \in \mathbb {C} [x, y, z, w]$
is a quasi-homogeneous polynomial of degree i with
![]() $w \notin f_8$
, and
$w \notin f_8$
, and
![]() $\mathsf {p} = \mathsf {p}_t$
. By the quasi-smoothness of X, we have
$\mathsf {p} = \mathsf {p}_t$
. By the quasi-smoothness of X, we have
![]() $z^6 \in f_{18}$
and we may assume
$z^6 \in f_{18}$
and we may assume
![]() $\operatorname {coeff}_{f_{18}} (z^6) = 1$
. Then we have
$\operatorname {coeff}_{f_{18}} (z^6) = 1$
. Then we have
We set
![]() $S = H_x$
and
$S = H_x$
and
![]() $T = H_y$
. We have
$T = H_y$
. We have
where
![]() $\Gamma = (x = y = z = 0)$
is a quasi-line of degree
$\Gamma = (x = y = z = 0)$
is a quasi-line of degree
![]() $1/40$
and
$1/40$
and
![]() $\Delta = (x = y = t^3 + z^5 = 0)$
is an irreducible and reduced curve of degree
$\Delta = (x = y = t^3 + z^5 = 0)$
is an irreducible and reduced curve of degree
![]() $1/8$
that does not pass through
$1/8$
that does not pass through
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Claim 13. The intersection matrix
![]() $M (\Gamma , \Delta )$
satisfies the condition
$M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 13.
By similar arguments as in the proof of Claim 12, we have
and
Thus,
![]() $M (\Gamma , \Delta )$
satisfies the condition
$M (\Gamma , \Delta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
By Claim 13 and Lemma 3.21, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{5 \cdot 2 \cdot (A^3) + \frac{1}{2} - 5 \deg \Gamma} \right\} = \frac{8}{9}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{5 \cdot 2 \cdot (A^3) + \frac{1}{2} - 5 \deg \Gamma} \right\} = \frac{8}{9}. \end{align*}$$
This completes the proof of Proposition 5.15.
5.5 QI centers: degenerate case
The aim of this section is to prove the following, which gives the exact value of
![]() $\alpha _{\mathsf {p}} (X)$
for a degenerate QI center
$\alpha _{\mathsf {p}} (X)$
for a degenerate QI center
![]() $\mathsf {p} \in X$
.
$\mathsf {p} \in X$
.
Let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
, where
$\mathsf {i} \in \mathsf {I}$
, where
![]() $1 = a_0 \le a_1 \le \cdots \le a_4$
, and let
$1 = a_0 \le a_1 \le \cdots \le a_4$
, and let
![]() $\mathsf {p} \in X$
be a degenerate QI center. We choose homogeneous coordinates as in Lemma 5.11.
$\mathsf {p} \in X$
be a degenerate QI center. We choose homogeneous coordinates as in Lemma 5.11.
Proposition 5.16. Let the notation as above, and let
![]() $\mathsf {p} = \mathsf {p}_{x_k} \in X$
be a degenerate QI center. Then
$\mathsf {p} = \mathsf {p}_{x_k} \in X$
be a degenerate QI center. Then
 $$\begin{align*}\alpha_{\mathsf{p}} (X) = \begin{cases} \frac{a_k + 1}{2 a_k + 1}, & \text{if}\ a_j = 1, \\ 1, & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) = \begin{cases} \frac{a_k + 1}{2 a_k + 1}, & \text{if}\ a_j = 1, \\ 1, & \text{otherwise}. \end{cases} \end{align*}$$
In particular, we have
![]() $\alpha _{\mathsf {p}} (X)> \frac {1}{2}$
.
$\alpha _{\mathsf {p}} (X)> \frac {1}{2}$
.
Proof. Let
![]() $\varphi \colon Y \to X$
be the Kawamata blowup at
$\varphi \colon Y \to X$
be the Kawamata blowup at
![]() $\mathsf {p}$
with exceptional divisor E. Note that we can choose
$\mathsf {p}$
with exceptional divisor E. Note that we can choose
![]() $x_{i_1}, x_{i_2}, x_{i_3}$
as a system of orbifold coordinates at
$x_{i_1}, x_{i_2}, x_{i_3}$
as a system of orbifold coordinates at
![]() $\mathsf {p}$
and
$\mathsf {p}$
and
![]() $\varphi $
is the weighted blowup with weight
$\varphi $
is the weighted blowup with weight
![]() $\operatorname {wt} (x_{i_1}, x_{i_2}, x_{i_3}) = \frac {1}{a_k} (a_{i_1}, a_{i_2}, a_{i_3})$
. Filtering off terms divisible by
$\operatorname {wt} (x_{i_1}, x_{i_2}, x_{i_3}) = \frac {1}{a_k} (a_{i_1}, a_{i_2}, a_{i_3})$
. Filtering off terms divisible by
![]() $x_j$
in equation (5.2), we have
$x_j$
in equation (5.2), we have
Since the polynomial
![]() $x_k^2 + \cdots $
does not vanish at
$x_k^2 + \cdots $
does not vanish at
![]() $\mathsf {p}$
, the vanishing order of
$\mathsf {p}$
, the vanishing order of
![]() $x_j$
along E coincides with that of
$x_j$
along E coincides with that of
![]() $\bar {g}$
, which is clearly
$\bar {g}$
, which is clearly
![]() $d/a_k$
. Hence, we have
$d/a_k$
. Hence, we have
 $$ \begin{align} K_Y + \frac{1}{a_j} \tilde{H}_{x_j} + \frac{2}{a_j} E = \varphi^* \left( K_X + \frac{1}{a_j} H_{x_j} \right), \end{align} $$
$$ \begin{align} K_Y + \frac{1}{a_j} \tilde{H}_{x_j} + \frac{2}{a_j} E = \varphi^* \left( K_X + \frac{1}{a_j} H_{x_j} \right), \end{align} $$
where
![]() $\tilde {H}_{x_j}$
is the proper transform of
$\tilde {H}_{x_j}$
is the proper transform of
![]() $H_{x_j}$
on Y. In particular,
$H_{x_j}$
on Y. In particular,
![]() $(X, \frac {1}{a_j} H_{x_j})$
is not canonical at
$(X, \frac {1}{a_j} H_{x_j})$
is not canonical at
![]() $\mathsf {p}$
. By Lemma 3.5, we have
$\mathsf {p}$
. By Lemma 3.5, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
if
$\alpha _{\mathsf {p}} (X) \ge 1$
if
![]() $(X, \frac {1}{a_j} H_{x_j})$
is log canonical at
$(X, \frac {1}{a_j} H_{x_j})$
is log canonical at
![]() $\mathsf {p}$
, and otherwise
$\mathsf {p}$
, and otherwise
![]() $\alpha _{\mathsf {p}} (X) = \operatorname {lct}_{\mathsf {p}} (X;\frac {1}{a_j} H_{x_j})$
.
$\alpha _{\mathsf {p}} (X) = \operatorname {lct}_{\mathsf {p}} (X;\frac {1}{a_j} H_{x_j})$
.
Suppose
![]() $a_j> 1$
. The pair
$a_j> 1$
. The pair
![]() $(E, \frac {1}{a_j} \tilde {H}_{x_j}|_E)$
is log canonical since
$(E, \frac {1}{a_j} \tilde {H}_{x_j}|_E)$
is log canonical since
![]() $\tilde {H}_{x_j}|_E$
is isomorphic to
$\tilde {H}_{x_j}|_E$
is isomorphic to
which is quasi-smooth by Lemma 5.11. By the inversion of adjunction, the pair
![]() $(Y, \frac {1}{a_j} \tilde {H}_{x_j} + E)$
is log canonical along E and so is the pair
$(Y, \frac {1}{a_j} \tilde {H}_{x_j} + E)$
is log canonical along E and so is the pair
![]() $(Y, \frac {1}{a_j} \tilde {H}_{x_j} + \frac {2}{a_j} E)$
since
$(Y, \frac {1}{a_j} \tilde {H}_{x_j} + \frac {2}{a_j} E)$
since
![]() $2/a_j \le 1$
. By equation (5.4), the pair
$2/a_j \le 1$
. By equation (5.4), the pair
![]() $(X, \frac {1}{a_j} H_{x_j})$
is log canonical at
$(X, \frac {1}{a_j} H_{x_j})$
is log canonical at
![]() $\mathsf {p}$
. Thus,
$\mathsf {p}$
. Thus,
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
. The existence of the prime divisor
$\alpha _{\mathsf {p}} (X) \ge 1$
. The existence of the prime divisor
![]() $H_{x_0} \in A$
passing through
$H_{x_0} \in A$
passing through
![]() $\mathsf {p}$
shows
$\mathsf {p}$
shows
![]() $\alpha _{\mathsf {p}} (X) \le 1$
, and we conclude
$\alpha _{\mathsf {p}} (X) \le 1$
, and we conclude
![]() $\alpha _{\mathsf {p}} (X) = 1$
in this case.
$\alpha _{\mathsf {p}} (X) = 1$
in this case.
Suppose
![]() $a_j = 1$
. We set
$a_j = 1$
. We set
and prove
![]() $\operatorname {lct}_{\mathsf {p}} (X;\frac {1}{a_j} H_{x_j}) = \theta $
. For a rational number
$\operatorname {lct}_{\mathsf {p}} (X;\frac {1}{a_j} H_{x_j}) = \theta $
. For a rational number
![]() $c \ge 0$
, it is easy to see that the discrepancy of the pair
$c \ge 0$
, it is easy to see that the discrepancy of the pair
![]() $(X, \frac {c}{a_j} H_{x_j})$
along E is
$(X, \frac {c}{a_j} H_{x_j})$
along E is
and it is at least
![]() $-1$
if and only if
$-1$
if and only if
![]() $c \le \theta $
. This shows
$c \le \theta $
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;\frac {1}{a_j} H_{x_j}) \le \theta $
. Moreover, since
$\operatorname {lct}_{\mathsf {p}} (X;\frac {1}{a_j} H_{x_j}) \le \theta $
. Moreover, since
 $$\begin{align*}K_Y + \frac{\theta}{a_j} \tilde{H}_{x_j} + E = \varphi^* \left( K_X + \frac{\theta}{a_j} H_{x_j} \right) \end{align*}$$
$$\begin{align*}K_Y + \frac{\theta}{a_j} \tilde{H}_{x_j} + E = \varphi^* \left( K_X + \frac{\theta}{a_j} H_{x_j} \right) \end{align*}$$
and the pair
![]() $(Y, \frac {\theta }{a_j} \tilde {H}_{x_j} + E)$
is log canonical along E, the pair
$(Y, \frac {\theta }{a_j} \tilde {H}_{x_j} + E)$
is log canonical along E, the pair
![]() $(X, \frac {\theta }{a_j} H_{x_j})$
is log canonical at
$(X, \frac {\theta }{a_j} H_{x_j})$
is log canonical at
![]() $\mathsf {p}$
. This shows
$\mathsf {p}$
. This shows
![]() $\alpha _{\mathsf {p}} (X) = \theta $
, and the proof is completed.
$\alpha _{\mathsf {p}} (X) = \theta $
, and the proof is completed.
Example 5.17. Let
![]() $X = X_{21} \subset \mathbb {P} (1,1,3,7,10)$
be a member of the family
$X = X_{21} \subset \mathbb {P} (1,1,3,7,10)$
be a member of the family
![]() $\mathcal {F}_{46}$
and
$\mathcal {F}_{46}$
and
![]() $\mathsf {p} = \mathsf {p}_w$
the
$\mathsf {p} = \mathsf {p}_w$
the
![]() $\frac {1}{10} (1,3,7)$
point, which is the center of a quadratic involution. Assume that
$\frac {1}{10} (1,3,7)$
point, which is the center of a quadratic involution. Assume that
![]() $\mathsf {p}$
is degenerate, which is equivalent to X being birationally superrigid. Then, by Proposition 5.16, we have
$\mathsf {p}$
is degenerate, which is equivalent to X being birationally superrigid. Then, by Proposition 5.16, we have
5.6 QI centers: nondegenerate case
The aim of this section is to prove the following.
Proposition 5.18. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I} \setminus \{2, 5, 8\}$
and
$\mathsf {i} \in \mathsf {I} \setminus \{2, 5, 8\}$
and
![]() $\mathsf {p} \in X$
be a nondegenerate QI center. Then
$\mathsf {p} \in X$
be a nondegenerate QI center. Then
The rest of this section is entirely devoted to the proof of Proposition 5.18, which will be done by dividing into several cases.
5.6.a Case: X has a unique QI center
By Lemma 5.12, we can choose homogeneous coordinates so that
where a is corprime to b,
![]() $a < b$
,
$a < b$
,
![]() $r = a + b$
and
$r = a + b$
and
![]() $c < r$
. Let
$c < r$
. Let
![]() $\mathsf {p} \in X$
be the QI center. Then
$\mathsf {p} \in X$
be the QI center. Then
![]() $\mathsf {p} = \mathsf {p}_w$
and the defining polynomial F of X can be written as
$\mathsf {p} = \mathsf {p}_w$
and the defining polynomial F of X can be written as
where
![]() $f_{r + c} = f_{r + c} (x, s, u)$
and
$f_{r + c} = f_{r + c} (x, s, u)$
and
![]() $f_{2 r + c} = f_{2 r + c} (x, s, u, v)$
are quasi-homogeneous polynomials of the indicated degree. We will show that
$f_{2 r + c} = f_{2 r + c} (x, s, u, v)$
are quasi-homogeneous polynomials of the indicated degree. We will show that
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{c} H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{c} H_v) \ge 1/2$
.
Claim 14. Suppose that
![]() $c \ge 2$
and
$c \ge 2$
and
![]() $2 r + c$
is divisible by b. Then
$2 r + c$
is divisible by b. Then
 $$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right) \ge \frac{1}{2}. \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right) \ge \frac{1}{2}. \end{align*}$$
Proof of Claim 14.
We first show that
![]() $\mathsf {p}_u \notin X$
unless X belongs to the family
$\mathsf {p}_u \notin X$
unless X belongs to the family
![]() $\mathcal {F}_7$
. Suppose
$\mathcal {F}_7$
. Suppose
![]() $\mathsf {p}_u \in X$
. By the quasi-smoothness of X at
$\mathsf {p}_u \in X$
. By the quasi-smoothness of X at
![]() $\mathsf {p}_u$
, we have
$\mathsf {p}_u$
, we have
![]() $d = m b + e$
, where
$d = m b + e$
, where
![]() $m \in \mathbb {Z}_{> 0}$
and
$m \in \mathbb {Z}_{> 0}$
and
![]() $e \in \{1, a, c, r\}$
. Since d is divisible by b, we see that e is divisible by b. This is possible only when
$e \in \{1, a, c, r\}$
. Since d is divisible by b, we see that e is divisible by b. This is possible only when
![]() $e = c$
since
$e = c$
since
![]() $r = a + b$
and a are both coprime to b. Thus, we can write
$r = a + b$
and a are both coprime to b. Thus, we can write
![]() $c = k b$
for some
$c = k b$
for some
![]() $k \in \mathbb {Z}_{> 0}$
. Take any point
$k \in \mathbb {Z}_{> 0}$
. Take any point
![]() $\mathsf {q} \in (x = s = w = 0) \cap X$
. The singularity
$\mathsf {q} \in (x = s = w = 0) \cap X$
. The singularity
![]() $\mathsf {q} \in X$
is of type
$\mathsf {q} \in X$
is of type
![]() $\frac {1}{b} (1, a, r) = \frac {1}{b} (1, a, a)$
. It follows that
$\frac {1}{b} (1, a, r) = \frac {1}{b} (1, a, a)$
. It follows that
![]() $a = 1$
and
$a = 1$
and
![]() $b = 2$
since
$b = 2$
since
![]() $\mathsf {q} \in X$
is terminal. We have
$\mathsf {q} \in X$
is terminal. We have
![]() $r = a + b = 3$
and
$r = a + b = 3$
and
![]() $c = 2$
since
$c = 2$
since
![]() $c = k b = 2 k < r = 3$
. Thus,
$c = k b = 2 k < r = 3$
. Thus,
![]() $X = X_8 \subset \mathbb {P} (1, 1, 2, 2, 3)$
and this belongs to
$X = X_8 \subset \mathbb {P} (1, 1, 2, 2, 3)$
and this belongs to
![]() $\mathcal {F}_7$
.
$\mathcal {F}_7$
.
We first consider the case where
![]() $\mathsf {p}_u \notin X$
. This means that
$\mathsf {p}_u \notin X$
. This means that
![]() $u^m \in F$
for some
$u^m \in F$
for some
![]() $m \in \mathbb {Z}_{> 0}$
. We have
$m \in \mathbb {Z}_{> 0}$
. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_v) \le m = (2 r + c)/b$
and hence
$\operatorname {omult}_{\mathsf {p}} (H_v) \le m = (2 r + c)/b$
and hence
 $$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left( X; \frac{1}{c} H_v \right) \ge \frac{b c}{2 r + c}. \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left( X; \frac{1}{c} H_v \right) \ge \frac{b c}{2 r + c}. \end{align*}$$
It remains to prove the inequality
![]() $bc/(2r + c) \ge 1/2$
, which is equivalent to
$bc/(2r + c) \ge 1/2$
, which is equivalent to
![]() $(2 b - 1) c \ge 2 r$
. We have
$(2 b - 1) c \ge 2 r$
. We have
since
![]() $c \ge 2$
and
$c \ge 2$
and
![]() $b> a$
. This shows
$b> a$
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{c} H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{c} H_v) \ge 1/2$
.
We next consider the case where
![]() $\mathsf {p}_u \in X$
. In this case, X belongs to the family
$\mathsf {p}_u \in X$
. In this case, X belongs to the family
![]() $\mathcal {F}_7$
and
$\mathcal {F}_7$
and
![]() $X = X_8 \subset \mathbb {P} (1, 1, 2, 2, 3)_{x, s, u, v, w}$
with defining polynomial
$X = X_8 \subset \mathbb {P} (1, 1, 2, 2, 3)_{x, s, u, v, w}$
with defining polynomial
We have
![]() $u^4 \notin F$
since
$u^4 \notin F$
since
![]() $\mathsf {p}_u \in X$
. We show that
$\mathsf {p}_u \in X$
. We show that
![]() $f_5 (x, s, u)$
contains a monomial involving u. Suppose to the contrary that
$f_5 (x, s, u)$
contains a monomial involving u. Suppose to the contrary that
![]() $f_5 = f_5 (x, s)$
is a polynomial in variables x and s. We can write
$f_5 = f_5 (x, s)$
is a polynomial in variables x and s. We can write
![]() $f_8 = u^3 g_2 + u^2 g_4 + u g_6 + g_8 + v h_6$
, where
$f_8 = u^3 g_2 + u^2 g_4 + u g_6 + g_8 + v h_6$
, where
![]() $g_i = g_i (x, s)$
and
$g_i = g_i (x, s)$
and
![]() $h_6 = h_6 (x, s, u, v)$
are quasi-homogeneous polynomials of indicated degree. Then we have
$h_6 = h_6 (x, s, u, v)$
are quasi-homogeneous polynomials of indicated degree. Then we have
![]() $F = v (w^2 + h_6) + g$
, where
$F = v (w^2 + h_6) + g$
, where
![]() $g = w f_5 + u^3 g_2 + u^2 g_4 + u g_6 + g_8 \in (x, s)^2$
, and we see that X is not quasi-smooth at any point in the nonempty set
$g = w f_5 + u^3 g_2 + u^2 g_4 + u g_6 + g_8 \in (x, s)^2$
, and we see that X is not quasi-smooth at any point in the nonempty set
This is a contradiction. It follows that there is a monomial involving u which appears in
![]() $f_5$
with nonzero coefficient. This implies
$f_5$
with nonzero coefficient. This implies
![]() $\operatorname {omult}_{\mathsf {p}} (H_v) \le 4$
, and we have
$\operatorname {omult}_{\mathsf {p}} (H_v) \le 4$
, and we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{2} H_v) \ge 1/2$
as desired.
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{2} H_v) \ge 1/2$
as desired.
Claim 15. Suppose that
![]() $c \ge 2$
and
$c \ge 2$
and
![]() $2 r + c$
is not divisible by b. Then
$2 r + c$
is not divisible by b. Then
 $$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right) \ge \frac{c}{5} \ge \frac{4}{5}. \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right) \ge \frac{c}{5} \ge \frac{4}{5}. \end{align*}$$
Proof of Claim 15.
By Lemma 5.13, we have
with
![]() $a \in \{2, 3, 4\}$
. Moreover,
$a \in \{2, 3, 4\}$
. Moreover,
![]() $\mathsf {p} = \mathsf {p}_w$
and the defining polynomial of X can be written as
$\mathsf {p} = \mathsf {p}_w$
and the defining polynomial of X can be written as
By the quasi-smoothness of X at
![]() $\mathsf {p}_z$
, we have either
$\mathsf {p}_z$
, we have either
![]() $u^3 \in f_{3 a + 3}$
or
$u^3 \in f_{3 a + 3}$
or
![]() $u^4 s \in f_{5 a + 4}$
. This implies
$u^4 s \in f_{5 a + 4}$
. This implies
![]() $\operatorname {omult}_{\mathsf {p}} (H_v) \le 5$
, and we have
$\operatorname {omult}_{\mathsf {p}} (H_v) \le 5$
, and we have
 $$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right) \ge \frac{c}{5} = \frac{a+2}{5} \ge \frac{4}{5}. \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right) \ge \frac{c}{5} = \frac{a+2}{5} \ge \frac{4}{5}. \end{align*}$$
This proves the claim.
It remains to consider the case where
![]() $c = 1$
. By Lemma 5.13, X belongs to a family
$c = 1$
. By Lemma 5.13, X belongs to a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \{24, 46\}$
.
$\mathsf {i} \in \{24, 46\}$
.
Claim 16. Suppose X is a member of the family
![]() $\mathcal {F}_{24}$
. Then
$\mathcal {F}_{24}$
. Then
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
Proof of Claim 16.
We have
and
![]() $\mathsf {p} = \mathsf {p}_w$
is of type
$\mathsf {p} = \mathsf {p}_w$
is of type
![]() $\frac {1}{7} (1, 2, 5)$
. We can write
$\frac {1}{7} (1, 2, 5)$
. We can write
where
![]() $f_8 = f_8 (x, s, u) \ne 0$
and
$f_8 = f_8 (x, s, u) \ne 0$
and
![]() $f_{15} = f_{15} (x, s, u, v)$
are quasi-homogeneous polynomials of degrees
$f_{15} = f_{15} (x, s, u, v)$
are quasi-homogeneous polynomials of degrees
![]() $8$
and
$8$
and
![]() $15$
, respectively. We have
$15$
, respectively. We have
![]() $u^3 \in f_{15}$
, and we may assume
$u^3 \in f_{15}$
, and we may assume
![]() $\operatorname {coeff}_{f_{15}} (u^3) = 1$
. We set
$\operatorname {coeff}_{f_{15}} (u^3) = 1$
. We set
![]() $\bar {F} := F (x, s, u, 0, 1)$
. For a given
$\bar {F} := F (x, s, u, 0, 1)$
. For a given
![]() $\underline {c} = (c_1, c_2, c_3) \in (\mathbb {Z}_{> 0})^3$
, we denote by
$\underline {c} = (c_1, c_2, c_3) \in (\mathbb {Z}_{> 0})^3$
, we denote by
![]() $G_{\underline {c}} \in \mathbb {C} [x, s, u]$
the lowest weight part of
$G_{\underline {c}} \in \mathbb {C} [x, s, u]$
the lowest weight part of
![]() $\bar {F}$
with respect to the weight
$\bar {F}$
with respect to the weight
![]() $\operatorname {wt} (x, s, u) = \underline {c}$
and let
$\operatorname {wt} (x, s, u) = \underline {c}$
and let
be the effective
![]() $\mathbb {Q}$
-divisor on
$\mathbb {Q}$
-divisor on
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
associated to
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
associated to
![]() $G_{\underline {c}}$
. By Lemma 3.27, we have
$G_{\underline {c}}$
. By Lemma 3.27, we have
 $$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X; H_v) \ge \min \left\{ \frac{c_1 + c_2 + c_3}{\deg G_{\underline{c}}}, \ \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \right\}, \end{align} $$
$$ \begin{align} \operatorname{lct}_{\mathsf{p}} (X; H_v) \ge \min \left\{ \frac{c_1 + c_2 + c_3}{\deg G_{\underline{c}}}, \ \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \right\}, \end{align} $$
where
![]() $\deg G_{\underline {c}}$
is the degree with respect to the weight
$\deg G_{\underline {c}}$
is the degree with respect to the weight
![]() $\operatorname {wt} (x, s, u) = \underline {c}$
.
$\operatorname {wt} (x, s, u) = \underline {c}$
.
Suppose
![]() $u s x \in f_8$
. In this case, we may assume
$u s x \in f_8$
. In this case, we may assume
![]() $\operatorname {coeff}_{f_8} (u s x) = 1$
and we have
$\operatorname {coeff}_{f_8} (u s x) = 1$
and we have
![]() $G_{\underline {c}} = u s x + u^3$
for
$G_{\underline {c}} = u s x + u^3$
for
![]() $\underline {c} = (1, 1, 1)$
. In this case,
$\underline {c} = (1, 1, 1)$
. In this case,
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}} = \mathbb {P}^2$
,
$\mathbb {P} (\underline {c})^{\operatorname {wf}} = \mathbb {P}^2$
,
![]() $\operatorname {Diff} = 0$
and
$\operatorname {Diff} = 0$
and
![]() $\mathcal {D}_{\underline {c}}$
is the sum of a line and a conic intersection at two distinct points. It is straightforward to check
$\mathcal {D}_{\underline {c}}$
is the sum of a line and a conic intersection at two distinct points. It is straightforward to check
and we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 1$
in this case.
$\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 1$
in this case.
Suppose that
![]() $u s x \notin f_8$
and
$u s x \notin f_8$
and
![]() $s^4 \in f_8$
. In this case, we may assume
$s^4 \in f_8$
. In this case, we may assume
![]() $\operatorname {coeff}_{f_8} (s^4) = 1$
and
$\operatorname {coeff}_{f_8} (s^4) = 1$
and
![]() $\operatorname {coeff}_{f_{15}} (u s^5) = 0$
by replacing s and w. Hence, we have
$\operatorname {coeff}_{f_{15}} (u s^5) = 0$
by replacing s and w. Hence, we have
and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge \operatorname {lct}_{\mathsf {p}} (H_x, H_v|_{H_x}) = 7/12$
, where the equality follows from [Reference KollárKol97, 8.21 Proposition] (or by Lemma 3.27 with
$\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge \operatorname {lct}_{\mathsf {p}} (H_x, H_v|_{H_x}) = 7/12$
, where the equality follows from [Reference KollárKol97, 8.21 Proposition] (or by Lemma 3.27 with
![]() $\operatorname {wt} (s, u) = (3, 4)$
).
$\operatorname {wt} (s, u) = (3, 4)$
).
Suppose
![]() $u x^3 \in f_8$
. In this case, we may assume
$u x^3 \in f_8$
. In this case, we may assume
![]() $\operatorname {coeff}_{f_8} (u s x) = 1$
by rescaling x. We consider a weight
$\operatorname {coeff}_{f_8} (u s x) = 1$
by rescaling x. We consider a weight
![]() $\underline {c} = (2, e, 3)$
, where e is a sufficiently large integer which is coprime to
$\underline {c} = (2, e, 3)$
, where e is a sufficiently large integer which is coprime to
![]() $6$
. Then
$6$
. Then
![]() $G_{\underline {c}} = u (x^3 + u^2)$
,
$G_{\underline {c}} = u (x^3 + u^2)$
,
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}} = \mathbb {P} (2, e, 3)$
,
$\mathbb {P} (\underline {c})^{\operatorname {wf}} = \mathbb {P} (2, e, 3)$
,
![]() $\operatorname {Diff} = 0$
and
$\operatorname {Diff} = 0$
and
![]() $\mathcal {D}_{\underline {c}}$
is the union of two quasi-smooth curves
$\mathcal {D}_{\underline {c}}$
is the union of two quasi-smooth curves
![]() $(u = 0)$
and
$(u = 0)$
and
![]() $(x^3 + u^2 = 0)$
. We have
$(x^3 + u^2 = 0)$
. We have
and thus
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 5/9$
in this case.
$\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 5/9$
in this case.
In the following, we assume
![]() $u s x, s^4, u x^3 \notin f_8$
. We can write
$u s x, s^4, u x^3 \notin f_8$
. We can write
where
![]() $\alpha _1, \dots , \alpha _4, \beta , \gamma \in \mathbb {C}$
and
$\alpha _1, \dots , \alpha _4, \beta , \gamma \in \mathbb {C}$
and
![]() $g_{15} = g_{15} (x, s, u) \not \ni u^3$
is a quasi-homogeneous polynomial of degree
$g_{15} = g_{15} (x, s, u) \not \ni u^3$
is a quasi-homogeneous polynomial of degree
![]() $15$
which is contained in the ideal
$15$
which is contained in the ideal
![]() $(x, u)^2 \subset \mathbb {C} [x, s, u]$
. Note that at least one of
$(x, u)^2 \subset \mathbb {C} [x, s, u]$
. Note that at least one of
![]() $\alpha , \beta , \gamma , \delta $
and
$\alpha , \beta , \gamma , \delta $
and
![]() $\varepsilon $
is nonzero since
$\varepsilon $
is nonzero since
![]() $f_8 (x, s, u) \ne 0$
. Note also that
$f_8 (x, s, u) \ne 0$
. Note also that
![]() $\lambda u s^5$
and
$\lambda u s^5$
and
![]() $\mu s^7 x$
are the only terms in
$\mu s^7 x$
are the only terms in
![]() $\bar {F}$
which is not contained in
$\bar {F}$
which is not contained in
![]() $(x, u)^2$
. It follows from the quasi-smoothness of X that
$(x, u)^2$
. It follows from the quasi-smoothness of X that
![]() $(\lambda , \mu ) \ne (0,0)$
.
$(\lambda , \mu ) \ne (0,0)$
.
Suppose
![]() $\beta \ne 0$
. Replacing u, we may assume
$\beta \ne 0$
. Replacing u, we may assume
![]() $\beta = 1$
and
$\beta = 1$
and
![]() $\gamma = 0$
. There exists
$\gamma = 0$
. There exists
![]() $j \in \{1, 2, 3, 4\}$
such that
$j \in \{1, 2, 3, 4\}$
such that
![]() $\alpha _j \ne 0$
since
$\alpha _j \ne 0$
since
![]() $f_8 \ne 0$
as a polynomial, and thus we set
$f_8 \ne 0$
as a polynomial, and thus we set
![]() $i = \min \{\, j \mid \alpha _j \ne 0 \,\} \in \{1, 2, 3, 4\}$
. We may assume
$i = \min \{\, j \mid \alpha _j \ne 0 \,\} \in \{1, 2, 3, 4\}$
. We may assume
![]() $\alpha _i = 1$
by rescaling x. We set
$\alpha _i = 1$
by rescaling x. We set
![]() $\underline {c} = (2 i + 7, 4 i, 10 i)$
. We have
$\underline {c} = (2 i + 7, 4 i, 10 i)$
. We have
![]() $G_{\underline {c}} = s^{4-i} x^{2 i} + u^3 + u s^5$
for
$G_{\underline {c}} = s^{4-i} x^{2 i} + u^3 + u s^5$
for
![]() $1 \le i \le 4$
. Moreover, we see that
$1 \le i \le 4$
. Moreover, we see that
 $$\begin{align*}\mathbb{P} (\underline{c})^{\operatorname{wf}} = \begin{cases} \mathbb{P} (2 i + 7, 2, 5)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ 1 \le i \le 3, \\ \mathbb{P} (3, 2, 1)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ i = 4, \end{cases} \end{align*}$$
$$\begin{align*}\mathbb{P} (\underline{c})^{\operatorname{wf}} = \begin{cases} \mathbb{P} (2 i + 7, 2, 5)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ 1 \le i \le 3, \\ \mathbb{P} (3, 2, 1)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ i = 4, \end{cases} \end{align*}$$
and
 $$\begin{align*}(\operatorname{Diff}, \mathcal{D}_{\underline{c}}) = \begin{cases} (\frac{2 i -1}{2 i} H_{\tilde{x}}, D_i), & \text{if}\ 1 \le i \le 3, \\ (\frac{7}{8} H_{\tilde{x}} + \frac{4}{5} H_{\tilde{s}}, D'), & \text{if}\ i = 4, \end{cases} \end{align*}$$
$$\begin{align*}(\operatorname{Diff}, \mathcal{D}_{\underline{c}}) = \begin{cases} (\frac{2 i -1}{2 i} H_{\tilde{x}}, D_i), & \text{if}\ 1 \le i \le 3, \\ (\frac{7}{8} H_{\tilde{x}} + \frac{4}{5} H_{\tilde{s}}, D'), & \text{if}\ i = 4, \end{cases} \end{align*}$$
where
are prime divisors on
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
. We first consider the case where
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
. We first consider the case where
![]() $1 \le i \le 3$
. We see that
$1 \le i \le 3$
. We see that
![]() $H_{\tilde {x}}$
is quasi-smooth, and
$H_{\tilde {x}}$
is quasi-smooth, and
![]() $D_i$
is quasi-smooth outside
$D_i$
is quasi-smooth outside
![]() $\{\mathsf {q}\}$
, where
$\{\mathsf {q}\}$
, where
![]() $\mathsf {q} = (1\!:\!0\!:\!0) \in \mathbb {P} (\underline {c})^{\operatorname {wf}}$
. Moreover, they intersect at two points
$\mathsf {q} = (1\!:\!0\!:\!0) \in \mathbb {P} (\underline {c})^{\operatorname {wf}}$
. Moreover, they intersect at two points
![]() $(0\!:\!1\!:\!0)$
and
$(0\!:\!1\!:\!0)$
and
![]() $(0\!:\!-1\!:\!1)$
transversally. It follows that
$(0\!:\!-1\!:\!1)$
transversally. It follows that
![]() $\operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}}) = \min \{1, \ \operatorname {lct}_{\mathsf {q}} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \mathcal {D}_{\underline {c}})\}$
since
$\operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}}) = \min \{1, \ \operatorname {lct}_{\mathsf {q}} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \mathcal {D}_{\underline {c}})\}$
since
![]() $H_{\tilde {x}}$
does not pass through
$H_{\tilde {x}}$
does not pass through
![]() $\mathsf {q}$
. If
$\mathsf {q}$
. If
![]() $i = 3$
, then
$i = 3$
, then
![]() $D_3$
is also quasi-smooth at
$D_3$
is also quasi-smooth at
![]() $\mathsf {q}$
, which implies
$\mathsf {q}$
, which implies
![]() $\operatorname {lct} (\mathbb {P} (\underline {c}), \operatorname {Diff}; \mathcal {D}_{\underline {c}}) = 1$
. If
$\operatorname {lct} (\mathbb {P} (\underline {c}), \operatorname {Diff}; \mathcal {D}_{\underline {c}}) = 1$
. If
![]() $i = 1, 2$
, then we have
$i = 1, 2$
, then we have
 $$ \begin{align*} \operatorname{lct}_{\mathsf{q}} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \mathcal{D}_{\underline{c}}) &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, (\tilde{s}^{4 - i} + \tilde{u}^3 + \tilde{u} \tilde{s}^5 = 0)) \\ &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, (\tilde{s}^{4-i} + \tilde{u}^3 = 0)) \\ &= \frac{3 + (4-i)}{3 (4-i)} = \frac{7 - i}{3 (4-i)} \end{align*} $$
$$ \begin{align*} \operatorname{lct}_{\mathsf{q}} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \mathcal{D}_{\underline{c}}) &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, (\tilde{s}^{4 - i} + \tilde{u}^3 + \tilde{u} \tilde{s}^5 = 0)) \\ &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, (\tilde{s}^{4-i} + \tilde{u}^3 = 0)) \\ &= \frac{3 + (4-i)}{3 (4-i)} = \frac{7 - i}{3 (4-i)} \end{align*} $$
since
![]() $(\tilde {s}^{4 - i} + \tilde {u}^3 + \tilde {u} \tilde {s}^5 = 0)$
is analytically equivalent to
$(\tilde {s}^{4 - i} + \tilde {u}^3 + \tilde {u} \tilde {s}^5 = 0)$
is analytically equivalent to
![]() $(\tilde {s}^{4-i} + \tilde {u}^3 = 0)$
. Thus, by Lemma 3.27, we have
$(\tilde {s}^{4-i} + \tilde {u}^3 = 0)$
. Thus, by Lemma 3.27, we have
 $$ \begin{align*} \operatorname{lct}_{\mathsf{p}} (X; H_v) &\ge \min \left\{ \frac{(2 i + 7) + 4 i + 10 i}{30 i}, \ \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \right\} \\ &= \begin{cases} \frac{2}{3}, & \text{if}\ i = 1, \\ \frac{13}{20}, & \text{if}\ i = 2, \\ \frac{11}{18}, & \text{if}\ i = 3. \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{lct}_{\mathsf{p}} (X; H_v) &\ge \min \left\{ \frac{(2 i + 7) + 4 i + 10 i}{30 i}, \ \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \right\} \\ &= \begin{cases} \frac{2}{3}, & \text{if}\ i = 1, \\ \frac{13}{20}, & \text{if}\ i = 2, \\ \frac{11}{18}, & \text{if}\ i = 3. \end{cases} \end{align*} $$
Suppose
![]() $\beta = 0$
. In this case, we have
$\beta = 0$
. In this case, we have
![]() $\gamma \ne 0$
. We set
$\gamma \ne 0$
. We set
![]() $i = \min \{\, j \mid \alpha _j \ne 0 \, \} \in \{1, 2, 3, 4\}$
. We may assume
$i = \min \{\, j \mid \alpha _j \ne 0 \, \} \in \{1, 2, 3, 4\}$
. We may assume
![]() $\gamma = \alpha _i = 1$
by rescaling x and s appropriately. We set
$\gamma = \alpha _i = 1$
by rescaling x and s appropriately. We set
 $$\begin{align*}\underline{c} = \begin{cases} (3 (i + 3), 3 (2 i - 1), 15 i - 4), & \text{if}\ 1 \le i \le 3, \\ (3, 3, 8), & \text{if}\ i = 4. \end{cases} \end{align*}$$
$$\begin{align*}\underline{c} = \begin{cases} (3 (i + 3), 3 (2 i - 1), 15 i - 4), & \text{if}\ 1 \le i \le 3, \\ (3, 3, 8), & \text{if}\ i = 4. \end{cases} \end{align*}$$
We have
![]() $G_{\underline {c}} = s^{4-i} x^{2 i} + u^3 + s^7 x$
for
$G_{\underline {c}} = s^{4-i} x^{2 i} + u^3 + s^7 x$
for
![]() $1 \le i \le 4$
. Moreover, we see that
$1 \le i \le 4$
. Moreover, we see that
 $$\begin{align*}\mathbb{P} (\underline{c})^{\operatorname{wf}} = \begin{cases} \mathbb{P} (i+3, 2 i - 1, 15 i - 4)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ 1 \le i \le 3, \\ \mathbb{P} (1, 1, 8)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ i = 4, \end{cases} \end{align*}$$
$$\begin{align*}\mathbb{P} (\underline{c})^{\operatorname{wf}} = \begin{cases} \mathbb{P} (i+3, 2 i - 1, 15 i - 4)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ 1 \le i \le 3, \\ \mathbb{P} (1, 1, 8)_{\tilde{x}, \tilde{s}, \tilde{u}}, & \text{if}\ i = 4, \end{cases} \end{align*}$$
and
We see that
![]() $H_{\tilde {u}}$
and
$H_{\tilde {u}}$
and
![]() $\mathcal {D}_{\underline {c}}$
are both quasi-smooth. If
$\mathcal {D}_{\underline {c}}$
are both quasi-smooth. If
![]() $i = 3, 4$
, then
$i = 3, 4$
, then
![]() $H_{\tilde {u}}$
and
$H_{\tilde {u}}$
and
![]() $\mathcal {D}_{\underline {c}}$
intersect transversally and thus we have
$\mathcal {D}_{\underline {c}}$
intersect transversally and thus we have
![]() $\operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}}) = 1$
. Suppose
$\operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}}) = 1$
. Suppose
![]() $i = 1, 2$
. Then
$i = 1, 2$
. Then
![]() $H_{\tilde {u}}$
and
$H_{\tilde {u}}$
and
![]() $\mathcal {D}_{\underline {c}}$
intersect transversally except at
$\mathcal {D}_{\underline {c}}$
intersect transversally except at
![]() $\mathsf {p}_{\tilde {x}} = (1\!:\!0\!:\!0) \in \mathbb {P} (\underline {c})^{\operatorname {wf}}$
, and we have
$\mathsf {p}_{\tilde {x}} = (1\!:\!0\!:\!0) \in \mathbb {P} (\underline {c})^{\operatorname {wf}}$
, and we have
 $$ \begin{align*} \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) &= \operatorname{lct}_{\mathsf{p}_{\tilde{x}}} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \\ &= \operatorname{lct} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^{4-i} + \tilde{u} + \tilde{s}^7 = 0)) \\ &= \operatorname{lct} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^{4-i} + \tilde{u} = 0)) \\ &= \begin{cases} \frac{2}{3}, & \text{if}\ i = 1, \\ 1, & \text{if}\ i = 2. \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) &= \operatorname{lct}_{\mathsf{p}_{\tilde{x}}} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \\ &= \operatorname{lct} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^{4-i} + \tilde{u} + \tilde{s}^7 = 0)) \\ &= \operatorname{lct} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^{4-i} + \tilde{u} = 0)) \\ &= \begin{cases} \frac{2}{3}, & \text{if}\ i = 1, \\ 1, & \text{if}\ i = 2. \end{cases} \end{align*} $$
Thus, by Lemma 3.27, we have
 $$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_v) \ge \begin{cases} \frac{2}{3}, & \text{if}\ i = 1, \\ \frac{25}{39}, & \text{if}\ i = 2, \\ \frac{74}{123}, & \text{if}\ i = 3, \\ \frac{7}{12}, & \text{if}\ i = 4. \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_v) \ge \begin{cases} \frac{2}{3}, & \text{if}\ i = 1, \\ \frac{25}{39}, & \text{if}\ i = 2, \\ \frac{74}{123}, & \text{if}\ i = 3, \\ \frac{7}{12}, & \text{if}\ i = 4. \end{cases} \end{align*}$$
This proves the claim.
Claim 17. Suppose X is a member of the family
![]() $\mathcal {F}_{46}$
. Then
$\mathcal {F}_{46}$
. Then
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
Proof of Claim 17.
We have
and
![]() $\mathsf {p} = \mathsf {p}_w$
is of type
$\mathsf {p} = \mathsf {p}_w$
is of type
![]() $\frac {1}{10} (1, 3, 7)$
. We can write
$\frac {1}{10} (1, 3, 7)$
. We can write
where
![]() $f_{11} = f_{11} (x, s, u) \ne 0$
and
$f_{11} = f_{11} (x, s, u) \ne 0$
and
![]() $f_{21} = f_{21} (x, s, u, v)$
are quasi-homogeneous polynomials of degree
$f_{21} = f_{21} (x, s, u, v)$
are quasi-homogeneous polynomials of degree
![]() $11$
and
$11$
and
![]() $21$
, respectively. We have
$21$
, respectively. We have
![]() $u^3, s^7 \in F$
by the quasi-smoothness of X, and we may assume
$u^3, s^7 \in F$
by the quasi-smoothness of X, and we may assume
![]() $\operatorname {coeff}_F (u^3) = \operatorname {coeff}_F (s^7) = 1$
. We set
$\operatorname {coeff}_F (u^3) = \operatorname {coeff}_F (s^7) = 1$
. We set
![]() $\bar {F} = F (x, s, u, 0, 1)$
, which can be written as
$\bar {F} = F (x, s, u, 0, 1)$
, which can be written as
where
![]() $\alpha , \beta , \dots , \zeta \in \mathbb {C}$
. We introduce various
$\alpha , \beta , \dots , \zeta \in \mathbb {C}$
. We introduce various
![]() $3$
-tuples
$3$
-tuples
![]() $(\underline {c} = (c_1, c_2, c_3)$
of positive integers according to the following division into cases. We denote by
$(\underline {c} = (c_1, c_2, c_3)$
of positive integers according to the following division into cases. We denote by
![]() $G_{\underline {c}}$
the lowest weight part of
$G_{\underline {c}}$
the lowest weight part of
![]() $\bar {F}$
with respect to
$\bar {F}$
with respect to
![]() $\operatorname {wt} (x, s, u) = \underline {c}$
.
$\operatorname {wt} (x, s, u) = \underline {c}$
.
-
(i)
 $\alpha \ne 0$
. In this case, we may assume
$\alpha \ne 0$
. In this case, we may assume
 $\alpha = 1$
. We set
$\alpha = 1$
. We set
 $\underline {c} = (1, 1, 1)$
. Then we have
$\underline {c} = (1, 1, 1)$
. Then we have
 $G_{\underline {c}} = u s x + u^3$
.
$G_{\underline {c}} = u s x + u^3$
. -
(ii)
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. In this case, we may assume
$\beta \ne 0$
. In this case, we may assume
 $\beta = 1$
. We set
$\beta = 1$
. We set
 $\underline {c} = (6, 3, 7)$
. Then we have
$\underline {c} = (6, 3, 7)$
. Then we have
 $G_{\underline {c}} = s^3 x^2 + u^3 + s^7$
.
$G_{\underline {c}} = s^3 x^2 + u^3 + s^7$
. -
(iii)
 $\alpha = \beta = 0$
and
$\alpha = \beta = 0$
and
 $\gamma \ne 0$
. In this case, we may assume
$\gamma \ne 0$
. In this case, we may assume
 $\gamma = 1$
. We set
$\gamma = 1$
. We set
 $\underline {c} = (7, 6, 14)$
. Then we have
$\underline {c} = (7, 6, 14)$
. Then we have
 $G_{\underline {c}} = u x^4 + u^3 + s^7$
.
$G_{\underline {c}} = u x^4 + u^3 + s^7$
. -
(iv)
 $\alpha = \beta = \gamma = 0$
and
$\alpha = \beta = \gamma = 0$
and
 $\delta \ne 0$
. In this case, we may assume
$\delta \ne 0$
. In this case, we may assume
 $\delta = 1$
. We set
$\delta = 1$
. We set
 $\underline {c} = (3, 3, 7)$
. In this case, we have
$\underline {c} = (3, 3, 7)$
. In this case, we have
 $G_{\underline {c}} = s^2 x^5 + u^3 + s^7$
.
$G_{\underline {c}} = s^2 x^5 + u^3 + s^7$
. -
(v)
 $\alpha = \beta = \gamma = \delta = 0$
and
$\alpha = \beta = \gamma = \delta = 0$
and
 $\varepsilon \ne 0$
. In this case, we may assume
$\varepsilon \ne 0$
. In this case, we may assume
 $\varepsilon = 1$
. We set
$\varepsilon = 1$
. We set
 $\underline {c} = (9, 12, 28)$
. In this case, we have
$\underline {c} = (9, 12, 28)$
. In this case, we have
 $G_{\underline {c}} = s x^8 + u^3 + s^7$
.
$G_{\underline {c}} = s x^8 + u^3 + s^7$
. -
(vi)
 $\alpha = \beta = \gamma = \delta = \varepsilon = 0$
. In this case, we may assume
$\alpha = \beta = \gamma = \delta = \varepsilon = 0$
. In this case, we may assume
 $\delta = 1$
. We set
$\delta = 1$
. We set
 $\underline {c} = (21, 33, 77)$
. In this case, we have
$\underline {c} = (21, 33, 77)$
. In this case, we have
 $x^{11} + u^3 + s^7$
.
$x^{11} + u^3 + s^7$
.
The descriptions of
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
,
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
,
![]() $\operatorname {Diff}$
and
$\operatorname {Diff}$
and
![]() $G_{\underline {c}} ^{\operatorname {wf}}$
are given in Table 4, where we choose
$G_{\underline {c}} ^{\operatorname {wf}}$
are given in Table 4, where we choose
![]() $\tilde {x}, \tilde {s}, \tilde {u}$
as homogeneous coordinates of
$\tilde {x}, \tilde {s}, \tilde {u}$
as homogeneous coordinates of
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
Table 4 Family
![]() $\mathcal {F}_{46}$
: Weights and LCT.
$\mathcal {F}_{46}$
: Weights and LCT.

We set
![]() $\mathcal {D}_{\underline {c}} = \mathcal {D}^{\operatorname {wf}}_{G_{\underline {c}}}$
. We explain the computation of
$\mathcal {D}_{\underline {c}} = \mathcal {D}^{\operatorname {wf}}_{G_{\underline {c}}}$
. We explain the computation of
![]() $\eta := \operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}})$
whose value is given in the fifth column of Table 4. The computation
$\eta := \operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}})$
whose value is given in the fifth column of Table 4. The computation
![]() $\eta = 1$
is straightforward when we are in case (i) since
$\eta = 1$
is straightforward when we are in case (i) since
![]() $\mathcal {D}_{\underline {c}}$
is the union of of a line and a conic on
$\mathcal {D}_{\underline {c}}$
is the union of of a line and a conic on
![]() $\mathbb {P}^2$
intersecting at two points. In the other cases,
$\mathbb {P}^2$
intersecting at two points. In the other cases,
![]() $\mathcal {D}_{\underline {c}}$
is the divisor defined by
$\mathcal {D}_{\underline {c}}$
is the divisor defined by
![]() $G_{\underline {c}}^{\operatorname {wf}} = 0$
which is a quasi-line in
$G_{\underline {c}}^{\operatorname {wf}} = 0$
which is a quasi-line in
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
. If we are in one of the cases (iii), (v) and (vi), then any two of the components of
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
. If we are in one of the cases (iii), (v) and (vi), then any two of the components of
![]() $\operatorname {Diff} + \mathcal {D}_{\underline {c}}$
intersect transversally, which implies
$\operatorname {Diff} + \mathcal {D}_{\underline {c}}$
intersect transversally, which implies
![]() $\eta = 1$
. If we are in case (ii) or (iv), then
$\eta = 1$
. If we are in case (ii) or (iv), then
![]() $H_{\tilde {u}}$
and
$H_{\tilde {u}}$
and
![]() $\mathcal {D}_{\underline {c}}$
intersect transversally except at
$\mathcal {D}_{\underline {c}}$
intersect transversally except at
![]() $\mathsf {q} = (1\!:\!0\!:\!0) \in \mathbb {P} (\underline {c})^{\operatorname {wf}}$
. We set
$\mathsf {q} = (1\!:\!0\!:\!0) \in \mathbb {P} (\underline {c})^{\operatorname {wf}}$
. We set
![]() $e = 3, 2$
if we are in case (ii), (iv), respectively. Then we have
$e = 3, 2$
if we are in case (ii), (iv), respectively. Then we have
 $$ \begin{align*} \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) &= \operatorname{lct}_{\mathsf{q}} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \\ &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^e + \tilde{u} + \tilde{s}^7 = 0)) \\ &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^e + \tilde{u} = 0)). \end{align*} $$
$$ \begin{align*} \operatorname{lct} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) &= \operatorname{lct}_{\mathsf{q}} (\mathbb{P} (\underline{c})^{\operatorname{wf}}, \operatorname{Diff}; \mathcal{D}_{\underline{c}}) \\ &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^e + \tilde{u} + \tilde{s}^7 = 0)) \\ &= \operatorname{lct}_{(0,0)} (\mathbb{A}^2_{\tilde{s}, \tilde{u}}, \tfrac{2}{3} (\tilde{u} = 0); (\tilde{s}^e + \tilde{u} = 0)). \end{align*} $$
This completes the explanations of the computations of
![]() $\eta $
. We set
$\eta $
. We set
 $$\begin{align*}\theta = \left\{\frac{c_1 + c_2 + c_3}{\deg_{\underline{c}} (G_{\underline{c}}^{\operatorname{wf}})}, \ \eta \right\} \end{align*}$$
$$\begin{align*}\theta = \left\{\frac{c_1 + c_2 + c_3}{\deg_{\underline{c}} (G_{\underline{c}}^{\operatorname{wf}})}, \ \eta \right\} \end{align*}$$
which is described in the sixth column of Table 4. By Lemma 3.27, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge \theta \ge 1/2$
and the claim is proved.
$\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge \theta \ge 1/2$
and the claim is proved.
By Claims 14, 15, 16 and 17, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{c} H_v) \ge 1/2$
. Let
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{c} H_v) \ge 1/2$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $\frac {1}{c} H_v$
. We set
$\frac {1}{c} H_v$
. We set
![]() $\lambda = (r + c)/(2 r + c)$
, and we will show that
$\lambda = (r + c)/(2 r + c)$
, and we will show that
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge \lambda $
. Suppose not, that is,
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge \lambda $
. Suppose not, that is,
![]() $(X, \lambda D)$
is not log canonical at
$(X, \lambda D)$
is not log canonical at
![]() $\mathsf {p}$
. Let
$\mathsf {p}$
. Let
![]() $\varphi \colon Y \to X$
be the Kawamata blowup of
$\varphi \colon Y \to X$
be the Kawamata blowup of
![]() $\mathsf {p} \in X$
. Then, for the proper transforms
$\mathsf {p} \in X$
. Then, for the proper transforms
![]() $\tilde {H}_t$
and
$\tilde {H}_t$
and
![]() $\tilde {D}$
of
$\tilde {D}$
of
![]() $H_t$
and D, respectively, we have
$H_t$
and D, respectively, we have
 $$ \begin{align*} \tilde{H}_t &\sim c \varphi^*A - \frac{r + c}{r} E, \\ \tilde{D} & \sim_{\mathbb{Q}} \varphi^*A - \frac{e}{r} E, \end{align*} $$
$$ \begin{align*} \tilde{H}_t &\sim c \varphi^*A - \frac{r + c}{r} E, \\ \tilde{D} & \sim_{\mathbb{Q}} \varphi^*A - \frac{e}{r} E, \end{align*} $$
where
![]() $e \in \mathbb {Q}_{\ge 0}$
. By [Reference KawamataKaw96], the discrepancy of the pair
$e \in \mathbb {Q}_{\ge 0}$
. By [Reference KawamataKaw96], the discrepancy of the pair
![]() $(X, \lambda D)$
along E is negative, and thus we have
$(X, \lambda D)$
along E is negative, and thus we have
![]() $e> 1/\lambda $
. By [Reference Corti, Pukhlikhov and ReidCPR00, Theorem 4.9],
$e> 1/\lambda $
. By [Reference Corti, Pukhlikhov and ReidCPR00, Theorem 4.9],
![]() $-K_Y \sim _{\mathbb {Q}} \varphi ^* A - \frac {1}{r} E$
is nef (more precisely,
$-K_Y \sim _{\mathbb {Q}} \varphi ^* A - \frac {1}{r} E$
is nef (more precisely,
![]() $- m K_Y$
defines the flopping contraction for a sufficiently divisible
$- m K_Y$
defines the flopping contraction for a sufficiently divisible
![]() $m> 0$
). Hence,
$m> 0$
). Hence,
![]() $(-K_Y \cdot \tilde {H}_t \cdot \tilde {D}) \ge 0$
and we have
$(-K_Y \cdot \tilde {H}_t \cdot \tilde {D}) \ge 0$
and we have
 $$ \begin{align*} 0 \le (-K_Y \cdot \tilde{H}_t \cdot \tilde{D}) &= c (A^3) - \frac{e (r+c)}{r^3} (E^3) \\ &= \frac{2 r + c}{a b r} - \frac{e (r+c)}{a b r} < \frac{2 r + c}{a b r} - \frac{r+c}{\lambda a b r} = 0. \end{align*} $$
$$ \begin{align*} 0 \le (-K_Y \cdot \tilde{H}_t \cdot \tilde{D}) &= c (A^3) - \frac{e (r+c)}{r^3} (E^3) \\ &= \frac{2 r + c}{a b r} - \frac{e (r+c)}{a b r} < \frac{2 r + c}{a b r} - \frac{r+c}{\lambda a b r} = 0. \end{align*} $$
This is a contradiction. Therefore,
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge \lambda $
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge \lambda $
and thus
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right), \ \frac{r + c}{2 r + c} \right\} \ge \frac{1}{2}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ \operatorname{lct}_{\mathsf{p}} \left(X; \frac{1}{c} H_v \right), \ \frac{r + c}{2 r + c} \right\} \ge \frac{1}{2}. \end{align*}$$
This completes the proof of Proposition 5.18 when X has a unique QI center.
5.6.b Case: X has exactly three distinct QI centers
By Lemma 5.12, we can choose homogeneous coordinates so that
where a is coprime to b,
![]() $a \le b$
and
$a \le b$
and
![]() $a + b = r$
. Let
$a + b = r$
. Let
![]() $\mathsf {p} \in X$
be a QI center. Then we may assume
$\mathsf {p} \in X$
be a QI center. Then we may assume
![]() $\mathsf {p} = \mathsf {p}_w$
by replacing t and w suitably. Then the defining polynomial F of X can be written as
$\mathsf {p} = \mathsf {p}_w$
by replacing t and w suitably. Then the defining polynomial F of X can be written as
where
![]() $f_{2 r} (x, y, z)$
and
$f_{2 r} (x, y, z)$
and
![]() $f_{3 r} (x, y, z, t)$
are quasi-homogeneous polynomials of degrees
$f_{3 r} (x, y, z, t)$
are quasi-homogeneous polynomials of degrees
![]() $2 r$
and
$2 r$
and
![]() $3 r$
, respectively. We have
$3 r$
, respectively. We have
![]() $(A^3) = 3 r/a b r^2 = 3 / a b r$
. By Lemma 3.29, we have
$(A^3) = 3 r/a b r^2 = 3 / a b r$
. By Lemma 3.29, we have
and Proposition 5.18 is proved when X has exactly three distinct QI centers.
5.6.c Case: X has exactly two distinct QI centers and their singularity types are equal
By Lemma 5.12, we can choose homogeneous coordinates so that
where a is coprime to b,
![]() $a \le b$
and
$a \le b$
and
![]() $a + b = r$
. Let
$a + b = r$
. Let
![]() $\mathsf {p} \in X$
be a QI center. We may assume
$\mathsf {p} \in X$
be a QI center. We may assume
![]() $\mathsf {p} = \mathsf {p}_t$
by replacing w suitably. Then the defining polynomial F of X can be written as
$\mathsf {p} = \mathsf {p}_t$
by replacing w suitably. Then the defining polynomial F of X can be written as
where
![]() $f_{3 r} (x, y, z)$
and
$f_{3 r} (x, y, z)$
and
![]() $f_{4 r} (x, y, z, w)$
are quasi-homogeneous polynomials of degrees
$f_{4 r} (x, y, z, w)$
are quasi-homogeneous polynomials of degrees
![]() $3 r$
and
$3 r$
and
![]() $4 r$
, respectively. Note that
$4 r$
, respectively. Note that
![]() $(A^3) = 4 r/2 a b r^2 = 2/a b r$
. By Lemma 3.29, we have
$(A^3) = 4 r/2 a b r^2 = 2/a b r$
. By Lemma 3.29, we have
and Proposition 5.18 is proved in this case.
5.6.d Case: X has exactly two distinct QI centers and their singularity types are distinct
By Lemma 5.12, we have
where a is coprime to b,
![]() $r_1 = a + b$
and
$r_1 = a + b$
and
![]() $r_2 = 2 a + b$
.
$r_2 = 2 a + b$
.
We first consider the QI center
![]() $\mathsf {p} = \mathsf {p}_t \in X$
of type
$\mathsf {p} = \mathsf {p}_t \in X$
of type
![]() $\frac {1}{r_1} (1, a, b)$
. The defining polynomial F of X can be written as
$\frac {1}{r_1} (1, a, b)$
. The defining polynomial F of X can be written as
where
![]() $f_{3 a + 2 b} = f_{3 a + 2 b} (x, u, v)$
and
$f_{3 a + 2 b} = f_{3 a + 2 b} (x, u, v)$
and
![]() $f_{4 a + 3 b} = f_{4 a + 3 b} (x, u, v, w)$
are quasi-homogeneous polynomials of the indicated degrees. Note that
$f_{4 a + 3 b} = f_{4 a + 3 b} (x, u, v, w)$
are quasi-homogeneous polynomials of the indicated degrees. Note that
![]() $(A^3) = (4 a + 3 b)/a b r_1 r_2$
. By Lemma 5.12, we have
$(A^3) = (4 a + 3 b)/a b r_1 r_2$
. By Lemma 5.12, we have
We next consider the QI center
![]() $\mathsf {p} = \mathsf {p}_w \in X$
of type
$\mathsf {p} = \mathsf {p}_w \in X$
of type
![]() $\frac {1}{r_2} (1, a, a + b)$
. Then the defining polynomial F of X can be written as
$\frac {1}{r_2} (1, a, a + b)$
. Then the defining polynomial F of X can be written as
where
![]() $f_{2 a + 2 b} = f_{2 a + 2 b} (x, u, t)$
and
$f_{2 a + 2 b} = f_{2 a + 2 b} (x, u, t)$
and
![]() $f_{4 a + 3 b} = f_{4 a + 3 b} (x, u, v, t)$
are quasi-homogeneous polynomials of the indicated degree.
$f_{4 a + 3 b} = f_{4 a + 3 b} (x, u, v, t)$
are quasi-homogeneous polynomials of the indicated degree.
Suppose
![]() $t^2 w \in F$
, that is,
$t^2 w \in F$
, that is,
![]() $t^2 \in f_{2 a + 2 b}$
. Then
$t^2 \in f_{2 a + 2 b}$
. Then
![]() $\operatorname {omult}_{\mathsf {p}} (H_v) = 2$
and we have
$\operatorname {omult}_{\mathsf {p}} (H_v) = 2$
and we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge b/2 \ge 1/2$
. Let
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge b/2 \ge 1/2$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $\frac {1}{b} H_v$
. We see that the set
$\frac {1}{b} H_v$
. We see that the set
![]() $\{x, u, v\}$
isolates
$\{x, u, v\}$
isolates
![]() $\mathsf {p}$
since
$\mathsf {p}$
since
![]() $t^2 w \in F$
. In particular, a general member
$t^2 w \in F$
. In particular, a general member
![]() $T \in |a A|$
does not contain any component of the effective
$T \in |a A|$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_z$
. Then we have
$D \cdot H_z$
. Then we have
 $$ \begin{align*} 2 \operatorname{omult}_{\mathsf{p}} (D) &\le (\rho_{\mathsf{p}}^*D \cdot \rho_{\mathsf{p}}^*H_v \cdot \rho_{\mathsf{p}}^*T)_{\check{\mathsf{p}}} \le r_2 (D \cdot H_v \cdot T) \\ &= r_2 b a (A^3) = \frac{4 a + 3 b}{a + b}. \end{align*} $$
$$ \begin{align*} 2 \operatorname{omult}_{\mathsf{p}} (D) &\le (\rho_{\mathsf{p}}^*D \cdot \rho_{\mathsf{p}}^*H_v \cdot \rho_{\mathsf{p}}^*T)_{\check{\mathsf{p}}} \le r_2 (D \cdot H_v \cdot T) \\ &= r_2 b a (A^3) = \frac{4 a + 3 b}{a + b}. \end{align*} $$
This implies
Therefore, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
In the following, we consider the case where
![]() $t^2 w \notin F$
.
$t^2 w \notin F$
.
Claim 18. If
![]() $b \ge 2$
, then
$b \ge 2$
, then
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge 1/2$
.
Proof of Claim 18.
By the quasi-smoothness of X at
![]() $\mathsf {p}_t$
, we have
$\mathsf {p}_t$
, we have
![]() $t^3 u \in f_{4 a + 3 b}$
since
$t^3 u \in f_{4 a + 3 b}$
since
![]() $t^2 w \notin F$
by assumption. Hence, we have
$t^2 w \notin F$
by assumption. Hence, we have
![]() $\operatorname {omult}_{\mathsf {p}} (H_v) \le 4$
and this shows
$\operatorname {omult}_{\mathsf {p}} (H_v) \le 4$
and this shows
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge 1/2$
.
If
![]() $b = 1$
, then X is a member of a family
$b = 1$
, then X is a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \{13, 25\}$
.
$\mathsf {i} \in \{13, 25\}$
.
Claim 19. If X is a member of the family
![]() $\mathcal {F}_{13}$
, then
$\mathcal {F}_{13}$
, then
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
Proof of Claim 19.
We have
Note that
![]() $f_6 (x, u, 0, t) \ne 0$
as a polynomial since
$f_6 (x, u, 0, t) \ne 0$
as a polynomial since
![]() $\mathsf {p} \in X$
is nondegenerate. We set
$\mathsf {p} \in X$
is nondegenerate. We set
![]() $\bar {F} = F (x, u, 0, t, 1) \in \mathbb {C} [x, u, t]$
. We have
$\bar {F} = F (x, u, 0, t, 1) \in \mathbb {C} [x, u, t]$
. We have
![]() $t^3 u \in F$
, and we may assume
$t^3 u \in F$
, and we may assume
![]() $\operatorname {coeff}_F (t^3 u) = 1$
. If
$\operatorname {coeff}_F (t^3 u) = 1$
. If
![]() $t u x \in f_6$
, then the cubic part of
$t u x \in f_6$
, then the cubic part of
![]() $\bar {F}$
is not a cube of a linear form, and thus we have
$\bar {F}$
is not a cube of a linear form, and thus we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 1/2$
by Lemma 3.28. In the following, we assume
$\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 1/2$
by Lemma 3.28. In the following, we assume
![]() $t u x \notin f_6$
. Then we can write
$t u x \notin f_6$
. Then we can write
where
![]() $\alpha , \beta , \dots , \varepsilon , \lambda \in \mathbb {C}$
and
$\alpha , \beta , \dots , \varepsilon , \lambda \in \mathbb {C}$
and
![]() $g_{10} = g_{10} (x, u, t)$
is a quasi-homogeneous polynomial of degree
$g_{10} = g_{10} (x, u, t)$
is a quasi-homogeneous polynomial of degree
![]() $10$
. We introduce
$10$
. We introduce
![]() $3$
-tuples
$3$
-tuples
![]() $\underline {c} = (c_1, c_2, c_3)$
of positive integers according to the following division into cases. We denote by
$\underline {c} = (c_1, c_2, c_3)$
of positive integers according to the following division into cases. We denote by
![]() $G_{\underline {c}}$
the lowest weight part of
$G_{\underline {c}}$
the lowest weight part of
![]() $\bar {F}$
with respect to
$\bar {F}$
with respect to
![]() $\operatorname {wt} (x, u, t) = \underline {c}$
.
$\operatorname {wt} (x, u, t) = \underline {c}$
.
-
(i)
 $\alpha \ne 0$
. In this case, we may assume
$\alpha \ne 0$
. In this case, we may assume
 $\alpha = 1$
. We choose and fix a sufficiently large integer e which is coprime to
$\alpha = 1$
. We choose and fix a sufficiently large integer e which is coprime to
 $2$
and
$2$
and
 $3$
, and we set
$3$
, and we set
 $\underline {c} = (e, 3, 2)$
. Then we have
$\underline {c} = (e, 3, 2)$
. Then we have
 $G_{\underline {c}} = u^3 + t^3 u$
.
$G_{\underline {c}} = u^3 + t^3 u$
. -
(ii)
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. In this case, we may assume
$\beta \ne 0$
. In this case, we may assume
 $\beta = 1$
. We set
$\beta = 1$
. We set
 $\underline {c} = (7, 4, 6)$
. Then we have
$\underline {c} = (7, 4, 6)$
. Then we have
 $G_{\underline {c}} = u^2 x^2 + t^3 u + \lambda t u^4$
.
$G_{\underline {c}} = u^2 x^2 + t^3 u + \lambda t u^4$
. -
(iii)
 $\alpha = \beta = 0$
and
$\alpha = \beta = 0$
and
 $\gamma \ne 0$
. In this case, we may assume
$\gamma \ne 0$
. In this case, we may assume
 $\gamma = 1$
. We set
$\gamma = 1$
. We set
 $\underline {c} = (8, 6, 9)$
. Then
$\underline {c} = (8, 6, 9)$
. Then
 $G_{\underline {c}} = t x^3 + t^3 u + \lambda t u^4$
.
$G_{\underline {c}} = t x^3 + t^3 u + \lambda t u^4$
. -
(iv)
 $\alpha = \beta = \gamma = 0$
and
$\alpha = \beta = \gamma = 0$
and
 $\delta \ne 0$
. In this case, we may assume
$\delta \ne 0$
. In this case, we may assume
 $\delta = 1$
. We set
$\delta = 1$
. We set
 $\underline {c} = (9, 8, 12)$
. Then
$\underline {c} = (9, 8, 12)$
. Then
 $G_{\underline {c}} = u x^4 + t^3 u + \lambda t u^4$
.
$G_{\underline {c}} = u x^4 + t^3 u + \lambda t u^4$
. -
(v)
 $\alpha = \beta = \gamma = \delta = 0$
. In this case, we may assume
$\alpha = \beta = \gamma = \delta = 0$
. In this case, we may assume
 $\varepsilon = 1$
. We set
$\varepsilon = 1$
. We set
 $\underline {c} = (11, 12, 18)$
. Then we have
$\underline {c} = (11, 12, 18)$
. Then we have
 $x^6 + t^3 u + \lambda t u^4$
.
$x^6 + t^3 u + \lambda t u^4$
.
The descriptions of
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
,
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
,
![]() $\operatorname {Diff}$
and
$\operatorname {Diff}$
and
![]() $G_{\underline {c}}^{\operatorname {wf}}$
are given in Table 5, where we choose
$G_{\underline {c}}^{\operatorname {wf}}$
are given in Table 5, where we choose
![]() $\tilde {x}, \tilde {u}, \tilde {t}$
as homogeneous coordinates of
$\tilde {x}, \tilde {u}, \tilde {t}$
as homogeneous coordinates of
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
Table 5 Family
![]() $\mathcal {F}_{13}$
: weights and LCT.
$\mathcal {F}_{13}$
: weights and LCT.

We set
![]() $\mathcal {D}_{\underline {c}} = \mathcal {D}_{G_{\underline {c}}}^{\operatorname {wf}}$
. We explain the computation of
$\mathcal {D}_{\underline {c}} = \mathcal {D}_{G_{\underline {c}}}^{\operatorname {wf}}$
. We explain the computation of
![]() $\eta := \operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}})$
whose value (or lower bound) is given in the fifth column of Table 5.
$\eta := \operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}})$
whose value (or lower bound) is given in the fifth column of Table 5.
Claim 20. If X is a member of the family
![]() $\mathcal {F}_{25}$
, then
$\mathcal {F}_{25}$
, then
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_v) \ge 1/2$
.
Proof of Claim 20.
We have
Note that
![]() $f_8 (x, u, 0, t) \ne 0$
as a polynomial since
$f_8 (x, u, 0, t) \ne 0$
as a polynomial since
![]() $\mathsf {p} \in X$
is nondegenerate. We set
$\mathsf {p} \in X$
is nondegenerate. We set
![]() $\bar {F} = F (x, u, 0, t, 1) \in \mathbb {C} [x, u, t]$
. We have
$\bar {F} = F (x, u, 0, t, 1) \in \mathbb {C} [x, u, t]$
. We have
![]() $t^3 u, u^5 \in F$
, and we may assume
$t^3 u, u^5 \in F$
, and we may assume
![]() $\operatorname {coeff}_F (t^3 u) = \operatorname {coeff}_F (u^5) = 1$
. If
$\operatorname {coeff}_F (t^3 u) = \operatorname {coeff}_F (u^5) = 1$
. If
![]() $t u x \in f_8$
, then the cubic part of
$t u x \in f_8$
, then the cubic part of
![]() $\bar {F}$
is not a cube of a linear form and thus we have
$\bar {F}$
is not a cube of a linear form and thus we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 1/2$
by Lemma 3.28. In the following, we assume
$\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge 1/2$
by Lemma 3.28. In the following, we assume
![]() $t u x \notin f_8$
. Then we can write
$t u x \notin f_8$
. Then we can write
where
![]() $\alpha , \beta , \gamma , \delta \in \mathbb {C}$
and
$\alpha , \beta , \gamma , \delta \in \mathbb {C}$
and
![]() $g_{14} = g_{14} (x, u, t)$
is a quasi-homogeneous polynomial of degree
$g_{14} = g_{14} (x, u, t)$
is a quasi-homogeneous polynomial of degree
![]() $14$
. We introduce
$14$
. We introduce
![]() $3$
-tuples
$3$
-tuples
![]() $\underline {c} = (c_1, c_2, c_3)$
of positive integers according to the following division into cases. We denote by
$\underline {c} = (c_1, c_2, c_3)$
of positive integers according to the following division into cases. We denote by
![]() $G_{\underline {c}}$
the lowest weight part of
$G_{\underline {c}}$
the lowest weight part of
![]() $\bar {F}$
with respect to
$\bar {F}$
with respect to
![]() $\operatorname {wt} (x, u, t) = \underline {c}$
.
$\operatorname {wt} (x, u, t) = \underline {c}$
.
-
(i)
 $\alpha \ne 0$
. In this case, we may assume
$\alpha \ne 0$
. In this case, we may assume
 $\alpha = 1$
. We set
$\alpha = 1$
. We set
 $\underline {c} = (9, 6, 8)$
. Then we have
$\underline {c} = (9, 6, 8)$
. Then we have
 $G_{\underline {c}} = u^2 x^2 + t^3 u + u^5$
.
$G_{\underline {c}} = u^2 x^2 + t^3 u + u^5$
. -
(ii)
 $\alpha = 0$
and
$\alpha = 0$
and
 $\beta \ne 0$
. In this case, we may assume
$\beta \ne 0$
. In this case, we may assume
 $\beta = 1$
. We set
$\beta = 1$
. We set
 $\underline {c} = (11, 12, 16)$
. Then we have
$\underline {c} = (11, 12, 16)$
. Then we have
 $G_{\underline {c}} = t x^4 + t^3 u + u^5$
.
$G_{\underline {c}} = t x^4 + t^3 u + u^5$
. -
(iii)
 $\alpha = \beta = 0$
and
$\alpha = \beta = 0$
and
 $\gamma \ne 0$
. In this case, we may assume
$\gamma \ne 0$
. In this case, we may assume
 $\gamma = 1$
. We set
$\gamma = 1$
. We set
 $\underline {c} = (12, 15, 20)$
. Then
$\underline {c} = (12, 15, 20)$
. Then
 $G_{\underline {c}} = u x^5 + t^3 u + u^5$
.
$G_{\underline {c}} = u x^5 + t^3 u + u^5$
. -
(iv)
 $\alpha = \beta = \gamma = 0$
and
$\alpha = \beta = \gamma = 0$
and
 $\delta \ne 0$
. In this case, we may assume
$\delta \ne 0$
. In this case, we may assume
 $\delta = 1$
. We set
$\delta = 1$
. We set
 $\underline {c} = (15, 24, 32)$
. Then
$\underline {c} = (15, 24, 32)$
. Then
 $G_{\underline {c}} = x^8 + t^3 u + u^5$
.
$G_{\underline {c}} = x^8 + t^3 u + u^5$
.
The descriptions of
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
,
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
,
![]() $\operatorname {Diff}$
and
$\operatorname {Diff}$
and
![]() $G_{\underline {c}}^{\operatorname {wf}}$
are given in Table 6, where we choose
$G_{\underline {c}}^{\operatorname {wf}}$
are given in Table 6, where we choose
![]() $\tilde {x}, \tilde {u}, \tilde {t}$
as homogeneous coordinates of
$\tilde {x}, \tilde {u}, \tilde {t}$
as homogeneous coordinates of
![]() $\mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
$\mathbb {P} (\underline {c})^{\operatorname {wf}}$
.
Table 6 Family
![]() $\mathcal {F}_{25}$
: Weights and LCT.
$\mathcal {F}_{25}$
: Weights and LCT.

We set
![]() $\mathcal {D}_{\underline {c}} = \mathcal {D}_{G_{\underline {c}}}^{\operatorname {wf}}$
. We explain the computation of
$\mathcal {D}_{\underline {c}} = \mathcal {D}_{G_{\underline {c}}}^{\operatorname {wf}}$
. We explain the computation of
![]() $\eta := \operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}})$
whose value is given in the fifth column of Table 6. Suppose that we are in case (ii) or (iv). Then
$\eta := \operatorname {lct} (\mathbb {P} (\underline {c})^{\operatorname {wf}}, \operatorname {Diff}; \mathcal {D}_{\underline {c}})$
whose value is given in the fifth column of Table 6. Suppose that we are in case (ii) or (iv). Then
![]() $\mathcal {D}_{\underline {c}}$
is a prime divisor which is quasi-smooth and intersects any component of
$\mathcal {D}_{\underline {c}}$
is a prime divisor which is quasi-smooth and intersects any component of
![]() $\operatorname {Diff}$
transversally. This shows
$\operatorname {Diff}$
transversally. This shows
![]() $\eta = 1$
. Suppose that we are in case (i). Then
$\eta = 1$
. Suppose that we are in case (i). Then
![]() $\mathcal {D}_{\underline {c}} = H_{\tilde {u}} + \Gamma $
, where
$\mathcal {D}_{\underline {c}} = H_{\tilde {u}} + \Gamma $
, where
![]() $\Gamma = (\tilde {u} \tilde {x} + \tilde {t} + \tilde {u}^4 = 0)$
is a quasi-line. We see that any two of
$\Gamma = (\tilde {u} \tilde {x} + \tilde {t} + \tilde {u}^4 = 0)$
is a quasi-line. We see that any two of
![]() $H_{\tilde {x}}, H_{\tilde {u}}, H_{\tilde {t}}, \Gamma $
intersect transversally, and thus
$H_{\tilde {x}}, H_{\tilde {u}}, H_{\tilde {t}}, \Gamma $
intersect transversally, and thus
![]() $\eta = 1$
. Suppose that we are in case (iii). Then
$\eta = 1$
. Suppose that we are in case (iii). Then
![]() $\mathcal {D}_{\underline {c}} = \frac {1}{4} H_{\tilde {u}} + \Gamma $
, where
$\mathcal {D}_{\underline {c}} = \frac {1}{4} H_{\tilde {u}} + \Gamma $
, where
![]() $\Gamma = (\tilde {x} + \tilde {t} \tilde {u} + \tilde {u}^5 = 0)$
is a quasi-line. We see that any two of
$\Gamma = (\tilde {x} + \tilde {t} \tilde {u} + \tilde {u}^5 = 0)$
is a quasi-line. We see that any two of
![]() $H_{\tilde {x}}, H_{\tilde {u}}, H_{\tilde {t}}$
and
$H_{\tilde {x}}, H_{\tilde {u}}, H_{\tilde {t}}$
and
![]() $\Gamma $
intersect transversally, and thus
$\Gamma $
intersect transversally, and thus
![]() $\eta = 1$
.
$\eta = 1$
.
We set
 $$\begin{align*}\theta := \min \left\{\ \frac{c_1 + c_2 + c_3}{\operatorname{wt}_{\underline{c}} (\bar{F})}, \eta \right\}, \end{align*}$$
$$\begin{align*}\theta := \min \left\{\ \frac{c_1 + c_2 + c_3}{\operatorname{wt}_{\underline{c}} (\bar{F})}, \eta \right\}, \end{align*}$$
which is listed in the sixth column of Table 6. By Lemma 3.27, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge \theta \ge 1/2$
and the claim is proved.
$\operatorname {lct}_{\mathsf {p}} (X; H_v) \ge \theta \ge 1/2$
and the claim is proved.
By Claims 18, 19 and 20, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge 1/2$
. Suppose
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{b} H_v) \ge 1/2$
. Suppose
![]() $\alpha _{\mathsf {p}} (X) < 1/2$
. Then there exists an irreducible
$\alpha _{\mathsf {p}} (X) < 1/2$
. Then there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
other than
$D \in |A|_{\mathbb {Q}}$
other than
![]() $\frac {1}{b} H_v$
such that
$\frac {1}{b} H_v$
such that
![]() $(X, \frac {1}{2} D)$
is not log canonical at
$(X, \frac {1}{2} D)$
is not log canonical at
![]() $\mathsf {p}$
. Let
$\mathsf {p}$
. Let
![]() $\varphi \colon Y \to X$
be the Kawamata blowup at
$\varphi \colon Y \to X$
be the Kawamata blowup at
![]() $\mathsf {p}$
with exceptional divisor E. We set
$\mathsf {p}$
with exceptional divisor E. We set
![]() $\lambda = \operatorname {ord}_E (D)$
. Since the pair
$\lambda = \operatorname {ord}_E (D)$
. Since the pair
![]() $(X, \frac {1}{2} D)$
is not canonical at
$(X, \frac {1}{2} D)$
is not canonical at
![]() $\mathsf {p}$
, the discrepancy of
$\mathsf {p}$
, the discrepancy of
![]() $(X, \frac {1}{2} D)$
along E is negative, which implies
$(X, \frac {1}{2} D)$
along E is negative, which implies
By [Reference Corti, Pukhlikhov and ReidCPR00, Theorem 4.9], the divisor
![]() $- K_Y \sim _{\mathbb {Q}} \varphi ^*A - \frac {1}{r_2} E$
is nef. We see that
$- K_Y \sim _{\mathbb {Q}} \varphi ^*A - \frac {1}{r_2} E$
is nef. We see that
![]() $\tilde {D} \cdot \tilde {H}_v$
is an effective
$\tilde {D} \cdot \tilde {H}_v$
is an effective
![]() $1$
-cycle on Y, where
$1$
-cycle on Y, where
![]() $\tilde {D}$
and
$\tilde {D}$
and
![]() $\tilde {H}_v$
are proper transforms of D and
$\tilde {H}_v$
are proper transforms of D and
![]() $H_v$
, respectively. It follows that
$H_v$
, respectively. It follows that
 $$ \begin{align*} 0 &\le (- K_Y \cdot \tilde{D} \cdot \tilde{H}_v) = b (A^3) - \frac{(2 a + 2 b) \lambda}{r_2^2} (E^3) \\ &= \frac{(4 a + 3 b) - (2 a + 2 b) r_2 \lambda}{a r_1 r_2} < - \frac{b}{a r_1 r_2} < 0. \end{align*} $$
$$ \begin{align*} 0 &\le (- K_Y \cdot \tilde{D} \cdot \tilde{H}_v) = b (A^3) - \frac{(2 a + 2 b) \lambda}{r_2^2} (E^3) \\ &= \frac{(4 a + 3 b) - (2 a + 2 b) r_2 \lambda}{a r_1 r_2} < - \frac{b}{a r_1 r_2} < 0. \end{align*} $$
This is a contradiction, and we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
. Therefore, the proof of Proposition 5.18 is completed.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
. Therefore, the proof of Proposition 5.18 is completed.
6 Families
 $\mathcal {F}_2$
,
$\mathcal {F}_2$
,
 $\mathcal {F}_{4}$
,
$\mathcal {F}_{4}$
,
 $\mathcal {F}_5$
,
$\mathcal {F}_5$
,
 $\mathcal {F}_6$
,
$\mathcal {F}_6$
,
 $\mathcal {F}_8$
,
$\mathcal {F}_8$
,
 $\mathcal {F}_{10}$
and
$\mathcal {F}_{10}$
and
 $\mathcal {F}_{14}$
$\mathcal {F}_{14}$
This section is devoted to the proof of the following theorem.
Theorem 6.1. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}_1$
. Then
$\mathsf {i} \in \mathsf {I}_1$
. Then
6.1 Families
 $\mathcal {F}_6$
,
$\mathcal {F}_6$
,
 $\mathcal {F}_{10}$
and
$\mathcal {F}_{10}$
and
 $\mathcal {F}_{14}$
$\mathcal {F}_{14}$
In this section, we prove Theorem 6.1 for families
![]() $\mathcal {F}_6$
,
$\mathcal {F}_6$
,
![]() $\mathcal {F}_{10}$
and
$\mathcal {F}_{10}$
and
![]() $\mathcal {F}_{14}$
whose member is a weighted hypersurface
$\mathcal {F}_{14}$
whose member is a weighted hypersurface
where
![]() $a = 2, 3, 4$
, respectively. Let X be a member of a family
$a = 2, 3, 4$
, respectively. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \{6, 10, 14\}$
.
$\mathsf {i} \in \{6, 10, 14\}$
.
Let
![]() $\mathsf {p} \in X$
be a smooth point. We may assume
$\mathsf {p} \in X$
be a smooth point. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
by a suitable choice of coordinates. By Lemma 4.3 (see also Remark 4.4), we have
$\mathsf {p} = \mathsf {p}_x$
by a suitable choice of coordinates. By Lemma 4.3 (see also Remark 4.4), we have
Let
![]() $\mathsf {p} \in X$
be a singular point. If
$\mathsf {p} \in X$
be a singular point. If
![]() $\mathsf {i} = 14$
, then
$\mathsf {i} = 14$
, then
![]() $\mathsf {p} \in X$
is of type
$\mathsf {p} \in X$
is of type
![]() $\frac {1}{2} (1, 1, 1)$
and we have
$\frac {1}{2} (1, 1, 1)$
and we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
by Proposition 5.2. If
$\alpha _{\mathsf {p}} (X) \ge 1$
by Proposition 5.2. If
![]() $\mathsf {i} = 6, 10$
, then
$\mathsf {i} = 6, 10$
, then
![]() $\mathsf {p} \in X$
is of type
$\mathsf {p} \in X$
is of type
![]() $\frac {1}{2} (1, 1, 1)$
,
$\frac {1}{2} (1, 1, 1)$
,
![]() $\frac {1}{3} (1, 1, 2)$
, respectively, and in both cases we have
$\frac {1}{3} (1, 1, 2)$
, respectively, and in both cases we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
by Proposition 5.4. Thus, the proof of Theorem 6.1 for families
$\alpha _{\mathsf {p}} (X) \ge 1/2$
by Proposition 5.4. Thus, the proof of Theorem 6.1 for families
![]() $\mathcal {F}_6$
,
$\mathcal {F}_6$
,
![]() $\mathcal {F}_{10}$
and
$\mathcal {F}_{10}$
and
![]() $\mathcal {F}_{14}$
is completed.
$\mathcal {F}_{14}$
is completed.
6.2 The family
 $\mathcal {F}_2$
$\mathcal {F}_2$
This section is devoted to the proof Theorem 6.1 for the family
![]() $\mathcal {F}_2$
. In the following, let
$\mathcal {F}_2$
. In the following, let
be a member of
![]() $\mathcal {F}_2$
with defining polynomial
$\mathcal {F}_2$
with defining polynomial
![]() $F = F (x,y,z,t,w)$
.
$F = F (x,y,z,t,w)$
.
6.2.a Smooth points
Let
![]() $\mathsf {p} \in X$
be a smooth point. In this subsection, we will prove
$\mathsf {p} \in X$
be a smooth point. In this subsection, we will prove
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
. We may assume
$\alpha _{\mathsf {p}} (X) \ge 1/2$
. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
by a choice of coordinates. The proof will be done by division into cases.
$\mathsf {p} = \mathsf {p}_x$
by a choice of coordinates. The proof will be done by division into cases.
6.2.a.1 Case:
 $x^3 w \in F$
$x^3 w \in F$
In this case, we can write
where
![]() $f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
$f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
![]() $\operatorname {mult}_{\mathsf {p}} (H_w) \ge 3$
.
$\operatorname {mult}_{\mathsf {p}} (H_w) \ge 3$
.
Claim 21.
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{2} H_w) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{2} H_w) \ge 1/2$
.
Proof of Claim 21.
This is obvious when
![]() $\operatorname {mult}_{\mathsf {p}} (H_w) \le 4$
, hence we assume
$\operatorname {mult}_{\mathsf {p}} (H_w) \le 4$
, hence we assume
![]() $\operatorname {mult}_{\mathsf {p}} (H_w) \ge 5$
. Then we can write
$\operatorname {mult}_{\mathsf {p}} (H_w) \ge 5$
. Then we can write
where
![]() $\alpha \in \mathbb {C}$
and
$\alpha \in \mathbb {C}$
and
![]() $a_1, b_2, c_1, d_3, e_5 \in \mathbb {C} [y,z,t]$
are quasi-homogeneous polynomials of indicated degrees. We show that
$a_1, b_2, c_1, d_3, e_5 \in \mathbb {C} [y,z,t]$
are quasi-homogeneous polynomials of indicated degrees. We show that
![]() $(e_5 = 0) \subset \mathbb {P} (1,1,1)_{y, z, t}$
is smooth. Indeed, if it has a singular point at
$(e_5 = 0) \subset \mathbb {P} (1,1,1)_{y, z, t}$
is smooth. Indeed, if it has a singular point at
![]() $(y\!:\!z\!:\!t) = (\lambda \!:\!\mu \!:\!\nu )$
, then, by setting
$(y\!:\!z\!:\!t) = (\lambda \!:\!\mu \!:\!\nu )$
, then, by setting
![]() $\theta \in \mathbb {C}$
to be a solution of the equation
$\theta \in \mathbb {C}$
to be a solution of the equation
we see that X is not quasi-smooth at the point
![]() $(\theta \!:\!\lambda \!:\!\mu \!:\!\nu \!:\!0)$
and this is a contradiction. The lowest weight part of
$(\theta \!:\!\lambda \!:\!\mu \!:\!\nu \!:\!0)$
and this is a contradiction. The lowest weight part of
![]() $F (1, y, z, t, 0) = e_5$
with respect to
$F (1, y, z, t, 0) = e_5$
with respect to
![]() $\operatorname {wt} (y, z, t) = (1, 1, 1)$
is
$\operatorname {wt} (y, z, t) = (1, 1, 1)$
is
![]() $e_5$
which defines a smooth hypersurface in
$e_5$
which defines a smooth hypersurface in
![]() $\mathbb {P}^2$
. By Lemma 3.27, we have
$\mathbb {P}^2$
. By Lemma 3.27, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X, H_w) \ge 3/5$
. Thus,
$\operatorname {lct}_{\mathsf {p}} (X, H_w) \ge 3/5$
. Thus,
![]() $\operatorname {lct}_{\mathsf {p}} (X;\frac {1}{2} H_w) \ge 6/5$
in this case and the claim is proved.
$\operatorname {lct}_{\mathsf {p}} (X;\frac {1}{2} H_w) \ge 6/5$
in this case and the claim is proved.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $\frac {1}{2} H_w$
. We can take a
$\frac {1}{2} H_w$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |A|_{\mathbb {Q}}$
such that
$T \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_w$
since
$D \cdot H_w$
since
![]() $\{y, z, t\}$
isolates
$\{y, z, t\}$
isolates
![]() $\mathsf {p}$
. It follows that
$\mathsf {p}$
. It follows that
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 3/5$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 3/5$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
6.2.a.2 Case:
 $x^3 w \notin F$
$x^3 w \notin F$
By a choice of coordinates, we can write
where
![]() $f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $w \notin f_2$
.
$w \notin f_2$
.
Suppose
![]() $w^2 \in f_4$
. In this case,
$w^2 \in f_4$
. In this case,
![]() $\operatorname {mult}_{\mathsf {p}} (H_t) = 2$
and hence
$\operatorname {mult}_{\mathsf {p}} (H_t) = 2$
and hence
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_t) \ge 1/2$
. Let
$\operatorname {lct}_{\mathsf {p}} (X;H_t) \ge 1/2$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_t$
. We can take a
$H_t$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |A|_{\mathbb {Q}}$
such that
$T \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_t$
since
$D \cdot H_t$
since
![]() $\{y, z, t\}$
isolates
$\{y, z, t\}$
isolates
![]() $\mathsf {p}$
so that
$\mathsf {p}$
so that
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/5$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/5$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
in this case.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
in this case.
Suppose
![]() $w^2 \notin f_4$
. We have
$w^2 \notin f_4$
. We have
![]() $\operatorname {Bs} |\mathcal {I}_{\mathsf {p}} (A)| = \Gamma $
, where
$\operatorname {Bs} |\mathcal {I}_{\mathsf {p}} (A)| = \Gamma $
, where
![]() $\Gamma = (y = z = t = 0) \subset X$
is a quasi-line. We assume
$\Gamma = (y = z = t = 0) \subset X$
is a quasi-line. We assume
![]() $\alpha _{\mathsf {p}} (X) < 1/2$
. Then there exists an irreducible
$\alpha _{\mathsf {p}} (X) < 1/2$
. Then there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
such that
$D \in |A|_{\mathbb {Q}}$
such that
![]() $(X, \frac {1}{2} D)$
is not log canonical at
$(X, \frac {1}{2} D)$
is not log canonical at
![]() $\mathsf {p}$
. Let
$\mathsf {p}$
. Let
![]() $S \in |\mathcal {I}_{\mathsf {p}} (A)|$
be a general member so that
$S \in |\mathcal {I}_{\mathsf {p}} (A)|$
be a general member so that
![]() $S \ne \operatorname {Supp} (D)$
. Then S is a normal surface by Lemma 3.7 and it is quasi-smooth along
$S \ne \operatorname {Supp} (D)$
. Then S is a normal surface by Lemma 3.7 and it is quasi-smooth along
![]() $\Gamma $
. Moreover, for another general
$\Gamma $
. Moreover, for another general
![]() $T \in |\mathcal {I}_{\mathsf {p}} (A)|$
, the multiplicity of
$T \in |\mathcal {I}_{\mathsf {p}} (A)|$
, the multiplicity of
![]() $T|_S$
along
$T|_S$
along
![]() $\Gamma $
is
$\Gamma $
is
![]() $1$
, that is, we can write
$1$
, that is, we can write
where
![]() $\Delta $
is an effective divisor on S such that
$\Delta $
is an effective divisor on S such that
![]() $\Gamma \not \subset \operatorname {Supp} (\Delta )$
. We see that
$\Gamma \not \subset \operatorname {Supp} (\Delta )$
. We see that
![]() $\Gamma $
is a quasi-line, S is quasi-smooth at
$\Gamma $
is a quasi-line, S is quasi-smooth at
![]() $\mathsf {p}_w$
,
$\mathsf {p}_w$
,
![]() $\Gamma $
passes through the
$\Gamma $
passes through the
![]() $\frac {1}{2} (1,1)$
point
$\frac {1}{2} (1,1)$
point
![]() $\mathsf {p}_w$
of S and
$\mathsf {p}_w$
of S and
![]() $(K_S \cdot \Gamma ) = 0$
. It follows that
$(K_S \cdot \Gamma ) = 0$
. It follows that
by Remark 3.10. Hence,
The divisor
![]() $D|_S$
on S is effective, and we write
$D|_S$
on S is effective, and we write
![]() $\frac {1}{2} D|_S = \gamma \Gamma + \Xi $
, where
$\frac {1}{2} D|_S = \gamma \Gamma + \Xi $
, where
![]() $\gamma \ge 0$
and
$\gamma \ge 0$
and
![]() $\Xi $
is an effective divisor on S such that
$\Xi $
is an effective divisor on S such that
![]() $\Gamma \not \subset \operatorname {Supp} (\Xi )$
. Since
$\Gamma \not \subset \operatorname {Supp} (\Xi )$
. Since
![]() $\operatorname {Bs} |\mathcal {I}_{\mathsf {p}} (A)| = \Gamma $
and S is general, we may assume that
$\operatorname {Bs} |\mathcal {I}_{\mathsf {p}} (A)| = \Gamma $
and S is general, we may assume that
![]() $\operatorname {Supp} (\Xi )$
does not contain any component of
$\operatorname {Supp} (\Xi )$
does not contain any component of
![]() $\operatorname {Supp} (\Delta )$
. In particular,
$\operatorname {Supp} (\Delta )$
. In particular,
![]() $(\Xi \cdot \Delta )_S \ge 0$
. Note also that
$(\Xi \cdot \Delta )_S \ge 0$
. Note also that
It follows that
which implies
![]() $\gamma \le \frac {1}{2}$
. We see that
$\gamma \le \frac {1}{2}$
. We see that
![]() $(X, \frac {1}{2} D|_S)$
is not log canonical at
$(X, \frac {1}{2} D|_S)$
is not log canonical at
![]() $\mathsf {p}$
, and hence
$\mathsf {p}$
, and hence
![]() $(S, \Gamma + \Xi ) = (S, \frac {1}{2} D|_S + (1-\gamma ) \Gamma )$
is not log canonical at
$(S, \Gamma + \Xi ) = (S, \frac {1}{2} D|_S + (1-\gamma ) \Gamma )$
is not log canonical at
![]() $\mathsf {p}$
. By the inversion of adjunction, we have
$\mathsf {p}$
. By the inversion of adjunction, we have
This is a contradiction and the inequality
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved.
6.2.b The singular point of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $\mathsf {p} = \mathsf {p}_w$
be the singular point of type
$\mathsf {p} = \mathsf {p}_w$
be the singular point of type
![]() $\frac {1}{2} (1,1,1)$
. Note that the point
$\frac {1}{2} (1,1,1)$
. Note that the point
![]() $\mathsf {p} \in X$
is a QI center.
$\mathsf {p} \in X$
is a QI center.
6.2.b.1 Case:
 $\mathsf {p}$
is nondegenerate
$\mathsf {p}$
is nondegenerate
By a choice of coordinates, we can write
where
![]() $f_3, g_5$
are nonzero homogeneous polynomials such that
$f_3, g_5$
are nonzero homogeneous polynomials such that
![]() $f_3 \ne 0$
as a polynomial. Let
$f_3 \ne 0$
as a polynomial. Let
![]() $\varphi \colon Y \to X$
be the Kawamata blowup at
$\varphi \colon Y \to X$
be the Kawamata blowup at
![]() $\mathsf {p}$
with exceptional divisor E.
$\mathsf {p}$
with exceptional divisor E.
Claim 22.
![]() $\operatorname {lct}_{\mathsf {p}} (X, H_t) \ge \frac {1}{2}$
.
$\operatorname {lct}_{\mathsf {p}} (X, H_t) \ge \frac {1}{2}$
.
Proof of Claim 22.
The lowest weight part of
![]() $F (x,y,z,0,1)$
with respect to
$F (x,y,z,0,1)$
with respect to
![]() $\operatorname {wt} (x,y,z) = (1,1,1)$
is
$\operatorname {wt} (x,y,z) = (1,1,1)$
is
![]() $f_3$
. By Lemma 3.28, we have
$f_3$
. By Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
unless
$\alpha _{\mathsf {p}} (X) \ge 1/2$
unless
![]() $f_3$
is a cube of a linear form. Hence, it remains to prove the claim assuming that
$f_3$
is a cube of a linear form. Hence, it remains to prove the claim assuming that
![]() $f_3$
is a cube of a linear form. By a choice of coordinates, we may assume
$f_3$
is a cube of a linear form. By a choice of coordinates, we may assume
![]() $f_3 = z^3$
. Let S be the divisor on X defined by
$f_3 = z^3$
. Let S be the divisor on X defined by
![]() $x - \lambda y = 0$
for a general
$x - \lambda y = 0$
for a general
![]() $\lambda \in \mathbb {C}$
. By the quasi-smoothness of X, the polynomial F cannot be contained in the ideal
$\lambda \in \mathbb {C}$
. By the quasi-smoothness of X, the polynomial F cannot be contained in the ideal
![]() $(z, t) \subset \mathbb {C} [x, y, z, t, w]$
. This implies
$(z, t) \subset \mathbb {C} [x, y, z, t, w]$
. This implies
![]() $g_5 (x, y, 0, 0) \ne 0$
, and hence
$g_5 (x, y, 0, 0) \ne 0$
, and hence
![]() $g_5 (\lambda y, y,0,0) \ne 0$
. By eliminating x, the surface S is isomorphic to the hypersurface in
$g_5 (\lambda y, y,0,0) \ne 0$
. By eliminating x, the surface S is isomorphic to the hypersurface in
![]() $\mathbb {P} (1, 1, 1, 2)_{y, z, t, w}$
defined by
$\mathbb {P} (1, 1, 1, 2)_{y, z, t, w}$
defined by
where
![]() $a_4 = a_4 (y, z), b_4 = b_4 (y, z, t)$
are homogeneous polynomials of degree
$a_4 = a_4 (y, z), b_4 = b_4 (y, z, t)$
are homogeneous polynomials of degree
![]() $4$
and
$4$
and
![]() $\alpha \ne 0$
is a constant. The lowest weight part of
$\alpha \ne 0$
is a constant. The lowest weight part of
![]() $G (x,z,0,1)$
with respect to
$G (x,z,0,1)$
with respect to
![]() $\operatorname {wt} (y, z) = (3, 5)$
is
$\operatorname {wt} (y, z) = (3, 5)$
is
![]() $z^3 + \alpha y^5$
which defines a smooth point of
$z^3 + \alpha y^5$
which defines a smooth point of
![]() $\mathbb {P} (3, 5)_{y, z}$
. By Lemma 3.27,
$\mathbb {P} (3, 5)_{y, z}$
. By Lemma 3.27,
![]() $\operatorname {lct}_{\mathsf {p}} (S; H_t|_S) \ge 8/15$
, and hence
$\operatorname {lct}_{\mathsf {p}} (S; H_t|_S) \ge 8/15$
, and hence
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_t) \ge 8/15$
. Thus, the claim is proved.
$\operatorname {lct}_{\mathsf {p}} (X;H_t) \ge 8/15$
. Thus, the claim is proved.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_t$
. We can take
$H_t$
. We can take
![]() $T \in |A|_{\mathbb {Q}}$
such that
$T \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
, and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
, and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_t$
since
$D \cdot H_t$
since
![]() $\{x, y, z, t\}$
isolates
$\{x, y, z, t\}$
isolates
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
since
![]() $\operatorname {omult}_{\mathsf {p}} (H_t) = 3$
. This shows
$\operatorname {omult}_{\mathsf {p}} (H_t) = 3$
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge \frac {3}{5}$
and thus
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge \frac {3}{5}$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge \frac {1}{2}$
.
$\alpha _{\mathsf {p}} (X) \ge \frac {1}{2}$
.
6.3 The family
 $\mathcal {F}_4$
$\mathcal {F}_4$
This subsection is devoted to the proof of Theorem 6.1 for the family
![]() $\mathcal {F}_4$
. In the following, let
$\mathcal {F}_4$
. In the following, let
be a member of
![]() $\mathcal {F}_4$
with defining polynomial
$\mathcal {F}_4$
with defining polynomial
![]() $F = F (x, y, z, t, w)$
.
$F = F (x, y, z, t, w)$
.
6.3.a Smooth points
Let
![]() $\mathsf {p}$
be a smooth point of X. We will prove
$\mathsf {p}$
be a smooth point of X. We will prove
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
. We may assume
$\alpha _{\mathsf {p}} (X) \ge 1/2$
. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
by a choice of coordinates. The proof will be done by division into cases.
$\mathsf {p} = \mathsf {p}_x$
by a choice of coordinates. The proof will be done by division into cases.
6.3.a.1 Case: Either
 $x^4 w \in F$
or
$x^4 w \in F$
or
 $x^4 t \in F$
$x^4 t \in F$
In this case, we have
by Lemma 3.29.
6.3.a.2 Case:
 $x^4 w, x^4 t \notin F$
$x^4 w, x^4 t \notin F$
We can write
where
![]() $f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t, w \notin f_2$
.
$t, w \notin f_2$
.
We claim
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
. This is obvious when
$\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
. This is obvious when
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \le 2$
and hence we assume
$\operatorname {mult}_{\mathsf {p}} (H_y) \le 2$
and hence we assume
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
. Then we can write
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
. Then we can write
 $$\begin{align*}\bar{F} := F (1, 0, z, t, w) = \sum_{i=2}^6 f_i (0, z, t, w) = \alpha z^3 + \beta t z^2 + \gamma w z^2 + c (t, w) + h, \end{align*}$$
$$\begin{align*}\bar{F} := F (1, 0, z, t, w) = \sum_{i=2}^6 f_i (0, z, t, w) = \alpha z^3 + \beta t z^2 + \gamma w z^2 + c (t, w) + h, \end{align*}$$
where
![]() $c (t, w) = f_6 (0, 0, z, t)$
and
$c (t, w) = f_6 (0, 0, z, t)$
and
![]() $h = h (y, t, w)$
is in the ideal
$h = h (y, t, w)$
is in the ideal
![]() $(y, t, w)^4$
. By the quasi-smoothness of X, c cannot be a cube of a linear form. This implies that the cubic part of
$(y, t, w)^4$
. By the quasi-smoothness of X, c cannot be a cube of a linear form. This implies that the cubic part of
![]() $\bar {F}$
is not a cube of a linear form. Thus,
$\bar {F}$
is not a cube of a linear form. Thus,
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
by Lemma 3.28 and the claim is proved.
$\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
by Lemma 3.28 and the claim is proved.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_y$
. We can take
$H_y$
. We can take
![]() $T \in |2 A|_{\mathbb {Q}}$
such that
$T \in |2 A|_{\mathbb {Q}}$
such that
![]() ${\operatorname {mult}_{\mathsf {p}} (T) \ge 1}$
and
${\operatorname {mult}_{\mathsf {p}} (T) \ge 1}$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_y$
since
$D \cdot H_y$
since
![]() $\{y, z, t, w\}$
isolates
$\{y, z, t, w\}$
isolates
![]() $\mathsf {p}$
. Then we have
$\mathsf {p}$
. Then we have
since
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 2$
. This implies
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 2$
. This implies
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 2/3$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 2/3$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
6.3.b Singular points of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $\mathsf {p}$
be a singular point of type
$\mathsf {p}$
be a singular point of type
![]() $\frac {1}{2} (1,1,1)$
. Then we have
$\frac {1}{2} (1,1,1)$
. Then we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
by Proposition 5.18 (actually we have
$\alpha _{\mathsf {p}} (X) \ge 1/2$
by Proposition 5.18 (actually we have
![]() $\alpha _{\mathsf {p}} (X) \ge 2/3$
by the argument in Section 5.6.b). Therefore, the proof of Theorem 6.1 for the family
$\alpha _{\mathsf {p}} (X) \ge 2/3$
by the argument in Section 5.6.b). Therefore, the proof of Theorem 6.1 for the family
![]() $\mathcal {F}_4$
is completed.
$\mathcal {F}_4$
is completed.
6.4 The family
 $\mathcal {F}_5$
$\mathcal {F}_5$
This subsection is devoted to the proof Theorem 6.1 for the family
![]() $\mathcal {F}_5$
. In the following, let
$\mathcal {F}_5$
. In the following, let
be a member of family
![]() $\mathcal {F}_5$
with defining polynomial
$\mathcal {F}_5$
with defining polynomial
![]() $F = F (x, y, z, t, w)$
.
$F = F (x, y, z, t, w)$
.
6.4.a Smooth points
Let
![]() $\mathsf {p}$
be a smooth point of X. We will prove
$\mathsf {p}$
be a smooth point of X. We will prove
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
. The proof will be done by division into cases.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
. The proof will be done by division into cases.
6.4.a.1 Case:
 $\mathsf {p} \in U_x \cup U_y \cup U_z$
$\mathsf {p} \in U_x \cup U_y \cup U_z$
By a choice of coordinates
![]() $x, y, z$
, we may assume
$x, y, z$
, we may assume
![]() $\mathsf {p} = \mathsf {p}_x$
. By Lemma 3.29, we have
$\mathsf {p} = \mathsf {p}_x$
. By Lemma 3.29, we have
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{1 \cdot 1 \cdot 2 \cdot (A^3)} = \frac{6}{7}, & \text{if}\ x^4w \in F, \\ \frac{2}{1 \cdot 1 \cdot 3 \cdot (A^3)} = \frac{4}{7}, & \text{if}\ x^4 w \notin F\ \text{and}\ x^5 t \in F. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \begin{cases} \frac{2}{1 \cdot 1 \cdot 2 \cdot (A^3)} = \frac{6}{7}, & \text{if}\ x^4w \in F, \\ \frac{2}{1 \cdot 1 \cdot 3 \cdot (A^3)} = \frac{4}{7}, & \text{if}\ x^4 w \notin F\ \text{and}\ x^5 t \in F. \end{cases} \end{align*}$$
It remains to consider the case where
![]() $x^4 w, x^5 t \notin F$
. In this case, we can write
$x^4 w, x^5 t \notin F$
. In this case, we can write
where
![]() $f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $t \notin f_2$
and
$t \notin f_2$
and
![]() $w \notin f_3$
.
$w \notin f_3$
.
Claim 23.
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
.
Proof of Claim 23.
This is obvious when
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) = 2$
, and we assume
$\operatorname {mult}_{\mathsf {p}} (H_y) = 2$
, and we assume
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
. It follows that each monomial appearing in F is contained in
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 3$
. It follows that each monomial appearing in F is contained in
![]() $(y) \cup (z, t, w)^3$
. A monomial of degree
$(y) \cup (z, t, w)^3$
. A monomial of degree
![]() $d \in \{2, 3, 4, 5, 6, 7\}$
in variables
$d \in \{2, 3, 4, 5, 6, 7\}$
in variables
![]() $y, z, t, w$
which is contained in
$y, z, t, w$
which is contained in
![]() $(y) \cup (z, t, w)^3$
is contained in
$(y) \cup (z, t, w)^3$
is contained in
![]() $(y) \cup (z, t)^2$
except for the monomial
$(y) \cup (z, t)^2$
except for the monomial
![]() $w^2 z$
of degree
$w^2 z$
of degree
![]() $7$
. Hence, we can write
$7$
. Hence, we can write
where
![]() $g = g (x, y, z, t, w) \in \mathbb {C} [x, y, z, t, w]$
and
$g = g (x, y, z, t, w) \in \mathbb {C} [x, y, z, t, w]$
and
![]() $h = h (x, z, t, w) \in (z, t)^2$
. If
$h = h (x, z, t, w) \in (z, t)^2$
. If
![]() $\alpha = 0$
, then X is not quasi-smooth at any point of the nonempty set
$\alpha = 0$
, then X is not quasi-smooth at any point of the nonempty set
Thus,
![]() $w^2 z \in F$
and we see that
$w^2 z \in F$
and we see that
![]() $\bar {F} = F (1,0,z,t,w) \in (z,t,w)^3$
and the cubic part of
$\bar {F} = F (1,0,z,t,w) \in (z,t,w)^3$
and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form since
$\bar {F}$
is not a cube of a linear form since
![]() $w^2 z \in \bar {F}$
and
$w^2 z \in \bar {F}$
and
![]() $w^3 \notin \bar {F}$
. By Lemma 3.28, we have
$w^3 \notin \bar {F}$
. By Lemma 3.28, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
, and the claim is proved.
$\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
, and the claim is proved.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_y$
. We can take a
$H_y$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |3 A|_{\mathbb {Q}}$
such that
$T \in |3 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_y$
since
$D \cdot H_y$
since
![]() $\{y, z, t, w\}$
isolates
$\{y, z, t, w\}$
isolates
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
since
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) \ge 2$
. This shows
$\operatorname {mult}_{\mathsf {p}} (H_y) \ge 2$
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
6.4.a.2 Case
 $\mathsf {p} \notin U_x \cup U_y \cup U_z$
$\mathsf {p} \notin U_x \cup U_y \cup U_z$
If
![]() $w t^2 \in F$
, then
$w t^2 \in F$
, then
![]() $X \setminus (U_x \cup U_y \cup U_z)$
consists of singular points. Hence, we have
$X \setminus (U_x \cup U_y \cup U_z)$
consists of singular points. Hence, we have
![]() $w t^2 \notin F$
in this case, and
$w t^2 \notin F$
in this case, and
![]() $\mathsf {p}$
is contained in the quasi-line
$\mathsf {p}$
is contained in the quasi-line
![]() $\Gamma := (x = y = z = 0) \subset X$
. We will show
$\Gamma := (x = y = z = 0) \subset X$
. We will show
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
. Assume to the contrary that
$\alpha _{\mathsf {p}} (X) \ge 1$
. Assume to the contrary that
![]() $\alpha _{\mathsf {p}} (X) < 1$
. Then there exists an irreducible
$\alpha _{\mathsf {p}} (X) < 1$
. Then there exists an irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
such that the pair
$D \in |A|_{\mathbb {Q}}$
such that the pair
![]() $(X, D)$
is not log canonical at
$(X, D)$
is not log canonical at
![]() $\mathsf {p}$
. Let
$\mathsf {p}$
. Let
![]() $S \in |A|$
be a general member and write
$S \in |A|$
be a general member and write
![]() $D|_S = \gamma \Gamma + \Delta $
, where
$D|_S = \gamma \Gamma + \Delta $
, where
![]() $\gamma \ge 0$
is a rational number and
$\gamma \ge 0$
is a rational number and
![]() $\Delta $
is an effective
$\Delta $
is an effective
![]() $1$
-cycle on S such that
$1$
-cycle on S such that
![]() $\Gamma \not \subset \operatorname {Supp} (\Delta )$
.
$\Gamma \not \subset \operatorname {Supp} (\Delta )$
.
Claim 24.
![]() $(\Gamma ^2)_S = - 5/6$
and
$(\Gamma ^2)_S = - 5/6$
and
![]() $\gamma \le 1$
.
$\gamma \le 1$
.
Proof of Claim 24.
We see that S has singular points of type
![]() $\frac {1}{2} (1,1)$
and
$\frac {1}{2} (1,1)$
and
![]() $\frac {1}{3} (1,2)$
at
$\frac {1}{3} (1,2)$
at
![]() $\mathsf {p}_t$
and
$\mathsf {p}_t$
and
![]() $\mathsf {p}_w$
, respectively, and smooth elsewhere since
$\mathsf {p}_w$
, respectively, and smooth elsewhere since
![]() $S \in |A|$
is general. Since
$S \in |A|$
is general. Since
![]() $\Gamma $
is a quasi-line on S passing through
$\Gamma $
is a quasi-line on S passing through
![]() $\mathsf {p}_t, \mathsf {p}_w$
and
$\mathsf {p}_t, \mathsf {p}_w$
and
![]() $K_S = (K_X + S)|_S \sim 0$
by adjunction, we have
$K_S = (K_X + S)|_S \sim 0$
by adjunction, we have
We choose a general member
![]() $T \in |A|$
which does not contain any component of
$T \in |A|$
which does not contain any component of
![]() $\Delta $
. This is possible since
$\Delta $
. This is possible since
![]() $\operatorname {Bs} |A| = \Gamma $
. We write
$\operatorname {Bs} |A| = \Gamma $
. We write
![]() $T|_S = \Gamma + \Xi $
, where
$T|_S = \Gamma + \Xi $
, where
![]() $\Xi $
is an effective divisor on S such that
$\Xi $
is an effective divisor on S such that
![]() $\Gamma \not \subset \operatorname {Supp} (\Xi )$
. We have
$\Gamma \not \subset \operatorname {Supp} (\Xi )$
. We have
 $$ \begin{align*} (D|_S \cdot \Xi)_S &= (D|_S \cdot (T|_S - \Gamma))_S = \frac{7}{6} - \frac{1}{6} = 1, \\ (\Gamma \cdot \Xi)_S &= (\Gamma \cdot (T|_S - \Gamma))_S = \frac{1}{6} + \frac{5}{6} = 1. \end{align*} $$
$$ \begin{align*} (D|_S \cdot \Xi)_S &= (D|_S \cdot (T|_S - \Gamma))_S = \frac{7}{6} - \frac{1}{6} = 1, \\ (\Gamma \cdot \Xi)_S &= (\Gamma \cdot (T|_S - \Gamma))_S = \frac{1}{6} + \frac{5}{6} = 1. \end{align*} $$
Note that
![]() $\Xi $
does not contain any component of
$\Xi $
does not contain any component of
![]() $\Delta $
by our choice of T, and hence
$\Delta $
by our choice of T, and hence
as desired.
The pair
![]() $(S, D|_S) = (S, \gamma \Gamma + \Delta )$
is not log canonical at
$(S, D|_S) = (S, \gamma \Gamma + \Delta )$
is not log canonical at
![]() $\mathsf {p}$
. Hence, the pair
$\mathsf {p}$
. Hence, the pair
![]() $(S, \Gamma + \Delta )$
is not log canonical at
$(S, \Gamma + \Delta )$
is not log canonical at
![]() $\mathsf {p}$
since
$\mathsf {p}$
since
![]() $\gamma \le 1$
. By the inversion of adjunction, we have
$\gamma \le 1$
. By the inversion of adjunction, we have
![]() $\operatorname {mult}_{\mathsf {p}} (\Delta |_{\Gamma })> 1$
and thus
$\operatorname {mult}_{\mathsf {p}} (\Delta |_{\Gamma })> 1$
and thus
This is a contradiction, and we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
6.4.b The singular point of type
 $\frac {1}{2} (1,1,1)$
$\frac {1}{2} (1,1,1)$
Let
![]() $\mathsf {p} = \mathsf {p}_t$
be the singular point of type
$\mathsf {p} = \mathsf {p}_t$
be the singular point of type
![]() $\frac {1}{2} (1,1,1)$
.
$\frac {1}{2} (1,1,1)$
.
6.4.b.1 Case:
 $t^2 w \in F$
$t^2 w \in F$
In this case, we have
by Lemma 3.29.
6.4.b.2 Case:
 $t^2 w \notin F$
$t^2 w \notin F$
Replacing
![]() $x, y, z$
, we can write
$x, y, z$
, we can write
where
![]() $f_i = f_i (x, y, z, w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (x, y, z, w)$
is a quasi-homogeneous polynomial of degree i with
![]() $w \notin f_3$
.
$w \notin f_3$
.
Claim 25. If
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) \ge 3$
, then either
$\operatorname {mult}_{\mathsf {p}} (H_x) \ge 3$
, then either
![]() $w^2 y \in F$
or
$w^2 y \in F$
or
![]() $w^2 z \in F$
.
$w^2 z \in F$
.
Proof of Claim 25.
Suppose
![]() $w^2 y, w^2 z \notin F$
. Then
$w^2 y, w^2 z \notin F$
. Then
![]() $h := F (0, y, z, t, w)$
is contained in the ideal
$h := F (0, y, z, t, w)$
is contained in the ideal
![]() $(y, z)^2 \subset \mathbb {C} [y, z, t, w]$
, and we can write
$(y, z)^2 \subset \mathbb {C} [y, z, t, w]$
, and we can write
![]() $F = x g + h$
, where
$F = x g + h$
, where
![]() $g = g (x, y, z, t, w)$
. We see that X is not quasi-smooth at any point in the nonempty subset
$g = g (x, y, z, t, w)$
. We see that X is not quasi-smooth at any point in the nonempty subset
This is a contradiction, and the claim is proved.
We set
![]() $\bar {F} := F (0, y, z, 1, w)$
. By Claim 25, either
$\bar {F} := F (0, y, z, 1, w)$
. By Claim 25, either
![]() $\bar {F} \in (y, z, w)^2 \setminus (y, z, w)^3$
or
$\bar {F} \in (y, z, w)^2 \setminus (y, z, w)^3$
or
![]() $\bar {F} \in (y, z, w)^3$
and the cubic part of
$\bar {F} \in (y, z, w)^3$
and the cubic part of
![]() $\bar {F}$
is not a cube of a linear form since
$\bar {F}$
is not a cube of a linear form since
![]() $w^3 \notin \bar {F}$
. By Lemma 3.28, we have
$w^3 \notin \bar {F}$
. By Lemma 3.28, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
since
$\alpha _{\mathsf {p}} (X) \ge 1/2$
since
![]() $\mathsf {p} \in X$
is not a maximal center.
$\mathsf {p} \in X$
is not a maximal center.
6.4.c Singular point of type
 $\frac {1}{3} (1,1,2)$
$\frac {1}{3} (1,1,2)$
Let
![]() $\mathsf {p} = \mathsf {p}_w$
be the singular point of type
$\mathsf {p} = \mathsf {p}_w$
be the singular point of type
![]() $\frac {1}{3} (1,1,2)$
. We can write
$\frac {1}{3} (1,1,2)$
. We can write
where
![]() $\alpha \in \mathbb {C}$
and
$\alpha \in \mathbb {C}$
and
![]() $a_2 = a_2 (x, y), b_4 = b_4 (y, z), f_7 = f_7 (x, y, z, t)$
are quasi-homogeneous polynomials of degree
$a_2 = a_2 (x, y), b_4 = b_4 (y, z), f_7 = f_7 (x, y, z, t)$
are quasi-homogeneous polynomials of degree
![]() $2, 4, 7$
, respectively. Let
$2, 4, 7$
, respectively. Let
![]() $q = q_{\mathsf {p}}$
be the quotient morphism of
$q = q_{\mathsf {p}}$
be the quotient morphism of
![]() $\mathsf {p} \in X$
and
$\mathsf {p} \in X$
and
![]() $\check {\mathsf {p}}$
be the preimage of
$\check {\mathsf {p}}$
be the preimage of
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
6.4.c.1 Case:
 $\alpha \ne 0$
$\alpha \ne 0$
We have
![]() $\operatorname {mult}_{\mathsf {p}} (H_x) = 2$
and
$\operatorname {mult}_{\mathsf {p}} (H_x) = 2$
and
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. Let
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_x$
. We can take a
$H_x$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |A|_{\mathbb {Q}}$
such that
$T \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
since
$D \cdot H_x$
since
![]() $\{x, y, z\}$
isolates
$\{x, y, z\}$
isolates
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
6.4.c.2 Case
 $\alpha = 0$
and
$\alpha = 0$
and
 $a_2 \ne 0$
$a_2 \ne 0$
The cubic part of
![]() $F (0, y, z, t, 1)$
is
$F (0, y, z, t, 1)$
is
![]() $t a_2$
, and, by Lemma 3.28, we have
$t a_2$
, and, by Lemma 3.28, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. Let
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 1/2$
. Let
![]() $D \sim _{\mathbb {Q}} A$
be an irreducible
$D \sim _{\mathbb {Q}} A$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X other than
$\mathbb {Q}$
-divisor on X other than
![]() $H_x$
. Then we can take a general
$H_x$
. Then we can take a general
![]() $T \in |\mathcal {I}_{\mathsf {p}} (2 A)| = |2 A|$
which does not contain any component of
$T \in |\mathcal {I}_{\mathsf {p}} (2 A)| = |2 A|$
which does not contain any component of
![]() $D \cap H_x$
since
$D \cap H_x$
since
![]() $\operatorname {Bs} |2 A| =\mathsf {p}$
. We see that T is defined by
$\operatorname {Bs} |2 A| =\mathsf {p}$
. We see that T is defined by
![]() $t - q (x, y, z) = 0$
on X, where
$t - q (x, y, z) = 0$
on X, where
![]() $q \in \mathbb {C} [x,y,z]$
is a general quadratic form. Let
$q \in \mathbb {C} [x,y,z]$
is a general quadratic form. Let
![]() $\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of X containing
$\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of X containing
![]() $\mathsf {p}$
and let
$\mathsf {p}$
and let
![]() $\breve {\mathsf {p}}$
be the preimage of
$\breve {\mathsf {p}}$
be the preimage of
![]() $\mathsf {p}$
. It is then easy to see that the effective
$\mathsf {p}$
. It is then easy to see that the effective
![]() $1$
-cycle
$1$
-cycle
![]() $\rho ^*H_x \cdot \rho ^*T$
on
$\rho ^*H_x \cdot \rho ^*T$
on
![]() $\breve {U}_{\mathsf {p}}$
has multiplicity
$\breve {U}_{\mathsf {p}}$
has multiplicity
![]() $4$
at
$4$
at
![]() $\breve {\mathsf {p}}$
. Then we have
$\breve {\mathsf {p}}$
. Then we have
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 4/7$
.
$\alpha _{\mathsf {p}} (X) \ge 4/7$
.
6.4.c.3 Case:
 $\alpha = a_2 = 0$
and
$\alpha = a_2 = 0$
and
 $b_4 \ne 0$
$b_4 \ne 0$
By similar arguments as in the proof of Claim 25, we see that either
![]() $t^3 y \in f_7$
or
$t^3 y \in f_7$
or
![]() $t^3 z \in f_7$
. We choose z and t so that
$t^3 z \in f_7$
. We choose z and t so that
![]() $b_4 (0,z) = z^4$
and
$b_4 (0,z) = z^4$
and
![]() $\operatorname {coeff}_{f_7} (t^3 z) = 1$
. Then we have
$\operatorname {coeff}_{f_7} (t^3 z) = 1$
. Then we have
where
![]() $\beta , \gamma , \delta \in \mathbb {C}$
. The lowest weight part of
$\beta , \gamma , \delta \in \mathbb {C}$
. The lowest weight part of
![]() $F (0,0,z,t,1)$
with respect to
$F (0,0,z,t,1)$
with respect to
![]() $\operatorname {wt} (z,t) = (1,1)$
is
$\operatorname {wt} (z,t) = (1,1)$
is
![]() $z^4 + t^3 z$
which defines four distinct points of
$z^4 + t^3 z$
which defines four distinct points of
![]() $\mathbb {P}^1_{z, t}$
. Hence, we have
$\mathbb {P}^1_{z, t}$
. Hence, we have
by Lemma 3.27. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_x$
. We can take a
$H_x$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |2 A|_{\mathbb {Q}}$
such that
$T \in |2 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_x$
since
$D \cdot H_x$
since
![]() $\{x, y, z, t\}$
isolates
$\{x, y, z, t\}$
isolates
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
since
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 4$
. This shows
$\operatorname {omult}_{\mathsf {p}} (H_x) = 4$
. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 4/7$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
6.4.c.4 Case:
 $\alpha = a_2 = b_4 = 0$
$\alpha = a_2 = b_4 = 0$
In this case, the point
![]() $\mathsf {p} \in X$
is a degenerate QI center and we have
$\mathsf {p} \in X$
is a degenerate QI center and we have
![]() $\alpha _{\mathsf {p}} (X) = 4/7$
by Proposition 5.16.
$\alpha _{\mathsf {p}} (X) = 4/7$
by Proposition 5.16.
6.5 The family
 $\mathcal {F}_8$
$\mathcal {F}_8$
This subsection is devoted to the proof of Theorem 6.1 for the family
![]() $\mathcal {F}_8$
. In the following, let
$\mathcal {F}_8$
. In the following, let
be a member of
![]() $\mathcal {F}_8$
with defining polynomial
$\mathcal {F}_8$
with defining polynomial
![]() $F = F (x, y, z, t, w)$
.
$F = F (x, y, z, t, w)$
.
6.5.a Smooth points
Let
![]() $\mathsf {p} \in X$
be a smooth point. We will prove
$\mathsf {p} \in X$
be a smooth point. We will prove
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
. We may assume
$\alpha _{\mathsf {p}} (X) \ge 1/2$
. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
. The proof will be done by division into cases.
$\mathsf {p} = \mathsf {p}_x$
. The proof will be done by division into cases.
6.5.a.1 Case:
 $x^5 w \in F$
$x^5 w \in F$
We can write
where
![]() $f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
$f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i. We have
![]() $\operatorname {mult}_{\mathsf {p}} (H_w) = 3$
since
$\operatorname {mult}_{\mathsf {p}} (H_w) = 3$
since
![]() $t^3 \in f_9$
. Let
$t^3 \in f_9$
. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor on X. Let
$\mathbb {Q}$
-divisor on X. Let
![]() $S \in |\mathcal {I}_{\mathsf {p}} (A)|$
be a general member so that
$S \in |\mathcal {I}_{\mathsf {p}} (A)|$
be a general member so that
![]() $\operatorname {Supp} (D) \ne S$
. Since
$\operatorname {Supp} (D) \ne S$
. Since
![]() $\{y, z, w\}$
isolates
$\{y, z, w\}$
isolates
![]() $\mathsf {p}$
, we can take a
$\mathsf {p}$
, we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |A|_{\mathbb {Q}}$
such that
$T \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot S$
and
$D \cdot S$
and
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 3/4$
(Note that T is one of
$\operatorname {mult}_{\mathsf {p}} (T) \ge 3/4$
(Note that T is one of
![]() $H_y, H_z$
and
$H_y, H_z$
and
![]() $\frac {1}{4} H_w$
). Then we have
$\frac {1}{4} H_w$
). Then we have
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
6.5.a.2 Case:
 $x^5 w \notin F$
and
$x^5 w \notin F$
and
 $x^6 t \in F$
$x^6 t \in F$
We can write
where
![]() $f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
$f_i = f_i (y,z,t,w)$
is a quasi-homogeneous polynomial of degree i with
![]() $w \notin f_4$
. Let
$w \notin f_4$
. Let
![]() $S, T \in |\mathcal {I}_{\mathsf {p}} (A)|$
be general members. Note that S is smooth at
$S, T \in |\mathcal {I}_{\mathsf {p}} (A)|$
be general members. Note that S is smooth at
![]() $\mathsf {p}$
. The intersection
$\mathsf {p}$
. The intersection
![]() $S \cap T$
is isomorphic to the subscheme in
$S \cap T$
is isomorphic to the subscheme in
![]() $\mathbb {P} (1_x, 3_t, 4_w)$
defined by the equation
$\mathbb {P} (1_x, 3_t, 4_w)$
defined by the equation
![]() $F (x,0,0,t,w) = 0$
, and we can write
$F (x,0,0,t,w) = 0$
, and we can write
where
![]() $\alpha , \beta , \gamma \in \mathbb {C}$
.
$\alpha , \beta , \gamma \in \mathbb {C}$
.
Claim 26. If
![]() $\gamma \ne 0$
, then
$\gamma \ne 0$
, then
![]() $S \cdot T = \Gamma $
, where
$S \cdot T = \Gamma $
, where
![]() $\Gamma $
is an irreducible and reduced curve of degree
$\Gamma $
is an irreducible and reduced curve of degree
![]() $3/4$
that is smooth at
$3/4$
that is smooth at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Proof of Claim 26.
Suppose
![]() $\gamma \ne 0$
. Then it is easy to see that the polynomial
$\gamma \ne 0$
. Then it is easy to see that the polynomial
![]() $F (x, 0, 0, t, w)$
is irreducible. Hence, the curve
$F (x, 0, 0, t, w)$
is irreducible. Hence, the curve
is irreducible and reduced. It is also obvious that
![]() $\deg \Gamma = 3/4$
and
$\deg \Gamma = 3/4$
and
![]() $\Gamma $
is smooth at
$\Gamma $
is smooth at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
If
![]() $\gamma \ne 0$
, then we have
$\gamma \ne 0$
, then we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
by Claim 26 and Lemma 3.17.
$\alpha _{\mathsf {p}} (X) \ge 1$
by Claim 26 and Lemma 3.17.
In the following, we consider the case where
![]() $\gamma = 0$
. We set
$\gamma = 0$
. We set
which is a quasi-line of degree
![]() $1/4$
passing through
$1/4$
passing through
![]() $\mathsf {p}$
. Note that
$\mathsf {p}$
. Note that
![]() $\Delta $
is smooth at
$\Delta $
is smooth at
![]() $\mathsf {p}$
.
$\mathsf {p}$
.
Claim 27. If
![]() $\gamma = 0$
and
$\gamma = 0$
and
![]() $\beta \ne 0$
, then
$\beta \ne 0$
, then
![]() $T|_S = \Delta + \Xi $
, where
$T|_S = \Delta + \Xi $
, where
![]() $\Xi $
is an irreducible and reduced curve which does not pass through
$\Xi $
is an irreducible and reduced curve which does not pass through
![]() $\mathsf {p}$
. Moreover, the intersection matrix
$\mathsf {p}$
. Moreover, the intersection matrix
![]() $M (\Delta , \Xi )$
satisfies the condition
$M (\Delta , \Xi )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 27.
We have
and the polynomial
![]() $x^6 + \alpha x^3 t + \beta x^2 w + t^2$
is irreducible since
$x^6 + \alpha x^3 t + \beta x^2 w + t^2$
is irreducible since
![]() $\beta \ne 0$
. It follows that
$\beta \ne 0$
. It follows that
![]() $T|_S = \Delta + \Xi $
, where
$T|_S = \Delta + \Xi $
, where
is an irreducible and reduced curve of degree
![]() $1/2$
that does not pass through
$1/2$
that does not pass through
![]() $\mathsf {p}$
. We have
$\mathsf {p}$
. We have
![]() $\Delta \cap \Xi = \{\mathsf {p}_w, \mathsf {q}\}$
, where
$\Delta \cap \Xi = \{\mathsf {p}_w, \mathsf {q}\}$
, where
![]() $\mathsf {q} = (1\!:\!0\!:\!0\!:\!0\!:\!-1/\beta )$
. It is easy to see that S is quasi-smooth at
$\mathsf {q} = (1\!:\!0\!:\!0\!:\!0\!:\!-1/\beta )$
. It is easy to see that S is quasi-smooth at
![]() $\mathsf {p}_w$
and
$\mathsf {p}_w$
and
![]() $\mathsf {q}$
, hence S is quasi-smooth along
$\mathsf {q}$
, hence S is quasi-smooth along
![]() $\Delta $
by Lemma 3.9. We have
$\Delta $
by Lemma 3.9. We have
![]() $\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_w\}$
and
$\operatorname {Sing}_{\Gamma } (S) = \{\mathsf {p}_w\}$
and
![]() $\mathsf {p}_w \in S$
is of type
$\mathsf {p}_w \in S$
is of type
![]() $\frac {1}{4} (1, 3)$
. By Remark 3.10, we have
$\frac {1}{4} (1, 3)$
. By Remark 3.10, we have
By taking intersection number of
![]() $T|_S = \Delta + \Xi $
and
$T|_S = \Delta + \Xi $
and
![]() $\Delta $
and then
$\Delta $
and then
![]() $T|_S$
and
$T|_S$
and
![]() $\Xi $
, we have
$\Xi $
, we have
It follows that the intersection matrix
![]() $M (\Delta , \Xi )$
satisfies the condition
$M (\Delta , \Xi )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Claim 28. If
![]() $\gamma = \beta = 0$
and
$\gamma = \beta = 0$
and
![]() $\alpha \ne \pm 2$
, then
$\alpha \ne \pm 2$
, then
![]() $T|_S = \Delta + \Theta _1 + \Theta _2$
, where
$T|_S = \Delta + \Theta _1 + \Theta _2$
, where
![]() $\Theta _1$
and
$\Theta _1$
and
![]() $\Theta _2$
are distinct quasi-lines which does not pass through
$\Theta _2$
are distinct quasi-lines which does not pass through
![]() $\mathsf {p}$
. Moreover, the intersection matrix
$\mathsf {p}$
. Moreover, the intersection matrix
![]() $M (\Delta , \Theta _1, \Theta _2)$
satisfies the condition
$M (\Delta , \Theta _1, \Theta _2)$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 28.
We have
where
![]() $\lambda \ne 0, 1$
is a complex number such that
$\lambda \ne 0, 1$
is a complex number such that
![]() $\alpha = \lambda + \lambda ^{-1}$
. Hence, we have
$\alpha = \lambda + \lambda ^{-1}$
. Hence, we have
where
are both quasi-lines of degree
![]() $1/4$
that do not pass through
$1/4$
that do not pass through
![]() $\mathsf {p}$
. We have
$\mathsf {p}$
. We have
![]() $\Delta \cap (\Theta _1 \cup \Theta _2) = \{\mathsf {p}_w\}$
and S is clearly quasi-smooth at
$\Delta \cap (\Theta _1 \cup \Theta _2) = \{\mathsf {p}_w\}$
and S is clearly quasi-smooth at
![]() $\mathsf {p}_w$
. It follows that S is quasi-smooth along
$\mathsf {p}_w$
. It follows that S is quasi-smooth along
![]() $\Gamma $
by Lemma 3.9, and
$\Gamma $
by Lemma 3.9, and
![]() $\operatorname {Sing}_{\Delta } (S) = \{\mathsf {p}_w\}$
, where
$\operatorname {Sing}_{\Delta } (S) = \{\mathsf {p}_w\}$
, where
![]() $\mathsf {p}_w \in S$
is of type
$\mathsf {p}_w \in S$
is of type
![]() $\frac {1}{4} (1, 3)$
. Thus, we have
$\frac {1}{4} (1, 3)$
. Thus, we have
By similar arguments, we see that S is quasi-smooth along
![]() $\Theta _i$
and
$\Theta _i$
and
![]() $\operatorname {Sing}_{\Theta } (S) = \{\mathsf {p}_w\}$
for
$\operatorname {Sing}_{\Theta } (S) = \{\mathsf {p}_w\}$
for
![]() $i = 1, 2$
, and hence
$i = 1, 2$
, and hence
By taking intersection number of
![]() $T|_S = \Delta + \Theta _1 + \Theta _2$
and
$T|_S = \Delta + \Theta _1 + \Theta _2$
and
![]() $\Delta , \Theta _1, \Theta _2$
, we conclude
$\Delta , \Theta _1, \Theta _2$
, we conclude
It is then straightforward to see that
![]() $M (\Delta , \Theta _1, \Theta _2)$
satisfies the condition
$M (\Delta , \Theta _1, \Theta _2)$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Claim 29. If
![]() $\gamma = \beta = 0$
and
$\gamma = \beta = 0$
and
![]() $\alpha = \pm 2$
, then
$\alpha = \pm 2$
, then
![]() $T|_S = \Delta + 2 \Theta $
, where
$T|_S = \Delta + 2 \Theta $
, where
![]() $\Theta $
is an irreducible and reduced curve which does not pass through
$\Theta $
is an irreducible and reduced curve which does not pass through
![]() $\mathsf {p}$
. Moreover, the intersection matrix
$\mathsf {p}$
. Moreover, the intersection matrix
![]() $M (\Delta , \Theta )$
satisfies the condition
$M (\Delta , \Theta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
Proof of Claim 29.
Without loss of generality, we may assume
![]() $\alpha = -2$
. We have
$\alpha = -2$
. We have
and hence
where
is a quasi-line of degree
![]() $1/4$
that does not pass through
$1/4$
that does not pass through
![]() $\mathsf {p}$
. By the same arguments as in Claim 28, we have
$\mathsf {p}$
. By the same arguments as in Claim 28, we have
Then, by taking intersection number of
![]() $T|_S = \Delta + 2 \Theta $
and
$T|_S = \Delta + 2 \Theta $
and
![]() $\Delta , \Theta $
, we have
$\Delta , \Theta $
, we have
Thus, the matrix
![]() $M (\Delta , \Theta )$
satisfies the condition
$M (\Delta , \Theta )$
satisfies the condition
![]() $(\star )$
.
$(\star )$
.
By Claims 27, 28, 29 and Lemma 3.21, we conclude
 $$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{(A^3) + 1 - \deg \Delta} \right\} = \frac{2}{3}. \end{align*}$$
$$\begin{align*}\alpha_{\mathsf{p}} (X) \ge \min \left\{ 1, \ \frac{1}{(A^3) + 1 - \deg \Delta} \right\} = \frac{2}{3}. \end{align*}$$
6.5.a.3 Case:
 $x^5 w, x^6 t \notin F$
$x^5 w, x^6 t \notin F$
Replacing y and z, we can write
where
![]() $f_i = f_i (y,z,t,w)$
is a homogeneous polynomial of degree i with
$f_i = f_i (y,z,t,w)$
is a homogeneous polynomial of degree i with
![]() $w \notin f_4$
and
$w \notin f_4$
and
![]() $t \notin f_3$
. Note that we have
$t \notin f_3$
. Note that we have
![]() $2 \le \operatorname {mult}_{\mathsf {p}} (H_y) \le 3$
since
$2 \le \operatorname {mult}_{\mathsf {p}} (H_y) \le 3$
since
![]() $t^3 \in F$
.
$t^3 \in F$
.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_y$
. We can take a
$H_y$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |4 A|_{\mathbb {Q}}$
such that
$T \in |4 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {mult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_y$
since
$D \cdot H_y$
since
![]() $\{y, z, t, w\}$
isolates
$\{y, z, t, w\}$
isolates
![]() $\mathsf {p}$
. Then
$\mathsf {p}$
. Then
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 2/3$
and thus it remains to show that
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 2/3$
and thus it remains to show that
![]() $\operatorname {lct} (X; H_y) \ge 1/2$
.
$\operatorname {lct} (X; H_y) \ge 1/2$
.
Suppose that either
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) = 2$
or
$\operatorname {mult}_{\mathsf {p}} (H_y) = 2$
or
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) = 3$
, and the cubic part of
$\operatorname {mult}_{\mathsf {p}} (H_y) = 3$
, and the cubic part of
![]() $\bar {F} := F (1,0,z,t,w)$
is a cube of a linear form. Then
$\bar {F} := F (1,0,z,t,w)$
is a cube of a linear form. Then
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
by Lemma 3.28, and we are done.
$\operatorname {lct}_{\mathsf {p}} (X;H_y) \ge 1/2$
by Lemma 3.28, and we are done.
In the following, we assume that
![]() $\operatorname {mult}_{\mathsf {p}} (H_y) = 3$
and the cubic part of
$\operatorname {mult}_{\mathsf {p}} (H_y) = 3$
and the cubic part of
![]() $\bar {F}$
is a cube of a linear form. Since
$\bar {F}$
is a cube of a linear form. Since
![]() $t^3 \in \bar {F}$
and
$t^3 \in \bar {F}$
and
![]() $w^3 \notin \bar {F}$
, we may assume that the cubic part of
$w^3 \notin \bar {F}$
, we may assume that the cubic part of
![]() $\bar {F}$
is
$\bar {F}$
is
![]() $t^3$
after replacing t.
$t^3$
after replacing t.
We claim
![]() $w^2 z \in F$
. We see that a monomial other than
$w^2 z \in F$
. We see that a monomial other than
![]() $w^2 z$
which appears in
$w^2 z$
which appears in
![]() $\bar {F}$
with nonzero coefficient is contained in the ideal
$\bar {F}$
with nonzero coefficient is contained in the ideal
![]() $(z, t)^2 \subset \mathbb {C} [z, t, w]$
. We can write
$(z, t)^2 \subset \mathbb {C} [z, t, w]$
. We can write
![]() $F = y G + F (x, 0, z, t, w)$
for some homogeneous polynomial
$F = y G + F (x, 0, z, t, w)$
for some homogeneous polynomial
![]() $G (x, y, z, t, w)$
. If
$G (x, y, z, t, w)$
. If
![]() $w^2 z \notin F$
, then
$w^2 z \notin F$
, then
![]() $F (x, 0, z, t, w) \in (z, t)^2$
and X is not quasi-smooth at any point contained in the nonempty set
$F (x, 0, z, t, w) \in (z, t)^2$
and X is not quasi-smooth at any point contained in the nonempty set
This is a contradiction and the claim is proved.
Then we may assume
![]() $\operatorname {coeff}_F (w^2 z) = 1$
and, by replacing t and w, we can write
$\operatorname {coeff}_F (w^2 z) = 1$
and, by replacing t and w, we can write
 $$ \begin{align*} \bar{F} = \alpha_4 z^4 & + \alpha_5 z^5 + (\beta t z^3 + \alpha_6 z^6) + (\gamma w z^3 + \delta t z^4 + \alpha_7 z^7) + \\ + & (\varepsilon w z^4 + \zeta t^2 z^2 + \eta t z^5 + \alpha_8 z^8) + (w^2 z + t^3 + \theta t^2 z^3 + \lambda t z^6 + \alpha_9 z^9), \end{align*} $$
$$ \begin{align*} \bar{F} = \alpha_4 z^4 & + \alpha_5 z^5 + (\beta t z^3 + \alpha_6 z^6) + (\gamma w z^3 + \delta t z^4 + \alpha_7 z^7) + \\ + & (\varepsilon w z^4 + \zeta t^2 z^2 + \eta t z^5 + \alpha_8 z^8) + (w^2 z + t^3 + \theta t^2 z^3 + \lambda t z^6 + \alpha_9 z^9), \end{align*} $$
where
![]() $\alpha _4, \dots , \alpha _9, \beta , \gamma , \dots , \lambda \in \mathbb {C}$
. The lowest weight part of
$\alpha _4, \dots , \alpha _9, \beta , \gamma , \dots , \lambda \in \mathbb {C}$
. The lowest weight part of
![]() $\bar {F}$
with respect to
$\bar {F}$
with respect to
![]() $\operatorname {wt} (z,t,w) = (6,8,9)$
is
$\operatorname {wt} (z,t,w) = (6,8,9)$
is
![]() $G := \alpha _4 z^4 + w^2 z + t^3$
. We set
$G := \alpha _4 z^4 + w^2 z + t^3$
. We set
![]() $\mathbb {P} = \mathbb {P} (6, 8, 9)$
. Then
$\mathbb {P} = \mathbb {P} (6, 8, 9)$
. Then
![]() $\mathbb {P}^{\operatorname {wf}} = \mathbb {P} (1, 4, 3)_{\tilde {z}, \tilde {t}, \tilde {w}}$
and, by Lemma 3.27, we have
$\mathbb {P}^{\operatorname {wf}} = \mathbb {P} (1, 4, 3)_{\tilde {z}, \tilde {t}, \tilde {w}}$
and, by Lemma 3.27, we have
 $$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_y) \ge \min \left\{ \frac{23}{24}, \ \operatorname{lct} (\mathbb{P}^{\operatorname{wf}}, \operatorname{Diff}; \Gamma) \right\}, \end{align*}$$
$$\begin{align*}\operatorname{lct}_{\mathsf{p}} (X; H_y) \ge \min \left\{ \frac{23}{24}, \ \operatorname{lct} (\mathbb{P}^{\operatorname{wf}}, \operatorname{Diff}; \Gamma) \right\}, \end{align*}$$
where
 $$ \begin{align*} \operatorname{Diff} &= \frac{2}{3} H^{\operatorname{wf}}_{\tilde{t}} + \frac{1}{2} H^{\operatorname{wf}}_{\tilde{w}}, \\ \Gamma &= \mathcal{D}^{\operatorname{wf}}_G = (\alpha_4 \tilde{z}^4 + \tilde{w} \tilde{z} + \tilde{t} = 0) \subset \mathbb{P} (1, 4, 3), \end{align*} $$
$$ \begin{align*} \operatorname{Diff} &= \frac{2}{3} H^{\operatorname{wf}}_{\tilde{t}} + \frac{1}{2} H^{\operatorname{wf}}_{\tilde{w}}, \\ \Gamma &= \mathcal{D}^{\operatorname{wf}}_G = (\alpha_4 \tilde{z}^4 + \tilde{w} \tilde{z} + \tilde{t} = 0) \subset \mathbb{P} (1, 4, 3), \end{align*} $$
are
![]() $(\mathbb {Q}$
-)divisors on
$(\mathbb {Q}$
-)divisors on
![]() $\mathbb {P}^{\operatorname {wf}}$
with
$\mathbb {P}^{\operatorname {wf}}$
with
![]() $H^{\operatorname {wf}}_{\tilde {t}} = (\tilde {t} = 0)$
and
$H^{\operatorname {wf}}_{\tilde {t}} = (\tilde {t} = 0)$
and
![]() $H^{\operatorname {wf}}_{\tilde {w}} = (\tilde {w} = 0)$
. It is easy to see that any pair of curves
$H^{\operatorname {wf}}_{\tilde {w}} = (\tilde {w} = 0)$
. It is easy to see that any pair of curves
![]() $H^{\operatorname {wf}}_{\tilde {t}}, H^{\operatorname {wf}}_{\tilde {w}}$
and
$H^{\operatorname {wf}}_{\tilde {t}}, H^{\operatorname {wf}}_{\tilde {w}}$
and
![]() $\Gamma $
intersect transversally. If
$\Gamma $
intersect transversally. If
![]() $\alpha _4 \ne 0$
, then
$\alpha _4 \ne 0$
, then
![]() $H^{\operatorname {wf}}_{\tilde {t}} \cap H^{\operatorname {wf}}_{\tilde {w}} \cap \Gamma = \emptyset $
, and thus
$H^{\operatorname {wf}}_{\tilde {t}} \cap H^{\operatorname {wf}}_{\tilde {w}} \cap \Gamma = \emptyset $
, and thus
![]() $\operatorname {lct} (\mathbb {P}^{\operatorname {wf}}, \operatorname {Diff}; \Gamma ) = 1$
. If
$\operatorname {lct} (\mathbb {P}^{\operatorname {wf}}, \operatorname {Diff}; \Gamma ) = 1$
. If
![]() $\alpha _4 = 0$
, then
$\alpha _4 = 0$
, then
![]() $H^{\operatorname {wf}}_{\tilde {t}} \cap H^{\operatorname {wf}}_{\tilde {w}} \cap \Gamma = \{\mathsf {p}_{\tilde {z}}\}$
. In this case, by consider the the blowup at
$H^{\operatorname {wf}}_{\tilde {t}} \cap H^{\operatorname {wf}}_{\tilde {w}} \cap \Gamma = \{\mathsf {p}_{\tilde {z}}\}$
. In this case, by consider the the blowup at
![]() $\mathsf {p}_{\tilde {z}}$
, we can confirm the equality
$\mathsf {p}_{\tilde {z}}$
, we can confirm the equality
![]() $\operatorname {lct} (\mathbb {P}^{\operatorname {wf}}, \operatorname {Diff}; \Gamma ) = 5/6$
. Thus, we have
$\operatorname {lct} (\mathbb {P}^{\operatorname {wf}}, \operatorname {Diff}; \Gamma ) = 5/6$
. Thus, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_y) \ge 5/6$
, and the proof is completed.
$\operatorname {lct}_{\mathsf {p}} (X; H_y) \ge 5/6$
, and the proof is completed.
6.5.b The singular point of type
 $\frac {1}{4} (1,1,3)$
$\frac {1}{4} (1,1,3)$
Let
![]() $\mathsf {p} = \mathsf {p}_w$
be the singular point of type
$\mathsf {p} = \mathsf {p}_w$
be the singular point of type
![]() $\frac {1}{4} (1,1,3)$
. We can write
$\frac {1}{4} (1,1,3)$
. We can write
where
![]() $a_2 = a_2 (y, z)$
,
$a_2 = a_2 (y, z)$
,
![]() $b_5 = b_5 (y, z)$
and
$b_5 = b_5 (y, z)$
and
![]() $f_9 =f_9 (x, y, z, t)$
are homogeneous polynomials of degrees
$f_9 =f_9 (x, y, z, t)$
are homogeneous polynomials of degrees
![]() $2$
,
$2$
,
![]() $5$
and
$5$
and
![]() $9$
, respectively.
$9$
, respectively.
Suppose that
![]() $a_2 \ne 0$
as a polynomial. Then
$a_2 \ne 0$
as a polynomial. Then
![]() $\bar {F} := F (0, y, z, t, 1) \in (y, z, t)^3$
and its cubic part
$\bar {F} := F (0, y, z, t, 1) \in (y, z, t)^3$
and its cubic part
![]() $t a_2 + t^3$
is not a cube of a linear form. It follows that
$t a_2 + t^3$
is not a cube of a linear form. It follows that
![]() $\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 2/3$
by Lemma 3.28. Let
$\operatorname {lct}_{\mathsf {p}} (X;H_x) \ge 2/3$
by Lemma 3.28. Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $H_x$
. Since the set
$H_x$
. Since the set
![]() $\{x, y, z\}$
isolates
$\{x, y, z\}$
isolates
![]() $\mathsf {p}$
, we can take a
$\mathsf {p}$
, we can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |A|_{\mathbb {Q}}$
such that
$T \in |A|_{\mathbb {Q}}$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of
$\operatorname {Supp} (T)$
does not contain any component of
![]() $D \cdot H_x$
. We have
$D \cdot H_x$
. We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 3$
. It follows that
$\operatorname {omult}_{\mathsf {p}} (H_x) = 3$
. It follows that
where
![]() $q = q_{\mathsf {p}}$
is the quotient morphism of
$q = q_{\mathsf {p}}$
is the quotient morphism of
![]() $\mathsf {p} \in X$
and
$\mathsf {p} \in X$
and
![]() $\check {\mathsf {p}}$
is the preimage of
$\check {\mathsf {p}}$
is the preimage of
![]() $\mathsf {p}$
via q. This shows
$\mathsf {p}$
via q. This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
and thus
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
Finally, suppose that
![]() $a_2 {\kern-0.5pt}={\kern-0.5pt} 0$
and
$a_2 {\kern-0.5pt}={\kern-0.5pt} 0$
and
![]() $b_5 {\kern-0.5pt}\ne{\kern-0.5pt} 0$
. Replacing y and z, we may assume
$b_5 {\kern-0.5pt}\ne{\kern-0.5pt} 0$
. Replacing y and z, we may assume
![]() $z^5 {\kern-0.5pt}\in{\kern-0.5pt} b_5$
and
$z^5 {\kern-0.5pt}\in{\kern-0.5pt} b_5$
and
![]() $\operatorname {coeff}_{b_5} (z^5) {\kern-0.5pt}={\kern-0.5pt} 1$
. We may also assume that
$\operatorname {coeff}_{b_5} (z^5) {\kern-0.5pt}={\kern-0.5pt} 1$
. We may also assume that
![]() $\operatorname {coeff}_{f_9} (t^3) = 1$
by rescaling t. Then we have
$\operatorname {coeff}_{f_9} (t^3) = 1$
by rescaling t. Then we have
The lowest weight part with respect to the weight
![]() $\operatorname {wt} (z,t) = (3,5)$
is
$\operatorname {wt} (z,t) = (3,5)$
is
![]() $z^5 + t^3$
and thus
$z^5 + t^3$
and thus
We have
![]() $\operatorname {omult}_{\mathsf {p}} (H_x) = 3$
and the set
$\operatorname {omult}_{\mathsf {p}} (H_x) = 3$
and the set
![]() $\{x, y, z\}$
isolates
$\{x, y, z\}$
isolates
![]() $\mathsf {p}$
. Hence, by the same argument as in the the case
$\mathsf {p}$
. Hence, by the same argument as in the the case
![]() $a_2 \ne 0$
, we have
$a_2 \ne 0$
, we have
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
for any irreducible
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
for any irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
other than
$D \in |A|_{\mathbb {Q}}$
other than
![]() $H_x$
. Thus,
$H_x$
. Thus,
![]() $\alpha _{\mathsf {p}} (X) \ge 1/2$
.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
.
Suppose that
![]() $a_2 = b_5 = 0$
. Then we have
$a_2 = b_5 = 0$
. Then we have
![]() $\alpha _{\mathsf {p}} (X) = 5/9$
by Proposition 5.16, and the proof is completed.
$\alpha _{\mathsf {p}} (X) = 5/9$
by Proposition 5.16, and the proof is completed.
Remark 6.2. The singular point
![]() $\mathsf {p} \in X$
of type
$\mathsf {p} \in X$
of type
![]() $\frac {1}{4} (1, 1, 3)$
is a QI center. When
$\frac {1}{4} (1, 1, 3)$
is a QI center. When
![]() $\mathsf {p}$
is nondegenerate, the above proof shows that
$\mathsf {p}$
is nondegenerate, the above proof shows that
![]() $\operatorname {lct}_{\mathsf {p}} (X; D) \ge 1$
for any irreducible
$\operatorname {lct}_{\mathsf {p}} (X; D) \ge 1$
for any irreducible
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \in |A|_{\mathbb {Q}}$
other than
$D \in |A|_{\mathbb {Q}}$
other than
![]() $H_x$
and
$H_x$
and
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x)> 1/2$
.
$\operatorname {lct}_{\mathsf {p}} (X; H_x)> 1/2$
.
7 Further results and discussion on related problems
7.1 Birationally superrigid Fano
 $3$
-folds of higher codimensions
$3$
-folds of higher codimensions
We can embed a Fano 3-fold into a weighted projective space by choosing (minimal) generators of the anticanonical graded ring. We consider embedded Fano 3-folds. We have satisfactory results on the classification of Fano 3-folds of low codimensions ([Reference Iano-FletcherIF00], [Reference Chen, Chen and ChenCCC11], [Reference Altınok, Brown and ReidABR02]), and the following are known for their birational (super)rigidity.
-
• Fano 3-folds of codimension
 $2$
are all weighted complete intersections and they consist of 85 families. Among them, there are exactly
$2$
are all weighted complete intersections and they consist of 85 families. Among them, there are exactly
 $19$
families whose members are birationally rigid ([Reference OkadaOka14], [Reference Ahmadinezhad and ZucconiAZ16]).
$19$
families whose members are birationally rigid ([Reference OkadaOka14], [Reference Ahmadinezhad and ZucconiAZ16]). -
• Fano 3-folds of codimension
 $3$
consist of 69 families of so-called Pfaffian Fano 3-folds and one family of complete intersections of three quadrics in
$3$
consist of 69 families of so-called Pfaffian Fano 3-folds and one family of complete intersections of three quadrics in
 $\mathbb {P}^6$
. Among them, there are exactly three families whose members are birationally rigid ([Reference Ahmadinezhad and OkadaAO18]).
$\mathbb {P}^6$
. Among them, there are exactly three families whose members are birationally rigid ([Reference Ahmadinezhad and OkadaAO18]). -
• Constructions of many families of Fano 3-folds of codimension 4 has been known (see, e.g., [Reference Brown, Kerber and ReidBKR12], [Reference Coughlan and DucatCD18]), but their classification is not completed. There are at least two families of birationally superrigid Fano 3-folds of codimension 4 ([Reference OkadaOka20a]).
For birationally rigid Fano 3-folds of codimension 2 and 3, K-stability and existence of KE metrics are known under some generality assumptions.
Theorem 7.1 [Reference Kim, Okada and WonKOW18].
Let X be a general quasi-smooth Fano 3-folds of codimension
![]() $c \in \{2, 3\}$
which is birationally rigid. We assume that X is a complete intersection of a quadric and cubic in
$c \in \{2, 3\}$
which is birationally rigid. We assume that X is a complete intersection of a quadric and cubic in
![]() $\mathbb {P}^5$
when
$\mathbb {P}^5$
when
![]() $c = 2$
. Then
$c = 2$
. Then
![]() $\alpha (X) \ge 1$
, X is K-stable and admits a KE metric.
$\alpha (X) \ge 1$
, X is K-stable and admits a KE metric.
Theorem 7.2 [Reference ZhuangZhu20b, Theorem 1.3].
Let X be a smooth complete intersection of a quadric and cubic in
![]() $\mathbb {P}^5$
. Then X is K-stable and admits a KE metric.
$\mathbb {P}^5$
. Then X is K-stable and admits a KE metric.
Question 7.3. Can we conclude K-stability for any quasi-smooth Fano 3-fold of codimension 2 and 3 which is birationally (super)rigid? How about for Fano 3-folds of codimension 4 or higher?
7.2 Lower bound of alpha invariants
In the context of Theorem 1.6, the following is a very natural question to ask.
Question 7.4. Is it true that
![]() $\alpha (X) \ge 1/2$
(or
$\alpha (X) \ge 1/2$
(or
![]() $\alpha (X)> 1/2$
) for any birationally superrigid Fano variety? If yes, can we find a lower bound better than
$\alpha (X)> 1/2$
) for any birationally superrigid Fano variety? If yes, can we find a lower bound better than
![]() $1/2$
?
$1/2$
?
The following example suggests that the number
![]() $1/2$
is optimal (or the lower bound can be even smaller).
$1/2$
is optimal (or the lower bound can be even smaller).
Example 7.5. For an integer
![]() $a \ge 2$
, let
$a \ge 2$
, let
![]() $X_a$
be a weighted hypersurfaces of degree
$X_a$
be a weighted hypersurfaces of degree
![]() $2 a + 1$
in
$2 a + 1$
in
![]() $\mathbb {P} (1^{a+2}, a) = \operatorname {Proj} \mathbb {C} [x_1,\dots ,x_{a+2},y]$
, given by the equation
$\mathbb {P} (1^{a+2}, a) = \operatorname {Proj} \mathbb {C} [x_1,\dots ,x_{a+2},y]$
, given by the equation
where f is a general homogeneous polynomial of degree
![]() $2 a + 1$
. Then
$2 a + 1$
. Then
![]() $X_a$
is a quasi-smooth Fano weighted hypersurface of dimension
$X_a$
is a quasi-smooth Fano weighted hypersurface of dimension
![]() $a+1$
and Picard number
$a+1$
and Picard number
![]() $1$
with the unique singular point
$1$
with the unique singular point
![]() $\mathsf {p}$
of type
$\mathsf {p}$
of type
 $$\begin{align*}\frac{1}{a} (\overbrace{1,\dots,1}^{a+1}). \end{align*}$$
$$\begin{align*}\frac{1}{a} (\overbrace{1,\dots,1}^{a+1}). \end{align*}$$
The singularity
![]() $\mathsf {p} \in X$
is terminal. By the same argument as in the proof of Proposition 5.16, we obtain
$\mathsf {p} \in X$
is terminal. By the same argument as in the proof of Proposition 5.16, we obtain
When
![]() $a = 2$
,
$a = 2$
,
![]() $X_a = X_2$
is a member of the family
$X_a = X_2$
is a member of the family
![]() $\mathcal {F}_2$
and it is birationally superrigid. We expect that
$\mathcal {F}_2$
and it is birationally superrigid. We expect that
![]() $X_a$
is birationally superrigid, although this is not proved at all when
$X_a$
is birationally superrigid, although this is not proved at all when
![]() $a \ge 3$
. If
$a \ge 3$
. If
![]() $X_a$
is birationally superrigid for
$X_a$
is birationally superrigid for
![]() $a \gg 0$
, then it follows that there exists a sequence of birationally superrigid Fano varieties whose alpha invariants are arbitrary close to (or less than)
$a \gg 0$
, then it follows that there exists a sequence of birationally superrigid Fano varieties whose alpha invariants are arbitrary close to (or less than)
![]() $\frac {1}{2}$
.
$\frac {1}{2}$
.
Question 7.6. Let
![]() $X_a$
be as in Example 7.5. Is
$X_a$
be as in Example 7.5. Is
![]() $X_a$
birationally superrigid for
$X_a$
birationally superrigid for
![]() $a \ge 3$
?
$a \ge 3$
?
7.3 Existence of KE metrics
For a quasi-smooth Fano 3-fold weighted hypersurface of index
![]() $1$
which is strictly birationally rigid, we are unable to conclude the existence of a KE metric as a direct consequence of Theorem 1.8. However, for a Fano variety X of dimension n with only quotient singularities, the implication
$1$
which is strictly birationally rigid, we are unable to conclude the existence of a KE metric as a direct consequence of Theorem 1.8. However, for a Fano variety X of dimension n with only quotient singularities, the implication
is proved in [Reference Demailly and KollárDK01, Section 6]. The aim of this section is to prove the existence of KE metrics on quasi-smooth members of suitable families.
We set
and
Note that
![]() $|\mathsf {I}_{\mathrm {KE}}| = 56$
. For a family
$|\mathsf {I}_{\mathrm {KE}}| = 56$
. For a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}$
, the mark ‘KE’ is given in the right-most column of Table 7 if and only if
$\mathsf {i} \in \mathsf {I}$
, the mark ‘KE’ is given in the right-most column of Table 7 if and only if
![]() $\mathsf {i} \in \mathsf {I}_{\mathrm {KE}}$
.
$\mathsf {i} \in \mathsf {I}_{\mathrm {KE}}$
.
Theorem 7.7. For a member X of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {KE}}$
, we have
$\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {KE}}$
, we have
In particular, any member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {I}_{\mathrm {KE}}$
admits a KE metric and is K-stable.
$\mathsf {I}_{\mathrm {KE}}$
admits a KE metric and is K-stable.
Proof. By Corollary 1.9 and the above arguments, it is enough to prove the first assertion. Let
be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {KE}}$
, where we assume
$\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {KE}}$
, where we assume
![]() $a_1 \le a_2 \le a_3 \le a_4$
. Note that
$a_1 \le a_2 \le a_3 \le a_4$
. Note that
![]() $1 < a_1 < a_2$
.
$1 < a_1 < a_2$
.
Claim 30.
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
![]() $\mathsf {p} \in U_1 \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in U_1 \cap \operatorname {Sm} (X)$
.
Proof of Claim 30.
Let
![]() $\mathsf {p}$
be a smooth point of X contained in
$\mathsf {p}$
be a smooth point of X contained in
![]() $U_1$
.
$U_1$
.
Suppose
![]() $\mathsf {i} = 42$
. Then
$\mathsf {i} = 42$
. Then
![]() $d = 20$
is divisible by
$d = 20$
is divisible by
![]() $a_4 = 10$
and
$a_4 = 10$
and
![]() $a_2 a_3 (A^3) = 1$
. By Lemma 4.3, we have
$a_2 a_3 (A^3) = 1$
. By Lemma 4.3, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha _{\mathsf {p}} (X) \ge 1$
.
Suppose
![]() $\mathsf {i} \in \{ 69, 74, 76, 79 \}$
. Then
$\mathsf {i} \in \{ 69, 74, 76, 79 \}$
. Then
![]() $a_2 a_4 (A^3) \le 1$
. By Lemma 4.2, we have
$a_2 a_4 (A^3) \le 1$
. By Lemma 4.2, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
in this case.
$\alpha _{\mathsf {p}} (X) \ge 1$
in this case.
Suppose
![]() $\mathsf {i} \in \{44, 45, 61\}$
. Then
$\mathsf {i} \in \{44, 45, 61\}$
. Then
![]() $a_3 a_4 (A^3) \le 2$
. We may assume
$a_3 a_4 (A^3) \le 2$
. We may assume
![]() $\mathsf {p} = \mathsf {p}_x$
. Then we have
$\mathsf {p} = \mathsf {p}_x$
. Then we have
![]() $\alpha _{\mathsf {p}} (X) \ge 2/a_3 a_4 (A^3) \ge 1$
by Lemma 3.29. This completes the proof.
$\alpha _{\mathsf {p}} (X) \ge 2/a_3 a_4 (A^3) \ge 1$
by Lemma 3.29. This completes the proof.
Claim 31.
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
![]() $\mathsf {p} \in (H_x \setminus L_{xy}) \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in (H_x \setminus L_{xy}) \cap \operatorname {Sm} (X)$
.
Claim 32.
![]() $\alpha _{\mathsf {p}} (X) \ge 43/54> 3/4$
for any
$\alpha _{\mathsf {p}} (X) \ge 43/54> 3/4$
for any
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
.
Proof of Claim 32.
Let
![]() $\mathsf {p}$
be a smooth point of X contained in
$\mathsf {p}$
be a smooth point of X contained in
![]() $L_{xy}$
. Suppose that X is a member of one of the families listed in Tables 1 or 2, that is, X is a member of a family
$L_{xy}$
. Suppose that X is a member of one of the families listed in Tables 1 or 2, that is, X is a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \{44, 45, 61, 69, 74, 76, 79\}$
. Then the claim follows immediately from Proposition 4.10.
$\mathsf {i} \in \{44, 45, 61, 69, 74, 76, 79\}$
. Then the claim follows immediately from Proposition 4.10.
Suppose
![]() $\mathsf {i} = 42$
. Then, by the proof of Proposition 4.11 (see Section 4.4.b), either
$\mathsf {i} = 42$
. Then, by the proof of Proposition 4.11 (see Section 4.4.b), either
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
for any
$\alpha _{\mathsf {p}} (X) \ge 1$
for any
![]() $\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
or X satisfies the assumption of Lemma 4.14. In the latter case, we have
$\mathsf {p} \in L_{xy} \cap \operatorname {Sm} (X)$
or X satisfies the assumption of Lemma 4.14. In the latter case, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 43/54$
by Remark 4.15. This completes the proof.
$\alpha _{\mathsf {p}} (X) \ge 43/54$
by Remark 4.15. This completes the proof.
By Claims 30, 31 and 32, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 3/4$
for any smooth point
$\alpha _{\mathsf {p}} (X) \ge 3/4$
for any smooth point
![]() $\mathsf {p} \in X$
. It remains to consider singular points.
$\mathsf {p} \in X$
. It remains to consider singular points.
Claim 33.
![]() $\alpha _{\mathsf {p}} (X)> 3/4$
for any
$\alpha _{\mathsf {p}} (X)> 3/4$
for any
![]() $\mathsf {p} \in \operatorname {Sing} (X)$
.
$\mathsf {p} \in \operatorname {Sing} (X)$
.
Proof of Claim 33.
Let
![]() $\mathsf {p} \in X$
be a singular point. If the subscript
$\mathsf {p} \in X$
be a singular point. If the subscript
![]() $\heartsuit $
(resp.
$\heartsuit $
(resp.
![]() $\diamondsuit $
) is given in Table 7, then
$\diamondsuit $
) is given in Table 7, then
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
by Proposition 5.2 (resp. Proposition 5.3). It remains to consider the case where
$\alpha _{\mathsf {p}} (X) \ge 1$
by Proposition 5.2 (resp. Proposition 5.3). It remains to consider the case where
![]() $\mathsf {i} = 42$
and
$\mathsf {i} = 42$
and
![]() $\mathsf {p}$
is of type
$\mathsf {p}$
is of type
![]() $\frac {1}{5} (1, 2, 3)$
. In this case, we have
$\frac {1}{5} (1, 2, 3)$
. In this case, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
by the proof of Proposition 5.18 (see Section 5.6.c).
$\alpha _{\mathsf {p}} (X) \ge 1$
by the proof of Proposition 5.18 (see Section 5.6.c).
This completes the proof of Theorem 7.7.
7.4 Birational rigidity and K-stability
7.4.a Generalizations of the conjecture
Birational superrigidity is a very strong property. It is natural to relax the assumption of birational superrigidity to birational rigidity in Conjecture 1.1, and we still expect a positive answer to the following.
Conjecture 7.8 [Reference Kim, Okada and WonKOW18, Conjecture 1.9].
A birationally rigid Fano variety is K-stable.
We explain the situation for smooth Fano 3-folds. There are exactly two families of smooth Fano 3-folds which is strictly birationally rigid: One is the family of complete intersections of a quadric and cubic in
![]() $\mathbb {P}^6$
([Reference Iskovskikh and PukhlikovIP96]), and another is the family of double covers V of a smooth quadric Q of dimension 3 branched along a smooth surface degree
$\mathbb {P}^6$
([Reference Iskovskikh and PukhlikovIP96]), and another is the family of double covers V of a smooth quadric Q of dimension 3 branched along a smooth surface degree
![]() $8$
on Q ([Reference IskovskikhIsk80]). Former Fano 3-folds are K-stable and admit KE metrics ([Reference ZhuangZhu20b]), and so are the latter Fano 3-folds (this follows from [Reference DervanDer16a] since Q is K-semistable). More evidence is already provided by Theorems 1.2 and 7.1, and we will provide further evidences in the next subsection (see Corollary 7.13).
$8$
on Q ([Reference IskovskikhIsk80]). Former Fano 3-folds are K-stable and admit KE metrics ([Reference ZhuangZhu20b]), and so are the latter Fano 3-folds (this follows from [Reference DervanDer16a] since Q is K-semistable). More evidence is already provided by Theorems 1.2 and 7.1, and we will provide further evidences in the next subsection (see Corollary 7.13).
It may be interesting to consider further generalization of Conjecture 7.8. According to systematic studies of Fano 3-folds of codimension 2 [Reference OkadaOka14; Reference OkadaOka18; Reference OkadaOka20b], existence of many birationally birigid Fano 3-folds are verified. Here, a Fano variety X of Picard number
![]() $1$
is birationally birigid if there exists a Fano variety
$1$
is birationally birigid if there exists a Fano variety
![]() $X'$
of Picard number
$X'$
of Picard number
![]() $1$
which is birational but not isomorphic to X, and up to isomorphism
$1$
which is birational but not isomorphic to X, and up to isomorphism
![]() $\{X, X'\}$
is all the Mori fiber space in the birational equivalence class of X. Extending the birigidity, tririgidity and so on notion of solid Fano variety is introduced in [Reference Ahmadinezhad and OkadaAO18]: A Fano variety of Picard number
$\{X, X'\}$
is all the Mori fiber space in the birational equivalence class of X. Extending the birigidity, tririgidity and so on notion of solid Fano variety is introduced in [Reference Ahmadinezhad and OkadaAO18]: A Fano variety of Picard number
![]() $1$
is solid if any Mori fiber space in the birational equivalence class is a Fano variety of Picard number
$1$
is solid if any Mori fiber space in the birational equivalence class is a Fano variety of Picard number
![]() $1$
. Solid Fano varieties are expected to behave nicely in moduli ([Reference ZhuangZhu20a]). Only some evidence is known ([Reference Kim, Okada and WonKOW19]) for the following question.
$1$
. Solid Fano varieties are expected to behave nicely in moduli ([Reference ZhuangZhu20a]). Only some evidence is known ([Reference Kim, Okada and WonKOW19]) for the following question.
Question 7.9. Is it true that any solid Fano variety is K-stable?
7.4.b On K-stability for 95 families
For strictly birationally rigid members of the 95 families, we are unable to conclude K-stability by Theorem 1.8, except for those treated in Theorem 7.7. The aim of this subsection is to prove K-stability for all the quasi-smooth members of suitable families indexed by
![]() $\mathsf {I}_{\mathrm {BR}}$
. This will be done by combining the inequality
$\mathsf {I}_{\mathrm {BR}}$
. This will be done by combining the inequality
![]() $\alpha \ge 1/2$
obtained by Theorem 1.8 and an additional information on local movable alpha invariants which are introduced below.
$\alpha \ge 1/2$
obtained by Theorem 1.8 and an additional information on local movable alpha invariants which are introduced below.
Definition 7.10. Let X be a Fano variety of Picard number
![]() $1$
and
$1$
and
![]() $\mathsf {p} \in X$
a point. For a nonempty linear system
$\mathsf {p} \in X$
a point. For a nonempty linear system
![]() $\mathcal {M}$
on X, we define
$\mathcal {M}$
on X, we define
![]() $\lambda _{\mathcal {M}} \in \mathbb {Q}_{> 0}$
to be the rational number such that
$\lambda _{\mathcal {M}} \in \mathbb {Q}_{> 0}$
to be the rational number such that
![]() $\mathcal {M} \sim _{\mathbb {Q}} - \lambda _{\mathcal {M}} K_X$
. For a movable linear system
$\mathcal {M} \sim _{\mathbb {Q}} - \lambda _{\mathcal {M}} K_X$
. For a movable linear system
![]() $\mathcal {M}$
on X and a positive rational number
$\mathcal {M}$
on X and a positive rational number
![]() $\mu $
, we define the movable log canonical threshold of
$\mu $
, we define the movable log canonical threshold of
![]() $(X, \mu \mathcal {M})$
at
$(X, \mu \mathcal {M})$
at
![]() $\mathsf {p}$
to be the number
$\mathsf {p}$
to be the number
and then we define the movable alpha invariant of X at
![]() $\mathsf {p}$
as
$\mathsf {p}$
as
Proposition 7.11 (cf. [Reference Stibitz and ZhuangSZ19, Corollary 3.1]).
Let X be a quasi-smooth Fano
![]() $3$
-fold weighted hypersurface of index
$3$
-fold weighted hypersurface of index
![]() $1$
. Assume that, for any maximal center
$1$
. Assume that, for any maximal center
![]() $\mathsf {p} \in X$
, we have
$\mathsf {p} \in X$
, we have
Then X is K-stable.
Proof. By the main result of [Reference Cheltsov and ParkCP17] (cf. Remark 2.25), we have
![]() $\alpha ^{\operatorname {mov}}_{\mathsf {q}} (X) \ge 1$
for any point
$\alpha ^{\operatorname {mov}}_{\mathsf {q}} (X) \ge 1$
for any point
![]() $\mathsf {q} \in X$
which is not a maximal center. It follows that the pair
$\mathsf {q} \in X$
which is not a maximal center. It follows that the pair
![]() $(X, \lambda _{\mathcal {M}}^{-1} \mathcal {M})$
is log canonical for any movable linear system
$(X, \lambda _{\mathcal {M}}^{-1} \mathcal {M})$
is log canonical for any movable linear system
![]() $\mathcal {M}$
on X. Combining this with the inequality
$\mathcal {M}$
on X. Combining this with the inequality
![]() $\alpha (X) \ge 1/2$
obtained by Theorem 1.8, we see that X is K-semistable by [Reference Stibitz and ZhuangSZ19, Theorem 1.2].
$\alpha (X) \ge 1/2$
obtained by Theorem 1.8, we see that X is K-semistable by [Reference Stibitz and ZhuangSZ19, Theorem 1.2].
Suppose that X is not K-stable. Then, by [Reference Stibitz and ZhuangSZ19, Corollary 3.1], there exists a prime divisor E over X, a movable linear system
![]() $\mathcal {M} \sim _{\mathbb {Q}} - n K_X$
and an effective
$\mathcal {M} \sim _{\mathbb {Q}} - n K_X$
and an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D \sim _{\mathbb {Q}} - K_X$
such that E is a log canonical place of
$D \sim _{\mathbb {Q}} - K_X$
such that E is a log canonical place of
![]() $(X, \frac {1}{n} \mathcal {M})$
and
$(X, \frac {1}{n} \mathcal {M})$
and
![]() $(X, \frac {1}{2} D)$
. Note that the center
$(X, \frac {1}{2} D)$
. Note that the center
![]() $\Gamma $
of E on X is necessarily a maximal center, and a maximal center on X is a BI center. Thus,
$\Gamma $
of E on X is necessarily a maximal center, and a maximal center on X is a BI center. Thus,
![]() $\Gamma = \mathsf {p}$
is a BI center, and this implies
$\Gamma = \mathsf {p}$
is a BI center, and this implies
![]() $(\alpha _{\mathsf {p}}^{\operatorname {mov}} (X), \alpha _{\mathsf {p}} (X)) = (1, 1/2)$
. This is impossible by the assumption. Therefore, X is K-stable.
$(\alpha _{\mathsf {p}}^{\operatorname {mov}} (X), \alpha _{\mathsf {p}} (X)) = (1, 1/2)$
. This is impossible by the assumption. Therefore, X is K-stable.
We define
Theorem 7.12. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {K}}$
. Then, for any BI center
$\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {K}}$
. Then, for any BI center
![]() $\mathsf {p} \in X$
, we have
$\mathsf {p} \in X$
, we have
In particular, X is K-stable.
Proof. Let X be a member of
![]() $\mathcal {F}_{\mathsf {i}}$
, where
$\mathcal {F}_{\mathsf {i}}$
, where
![]() $\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {K}}$
. We first show that the inequalities (7.12) are satisfied.
$\mathsf {i} \in \mathsf {I}^{\prime }_{\mathrm {K}}$
. We first show that the inequalities (7.12) are satisfied.
Suppose
![]() $\mathsf {i} \in \{16, 17, 26, 27, 36, 47, 48, 54, 65\}$
. Then the subscript
$\mathsf {i} \in \{16, 17, 26, 27, 36, 47, 48, 54, 65\}$
. Then the subscript
![]() $\diamondsuit $
is given in the fourth column of Table 7 for any BI center on X. By Proposition 5.3, we have
$\diamondsuit $
is given in the fourth column of Table 7 for any BI center on X. By Proposition 5.3, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
, and hence
$\alpha _{\mathsf {p}} (X) \ge 1$
, and hence
![]() $\alpha ^{\operatorname {mov}}_{\mathsf {p}} (X) \ge 1$
, for any BI center
$\alpha ^{\operatorname {mov}}_{\mathsf {p}} (X) \ge 1$
, for any BI center
![]() $\mathsf {p} \in X$
.
$\mathsf {p} \in X$
.
Suppose
![]() $\mathsf {i} \in \{6, 15, 30, 41, 68\}$
. In this case, X admits two QI centers of equal singularity type and does not admit any other BI center. By the proof of Proposition 5.18 (see Section 5.6.c), we have
$\mathsf {i} \in \{6, 15, 30, 41, 68\}$
. In this case, X admits two QI centers of equal singularity type and does not admit any other BI center. By the proof of Proposition 5.18 (see Section 5.6.c), we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
for any QI center
$\alpha _{\mathsf {p}} (X) \ge 1$
for any QI center
![]() $\mathsf {p} \in X$
. In particular, we have
$\mathsf {p} \in X$
. In particular, we have
![]() $\alpha ^{\operatorname {mov}}_{\mathsf {p}} (X) \ge \alpha _{\mathsf {p}} (X) \ge 1$
.
$\alpha ^{\operatorname {mov}}_{\mathsf {p}} (X) \ge \alpha _{\mathsf {p}} (X) \ge 1$
.
Suppose
![]() $\mathsf {i} \in \{8, 56, 60\}$
. In this case, X admits a unique BI center and it is a QI center. The inequalities (7.1) follow from Remark 6.2 and Propositions 7.14, 7.15. This completes the verifications for the inequalities (7.1).
$\mathsf {i} \in \{8, 56, 60\}$
. In this case, X admits a unique BI center and it is a QI center. The inequalities (7.1) follow from Remark 6.2 and Propositions 7.14, 7.15. This completes the verifications for the inequalities (7.1).
The K-stability of X follows from the inequalities (7.1), Theorem 1.8 and Proposition 7.11.
We define
Note that
![]() $|\mathsf {I}_{\mathrm {K}}| = 73$
. Combining Theorems 7.7, 7.12 and Corollary 1.9, we obtain the K-stability of arbitrary quasi-smooth member for families indexed by
$|\mathsf {I}_{\mathrm {K}}| = 73$
. Combining Theorems 7.7, 7.12 and Corollary 1.9, we obtain the K-stability of arbitrary quasi-smooth member for families indexed by
![]() $\mathsf {I}_{\mathrm {K}}$
.
$\mathsf {I}_{\mathrm {K}}$
.
Corollary 7.13. Let X be a member of a family
![]() $\mathcal {F}_{\mathsf {i}}$
with
$\mathcal {F}_{\mathsf {i}}$
with
![]() $\mathsf {i} \in \mathsf {I}_{\mathrm {K}}$
. Then X is K-stable.
$\mathsf {i} \in \mathsf {I}_{\mathrm {K}}$
. Then X is K-stable.
7.5 Further computations of alpha invariants
In this section, we compute local alpha invariants for a few families in order to give better lower bounds. The results obtained in this section are used only in the proof of Theorem 7.12.
Proposition 7.14. Let X be a member of the family
![]() $\mathcal {F}_{56}$
and
$\mathcal {F}_{56}$
and
![]() $\mathsf {p} = \mathsf {p}_w \in X$
be the singular point of type
$\mathsf {p} = \mathsf {p}_w \in X$
be the singular point of type
![]() $\frac {1}{11} (1, 3, 8)$
. Then
$\frac {1}{11} (1, 3, 8)$
. Then
Proof. We set
![]() $\mathsf {p} = \mathsf {p}_w$
. We can write the defining polynomial of X as
$\mathsf {p} = \mathsf {p}_w$
. We can write the defining polynomial of X as
where
![]() $f_i = f_i (x, y, z, t)$
is a quasi-homogeneous polynomial of degree i. By the quasi-smoothness of X, we have
$f_i = f_i (x, y, z, t)$
is a quasi-homogeneous polynomial of degree i. By the quasi-smoothness of X, we have
![]() $t^3 \in F$
. It is easy to see that
$t^3 \in F$
. It is easy to see that
![]() $F (x, 0, z, t, 1) \in (x, z, t)^3$
. It follows that
$F (x, 0, z, t, 1) \in (x, z, t)^3$
. It follows that
![]() $\operatorname {omult}_{\mathsf {p}} (H_y) = 3$
, which in particular implies
$\operatorname {omult}_{\mathsf {p}} (H_y) = 3$
, which in particular implies
![]() $\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{2} H_y) \ge 2/3$
.
$\operatorname {lct}_{\mathsf {p}} (X; \frac {1}{2} H_y) \ge 2/3$
.
Let
![]() $D \in |A|_{\mathbb {Q}}$
be an irreducible
$D \in |A|_{\mathbb {Q}}$
be an irreducible
![]() $\mathbb {Q}$
-divisor other than
$\mathbb {Q}$
-divisor other than
![]() $\frac {1}{2} H_y$
. We can take a
$\frac {1}{2} H_y$
. We can take a
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T \in |3 A|_{\mathbb {Q}}$
such that
$T \in |3 A|_{\mathbb {Q}}$
such that
![]() $\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
$\operatorname {omult}_{\mathsf {p}} (T) \ge 1$
and
![]() $\operatorname {Supp} (T)$
does not contain any component of the effective
$\operatorname {Supp} (T)$
does not contain any component of the effective
![]() $1$
-cycle
$1$
-cycle
![]() $D \cdot H_y$
. We have
$D \cdot H_y$
. We have
This shows
![]() $\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
. Therefore,
$\operatorname {lct}_{\mathsf {p}} (X;D) \ge 1$
. Therefore,
![]() $\alpha ^{\operatorname {mov}}_{\mathsf {p}} (X) \ge 1$
and
$\alpha ^{\operatorname {mov}}_{\mathsf {p}} (X) \ge 1$
and
![]() $\alpha _{\mathsf {p}} (X) \ge 2/3$
.
$\alpha _{\mathsf {p}} (X) \ge 2/3$
.
Proposition 7.15. Let X be a member of the family
![]() $\mathcal {F}_{60}$
, and let
$\mathcal {F}_{60}$
, and let
![]() $\mathsf {p} = \mathsf {p}_w$
be the singular point of type
$\mathsf {p} = \mathsf {p}_w$
be the singular point of type
![]() $\frac {1}{9} (1, 4, 5)$
. Then
$\frac {1}{9} (1, 4, 5)$
. Then
Proof. We set
![]() $S = H_x \sim A$
,
$S = H_x \sim A$
,
![]() $T = H_z$
and
$T = H_z$
and
![]() $\Gamma = S \cap T = (x = z = 0)_X$
. Let
$\Gamma = S \cap T = (x = z = 0)_X$
. Let
![]() $\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of
$\rho = \rho _{\mathsf {p}} \colon \breve {U}_{\mathsf {p}} \to U_{\mathsf {p}}$
be the orbifold chart of
![]() $\mathsf {p} \in X$
, and we set
$\mathsf {p} \in X$
, and we set
![]() $\breve {\Gamma } = (\breve {x} = \breve {z} = 0) \subset \breve {U}_{\mathsf {p}}$
. We can write the defining polynomial of X as
$\breve {\Gamma } = (\breve {x} = \breve {z} = 0) \subset \breve {U}_{\mathsf {p}}$
. We can write the defining polynomial of X as
where
![]() $f_i = f_i (x, y, z, t)$
is a quasi-homogeneous polynomial of degree i. By the quasi-smoothness of X, we have
$f_i = f_i (x, y, z, t)$
is a quasi-homogeneous polynomial of degree i. By the quasi-smoothness of X, we have
![]() $t^4, y^6 \in F$
, and we may assume
$t^4, y^6 \in F$
, and we may assume
![]() $\operatorname {coeff}_F (t^4) = \operatorname {coeff}_F (y^6) = 1$
by rescaling y and t. We set
$\operatorname {coeff}_F (t^4) = \operatorname {coeff}_F (y^6) = 1$
by rescaling y and t. We set
![]() $\lambda = \operatorname {coeff}_F (t^2 y^3) \in \mathbb {C}$
. Then
$\lambda = \operatorname {coeff}_F (t^2 y^3) \in \mathbb {C}$
. Then
 $$ \begin{align*} \Gamma &\cong (w^2 t + t^4 + \lambda t^2 y^3 + y^6 = 0) \subset \mathbb{P} (3, 10, 17)_{y, t, w}, \\ \breve{\Gamma} & \cong (\breve{w}^2 \breve{t} + \breve{t}^4 + \lambda \breve{t}^{\hspace{0.3mm} 2} \breve{y}^3 + \breve{y}^6 = 0) \subset \mathbb{A}^3_{\breve{y}, \breve{t}, \breve{w}}. \end{align*} $$
$$ \begin{align*} \Gamma &\cong (w^2 t + t^4 + \lambda t^2 y^3 + y^6 = 0) \subset \mathbb{P} (3, 10, 17)_{y, t, w}, \\ \breve{\Gamma} & \cong (\breve{w}^2 \breve{t} + \breve{t}^4 + \lambda \breve{t}^{\hspace{0.3mm} 2} \breve{y}^3 + \breve{y}^6 = 0) \subset \mathbb{A}^3_{\breve{y}, \breve{t}, \breve{w}}. \end{align*} $$
It is easy to see that
![]() $\Gamma $
is an irreducible and reduced curve, and
$\Gamma $
is an irreducible and reduced curve, and
![]() $\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) = 1$
, where
$\operatorname {mult}_{\breve {\mathsf {p}}} (\breve {\Gamma }) = 1$
, where
![]() $\breve {\mathsf {p}} = o \in \mathbb {A}^3$
is the preimage of
$\breve {\mathsf {p}} = o \in \mathbb {A}^3$
is the preimage of
![]() $\mathsf {p}$
via
$\mathsf {p}$
via
![]() $\rho $
.
$\rho $
.
We see that
![]() $H_x$
is quasi-smooth at
$H_x$
is quasi-smooth at
![]() $\mathsf {p}$
, and hence
$\mathsf {p}$
, and hence
![]() $\operatorname {lct}_{\mathsf {p}} (X; H_x) = 1$
. Therefore, we have
$\operatorname {lct}_{\mathsf {p}} (X; H_x) = 1$
. Therefore, we have
![]() $\alpha _{\mathsf {p}} (X) \ge 1$
by Lemma 3.17.
$\alpha _{\mathsf {p}} (X) \ge 1$
by Lemma 3.17.
8 The table
The list of the 93 families together with their basic information are summarized in Table 7, and we explain the contents.
Table 7 The 93 families.

The first two columns indicate basic information of each family and the anticanonical degree
![]() $(A^3) = (-K_X)^3$
is indicated in the third column.
$(A^3) = (-K_X)^3$
is indicated in the third column.
In the fourth column, the number and the singularities of X are described. The symbol
![]() $\frac {1}{r} [a, r-a]$
stands for the cyclic quotient singularity of type
$\frac {1}{r} [a, r-a]$
stands for the cyclic quotient singularity of type
![]() $\frac {1}{r} (1, a, r-a)$
, where
$\frac {1}{r} (1, a, r-a)$
, where
![]() $1 \le a \le r/2$
. Moreover, the symbols
$1 \le a \le r/2$
. Moreover, the symbols
![]() $\frac {1}{2}$
,
$\frac {1}{2}$
,
![]() $\frac {1}{3}$
and
$\frac {1}{3}$
and
![]() $\frac {1}{4}$
stand for singularities of types
$\frac {1}{4}$
stand for singularities of types
![]() $\frac {1}{2} (1, 1, 1)$
,
$\frac {1}{2} (1, 1, 1)$
,
![]() $\frac {1}{3} (1, 1, 2)$
and
$\frac {1}{3} (1, 1, 2)$
and
![]() $\frac {1}{4} (1, 1, 3)$
. The superscripts
$\frac {1}{4} (1, 1, 3)$
. The superscripts
![]() $\mathrm {QI}$
and
$\mathrm {QI}$
and
![]() $\mathrm {EI}$
indicate that the corresponding singular point
$\mathrm {EI}$
indicate that the corresponding singular point
![]() $\mathsf {p}$
is a QI center and EI center, respectively (see Section 2.3.b for definitions). The meaning of the subscripts is explained as follows.
$\mathsf {p}$
is a QI center and EI center, respectively (see Section 2.3.b for definitions). The meaning of the subscripts is explained as follows.
-
• The subscript
 $\heartsuit $
indicates that
$\heartsuit $
indicates that
 $\alpha _{\mathsf {p}} (X) \ge 1$
is proved by Proposition 5.2.
$\alpha _{\mathsf {p}} (X) \ge 1$
is proved by Proposition 5.2. -
• The subscript
 $\diamondsuit $
(resp.
$\diamondsuit $
(resp.
 $\diamondsuit '$
) indicates that
$\diamondsuit '$
) indicates that
 $\alpha _{\mathsf {p}} (X) \ge 1$
(resp.
$\alpha _{\mathsf {p}} (X) \ge 1$
(resp.
 $\alpha _{\mathsf {p}} (X) \ge 2/3$
) is proved by Proposition 5.3.
$\alpha _{\mathsf {p}} (X) \ge 2/3$
) is proved by Proposition 5.3. -
• The subscript
 $\clubsuit $
indicates that
$\clubsuit $
indicates that
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved by Proposition 5.4.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved by Proposition 5.4. -
• The subscript
 $\spadesuit $
indicates that
$\spadesuit $
indicates that
 $\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved by Proposition 5.5.
$\alpha _{\mathsf {p}} (X) \ge 1/2$
is proved by Proposition 5.5.
In Theorem 1.8, any birational superrigid member of each of the 95 families is proved. Apart from this main result, we have results on the existence of KE metrics or K-stability for any quasi-smooth member of suitable families. In the right-most column the mark ‘KE’ and ‘K’ are given and their meanings are as follows.
-
• The mark ‘KE’ in the right-most column means that any quasi-smooth member admits a KE metric and is K-stable (see Section 7.3).
-
• The mark ‘K’ in the right-most column means that any quasi-smooth member is K-stable (see Section 7.4.b).
Remark 8.1. We explain what is left about K-stability of quasi-smooth Fano
![]() $3$
-fold weighted hypersurfaces of index
$3$
-fold weighted hypersurfaces of index
![]() $1$
.
$1$
.
As it is explained in Section 1.4, the result [Reference Liu, Xu and ZhuangLXZ22] obtained after this paper is written in particular implies that the K-stability of a quasi-smooth Fano
![]() $3$
-fold weighted hypersurface is equivalent to the existence of a KE metric. It follows that the meaning of the mark ‘KE’ and ‘K’ in the right-most column of Table 7 are the same: It indicates that any quasi-smooth member is K-stable (and admits a KE metric). All in all, we obtain the following results in this article:
$3$
-fold weighted hypersurface is equivalent to the existence of a KE metric. It follows that the meaning of the mark ‘KE’ and ‘K’ in the right-most column of Table 7 are the same: It indicates that any quasi-smooth member is K-stable (and admits a KE metric). All in all, we obtain the following results in this article:
-
• Any quasi-smooth member in a family
 $\mathcal {F}_{\mathsf {i}}$
with a mark ‘K’ or ‘KE’ in the right-most column of Table 7 is K-stable.
$\mathcal {F}_{\mathsf {i}}$
with a mark ‘K’ or ‘KE’ in the right-most column of Table 7 is K-stable. -
• Any quasi-smooth and birationally superrigid member in a family
 $\mathcal {F}_{\mathsf {i}}$
with a blank right-most column in Table 7 is K-stable.
$\mathcal {F}_{\mathsf {i}}$
with a blank right-most column in Table 7 is K-stable.
Therefore, it remains to determine K-stability for quasi-smooth members in a family
![]() $\mathcal {F}_{\mathsf {i}}$
with a blank right-most column that are not birationally superrigid.
$\mathcal {F}_{\mathsf {i}}$
with a blank right-most column that are not birationally superrigid.
Acknowledgements
We would like to thank Professors C. Xu and Z. Zhuang for valuable comments and especially for informing us of Theorem 1.7. We also would like to thank the anonymous referee for his/her suggestion on adding Section 1.4 explaining some relevant results in K-stability that have been developed during the preparation and after the completion of this article and Remark 8.1 that makes it clear what is left about K-stability of quasi-smooth Fano
![]() $3$
-fold weighted hypersurfaces of index
$3$
-fold weighted hypersurfaces of index
![]() $1$
.
$1$
.
Competing interest
The authors have no competing interest to declare.
Funding statement
The first author was supported by the National Research Foundation of Korea (NRF-2023R1A2C1003390 and NRF-2022M3C1C8094326). The second author was supported by JSPS KAKENHI Grant Numbers JP18K03216 and JP22H01118. The third author was supported by the National Research Foundation of Korea (NRF-2020R1A2C1A01008018 and NRF-2022M3C1C8094326).