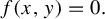1. Introduction
Let A be a rational function of one complex variable of degree at least two, and
![]() $z_0$
its repelling fixed point with the multiplier
$z_0$
its repelling fixed point with the multiplier
![]() $\unicode{x3bb} .$
We recall that a Poincaré function
$\unicode{x3bb} .$
We recall that a Poincaré function ![]() associated with
associated with
![]() $z_0$
is a function meromorphic on
$z_0$
is a function meromorphic on
![]() ${\mathbb C}$
such that
${\mathbb C}$
such that ![]() and the diagram
and the diagram

commutes. The Poincaré function exists and is defined up to the transformation of argument
![]() $z\rightarrow cz,$
where
$z\rightarrow cz,$
where
![]() $c\in {\mathbb C}^*$
(see e.g. [Reference Milnor12]). In particular, it is defined in a unique way if to assume that
$c\in {\mathbb C}^*$
(see e.g. [Reference Milnor12]). In particular, it is defined in a unique way if to assume that ![]() . Such Poincaré functions are called normalized. In this paper, we will consider non-normalized Poincaré functions, so the explicit meaning of the notation
. Such Poincaré functions are called normalized. In this paper, we will consider non-normalized Poincaré functions, so the explicit meaning of the notation ![]() is as follows:
is as follows: ![]() is some meromorphic function satisfying the above conditions. We say that a rational function A is special if it is either a Lattès map, or it is conjugate to
is some meromorphic function satisfying the above conditions. We say that a rational function A is special if it is either a Lattès map, or it is conjugate to
![]() $z^{\pm n}$
or
$z^{\pm n}$
or
![]() $\pm T_n.$
Poincaré functions associated with special functions can be described in terms of classical functions. Moreover, by the result of Ritt [Reference Ritt27], these functions are the only Poincaré functions that are periodic.
$\pm T_n.$
Poincaré functions associated with special functions can be described in terms of classical functions. Moreover, by the result of Ritt [Reference Ritt27], these functions are the only Poincaré functions that are periodic.
In this paper, we study the following problem. Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
be non-special rational functions of degree at least two with repelling fixed points
$A_2$
be non-special rational functions of degree at least two with repelling fixed points
![]() $z_1$
,
$z_1$
,
![]() $z_2$
, and
$z_2$
, and ![]() ,
, ![]() corresponding Poincaré functions. Under what conditions does there exist an algebraic curve
corresponding Poincaré functions. Under what conditions does there exist an algebraic curve
![]() $f(x,y)=0$
such that
$f(x,y)=0$
such that
and, if such a curve exists, how it can be described? The simplest example of relation (1) is just the equality
which is known to have strong dynamical consequences. Specifically, equality (2) implies easily that
![]() $A_1$
and
$A_1$
and
![]() $A_2$
commute. On the other hand, by the theorem of Ritt (see [Reference Ritt28] and also [Reference Eremenko6, Reference Pakovich23]), every two non-special commuting rational functions of degree at least two have a common iterate. Thus, equality (2) implies that
$A_2$
commute. On the other hand, by the theorem of Ritt (see [Reference Ritt28] and also [Reference Eremenko6, Reference Pakovich23]), every two non-special commuting rational functions of degree at least two have a common iterate. Thus, equality (2) implies that
for some integers
![]() $l_1,l_2\geq 1$
. Moreover, the Ritt theorem essentially is equivalent to the statement that equality (2) implies equality (3), since it was observed already by Fatou and Julia [Reference Fatou8, Reference Julia10] that if two rational functions commute, then some of their iterates share a repelling fixed point and a corresponding Poincaré function.
$l_1,l_2\geq 1$
. Moreover, the Ritt theorem essentially is equivalent to the statement that equality (2) implies equality (3), since it was observed already by Fatou and Julia [Reference Fatou8, Reference Julia10] that if two rational functions commute, then some of their iterates share a repelling fixed point and a corresponding Poincaré function.
To the best of our knowledge, the problem of describing algebraic dependencies between Poincaré functions has never been considered in the literature. Nevertheless, the problem of describing algebraic dependencies between Böttcher functions, similar in spirit, has been investigated previously [Reference Becker and Bergweiler2, Reference Nguyen14]. We recall that for a polynomial A of degree n, a corresponding Böttcher function ![]() is a Laurent series
is a Laurent series
that makes the diagram

commutative. In this notation, the result of Becker and Bergweiler [Reference Becker and Bergweiler2] (see also [Reference Becker and Bergweiler3]), states that if
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are polynomials of the same degree d, then the function
$A_2$
are polynomials of the same degree d, then the function ![]() is transcendental, unless either
is transcendental, unless either
![]() $\beta $
is linear, or
$\beta $
is linear, or
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are special (notice that since a polynomial cannot be a Lattès map, a polynomial is special if and only if it is conjugate to
$A_2$
are special (notice that since a polynomial cannot be a Lattès map, a polynomial is special if and only if it is conjugate to
![]() $z^n$
or
$z^n$
or
![]() $\pm T_n$
). Since the equality
$\pm T_n$
). Since the equality
holds for some
![]() $f(x,y)\in {\mathbb C}[x,y]$
if and only if the function
$f(x,y)\in {\mathbb C}[x,y]$
if and only if the function
![]() $\beta $
is algebraic, this result implies the absence of algebraic dependencies of degree greater than one between
$\beta $
is algebraic, this result implies the absence of algebraic dependencies of degree greater than one between ![]() and
and ![]() for non-special
for non-special
![]() $A_1$
and
$A_1$
and
![]() $A_2$
of the same degree.
$A_2$
of the same degree.
Subsequently, it was proved by Nguyen in [Reference Nguyen14] that the equality
holds for some integers
![]() $d_1,d_2\geq 1$
if and only if there exist polynomials
$d_1,d_2\geq 1$
if and only if there exist polynomials
![]() $X_1,X_2, B$
and integers
$X_1,X_2, B$
and integers
![]() $l_1, l_2\geq 1$
such that the diagram
$l_1, l_2\geq 1$
such that the diagram

commutes. Notice that although the result of Nguyen deals with the more general situation than the result of Becker and Bergweiler, the former does not formally imply the latter.
Let us recall that an algebraic curve
![]() $C: f(x,y)=0$
has genus zero if and only if it admits a parameterization
$C: f(x,y)=0$
has genus zero if and only if it admits a parameterization
![]() $z\rightarrow (X_1(z),X_2(z))$
by rational functions
$z\rightarrow (X_1(z),X_2(z))$
by rational functions
![]() $X_1, X_2.$
Such a parameterization is called generically one-to-one if it is one-to-one except for finitely many points. By the Lüroth theorem, this is equivalent to saying that
$X_1, X_2.$
Such a parameterization is called generically one-to-one if it is one-to-one except for finitely many points. By the Lüroth theorem, this is equivalent to saying that
![]() $X_1$
and
$X_1$
and
![]() $X_2$
generate the whole field of rational functions
$X_2$
generate the whole field of rational functions
![]() ${\mathbb C}(z)$
. In this notation, our main result is the following analog of the result of Nguyen.
${\mathbb C}(z)$
. In this notation, our main result is the following analog of the result of Nguyen.
Theorem 1.1. Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
be non-special rational functions of degree at least two,
$A_2$
be non-special rational functions of degree at least two,
![]() $z_1$
,
$z_1$
,
![]() $z_2$
their repelling fixed points with multipliers
$z_2$
their repelling fixed points with multipliers
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2$
, and
$\unicode{x3bb} _1, \unicode{x3bb} _2$
, and ![]() ,
, ![]() Poincaré functions. Assume that
Poincaré functions. Assume that
![]() $C: f(x,y)=0$
is an irreducible algebraic curve, and
$C: f(x,y)=0$
is an irreducible algebraic curve, and
![]() $d_1, d_2$
are coprime positive integers such that the equality
$d_1, d_2$
are coprime positive integers such that the equality
holds. Then, C has genus zero. Furthermore, if
![]() $C: f(x,y)=0$
is an irreducible algebraic curve of genus zero with a generically one-to-one parameterization by rational functions
$C: f(x,y)=0$
is an irreducible algebraic curve of genus zero with a generically one-to-one parameterization by rational functions
![]() $z\rightarrow (X_1(z),X_2(z))$
, and
$z\rightarrow (X_1(z),X_2(z))$
, and
![]() $d_1, d_2$
are coprime positive integers, then equality (7) holds for some Poincaré functions
$d_1, d_2$
are coprime positive integers, then equality (7) holds for some Poincaré functions ![]() ,
, ![]() if and only if there exist positive integers
if and only if there exist positive integers
![]() $l_1,l_2,k$
and a rational function B with a repelling fixed point
$l_1,l_2,k$
and a rational function B with a repelling fixed point
![]() $z_0$
such that the diagram
$z_0$
such that the diagram

commutes and the equalities
hold.
Notice that Theorem 1.1 can be considered as a refinement of the Ritt theorem. Indeed, equality (2) is a particular case of the condition (7), where the curve
is parameterized by the functions
![]() $X_1=z, X_2=z.$
Thus, in this case, the diagram (8) reduces to equality (3). More generally, considering the curve
$X_1=z, X_2=z.$
Thus, in this case, the diagram (8) reduces to equality (3). More generally, considering the curve
![]() $x-R(y)=0,$
where R is a rational function, we conclude that the equality
$x-R(y)=0,$
where R is a rational function, we conclude that the equality
implies that there exist
![]() $l_1,l_2\geq 1$
such that the diagram
$l_1,l_2\geq 1$
such that the diagram

commutes.
Notice also that Theorem 1.1 implies the following handy criterion for the algebraic independence of Poincaré functions.
Corollary 1.2. Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
be non-special rational functions of degrees
$A_2$
be non-special rational functions of degrees
![]() $n_1\geq 2$
,
$n_1\geq 2$
,
![]() $n_2\geq 2$
, and
$n_2\geq 2$
, and
![]() $z_1$
,
$z_1$
,
![]() $z_2$
their repelling fixed points with multipliers
$z_2$
their repelling fixed points with multipliers
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2$
. Then, Poincaré functions
$\unicode{x3bb} _1, \unicode{x3bb} _2$
. Then, Poincaré functions ![]() ,
, ![]() are algebraically independent, unless there exist positive integers
are algebraically independent, unless there exist positive integers
![]() $l_1,l_2$
and
$l_1,l_2$
and
![]() $l_1',l_2'$
such that
$l_1',l_2'$
such that
![]() $n_1^{l_1}=n_2^{l_2}$
and
$n_1^{l_1}=n_2^{l_2}$
and
![]() $\unicode{x3bb} _1^{l_1'}=\unicode{x3bb} _2^{l_2'}$
.
$\unicode{x3bb} _1^{l_1'}=\unicode{x3bb} _2^{l_2'}$
.
In addition to Theorem 1.1, we prove the following more precise version of the theorem of Nguyen, which formally includes and generalizes the result of Becker and Bergweiler.
Theorem 1.3. Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
be non-special polynomials of degree at least two, and
$A_2$
be non-special polynomials of degree at least two, and ![]() ,
, ![]() Böttcher functions. Assume that
Böttcher functions. Assume that
![]() $C: f(x,y)=0$
is an irreducible algebraic curve, and
$C: f(x,y)=0$
is an irreducible algebraic curve, and
![]() $d_1, d_2$
are coprime positive integers such that the equality
$d_1, d_2$
are coprime positive integers such that the equality
holds. Then, C has the form
![]() $Y_1(x)-Y_2(y)=0$
, where
$Y_1(x)-Y_2(y)=0$
, where
![]() $Y_1,Y_2$
are polynomials of coprime degrees, and can be parameterized by polynomials. Furthermore, if
$Y_1,Y_2$
are polynomials of coprime degrees, and can be parameterized by polynomials. Furthermore, if
![]() $C: f(x,y)=0$
is an irreducible algebraic curve as above with a generically one-to-one parameterization by polynomials
$C: f(x,y)=0$
is an irreducible algebraic curve as above with a generically one-to-one parameterization by polynomials
![]() $z\rightarrow (X_1(z),X_2(z))$
, and
$z\rightarrow (X_1(z),X_2(z))$
, and
![]() $d_1, d_2$
are coprime positive integers, then equality (11) holds for some Böttcher functions
$d_1, d_2$
are coprime positive integers, then equality (11) holds for some Böttcher functions ![]() ,
, ![]() if and only if there exist positive integers
if and only if there exist positive integers
![]() $l_1,l_2$
and a polynomial B such that the diagram
$l_1,l_2$
and a polynomial B such that the diagram

commutes, and the equalities
hold. In particular, the equality
implies that
![]() $C: f(x,y)=0$
has degree one and some iterates of
$C: f(x,y)=0$
has degree one and some iterates of
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are conjugate.
$A_2$
are conjugate.
Notice that the parameters
![]() $d_1,d_2$
appear in conclusions of both Theorems 1.1 and 1.3. However, the condition (10) is less restrictive than the condition (13). In particular, applying Theorem 1.3 for
$d_1,d_2$
appear in conclusions of both Theorems 1.1 and 1.3. However, the condition (10) is less restrictive than the condition (13). In particular, applying Theorem 1.3 for
![]() $d_1=d_2=1$
, we conclude that algebraic dependencies between Bötcher functions are essentially trivial. However, algebraic dependencies between Poincaré functions do exist (see §3).
$d_1=d_2=1$
, we conclude that algebraic dependencies between Bötcher functions are essentially trivial. However, algebraic dependencies between Poincaré functions do exist (see §3).
The approach of Nguyen to the study of algebraic dependencies (6) relies on the fact that such dependencies give rise to invariant algebraic curves for endomorphisms
given by the formula
where
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are polynomials. Say, for
$A_2$
are polynomials. Say, for
![]() $A_1$
and
$A_1$
and
![]() $A_2$
of the same degree n, this can be seen immediately, since after substituting
$A_2$
of the same degree n, this can be seen immediately, since after substituting
![]() $z^n$
for z into equation (6), we obtain the equality
$z^n$
for z into equation (6), we obtain the equality
implying that
![]() $f(x,y)=0$
is
$f(x,y)=0$
is
![]() $(A_1,A_2)$
-invariant. Invariant curves for polynomial endomorphisms of the form (14) were classified by Medvedev and Scanlon [Reference Medvedev and Scanlon11], and the proof of the theorem of Nguyen relies crucially on this classification.
$(A_1,A_2)$
-invariant. Invariant curves for polynomial endomorphisms of the form (14) were classified by Medvedev and Scanlon [Reference Medvedev and Scanlon11], and the proof of the theorem of Nguyen relies crucially on this classification.
Our approach to the study of algebraic dependencies (1) is similar. However, instead of the paper [Reference Medvedev and Scanlon11], we use the results of the recent paper [Reference Pakovich25] providing a classification of invariant curves for endomorphisms (15) defined by arbitrary non-special rational functions
![]() $A_1, A_2$
. Notice that [Reference Medvedev and Scanlon11] is based on the Ritt theory of polynomial decompositions [Reference Ritt26], which does not extend to rational functions. Accordingly, the approach of [Reference Pakovich25] is completely different and relies on the recent results [Reference Pakovich16, Reference Pakovich18–Reference Pakovich21] about semiconjugate rational functions, which appear naturally in a variety of different contexts (see e.g. [Reference Buff and Epstein4, Reference Eremenko7, Reference Inou9, Reference Medvedev and Scanlon11, Reference Nguyen14, Reference Pakovich17, Reference Pakovich20, Reference Pakovich22, Reference Pakovich25]).
$A_1, A_2$
. Notice that [Reference Medvedev and Scanlon11] is based on the Ritt theory of polynomial decompositions [Reference Ritt26], which does not extend to rational functions. Accordingly, the approach of [Reference Pakovich25] is completely different and relies on the recent results [Reference Pakovich16, Reference Pakovich18–Reference Pakovich21] about semiconjugate rational functions, which appear naturally in a variety of different contexts (see e.g. [Reference Buff and Epstein4, Reference Eremenko7, Reference Inou9, Reference Medvedev and Scanlon11, Reference Nguyen14, Reference Pakovich17, Reference Pakovich20, Reference Pakovich22, Reference Pakovich25]).
This paper is organized as follows. In §2, we review the notion of a generalized Lattès map, introduced in [Reference Pakovich20], and recall some results about semiconjugate rational functions and invariant curves proved in [Reference Pakovich25]. In §3, we prove Theorem 1.1. We also show that for rational functions that are not generalized Lattès maps, equality (7) under the condition
![]() $\mathrm {GCD }(d_1,d_2)=1$
implies the equality
$\mathrm {GCD }(d_1,d_2)=1$
implies the equality
![]() $d_1=d_2=1$
(Theorem 3.6). Finally, in §4, based on results of [Reference Pakovich17], which complements some of results of [Reference Medvedev and Scanlon11], we reconsider algebraic dependencies between Böttcher functions and prove Theorem 1.3.
$d_1=d_2=1$
(Theorem 3.6). Finally, in §4, based on results of [Reference Pakovich17], which complements some of results of [Reference Medvedev and Scanlon11], we reconsider algebraic dependencies between Böttcher functions and prove Theorem 1.3.
2. Generalized Lattès maps and invariant curves
2.1. Generalized Lattès maps and semiconjugacies
Let us recall that a Riemann surface orbifold is a pair ![]() consisting of a Riemann surface R and a ramification function
consisting of a Riemann surface R and a ramification function
![]() $\nu :R\rightarrow \mathbb N$
, which takes the value
$\nu :R\rightarrow \mathbb N$
, which takes the value
![]() $\nu (z)=1$
except at isolated points. For an orbifold
$\nu (z)=1$
except at isolated points. For an orbifold ![]() , the Euler characteristic of
, the Euler characteristic of ![]() is the number
is the number

For orbifolds ![]() and
and ![]() , we write
, we write ![]() if
if
![]() $R_1=R_2$
and for any
$R_1=R_2$
and for any
![]() $z\in R_1$
, the condition
$z\in R_1$
, the condition
![]() $\nu _1(z)\mid \nu _2(z)$
holds.
$\nu _1(z)\mid \nu _2(z)$
holds.
Let ![]() and
and ![]() be orbifolds, and let
be orbifolds, and let
![]() $f:\, R_1\rightarrow R_2$
be a holomorphic branched covering map. We say that
$f:\, R_1\rightarrow R_2$
be a holomorphic branched covering map. We say that ![]() is a covering map between orbifolds if for any
is a covering map between orbifolds if for any
![]() $z\in R_1$
, the equality
$z\in R_1$
, the equality
holds, where
![]() $\mathrm {deg\,}_zf$
is the local degree of f at the point z. If for any
$\mathrm {deg\,}_zf$
is the local degree of f at the point z. If for any
![]() $z\in R_1$
the weaker condition
$z\in R_1$
the weaker condition
is satisfied, we say that ![]() is a holomorphic map between orbifolds. If
is a holomorphic map between orbifolds. If ![]() is a covering map between orbifolds with compact supports, then the Riemann–Hurwitz formula implies that
is a covering map between orbifolds with compact supports, then the Riemann–Hurwitz formula implies that
More generally, if ![]() is a holomorphic map, then
is a holomorphic map, then
and the equality is attained if and only if ![]() is a covering map between orbifolds (see [Reference Pakovich16, Proposition 3.2]).
is a covering map between orbifolds (see [Reference Pakovich16, Proposition 3.2]).
Let
![]() $R_1$
,
$R_1$
,
![]() $R_2$
be Riemann surfaces and
$R_2$
be Riemann surfaces and
![]() $f:\, R_1\rightarrow R_2$
a holomorphic branched covering map. Assume that
$f:\, R_1\rightarrow R_2$
a holomorphic branched covering map. Assume that
![]() $R_2$
is provided with a ramification function
$R_2$
is provided with a ramification function
![]() $\nu _2$
. To define a ramification function
$\nu _2$
. To define a ramification function
![]() $\nu _1$
on
$\nu _1$
on
![]() $R_1$
so that f would be a holomorphic map between orbifolds
$R_1$
so that f would be a holomorphic map between orbifolds ![]() and
and ![]() , we must satisfy the condition (16), and it is easy to see that for any
, we must satisfy the condition (16), and it is easy to see that for any
![]() $z\in R_1$
, a minimum possible value for
$z\in R_1$
, a minimum possible value for
![]() $\nu _1(z)$
is defined by the equality
$\nu _1(z)$
is defined by the equality
In the case where equation (19) is satisfied for any
![]() $z\in R_1$
, we say that f is a minimal holomorphic map between orbifolds
$z\in R_1$
, we say that f is a minimal holomorphic map between orbifolds ![]() and
and ![]() .
.
We recall that a Lattès map can be defined as a rational function A such that ![]() is a covering self-map for some orbifold
is a covering self-map for some orbifold ![]() on
on
![]() ${\mathbb C}{\mathbb P}^1$
(see [Reference Milnor, Hjorth and Petersen13, Reference Pakovich20]). Thus, A is a Lattès map if there exists an orbifold
${\mathbb C}{\mathbb P}^1$
(see [Reference Milnor, Hjorth and Petersen13, Reference Pakovich20]). Thus, A is a Lattès map if there exists an orbifold ![]() such that for any
such that for any
![]() $z\in {\mathbb C}{\mathbb P}^1$
, the equality
$z\in {\mathbb C}{\mathbb P}^1$
, the equality
holds. By equality (17), such ![]() necessarily satisfies
necessarily satisfies ![]() Following [Reference Pakovich20], we say that a rational function A of degree at least two is a generalized Lattès map if there exists an orbifold
Following [Reference Pakovich20], we say that a rational function A of degree at least two is a generalized Lattès map if there exists an orbifold ![]() , distinct from the non-ramified sphere, such that
, distinct from the non-ramified sphere, such that ![]() is a minimal holomorphic self-map between orbifolds; that is, for any
is a minimal holomorphic self-map between orbifolds; that is, for any
![]() $z\in {\mathbb C}{\mathbb P}^1$
, the equality
$z\in {\mathbb C}{\mathbb P}^1$
, the equality
holds. By inequality (18), such ![]() satisfies
satisfies ![]() . Notice that any special rational function is a generalized Lattès map, and that some iterate
. Notice that any special rational function is a generalized Lattès map, and that some iterate
![]() $A^{\circ l}$
,
$A^{\circ l}$
,
![]() $l\geq 1,$
of a rational function A is a generalized Lattès map if and only if A is a generalized Lattès map (see [Reference Pakovich25, §2.3].
$l\geq 1,$
of a rational function A is a generalized Lattès map if and only if A is a generalized Lattès map (see [Reference Pakovich25, §2.3].
Generalized Lattès maps are closely related to the problem of describing semiconjugate rational functions, that is, rational functions that make the diagram

commutative. For a general theory, we refer the reader to [Reference Pakovich16, Reference Pakovich18–Reference Pakovich21]. Below, we need only the following two results, which are simplified reformulations of [Reference Pakovich25, Proposition 3.3 and Theorem 4.14].
The first result states that if the function A in diagram (20) is not a generalized Lattès map, then diagram (20) can be completed to a diagram of the very special form.
Proposition 2.1. Let A be a rational function of degree at least two that is not a generalized Lattes map, and
![]() $X, B$
rational functions such that the diagram (20) commutes. Then there exists a rational function Y such that the diagram
$X, B$
rational functions such that the diagram (20) commutes. Then there exists a rational function Y such that the diagram

commutes, and the equalities
hold for some
![]() $d\geq 0$
.
$d\geq 0$
.
The second result relates an arbitrary non-special rational function with some rational function that is not a generalized Lattès map through the semiconjugacy relation.
Theorem 2.2. Let A be a non-special rational function of degree at least two. Then there exist rational functions
![]() $\theta $
and F such that F is not a generalized Lattès map and the diagram
$\theta $
and F such that F is not a generalized Lattès map and the diagram

commutes.
2.2. Invariant curves
Let
![]() $A_1,A_2$
be rational functions,
$A_1,A_2$
be rational functions,
![]() $(A_1,A_2)$
the map given by formulas (14) and (15), and C an irreducible algebraic curve in
$(A_1,A_2)$
the map given by formulas (14) and (15), and C an irreducible algebraic curve in
![]() $( {\mathbb C}{\mathbb P}^1)^2$
. We say that C is
$( {\mathbb C}{\mathbb P}^1)^2$
. We say that C is
![]() $(A_1,A_2)$
- invariant if
$(A_1,A_2)$
- invariant if
![]() $(A_1,A_2)( C)= C.$
We recall that a desingularization of
$(A_1,A_2)( C)= C.$
We recall that a desingularization of
![]() $ C$
is a compact Riemann surface
$ C$
is a compact Riemann surface
![]() $\widetilde C$
together with a map
$\widetilde C$
together with a map
![]() $\pi :\widetilde C\rightarrow C$
, which is biholomorphic except for finitely many points.
$\pi :\widetilde C\rightarrow C$
, which is biholomorphic except for finitely many points.
The simplest
![]() $(A_1,A_2)$
-invariant curves are vertical lines
$(A_1,A_2)$
-invariant curves are vertical lines
![]() $x=a$
, where a is a fixed point of
$x=a$
, where a is a fixed point of
![]() $A_1$
, and horizontal lines
$A_1$
, and horizontal lines
![]() $y=b$
, where b is a fixed point of
$y=b$
, where b is a fixed point of
![]() $A_2$
. Other invariant curves are described as follows (see [Reference Pakovich25, Theorem 4.1]).
$A_2$
. Other invariant curves are described as follows (see [Reference Pakovich25, Theorem 4.1]).
Theorem 2.3. Let
![]() $A_1,A_2$
be rational functions of degree at least two, and
$A_1,A_2$
be rational functions of degree at least two, and
![]() $ C$
an irreducible
$ C$
an irreducible
![]() $(A_1,A_2)$
-invariant curve that is not a vertical or horizontal line. Then the desingularization
$(A_1,A_2)$
-invariant curve that is not a vertical or horizontal line. Then the desingularization
![]() $\widetilde { C}$
of
$\widetilde { C}$
of
![]() $ C$
has genus zero or one, and there exist non-constant holomorphic maps
$ C$
has genus zero or one, and there exist non-constant holomorphic maps
![]() $X_1,X_2:\widetilde { C}\rightarrow {\mathbb C}{\mathbb P}^1$
and
$X_1,X_2:\widetilde { C}\rightarrow {\mathbb C}{\mathbb P}^1$
and
![]() $B:\widetilde { C}\rightarrow \widetilde { C}$
such that the diagram
$B:\widetilde { C}\rightarrow \widetilde { C}$
such that the diagram

commutes and the map
![]() $t\rightarrow (X_1(t),X_2(t))$
is a generically one-to-one parameterization of
$t\rightarrow (X_1(t),X_2(t))$
is a generically one-to-one parameterization of
![]() $ C.$
Finally, unless both
$ C.$
Finally, unless both
![]() $A_1, A_2$
are Lattès maps,
$A_1, A_2$
are Lattès maps,
![]() $\widetilde { C}$
has genus zero.
$\widetilde { C}$
has genus zero.
For a general description of
![]() $(A_1,A_2)$
-invariant curves, we refer the reader to [Reference Pakovich25]. Below, we need only the following description of invariant curves in the case where
$(A_1,A_2)$
-invariant curves, we refer the reader to [Reference Pakovich25]. Below, we need only the following description of invariant curves in the case where
![]() $A_1=A_2$
(see [Reference Pakovich25, Theorem 1.2]).
$A_1=A_2$
(see [Reference Pakovich25, Theorem 1.2]).
Theorem 2.4. Let A be a rational function of degree at least two that is not a generalized Lattès map, and
![]() $ C$
an irreducible algebraic curve in
$ C$
an irreducible algebraic curve in
![]() $( {\mathbb C}{\mathbb P}^1)^2$
that is not a vertical or horizontal line. Then,
$( {\mathbb C}{\mathbb P}^1)^2$
that is not a vertical or horizontal line. Then,
![]() $ C$
is
$ C$
is
![]() $(A,A)$
-invariant if and only if there exist rational functions
$(A,A)$
-invariant if and only if there exist rational functions
![]() $U_1, U_2, V_1, V_2$
commuting with A such that the equalities
$U_1, U_2, V_1, V_2$
commuting with A such that the equalities
 $$ \begin{align*} U_1\circ V_1&=U_2\circ V_2=A^{\circ d},\\V_1\circ U_1&=V_2\circ U_2=A^{\circ d} \end{align*} $$
$$ \begin{align*} U_1\circ V_1&=U_2\circ V_2=A^{\circ d},\\V_1\circ U_1&=V_2\circ U_2=A^{\circ d} \end{align*} $$
hold for some
![]() $d\geq 0$
and the map
$d\geq 0$
and the map
![]() $t\rightarrow (U_1(t),U_2(t))$
is a parameterization of
$t\rightarrow (U_1(t),U_2(t))$
is a parameterization of
![]() $ C$
.
$ C$
.
Notice that, in general, the parameterization
![]() $t\rightarrow (U_1(t),U_2(t))$
provided by Theorem 2.4 is not generically one-to-one.
$t\rightarrow (U_1(t),U_2(t))$
provided by Theorem 2.4 is not generically one-to-one.
3. Algebraic dependencies between Poincaré functions
Our proof of Theorem 1.1 is based on the results of §2 and the lemmas below.
Lemma 3.1. Let
![]() $C:\, f(x,y)=0$
be an irreducible algebraic curve that admits a parameterization
$C:\, f(x,y)=0$
be an irreducible algebraic curve that admits a parameterization
![]() $z\rightarrow ({\varphi }_1(z), {\varphi }_2(z))$
by functions meromorphic on
$z\rightarrow ({\varphi }_1(z), {\varphi }_2(z))$
by functions meromorphic on
![]() ${\mathbb C}.$
Then the desingularization
${\mathbb C}.$
Then the desingularization
![]() $\widetilde {C}$
of C has genus zero or one, and there exist meromorphic functions
$\widetilde {C}$
of C has genus zero or one, and there exist meromorphic functions
![]() ${\varphi }:\, {\mathbb C} \rightarrow \widetilde {C}$
and
${\varphi }:\, {\mathbb C} \rightarrow \widetilde {C}$
and
![]() $\widetilde {\varphi }_1:\, \widetilde {C}\rightarrow {\mathbb C}{\mathbb P}^1$
,
$\widetilde {\varphi }_1:\, \widetilde {C}\rightarrow {\mathbb C}{\mathbb P}^1$
,
![]() $\widetilde {\varphi }_2:\, \widetilde {C}\rightarrow {\mathbb C}{\mathbb P}^1$
such that
$\widetilde {\varphi }_2:\, \widetilde {C}\rightarrow {\mathbb C}{\mathbb P}^1$
such that
and the map
![]() $z\rightarrow (\widetilde {\varphi }_1(z),\widetilde {\varphi }_2(z))$
from
$z\rightarrow (\widetilde {\varphi }_1(z),\widetilde {\varphi }_2(z))$
from
![]() $\widetilde {C}$
to C is generically one-to-one.
$\widetilde {C}$
to C is generically one-to-one.
Proof. The lemma follows from the Picard theorem (see [Reference Beardon and Ng1, Theorems 1 and 2]).
Lemma 3.2. Let A be a non-special rational function of degree at least two, and
![]() $z_0$
its fixed point with the multiplier
$z_0$
its fixed point with the multiplier
![]() $\unicode{x3bb} .$
Assume that W is a rational function of degree at least two commuting with A such that
$\unicode{x3bb} .$
Assume that W is a rational function of degree at least two commuting with A such that
![]() $z_0$
is a fixed point of W with the multiplier
$z_0$
is a fixed point of W with the multiplier
![]() $\mu .$
Then there exist positive integers l and k such that
$\mu .$
Then there exist positive integers l and k such that
![]() $\mu ^l=\unicode{x3bb} ^k.$
$\mu ^l=\unicode{x3bb} ^k.$
Proof. By the theorem of Ritt, there exist positive integers l and k such that
![]() $W^{\circ l}=A^{\circ k}$
, and differentiating this equality at
$W^{\circ l}=A^{\circ k}$
, and differentiating this equality at
![]() $z_0$
, we conclude that
$z_0$
, we conclude that
![]() $\mu ^l=\unicode{x3bb} ^k.$
$\mu ^l=\unicode{x3bb} ^k.$
Lemma 3.3. Let A, B be rational functions of degree at least two, and X a non-constant rational function such that the diagram

commutes. Assume that
![]() $z_0$
is a fixed point of B with the multiplier
$z_0$
is a fixed point of B with the multiplier
![]() $\unicode{x3bb} _0$
. Then
$\unicode{x3bb} _0$
. Then
![]() $z_1=X(z_0)$
is a fixed point
$z_1=X(z_0)$
is a fixed point
![]() $z_1$
of A with the multiplier
$z_1$
of A with the multiplier
In particular,
![]() $z_0$
is a repelling fixed point of B if and only if
$z_0$
is a repelling fixed point of B if and only if
![]() $z_1$
is a repelling fixed point of A. Furthermore, if
$z_1$
is a repelling fixed point of A. Furthermore, if
![]() $z_0$
is repelling and
$z_0$
is repelling and ![]() is a Poincaré function, then the equality
is a Poincaré function, then the equality
holds for some Poincaré function ![]() .
.
Proof. It is clear that
![]() $z_1$
is a fixed point of A, and a local calculation shows that equality (21) holds. Thus,
$z_1$
is a fixed point of A, and a local calculation shows that equality (21) holds. Thus,
![]() $z_1$
is a repelling fixed point of A if and only if
$z_1$
is a repelling fixed point of A if and only if
![]() $z_0$
is a repelling fixed point of B.
$z_0$
is a repelling fixed point of B.
The rest of the proof is obtained by a modification of the proof of the uniqueness of a Poincaré function (see e.g. [Reference Milnor12]). Namely, considering the function
holomorphic in a neighborhood of zero and satisfying
![]() $G(0)=0,$
we see that
$G(0)=0,$
we see that

Comparing now coefficients of the Taylor expansions in the left and the right parts of this equality, and taking into account that
![]() $\unicode{x3bb} _0$
is not a root of unity, we conclude that
$\unicode{x3bb} _0$
is not a root of unity, we conclude that
![]() $G=z^{\mathrm {ord}_{z_0} X}$
for some choice of
$G=z^{\mathrm {ord}_{z_0} X}$
for some choice of ![]() , implying equality (22).
, implying equality (22).
Lemma 3.4. Let A be a rational function of degree at least two,
![]() $z_0$
its repelling fixed point with the multiplier
$z_0$
its repelling fixed point with the multiplier
![]() $\unicode{x3bb} ,$
and
$\unicode{x3bb} ,$
and ![]() a Poincaré function. Assume that
a Poincaré function. Assume that
![]() $C: f(x,y)=0$
is an irreducible algebraic curve, and
$C: f(x,y)=0$
is an irreducible algebraic curve, and
![]() $d_1,d_2$
are positive integers such that the equality
$d_1,d_2$
are positive integers such that the equality
holds. Then
![]() $d_1=d_2$
, and C is the diagonal
$d_1=d_2$
, and C is the diagonal
![]() $x=y$
.
$x=y$
.
Proof. Since
is a parameterization of C, it is clear that C is not a vertical or horizontal line. Furthermore, substituting
![]() $\unicode{x3bb} _0z$
for z into equality (23), we see that the curve C is
$\unicode{x3bb} _0z$
for z into equality (23), we see that the curve C is
![]() $(A^{\circ d_1}, A^{\circ d_2})$
-invariant. Therefore, by Theorem 2.3, there exist non-constant holomorphic maps
$(A^{\circ d_1}, A^{\circ d_2})$
-invariant. Therefore, by Theorem 2.3, there exist non-constant holomorphic maps
![]() $X_1,X_2: \widetilde {\mathcal C}\rightarrow {\mathbb C}{\mathbb P}^1$
and
$X_1,X_2: \widetilde {\mathcal C}\rightarrow {\mathbb C}{\mathbb P}^1$
and
![]() $B:\widetilde {\mathcal C}\rightarrow \widetilde {\mathcal C}$
such that the diagram
$B:\widetilde {\mathcal C}\rightarrow \widetilde {\mathcal C}$
such that the diagram

commutes. Thus,
and hence
![]() $d_1=d_2.$
Since the parameterization of C has the form (24), this implies that C is the diagonal.
$d_1=d_2.$
Since the parameterization of C has the form (24), this implies that C is the diagonal.
Corollary 3.5. Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
be rational functions of degree at least two,
$A_2$
be rational functions of degree at least two,
![]() $z_1$
,
$z_1$
,
![]() $z_2$
their repelling fixed points with multipliers
$z_2$
their repelling fixed points with multipliers
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2$
, and
$\unicode{x3bb} _1, \unicode{x3bb} _2$
, and ![]() ,
, ![]() Poincaré functions. Assume that
Poincaré functions. Assume that
![]() $C: f(x,y)=0$
is an irreducible algebraic curve and
$C: f(x,y)=0$
is an irreducible algebraic curve and
![]() $d_1,d_2,\widetilde d_1,\widetilde d_2$
are positive integers such that
$d_1,d_2,\widetilde d_1,\widetilde d_2$
are positive integers such that
![]() $\mathrm {GCD }(d_1,d_2)=1$
and the equalities
$\mathrm {GCD }(d_1,d_2)=1$
and the equalities
hold. Then there exists a positive integer k such that the equalities
hold.
Proof. It is clear that equalities (25) and (26) imply the equalities
and
Eliminating now from these equalities ![]() , we conclude that the functions
, we conclude that the functions ![]() and
and ![]() are algebraically dependent. Therefore,
are algebraically dependent. Therefore,
![]() $\widetilde d_1d_2=d_1\widetilde d_2$
by Lemma 3.4, implying equalities (27).
$\widetilde d_1d_2=d_1\widetilde d_2$
by Lemma 3.4, implying equalities (27).
Proof of Theorem 1.1
Let
![]() $C: f(x,y)=0$
be an irreducible algebraic curve with a generically one-to-one parameterization by rational functions
$C: f(x,y)=0$
be an irreducible algebraic curve with a generically one-to-one parameterization by rational functions
![]() $z\rightarrow (X_1(z),X_2(z))$
, and
$z\rightarrow (X_1(z),X_2(z))$
, and
![]() $d_1, d_2$
coprime positive integers. Assume that the diagram (8) commutes for some rational function B with a repelling fixed point
$d_1, d_2$
coprime positive integers. Assume that the diagram (8) commutes for some rational function B with a repelling fixed point
![]() $z_0$
, and equalities (9) and (10) hold. Then, denoting the multiplier of
$z_0$
, and equalities (9) and (10) hold. Then, denoting the multiplier of
![]() $z_0$
by
$z_0$
by
![]() $\unicode{x3bb} $
and using Lemma 3.3, we see that
$\unicode{x3bb} $
and using Lemma 3.3, we see that
and

Since
this implies that
Finally, equality (10) implies that if equality (29) holds, then equality (7) also holds. This proves the ‘if’ part of the theorem.
To prove the ‘only if’ part, it is enough to show that equality (7) implies that there exist positive integers
![]() $r_1,r_2$
such that
$r_1,r_2$
such that
Indeed, in this case, substituting
![]() $\unicode{x3bb} z$
for z into equality (7), we obtain the equality
$\unicode{x3bb} z$
for z into equality (7), we obtain the equality
Therefore, for
the curve C is
![]() $(A_1^{\circ l_1}, A_2^{\circ l_2})$
-invariant, implying by Theorem 2.3 that C has genus zero and there exist rational functions
$(A_1^{\circ l_1}, A_2^{\circ l_2})$
-invariant, implying by Theorem 2.3 that C has genus zero and there exist rational functions
![]() $X_1,X_2$
and B such that the diagram (8) commutes and the map
$X_1,X_2$
and B such that the diagram (8) commutes and the map
![]() $z\rightarrow (X_1(z),X_2(z))$
is a generically one-to-one parameterization of C. It follows now from Lemma 3.1 that there exists a meromorphic function
$z\rightarrow (X_1(z),X_2(z))$
is a generically one-to-one parameterization of C. It follows now from Lemma 3.1 that there exists a meromorphic function
![]() ${\varphi }$
such that the equalities
${\varphi }$
such that the equalities
hold. Thus,
implying that equalities (9) hold for the point
![]() $z_0={\varphi }(0).$
$z_0={\varphi }(0).$
Further, since
![]() $z_1$
and
$z_1$
and
![]() $z_2$
are fixed points of
$z_2$
are fixed points of
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, the point
$A_2$
, the point
![]() $z_0$
is a preperiodic point of B. Thus, changing in equation (8) the functions B and
$z_0$
is a preperiodic point of B. Thus, changing in equation (8) the functions B and
![]() $A_1^{\circ l_1}, A_2^{\circ l_2}$
to some of their iterates, and the point
$A_1^{\circ l_1}, A_2^{\circ l_2}$
to some of their iterates, and the point
![]() $z_0$
to some point in its B-orbit, we may assume that
$z_0$
to some point in its B-orbit, we may assume that
![]() $z_0$
is a fixed point of B. Moreover,
$z_0$
is a fixed point of B. Moreover,
![]() $z_0$
is repelling by Lemma 3.3. Let us recall now that, by what is proved above, equalities (8) and (9) imply equality (29). Thus, equalities (7) and (29) hold simultaneously and hence equality (10) holds by Corollary 3.5.
$z_0$
is repelling by Lemma 3.3. Let us recall now that, by what is proved above, equalities (8) and (9) imply equality (29). Thus, equalities (7) and (29) hold simultaneously and hence equality (10) holds by Corollary 3.5.
Let us show now that equality (7) implies equality (30). Assume first that
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are not generalized Lattès maps. Substituting
$A_2$
are not generalized Lattès maps. Substituting
![]() $\unicode{x3bb} _2z$
for z into equality (7), we obtain the equality
$\unicode{x3bb} _2z$
for z into equality (7), we obtain the equality

implying that the functions ![]() and
and ![]() satisfy the equality
satisfy the equality
where
![]() $g(x,y)=f(x,A_2^{\circ d_2}(y)).$
Eliminating now from equalities (7) and (31) the function
$g(x,y)=f(x,A_2^{\circ d_2}(y)).$
Eliminating now from equalities (7) and (31) the function ![]() , we conclude that the functions
, we conclude that the functions ![]() and
and ![]() are algebraically dependent. In turn, this implies that the functions
are algebraically dependent. In turn, this implies that the functions ![]() and
and ![]() also are algebraically dependent.
also are algebraically dependent.
Let
![]() $\widetilde C: \widetilde f(x,y)=0$
be a curve such that
$\widetilde C: \widetilde f(x,y)=0$
be a curve such that
Then, substituting
![]() $\unicode{x3bb} _1 z$
for z, we see that
$\unicode{x3bb} _1 z$
for z, we see that
![]() $\widetilde f$
is
$\widetilde f$
is
![]() $(A_1,A_1)$
-invariant. Therefore, by Theorem 2.4, there exist rational functions
$(A_1,A_1)$
-invariant. Therefore, by Theorem 2.4, there exist rational functions
![]() $V_1$
and
$V_1$
and
![]() $V_2$
commuting with
$V_2$
commuting with
![]() $A_1$
such that
$A_1$
such that
![]() $\widetilde C$
is a component of the curve
$\widetilde C$
is a component of the curve
implying that the equality
holds. Furthermore, it follows from the Ritt theorem that there exist positive integers
![]() $s_1,s_2$
, and s such that
$s_1,s_2$
, and s such that
Since equality (32) implies that for every
![]() $l\geq 1$
, the equality
$l\geq 1$
, the equality
holds, setting
we see that
![]() $W_1$
and
$W_1$
and
![]() $W_2$
also commute with
$W_2$
also commute with
![]() $A_1$
and satisfy
$A_1$
and satisfy
In addition,
![]() $z_1$
is a fixed point of
$z_1$
is a fixed point of
![]() $W_1$
by equality (33). Finally, since equality (34) implies the equality
$W_1$
by equality (33). Finally, since equality (34) implies the equality
the point
![]() $z_1$
is also a fixed point of
$z_1$
is also a fixed point of
![]() $W_2$
.
$W_2$
.
Differentiating equality (34) at zero, we see that the multipliers
satisfy the equality
On the other hand, Lemma 3.2 yields that there exist positive integers
![]() $k_1, k_2,$
and k such that
$k_1, k_2,$
and k such that
It follows now from equalities (35) and (36) that
implying that
Moreover, since
![]() $\vert \unicode{x3bb} _1 \vert>1, \vert \unicode{x3bb} _2 \vert >1,$
the number
$\vert \unicode{x3bb} _1 \vert>1, \vert \unicode{x3bb} _2 \vert >1,$
the number
![]() $k_2- k_1$
is positive. This proves the implication (7)
$k_2- k_1$
is positive. This proves the implication (7)
![]() $\Rightarrow $
(30) in the case where
$\Rightarrow $
(30) in the case where
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are not generalized Lattès maps.
$A_2$
are not generalized Lattès maps.
Assume now that
![]() $A_1$
,
$A_1$
,
![]() $A_2$
are arbitrary non-special rational functions. Then, by Theorem 2.2, there exist rational functions
$A_2$
are arbitrary non-special rational functions. Then, by Theorem 2.2, there exist rational functions
![]() $F_1$
,
$F_1$
,
![]() $F_2, \theta _1, \theta _2$
such that the diagrams
$F_2, \theta _1, \theta _2$
such that the diagrams

commute, and
![]() $F_1$
,
$F_1$
,
![]() $F_2$
are not generalized Lattès maps. Further, since all the points in the preimage
$F_2$
are not generalized Lattès maps. Further, since all the points in the preimage
![]() $\theta _{A_i}^{-1}\{z_i\}, i=1,2$
, are
$\theta _{A_i}^{-1}\{z_i\}, i=1,2$
, are
![]() $F_i$
-preperiodic, there exist a positive integer N and fixed points
$F_i$
-preperiodic, there exist a positive integer N and fixed points
![]() $z_1', z_2'$
of
$z_1', z_2'$
of
![]() $F_1^{\circ N}, F_2^{\circ N}$
such that the diagrams
$F_1^{\circ N}, F_2^{\circ N}$
such that the diagrams

commute, and the equalities
hold. Moreover, if
![]() $\mu _i$
is the multiplier of
$\mu _i$
is the multiplier of
![]() $F_i^{\circ N}$
at
$F_i^{\circ N}$
at
![]() $z_i'$
,
$z_i'$
,
![]() $i=1,2,$
then, by Lemma 3.3, the equalities
$i=1,2,$
then, by Lemma 3.3, the equalities
hold.
Setting
and substituting
![]() $z^{d_1f_2}$
and
$z^{d_1f_2}$
and
![]() $z^{d_2f_1}$
for z into equalities (38) and (39), we obtain that
$z^{d_2f_1}$
for z into equalities (38) and (39), we obtain that

Thus, equality (7) implies that the functions ![]() and
and ![]() satisfy the equality
satisfy the equality
where
Since
![]() $F_1^{\circ N}, F_2^{\circ N}$
are not generalized Lattès maps, by what is proved above, there exist positive integers
$F_1^{\circ N}, F_2^{\circ N}$
are not generalized Lattès maps, by what is proved above, there exist positive integers
![]() $p_1,p_2$
such that
$p_1,p_2$
such that
![]() $\mu _1^{p_1}= \mu _2^{p_2},$
implying by equalities (37) that
$\mu _1^{p_1}= \mu _2^{p_2},$
implying by equalities (37) that
Thus, equality (30) holds for the integers
Proof of Corollary 1.2
If ![]() ,
, ![]() are algebraically dependent, then it follows from the commutativity of the diagram (8) that
are algebraically dependent, then it follows from the commutativity of the diagram (8) that
implying that
![]() $n_1^{l_1}=n_2^{l_2}.$
Furthermore, it follows from equalities (28) that
$n_1^{l_1}=n_2^{l_2}.$
Furthermore, it follows from equalities (28) that
The following result shows that if
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are not generalized Lattès maps, then dependencies of the form (7) actually reduce to dependencies of the form (1).
$A_2$
are not generalized Lattès maps, then dependencies of the form (7) actually reduce to dependencies of the form (1).
Theorem 3.6. Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
be rational functions of degree at least two that are not generalized Lattès maps,
$A_2$
be rational functions of degree at least two that are not generalized Lattès maps,
![]() $z_1$
,
$z_1$
,
![]() $z_2$
their repelling fixed points with multipliers
$z_2$
their repelling fixed points with multipliers
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2$
, and
$\unicode{x3bb} _1, \unicode{x3bb} _2$
, and ![]() ,
, ![]() Poincaré functions. Assume that
Poincaré functions. Assume that
![]() $C: f(x,y)=0$
is an irreducible algebraic curve, and
$C: f(x,y)=0$
is an irreducible algebraic curve, and
![]() $d_1, d_2$
are coprime positive integers such that the equality
$d_1, d_2$
are coprime positive integers such that the equality
holds. Then,
![]() $d_1=d_2=1$
and C has genus zero. Furthermore, if
$d_1=d_2=1$
and C has genus zero. Furthermore, if
![]() $C: f(x,y)=0$
is an irreducible curve of genus zero with a generically one-to-one parameterization by rational functions
$C: f(x,y)=0$
is an irreducible curve of genus zero with a generically one-to-one parameterization by rational functions
![]() $z\rightarrow (X_1(z),X_2(z))$
, then the equality
$z\rightarrow (X_1(z),X_2(z))$
, then the equality
holds for some Poincaré functions ![]() ,
, ![]() if and only if there exist positive integers
if and only if there exist positive integers
![]() $l_1,l_2$
and a rational function B with a repelling fixed point
$l_1,l_2$
and a rational function B with a repelling fixed point
![]() $z_0$
such that the diagram
$z_0$
such that the diagram

commutes, and the equalities
hold.
Proof. The proof is obtained by a modification of the proof of Theorem 1.1, taking into account that if
![]() $A_1, A_2$
are not generalized Lattès maps, then it follows from the commutativity of the diagram (8) by Proposition 2.1 that there exist rational functions
$A_1, A_2$
are not generalized Lattès maps, then it follows from the commutativity of the diagram (8) by Proposition 2.1 that there exist rational functions
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
such that the equalities
$Y_2$
such that the equalities
hold for some
![]() $d_1,d_2\geq 0$
. Therefore, for any repelling fixed point
$d_1,d_2\geq 0$
. Therefore, for any repelling fixed point
![]() $z_0$
of B, the inequalities (40) hold by the chain rule. Thus,
$z_0$
of B, the inequalities (40) hold by the chain rule. Thus,
![]() $d_1=d_2=1$
by equalities (10).
$d_1=d_2=1$
by equalities (10).
Notice that unlike the case of Böttcher functions, algebraic dependencies of the form (1) of degree greater than one between Poincaré functions do exist. The simplest of them are graphs constructed as follows. Let us take any two rational functions U and V, and set
Then the diagram

obviously commutes. Moreover, if
![]() $z_0$
is a repelling fixed point of
$z_0$
is a repelling fixed point of
![]() $A_1$
, then the point
$A_1$
, then the point
![]() $z_1=V(z_0)$
is a repelling fixed point of
$z_1=V(z_0)$
is a repelling fixed point of
![]() $A_2$
by Lemma 3.3. Finally, the first equality in (41) implies that
$A_2$
by Lemma 3.3. Finally, the first equality in (41) implies that
![]() $V'(z_1)\neq 0.$
Therefore,
$V'(z_1)\neq 0.$
Therefore,
by Lemma 3.3.
Notice also that the equality
![]() $d_1=d_2=1$
provided by Theorem 3.6 does not hold for arbitrary non-special
$d_1=d_2=1$
provided by Theorem 3.6 does not hold for arbitrary non-special
![]() $A_1, A_2$
. For example, let A be any rational function of the form
$A_1, A_2$
. For example, let A be any rational function of the form
![]() $A=zR^d(z)$
, where
$A=zR^d(z)$
, where
![]() $R\in {\mathbb C}(z)$
and
$R\in {\mathbb C}(z)$
and
![]() $d>1.$
Then one can easily check that
$d>1.$
Then one can easily check that ![]() , where
, where ![]() is defined by the equalities
is defined by the equalities
is a minimal holomorphic map between orbifolds. Thus, A is a generalized Lattès map. Furthermore, the diagram

obviously commutes. Choosing now R in such a way that zero is a repelling fixed point of
![]() $zR(z^d)$
and denoting by
$zR(z^d)$
and denoting by
![]() $\unicode{x3bb} $
the multiplier of
$\unicode{x3bb} $
the multiplier of
![]() $zR^d(z)$
at zero, we obtain by Lemma 3.3 that
$zR^d(z)$
at zero, we obtain by Lemma 3.3 that
Thus, ![]() and
and ![]() are algebraically dependent.
are algebraically dependent.
4. Algebraic dependencies between Böttcher functions
4.1. Polynomial semiconjugacies and invariant curves
If
![]() $A_1$
,
$A_1$
,
![]() $A_2$
are non-special polynomials of degree at least two, then any irreducible
$A_2$
are non-special polynomials of degree at least two, then any irreducible
![]() $(A_1,A_2)$
-invariant curve C that is not a vertical or horizontal line has genus zero and allows for a generically one-to-one parameterization by polynomials
$(A_1,A_2)$
-invariant curve C that is not a vertical or horizontal line has genus zero and allows for a generically one-to-one parameterization by polynomials
![]() $X_1,X_2$
such that the diagram
$X_1,X_2$
such that the diagram

commutes for some polynomial B (see [Reference Medvedev and Scanlon11, Proposition 2.34] or [Reference Pakovich17, §4.3]).
For fixed polynomials A, B of degree at least two, we denote by ![]() the set (possibly empty) consisting of polynomials X of degree at least two such that the diagram (20) commutes. The following result was proved in [Reference Pakovich17] as a corollary of the results in [Reference Pakovich15].
the set (possibly empty) consisting of polynomials X of degree at least two such that the diagram (20) commutes. The following result was proved in [Reference Pakovich17] as a corollary of the results in [Reference Pakovich15].
Theorem 4.1. Let A and B be fixed non-special polynomials of degree at least two such that the set ![]() is non-empty, and let
is non-empty, and let
![]() $X_0$
be an element of
$X_0$
be an element of ![]() of the minimum possible degree. Then a polynomial X belongs to
of the minimum possible degree. Then a polynomial X belongs to ![]() if and only if
if and only if
![]() $X= \widetilde A\circ X_0$
for some polynomial
$X= \widetilde A\circ X_0$
for some polynomial
![]() $\widetilde A$
commuting with
$\widetilde A$
commuting with
![]() $A.$
$A.$
Notice that applying Theorem 4.1 for
![]() $B=A$
, one can reprove the classification of commuting polynomials and, more generally, of commutative semigroups of
$B=A$
, one can reprove the classification of commuting polynomials and, more generally, of commutative semigroups of
![]() ${\mathbb C}[z]$
obtained in [Reference Eigenthaler and Woracek5, Reference Ritt28, Reference Ritt29] (see [Reference Pakovich24, §7.1], for more detail). On the other hand, applying Theorem 4.1 to the system of equation (42) with
${\mathbb C}[z]$
obtained in [Reference Eigenthaler and Woracek5, Reference Ritt28, Reference Ritt29] (see [Reference Pakovich24, §7.1], for more detail). On the other hand, applying Theorem 4.1 to the system of equation (42) with
![]() $A_1=A_2=A$
, we see that
$A_1=A_2=A$
, we see that
![]() $X_1, X_2$
cannot provide a generically one-to-one parameterization of C, unless one of the polynomials
$X_1, X_2$
cannot provide a generically one-to-one parameterization of C, unless one of the polynomials
![]() $X_1$
,
$X_1$
,
![]() $X_2$
has degree one. Moreover if, say,
$X_2$
has degree one. Moreover if, say,
![]() $X_1$
has degree one, then without loss of generality, we may assume that
$X_1$
has degree one, then without loss of generality, we may assume that
![]() $X_1=z,$
implying that
$X_1=z,$
implying that
![]() $B=A$
and
$B=A$
and
![]() $X_2$
commutes with A. Thus, we obtain the following result obtained by Medvedev and Scanlon [Reference Medvedev and Scanlon11].
$X_2$
commutes with A. Thus, we obtain the following result obtained by Medvedev and Scanlon [Reference Medvedev and Scanlon11].
Theorem 4.2. Let A be a non-special polynomial of degree at least two, and C an irreducible algebraic curve that is not a vertical or horizontal line. Then, C is
![]() $(A,A)$
-invariant if and only if C has the form
$(A,A)$
-invariant if and only if C has the form
![]() $x= P(y)$
or
$x= P(y)$
or
![]() $y=P(x)$
, where P is a polynomial commuting with A.
$y=P(x)$
, where P is a polynomial commuting with A.
Finally, yet another corollary of Theorem 4.1 is the following result, which complements the classification of
![]() $(A_1,A_2)$
-invariant curves obtained in [Reference Medvedev and Scanlon11] (see [Reference Pakovich17, Theorem 1.4]).
$(A_1,A_2)$
-invariant curves obtained in [Reference Medvedev and Scanlon11] (see [Reference Pakovich17, Theorem 1.4]).
Theorem 4.3. Let
![]() $A_1$
,
$A_1$
,
![]() $A_2$
be non-special polynomials of degree at least two, and C a curve. Then C is an irreducible
$A_2$
be non-special polynomials of degree at least two, and C a curve. Then C is an irreducible
![]() $(A_1,A_2)$
-invariant curve if and only if C has the form
$(A_1,A_2)$
-invariant curve if and only if C has the form
![]() $Y_1(x)-Y_2(y)=0$
, where
$Y_1(x)-Y_2(y)=0$
, where
![]() $Y_1,Y_2$
are polynomials of coprime degrees satisfying the equations
$Y_1,Y_2$
are polynomials of coprime degrees satisfying the equations
for some polynomial
![]() $T.$
$T.$
4.2. Proof of Theorem 1.3
As in the case of Poincaré functions, we do not assume that considered Böttcher functions are normalized. Thus, the notation ![]() is used to denote some function satisfying the conditions (4) and (5).
is used to denote some function satisfying the conditions (4) and (5).
To prove Theorem 1.3, we need the following two lemmas.
Lemma 4.4. Let A, B be polynomials of degree at least two, and X a non-constant polynomial such that the diagram

commutes. Assume that ![]() is a Böttcher function. Then,
is a Böttcher function. Then,
for some Böttcher function ![]() .
.
Proof. The lemma follows from [Reference Nguyen14, Lemma 2.1].
Lemma 4.5. Let A be a polynomial of degree
![]() $n\geq 2$
, and
$n\geq 2$
, and ![]() a Böttcher function. Assume that
a Böttcher function. Assume that
![]() $C: f(x,y)=0$
is an irreducible algebraic curve, and
$C: f(x,y)=0$
is an irreducible algebraic curve, and
![]() $d_1,d_2$
are positive integers such that
$d_1,d_2$
are positive integers such that
![]() $d_1\leq d_2$
and the equality
$d_1\leq d_2$
and the equality
holds. Then, C is a graph
where P is a polynomial commuting with A, and the equality
holds.
Proof. Substituting
![]() $z^n$
for z in equation (43), we see that the curve C is
$z^n$
for z in equation (43), we see that the curve C is
![]() $(A, A)$
-invariant. Therefore, by Theorem 4.2, C is a graph of the form
$(A, A)$
-invariant. Therefore, by Theorem 4.2, C is a graph of the form
![]() $x= P(y)$
or
$x= P(y)$
or
![]() $y=P(x)$
, where P is a polynomial commuting with A. Taking into account that
$y=P(x)$
, where P is a polynomial commuting with A. Taking into account that
![]() $d_1\leq d_2$
, this implies that equalities (44) and (45) hold.
$d_1\leq d_2$
, this implies that equalities (44) and (45) hold.
Corollary 4.6. Let
![]() $A_1, A_2$
be polynomials of degree at least two, and
$A_1, A_2$
be polynomials of degree at least two, and ![]() Böttcher functions. Assume that
Böttcher functions. Assume that
![]() $C: f(x,y)=0$
is an irreducible algebraic curve of genus zero, and
$C: f(x,y)=0$
is an irreducible algebraic curve of genus zero, and
![]() $d_1,d_2,\widetilde d_1,\widetilde d_2$
are positive integers such that
$d_1,d_2,\widetilde d_1,\widetilde d_2$
are positive integers such that
![]() $\mathrm {GCD }(d_1,d_2)=1$
and the equalities
$\mathrm {GCD }(d_1,d_2)=1$
and the equalities
hold. Then there exists a positive integer k such that the equalities
hold.
Proof. It is clear that equalities (46) and (47) imply the equalities
and
and eliminating from these equalities the function ![]() , we conclude that the functions
, we conclude that the functions ![]() and
and ![]() are algebraically dependent. Therefore, by Lemma 4.5, one of these functions is a polynomial in the other.
are algebraically dependent. Therefore, by Lemma 4.5, one of these functions is a polynomial in the other.
Assume, say, that
(the other case is considered similarly). Then substituting the right part of this equality for the left part in equality (49), we conclude that
implying that
Let us observe now that equalities (47) and (51) imply that the curve
![]() $f(x,y)=0$
is invariant under the map
$f(x,y)=0$
is invariant under the map
Since the commutativity of diagram (42) implies that
![]() $\mathrm {deg\,} A_1=\mathrm {deg\,} A_2,$
this yields that
$\mathrm {deg\,} A_1=\mathrm {deg\,} A_2,$
this yields that
![]() $\mathrm {deg\,} R=1$
. It follows now from equality (50) that
$\mathrm {deg\,} R=1$
. It follows now from equality (50) that
implying equality (48).
Proof of Theorem 1.3
To prove the ‘if’ part, it is enough to observe that if equalities (12) and (13) hold, then by Lemma 4.4,

In the other direction, if equality (11) holds, then setting
![]() $n_1=\mathrm {deg\,} A_1, n_2=\mathrm {deg\,} A_2$
, and substituting
$n_1=\mathrm {deg\,} A_1, n_2=\mathrm {deg\,} A_2$
, and substituting
![]() $z^{n_2}$
for z into equality (11), we obtain the equality
$z^{n_2}$
for z into equality (11), we obtain the equality
Eliminating now ![]() from equalities (11) and (52), we conclude that the functions
from equalities (11) and (52), we conclude that the functions ![]() and
and ![]() are algebraically dependent. Since the corresponding algebraic curve
are algebraically dependent. Since the corresponding algebraic curve
![]() $\widetilde f(x,y)=0$
such that
$\widetilde f(x,y)=0$
such that
is
![]() $(A_1,A_1)$
-invariant, it follows from Theorem 4.2 that
$(A_1,A_1)$
-invariant, it follows from Theorem 4.2 that
for some polynomial P commuting with
![]() $A_1.$
Clearly, equality (53) implies that
$A_1.$
Clearly, equality (53) implies that
![]() $\mathrm {deg\,} P=n_2.$
On the other hand, by the Ritt theorem, P and
$\mathrm {deg\,} P=n_2.$
On the other hand, by the Ritt theorem, P and
![]() $A_1$
have a common iterate. Therefore, there exist positive integers
$A_1$
have a common iterate. Therefore, there exist positive integers
![]() $l_1, l_2$
such that
$l_1, l_2$
such that
![]() $n_1^{l_1}=n_2^{l_2}.$
$n_1^{l_1}=n_2^{l_2}.$
Setting now
and substituting
![]() $z^{n}$
for z into equality (11), we obtain that
$z^{n}$
for z into equality (11), we obtain that
![]() $f(x,y)=0$
is
$f(x,y)=0$
is
![]() $(A_1^{\circ l_1}, A_2^{\circ l_2})$
-invariant, implying that condition (12) holds. Moreover, by Theorem 4.3,
$(A_1^{\circ l_1}, A_2^{\circ l_2})$
-invariant, implying that condition (12) holds. Moreover, by Theorem 4.3,
![]() $f(x,y)=0$
has the form
$f(x,y)=0$
has the form
where
![]() $Y_1,Y_2$
are polynomials of coprime degrees. Since a generically one-to-one parameterization
$Y_1,Y_2$
are polynomials of coprime degrees. Since a generically one-to-one parameterization
![]() $z\rightarrow (X_1(z),X_2(z))$
of curve (54) satisfies the conditions
$z\rightarrow (X_1(z),X_2(z))$
of curve (54) satisfies the conditions
we conclude that the degrees
of the functions
![]() $X_1$
and
$X_1$
and
![]() $X_2$
in diagram (12) satisfy
$X_2$
in diagram (12) satisfy
![]() $\mathrm {GCD }(d_1',d_2')=1.$
Using now the ‘if’ part of the theorem, we see that the equalities (11) and
$\mathrm {GCD }(d_1',d_2')=1.$
Using now the ‘if’ part of the theorem, we see that the equalities (11) and
hold simultaneously, implying by Corollary 4.6 that equalities
![]() $d_1'=d_1, d_2'=d_2,$
and equality (13) hold.
$d_1'=d_1, d_2'=d_2,$
and equality (13) hold.
Acknowledgement
This research was supported by ISF Grant No. 1092/22.


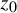
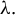
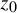
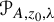 meromorphic on
meromorphic on 
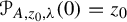 ,
, 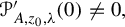 and
and 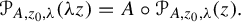 In this paper, we study the following problem: given Poincaré functions
In this paper, we study the following problem: given Poincaré functions 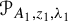 and
and 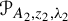 , find out if there is an algebraic relation
, find out if there is an algebraic relation 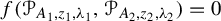 between them and, if such a relation exists, describe the corresponding algebraic curve
between them and, if such a relation exists, describe the corresponding algebraic curve