Genome-wide association studies (GWAS) have conventionally focused on identifying associations between individual single-nucleotide polymorphisms (SNPs) and the phenotype, but there is growing interest in modeling more complex effects such as interactions. Genome-wide studies of pairwise interactions between SNPs have shown promising results (e.g., Hu et al., Reference Hu, Liu, Zhang, Li, Wang, He and Shi2010; Lippert et al., Reference Lippert, Listgarten, Davidson, Baxter, Poon, Kadie and Heckerman2013; Wan et al., Reference Wan, Yang, Yang, Xue, Fan, Tang and Yu2010a; Wan et al., Reference Wan, Yang, Yang, Xue, Tang and Yu2010b). For instance, Hemani et al. (Reference Hemani, Shakhbazov, Westra, Esko, Henders, McRae and Powell2014) recently identified and replicated 30 pairwise interactions associated with gene expression levels. Identifying SNP–SNP interactions could help close the gap of ‘missing heritability’ from GWAS by reducing estimates of narrow-sense heritability inflated by ‘phantom heritability’ from interactions (Zuk et al., Reference Zuk, Hechter, Sunyaev and Lander2012). Epistatic effects could also contribute large components of broad-sense heritability that would not be detected by univariate tests of association (Culverhouse et al., Reference Culverhouse, Suarez, Lin and Reich2002). In either case, however, the abundance of competing models for these interactions can lead to confusion and slow research efforts.
One primary source of confusion is the distinction between the biological definition of epistasis as a masking effect (Bateson, Reference Bateson1909) and the statistical definition involving deviation from additivity for the effects of genetic factors on quantitative outcomes (Fisher, Reference Fisher1918). As a further complication, the statistical definition of epistasis is scale-dependent. Cordell (Reference Cordell2009) provides an excellent review of these historical issues.
As a result of the diversity of definitions of epistasis in the literature, there are a multitude of statistical models for epistasis and, more recently, interactions between SNPs. Efforts to estimate all possible patterns of epistasis have identified numerous interpretable models (Li & Reich, Reference Li and Reich2000; Niu et al., Reference Niu, Zhang and Sha2009). The different software packages intended to test SNP–SNP interactions mirror this diversity (e.g., Herold et al., Reference Herold, Steffens, Brockschmidt, Baur and Becker2009; Purcell et al., Reference Purcell, Neale, Todd-Brown, Thomas, Ferreira, Bender and Sham2007; Ueki & Cordell, Reference Ueki and Cordell2012).
Although the implemented epistatic models are useful, the variety of models can make it difficult for researchers to meaningfully compare the results from different studies of epistasis. In particular, comparison of effect sizes and accumulation of studies of epistasis in meta-analysis are complicated by the use of differing models.
Therefore, in order to facilitate comparisons between differing studies of epistasis we have developed Epi2Loc, an R package for epistatic two-locus models, to easily convert between common models of pairwise epistasis for both dichotomous and continuous outcomes. Additional tools for power analysis and simulation studies using each available model are also included in the package.
Methods
Epistasis between two loci can be modeled using penetrance models, variance components, or the generalized linear model (GLM). Although each of these approaches models the same set of possible two-locus interactions, they rely on very different frameworks for describing the interaction. The models implemented in the Epi2Loc package are briefly introduced here.
Penetrance Models
Following the biological approach to epistasis, the first approach is to present the model as a table of conditional outcomes relative to the genotypes at two bi-allelic loci (Table 1). For dichotomous phenotypes, the outcome of interest is the penetrance. The penetrance is the probability of being affected (i.e., the probability of being in the ‘case’ group), conditional on genotype. Each entry in the table denotes the penetrance conditional on the corresponding genotypes; for example, f
5 = P(Y = 1|AaBb). Alternatively these risk models may be stated using log odds (
![]() $\log \frac{{P\left( {Y = 1|{\rm AaBb}} \right)}}{{P\left( {Y = 0|{\rm AaBb}} \right)}} = u\left( {f_5 } \right)$
; see Marchini et al., Reference Marchini, Donnelly and Cardon2005).
$\log \frac{{P\left( {Y = 1|{\rm AaBb}} \right)}}{{P\left( {Y = 0|{\rm AaBb}} \right)}} = u\left( {f_5 } \right)$
; see Marchini et al., Reference Marchini, Donnelly and Cardon2005).
TABLE 1 Saturated Model of Conditional Phenotypes at Two Bi-allelic Loci

As this model has a separate parameter for each cell it is saturated and fits any observable pattern of penetrances. Certain patterns of penetrances are biologically or statistically meaningful, such as patterns showing dominance of one locus over another. Such useful patterns can be modeled by imposing constraints on the cells of the penetrance table (Hallgrimsdottir & Yuster, Reference Hallgrimsdottir and Yuster2008; Li & Reich, Reference Li and Reich2000; Neuman & Rice, Reference Neuman and Rice1992; Niu et al., Reference Niu, Zhang and Sha2009; Todorov et al., Reference Todorov, Borecki and Rao1997; Vieland & Huang, Reference Vieland and Huang2003).
However, while the pattern of penetrances may be biologically meaningful, the individual parameters do not correspond to effects that have an easy conceptual interpretation. In order to get more interpretable parameters, it is common to define effects within the GLM framework.
Generalized Linear Models
The GLM relates the expected value of the phenotype to a linear function of the genotypes. Most commonly, this takes the form of linear regression, for a continuous phenotype, or logistic regression, for dichotomous phenotypes. For example, in the general case, logistic regression defines the probability of being affected conditional on the genotype as
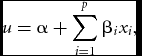 \begin{equation}
u = \alpha + \mathop \sum \limits_{i = 1}^p \beta _i x_i,
\end{equation}
\begin{equation}
u = \alpha + \mathop \sum \limits_{i = 1}^p \beta _i x_i,
\end{equation}
Using this structure, xi can be coded in a variety of ways to model the desired effects. The parameterization of xi is the key feature that distinguishes between many models for two-locus interactions. For instance, for a single locus let x 1 = ( − 1, 0, 1) and x 2 = ( − 0.5, 0.5, −0.5) code the genotypes (AA,Aa,aa) in order to reflect the additive trend and dominance deviation, respectively, at that locus. Define z 1 and z 2 similarly for the second locus. Then the linear model containing these variables and their cross products is
 \begin{eqnarray}
u &=& \alpha + \beta _1 x_1 + \beta _2 x_2 + \beta _3 z_1 + \beta _4 z_2 + \beta _5 x_1 z_1 + \beta _6 x_2 z_1 \nonumber\\
&& +\, \beta _7 x_1 z_2 + \beta _8 x_2 z_2 ,\end{eqnarray}
\begin{eqnarray}
u &=& \alpha + \beta _1 x_1 + \beta _2 x_2 + \beta _3 z_1 + \beta _4 z_2 + \beta _5 x_1 z_1 + \beta _6 x_2 z_1 \nonumber\\
&& +\, \beta _7 x_1 z_2 + \beta _8 x_2 z_2 ,\end{eqnarray}
which is the F 2 model described by Anderson and Kempthorne (Reference Anderson and Kempthorne1954). If x 2 and z 2 are instead coded (0,1,0) for the three genotypes at each locus, then Equation 3 corresponds to the F ∞ model (Hayman & Mather, Reference Hayman and Mather1955).
In either case, the model contains 9 degrees of freedom, providing a saturated model for the nine possible haplotypes for two bi-allelic loci. The resulting regression coefficients correspond to the additive effects of each locus (β1and β3, respectively), the dominance effects of each locus (β2 and β4, respectively), and their interactions (β5,β6, β7, and β8).
Other noteworthy parameterizations of the GLM include the Natural and Orthogonal Interactions (NOIA) model (Alvarez-Castro & Carlborg, Reference Alvarez-Castro and Carlborg2007), the General Two-Allele model (Zeng et al., Reference Zeng, Wang and Zou2005), and the Unweighted model (Cheverud & Routman, Reference Cheverud and Routman1995). Each of these models, as well as the F 2 and F ∞ models, is implemented in the Epi2Loc package, allowing simple conversion between these formulations. The reasons for this variety of parameterizations are highlighted by comparing the GLM framework to the variance components model.
Variance Components
The third common approach is to formulate epistasis in terms of a decomposition of the phenotypic variance. The total genetic effect of two loci Vg is partitioned into components for the additive (V A), dominance (V D), and interaction (V I) effects (Falconer & Mackay, Reference Falconer and Mackay1996).
Note that this is equivalent to a decomposition of the (broad sense) heritability since
where V ε is the remaining phenotypic variance due to environmental factors. The additive and dominance variance components can each be decomposed into the univariate effects of each locus (i.e., V A = V Aa + V Ab and V D = V Da + V Db ). Optionally, the phenotypic variance due to the interaction can also be further partitioned into an additive-by-additive effect, an additive-by-dominant effect, and a dominant-by-dominant effect.
with V AD further divisible to V AD + V DA to indicate whether the first or second locus is dominant in the interaction.
This complete decomposition loosely corresponds to the GLM parameters described for Equation 3, with V Acorresponding to β1 and β3, V D corresponding to β2and β4, and the components of V Icorresponding to the remaining four βs. The key distinction, however, is that the variance components are defined to be orthogonal whereas the GLM parameters are not necessarily independent. Due to the orthogonality of components, each component has a clear intuitive interpretation. For instance, V Aa = V Ab = V Da = V Db = 0 indicates an absence of marginal univariate effects for the two loci, but depending on the selected parameterization β1 = β2 = β3 = β4 = 0in the GLM framework (Equation 3) may not necessarily imply a lack of univariate effects if the remaining coefficients are non-zero. Furthermore, the variance components provide an intuitively meaningful scale for the magnitude of the effects, placing the observed effect on the same scale as broader heritability estimates.
To obtain independent GLM parameters that correspond to the classical variance components, it is necessary to consider the genotype frequencies for the two loci. The NOIA statistical model weights its variables in Equation 3 to ensure that the parameters are independent as long as the loci are uncorrelated (Alvarez-Castro & Carlborg, Reference Alvarez-Castro and Carlborg2007). This model allows direct conversion between GLM models and the variance components model. Other GLM parameterizations may similarly maintain orthogonal components under stronger restrictions. For instance, the G2 A model corresponds to the variance component decomposition if the loci are uncorrelated and Hardy–Weinberg equilibrium holds for both loci (Zeng et al., Reference Zeng, Wang and Zou2005).
It should be noted, however, that a given set of variance components does not uniquely define a two-locus GLM model. The variance components do not indicate the sign of any of the component effects, nor do they indicate the population mean. Only the magnitude of the effects is determined, with the resulting GLM parameters conditional on the allele frequencies. In addition, treating the variance components as a two-locus model only models the genetic effects for two loci, so any variance explained by covariates or other genetic effects must be modeled separately (i.e., by defining the components of V g as only the contribution of two loci, with any other genetic effects treated as independent and included in V ε).
Package Utilities
The Epi2Loc package provides functions for converting between the above models, generating data under a selected model, and performing power analysis. The methodology for accomplishing these tasks is summarized here. The Epi2Loc package is available from the Comprehensive R Archive Network (CRAN, http://cran.us.r-project.org/index.html).
Model conversions. Because the full model for each of the parameterizations described above is a saturated model for the nine possible two-locus genotype combinations, it is possible to equate any pair of models and convert to a different set of model parameters. In most cases, we rely on the GLM framework, rewriting Equation 2 in matrix form
where u is the vector (u AABB, u AaBB, u aaBB, u AABb, u AaBb, u aaBb, u AAbb, u Aabb, u aabb) and D is an appropriate design matrix. As before, the elements of u correspond to the conditional expected value of the phenotype such that g −1(u AABB) = E(y|AABB) for the selected link function g(·). Then, given a model with design matrix D 1, known parameters β1, and link function g 1(·), in order to compute the unknown model parameters for a model with design matrix D 2, and link function g 2(·), we solve
For conversions involving variance components, closed-form solutions exist relating each variance component to a parameter in the NOIA statistical model. For instance,
where p aa and p Aa are frequencies of the indicated genotype at the first locus. The full set of solutions for the NOIA statistical model is provided in Supplementary Materials (Section S2). Further conversions beyond the NOIA model can then be performed as described above. Utilizing the NOIA statistical model in this way ensures that the defined variance components will be orthogonal regardless of the minor allele frequency or violations of Hardy–Weinberg equilibrium at each locus. The only required assumption is that the two loci are uncorrelated (Alvarez-Castro & Carlborg, Reference Alvarez-Castro and Carlborg2007).
These conversions between models are useful to aid the interpretation of results from studying epistatic effects. Although the saturated model and the 4-df test of all interaction parameters are equivalent for all models, the individual parameters in each parameterization correspond to different effects under different assumptions. For example, the parameters for univariate effects estimate average marginal effects in the NOIA statistical model, average marginal effects under Hardy–Weinberg equilibrium in the G2 A model, marginal effects of allele substitution in the NOIA functional model, and marginal effects of genotype substitution in the genotype model (for further discussion of interpretation for these models, see Alvarez-Castro & Carlborg, Reference Alvarez-Castro and Carlborg2007; Zeng et al., Reference Zeng, Wang and Zou2005). In addition, the effects are estimated conditional on the remaining effects in the model; therefore, if the parameters are not orthogonal the estimates may vary depending on which other effects are included. In sum, it is important to select a model that estimates the genetic effects that are the focus of the investigation.
Data generation. Data generation from a selected two-locus model proceeds by constructing the appropriate N × 9 design matrix D as described above with rows corresponding to simulated or observed genotypes at two loci (Supplementary Materials, Section S1). The design matrix and model parameters are then used to compute the conditional expected value of the phenotype for each individual as E(y|D) = g −1(Dβ). For dichotomous phenotypes, the phenotype is then generated from a Bernoulli distribution with the defined probability. For continuous phenotypes, normally distributed random error is added to the expected value for each individual to obtain the desired phenotype.
Power analysis. The Epi2Loc package provides a power analysis tool for tests of parameters in a two-locus GLM model. Unsurprisingly, the power for a given hypothesis test in the two-locus model will depend on the effect to be tested based on the selected model. For linear regression with continuous phenotypes, power may be computed based on Cohen's f 2 effect size (Cohen, Reference Cohen1988). Specifically,
where R 2 F and R 2 R are the multiple R 2 for the full model (i.e., most often the saturated model) and the restricted model, respectively. The restricted model is defined by constraining one or more parameters β to zero. This effect size is then used to estimate the non-centrality parameter for the distribution of the F-test corresponding to this hypothesis test, providing an estimate of power at a given sample size as described by Cohen (Reference Cohen1988).
For dichotomous outcomes, power may instead be computed based on the asymptotic power of the likelihood ratio test comparing the full and restricted models. Briefly, the saturated model and the genotype frequencies of the two loci are used to compute the expected value of the information matrix for logistic or probit regression. The Epi2Loc package then estimates the power for the test by computing the non-centrality parameter for the likelihood ratio test of the full and reduced models based on the expected information matrix (Cox & Hinkley, Reference Cox and Hinkley1974), using an implementation of this approach in the R package asypow (Halvorsen et al., Reference Halvorsen, Brown, Lovato and Russel2013).
Results and Discussion
Sample Analysis
To demonstrate the use of the Epi2Loc package, we consider data on two SNPs associated with rheumatoid arthritis. In analysis of the transcriptional regulatory network of NF-κB using multifactor dimensionality reduction (MDR; Hahn et al., Reference Hahn, Ritchie and Moore2003), Julia et al. (Reference Julia, Moore, Miquel, Alegre, Barcelo, Ritchie and Marsal2007) identified an interaction between rs1290754 and rs1800797 associated with risk for rheumatoid arthritis. The reported penetrance and genotype frequencies for these two loci are summarized in Table 2. The genotype frequencies suggest the two loci are uncorrelated (r = -0.06, p = .19).
TABLE 2 Interaction of rs1290754 and rs1800797 Associated with Rheumatoid Arthritis

aConditional penetrances of rheumatoid arthritis reported by Julia et al. (Reference Julia, Moore, Miquel, Alegre, Barcelo, Ritchie and Marsal2007).bReported genotype frequencies. Total N = 439.
Because this interaction was identified using MDR, parametric effect sizes were not computed. To aid in understanding the magnitude of the effect for these two loci, the Epi2Loc package may be used to convert the reported penetrances to a variance components model. The resulting variance components indicate that the two loci jointly explain 7.3% of the phenotypic variance, with the largest effects attributable to an additive by dominance interaction explaining 3.5% of the phenotypic variance and followed by a dominance effect of rs1290754 explaining 1.8% of the variance.
The Epi2Loc package may also be used to construct a design matrix to test the significance of specific GLM model parameters for this data. Using the NOIA statistical model, the Wald test for the additive (rs1290754) by dominant (rs1800797) interaction is significant (p = .001). There is also strong evidence of dominance deviation for rs1290754, but the effect is not significant after correcting for multiple testing of eight coefficients (uncorrected p = .015).
Lastly, treating the observed penetrances as the population values, we can investigate the power to detect the additive by dominance interaction and the dominance effect of rs1290754. As shown by Figure 1, the sample of N = 439 provides sufficient power to detect the interaction explaining 3.5% of the phenotypic variance at the α = 0.05 level, but a larger sample would be required to reliably detect the dominance effect.

FIGURE 1 Power analysis for effects of rs1290754 and rs1800797. Note: Post-hoc power analysis for the additive-by-dominant interaction of rs1290754 and rs1800797 and the dominance deviation of rs1800797 estimated from data reported by Julia et al. (Reference Julia, Moore, Miquel, Alegre, Barcelo, Ritchie and Marsal2007). Vertical reference line indicates observed sample size N = 439.
These power estimates are likely to be optimistic, however, compared to many genome-wide studies. Notably, the effect sizes observed by Julia et al. (Reference Julia, Moore, Miquel, Alegre, Barcelo, Ritchie and Marsal2007) are quite large; in comparison, the epistatic interactions among 238 SNPs identified by Hemani et al. (Reference Hemani, Shakhbazov, Westra, Esko, Henders, McRae and Powell2014) jointly explained only 0.22% of the phenotypic variance in the discovery sample. In addition, considering power at α = 0.05 does not account for the multiple testing burdens in the likely scenario of testing pairwise interactions for large sets of genome-wide SNPs. For example, achieving power of 0.8 to detect an additive-by-additive interaction explaining 0.25% of the variance with α = 10−8 requires over 17,000 individuals.
Existing Software
Existing software offers some support for studying epistatic effects, but does not offer the same flexibility of the Epi2Loc package for working with a wide range of model parameterizations. For instance, the epistatic model implemented in PLINK (Purcell et al., Reference Purcell, Neale, Todd-Brown, Thomas, Ferreira, Bender and Sham2007) by default only considers additive-by-additive interactions (V AA) with limited parameterizations of the single locus effects. CASSI (Ueki & Cordell, Reference Ueki and Cordell2012) similarly limits testing of epistasis to the 1-df test of the additive-by-additive interaction. As epistatic variance components may be evenly split among V AA, V AD, V DA, and V DD (Hemani et al., Reference Hemani, Shakhbazov, Westra, Esko, Henders, McRae and Powell2014), this testing approach may not identify a large proportion of existing epistatic effects. More options for considering these additional interaction components are available in INTERSNP (Herold et al., Reference Herold, Steffens, Brockschmidt, Baur and Becker2009), but GLM model parameterization in INTERSNP is restricted to the F 2 model (Anderson & Kempthorne, Reference Anderson and Kempthorne1954). In comparison, the Epi2Loc package offers support for seven GLM model parameterizations, as well as penetrance and variance component models.
Additional software packages have pursued a model-free heuristic approach to identifying epistasis (e.g., GWIS — Goudey et al., Reference Goudey, Rawlinson, Wang, Shi, Ferra, Campbell and Kowalczyk2013; MDR — Hahn et al., Reference Hahn, Ritchie and Moore2003). Although these methods are useful, the lack of effect sizes for these models can make the interpretation of results and comparisons across studies challenging. In contrast, the Epi2Loc package supports computation of variance components from any included model to simplify interpretation and comparison.
As a result, the Epi2Loc package offers a useful supplement to the existing software in order to interpret the results of genome-wide interaction studies. For instance, a genome-wide scan using saturated two-locus models may be performed using INTERSNP, and the Epi2Loc package may then be used to compute variance components for the resulting F 2 model parameters. Alternatively, the Epi2Loc package could be used to perform the complete analysis, but computing all pairwise interactions genome-wide is computationally expensive and likely to benefit from optimization in stand-alone software. Therefore, use of the Epi2Loc package is recommended for interpreting results, as well as preparing for genome-wide interaction analyses through simulations and power analysis.
Conclusion
The Epi2Loc package provides a convenient utility for converting, comparing, and interpreting epistatic models with more flexibility than existing software. The included utilities are useful for performing simulation studies of two-locus interactions and planning future analyses of epistasis in genome-wide SNP data. This tool should facilitate future efforts to uncover the contribution of SNP–SNP interactions to the genetics of complex phenotypes.
Acknowledgments
The authors would like to thank Patrick Miller, Daniel McArtor, and two anonymous reviewers for their helpful comments on earlier versions of this manuscript. This work was supported by the National Institute on Drug Abuse (G.L., grant number R37DA018673).
Supplementary Material
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/thg.2014.38.





