Article contents
Logic programming with function symbols: Checking termination of bottom-up evaluation through program adornments
Published online by Cambridge University Press: 25 September 2013
Abstract
Recent years have witnessed an increasing interest in enhancing answer set solvers by allowing function symbols. Since the introduction of function symbols makes common inference tasks undecidable, research has focused on identifying classes of programs allowing only a restricted use of function symbols while ensuring decidability of common inference tasks. Finitely-ground programs, introduced in Calimeri et al. (2008), are guaranteed to admit a finite number of stable models with each of them of finite size. Stable models of such programs can be computed and thus common inference tasks become decidable. Unfortunately, checking whether a program is finitely-ground is semi-decidable. This has led to several decidable criteria, called termination criteria, providing sufficient conditions for a program to be finitely-ground. This paper presents a new technique that, used in conjunction with current termination criteria, allows us to detect more programs as finitely-ground. Specifically, the proposed technique takes a logic program 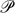 ${\cal P}$ and transforms it into an adorned program
${\cal P}$ and transforms it into an adorned program 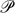 ${{\cal P}}$μ with the aim of applying termination criteria to
${{\cal P}}$μ with the aim of applying termination criteria to 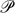 ${{\cal P}}$μ rather than
${{\cal P}}$μ rather than 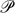 ${\cal P}$. The transformation is sound in that if the adorned program satisfies a certain termination criterion, then the original program is finitely-ground. Importantly, applying termination criteria to adorned programs rather than the original ones strictly enlarges the class of programs recognized as finitely-ground.
${\cal P}$. The transformation is sound in that if the adorned program satisfies a certain termination criterion, then the original program is finitely-ground. Importantly, applying termination criteria to adorned programs rather than the original ones strictly enlarges the class of programs recognized as finitely-ground.
Keywords
- Type
- Regular Papers
- Information
- Theory and Practice of Logic Programming , Volume 13 , Special Issue 4-5: 29th International Conference on Logic Programming , July 2013 , pp. 737 - 752
- Copyright
- Copyright © 2013 [SERGIO GRECO, CRISTIAN MOLINARO and IRINA TRUBITSYNA]
References
- 7
- Cited by




