Symmetrical Implications
Symmetry is inherent in a Monophonic scale. It is not planned; it is inevitable.Footnote 1
Jean-Philippe Rameau's mid-eighteenth century attempt to justify the existence of the minor triad as a ‘natural phenomenon of vibrating strings’ put forth a notion of ‘dual generators’, where the 4:5:6 triad is mirrored above and below a central pitch (C).Footnote 2 Although Rameau's symmetrical justification was rejected by L'Académie des Sciences,Footnote 3 several theorists and composers have continued to put forth conceptions that include undertones.
As Bob Gilmore points out in ‘Changing the Metaphor’, James Tenney disagreed with Harry Partch on the undertonal origin of the minor triad: ‘the problem with the U-tonality configuration as Tenney sees it, lies in the ambiguity surrounding the root’.Footnote 4 But roots can be disambiguated by measuring intervals independently of any relationship they may have to a centralised pitch identity. Nevertheless, Tenney also constructed similarly symmetrical crystalline structures within his own practice.Footnote 5 For reasons discussed later I use an approximate microtonal notation that expresses ratios to the nearest 8th tone accidental. Sound files that accompany this article's figures can be found online.Footnote 6
Figure 1 shows one just minor triad as both negative partial relationships in 5-limit tuning, extending downwards: –4:–5:–6, and as positive integers: 10:12:15. Using objective numerical distances, Figure 1 reveals not two (dual) ‘generators’ but four possible harmonic implications of the mirrored triad collection of five pitches. The C, D♭ (up-arrow), F and A♭ (up-arrow) are each implied from this aggregate, in the centre of Figure 1. If this entire 5-note collection is viewed from the perspective of a single harmonic generator, however, the fundamental implication is the D♭ (up-arrow) [1:40:48:60:75:90] (see Figure 1).

Figure 1: ‘Dual generators’ unpacked.
In The Musician's Arithmetic Max F. Meyer includes a 7-limit tonality diamond that evidently influenced Harry Partch in the construction of his own 11-limit diamond marimba.Footnote 7, Footnote 8 Like Rameau's ‘dual generators’ this diamond marimba mirrors its pitch contents around a central pitch, G. This G is repeated across six central marimba bars, fixed and functioning as a different partial in relation to the others (see Figure 2).

Figure 2: Diamond Marimba pitches low to high, line dividing the U- from O-tonalities.
As Cris Forster shows in Musical Mathematics: On the Art and Science of Acoustic Instruments, the sequence 4:5:6:7:9:11 is found along all the diagonals of the instrument: upwards from left to right, and also downwards from left to right: −4:−5:−6:−7:−9:−11. When the diamond is played ascending from left to right, the first G functions as the 4th partial, the second as the 5th, the 3rd as the 6th, the 4th as the 7th, the 5th as the 9th and finally the 6th as the 11th partial of the D quarter-flat, 4:11.
Unique intervals on the 11-limit diamond are found within the aggregate collection: [16, 20, 24, 25, 28, 30, 35, 36, 42, 44, 45, 49, 54, 55, 63, 66, 77, 81, 99, 121]. The subset [4:5:6:7:9:11] appears within the above collection (as 16, 20, 24, 28, 36, 44). If one were to compose for this instrument, or any other instrument, measuring intervals in ratios would help determine which intervals are repeated on the instrument and which are unique to certain registers. Repeating or avoiding the repetition of intervals or pitches is discussed further later. The following device enables the above determinations.
Maya Intervallic Measuring Device
The Maya device is a handheld tool that allows for the conversion from linear to logarithmic intervallic measurement, from pitch names to ratios and ratios to cents, or vice versa. An online version is available.Footnote 9 To use, drag the pitch-name ring with the cursor to the desired cent. The harmonic potential of any tuning system can be explored using the data provided in the interval appendix in conjunction with the Maya device (Figure 3).

Figure 3: Maya device.
The Maya device enables its user to work in just intonation and equal temperament simultaneously. One can convert from one system of measurement to the other and make relative interval calculations to the nearest cent (one hundredth of a half-tone). The innermost disc of the device displays a spiral representation of the overtone series to the 256th partial (eight octaves). Partial numbers are listed extending out from the centre, with prime number partials in red. To correlate and convert to linear units, the middle ring includes 1200 tick marks indicating cents, (1200 equal divisions of the octave). At each 25-cent increment, a pitch letter-name reflecting equal temperament in eighth-tones (48-tet) is marked. This middle ring can be compared to both the inner and outer rings for equivalence to ratios or cents. In the interval appendix, 10,024 unique intervals are presented in harmonic ratios within a single octave space.Footnote 10 These distances include many decimals for more precise comparisons to adjacent-in-size intervals within the numerical range of eight-plus octaves (1:256).
Representations in Notation
Using microtonal accidentals that represent specific ‘tuneable’ partial deviations, Marc Sabat's Extended Helmholtz-Ellis JI Pitch Notation accounts for the ‘natural’ intervals within the span of six octaves (1:64).Footnote 11 In this notation system dozens of specific microtonal accidentals are used to reference a tuning relationship with a fundamental. While specific, this notation can have the effect of limiting a composer from utilising the same notated partial as another partial of a different fundamental. For this reason, instead of using partial-specific and more complex additive microtonal accidentals as James Tenney or Marc Sabat have done, my approach uses a limited number of microtonal accidentals to approximate an unlimited number of proportional relationships. This approach to notation greatly reduces the number of microtonal accidentals while welcoming harmonic reinterpretation.
An approximate notation system also means that relative intervallic constructions can be explored to imply ‘microtonal’ fundamentals, where a symmetrical approach to notation can have the unfortunate effect of tacitly restricting one's construction of harmonies, encouraging composers to build harmonic structures only on known (standard, 12-tet) fundamentals, from the fundamental up the overtone series, in lieu of utilising the real (measured) ratios of intervals found on any specific instrument. For these reasons, in the following approach to notation the number of accidentals used to modify the known note names (~12-tet) are reduced to an arrow, to indicate approximately +/−25¢, and two quarter-tone symbols, to indicate approximately +/−50¢. More precisely, the arrows are used to indicate a microtonal deviation that ranges between +/−12.5¢ and +/−38.5¢ at which point a +/−38.6¢ deviation would include a quartertone accidental.
In contrast to lists of intervals produced by Helmholtz in On the Sensations of Tone,Footnote 12 or those of Partch's ‘Monophonic fabric’, this article's appendix (https://static1.squarespace.com/static/545e8246e4b01d77329f0dbf/t/63fe51f0f0942b7efc2e6176/1677611504652/Pratt_Adjacent_Interval_Chart_1-256.pdf) is inclusive of all intervals numerically available to a limited range of octaves.Footnote 13 When all of the different intervals within a certain range are listed, a structure known as a Farey sequence is produced. For example, below are listed all the intervals numerically available to 1:32 (a five-octave range) in descending-in-size order within a single octave.
Farey Sequences
Ratios from Figure 4 are notated in Figure 5. The top stave shows the Farey sequence that results when all these intervals are plotted along a theoretical string, moving from the octave node in the centre of the string (2) to either of its ends (see Figure 5).Footnote 14

Figure 4: All ratios within five octaves (1:32).

Figure 5: 1–32 half-string melodic/harmonic sequence.
The fundamental implication of the interval C to B (up-arrow) (11:21) is the G quarter-flat in the bass clef. The F (down-arrow) in the top stave coincides with the 21st partial of the constant C (here as partial 16) and forms the upper Farey sequence (see Figure 6).

Figure 6: Explanation of the numbers in Figure 5 (one random interval selected)
The lower Farey sequence may appear symmetrical with the above sequence in Figure 5 but is in actuality a result of calculating the difference tones of the descending-in-size intervals of the central stave.
In his ‘spectral canons’ James TenneyFootnote 15 generated Farey sequences from an application of partial numbers to duration. The polyrhythms, created by assigning each partial a rhythmic value, form a similar sequence, one difference being the lack of simultaneous notes in the above sequences. A Farey sequence generator can be found online.Footnote 16
Alternate Farey sequences are constructed through a process of instrumental filtration in some of my own compositions.Footnote 17 In these pieces, sequences are formed using only some of the partials derived from a full Farey sequence which is subjected to filtration through the microtonal limitations of various instruments.
Instrumental Filters
Intervallic uniqueness can be determined using the numbers of ratios, whether they are odd, even or prime. This approach contrasts one of prime limits, where the same intervals are added or multiplied indefinitely, producing very high-number ratios that imply fundamentals beyond the range of human hearing, such as 59049:65536. Ratios such as 59049:65536 extend into the tens of thousands, this one indicating a distance built on a fundamental that extends 16 octaves lower. Where Harry Partch and others multiplied the same lower-limit ratios, sometimes resulting in large-number ratios such as 59049:65536, or (3^10: 2^16), I have instead calculated all of the different intervals within 1:256 (eight octaves) and placed them in descending-in-size order.
These intervals are generally within less than 1 cent of one another in size and, given this data, can be reinterpreted for one another in order to explore alternate harmonic implications. For example, within an eight-octave (1:256) range, several intervals exist in very near proximity to the interval 59049:65536. Near 180¢ intervals are listed in the supplemental appendix, excerpted below. If the interval 59049:65536 = 180.449991346¢ was not available to an instrument, given its proximity in size, it could be reinterpreted as one of the following intervals.
-
9:10 = 182.403712134¢
-
226:251 = 181.637509843
-
217:241 = 181.605724543
-
208:231 = 181.57118793
-
199:221 = 181.533526617
-
190:211 = 181.492296451
-
181:201 = 181.446964915
-
172:191 = 181.396888
-
163:181 = 181.341279423
-
154:171 = 181.279169029
-
145:161 = 181.20934572
-
136:151 = 181.13027769
-
127:141 = 181.039998752
-
118:131 = 180.935942611
-
227:252 = 180.877723451
-
109:121 = 180.814694997
-
209:232 = 180.746235656
-
100:111 = 180.67161189
-
191:212 = 180.589951833
-
91:101 = 180.500211064
-
173:192 = 180.401127701
The reinterpretation of intervals is discussed in the subsequent sections of this article. Using data included in the appendix, any tuning system, including 12-tet, can be utilised for its proportional intervals.
Equal Temperament as Myth
In The Myth of Equal Temperament Ll. S. Lloyd showed that ‘not even the piano is exempt from the charge of inexactness’, arguing against the rigidity of fixed tuning systems.Footnote 18 The following figure reveals some of the other ratios, such as 17:18, which could potentially be reinterpreted as the 100-cent distances of 12-tet.
Equal temperament has been determined to varying degrees across the globe; perhaps the earliest calculation is attributed to Huainanzi (淮南子), 122 bce, China. Others, including Zhu Zaiyu (1536–1611), calculated 12-tone equal temperament (12-tet) to a different degree of precision working from the Huainanzi text.Footnote 19 According to James Murray Barbour, at around the same time in Europe Vincenzo Galilei (1520–1591) and others were using the ratio 17:18 (17:18 = ~98.95 cents) and making intuitive adjustments when placing the frets on a lute.Footnote 20 The ambiguity even within 100-cent distances allows for a myriad of numerical interpretations of the supposedly equal-tempered notes.
In Figure 7, overtone series pitches are notated with a harmonic diamond to the nearest eighth-tone accidental, on the fundamental E ~36-cent flat. The deviation of this fundamental from equal temperament means that some higher partials fall close enough to 12-tet to be included within a potential chord. Using this perspective and the Maya device, numerical proportions, tempered or not, can be utilised to filter unique harmonic collections in conjunction with instrumental availability (see Figure 7).

Figure 7: Maya device, positioned at fundamental E~ 36-cent flat, available ~12-tet partials.
Further 12-tet/JI Harmonic Filtration
In Figure 8, approximate ratios appear within the limits of the linear grid of 12-tone equal temperament. Here partials that deviate by more than +/−12.5 cents are filtered out of the sonorities, revealing a near-harmonic ‘progression’ of chords that imply ‘microtonal’ fundamentals shown in the bottom stave. Beginning on a G fundamental, the first chord allows the partials 3:9:15:17:19:27:43:45:51:57 through an imposed filter of 12-tone equal temperament. Within each half-step the same filter pattern will repeat. Here G to A♭ is shown on fundamentals spaced 2 cents apart (see Figure 8).

Figure 8: 12-tet filtered by temperament (every two cents) in (1:64, six octaves.
Calculating Virtual Intervals
As shown above, intervals can be reinterpreted for others that approach them in size. For example, although the following ‘minor 3rds’ approach one another in size and share the notation C to E♭, each interval can be ‘unpacked’ and used to imply distinct harmonic territories.
Through the following procedure, the ‘territory’ contained within each interval is revealed to be distinct from the next. In Figure 9 C to E♭ is first interpreted as a 26:31 ‘minor third’, equal to 304.5 cents. The harmonic implication of 26:31, when C is fixed as the 26th partial, is the fundamental E quarter-tone-flat +9 cents, 359.47 cents.

Figure 9: Virtual fundamental comparison: 304.5 cents and 303.3 cents.
To determine the fundamental (1) of this interval (26:31), first find the distance from the upper partial of the interval (31) to an octave multiple of the fundamental (16), 16:31. To convert 16:31 into cents, use the following ‘ratios to cents’ equation, or simply search the supplemental ‘Adjacent Interval Chart’: 16:31 = 1145.03557246 cents. log(31 ÷ 16) ÷ log(2) × 1200 = 1145.03557246 cents. Next, find the nearest lower multiple of the fundamental (16) to the lower partial of the interval (16:26): 16:26 = 8:13 and 8:13 = 840.52 cents. Finally, subtract this distance from an octave (1200 cents): 1200 cents – 840.52 cents = 359.47 cents. Because the C is fixed here, in this instance the virtual fundamental is equal to E quarter-tone-flat +9 cents, 359.47 cents; when the notation C to E♭ is interpreted as 47:56 in the second chord in Figure 9, however, the implied fundamental is an F ~36-cent sharp.
Intervals and ratios that repeat (up the series) can be filtered out in order to create numerically distinct adjacent harmonic structures that automatically avoid parallel intervals and repeated sonorities. Filtering the harmonic series so that only prime-number partials are included removes intervallic repetition up the series (10:15 = 6:9 or 2:3), while removing even-number partials deletes all octave repetition. The specific range and irregularities of instrumental tuning structures can also act as a kind of harmonic filter even prior to the start of a composition.
Harmonies Derived from an Ensemble
In my composition Invariance (2016), for ensemble, the available fixed microtones of natural harmonics found on string and brass instruments heavily influenced the formation of harmonies. These inherent instrumental restrictions acted as filters on the harmonic progression to-be, playing a central role in the composition's conception. Figure 10 includes some of the microtones available to the instruments used in Invariance. The harmonics palette of the strings includes only the first seven partials of each open string in standard tunings, but higher-number ratios are utilised through the objective ratios found between all of the instruments, and not building from tempered pitches (see Figure 10).

Figure 10: Some fixed microtones: horn, trumpet, violin, viola, cello and double bass.
Rather than building uniquely tuned instruments or using scordatura, Invariance relies on this given skeleton of fixed natural harmonics. The composition biases these ‘natural’ pitches using this structure as an irregular harmonic filter, which is itself revealed through a series of horizontally related fundamentals. In the following figure, chords 149 and 147 (from the middle of the composition) are first grouped by instrument and then the full chord is arpeggiated for each of the two sections, 149 and 147 (see Figure 11).

Figure 11: Ryan Pratt, Invariance (2016): chords 149 and 147, instrumental sections.
In the first chord section (chord 149), partials 9, 17, 23, 27, 51, 77 and 115 are found in string and brass harmonics within the overtone series of a fundamental E ~36-cent flat. 12-tet pitches are found on the piano, vibraphone and glockenspiel and include partials 13, 23, 29, 31, 39, 41, 49, 55, 69, 73 and 87. In the second chord section (chord 147), some of the same harmonics are utilised as other partials, (13, 23, 37, 39, 55, 117), of the new fundamental (Figure 12).

Figure 12: Ryan Pratt, Invariance (2016): chords 149 and 147, bars 121–26.
Tuning Systems that Evade the Octave
While exploring all the different intervals within the span of just over a single octave (203:101), this composition specifically avoids any duplications of the octave within any of its vertical sonorities. In this section, I examine three musical practices that ‘evade’ the octave (1:2) within their own tuning systems: a single Indonesian gamelan instrument, an mbira dza vadzimu from Zimbabwe and three scales of Wendy Carlos. Interval ratios are used to measure precisely the relationships between the notes of each practice because notation may not capture each expression. This approach also examines the extent to which tuning systems vary.
Measuring Slendro
With its five near-240-cent distances, the Slendro tuning system might be mistaken for a 5-equal pitch equal-tuning system, but its unequal octaves and inner interval variations fall outside of equal distances, allowing for an extraordinary variety of subtle differences from orchestra to orchestra. Musicologist, composer and inventor of the Sundanese solfège system, Raden Machjar Angga Koesoemadinata, identified 17 vocal pitches used in the Slendro scale that is found throughout Indonesia.Footnote 21 As Sambamurthy observed, ‘These additional ornamental tones function much like the sruti of traditional Indian music’; they decorate the ‘main’ tones that also vary from island to island.Footnote 22
In A Mathematical Model for Optimal Tuning Systems, Douglas Repetto, Larry Polansky, Daniel Rockmore, Micah J. Johnson and Wei Pan note that gamelans change in their pitch and that it is also difficult to know when to measure the fundamental within the envelope of the bronze keys.Footnote 23 In their research, they observe a ~51¢ variation in cents (between 267 and 216 cents) within the Slendro scales they measured. The intervals listed below are some of the ‘simpler’ (lower-number) ratios within a distance of ~290 to ~216 cents, referred to in their ‘GM’ study.
-
11:13 = 289.2¢
-
28:33 = 284.4
-
17:20 = 281.4
-
23:27 = 277.6
-
29:34 = 275.4
-
6:7 = 266.9
-
31:36 = 258.9
-
19:22 = 253.8
-
32:37 = 251.3
-
13:15 = 247.7
-
33:38 = 244.2
-
20:23 = 241.9
-
27:31 = 239.2
-
34:39 = 237.5
-
7:8 = 231.2
-
29:33 = 223.7
-
22:25 = 221.3
-
15:17 = 216.7
Notation
In Traditional Music in Modern Java: Gamelan in a Changing Society, Judith Becker writes:
Unlike other types of borrowings such as musical instruments, which are relatively easy to incorporate and absorb, notation is not an object but a technology that implies its own theory. Notation presupposes a linear concept of time, necessitates decisions as to what should be notated, and forces a perceptual bias on the user. The implicit bias of any given notation system is all the more powerful because the user is unaware of the implications of the new technology and therefore offers no conscious resistance.
As an example she cites the Kepatihan system, ‘one of seven or more experimental notation systems attempted between the years 1886 and 1942, [which] came to dominate all others and, with slight variations, is the basis of all contemporary notation of Gamelan music’.Footnote 24 Where the Kepatihan notation system uses numbers for the pitches of each scale, independent of the tuning of these pitches (so that other Gamelans can perform the same piece), the following ‘microtonal’ notation functions more as a graph where absolute pitch points are represented with approximate accidentals. The following notation is used only to demonstrate the ambiguity inherent to intervallic measurements. This is not an effort to re-transcribe gamelan music and is used here to show multiple units of measurement (cents, approximate microtonal accidentals and multiple ratios) in order to reveal the multiplicity inherent to the potential of intervallic interpretation.
Measuring a Polo
The Slendro scales analysed by Repetto et al. vary within a range of roughly 216¢ to 266¢ adjacent scale note distances. Using the Maya device, other approximations of the following randomly selected Polo (gamelan instrument) scale can be determined. The frequencies were determined using the application S P E A R.Footnote 25 Distances approaching the 278¢, 225¢, 226¢, 231¢ and 255¢ adjacent distances (measured on one polo) are found by shifting the Maya device to the lowest note of each number, to determine the ratios available within the tuning. Figure 13 lists five potential ratio interpretations of the midi cents notated below the stave.

Figure 13: Additional ratio interpretations of Polo scale.
A collection, in this case a 5-note scale, can be interpreted as being of a single fundamental or, more precisely, as of (implying) several different fundamentals. These non-tempered collections are reinterpreted above as multiple different ratios within cents of one another. Instead of attempting to precisely determine any tuning system's intervals, the point here is to note the extent to which intervals can be reinterpreted within cents in order to explore the multiplicity of harmonic depth inherent to some practices.
Asymmetry about the Octave
Intervals slightly larger and smaller than 1200 cents appear in numerous musical practices including gamelan music and mbira music. A similar variation occurs also in the tuning systems found in mbira music, to the extent that in mbira music the name of the song might more accurately refer to the fingering pattern on the lamellophone than the sound produced from it. According to the Tinotenda website, ‘different tunings use different pitch intervals. But even with mbiras of the “same tuning” mbira makers and players tune their mbiras with varying internal relationships among the intervals of an mbira, including tuning octaves not exactly an octave apart.’Footnote 26 One online resource, sympathetic-resonances.org, allows users to substitute different finger patterns with different instrumental tunings and hear the differences.Footnote 27
Mbira Tunings: Inharmonicity and Indeterminacy
The mbira dza vadzimu is specifically played in the invocation of the ancestral spirits. This particular mbira, of the Shona people of Zimbabwe, dates back more than 3,000 years. Much of its known repertoire is widely described as heptatonic with some unequal octaves. According to the Tinotenda website, ‘although discussions of mbira tunings tend to focus on the configuration of intervals, Shona musicians also take into consideration qualities of tone, sound projection, pitch level, and overtones’, and ‘the existence of mbiras with different interval relationships allows mbira players to play “the same song” (using the same fingering pattern) in different tunings’.
In his 1978 book The Soul of Mbira, Paul Berliner compared five mbira dza vadzimu tunings calling into question the then prevailing theory that ‘Shona mbira makers used a distinctive, well-defined scale, with only slight variation in different parts of the country… It can be described as a 7-note scale, with all the intervals equal’ (Figure 14).

Figure 14: Tuning of John Kunaka's mbira from Berliner, midi cents notated below.
Mbira Maker John Kunaka
Some mbiras have overtones that are more present than the fundamentals. ‘The presence or absence of tuned overtones is an additional factor in distinguishing the chuning of different mbira. John Kunaka reported that the instruments he builds are different from those constructed by other local blacksmiths because he “gives two voices” to the lowest pitch of his instruments.’Footnote 28
Mbira.org Tunings
On mbira.org, a non-profit organisation devoted to traditional music of Zimbabwe, mbirist Erica Azim has included several audio and visual resources such, as the following G Nyamaropa tuning.Footnote 29
The upper stave in Figure 15 shows the ‘main’ pitches of each mbira key and proposes ratios that reveal a single fundamental implication for the aggregate. Partial 256 is the octave multiple of the implied fundamental G. The lower-stave system includes ratios within the inharmonic spectrum of each key (see Figure 15).

Figure 15: Mbira G Nyamaropa tuning, ratios notated.
While there may be a tendency for Western ears to analyse non-Western practices within the context of tonality, I am not interested in redefining this music in ways that the musicians who play it would generally not consider. My interest instead is to approach this music outside the limitations within which our ears might be tempted to hear it, if possible, and ideally to shed light on the sometimes subtle differences within these unique tuning systems that vary differently from how 12-tet itself varies. Rather than squeezing any of these found intervals into ‘simpler’, more ‘ideal’ (lower-number), ratios, I have found ratios that closely approximate the distances of recorded instruments.
Wendy Carlos’ Scales
The variation within gamelan and mbira dza vadzimu tunings does not exist in the digitally synthesised scales of Wendy Carlos, although in her practice multiple scales are sometimes superimposed.Footnote 30 Wendy Carlos’ scales more closely approximate some of the same lower ‘ideal’ ratios (2:3, 4:5, but interestingly not the octave, 1:2). By breaking ‘desirable’ ratios into equal portions and adding these equal steps together, Carlos was able to approach the ‘ideal’ intervals in a closer approximation than other equal temperaments that do include the octave (1:2) relationship. In this approach, she constructed three new scales of equal steps that bypass the octave in favour of these other relationships. Her Alpha scale includes distances of 78¢, the Beta scale 63.8¢ and the Gamma scale 35.1¢. While these scales are asymmetrical about the octave, intervals within them can form other symmetries. Unlike another whole-number equal temperament (such as 17-tet), the 15.385 equal steps do not include a repetition of pitches at the octave (see Figure 16).
You really have to go further, up to 53-step E.T., to find another nearly perfect equal division, yet Gamma is noticeably freer of beats than even that venerable tuning. Why was it overlooked for so long? You guessed it, it's not symmetrical about the octave, and so was excluded a priori from everybody's search.
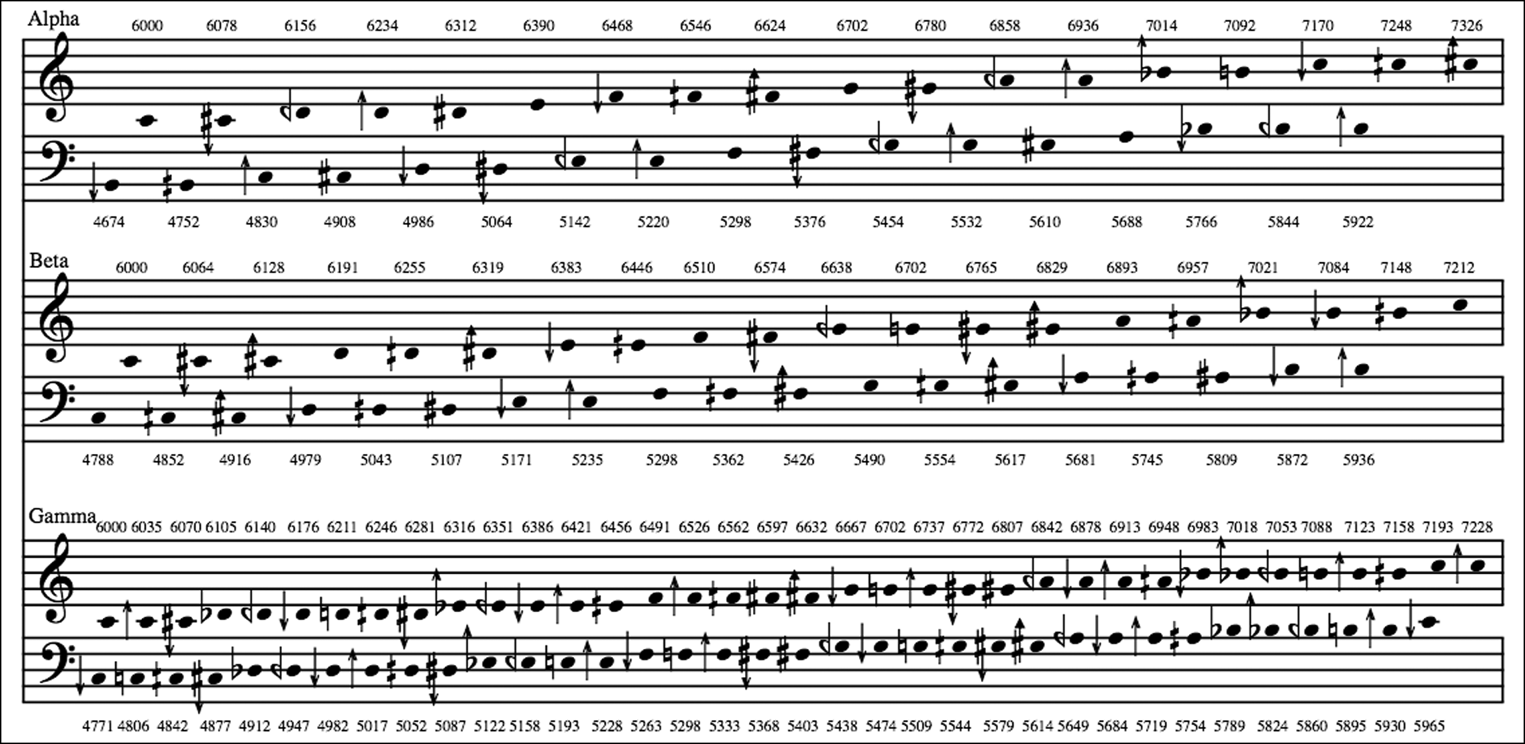
Figure 16: Wendy Carlos’ Alpha, Beta, Gamma scales, notated above and below middle ‘C’.
[…] Alpha has a musically interesting property not found in Western music: it splits the minor third exactly in half (also in quarters). This is what initially led me to look for it, and I merely called it my ‘split minor 3rd scale of 78-cents-steps.’ Beta, like the symmetric 19 division, does the same things to the perfect fourth. The whole formal discovery came a few weeks after I had completed the album, Beauty in the Beast, which is wholly in new tunings and timbres. The title cut from the album contains and extended study of some ‘beta’ but is mostly in ‘alpha’.Footnote 31
Logarithmic Scales of Chords
The logarithmic approach described in this section avoids dividing the octave or any interval into any equal distances, and instead explores the extent to which different distances are available within numerical (not instrumental) restrictions alone. I expand upon a ‘scale of chords’ construction, taking this concept outside of linear units of equal temperament into logarithmic (microtonal) units expressed in ratios. In lieu of a symmetrical approach of prime limits where the same intervals are stacked indefinitely, intervallic difference is utilised in the creation of distinct harmonies within each scale system here. Having previously detailed an orchestration-led approach to composition, I now explore purely numerical harmonic systems in the absence of any instrumental influence. By constructing harmonies through the simultaneous use of both systems of measurement (linear and logarithmic), one can make use of the generative properties of each structure's recursion (Figure 17).

Figure 17: Scales of chords in two measurements.
An 8-note ‘major’ scale (with an extra 6th note, A♭) is harmonised above. This ‘6th diminished’ scale of chords is used as a tool of improvisation within jazz standards, as demonstrated by Barry Harris and several of his students in various online masterclasses.Footnote 32
Constructing Scales of Chords beyond 12-tet
The ‘scale of chords’ technique can also be applied outside 12-tet, using a scale with x number of notes to create chords with y number of notes, and each closed system contains a different consistency determined by the chosen x and y values. In the following examples, pitches are not doubled within the same chord, partly so that all the unique chords can be determined. Some 8-note collections (and other collections containing an even number of notes) alternate such that every other chord is an inversion of itself. Where these even-number ‘binary’ scales alternate the same notes in inversion [1 0 1 0 1 0 1 0], scales with an odd number of notes contain the potential to form distinct chords, because an odd number of scale notes prevents a binary alternation of two pitch groups. One might choose to construct a scale with an odd number of notes for greater harmonic variety. The 12-tet 7-note scale below produces four different 7th chords, but in equal temperament some of these chords are transpositions of the same structure, whereas outside of an equal temperament, logarithmic units can yield unique chords (those that do not repeat within the system).
To construct a scale with x number of pitches, start from partial x and count upwards to its octave double (x^2). There will always be x pitches in this scale before the octave (regardless of x). For example, a ‘scale’ containing only partials 3, 4 and 5 contains 3 notes before its octave multiple (6); a 4-note scale beginning on partial 4 contains 4 notes until its octave duplicate (8), etc.
‘Close’ Position Harmonic Motion
Figures 18–20 show ‘close’ position movement by limiting the range of the harmony to the octave within which the scale is already situated. Voices move to the nearest note within the octave space producing the up and down motion of each inner voice (see Figures 18 and 19).

Figure 18: ‘Close’ position scales of chords voicing.

Figure 19: 11–21 scale of chords; ‘Close’ voicings.

Figure 20: Scale from 16th to 31st partial on D; 16 and 19 May scales of chords in close position.
In Figure 19, 5-note chords are formed in an ascending odd-number scale of chords, within the scale space of 11–21 (see Figure 19).
May 16th and 19th ‘Progressions’ Comparison
In Figure 20, calendar dates were utilised in the construction of two scale systems. For 16 May, 16 different 5-note chords were formed. Below this, the date 19 May led to the creation of a 19-note scale with 5-note chords for each pitch. The scale is displaced when the chords are re-voiced. Each note of each scale is shown in open note heads below.
The first chord of the 16 May scale begins on D4 and includes partials 3, 5, 7 and 9. Using the scale, the following chords are determined by moving up stepwise, here in a two-octave voicing limitation. The 19 May scale of chords was initiated by combining the multiple of the fundamental (within 19–37), which is 32, with the partial multiple of the 3rd, 5th, 7th and 9th overtone, and then moving stepwise up the scale in all voices. Therefore (within this partial range), this chord contains partials 32, 24, 20, 28 and 36 (respective multiples of partials 3, 5, 7 and 9) and is found 6 from the end of Figure 20.
Extraction or Erasure
The 8-note scale at the top of Figure 21 was extracted from the larger 15-note scale below it, [15–29] (partial 26 is shown here as partial 13, down an octave). A 6-note scale of chords is shown below these scales (see Figure 21).

Figure 21: 15-note scale [15–29] and scale of chords up to 29th partial.
In this approach one must first construct a full 6-note scale of chords, 6-note chords on every note of the 15-note scale, and then utilise only the chords built upon the 8-note scale tones [15 17 18 20 21 23 25 26]. In Figure 22, a scale of chords is formed that includes the 8 notes of the subset scale in Figure 21. Here the scale is rearticulated with 26 down the octave to 13 [13 15 17 18 20 21 23 25].

Figure 22: Scale of chords; subset and erasure.
First, 4-note chords are formed, using only this extracted 8-note scale. Then, 6-note chords are formed, utilising the full 15–29 scale. The lowest stave in Figure 22 re-voices the same collection in a close position that, because of the chosen partial numbers, includes distinct melodic lines for each of the six voices, avoiding intervallic parallels and transpositions of the same chord on different scale degrees.
Parallel (repeated) intervals can be entirely excluded at the point of determining a scale, prior to harmonising it. Parallel intervals will be found within a scale that includes repeated intervals. For example, if a scale includes multiples of partials: [2 9 5 21 3 27 15], written within a single octave [16 18 20 21 24 27 30], repeated intervals will be found between 16:24, 18:27, 20:30, etc. But if a scale includes only odd-number partials or odd-number partials with non-duplicate even-numbered partials, repeated/parallel intervals will already be numerically excluded from the scale system.
The examples given here illustrate both the formation of distinct harmonic structures through ratios, independent of instrumental influences, and the formation of those specifically derived from the limitations of instrumental spaces.
Acknowledgements
I would like to thank Izumi Miyahara, Mahir Cetiz, Miya Masaoka, James Ilgenfritz and Tansy Xiao, who helped me bring this article to its current state.



























