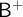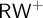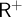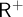1 Ternary Relational Frames
The ternary relational semantics for relevant logics is a triumph. The groundbreaking results of Routley and Meyer [Reference Routley and Meyer45–Reference Routley, Meyer and Leblanc47] have significantly clarified our understanding of relevant logics.Footnote 1 After 20 years of viewing relevant logics with Hilbert-style axiomatisations, natural deduction systems and algebraic semantics, we finally had a truth-conditional semantics which modelled relevant logics in the same way that Kripke semantics provide models for normal modal logics and intuitionistic and intermediate logics.Footnote 2
Propositions are modelled as sets of points, and connectives are interpreted as operations on such sets, some (namely the modal operators, intuitionistic conditional and negation, and in the case of relevant logics, relevant implication and the intensional conjunction, fusion) using accessibility relations on the class of points. In the case of the distinctively relevant conditional connective ‘
![]() $\to $
’, the two-place connective is naturally interpreted by a three-place accessibility relation, the eponymous ternary relation of the ternary relational semantics.
$\to $
’, the two-place connective is naturally interpreted by a three-place accessibility relation, the eponymous ternary relation of the ternary relational semantics.
That a ternary relation should feature in a frame semantics for relevant logics should not have surprised anyone. The pieces had been in place for quite some time. Jónsson and Tarski’s papers, from the 1950s, on Boolean algebras with operators [Reference Jónsson and Tarski26, Reference Jónsson and Tarski27], showed how Boolean algebras with n-ary operators satisfying appropriate distributive laws can be concretely modelled as power set algebras where each n-place operator is interpreted using an (
![]() $n+1$
)-place relation. Generalising these results from Boolean algebras to distributive lattices makes some of the details a little more complicated, but the picture is mostly unchanged. The details for how to make that generalisation of Jónsson and Tarski’s work to arbitrary distributive lattices with operators—including relevant logics—were worked out by Dunn in his papers on gaggle theory in the early 1990s [Reference Dunn14–Reference Dunn, Max and Stelzner17].Footnote
3
The picture is extremely natural and well motivated. The ternary relational semantics for relevant and substructural logics is powerful, and it has resulted in significant advances in our understandings of these logics.
$n+1$
)-place relation. Generalising these results from Boolean algebras to distributive lattices makes some of the details a little more complicated, but the picture is mostly unchanged. The details for how to make that generalisation of Jónsson and Tarski’s work to arbitrary distributive lattices with operators—including relevant logics—were worked out by Dunn in his papers on gaggle theory in the early 1990s [Reference Dunn14–Reference Dunn, Max and Stelzner17].Footnote
3
The picture is extremely natural and well motivated. The ternary relational semantics for relevant and substructural logics is powerful, and it has resulted in significant advances in our understandings of these logics.
Nonetheless, it cannot be said that the ternary relational semantics has met with anything like the reception of the Kripke semantics for modal and constructive logics. Some of the difference is no doubt due to the size of the respective audiences. Substructural and relevant logic is a boutique interest when compared to the modal industrial complex of the late twentieth and early twenty-first centuries. However, it seems to us that this does not explain all of the differences in the scale and quality of the reception of the respective semantic frameworks. Some of the relative dissatisfaction with the ternary relational semantics centres on philosophy and the question of the intelligibility of the semantics [Reference Beall, Brady, Dunn, Hazen, Mares, Meyer, Priest, Restall, Ripley, Slaney and Sylvan2, Reference Copeland11]. We think those questions have been well dealt with in the literature, and that to a large degree the proof of this pudding is in the eating, rather than adding to the already long discussion of pudding interpretation. The ternary relational semantics is not problematic because it lacks interpretive power or philosophical intelligibility. The problem with the ternary relational semantics is that it is fiddly.
Consider Kripke semantics for modal logics. All you need to make a Kripke frame is a non-empty set of points, and a binary relation on those points. Nothing more. Propositions are modelled by sets of points. The Boolean operators correspond to the set functions of union, intersection and complementation, and the modal operators are simple universal or existential projections along the binary relation. This is simple, it is robust, and once you see it, you find this pattern everywhere. Structures for modal logics are ubiquitous.
Kripke semantics for intuitionistic logic is a little more complicated, but not by much. We must have a partial order on our set of points (or possibly a preorder) and propositions are sets of points closed upward along that order. Conjunction and disjunction are unchanged from the modal case, as intersection and union preserve the property of being upward closed. However, complementation, and the corresponding operation to model the material conditional, do not preserve the property of being closed, so they are replaced by operations that utilise the partial order and respect the upward closure condition. Again, this is all very straightforward. When you have an ordered collection of states, carrying information preserved along that order, constructive logic is a natural tool, and Kripke models for intuitionistic logic are correspondingly natural.
Now compare the general framework for substructural logics.Footnote
4
One natural presentation of the semantics takes this form: a frame is a 4-tuple
![]() $\langle P,R,\sqsubseteq ,N\rangle $
, where P is a non-empty set of points, R is a ternary relation on P,
$\langle P,R,\sqsubseteq ,N\rangle $
, where P is a non-empty set of points, R is a ternary relation on P,
![]() $\sqsubseteq $
is a binary relation on P, and N is a subset of P, where the following conditions are satisfied.
$\sqsubseteq $
is a binary relation on P, and N is a subset of P, where the following conditions are satisfied.
-
•
 $\sqsubseteq $
is a partial order.
$\sqsubseteq $
is a partial order. -
• R is
 $\sqsubseteq $
-downward preserved in the first two positions, and
$\sqsubseteq $
-downward preserved in the first two positions, and
 $\sqsubseteq $
-upward preserved in the third. That is, if
$\sqsubseteq $
-upward preserved in the third. That is, if
 $Rxyz$
and
$Rxyz$
and
 $x^-\sqsubseteq x$
,
$x^-\sqsubseteq x$
,
 $y^-\sqsubseteq y$
and
$y^-\sqsubseteq y$
and
 $z\sqsubseteq z^+$
then
$z\sqsubseteq z^+$
then
 $Rx^-y^-z^+$
.
$Rx^-y^-z^+$
. -
•
 $y\sqsubseteq z$
if and only if there is some x where
$y\sqsubseteq z$
if and only if there is some x where
 $Nx$
and
$Nx$
and
 $Rxyz$
.
$Rxyz$
.
Notice that these models have three distinct moving parts: the ternary relation R, the partial order
![]() $\sqsubseteq $
, and the distinguished set N of points. Propositions are sets of points closed upward under the partial order
$\sqsubseteq $
, and the distinguished set N of points. Propositions are sets of points closed upward under the partial order
![]() $\sqsubseteq $
. R is used to interpret the conditional connective ‘
$\sqsubseteq $
. R is used to interpret the conditional connective ‘
![]() $\to $
’ (and the intensional conjunction ‘
$\to $
’ (and the intensional conjunction ‘
![]() $\circ $
’, if present), while the set N of so-called normal, or regular, points is the set of points at which logical truths are taken hold.Footnote
5
The need for N is a distinctive feature of relevant logics, as logical truths (like, say,
$\circ $
’, if present), while the set N of so-called normal, or regular, points is the set of points at which logical truths are taken hold.Footnote
5
The need for N is a distinctive feature of relevant logics, as logical truths (like, say,
![]() $p\to p$
) need not hold at all points. Since, for example,
$p\to p$
) need not hold at all points. Since, for example,
![]() $q\to (p\to p)$
is not a theorem of
$q\to (p\to p)$
is not a theorem of
![]() $\mathsf {R}^+$
, so some models feature have counterexamples to the conditional. Those models have at least one point where q is supported but
$\mathsf {R}^+$
, so some models feature have counterexamples to the conditional. Those models have at least one point where q is supported but
![]() $p\to p$
is not. But
$p\to p$
is not. But
![]() $p\to p$
is still a logical truth according to
$p\to p$
is still a logical truth according to
![]() $\mathsf {R}^+$
. Logical truths are guaranteed to hold at some points (namely, those in N), but not necessarily at all points. So, our models have three distinct moving parts:
$\mathsf {R}^+$
. Logical truths are guaranteed to hold at some points (namely, those in N), but not necessarily at all points. So, our models have three distinct moving parts:
![]() $\sqsubseteq $
for providing our closure conditions for propositions,Footnote
6
R for modelling ‘
$\sqsubseteq $
for providing our closure conditions for propositions,Footnote
6
R for modelling ‘
![]() $\to $
’ and ‘
$\to $
’ and ‘
![]() $\circ $
’, and N for modelling the logical truths.
$\circ $
’, and N for modelling the logical truths.
We challenge anyone to find this kind of formal semantics to be as straightforward to apply as the Kripke semantics for modal and constructive logics. While it is relatively easy to find preorders or binary relations on sets under every bush, it is rather harder to see where ternary relations, partial orders and special sets of normal points are to be found. Perhaps they are there somewhere, but they do not seem particularly easy to spot. It is not for nothing that modal and constructive logics have been applied in many domains where relevant and substructural logics have not.Footnote 7
It is true that the choice of primitives in the ternary frame semantics is somewhat arbitrary. We could take
![]() $\sqsubseteq $
to be defined in terms of N and R, but then the condition that it is a partial order (or a preorder) and that R is preserved along that order become even more complex and unnatural to state. In models for some of our logics (not all) we could impose the condition that
$\sqsubseteq $
to be defined in terms of N and R, but then the condition that it is a partial order (or a preorder) and that R is preserved along that order become even more complex and unnatural to state. In models for some of our logics (not all) we could impose the condition that
![]() $\sqsubseteq $
is the identity relation (and hence, all algebras of propositions arising out of such frames would be at least implicitly Boolean algebras, so this works only for logics conservatively extended with Boolean negation) [Reference Priest and Sylvan38]. It is possible, for some substructural logics, to trade in our set N for a single point g (and restrict our attention to so-called reduced models), cutting down further on the number of models generated, but the conceptual complexity remains [Reference Giambrone21, Reference Routley, Plumwood, Meyer and Brady48–Reference Standefer and Bimbó51].
$\sqsubseteq $
is the identity relation (and hence, all algebras of propositions arising out of such frames would be at least implicitly Boolean algebras, so this works only for logics conservatively extended with Boolean negation) [Reference Priest and Sylvan38]. It is possible, for some substructural logics, to trade in our set N for a single point g (and restrict our attention to so-called reduced models), cutting down further on the number of models generated, but the conceptual complexity remains [Reference Giambrone21, Reference Routley, Plumwood, Meyer and Brady48–Reference Standefer and Bimbó51].
When you consider ternary relational models alongside point semantics for normal modal logics and constructive logics, the contrast is plain for all to see. Ternary relational models are significantly less elegant, and they have many different moving parts than Kripke models for modal and constructive logics. It is not for nothing that those of us working in the area have sought to simplify the semantics, but try as we might, significant complexity remains after such all such efforts [Reference Priest and Sylvan38, Reference Restall39].Footnote 8
In this paper we introduce a new class of models for positive relevant and substructural logics, which at the same time generalises and simplifies the ternary relational semantics. Collection frames generalise ternary relational frames in the sense that every ternary relational frame can be seen as a collection frame, but that there are also collection frames that do not arise as ternary relational frames. Collection frames simplify ternary relational frames in the sense that there are significantly fewer independent parts and conditions connecting different components of the semantics. While the resulting models are not quite as simple as Kripke semantics for modal logics—some complexity is inevitable, given that we are aiming to model an intensional two-place connective—the gain in simplicity over the traditional presentation of the ternary relational frame semantics for relevant logics is significant.
Simplifying the semantics is one motivation for our work. The second motivation for an alternate approach to frames for these logics arises out of noticing the following fact: When we work with particular substructural logics—such as
![]() $\mathsf {R}^+$
,
$\mathsf {R}^+$
,
![]() $\mathsf {RW}^+$
, and
$\mathsf {RW}^+$
, and
![]() $\mathsf {TW}^+$
—it is very natural to consider not only the ternary relation R but its generalisations to more places:
$\mathsf {TW}^+$
—it is very natural to consider not only the ternary relation R but its generalisations to more places:
![]() $R^2a(bc)d$
is defined as
$R^2a(bc)d$
is defined as
![]() $(\exists x)(Rbcx \land Raxd)$
, and
$(\exists x)(Rbcx \land Raxd)$
, and
![]() $R^2(ab)cd$
is defined as
$R^2(ab)cd$
is defined as
![]() $(\exists x)(Rabx\land Rxcd)$
. In
$(\exists x)(Rabx\land Rxcd)$
. In
![]() $\mathsf {R}^+$
and
$\mathsf {R}^+$
and
![]() $\mathsf {RW}^+$
,
$\mathsf {RW}^+$
,
![]() $R^2a(bc)d$
holds if and only if
$R^2a(bc)d$
holds if and only if
![]() $R^2(ab)cd$
holds, so we can simplify our notation, and generalise further: for
$R^2(ab)cd$
holds, so we can simplify our notation, and generalise further: for
![]() $n>0$
, we define
$n>0$
, we define
![]() $R^{n}$
to be the
$R^{n}$
to be the
![]() $(n+2)$
-ary relation on P, setting
$(n+2)$
-ary relation on P, setting
![]() $R^1=R$
, and setting
$R^1=R$
, and setting
![]() $R^{n+1}a_1a_2a_3\cdots a_{n+3}$
to hold if and only if
$R^{n+1}a_1a_2a_3\cdots a_{n+3}$
to hold if and only if
![]() $(\exists x)(Ra_1a_2x\land R^{n}xa_3\cdots a_{n+3})$
. This generalisation into an arbitrary n-ary relation, where
$(\exists x)(Ra_1a_2x\land R^{n}xa_3\cdots a_{n+3})$
. This generalisation into an arbitrary n-ary relation, where
![]() $n\ge 3$
is extremely natural, and conditions on
$n\ge 3$
is extremely natural, and conditions on
![]() $R^2$
and still higher orders of R play a role in the specification of various substructural logics.Footnote
9
$R^2$
and still higher orders of R play a role in the specification of various substructural logics.Footnote
9
Our attempt to understand the phenomenon of higher order accessibility relations—and how they relate to each other—is the starting point for a new, simpler characterisation of frame semantics for substructural logics. In the next section we will start with one case, frames for the logics
![]() $\mathsf {RW}^+$
and
$\mathsf {RW}^+$
and
![]() $\mathsf {R}^+$
. In later sections we will then branch out to a wider class of substructural logics.
$\mathsf {R}^+$
. In later sections we will then branch out to a wider class of substructural logics.
2 Multiset Frames
A guiding idea in ternary relational semantics for relevant logics is the notion of information application or combination. The ternary relation R relates the triple of points
![]() $x,y,z$
(that is,
$x,y,z$
(that is,
![]() $Rxyz$
) if and only if applying the information in x to the information in y results in information that is in z. In the logics
$Rxyz$
) if and only if applying the information in x to the information in y results in information that is in z. In the logics
![]() $\mathsf {R}^+$
and
$\mathsf {R}^+$
and
![]() $\mathsf {RW}^+$
, information application is commutative (applying x to y results in the same information as applying y to x), and associative (applying x to y and then applying the results to z results in the same things as applying x to a result of applying y to z). In models for
$\mathsf {RW}^+$
, information application is commutative (applying x to y results in the same information as applying y to x), and associative (applying x to y and then applying the results to z results in the same things as applying x to a result of applying y to z). In models for
![]() $\mathsf {R}^+$
, combination is also idempotent, to the effect that the result of applying x to itself doesn’t take you outside x (so we have
$\mathsf {R}^+$
, combination is also idempotent, to the effect that the result of applying x to itself doesn’t take you outside x (so we have
![]() $Rxxx$
). Associativity and commutativity of application (or combination) means that we could simplify our ternary relation R by thinking of it not so much as a ternary relation where all three slots act independently, but rather, at least in the case of these logics, as a relation between unordered pairs of points on the one hand, and points on the other. The fact rendered as
$Rxxx$
). Associativity and commutativity of application (or combination) means that we could simplify our ternary relation R by thinking of it not so much as a ternary relation where all three slots act independently, but rather, at least in the case of these logics, as a relation between unordered pairs of points on the one hand, and points on the other. The fact rendered as
![]() $Rxyz$
in the ternary semantics could instead be represented as
$Rxyz$
in the ternary semantics could instead be represented as
where we have the (unordered) pair of x and y on the one hand, and the z on the other. The fact that this is an unordered pair, and not a set is important, because when we consider
![]() $Rxxz$
what we have is
$Rxxz$
what we have is
where x is applied to itself. But as far as order of application goes,
![]() $[x,y]Rz$
is the very same fact as
$[x,y]Rz$
is the very same fact as
![]() $[y,x]Rz$
. When it comes to associativity, what we have in models for
$[y,x]Rz$
. When it comes to associativity, what we have in models for
![]() $\mathsf {RW}^+$
, traditionally presented, is the following complex fact:
$\mathsf {RW}^+$
, traditionally presented, is the following complex fact:
If we are willing to abuse notation a little more, what we have in this biconditional is two different ways of representing the one single fact
to the effect that x, y and z together, combined in any order, are related to w. Collection frames arise from taking what was an abuse of notation literally. In collection frames, an accessibility relation relates collections of points to points.
This shifted perspective on R comes with advantages. Not only will this relation R do the job of the original ternary relation, in the case where the multiset has two elements, and not only can it represent
![]() $R^2$
and relations of higher arities with larger multisets. It also has the capacity to represent the binary relation
$R^2$
and relations of higher arities with larger multisets. It also has the capacity to represent the binary relation
![]() $\sqsubseteq $
in the case where the collection being related is a singleton, and it also represents the predicate N, in the case where the collection being related is the empty multiset. The translation manual is straightforward:
$\sqsubseteq $
in the case where the collection being related is a singleton, and it also represents the predicate N, in the case where the collection being related is the empty multiset. The translation manual is straightforward:
 $$\begin{align*}\begin{array}{lrcl} \mathrm{(F1)} & Nx & \textit{becomes} & [\;] Rx, \\ \mathrm{(F2)} & x\sqsubseteq y & \textit{becomes} & [x]Ry, \\ \mathrm{(F3)} & Rxyz & \textit{becomes} & [x,y]Rz. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{lrcl} \mathrm{(F1)} & Nx & \textit{becomes} & [\;] Rx, \\ \mathrm{(F2)} & x\sqsubseteq y & \textit{becomes} & [x]Ry, \\ \mathrm{(F3)} & Rxyz & \textit{becomes} & [x,y]Rz. \end{array} \end{align*}$$
What was represented by three different fundamental concepts in traditional Routley–Meyer frames becomes three different aspects of one underlying relation. The conditions linking N,
![]() $\sqsubseteq $
and (ternary) R become corollaries of the fundamental structure of the one multiset relation R.
$\sqsubseteq $
and (ternary) R become corollaries of the fundamental structure of the one multiset relation R.
To make things explicit, a collection frame for
![]() $\mathsf {RW}^+$
has a non-empty set P of points and a single accessibility relation R on
$\mathsf {RW}^+$
has a non-empty set P of points and a single accessibility relation R on
![]() $M(P)\times P$
, where
$M(P)\times P$
, where
![]() $M(P)$
is the class of finite multisets of elements of P. Since multisets are not in very wide use,Footnote
10
we would do well to be explicit about them and their properties.
$M(P)$
is the class of finite multisets of elements of P. Since multisets are not in very wide use,Footnote
10
we would do well to be explicit about them and their properties.
Definition 1 (Finite multisets, ground)
A multiset is a collection in which order is irrelevant, but multiplicity of membership is relevant. There are various ways to formally define the notion. One way is this: a finite multiset of objects taken from some class P can be represented as a function
![]() $m:P\to \omega $
where
$m:P\to \omega $
where
![]() $m(x)=0$
for all but finitely many values of x. If x is in P, then
$m(x)=0$
for all but finitely many values of x. If x is in P, then
![]() $m(x)$
is the number of times
$m(x)$
is the number of times
![]() $x$
is a member of the multiset m. The multisets
$x$
is a member of the multiset m. The multisets
![]() $m_1$
and
$m_1$
and
![]() $m_2$
from P are identical if they have the same members to the same multiplicities: that is,
$m_2$
from P are identical if they have the same members to the same multiplicities: that is,
![]() $m_1=m_2$
if and only if
$m_1=m_2$
if and only if
![]() $m_1(x)=m_2(x)$
for each
$m_1(x)=m_2(x)$
for each
![]() $x$
in P.
$x$
in P.
For any two multisets
![]() $m_1$
and
$m_1$
and
![]() $m_2$
, their union is the multiset with function
$m_2$
, their union is the multiset with function
![]() $m_1+m_2$
. We also write ‘
$m_1+m_2$
. We also write ‘
![]() $m_1\cup m_2$
’ using the traditional notation for union. Note, however, that
$m_1\cup m_2$
’ using the traditional notation for union. Note, however, that
![]() $m_1\cup m_1$
is now not (typically) the same multiset as
$m_1\cup m_1$
is now not (typically) the same multiset as
![]() $m_1$
.
$m_1$
.
We say that
![]() $m_1\le m_2$
(a generalisation of the subset relation to multisets) if
$m_1\le m_2$
(a generalisation of the subset relation to multisets) if
![]() $m_1(a)\le m_2(a)$
for all a in P.
$m_1(a)\le m_2(a)$
for all a in P.
We use the familiar bracket notation for multisets: for example,
![]() $[a,a,b]$
is the multiset where
$[a,a,b]$
is the multiset where
![]() $m(a)=2$
and
$m(a)=2$
and
![]() $m(b)=1$
and
$m(b)=1$
and
![]() $m(x)=0$
for every other value of
$m(x)=0$
for every other value of
![]() $x$
. So,
$x$
. So,
![]() $[a,b]\cup [a,c,c]=[a,a,b,c,c]$
.
$[a,b]\cup [a,c,c]=[a,a,b,c,c]$
.
As with sets, we will use the symbol ‘
![]() $\in $
’ for multiset membership. Here, ‘
$\in $
’ for multiset membership. Here, ‘
![]() $x\in m$
’ will be taken to mean that
$x\in m$
’ will be taken to mean that
![]() $m(x)>0$
, that is, the object
$m(x)>0$
, that is, the object
![]() $x$
is in the multiset m a non-zero number of times.
$x$
is in the multiset m a non-zero number of times.
For any multiset m on P, its ground
![]() $g(m)$
is the subset of P consisting of all objects x with non-zero multiplicity in m, that is,
$g(m)$
is the subset of P consisting of all objects x with non-zero multiplicity in m, that is,
![]() $g(m)=\{x\in P~|~m(x)>0\}$
.
$g(m)=\{x\in P~|~m(x)>0\}$
.
Now we know enough about multisets for us to introduce the multiset semantics for
![]() $\mathsf {RW}^+$
and for
$\mathsf {RW}^+$
and for
![]() $\mathsf {R}^+$
. As we have already indicated, a collection frame consists of a set P of points (with at least one member), and a relation R on
$\mathsf {R}^+$
. As we have already indicated, a collection frame consists of a set P of points (with at least one member), and a relation R on
![]() $M(P)\times P$
, which relates multisets of points to points. Henceforth, we will call relations R on
$M(P)\times P$
, which relates multisets of points to points. Henceforth, we will call relations R on
![]() $M(P)\times P$
multiset relations.
$M(P)\times P$
multiset relations.
The intended application of R in a multiset frame is straightforward:
![]() $X R y$
holds when, and only when, the information in the points X taken together also holds in y. There are aspects, in this reading, of the partial order from constructive logics, and just like that case, there must be at least some condition on this relation for such an interpretation to make sense. The relation R cannot be entirely arbitrary. In the case of the semantics for constructive logic, there are two parts to the constraint on the order relation. First, that it be reflexive, and second, that it is transitive.Footnote
11
In the case of multiset relations for frames for
$X R y$
holds when, and only when, the information in the points X taken together also holds in y. There are aspects, in this reading, of the partial order from constructive logics, and just like that case, there must be at least some condition on this relation for such an interpretation to make sense. The relation R cannot be entirely arbitrary. In the case of the semantics for constructive logic, there are two parts to the constraint on the order relation. First, that it be reflexive, and second, that it is transitive.Footnote
11
In the case of multiset relations for frames for
![]() $\mathsf {RW}^+$
, the condition has much the same form: a transitivity component and a reflexivity component. The strictest and most natural form of reflexivity would be we require that the information in the singleton multiset of points
$\mathsf {RW}^+$
, the condition has much the same form: a transitivity component and a reflexivity component. The strictest and most natural form of reflexivity would be we require that the information in the singleton multiset of points
![]() $[x]$
is indeed carried by the x itself. This says very little about combining points, of course. For transitivity, we require that combination compose in a straightforward manner: if
$[x]$
is indeed carried by the x itself. This says very little about combining points, of course. For transitivity, we require that combination compose in a straightforward manner: if
![]() $XRy$
and
$XRy$
and
![]() $[y]\cup YRz$
then
$[y]\cup YRz$
then
![]() $(X\cup Y)Rz$
.Footnote
12
However, we require something stronger than just composition in this direction: we also require its converse. That is, if
$(X\cup Y)Rz$
.Footnote
12
However, we require something stronger than just composition in this direction: we also require its converse. That is, if
![]() $(X\cup Y)Rz$
then we can find some ‘value’ y where
$(X\cup Y)Rz$
then we can find some ‘value’ y where
![]() $XRy$
and
$XRy$
and
![]() $([y]\cup Y)Rz$
. We call these two conditions compositionality because we think of R as a generalised combination relation, selecting for each collection of points the single points which are suitable to represent it. The compositionality condition says that this relation can be composed or decomposed piecewise. So, we have the following definition:
$([y]\cup Y)Rz$
. We call these two conditions compositionality because we think of R as a generalised combination relation, selecting for each collection of points the single points which are suitable to represent it. The compositionality condition says that this relation can be composed or decomposed piecewise. So, we have the following definition:
Definition 2 (Compositionality)
A multiset relation
![]() $R$
on
$R$
on
![]() $M(P)\times P$
is said to be compositional if and only if for all multisets X and Y and for all points z,
$M(P)\times P$
is said to be compositional if and only if for all multisets X and Y and for all points z,
In addition, a compositional multiset relation is reflexive iff for all points x, we have
We break the compositionality condition into two parts, the left to right direction we will call Transitivity, for obvious reasons. The right to left direction we will call Splitting.Footnote 13 These two parts of the condition play different roles in exploring the properties of this semantics, so we will highlight these roles by mentioning at each point whether Transitivity or Splitting is being appealed to.

Fig. 1 The two directions of compositionality.
The intuitions behind the two directions are represented in Figure 1. The intuition behind Transitivity is that if one can combine the information in X to obtain x and combine the information in Y together with x to obtain y, represented by the solid lines, then one could have just as well have used the information in the combination of X and Y to obtain y, represented by the broken lines. If we restrict our attention to the case where
![]() $X=[x]$
and
$X=[x]$
and
![]() $Y=[\;]$
then we see that Transitivity gives us the transitivity of the binary relation
$Y=[\;]$
then we see that Transitivity gives us the transitivity of the binary relation
![]() $\lambda x.\lambda y.[x]Ry$
on points.
$\lambda x.\lambda y.[x]Ry$
on points.
The intuition behind Splitting is that if one can obtain y from some information Z, which can be split into components X and Y, then one could evaluate the X portion to obtain something, x, which can be combined with the information in Y to obtain y.Footnote
14
If we restrict our attention to the case where
![]() $X=[x]$
and
$X=[x]$
and
![]() $Y=[\;]$
, then Splitting gives us the density of the binary relation
$Y=[\;]$
, then Splitting gives us the density of the binary relation
![]() $\lambda x.\lambda y.[x]Ry$
. That is, if
$\lambda x.\lambda y.[x]Ry$
. That is, if
![]() $[x]Rz$
then there is some y where
$[x]Rz$
then there is some y where
![]() $[x]Ry$
and
$[x]Ry$
and
![]() $[y]Rz$
. Notice that the density of this relation holds automatically in the case where reflexivity holds, but this condition is strictly weaker than reflexivity.Footnote
15
$[y]Rz$
. Notice that the density of this relation holds automatically in the case where reflexivity holds, but this condition is strictly weaker than reflexivity.Footnote
15
Since this binary relation
![]() $\lambda x.\lambda y.[x]Ry$
is so important in our frames, we will reserve special notation for it. In ternary frames the usual notation is ‘
$\lambda x.\lambda y.[x]Ry$
is so important in our frames, we will reserve special notation for it. In ternary frames the usual notation is ‘
![]() $\sqsubseteq $
’. Since our frames will not require reflexivity (but we will allow it), let us write ‘
$\sqsubseteq $
’. Since our frames will not require reflexivity (but we will allow it), let us write ‘
![]() $\sqsubset $
’ for this binary relation induced by the multiset relation R. We have seen proved the following lemma.
$\sqsubset $
’ for this binary relation induced by the multiset relation R. We have seen proved the following lemma.
Lemma 3. If R is a compositional multiset relation then the induced binary relation
![]() $\sqsubset $
(given by setting
$\sqsubset $
(given by setting
![]() $x\sqsubset y$
iff
$x\sqsubset y$
iff
![]() $[x]Ry$
) is transitive and dense.
$[x]Ry$
) is transitive and dense.
Before we continue spelling out the semantics, we would do well to pause to consider some examples of simple multiset relations, and their properties.
Example 4 (Compositional multiset relations on
 $\omega $
)
$\omega $
)
Here are some examples of compositional multiset relations on the set
![]() $\omega $
of natural numbers.
$\omega $
of natural numbers.
-
[ The Product]
 $XRy$
if and only if y is the product of all the members of X.Footnote
16
(This is genuinely and distinctively a multiset relation, which distinguishes repeated elements in the multiset. For this relation,
$XRy$
if and only if y is the product of all the members of X.Footnote
16
(This is genuinely and distinctively a multiset relation, which distinguishes repeated elements in the multiset. For this relation,
 $[2,2]R4$
holds, but
$[2,2]R4$
holds, but
 $[2]R4$
does not.) This is compositional, which fact is left to the reader.
$[2]R4$
does not.) This is compositional, which fact is left to the reader. -
[ Some Product]
 $XRy$
if and only if y is some product of the members of X, using each instance in X at most once. (Unlike the product, this relation is not functional.
$XRy$
if and only if y is some product of the members of X, using each instance in X at most once. (Unlike the product, this relation is not functional. -
[ The Sum, and Some Sum] In the same way, the relation R given by setting
 $XRy$
iff
$XRy$
iff
 $\Sigma X=y$
is compositional (given that we set
$\Sigma X=y$
is compositional (given that we set
 $\Sigma [\;]=0$
), as is the relation given by setting
$\Sigma [\;]=0$
), as is the relation given by setting
 $XRy$
iff
$XRy$
iff
 $\Sigma X'=y$
for some
$\Sigma X'=y$
for some
 $X'\le X$
. As with the product relations, one is functional, and the other is not. Each of the relations discussed so far makes essential use of the multiset structure. The multiset
$X'\le X$
. As with the product relations, one is functional, and the other is not. Each of the relations discussed so far makes essential use of the multiset structure. The multiset
 $[2,2]$
is related to different numbers in each case, than the singleton multiset
$[2,2]$
is related to different numbers in each case, than the singleton multiset
 $[2]$
. In the next example, the multiplicity of members makes no difference at all.
$[2]$
. In the next example, the multiplicity of members makes no difference at all. -
[Maximum-or-zero-if-empty] In this case,
 $XRy$
if and only if y is the largest member of X, and is
$XRy$
if and only if y is the largest member of X, and is
 $0$
if X is empty. This satisfies the reflexivity condition, as well as Transitivity and Splitting.
$0$
if X is empty. This satisfies the reflexivity condition, as well as Transitivity and Splitting. -
[The Empty Relation] Another multiset relation, trivially compositional, is the empty multiset relation. It is straightforward to verify that this relation satisfies both the Transitivity and the Splitting conditions. Of course, this relation fails to be reflexive, unlike the other relations we have considered so far.
That is a range of compositional multiset relations on
![]() $\omega $
. Not every multiset relation, however, is compositional.
$\omega $
. Not every multiset relation, however, is compositional.
Example 5 (Non-compositional multiset relations on
 $\omega $
)
$\omega $
)
These relations fail to be compositional in different ways.
-
[Larger than the product of]
 $XRy$
holds if and only if
$XRy$
holds if and only if
 $y>\Pi X$
. Clearly this is not reflexive. While Splitting holds, the Transitivity direction of compositionality fails.
$y>\Pi X$
. Clearly this is not reflexive. While Splitting holds, the Transitivity direction of compositionality fails. -
[Largest two]
 $XRy$
if and only if y is one of the largest two elements of X. This relation fails transitivity.
$XRy$
if and only if y is one of the largest two elements of X. This relation fails transitivity. -
[Membership]
 $XRy$
if and only if
$XRy$
if and only if
 $y\in X$
. This relation enjoys Transitivity but not Splitting.
$y\in X$
. This relation enjoys Transitivity but not Splitting.Although membership is not a compositional multiset relation on
 $M(P)\times P$
, it is compositional if we restrict our attention to inhabited
Footnote
17
multisets. (We will discuss this restricted form of compositionality below.)
$M(P)\times P$
, it is compositional if we restrict our attention to inhabited
Footnote
17
multisets. (We will discuss this restricted form of compositionality below.) -
[Between]
 $XRy$
iff y occurs between the smallest and the largest members of X, inclusive. So
$XRy$
iff y occurs between the smallest and the largest members of X, inclusive. So
 $[2,4]$
is related to
$[2,4]$
is related to
 $2$
and to
$2$
and to
 $4$
and to
$4$
and to
 $3$
but to no other number. This, like membership, is compositional on the inhabited multisets but not the full collection of multisets.
$3$
but to no other number. This, like membership, is compositional on the inhabited multisets but not the full collection of multisets.
We will end this series of examples with two more compositional relations, this time, on the rational numbers
![]() ${\mathbb Q}$
and the reals,
${\mathbb Q}$
and the reals,
![]() ${\mathbb R}$
, rather than on
${\mathbb R}$
, rather than on
![]() $\omega $
, so we have scope for examples of non-reflexive but dense order relations.
$\omega $
, so we have scope for examples of non-reflexive but dense order relations.
Example 6 (Non-reflexive multiset relations)
These examples of multiset relations make use of the density of the underlying order
![]() $<$
on
$<$
on
![]() ${\mathbb Q}$
and on
${\mathbb Q}$
and on
![]() ${\mathbb R}$
.
${\mathbb R}$
.
-
[larger than]
 $XRy$
if and only if
$XRy$
if and only if
 $y>x$
for each
$y>x$
for each
 $x\in X$
. So,
$x\in X$
. So,
 $[\;] Ry$
for every y (in this case, the condition is vacuously satisfied). This relation satisfies Transitivity and Splitting but not reflexivity.
$[\;] Ry$
for every y (in this case, the condition is vacuously satisfied). This relation satisfies Transitivity and Splitting but not reflexivity.In this case, the relation makes no distinction between multisets with the same ground.
 $[2,2]$
is related to all the numbers greater than
$[2,2]$
is related to all the numbers greater than
 $2$
, as is
$2$
, as is
 $[2]$
and
$[2]$
and
 $[2,2,2]$
.
$[2,2,2]$
. -
[larger than the sum of] Here,
 $XRy$
if and only if
$XRy$
if and only if
 $y$
is larger than the sum of all the members of X (counting their multiplicities, as in the case of the sum relation given previously). As before, we set
$y$
is larger than the sum of all the members of X (counting their multiplicities, as in the case of the sum relation given previously). As before, we set
 $\Sigma [\;]=0$
. While this fails to be reflexive, it is compositional.
$\Sigma [\;]=0$
. While this fails to be reflexive, it is compositional.
This flock of examples was longer than it strictly needed to be, if not for one thing. A complaint about the ternary relational semantics is that examples are hard to come by, hard to construct and above all, hard to picture. That there is such a list of naturally occurring examples of compositional multiset relations, both reflexive and irreflexive, and which exhibit significantly different behaviours, but are straightforward both to reason with and to understand, goes quite some way towards answering that complaint.
It is disappointing, however, that membership and betweenness failed to count as compositional relations. In fact, as we noted, those multiset relations are compositional if we restrict our attention to the class
![]() $M'(P)$
of inhabited multisets of points. We can make this notion precise in a definition.
$M'(P)$
of inhabited multisets of points. We can make this notion precise in a definition.
Definition 7 (Compositional inhabited-multiset relations)
A relation R on
![]() $M'(P)\times P$
is said to be compositional if and only if for all multisets X and Y where
$M'(P)\times P$
is said to be compositional if and only if for all multisets X and Y where
![]() $X\neq [\;]$
, and for all points z,
$X\neq [\;]$
, and for all points z,
This is the appropriate definition of compositionality for a relation on inhabited multisets. You may wonder why, in this definition, X inhabited, but Y is allowed to be empty. Isn’t that outside the spirit of restricting our attention to inhabited multisets? This is a natural restriction of compositionality to this setting, because it is the smallest modification to the condition that ensures that the left relatum of any R-fact is nonempty. (Since we require that X be inhabited, for
![]() $XRy$
to make sense in this context, this is enough to guarantee that
$XRy$
to make sense in this context, this is enough to guarantee that
![]() $X\cup Y$
is also inhabited, and
$X\cup Y$
is also inhabited, and
![]() $[y]\cup Y$
is inhabited by design.) A satisfying upshot of this result is the fact under this condition (allowing for Y to be empty), the proof of Lemma 15 works in the case of inhabited-multiset relations, too. That special case of transitivity, spelled out, is this:
$[y]\cup Y$
is inhabited by design.) A satisfying upshot of this result is the fact under this condition (allowing for Y to be empty), the proof of Lemma 15 works in the case of inhabited-multiset relations, too. That special case of transitivity, spelled out, is this:
![]() $XRy$
and
$XRy$
and
![]() $[y]Rz$
implies
$[y]Rz$
implies
![]() $XRz$
. We have also appealed to this condition in the proof Lemma 3. We will also see below, when we turn to more general structures, like lists and trees, that the general form of compositionality involves trading in a single item in a structure (here, a member of a multiset) for another structure. In the case of a multiset, any multiset with a member y can be written in the form
$XRz$
. We have also appealed to this condition in the proof Lemma 3. We will also see below, when we turn to more general structures, like lists and trees, that the general form of compositionality involves trading in a single item in a structure (here, a member of a multiset) for another structure. In the case of a multiset, any multiset with a member y can be written in the form
![]() $X\cup [y]$
. For this representation to work, in general, we need to allow the case where X is empty, even if our attention is fixed on inhabited multisets, for we may wish to trade in the y in a singleton multiset
$X\cup [y]$
. For this representation to work, in general, we need to allow the case where X is empty, even if our attention is fixed on inhabited multisets, for we may wish to trade in the y in a singleton multiset
![]() $[y]$
for some other multiset.
$[y]$
for some other multiset.
Example 8 (Compositional inhabited-multiset relations)
With this expanded definition, we can enlarge our class of models even further. We have already seen that membership and between give us compositional relations on inhabited multisets. So are these:
-
[maximum, and minimum] maximum-or-zero-if-empty is a compositional multiset relation on
 $\omega $
. Without the need to have a maximum for
$\omega $
. Without the need to have a maximum for
 $[\;]$
, we can remove the “or-zero-if-empty” dodge, and restrict our attention to the largest member of the multiset. Or the smallest, if we choose, and the result is a compositional inhabited-multiset relation.
$[\;]$
, we can remove the “or-zero-if-empty” dodge, and restrict our attention to the largest member of the multiset. Or the smallest, if we choose, and the result is a compositional inhabited-multiset relation. -
[ the sum, and some sum on subsets of ω] If we no longer have the requirement that the empty multiset
 $[\;]$
have a sum, then given any subset
$[\;]$
have a sum, then given any subset
 $S$
of
$S$
of
 $\omega $
, closed under addition (so if
$\omega $
, closed under addition (so if
 $x,y\in S$
, then so is
$x,y\in S$
, then so is
 $x+y$
) we can define a compositional inhabited-multiset relations R and
$x+y$
) we can define a compositional inhabited-multiset relations R and
 $R'$
on S, setting
$R'$
on S, setting
 $XRy$
iff
$XRy$
iff
 $y=\Sigma X$
, and
$y=\Sigma X$
, and
 $XR'y$
iff
$XR'y$
iff
 $y=\Sigma X'$
where
$y=\Sigma X'$
where
 $X'$
is an inhabited multiset where
$X'$
is an inhabited multiset where
 $X'\le X$
. For example, we can let
$X'\le X$
. For example, we can let
 $S=\{1,2,3,\ldots \}=\omega \backslash \{0\}$
to provide a very different kind of model, once
$S=\{1,2,3,\ldots \}=\omega \backslash \{0\}$
to provide a very different kind of model, once
 $0$
is left out of the domain.
$0$
is left out of the domain. -
[ the product, and some product on subsets of ω] In exactly the same way, we can generate models defining R on subsets of
 $\omega $
closed under product, without having to include
$\omega $
closed under product, without having to include
 $1$
as the product of the empty multiset.
$1$
as the product of the empty multiset.
In what follows, we will consider both compositional multiset relations and, at times, compositional inhabited-multiset relations. For any compositional multiset relation, its restriction to inhabited multisets is, of course, also compositional. For the converse, we have the following lemma, which shows that there is a way to extend a compositional inhabited multiset relation R on
![]() $M'(P)\times P$
to a compositional multiset relation on
$M'(P)\times P$
to a compositional multiset relation on
![]() $M(P\cup \{\infty \})\times (P\cup \{\infty \})$
, where we add a new ‘point at infinity’ to our point set.
$M(P\cup \{\infty \})\times (P\cup \{\infty \})$
, where we add a new ‘point at infinity’ to our point set.
Lemma 9. If R is a compositional inhabited-multiset relation on
![]() $M'(P)\times P$
, and
$M'(P)\times P$
, and
![]() $\infty \not \in P$
, then the multiset relation
$\infty \not \in P$
, then the multiset relation
![]() $R^{\times }$
on
$R^{\times }$
on
![]() $M(P\cup \{\infty \})\times (P\cup \{\infty \})$
, defined as follows, is compositional.
$M(P\cup \{\infty \})\times (P\cup \{\infty \})$
, defined as follows, is compositional.
 $$\begin{align*}XR^{\times} z\textrm{ iff } \begin{cases} z=\infty, & \textrm{if }X\backslash \infty=[\;], \\ (X\backslash\infty)Rz, & \textrm{if }{X\backslash\infty}\neq[\;].\end{cases} \end{align*}$$
$$\begin{align*}XR^{\times} z\textrm{ iff } \begin{cases} z=\infty, & \textrm{if }X\backslash \infty=[\;], \\ (X\backslash\infty)Rz, & \textrm{if }{X\backslash\infty}\neq[\;].\end{cases} \end{align*}$$
Furthermore, if R is reflexive, then so is
![]() $R^{\times }$
.
$R^{\times }$
.
(In the definition of
![]() $R^{\times }$
we use the notation ‘
$R^{\times }$
we use the notation ‘
![]() $X\backslash y$
’ for the multiset formed by removing all instances of y from X. So, for example,
$X\backslash y$
’ for the multiset formed by removing all instances of y from X. So, for example,
![]() $[a,b,b,c,c]\backslash c=[a,b,b]$
. We reserve ‘
$[a,b,b,c,c]\backslash c=[a,b,b]$
. We reserve ‘
![]() $X\backslash Y$
’ for the multiset formed by removing the number of occurrences in Y from X, so
$X\backslash Y$
’ for the multiset formed by removing the number of occurrences in Y from X, so
![]() $[a,b,b,c,c]\backslash [c]=[a,b,b,c]$
.)
$[a,b,b,c,c]\backslash [c]=[a,b,b,c]$
.)
Proof. Let’s suppose that
![]() $(X\cup Y)R^{\times } z$
, in order to find some y where
$(X\cup Y)R^{\times } z$
, in order to find some y where
![]() $YR^{\times } y$
and
$YR^{\times } y$
and
![]() $(X\cup [y])R^{\times } z$
. By definition
$(X\cup [y])R^{\times } z$
. By definition
![]() $(X\cup Y)R^{\times } z$
holds if and only if
$(X\cup Y)R^{\times } z$
holds if and only if
![]() $z=\infty $
(if
$z=\infty $
(if
![]() $(X\cup Y)\backslash \infty =[\;]$
) or
$(X\cup Y)\backslash \infty =[\;]$
) or
![]() $((X\cup Y)\backslash \infty ))Rz$
(otherwise). Let’s take these cases in turn. If
$((X\cup Y)\backslash \infty ))Rz$
(otherwise). Let’s take these cases in turn. If
![]() $(X\cup Y)\backslash \infty =[\;]$
then clearly
$(X\cup Y)\backslash \infty =[\;]$
then clearly
![]() $X\backslash [\;]$
and
$X\backslash [\;]$
and
![]() $Y\backslash [\;]$
, so in this case, both
$Y\backslash [\;]$
, so in this case, both
![]() $YR^{\times }\infty $
and
$YR^{\times }\infty $
and
![]() $(X\cup [\infty])R^{\times } \infty $
, as desired. So, now consider the second case: we have
$(X\cup [\infty])R^{\times } \infty $
, as desired. So, now consider the second case: we have
![]() $((X\cup Y)\backslash \infty ))Rz$
and
$((X\cup Y)\backslash \infty ))Rz$
and
![]() $(X\cup Y)\backslash \infty \neq [\;]$
. We aim to find some y where
$(X\cup Y)\backslash \infty \neq [\;]$
. We aim to find some y where
![]() $YR^{\times } y$
and
$YR^{\times } y$
and
![]() $(X\cup [y])R^{\times } z$
. If
$(X\cup [y])R^{\times } z$
. If
![]() $Y\backslash \infty =[\;]$
, then we choose
$Y\backslash \infty =[\;]$
, then we choose
![]() $\infty $
for y. We have, then,
$\infty $
for y. We have, then,
![]() $YR^{\times } \infty $
and since
$YR^{\times } \infty $
and since
![]() $((X\cup Y)\backslash \infty ))Rz$
, we have
$((X\cup Y)\backslash \infty ))Rz$
, we have
![]() $(X\backslash \infty )Rz$
, so we have
$(X\backslash \infty )Rz$
, so we have
![]() $(X\cup \{\infty \})R^{\times } z$
as desired. On the other hand, if Y has some element other than
$(X\cup \{\infty \})R^{\times } z$
as desired. On the other hand, if Y has some element other than
![]() $\infty $
, since
$\infty $
, since
![]() $((X\cup Y)\backslash \infty ))Rz$
, we have
$((X\cup Y)\backslash \infty ))Rz$
, we have
![]() $((X\backslash \infty )\cup (Y\backslash \infty ))Rz$
, and since R is compositional, there is some y where
$((X\backslash \infty )\cup (Y\backslash \infty ))Rz$
, and since R is compositional, there is some y where
![]() $(Y\backslash \infty )Ry$
and
$(Y\backslash \infty )Ry$
and
![]() $((X\backslash \infty )\cup [y])Rz$
, which gives us
$((X\backslash \infty )\cup [y])Rz$
, which gives us
![]() $YR^{\times } y$
and
$YR^{\times } y$
and
![]() $(X\cup [y])R^{\times } z$
as desired.
$(X\cup [y])R^{\times } z$
as desired.
Now for the second half of the compositionality condition for
![]() $R^{\times }$
, suppose that there is some y where
$R^{\times }$
, suppose that there is some y where
![]() $YR^{\times } y$
and
$YR^{\times } y$
and
![]() $(X\cup [y])R^{\times } z$
. We aim to show that
$(X\cup [y])R^{\times } z$
. We aim to show that
![]() $(X\cup Y)R^{\times } z$
. If
$(X\cup Y)R^{\times } z$
. If
![]() $YR^{\times } y$
then either
$YR^{\times } y$
then either
![]() $y=\infty $
and Y contains at most
$y=\infty $
and Y contains at most
![]() $\infty $
, or otherwise
$\infty $
, or otherwise
![]() $(Y\backslash \infty )Ry$
. In the first case,
$(Y\backslash \infty )Ry$
. In the first case,
![]() $(X\cup [y])R^{\times } z$
tells us that
$(X\cup [y])R^{\times } z$
tells us that
![]() $(X\cup [\infty])R^{\times } z$
, which means either that
$(X\cup [\infty])R^{\times } z$
, which means either that
![]() $(X\backslash \infty )Rz$
, or X also contains at most
$(X\backslash \infty )Rz$
, or X also contains at most
![]() $\infty $
and then
$\infty $
and then
![]() $z=\infty $
. In the either of these cases, we have
$z=\infty $
. In the either of these cases, we have
![]() $(X\cup Y)R^{\times } z$
, as desired. So, let’s suppose
$(X\cup Y)R^{\times } z$
, as desired. So, let’s suppose
![]() $y\neq \infty $
. In that case we have
$y\neq \infty $
. In that case we have
![]() $(Y\backslash \infty )Ry$
, and then, since
$(Y\backslash \infty )Ry$
, and then, since
![]() $(X\cup [y]))R^{\times } z$
, we have
$(X\cup [y]))R^{\times } z$
, we have
![]() $((X\cup [y])\backslash \infty )Rz$
, and by the compositionality of R,
$((X\cup [y])\backslash \infty )Rz$
, and by the compositionality of R,
![]() $((X\cup Y)\backslash {\infty })Rz$
, which gives
$((X\cup Y)\backslash {\infty })Rz$
, which gives
![]() $(X\cup Y)R^{\times } z$
, as desired.
$(X\cup Y)R^{\times } z$
, as desired.
Finally,
![]() $R^{\times }$
is reflexive follows immediately from the reflexivity of R and the fact that
$R^{\times }$
is reflexive follows immediately from the reflexivity of R and the fact that
![]() $[\infty]R^{\times }\infty $
.
$[\infty]R^{\times }\infty $
.
With this result, it is possible for us to use examples like membership and betweenness as compositional multiset relations, with the full complement of logical resources, including the set of normal points, identified as those related to the empty multiset
![]() $[\;]$
.
$[\;]$
.
Now we are in a position to define multiset frames and models. We will begin with the more standard ternary relational frames for
![]() $\mathsf {RW}^+$
.
$\mathsf {RW}^+$
.
Definition 10 (Ternary relational
 $\mathsf {RW}^+$
frames, models)
$\mathsf {RW}^+$
frames, models)
A ternary relational frame for
![]() $\mathsf {RW}^+$
is a quadruple
$\mathsf {RW}^+$
is a quadruple
![]() $\langle P,R,\sqsubseteq , N\rangle $
obeying the following conditions.
$\langle P,R,\sqsubseteq , N\rangle $
obeying the following conditions.
-
1.
 $\sqsubseteq $
is a partial order.
$\sqsubseteq $
is a partial order. -
2. If
 $x\sqsubseteq w$
,
$x\sqsubseteq w$
,
 $y\sqsubseteq u$
,
$y\sqsubseteq u$
,
 $v\sqsubseteq z$
, and
$v\sqsubseteq z$
, and
 $Rwuv$
, then
$Rwuv$
, then
 $Rxyz$
.
$Rxyz$
. -
3.
 $y\sqsubseteq z$
iff
$y\sqsubseteq z$
iff
 $\exists x\in N$
,
$\exists x\in N$
,
 $Rxyz$
.
$Rxyz$
. -
4. If
 $x\in N$
and
$x\in N$
and
 $x\sqsubseteq y$
, then
$x\sqsubseteq y$
, then
 $y\in N$
.
$y\in N$
. -
5.
 $Rxyz$
only if
$Rxyz$
only if
 $Ryxz$
.
$Ryxz$
. -
6.
 $Rwxyz$
only if
$Rwxyz$
only if
 $Rw(xy)z$
.
$Rw(xy)z$
.
To get a ternary relational frame for
![]() $\mathsf {R}^+$
, one adds the condition that if
$\mathsf {R}^+$
, one adds the condition that if
![]() $Rxyz$
, then
$Rxyz$
, then
![]() $Rxyyz$
.
$Rxyyz$
.
A ternary relational model is a quintuple
![]() $\langle P, R, \sqsubseteq , N, \Vdash \rangle $
where the first four components make up a frame and the final component is a binary relation between P and the set of atoms such that if
$\langle P, R, \sqsubseteq , N, \Vdash \rangle $
where the first four components make up a frame and the final component is a binary relation between P and the set of atoms such that if
![]() $x\Vdash p$
and
$x\Vdash p$
and
![]() $x\sqsubseteq y$
, then
$x\sqsubseteq y$
, then
![]() $y\Vdash p$
. This is extended to the whole language according to the following clauses.
$y\Vdash p$
. This is extended to the whole language according to the following clauses.
-
•
 $x\Vdash A\land B$
iff
$x\Vdash A\land B$
iff
 $x\Vdash A$
and
$x\Vdash A$
and
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\lor B$
iff
$x\Vdash A\lor B$
iff
 $x\Vdash A$
or
$x\Vdash A$
or
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\to B$
iff for each
$x\Vdash A\to B$
iff for each
 $y,z$
where
$y,z$
where
 $Rxyz$
, if
$Rxyz$
, if
 $y\Vdash A$
then
$y\Vdash A$
then
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash A\circ B$
iff for some
$x\Vdash A\circ B$
iff for some
 $y,z$
where
$y,z$
where
 $Rxyz$
, both
$Rxyz$
, both
 $y\Vdash A$
and
$y\Vdash A$
and
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash \mathsf {t}$
iff
$x\Vdash \mathsf {t}$
iff
 $x\in N$
.
$x\in N$
. -
•
 $x\Vdash \bot $
never.
$x\Vdash \bot $
never.
Next, we define multiset frames.
Definition 11 (Multiset frame)
A multiset frame
![]() $\langle P,R\rangle $
is an inhabited set P of points together with a compositional multiset relation R on P.
$\langle P,R\rangle $
is an inhabited set P of points together with a compositional multiset relation R on P.
This definition is, in one sense, starkly simpler than the traditional frame semantics for
![]() $\mathsf {RW}^+$
, in that the three elements N,
$\mathsf {RW}^+$
, in that the three elements N,
![]() $\sqsubseteq $
and the ternary relation R are subsumed into one fundamental relation, the compositional multiset relation. They are also more general, because we consider not only models in which
$\sqsubseteq $
and the ternary relation R are subsumed into one fundamental relation, the compositional multiset relation. They are also more general, because we consider not only models in which
![]() $\sqsubset $
is reflexive (as it is in ternary relational frames), but the more general class of frames allowing for the underlying order relation
$\sqsubset $
is reflexive (as it is in ternary relational frames), but the more general class of frames allowing for the underlying order relation
![]() $\sqsubset $
to be non-reflexive, or even irreflexive. In fact, we allow as a frame the case where R is the empty relation. So, this is a wider class of frames. The multiset frames subsume the traditional ternary relational frames for
$\sqsubset $
to be non-reflexive, or even irreflexive. In fact, we allow as a frame the case where R is the empty relation. So, this is a wider class of frames. The multiset frames subsume the traditional ternary relational frames for
![]() $\mathsf {RW}^+$
, following the conditions (F1), (F2), and (F3) from Section 2. The one relation in a multiset frame encodes the three different moving parts of a ternary frame. We have the following fact:
$\mathsf {RW}^+$
, following the conditions (F1), (F2), and (F3) from Section 2. The one relation in a multiset frame encodes the three different moving parts of a ternary frame. We have the following fact:
Lemma 12. Each ternary frame
![]() $\langle P,R,\sqsubseteq ,N\rangle $
for
$\langle P,R,\sqsubseteq ,N\rangle $
for
![]() $\mathsf {RW}^+$
determines a reflexive multiset frame
$\mathsf {RW}^+$
determines a reflexive multiset frame
![]() $\langle P,R'\rangle $
, defined by setting:
$\langle P,R'\rangle $
, defined by setting:
-
•
 $[\;] R'x$
iff
$[\;] R'x$
iff
 $x\in N$
,
$x\in N$
, -
•
 $[x]R'y$
iff
$[x]R'y$
iff
 $x\sqsubseteq y$
,
$x\sqsubseteq y$
, -
•
 $[x,y]R'z$
iff
$[x,y]R'z$
iff
 $Rxyz$
,
$Rxyz$
, -
• If Y is a multiset of size two or more,
 $([x]\cup Y)R'z$
iff for some y,
$([x]\cup Y)R'z$
iff for some y,
 $YR'y$
and
$YR'y$
and
 $[x,y]R'z$
.
$[x,y]R'z$
.
Proof. We first need to show that the definition is
![]() $R'$
coherent: that the third clause, to the effect that
$R'$
coherent: that the third clause, to the effect that
![]() $[x,y]R'z$
iff
$[x,y]R'z$
iff
![]() $Rxyz$
, that the last clause, according to which
$Rxyz$
, that the last clause, according to which
![]() $([x]\cup Y)R'z$
iff for some y,
$([x]\cup Y)R'z$
iff for some y,
![]() $YR'y$
and
$YR'y$
and
![]() $[x,y]R'z$
, could both hold. For the third clause, we need to be sure that
$[x,y]R'z$
, could both hold. For the third clause, we need to be sure that
![]() $Rxyz$
holds iff
$Rxyz$
holds iff
![]() $Ryxz$
holds, since
$Ryxz$
holds, since
![]() $[x,y]=[y,x]$
, lest the clause give inconsistent guidance as about
$[x,y]=[y,x]$
, lest the clause give inconsistent guidance as about
![]() $[x,y]R'z$
. But in any ternary frame
$[x,y]R'z$
. But in any ternary frame
![]() $\langle P,R,\sqsubseteq ,N\rangle $
for
$\langle P,R,\sqsubseteq ,N\rangle $
for
![]() $\mathsf {RW}^+$
, we have
$\mathsf {RW}^+$
, we have
![]() $Rxyz$
iff
$Rxyz$
iff
![]() $Ryxz$
, so this clause is coherent.
$Ryxz$
, so this clause is coherent.
For the last clause, if
![]() $[x]\cup Y$
is the same multiset as
$[x]\cup Y$
is the same multiset as
![]() $[x']\cup Y'$
, we need to show that
$[x']\cup Y'$
, we need to show that
in order to ensure that this clause also gives consistent guidance concerning
![]() $R'$
. We prove this by induction on the size of
$R'$
. We prove this by induction on the size of
![]() $[x]\cup Y$
. When Y has size
$[x]\cup Y$
. When Y has size
![]() $2$
, this reduces to the case
$2$
, this reduces to the case
![]() $(\exists y)([x_2,x_3]R'y\land [x_1,y]R'z$
iff
$(\exists y)([x_2,x_3]R'y\land [x_1,y]R'z$
iff
![]() $(\exists y')([x_1,x_3]R'y'\land [x_2,y']R'z)$
, but given the definition of
$(\exists y')([x_1,x_3]R'y'\land [x_2,y']R'z)$
, but given the definition of
![]() $R'$
on two-element multisets in terms of the ternary R, this reduces to the biconditional
$R'$
on two-element multisets in terms of the ternary R, this reduces to the biconditional
![]() $(\exists y)(Rx_2x_3y\land Rx_1yz)$
iff
$(\exists y)(Rx_2x_3y\land Rx_1yz)$
iff
![]() $(\exists y)(Rx_1x_3y'\land Rx_2y'z)$
, but this is the biconditional between
$(\exists y)(Rx_1x_3y'\land Rx_2y'z)$
, but this is the biconditional between
![]() $R^2x_1(x_2x_3)z$
and
$R^2x_1(x_2x_3)z$
and
![]() $R^2x_2(x_1x_3)z$
, which indeed holds in our
$R^2x_2(x_1x_3)z$
, which indeed holds in our
![]() $\mathsf {RW}^+$
frame.
$\mathsf {RW}^+$
frame.
Suppose the equivalence has been proved for all multisets of size n (where
![]() $n>2$
) and we have a multiset
$n>2$
) and we have a multiset
![]() $[x_1]\cup Y=[x_2]\cup Y'$
of size
$[x_1]\cup Y=[x_2]\cup Y'$
of size
![]() $n+1$
. Let Z be such that
$n+1$
. Let Z be such that
![]() $Z\cup [x_{2}]=Y$
and
$Z\cup [x_{2}]=Y$
and
![]() $Z\cup [x_{1}]=Y'$
. Note that we may assume
$Z\cup [x_{1}]=Y'$
. Note that we may assume
![]() $x_{1}\neq x_{2}$
, as otherwise the case is trivial. We wish to show that
$x_{1}\neq x_{2}$
, as otherwise the case is trivial. We wish to show that
By the inductive hypothesis,
![]() $(\exists y)(([x_{2}]\cup Z)R'y\land [x_1,y]R'z)$
is equivalent to
$(\exists y)(([x_{2}]\cup Z)R'y\land [x_1,y]R'z)$
is equivalent to
From the definition of
![]() $R'$
, the latter two conjuncts suffice for
$R'$
, the latter two conjuncts suffice for
![]() $Rx_{1}(x_{2}w)z$
, which is equivalent to
$Rx_{1}(x_{2}w)z$
, which is equivalent to
![]() $Rx_{2}(x_{1}w)z$
, as in the base case. Therefore,
$Rx_{2}(x_{1}w)z$
, as in the base case. Therefore,
which in turn is equivalent, by the inductive hypothesis, to
So, we have shown by induction that the definition is coherent.
Now, it suffices to show that
![]() $R'$
, so defined, is reflexive and compositional. Reflexivity follows from the reflexivity of
$R'$
, so defined, is reflexive and compositional. Reflexivity follows from the reflexivity of
![]() $\sqsubseteq $
, and Transitivity follows straightforwardly from the definition of
$\sqsubseteq $
, and Transitivity follows straightforwardly from the definition of
![]() $R'$
itself, albeit with many cases to check. It remains to show that Splitting holds.
$R'$
itself, albeit with many cases to check. It remains to show that Splitting holds.
We want to show that if
![]() $(X\cup Y)R'z$
, then there is some y where
$(X\cup Y)R'z$
, then there is some y where
![]() $XR'y$
and
$XR'y$
and
![]() $([y]\cup Y)R'z$
. Given the definitions, we need to consider the cases where
$([y]\cup Y)R'z$
. Given the definitions, we need to consider the cases where
![]() $X\cup Y$
has zero, one, two, or more elements. In the case where
$X\cup Y$
has zero, one, two, or more elements. In the case where
![]() $X\cup Y$
is empty, then we have
$X\cup Y$
is empty, then we have
![]() $[]R'z$
. So, then we have
$[]R'z$
. So, then we have
![]() $[]R'z$
and
$[]R'z$
and
![]() $[z]R'z$
, as desired.
$[z]R'z$
, as desired.
If
![]() $X\cup Y$
has size 1, then there are two subcases. Subcase: X is
$X\cup Y$
has size 1, then there are two subcases. Subcase: X is
![]() $[x]$
. By assumption we have
$[x]$
. By assumption we have
![]() $[x]R'z$
, so we then have
$[x]R'z$
, so we then have
![]() $[x]R'x$
, by Reflexivity, and
$[x]R'x$
, by Reflexivity, and
![]() $[x]R'z$
, satisfying Splitting. Subcase: X is empty and Y is
$[x]R'z$
, satisfying Splitting. Subcase: X is empty and Y is
![]() $[x]$
. Since
$[x]$
. Since
![]() $[x]R'z$
,
$[x]R'z$
,
![]() $x\sqsubseteq z$
, so there is some
$x\sqsubseteq z$
, so there is some
![]() $y\in N$
such that
$y\in N$
such that
![]() $Ryxz$
. We then have
$Ryxz$
. We then have
![]() $[]R'y$
and
$[]R'y$
and
![]() $[y,x]R'z$
, satisfying Splitting.
$[y,x]R'z$
, satisfying Splitting.
Suppose
![]() $X\cup Y$
has size 2. Subcase: X is empty. We need a y such that
$X\cup Y$
has size 2. Subcase: X is empty. We need a y such that
![]() $[]R'y$
and
$[]R'y$
and
![]() $[y,y_{1},y_{2}]R'z$
. Since
$[y,y_{1},y_{2}]R'z$
. Since
![]() $y_{1}\sqsubseteq y_{1}$
, there is a
$y_{1}\sqsubseteq y_{1}$
, there is a
![]() $u\in N$
such that
$u\in N$
such that
![]() $Ruy_{1}y_{1}$
. By assumption we have
$Ruy_{1}y_{1}$
. By assumption we have
![]() $Ry_{1}y_{2}z$
, so it follows that
$Ry_{1}y_{2}z$
, so it follows that
![]() $Ruy_{1}y_{2}z$
, which is
$Ruy_{1}y_{2}z$
, which is
![]() $[uy_{1}y_{2}]R'z$
, as desired. Subcase: X is [x] and Y is
$[uy_{1}y_{2}]R'z$
, as desired. Subcase: X is [x] and Y is
![]() $[y_{1}]$
. In this subcase we have
$[y_{1}]$
. In this subcase we have
![]() $[x,y_{1}]R'z$
. Since
$[x,y_{1}]R'z$
. Since
![]() $[x]R'x$
, it follows that there is a y such that
$[x]R'x$
, it follows that there is a y such that
![]() $[x]R'y$
and
$[x]R'y$
and
![]() $[y,y_{1}]R'z$
, namely x. Subcase: X is
$[y,y_{1}]R'z$
, namely x. Subcase: X is
![]() $[x_{1},x_{2}]$
and Y is empty. By assumption we have
$[x_{1},x_{2}]$
and Y is empty. By assumption we have
![]() $[x_{1},x_{2}]R'z$
and we need a y such that
$[x_{1},x_{2}]R'z$
and we need a y such that
![]() $[x_{1},x_{2}]R'y$
and
$[x_{1},x_{2}]R'y$
and
![]() $[y]R'z$
. Since
$[y]R'z$
. Since
![]() $[z]R'z$
, we can simply take z as y.
$[z]R'z$
, we can simply take z as y.
Suppose
![]() $X\cup Y$
has size 3 or greater. Subcase: X is empty. The argument is similar to the subcase of the previous case where X is empty. Subcase: Y is empty. The argument is similar to the subcase of the previous case where Y is empty. Subcase: X and Y are inhabited, so
$X\cup Y$
has size 3 or greater. Subcase: X is empty. The argument is similar to the subcase of the previous case where X is empty. Subcase: Y is empty. The argument is similar to the subcase of the previous case where Y is empty. Subcase: X and Y are inhabited, so
![]() $X= [x]\cup X'$
and
$X= [x]\cup X'$
and
![]() $Y=[y_{1},\ldots ,y_{n}]$
and
$Y=[y_{1},\ldots ,y_{n}]$
and
![]() $([x]\cup X'\cup [y_{1},\ldots ,y_{n})R'z$
. From the definition of
$([x]\cup X'\cup [y_{1},\ldots ,y_{n})R'z$
. From the definition of
![]() $R'$
, it follows that for some
$R'$
, it follows that for some
![]() $z_{1}$
,
$z_{1}$
,
![]() $([x]\cup X'\cup [y_{2},\ldots ,y_{n}])R'z_{1}$
and
$([x]\cup X'\cup [y_{2},\ldots ,y_{n}])R'z_{1}$
and
![]() $[y_{1}, z_{1}]R'z$
. Repeated use of the definition results in
$[y_{1}, z_{1}]R'z$
. Repeated use of the definition results in
![]() $z_{2},\ldots ,z_{n}$
such that
$z_{2},\ldots ,z_{n}$
such that
![]() $[y_{1}, z_{1}]R'z$
,
$[y_{1}, z_{1}]R'z$
,
![]() $[y_{2}, z_{2}]R'z_{1}$
, …,
$[y_{2}, z_{2}]R'z_{1}$
, …,
![]() $[y_{n}, z_{n}]R'z_{n-1}$
, and
$[y_{n}, z_{n}]R'z_{n-1}$
, and
![]() $([x]\cup X')R'z_{n}$
. Repeated use of Transitivity then yields
$([x]\cup X')R'z_{n}$
. Repeated use of Transitivity then yields
![]() $[y_{1},\ldots ,y_{n}, z_{n}]R'z$
, so we can let
$[y_{1},\ldots ,y_{n}, z_{n}]R'z$
, so we can let
![]() $z_{n}$
be the desired y.
$z_{n}$
be the desired y.
All of the cases have been covered, so we conclude that
![]() $R'$
obeys Splitting.
$R'$
obeys Splitting.
So, the lemma is proved.
Now let us turn to consider what it is for a formula to hold at a point in a multiset frame. Given our understanding of the relation R, if
![]() $[x]Ry$
then the information in x also holds in y. So, if a formula holds at x, it is given by the multiset consisting of
$[x]Ry$
then the information in x also holds in y. So, if a formula holds at x, it is given by the multiset consisting of
![]() $[x]$
alone. But then, it should also hold at y, since the information given by
$[x]$
alone. But then, it should also hold at y, since the information given by
![]() $[x]$
is (perforce, according to R at least) also true at y, and there is nothing else in
$[x]$
is (perforce, according to R at least) also true at y, and there is nothing else in
![]() $[x]$
to take together with x. So, an appropriate heredity condition for truth-at-a-point in a multiset frame is given by the multiset relation R:
$[x]$
to take together with x. So, an appropriate heredity condition for truth-at-a-point in a multiset frame is given by the multiset relation R:
Definition 13 (Heredity)
A relation
![]() $\Vdash $
between points and formulas is hereditary along R for some class
$\Vdash $
between points and formulas is hereditary along R for some class
![]() $\mathcal {F}$
of formulas if and only if whenever
$\mathcal {F}$
of formulas if and only if whenever
![]() $[x]Ry$
(that is, when
$[x]Ry$
(that is, when
![]() $x\sqsubset y$
) and
$x\sqsubset y$
) and
![]() $x\Vdash A$
then
$x\Vdash A$
then
![]() $y\Vdash A$
, for each formula
$y\Vdash A$
, for each formula
![]() $A$
in
$A$
in
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Given a hereditary relation
![]() $\Vdash $
for all atomic formulas on a multiset frame, we can extend it to a hereditary relation on all formulas in the language of
$\Vdash $
for all atomic formulas on a multiset frame, we can extend it to a hereditary relation on all formulas in the language of
![]() $\mathsf {RW}^+$
as follows:
$\mathsf {RW}^+$
as follows:
Definition 14 (Truth-at-a-point in a multiset model)
For any multiset frame
![]() $\langle P,R\rangle $
and a hereditary relation
$\langle P,R\rangle $
and a hereditary relation
![]() $\Vdash $
defined on atomic formulas in our language, we extend the relation
$\Vdash $
defined on atomic formulas in our language, we extend the relation
![]() $\Vdash $
to the whole vocabulary, defining
$\Vdash $
to the whole vocabulary, defining
![]() $x\Vdash A$
recursively as follows:
$x\Vdash A$
recursively as follows:
-
•
 $x\Vdash A\land B$
iff
$x\Vdash A\land B$
iff
 $x\Vdash A$
and
$x\Vdash A$
and
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\lor B$
iff
$x\Vdash A\lor B$
iff
 $x\Vdash A$
or
$x\Vdash A$
or
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\to B$
iff for each
$x\Vdash A\to B$
iff for each
 $y,z$
where
$y,z$
where
 $[x,y]Rz$
, if
$[x,y]Rz$
, if
 $y\Vdash A$
then
$y\Vdash A$
then
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash A\circ B$
iff for some
$x\Vdash A\circ B$
iff for some
 $y,z$
where
$y,z$
where
 $[y,z]Rx$
, both
$[y,z]Rx$
, both
 $y\Vdash A$
and
$y\Vdash A$
and
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash \mathsf {t}$
iff
$x\Vdash \mathsf {t}$
iff
 $[\;] Rx$
.
$[\;] Rx$
. -
•
 $x\Vdash \bot $
never.
$x\Vdash \bot $
never.
Lemma 15. In any multiset frame
![]() $\langle P,R\rangle $
, the evaluation relation
$\langle P,R\rangle $
, the evaluation relation
![]() $\Vdash $
defined above, between points and arbitrary formulas is hereditary along R.
$\Vdash $
defined above, between points and arbitrary formulas is hereditary along R.
Proof. We aim to show that whenever
![]() $[x]Ry$
and
$[x]Ry$
and
![]() $x\Vdash A$
then
$x\Vdash A$
then
![]() $y\Vdash A$
. This is an easy induction on the structure of the formula A. The result holds by fiat for atomic formulas, and the induction step is trivial for conjunctions and disjunctions.
$y\Vdash A$
. This is an easy induction on the structure of the formula A. The result holds by fiat for atomic formulas, and the induction step is trivial for conjunctions and disjunctions.
For conditionals, suppose
![]() $[x]Ry$
and
$[x]Ry$
and
![]() $x\Vdash A\to B$
. We wish to show that
$x\Vdash A\to B$
. We wish to show that
![]() $y\Vdash A\to B$
too. Take
$y\Vdash A\to B$
too. Take
![]() $u,v$
where
$u,v$
where
![]() $[y,u]Rv$
. We wish to show that if
$[y,u]Rv$
. We wish to show that if
![]() $u\Vdash A$
then
$u\Vdash A$
then
![]() $v\Vdash B$
. By compositionality, since
$v\Vdash B$
. By compositionality, since
![]() $[x]Ry$
and
$[x]Ry$
and
![]() $[y,u]Rv$
, we have
$[y,u]Rv$
, we have
![]() $[x,u]Rv$
. Since
$[x,u]Rv$
. Since
![]() $x\Vdash A\to B$
, if
$x\Vdash A\to B$
, if
![]() $u\Vdash A$
then
$u\Vdash A$
then
![]() $v\Vdash B$
as desired.
$v\Vdash B$
as desired.
Similarly, if
![]() $[x]Ry$
and
$[x]Ry$
and
![]() $x\Vdash A\circ B$
, we wish to show that
$x\Vdash A\circ B$
, we wish to show that
![]() $y\Vdash A\circ B$
. So, we wish to find
$y\Vdash A\circ B$
. So, we wish to find
![]() $u,v$
where
$u,v$
where
![]() $[u,v]Ry$
,
$[u,v]Ry$
,
![]() $u\Vdash A$
and
$u\Vdash A$
and
![]() $v\Vdash B$
. Since
$v\Vdash B$
. Since
![]() $x\Vdash A\circ B$
, we have
$x\Vdash A\circ B$
, we have
![]() $u,v$
where
$u,v$
where
![]() $[u,v]Rx$
,
$[u,v]Rx$
,
![]() $u\Vdash A$
and
$u\Vdash A$
and
![]() $v\Vdash B$
. By compositionality,
$v\Vdash B$
. By compositionality,
![]() $[u,v]Rx$
and
$[u,v]Rx$
and
![]() $([x]\cup [\;])Ry$
gives us
$([x]\cup [\;])Ry$
gives us
![]() $([u,v]\cup [\;])Ry$
, i.e.,
$([u,v]\cup [\;])Ry$
, i.e.,
![]() $[u,v]Ry$
as desired.
$[u,v]Ry$
as desired.
Finally, if
![]() $[x]Ry$
and
$[x]Ry$
and
![]() $x\Vdash \mathsf {t}$
, then we have
$x\Vdash \mathsf {t}$
, then we have
![]() $[\;] Rx$
. Notice that compositionality ensures that
$[\;] Rx$
. Notice that compositionality ensures that
![]() $[\;] Rx$
and
$[\;] Rx$
and
![]() $([x]\cup [\;] )Ry$
give
$([x]\cup [\;] )Ry$
give
![]() $([\;]\cup [\;])Ry$
, i.e., from
$([\;]\cup [\;])Ry$
, i.e., from
![]() $[\;] Rx$
and
$[\;] Rx$
and
![]() $[x]Ry$
, we have
$[x]Ry$
, we have
![]() $[\;] Ry$
, so if
$[\;] Ry$
, so if
![]() $\mathsf {t}$
holds at x and
$\mathsf {t}$
holds at x and
![]() $[x]Ry$
, then
$[x]Ry$
, then
![]() $\mathsf {t}$
holds at y too.
$\mathsf {t}$
holds at y too.
So, evaluation relations on frames allow us to interpret formulas from the language of
![]() $\mathsf {RW}^+$
or
$\mathsf {RW}^+$
or
![]() $\mathsf {R}^+$
at points. Note that in the case for fusion, we needed to consider the multiset
$\mathsf {R}^+$
at points. Note that in the case for fusion, we needed to consider the multiset
![]() $[x]\cup [\;]$
, which is the special case highlighted in the definition of compositionality for inhabited-multiset relations. We call the combination of a frame
$[x]\cup [\;]$
, which is the special case highlighted in the definition of compositionality for inhabited-multiset relations. We call the combination of a frame
![]() $\langle P,R\rangle $
and an evaluation relation
$\langle P,R\rangle $
and an evaluation relation
![]() $\Vdash $
on that frame a model, and we abuse notation slightly to think of the triple
$\Vdash $
on that frame a model, and we abuse notation slightly to think of the triple
![]() $\langle P,R,\Vdash \rangle $
as a model.
$\langle P,R,\Vdash \rangle $
as a model.
Another way to represent how formulas are evaluated at points in frames is, for each formula A, to collect together the points that support A. We use the notation
![]() for the set
for the set
![]() $\{x\in P:x\Vdash A\}$
, the extension of the formula A in the model. The results of this section show that the set
$\{x\in P:x\Vdash A\}$
, the extension of the formula A in the model. The results of this section show that the set
![]() is upwardly closed along the relation
is upwardly closed along the relation
![]() $\sqsubset $
, and the evaluation conditions for atomic formulas are simply that for each atomic formula p, its extension
$\sqsubset $
, and the evaluation conditions for atomic formulas are simply that for each atomic formula p, its extension
![]() is an upwardly closed set.
is an upwardly closed set.
We pause to note that the evaluation conditions on ternary frames agree with those on multiset frames. In other words we have the following lemma:
Lemma 16 (Model equivalence)
If
![]() $\langle P,R,\sqsubseteq ,N,\Vdash \rangle $
is a ternary relational model for
$\langle P,R,\sqsubseteq ,N,\Vdash \rangle $
is a ternary relational model for
![]() $\mathsf {RW}^+$
(or
$\mathsf {RW}^+$
(or
![]() $\mathsf {R}^+$
), then
$\mathsf {R}^+$
), then
![]() $\langle P,R',\Vdash \rangle $
is a multiset model defined on the multiset frame
$\langle P,R',\Vdash \rangle $
is a multiset model defined on the multiset frame
![]() $\langle P,R'\rangle $
.
$\langle P,R'\rangle $
.
The proof is immediate, given that
![]() $[x,y]R'z$
iff
$[x,y]R'z$
iff
![]() $Rxyz$
, and
$Rxyz$
, and
![]() $[\;] R'x$
iff
$[\;] R'x$
iff
![]() $x\in N$
.
$x\in N$
.
So, we have shown that reflexive multiset frames correspond tightly to ternary relational frames. We have also seen that compositional inhabited-multiset relations arise naturally as structures in the same general family as compositional multiset relation. A frame
![]() $\langle P,R\rangle $
which is furnished with an inhabited-multiset relation R can also be used to model our propositional vocabulary. Given an inhabited-multiset frame
$\langle P,R\rangle $
which is furnished with an inhabited-multiset relation R can also be used to model our propositional vocabulary. Given an inhabited-multiset frame
![]() $\langle P,R\rangle $
and a hereditary evaluation relation
$\langle P,R\rangle $
and a hereditary evaluation relation
![]() $\Vdash $
on atomic formulas, we can extend
$\Vdash $
on atomic formulas, we can extend
![]() $\Vdash $
to the propositional language except for the Ackermann constant
$\Vdash $
to the propositional language except for the Ackermann constant
![]() $\mathsf {t}$
, in the manner given in Definition 14. The proof that
$\mathsf {t}$
, in the manner given in Definition 14. The proof that
![]() $\Vdash $
so defined is heredity follows in exactly the same way. The only point at which the condition that R relate only inhabited multisets is violated in that proof is at the clause for
$\Vdash $
so defined is heredity follows in exactly the same way. The only point at which the condition that R relate only inhabited multisets is violated in that proof is at the clause for
![]() $\mathsf {t}$
. The rest of the proof goes through as expected.
$\mathsf {t}$
. The rest of the proof goes through as expected.
With multiset frames, we can model the relevant logic
![]() $\mathsf {RW}^+$
. To make this precise, we introduce the logic
$\mathsf {RW}^+$
. To make this precise, we introduce the logic
![]() $\mathsf {RW}^+$
by way of a sequent calculus. The calculus utilises sequents of the form
$\mathsf {RW}^+$
by way of a sequent calculus. The calculus utilises sequents of the form
![]() , where A is a formula and
, where A is a formula and
![]() $\Gamma $
is a structure, generated by the following grammar:
$\Gamma $
is a structure, generated by the following grammar:
In other words, a structure is a formula A, the empty structure
![]() $\epsilon $
, the extensional combination
$\epsilon $
, the extensional combination
![]() $(\Gamma ,\Gamma ')$
of two structures, or the intensional combination
$(\Gamma ,\Gamma ')$
of two structures, or the intensional combination
![]() $(\Gamma ;\Gamma ')$
of two structures. When presenting structures, we often omit the outer layer of parentheses (so
$(\Gamma ;\Gamma ')$
of two structures. When presenting structures, we often omit the outer layer of parentheses (so
![]() $A,B$
is a structure, as is
$A,B$
is a structure, as is
![]() $A;(B,C)$
), but we do not omit interior parentheses:
$A;(B,C)$
), but we do not omit interior parentheses:
![]() $A,(B,C)$
differs from
$A,(B,C)$
differs from
![]() $(A,B),C$
in the order of combination, even though they will end up having the same logical force, due to the structural rules of the proof calculus.Footnote
18
We will also treat binary structural connectives as binding less tightly than any formula connectives, so
$(A,B),C$
in the order of combination, even though they will end up having the same logical force, due to the structural rules of the proof calculus.Footnote
18
We will also treat binary structural connectives as binding less tightly than any formula connectives, so
![]() $A\to B; C$
will be
$A\to B; C$
will be
![]() $(A\to B); C$
.
$(A\to B); C$
.
When specifying rules of inference, we use parentheses in another way:
![]() $\Gamma (A)$
is a structure with a particular subformula A singled out. Given
$\Gamma (A)$
is a structure with a particular subformula A singled out. Given
![]() $\Gamma (A)$
, the structure
$\Gamma (A)$
, the structure
![]() $\Gamma (\Gamma ')$
is found by substituting that instance of A by
$\Gamma (\Gamma ')$
is found by substituting that instance of A by
![]() $\Gamma '$
. The same goes for other structures. So,
$\Gamma '$
. The same goes for other structures. So,
![]() $\Gamma (\Gamma ',\Gamma '')$
is a structure in which the structure
$\Gamma (\Gamma ',\Gamma '')$
is a structure in which the structure
![]() $\Gamma ',\Gamma ''$
is found somewhere as a constituent, and the structure
$\Gamma ',\Gamma ''$
is found somewhere as a constituent, and the structure
![]() $\Gamma (\Gamma '',\Gamma ')$
is found by reversing the order of
$\Gamma (\Gamma '',\Gamma ')$
is found by reversing the order of
![]() $\Gamma '$
and
$\Gamma '$
and
![]() $\Gamma ''$
inside that structure. For future reference, we will call the part of the structure
$\Gamma ''$
inside that structure. For future reference, we will call the part of the structure
![]() $\Gamma (A)$
around the instance A the context of A in
$\Gamma (A)$
around the instance A the context of A in
![]() $\Gamma (A)$
, and we will use the notation ‘
$\Gamma (A)$
, and we will use the notation ‘
![]() $\Gamma (-)$
’ to refer to that context.
$\Gamma (-)$
’ to refer to that context.
A derivation in this sequent calculus is a tree of sequents, of which every leaf is an axiom, where each transition is an inference rule. The fundamental rules in the sequent calculus are the axioms of Identity and the inference rule, Cut.Footnote 19

The next series of rules are structural rules, governing extensional and intensional structure combination respectively. Extensional combination allows for commutativity and associativity (at arbitrary depth inside a structure), as well as contraction and weakening, while intensional combination allows for only commutativity and associativity. In addition,
![]() $\epsilon $
acts as an identity for intensional combination.
$\epsilon $
acts as an identity for intensional combination.


The remaining rules are left and right rules for each connective. These are totally modular, in the sense that we can choose to include a connective or to leave it out. No rule for one connective requires the presence of any other connective in the vocabulary.




For
![]() $\mathsf {R}^+$
, we add one more rule: contraction for intensional combination.
$\mathsf {R}^+$
, we add one more rule: contraction for intensional combination.

With IW, we can derive new sequents, which could not be derived without it. For example, we can derive
.

The proof theory for logics like
![]() $\mathsf {RW}^+$
and
$\mathsf {RW}^+$
and
![]() $\mathsf {R}^+$
is well known, and so is the ternary relational semantics. Given our perspective on collection frames, it is worth taking the time to reconsider the relationship between proofs and models. Consider the proof given above, of the sequent
$\mathsf {R}^+$
is well known, and so is the ternary relational semantics. Given our perspective on collection frames, it is worth taking the time to reconsider the relationship between proofs and models. Consider the proof given above, of the sequent
. What does this say about
![]() $\mathsf {R}^+$
models? It does not tell us that
$\mathsf {R}^+$
models? It does not tell us that
![]() $(A\land (A\to B))\to B$
holds at every point in those models, only that it holds at normal points, those points x where
$(A\land (A\to B))\to B$
holds at every point in those models, only that it holds at normal points, those points x where
![]() $[\;] Rx$
. In other words, the sequent
$[\;] Rx$
. In other words, the sequent
should tell us that
For every point x, if
![]() $[\;] Rx$
then
$[\;] Rx$
then
![]() $x\Vdash (A\land (A\to B))\to B$
.
$x\Vdash (A\land (A\to B))\to B$
.
Scanning back to our derivation to its second line, we have
. This does not tell us that if
![]() $A\to B$
is true at a point and that A is true at that point, then B is true there too (if that were all the sequent said, the conditional would be irrelevant). The appropriate way to understand the ‘cash value’ of the derivation of this sequent according to our frames is that
$A\to B$
is true at a point and that A is true at that point, then B is true there too (if that were all the sequent said, the conditional would be irrelevant). The appropriate way to understand the ‘cash value’ of the derivation of this sequent according to our frames is that
For all x, y and z, if
![]() $x\Vdash A\to B$
and
$x\Vdash A\to B$
and
![]() $y\Vdash A$
, if
$y\Vdash A$
, if
![]() $[x,y]Rz$
then
$[x,y]Rz$
then
![]() $z\Vdash B$
.
$z\Vdash B$
.
In the first of these cases, we have involved the R relation on empty multiset. In the second of these cases, we have used the R relation on a two-element multiset. The natural thing to consider when it comes to the sequent
, then, would be to understand the sequent as telling us this:
For all x and y, if
![]() $x\Vdash A\land (A\to B)$
and
$x\Vdash A\land (A\to B)$
and
![]() $[x]Ry$
then
$[x]Ry$
then
![]() $y\Vdash B$
.
$y\Vdash B$
.
This is how we will understand validity of sequents on our frames. A single-premise single-conclusion sequent
is valid on a frame if and only if:
For all x and y, if
![]() $x\Vdash A$
and
$x\Vdash A$
and
![]() $[x]Ry$
then
$[x]Ry$
then
![]() $y\Vdash B$
.
$y\Vdash B$
.
This agrees with the traditional understanding of validity of a sequent
![]() on a frame (that for each point x, if
on a frame (that for each point x, if
![]() $x\Vdash A$
then
$x\Vdash A$
then
![]() $x\Vdash B$
too) when that frame is reflexive. (Take any reflexive frame. If a sequent has a counterexample according to the old definition, that provides a counterexample in the new definition too, by the reflexivity of the frame. Conversely, if we had points x and y where
$x\Vdash B$
too) when that frame is reflexive. (Take any reflexive frame. If a sequent has a counterexample according to the old definition, that provides a counterexample in the new definition too, by the reflexivity of the frame. Conversely, if we had points x and y where
![]() $[x]Ry$
and A holds at x but B fails at y, then by heredity on our frame, B must also fail at x, since
$[x]Ry$
and A holds at x but B fails at y, then by heredity on our frame, B must also fail at x, since
![]() $[x]Ry$
, and so we have a counterexample according to the traditional definition). This understanding of validity diverges only in cases where the frame is not reflexive.Footnote
20
Since non-reflexive frames are a proper generalisation of ternary relational frames, the question of how to interpret sequents on them is open. We have argued here that invoking R, and evaluating the lhs of our sequent at one point and the rhs at another is in keeping with how we have always interpreted zero-premise and multiple-premise sequents on ternary frames. It is also in keeping with the interpretation of conditionals in these frames. It would be surprising if the conditional-like notion of entailment in a relevant logic did not share in the features that the semantics ascribes to the conditional in that logic. So, we proceed with this new understanding of what it is for a sequent to be valid in a model.Footnote
21
$[x]Ry$
, and so we have a counterexample according to the traditional definition). This understanding of validity diverges only in cases where the frame is not reflexive.Footnote
20
Since non-reflexive frames are a proper generalisation of ternary relational frames, the question of how to interpret sequents on them is open. We have argued here that invoking R, and evaluating the lhs of our sequent at one point and the rhs at another is in keeping with how we have always interpreted zero-premise and multiple-premise sequents on ternary frames. It is also in keeping with the interpretation of conditionals in these frames. It would be surprising if the conditional-like notion of entailment in a relevant logic did not share in the features that the semantics ascribes to the conditional in that logic. So, we proceed with this new understanding of what it is for a sequent to be valid in a model.Footnote
21
So, when is a sequent
![]() valid in some model
valid in some model
![]() $\langle P,R,\Vdash \rangle $
? We have considered sequents of the form
$\langle P,R,\Vdash \rangle $
? We have considered sequents of the form
![]() , those of the form
, those of the form
![]() and those of the form
and those of the form
![]() . What about those involving the extensional combiner, the comma? When is the sequent
. What about those involving the extensional combiner, the comma? When is the sequent
![]() valid in our frame? One candidate (generalising the case of the single formula on the left) is to say that whenever
valid in our frame? One candidate (generalising the case of the single formula on the left) is to say that whenever
![]() $x\Vdash A$
and
$x\Vdash A$
and
![]() $x\Vdash B$
then when
$x\Vdash B$
then when
![]() $[x]Ry$
, we have
$[x]Ry$
, we have
![]() $y\Vdash C$
. However, an equivalent way of formulating this claim will be more natural in our setting. Instead, we can say that
$y\Vdash C$
. However, an equivalent way of formulating this claim will be more natural in our setting. Instead, we can say that
![]() is valid on a frame if and only if
is valid on a frame if and only if
For all x, y and z, if
![]() $x\Vdash A$
and
$x\Vdash A$
and
![]() $y\Vdash B$
, if
$y\Vdash B$
, if
![]() $[x]Rz$
and
$[x]Rz$
and
![]() $[y]Rz$
, then
$[y]Rz$
, then
![]() $z\Vdash C$
.
$z\Vdash C$
.
The parallel with the case for the semicolon is clear. We look for points where the lhs formulas are true, and we combine them, using R to locate where to check the rhs formula. Here we check C at all common descendants of x and of y, rather than those points found by combining x and y together. This choice allows us to give a particularly straightforward interpretation of the validity of sequents in our models. We start with the notion of the shadow cast by a structure in a model.
Definition 17 (The shadow cast by a structure)
For a structure
![]() $\Gamma $
its shadow
$\Gamma $
its shadow
![]() $\{\!\{\Gamma \}\!\}$
in the model
$\{\!\{\Gamma \}\!\}$
in the model
![]() $\langle P,R,\Vdash \rangle $
is a set of points, defined recursively as follows:
$\langle P,R,\Vdash \rangle $
is a set of points, defined recursively as follows:
-
•
 $\{\!\{\epsilon \}\!\} = \{x\in P:[\;] Rx\}$
,
$\{\!\{\epsilon \}\!\} = \{x\in P:[\;] Rx\}$
, -
•
 ,
, -
•
 $\{\!\{\Gamma ,\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})([y]Rx\land [z]Rx)\}$
,
$\{\!\{\Gamma ,\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})([y]Rx\land [z]Rx)\}$
, -
•
 $\{\!\{\Gamma ;\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})[y,z]Rx\}$
.
$\{\!\{\Gamma ;\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})[y,z]Rx\}$
.
When a structure is a single formula A, then
![]() $\{\!\{A\}\!\}$
, the shadow it casts is not the formula’s extension,
$\{\!\{A\}\!\}$
, the shadow it casts is not the formula’s extension,
![]() , but rather, it is the set of points upward from some point in the extension. If R is reflexive, then
, but rather, it is the set of points upward from some point in the extension. If R is reflexive, then
![]() , so where R is reflexive, the distinction between shadows and extensions makes no significant difference. In any model, whether reflexive or not,
, so where R is reflexive, the distinction between shadows and extensions makes no significant difference. In any model, whether reflexive or not,
![]() .
.
It is worth pausing to understand the behaviour of shadows in a specific non-reflexive frame. Consider the multiset frame
![]() $\langle {\mathbb R},<\rangle $
with the multiset relation given by taking a multiset X of reals to relate to all and only those reals larger than each member of X. Here, the underlying order
$\langle {\mathbb R},<\rangle $
with the multiset relation given by taking a multiset X of reals to relate to all and only those reals larger than each member of X. Here, the underlying order
![]() $\sqsubset $
is the order
$\sqsubset $
is the order
![]() $<$
on
$<$
on
![]() ${\mathbb R}$
. So, the extension
${\mathbb R}$
. So, the extension
![]() of a formula must be upwardly closed on
of a formula must be upwardly closed on
![]() ${\mathbb R}$
. So, an extension must have one of the forms
${\mathbb R}$
. So, an extension must have one of the forms
![]() $(-\infty ,\infty )$
,
$(-\infty ,\infty )$
,
![]() $[r,\infty )$
, or
$[r,\infty )$
, or
![]() $(r,\infty )$
for some real r, or be empty. A shadow, on the other hand, cannot have the form
$(r,\infty )$
for some real r, or be empty. A shadow, on the other hand, cannot have the form
![]() $[r,\infty )$
. If
$[r,\infty )$
. If
![]() , then
, then
![]() $\{\!\{A\}\!\}=(r,\infty )$
, and if
$\{\!\{A\}\!\}=(r,\infty )$
, and if
![]() then
then
![]() $\{\!\{A\}\!\}=(r,\infty )$
too. The possible values of shadows are
$\{\!\{A\}\!\}=(r,\infty )$
too. The possible values of shadows are
![]() $(-\infty ,\infty )$
, and
$(-\infty ,\infty )$
, and
![]() $(r,\infty )$
for each real r, and the empty set of reals.
$(r,\infty )$
for each real r, and the empty set of reals.
It is also worth pausing to note that the notion of a shadow can be applied equally well in inhabited-multiset frames, provided that our structures do not contain the marker ‘
![]() $\epsilon $
’ for the empty structure. So, for the rest of this section, we will consider two kinds of models: those on multiset frames, and those on inhabited-multiset frames. The first kind will be models of the whole calculus, while inhabited-multiset frames can be used as models for the fragment of the proof calculus in which
$\epsilon $
’ for the empty structure. So, for the rest of this section, we will consider two kinds of models: those on multiset frames, and those on inhabited-multiset frames. The first kind will be models of the whole calculus, while inhabited-multiset frames can be used as models for the fragment of the proof calculus in which
![]() $\epsilon $
is absent: that is, the calculus without the rules
$\epsilon $
is absent: that is, the calculus without the rules
![]() $\epsilon \textit {I}$
,
$\epsilon \textit {I}$
,
![]() $\epsilon \textit {E}$
,
$\epsilon \textit {E}$
,
![]() $\mathsf {t}\textit {L}$
and
$\mathsf {t}\textit {L}$
and
![]() $\mathsf {t}\textit {R}$
. We will call the calculi for
$\mathsf {t}\textit {R}$
. We will call the calculi for
![]() $\mathsf {RW}^+$
and
$\mathsf {RW}^+$
and
![]() $\mathsf {R}^+$
without
$\mathsf {R}^+$
without
![]() $\epsilon $
,
$\epsilon $
,
![]() $\mathsf {RW}^+_{-\epsilon }$
and
$\mathsf {RW}^+_{-\epsilon }$
and
![]() $\mathsf {R}^+_{-\epsilon }$
respectively, to make explicit the absence of sequents with
$\mathsf {R}^+_{-\epsilon }$
respectively, to make explicit the absence of sequents with
![]() $\epsilon $
.
$\epsilon $
.
We have seen that the shadow
![]() $\{\!\{A\}\!\}$
of a formula A is related to its extension
$\{\!\{A\}\!\}$
of a formula A is related to its extension
![]() in a natural way.
in a natural way.
![]() $x\in \{\!\{A\}\!\}$
iff there is some
$x\in \{\!\{A\}\!\}$
iff there is some
![]() where
where
![]() $[y]Rx$
(that is,
$[y]Rx$
(that is,
![]() $y\sqsubset x$
). This transition from extension to shadow is an operation on sets of points, and it is worth singling out with some notation.
$y\sqsubset x$
). This transition from extension to shadow is an operation on sets of points, and it is worth singling out with some notation.
Definition 18 (
 $\sqsubset $
on sets of points)
$\sqsubset $
on sets of points)
![]() $X_{\sqsubset }$
is defined as
$X_{\sqsubset }$
is defined as
![]() $\{x\in P:(\exists y\in X)y\sqsubset x\}$
.
$\{x\in P:(\exists y\in X)y\sqsubset x\}$
.
So, this lemma is immediate:
Lemma 19 (From extensions to shadows)
![]() .
.
This operation satisfies two useful conditions.
Lemma 20 (
 $\sqsubset $
is monotone and idempotent)
$\sqsubset $
is monotone and idempotent)
For any sets X and Y, if
![]() $X\subseteq Y$
then
$X\subseteq Y$
then
![]() $X_{\sqsubset } \subseteq Y_{\sqsubset }$
. Furthermore,
$X_{\sqsubset } \subseteq Y_{\sqsubset }$
. Furthermore,
![]() $X_{\sqsubset }=X_{\sqsubset \sqsubset }$
.
$X_{\sqsubset }=X_{\sqsubset \sqsubset }$
.
Proof. For monotony, if
![]() $z\in X_{\sqsubset }$
then there is some
$z\in X_{\sqsubset }$
then there is some
![]() $x\in X$
where
$x\in X$
where
![]() $[x]Rz$
. Since
$[x]Rz$
. Since
![]() $x\in Y$
,
$x\in Y$
,
![]() $z\in Y_{\sqsubset }$
too. For idempotence, we appeal to the density and transitivity of
$z\in Y_{\sqsubset }$
too. For idempotence, we appeal to the density and transitivity of
![]() $\sqsubset $
. If
$\sqsubset $
. If
![]() $z\in X_{\sqsubset }$
then since there is some
$z\in X_{\sqsubset }$
then since there is some
![]() $x\in X$
where
$x\in X$
where
![]() $[x]Rz$
then by density there is some y where
$[x]Rz$
then by density there is some y where
![]() $[x]Ry$
(so
$[x]Ry$
(so
![]() $y\in X_{\sqsubset }$
) and
$y\in X_{\sqsubset }$
) and
![]() $[y]Rz$
, ensuring that
$[y]Rz$
, ensuring that
![]() $x\in X_{\sqsubset \sqsubset }$
. Conversely, if
$x\in X_{\sqsubset \sqsubset }$
. Conversely, if
![]() $z\in X_{\sqsubset \sqsubset }$
then there is some
$z\in X_{\sqsubset \sqsubset }$
then there is some
![]() $y\in X_{\sqsubset }$
where
$y\in X_{\sqsubset }$
where
![]() $[y]Rz$
and some
$[y]Rz$
and some
![]() $x\in X$
where
$x\in X$
where
![]() $[x]Ry$
. By transitivity,
$[x]Ry$
. By transitivity,
![]() $[x]Rz$
, ensuring that
$[x]Rz$
, ensuring that
![]() $z\in X_{\sqsubset }$
.
$z\in X_{\sqsubset }$
.
The shadow of a formula A is the set of points above that formula’s extension,
![]() . A shadow of a structure is not defined by taking the points above the extension of some formula, but nonetheless, it too is a fixed point for the operation
. A shadow of a structure is not defined by taking the points above the extension of some formula, but nonetheless, it too is a fixed point for the operation
![]() $\sqsubset $
.
$\sqsubset $
.
Lemma 21 (Shadows and order)
For each shadow
![]() $\{\!\{\Gamma \}\!\}$
, we have
$\{\!\{\Gamma \}\!\}$
, we have
![]() $\{\!\{\Gamma \}\!\}=\{\!\{\Gamma \}\!\}_{\sqsubset }$
.
$\{\!\{\Gamma \}\!\}=\{\!\{\Gamma \}\!\}_{\sqsubset }$
.
To prove this, it is simplest to characterise the sets fixed under
![]() $\sqsubset $
in general terms. We first prove a more general lemma, for which Lemma 21 is a corollary. For this, we need one more definition:
$\sqsubset $
in general terms. We first prove a more general lemma, for which Lemma 21 is a corollary. For this, we need one more definition:
Definition 22 (Closed upwards and open downwards)
A set X is closed upwards along
![]() $\sqsubset $
if whenever
$\sqsubset $
if whenever
![]() $x\in X$
and
$x\in X$
and
![]() $x\sqsubset x'$
then
$x\sqsubset x'$
then
![]() $x'\in X$
too. A set X is open downwards along
$x'\in X$
too. A set X is open downwards along
![]() $\sqsubset $
if whenever
$\sqsubset $
if whenever
![]() $x\in X$
, there is some
$x\in X$
, there is some
![]() $x'\sqsubset x$
where
$x'\sqsubset x$
where
![]() $x'\in X$
too.
$x'\in X$
too.
In the multiset frame
![]() $\langle {\mathbb R},<\rangle $
discussed above, the intervals
$\langle {\mathbb R},<\rangle $
discussed above, the intervals
![]() $[r,\infty )$
are closed upwards but not open downwards, while the intervals
$[r,\infty )$
are closed upwards but not open downwards, while the intervals
![]() $(r,\infty )$
are both closed upwards and open downwards along the order
$(r,\infty )$
are both closed upwards and open downwards along the order
![]() $<$
. The properties of being closed upwards and open downwards are related to the operation
$<$
. The properties of being closed upwards and open downwards are related to the operation
![]() $\sqsubset $
as follows:
$\sqsubset $
as follows:
Lemma 23 (Open and closed sets)
If the relation
![]() $\sqsubset $
is transitive, then if X is closed upwards, then
$\sqsubset $
is transitive, then if X is closed upwards, then
![]() $X_{\sqsubset }\subseteq X$
. If
$X_{\sqsubset }\subseteq X$
. If
![]() $\sqsubset $
is dense, then if X is open downwards, then
$\sqsubset $
is dense, then if X is open downwards, then
![]() $X\subseteq X_{\sqsubset }$
.
$X\subseteq X_{\sqsubset }$
.
The proof is a simple matter of unpacking the definitions:
Proof. Suppose
![]() $\sqsubset $
is transitive and that X is closed upwards. Take
$\sqsubset $
is transitive and that X is closed upwards. Take
![]() $x\in X_{\sqsubset }$
. So there is some
$x\in X_{\sqsubset }$
. So there is some
![]() $x'\in X$
where
$x'\in X$
where
![]() $x'\sqsubset x$
. Since X is closed upwards, we have
$x'\sqsubset x$
. Since X is closed upwards, we have
![]() $x\in X$
. Suppose
$x\in X$
. Suppose
![]() $\sqsubset $
is dense and X is open downwards. Take
$\sqsubset $
is dense and X is open downwards. Take
![]() $x\in X$
. Since X is open downwards we have some
$x\in X$
. Since X is open downwards we have some
![]() $x'\in X$
where
$x'\in X$
where
![]() $x'\sqsubset x$
. It follows that
$x'\sqsubset x$
. It follows that
![]() $x\in X_{\sqsubset }$
.
$x\in X_{\sqsubset }$
.
So, the sets X that are closed upwards and open downwards are fixed points for the operation
![]() $\sqsubset $
. Since on any collection frame,
$\sqsubset $
. Since on any collection frame,
![]() $\sqsubset $
is transitive and dense, the shadow
$\sqsubset $
is transitive and dense, the shadow
![]() $\{\!\{\Gamma \}\!\}$
of any structure
$\{\!\{\Gamma \}\!\}$
of any structure
![]() $\Gamma $
is both closed upwards and open downwards, and is a fixed point for the operation
$\Gamma $
is both closed upwards and open downwards, and is a fixed point for the operation
![]() $\sqsubset $
.
$\sqsubset $
.
Now we can return to the proof of Lemma 21.
Proof. Consider each kind of shadow, as given in Definition 17. A quick inspection of each clause shows that if R satisfies Transitivity and Splitting, then the shadow is closed upward and open downward. For one example, for
![]() $\{\!\{\epsilon \}\!\}$
, if
$\{\!\{\epsilon \}\!\}$
, if
![]() $x\in \{\!\{\epsilon \}\!\}$
, for upward closure, assume that
$x\in \{\!\{\epsilon \}\!\}$
, for upward closure, assume that
![]() $x\sqsubset x'$
. Since
$x\sqsubset x'$
. Since
![]() $[\;] Rx$
and
$[\;] Rx$
and
![]() $x\sqsubset x'$
we have
$x\sqsubset x'$
we have
![]() $[\;] Rx'$
by transitivity, and
$[\;] Rx'$
by transitivity, and
![]() $x'\in \{\!\{\epsilon \}\!\}$
. For downward openness, since
$x'\in \{\!\{\epsilon \}\!\}$
. For downward openness, since
![]() $[\;] R x$
, by Splitting we have some
$[\;] R x$
, by Splitting we have some
![]() $x'$
where
$x'$
where
![]() $[\;] Rx'$
(so
$[\;] Rx'$
(so
![]() $x'\in \{\!\{\epsilon \}\!\}$
) and
$x'\in \{\!\{\epsilon \}\!\}$
) and
![]() $x'\sqsubset x$
, as desired.
$x'\sqsubset x$
, as desired.
For the intensional composition case, if
![]() $x\in \{\!\{\Gamma ;\Gamma '\}\!\}$
, for upward closure, assume that
$x\in \{\!\{\Gamma ;\Gamma '\}\!\}$
, for upward closure, assume that
![]() $x\sqsubset x'$
. Since we have
$x\sqsubset x'$
. Since we have
![]() $y\in \{\!\{\Gamma \}\!\}$
and
$y\in \{\!\{\Gamma \}\!\}$
and
![]() $z\in \{\!\{\Gamma '\}\!\}$
where
$z\in \{\!\{\Gamma '\}\!\}$
where
![]() $[y,z]Rx$
, and since
$[y,z]Rx$
, and since
![]() $x\sqsubset x'$
, by transitivity we have
$x\sqsubset x'$
, by transitivity we have
![]() $[y,z]Rx'$
, and
$[y,z]Rx'$
, and
![]() $x'\in \{\!\{\Gamma ;\Gamma '\}\!\}$
as desired. For downward openness, since
$x'\in \{\!\{\Gamma ;\Gamma '\}\!\}$
as desired. For downward openness, since
![]() $[y,z]Rx$
, by Splitting we have some
$[y,z]Rx$
, by Splitting we have some
![]() $x'$
where
$x'$
where
![]() $[y,z]Rx'$
and
$[y,z]Rx'$
and
![]() $[x']Rx$
(so
$[x']Rx$
(so
![]() $x'\in \{\!\{\Gamma ;\Gamma '\}\!\}$
) and
$x'\in \{\!\{\Gamma ;\Gamma '\}\!\}$
) and
![]() $x'\sqsubset x$
, as desired.
$x'\sqsubset x$
, as desired.
The other two cases follow in the same way, so we can declare this lemma proved.
With this behaviour of shadows proved, we can see that the definition of the shadow of an extensional structure can be simplified. Since
![]() $\{\!\{\Gamma ,\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})[y]Rx\}\cap \{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})[z]Rx\}=\{\!\{\Gamma \}\!\}_{\sqsubset }\cap \{\!\{\Gamma '\}\!\}_{\sqsubset }$
, we have the following consequence:
$\{\!\{\Gamma ,\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})[y]Rx\}\cap \{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})[z]Rx\}=\{\!\{\Gamma \}\!\}_{\sqsubset }\cap \{\!\{\Gamma '\}\!\}_{\sqsubset }$
, we have the following consequence:
Corollary 24.
![]() $\{\!\{\Gamma ,\Gamma '\}\!\}=\{\!\{\Gamma \}\!\}\cap \{\!\{\Gamma '\}\!\}$
.
$\{\!\{\Gamma ,\Gamma '\}\!\}=\{\!\{\Gamma \}\!\}\cap \{\!\{\Gamma '\}\!\}$
.
With the definition of a structure’s shadow, the statement the condition for validity on a model is straightforward.
Definition 25 (Model validity)
A sequent
![]() is valid in the model
is valid in the model
![]() $\langle P,R,\Vdash \rangle $
if and only if
$\langle P,R,\Vdash \rangle $
if and only if
![]() . That is, the shadow cast by the structure
. That is, the shadow cast by the structure
![]() $\Gamma $
is restricted to the extension of the formula A.
$\Gamma $
is restricted to the extension of the formula A.
So, we are in a position to state our soundness theorem:
Theorem 26 (
 $\mathsf {RW}^+$
is sound for multiset frames)
$\mathsf {RW}^+$
is sound for multiset frames)
Any
![]() $\mathsf {RW}^+$
derivable sequent
$\mathsf {RW}^+$
derivable sequent
![]() holds in each model
holds in each model
![]() $\langle P,R,\Vdash \rangle $
on a multiset frame. Furthermore, any
$\langle P,R,\Vdash \rangle $
on a multiset frame. Furthermore, any
![]() $\mathsf {RW}^+_{-\epsilon }$
derivable sequent holds in each model on an inhabited-multiset frame.
$\mathsf {RW}^+_{-\epsilon }$
derivable sequent holds in each model on an inhabited-multiset frame.
To prove the soundness theorem, it helps to establish the following facts about shadows and contexts.
Lemma 27 (Contexts preserve order, and are prime)
If
![]() , then for any context
, then for any context
![]() $\Gamma '(-)$
, we have
$\Gamma '(-)$
, we have
![]() $\{\!\{\Gamma '(\Gamma )\}\!\}\subseteq \{\!\{\Gamma '(A)\}\!\}$
. In this sense, contexts are order preserving over valid sequents. Furthermore,
$\{\!\{\Gamma '(\Gamma )\}\!\}\subseteq \{\!\{\Gamma '(A)\}\!\}$
. In this sense, contexts are order preserving over valid sequents. Furthermore,
![]() $\{\!\{\Gamma '(A\lor B)\}\!\}=\{\!\{\Gamma '(A)\}\!\}\cup \{\!\{\Gamma '(B)\}\!\}$
, so contexts are prime, and
$\{\!\{\Gamma '(A\lor B)\}\!\}=\{\!\{\Gamma '(A)\}\!\}\cup \{\!\{\Gamma '(B)\}\!\}$
, so contexts are prime, and
![]() $\{\!\{\Gamma '(\bot )\}\!\}=\{\!\{\bot \}\!\}=\emptyset $
.
$\{\!\{\Gamma '(\bot )\}\!\}=\{\!\{\bot \}\!\}=\emptyset $
.
Proof. Both facts follow from an easy induction on the construction of the context
![]() $\Gamma '(-)$
. An atomic context
$\Gamma '(-)$
. An atomic context
![]() $\Gamma '(-)$
the hole ‘
$\Gamma '(-)$
the hole ‘
![]() $-$
’ itself. In this case, primeness is trivial, and order preservation follows from the monotony and idempotence (Lemma 20). If
$-$
’ itself. In this case, primeness is trivial, and order preservation follows from the monotony and idempotence (Lemma 20). If
![]() , then by monotony,
, then by monotony,
![]() , but
, but
![]() , so
, so
![]() $\{\!\{A\}\!\}_{\sqsubset }\subseteq \{\!\{B\}\!\}$
, and since idempotence gives
$\{\!\{A\}\!\}_{\sqsubset }\subseteq \{\!\{B\}\!\}$
, and since idempotence gives
![]() $\{\!\{A\}\!\}=\{\!\{A\}\!\}_{\sqsubset }$
, we have
$\{\!\{A\}\!\}=\{\!\{A\}\!\}_{\sqsubset }$
, we have
![]() $\{\!\{A\}\!\}\subseteq \{\!\{B\}\!\}$
as desired.
$\{\!\{A\}\!\}\subseteq \{\!\{B\}\!\}$
as desired.
For the induction steps,
![]() $\Gamma '(-)$
either has the form
$\Gamma '(-)$
either has the form
![]() $\Gamma ''(-),\Gamma '''$
, or
$\Gamma ''(-),\Gamma '''$
, or
![]() $\Gamma ''',\Gamma ''(-)$
, or
$\Gamma ''',\Gamma ''(-)$
, or
![]() $\Gamma ''(-);\Gamma '''$
, or
$\Gamma ''(-);\Gamma '''$
, or
![]() $\Gamma ''';\Gamma ''(-)$
, in which case preservation and primeness follow immediately from the properties holding for the simpler context
$\Gamma ''';\Gamma ''(-)$
, in which case preservation and primeness follow immediately from the properties holding for the simpler context
![]() $\Gamma ''(-)$
.
$\Gamma ''(-)$
.
For example, if
![]() $\{\!\{\Gamma ''(\Gamma )\}\!\}\subseteq \{\!\{\Gamma ''(A)\}\!\}$
, then
$\{\!\{\Gamma ''(\Gamma )\}\!\}\subseteq \{\!\{\Gamma ''(A)\}\!\}$
, then
![]() $\{\!\{\Gamma ';\Gamma ''(\Gamma )\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(\Gamma )\}\!\})[y,z]Rx\}$
, but since
$\{\!\{\Gamma ';\Gamma ''(\Gamma )\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(\Gamma )\}\!\})[y,z]Rx\}$
, but since
![]() $\{\!\{\Gamma ''(\Gamma )\}\!\}\subseteq \{\!\{\Gamma ''(A)\}\!\}$
, it follows that this set is a subset of
$\{\!\{\Gamma ''(\Gamma )\}\!\}\subseteq \{\!\{\Gamma ''(A)\}\!\}$
, it follows that this set is a subset of
![]() $\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A)\}\!\})[y,z]Rx\}$
, which is
$\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A)\}\!\})[y,z]Rx\}$
, which is
![]() $\{\!\{\Gamma ';\Gamma ''(A)\}\!\}$
, as desired. Similarly, given that
$\{\!\{\Gamma ';\Gamma ''(A)\}\!\}$
, as desired. Similarly, given that
![]() $\{\!\{\Gamma ''(A\lor B)\}\!\}=\{\!\{\Gamma ''(A)\cup \Gamma ''(B)\}\!\}$
, then
$\{\!\{\Gamma ''(A\lor B)\}\!\}=\{\!\{\Gamma ''(A)\cup \Gamma ''(B)\}\!\}$
, then
![]() $\{\!\{\Gamma ';\Gamma ''(A\lor B)\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A\lor B)\}\!\})[y,z]Rx\}$
, which is equal to
$\{\!\{\Gamma ';\Gamma ''(A\lor B)\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A\lor B)\}\!\})[y,z]Rx\}$
, which is equal to
![]() $\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A)\}\!\}\cup \{\!\{\Gamma ''(B)\}\!\})[y,z]Rx\}$
, which is
$\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A)\}\!\}\cup \{\!\{\Gamma ''(B)\}\!\})[y,z]Rx\}$
, which is
![]() $\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A)\}\!\})[y,z]Rx\}\cup \{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\}) (\exists z\in \{\!\{\Gamma ''(B)\}\!\})[y,z]Rx\}$
, which is in turn
$\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(A)\}\!\})[y,z]Rx\}\cup \{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\}) (\exists z\in \{\!\{\Gamma ''(B)\}\!\})[y,z]Rx\}$
, which is in turn
![]() $\{\!\{\Gamma ';\Gamma ''(A)\}\!\}\cup \{\!\{\Gamma ';\Gamma ''(B)\}\!\}$
. Finally, given that
$\{\!\{\Gamma ';\Gamma ''(A)\}\!\}\cup \{\!\{\Gamma ';\Gamma ''(B)\}\!\}$
. Finally, given that
![]() $\{\!\{\Gamma ''(\bot )\}\!\}=\emptyset $
, clearly
$\{\!\{\Gamma ''(\bot )\}\!\}=\emptyset $
, clearly
![]() $\{\!\{\Gamma ';\Gamma ''(\bot )\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(\bot )\}\!\})[y,z]Rx\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \emptyset )[y,z]Rx\}=\emptyset $
, as desired.
$\{\!\{\Gamma ';\Gamma ''(\bot )\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \{\!\{\Gamma ''(\bot )\}\!\})[y,z]Rx\}=\{x\in P:(\exists y\in \{\!\{\Gamma '\}\!\})(\exists z\in \emptyset )[y,z]Rx\}=\emptyset $
, as desired.
Now we can return to our proof of the soundness theorem. As is usual, it is a straightforward induction on the length of a derivation. The technique is standard, and there are no surprises, despite the idiosyncratic interpretation of sequents to allow for the non-reflexive frames.Footnote 22
Proof. We prove soundness by induction on the length of a derivation for the sequent
![]() . The axiomatic sequent
. The axiomatic sequent
![]() holds in every multiset frame and in every inhabited-multiset frame since
holds in every multiset frame and in every inhabited-multiset frame since
![]() . The sequent
. The sequent
![]() holds in every multiset frame, since in these frames we have
holds in every multiset frame, since in these frames we have
![]() .
.
For the Cut rule, suppose we have
![]() and
and
![]() . We wish to show that
. We wish to show that
![]() . Here we appeal to the fact that the context
. Here we appeal to the fact that the context
![]() $\Gamma '$
preserves order. Since
$\Gamma '$
preserves order. Since
![]() , we have
, we have
![]() $\{\!\{\Gamma '(\Gamma )\}\!\}\subseteq \{\!\{\Gamma '(A)\}\!\}$
, and since
$\{\!\{\Gamma '(\Gamma )\}\!\}\subseteq \{\!\{\Gamma '(A)\}\!\}$
, and since
![]() , we have
, we have
![]() as desired.
as desired.
That the extensional structural rules preserve validity on frames is an immediate consequence of the fact that the outer context
![]() $\Gamma (-)$
preserves order, and the extensional structure is modelled by intersection of shadows. For example, for the weakening rule EK, since
$\Gamma (-)$
preserves order, and the extensional structure is modelled by intersection of shadows. For example, for the weakening rule EK, since
![]() $\{\!\{\Gamma ',\Gamma ''\}\!\}=\{\!\{\Gamma '\}\!\}\cap \{\!\{\Gamma ''\}\!\}\subseteq \{\!\{\Gamma '\}\!\}$
, and since
$\{\!\{\Gamma ',\Gamma ''\}\!\}=\{\!\{\Gamma '\}\!\}\cap \{\!\{\Gamma ''\}\!\}\subseteq \{\!\{\Gamma '\}\!\}$
, and since
![]() $\Gamma (-)$
preserves order, we know that if
$\Gamma (-)$
preserves order, we know that if
![]() then we also have
then we also have
![]() . In the same way, associativity, commutativity and contraction are assured.
. In the same way, associativity, commutativity and contraction are assured.
Most of the intensional structural rules follow in the same way from the properties of multisets. For example, the associativity rule IB follows appeals to the compositionality of R.
![]() $\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{x\in P:(\exists y\in \{\!\{(\Gamma ';\Gamma '')\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})[y,z]Rx\}$
unpacking the definition of
$\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{x\in P:(\exists y\in \{\!\{(\Gamma ';\Gamma '')\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})[y,z]Rx\}$
unpacking the definition of
![]() $\{\!\{\Gamma ';\Gamma ''\}\!\}$
this set is identical to
$\{\!\{\Gamma ';\Gamma ''\}\!\}$
this set is identical to
![]() $\{x\in P:(\exists y\in P)(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})([u,v]Ry\land [y,z]Rx)\}$
. Applying compositionality, we see that
$\{x\in P:(\exists y\in P)(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})([u,v]Ry\land [y,z]Rx)\}$
. Applying compositionality, we see that
![]() $(\exists y\in P)([u,v]Ry\land [y,z]Rx)$
is equivalent to
$(\exists y\in P)([u,v]Ry\land [y,z]Rx)$
is equivalent to
![]() $[u,v,z]Rx$
, using Transitivity in one direction and Splitting in the other. Thus, the set
$[u,v,z]Rx$
, using Transitivity in one direction and Splitting in the other. Thus, the set
![]() $\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}$
simplifies (as expected) to
$\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}$
simplifies (as expected) to
![]() $\{x\in P:(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})[u,v,z]Rx\}$
where the left-associated structure
$\{x\in P:(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})[u,v,z]Rx\}$
where the left-associated structure
![]() $(\Gamma ';\Gamma '');\Gamma '''$
unwraps into the unassociated multiset
$(\Gamma ';\Gamma '');\Gamma '''$
unwraps into the unassociated multiset
![]() $[u,v,z]$
. A moment’s reflection shows that the right-associated structure
$[u,v,z]$
. A moment’s reflection shows that the right-associated structure
![]() $\Gamma ';(\Gamma '';\Gamma ''')$
unwraps to exactly the same set, so
$\Gamma ';(\Gamma '';\Gamma ''')$
unwraps to exactly the same set, so
![]() $\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{\!\{\Gamma ';(\Gamma '';\Gamma ''')\}\!\}$
, showing that the associativity structural rule IB is valid on frames. It is simpler to show that IC holds, since
$\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{\!\{\Gamma ';(\Gamma '';\Gamma ''')\}\!\}$
, showing that the associativity structural rule IB is valid on frames. It is simpler to show that IC holds, since
![]() $\{\!\{\Gamma ';\Gamma ''\}\!\}=\{\!\{\Gamma '';\Gamma '\}\!\}$
straightforwardly, given that
$\{\!\{\Gamma ';\Gamma ''\}\!\}=\{\!\{\Gamma '';\Gamma '\}\!\}$
straightforwardly, given that
![]() $[y,z]=[z,y]$
for each y and z.
$[y,z]=[z,y]$
for each y and z.
The
![]() $\epsilon $
I and
$\epsilon $
I and
![]() $\epsilon $
E rules hold in models on multiset frames (but not in models on inhabited-multiset frames). Here, we have
$\epsilon $
E rules hold in models on multiset frames (but not in models on inhabited-multiset frames). Here, we have
![]() $\{\!\{\epsilon ;\Gamma '\}\!\}=\{\!\{\Gamma '\}\!\}$
since
$\{\!\{\epsilon ;\Gamma '\}\!\}=\{\!\{\Gamma '\}\!\}$
since
![]() $\{\!\{\epsilon \}\!\}=\{x\in P:[\;] Rx\}$
and so
$\{\!\{\epsilon \}\!\}=\{x\in P:[\;] Rx\}$
and so
![]() $\{\!\{\epsilon ;\Gamma '\}\!\}=\{x\in P:\exists y ([\;] Ry \land \exists z\in \{\!\{\Gamma '\}\!\}[y,z]Rx)\}$
. However, if
$\{\!\{\epsilon ;\Gamma '\}\!\}=\{x\in P:\exists y ([\;] Ry \land \exists z\in \{\!\{\Gamma '\}\!\}[y,z]Rx)\}$
. However, if
![]() $[\;] Ry$
and
$[\;] Ry$
and
![]() $[y,z]Rx$
then by transitivity,
$[y,z]Rx$
then by transitivity,
![]() $[\;]\cup [z]Rx$
, i.e.,
$[\;]\cup [z]Rx$
, i.e.,
![]() $[z]Rx$
. And conversely, by Splitting, if
$[z]Rx$
. And conversely, by Splitting, if
![]() $[z]Rx$
then
$[z]Rx$
then
![]() $[\;]\cup [z]Rx$
and so, there is some y where
$[\;]\cup [z]Rx$
and so, there is some y where
![]() $[\;] Ry$
and
$[\;] Ry$
and
![]() $[y,z]Rx$
. So, our set
$[y,z]Rx$
. So, our set
![]() $\{x\in P:\exists y([\;] Ry \land \exists z\in \{\!\{\Gamma '\}\!\}[y,z]Rx)\}$
is the set
$\{x\in P:\exists y([\;] Ry \land \exists z\in \{\!\{\Gamma '\}\!\}[y,z]Rx)\}$
is the set
![]() $\{x\in P:\exists z\in \{\!\{\Gamma '\}\!\}[z]Rx\}$
, which is
$\{x\in P:\exists z\in \{\!\{\Gamma '\}\!\}[z]Rx\}$
, which is
![]() $\{\!\{\Gamma '\}\!\}$
itself, by Lemma 21.
$\{\!\{\Gamma '\}\!\}$
itself, by Lemma 21.
It remains to verify the validity of each of the connective rules. The validity of the left rules for conjunction, disjunction, and fusion follow immediately from the truth conditions for these connectives and the fact that the context
![]() $\Gamma (-)$
preserves order. For example, for
$\Gamma (-)$
preserves order. For example, for
![]() $\circ $
L, if we know that
$\circ $
L, if we know that
![]() holds in the model, then since
holds in the model, then since
![]() , and the context
, and the context
![]() $\Gamma (-)$
preserves order, it follows that
$\Gamma (-)$
preserves order, it follows that
![]() too. The reasoning for the left rules for conjunction is similar, and so is the left rule for
too. The reasoning for the left rules for conjunction is similar, and so is the left rule for
![]() $\mathsf {t}$
when our attention is restricted to multiset frames.
$\mathsf {t}$
when our attention is restricted to multiset frames.
The reasoning for the left rule for disjunction follows immediately from the primeness of the context
![]() $\Gamma (-)$
. If
$\Gamma (-)$
. If
![]() and
and
![]() then indeed
then indeed
![]() . The left rule for
. The left rule for
![]() $\bot $
is trivial, given that
$\bot $
is trivial, given that
![]() $\{\!\{\bot \}\!\}=\emptyset $
.
$\{\!\{\bot \}\!\}=\emptyset $
.
For the last left rule, for the conditional, to show that
![]() and
and
![]() ensures that
ensures that
![]() , we appeal to the fact that
, we appeal to the fact that
![]() $\Gamma '(-)$
preserves order. Using this fact, it suffices to show that
$\Gamma '(-)$
preserves order. Using this fact, it suffices to show that
![]() , for then we indeed have
, for then we indeed have
![]() as desired. That
as desired. That
![]() follows from
follows from
![]() by the definition of shadows for intensional combination. If
by the definition of shadows for intensional combination. If
![]() $x\in \{\!\{A\to B;\Gamma \}\!\}$
then there are y and z where
$x\in \{\!\{A\to B;\Gamma \}\!\}$
then there are y and z where
![]() $y\in \{\!\{A\to B\}\!\}$
and
$y\in \{\!\{A\to B\}\!\}$
and
![]() $z\in \{\!\{\Gamma \}\!\}$
such that
$z\in \{\!\{\Gamma \}\!\}$
such that
![]() $[y,z]Rx$
. Since
$[y,z]Rx$
. Since
![]() we have
we have
![]() $z\Vdash A$
. Since
$z\Vdash A$
. Since
![]() $y\in \{\!\{A\to B\}\!\}$
we have
$y\in \{\!\{A\to B\}\!\}$
we have
![]() $y\Vdash A\to B$
. It follows from
$y\Vdash A\to B$
. It follows from
![]() $[y,z]Rx$
that
$[y,z]Rx$
that
![]() $x\Vdash B$
, i.e.,
$x\Vdash B$
, i.e.,
![]() , as desired.
, as desired.
That completes the verification of the left connective rules. The right rules
![]() $\lor $
R and
$\lor $
R and
![]() $\land $
R follow immediately from the truth conditions for the connectives, and we have already dealt with
$\land $
R follow immediately from the truth conditions for the connectives, and we have already dealt with
![]() $\mathsf {t}$
R as an axiom. For
$\mathsf {t}$
R as an axiom. For
![]() $\to $
R and
$\to $
R and
![]() $\circ $
R the verification is also straightforward. For
$\circ $
R the verification is also straightforward. For
![]() $\circ $
R, if
$\circ $
R, if
![]() and
and
![]() , we wish to show that
, we wish to show that
![]() . If
. If
![]() $x\in \{\!\{\Gamma ;\Gamma '\}\!\}$
then there are
$x\in \{\!\{\Gamma ;\Gamma '\}\!\}$
then there are
![]() $y,z$
where
$y,z$
where
![]() $[y,z]Rx$
,
$[y,z]Rx$
,
![]() $y\in \{\!\{\Gamma \}\!\}$
and
$y\in \{\!\{\Gamma \}\!\}$
and
![]() $z\in \{\!\{\Gamma '\}\!\}$
. So, we also have
$z\in \{\!\{\Gamma '\}\!\}$
. So, we also have
![]() and
and
![]() , so
, so
![]() as desired. For
as desired. For
![]() $\to $
R, suppose
$\to $
R, suppose
![]() . To show that
. To show that
![]() , suppose we have
, suppose we have
![]() $x\in \{\!\{\Gamma \}\!\}$
. To show that
$x\in \{\!\{\Gamma \}\!\}$
. To show that
![]() , suppose we have a y where
, suppose we have a y where
![]() $y\Vdash A$
and
$y\Vdash A$
and
![]() $[x,y]Rz$
. By Splitting, we have some
$[x,y]Rz$
. By Splitting, we have some
![]() $y'$
where
$y'$
where
![]() $[y]Ry'$
and
$[y]Ry'$
and
![]() $[x,y']Rz$
. Since
$[x,y']Rz$
. Since
![]() and
and
![]() $[y]Ry'$
we have
$[y]Ry'$
we have
![]() $y\in \{\!\{A\}\!\}$
, and since
$y\in \{\!\{A\}\!\}$
, and since
![]() $x\in \{\!\{\Gamma \}\!\}$
and
$x\in \{\!\{\Gamma \}\!\}$
and
![]() $[x,y']Rz$
we have
$[x,y']Rz$
we have
![]() $z\in \{\!\{\Gamma ;A\}\!\}$
, so
$z\in \{\!\{\Gamma ;A\}\!\}$
, so
![]() , as desired.
, as desired.
This completes the proof. Each rule of the sequent calculus is sound on multiset frames. So, if a sequent
![]() can be derived in
can be derived in
![]() $\mathsf {RW}^+$
, on any multiset frame (whether reflexive or not) we have
$\mathsf {RW}^+$
, on any multiset frame (whether reflexive or not) we have
![]() . Furthermore, if that sequent can be derived in
. Furthermore, if that sequent can be derived in
![]() $\mathsf {RW}^+_{-\epsilon }$
, it also holds on any inhabited-multiset frame.
$\mathsf {RW}^+_{-\epsilon }$
, it also holds on any inhabited-multiset frame.
It is worth remarking on the role of the Transitivity portion of compositionality in the proof of the soundness of the Cut rule. That case is handled by appeal to Lemma 27, the fact that contexts preserve order. Inspection of the proof of Lemma 27 reveals that it hinges on the monotony and idempotency of the
![]() $\sqsubset $
operator, Lemma 20. Showing that
$\sqsubset $
operator, Lemma 20. Showing that
![]() $\sqsubset $
is idempotent, in particular, appeals to the density and transitivity of
$\sqsubset $
is idempotent, in particular, appeals to the density and transitivity of
![]() $\sqsubset $
. That appeal does not use the full Transitivity principle, but rather a restricted form involving only singletons on the left, much as density is a restricted form of the full Splitting principle. These observations suggest that collection frames that adopt only the restricted forms of Transitivity and Splitting may be of interest for the study of weaker logics.Footnote
23
$\sqsubset $
. That appeal does not use the full Transitivity principle, but rather a restricted form involving only singletons on the left, much as density is a restricted form of the full Splitting principle. These observations suggest that collection frames that adopt only the restricted forms of Transitivity and Splitting may be of interest for the study of weaker logics.Footnote
23
Before proceeding with further results, let’s put this soundness proof to work, by showing how to use some of the frames we have constructed can provide counterexamples to sequents.
Example 28 (Refuting
 and
and
 )
)
Start with
![]() $\langle {\mathbb R},R\rangle $
, where
$\langle {\mathbb R},R\rangle $
, where
![]() $XRy$
iff
$XRy$
iff
![]() $y>\Sigma X$
. This is a non-reflexive frame on
$y>\Sigma X$
. This is a non-reflexive frame on
![]() ${\mathbb R}$
, in which the underlying order on points is
${\mathbb R}$
, in which the underlying order on points is
![]() $<$
. So, extensions of formulas are the intervals
$<$
. So, extensions of formulas are the intervals
![]() $[r,\infty )$
or
$[r,\infty )$
or
![]() $(r,\infty )$
closed or open at the left, together with
$(r,\infty )$
closed or open at the left, together with
![]() ${\mathbb R}$
as a whole and the empty set. If we take
${\mathbb R}$
as a whole and the empty set. If we take
![]() and
and
![]() , then we have
, then we have
![]() $x\Vdash p\to q$
iff for each
$x\Vdash p\to q$
iff for each
![]() $y$
, if
$y$
, if
![]() $y\Vdash p$
(that is, if
$y\Vdash p$
(that is, if
![]() $y\ge 1$
) and
$y\ge 1$
) and
![]() $x+y<z$
, we have
$x+y<z$
, we have
![]() $z\Vdash q$
(that is,
$z\Vdash q$
(that is,
![]() $z\ge 2$
). It is easy to see that this obtains when
$z\ge 2$
). It is easy to see that this obtains when
![]() $x\ge 1$
, but if
$x\ge 1$
, but if
![]() $x<1$
, we can find some value of y, (e.g.,
$x<1$
, we can find some value of y, (e.g.,
![]() $1$
) and a value of z (e.g.,
$1$
) and a value of z (e.g.,
![]() $1+x$
) such that
$1+x$
) such that
![]() $x+y<z$
and
$x+y<z$
and
![]() $z\not \ge 2$
. So,
$z\not \ge 2$
. So,
![]() . So, in particular,
. So, in particular,
![]() $1\Vdash p\land (p\to q)$
, and so, for example,
$1\Vdash p\land (p\to q)$
, and so, for example,
![]() $1\frac {1}{2}\in \{\!\{p\land (p\to q)\}\!\}$
and
$1\frac {1}{2}\in \{\!\{p\land (p\to q)\}\!\}$
and
![]() . So this model provides a counterexample to the sequent
. So this model provides a counterexample to the sequent
![]() . As we would expect in at least some frames for
. As we would expect in at least some frames for
![]() $\mathsf {RW}^+$
, we have a violation of contraction.
$\mathsf {RW}^+$
, we have a violation of contraction.
This frame also provides a counterexample to sequents involving failures of relevance, such as
![]() . If we set
. If we set
![]() and
and
![]() then it is easy to see that
then it is easy to see that
![]() $1\in \{\!\{s\}\!\}$
, while
$1\in \{\!\{s\}\!\}$
, while
![]() , since
, since
![]() $-3\Vdash r$
and
$-3\Vdash r$
and
![]() $[-3,1]R-1$
(since
$[-3,1]R-1$
(since
![]() ${-}3+1 = {-}2 < {-}1$
) and
${-}3+1 = {-}2 < {-}1$
) and
![]() $-1\not \Vdash s$
. These simple numerical frames provide the leeway to explore a number of the distinctive features of the substructural logic
$-1\not \Vdash s$
. These simple numerical frames provide the leeway to explore a number of the distinctive features of the substructural logic
![]() $\mathsf {RW}^+$
.
$\mathsf {RW}^+$
.
Another result that follows immediately is the fact that
![]() $\mathsf {RW}^+$
is a non-conservative extension of
$\mathsf {RW}^+$
is a non-conservative extension of
![]() $\mathsf {RW}^+_{-\epsilon }$
. The sequent
$\mathsf {RW}^+_{-\epsilon }$
. The sequent
is derivable in
![]() $\mathsf {RW}^+$
as follows:
$\mathsf {RW}^+$
as follows:

This derivation makes use of
![]() $\epsilon $
. It might be asked whether any
$\epsilon $
. It might be asked whether any
![]() $\mathsf {RW}^+$
derivation of this sequent must go through
$\mathsf {RW}^+$
derivation of this sequent must go through
![]() $\epsilon $
in this way. Inhabited-multiset frames give us an answer. This sequent is not derivable in
$\epsilon $
in this way. Inhabited-multiset frames give us an answer. This sequent is not derivable in
![]() $\mathsf {RW}^+_{-\epsilon }$
.Footnote
24
$\mathsf {RW}^+_{-\epsilon }$
.Footnote
24
Example 29 (
 $\mathsf {RW}^+$
is not conservative over
$\mathsf {RW}^+$
is not conservative over
 $\mathsf {RW}^+_{-\epsilon }$
)
$\mathsf {RW}^+_{-\epsilon }$
)
Consider
![]() $\langle P,R\rangle $
where
$\langle P,R\rangle $
where
![]() $P$
is the set
$P$
is the set
![]() $\{1,2,3,\ldots \}$
of positive natural numbers, and for inhabited multisets X,
$\{1,2,3,\ldots \}$
of positive natural numbers, and for inhabited multisets X,
![]() $XRy$
iff
$XRy$
iff
![]() $y=\Sigma X$
. R, defined in this way, is both compositional and reflexive. This is an inhabited-multiset frame. The underlying order
$y=\Sigma X$
. R, defined in this way, is both compositional and reflexive. This is an inhabited-multiset frame. The underlying order
![]() $\sqsubset $
is identity, so any set of points may be used as the extension of a formula. Define
$\sqsubset $
is identity, so any set of points may be used as the extension of a formula. Define
![]() $\Vdash $
by setting
$\Vdash $
by setting
![]() (so
(so
![]() $p$
is true everywhere) and
$p$
is true everywhere) and
![]() (so
(so
![]() $q$
holds everywhere other than
$q$
holds everywhere other than
![]() $1$
). In this model
$1$
). In this model
![]() , trivially. It follows that
, trivially. It follows that
![]() $(p\to p)\to q$
is true at every number
$(p\to p)\to q$
is true at every number
![]() $n\ge 1$
, too, since for any such n, and for any
$n\ge 1$
, too, since for any such n, and for any
![]() $m\ge 1$
where
$m\ge 1$
where
![]() $m\Vdash p\to p$
(i.e., for any
$m\Vdash p\to p$
(i.e., for any
![]() $m\ge 1$
) then
$m\ge 1$
) then
![]() $n+m\Vdash q$
, since clearly,
$n+m\Vdash q$
, since clearly,
![]() $n+m\ge 2$
. So, we have a counterexample to our sequent
$n+m\ge 2$
. So, we have a counterexample to our sequent
![]() on our model. In particular, we have
on our model. In particular, we have
![]() $1\in \{\!\{(p\to p)\to q\}\!\}$
while
$1\in \{\!\{(p\to p)\to q\}\!\}$
while
![]() .
.
If we wish to model the stronger logic
![]() $\mathsf {R}^+$
, we must restrict our attention to a smaller class of multiset frames. In ternary relational semantics, the traditional frame condition to impose on
$\mathsf {R}^+$
, we must restrict our attention to a smaller class of multiset frames. In ternary relational semantics, the traditional frame condition to impose on
![]() $\mathsf {RW}^+$
models to validate contraction is
$\mathsf {RW}^+$
models to validate contraction is
![]() $Rxxx$
. Its analogue in multiset frames is straightforward:
$Rxxx$
. Its analogue in multiset frames is straightforward:
![]() $[x,x]Rx$
. Once we have non-reflexive frames in view, however, we can see that this frame condition is not general enough. A more general form of contraction on ternary frames is this condition:
$[x,x]Rx$
. Once we have non-reflexive frames in view, however, we can see that this frame condition is not general enough. A more general form of contraction on ternary frames is this condition:
corresponding to the validity of the sequent
![]() . If we choose a normal point for y, then the condition becomes
. If we choose a normal point for y, then the condition becomes
which, in the presence of reflexivity gives us
![]() $Rxxx$
for every x. In the absence of reflexivity, no such consequence need follow. In the multiset frame on
$Rxxx$
for every x. In the absence of reflexivity, no such consequence need follow. In the multiset frame on
![]() ${\mathbb R}$
where we set
${\mathbb R}$
where we set
![]() $XRy$
iff y is greater than every member of X, it is clear that whenever
$XRy$
iff y is greater than every member of X, it is clear that whenever
![]() $x\sqsubset z$
(that is,
$x\sqsubset z$
(that is,
![]() $x<z$
) we have
$x<z$
) we have
![]() $Rxxz$
(that is,
$Rxxz$
(that is,
![]() $x<z$
). However, we never have
$x<z$
). However, we never have
![]() $Rxxx$
on this frame.
$Rxxx$
on this frame.
The appropriate understanding of contraction on arbitrary multiset frames, whether reflexive or not, is simple. A multiset rendering of the condition goes like this:
The relation R is preserved when the multiset expands from one repetition of x to two. If R is compositional, this condition will continue to hold in a more general form, using the ground function g from Definition 1:
Lemma 30 (Preservation for contracting relations)
Whenever R is compositional multiset relation where
![]() $[x]Rz\Rightarrow [x,x]Rz$
for every x and z then if
$[x]Rz\Rightarrow [x,x]Rz$
for every x and z then if
![]() $XRy$
and
$XRy$
and
![]() $X'$
is another multiset where
$X'$
is another multiset where
![]() $X\le X'$
and
$X\le X'$
and
![]() $g(X)=g(X')$
, then
$g(X)=g(X')$
, then
![]() $X'Ry$
too.
$X'Ry$
too.
Proof. Recall that
![]() $X\le X'$
iff any object that is an element of
$X\le X'$
iff any object that is an element of
![]() $X \ i$
times is a member of
$X \ i$
times is a member of
![]() $X'$
at least that many times. The constraint that
$X'$
at least that many times. The constraint that
![]() $g(X')=g(X)$
means that the only elements with non-zero multiplicity in
$g(X')=g(X)$
means that the only elements with non-zero multiplicity in
![]() $X'$
have non-zero multiplicity in X too. So,
$X'$
have non-zero multiplicity in X too. So,
![]() $X'$
differs from X only by allowing elements that were already in X to be in
$X'$
differs from X only by allowing elements that were already in X to be in
![]() $X'$
more times. Since X and
$X'$
more times. Since X and
![]() $X'$
are finite multisets, if we prove that
$X'$
are finite multisets, if we prove that
![]() $XRy$
implies
$XRy$
implies
![]() $([x]\cup X)Ry$
, when
$([x]\cup X)Ry$
, when
![]() $x\in X$
, we can repeat this process until we have built
$x\in X$
, we can repeat this process until we have built
![]() $X'$
from X in a series of additions of single elements.
$X'$
from X in a series of additions of single elements.
Now, if
![]() $XRy$
and
$XRy$
and
![]() $x\in X$
, then we have
$x\in X$
, then we have
![]() $([x]\cup (X\backslash x))Ry$
. By Splitting there is some z where
$([x]\cup (X\backslash x))Ry$
. By Splitting there is some z where
![]() $[x]Rz$
and
$[x]Rz$
and
![]() $([z]\cup (X\backslash x))Ry$
. Since
$([z]\cup (X\backslash x))Ry$
. Since
![]() $[x]Rz$
we have
$[x]Rz$
we have
![]() $[x,x]Rz$
, and so, by transitivity,
$[x,x]Rz$
, and so, by transitivity,
![]() $([x,x]\cup (X\backslash x))Ry$
, i.e.,
$([x,x]\cup (X\backslash x))Ry$
, i.e.,
![]() $([x]\cup X)Ry$
, as desired. Applying this process repeatedly, for each additional element in
$([x]\cup X)Ry$
, as desired. Applying this process repeatedly, for each additional element in
![]() $X'$
, we see that
$X'$
, we see that
![]() $X'Ry$
, and we have completed the proof.
$X'Ry$
, and we have completed the proof.
To show that
![]() $\mathsf {R}^+$
is indeed sound for contracting multiset frames, we need to verify that on each model on such a frame
$\mathsf {R}^+$
is indeed sound for contracting multiset frames, we need to verify that on each model on such a frame
![]() $\{\!\{\Gamma \}\!\}\subseteq \{\!\{\Gamma ;\Gamma \}\!\}$
. But this is immediate: let’s suppose that
$\{\!\{\Gamma \}\!\}\subseteq \{\!\{\Gamma ;\Gamma \}\!\}$
. But this is immediate: let’s suppose that
![]() $x\in \{\!\{\Gamma \}\!\}$
. Then by Lemma 21, there is some
$x\in \{\!\{\Gamma \}\!\}$
. Then by Lemma 21, there is some
![]() $[y]Rx$
where
$[y]Rx$
where
![]() $y\in \{\!\{\Gamma \}\!\}$
too. Now, since
$y\in \{\!\{\Gamma \}\!\}$
too. Now, since
![]() $[y]Rx$
, we have
$[y]Rx$
, we have
![]() $[y,y]Rx$
and so, we have that
$[y,y]Rx$
and so, we have that
![]() $x\in \{\!\{\Gamma ;\Gamma \}\!\}$
. With this reasoning, the soundness result for
$x\in \{\!\{\Gamma ;\Gamma \}\!\}$
. With this reasoning, the soundness result for
![]() $\mathsf {R}^+$
on contracting multiset frames is proved.
$\mathsf {R}^+$
on contracting multiset frames is proved.
Theorem 31 (
 $\mathsf {R}^+$
is sound for contracting multiset frames)
$\mathsf {R}^+$
is sound for contracting multiset frames)
Any sequent
![]() derivable in
derivable in
![]() $\mathsf {R}^+$
also holds in each model
$\mathsf {R}^+$
also holds in each model
![]() $\langle P,R,\Vdash \rangle $
on a contracting multiset frame.
$\langle P,R,\Vdash \rangle $
on a contracting multiset frame.
For completeness, we need to show that if a sequent holds in all multiset frames then it is derivable in
![]() $\mathsf {RW}^+$
, and that if a sequent holds in all contracting multiset frames, then it is derivable in
$\mathsf {RW}^+$
, and that if a sequent holds in all contracting multiset frames, then it is derivable in
![]() $\mathsf {R}^+$
. As is usual, the most straightforward way to prove completeness is to prove the contrapositive, by showing that for any underivable sequent, one can find a counterexample in some frame. In the case of the ternary relational semantics, as with Kripke models for normal modal logics and intuitionistic logics, this is achieved by constructing the canonical frame [Reference Restall41, Reference Routley and Meyer45–Reference Routley, Meyer and Leblanc47], whose points are prime theories,Footnote
25
and where the normal points are those theories containing all logical truths, where
$\mathsf {R}^+$
. As is usual, the most straightforward way to prove completeness is to prove the contrapositive, by showing that for any underivable sequent, one can find a counterexample in some frame. In the case of the ternary relational semantics, as with Kripke models for normal modal logics and intuitionistic logics, this is achieved by constructing the canonical frame [Reference Restall41, Reference Routley and Meyer45–Reference Routley, Meyer and Leblanc47], whose points are prime theories,Footnote
25
and where the normal points are those theories containing all logical truths, where
![]() $\sqsubseteq $
is the subset relation, and where R is defined syntactically:
$\sqsubseteq $
is the subset relation, and where R is defined syntactically:
![]() $R\alpha \beta \gamma $
iff for each
$R\alpha \beta \gamma $
iff for each
![]() $A\to B\in \alpha $
, if
$A\to B\in \alpha $
, if
![]() $A\in \beta $
then
$A\in \beta $
then
![]() $B\in \gamma $
. It is a standard result that membership is an evaluation relation on the canonical frame, defining
$B\in \gamma $
. It is a standard result that membership is an evaluation relation on the canonical frame, defining
![]() $\alpha \Vdash A$
iff
$\alpha \Vdash A$
iff
![]() $A\in \alpha $
, which gives us a relation satisfying the expected truth conditions, and that that any underivable sequent has a counterexample in the resulting canonical model. In addition, the
$A\in \alpha $
, which gives us a relation satisfying the expected truth conditions, and that that any underivable sequent has a counterexample in the resulting canonical model. In addition, the
![]() $\mathsf {RW}^+$
canonical frame satisfies the
$\mathsf {RW}^+$
canonical frame satisfies the
![]() $\mathsf {RW}^+$
conditions on the ternary relation, and the
$\mathsf {RW}^+$
conditions on the ternary relation, and the
![]() $\mathsf {R}^+$
canonical frame satisfies the contraction condition. So, we can appeal to Lemma 16, to show that the canonical ternary relational model for
$\mathsf {R}^+$
canonical frame satisfies the contraction condition. So, we can appeal to Lemma 16, to show that the canonical ternary relational model for
![]() $\mathsf {RW}^+$
(or for
$\mathsf {RW}^+$
(or for
![]() $\mathsf {R}^+$
) will also provide a multiset model (or contracting multiset model), which gives exactly the same truth conditions on points, and so, counterexamples to the same sequents. So, we have completeness for free:
$\mathsf {R}^+$
) will also provide a multiset model (or contracting multiset model), which gives exactly the same truth conditions on points, and so, counterexamples to the same sequents. So, we have completeness for free:
Theorem 32 (Completeness for multiset frames)
Each sequent that holds on every reflexive multiset frame is derivable in
![]() $\mathsf {RW}^+$
. Furthermore, each sequent that holds on every contracting, reflexive multiset frame is derivable in
$\mathsf {RW}^+$
. Furthermore, each sequent that holds on every contracting, reflexive multiset frame is derivable in
![]() $\mathsf {R}^+$
.
$\mathsf {R}^+$
.
So, multiset frames provide an elegant, simple class of models for
![]() $\mathsf {RW}^+$
, unifying the parts of the ternary relational frames. The compositionality condition on the multiset relation R is a natural generalisation of the condition that inclusion (
$\mathsf {RW}^+$
, unifying the parts of the ternary relational frames. The compositionality condition on the multiset relation R is a natural generalisation of the condition that inclusion (
![]() $\sqsubseteq $
) be a preorder, to the general setting that we relate a collection of points to a point. The generalisation goes so far as to include models in which the underlying order is not even reflexive.
$\sqsubseteq $
) be a preorder, to the general setting that we relate a collection of points to a point. The generalisation goes so far as to include models in which the underlying order is not even reflexive.
However, not all collections are multisets. In the rest of this paper, we will show that we can generalise these results to other kinds of collections in a natural way. We will start by considering sets.
3 Set frames
Once you understand multiset frames, it is straightforward to define set frames. We start with the definition of compositionality for relations on
![]() ${\mathcal P}^*(P)\times P$
, where
${\mathcal P}^*(P)\times P$
, where
![]() ${\mathcal P}^*(P)$
is the set of finite subsets of P.
${\mathcal P}^*(P)$
is the set of finite subsets of P.
Definition 33 (Compositionality for set relations)
A relation R on
![]() ${\mathcal P}^*(P)\times P$
is said to be compositional if and only if for all sets
${\mathcal P}^*(P)\times P$
is said to be compositional if and only if for all sets
![]() $X,Y$
and all points x and z,
$X,Y$
and all points x and z,
Such a set relation R is reflexive iff for all points
![]() $x\in P$
, we have
$x\in P$
, we have
We have replaced talk of multisets of elements of P with finite subsets of P. The compositional multiset relations discussed in Example 4 can be all reframed as set relations. Membership, Maximum, The Product, Some Product of and Between can all be defined as set relations on
![]() $\omega $
, and each is set relation so defined is compositional.
$\omega $
, and each is set relation so defined is compositional.
The novelty with set relations, as opposed to multiset relations, is that they are, by construction, contracting. There is no difference at all between
![]() $\{x,x\} Ry$
and
$\{x,x\} Ry$
and
![]() $\{x\}Ry$
, and since by reflexivity, we have
$\{x\}Ry$
, and since by reflexivity, we have
![]() $\{x\}Rx$
, it follows that
$\{x\}Rx$
, it follows that
![]() $\{x,x\}Rx$
holds in every compositional set relation R. Once we define the notion of a set frame, and the corresponding notion of a set model, it will follow immediately that
$\{x,x\}Rx$
holds in every compositional set relation R. Once we define the notion of a set frame, and the corresponding notion of a set model, it will follow immediately that
![]() $\mathsf {R}^+$
is sound for set models.
$\mathsf {R}^+$
is sound for set models.
Definition 34 (Set frames and set models)
If P is an inhabited set and R is a compositional set relation on P, then
![]() $\langle P,R\rangle $
is said to be a set frame. If
$\langle P,R\rangle $
is said to be a set frame. If
![]() $\Vdash $
is a relation between the set P and the set of atomic formulas, which is hereditary along R (so if
$\Vdash $
is a relation between the set P and the set of atomic formulas, which is hereditary along R (so if
![]() $x\Vdash p$
and
$x\Vdash p$
and
![]() $\{x\}Ry$
then
$\{x\}Ry$
then
![]() $y\Vdash p$
too), then
$y\Vdash p$
too), then
![]() $\langle P,R,\Vdash \rangle $
is said to be a set model, where
$\langle P,R,\Vdash \rangle $
is said to be a set model, where
![]() $\Vdash $
evaluates all formulas in the language of
$\Vdash $
evaluates all formulas in the language of
![]() $\mathsf {R}^+$
as follows:
$\mathsf {R}^+$
as follows:
-
•
 $x\Vdash A\land B$
iff
$x\Vdash A\land B$
iff
 $x\Vdash A$
and
$x\Vdash A$
and
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\lor B$
iff
$x\Vdash A\lor B$
iff
 $x\Vdash A$
or
$x\Vdash A$
or
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\to B$
iff for each
$x\Vdash A\to B$
iff for each
 $y,z$
where
$y,z$
where
 $\{x,y\}Rz$
, if
$\{x,y\}Rz$
, if
 $y\Vdash A$
then
$y\Vdash A$
then
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash A\circ B$
iff for some
$x\Vdash A\circ B$
iff for some
 $y,z$
where
$y,z$
where
 $\{y,z\}Rx$
, both
$\{y,z\}Rx$
, both
 $y\Vdash A$
and
$y\Vdash A$
and
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash \mathsf {t}$
iff
$x\Vdash \mathsf {t}$
iff
 $\{\;\} Rx$
.
$\{\;\} Rx$
. -
•
 $x\Vdash \bot $
never.
$x\Vdash \bot $
never.
As with multiset models, the evaluation relation
![]() $\Vdash $
on set models is hereditary across the relation R. And as with contracting multiset models, the logic
$\Vdash $
on set models is hereditary across the relation R. And as with contracting multiset models, the logic
![]() $\mathsf {R}^+$
is sound for set. The soundness proof for
$\mathsf {R}^+$
is sound for set. The soundness proof for
![]() $\mathsf {RW}^+$
can be rewritten, word-for-word, with set singletons and set union replacing multiset singletons and multiset union. Furthermore, any relation compositional set relation R satisfies the contraction condition vacuously, so the contraction rule preserves validity on all set models. We have the following soundness theorem for free:
$\mathsf {RW}^+$
can be rewritten, word-for-word, with set singletons and set union replacing multiset singletons and multiset union. Furthermore, any relation compositional set relation R satisfies the contraction condition vacuously, so the contraction rule preserves validity on all set models. We have the following soundness theorem for free:
Theorem 35 (
 $\mathsf {R}^+$
is sound for set frames)
$\mathsf {R}^+$
is sound for set frames)
Any
![]() $\mathsf {R}^+$
derivable sequent
$\mathsf {R}^+$
derivable sequent
![]() holds in each model
holds in each model
![]() $\langle P,R,\Vdash \rangle $
on a set frame.
$\langle P,R,\Vdash \rangle $
on a set frame.
A natural question arises. Is
![]() $\mathsf {R}^+$
complete for set frames? Here, any completeness theorem will not be quite as straightforward as in the case for multiset frames and
$\mathsf {R}^+$
complete for set frames? Here, any completeness theorem will not be quite as straightforward as in the case for multiset frames and
![]() $\mathsf {RW}^+$
. We cannot simply take the canonical frame and show that it is a set frame. In general, contracting ternary frames (or contracting multiset frames) do not turn out to be equivalent to set frames. In any set frame we have
$\mathsf {RW}^+$
. We cannot simply take the canonical frame and show that it is a set frame. In general, contracting ternary frames (or contracting multiset frames) do not turn out to be equivalent to set frames. In any set frame we have
![]() $\{x,x\}Ry$
if and only if
$\{x,x\}Ry$
if and only if
![]() $\{x\}Ry$
trivially, but the corresponding biconditional—
$\{x\}Ry$
trivially, but the corresponding biconditional—
![]() $Rxxy$
if and only if
$Rxxy$
if and only if
![]() $x\sqsubseteq y$
(or
$x\sqsubseteq y$
(or
![]() $[x,x]Ry$
iff
$[x,x]Ry$
iff
![]() $[x]Ry$
)—does not hold in all ternary relational frames for
$[x]Ry$
)—does not hold in all ternary relational frames for
![]() $\mathsf {R}^+$
, or on all contracting multiset frames. In general, only one direction of the biconditional holds.
$\mathsf {R}^+$
, or on all contracting multiset frames. In general, only one direction of the biconditional holds.
Example 36 (A ternary
 $\mathsf {R}^+$
frame that isn’t (equivalent to) a set frame)
$\mathsf {R}^+$
frame that isn’t (equivalent to) a set frame)
The frame on the set
![]() $P=\{0,a,b\}$
of points with
$P=\{0,a,b\}$
of points with
![]() $N=\{0\}$
, where
$N=\{0\}$
, where
![]() $\sqsubseteq $
is identity and where R is defined with the following table
$\sqsubseteq $
is identity and where R is defined with the following table
 $$\begin{align*}\begin{array}{c|ccc} R & 0 & a & b \\ \hline 0 & 0 & a & b \\ a & a & ab & 0ab \\ b & b & 0ab & ab \end{array}\end{align*}$$
$$\begin{align*}\begin{array}{c|ccc} R & 0 & a & b \\ \hline 0 & 0 & a & b \\ a & a & ab & 0ab \\ b & b & 0ab & ab \end{array}\end{align*}$$
is not equivalent to a set frame. To read the table, the values in the x row and y column in the table are the different values of z such that
![]() $Rxyz$
. So, the
$Rxyz$
. So, the
![]() $ab$
in the a row and a column indicates that
$ab$
in the a row and a column indicates that
![]() $Raaa$
and
$Raaa$
and
![]() $Raab$
. It is not too difficult to check that this is a ternary
$Raab$
. It is not too difficult to check that this is a ternary
![]() $\mathsf {R}^+$
frame (it is associative, commutative and contracting), but it does not satisfy the condition needed for equivalence to a set frame: that
$\mathsf {R}^+$
frame (it is associative, commutative and contracting), but it does not satisfy the condition needed for equivalence to a set frame: that
![]() $Rxxy$
if and only if
$Rxxy$
if and only if
![]() $x\sqsubseteq y$
. Here,
$x\sqsubseteq y$
. Here,
![]() $Raab$
, but
$Raab$
, but
![]() $a\not \sqsubseteq b$
. This is a ternary frame that is not equivalent to a set frame.
$a\not \sqsubseteq b$
. This is a ternary frame that is not equivalent to a set frame.
What goes for this ternary frame can go for the canonical frame for
![]() $\mathsf {R}^+$
.Footnote
26
So, there is no guarantee that any canonical frame for
$\mathsf {R}^+$
.Footnote
26
So, there is no guarantee that any canonical frame for
![]() $\mathsf {R}^+$
will be (equivalent to) a set frame. This raises the question of whether set frames overgenerate, whether they determine a logic stronger than
$\mathsf {R}^+$
will be (equivalent to) a set frame. This raises the question of whether set frames overgenerate, whether they determine a logic stronger than
![]() $\mathsf {R}^+$
. It might be thought that the stronger frame condition induced on a set frame means that the mingle axiom
$\mathsf {R}^+$
. It might be thought that the stronger frame condition induced on a set frame means that the mingle axiom
![]() $p\to (p\to p)$
(which is equivalent to
$p\to (p\to p)$
(which is equivalent to
![]() $(p\circ p)\to p$
) holds on our frames. It fails, as the following example shows.
$(p\circ p)\to p$
) holds on our frames. It fails, as the following example shows.
Example 37 (A set frame counterexample to mingle)
Consider the inhabited-set frame on
![]() $\omega $
, where
$\omega $
, where
![]() $XRy$
iff
$XRy$
iff
![]() $y$
is in the interval bound by the set X. So, for example, the set
$y$
is in the interval bound by the set X. So, for example, the set
![]() $\{0,2\}$
is related to
$\{0,2\}$
is related to
![]() $0$
,
$0$
,
![]() $1$
and
$1$
and
![]() $2$
but no other elements of
$2$
but no other elements of
![]() $\omega $
. This is frame on inhabited sets. We can then extend this frame to construct a set frame using the technique of Lemma 8, by adjoining an element
$\omega $
. This is frame on inhabited sets. We can then extend this frame to construct a set frame using the technique of Lemma 8, by adjoining an element
![]() $\infty $
and choosing the
$\infty $
and choosing the
![]() $R^{\times }$
extension of the relation R. Here,
$R^{\times }$
extension of the relation R. Here,
![]() $\{\;\} R^{\times } \infty $
and
$\{\;\} R^{\times } \infty $
and
![]() $\{\infty \}R^{\times } \infty $
and for every other set X,
$\{\infty \}R^{\times } \infty $
and for every other set X,
![]() $XR^{\times } z$
iff
$XR^{\times } z$
iff
![]() $(X\backslash \infty )Rz$
, to make this a model for the whole of
$(X\backslash \infty )Rz$
, to make this a model for the whole of
![]() $\mathsf {R}^+$
, including
$\mathsf {R}^+$
, including
![]() $\mathsf {t}$
. In this model, the order relation
$\mathsf {t}$
. In this model, the order relation
![]() $\sqsubset $
is the identity relation, since
$\sqsubset $
is the identity relation, since
![]() $\{x\}R^{\times } y$
iff
$\{x\}R^{\times } y$
iff
![]() $y=x$
, for every
$y=x$
, for every
![]() $x$
(including
$x$
(including
![]() $\infty $
). Let’s take
$\infty $
). Let’s take
![]() . Then it is straightforward that
. Then it is straightforward that
![]() $0\Vdash p$
but
$0\Vdash p$
but
![]() $0\not \Vdash p\to p$
, since
$0\not \Vdash p\to p$
, since
![]() $2\Vdash p$
and
$2\Vdash p$
and
![]() $1\not \Vdash p$
and
$1\not \Vdash p$
and
![]() $\{0,2\}R^{\times } 1$
. So, since
$\{0,2\}R^{\times } 1$
. So, since
![]() $\{0,\infty \}R^{\times } 0$
, we have
$\{0,\infty \}R^{\times } 0$
, we have
![]() $\infty \not \Vdash p\to (p\to p)$
, and since
$\infty \not \Vdash p\to (p\to p)$
, and since
![]() $\{\;\} R^{\times }\infty $
, we see that
$\{\;\} R^{\times }\infty $
, we see that
![]() $p\to (p\to p)$
fails at a normal point (at the only normal point,
$p\to (p\to p)$
fails at a normal point (at the only normal point,
![]() $\infty $
), giving us a counterexample to the sequent
$\infty $
), giving us a counterexample to the sequent
![]() , as desired.
, as desired.
So, set frames are sound for
![]() $\mathsf {R}^+$
, but the standard techniques for completeness do not suffice to show completeness for
$\mathsf {R}^+$
, but the standard techniques for completeness do not suffice to show completeness for
![]() $\mathsf {R}^+$
. It seems we must use another approach, or find some way that these frames overgenerate
$\mathsf {R}^+$
. It seems we must use another approach, or find some way that these frames overgenerate
![]() $\mathsf {R}^+$
. We will not, however, settle the question here, so we leave it as a topic for further research.Footnote
27
$\mathsf {R}^+$
. We will not, however, settle the question here, so we leave it as a topic for further research.Footnote
27
-
[open question] Is
 $\mathsf {R}^+$
complete for the class of all set frames?
$\mathsf {R}^+$
complete for the class of all set frames?
As with multiset frames, we can move from set frames to inhabited-set frames, if we loosen the requirement that the compositional relation R relates the empty set to points. All of the results concerning inhabited-multiset frames generalise to inhabited-set frames. Inhabited-set frames on the real plane are surprisingly straightforward to construct, and they have interesting properties of their own.Footnote 28 We have the following result.
Theorem 38 (
 $\mathsf {R}^+_{-\epsilon }$
is sound for set frames)
$\mathsf {R}^+_{-\epsilon }$
is sound for set frames)
Any
![]() $\mathsf {R}^+_{-\epsilon }$
derivable sequent
$\mathsf {R}^+_{-\epsilon }$
derivable sequent
![]() holds in each model
holds in each model
![]() $\langle P,R,\Vdash \rangle $
on an inhabited-set frame.
$\langle P,R,\Vdash \rangle $
on an inhabited-set frame.
Again, the proof of this theorem comes essentially for free, once we recognise that the structural rule IW of intensional contraction satisfied on inhabited-set frames. We can use an inhabited-set frame to show that the sequent
![]() also fails in
also fails in
![]() $\mathsf {R}^+_{-\epsilon }$
, so
$\mathsf {R}^+_{-\epsilon }$
, so
![]() $\mathsf {R}^+$
fails to be conservative over
$\mathsf {R}^+$
fails to be conservative over
![]() $\mathsf {R}^+_{-\epsilon }$
, just as
$\mathsf {R}^+_{-\epsilon }$
, just as
![]() $\mathsf {RW}^+$
is not conservative over
$\mathsf {RW}^+$
is not conservative over
![]() $\mathsf {RW}^+_{-\epsilon }$
.
$\mathsf {RW}^+_{-\epsilon }$
.
Example 39 (
 $\mathsf {R}^+$
is not conservative over
$\mathsf {R}^+$
is not conservative over
 $\mathsf {R}^+_{-\epsilon }$
)
$\mathsf {R}^+_{-\epsilon }$
)
This time, consider the inhabited-set frame
![]() $\langle P,R\rangle $
where
$\langle P,R\rangle $
where
![]() $P=\{0,1,2\}$
and
$P=\{0,1,2\}$
and
![]() $XRy$
holds when y is bounded by the set X. In other words,
$XRy$
holds when y is bounded by the set X. In other words,
![]() $XRy$
if and only if
$XRy$
if and only if
![]() $\min (X)\le y\le \max (Y)$
. In this frame, the underlying order is identity, so the relation is reflexive, and any set of points is a possible extension of a formula. Let
$\min (X)\le y\le \max (Y)$
. In this frame, the underlying order is identity, so the relation is reflexive, and any set of points is a possible extension of a formula. Let
![]() . Then at
. Then at
![]() $p\to p$
is satisfied nowhere, since for any point
$p\to p$
is satisfied nowhere, since for any point
![]() $x$
you choose, there is some point y (choose
$x$
you choose, there is some point y (choose
![]() $2$
if
$2$
if
![]() $x$
is
$x$
is
![]() $0$
, and choose
$0$
, and choose
![]() $0$
otherwise) where
$0$
otherwise) where
![]() $y\Vdash p$
, and where
$y\Vdash p$
, and where
![]() $\{x,y\}R1$
, where
$\{x,y\}R1$
, where
![]() $1\not \Vdash p$
. So, at every point we have a counterexample to the identity statement
$1\not \Vdash p$
. So, at every point we have a counterexample to the identity statement
![]() $p\to p$
.
$p\to p$
.
This means that every point in our frame supports
![]() $(p\to p)\to q$
, since
$(p\to p)\to q$
, since
![]() $p\to p$
fails everywhere. In particular,
$p\to p$
fails everywhere. In particular,
![]() $1\Vdash (p\to p)\to p$
, while
$1\Vdash (p\to p)\to p$
, while
![]() $1\not \Vdash p$
, so
$1\not \Vdash p$
, so
![]() fails on this frame, and hence, it is not derivable in
fails on this frame, and hence, it is not derivable in
![]() $\mathsf {R}^+_{-\epsilon }$
. A fortiori, neither is the sequent
$\mathsf {R}^+_{-\epsilon }$
. A fortiori, neither is the sequent
![]() .
.
4 List frames and tree frames
Different collections gather their elements in different ways. Sets collect elements with no regard to order or multiplicity. Multisets allow their members to occur repeatedly, but there is no record of the order of their arrival. It is natural to consider collections that keep track of both multiplicity and order: lists. The list
![]() $\langle a,a,b,c\rangle $
is distinct from the list
$\langle a,a,b,c\rangle $
is distinct from the list
![]() $\langle a,b,a,c\rangle $
, both of which are distinct from the list
$\langle a,b,a,c\rangle $
, both of which are distinct from the list
![]() $\langle a,b,c\rangle $
.
$\langle a,b,c\rangle $
.
The definition given for compositionality in set and multiset frames generalises nicely to the context of list frames, but we will need to be careful when doing so: the definitions were not attentive to matters of ordering, so we will need to pay attention to that here when defining what it is to replace an element y occurring in some list by another list. To this we turn, now.
Definition 40 (List composition)
If the list
![]() $X$
is
$X$
is
![]() $\langle x_{1},\ldots ,x_{n}\rangle $
and the inhabited list
$\langle x_{1},\ldots ,x_{n}\rangle $
and the inhabited list
![]() $Y(y_{j})$
is
$Y(y_{j})$
is
![]() $\langle y_{1},\ldots , y_{j}, \ldots ,y_{m}\rangle $
, then
$\langle y_{1},\ldots , y_{j}, \ldots ,y_{m}\rangle $
, then
![]() $Y(X)$
is
$Y(X)$
is
![]() $\langle y_{1},\ldots , y_{j-1},x_{1},\ldots ,x_{n},y_{j+1}, \ldots ,y_{m}\rangle $
.
$\langle y_{1},\ldots , y_{j-1},x_{1},\ldots ,x_{n},y_{j+1}, \ldots ,y_{m}\rangle $
.
Given an inhabited set P, the set
![]() $L(P)$
is the set of all finite lists of elements from P.
$L(P)$
is the set of all finite lists of elements from P.
Definition 41 (Compositionality)
A list relation R on
![]() $L(P)\times P$
is said to be compositional if and only if for all lists X and Y and for all points z,
$L(P)\times P$
is said to be compositional if and only if for all lists X and Y and for all points z,
A list relation R is reflexive iff for all points x, we have
As with multisets, a compositional list relation between inhabited lists and points adds the requirement that X be inhabited to the preceding definition. (
![]() $Y(y)$
must of course be inhabited, though of course it may just be the singleton list
$Y(y)$
must of course be inhabited, though of course it may just be the singleton list
![]() $\langle y\rangle $
.)
$\langle y\rangle $
.)
Definition 42 (List frames and list models)
If P is an inhabited set and R is a compositional list relation on P, then
![]() $\langle P,R\rangle $
is said to be a list frame. (If R is an inhabited-list relation, then this is an inhabited-list frame.) If
$\langle P,R\rangle $
is said to be a list frame. (If R is an inhabited-list relation, then this is an inhabited-list frame.) If
![]() $\Vdash $
is a relation between the set P and the set of atomic formulas, which is hereditary along R (so if
$\Vdash $
is a relation between the set P and the set of atomic formulas, which is hereditary along R (so if
![]() $x\Vdash p$
and
$x\Vdash p$
and
![]() $\langle x\rangle Ry$
then
$\langle x\rangle Ry$
then
![]() $y\Vdash p$
too), then
$y\Vdash p$
too), then
![]() $\langle P,R,\Vdash \rangle $
is said to be a list model, where
$\langle P,R,\Vdash \rangle $
is said to be a list model, where
![]() $\Vdash $
evaluates all formulas in the language of
$\Vdash $
evaluates all formulas in the language of
![]() $\mathsf {R}^+$
as follows:
$\mathsf {R}^+$
as follows:
-
•
 $x\Vdash A\land B$
iff
$x\Vdash A\land B$
iff
 $x\Vdash A$
and
$x\Vdash A$
and
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\lor B$
iff
$x\Vdash A\lor B$
iff
 $x\Vdash A$
or
$x\Vdash A$
or
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\to B$
iff for each
$x\Vdash A\to B$
iff for each
 $y,z$
where
$y,z$
where
 $\langle x,y\rangle Rz$
, if
$\langle x,y\rangle Rz$
, if
 $y\Vdash A$
then
$y\Vdash A$
then
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash A\circ B$
iff for some
$x\Vdash A\circ B$
iff for some
 $y,z$
where
$y,z$
where
 $\langle y,z\rangle Rx$
, both
$\langle y,z\rangle Rx$
, both
 $y\Vdash A$
and
$y\Vdash A$
and
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash \bot $
never.
$x\Vdash \bot $
never.
If R is a list relation, and not merely an inhabited-list relation, we can add the
![]() $\mathsf {t}$
clause.
$\mathsf {t}$
clause.
-
•
 $x\Vdash \mathsf {t}$
iff
$x\Vdash \mathsf {t}$
iff
 $\langle \;\rangle Rx$
.
$\langle \;\rangle Rx$
.
We can define validity for sequents on our models in the usual way. In fact, the definitions the extension
![]() of a formula A carries over unchanged in the setting of list frames, and the definition of the shadow
of a formula A carries over unchanged in the setting of list frames, and the definition of the shadow
![]() $\{\!\{\Gamma \}\!\}$
of a structure requires only one small tweak, given the move from multiset or set frames to list frames. References to multisets must be replaced by the corresponding references to lists, as follows:
$\{\!\{\Gamma \}\!\}$
of a structure requires only one small tweak, given the move from multiset or set frames to list frames. References to multisets must be replaced by the corresponding references to lists, as follows:
-
•
 $\{\!\{\epsilon \}\!\} = \{x\in P:\langle \;\rangle Rx\}$
,
$\{\!\{\epsilon \}\!\} = \{x\in P:\langle \;\rangle Rx\}$
, -
•
 ,
, -
•
 $\{\!\{\Gamma ,\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})\langle y\rangle Rx\land \langle z\rangle Rx\}$
,
$\{\!\{\Gamma ,\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})\langle y\rangle Rx\land \langle z\rangle Rx\}$
, -
•
 $\{\!\{\Gamma ;\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})\langle y,z\rangle Rx\}$
.
$\{\!\{\Gamma ;\Gamma '\}\!\}=\{x\in P:(\exists y\in \{\!\{\Gamma \}\!\})(\exists z\in \{\!\{\Gamma '\}\!\})\langle y,z\rangle Rx\}$
.
With this, we can define validity on a model as before. The sequent
![]() is valid on
is valid on
![]() $\langle P,R,\Vdash \rangle $
iff
$\langle P,R,\Vdash \rangle $
iff
![]() .
.
We have seen that logic
![]() $\mathsf {RW}^+$
is sound and complete for multiset frames. The logic
$\mathsf {RW}^+$
is sound and complete for multiset frames. The logic
![]() $\mathsf {R}^+$
is sound and complete for multiset frames with contraction, and that
$\mathsf {R}^+$
is sound and complete for multiset frames with contraction, and that
![]() $\mathsf {R}^+$
is sound for set frames. A natural question is what logic is sound and complete for list frames. List frames will not validate the structural rules
$\mathsf {R}^+$
is sound for set frames. A natural question is what logic is sound and complete for list frames. List frames will not validate the structural rules
![]() $IC$
and
$IC$
and
![]() $IW$
, so the logic will be weaker than
$IW$
, so the logic will be weaker than
![]() $\mathsf {RW}^+$
. One might think that list frames validate
$\mathsf {RW}^+$
. One might think that list frames validate
![]() $\mathsf {TW}^+$
, a close relative of
$\mathsf {TW}^+$
, a close relative of
![]() $\mathsf {RW}^+$
that eschews the structural rules
$\mathsf {RW}^+$
that eschews the structural rules
![]() $IC$
and
$IC$
and
![]() $IW$
, but that thought is not borne out, as we will show.
$IW$
, but that thought is not borne out, as we will show.
Lemma 43. The following structural rules are valid on list frames.

Proof. It is straightforward to show that
![]() $\{\!\{\Gamma ';(\Gamma '';\Gamma ''')\}\!\}=\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}$
, given the associativity of list composition, and the compositionality of the relation R. The proof used for Theorem 26 carries over here with only notational changes, like so:
$\{\!\{\Gamma ';(\Gamma '';\Gamma ''')\}\!\}=\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}$
, given the associativity of list composition, and the compositionality of the relation R. The proof used for Theorem 26 carries over here with only notational changes, like so:
![]() $\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{x\in P:(\exists y\in \{\!\{(\Gamma ';\Gamma '')\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})\langle y,z\rangle Rx\}$
unpacking the definition of
$\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{x\in P:(\exists y\in \{\!\{(\Gamma ';\Gamma '')\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})\langle y,z\rangle Rx\}$
unpacking the definition of
![]() $\{\!\{\Gamma ';\Gamma ''\}\!\}$
this set is identical to
$\{\!\{\Gamma ';\Gamma ''\}\!\}$
this set is identical to
![]() $\{x\in P:(\exists y\in P)(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})(\langle u,v\rangle Ry\land \langle y,z\rangle Rx)\}$
. Applying compositionality, we see that
$\{x\in P:(\exists y\in P)(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})(\langle u,v\rangle Ry\land \langle y,z\rangle Rx)\}$
. Applying compositionality, we see that
![]() $(\exists y\in P)(\langle u,v\rangle Ry\land \langle y,z\rangle Rx)$
is equivalent to
$(\exists y\in P)(\langle u,v\rangle Ry\land \langle y,z\rangle Rx)$
is equivalent to
![]() $\langle u,v,z\rangle Rx$
so the set
$\langle u,v,z\rangle Rx$
so the set
![]() $\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}$
simplifies (as expected) to
$\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}$
simplifies (as expected) to
![]() $\{x\in P:(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})\langle u,v,z\rangle Rx\}$
where the left-associated structure
$\{x\in P:(\exists u\in \{\!\{\Gamma '\}\!\})(\exists v\in \{\!\{\Gamma ''\}\!\})(\exists z\in \{\!\{\Gamma '''\}\!\})\langle u,v,z\rangle Rx\}$
where the left-associated structure
![]() $(\Gamma ';\Gamma '');\Gamma '''$
unwraps into the unassociated list
$(\Gamma ';\Gamma '');\Gamma '''$
unwraps into the unassociated list
![]() $\langle u,v,z\rangle $
. Similarly, the right-associated structure
$\langle u,v,z\rangle $
. Similarly, the right-associated structure
![]() $\Gamma ';(\Gamma '';\Gamma ''')$
unwraps to exactly the same set, so
$\Gamma ';(\Gamma '';\Gamma ''')$
unwraps to exactly the same set, so
![]() $\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{\!\{\Gamma ';(\Gamma '';\Gamma ''')\}\!\}$
, showing that the associativity structural rule IB is valid on list frames.
$\{\!\{(\Gamma ';\Gamma '');\Gamma '''\}\!\}=\{\!\{\Gamma ';(\Gamma '';\Gamma ''')\}\!\}$
, showing that the associativity structural rule IB is valid on list frames.
The structural rule IB is valid in ternary frames for
![]() $\mathsf {TW}^+$
, but the rule IBc is not. The latter rule can be used to derive the sequent
$\mathsf {TW}^+$
, but the rule IBc is not. The latter rule can be used to derive the sequent
, which does not hold in
![]() $\mathsf {TW}^+$
.Footnote
29
Rather than the structural rule IBc, the usual structural rule paired with IB for
$\mathsf {TW}^+$
.Footnote
29
Rather than the structural rule IBc, the usual structural rule paired with IB for
![]() $\mathsf {TW}^+$
is the rule IB
$\mathsf {TW}^+$
is the rule IB
![]() $'$
.
$'$
.

This rule, despite its importance in the study of relevant logics, is not valid on inhabited list frames.
Lemma 44. The rule IB
![]() $'$
is not valid on list frames.
$'$
is not valid on list frames.
Proof. For the counterexample, let the frame be
![]() $\langle \omega ,R\rangle $
on inhabited lists from
$\langle \omega ,R\rangle $
on inhabited lists from
![]() $\omega $
, where
$\omega $
, where
![]() $\langle x_{1},\ldots ,x_{n}\rangle Ry$
iff
$\langle x_{1},\ldots ,x_{n}\rangle Ry$
iff
![]() $x_{1}=y$
. For this frame,
$x_{1}=y$
. For this frame,
![]() $x\sqsubset y$
iff
$x\sqsubset y$
iff
![]() $x=y$
, so any set of points is an extension, and this frame is reflexive. On this frame, set
$x=y$
, so any set of points is an extension, and this frame is reflexive. On this frame, set
![]() ,
,
![]() and
and
![]() . Let’s check the validity of
. Let’s check the validity of
![]() on this model. Here,
on this model. Here,
![]() $\{\!\{q;p\}\!\}=\{x:\langle 2,1\rangle Rx\}=\{2\}$
, and so,
$\{\!\{q;p\}\!\}=\{x:\langle 2,1\rangle Rx\}=\{2\}$
, and so,
![]() $\{\!\{(q;p);r\}\!\}=\{x:\langle 2,3\rangle Rx\}=\{2\}$
, too. On the other hand,
$\{\!\{(q;p);r\}\!\}=\{x:\langle 2,3\rangle Rx\}=\{2\}$
, too. On the other hand,
![]() , and so,
, and so,
![]() , and hence,
, and hence,
![]() , and
, and
![]() is not valid on our model. Since it is derivable, using IB
is not valid on our model. Since it is derivable, using IB
![]() $'$
, this rule is not valid on list frames.
$'$
, this rule is not valid on list frames.
This counterexample uses one natural way of forming inhabited list frames from a given set P of points and suggests another natural example.
-
[First] Say that
 $XRy$
iff
$XRy$
iff
 $X=\langle x_{1},\ldots ,x_{n}\rangle $
and
$X=\langle x_{1},\ldots ,x_{n}\rangle $
and
 $x=x_{1}$
.
$x=x_{1}$
.
 $\langle x\rangle Rx$
clearly holds. It is only slightly more work to see that the compositionality condition,
$\langle x\rangle Rx$
clearly holds. It is only slightly more work to see that the compositionality condition,
 $\exists z(XRz$
and
$\exists z(XRz$
and
 $Y(z)Ry)$
iff
$Y(z)Ry)$
iff
 $Y(X)Ry$
, holds.
$Y(X)Ry$
, holds. -
[Last] Say that
 $XRy$
iff
$XRy$
iff
 $X=\langle x_{1},\ldots ,x_{n}\rangle $
and
$X=\langle x_{1},\ldots ,x_{n}\rangle $
and
 $x=x_{n}$
.
$x=x_{n}$
.
Each compositional multiset relation R (on inhabited multisets, or on all multisets) can be lifted to a list relation (correspondingly, on inhabited lists, or all lists) too, where we set
![]() $XR'x$
if and only if
$XR'x$
if and only if
![]() $m(X)Rx$
, where
$m(X)Rx$
, where
![]() $m(X)$
is the multiset of members of the list X defined in the obvious way.Footnote
30
So, all of the other compositional multiset relations we have considered, like
sum
,
product
,
membership
, etc., transfer naturally to this setting, albeit without making any use of the distinctively non-commutative nature of the list structures being related. Another example of a functional compositional list relation is given by any semigroup.
$m(X)$
is the multiset of members of the list X defined in the obvious way.Footnote
30
So, all of the other compositional multiset relations we have considered, like
sum
,
product
,
membership
, etc., transfer naturally to this setting, albeit without making any use of the distinctively non-commutative nature of the list structures being related. Another example of a functional compositional list relation is given by any semigroup.
Example 45 (Lifting a semigroup)
If
![]() $\langle P,*\rangle $
is a semigroup (if
$\langle P,*\rangle $
is a semigroup (if
![]() $*$
is an associative binary operation on P) then the inhabited-list relation
$*$
is an associative binary operation on P) then the inhabited-list relation
![]() $R^*$
, given by setting
$R^*$
, given by setting
![]() $\langle x\rangle R^* y$
iff
$\langle x\rangle R^* y$
iff
![]() $x=y$
and
$x=y$
and
![]() $\langle x, x_{1},\ldots ,x_{n}\rangle R^* y$
iff there is some z where
$\langle x, x_{1},\ldots ,x_{n}\rangle R^* y$
iff there is some z where
![]() $\langle x, x_{1},\ldots ,x_{n}\rangle R^* z$
and
$\langle x, x_{1},\ldots ,x_{n}\rangle R^* z$
and
![]() $y=x*z$
, is both compositional and functional. If, in addition, P is a monoid with identity e, then we can extend this to a list relation, setting
$y=x*z$
, is both compositional and functional. If, in addition, P is a monoid with identity e, then we can extend this to a list relation, setting
![]() $\langle \,\rangle R^* y$
iff
$\langle \,\rangle R^* y$
iff
![]() $y=e$
.
$y=e$
.
The logic that is sound and complete for list is not
![]() $\mathsf {TW}^+$
, but rather the associative Lambek calculus.Footnote
31
Much work on associative Lambek calculus uses a different language than the one we have been considering, often with the addition of another conditional,
$\mathsf {TW}^+$
, but rather the associative Lambek calculus.Footnote
31
Much work on associative Lambek calculus uses a different language than the one we have been considering, often with the addition of another conditional,
![]() $\leftarrow $
and without
$\leftarrow $
and without
![]() $\mathsf {t}$
.Footnote
32
$\mathsf {t}$
.Footnote
32
In the transition from multisets to lists, we noted that multisets take account of multiplicity but not order, whereas lists mind them both. There is still more structure to jettison. Lists are implicitly associative. For example, the list
![]() $\langle a,b,c\rangle $
is indifferent to whether it was formed by concatenating
$\langle a,b,c\rangle $
is indifferent to whether it was formed by concatenating
![]() $\langle a\rangle $
with
$\langle a\rangle $
with
![]() $\langle b,c\rangle $
or by concatenating
$\langle b,c\rangle $
or by concatenating
![]() $\langle a,b\rangle $
with
$\langle a,b\rangle $
with
![]() $\langle c\rangle $
. The final collections we will look at are ones that pay more attention to how the collections were formed, namely trees. We will focus on rooted binary-branching trees.
$\langle c\rangle $
. The final collections we will look at are ones that pay more attention to how the collections were formed, namely trees. We will focus on rooted binary-branching trees.
Leaf-labelled, rooted, binary-branching trees, or just trees, for the remainder of the section, are familiar objects. Given a set P of points,
![]() $T(P)$
is the set of all inhabited, finite trees where each node has exactly zero or two successors and each of whose leaves is labelled with an element of P. The trees will be oriented, so that they distinguish the left successor node from the right successor node. As an example, let
$T(P)$
is the set of all inhabited, finite trees where each node has exactly zero or two successors and each of whose leaves is labelled with an element of P. The trees will be oriented, so that they distinguish the left successor node from the right successor node. As an example, let
![]() $P=\{b,c\}$
, then the following three (distinct) trees are elements of
$P=\{b,c\}$
, then the following three (distinct) trees are elements of
![]() $T(P)$
.
$T(P)$
.

Rather than draw trees in a two-dimensional array, we will adopt a more compact notation, specifying the leaves of the tree by their labels. The example trees above would be represented as follows:
![]() $(b,c)$
,
$(b,c)$
,
![]() $(c,b)$
, and
$(c,b)$
, and
![]() $(c,(b,c))$
.Footnote
33
The following definition formalises this idea.
$(c,(b,c))$
.Footnote
33
The following definition formalises this idea.
Definition 46 (Trees)
Given a set of points P, the binary trees over P are defined as follows.
-
• For all
 $x\in P$
, x is a tree.
$x\in P$
, x is a tree. -
• If L and R are trees,
 $(L,R)$
is a tree.
$(L,R)$
is a tree.
To maintain the notational similarity with the other collections, we will use
![]() $(x)$
for the singleton tree of x.
$(x)$
for the singleton tree of x.
Definition 47 (Tree composition)
If X is an inhabited tree and
![]() $Y(x)$
is a tree with a distinguished leaf labelled x, then
$Y(x)$
is a tree with a distinguished leaf labelled x, then
![]() $Y(X)$
is the tree that results by replacing the leaf x with the tree X.
$Y(X)$
is the tree that results by replacing the leaf x with the tree X.
As an example of tree composition, let X be
![]() $(b,c)$
and let
$(b,c)$
and let
![]() $Y(b)$
be
$Y(b)$
be
![]() $(c,b)$
. Then
$(c,b)$
. Then
![]() $Y(X)$
is
$Y(X)$
is
![]() $(c,(b,c))$
, which is the rightmost tree in the diagram above, obtained by replacing the b node in the middle tree by the leftmost tree.
$(c,(b,c))$
, which is the rightmost tree in the diagram above, obtained by replacing the b node in the middle tree by the leftmost tree.
Definition 48 (Compositionality)
A tree relation R on
![]() $T(P)\times P$
is said to be compositional if and only if for all trees
$T(P)\times P$
is said to be compositional if and only if for all trees
![]() $X,Y\in T(P)$
and for all points
$X,Y\in T(P)$
and for all points
![]() $z$
,
$z$
,
A tree relation R is reflexive iff for all points
![]() $x$
, we have
$x$
, we have
Definition 49 (Tree frame and tree model)
If P is an inhabited set and R is a compositional tree relation on P, then
![]() $\langle P,R\rangle $
is said to be a tree frame. If
$\langle P,R\rangle $
is said to be a tree frame. If
![]() $\Vdash $
is a relation between the set P and the set of atomic formulas, which is hereditary along R (so if
$\Vdash $
is a relation between the set P and the set of atomic formulas, which is hereditary along R (so if
![]() $x\Vdash p$
and
$x\Vdash p$
and
![]() $(x) Ry$
then
$(x) Ry$
then
![]() $y\Vdash p$
too), then
$y\Vdash p$
too), then
![]() $\langle P,R,\Vdash \rangle $
is said to be a list model, where
$\langle P,R,\Vdash \rangle $
is said to be a list model, where
![]() $\Vdash $
evaluates all formulas in the language of
$\Vdash $
evaluates all formulas in the language of
![]() $\mathsf {R}^+$
as follows:Footnote
34
$\mathsf {R}^+$
as follows:Footnote
34
-
•
 $x\Vdash A\land B$
iff
$x\Vdash A\land B$
iff
 $x\Vdash A$
and
$x\Vdash A$
and
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\lor B$
iff
$x\Vdash A\lor B$
iff
 $x\Vdash A$
or
$x\Vdash A$
or
 $x\Vdash B$
.
$x\Vdash B$
. -
•
 $x\Vdash A\to B$
iff for each
$x\Vdash A\to B$
iff for each
 $y,z$
where
$y,z$
where
 $(x,y)Rz$
, if
$(x,y)Rz$
, if
 $y\Vdash A$
then
$y\Vdash A$
then
 $z\Vdash B$
.
$z\Vdash B$
. -
•
 $x\Vdash A\circ B$
iff for some
$x\Vdash A\circ B$
iff for some
 $y,z$
where
$y,z$
where
 $(y,z)Rx$
, both
$(y,z)Rx$
, both
 $y\Vdash A$
and
$y\Vdash A$
and
 $z\Vdash B$
.
$z\Vdash B$
.
Tree frames are rather easy to come by. Here are two examples.
-
[groupoid] Let
 $(G,\cdot )$
be a groupoid. To define R, we will use a mapping
$(G,\cdot )$
be a groupoid. To define R, we will use a mapping
 $\tau $
from
$\tau $
from
 $T(G)$
to G as follows:
$T(G)$
to G as follows:
 $\tau ((x))=x$
and
$\tau ((x))=x$
and
 $\tau ((X,Y))=\tau (X)\cdot \tau (Y)$
. Define R as follows:
$\tau ((X,Y))=\tau (X)\cdot \tau (Y)$
. Define R as follows:
 $(x)Rx$
, for all x, and
$(x)Rx$
, for all x, and
 $XRy$
iff
$XRy$
iff
 $\tau (X)=y$
. It is straightforward to see that R is a compositional.
$\tau (X)=y$
. It is straightforward to see that R is a compositional. -
[join semi-lattice] Let
 $(S,+)$
be a join semi-lattice. Define
$(S,+)$
be a join semi-lattice. Define
 $x\preceq y$
iff
$x\preceq y$
iff
 $x+y=y$
. Set
$x+y=y$
. Set
 $(x)Rx$
and, adapting
$(x)Rx$
and, adapting
 $\tau $
from the previous example, define
$\tau $
from the previous example, define
 $XRy$
iff
$XRy$
iff
 $\tau (X)\preceq y$
. As in the previous example, it is straightforward to show that R is compositional.
$\tau (X)\preceq y$
. As in the previous example, it is straightforward to show that R is compositional.
We will now relate the tree frames to some more standard ternary frames. For this, we will introduce some notation using square brackets, which should not be confused for multisets as in earlier sections: Here,
![]() $Y[x]$
is to be understood as the tree Y with a distinguished leaf x, while
$Y[x]$
is to be understood as the tree Y with a distinguished leaf x, while
![]() $Y[x,y]$
is Y with two distinguished leaves,
$Y[x,y]$
is Y with two distinguished leaves,
![]() $Y[(x,y)]$
is Y with a distinguished pair of adjacent leaves
$Y[(x,y)]$
is Y with a distinguished pair of adjacent leaves
![]() $(x,y)$
,
$(x,y)$
,
![]() $Y[(x,y), (u,v)]$
with two distinguished pairs of adjacent nodes, and
$Y[(x,y), (u,v)]$
with two distinguished pairs of adjacent nodes, and
![]() $Y[x, (y,z)]$
is a distinguished triple of leaves, where one is adjacent to a pair.
$Y[x, (y,z)]$
is a distinguished triple of leaves, where one is adjacent to a pair.
Lemma 50. Each ternary frame
![]() $\langle P,R,\sqsubseteq , N\rangle $
determines a reflexive tree frame
$\langle P,R,\sqsubseteq , N\rangle $
determines a reflexive tree frame
![]() $\langle P, R'\rangle $
by setting:
$\langle P, R'\rangle $
by setting:
-
•
 $(x)Ry$
iff
$(x)Ry$
iff
 $x\sqsubseteq y$
.
$x\sqsubseteq y$
. -
•
 $(x,y)R'z$
iff
$(x,y)R'z$
iff
 $Rxyz$
.
$Rxyz$
. -
• If Y is a tree with two or more leaves, then
 $Y[(x,y)]R'z$
iff for some u,
$Y[(x,y)]R'z$
iff for some u,
 $Y(u)R'z$
and
$Y(u)R'z$
and
 $(x,y)R'u$
.
$(x,y)R'u$
.
You will notice here that there is nothing in the tree frame that corresponds to the set N of normal points, since our trees are essentially inhabited.
Proof. The proof proceeds much as in the proof of Lemma 12. We need to verify that
![]() $R'$
is coherent. There is nothing to check for clause 2.
$R'$
is coherent. There is nothing to check for clause 2.
To check the final clause, we need to prove that if
![]() $Y[(x,y)]$
is the same tree as
$Y[(x,y)]$
is the same tree as
![]() $Y'[(x',y')]$
, then
$Y'[(x',y')]$
, then
If Y has one leaf, then
![]() $x=y=x'=y'$
, and the displayed biconditional is satisfied by the first and second clauses of the definition. If Y has either two or three leaves, then
$x=y=x'=y'$
, and the displayed biconditional is satisfied by the first and second clauses of the definition. If Y has either two or three leaves, then
![]() $x=x'$
and
$x=x'$
and
![]() $y=y'$
, and the displayed biconditional is satisfied.
$y=y'$
, and the displayed biconditional is satisfied.
Let
![]() $X[(x,y), (x',y')]$
be the tree Y with the two distinguished pairs of adjacent leaves
$X[(x,y), (x',y')]$
be the tree Y with the two distinguished pairs of adjacent leaves
![]() $(x,y)$
and
$(x,y)$
and
![]() $(x',y')$
. Assume X has
$(x',y')$
. Assume X has
![]() $n>3$
leaves. Suppose
$n>3$
leaves. Suppose
![]() $(\exists z)(X[z, (x',y')]R' u\land (x,y)R'z)$
. The tree
$(\exists z)(X[z, (x',y')]R' u\land (x,y)R'z)$
. The tree
![]() $X[z,(x',y')]$
has
$X[z,(x',y')]$
has
![]() $n-1$
leaves, so by the inductive hypothesis, this is equivalent to
$n-1$
leaves, so by the inductive hypothesis, this is equivalent to
![]() $(\exists z)(\exists z')(X[z, z']R' u\land (x,y)R'z\land (x',y')R'z')$
. This, in turn, is equivalent to
$(\exists z)(\exists z')(X[z, z']R' u\land (x,y)R'z\land (x',y')R'z')$
. This, in turn, is equivalent to
![]() $(\exists z')(X[(x,y),z']R' u\land (x',y')R'z')$
by the inductive hypothesis, which establishes the desired biconditional.
$(\exists z')(X[(x,y),z']R' u\land (x',y')R'z')$
by the inductive hypothesis, which establishes the desired biconditional.
The reflexivity condition on
![]() $R'$
is satisfied by the reflexivity of
$R'$
is satisfied by the reflexivity of
![]() $\sqsubseteq $
and an argument similar to that of Lemma 12 establishes the compositionality conditions.
$\sqsubseteq $
and an argument similar to that of Lemma 12 establishes the compositionality conditions.
So, every ternary frame generates a tree frame. A straightforward inductive argument shows that the extensional structural rules are all sound for tree frames, as are the operational rules, excluding the rules for
![]() $\mathsf {t}$
and for
$\mathsf {t}$
and for
![]() $\epsilon $
. This suffices for the adequacy of the logic
$\epsilon $
. This suffices for the adequacy of the logic
![]() $\mathsf {B}^+_{-\epsilon }$
, given by the connective rules and the extensional structural rules, but without the intensional structural rules and IC, IB, and without
$\mathsf {B}^+_{-\epsilon }$
, given by the connective rules and the extensional structural rules, but without the intensional structural rules and IC, IB, and without
![]() $\epsilon \textit {I}$
or
$\epsilon \textit {I}$
or
![]() $\epsilon \textit {E}$
, with respect to tree frames.
$\epsilon \textit {E}$
, with respect to tree frames.
Theorem 51. The logic
![]() $\mathsf {B}^+_{-\epsilon }$
is sound and complete with respect to tree frames.
$\mathsf {B}^+_{-\epsilon }$
is sound and complete with respect to tree frames.
To model the basic substructural logic
![]() $\mathsf {B}^+$
, we need to add
$\mathsf {B}^+$
, we need to add
![]() $\epsilon \textit {I}$
and
$\epsilon \textit {I}$
and
![]() $\epsilon \textit {E}$
to our repertoire of rules, and to do this in a natural way corresponding to our treatments of lists, multisets and sets, we would need to allow an empty tree,
$\epsilon \textit {E}$
to our repertoire of rules, and to do this in a natural way corresponding to our treatments of lists, multisets and sets, we would need to allow an empty tree,
![]() $(\;)$
, such that the tree
$(\;)$
, such that the tree
![]() $((\;),R)$
is identical to the tree R. We leave exploration of this, and further developments in collection frames, to future work.
$((\;),R)$
is identical to the tree R. We leave exploration of this, and further developments in collection frames, to future work.
Acknowledgements
We would like to thank Bogdan Dicher, Lloyd Humberstone, Tomasz Kowalski, Ed Mares, Graham Priest, Dave Ripley, Kai Tanter and members of the Melbourne Logic Group, and an audience at the LanCog workshop on Substructural Logics in Lisbon, for feedback on earlier versions of this paper. We would especially like to thank two anonymous reviewers of this journal for questions and comments that have greatly improved the presentation of this paper. This research was supported by the Australian Research Council, Discovery Grant dp150103801.