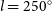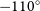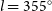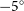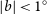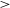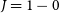1. Introduction
Carbon monoxide (CO) is the second most abundant molecule in the Galaxy and a commonly observed tracer of molecular gas in the Milky Way and beyond. A low electric dipole moment (0.122 D) means that CO readily emits the rotational
![]() $J=1$
-0 transition within cold molecular gas, as discovered by Wilson, Jefferts, & Penzias (Reference Wilson, Jefferts and Penzias1970). CO is thus a good tracer of the most common molecule in the Galaxy, H
$J=1$
-0 transition within cold molecular gas, as discovered by Wilson, Jefferts, & Penzias (Reference Wilson, Jefferts and Penzias1970). CO is thus a good tracer of the most common molecule in the Galaxy, H
![]() $_2$
, which itself is not easily excited to emit within quiescent environments common to interstellar molecular clouds.
$_2$
, which itself is not easily excited to emit within quiescent environments common to interstellar molecular clouds.
The CO
![]() $(J=1$
-0) transition has been extensively mapped in order to investigate the structure and nature of the Milky Way, and with this paper we contribute to the highest-resolution, large-scale CO(1-0), 3-dimensional survey of the Southern Galactic Plane yet to the astronomical community – The Mopra Southern Galactic Plane CO SurveyFootnote a (Burton et al. Reference Burton2013) Data Release 0 (DR0).
$(J=1$
-0) transition has been extensively mapped in order to investigate the structure and nature of the Milky Way, and with this paper we contribute to the highest-resolution, large-scale CO(1-0), 3-dimensional survey of the Southern Galactic Plane yet to the astronomical community – The Mopra Southern Galactic Plane CO SurveyFootnote a (Burton et al. Reference Burton2013) Data Release 0 (DR0).
The primary targets in the Mopra CO survey were
![]() $^{12}$
CO(1-0),
$^{12}$
CO(1-0),
![]() $^{13}$
CO(1-0), C
$^{13}$
CO(1-0), C
![]() $^{18}$
O(1-0), and C
$^{18}$
O(1-0), and C
![]() $^{17}$
O(1-0).Footnote b With a view of these four most common CO isotopologues, a comprehensive range of optical depths become available for studies of molecular gas.
$^{17}$
O(1-0).Footnote b With a view of these four most common CO isotopologues, a comprehensive range of optical depths become available for studies of molecular gas.
Previously, the largest release of data from our team was DR3 (Braiding et al. Reference Braiding2018), which covered 50 deg
![]() $^{2}$
of the Southern Galactic Plane (
$^{2}$
of the Southern Galactic Plane (
![]() $l=$
300–350
$l=$
300–350
![]() $^{\circ}$
,
$^{\circ}$
,
![]() $|b|$
< 0.5
$|b|$
< 0.5
![]() $^{\circ}$
) and traced
$^{\circ}$
) and traced
![]() $\sim$
2–9
$\sim$
2–9
![]() $\times$
10
$\times$
10
![]() $^8$
M
$^8$
M
![]() $_{\odot}$
of molecular mass within the solar circle. Prior to this release, we presented and examined l = 320–330
$_{\odot}$
of molecular mass within the solar circle. Prior to this release, we presented and examined l = 320–330
![]() $^{\circ}$
(Braiding et al. Reference Braiding2018) DR1, the Carina/Gum 31 region (Rebolledo et al. Reference Rebolledo2016); DR2 and the Central Molecular Zone (Blackwell, Burton, & Rowell Reference Blackwell, Burton and Rowell2016), which all followed the successful pilot study of the Mopra CO fast-mapping technique in DR0 (Burton et al. Reference Burton2013). The observational strategy took advantage of the strong Galactic Plane CO(1-0) flux, such that we reduced the integration time of each sky position to make large-scale mapping campaigns feasible, while maintaining the fine beam of Mopra (FWHM
$^{\circ}$
(Braiding et al. Reference Braiding2018) DR1, the Carina/Gum 31 region (Rebolledo et al. Reference Rebolledo2016); DR2 and the Central Molecular Zone (Blackwell, Burton, & Rowell Reference Blackwell, Burton and Rowell2016), which all followed the successful pilot study of the Mopra CO fast-mapping technique in DR0 (Burton et al. Reference Burton2013). The observational strategy took advantage of the strong Galactic Plane CO(1-0) flux, such that we reduced the integration time of each sky position to make large-scale mapping campaigns feasible, while maintaining the fine beam of Mopra (FWHM
![]() $\sim$
36
$\sim$
36
![]() $^{\prime\prime}$
).Footnote c
$^{\prime\prime}$
).Footnote c
This Mopra CO data release will be well-complemented by the FOREST Unbiased Galactic Plane Imaging (FUGIN) CO survey (Minamidani et al. Reference Minamidani2016), and The Milky Way Imaging Scroll Painting (MWISP) CO survey (Su et al. Reference Su2019). Together, the FUGIN, Mopra, and MWISP CO surveys will have full 360
![]() $^{\circ}$
longitude coverage of the inner Southern and Northern Galactic Plane (
$^{\circ}$
longitude coverage of the inner Southern and Northern Galactic Plane (
![]() $|b|$
< 1
$|b|$
< 1
![]() $^{\circ}$
), and the 20
$^{\circ}$
), and the 20
![]() $^{\prime\prime}$
, 36
$^{\prime\prime}$
, 36
![]() $^{\prime\prime}$
, and 50
$^{\prime\prime}$
, and 50
![]() $^{\prime\prime}$
angular resolutions, respectively, will improve on the 8
$^{\prime\prime}$
angular resolutions, respectively, will improve on the 8
![]() $^{\prime}$
angular resolution of the well-known Columbia CO survey (Dame, Hartmann, & Thaddeus Reference Dame, Hartmann and Thaddeus2001) that helped to characterise the structure of the Milky Way (e.g., Vallée 2014).
$^{\prime}$
angular resolution of the well-known Columbia CO survey (Dame, Hartmann, & Thaddeus Reference Dame, Hartmann and Thaddeus2001) that helped to characterise the structure of the Milky Way (e.g., Vallée 2014).
In calculating H
![]() $_2$
column densities or masses, it is common to assume a CO abundance relative to molecular hydrogen, usually
$_2$
column densities or masses, it is common to assume a CO abundance relative to molecular hydrogen, usually
![]() $\sim$
10
$\sim$
10
![]() $^{-4}$
. This value, however, is observed to fluctuate with varying interstellar medium chemistry and dust grain evolution (see, e.g., Bolatto, Wolfire, & Leroy Reference Bolatto, Wolfire and Leroy2013). Comparisons of three independent tracers of mass: infrared opacity, diffuse gamma-ray emission from p-p interactions and CO(1-0) + HI have pointed towards inconsistencies that may be explained by a ‘dark’ component of gas (e.g. Ade et al. Reference Ade2015). ‘Dark’ gas may simply be a transition phase of gas where carbon is in atomic/ionic form, while hydrogen is molecular. This would perhaps be due to the stronger self-shielding effects of H
$^{-4}$
. This value, however, is observed to fluctuate with varying interstellar medium chemistry and dust grain evolution (see, e.g., Bolatto, Wolfire, & Leroy Reference Bolatto, Wolfire and Leroy2013). Comparisons of three independent tracers of mass: infrared opacity, diffuse gamma-ray emission from p-p interactions and CO(1-0) + HI have pointed towards inconsistencies that may be explained by a ‘dark’ component of gas (e.g. Ade et al. Reference Ade2015). ‘Dark’ gas may simply be a transition phase of gas where carbon is in atomic/ionic form, while hydrogen is molecular. This would perhaps be due to the stronger self-shielding effects of H
![]() $_2$
, guarding against ionising radiation that dissociates a large proportion of CO molecules, particularly in low molecular density regions (e.g., Wolfire, Hollenbach, & Mc-Kee 2010). In such transition regions, atomic or ionic transitions of carbon are expected to trace molecular H
$_2$
, guarding against ionising radiation that dissociates a large proportion of CO molecules, particularly in low molecular density regions (e.g., Wolfire, Hollenbach, & Mc-Kee 2010). In such transition regions, atomic or ionic transitions of carbon are expected to trace molecular H
![]() $_2$
mass, so complementing CO(1-0) and HI observations.
$_2$
mass, so complementing CO(1-0) and HI observations.
A large component of mysterious ‘dark’ gas has alternatively been suggested to be in atomic form (Fukui et al. 2014a,b). Observations of some off-plane molecular clouds show that cold (<20 K) atomic clumps may contain a significant component of mass unobservable in HI emission, yet indirectly observable by infrared opacity or by hints of absorption in HI spectra (Fukui et al. 2014a,b). If present, the proposed low volume-filling factor (
![]() $\sim$
4%) of this high-mass component would make studies using observations of background sources difficult.
$\sim$
4%) of this high-mass component would make studies using observations of background sources difficult.
Some previous studies (Remy et al. Reference Remy, Grenier, Marshall and Casandjian2017, Reference Remy, Grenier, Marshall and Casandjian2018a,Reference Remy, Grenier, Marshall and Casandjianb) similarly find inconsistencies between infrared-derived and CO+HI-derived column densities. A comparison of these with gamma-ray data lead the authors to support a notion that dust grain opacity increases towards high column density regions (both atomic and molecular), sometimes leading to overestimations in calculations of X-factor. The authors note that where grain opacity may increase 4
![]() $-$
6 fold (consistent with grain evolution modelling, e.g., Jones & Braiding Reference Jones and Braiding2015; Köhler, Ysard, & Jones Reference Köhler, Ysard and Jones2015), both the flux of gamma-ray emission from p-p interactions, and the reddening of optical light from dust grains, seems to remain proportional to mass (Remy et al. Reference Remy, Grenier, Marshall and Casandjian2017) at the scale of Columbia CO data (8
$-$
6 fold (consistent with grain evolution modelling, e.g., Jones & Braiding Reference Jones and Braiding2015; Köhler, Ysard, & Jones Reference Köhler, Ysard and Jones2015), both the flux of gamma-ray emission from p-p interactions, and the reddening of optical light from dust grains, seems to remain proportional to mass (Remy et al. Reference Remy, Grenier, Marshall and Casandjian2017) at the scale of Columbia CO data (8
![]() $^{\prime}$
). This former observation suggests that GeV cosmic rays (CRs) uniformly penetrate dense gas at this scale, however it is possible that at smaller scales, energy-dependent diffusion into gas plays a significant role (e.g., Gabici, Aharonian, & Blasi Reference Gabici, Aharonian and Blasi2007; Gabici, Aharonian, & Casanova Reference Gabici, Aharonian and Casanova2009), particularly in the presence of strong turbulence (Zirakashvili & Aharonian Reference Zirakashvili and Aharonian2009; Inoue et al. Reference Inoue, Yamazaki, Inutsuka and Fukui2011; Maxted et al. Reference Maxted2012; Fukui et al. Reference Fukui2012).
$^{\prime}$
). This former observation suggests that GeV cosmic rays (CRs) uniformly penetrate dense gas at this scale, however it is possible that at smaller scales, energy-dependent diffusion into gas plays a significant role (e.g., Gabici, Aharonian, & Blasi Reference Gabici, Aharonian and Blasi2007; Gabici, Aharonian, & Casanova Reference Gabici, Aharonian and Casanova2009), particularly in the presence of strong turbulence (Zirakashvili & Aharonian Reference Zirakashvili and Aharonian2009; Inoue et al. Reference Inoue, Yamazaki, Inutsuka and Fukui2011; Maxted et al. Reference Maxted2012; Fukui et al. Reference Fukui2012).
The sub-arcminute resolution of the Mopra CO data will be able to examine CR diffusion into dense gas in fine detail to test models that predict energy-dependent CR exclusion in high column density regions, complementing gamma-ray instruments such as Fermi-LAT (Atwood et al. Reference Atwood2009) and the Cherenkov Telescope Array (e.g. Consortium et al. 2017) Mopra CO data will provide smaller-scale investigations of CO X-factor in comparison to both infrared opacity with instruments such as Planck (Ade et al. Reference Ade2015) and diffuse gamma-ray emission. Furthermore, a comparison of Mopra CO data with carbon line observations (e.g., HEAT, Walker et al. Reference Walker2004) and comparable resolution HI data (e.g., from GASKAP, see Dickey et al. Reference Dickey2013) will provide a better understanding of how carbon chemistry varies throughout the ISM (e.g., Burton et al. Reference Burton2014, Reference Burton2015), towards a goal of understanding what constitutes ‘dark’ gas.
2. Observations and data processing
2.1. Observations
The observations were carried out using Mopra, a 22 m single-dish radio telescope located
![]() $\sim$
450 km north-west of Sydney, Australia (at 31
$\sim$
450 km north-west of Sydney, Australia (at 31
![]() $^{\circ}$
16
$^{\circ}$
16
![]() $^{\prime}$
04
$^{\prime}$
04
![]() $^{\prime\prime}$
S, 149
$^{\prime\prime}$
S, 149
![]() $^{\circ}$
05
$^{\circ}$
05
![]() $^{\prime}$
59
$^{\prime}$
59
![]() $^{\prime\prime}$
E, 866 m a.s.l.), over the Southern Hemisphere winters of 2011–2018.
$^{\prime\prime}$
E, 866 m a.s.l.), over the Southern Hemisphere winters of 2011–2018.
We targeted four isotopologue
![]() $J=1$
–0 transition spectral lines:
$J=1$
–0 transition spectral lines:
![]() $^{12}$
CO,
$^{12}$
CO,
![]() $^{13}$
CO, C
$^{13}$
CO, C
![]() $^{18}$
O, and C
$^{18}$
O, and C
![]() $^{17}$
O (with central frequencies of 115 271.202, 110 201.354, 109 782.176, and 112 358.988 MHzFootnote d, respectively). Using the UNSW Digital Filter Bank (the UNSW-MOPS) in its ‘zoom’ mode, we divided the spectral range of the 8
$^{17}$
O (with central frequencies of 115 271.202, 110 201.354, 109 782.176, and 112 358.988 MHzFootnote d, respectively). Using the UNSW Digital Filter Bank (the UNSW-MOPS) in its ‘zoom’ mode, we divided the spectral range of the 8
![]() $\times$
137.5 MHz dual-polarisation bands unequally amongst the 4 isotopologue transitions, favouring the most abundant species – 3 bands allocated to
$\times$
137.5 MHz dual-polarisation bands unequally amongst the 4 isotopologue transitions, favouring the most abundant species – 3 bands allocated to
![]() $^{12}$
CO, 2 bands each to
$^{12}$
CO, 2 bands each to
![]() $^{13}$
CO and C
$^{13}$
CO and C
![]() $^{18}$
O, and 1 band to C
$^{18}$
O, and 1 band to C
![]() $^{17}$
O. The resultant spectral coverage in velocity space was
$^{17}$
O. The resultant spectral coverage in velocity space was
![]() $\sim$
1 100,
$\sim$
1 100,
![]() $\sim$
770, and
$\sim$
770, and
![]() $\sim$
380 km s
$\sim$
380 km s
![]() $^{-1}$
, respectively. The targeted central frequencies were offset according to Galactic Longitude to maximise overlap with expected Galactic rotation velocities.
$^{-1}$
, respectively. The targeted central frequencies were offset according to Galactic Longitude to maximise overlap with expected Galactic rotation velocities.
This fourth data release is comprised of both unpublished and previously released data (Burton et al. Reference Burton2013; Braiding et al. Reference Braiding2015; Rebolledo et al. Reference Rebolledo2016; Braiding et al. Reference Braiding2018), in addition to small-scale CO studies around sources of interest with preliminary Mopra CO survey data (Burton et al. Reference Burton2014, Reference Burton2015; Lau et al. Reference Lau2016, Reference Lau2017; Maxted et al. Reference Maxted2017, Reference Maxted2018; Feijen et al. Reference Feijen, Rowell, Einecke, Braiding, Burton, Maxted, Voisin and Wong2020). As described in DR0 (Burton et al. Reference Burton2013), Fast-On-The-Fly mapping has been carried out in 1 square degree segments, with each segment being comprised of orthogonal scans (in longitudinal and latitudinal directions) to reduce scanning artefacts. The exposure of each square degree is at least
![]() $\sim$
20 h, more in places where poor weather or technical issues interrupt observations and triggered a repeat of the affected scans. Accounting for both instrumental resolution and image processing, the final angular resolution of Mopra 3 mm (115 GHz) data is
$\sim$
20 h, more in places where poor weather or technical issues interrupt observations and triggered a repeat of the affected scans. Accounting for both instrumental resolution and image processing, the final angular resolution of Mopra 3 mm (115 GHz) data is
![]() $\sim$
36
$\sim$
36
![]() $\pm$
3
$\pm$
3
![]() $^{\prime\prime}$
. The pointing accuracy was regularly corrected to be
$^{\prime\prime}$
. The pointing accuracy was regularly corrected to be
![]() $\sim$
6
$\sim$
6
![]() $^{\prime\prime}$
via recalibration using a standard 3mm SiO maser source between
$^{\prime\prime}$
via recalibration using a standard 3mm SiO maser source between
![]() $\sim$
1 h-length maps. The extended beam efficiency of Mopra CO data is expected to be
$\sim$
1 h-length maps. The extended beam efficiency of Mopra CO data is expected to be
![]() $\sim$
0.55
$\sim$
0.55
![]() $\times$
the true flux from source (Ladd et al. Reference Ladd, Purcell, Wong and Robertson2005).
$\times$
the true flux from source (Ladd et al. Reference Ladd, Purcell, Wong and Robertson2005).

Figure 1. The coverage of the Mopra Southern Galactic Plane CO Survey and the Central Molecular Zone CO Survey. Each rectangular cell corresponds to 1
![]() $^\circ$
in Galactic Longitude and 0.5
$^\circ$
in Galactic Longitude and 0.5
![]() $^\circ$
in Galactic Latitude. The region shown in cyan is the published data in the previous data releases. The blue region shows the data we release with this study (DR4). The yellow and orange region are part of the Central Molecular Zone CO Survey.
$^\circ$
in Galactic Latitude. The region shown in cyan is the published data in the previous data releases. The blue region shows the data we release with this study (DR4). The yellow and orange region are part of the Central Molecular Zone CO Survey.
2.2. Data processing
The dataset has been processed in the same way as that described in the DR3 (Braiding et al. Reference Braiding2018). This includes all the steps in the pipeline, custom IDL routines, Livedata, and Gridzilla.Footnote e
The reduced data products will be made publicly available.Footnote f This will include the data cubes (
![]() $l \times b \times v$
) for each degree in longitude (
$l \times b \times v$
) for each degree in longitude (
![]() $l \times b = 1^{\circ} \times 2^{\circ}$
at 0.1 km s
$l \times b = 1^{\circ} \times 2^{\circ}$
at 0.1 km s
![]() $^{-1}$
resolution and stepped by
$^{-1}$
resolution and stepped by
![]() $0.5^{\circ}$
in l; also for every 10 degrees in longitude (
$0.5^{\circ}$
in l; also for every 10 degrees in longitude (
![]() $l \times b = 10^{\circ} \times 2^{\circ}$
at both full (0.1 km s
$l \times b = 10^{\circ} \times 2^{\circ}$
at both full (0.1 km s
![]() $^{-1}$
) and binned (1 km s
$^{-1}$
) and binned (1 km s
![]() $^{-1}$
) spectral resolution; moment (integrated intensity) maps for each 10 km s
$^{-1}$
) spectral resolution; moment (integrated intensity) maps for each 10 km s
![]() $^{-1}$
in bandwidth, and averaged line profiles for each degree in longitude. The longitude-velocity plots are also provided. In addition, the corresponding system temperature (
$^{-1}$
in bandwidth, and averaged line profiles for each degree in longitude. The longitude-velocity plots are also provided. In addition, the corresponding system temperature (
![]() $T_{sys}$
) and noise (
$T_{sys}$
) and noise (
![]() $1 \sigma$
) maps are also provided. The data covers from
$1 \sigma$
) maps are also provided. The data covers from
![]() $l=250^{\circ}$
to
$l=250^{\circ}$
to
![]() $l=355^{\circ}$
with
$l=355^{\circ}$
with
![]() $b=\pm 1^{\circ}$
.
$b=\pm 1^{\circ}$
.
In 2018 May, we identified a new problem that sometimes resulted in the reference positions being offset by 0.5
![]() $^{\circ}$
in Galactic Latitude. Although the problem was remedied at software level such that no subsequent observations used an erroneous ‘offset’ reference position, maps that were taken prior to 2018 May sometimes used a sub-optimal OFF position for the subtraction sky emission. As described in the DR1 (Braiding et al. Reference Braiding2015), contamination of maps by reference position CO emission was routinely corrected for by modelling the contaminant spectrum and adding the component back into the final map. The ‘offset’ reference position problem simply involved applying this method more extensively.
$^{\circ}$
in Galactic Latitude. Although the problem was remedied at software level such that no subsequent observations used an erroneous ‘offset’ reference position, maps that were taken prior to 2018 May sometimes used a sub-optimal OFF position for the subtraction sky emission. As described in the DR1 (Braiding et al. Reference Braiding2015), contamination of maps by reference position CO emission was routinely corrected for by modelling the contaminant spectrum and adding the component back into the final map. The ‘offset’ reference position problem simply involved applying this method more extensively.
In 2020 September, we identified a further problem with 76 data cubes, approximately a quarter of the whole dataset, that was caused by the baselining step in the pipeline. The problem was overlooked because the bad baselining was not visible in full resolution profiles. During the data analysis, we noticed some drops in one of the binned cubes’ profile that were binned by a factor of ten. The systematic error was only appearing in the binned, higher S/N, data cubes. Further analysis of this problem revealed that the issue was caused by incorrectly set continuum limits. Weak features were not visible to the eye in full resolution data cubes, thus it led our team to consider some velocity channels as continuum although they had emission in them. All 76 cubes were re-baselined by checking their continuum ranges from binned cubes. Some of these data cubes were published in DR3.
3. Results
We present here the average line profiles, moment maps, position–velocity (PV) images and the mass calculation results of Data Release 4 (DR4). We have extended the survey coverage from 300
![]() $^{\circ}$
–350
$^{\circ}$
–350
![]() $^\circ$
in Galactic longitude and from
$^\circ$
in Galactic longitude and from
![]() $\pm$
0.5
$\pm$
0.5
![]() $^\circ$
in Galactic latitude to 250–355
$^\circ$
in Galactic latitude to 250–355
![]() $^\circ$
in Galactic longitude (l = 250
$^\circ$
in Galactic longitude (l = 250
![]() $^{\circ}$
–355
$^{\circ}$
–355
![]() $^{\circ}$
) and
$^{\circ}$
) and
![]() $\pm$
1.0
$\pm$
1.0
![]() $^\circ$
in Galactic latitude (
$^\circ$
in Galactic latitude (
![]() $|b|$
< 1
$|b|$
< 1
![]() $^{\circ}$
). The final data release of the Mopra Southern Galactic Plane CO Survey covers more than 210 deg
$^{\circ}$
). The final data release of the Mopra Southern Galactic Plane CO Survey covers more than 210 deg
![]() $^2$
. Furthermore, the region from l = 355
$^2$
. Furthermore, the region from l = 355
![]() $^{\circ}$
to l = +11
$^{\circ}$
to l = +11
![]() $^{\circ}$
has been observed, and the data will be published in a future work as part of the extended Central Molecular Zone Survey (Blackwell et al. in preparation). Fig. 1 shows both surveys’ coverage and the status of the various datasets in different colours.
$^{\circ}$
has been observed, and the data will be published in a future work as part of the extended Central Molecular Zone Survey (Blackwell et al. in preparation). Fig. 1 shows both surveys’ coverage and the status of the various datasets in different colours.
3.1. Spectra
The average line profiles for both
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO cubes are presented in the Appendix (from Figs. 12 to 32). All cubes cover
$^{13}$
CO cubes are presented in the Appendix (from Figs. 12 to 32). All cubes cover
![]() $1\times 2$
degrees area (
$1\times 2$
degrees area (
![]() $l\times b$
,
$l\times b$
,
![]() $|b|<1^\circ$
), and the cubes are centred at each longitude degree. An illustrative example of this is the line profile of G300, Fig. 22a. This covers an area between
$|b|<1^\circ$
), and the cubes are centred at each longitude degree. An illustrative example of this is the line profile of G300, Fig. 22a. This covers an area between
![]() $\pm$
1
$\pm$
1
![]() $^\circ$
in latitude and from longitude 300
$^\circ$
in latitude and from longitude 300
![]() $^\circ$
to longitude 301
$^\circ$
to longitude 301
![]() $^\circ$
, centred at 300.5
$^\circ$
, centred at 300.5
![]() $^\circ$
.
$^\circ$
.
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO data from the Mopra CO Survey was compared to
$^{13}$
CO data from the Mopra CO Survey was compared to
![]() $^{12}$
CO data from the Columbia CO Survey (Dame et al. Reference Dame, Hartmann and Thaddeus2001). As was previously discussed in the DR0 (Burton et al. Reference Burton2013) and DR3 (Braiding et al. Reference Braiding2018) papers, we found a factor of 1.35 systematic difference in the flux scale between the Mopra and Columbia surveys. However, after extending our Mopra survey coverage in DR4, we have found that the difference in flux scale now varies for different parts of the survey, arising from variable sampling in the Columbia survey. We discuss this in more detail in the Discussion section.
$^{12}$
CO data from the Columbia CO Survey (Dame et al. Reference Dame, Hartmann and Thaddeus2001). As was previously discussed in the DR0 (Burton et al. Reference Burton2013) and DR3 (Braiding et al. Reference Braiding2018) papers, we found a factor of 1.35 systematic difference in the flux scale between the Mopra and Columbia surveys. However, after extending our Mopra survey coverage in DR4, we have found that the difference in flux scale now varies for different parts of the survey, arising from variable sampling in the Columbia survey. We discuss this in more detail in the Discussion section.
The peaks of the spectra of the cubes usually correspond to the spiral arms. The velocity of the peak positions change as we move through Galactic longitude. Thus the position and the velocity change of the spiral arms can be inspected using spectra of the cubes. The expected line of sight velocity for the emission from any position within the survey region under the assumption of Galactic rotation can be seen in Fig. 2, overlaid with the position of the spiral arms from the model of Vallée (Reference Vallée2016).

Figure 2. A schematic of the Galactic rotation curve to illustrate how the CO profiles are used to determine location of molecular clouds. The colour-scale displays the expected kinematic line-of-sight velocity (km s
![]() $^{-1}$
) from the reference point of the Sun for the entire coverage of the Mopra CO Survey. Four spiral arms, the Galactic Centre, and the location of the Sun are also overlaid. The spiral arms are modelled as having a pitch angle of 13.1
$^{-1}$
) from the reference point of the Sun for the entire coverage of the Mopra CO Survey. Four spiral arms, the Galactic Centre, and the location of the Sun are also overlaid. The spiral arms are modelled as having a pitch angle of 13.1
![]() $^\circ$
, a central bar length of 2.2 kpc inclined at
$^\circ$
, a central bar length of 2.2 kpc inclined at
![]() $-30^\circ$
to our sightline, a Galactic Centre distance of 8.0 kpc and a flat rotation curve with velocity 220 km s
$-30^\circ$
to our sightline, a Galactic Centre distance of 8.0 kpc and a flat rotation curve with velocity 220 km s
![]() $^{-1}$
(Vallée Reference Vallée2016).
$^{-1}$
(Vallée Reference Vallée2016).
Some line profiles show broad emission (FWHM
![]() $> 20$
km s
$> 20$
km s
![]() $^{-1}$
). This is usually caused by multiple spiral arms along the line of sight. A notable example of this is G310’s spectrum (Figure Appendix 24a). One of the two prominent peaks is from the Sagittarius Arm
$^{-1}$
). This is usually caused by multiple spiral arms along the line of sight. A notable example of this is G310’s spectrum (Figure Appendix 24a). One of the two prominent peaks is from the Sagittarius Arm
![]() $(v = -40$
km s
$(v = -40$
km s
![]() $^{-1}$
) whereas the higher peak emission comes from the Scutum-Crux Arm (
$^{-1}$
) whereas the higher peak emission comes from the Scutum-Crux Arm (
![]() $v = -53$
km s
$v = -53$
km s
![]() $^{-1}$
). G330 is another useful example as its spectrum shows three prominent peaks caused by the Sagittarius Arm, Scutum Arm, and Norma Arm with peak velocities at
$^{-1}$
). G330 is another useful example as its spectrum shows three prominent peaks caused by the Sagittarius Arm, Scutum Arm, and Norma Arm with peak velocities at
![]() $-45$
,
$-45$
,
![]() $-64$
, and
$-64$
, and
![]() $-97$
km s
$-97$
km s
![]() $^{-1}$
respectively (Figure Appendix 28a).
$^{-1}$
respectively (Figure Appendix 28a).
3.2. Intensity maps
Integrated intensity (Moment 0) maps from DR4 are presented in the Appendix (from Figs. 33 to 184), calculated over an interval of 10 km s
![]() $^{-1}$
in the velocity range of
$^{-1}$
in the velocity range of
![]() $-$
200 to 100 km s
$-$
200 to 100 km s
![]() $^{-1}$
. All moment maps cover 10 degrees in longitude and 2 degrees in latitude. Each figure shows the
$^{-1}$
. All moment maps cover 10 degrees in longitude and 2 degrees in latitude. Each figure shows the
![]() $^{12}$
CO moment map in the top panel and the
$^{12}$
CO moment map in the top panel and the
![]() $^{13}$
CO moment map in the bottom panel.
$^{13}$
CO moment map in the bottom panel.
In order to obtain each 10 km s
![]() $^{-1}$
moment map, a hundred channels have been integrated since the original spectral resolution is 0.1 km s
$^{-1}$
moment map, a hundred channels have been integrated since the original spectral resolution is 0.1 km s
![]() $^{-1}$
. Thanks to our survey’s improved spatial and spectral resolution for the covered region, the distribution and the shape of the molecular clouds are easily seen.
$^{-1}$
. Thanks to our survey’s improved spatial and spectral resolution for the covered region, the distribution and the shape of the molecular clouds are easily seen.
However, if the flux of the features in a region is weak, and over a limited velocity range then the S/N is not improved when summing over this range. This can lead to a noisy moment map. We have not included these noisy moment maps in the appendix. In addition to this, during the observations, artificial features/emissions may occasionally occur due to various problems: weather changes, hardware or software issues, etc. If this is the case, those artificial features are generally enhanced in the moment images as they affect all channels. However, they are generally readily identified due to their appearance. The vertical line in Figure Appendix 105 around G327 is a typical example of such behaviour.
Previously, in the DR3 paper, moment maps were published for the region between Galactic longitude 300
![]() $^{\circ}$
and 350
$^{\circ}$
and 350
![]() $^{\circ}$
, and Galactic latitude
$^{\circ}$
, and Galactic latitude
![]() $\pm$
0.5
$\pm$
0.5
![]() $^\circ$
. Now, we have extended this area from longitude 250
$^\circ$
. Now, we have extended this area from longitude 250
![]() $^{\circ}$
to 355
$^{\circ}$
to 355
![]() $^{\circ}$
, and latitude
$^{\circ}$
, and latitude
![]() $\pm$
1.0
$\pm$
1.0
![]() $^\circ$
. Another difference is the threshold levels chosen for the moment maps. These were 5 sigma in the DR3 paper. Thus, few artificial features were seen in them. On the other hand, many real features were masked out due to the high-sigma level selection. We have now selected 3 sigma for the threshold value in the DR4.Footnote g In this way, the maps show extended and more detailed cloud structures. For instance, many examples of bubble and arc-like structures are seen throughout the survey. Figure Appendix 112 shows both bubble and arc-like features (e.g., l = 328.7
$^\circ$
. Another difference is the threshold levels chosen for the moment maps. These were 5 sigma in the DR3 paper. Thus, few artificial features were seen in them. On the other hand, many real features were masked out due to the high-sigma level selection. We have now selected 3 sigma for the threshold value in the DR4.Footnote g In this way, the maps show extended and more detailed cloud structures. For instance, many examples of bubble and arc-like structures are seen throughout the survey. Figure Appendix 112 shows both bubble and arc-like features (e.g., l = 328.7
![]() $^\circ$
, b = -0.5
$^\circ$
, b = -0.5
![]() $^\circ$
and l = 326.8
$^\circ$
and l = 326.8
![]() $^\circ$
, b = 0.1
$^\circ$
, b = 0.1
![]() $^\circ$
).
$^\circ$
).
We also present
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO peak intensity maps to highlight the most prominent molecular cloud structures (Figs. 3 and 4). The five panels in each figure cover the entire survey range (with each panel spanning a
$^{13}$
CO peak intensity maps to highlight the most prominent molecular cloud structures (Figs. 3 and 4). The five panels in each figure cover the entire survey range (with each panel spanning a
![]() $21^{\circ}$
in longitude). The display range begins at 0 in order to display diffuse, extended emission, however we note that this means that some scanning artefacts appear in the images. In particular, these occur in regions with weak or no intrinsic line emission, when they arise from sky variations during the observations. The images illustrate the wide spread extent of the CO emission along the Galactic plane, with the brightest cloud complexes prominent within them. Interestingly, more compact bright features are apparent in the
$21^{\circ}$
in longitude). The display range begins at 0 in order to display diffuse, extended emission, however we note that this means that some scanning artefacts appear in the images. In particular, these occur in regions with weak or no intrinsic line emission, when they arise from sky variations during the observations. The images illustrate the wide spread extent of the CO emission along the Galactic plane, with the brightest cloud complexes prominent within them. Interestingly, more compact bright features are apparent in the
![]() $^{13}$
CO maps. This is because this line is less optically thick than
$^{13}$
CO maps. This is because this line is less optically thick than
![]() $^{12}$
CO, hence it better picks out the peaks, which can be saturated in
$^{12}$
CO, hence it better picks out the peaks, which can be saturated in
![]() $^{12}$
CO.
$^{12}$
CO.

Figure 3.
![]() $^{12}$
CO peak intensity map per voxel showing the entire survey coverage. The display range is from 0 to 20 K T
$^{12}$
CO peak intensity map per voxel showing the entire survey coverage. The display range is from 0 to 20 K T
![]() $_{\rm MB}$
.
$_{\rm MB}$
.

Figure 4.
![]() $^{13}$
CO peak intensity map per voxel showing the entire survey coverage. The display range is from 0 to 5 K T
$^{13}$
CO peak intensity map per voxel showing the entire survey coverage. The display range is from 0 to 5 K T
![]() $_{\rm MB}$
.
$_{\rm MB}$
.
3.3. Velocity distribution
The panels of Fig. 5 show PV slices of the
![]() $^{12}$
CO emission, averaged over three different ranges in latitude, overlaid with the positions of three spiral arms from the Galaxy model of Vallée (2016).Footnote h
$^{12}$
CO emission, averaged over three different ranges in latitude, overlaid with the positions of three spiral arms from the Galaxy model of Vallée (2016).Footnote h

Figure 5.
![]() $^{12}$
CO position–velocity (PV) plots as a function of Galactic Longitude, l, on the x-axis and the radial velocity, V
$^{12}$
CO position–velocity (PV) plots as a function of Galactic Longitude, l, on the x-axis and the radial velocity, V
![]() $_{LSR}$
, in km s
$_{LSR}$
, in km s
![]() $^{-1}$
on the y-axis. The data has been averaged between three different latitude ranges (
$^{-1}$
on the y-axis. The data has been averaged between three different latitude ranges (
![]() $b=\pm0.05^\circ$
,
$b=\pm0.05^\circ$
,
![]() $b=\pm0.5^\circ$
,
$b=\pm0.5^\circ$
,
![]() $b=\pm1.0^\circ$
from top to bottom panel, respectively). The solid lines are the positions for the centres of the three spiral arms (Norma, Sgr-Carina, Scutum + Cen-Crux) from the model of Valée (2016). The display range is 0.3–6 K.
$b=\pm1.0^\circ$
from top to bottom panel, respectively). The solid lines are the positions for the centres of the three spiral arms (Norma, Sgr-Carina, Scutum + Cen-Crux) from the model of Valée (2016). The display range is 0.3–6 K.
The Galactic latitude coverage of the PV plot shown in Fig. 5a is from -0.05
![]() $^{\circ}$
to 0.05
$^{\circ}$
to 0.05
![]() $^{\circ}$
, in Fig. 5b from -0.5
$^{\circ}$
, in Fig. 5b from -0.5
![]() $^{\circ}$
to 0.5
$^{\circ}$
to 0.5
![]() $^{\circ}$
, and in Fig. 5c from -1.0
$^{\circ}$
, and in Fig. 5c from -1.0
![]() $^{\circ}$
to 1.0
$^{\circ}$
to 1.0
![]() $^{\circ}$
. The Galactic longitude coverage (
$^{\circ}$
. The Galactic longitude coverage (
![]() $l=250^{\circ}$
–
$l=250^{\circ}$
–
![]() $355^{\circ}$
) and the velocity axes are the same for all these PV plots. In addition, all display ranges are kept the same, with the minimum 0.3 K and the maximum 6.0 K.
$355^{\circ}$
) and the velocity axes are the same for all these PV plots. In addition, all display ranges are kept the same, with the minimum 0.3 K and the maximum 6.0 K.
There is almost no emission seen at negative velocities between
![]() $l=250^\circ$
and
$l=250^\circ$
and
![]() $l=270^\circ$
. Although we note some high positive velocity features in this region,
$l=270^\circ$
. Although we note some high positive velocity features in this region,
![]() $\sim$
90 km s
$\sim$
90 km s
![]() $^{-1}$
(
$^{-1}$
(
![]() $|b|>0.1^\circ$
), they are suppressed on the PV plots as these are integrated over a large latitude range. The molecular gas gradually shifts towards negative velocities as we move towards the Galactic centre. The most extreme negative velocity features,
$|b|>0.1^\circ$
), they are suppressed on the PV plots as these are integrated over a large latitude range. The molecular gas gradually shifts towards negative velocities as we move towards the Galactic centre. The most extreme negative velocity features,
![]() $\sim$
$\sim$
![]() $-200$
km s
$-200$
km s
![]() $^{-1}$
(
$^{-1}$
(
![]() $|b|>0.1^\circ$
), are seen between
$|b|>0.1^\circ$
), are seen between
![]() $l=340^\circ$
and
$l=340^\circ$
and
![]() $l=355^\circ$
. However, these features are not visible in the PV plots as their fluxes are not sufficiently strong when averaged over the entire latitude range. The features can be seen in the moment maps, however.
$l=355^\circ$
. However, these features are not visible in the PV plots as their fluxes are not sufficiently strong when averaged over the entire latitude range. The features can be seen in the moment maps, however.
Fig. 6 shows a comparison of the PV plots for the different isotopologues for the innermost latitude range (
![]() $b = -0.05^{\circ}$
to
$b = -0.05^{\circ}$
to
![]() $0.05^{\circ}$
), with
$0.05^{\circ}$
), with
![]() $^{12}$
CO upper,
$^{12}$
CO upper,
![]() $^{13}$
CO middle, and C
$^{13}$
CO middle, and C
![]() $^{18}$
O lower. The C
$^{18}$
O lower. The C
![]()
![]() $^{18}$
O provides a good indicator of the location of the cores, since the weak emission in this line is only seen along the highest column density sight lines.
$^{18}$
O provides a good indicator of the location of the cores, since the weak emission in this line is only seen along the highest column density sight lines.

Figure 6. All the panels cover the entire survey range and show
![]() $^{12}$
CO (a),
$^{12}$
CO (a),
![]() $^{13}$
CO (b), and C
$^{13}$
CO (b), and C
![]() $^{18}$
O (c) data from top to bottom, respectively. All three PV plots show the data averaged between the same latitude range,
$^{18}$
O (c) data from top to bottom, respectively. All three PV plots show the data averaged between the same latitude range,
![]() $b=\pm0.05^\circ$
. The display range is 0.3–6 K for
$b=\pm0.05^\circ$
. The display range is 0.3–6 K for
![]() $^{12}$
CO, 0.3–1 K for
$^{12}$
CO, 0.3–1 K for
![]() $^{13}$
CO, and 0.3–0.6 K for C
$^{13}$
CO, and 0.3–0.6 K for C
![]() $^{18}$
O.
$^{18}$
O.
3.4. Integrated intensity and mass distribution
We have used a CO X-factor in order to convert the
![]() $^{12}$
CO line fluxes into column densities, and from there to cloud masses and so to the overall mass distribution along the Southern Galactic Plane.
$^{12}$
CO line fluxes into column densities, and from there to cloud masses and so to the overall mass distribution along the Southern Galactic Plane.
We used a conversion factor of
![]() $2.7 \times 10^{20}$
cm
$2.7 \times 10^{20}$
cm
![]() $^{-2}$
(K km s
$^{-2}$
(K km s
![]() $^{-1}$
)
$^{-1}$
)
![]() $^{-1}$
, the value derived for
$^{-1}$
, the value derived for
![]() $|b| < 1^\circ$
in Dame et al. (Reference Dame, Hartmann and Thaddeus2001). This is for consistency with our previous papers on the Mopra survey which used this value. Bolatto et al. (Reference Bolatto, Wolfire and Leroy2013) have suggested using a coefficient of 2 rather than 2.7, however this has a
$|b| < 1^\circ$
in Dame et al. (Reference Dame, Hartmann and Thaddeus2001). This is for consistency with our previous papers on the Mopra survey which used this value. Bolatto et al. (Reference Bolatto, Wolfire and Leroy2013) have suggested using a coefficient of 2 rather than 2.7, however this has a
![]() $\pm 30\%$
uncertainty. A range of X-factors are used in the literature, with this coefficient ranging from 0.7 to 4.2 (see the discussion in (see the discussion in Bolatto et al. Reference Bolatto, Wolfire and Leroy2013)
$\pm 30\%$
uncertainty. A range of X-factors are used in the literature, with this coefficient ranging from 0.7 to 4.2 (see the discussion in (see the discussion in Bolatto et al. Reference Bolatto, Wolfire and Leroy2013)

Figure 7. Molecular mass distribution for the inner two degrees of latitude (
![]() $b=\pm1^\circ$
) across the Galaxy, extending from l = 250
$b=\pm1^\circ$
) across the Galaxy, extending from l = 250
![]() $^\circ$
-350
$^\circ$
-350
![]() $^\circ$
. Masses are calculated using a
$^\circ$
. Masses are calculated using a
![]() $^{12}$
CO X-factor to convert line fluxes to column densities for all gas detected within the solar circle (i.e. that with negative velocities, except for the third quadrant (l = 250
$^{12}$
CO X-factor to convert line fluxes to column densities for all gas detected within the solar circle (i.e. that with negative velocities, except for the third quadrant (l = 250
![]() $^\circ$
–270
$^\circ$
–270
![]() $^\circ$
). The solid line illustrates the mass calculated using the assumption of near-side distances (y-axis on left); whereas the dotted line assumes far-side distances (y-axis on right). All mass values divided by 10
$^\circ$
). The solid line illustrates the mass calculated using the assumption of near-side distances (y-axis on left); whereas the dotted line assumes far-side distances (y-axis on right). All mass values divided by 10
![]() $^6$
.
$^6$
.
This is an empirical approach, the X-factor undoubtedly varies from source to source as well as across the Galaxy. CO emission is heavily optically thick, in general we are only seeing the front surfaces of molecular clouds along the sight lines. However, a full calculation requires an estimation of the optical depth as well as the temperature of the gas and so must be done for each cloud that is observed, a considerable task beyond the scope of this paper. Given the additional uncertainty in the absolute flux calibration such an effort is not justified here. Using an X-factor is equivalent to the approach usually applied to extra-galactic studies, it provides an overall mass estimate.
We have additionally also applied a
![]() $^{13}$
CO X-factor, however simply by averaging the overall
$^{13}$
CO X-factor, however simply by averaging the overall
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}CO$
fluxes to determine the relative ratio of the X-factor.
$^{13}CO$
fluxes to determine the relative ratio of the X-factor.
![]() $^{13}$
CO is less optically thick than
$^{13}$
CO is less optically thick than
![]() $^{12}$
CO so does probe further into the highest column density region of molecular clouds. However, being a weaker line, it is also less sensitive to the more diffuse, extended gas. It thus provides a consistency check for the
$^{12}$
CO so does probe further into the highest column density region of molecular clouds. However, being a weaker line, it is also less sensitive to the more diffuse, extended gas. It thus provides a consistency check for the
![]() $^{12}$
CO mass estimates, but not an independent measurement of it.
$^{12}$
CO mass estimates, but not an independent measurement of it.
While C
![]() $^{18}$
O has also been measured in our survey, the line is very much weaker than for the first two isotopologues. It is only sensitive to the highest column density sight lines, so is not useful for estimating overall molecular masses.
$^{18}$
O has also been measured in our survey, the line is very much weaker than for the first two isotopologues. It is only sensitive to the highest column density sight lines, so is not useful for estimating overall molecular masses.
Following this approach, the distribution of molecular mass along Galactic longitude has been calculated and is shown in Fig. 7. This plot is averaged for each degree in longitude of the survey range over the two degrees in latitude (l
![]() $\times$
b = 1
$\times$
b = 1
![]() $^\circ$
$^\circ$
![]() $\times$
2
$\times$
2
![]() $^\circ$
). The calculation is as in Braiding et al. (Reference Braiding2015) for l = 320
$^\circ$
). The calculation is as in Braiding et al. (Reference Braiding2015) for l = 320
![]() $^{\circ}$
–330
$^{\circ}$
–330
![]() $^{\circ}$
, now extended to l = 250
$^{\circ}$
, now extended to l = 250
![]() $^{\circ}$
–350
$^{\circ}$
–350
![]() $^{\circ}$
and to |b| < 1
$^{\circ}$
and to |b| < 1
![]() $^\circ$
, so covering the entirety of the survey.
$^\circ$
, so covering the entirety of the survey.
Moreover, we also calculated the total mass by using
![]() $^{13}$
CO flux, and a
$^{13}$
CO flux, and a
![]() $^{13}$
CO X-factor value, 2.3
$^{13}$
CO X-factor value, 2.3
![]() $\times$
10
$\times$
10
![]() $^{21}$
cm
$^{21}$
cm
![]() $^{-2}$
(K km s
$^{-2}$
(K km s
![]() $^{-1}$
)
$^{-1}$
)
![]() $^{-1}$
, a factor of 8.5 higher value than
$^{-1}$
, a factor of 8.5 higher value than
![]() $^{12}$
CO X-factor. We derived this X-factor from the
$^{12}$
CO X-factor. We derived this X-factor from the
![]() $^{12}$
CO/
$^{12}$
CO/
![]() $^{13}$
CO total flux ratio (R
$^{13}$
CO total flux ratio (R
![]() $_{12}$
/R
$_{12}$
/R
![]() $_{13}$
) between l = 250
$_{13}$
) between l = 250
![]() $^{\circ}$
–350
$^{\circ}$
–350
![]() $^{\circ}$
.
$^{\circ}$
.
We find that there are typically a few
![]() $\times$
10
$\times$
10
![]() $^{6}$
M
$^{6}$
M
![]() $_{\odot}$
of molecular gas per degree in longitude from
$_{\odot}$
of molecular gas per degree in longitude from
![]() $l=300$
$l=300$
![]() $^{\circ}$
to
$^{\circ}$
to
![]() $l=325$
$l=325$
![]() $^{\circ}$
. The mass distribution peaks around 10
$^{\circ}$
. The mass distribution peaks around 10
![]() $^{7}$
M
$^{7}$
M
![]() $_{\odot}$
per degree between
$_{\odot}$
per degree between
![]() $l=326^{\circ}$
and
$l=326^{\circ}$
and
![]() $l=334$
$l=334$
![]() $^{\circ}$
, where it corresponds to the Norma spiral arm. Then the mass decreases gradually as we move to the Galactic centre, and around
$^{\circ}$
, where it corresponds to the Norma spiral arm. Then the mass decreases gradually as we move to the Galactic centre, and around
![]() $l=350^{\circ}$
is almost half of the peak.
$l=350^{\circ}$
is almost half of the peak.
The sum of the molecular mass for each degree shows that the total molecular mass found in the Mopra CO Survey’s coverage is 2.7
![]() $\times$
10
$\times$
10
![]() $^{8}$
M
$^{8}$
M
![]() $_{\odot}$
considered all mass at the near distance, 1.4
$_{\odot}$
considered all mass at the near distance, 1.4
![]() $\times$
10
$\times$
10
![]() $^{9}$
M
$^{9}$
M
![]() $_{\odot}$
considered all mass at the far distance. The very same calculation was done using
$_{\odot}$
considered all mass at the far distance. The very same calculation was done using
![]() $^{13}$
CO flux values and a
$^{13}$
CO flux values and a
![]() $^{13}$
CO X-factor value (a factor of 8.5 higher than
$^{13}$
CO X-factor value (a factor of 8.5 higher than
![]() $^{12}$
CO X-factor). The total mass results for near distance and far distance are 2.8
$^{12}$
CO X-factor). The total mass results for near distance and far distance are 2.8
![]() $\times$
10
$\times$
10
![]() $^{8}$
M
$^{8}$
M
![]() $_{\odot}$
and 1.5
$_{\odot}$
and 1.5
![]() $\times$
10
$\times$
10
![]() $^{9}$
M
$^{9}$
M
![]() $_{\odot}$
, respectively.
$_{\odot}$
, respectively.
The results show that the
![]() $^{12}$
CO integrated intensity between Galactic longitude 250
$^{12}$
CO integrated intensity between Galactic longitude 250
![]() ${}^{\circ}$
and 300
${}^{\circ}$
and 300
![]() ${}^{\circ}$
only corresponds to 6% of the integrated intensity of the survey coverage (l = 250
${}^{\circ}$
only corresponds to 6% of the integrated intensity of the survey coverage (l = 250
![]() $^{\circ}$
–350
$^{\circ}$
–350
![]() $^{\circ}$
). In addition to this, the total near mass and the total far mass only correspond to 2% and 1%, respectively, for the same comparison (see Table 1). We have made the same comparisons for
$^{\circ}$
). In addition to this, the total near mass and the total far mass only correspond to 2% and 1%, respectively, for the same comparison (see Table 1). We have made the same comparisons for
![]() $^{13}$
CO results, finding proportions of 5%, 2%, and 1%, respectively (see Table 2).
$^{13}$
CO results, finding proportions of 5%, 2%, and 1%, respectively (see Table 2).
We note that as we move towards the Galactic centre, using the Galactic rotation curve to determine the distances becomes less useful and leads to large uncertainties. Although we observed features at extreme velocities between
![]() $l=350^{\circ}$
and
$l=350^{\circ}$
and
![]() $l=355^{\circ}$
, i.e.
$l=355^{\circ}$
, i.e.
![]() $+$
130 km s
$+$
130 km s
![]() $^{-1}$
or
$^{-1}$
or
![]() $-$
230 km s
$-$
230 km s
![]() $^{-1}$
, we have not included this region to the mass calculation. However, the integrated
$^{-1}$
, we have not included this region to the mass calculation. However, the integrated
![]() $^{12}$
CO intensity between
$^{12}$
CO intensity between
![]() $l=350^{\circ}$
and
$l=350^{\circ}$
and
![]() $l=355^{\circ}$
is
$l=355^{\circ}$
is
![]() $1.6 \times 10^7$
K km s
$1.6 \times 10^7$
K km s
![]() $^{-1}$
whilst the integrated
$^{-1}$
whilst the integrated
![]() $^{13}$
CO intensity for the same region is
$^{13}$
CO intensity for the same region is
![]() $1.6 \times 10^6$
K km s
$1.6 \times 10^6$
K km s
![]() $^{-1}$
.
$^{-1}$
.
As discussed in DR3, we have not included positive velocity features in the 4th quadrant (beyond the solar circle) in the mass calculation due to the uncertainties as the distances are large and emission is relatively weak. However, almost all of the gas is present at positive velocities in the 3rd quadrant (l = 250
![]() $^{\circ}$
–270
$^{\circ}$
–270
![]() $^{\circ}$
), and we have included the region in the mass calculation since the distances are nearby. We note that the
$^{\circ}$
), and we have included the region in the mass calculation since the distances are nearby. We note that the
![]() $^{12}$
CO integrated intensity in the region is only 1% of the entire survey, and the total mass in the region only corresponds to 0.1% of the total mass of the entire survey.
$^{12}$
CO integrated intensity in the region is only 1% of the entire survey, and the total mass in the region only corresponds to 0.1% of the total mass of the entire survey.
Table 1. Integrated intensity and total mass values of
![]() $^{12}$
CO for the covered region. Near and far mass values are calculated assuming either all flux is at the near side or at the far side distance solution. Mass between
$^{12}$
CO for the covered region. Near and far mass values are calculated assuming either all flux is at the near side or at the far side distance solution. Mass between
![]() $l=350^{\circ}$
–355
$l=350^{\circ}$
–355
![]() $^{\circ}$
is not calculated as the distance is unreliable.
$^{\circ}$
is not calculated as the distance is unreliable.

Table 2. As in Table 1, but for
![]() $^{13}$
CO.
$^{13}$
CO.

4. Discussion
4.1. DR3 and DR4 comparison
In this section we present some initial data analysis, and a comparison between DR3 and DR4. As mentioned in Section 3, the size of the released data have been significantly increased with DR4 from 50 to 210 deg
![]() $^2$
.
$^2$
.
We note that after the data correction described earlier in the Data Processing section (mainly re-baselining, occasionally re-reduction) the total integrated intensity in the DR3 region has been increased by 4%. Subsequently, this results in an increased total near mass by
![]() $\sim$
10% and total far mass by
$\sim$
10% and total far mass by
![]() $\sim6\%$
from results reported in DR3.
$\sim6\%$
from results reported in DR3.
4.2. Integrated intensity distribution
Fig. 8a shows the distribution of integrated intensity along the Galactic Plane. We have divided the total coverage of the survey into a
![]() $105 \times 20$
pixel grid. Each pixel size is 1 degree in longitude and 0.1 degree in latitude. The colour-bar shows the percentage distribution of the total integrated intensity of the entire survey. The brightest pixel of the heat-map is located at l = 337.5
$105 \times 20$
pixel grid. Each pixel size is 1 degree in longitude and 0.1 degree in latitude. The colour-bar shows the percentage distribution of the total integrated intensity of the entire survey. The brightest pixel of the heat-map is located at l = 337.5
![]() $^\circ$
, b =
$^\circ$
, b =
![]() $-$
0.05
$-$
0.05
![]() $^\circ$
. This pixel has 0.35% of the integrated intensity of the entire survey.
$^\circ$
. This pixel has 0.35% of the integrated intensity of the entire survey.

Figure 8. The top panel shows the total (velocity integrated) of
![]() $^{12}$
CO intensity distribution across the survey (divided by 10
$^{12}$
CO intensity distribution across the survey (divided by 10
![]() $^5$
K km s
$^5$
K km s
![]() $^{-1}$
). X-axis shows Galactic longitude, from l = 250
$^{-1}$
). X-axis shows Galactic longitude, from l = 250
![]() $^\circ$
–355
$^\circ$
–355
![]() $^\circ$
. Y-axis shows Galactic latitude, from b = –1
$^\circ$
. Y-axis shows Galactic latitude, from b = –1
![]() $^\circ$
–1
$^\circ$
–1
![]() $^\circ$
. The colour-bar is square root function to provide contrast. The bottom panel shows each pixels’ percentage contribution to the total flux measured across the survey region. The pixel size is
$^\circ$
. The colour-bar is square root function to provide contrast. The bottom panel shows each pixels’ percentage contribution to the total flux measured across the survey region. The pixel size is
![]() $1.0^\circ$
x
$1.0^\circ$
x
![]() $0.1^\circ$
for both panels.
$0.1^\circ$
for both panels.
Two-thirds of the total integrated intensity is present between Galactic longitude 326
![]() $^\circ$
and 355
$^\circ$
and 355
![]() $^\circ$
, an area of almost one quarter of the survey coverage. There are sharp transitions in the values for the integrated intensity along the Galactic Plane as we move towards Galactic Centre. The first occurs at longitude 301
$^\circ$
, an area of almost one quarter of the survey coverage. There are sharp transitions in the values for the integrated intensity along the Galactic Plane as we move towards Galactic Centre. The first occurs at longitude 301
![]() $^\circ$
where the Scutum arm joins the line of sight. Between longitude 319
$^\circ$
where the Scutum arm joins the line of sight. Between longitude 319
![]() $^\circ$
and 326
$^\circ$
and 326
![]() $^\circ$
, there is also a drop in intensity. This should correspond to the relatively less dense region between Scutum and Norma arms. A sharp rise occurs at G326
$^\circ$
, there is also a drop in intensity. This should correspond to the relatively less dense region between Scutum and Norma arms. A sharp rise occurs at G326
![]() $^\circ$
as Norma arm joins the line of sight. The Norma arm leaves the line of sight at G335
$^\circ$
as Norma arm joins the line of sight. The Norma arm leaves the line of sight at G335
![]() $^\circ$
, and 3-kpc arm joins the sightline at G336
$^\circ$
, and 3-kpc arm joins the sightline at G336
![]() $^\circ$
.
$^\circ$
.
The molecular gas distribution is also clearly not homogeneous with Galactic latitude. Generally, the strongest CO emission along the Galactic Plane is present in the inner 0.2 degrees (i.e., between
![]() $b=-0.1^\circ$
and
$b=-0.1^\circ$
and
![]() $b=0.1^\circ$
). However, exceptionally, the strongest emission between
$b=0.1^\circ$
). However, exceptionally, the strongest emission between
![]() $l=347^\circ$
and
$l=347^\circ$
and
![]() $l=350^\circ$
is present between
$l=350^\circ$
is present between
![]() $b=0.2^\circ$
and
$b=0.2^\circ$
and
![]() $b=0.4^\circ$
. We find that 65% of the total emission in latitude lies in the inner
$b=0.4^\circ$
. We find that 65% of the total emission in latitude lies in the inner
![]() $1^\circ$
(
$1^\circ$
(
![]() $|b|$
< 0.5
$|b|$
< 0.5
![]() $^{\circ}$
).
$^{\circ}$
).
In latitude between
![]() $l=300^\circ$
and
$l=300^\circ$
and
![]() $l=250^\circ$
the CO features seem irregularly distributed along the Galactic Plane. The concentration of molecular gas is, however, much reduced from the inner Galaxy as there are no prominent spiral arms here to contribute to the molecular emission.
$l=250^\circ$
the CO features seem irregularly distributed along the Galactic Plane. The concentration of molecular gas is, however, much reduced from the inner Galaxy as there are no prominent spiral arms here to contribute to the molecular emission.
4.3.
 $^{12}$
CO &
$^{12}$
CO &
 $^{13}$
CO integrated intensity comparison
$^{13}$
CO integrated intensity comparison
The total measured
![]() $^{12}$
CO integrated intensity of the entire survey is
$^{12}$
CO integrated intensity of the entire survey is
![]() $1.53\times10^8$
K km s
$1.53\times10^8$
K km s
![]() $^{-1}$
(
$^{-1}$
(
![]() $l=250^\circ-355^\circ$
,
$l=250^\circ-355^\circ$
,
![]() $b=\pm1.0$
) whereas the total measured
$b=\pm1.0$
) whereas the total measured
![]() $^{13}$
CO integrated intensity for the same area is
$^{13}$
CO integrated intensity for the same area is
![]() $1.77\times10^7$
K km s
$1.77\times10^7$
K km s
![]() $^{-1}$
. We note a factor of
$^{-1}$
. We note a factor of
![]() $\sim$
8.5 difference between the totals for
$\sim$
8.5 difference between the totals for
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO here. As a result, we have used a factor of 8.5 higher X-factor value than
$^{13}$
CO here. As a result, we have used a factor of 8.5 higher X-factor value than
![]() $^{12}$
CO X-factor in order to calculate the total mass using
$^{12}$
CO X-factor in order to calculate the total mass using
![]() $^{13}$
CO integrated intensity as mentioned earlier.
$^{13}$
CO integrated intensity as mentioned earlier.
The comparison of the integrated intensity distributions of
![]() $^{12}$
CO to
$^{12}$
CO to
![]() $^{13}$
CO look similar along the Galactic Plane. However, on closer inspection the
$^{13}$
CO look similar along the Galactic Plane. However, on closer inspection the
![]() $^{12}$
CO distribution is more spread out towards the higher latitudes than
$^{12}$
CO distribution is more spread out towards the higher latitudes than
![]() $^{13}$
CO. This was quantified as follows:
$^{13}$
CO. This was quantified as follows:
We first determined the velocity ranges for the
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO emission using PV plots. Then we calculated the total integrated intensity in each line for the same velocity range, with
$^{13}$
CO emission using PV plots. Then we calculated the total integrated intensity in each line for the same velocity range, with
![]() $0.1^\circ$
latitude increments in both positive and negative directions (i.e., from
$0.1^\circ$
latitude increments in both positive and negative directions (i.e., from
![]() $b=0.0$
to
$b=0.0$
to
![]() $b=0.1$
, from
$b=0.1$
, from
![]() $b=0.0$
to
$b=0.0$
to
![]() $b=0.2$
, from
$b=0.2$
, from
![]() $b=0.0$
to
$b=0.0$
to
![]() $b=-0.1$
etc. until from
$b=-0.1$
etc. until from
![]() $b=0.0$
to
$b=0.0$
to
![]() $1.0$
and from
$1.0$
and from
![]() $b=0.0$
to
$b=0.0$
to
![]() $-1.0$
). From these calculations we produced the integrated intensity and mass distribution plots shown in Figs. 8a and 8b).
$-1.0$
). From these calculations we produced the integrated intensity and mass distribution plots shown in Figs. 8a and 8b).
We then compared the intensity distributions for
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO separately, starting from
$^{13}$
CO separately, starting from
![]() $b=0^\circ$
and moving towards higher latitudes. The
$b=0^\circ$
and moving towards higher latitudes. The
![]() $^{12}$
CO data shows that the region to
$^{12}$
CO data shows that the region to
![]() $b=\pm0.4^\circ$
contains more than half, and the region to
$b=\pm0.4^\circ$
contains more than half, and the region to
![]() $b=\pm0.7^\circ$
contains more than 80%, of the total integrated intensity for the entire Galactic Plane. On the other hand, the
$b=\pm0.7^\circ$
contains more than 80%, of the total integrated intensity for the entire Galactic Plane. On the other hand, the
![]() $^{13}$
CO data shows that in just the inner 0.6
$^{13}$
CO data shows that in just the inner 0.6
![]() $^\circ$
of the Galactic Plane (
$^\circ$
of the Galactic Plane (
![]() $b=\pm0.3^\circ$
) is contained half of the total integrated flux in this isotopologue.
$b=\pm0.3^\circ$
) is contained half of the total integrated flux in this isotopologue.
Considering the drop in the rate of increase of integrated intensity towards higher latitudes, we can predict the latitude after which this increase becomes negligible. We fitted a quadratic polynomial to both
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO data separately. The
$^{13}$
CO data separately. The
![]() $^{12}$
CO trend line suggests that beyond
$^{12}$
CO trend line suggests that beyond
![]() $b=\pm1.4^\circ$
total integrated intensity increase should be negligible, with only an additional
$b=\pm1.4^\circ$
total integrated intensity increase should be negligible, with only an additional
![]() $\sim$
10% occurring from b = 1.0
$\sim$
10% occurring from b = 1.0
![]() $^\circ$
to 1.4
$^\circ$
to 1.4
![]() $^\circ$
. The same extrapolation was also applied using
$^\circ$
. The same extrapolation was also applied using
![]() $^{13}$
CO data. The
$^{13}$
CO data. The
![]() $^{13}$
CO trend line suggests that almost all of the molecular gas within the Galactic Plane lies between
$^{13}$
CO trend line suggests that almost all of the molecular gas within the Galactic Plane lies between
![]() $b=\pm1.0$
. Finally, we compared the increase of integrated intensity for both lines (
$b=\pm1.0$
. Finally, we compared the increase of integrated intensity for both lines (
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO) by simply looking at their ratio moving towards higher latitudes. 15.9% of total
$^{13}$
CO) by simply looking at their ratio moving towards higher latitudes. 15.9% of total
![]() $^{12}$
CO integrated intensity lies between
$^{12}$
CO integrated intensity lies between
![]() $b=\pm 0.1$
whilst 18.9% of total
$b=\pm 0.1$
whilst 18.9% of total
![]() $^{13}$
CO integrated intensity is present in the same region. The ratio between these is 84%. The percentage increases towards higher latitudes, and reaches 100% at
$^{13}$
CO integrated intensity is present in the same region. The ratio between these is 84%. The percentage increases towards higher latitudes, and reaches 100% at
![]() $b=\pm 1.0$
, i.e. the total
$b=\pm 1.0$
, i.e. the total
![]() $^{12}$
CO flux is increasing more rapidly than is
$^{12}$
CO flux is increasing more rapidly than is
![]() $^{13}$
CO as
$^{13}$
CO as
![]() $|b|$
rises. Although
$|b|$
rises. Although
![]() $^{12}$
CO is more optically thick than
$^{12}$
CO is more optically thick than
![]() $^{13}$
CO, our results show that
$^{13}$
CO, our results show that
![]() $^{12}$
CO is even more optically thick near the Galactic Plane compared to
$^{12}$
CO is even more optically thick near the Galactic Plane compared to
![]() $^{13}$
CO (Fig. 9).
$^{13}$
CO (Fig. 9).

Figure 9. Fraction of the total integrated intensity measured in the survey as a function of latitude range for
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO from
$^{13}$
CO from
![]() $|b|$
= 0
$|b|$
= 0
![]() $^\circ$
to 1
$^\circ$
to 1
![]() $^\circ$
. Blue and red data points represent
$^\circ$
. Blue and red data points represent
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO data respectively, whilst black data points represent ratio between the detected fractions of the
$^{13}$
CO data respectively, whilst black data points represent ratio between the detected fractions of the
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO intensities. The blue and red lines show quadratic polynomial fits to the corresponding data points. The
$^{13}$
CO intensities. The blue and red lines show quadratic polynomial fits to the corresponding data points. The
![]() $^{12}$
CO fit has been extrapolated to its peak, which occurs at
$^{12}$
CO fit has been extrapolated to its peak, which occurs at
![]() $|b|=1.4^\circ$
$|b|=1.4^\circ$
The difference between these
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO distributions is significant. Since
$^{13}$
CO distributions is significant. Since
![]() $^{13}$
CO emission is less optically thick than
$^{13}$
CO emission is less optically thick than
![]() $^{12}$
CO, it should be a better indicator for the entirety of the gas. This result shows that the latitude coverage of the Mopra CO survey is optimal when balancing limited survey time with areal coverage, and obtaining significantly more flux would be unlikely if the latitude coverage has been extended beyond
$^{12}$
CO, it should be a better indicator for the entirety of the gas. This result shows that the latitude coverage of the Mopra CO survey is optimal when balancing limited survey time with areal coverage, and obtaining significantly more flux would be unlikely if the latitude coverage has been extended beyond
![]() $|b|<1^\circ$
.
$|b|<1^\circ$
.
4.4. Mass distribution
The total molecular gas within the DR3 region was found to be
![]() $\sim$
2
$\sim$
2
![]() $\times$
10
$\times$
10
![]() $^{8}$
M
$^{8}$
M
![]() $_{\odot}$
(if all were at the near distance) and
$_{\odot}$
(if all were at the near distance) and
![]() $\sim$
9
$\sim$
9
![]() $\times$
10
$\times$
10
![]() $^{8}$
M
$^{8}$
M
![]() $_{\odot}$
(if all were at the far distance). We have now calculated the mass of total molecular gas for the same longitude coverage but with the latitude coverage increased from
$_{\odot}$
(if all were at the far distance). We have now calculated the mass of total molecular gas for the same longitude coverage but with the latitude coverage increased from
![]() $\pm$
0.5 to
$\pm$
0.5 to
![]() $\pm$
1.0, a factor of two. The new results for the extended region are
$\pm$
1.0, a factor of two. The new results for the extended region are
![]() $\sim$
2.7
$\sim$
2.7
![]() $\times$
10
$\times$
10
![]() $^{8}$
M
$^{8}$
M
![]() $_{\odot}$
(all at near distance) and
$_{\odot}$
(all at near distance) and
![]() $\sim$
1.4
$\sim$
1.4
![]() $\times$
10
$\times$
10
![]() $^{9}$
M
$^{9}$
M
![]() $_{\odot}$
(all at far distance), an increase of just
$_{\odot}$
(all at far distance), an increase of just
![]() $\sim$
40–60
$\sim$
40–60
![]() $\%$
despite doubling the coverage.
$\%$
despite doubling the coverage.
The mass distribution plots (Fig. 10a and 10b) of the near/far assumption generally look morphologically similar. However, there are some differences. The peak which is present at
![]() $l=343^\circ$
and
$l=343^\circ$
and
![]() $b=-0.7^\circ$
in the far side distribution is not present in the near side mass distribution. Similarly, the peak seen at
$b=-0.7^\circ$
in the far side distribution is not present in the near side mass distribution. Similarly, the peak seen at
![]() $l=328^\circ$
and
$l=328^\circ$
and
![]() $b=0.7^\circ$
in the near distribution is not seen in the far distribution. These differences are caused by the mass being directly proportional to distance squared (M
$b=0.7^\circ$
in the near distribution is not seen in the far distribution. These differences are caused by the mass being directly proportional to distance squared (M
![]() $\propto$
d
$\propto$
d
![]() $^2$
). If a feature is very close in the near side distribution, it means it would be too far away in the far side distribution, thus significantly different mass values are seen.
$^2$
). If a feature is very close in the near side distribution, it means it would be too far away in the far side distribution, thus significantly different mass values are seen.

Figure 10. Both panels show the mass distribution per
![]() $1.0^\circ$
x
$1.0^\circ$
x
![]() $0.1^\circ$
pixel. The top panel assumes all features at the near distance whilst the bottom panel shows the same distribution for the far distance. All mass values in the pixels are divided by 10
$0.1^\circ$
pixel. The top panel assumes all features at the near distance whilst the bottom panel shows the same distribution for the far distance. All mass values in the pixels are divided by 10
![]() $^5$
M
$^5$
M
![]() $_{\odot}$
and the colour-bars are square root function to provide contrast.
$_{\odot}$
and the colour-bars are square root function to provide contrast.
We note that the Galactic rotation curve is less useful to determine distances for sightlines close to the Galactic centre, and we have not included the longitude range between
![]() $l=355^\circ$
and
$l=355^\circ$
and
![]() $l=350^\circ$
in our mass distribution and calculation plots.Footnote i
$l=350^\circ$
in our mass distribution and calculation plots.Footnote i
4.5. PV–Plot comparison
Three spiral arms have been over-plotted on the PV maps shown in Fig. 5 using parameters taken from Vallée (2016). There are three spiral arms in the line of sight; Norma (red), Sgr-Carina (green), and Scutum + Cen-Crux (blue). We note that none of the plotted spiral arms perfectly match the features in the PV maps as the model assumes perfectly shaped spiral arms.

Figure 11. Comparison between the Columbia CO Survey and the Mopra Southern Galactic Plane CO Survey to illustrate the difference in angular resolution. Both panels show the moment 0 map for the same region (
![]() $l=300^\circ$
–
$l=300^\circ$
–
![]() $310^\circ$
,
$310^\circ$
,
![]() $b=\pm$
1.0,
$b=\pm$
1.0,
![]() $v=-50$
–
$v=-50$
–
![]() $-40$
km s
$-40$
km s
![]() $^{-1}$
).
$^{-1}$
).
Approximately 16% of the total flux lies between
![]() $b=-0.1^\circ$
and
$b=-0.1^\circ$
and
![]() $b=0.1^\circ$
. However, almost all the features seen in Fig. 5a are also present in Fig. 5b and 5c. This suggests that since the flux in the inner 0.1 degrees dominates the rest of the latitude coverage, it is unlikely to find other strong features in the higher latitudes PV plots (Fig. 5b and 5c) as flux being integrated over larger latitude ranges.
$b=0.1^\circ$
. However, almost all the features seen in Fig. 5a are also present in Fig. 5b and 5c. This suggests that since the flux in the inner 0.1 degrees dominates the rest of the latitude coverage, it is unlikely to find other strong features in the higher latitudes PV plots (Fig. 5b and 5c) as flux being integrated over larger latitude ranges.
The features look more prominent in Fig. 5a as the data has been integrated over only 0.1
![]() $^\circ$
in latitude. In Fig. 5b, data has been integrated over 1
$^\circ$
in latitude. In Fig. 5b, data has been integrated over 1
![]() $^\circ$
in latitude and a result of this, some weaker features started to disappear. Since Fig. 5c has been integrated over 2
$^\circ$
in latitude and a result of this, some weaker features started to disappear. Since Fig. 5c has been integrated over 2
![]() $^\circ$
in latitude, all the weak features have disappeared. This indicates the concentration towards the Galactic Plane itself.
$^\circ$
in latitude, all the weak features have disappeared. This indicates the concentration towards the Galactic Plane itself.
4.6. Comparison with Columbia CO survey
The Columbia CO Survey, Dame et al. (Reference Dame, Hartmann and Thaddeus2001), has provided an exceptional tool for the Milky Way studies. However, the improvements of the radio telescope arrays in the last two decades require higher-resolution surveys for future studies. The Mopra Southern Galactic Plane CO Survey has a significantly better spectral and spatial resolution (an order of magnitude in each) than the Columbia CO Survey (Fig. 11). In addition, the Columbia CO Survey does not have a uniform sampling since it is a combination of multiple separate surveys. The Mopra CO Survey has the same uniform sampling throughout its region of coverage. This provides more reliability and integrity for the data set.
On the other hand, challenges for conducting the higher resolution Mopra survey included the much longer total observing time, the computationally more expensive data reduction process, and the total size of the resulting data set.
In comparing the two surveys over our now extended coverage (i.e., DR4) we still find general agreement between the shapes of the CO line profiles between Mopra and Columbia for each two square degrees of coverage (i.e., 1 degree in l, 2 degrees in b; see Fig. 12 and following pages). Nonetheless, the factor of 1.35 systematic difference in flux scale found between the two surveys in our DR3 paper does not hold over the larger survey region presented here. We note that the area covered in the full Mopra survey (DR4) corresponds to 4 different sub-surveys in the Columbia dataset. The samplings used in these sub-surveys was not uniform. This results in varying total integrated intensities when comparing to the corresponding values determined in the Mopra survey.
For instance, in the fourth quadrant (
![]() $l=270$
–
$l=270$
–
![]() $360^{\circ}$
), the sampling of the Columbia CO Survey is not the same as in the inner Galactic Plane and beyond
$360^{\circ}$
), the sampling of the Columbia CO Survey is not the same as in the inner Galactic Plane and beyond
![]() $\pm$
0.75 in latitude. Also, in the third quadrant (
$\pm$
0.75 in latitude. Also, in the third quadrant (
![]() $l=180$
–
$l=180$
–
![]() $270^{\circ}$
), multiple variations are present in the sampling. As a result, differences in the ratio of the total integrated intensity occur between the two surveys for each degree in longitude varies. These vary between factors of 1.3 and 2.4 from
$270^{\circ}$
), multiple variations are present in the sampling. As a result, differences in the ratio of the total integrated intensity occur between the two surveys for each degree in longitude varies. These vary between factors of 1.3 and 2.4 from
![]() $l=250^{\circ}$
to
$l=250^{\circ}$
to
![]() $310^{\circ}$
(see Figs. 12–23). We emphasise that the flux calibration for the integrated intensities of the Mopra survey is the same throughout these spectra.
$310^{\circ}$
(see Figs. 12–23). We emphasise that the flux calibration for the integrated intensities of the Mopra survey is the same throughout these spectra.
5. Summary
We present the fourth and the final data release of the Mopra Southern Galactic Plane CO Survey, covering more than 210 square degrees between Galactic longitude
![]() $l = 250$
–
$l = 250$
–
![]() $355^\circ$
and
$355^\circ$
and
![]() $b = \pm 1.0^\circ$
.
$b = \pm 1.0^\circ$
.
We showed the distribution of total flux along the Galactic Plane. We also calculated the total mass, and showed the mass distribution for the entire survey coverage. Mass calculation was done using a canonical X-factor for both near distance and far distance assumptions.
We compared the total flux of
![]() $^{12}$
CO to
$^{12}$
CO to
![]() $^{13}$
CO, and noted that there is approximately a factor of 9 difference between
$^{13}$
CO, and noted that there is approximately a factor of 9 difference between
![]() $^{12}$
CO and
$^{12}$
CO and
![]() $^{13}$
CO fluxes in the favour of
$^{13}$
CO fluxes in the favour of
![]() $^{12}$
CO.
$^{12}$
CO.
We checked the total flux increase as we move from the Galactic Plane (b = 0.0
![]() $^\circ$
) towards higher latitudes (b =
$^\circ$
) towards higher latitudes (b =
![]() $\pm 1.0^\circ$
). The
$\pm 1.0^\circ$
). The
![]() $^{12}$
CO total flux increases by the latitude changes were extrapolated to predict the total flux increase beyond b =
$^{12}$
CO total flux increases by the latitude changes were extrapolated to predict the total flux increase beyond b =
![]() $\pm 1.0^\circ$
. Our data suggest that the increase in
$\pm 1.0^\circ$
. Our data suggest that the increase in
![]() $^{12}$
CO total flux would be small beyond b =
$^{12}$
CO total flux would be small beyond b =
![]() $\pm 1.4^\circ$
. Also, we find that by extending the latitude coverage from b =
$\pm 1.4^\circ$
. Also, we find that by extending the latitude coverage from b =
![]() $\pm 1.0^\circ$
to b =
$\pm 1.0^\circ$
to b =
![]() $\pm 1.4^\circ$
would only increase the total flux by 10% in
$\pm 1.4^\circ$
would only increase the total flux by 10% in
![]() $^{12}$
CO and negligible amount in
$^{12}$
CO and negligible amount in
![]() $^{13}$
CO. The optimal latitude range for CO distribution is found b =
$^{13}$
CO. The optimal latitude range for CO distribution is found b =
![]() $\pm 1.0^\circ$
as our survey used.
$\pm 1.0^\circ$
as our survey used.
In this final data release, we present PV, moment 0, mean line profile, RMS, and T
![]() $_{sys}$
maps of the entire dataset.
$_{sys}$
maps of the entire dataset.
Acknowledgement
The Mopra radio telescope is part of the Australia Telescope National Facility. Operations support was provided by the University of New South Wales, the University of Adelaide, and Western Sydney University. Many staff of the ATNF have contributed to the success of the remote operations at Mopra. We particularly wish to acknowledge the contributions of David Brodrick, Philip Edwards, Brett Hiscock, and Peter Mirtschin.
This research made use of Astropy, a community-developed core Python package for Astronomy (Robitaille et al. Reference Robitaille2013) and the IDL Astronomy Library (Landsman Reference Landsman1993).
We are indebted also to the financial support of the #TeamMopra kickstarter contributors, listed at mopracosurvey.wordpress.com. The University of New South Wales Digital Filter Bank used for the observations with the Mopra Telescope (the UNSW–MOPS) was provided with support from the Australian Research Council (ARC). We also acknowledge ARC support through Discovery Project DP120101585 and Linkage, Infrastructure, Equipment and Facilities project LE160100094.
We are also grateful to the Department for Communities of the Northern Ireland Executive for their support while this thesis work was undertaken.
We thank the anonymous referee for their critical review of our manuscript which has helped us to improve it.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/pasa.2023.44
Data Availability
All the information and links related to this study can be found at the following link mopracosurvey.wordpress.com