No CrossRef data available.
Article contents
The Generalization of de Finetti's Representation Theorem to Stationary Probabilities
Published online by Cambridge University Press: 28 February 2022
Extract
According to de Finetti's representation theorem, probabilities of exchangeable sequences of events are unique mixtures of Bernoullian probabilities. The exchangeable probability P(E) of the sequence E equals an integral of the form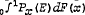 
, where Px(E) is for each x (0≦x≦1) a Bernoullian measure with the probability x for ‘success’ and independence between consecutive events, and F a uniquely determined distribution of the parameter x. P(E) equals the expected value of Px(E). If F has a derivative f, 
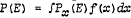Probabilities can be calculated under the integral sign as if events were independent and had a constant success probability. Therefore there cannot be anything one can do with Bernoullian probabilities, but could not do with the exchangeable ones, de Finetti thinks that he has, because of the unique correspondence between exchangeable measures and distributions over a parameter each value of which gives a Bernoullian probability, shown the unnecessity of the latter.
- Type
- Part IV. Probability and Statistical Inference
- Information
- Copyright
- Copyright © Philosophy of Science Association 1982
References
de Finetti, B. (1937). “La prévision: ses lois logiques, ses sources subjetives.” Annales de l‘Institut Henri Poincaré 7: 1–68. (As reprinted as “Foresight: Its Logical Laws, Its Subjective Sources.” (trans.) H.E. Kyburg. In Studies in Subjective Probability. Edited by H.E. Kyburg and H.E. Smokier. New York: Wiley, 1964. Pages 95-158.)Google Scholar
de Finetti, B. (1938). “Sur la condition d'équivalence partielle.” Actualités Scientifiques et Industrielles 737: 5–18. (As reprinted as “On the Condition of Partial Exchangeability.” (trans.) P. Benacerraf and R. Jeffrey. In Jeffre. (1980). Pages 193-205.)Google Scholar
Diaconis, P. and Freedman, D. (1980). “De Finetti‘s Generalizations of Exchangeability.” In Jeffre. (1980). Pages 233–249.CrossRefGoogle Scholar
Farrell, R.H. (1962). “Representation of Invariant Measures.” Illinois Journal of Mathematics 6: 447–467.CrossRefGoogle Scholar
Feller, H. (1971). An Introduction to Probability Theory and Its Applications. Volume II. New York: Wiley.Google Scholar
Freedman, D. (1962). “Invariants Under Mixing Which Generalize de Finetti‘s Theorem.” Annals of Mathematical Statistics 33: 916–923.CrossRefGoogle Scholar
Jacobs, K. (1963). Lecture Notes on Ergodic Theory. 2 vols. Aarhus: Mathematical Institute of Aarhus University.Google Scholar
Jeffrey, R. (ed.). (1980). Studies in Inductive Logic and Probability, Volume II. Berkeley: University of California Press.10.1525/9780520318328CrossRefGoogle Scholar
Link, G. (1980). “Representation Theorems of the de Finetti Type.” In Jeffre. (1980). Pages 207–231.Google Scholar
Ryll-Nardzewski, C. (1957). “On Stationary Sequences of Random Variables and the de Finetti‘s Equivalence.” Colloquium Mathematicum 4; 149–156.CrossRefGoogle Scholar
von Neumann, J. (1932). “Zur Operatorenmethode in der klassischen Mechanik.” Annals of Mathematics 33: 587–642. (As reprinted in Collected Works, Volume II. (ed.) A.H. Taub. Pages 307-362.)CrossRefGoogle Scholar
von Plato, J. (1981). “Reductive Relations in Interpretations of Probability.” Synthese 48: 61–75.CrossRefGoogle Scholar
von Plato, J. (1982a). “Probability and Determinism.” Philosophy of Science 49: 51–66.CrossRefGoogle Scholar
Plato, J. (1982b). “The Method of Arbitrary Functions.” The British Journal for the Philosophy of Science (Forthcoming).Google Scholar