No CrossRef data available.
Article contents
XLI.—On Sommerfeld's Form of Fourier's Repeated Integrals
Published online by Cambridge University Press: 15 September 2014
Extract
§ 1. In his treatise on Fourier Series and Integrals Carslaw quotes without proof Sommerfeld's theorem that
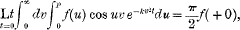
when the limit on the right-hand side exists. In applied mathematics, he remarks, it is this limit, rather than the corresponding Fourier repeated integral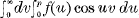 
which occurs.
In the present paper I propose to extend this result in various ways. After proving Sommerfeld's result on the general hypothesis, not considered by him, that the integral is a Lebesgue integral, I show that the limit in question is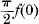 
whenever the origin is a point at which f(u) is the differential coefficient of its integral, and I obtain the corresponding results for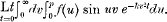 
In all their generality these statements are only true when the interval (0, p) is a finite one. I then show how, under a variety of hypotheses with respect to the nature of f(x) at infinity, they can be extended so as to be still true when p = + ∞ . These hypotheses correspond precisely to those which have been proved f to be sufficient for the corresponding statements as to the Fourier sine and cosine repeated integrals in their usual forms.
- Type
- Research Article
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1912
References
page 587 note * Cf. Carslaw, , op. cit., p. 186.Google Scholar The theorem as there stated differs only in form from the above, from which it may be easily deduced. The proviso as to the existence of the limit ƒ( + 0) is moreover, though tacitly assumed, not expressly stated in the enunciation.
page 587 note † Pringsheim, A., “Ueber neue Giiltigkeitsbedingungen fur die Fouriersche Integralformel,” 1909, Math. Ann., lxviii. pp. 367–408.Google Scholar Young, W. H., “On Fourier's Repeated Integrals,” 1910 Google Scholar, presented to the Royal Society of Edinburgh.
page 588 note * The statement and indications of proof of this theorem are given in my recent paper on the “Theory of the Application of Expansions to Definite Integrals,” § 4, presented to the London Mathematical Society.
page 589 note * Young, W. H., “On the Change of Order of Integration in an Improper Repeated Integral,” 1910, Trans. Gamb. Phil. Soc., vol. xxi. p. 364, § 4.Google Scholar
page 589 note † By the theorem enunciated at the end of § 1.
page 589 note ‡ Young, W. H., “On a Theorem of Tannery's and its Analogue in the Theory of Definite Integrals,” 1910, Mess. Math., p. 58 Google Scholar, Cor. 2. See also Bromwich's Introduction to the Theory of Infinite Series (1908), p. 438, where the condition of uniform convergence may be changed to bounded convergence.
page 591 note * This extension to an infinite interval of integration may be found in my recent paper on “Fourier's Repeated Integrals,” § 10, presented to the Royal Society of Edinburgh. For the original theorem see Riemann, B., Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe, § 10 Google Scholar; and H. Lebesgue, Leçons sur les séries trigmiométriques; also Hobson's, Theory of Functions of a Real Variable, p. 67.Google Scholar
page 591 note † See my paper on “Change of Order of Integration in an Improper Repeated Integral,” already quoted, § 9 (B).
page 595 note * This theorem, and that of § 15, can also be proved even more simply by the method of § 14.
page 599 note *
In fact, the series whose general terms are 
where O<e, converge absolutely. See my recent paper on Fourier integrals already cited, § 16.
page 599 note † Young, W. H., “On the Integration of Fourier Series” (1910)Google Scholar, Theorem 2, presented to the London Mathematical Society.
page 603 note * Young, W. H., “On the Theory of the Application of Expansions to Definite Integrals,” 1910, presented to the London Mathematical Society.Google Scholar