No CrossRef data available.
Article contents
XIII.—The Theory of Orthogonants in the Historical Order of Development up to 1860
Published online by Cambridge University Press: 15 September 2014
Extract
Notwithstanding the generalisations made by Jacobi and Cauchy, the special case with which the whole theory originated continued from time to time to attract attention. In 1843 William Thomson, afterwards known as Lord Kelvin, published under the signature “T.” in the Cambridge Math. Journ., iii. pp. 247–248, a short note in which he proved the detached theorem that if l1, m1, n1, l2, … be nine quantitiessuch that
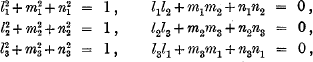
then it follows that
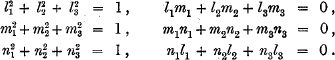
This led to a short paper by A. Göpel in the Archiv d. Math. u. Phys., iv. (1843) pp. 244–246.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1910
References
page 265 note * Published also in Archiv d. Math. u. Phys., xiii. pp. 276–281.
page 266 note *
I.e.
![]() of what afterwards came to be called the discriminant of x
3 − Px
2
y+Qxy
2 − Ry
3.
of what afterwards came to be called the discriminant of x
3 − Px
2
y+Qxy
2 − Ry
3.
page 267 note * The modern reader would do well to use Binet's theorem regarding the determinant which is viewable as the product of two rectangular arrays. Thus

and so forth.
page 268 note * The most appropriate designation would seem to be “Lagrange's determinantal equation,” because of this mathematician's early (1773) and successful investigation of the cubic. See his Œuvres complètes, iii. pp. 600–603.
page 272 note * Cayley, A., “On the motion of rotation of a solid body.” Cambridge Math. Journ., iii. pp. 224–232 Google Scholar: or Collected Math. Papers, i. pp. 28–35.
page 272 note † Cayley, A., “On certain results relating to quaternions.” Philos. Magazine, xxvi. pp. 141–145 Google Scholar: or Collected Math. Papers, i. pp. 123–126.
page 277 note * It should be noted that the theorem holds when δ is any determinant whatever. Further, there is implied in it another of at least equal importance, namely:—If δ stand for | a11a22…ann|, the equation whose roots are δ times the reciprocals of the roots of the equation is

An independent proof of this is readily obtained by substituting δ/Θ for Θ in the original equation, expanding the determinant in a series arranged according to descending powers of δ/Θ, using Θ n /δ as a multiplier, substituting A11, A12…for their equivalents, and returning to the determinant form.
page 278 note * On verifying this, see also the account of the related paper published in the Nouv. Annales de Math, for November 1852.
page 279 note * This proof, for the case where n = 3, is given free of determinants by Grunert, in the Archiv d. Math. u. Phys., xxix. (1857), pp. 442–446.Google Scholar
page 281 note * Cayley, A., “Sur la transformation d'une fonction quadratique en elle-même par des substitutions linéaires,” crelle's Journ., 1. pp. 288–299 Google Scholar: or Collected Math. Papers, ii. pp. 192–201. See also Brioschi in Annali di Sci. Mat. e Fis., v. pp. 201–206.
page 281 note † Cayley, A., “A Memoir on the Automorphic Linear Transformation of a Bipartite Quadric Function,” Philos. Trans. Roy. Soc. London, cxlviii. pp. 39–46 Google Scholar: or Collected Math. Papers, ii. pp. 497–505.
page 281 note ‡ Cambridge and Dublin Math. Journ., iv. pp. 47–50; and Quart. Journ. of Math., ii. pp. 192–195: or Collected Math. Papers, i. pp. 428–431, and iii. pp. 129–131.




