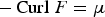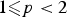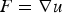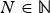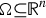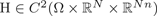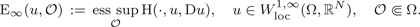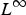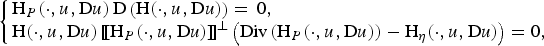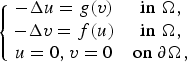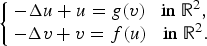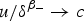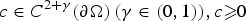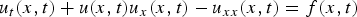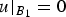Research Article
Analytic and geometric properties of dislocation singularities
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
-
- Article
- Export citation
A pointwise characterisation of the PDE system of vectorial calculus of variations in L∞
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1653-1669
-
- Article
- Export citation
Axisymmetric flows in the exterior of a cylinder
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1671-1698
-
- Article
- Export citation
An optimal improvement for the Hardy inequality on the hyperbolic space and related manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1699-1736
-
- Article
- Export citation
Ground state solutions of Hamiltonian elliptic systems in dimension two
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2019, pp. 1737-1768
-
- Article
- Export citation
Spectra of a class of non-symmetric operators in Hilbert spaces with applications to singular differential operators
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2019, pp. 1769-1790
-
- Article
- Export citation
Positive solutions of semilinear elliptic problems with a Hardy potential
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2019, pp. 1791-1804
-
- Article
- Export citation
Mass-conserving solutions to the Smoluchowski coagulation equation with singular kernel
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2019, pp. 1805-1825
-
- Article
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of:
-
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
-
- Article
-
- You have access
- Export citation
Multidimensional regular C-fraction with independent variables corresponding to formal multiple power series
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1853-1870
-
- Article
- Export citation
Regularity results for the 2D critical Oldroyd-B model in the corotational case
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1871-1913
-
- Article
- Export citation
Standing waves of modified Schrödinger equations coupled with the Chern–Simons gauge theory
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1915-1936
-
- Article
- Export citation
EXPLICIT cocycle formulas on finite abelian groups with applications to braided linear Gr-categories and Dijkgraaf–Witten invariants
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2019, pp. 1937-1964
-
- Article
- Export citation
Wave propagation for a class of non-local dispersal non-cooperative systems
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2019, pp. 1965-1997
-
- Article
- Export citation
Global well-posedness and large time behaviour of the viscous liquid-gas two-phase flow model in ℝ3
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2019, pp. 1999-2024
-
- Article
- Export citation
On non-autonomously forced Burgers equation with periodic and Dirichlet boundary conditions
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2019, pp. 2025-2054
-
- Article
- Export citation
Division algebras of slice functions
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2019, pp. 2055-2082
-
- Article
- Export citation
Sharp estimates of semistable radial solutions of k-Hessian equations
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2019, pp. 2083-2115
-
- Article
- Export citation
Bilinear forms on potential spaces in the unit circle
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2019, pp. 2117-2154
-
- Article
- Export citation
Spectral partitions for Sturm–Liouville problems
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2019, pp. 2155-2173
-
- Article
- Export citation