The two-well problem with surface energy
Published online by Cambridge University Press: 12 July 2007
Abstract
Let Ω be a bounded Lipschitz domain in R2, let H be a 2 × 2 diagonal matrix with det(H) = 1. Let ε > 0 and consider the functional
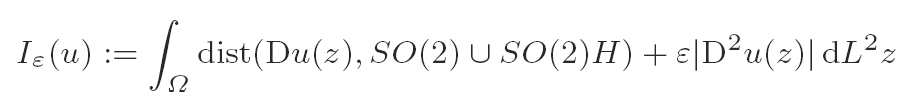 over AF ∩ W2,1(Ω), where AF is the class of functions from Ω satisfying affine boundary condition F. It can be shown by convex integration that there exists F ∉ SO(2) ∪ SO(2)H and u ∈ AF with I0(u) = 0. Let 0 < ζ1 < 1 < ζ2 < ∞,
over AF ∩ W2,1(Ω), where AF is the class of functions from Ω satisfying affine boundary condition F. It can be shown by convex integration that there exists F ∉ SO(2) ∪ SO(2)H and u ∈ AF with I0(u) = 0. Let 0 < ζ1 < 1 < ζ2 < ∞,
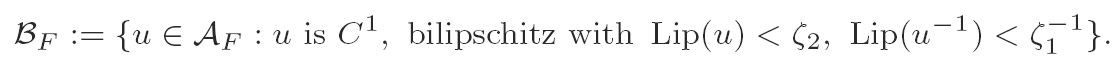 .
.
In this paper we begin the study of the asymptotics of mε ≔ infBF∩W2,1Iε for such F. This is one of the simplest minimization problems involving surface energy for which we can hope to see the effects of convex integration solutions. The only known lower bounds are lim infε→0mε/ε = ∞.
We link the behaviour of mε to the minimum of I0 over a suitable class of piecewise affine functions. Let {τi} be a triangulation of Ω by triangles of diameter less than h and let 

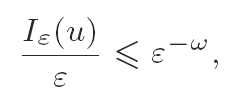 then, for h = ε(1+6399ω)/3201, the interpolant
then, for h = ε(1+6399ω)/3201, the interpolant 
Note that it is trivial that 

- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 136 , Issue 4 , August 2006 , pp. 795 - 805
- Copyright
- Copyright © Royal Society of Edinburgh 2006
- 5
- Cited by




