Article contents
Semi-classical solutions for Kirchhoff type problem with a critical frequency
Published online by Cambridge University Press: 27 May 2020
Abstract
In the present paper, we consider the following Kirchhoff type problem
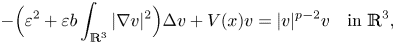 $$ -\Big(\varepsilon^2+\varepsilon b \int_{\mathbb R^3} | \nabla v|^2\Big) \Delta v+V(x)v=|v|^{p-2}v \quad {\rm in}\ \mathbb{R}^3, $$
$$ -\Big(\varepsilon^2+\varepsilon b \int_{\mathbb R^3} | \nabla v|^2\Big) \Delta v+V(x)v=|v|^{p-2}v \quad {\rm in}\ \mathbb{R}^3, $$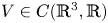 $V\in C(\mathbb R^3,\mathbb R)$ and ɛ is a positive parameter. The existence and multiplicity of semi-classical state solutions are obtained by variational method for this problem with several classes of critical frequency potentials, i.e.,
$V\in C(\mathbb R^3,\mathbb R)$ and ɛ is a positive parameter. The existence and multiplicity of semi-classical state solutions are obtained by variational method for this problem with several classes of critical frequency potentials, i.e., 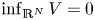 $\inf _{\mathbb R^N} V=0$. As to Kirchhoff type problem, little has been done for the critical frequency cases in the literature, especially the potential may vanish at infinity.
$\inf _{\mathbb R^N} V=0$. As to Kirchhoff type problem, little has been done for the critical frequency cases in the literature, especially the potential may vanish at infinity.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 2 , April 2021 , pp. 761 - 798
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 6
- Cited by





