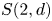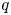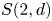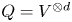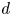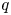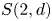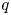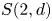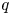1. Introduction
The theory of quasi-hereditary covers, introduced in [Reference Rouquier49], gives a framework to study finite-dimensional algebras of infinite global dimension through algebras having nicer homological properties, for instance, quasi-hereditary algebras via an exact functor known as Schur functor. Quasi-hereditary covers appear naturally and are useful in algebraic Lie theory, representation, theory and homological algebra. In particular, they are in the background of Auslander's correspondence [Reference Auslander2] and in Iyama's proof of finiteness of representation dimension [Reference Iyama37]. Further, quasi-hereditary algebras arise quite naturally in the representation theory of algebraic groups [Reference Cline, Parshall and Scott4, Reference Parshall and Scott47] and algebras of global dimension at most two are quasi-hereditary.
Schur algebras $S(n,d)$![]() form an important class of quasi-hereditary algebras, they provide a link between polynomial representations of general linear groups and representations of symmetric groups. Classically, when $n\geq d$
form an important class of quasi-hereditary algebras, they provide a link between polynomial representations of general linear groups and representations of symmetric groups. Classically, when $n\geq d$![]() , the Schur algebra, via the Schur functor, is a quasi-hereditary cover of the group algebra of the symmetric group $\mathcal {S}_d$
, the Schur algebra, via the Schur functor, is a quasi-hereditary cover of the group algebra of the symmetric group $\mathcal {S}_d$![]() . This connection is one of the versions of Schur–Weyl duality. Indeed, this formulation clarifies the connection between the representation theory of symmetric groups and the representation theory of Schur algebras, by detecting how the subcategories of modules with Weyl filtrations and of modules with dual Specht filtrations are related and how the Yoneda extension groups in these subcategories are related by the Schur functor (see also [Reference Hemmer and Nakano35]). Further, this connection becomes stronger as the characteristic of the ground field increases. It was first observed in [Reference Fang and Koenig29] that this behaviour is captured by the classical dominant dimension. However, this is not the case for all quasi-hereditary covers.
. This connection is one of the versions of Schur–Weyl duality. Indeed, this formulation clarifies the connection between the representation theory of symmetric groups and the representation theory of Schur algebras, by detecting how the subcategories of modules with Weyl filtrations and of modules with dual Specht filtrations are related and how the Yoneda extension groups in these subcategories are related by the Schur functor (see also [Reference Hemmer and Nakano35]). Further, this connection becomes stronger as the characteristic of the ground field increases. It was first observed in [Reference Fang and Koenig29] that this behaviour is captured by the classical dominant dimension. However, this is not the case for all quasi-hereditary covers.
To fix this, in [Reference Cruz10] the concepts of relative dominant dimension and relative codominant dimension with respect to a module were introduced. Further, in [Reference Cruz10] these homological invariants were exploited to create new quasi-hereditary covers. With this, the link between Schur algebras and symmetric groups can be regarded as a special case of quasi-hereditary covers of quotients of Iwahori–Hecke algebras.
Temperley–Lieb algebras are quotients of Iwahori–Hecke algebras and they sometimes have infinite global dimension. They were introduced in [Reference Temperley and Lieb50] in the context of statistical mechanics and they were popularized by Jones, in particular, they are used to define the Jones polynomial (see [Reference Jones41]). However, contrary to Iwahori–Hecke algebras no Hemmer–Nakano type result was known for Temperley–Lieb algebras until now. Both classes of algebras are cellular (see e.g. [Reference Graham and Lehrer32]) and so an important property that they have in common is the existence of a simple preserving duality.
Quasi-hereditary algebras with a simple preserving duality always have even global dimension. Mazorchuk and Ovsienko have shown this fact in [Reference Mazorchuk and Ovsienko45] by proving that the global dimension of a quasi-hereditary algebra with a simple preserving duality is exactly twice the projective dimension of the characteristic tilting module. Later, under much stronger conditions, the analogue result for dominant dimension was obtained in [Reference Fang and Koenig29] by Fang and Koenig exploiting that a faithful projective–injective module is a summand of the characteristic tilting module.
The present paper has two aims. First, we will establish that the relative dominant dimension of a quasi-hereditary algebra with respect to any summand of its characteristic tilting module is always twice as large as that of the characteristic tilting module, in the case when the algebra has a simple preserving duality. In particular, this homological invariant is always even for such quasi-hereditary algebras. Further, Fang and Koenig's result can then be recovered from ours by just fixing the summand to be a projective–injective module. Therefore, we obtain an alternative approach to the classical case of dominant dimension without any further assumptions.
The second aim is to study classes of quasi-hereditary covers of Temperley–Lieb algebras and their link to the representation theory of Temperley–Lieb algebras. In particular, we aim to completely understand such a connection using the representation theory of $q$![]() -Schur algebras and their Ringel duals.
-Schur algebras and their Ringel duals.
Questions to be addressed and setup
To make our results precise, we need further notation. In general, assume that $B$![]() is a finite-dimensional algebra over an algebraically closed field. A pair $(A, P)$
is a finite-dimensional algebra over an algebraically closed field. A pair $(A, P)$![]() is a quasi-hereditary cover of $B$
is a quasi-hereditary cover of $B$![]() if $A$
if $A$![]() is a quasi-hereditary algebra, $P$
is a quasi-hereditary algebra, $P$![]() is a finitely generated projective $A$
is a finitely generated projective $A$![]() -module such that $B=\operatorname {End}_A(P)^{op}$
-module such that $B=\operatorname {End}_A(P)^{op}$![]() , and in addition the restriction of the associated Schur functor $F:= \operatorname {Hom}_A(P, -)\colon A\!\operatorname {-mod} \rightarrow B\!\operatorname {-mod}$
, and in addition the restriction of the associated Schur functor $F:= \operatorname {Hom}_A(P, -)\colon A\!\operatorname {-mod} \rightarrow B\!\operatorname {-mod}$![]() to the subcategory of finitely generated projective $A$
to the subcategory of finitely generated projective $A$![]() -modules is full and faithful.
-modules is full and faithful.
Let $\mathcal {F}(\Delta )$![]() be the category of $A$
be the category of $A$![]() -modules which have a filtration by standard modules. We would like to get information on the category $\mathcal {F}(F\Delta )$
-modules which have a filtration by standard modules. We would like to get information on the category $\mathcal {F}(F\Delta )$![]() of $B$
of $B$![]() -modules which have a filtration by images under $F$
-modules which have a filtration by images under $F$![]() of standard modules. Specifically, we would like the functor $F$
of standard modules. Specifically, we would like the functor $F$![]() to be faithful on $\mathcal {F}(\Delta )$
to be faithful on $\mathcal {F}(\Delta )$![]() and to induce isomorphisms ${\rm Ext}_A^j(X, Y) \to {\rm Ext}^j_B(FX, FY)$
and to induce isomorphisms ${\rm Ext}_A^j(X, Y) \to {\rm Ext}^j_B(FX, FY)$![]() for $X, Y$
for $X, Y$![]() modules in $\mathcal {F}(\Delta )$
modules in $\mathcal {F}(\Delta )$![]() . If this is the case for $0\leq j\leq i$
. If this is the case for $0\leq j\leq i$![]() , then $(A, P)$
, then $(A, P)$![]() is called an $i$
is called an $i$![]() -$\mathcal {F}(\Delta )$
-$\mathcal {F}(\Delta )$![]() cover of $B$
cover of $B$![]() . The largest $n$
. The largest $n$![]() such that $(A, P)$
such that $(A, P)$![]() is an $n$
is an $n$![]() -$\mathcal {F}(\Delta )$
-$\mathcal {F}(\Delta )$![]() cover of $B$
cover of $B$![]() is called the Hemmer–Nakano dimension of $\mathcal {F}(\Delta )$
is called the Hemmer–Nakano dimension of $\mathcal {F}(\Delta )$![]() in [Reference Fang and Koenig29]. When $n \geq 1$
in [Reference Fang and Koenig29]. When $n \geq 1$![]() , filtration multiplicities in the category $\mathcal {F}(F\Delta )$
, filtration multiplicities in the category $\mathcal {F}(F\Delta )$![]() are well-defined, which places the Hemmer–Nakano theorem on Specht filtrations into a wider context. When $B$
are well-defined, which places the Hemmer–Nakano theorem on Specht filtrations into a wider context. When $B$![]() is self-injective, Fang and Koenig showed that this dimension is controlled by the dominant dimension of a characteristic tilting module. In addition, they proved that if $B$
is self-injective, Fang and Koenig showed that this dimension is controlled by the dominant dimension of a characteristic tilting module. In addition, they proved that if $B$![]() is a symmetric algebra and the quasi-hereditary cover admits a certain simple preserving duality, then the dominant dimension of a characteristic tilting module is exactly half of the dominant dimension of $A$
is a symmetric algebra and the quasi-hereditary cover admits a certain simple preserving duality, then the dominant dimension of a characteristic tilting module is exactly half of the dominant dimension of $A$![]() .
.
Recently, in [Reference Cruz10], the situation was generalized to include cases where $B$![]() is not necessarily self-injective. Moreover, it was proved in [Reference Cruz10] that the Hemmer–Nakano dimension of $\mathcal {F}(\Delta )$
is not necessarily self-injective. Moreover, it was proved in [Reference Cruz10] that the Hemmer–Nakano dimension of $\mathcal {F}(\Delta )$![]() associated with a $0$
associated with a $0$![]() -$\mathcal {F}(\Delta )$
-$\mathcal {F}(\Delta )$![]() cover can be determined using the relative codominant dimension of a characteristic tilting module with respect to a certain summand of the characteristic tilting module.
cover can be determined using the relative codominant dimension of a characteristic tilting module with respect to a certain summand of the characteristic tilting module.
The concepts of relative dominant and relative codominant dimension (see the definition below in § 2.3) and the concept of quasi-hereditary cover can be considered in an integral setup, that is, both of these concepts can be studied for Noetherian algebras which are finitely generated and projective as modules over a regular commutative Noetherian ring. In [Reference Cruz9], methods were developed to reduce the computations of Hemmer–Nakano dimensions in the integral setup to the setup where the ground ring is an algebraically closed field. So, it will be enough for our purposes to concentrate on the case when the coefficient ring is an algebraically closed field.
The new approach to construct quasi-hereditary covers appears in [Reference Cruz10, Theorem 5.3.1] and [Reference Cruz10, Theorem 8.1.5] when applied to Schur algebras (and $q$![]() -Schur algebras). The novelty is that it uses the Ringel dual of a Schur algebra, rather than a Schur algebra, and works for arbitrary parameters $n, d$
-Schur algebras). The novelty is that it uses the Ringel dual of a Schur algebra, rather than a Schur algebra, and works for arbitrary parameters $n, d$![]() .
.
This can, in particular, be applied to the study of Temperley–Lieb algebras. Recall that $S(n, d)$![]() is isomorphic to the centralizer algebra of $\mathcal {S}_d$
is isomorphic to the centralizer algebra of $\mathcal {S}_d$![]() in the endomorphism algebra of the tensor power $(K^n)^{\otimes d}$
in the endomorphism algebra of the tensor power $(K^n)^{\otimes d}$![]() , where $(K^n)^{\otimes d}$
, where $(K^n)^{\otimes d}$![]() affords a module structure over $\mathcal {S}_d$
affords a module structure over $\mathcal {S}_d$![]() by place permutation for a field $K$
by place permutation for a field $K$![]() . Furthermore, $V^{\otimes d}:=(K^n)^{\otimes d}$
. Furthermore, $V^{\otimes d}:=(K^n)^{\otimes d}$![]() is in the additive closure of a characteristic tilting module over $S(n, d)$
is in the additive closure of a characteristic tilting module over $S(n, d)$![]() . When $n=2$
. When $n=2$![]() , the centralizer of $S(2, d)$
, the centralizer of $S(2, d)$![]() (and its $q$
(and its $q$![]() -analogue) in the endomorphism algebra of the tensor power can be identified with a Temperley–Lieb algebra. Indeed, all Temperley–Lieb algebras arise in this way. Our cases of interest have a simple preserving duality, and in such a case, for this situation, we can without ambiguity interchange the concepts relative dominant dimension and relative codominant dimension.
-analogue) in the endomorphism algebra of the tensor power can be identified with a Temperley–Lieb algebra. Indeed, all Temperley–Lieb algebras arise in this way. Our cases of interest have a simple preserving duality, and in such a case, for this situation, we can without ambiguity interchange the concepts relative dominant dimension and relative codominant dimension.
Denote by $Q\!\operatorname {-domdim}_A X$![]() the relative dominant dimension of an $A$
the relative dominant dimension of an $A$![]() -module $X$
-module $X$![]() with respect to $Q$
with respect to $Q$![]() . In this context, the following questions arise:
. In this context, the following questions arise:
(1) What is the value of $V^{\otimes d}\!\operatorname {-domdim}_{S(2, d)} T$
 , where $T$
, where $T$ is a characteristic tilting module of the quasi-hereditary algebra $S(2, d)$
is a characteristic tilting module of the quasi-hereditary algebra $S(2, d)$ ? What happens to this value when we replace a Schur algebra by a $q$
? What happens to this value when we replace a Schur algebra by a $q$ -Schur algebra?
-Schur algebra?(2) The Ringel duals of Schur algebras as well as Schur algebras have a simple preserving duality. Can we expect, like in the classical case (see [Reference Fang and Koenig29, Theorem 4.3]), the equality $V^{\otimes d}\!\operatorname {-domdim} S(n, d)=2\cdot V^{\otimes d}\!\operatorname {-domdim}_{S(n, d)} T$
 to hold in general?
to hold in general?(3) Can we expect the quasi-hereditary cover of the Temperley–Lieb algebra constructed in [Reference Cruz10, Theorem 8.1.5] to be unique, in some meaningful way?
Our goal in this paper is to provide answers to these three questions.
Main results
Surprisingly, the answer to (2) is positive without using extra structure on $S(n, d)$![]() besides the quasi-hereditary structure and the existence of a simple preserving duality.
besides the quasi-hereditary structure and the existence of a simple preserving duality.
Theorem A (see theorem 3.1)
Let $A$![]() be a quasi-hereditary algebra over a field $K$
be a quasi-hereditary algebra over a field $K$![]() . Suppose that there exists a simple preserving duality ${}^\diamond \! (-) \colon A\!\operatorname {-mod} \to A\!\operatorname {-mod}$
. Suppose that there exists a simple preserving duality ${}^\diamond \! (-) \colon A\!\operatorname {-mod} \to A\!\operatorname {-mod}$![]() . Let $T$
. Let $T$![]() be the characteristic tilting module of $A$
be the characteristic tilting module of $A$![]() . Assume that $Q\in {\rm add}(T)$
. Assume that $Q\in {\rm add}(T)$![]() . Then
. Then
This means that for $A$![]() as in the theorem, the characteristic tilting module $T$
as in the theorem, the characteristic tilting module $T$![]() is a test module to compute the relative dominant dimension of $A$
is a test module to compute the relative dominant dimension of $A$![]() with respect to direct summands of $T$
with respect to direct summands of $T$![]() . By fixing $Q$
. By fixing $Q$![]() to be a projective–injective module in this setting, this result generalizes [Reference Fang and Koenig29, Theorem 4.3] and our methods provide a new proof to their case without using any information on $A$
to be a projective–injective module in this setting, this result generalizes [Reference Fang and Koenig29, Theorem 4.3] and our methods provide a new proof to their case without using any information on $A$![]() being an endomorphism algebra of a faithful module over a symmetric algebra. In particular, our result also works for dominant dimension exactly zero and when $A$
being an endomorphism algebra of a faithful module over a symmetric algebra. In particular, our result also works for dominant dimension exactly zero and when $A$![]() is the endomorphism algebra of a faithful module over a self-injective algebra. The left-hand side of the equation in theorem A is also known as the faithful dimension of $Q$
is the endomorphism algebra of a faithful module over a self-injective algebra. The left-hand side of the equation in theorem A is also known as the faithful dimension of $Q$![]() in the sense of [Reference Buan and Solberg3]. This means that the faithful dimension of $Q$
in the sense of [Reference Buan and Solberg3]. This means that the faithful dimension of $Q$![]() fully determines the connection between $\operatorname {End}_A(Q)$
fully determines the connection between $\operatorname {End}_A(Q)$![]() and its quasi-hereditary cover formed by the Ringel dual when the $A$
and its quasi-hereditary cover formed by the Ringel dual when the $A$![]() is a quasi-hereditary with a simple preserving duality.
is a quasi-hereditary with a simple preserving duality.
Theorem A has many applications for quasi-hereditary algebras with a simple preserving duality. For instance, it can be used to reprove a result of [Reference Hu and Xiao36] which states that there exists a unique minimal direct summand of the characteristic tilting module affording a double centralizer property (see Appendix A). It can also be used to reprove that Ringel duality preserves dominant dimension in this setting.
Combining techniques of Frobenius twisted tensor products with theorem A we obtain a complete answer to (1):
Theorem B (see also theorem 5.8 for the $q$ -version)
-version)
Let $K$![]() be a field and let $A$
be a field and let $A$![]() be the Schur algebra $S_{K}(2, d)$
be the Schur algebra $S_{K}(2, d)$![]() and $T$
and $T$![]() be the characteristic tilting module of $A$
be the characteristic tilting module of $A$![]() . Then,
. Then,

In this case, $Q=V^{\otimes d}$![]() and ${\rm End}_A(Q)$
and ${\rm End}_A(Q)$![]() is the quotient of the symmetric group algebra, modulo the kernel of the action on $V^{\otimes d}$
is the quotient of the symmetric group algebra, modulo the kernel of the action on $V^{\otimes d}$![]() , and theorem B provides information about this quotient. When the relative dominant dimension is infinite, this quotient is Morita equivalent to the Ringel dual of $A$
, and theorem B provides information about this quotient. When the relative dominant dimension is infinite, this quotient is Morita equivalent to the Ringel dual of $A$![]() . When $\operatorname {char} K=2$
. When $\operatorname {char} K=2$![]() and $d$
and $d$![]() is even theorem B shows that for $d\geq 6$
is even theorem B shows that for $d\geq 6$![]() , the Hemmer–Nakano dimension is positive. Hence, in this case, the filtration multiplicities in the category $\mathcal {F}(F\Delta )$
, the Hemmer–Nakano dimension is positive. Hence, in this case, the filtration multiplicities in the category $\mathcal {F}(F\Delta )$![]() are well-defined. These are the modules filtered by Specht modules labelled by 2-part partitions and this provides new information: in contrast, filtration multiplicities for arbitrary Specht modules are not well-defined for $p=2$
are well-defined. These are the modules filtered by Specht modules labelled by 2-part partitions and this provides new information: in contrast, filtration multiplicities for arbitrary Specht modules are not well-defined for $p=2$![]() , as shown in [Reference Hemmer and Nakano35]. Further, theorem B and its $q$
, as shown in [Reference Hemmer and Nakano35]. Further, theorem B and its $q$![]() -version generalizes [Reference Coulembier and Zhang7, Theorem C (3), (4)] for Temperley–Lieb algebras. For the quantum case, the same approach works. In the quantum case, the algebra $A$
-version generalizes [Reference Coulembier and Zhang7, Theorem C (3), (4)] for Temperley–Lieb algebras. For the quantum case, the same approach works. In the quantum case, the algebra $A$![]() is the $q$
is the $q$![]() -Schur algebra $S_{K, q}(2, d)$
-Schur algebra $S_{K, q}(2, d)$![]() , which can be defined as the centralizer of the Hecke algebra $H_q(d)$
, which can be defined as the centralizer of the Hecke algebra $H_q(d)$![]() acting on $V^{\otimes d}$
acting on $V^{\otimes d}$![]() , again for $\dim V=2$
, again for $\dim V=2$![]() and in the theorem the characteristic is replaced by the quantum characteristic. When we have $v\in K$
and in the theorem the characteristic is replaced by the quantum characteristic. When we have $v\in K$![]() such that $v^2=q$
such that $v^2=q$![]() and $\delta = -v-v^{-1}$
and $\delta = -v-v^{-1}$![]() , the Temperley–Lieb algebra $TL_{K,d}(\delta )$
, the Temperley–Lieb algebra $TL_{K,d}(\delta )$![]() is a quotient of this action. In both cases, the real difficulty lies in the case in which the characteristic (resp. quantum characteristic) is two.
is a quotient of this action. In both cases, the real difficulty lies in the case in which the characteristic (resp. quantum characteristic) is two.
For tilting modules in general, going beyond the characteristic tilting module, we can construct, via mutation, new tilting modules. In the context of Buan and Solberg's work [Reference Buan and Solberg3], theorem B means that $V^{\otimes d}$![]() over $S(2, d)$
over $S(2, d)$![]() is either a full tilting module or there are precisely $d+1$
is either a full tilting module or there are precisely $d+1$![]() indecomposable $S(2, d)$
indecomposable $S(2, d)$![]() -modules $X$
-modules $X$![]() making $X\oplus V^{\otimes d}$
making $X\oplus V^{\otimes d}$![]() a full tilting module.
a full tilting module.
Using theorem B together with cover theory, we obtain a positive answer to question (3) when we consider the Laurent polynomial ring over the integers as coefficient ring and $d>2$![]() (see § 7 and corollary 7.5). In such a case, the (integral) Schur functor $F$
(see § 7 and corollary 7.5). In such a case, the (integral) Schur functor $F$![]() induces an exact equivalence $\mathcal {F}(\Delta )\rightarrow \mathcal {F}(F\Delta ).$
induces an exact equivalence $\mathcal {F}(\Delta )\rightarrow \mathcal {F}(F\Delta ).$![]() The quasi-hereditary cover of the integral Temperley–Lieb algebra formed by the Ringel dual of a $q$
The quasi-hereditary cover of the integral Temperley–Lieb algebra formed by the Ringel dual of a $q$![]() -Schur algebra is the unique quasi-hereditary cover which induces this exact equivalence. If $d=2$
-Schur algebra is the unique quasi-hereditary cover which induces this exact equivalence. If $d=2$![]() , the Temperley–Lieb algebra is exactly an Iwahori–Hecke algebra, but this is new information when $d>2$
, the Temperley–Lieb algebra is exactly an Iwahori–Hecke algebra, but this is new information when $d>2$![]() .
.
We emphasize that the specialization of theorem A to projective–injective modules played a key role in determining the dominant dimension of Schur algebras $S(n, d)$![]() with $n\geq d$
with $n\geq d$![]() in [Reference Fang and Koenig29] (also their $q$
in [Reference Fang and Koenig29] (also their $q$![]() -analogues [Reference Fang and Miyachi30]). It is our expectation that its use will be crucial to determine, in particular, $V^{\otimes d}\!\operatorname {-domdim} S(n, d)$
-analogues [Reference Fang and Miyachi30]). It is our expectation that its use will be crucial to determine, in particular, $V^{\otimes d}\!\operatorname {-domdim} S(n, d)$![]() and $\operatorname {domdim} S(n, d)$
and $\operatorname {domdim} S(n, d)$![]() also in the cases $2< n< d$
also in the cases $2< n< d$![]() while the latter is also an open problem for $n=2$
while the latter is also an open problem for $n=2$![]() .
.
This article is organized as follows: in § 2, we introduce the notation and the main properties of relative dominant dimension with respect to a module, split quasi-hereditary algebras with a simple preserving duality, and cover theory to be used throughout the paper. In § 3, we discuss elementary results on relative injective dimensions and we give the proof of theorem A. We then deduce that the dominant dimension is a lower bound for the faithful dimension of a faithful direct summand of a characteristic tilting module fixed by a simple preserving duality (see proposition 3.6). In § 4, we collect results on the quasi-hereditary structure of Schur algebras $S(2, d)$![]() , in particular, reduction techniques and how to construct partial tilting and standard modules inductively using the Frobenius twist functor. In § 5, we compute the relative dominant dimension of $S(2, d)$
, in particular, reduction techniques and how to construct partial tilting and standard modules inductively using the Frobenius twist functor. In § 5, we compute the relative dominant dimension of $S(2, d)$![]() with respect to $V^{\otimes d}$
with respect to $V^{\otimes d}$![]() in terms of $V^{\otimes d}\!\operatorname {-domdim}_{S(2, d)} T$
in terms of $V^{\otimes d}\!\operatorname {-domdim}_{S(2, d)} T$![]() , where $T$
, where $T$![]() is a characteristic tilting module of $S(2, d)$
is a characteristic tilting module of $S(2, d)$![]() . In particular, we give the proof of theorem B and its $q$
. In particular, we give the proof of theorem B and its $q$![]() -analogue (see theorem 5.8). As an application, we compute all complements of the almost complete tilting module $V^{\otimes 4}$
-analogue (see theorem 5.8). As an application, we compute all complements of the almost complete tilting module $V^{\otimes 4}$![]() when the ground field has characteristic two (see § 5.3). In § 6, we recall that all Temperley–Lieb algebras can be realized as the centralizer algebras of $q$
when the ground field has characteristic two (see § 5.3). In § 6, we recall that all Temperley–Lieb algebras can be realized as the centralizer algebras of $q$![]() -Schur algebras in the endomorphism algebra of the tensor power $V^{\otimes d}$
-Schur algebras in the endomorphism algebra of the tensor power $V^{\otimes d}$![]() . As a consequence, we determine the value of Hemmer–Nakano dimension of $\mathcal {F}(\Delta )$
. As a consequence, we determine the value of Hemmer–Nakano dimension of $\mathcal {F}(\Delta )$![]() in all cases associated with the cover of the Temperley–Lieb algebra formed by the Ringel dual of a $q$
in all cases associated with the cover of the Temperley–Lieb algebra formed by the Ringel dual of a $q$![]() -Schur algebra. This computation is contained in corollary 6.8. In § 7, we determine the Hemmer–Nakano dimension of the abovementioned quasi-hereditary cover in the integral setup, dividing the study into two cases: the coefficient ring being or not $2$
-Schur algebra. This computation is contained in corollary 6.8. In § 7, we determine the Hemmer–Nakano dimension of the abovementioned quasi-hereditary cover in the integral setup, dividing the study into two cases: the coefficient ring being or not $2$![]() -partially $q$
-partially $q$![]() -divisible (see § 7.1). When the coefficient ring does not have such property, we show that a quasi-hereditary cover with such coefficient ring has better properties. We conclude by addressing the problem of the uniqueness of this cover (see § 7.2). In Appendix A, we provide two applications of theorem A that involve faithful direct summands of the characteristic tilting module.
-divisible (see § 7.1). When the coefficient ring does not have such property, we show that a quasi-hereditary cover with such coefficient ring has better properties. We conclude by addressing the problem of the uniqueness of this cover (see § 7.2). In Appendix A, we provide two applications of theorem A that involve faithful direct summands of the characteristic tilting module.
2. Preliminaries
2.1. The setting
This follows [Reference Cruz10]. Throughout we fix a Noetherian commutative ring $R$![]() with identity, and $A$
with identity, and $A$![]() is an $R$
is an $R$![]() -algebra which is finitely generated and projective as an $R$
-algebra which is finitely generated and projective as an $R$![]() -module. We refer to $A$
-module. We refer to $A$![]() as a projective Noetherian $R$
as a projective Noetherian $R$![]() -algebra. The set of invertible elements of $R$
-algebra. The set of invertible elements of $R$![]() is denoted by $R^\times$
is denoted by $R^\times$![]() .
.
We denote by $A\!\operatorname {-mod}$![]() the category of finitely generated (left) $A$
the category of finitely generated (left) $A$![]() -modules. Given $M\in A\!\operatorname {-mod}$
-modules. Given $M\in A\!\operatorname {-mod}$![]() , we denote by $\!\operatorname {add}_A M$
, we denote by $\!\operatorname {add}_A M$![]() (or just $\!\operatorname {add} M$
(or just $\!\operatorname {add} M$![]() ) the full subcategory of $A\!\operatorname {-mod}$
) the full subcategory of $A\!\operatorname {-mod}$![]() whose modules are direct summands of a finite direct sum of copies of $M$
whose modules are direct summands of a finite direct sum of copies of $M$![]() . We also denote $\!\operatorname {add} A$
. We also denote $\!\operatorname {add} A$![]() by $A\!\operatorname {-proj}$
by $A\!\operatorname {-proj}$![]() .
.
The endomorphism algebra of a module $M\in A\!\operatorname {-mod}$![]() is denoted by ${\rm End}_A(M)$
is denoted by ${\rm End}_A(M)$![]() . We denote by $D_R$
. We denote by $D_R$![]() or just $D$
or just $D$![]() the standard duality ${\rm Hom}_R(-, R): A\!\operatorname {-mod} \to A^{op}\!\operatorname {-mod}$
the standard duality ${\rm Hom}_R(-, R): A\!\operatorname {-mod} \to A^{op}\!\operatorname {-mod}$![]() where $A^{op}$
where $A^{op}$![]() is the opposite algebra of $A$
is the opposite algebra of $A$![]() .
.
A module $M \in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() is said to be $(A, R)$
is said to be $(A, R)$![]() -injective if it belongs to ${\rm add}\, DA$
-injective if it belongs to ${\rm add}\, DA$![]() , and we write $(A,R)\!\operatorname {-inj}\cap R\!\operatorname {-proj}$
, and we write $(A,R)\!\operatorname {-inj}\cap R\!\operatorname {-proj}$![]() for the full subcategory of $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$
for the full subcategory of $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() whose modules are $(A, R)$
whose modules are $(A, R)$![]() -injective.
-injective.
Furthermore, an exact sequence of $A$![]() -modules which is split as an exact sequence of $R$
-modules which is split as an exact sequence of $R$![]() -modules is said to be $(A, R)$
-modules is said to be $(A, R)$![]() -exact. In particular, an $(A, R)$
-exact. In particular, an $(A, R)$![]() -monomorphism is a homomorphism $f: M\to N$
-monomorphism is a homomorphism $f: M\to N$![]() that fits into an $(A,R)$
that fits into an $(A,R)$![]() -exact sequence $0\to M\stackrel {f}\to N$
-exact sequence $0\to M\stackrel {f}\to N$![]() .
.
Given a left exact covariant additive functor $G$![]() , we say that $X$
, we say that $X$![]() is a $G$
is a $G$![]() -acyclic object if $\operatorname {R}^{i>0}G(X)=0$
-acyclic object if $\operatorname {R}^{i>0}G(X)=0$![]() . An exact sequence $0\rightarrow L\rightarrow X_0\rightarrow X_1\rightarrow \cdots$
. An exact sequence $0\rightarrow L\rightarrow X_0\rightarrow X_1\rightarrow \cdots$![]() is called a $G$
is called a $G$![]() -acyclic coresolution of $L$
-acyclic coresolution of $L$![]() if all objects $X_0, X_1, \ldots$
if all objects $X_0, X_1, \ldots$![]() are $G$
are $G$![]() -acyclic. Given $X\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$
-acyclic. Given $X\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() , we denote by $X^\perp$
, we denote by $X^\perp$![]() the full subcategory
the full subcategory
and by ${}^\perp X$![]() the full subcategory
the full subcategory
2.2. Approximations
Assume that $A$![]() is an $R$
is an $R$![]() -algebra as above, and $Q$
-algebra as above, and $Q$![]() is a fixed module in $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$
is a fixed module in $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() .
.
An $A$![]() -homomorphism $f: M\to N$
-homomorphism $f: M\to N$![]() is a left $\!\operatorname {add}_A Q$
is a left $\!\operatorname {add}_A Q$![]() -approximation of $M$
-approximation of $M$![]() provided that $N$
provided that $N$![]() belongs to $\!\operatorname {add}_A Q$
belongs to $\!\operatorname {add}_A Q$![]() , and moreover the induced map
, and moreover the induced map
is surjective for every $X\in \!\operatorname {add}_A Q$![]() . Dually, one defines right $\!\operatorname {add}_A Q$
. Dually, one defines right $\!\operatorname {add}_A Q$![]() -approximations. Note that every module $M \in A\!\operatorname {-mod}$
-approximations. Note that every module $M \in A\!\operatorname {-mod}$![]() has a left and a right $\!\operatorname {add}_A Q$
has a left and a right $\!\operatorname {add}_A Q$![]() -approximation.
-approximation.
2.3. Relative (co)dominant dimension with respect to a module
We recall from [Reference Cruz10] the definition of relative (co)dominant dimensions.
Let $Q, X\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() . If $X$
. If $X$![]() does not admit a left $\!\operatorname {add} Q$
does not admit a left $\!\operatorname {add} Q$![]() -approximation which is an $(A, R)$
-approximation which is an $(A, R)$![]() -monomorphism then the relative dominant dimension of $X$
-monomorphism then the relative dominant dimension of $X$![]() with respect to $Q$
with respect to $Q$![]() is zero. Otherwise, the relative dominant dimension of $X$
is zero. Otherwise, the relative dominant dimension of $X$![]() with respect to $Q$
with respect to $Q$![]() , denoted by $Q\!\operatorname {-domdim}_{(A, R)}X$
, denoted by $Q\!\operatorname {-domdim}_{(A, R)}X$![]() , or $Q\!\operatorname {-domdim}_A X$
, or $Q\!\operatorname {-domdim}_A X$![]() when $R$
when $R$![]() is a field, is the supremum of all $n\in \mathbb {N}$
is a field, is the supremum of all $n\in \mathbb {N}$![]() such that there is an $(A, R)$
such that there is an $(A, R)$![]() -exact sequence:
-exact sequence:
with all $Q_i\in \!\operatorname {add} Q$![]() , which remains exact under ${\rm Hom}_A(-, Q)$
, which remains exact under ${\rm Hom}_A(-, Q)$![]() .
.
Dually, one defines the relative codominant dimension, denoted by $Q{\rm }\hbox{-}{\rm codomdim}_{(A, R)}(X)$![]() with $Q, X$
with $Q, X$![]() as above: if $X$
as above: if $X$![]() does not admit a surjective right $\!\operatorname {add} Q$
does not admit a surjective right $\!\operatorname {add} Q$![]() -approximation, then ${Q\!\operatorname {-codomdim}_{(A, R)}(X)} = 0$
-approximation, then ${Q\!\operatorname {-codomdim}_{(A, R)}(X)} = 0$![]() . Otherwise it is the supremum of all $n\in \mathbb {N}$
. Otherwise it is the supremum of all $n\in \mathbb {N}$![]() such that there is an $(A, R)$
such that there is an $(A, R)$![]() -exact sequence:
-exact sequence:
with all $Q_i\in \!\operatorname {add} Q$![]() , which remains exact under ${\rm Hom}_A(Q, -)$
, which remains exact under ${\rm Hom}_A(Q, -)$![]() .
.
Hence, $Q\!\operatorname {-codomdim}_{(A, R)} X=DQ\!\operatorname {-domdim}_{(A^{op}, R)} DX$![]() . By $Q\!\operatorname {-domdim} {(A, R)}$
. By $Q\!\operatorname {-domdim} {(A, R)}$![]() we mean the value $Q\!\operatorname {-domdim}_{(A, R)} A$
we mean the value $Q\!\operatorname {-domdim}_{(A, R)} A$![]() . We will write $Q\!\operatorname {-codomdim}_A X$
. We will write $Q\!\operatorname {-codomdim}_A X$![]() to denote $Q\!\operatorname {-codomdim}_{(A, R)} X$
to denote $Q\!\operatorname {-codomdim}_{(A, R)} X$![]() when $R$
when $R$![]() is a field.
is a field.
2.3.1. Results from [10]
We will give criteria towards finding these invariants. These depend essentially on the theorems [Reference Cruz10, Theorems 3.1.1, 3.1.4] and their dual versions. We briefly describe part of it. Assume $Q\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() such that the endomorphism algebra of $Q$
such that the endomorphism algebra of $Q$![]() , $B=\operatorname {End}_A(Q)$
, $B=\operatorname {End}_A(Q)$![]() , is a projective Noetherian $R$
, is a projective Noetherian $R$![]() -algebra. The Schur functor $F=\operatorname {Hom}_A(Q, -)$
-algebra. The Schur functor $F=\operatorname {Hom}_A(Q, -)$![]() has a left adjoint $\mathcal {I}:=Q\otimes _B -$
has a left adjoint $\mathcal {I}:=Q\otimes _B -$![]() . Let $\chi$
. Let $\chi$![]() be the associated counit $\chi \colon \mathcal {I}F\rightarrow \operatorname {id}_{A\!\operatorname {-mod}}$
be the associated counit $\chi \colon \mathcal {I}F\rightarrow \operatorname {id}_{A\!\operatorname {-mod}}$![]() . Explicitly, if $M$
. Explicitly, if $M$![]() belongs to $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$
belongs to $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() , then $\chi _M$
, then $\chi _M$![]() is the $A$
is the $A$![]() -homomorphism:
-homomorphism:
By Theorem 3.1.1 of [Reference Cruz10], for a module $M\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() , $Q\!\operatorname {-codomdim}_{(A, R)} M\geq 2$
, $Q\!\operatorname {-codomdim}_{(A, R)} M\geq 2$![]() if and only if $\chi _M$
if and only if $\chi _M$![]() is an isomorphism. Theorem 3.1.4 of [Reference Cruz10] states that $Q\!\operatorname {-codomdim}_{(A, R)}\geq n$
is an isomorphism. Theorem 3.1.4 of [Reference Cruz10] states that $Q\!\operatorname {-codomdim}_{(A, R)}\geq n$![]() for $n\geq 2$
for $n\geq 2$![]() if and only if $\chi _M$
if and only if $\chi _M$![]() is an isomorphism and $Q\otimes _B -$
is an isomorphism and $Q\otimes _B -$![]() is exact on the first part of a projective resolution of $\operatorname {Hom}_A(Q, M)$
is exact on the first part of a projective resolution of $\operatorname {Hom}_A(Q, M)$![]() as a $B$
as a $B$![]() -module.
-module.
Section 3.1 of [Reference Cruz10] describes several consequences; we will use especially [Reference Cruz10, Corollary 3.1.5, Corollary 3.1.8, Proposition 3.1.11 and Corollary 3.1.12].
Lemma 2.1 Assume $M \in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() , and let $Q_i \in \!\operatorname {add} Q$
, and let $Q_i \in \!\operatorname {add} Q$![]() . An exact sequence
. An exact sequence
remains exact under ${\rm Hom}_A(-, Q)$![]() if and only if for every factorization $Q_i\to {\rm im}\, \alpha _{i+1} \to Q_{i+1}$
if and only if for every factorization $Q_i\to {\rm im}\, \alpha _{i+1} \to Q_{i+1}$![]() of $\alpha _{i+1}$
of $\alpha _{i+1}$![]() , the $(A,R)$
, the $(A,R)$![]() -monomorphism ${\rm im}\,\alpha _{i+1}\to Q_{i+1}$
-monomorphism ${\rm im}\,\alpha _{i+1}\to Q_{i+1}$![]() and $\alpha _0$
and $\alpha _0$![]() are left $\!\operatorname {add} Q$
are left $\!\operatorname {add} Q$![]() -approximations.
-approximations.
Proof. See [Reference Cruz10, Lemma 2.1.4].
In addition to the assumptions on $R, A$![]() , and $Q$
, and $Q$![]() , in the following, we also assume that $\operatorname {Hom}_A(Q, Q) \in R\!\operatorname {-proj}$
, in the following, we also assume that $\operatorname {Hom}_A(Q, Q) \in R\!\operatorname {-proj}$![]() .
.
It is crucial to compare relative dominant dimensions for end terms of a short exact sequence which remains exact under ${\rm Hom}_A(-, Q)$![]() . This is completely described in [Reference Cruz10, Lemma 3.1.7], part of it is as follows.
. This is completely described in [Reference Cruz10, Lemma 3.1.7], part of it is as follows.
Lemma 2.2 Let $M\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() and consider an $(A,R)$
and consider an $(A,R)$![]() -exact sequence
-exact sequence
which remains exact under ${\rm Hom}_A(-, Q)$![]() . Let $n=Q\!\operatorname {-domdim}_AM$
. Let $n=Q\!\operatorname {-domdim}_AM$![]() and $n_i= Q\!\operatorname {-domdim}_AM_i$
and $n_i= Q\!\operatorname {-domdim}_AM_i$![]() for $i=1, 2$
for $i=1, 2$![]() , then$:$
, then$:$![]()
(a) $n\geq {\rm min}\{ n_1, n_2\}$
 .
.(b) If $n=\infty$
 and $n_1 < \infty$
and $n_1 < \infty$ then $n_2 = n_1-1$
then $n_2 = n_1-1$ .
.
Corollary 2.3 Let $M_i$![]() for $i\in I$
for $i\in I$![]() be a finite set of modules in $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$
be a finite set of modules in $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() . Then
. Then

Proof. See [Reference Cruz10, Corollary 3.1.8].
Recall ${}^{\perp }Q = \{ M \in A\!\operatorname {-mod}\cap R\!\operatorname {-proj} \mid {\rm Ext}_A^{i>0}(M, Q)=0\}$![]() . The following is proved in [Reference Cruz10, Proposition 3.1.11].
. The following is proved in [Reference Cruz10, Proposition 3.1.11].
Proposition 2.4 Assume ${\rm Ext}^{i>0}_A(Q, Q)=0$![]() , and $M \in {}^{\perp }Q$
, and $M \in {}^{\perp }Q$![]() . An exact sequence
. An exact sequence
yields $Q\!\operatorname {-domdim}_{(A, R)}(M)\geq n$![]() if and only if $Q_i \in \!\operatorname {add} Q$
if and only if $Q_i \in \!\operatorname {add} Q$![]() and the cokernel of $Q_{n-1}\to Q_n$
and the cokernel of $Q_{n-1}\to Q_n$![]() belongs to ${}^{\perp }Q$
belongs to ${}^{\perp }Q$![]() .
.
The following is an application of lemma 2.2.
Corollary 2.5 Assume $Q\in {}^\perp Q$![]() . Let $M\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$
. Let $M\in A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() , and consider an $(A, R)$
, and consider an $(A, R)$![]() -exact sequence:
-exact sequence:
with $Q_i\in \!\operatorname {add} Q$![]() and $t\in \mathbb {N}$
and $t\in \mathbb {N}$![]() . If ${\rm Ext}_A^i(X, Q)=0$
. If ${\rm Ext}_A^i(X, Q)=0$![]() for $1\leq i\leq t$
for $1\leq i\leq t$![]() , then
, then
Proof. See [Reference Cruz10, Corollary 3.1.12].
2.4. Split quasi-hereditary algebras with duality
For the definition and general properties of split quasi-hereditary algebras we refer to [Reference Cline, Parshall and Scott5, Reference Cruz9–Reference Cruz11, Reference Rouquier49]. In particular, we follow the notation of [Reference Cruz9–Reference Cruz11]. One of the advantages to use such setup stems from the fact that split quasi-hereditary $R$![]() -algebras $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$
-algebras $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() are exactly the algebras so that $(S\otimes _R A, \{S\otimes _R \Delta (\lambda )_{\lambda \in \Lambda }\})$
are exactly the algebras so that $(S\otimes _R A, \{S\otimes _R \Delta (\lambda )_{\lambda \in \Lambda }\})$![]() are quasi-hereditary algebras for every commutative Noetherian ring $S$
are quasi-hereditary algebras for every commutative Noetherian ring $S$![]() which is an $R$
which is an $R$![]() -algebra. Concerning the terminology, we remark the word split arises from the endomorphism algebra $\operatorname {End}_A(\Delta (\lambda ))$
-algebra. Concerning the terminology, we remark the word split arises from the endomorphism algebra $\operatorname {End}_A(\Delta (\lambda ))$![]() being isomorphic to the ground ring $R$
being isomorphic to the ground ring $R$![]() . As it was observed in [Reference Rouquier49], when $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$
. As it was observed in [Reference Rouquier49], when $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() is a split quasi-hereditary $R$
is a split quasi-hereditary $R$![]() -algebra, the objects $T(\lambda )$
-algebra, the objects $T(\lambda )$![]() satisfying $\!\operatorname {add} \bigoplus _{\lambda \in \Lambda } T(\lambda )=\mathcal {F}(\tilde {\Delta })\cap \mathcal {F}(\tilde {\nabla })$
satisfying $\!\operatorname {add} \bigoplus _{\lambda \in \Lambda } T(\lambda )=\mathcal {F}(\tilde {\Delta })\cap \mathcal {F}(\tilde {\nabla })$![]() are no longer unique, in contrast to quasi-hereditary algebras over a field. For this reason, we will say that $T$
are no longer unique, in contrast to quasi-hereditary algebras over a field. For this reason, we will say that $T$![]() is a characteristic tilting module of $A$
is a characteristic tilting module of $A$![]() if $\!\operatorname {add} T=\mathcal {F}(\tilde {\Delta })\cap \mathcal {F}(\tilde {\nabla })$
if $\!\operatorname {add} T=\mathcal {F}(\tilde {\Delta })\cap \mathcal {F}(\tilde {\nabla })$![]() and $T$
and $T$![]() is the (basic) characteristic tilting module of $A$
is the (basic) characteristic tilting module of $A$![]() if $A$
if $A$![]() is a quasi-hereditary algebra over a field and $T=\bigoplus _{\lambda \in \Lambda } T(\lambda )$
is a quasi-hereditary algebra over a field and $T=\bigoplus _{\lambda \in \Lambda } T(\lambda )$![]() .
.
The following prepares the ground for quasi-hereditary covers, constructed from the Ringel dual $R(A)= {\rm End}_A(T)^{op}$![]() of a quasi-hereditary algebra $A$
of a quasi-hereditary algebra $A$![]() with a characteristic tilting module $T$
with a characteristic tilting module $T$![]() . To see that Ringel duality is well defined in the integral setup, we refer to [Reference Cruz10, Subsection 2.2.3].
. To see that Ringel duality is well defined in the integral setup, we refer to [Reference Cruz10, Subsection 2.2.3].
Proposition 2.6 Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary $R$
be a split quasi-hereditary $R$![]() -algebra with a characteristic tilting module $T$
-algebra with a characteristic tilting module $T$![]() . Denote by $R(A)$
. Denote by $R(A)$![]() the Ringel dual $\operatorname {End}_A(T)^{op}$
the Ringel dual $\operatorname {End}_A(T)^{op}$![]() of $A$
of $A$![]() . Suppose that $Q\in \!\operatorname {add}_A T$
. Suppose that $Q\in \!\operatorname {add}_A T$![]() is a partial tilting module. Then,
is a partial tilting module. Then,
(i) $\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{(R(A), R)} DT=Q\!\operatorname {-domdim}_{(A, R)} T$
 .
.(ii) $DQ\!\operatorname {-domdim}{(A, R)} = Q\!\operatorname {-codomdim}_{(A, R)} DA= Q\!\operatorname {-domdim} {(A,R)}$
 .
.(iii) $\inf \{Q\!\operatorname {-codomdim}_{(A, R)} M \colon M\in \mathcal {F}(\tilde {\nabla })\} = Q\!\operatorname {-codomdim}_{(A, R)} T$
 .
.
Proof. For (i), see [Reference Cruz10, Proposition 6.1.1]. For (ii), see [Reference Cruz10, Corollary 3.1.5]. For (iii), see [Reference Cruz10, Theorem 5.3.1].
Recall that $\operatorname {Hom}_A(T, DA)\simeq DT$![]() is a characteristic tilting module over $R(A)$
is a characteristic tilting module over $R(A)$![]() . Relative codominant dimension can also be used to observe that a characteristic tilting module behaves like a flat module in $\mathcal {F}(\tilde {\Delta }_{R(A)})$
. Relative codominant dimension can also be used to observe that a characteristic tilting module behaves like a flat module in $\mathcal {F}(\tilde {\Delta }_{R(A)})$![]() .
.
Proposition 2.7 The functor $\operatorname {Hom}_A(T, -)\colon \mathcal {F}(\tilde {\nabla })\rightarrow \mathcal {F}(\tilde {\Delta }_{R(A)})$![]() is an exact equivalence with quasi-inverse the exact functor $T\otimes _{R(A)} -\colon \mathcal {F}(\tilde {\Delta }_{R(A)})\rightarrow \mathcal {F}(\tilde {\nabla })$
is an exact equivalence with quasi-inverse the exact functor $T\otimes _{R(A)} -\colon \mathcal {F}(\tilde {\Delta }_{R(A)})\rightarrow \mathcal {F}(\tilde {\nabla })$![]() .
.
Proof. The fact that the functor $\operatorname {Hom}_A(T, -)\colon \mathcal {F}(\tilde {\nabla })\rightarrow \mathcal {F}(\tilde {\Delta }_{R(A)})$![]() is an exact equivalence follows from Ringel duality (see e.g. [Reference Cruz10, 2.2.3], or [Reference Ringel48, Theorem 6] in the field case).
is an exact equivalence follows from Ringel duality (see e.g. [Reference Cruz10, 2.2.3], or [Reference Ringel48, Theorem 6] in the field case).
By proposition 2.6, $T\!\operatorname {-codomdim}_{(A, R)} M\geq T\!\operatorname {-codomdim}_{(A, R)} T=+\infty$![]() for every $M\in \mathcal {F}(\tilde {\nabla })$
for every $M\in \mathcal {F}(\tilde {\nabla })$![]() . By Theorem 3.1.4 of [Reference Cruz10], $T\otimes _{R(A)} \operatorname {Hom}_A(T, M)\rightarrow M$
. By Theorem 3.1.4 of [Reference Cruz10], $T\otimes _{R(A)} \operatorname {Hom}_A(T, M)\rightarrow M$![]() is an isomorphism and $\operatorname {Tor}^A_{i>0}(T, \operatorname {Hom}_A(T, M))=0$
is an isomorphism and $\operatorname {Tor}^A_{i>0}(T, \operatorname {Hom}_A(T, M))=0$![]() for every $M\in \mathcal {F}(\tilde {\nabla })$
for every $M\in \mathcal {F}(\tilde {\nabla })$![]() . Since $\operatorname {Hom}_A(T, -)\colon \mathcal {F}(\tilde {\nabla })\rightarrow \mathcal {F}(\tilde {\Delta }_{R(A)})$
. Since $\operatorname {Hom}_A(T, -)\colon \mathcal {F}(\tilde {\nabla })\rightarrow \mathcal {F}(\tilde {\Delta }_{R(A)})$![]() is essentially surjective, the result follows.
is essentially surjective, the result follows.
Proposition 2.8 Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary algebra over a field $k$
be a split quasi-hereditary algebra over a field $k$![]() . Assume that there exists a simple preserving duality ${}^\diamond \! (-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$
. Assume that there exists a simple preserving duality ${}^\diamond \! (-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$![]() . Let $T$
. Let $T$![]() be the characteristic tilting module of $A$
be the characteristic tilting module of $A$![]() and assume that $Q\in \!\operatorname {add}_A T$
and assume that $Q\in \!\operatorname {add}_A T$![]() . Then,
. Then,
(i) ${}^\diamond \! \Delta (\lambda )\simeq \nabla (\lambda )$
 for all $\lambda \in \Lambda$
for all $\lambda \in \Lambda$ ;
;(ii) ${}^\diamond \! T(\lambda )\simeq T(\lambda )$
 for all indecomposable direct summands of $T$
for all indecomposable direct summands of $T$ ;
;(iii) $Q\!\operatorname {-domdim}_{(A, R)} T=Q\!\operatorname {-codomdim}_{(A, R)} T$
 .
.
Proof. (i) and (ii) follow by applying the simple preserving duality to the canonical exact sequences defining $\Delta (\lambda )$![]() and $T(\lambda )$
and $T(\lambda )$![]() , respectively. For (iii), see [Reference Cruz10, Proposition 3.1.6].
, respectively. For (iii), see [Reference Cruz10, Proposition 3.1.6].
Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary algebra over a field $k$
be a split quasi-hereditary algebra over a field $k$![]() . The $\nabla$
. The $\nabla$![]() -filtration dimension of $X$
-filtration dimension of $X$![]() , denoted by $\dim _{\mathcal {F}(\nabla )} X$
, denoted by $\dim _{\mathcal {F}(\nabla )} X$![]() , is the infimum of all $n\geq 0$
, is the infimum of all $n\geq 0$![]() such that there exists an exact sequence:
such that there exists an exact sequence:
with $M_0, \ldots, M_n \in \mathcal {F}(\nabla )$![]() . Analogously, the $\Delta$
. Analogously, the $\Delta$![]() -filtration dimension is defined. The $\nabla$
-filtration dimension is defined. The $\nabla$![]() -filtration dimensions first appeared in [Reference Friedlander and Parshall31] in the study of cohomology of algebraic groups.
-filtration dimensions first appeared in [Reference Friedlander and Parshall31] in the study of cohomology of algebraic groups.
$\nabla$![]() - and $\Delta$
- and $\Delta$![]() -filtration dimensions play a crucial role in [Reference Erdmann and Parker25, Reference Mazorchuk and Ovsienko45] establishing that the global dimension of a quasi-hereditary algebra having a simple preserving duality is always an even number. For us, they are of importance due to the following result.
-filtration dimensions play a crucial role in [Reference Erdmann and Parker25, Reference Mazorchuk and Ovsienko45] establishing that the global dimension of a quasi-hereditary algebra having a simple preserving duality is always an even number. For us, they are of importance due to the following result.
Proposition 2.9 Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary algebra over a field $k$
be a split quasi-hereditary algebra over a field $k$![]() . Assume that there exists a simple preserving duality ${}^\diamond \! (-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$
. Assume that there exists a simple preserving duality ${}^\diamond \! (-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$![]() . If $M\in A\!\operatorname {-mod}$
. If $M\in A\!\operatorname {-mod}$![]() satisfies $\dim _{\mathcal {F}(\Delta )} M=t<+\infty$
satisfies $\dim _{\mathcal {F}(\Delta )} M=t<+\infty$![]() , then $\operatorname {Ext}_A^{2t}(M, {}^\diamond \! M)\neq 0$
, then $\operatorname {Ext}_A^{2t}(M, {}^\diamond \! M)\neq 0$![]() .
.
Proof. See [Reference Mazorchuk and Ovsienko45, Corollary 6].
2.5. Cover theory
The concept of a cover, and in particular, of a split quasi-hereditary cover was introduced in [Reference Rouquier49] to give an abstract framework to connections in representation theory like Schur–Weyl duality. Given a split quasi-hereditary algebra $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() over a commutative Noetherian ring $R$
over a commutative Noetherian ring $R$![]() and a finitely generated projective $A$
and a finitely generated projective $A$![]() -module $P$
-module $P$![]() , let $B:= {\rm End}_A(P)^{op}$
, let $B:= {\rm End}_A(P)^{op}$![]() . We say that $(A, P)$
. We say that $(A, P)$![]() is a split quasi-hereditary cover of $B$
is a split quasi-hereditary cover of $B$![]() if the restriction of the functor
if the restriction of the functor
known as Schur functor, to $A\!\operatorname {-proj}$![]() is fully faithful. Given, in addition, $i\in \mathbb {N}\cup \{-1, 0, +\infty \}$
is fully faithful. Given, in addition, $i\in \mathbb {N}\cup \{-1, 0, +\infty \}$![]() , following the notation of [Reference Cruz9], we say that $(A, P)$
, following the notation of [Reference Cruz9], we say that $(A, P)$![]() is an $i$
is an $i$![]() - $\mathcal {F}(\tilde {\Delta })$
- $\mathcal {F}(\tilde {\Delta })$![]() (quasi-hereditary) cover of $B$
(quasi-hereditary) cover of $B$![]() if the following conditions hold:
if the following conditions hold:
• $(A, P)$
 is a split quasi-hereditary cover of $\operatorname {End}_A(P)^{op}$
is a split quasi-hereditary cover of $\operatorname {End}_A(P)^{op}$ ;
;• The restriction of $F$
 to $\mathcal {F}(\tilde {\Delta })$
to $\mathcal {F}(\tilde {\Delta })$ is faithful;
is faithful;• The Schur functor $F$
 induces bijections $\operatorname {Ext}_A^j(M, N)\simeq \operatorname {Ext}^j_{B}(FM, FN)$
induces bijections $\operatorname {Ext}_A^j(M, N)\simeq \operatorname {Ext}^j_{B}(FM, FN)$ , for every $M, N\in \mathcal {F}(\tilde {\Delta })$
, for every $M, N\in \mathcal {F}(\tilde {\Delta })$ and $0\leq j\leq i$
and $0\leq j\leq i$ .
.
Here, $\mathcal {F}(\tilde {\Delta })$![]() denotes the resolving subcategory of $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$
denotes the resolving subcategory of $A\!\operatorname {-mod}\cap R\!\operatorname {-proj}$![]() whose modules admit a finite filtration into direct summands of direct sums of standard modules $\Delta (\lambda )$
whose modules admit a finite filtration into direct summands of direct sums of standard modules $\Delta (\lambda )$![]() , $\lambda \in \Lambda$
, $\lambda \in \Lambda$![]() .
.
The optimal value of the quality of a cover is known as the Hemmer–Nakano dimension. More precisely, if $(A, P)$![]() is a $(-1)$
is a $(-1)$![]() -$\mathcal {F}(\tilde {\Delta })$
-$\mathcal {F}(\tilde {\Delta })$![]() (quasi-hereditary) cover of $B$
(quasi-hereditary) cover of $B$![]() , the Hemmer–Nakano dimension of $\mathcal {F}(\tilde {\Delta })$
, the Hemmer–Nakano dimension of $\mathcal {F}(\tilde {\Delta })$![]() with respect to $F$
with respect to $F$![]() is $i\in \mathbb {N}\cup \{-1, 0, +\infty \}$
is $i\in \mathbb {N}\cup \{-1, 0, +\infty \}$![]() if $(A, P)$
if $(A, P)$![]() is an $i$
is an $i$![]() -$\mathcal {F}(\tilde {\Delta })$
-$\mathcal {F}(\tilde {\Delta })$![]() (quasi-hereditary) cover of $\operatorname {End}_A(P)^{op}$
(quasi-hereditary) cover of $\operatorname {End}_A(P)^{op}$![]() but $(A, P)$
but $(A, P)$![]() is not an $(i+1)$
is not an $(i+1)$![]() -$\mathcal {F}(\tilde {\Delta })$
-$\mathcal {F}(\tilde {\Delta })$![]() (quasi-hereditary) cover of $B$
(quasi-hereditary) cover of $B$![]() . The Hemmer–Nakano dimension of $\mathcal {F}(\tilde {\Delta })$
. The Hemmer–Nakano dimension of $\mathcal {F}(\tilde {\Delta })$![]() is denoted by $\operatorname {HNdim}_{F}(\mathcal {F}(\tilde {\Delta }))$
is denoted by $\operatorname {HNdim}_{F}(\mathcal {F}(\tilde {\Delta }))$![]() .
.
Major tools to compute Hemmer–Nakano dimensions are classical dominant dimension and relative dominant dimensions. This can be traced back to [Reference Fang and Koenig29] which was later amplified in several directions in [Reference Cruz9] and in [Reference Cruz10], and it is briefly summarized in the following result proved in [Reference Cruz10, Theorem 5.3.1, Corollary 5.3.4]. Note that ${\rm Hom}_A(T, Q)$![]() is projective as a $B$
is projective as a $B$![]() -module.
-module.
Theorem 2.10 Let $R$![]() be a commutative Noetherian ring. Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$
be a commutative Noetherian ring. Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary $R$
be a split quasi-hereditary $R$![]() -algebra with a characteristic tilting module $T$
-algebra with a characteristic tilting module $T$![]() . Denote by $R(A)$
. Denote by $R(A)$![]() the Ringel dual $\operatorname {End}_A(T)^{op}$
the Ringel dual $\operatorname {End}_A(T)^{op}$![]() of $A$
of $A$![]() . Assume that $Q\in \!\operatorname {add} T$
. Assume that $Q\in \!\operatorname {add} T$![]() is a (partial) tilting module of $A$
is a (partial) tilting module of $A$![]() . Then, the following assertions hold.
. Then, the following assertions hold.
(a) If $Q\!\operatorname {-codomdim}_{(A, R)} T \geq n\geq 2$
 , then $(R(A), \operatorname {Hom}_A(T, Q))$
, then $(R(A), \operatorname {Hom}_A(T, Q))$ is an $(n-2)$
is an $(n-2)$ -$\mathcal {F}(\tilde {\Delta }_{R(A)})$
-$\mathcal {F}(\tilde {\Delta }_{R(A)})$ split quasi-hereditary cover of $\operatorname {End}_A(Q)^{op}$
split quasi-hereditary cover of $\operatorname {End}_A(Q)^{op}$ .
.(b) Assume, in addition, that $R$
 is a field. Then, $Q\!\operatorname {-codomdim}_{(A, R)} T \geq n\geq 2$
is a field. Then, $Q\!\operatorname {-codomdim}_{(A, R)} T \geq n\geq 2$ if and only if $(R(A), \operatorname {Hom}_A(T, Q))$
if and only if $(R(A), \operatorname {Hom}_A(T, Q))$ is an $(n-2)$
is an $(n-2)$ -$\mathcal {F}(\tilde {\Delta }_{R(A)})$
-$\mathcal {F}(\tilde {\Delta }_{R(A)})$ split quasi-hereditary cover of $\operatorname {End}_A(Q)^{op}$
split quasi-hereditary cover of $\operatorname {End}_A(Q)^{op}$ .
.
Let $B$![]() be a projective Noetherian $R$
be a projective Noetherian $R$![]() -algebra, $(A, P)$
-algebra, $(A, P)$![]() be an $(-1)$
be an $(-1)$![]() -$\mathcal {F}(\tilde {\Delta })$
-$\mathcal {F}(\tilde {\Delta })$![]() (quasi-hereditary) cover of $B$
(quasi-hereditary) cover of $B$![]() and $(A', P')$
and $(A', P')$![]() be an $(-1)$
be an $(-1)$![]() -$\mathcal {F}(\tilde {\Delta }')$
-$\mathcal {F}(\tilde {\Delta }')$![]() (quasi-hereditary) cover of $B$
(quasi-hereditary) cover of $B$![]() . We say that $(A, P)$
. We say that $(A, P)$![]() is equivalent to $(A', P')$
is equivalent to $(A', P')$![]() as quasi-hereditary covers if there exists an equivalence $H\colon A\!\operatorname {-mod}\rightarrow A'\!\operatorname {-mod}$
as quasi-hereditary covers if there exists an equivalence $H\colon A\!\operatorname {-mod}\rightarrow A'\!\operatorname {-mod}$![]() which restricts to an equivalence of categories between $\mathcal {F}(\tilde {\Delta })$
which restricts to an equivalence of categories between $\mathcal {F}(\tilde {\Delta })$![]() and $\mathcal {F}(\tilde {\Delta }')$
and $\mathcal {F}(\tilde {\Delta }')$![]() making the following diagram commutative:
making the following diagram commutative:

for some equivalence of categories $L$![]() . The first application of uniqueness of covers goes back to [Reference Rouquier49]. Split quasi-hereditary covers with higher values of Hemmer–Nakano dimension associated with them are essentially unique. In fact, this is due to the following result which can be found in [Reference Cruz9, Corollary 4.3.6].
. The first application of uniqueness of covers goes back to [Reference Rouquier49]. Split quasi-hereditary covers with higher values of Hemmer–Nakano dimension associated with them are essentially unique. In fact, this is due to the following result which can be found in [Reference Cruz9, Corollary 4.3.6].
Corollary 2.11 Let $B$![]() be a projective Noetherian $R$
be a projective Noetherian $R$![]() -algebra, $(A, P)$
-algebra, $(A, P)$![]() be a $1$
be a $1$![]() -$\mathcal {F}(\tilde {\Delta })$
-$\mathcal {F}(\tilde {\Delta })$![]() (quasi-hereditary) cover of $B$
(quasi-hereditary) cover of $B$![]() and $(A', P')$
and $(A', P')$![]() be a $1$
be a $1$![]() -$\mathcal {F}(\tilde {\Delta }')$
-$\mathcal {F}(\tilde {\Delta }')$![]() (quasi-hereditary) cover of $B$
(quasi-hereditary) cover of $B$![]() . If there exists an exact equivalence $L\colon B\!\operatorname {-mod}\rightarrow B\!\operatorname {-mod}$
. If there exists an exact equivalence $L\colon B\!\operatorname {-mod}\rightarrow B\!\operatorname {-mod}$![]() which restricts to an exact equivalence between $\mathcal {F}(\operatorname {Hom}_A(P, -)\tilde {\Delta })$
which restricts to an exact equivalence between $\mathcal {F}(\operatorname {Hom}_A(P, -)\tilde {\Delta })$![]() and $\mathcal {F}(\operatorname {Hom}_{A'}(P', -)\tilde {\Delta }')$
and $\mathcal {F}(\operatorname {Hom}_{A'}(P', -)\tilde {\Delta }')$![]() , then $(A, P)$
, then $(A, P)$![]() is equivalent as split quasi-hereditary cover to $(A', P')$
is equivalent as split quasi-hereditary cover to $(A', P')$![]() .
.
For a more detailed exposition on cover theory and Hemmer–Nakano dimensions we refer to [Reference Cruz9, Reference Cruz10].
3. The first main result
The aim of this section is to prove theorem A, that is, to prove the following.
Theorem 3.1 Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary algebra over a field $k$
be a split quasi-hereditary algebra over a field $k$![]() . Suppose that there exists a simple preserving duality ${}^\diamond \!(-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$
. Suppose that there exists a simple preserving duality ${}^\diamond \!(-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$![]() . Let $T$
. Let $T$![]() be a characteristic tilting module of $A$
be a characteristic tilting module of $A$![]() . Assume that $Q\in \!\operatorname {add} T$
. Assume that $Q\in \!\operatorname {add} T$![]() . Then,
. Then,
3.1. Outline of the proof
The proof will be divided in two parts: $\leq$![]() , $\geq$
, $\geq$![]() . The easier part is $\geq$
. The easier part is $\geq$![]() , that is, to prove that:
, that is, to prove that:
the latter being a particular case of lemma 3.4. For this inequality, there are two main ideas. First, we construct (using Ringel duality) an exact sequence:
with the following properties:
• $n=Q\!\operatorname {-domdim}_A T$
 ;
;• $\overline {C}\in \mathcal {F}(\nabla )$
 and $\overline {X_i}\in \!\operatorname {add} Q$
and $\overline {X_i}\in \!\operatorname {add} Q$ .
.
Hence, (3.2) remains exact under $\operatorname {Hom}_A(T, -)$![]() and under $\operatorname {Hom}_A(Q, -)$
and under $\operatorname {Hom}_A(Q, -)$![]() . Second, we use the formula:
. Second, we use the formula:
On the other hand, to establish the part $\leq$![]() , that is, to prove that $Q\!\operatorname {-codomdim}_A DA$
, that is, to prove that $Q\!\operatorname {-codomdim}_A DA$![]() cannot be larger than $2Q\!\operatorname {-codomdim}_A T=2n$
cannot be larger than $2Q\!\operatorname {-codomdim}_A T=2n$![]() , there are two key steps:
, there are two key steps:
(1) From any exact sequence $\overline {X_{n+1}}\rightarrow \overline {X_n}\rightarrow \cdots \rightarrow \overline {X_1}\rightarrow DA\rightarrow 0$
 that gives ${Q\!\operatorname {-codomdim}_A DA\geq n+1}$
that gives ${Q\!\operatorname {-codomdim}_A DA\geq n+1}$ we can infer that the kernel of $\overline {X_{n+1}}\rightarrow \overline {X_n}$
we can infer that the kernel of $\overline {X_{n+1}}\rightarrow \overline {X_n}$ , denoted here by $E$
, denoted here by $E$ (with $\overline {X_0}:=DA$
(with $\overline {X_0}:=DA$ if $n=0$
if $n=0$ ) satisfies $\operatorname {Ext}_A^{i\geq n+2}(X, E)=0$
) satisfies $\operatorname {Ext}_A^{i\geq n+2}(X, E)=0$ for every $X\in {}^\perp Q$
for every $X\in {}^\perp Q$ ;
;(2) Proposition 2.9 provides a method to use the simple preserving duality functor to construct a module $X\in {}^\perp Q$
 that satisfies $\operatorname {Ext}_A^{n+2}(X, E)\neq 0$
that satisfies $\operatorname {Ext}_A^{n+2}(X, E)\neq 0$ if $Q\!\operatorname {-codomdim}_A DA>2n$
if $Q\!\operatorname {-codomdim}_A DA>2n$ .
.
3.2. Relative injective dimension
Before we start with the proof of theorem A we need to discuss the concept of relative injective dimension.
Definition 3.2 Let $\mathcal {A}$![]() be a full subcategory of $A\!\operatorname {-mod}$
be a full subcategory of $A\!\operatorname {-mod}$![]() . We define the $\mathcal {A}$
. We define the $\mathcal {A}$![]() -injective dimension of $N\in A\!\operatorname {-mod}$
-injective dimension of $N\in A\!\operatorname {-mod}$![]() (or the relative injective dimension of $N$
(or the relative injective dimension of $N$![]() with respect to $\mathcal {A}$
with respect to $\mathcal {A}$![]() ) as the value:
) as the value:
We denote by $\operatorname {idim}_\mathcal {A} N$![]() the $\mathcal {A}$
the $\mathcal {A}$![]() -injective dimension of $N$
-injective dimension of $N$![]() . Analogously, we define the $\mathcal {A}$
. Analogously, we define the $\mathcal {A}$![]() -projective dimension of $N\in A\!\operatorname {-mod}$
-projective dimension of $N\in A\!\operatorname {-mod}$![]() as the value:
as the value:
Lemma 3.3 Let $A$![]() be a projective Noetherian $R$
be a projective Noetherian $R$![]() -algebra and let $Q\in A\!\operatorname {-mod}$
-algebra and let $Q\in A\!\operatorname {-mod}$![]() such that $\operatorname {Ext}_A^{i>0}(Q, Q)=0$
such that $\operatorname {Ext}_A^{i>0}(Q, Q)=0$![]() . Then, the following assertions hold.
. Then, the following assertions hold.
(1) If there exists an exact sequence $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$
 with $Y\in \!\operatorname {add} Q$
with $Y\in \!\operatorname {add} Q$ , then $\operatorname{idim}_{{}^\perp Q} X\leq 1+\operatorname{idim}_{{}^\perp Q} Z.$
, then $\operatorname{idim}_{{}^\perp Q} X\leq 1+\operatorname{idim}_{{}^\perp Q} Z.$
(2) If there exists an exact sequence $0\rightarrow X\rightarrow X_r\rightarrow \cdots \rightarrow X_1 \rightarrow Z\rightarrow 0$
 with $X_1, \ldots, X_r\in \!\operatorname {add} Q$
with $X_1, \ldots, X_r\in \!\operatorname {add} Q$ , then $\operatorname {idim}_{{}^\perp Q} X\leq r+\operatorname {idim}_{{}^\perp Q} Z$
, then $\operatorname {idim}_{{}^\perp Q} X\leq r+\operatorname {idim}_{{}^\perp Q} Z$ .
.(3) If there exists an exact sequence $0\rightarrow X\rightarrow X_r\rightarrow \cdots \rightarrow X_1 \rightarrow Z\rightarrow 0$
 with $X_1, \ldots, X_r\in \!\operatorname {add} Q$
with $X_1, \ldots, X_r\in \!\operatorname {add} Q$ , then for every $Y\in Q^{\perp }$
, then for every $Y\in Q^{\perp }$ , $\operatorname {Ext}_A^i(X, Y)\simeq \operatorname {Ext}_A^{i+r}(Z,Y)$
, $\operatorname {Ext}_A^i(X, Y)\simeq \operatorname {Ext}_A^{i+r}(Z,Y)$ for all $i\in \mathbb {N}$
for all $i\in \mathbb {N}$ .
.
Proof. For each $M\in {}^\perp Q$![]() , applying $\operatorname {Hom}_A(M, -)$
, applying $\operatorname {Hom}_A(M, -)$![]() yields that $\operatorname {Ext}_A^i(M, Z)\simeq \operatorname {Ext}_A^{i+1}(M, X)$
yields that $\operatorname {Ext}_A^i(M, Z)\simeq \operatorname {Ext}_A^{i+1}(M, X)$![]() for all $i\geq 1$
for all $i\geq 1$![]() . Hence, (i) follows. By induction and using (i), (ii) follows. Denote by $C_i$
. Hence, (i) follows. By induction and using (i), (ii) follows. Denote by $C_i$![]() the image of $X_{i+1}\rightarrow X_i$
the image of $X_{i+1}\rightarrow X_i$![]() for all $i=1, \ldots, r-1$
for all $i=1, \ldots, r-1$![]() . By applying $\operatorname {Hom}_A(-, Y)$
. By applying $\operatorname {Hom}_A(-, Y)$![]() we deduce that $\operatorname {Ext}_A^i(X, Y)\simeq \operatorname {Ext}_A^{i+1}(C_{r-1}, Y)\simeq \operatorname {Ext}_A^{i+2}(C_{r-2}, Y)$
we deduce that $\operatorname {Ext}_A^i(X, Y)\simeq \operatorname {Ext}_A^{i+1}(C_{r-1}, Y)\simeq \operatorname {Ext}_A^{i+2}(C_{r-2}, Y)$![]() $\simeq \operatorname {Ext}_A^{i+r-1}(C_1, Y)\simeq \operatorname {Ext}_A^{i+r}(Z, Y)$
$\simeq \operatorname {Ext}_A^{i+r-1}(C_1, Y)\simeq \operatorname {Ext}_A^{i+r}(Z, Y)$![]() .
.
3.3. Computing relative dominant dimension of the regular module using a characteristic tilting module
Let $T$![]() be a characteristic tilting module of a split quasi-hereditary algebra $A$
be a characteristic tilting module of a split quasi-hereditary algebra $A$![]() and let $Q$
and let $Q$![]() be a partial tilting module. By proposition 2.6(ii)–(iii), the relative codominant dimension of $T$
be a partial tilting module. By proposition 2.6(ii)–(iii), the relative codominant dimension of $T$![]() with respect to $Q$
with respect to $Q$![]() is a lower bound to the relative dominant dimension of $A$
is a lower bound to the relative dominant dimension of $A$![]() with respect to $Q$
with respect to $Q$![]() . In the following we will see that this lower bound can be sharpened.
. In the following we will see that this lower bound can be sharpened.
Lemma 3.4 Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary $R$
be a split quasi-hereditary $R$![]() -algebra with a characteristic tilting module $T$
-algebra with a characteristic tilting module $T$![]() . Denote by $R(A)$
. Denote by $R(A)$![]() the Ringel dual $\operatorname {End}_A(T)^{op}$
the Ringel dual $\operatorname {End}_A(T)^{op}$![]() of $A$
of $A$![]() . Suppose that $Q\in \!\operatorname {add} T$
. Suppose that $Q\in \!\operatorname {add} T$![]() . Then,
. Then,
Proof. Observe that $DQ\otimes _A Q\in R\!\operatorname {-proj}$![]() (see e.g. [Reference Cruz9, A.4.3]). By proposition 2.6(ii) and (iii), we obtain that:
(see e.g. [Reference Cruz9, A.4.3]). By proposition 2.6(ii) and (iii), we obtain that:
If $Q\!\operatorname {-domdim}_A T=0$![]() , then there is nothing more to prove. Assume that $n:= {Q\!\operatorname {-domdim}_{(A, R)} T}\geq 1$
, then there is nothing more to prove. Assume that $n:= {Q\!\operatorname {-domdim}_{(A, R)} T}\geq 1$![]() . By proposition 2.6(i), $\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{R(A)} DT=n$
. By proposition 2.6(i), $\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{R(A)} DT=n$![]() . That is, there exists an exact sequence:
. That is, there exists an exact sequence:
with all $X_i\in \!\operatorname {add} (\operatorname {Hom}_A(T, Q))$![]() , and so they are projective modules over $R(A)$
, and so they are projective modules over $R(A)$![]() . The modules $DT$
. The modules $DT$![]() and $X_i$
and $X_i$![]() are in $\mathcal {F}(\tilde {\Delta }_{R(A)})$
are in $\mathcal {F}(\tilde {\Delta }_{R(A)})$![]() , which is closed under kernels of epimorphisms and hence also $C$
, which is closed under kernels of epimorphisms and hence also $C$![]() is in $\mathcal {F}(\tilde {\Delta }_{R(A)})$
is in $\mathcal {F}(\tilde {\Delta }_{R(A)})$![]() .
.
By the Ringel dual equivalence described in proposition 2.7, the functor $T\otimes _{R(A)} -$![]() takes (3.7) to the exact sequence:
takes (3.7) to the exact sequence:
and $\overline {X_i}\in \!\operatorname {add} Q$![]() since $T\otimes _{R(A)} \operatorname {Hom}_A(T, Q)=\!\operatorname {add} Q$
since $T\otimes _{R(A)} \operatorname {Hom}_A(T, Q)=\!\operatorname {add} Q$![]() . Moreover,
. Moreover,
and $\overline {C}\in \mathcal {F}(\tilde {\nabla })$![]() . Thus, the exact sequence (3.8) remains exact under $\operatorname {Hom}_A(Q, -)$
. Thus, the exact sequence (3.8) remains exact under $\operatorname {Hom}_A(Q, -)$![]() . By the dual version of corollary 2.5, we obtain that
. By the dual version of corollary 2.5, we obtain that
Applying again proposition 2.6(iii) gives that ${Q\!\operatorname {-codomdim}_{(A, R)} \overline {C}}\geq Q\!\operatorname {-codomdim}_{(A, R)} T.$![]()
Remark 3.5 An alternative proof to lemma 3.4 would be to repeat the steps of lemma 3.4 but only for quasi-hereditary algebras over a field. Then, since relative dominant dimension of modules with a standard filtration with respect to direct summands of a characteristic tilting module remains invariant under change of ground ring, the result would follow for split quasi-hereditary algebras with arbitrary commutative Noetherian ground ring.
Surprisingly, theorem 3.1 generalizes [Reference Fang and Koenig29, Theorem 4.3] without using any techniques on symmetric algebras. In particular, for the following proof we do not need to require $A$![]() to be an endomorphism algebra of a generator over a symmetric algebra.
to be an endomorphism algebra of a generator over a symmetric algebra.
Proof of theorem 3.1 By proposition 2.6(ii), proposition 2.8, and lemma 3.4, part $\geq$![]() follows. So, it remains to show that
follows. So, it remains to show that
If $Q\!\operatorname {-codomdim}_A T=+\infty$![]() , then there is nothing to prove. Denote by $n$
, then there is nothing to prove. Denote by $n$![]() the value $Q\!\operatorname {-domdim}_A T=Q\!\operatorname {-codomdim}_A T$
the value $Q\!\operatorname {-domdim}_A T=Q\!\operatorname {-codomdim}_A T$![]() . Assume first that $n>0$
. Assume first that $n>0$![]() . So, we can consider again exact sequences of the form (3.7) and (3.8). Assume, for a contradiction, that $Q\!\operatorname {-codomdim}_A DA>2n$
. So, we can consider again exact sequences of the form (3.7) and (3.8). Assume, for a contradiction, that $Q\!\operatorname {-codomdim}_A DA>2n$![]() . Hence, also $Q\!\operatorname {-codomdim}_A \overline {C}>n$
. Hence, also $Q\!\operatorname {-codomdim}_A \overline {C}>n$![]() according to the dual of corollary 2.5. So, there exists an exact sequence:
according to the dual of corollary 2.5. So, there exists an exact sequence:
which remains exact under $\operatorname {Hom}_A(Q, -)$![]() and $\overline {X_i}\in \!\operatorname {add} Q$
and $\overline {X_i}\in \!\operatorname {add} Q$![]() , $i=n+1, \ldots, 2n+1$
, $i=n+1, \ldots, 2n+1$![]() . In particular, $0\rightarrow L\rightarrow \overline {X_{2n+1}}\rightarrow \cdots \rightarrow \overline {X_1}\rightarrow DA\rightarrow 0$
. In particular, $0\rightarrow L\rightarrow \overline {X_{2n+1}}\rightarrow \cdots \rightarrow \overline {X_1}\rightarrow DA\rightarrow 0$![]() is an $\operatorname {Hom}_A(Q, -)$
is an $\operatorname {Hom}_A(Q, -)$![]() -acyclic coresolution of $L$
-acyclic coresolution of $L$![]() , so it can be used to compute $\operatorname {Ext}_A^i(Q, L)$
, so it can be used to compute $\operatorname {Ext}_A^i(Q, L)$![]() for all $i$
for all $i$![]() . Since it remains exact under $\operatorname {Hom}_A(Q, -)$
. Since it remains exact under $\operatorname {Hom}_A(Q, -)$![]() we obtain that $\operatorname {Ext}_A^{i>0}(Q, L)=0$
we obtain that $\operatorname {Ext}_A^{i>0}(Q, L)=0$![]() and so $L\in Q^\perp$
and so $L\in Q^\perp$![]() and ${}^\diamond \! L\in {}^\perp Q$
and ${}^\diamond \! L\in {}^\perp Q$![]() . Let $E$
. Let $E$![]() be the kernel of the map $\overline {X_{n+1}}\rightarrow \overline {C}$
be the kernel of the map $\overline {X_{n+1}}\rightarrow \overline {C}$![]() and consider the exact sequence:
and consider the exact sequence:
By lemma 3.3(2), $\operatorname {idim}_{{}^\perp Q} E\leq n+1$![]() . Since (3.10) remains exact under $\operatorname {Hom}_A(Q, -)$
. Since (3.10) remains exact under $\operatorname {Hom}_A(Q, -)$![]() we have that $E\in Q^{\perp }$
we have that $E\in Q^{\perp }$![]() . On the other hand, observe that $E$
. On the other hand, observe that $E$![]() cannot belong to $\mathcal {F}(\nabla )$
cannot belong to $\mathcal {F}(\nabla )$![]() because otherwise (3.10) would remain exact under $\operatorname {Hom}_A(T, -)$
because otherwise (3.10) would remain exact under $\operatorname {Hom}_A(T, -)$![]() yielding that $n<\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{R(A)} DT$
yielding that $n<\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{R(A)} DT$![]() contradicting the definition of $n$
contradicting the definition of $n$![]() .
.
So, the exact sequence $0\rightarrow E\rightarrow \overline {X_{n+1}}\rightarrow \overline {C}\rightarrow 0$![]() yields that $\dim _{\mathcal {F}(\nabla )}E=1$
yields that $\dim _{\mathcal {F}(\nabla )}E=1$![]() . Hence, $\dim _{\mathcal {F}(\Delta )}{}^\diamond \! E=1$
. Hence, $\dim _{\mathcal {F}(\Delta )}{}^\diamond \! E=1$![]() . By proposition 2.9, we obtain that $0\neq \operatorname {Ext}_A^2({}^\diamond \! E, {}^\diamond \! {}^\diamond \! E)\simeq \operatorname {Ext}_A^2({}^\diamond \! E, E)$
. By proposition 2.9, we obtain that $0\neq \operatorname {Ext}_A^2({}^\diamond \! E, {}^\diamond \! {}^\diamond \! E)\simeq \operatorname {Ext}_A^2({}^\diamond \! E, E)$![]() . By lemma 3.3(3) on the exact sequence $0\rightarrow {}^\diamond \! E\rightarrow {}^\diamond \! \overline {X_{n+2}}\rightarrow \cdots \rightarrow {}^\diamond \! \overline {X_{2n+1}}\rightarrow {}^\diamond \! L\rightarrow 0$
. By lemma 3.3(3) on the exact sequence $0\rightarrow {}^\diamond \! E\rightarrow {}^\diamond \! \overline {X_{n+2}}\rightarrow \cdots \rightarrow {}^\diamond \! \overline {X_{2n+1}}\rightarrow {}^\diamond \! L\rightarrow 0$![]() we obtain $0\neq \operatorname {Ext}_A^2({}^\diamond \! E, E)\simeq \operatorname {Ext}_A^{n+2}({}^\diamond \! L, E)$
we obtain $0\neq \operatorname {Ext}_A^2({}^\diamond \! E, E)\simeq \operatorname {Ext}_A^{n+2}({}^\diamond \! L, E)$![]() . This contradicts $\operatorname {idim}_{{}^\perp Q} E$
. This contradicts $\operatorname {idim}_{{}^\perp Q} E$![]() being at most $n+1$
being at most $n+1$![]() . We will now treat the case $n=0$
. We will now treat the case $n=0$![]() . Assume, for the sake of contradiction, that $Q\!\operatorname {-codomdim}_A DA\geq 1$
. Assume, for the sake of contradiction, that $Q\!\operatorname {-codomdim}_A DA\geq 1$![]() , then there exists an exact sequence $0\rightarrow L\rightarrow X_1\rightarrow DA\rightarrow 0$
, then there exists an exact sequence $0\rightarrow L\rightarrow X_1\rightarrow DA\rightarrow 0$![]() which remains exact under $\operatorname {Hom}_A(Q, -)$
which remains exact under $\operatorname {Hom}_A(Q, -)$![]() and $X_1\in \!\operatorname {add} Q$
and $X_1\in \!\operatorname {add} Q$![]() . Hence, $L\in Q^{\perp }$
. Hence, $L\in Q^{\perp }$![]() , ${}^\diamond \! L\in {}^\perp Q$
, ${}^\diamond \! L\in {}^\perp Q$![]() , $\dim _{\mathcal {F}(\nabla )}(L)\leq 1$
, $\dim _{\mathcal {F}(\nabla )}(L)\leq 1$![]() and the ${}^\perp Q$
and the ${}^\perp Q$![]() -injective dimension of $L$
-injective dimension of $L$![]() is at most one. In particular, $\operatorname {Ext}_A^2({}^\diamond \! L, L)= 0$
is at most one. In particular, $\operatorname {Ext}_A^2({}^\diamond \! L, L)= 0$![]() . By proposition 2.9, we must have that $L\in \mathcal {F}(\nabla )$
. By proposition 2.9, we must have that $L\in \mathcal {F}(\nabla )$![]() . But, then applying $\operatorname {Hom}_A(T, -)$
. But, then applying $\operatorname {Hom}_A(T, -)$![]() to $0\rightarrow L\rightarrow X_1\rightarrow DA\rightarrow 0$
to $0\rightarrow L\rightarrow X_1\rightarrow DA\rightarrow 0$![]() yields that $\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{R(A)} \operatorname {Hom}_A(T, DA)\geq 1$
yields that $\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{R(A)} \operatorname {Hom}_A(T, DA)\geq 1$![]() which, in turn, implies that $n=Q\!\operatorname {-domdim} T\geq 1$
which, in turn, implies that $n=Q\!\operatorname {-domdim} T\geq 1$![]() by proposition 2.6(i).
by proposition 2.6(i).
The following gives a positive answer to the Conjecture 6.2.4 of [Reference Cruz8], which is a special case by taking $A$![]() to be a Schur algebra and $Q$
to be a Schur algebra and $Q$![]() the tensor space $V^{\otimes d}$
the tensor space $V^{\otimes d}$![]() .
.
Proposition 3.6 Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary algebra over a field $k$
be a split quasi-hereditary algebra over a field $k$![]() with a simple preserving duality. Let $T$
with a simple preserving duality. Let $T$![]() be a characteristic tilting module of $A$
be a characteristic tilting module of $A$![]() . Assume that $Q\in \!\operatorname {add} T$
. Assume that $Q\in \!\operatorname {add} T$![]() satisfies $Q\!\operatorname {-domdim}_A A\geq 2$
satisfies $Q\!\operatorname {-domdim}_A A\geq 2$![]() . Then,
. Then,
Proof. Let $P$![]() be a faithful projective–injective module over $A$
be a faithful projective–injective module over $A$![]() . By assumption, $Q\!\operatorname {-domdim}_A A\geq 2$
. By assumption, $Q\!\operatorname {-domdim}_A A\geq 2$![]() , so by corollary 2.3 it follows that $Q\!\operatorname {-domdim}_A P\geq 2$
, so by corollary 2.3 it follows that $Q\!\operatorname {-domdim}_A P\geq 2$![]() . Since $P$
. Since $P$![]() is injective we must have that $P\in \!\operatorname {add} Q$
is injective we must have that $P\in \!\operatorname {add} Q$![]() . Hence, $\operatorname {Hom}_A(T, P)\in \!\operatorname {add} \operatorname {Hom}_A(T, Q)$
. Hence, $\operatorname {Hom}_A(T, P)\in \!\operatorname {add} \operatorname {Hom}_A(T, Q)$![]() .
.
By proposition 2.6(i),

Applying theorem 3.1 to the partial tilting modules $P$![]() and $Q$
and $Q$![]() , the result follows.
, the result follows.
Example 3.7 We illustrate the proof of theorem A, using the Schur algebra $S(2, 4)$![]() over a field of characteristic $2$
over a field of characteristic $2$![]() . Its basic algebra $A$
. Its basic algebra $A$![]() is isomorphic to $KQ/I$
is isomorphic to $KQ/I$![]() where $Q$
where $Q$![]() is the quiver
is the quiver

and $I = \langle \beta \alpha, \gamma \delta, (\alpha \beta )\delta, \gamma (\alpha \beta )\rangle$![]() (see [Reference Erdmann26, 5.6]). (Here, we label vertices consistent with later sections.) The partial order is $4> 2 > 0$
(see [Reference Erdmann26, 5.6]). (Here, we label vertices consistent with later sections.) The partial order is $4> 2 > 0$![]() , all standard modules are uniserial, $\Delta (2)$
, all standard modules are uniserial, $\Delta (2)$![]() has composition factors labelled $2, 0$
has composition factors labelled $2, 0$![]() and $\Delta (4)$
and $\Delta (4)$![]() has composition factors labelled $4, 0, 2$
has composition factors labelled $4, 0, 2$![]() . Then, $T(4)$
. Then, $T(4)$![]() and $T(2)$
and $T(2)$![]() are uniserial, with
are uniserial, with
We take $Q= T(4)\oplus T(2)$![]() , then the characteristic tilting module is $Q\oplus T(0)$
, then the characteristic tilting module is $Q\oplus T(0)$![]() and $T(0)$
and $T(0)$![]() is the simple module $L(0)$
is the simple module $L(0)$![]() .
.
Consider the sequences in the proof of lemma 3.4. First, sequence (3.7) is the start of a minimal projective resolution of $DT$![]() as a module for $R(A)$
as a module for $R(A)$![]() . We apply $T\otimes _{R(A)}(-)$
. We apply $T\otimes _{R(A)}(-)$![]() which gives sequence (3.8). We know that it is a resolution of $D(A)$
which gives sequence (3.8). We know that it is a resolution of $D(A)$![]() with terms in ${\rm add}(Q)$
with terms in ${\rm add}(Q)$![]() which is exact under ${\rm Hom}(Q, -)$
which is exact under ${\rm Hom}(Q, -)$![]() , and from this information we see that it is
, and from this information we see that it is
(where $\overline {X_1}= T(4)^3\oplus T(2)$![]() and $\overline {X_2}\simeq T(2)^2$
and $\overline {X_2}\simeq T(2)^2$![]() ). This shows, by the dual of corollary 2.5, that
). This shows, by the dual of corollary 2.5, that
In particular, $\operatorname {Hom}_A(T, Q)\!\operatorname {-codomdim}_{R(A)} DT=2$![]() . By proposition 2.6(i), $n=Q\!\operatorname {-domdim}_A T=2$
. By proposition 2.6(i), $n=Q\!\operatorname {-domdim}_A T=2$![]() . In this case, $\overline {C}$
. In this case, $\overline {C}$![]() is already too simple and we know its relative codominant dimension using the simple preserving duality, thus this is enough already to deduce that $Q\!\operatorname {-codomdim}_A DA=4$
is already too simple and we know its relative codominant dimension using the simple preserving duality, thus this is enough already to deduce that $Q\!\operatorname {-codomdim}_A DA=4$![]() .
.
Assume, for the moment, that at this point we did not know the value of $Q\!\operatorname {-codomdim}_A \overline {C}$![]() . We consider now the proof of theorem 3.1. The exact sequence (3.10) is precisely:
. We consider now the proof of theorem 3.1. The exact sequence (3.10) is precisely:
where the map $T(2)\rightarrow \overline {X_2}$![]() factors through $T(0)$
factors through $T(0)$![]() . Hence, $E= \Delta (2)$
. Hence, $E= \Delta (2)$![]() . Step (1), that is, (3.10) together with lemma 3.3(2) gives that $\operatorname {idim}_{{}^\perp Q} \Delta (2)\leq 3.$
. Step (1), that is, (3.10) together with lemma 3.3(2) gives that $\operatorname {idim}_{{}^\perp Q} \Delta (2)\leq 3.$![]() Indeed, the (absolute) injective dimension $\operatorname {idim}_A \Delta (2)$
Indeed, the (absolute) injective dimension $\operatorname {idim}_A \Delta (2)$![]() is exactly $3$
is exactly $3$![]() , so $\operatorname {idim}_{{}^\perp Q} \Delta (2)$
, so $\operatorname {idim}_{{}^\perp Q} \Delta (2)$![]() must be at most 3. By the proof of theorem 3.1, if $Q\!\operatorname {-codomdim}_A DA>2\cdot 2=4$
must be at most 3. By the proof of theorem 3.1, if $Q\!\operatorname {-codomdim}_A DA>2\cdot 2=4$![]() , then proposition 2.9 through the object ${}^\diamond \! L$
, then proposition 2.9 through the object ${}^\diamond \! L$![]() would give that $\operatorname {idim}_{{}^\perp Q} \Delta (2)>3$
would give that $\operatorname {idim}_{{}^\perp Q} \Delta (2)>3$![]() which does not happen.
which does not happen.
4. Input from Schur algebras
The main work to prove the second main result, to determine the Hemmer–Nakano dimension of $\mathcal {F}(\Delta )$![]() over the quasi-hereditary cover for the Temperley–Lieb algebra, in §6 and 7, will be done for Schur algebras, and we can work over an algebraically closed field. In this section, we give an outline of the background. To keep the notation simple, we do this for the classical case.
over the quasi-hereditary cover for the Temperley–Lieb algebra, in §6 and 7, will be done for Schur algebras, and we can work over an algebraically closed field. In this section, we give an outline of the background. To keep the notation simple, we do this for the classical case.
Assume $K$![]() is an algebraically closed field. The Schur algebra $S=S_K(n,d)$
is an algebraically closed field. The Schur algebra $S=S_K(n,d)$![]() (or just $S(n, d)$
(or just $S(n, d)$![]() ) of degree $d$
) of degree $d$![]() over $K$
over $K$![]() can be defined in different ways. One can start with the symmetric group $\mathcal {S}_d$
can be defined in different ways. One can start with the symmetric group $\mathcal {S}_d$![]() which acts (on the right) by place permutations on the tensor power $V^{\otimes d}$
which acts (on the right) by place permutations on the tensor power $V^{\otimes d}$![]() where $V$
where $V$![]() is an $n$
is an $n$![]() -dimensional vector space. Then, the Schur algebra $S(n, d)$
-dimensional vector space. Then, the Schur algebra $S(n, d)$![]() is the endomorphism algebra ${\rm End}_{K\mathcal {S}_d}(V^{\otimes d})$
is the endomorphism algebra ${\rm End}_{K\mathcal {S}_d}(V^{\otimes d})$![]() . Analogously, the integral Schur algebra $S_R(2, d)$
. Analogously, the integral Schur algebra $S_R(2, d)$![]() is defined as the endomorphism algebra ${\rm End}_{R\mathcal {S}_d}((R^2)^{\otimes d})$
is defined as the endomorphism algebra ${\rm End}_{R\mathcal {S}_d}((R^2)^{\otimes d})$![]() where $(R^2)^{\otimes d}$
where $(R^2)^{\otimes d}$![]() affords a right $R\mathcal {S}_d$
affords a right $R\mathcal {S}_d$![]() -module structure via place permutations with $R$
-module structure via place permutations with $R$![]() being a commutative Noetherian regular ring (of positive Krull dimension). Alternatively one can construct $S(n, d)$
being a commutative Noetherian regular ring (of positive Krull dimension). Alternatively one can construct $S(n, d)$![]() via the general linear group $GL(V)$
via the general linear group $GL(V)$![]() , for details see for example [Reference Green33, 2.3] or [Reference Donkin16, Section 1]. The first route shows that the endomorphism algebra of $S(n,d)$
, for details see for example [Reference Green33, 2.3] or [Reference Donkin16, Section 1]. The first route shows that the endomorphism algebra of $S(n,d)$![]() acting on $V^{\otimes d}$
acting on $V^{\otimes d}$![]() is a quotient of $K\mathcal {S}_d$
is a quotient of $K\mathcal {S}_d$![]() . The second approach allows one to use tensor products and Frobenius twists as tools to study representations.
. The second approach allows one to use tensor products and Frobenius twists as tools to study representations.
The Schur algebra $S(n, d)$![]() is quasi-hereditary, with respect to the dominance order on the set $\Lambda ^+(n, d)$
is quasi-hereditary, with respect to the dominance order on the set $\Lambda ^+(n, d)$![]() of partitions of $d$
of partitions of $d$![]() with at most $n$
with at most $n$![]() parts, which is the standard labelling set for simple modules. It has a simple preserving duality ${}^\diamond \!(-)$
parts, which is the standard labelling set for simple modules. It has a simple preserving duality ${}^\diamond \!(-)$![]() (see e.g. [Reference Donkin20, p. 83]). For each partition $\lambda$
(see e.g. [Reference Donkin20, p. 83]). For each partition $\lambda$![]() of $d$
of $d$![]() with at most $n$
with at most $n$![]() parts, the corresponding simple module will be denoted by $L(\lambda )$
parts, the corresponding simple module will be denoted by $L(\lambda )$![]() . We denote the standard module with simple top $L(\lambda )$
. We denote the standard module with simple top $L(\lambda )$![]() by $\Delta (\lambda )$
by $\Delta (\lambda )$![]() , then the costandard module with simple socle $L(\lambda )$
, then the costandard module with simple socle $L(\lambda )$![]() is $\nabla (\lambda ) = {}^\diamond \!\Delta (\lambda )$
is $\nabla (\lambda ) = {}^\diamond \!\Delta (\lambda )$![]() . For background we refer to [Reference Dlab and Ringel21, Reference Dlab and Ringel22, Reference Erdmann27].
. For background we refer to [Reference Dlab and Ringel21, Reference Dlab and Ringel22, Reference Erdmann27].
Of central importance for the quasi-hereditary structure is the characteristic tilting module $T$![]() : by [Reference Ringel48] the indecomposable modules in $\mathcal {F}(\Delta )\cap \mathcal {F}(\nabla )$
: by [Reference Ringel48] the indecomposable modules in $\mathcal {F}(\Delta )\cap \mathcal {F}(\nabla )$![]() are in bijection with the weights. Write $T(\lambda )$
are in bijection with the weights. Write $T(\lambda )$![]() for the indecomposable labelled by $\lambda \in \Lambda ^+(n, d)$
for the indecomposable labelled by $\lambda \in \Lambda ^+(n, d)$![]() . Then, the direct sum $T:= \bigoplus _{\lambda \in \Lambda ^+(n, d)} T(\lambda )$
. Then, the direct sum $T:= \bigoplus _{\lambda \in \Lambda ^+(n, d)} T(\lambda )$![]() (or a module with the same indecomposable summands) is a distinguished tilting module, known as the characteristic tilting module of $S$
(or a module with the same indecomposable summands) is a distinguished tilting module, known as the characteristic tilting module of $S$![]() . Its endomorphism algebra $R(S):= {\rm End}_S(T)^{op}$
. Its endomorphism algebra $R(S):= {\rm End}_S(T)^{op}$![]() is again quasi-hereditary and $R(R(S))$
is again quasi-hereditary and $R(R(S))$![]() is Morita equivalent (as quasi-hereditary algebra) to $S$
is Morita equivalent (as quasi-hereditary algebra) to $S$![]() .
.
For each $\lambda$![]() , there is an associated exact sequence:
, there is an associated exact sequence:
where $X(\lambda )$![]() has $\Delta$
has $\Delta$![]() -filtration where only $\Delta (\mu )$
-filtration where only $\Delta (\mu )$![]() with $\mu < \lambda$
with $\mu < \lambda$![]() occur. We will refer to this as a standard sequence.
occur. We will refer to this as a standard sequence.
We follow the usual practice in algebraic Lie theory to refer to a module in ${\rm add}(T)$![]() as a tilting module, and to $T$
as a tilting module, and to $T$![]() as a full tilting module (this will not be ambiguous here).
as a full tilting module (this will not be ambiguous here).
For the connection between Schur algebras and symmetric groups, the tensor space $V^{\otimes d}$![]() is of central importance. As it happens, the tensor space is a direct sum of tilting modules, and $T(\lambda )$
is of central importance. As it happens, the tensor space is a direct sum of tilting modules, and $T(\lambda )$![]() occurs as a summand if and only if $\lambda$
occurs as a summand if and only if $\lambda$![]() is $p$
is $p$![]() -regular (i.e. does not have $p$
-regular (i.e. does not have $p$![]() equal parts). For the quantum case, $T(\lambda )$
equal parts). For the quantum case, $T(\lambda )$![]() occurs in the tensor space if and only if $\lambda$
occurs in the tensor space if and only if $\lambda$![]() is $\ell$
is $\ell$![]() -regular where $q$
-regular where $q$![]() is a primitive $\ell$
is a primitive $\ell$![]() -th root of 1. This is proved in [Reference Erdmann27, 4.2], or combining the reasoning of [Reference Erdmann27, 4.2] with [Reference Donkin20, 2.2(1), 4.3, 4.7] respectively. Hence, the following result has become folklore.
-th root of 1. This is proved in [Reference Erdmann27, 4.2], or combining the reasoning of [Reference Erdmann27, 4.2] with [Reference Donkin20, 2.2(1), 4.3, 4.7] respectively. Hence, the following result has become folklore.
Lemma 4.1 Assume that $n=2$![]() and $d$
and $d$![]() is a natural number. If $\operatorname {char} K\neq 2$
is a natural number. If $\operatorname {char} K\neq 2$![]() or $d$
or $d$![]() is odd, then $V^{\otimes d}$
is odd, then $V^{\otimes d}$![]() is a characteristic tilting module over $S_K(2, d)$
is a characteristic tilting module over $S_K(2, d)$![]() .
.
Proof. If $K$![]() has characteristic zero, then the Schur algebra $S(2, d)$
has characteristic zero, then the Schur algebra $S(2, d)$![]() is semi-simple (see e.g. [Reference Green33, (2.6)e]) and since $V^{\otimes d}$
is semi-simple (see e.g. [Reference Green33, (2.6)e]) and since $V^{\otimes d}$![]() is faithful over $S(2, d)$
is faithful over $S(2, d)$![]() it contains the regular module in its additive closure, and in particular, $V^{\otimes d}$
it contains the regular module in its additive closure, and in particular, $V^{\otimes d}$![]() is a characteristic tilting module. If $K$
is a characteristic tilting module. If $K$![]() has positive characteristic, as discussed before $V^{\otimes d}$
has positive characteristic, as discussed before $V^{\otimes d}$![]() is a characteristic tilting module over $S(2, d)$
is a characteristic tilting module over $S(2, d)$![]() if and only if all partitions of $d$
if and only if all partitions of $d$![]() in at most $2$
in at most $2$![]() parts are $\operatorname {char} K$
parts are $\operatorname {char} K$![]() -regular partitions of $d$
-regular partitions of $d$![]() . Of course, all partitions of $d$
. Of course, all partitions of $d$![]() in at most $2$
in at most $2$![]() parts are $p$
parts are $p$![]() -regular if $p>2$
-regular if $p>2$![]() . If $d$
. If $d$![]() is odd, then there are no partitions of $d$
is odd, then there are no partitions of $d$![]() in exactly two equal parts.
in exactly two equal parts.
From now on we assume $n=2$![]() and $\operatorname {char} K =2$
and $\operatorname {char} K =2$![]() , or in the quantum case that $\ell = 2$
, or in the quantum case that $\ell = 2$![]() . We also assume $d$
. We also assume $d$![]() is even (unless specified differently).
is even (unless specified differently).
4.1. On the quasi-hereditary structure of $S(2, d)$
Let $S=S(2, d)$![]() , and let $e=\xi _{(d)}$
, and let $e=\xi _{(d)}$![]() be the idempotent corresponding to the largest weight (in the notation of [Reference Green33, 3.2]). Then, $SeS$
be the idempotent corresponding to the largest weight (in the notation of [Reference Green33, 3.2]). Then, $SeS$![]() is an idempotent heredity ideal and $S/SeS$
is an idempotent heredity ideal and $S/SeS$![]() is isomorphic to $S(2, d-2)$
is isomorphic to $S(2, d-2)$![]() (for details see e.g. [Reference Erdmann26, 1.3]). Since $SeS$
(for details see e.g. [Reference Erdmann26, 1.3]). Since $SeS$![]() is a heredity ideal corresponding to $(d)$
is a heredity ideal corresponding to $(d)$![]() , factoring it out is compatible with the quasi-hereditary structure. Furthermore, as it is proved in the appendix of [Reference Dlab and Ringel22] computing ${\rm Ext}^i$
, factoring it out is compatible with the quasi-hereditary structure. Furthermore, as it is proved in the appendix of [Reference Dlab and Ringel22] computing ${\rm Ext}^i$![]() 's for $S/SeS$
's for $S/SeS$![]() -modules is the same whether in $S$
-modules is the same whether in $S$![]() or in $S/SeS$
or in $S/SeS$![]() . In particular, $S(2, d)\!\operatorname {-mod}$
. In particular, $S(2, d)\!\operatorname {-mod}$![]() is the full subcategory of $S(2, d+2)\!\operatorname {-mod}$
is the full subcategory of $S(2, d+2)\!\operatorname {-mod}$![]() consisting of modules whose composition factors are different from those appearing in the top of $Se$
consisting of modules whose composition factors are different from those appearing in the top of $Se$![]() .
.
We work mostly with the restrictions of simple modules, (co)standard modules and tilting modules to $SL(2, K)$![]() . Recall that $L(\lambda )$
. Recall that $L(\lambda )$![]() and $L(\mu )$
and $L(\mu )$![]() are isomorphic as $SL(2, K)$
are isomorphic as $SL(2, K)$![]() -modules if and only if they can be regarded both as $S(2, d)$
-modules if and only if they can be regarded both as $S(2, d)$![]() -modules for some large $d$
-modules for some large $d$![]() and they are isomorphic as $S(2, d)$
and they are isomorphic as $S(2, d)$![]() -modules. This fact can be seen using the canonical surjective map of $KSL(2, K)$
-modules. This fact can be seen using the canonical surjective map of $KSL(2, K)$![]() onto $S(2, d)$
onto $S(2, d)$![]() . Since every partition $(\lambda _1, \lambda _2)$
. Since every partition $(\lambda _1, \lambda _2)$![]() of $d$
of $d$![]() in at most two parts is completely determined by the value $\lambda _1-\lambda _2$
in at most two parts is completely determined by the value $\lambda _1-\lambda _2$![]() , it follows that $L(\lambda )$
, it follows that $L(\lambda )$![]() and $L(\mu )$
and $L(\mu )$![]() are isomorphic as $SL(2, K)$
are isomorphic as $SL(2, K)$![]() -modules if and only if $\lambda _1-\lambda _2 = \mu _1 - \mu _2$
-modules if and only if $\lambda _1-\lambda _2 = \mu _1 - \mu _2$![]() . Similarly, we may label the standard modules and tilting modules.
. Similarly, we may label the standard modules and tilting modules.
We therefore label these modules by $m =\lambda _1-\lambda _2$![]() if $\lambda = (\lambda _1, \lambda _2)$
if $\lambda = (\lambda _1, \lambda _2)$![]() (such labellings can also be found e.g. in [Reference Erdmann and Law24, Subsection 3.2]). This means that we consider Schur algebras $S=S(2,d)$
(such labellings can also be found e.g. in [Reference Erdmann and Law24, Subsection 3.2]). This means that we consider Schur algebras $S=S(2,d)$![]() , allowing degrees to vary but keeping the parity. We make the convention that we view tacitly modules for $S(2, d')$
, allowing degrees to vary but keeping the parity. We make the convention that we view tacitly modules for $S(2, d')$![]() with $d'\leq d$
with $d'\leq d$![]() of the same parity as modules for $S(2, d)$
of the same parity as modules for $S(2, d)$![]() . We say that such a degree $d'$
. We say that such a degree $d'$![]() is admissible for the module defined in degree $d$
is admissible for the module defined in degree $d$![]() . With this, the weights labelling the simple modules for $S(2, d)$
. With this, the weights labelling the simple modules for $S(2, d)$![]() are precisely all non-negative integers $m\leq d$
are precisely all non-negative integers $m\leq d$![]() of the same parity. The dominance order when $p=2$
of the same parity. The dominance order when $p=2$![]() and the degree is even, is the linear order.
and the degree is even, is the linear order.
The tilting module $T(0)$![]() is simple, it is the trivial module for $SL(2, K)$
is simple, it is the trivial module for $SL(2, K)$![]() . As a building block, the tilting module $T(1)$
. As a building block, the tilting module $T(1)$![]() appears, which is isomorphic to the natural $SL(2, K)$
appears, which is isomorphic to the natural $SL(2, K)$![]() -module $V$
-module $V$![]() . Furthermore, $T(2) \cong V^{\otimes 2}$
. Furthermore, $T(2) \cong V^{\otimes 2}$![]() . For $d\geq 4$
. For $d\geq 4$![]() we have that $V^{\otimes d}$
we have that $V^{\otimes d}$![]() is the direct sum of $T(k)$
is the direct sum of $T(k)$![]() where all $T(k)$
where all $T(k)$![]() occur for $k$
occur for $k$![]() of the same parity of $d$
of the same parity of $d$![]() , except that $T(0)$
, except that $T(0)$![]() does not occur when $d$
does not occur when $d$![]() is even. (See e.g. [Reference Erdmann27, 4.2], it is implicitly in [Reference Donkin17, 3.4].)
is even. (See e.g. [Reference Erdmann27, 4.2], it is implicitly in [Reference Donkin17, 3.4].)
4.2. The category $\mathcal {F}(\Delta )$ and projective modules
and projective modules
Non-split extensions of standard modules satisfy a directedness property, that is:
This has the following immediate consequence:
Lemma 4.2 Every module in $\mathcal {F}(\Delta )$![]() has a filtration in which weights of $\Delta$
has a filtration in which weights of $\Delta$![]() -quotients increase from top to bottom.
-quotients increase from top to bottom.
Proof. This follows for example from [Reference Dlab and Ringel22, Lemma 1.4], see also [Reference Cruz11, B.0.6]. See [Reference Jantzen38], for an earlier reference.
Of main interest for us are the indecomposable projective modules. Let $P_d(m)$![]() denote the indecomposable projective of $S(2, d)$
denote the indecomposable projective of $S(2, d)$![]() with simple quotient $L(m)$
with simple quotient $L(m)$![]() . Recall $P_d(m)$
. Recall $P_d(m)$![]() has a $\Delta$
has a $\Delta$![]() -filtration, and that the filtration multiplicities $[P_d(m):\Delta (w)]$
-filtration, and that the filtration multiplicities $[P_d(m):\Delta (w)]$![]() are the same as the decomposition numbers. That is,
are the same as the decomposition numbers. That is,
where we write $(M:L(m))$![]() for the multiplicity of $L(m)$
for the multiplicity of $L(m)$![]() as a composition factor of the module $M$
as a composition factor of the module $M$![]() . Note this also shows that projective modules depend on the degree $d$
. Note this also shows that projective modules depend on the degree $d$![]() . In this case, decomposition numbers are always $0$
. In this case, decomposition numbers are always $0$![]() or $1$
or $1$![]() , see [Reference Henke34, Prop. 2.2, Theorem 3.2]. We give an example in figure 1.
, see [Reference Henke34, Prop. 2.2, Theorem 3.2]. We give an example in figure 1.

Figure 1. Decomposition matrix for $S(2, 46)$![]() for $p=2$
for $p=2$![]() . The $(m,n)$
. The $(m,n)$![]() -entry denotes $(\Delta (m):L(n))$
-entry denotes $(\Delta (m):L(n))$![]() , the column label is the same as the row label.
, the column label is the same as the row label.
It follows that either $P_{d}(m) \cong P_{d-2}(m)$![]() as a module for $S(2, d)$
as a module for $S(2, d)$![]() , or else there is a non-split exact sequence:
, or else there is a non-split exact sequence:
Namely, the top of $P_{d-2}(m)$![]() is $L(m)$
is $L(m)$![]() , so there is a surjective homomorphism from $P_{d}(m)$
, so there is a surjective homomorphism from $P_{d}(m)$![]() onto $P_{d-2}(m)$
onto $P_{d-2}(m)$![]() . Recall that $\mathcal {F}(\Delta )$
. Recall that $\mathcal {F}(\Delta )$![]() is closed under kernels of epimorphisms. By the filtration property in lemma 4.2 if this is not an isomorphism, then its kernel is a direct sum of copies of $\Delta (d)$
is closed under kernels of epimorphisms. By the filtration property in lemma 4.2 if this is not an isomorphism, then its kernel is a direct sum of copies of $\Delta (d)$![]() and there is only one since the decomposition numbers are $\leq \! 1$
and there is only one since the decomposition numbers are $\leq \! 1$![]() .
.
4.3. Twisted tensor product methods
Let $(-)^F$![]() denote the Frobenius twist (see [Reference Donkin20, p. 64]), this is an exact functor. In our setting, that is for even characteristic, we have the following tools, due to [Reference Donkin17]. Odd degrees when $p=2$
denote the Frobenius twist (see [Reference Donkin20, p. 64]), this is an exact functor. In our setting, that is for even characteristic, we have the following tools, due to [Reference Donkin17]. Odd degrees when $p=2$![]() are less important. Namely, each block of $S(2, d)$
are less important. Namely, each block of $S(2, d)$![]() for $d$
for $d$![]() odd is Morita equivalent to some block of some Schur algebra $S(2, x)$
odd is Morita equivalent to some block of some Schur algebra $S(2, x)$![]() with $x=(d-1)/2$
with $x=(d-1)/2$![]() via the functor $\Delta (1)\otimes (-)^F$
via the functor $\Delta (1)\otimes (-)^F$![]() , see for example [Reference Erdmann and Henke23, Lemma 1] or [Reference Donkin18, Section 4, Theorem].
, see for example [Reference Erdmann and Henke23, Lemma 1] or [Reference Donkin18, Section 4, Theorem].
(1)
(a) Let $m=2t$
 . There is an exact sequence of $S$
. There is an exact sequence of $S$ -modules:
\[ 0\to \Delta(t-1)^F\to \Delta(m)\to \Delta(t)^F\to 0 \]Taking contravariant duals gives the analogue for costandard modules.
-modules:
\[ 0\to \Delta(t-1)^F\to \Delta(m)\to \Delta(t)^F\to 0 \]Taking contravariant duals gives the analogue for costandard modules.
(b) Let $m=2t+1$
 , then $\Delta (m)\cong L(1)\otimes \Delta (t)^F$
, then $\Delta (m)\cong L(1)\otimes \Delta (t)^F$ .
.
(See e.g. [Reference Cox6, Prop. 3.3]).
We note that this determines recursively the decomposition numbers, as input using that $\Delta (t)$![]() is simple and isomorphic to $L(t)$
is simple and isomorphic to $L(t)$![]() for $t=0, 1$
for $t=0, 1$![]() , recall $p=2$
, recall $p=2$![]() . This can also be used to show that when $p=2$
. This can also be used to show that when $p=2$![]() and $d$
and $d$![]() is even, the algebra $S(2, d)$
is even, the algebra $S(2, d)$![]() is indecomposable. Further, this also implies, by induction, that the decomposition numbers are always $0$
is indecomposable. Further, this also implies, by induction, that the decomposition numbers are always $0$![]() and $1$
and $1$![]() when $p=2$
when $p=2$![]() and $d$
and $d$![]() is even.
is even.
(2) We have a complete description of the indecomposable tilting modules in this case. We have already described $T(m)$
 for $m\leq 2$
for $m\leq 2$ . The following is due to Donkin, see [Reference Donkin17, Example 2, p. 47].
. The following is due to Donkin, see [Reference Donkin17, Example 2, p. 47].
Proposition 4.3 Let $m=2s$![]() and $m\geq 2$
and $m\geq 2$![]() , then
, then
If $m=2s+1$![]() , then $T(r) \cong T(1) \otimes T(s)^F$
, then $T(r) \cong T(1) \otimes T(s)^F$![]() .
.
This describes recursively all indecomposable tilting modules.
The following shows that filtration multiplicities $[T(m):\Delta (w)]$![]() are $\leq 1$
are $\leq 1$![]() .
.
Proposition 4.4 The $\Delta$![]() -filtration multiplicities of indecomposable tilting modules in even degree can be computed recursively from:
-filtration multiplicities of indecomposable tilting modules in even degree can be computed recursively from:
To prove this, one may specialize [Reference Cox6, Prop. 3.4].
We will see below that modules $T(2)\otimes X^F$![]() for $X$
for $X$![]() in $\mathcal {F}(\Delta )$
in $\mathcal {F}(\Delta )$![]() have infinite relative dominant dimension with respect to $V^{\otimes d}$
have infinite relative dominant dimension with respect to $V^{\otimes d}$![]() . This means that we can use lemma 2.2 (from Lemma 3.1.7 of [Reference Cruz10]) to relate the relative $V^{\otimes d}$
. This means that we can use lemma 2.2 (from Lemma 3.1.7 of [Reference Cruz10]) to relate the relative $V^{\otimes d}$![]() -dominant dimension of the end terms, and this suggests a route towards the proof of our second main result.
-dominant dimension of the end terms, and this suggests a route towards the proof of our second main result.
We define a twisted filtration of a module $M\in \mathcal {F}(\Delta )$![]() to be a filtration where each quotient is isomorphic to $T(2)\otimes \Delta (t)^F$
to be a filtration where each quotient is isomorphic to $T(2)\otimes \Delta (t)^F$![]() for some $t$
for some $t$![]() .
.
Lemma 4.5 Let $m=2s\geq 1$![]() . Then, the tilting module $T(m)$
. Then, the tilting module $T(m)$![]() has a twisted filtration
has a twisted filtration
with $M_{i-1}/M_i \cong T(2)\otimes \Delta (s_i)^F$![]() , with quotients $\Delta (2s_i)$
, with quotients $\Delta (2s_i)$![]() and $\Delta (2s_i+2)$
and $\Delta (2s_i+2)$![]() , for $s_1 < s_2<\cdots < s_k$
, for $s_1 < s_2<\cdots < s_k$![]() .
.
Proof. We have $T(m)\cong T(2)\otimes T(s-1)^F$![]() . The module $T(s-1)$
. The module $T(s-1)$![]() has a $\Delta$
has a $\Delta$![]() -filtration
-filtration
with $N_{i-1}/N_i \cong \Delta (s_i)$![]() and such that $s_1 < s_2 < \cdots < s_k$
and such that $s_1 < s_2 < \cdots < s_k$![]() , by lemma 4.2. Applying the exact functor $T(2)\otimes (-)^F$
, by lemma 4.2. Applying the exact functor $T(2)\otimes (-)^F$![]() gives the claim.
gives the claim.
Remark 4.6
(1) The algebra $S(2, d)$
 is Ringel self-dual for $p=2$
is Ringel self-dual for $p=2$ and $d$
and $d$ even if and only if $d=2^{n+1}-2$
even if and only if $d=2^{n+1}-2$ for some $n$
for some $n$ , see [Reference Erdmann and Henke23, Theorem 27] and for a functorial proof see [Reference Erdmann and Law24, 5.4]. In [Reference Erdmann and Henke23, Corollary 21] and [Reference Erdmann and Law24, Section 5], the projective tilting modules (and also the injective tilting modules) have been identified for these degrees.
, see [Reference Erdmann and Henke23, Theorem 27] and for a functorial proof see [Reference Erdmann and Law24, 5.4]. In [Reference Erdmann and Henke23, Corollary 21] and [Reference Erdmann and Law24, Section 5], the projective tilting modules (and also the injective tilting modules) have been identified for these degrees.(2) Each $T(m)$
 has a simple top, by proposition 4.3, using [Reference Erdmann and Henke23, Lemma 11], or [Reference Erdmann and Law24, 3.4].
has a simple top, by proposition 4.3, using [Reference Erdmann and Henke23, Lemma 11], or [Reference Erdmann and Law24, 3.4].
5. The relative dominant dimension of the regular module with respect to $V^{\otimes d}$
Let $S=S(2, d)$![]() and assume that $K$
and assume that $K$![]() has characteristic $p$
has characteristic $p$![]() . Recall that the indecomposable summands of $V^{\otimes d}$
. Recall that the indecomposable summands of $V^{\otimes d}$![]() are precisely the $T(\lambda )$
are precisely the $T(\lambda )$![]() where $\lambda$
where $\lambda$![]() is a partition of $d$
is a partition of $d$![]() with at most two parts, such that $\lambda$
with at most two parts, such that $\lambda$![]() does not have $p$
does not have $p$![]() equal parts. Recall that we identify $\lambda$
equal parts. Recall that we identify $\lambda$![]() with $m=\lambda _1-\lambda _2$
with $m=\lambda _1-\lambda _2$![]() . Hence, unless $p=2$
. Hence, unless $p=2$![]() and $d$
and $d$![]() is even, all indecomposable summands of $T$
is even, all indecomposable summands of $T$![]() occur in $V^{\otimes d}$
occur in $V^{\otimes d}$![]() , and then $V^{\otimes d}\!\operatorname {-domdim}_S S=\infty$
, and then $V^{\otimes d}\!\operatorname {-domdim}_S S=\infty$![]() , by the following:
, by the following:
Lemma 5.1 If $V^{\otimes d}$![]() has all $T(\lambda )$
has all $T(\lambda )$![]() as direct summands, then
as direct summands, then
Proof. Every module in $\mathcal {F}(\Delta )$![]() admits a finite $\ \!\operatorname {add} T$
admits a finite $\ \!\operatorname {add} T$![]() -coresolution (see e.g. [Reference Ringel48, lemma 6] or [Reference Donkin15]) which, in particular, remains exact under $\operatorname {Hom}_S(-,V^{\otimes d})$
-coresolution (see e.g. [Reference Ringel48, lemma 6] or [Reference Donkin15]) which, in particular, remains exact under $\operatorname {Hom}_S(-,V^{\otimes d})$![]() . By corollary 2.5, the result follows.
. By corollary 2.5, the result follows.
5.1. The characteristic two case
Lemma 5.1 leaves us to consider $p=2$![]() and $d$
and $d$![]() even $(\neq 0$
even $(\neq 0$![]() ). In this case, as mentioned above, the components of $V^{\otimes d}$
). In this case, as mentioned above, the components of $V^{\otimes d}$![]() are the $T(m)$
are the $T(m)$![]() with $m\neq 0$
with $m\neq 0$![]() . The standard sequence (4.1) is an $\!\operatorname {add} T$
. The standard sequence (4.1) is an $\!\operatorname {add} T$![]() -approximation, this follows from a special case of proposition 2.4. In particular,
-approximation, this follows from a special case of proposition 2.4. In particular,
Theorem 5.2 Let $d=2s> 0$![]() . We have
. We have
To prove this, we will use lemma 2.2 on extensions of $\Delta (t)$![]() by $\Delta (2+t)$
by $\Delta (2+t)$![]() .
.
The cases $d=2$![]() and $d=4$
and $d=4$![]() are easy.
are easy.
(1) For $d=2$
 we have the exact sequence $0\to \Delta (2) \to T(2) \to \Delta (0) = T(0)\to 0$
we have the exact sequence $0\to \Delta (2) \to T(2) \to \Delta (0) = T(0)\to 0$ , which proves the statement of the theorem by corollary 2.5.
, which proves the statement of the theorem by corollary 2.5.(2) Let $d=4$
 , we have the exact sequence $0\to \Delta (4) \to T(4) \to \Delta (2)\to 0$
, we have the exact sequence $0\to \Delta (4) \to T(4) \to \Delta (2)\to 0$ . Splicing this with the sequence for $\Delta (2)$
. Splicing this with the sequence for $\Delta (2)$ gives the claim.
gives the claim.
Degrees $d\geq 6$![]() need more work. The main ingredient is the observation that subquotients of the form $T(2)\otimes N^F$
need more work. The main ingredient is the observation that subquotients of the form $T(2)\otimes N^F$![]() with $N\in \mathcal {F}(\Delta )$
with $N\in \mathcal {F}(\Delta )$![]() are not relevant for a minimal $V^{\otimes d}$
are not relevant for a minimal $V^{\otimes d}$![]() -approximation.
-approximation.
Lemma 5.3 Let $X\in S(2, s)\!\operatorname {-mod}$![]() . Assume that $X\in \mathcal {F}(\Delta )$
. Assume that $X\in \mathcal {F}(\Delta )$![]() . Then, the module $T(2)\otimes X^F$
. Then, the module $T(2)\otimes X^F$![]() has infinite relative dominant dimension with respect to $V^{\otimes d}$
has infinite relative dominant dimension with respect to $V^{\otimes d}$![]() for any even degree $d$
for any even degree $d$![]() greater or equal to $2s+2$
greater or equal to $2s+2$![]() .
.
Proof. By lemma 2.2 it suffices to prove this when $X=\Delta (s)$![]() . We proceed by induction on $s$
. We proceed by induction on $s$![]() . When $s=0$
. When $s=0$![]() or $s=1$
or $s=1$![]() we see that $T(2)\otimes \Delta (s)^F$
we see that $T(2)\otimes \Delta (s)^F$![]() is a summand of $V^{\otimes d}$
is a summand of $V^{\otimes d}$![]() . For the inductive step consider the exact sequence:
. For the inductive step consider the exact sequence:
The middle term is isomorphic to $T(2 + 2s)$![]() . Since $X(s)$
. Since $X(s)$![]() has a filtration with quotients $\Delta (t)$
has a filtration with quotients $\Delta (t)$![]() for $t< s$
for $t< s$![]() it follows by induction (and lemma 2.2) that the module $T(2)\otimes X(s)^F$
it follows by induction (and lemma 2.2) that the module $T(2)\otimes X(s)^F$![]() has infinite $V^{\otimes d}$
has infinite $V^{\otimes d}$![]() -dominant dimension for any even degree $d\geq 2s+2$
-dominant dimension for any even degree $d\geq 2s+2$![]() . We deduce that the module ${T(2)\otimes \Delta (s)^F}$
. We deduce that the module ${T(2)\otimes \Delta (s)^F}$![]() has infinite $V^{\otimes d}$
has infinite $V^{\otimes d}$![]() -dominant dimension as well.
-dominant dimension as well.
Proof of theorem 5.2 Assume $d=2s\geq 4$![]() . By proposition 4.4, there exists $S(2, d)$
. By proposition 4.4, there exists $S(2, d)$![]() -exact sequences
-exact sequences
for every $0\leq t\leq s-1$![]() . Moreover, they remain exact over $\operatorname {Hom}_{S(2, d)}(-, V^{\otimes d})$
. Moreover, they remain exact over $\operatorname {Hom}_{S(2, d)}(-, V^{\otimes d})$![]() since $V^{\otimes d}$
since $V^{\otimes d}$![]() is a partial tilting module and so $\operatorname {Ext}_{S(2,d)}^1(\Delta (2t+2), V^{\otimes d})=0$
is a partial tilting module and so $\operatorname {Ext}_{S(2,d)}^1(\Delta (2t+2), V^{\otimes d})=0$![]() . By lemma 5.3, $T(2)\otimes \Delta (t)^F$
. By lemma 5.3, $T(2)\otimes \Delta (t)^F$![]() has infinite relative dominant dimension with respect to $V^{\otimes d}$
has infinite relative dominant dimension with respect to $V^{\otimes d}$![]() for $0\leq t\leq s-1$
for $0\leq t\leq s-1$![]() . By lemma 2.2,
. By lemma 2.2,
Hence, $V^{\otimes d}\!\operatorname {-domdim}_{S(2, d)} \Delta (0)=s+V^{\otimes d}\!\operatorname {-domdim}_{S(2, d)} \Delta (d)$![]() .
.
We will now determine the relative dominant dimension of $S(2,d)$![]() with respect to $V^{\otimes d}$
with respect to $V^{\otimes d}$![]() . Let $P_d(m)$
. Let $P_d(m)$![]() be the indecomposable projective $S(2, d)$
be the indecomposable projective $S(2, d)$![]() -module with homomorphic image $L(m)$
-module with homomorphic image $L(m)$![]() . Throughout, $d$
. Throughout, $d$![]() and $m$
and $m$![]() are even.
are even.
Lemma 5.4 Consider a projective module $P_d(m)$![]() where $d$
where $d$![]() and $m$
and $m$![]() are even with $m < d$
are even with $m < d$![]() . Then, one of the following holds.
. Then, one of the following holds.
(a) The number of quotients in a $\Delta$
 -filtration of $P_d(m)$
-filtration of $P_d(m)$ is even and $P_d(m)$
is even and $P_d(m)$ has a twisted filtration.
has a twisted filtration.(b) There is an exact sequence
\[ 0\to \Delta(d) \to P_d(m) \to P_{d-2}(m)\to 0 \]and $P_{d-2}(m)$
 has a twisted filtration.
has a twisted filtration.
Proof. Our strategy consists of proving that the projective module $P_d(m)$![]() is a quotient of a tilting module and then to combine this fact with lemma 4.5. Let $r_n:= 2^{n+1}-2$
is a quotient of a tilting module and then to combine this fact with lemma 4.5. Let $r_n:= 2^{n+1}-2$![]() . There is a unique $n$
. There is a unique $n$![]() such that $r_{n-1} < d \leq r_{n}$
such that $r_{n-1} < d \leq r_{n}$![]() . By our convention, we can view $P_d(m)$
. By our convention, we can view $P_d(m)$![]() as a module in degree $r_n$
as a module in degree $r_n$![]() . Since it has a simple top isomorphic to $L(m)$
. Since it has a simple top isomorphic to $L(m)$![]() , it is isomorphic to a quotient of $P_{r_n}(m)$
, it is isomorphic to a quotient of $P_{r_n}(m)$![]() .
.
By [Reference Erdmann and Henke23, Corollary 21] or [Reference Erdmann and Law24, Section 5], we have the following.
(i) If $0\leq m < (r_n)/2$
 , then $P_{r_n}(m)$
, then $P_{r_n}(m)$ is a tilting module (in fact, it is isomorphic to $T(r_n-m)$
is a tilting module (in fact, it is isomorphic to $T(r_n-m)$ ).
).(ii) For $(r_n)/2 < m \leq r_n$
 , the projective module $P_{r_n}(m)$
, the projective module $P_{r_n}(m)$ is a factor module of the tilting module $T(r_{n+1}-m)$
is a factor module of the tilting module $T(r_{n+1}-m)$ .
.
We exploit this now. Let $\hat {m}$![]() be the weight as above such that $P_d(m)$
be the weight as above such that $P_d(m)$![]() is a quotient of $T(\hat {m})$
is a quotient of $T(\hat {m})$![]() . With the notation as in lemma 4.5, since $\mathcal {F}(\Delta )$
. With the notation as in lemma 4.5, since $\mathcal {F}(\Delta )$![]() is closed under kernels of epimorphisms there is a submodule $U\subseteq T(\hat {m})$
is closed under kernels of epimorphisms there is a submodule $U\subseteq T(\hat {m})$![]() which has a $\Delta$
which has a $\Delta$![]() -filtration, with $M_i \subseteq U \subset M_{i-1}$
-filtration, with $M_i \subseteq U \subset M_{i-1}$![]() where $0< i\leq k$
where $0< i\leq k$![]() , and $P_{d}(m) \cong T(\hat {m})/U$
, and $P_{d}(m) \cong T(\hat {m})/U$![]() .
.
If $U=M_i$![]() then we have part (a). Otherwise, $P_d(m)$
then we have part (a). Otherwise, $P_d(m)$![]() has the submodule $M_{i-1}/U$
has the submodule $M_{i-1}/U$![]() which is isomorphic to $\Delta (2s_i)$
which is isomorphic to $\Delta (2s_i)$![]() and $U/M_i \cong \Delta (2s_i+2)$
and $U/M_i \cong \Delta (2s_i+2)$![]() . Moreover, $P_d(m)/\Delta (2s_i)\simeq T(\hat {m})/M_{i-1}$
. Moreover, $P_d(m)/\Delta (2s_i)\simeq T(\hat {m})/M_{i-1}$![]() which has a twisted filtration. Since $\Delta (2s_i)\subset P_d(m)$
which has a twisted filtration. Since $\Delta (2s_i)\subset P_d(m)$![]() we deduce $2s_i\leq d$
we deduce $2s_i\leq d$![]() . Suppose we have $2s_i < d$
. Suppose we have $2s_i < d$![]() , then $2s_i+2 \leq d$
, then $2s_i+2 \leq d$![]() . Hence, $T(\hat {m})/M_i\in S(2, d)\!\operatorname {-mod}$
. Hence, $T(\hat {m})/M_i\in S(2, d)\!\operatorname {-mod}$![]() . Since $P_d(m)$
. Since $P_d(m)$![]() is a quotient of the indecomposable $T(\hat {m})$
is a quotient of the indecomposable $T(\hat {m})$![]() , $T(\hat {m})$
, $T(\hat {m})$![]() has a simple top isomorphic to $L(m)$
has a simple top isomorphic to $L(m)$![]() . So, the module $T(\hat {m})/M_i$
. So, the module $T(\hat {m})/M_i$![]() has a simple top isomorphic to $L(m)$
has a simple top isomorphic to $L(m)$![]() and is in degree $d$
and is in degree $d$![]() , and therefore must be a quotient of $P_d(m)$
, and therefore must be a quotient of $P_d(m)$![]() . In particular, we would obtain $M_i=U$
. In particular, we would obtain $M_i=U$![]() . This is not so in the case considered. Therefore, $2s_i=d$
. This is not so in the case considered. Therefore, $2s_i=d$![]() and the result follows from (4.2).
and the result follows from (4.2).
Example 5.5 Consider figure 1, with $d=28$![]() . Then, $r_n=30$
. Then, $r_n=30$![]() and the projective modules $P_d(m)$
and the projective modules $P_d(m)$![]() for $15 < m < 28$
for $15 < m < 28$![]() are as follows. We have (a) when $m=18, 20, 22, 26$
are as follows. We have (a) when $m=18, 20, 22, 26$![]() and we have (b) when $m=16, 24$
and we have (b) when $m=16, 24$![]() . Note that cases $P_d(m) \cong P_{d-2}(m)$
. Note that cases $P_d(m) \cong P_{d-2}(m)$![]() occur in (a).
occur in (a).
Corollary 5.6 With the setting as in lemma 5.4,
if (a) occurs, then $V^{\otimes d}\!\operatorname {-domdim}_S P_d(m) = +\infty$![]() .
.
If (b) occurs, then for $d=2s$![]() we have $V^{\otimes d}\!\operatorname {-domdim}_S P_d(m) = V^{\otimes d}\!\operatorname {-domdim}_S \Delta (d).$
we have $V^{\otimes d}\!\operatorname {-domdim}_S P_d(m) = V^{\otimes d}\!\operatorname {-domdim}_S \Delta (d).$![]() In particular,
In particular,
This completes the proof of theorem B for algebraically closed fields. By [Reference Cruz10, Lemma 3.2.3], the result also holds over arbitrary fields.
5.2. The quantum case
Remark 5.7 If $q$![]() is not a root of unity, then $S_{K, q}(2, d)$
is not a root of unity, then $S_{K, q}(2, d)$![]() is semi-simple [Reference Donkin20, 4.3(7)] and $V^{\otimes d}$
is semi-simple [Reference Donkin20, 4.3(7)] and $V^{\otimes d}$![]() being faithful is a characteristic tilting module. Otherwise, the summands of $V^{\otimes d}$
being faithful is a characteristic tilting module. Otherwise, the summands of $V^{\otimes d}$![]() over $S_{K, q}(2, d)$
over $S_{K, q}(2, d)$![]() are the tilting modules labelled by the $\ell$
are the tilting modules labelled by the $\ell$![]() -regular partitions of $d$
-regular partitions of $d$![]() in at most two parts, where $q$
in at most two parts, where $q$![]() is an $\ell$
is an $\ell$![]() -root of unity. Hence, replacing $\operatorname {char} K$
-root of unity. Hence, replacing $\operatorname {char} K$![]() by $\ell$
by $\ell$![]() in lemma 4.1, we obtain that $V^{\otimes d}$
in lemma 4.1, we obtain that $V^{\otimes d}$![]() is a characteristic tilting module over $S_{K, q}(2, d)$
is a characteristic tilting module over $S_{K, q}(2, d)$![]() if $q+1\neq 0$
if $q+1\neq 0$![]() or $d$
or $d$![]() is odd.
is odd.
For the quantum case, it is enough to take $S=S_{K, q}(2, d)$![]() where $q+1=0$
where $q+1=0$![]() . In this case, everything is exactly the same as over $S(2, d)$
. In this case, everything is exactly the same as over $S(2, d)$![]() when $\operatorname {char} K=2$
when $\operatorname {char} K=2$![]() . Namely, we may take $S_{K, q}(2, d)$
. Namely, we may take $S_{K, q}(2, d)$![]() as $A_q(2, d)^*$
as $A_q(2, d)^*$![]() as it is done in [Reference Cox6, Reference Donkin20], and also in [Reference Dipper and Donkin12, Reference Donkin19]. The definition of $A_q(2)$
as it is done in [Reference Cox6, Reference Donkin20], and also in [Reference Dipper and Donkin12, Reference Donkin19]. The definition of $A_q(2)$![]() may be found in [Reference Dipper and Donkin12, p. 16]. This means that one takes the quantum group $G(2)$
may be found in [Reference Dipper and Donkin12, p. 16]. This means that one takes the quantum group $G(2)$![]() as defined in [Reference Dipper and Donkin12] instead of $SL(2, K)$
as defined in [Reference Dipper and Donkin12] instead of $SL(2, K)$![]() .
.
As it is explained in [Reference Erdmann and Law24, Sections 3.1 and 3.2], we can use the same labelling for weights; in that paper the parameter $q$![]() is a primitive $\ell$
is a primitive $\ell$![]() -th root of $1$
-th root of $1$![]() and we only need $\ell =2$
and we only need $\ell =2$![]() . We can regard $S_{K, q}(2, d)$
. We can regard $S_{K, q}(2, d)$![]() as a factor algebra of $S_{K, q}(2, d+2)$
as a factor algebra of $S_{K, q}(2, d+2)$![]() , using [Reference Donkin20, Section 4.2], and therefore regard modules in degree $d$
, using [Reference Donkin20, Section 4.2], and therefore regard modules in degree $d$![]() again as modules in degree $d'$
again as modules in degree $d'$![]() for $d'>d$
for $d'>d$![]() of the same parity.
of the same parity.
There is a Frobenius morphism from the quantum group $G(2)$![]() to the classical setting, hence if $\Delta (m)$
to the classical setting, hence if $\Delta (m)$![]() (resp. $T(m)$
(resp. $T(m)$![]() ) is a standard module (resp. a tilting module) for the classical setting, then $\Delta (m)^F$
) is a standard module (resp. a tilting module) for the classical setting, then $\Delta (m)^F$![]() (resp. $T(m)^F$
(resp. $T(m)^F$![]() ) is a module for the quantum group, and so are the tensor products $T(2)\otimes \Delta (m)^F$
) is a module for the quantum group, and so are the tensor products $T(2)\otimes \Delta (m)^F$![]() and $T(2)\otimes T(m)^F$
and $T(2)\otimes T(m)^F$![]() modules for the quantum group. The $q$
modules for the quantum group. The $q$![]() -analogues of the exact sequences in § 4.3 and proposition 4.4 exist by [Reference Cox6, Prop. 3.3 and 3.4]. See also [Reference Erdmann and Law24, Proposition 3.1] (our situation of interest is recovered by fixing $l=2$
-analogues of the exact sequences in § 4.3 and proposition 4.4 exist by [Reference Cox6, Prop. 3.3 and 3.4]. See also [Reference Erdmann and Law24, Proposition 3.1] (our situation of interest is recovered by fixing $l=2$![]() in their setup). The $q$
in their setup). The $q$![]() -analogue of proposition 4.3 can be found in [Reference Donkin20, Section 3.4, p. 73, (8)].
-analogue of proposition 4.3 can be found in [Reference Donkin20, Section 3.4, p. 73, (8)].
We note that (1) of § 4.3 and the $q$![]() -analogue imply, by induction, that all decomposition numbers are $0$
-analogue imply, by induction, that all decomposition numbers are $0$![]() or $1$
or $1$![]() .
.
In [Reference Dipper and Donkin12], it is shown that this version of the $q$![]() -Schur algebra is the same as our definition, as the endomorphism algebra of the action of the Iwahori–Hecke algebra on the tensor space $V^{\otimes d}$
-Schur algebra is the same as our definition, as the endomorphism algebra of the action of the Iwahori–Hecke algebra on the tensor space $V^{\otimes d}$![]() , see § 6. The definition of the Iwahori–Hecke algebra, as we take it is given in 6.2. In particular, we denote by $H$
, see § 6. The definition of the Iwahori–Hecke algebra, as we take it is given in 6.2. In particular, we denote by $H$![]() the Iwahori–Hecke algebra. Their strategy in [Reference Dipper and Donkin12, Section 3] is to show that the action of the Iwahori–Hecke algebra on the tensor space is a comodule homomorphism (see 3.1.6 of [Reference Dipper and Donkin12]). The $H$
the Iwahori–Hecke algebra. Their strategy in [Reference Dipper and Donkin12, Section 3] is to show that the action of the Iwahori–Hecke algebra on the tensor space is a comodule homomorphism (see 3.1.6 of [Reference Dipper and Donkin12]). The $H$![]() -action in [Reference Dipper and Donkin12, 3.1.6] is not the same as ours, but it is explained in detail (see 4.4.3 of [Reference Dipper and Donkin12]) that the action we use also can be taken.
-action in [Reference Dipper and Donkin12, 3.1.6] is not the same as ours, but it is explained in detail (see 4.4.3 of [Reference Dipper and Donkin12]) that the action we use also can be taken.
Hence, the arguments of § 5 remain valid in the quantum case and therefore, we obtain the following:
Theorem 5.8 Let $K$![]() be a field and fix $q=u^{-2}$
be a field and fix $q=u^{-2}$![]() for some $u\in K$
for some $u\in K$![]() . Let $S$
. Let $S$![]() be the $q$
be the $q$![]() -Schur algebra $S_{K, q}(2, d)$
-Schur algebra $S_{K, q}(2, d)$![]() and $T$
and $T$![]() be the characteristic tilting module of $S$
be the characteristic tilting module of $S$![]() . Then,
. Then,

Remark 5.9 One might want to know for which $m$![]() it is true that $V^{\otimes d}\!\operatorname {-domdim}_S P_d(m)$
it is true that $V^{\otimes d}\!\operatorname {-domdim}_S P_d(m)$![]() is finite. In principle, one can answer this, using the formula in [Reference Henke34] for decomposition numbers. Namely, this $V^{\otimes d}$
is finite. In principle, one can answer this, using the formula in [Reference Henke34] for decomposition numbers. Namely, this $V^{\otimes d}$![]() -dominant dimension is finite if and only the number of $\Delta$
-dominant dimension is finite if and only the number of $\Delta$![]() -quotients of $P_d(m)$
-quotients of $P_d(m)$![]() is odd, that is the number of $1$
is odd, that is the number of $1$![]() s in the column of $L(m)$
s in the column of $L(m)$![]() .
.
Example 5.10 We give an illustration of theorem B, we continue with example 3.7. Let $A=S(2,4)$![]() where $K$
where $K$![]() has characteristic $2$
has characteristic $2$![]() , then ${\rm add} (V^{\otimes 4}) = {\rm add} [T(2)\oplus T(4)]$
, then ${\rm add} (V^{\otimes 4}) = {\rm add} [T(2)\oplus T(4)]$![]() .
.
The fact that $Q\!\operatorname {-domdim} \Delta (4)=2+Q\!\operatorname {-domdim}_A T(0)$![]() for this example was already done in the proof of theorem 5.2. Case (a) of lemma 5.4 occurs for $P(2)$
for this example was already done in the proof of theorem 5.2. Case (a) of lemma 5.4 occurs for $P(2)$![]() . Indeed, $Q\!\operatorname {-domdim}_A P(2)=+\infty$
. Indeed, $Q\!\operatorname {-domdim}_A P(2)=+\infty$![]() since $P(2)\simeq T(4)$
since $P(2)\simeq T(4)$![]() . Case (b) of lemma 5.4 occurs for $P(0)$
. Case (b) of lemma 5.4 occurs for $P(0)$![]() . Indeed, there exists an exact sequence $0\rightarrow \Delta (4)\rightarrow P(0)\rightarrow T(2)\rightarrow 0$
. Indeed, there exists an exact sequence $0\rightarrow \Delta (4)\rightarrow P(0)\rightarrow T(2)\rightarrow 0$![]() , where $Q\!\operatorname {-domdim}_A T(2)=+\infty$
, where $Q\!\operatorname {-domdim}_A T(2)=+\infty$![]() . So, lemma 2.2 gives that $Q\!\operatorname {-domdim}_A P(0)=Q\!\operatorname {-domdim}_A \Delta (4)$
. So, lemma 2.2 gives that $Q\!\operatorname {-domdim}_A P(0)=Q\!\operatorname {-domdim}_A \Delta (4)$![]() . Therefore, $Q\!\operatorname {-domdim} A=Q\!\operatorname {-domdim}_A \Delta (4)=2+Q\!\operatorname {-domdim}_A T(0)$
. Therefore, $Q\!\operatorname {-domdim} A=Q\!\operatorname {-domdim}_A \Delta (4)=2+Q\!\operatorname {-domdim}_A T(0)$![]() $=2+Q\!\operatorname {-domdim}_AT=4$
$=2+Q\!\operatorname {-domdim}_AT=4$![]() .
.
5.3. An application of theorem B
In [Reference Buan and Solberg3], Buan and Solberg characterize complements of almost complete (co) tilting modules. Let $Q$![]() be an $A$
be an $A$![]() -module, then the faithful dimension of $Q$
-module, then the faithful dimension of $Q$![]() as they define it, is equal to $Q\!\operatorname {-domdim}_A A$
as they define it, is equal to $Q\!\operatorname {-domdim}_A A$![]() . A partial tilting module $Q$
. A partial tilting module $Q$![]() is almost complete if it is not a tilting module, but there is an indecomposable module $X$
is almost complete if it is not a tilting module, but there is an indecomposable module $X$![]() such that $Q\oplus X$
such that $Q\oplus X$![]() is a tilting module. In this case, call $X$
is a tilting module. In this case, call $X$![]() a complement of $Q$
a complement of $Q$![]() . Recall that a module $M$
. Recall that a module $M$![]() is a tilting module over $A$
is a tilting module over $A$![]() if and only if $DM$
if and only if $DM$![]() is a cotilting module over $A^{op}$
is a cotilting module over $A^{op}$![]() and $M\!\operatorname {-domdim} A=DM\!\operatorname {-domdim}_{A^{op}}A$
and $M\!\operatorname {-domdim} A=DM\!\operatorname {-domdim}_{A^{op}}A$![]() .
.
Hence, dualizing [Reference Buan and Solberg3, Theorem 3.6] and [Reference Buan and Solberg3, Proposition 3.2] of Buan and Solberg we have the following.
Theorem 5.11 Let $A$![]() be a finite-dimensional algebra over a field.
be a finite-dimensional algebra over a field.
(1) Let $n$
 be a non-negative integer. An almost complete tilting $A$
be a non-negative integer. An almost complete tilting $A$ -module $Q$
-module $Q$ has $n+1$
has $n+1$ complements if and only if ${Q\!\operatorname {-domdim}_A A = n}$
complements if and only if ${Q\!\operatorname {-domdim}_A A = n}$ .
.(2) Let $Q\in A\!\operatorname {-mod}$
 so that $Q\oplus X$
so that $Q\oplus X$ is a tilting $A$
is a tilting $A$ -module. If $g\colon M_0\rightarrow X$
-module. If $g\colon M_0\rightarrow X$ is a surjective minimal right $\!\operatorname {add}_A Q$
is a surjective minimal right $\!\operatorname {add}_A Q$ -approximation of $X$
-approximation of $X$ , then $\ker g$
, then $\ker g$ is a complement of $Q$
is a complement of $Q$ .
.(3) Let $Q\in A\!\operatorname {-mod}$
 so that $Q\oplus X$
so that $Q\oplus X$ is a tilting $A$
is a tilting $A$ -module. If $f\colon X\rightarrow M_0$
-module. If $f\colon X\rightarrow M_0$ is an injective minimal left $\!\operatorname {add}_A Q$
is an injective minimal left $\!\operatorname {add}_A Q$ -approximation of $X$
-approximation of $X$ , then $\operatorname {coker} f$
, then $\operatorname {coker} f$ is a complement of $Q$
is a complement of $Q$ .
.
Assume $A=S(2, d)$![]() for char$(K)=2$
for char$(K)=2$![]() and $d$
and $d$![]() even, then $Q=V^{\otimes d}$
even, then $Q=V^{\otimes d}$![]() is an almost complete tilting module. We have proved that $Q\!\operatorname {-domdim} A=d$
is an almost complete tilting module. We have proved that $Q\!\operatorname {-domdim} A=d$![]() , so there should be in general $d+1$
, so there should be in general $d+1$![]() complements.
complements.
Example 5.12 Assume $A=S(2, 4)$![]() when $p=2$
when $p=2$![]() , we continue with the notation as in example 5.10. Consider $Q=V^{\otimes 4}$
, we continue with the notation as in example 5.10. Consider $Q=V^{\otimes 4}$![]() . We know $T(0)$
. We know $T(0)$![]() is a complement of $Q$
is a complement of $Q$![]() . By computing minimal right ${\rm add}( Q)$
. By computing minimal right ${\rm add}( Q)$![]() -approximations, we get the following exact sequence:
-approximations, we get the following exact sequence:
Namely, the kernel of the surjection $f_0: T(2)\to \Delta (0)\cong T(0)$![]() is $\Delta (2)$
is $\Delta (2)$![]() . Take $f_1$
. Take $f_1$![]() to be the map where the first component has image $L(0)$
to be the map where the first component has image $L(0)$![]() and the second component has image $\Delta (2)$
and the second component has image $\Delta (2)$![]() , this is a right ${\rm add}\, Q$
, this is a right ${\rm add}\, Q$![]() approximation, and its kernel is isomorphic to $P(0)$
approximation, and its kernel is isomorphic to $P(0)$![]() . It is minimal since $P(0)$
. It is minimal since $P(0)$![]() is indecomposable. A minimal right ${\rm add}\, Q$
is indecomposable. A minimal right ${\rm add}\, Q$![]() approximation of $P(0)$
approximation of $P(0)$![]() cannot be surjective since $P(0)$
cannot be surjective since $P(0)$![]() is projective but not a direct summand of $Q$
is projective but not a direct summand of $Q$![]() .
.
By (2) of theorem 5.11 on (5.4), we get that ${\rm ker} f_0 = \Delta (2)$![]() and $P(0)$
and $P(0)$![]() are complements of $Q$
are complements of $Q$![]() . Now, applying the simple preserving duality functor to (5.4) we get an exact sequence:
. Now, applying the simple preserving duality functor to (5.4) we get an exact sequence:
and surjective minimal right approximations are sent to injective minimal left approximations. Thus, the complements of $Q$![]() are
are
6. Temperley–Lieb algebras
These algebras were introduced in the context of statistical mechanics [Reference Temperley and Lieb50], and then became popular through the work of Jones. In particular, he noticed that they occur as quotients of Iwahori–Hecke algebras [Reference Jones40, Reference Jones41]. See also [Reference Westbury51] for further details. We give the definition and discuss the connections with Schur algebras.
Definition 6.1 Let $R$![]() be a commutative ring and $\delta$
be a commutative ring and $\delta$![]() an element of $R$
an element of $R$![]() . The Temperley–Lieb algebra $TL_{R,d}(\delta )$
. The Temperley–Lieb algebra $TL_{R,d}(\delta )$![]() over $R$
over $R$![]() is the $R$
is the $R$![]() -algebra generated by elements $U_1, U_2, \ldots, U_{d-1}$
-algebra generated by elements $U_1, U_2, \ldots, U_{d-1}$![]() with defining relations, here $1\leq i, j\leq d-1$
with defining relations, here $1\leq i, j\leq d-1$![]() such that each term is defined:
such that each term is defined:
(a) $U_iU_j=U_jU_i$
 ($|i-j|>1$
($|i-j|>1$ ),
),(b) $U_i^2 = \delta U_i$
 ,
,(c) $U_{i}U_{i+1}U_i = U_i$
 , $1\leq i\leq n-2,$
, $1\leq i\leq n-2,$
(d) $U_{i}U_{i- 1}U_i = U_i$
 , $2\leq i\leq n-1.$
, $2\leq i\leq n-1.$
It can be viewed as a diagram algebra, with a very extensive literature, but we will not give details since we do not use diagram calculations.
6.1. The classical case
We will start by considering the class of Temperley–Lieb algebras of the form $TL_{R, d}(-2)$![]() which can be viewed as quotients of group algebras of the symmetric group.
which can be viewed as quotients of group algebras of the symmetric group.
Lemma 6.2 There is a surjective algebra homomorphism $\Phi : R\mathcal {S}_d \to TL_{R,d}(-2)$![]() taking the generator $T_i = (i \ i+1)$
taking the generator $T_i = (i \ i+1)$![]() of $\mathcal {S}_d$
of $\mathcal {S}_d$![]() to $U_i+1$
to $U_i+1$![]() for $1\leq i\leq d-1$
for $1\leq i\leq d-1$![]() .
.
Proof. Recall that the group algebra $R\mathcal {S}_d$![]() is generated by the $T_i$
is generated by the $T_i$![]() subject to the relations:
subject to the relations:
(a) $T_iT_{i+1}T_i = T_{i+1}T_iT_{i+1}$
 ,
,(b) $T_iT_j = T_jT_i$
 ($|i-j| > 1$
($|i-j| > 1$ ),
),(c) $T_i^2=1$
 ,
,
for $1\leq i, j \leq d-1$![]() such that each factor is defined. To show that the map is well-defined one has to check that it preserves these relations; this is straightforward. It is clear that $\Phi$
such that each factor is defined. To show that the map is well-defined one has to check that it preserves these relations; this is straightforward. It is clear that $\Phi$![]() is surjective, noting that $U_i = \Phi (T_i-T_i^2)$
is surjective, noting that $U_i = \Phi (T_i-T_i^2)$![]() .
.
The following description of the kernel of $\Phi$![]() goes back to [Reference Jones42, p. 364].
goes back to [Reference Jones42, p. 364].
Theorem 6.3 For each $i=1, 2, \ldots, d-2$![]() define
define
Let $I$![]() be the ideal of $R\mathcal {S}_d$
be the ideal of $R\mathcal {S}_d$![]() generated by the $x_i$
generated by the $x_i$![]() for $1\leq i\leq d-2$
for $1\leq i\leq d-2$![]() . Then, there is an exact sequence
. Then, there is an exact sequence
Proof. One checks that $\Phi (x_i)=0$![]() for each $i=1, \ldots, d-2$
for each $i=1, \ldots, d-2$![]() . So, we have a commutative diagram:
. So, we have a commutative diagram:

where $\pi$![]() maps the image of $T_i$
maps the image of $T_i$![]() in $RS_d/I$
in $RS_d/I$![]() to $\Phi (T_i) = U_i+1$
to $\Phi (T_i) = U_i+1$![]() , and $\iota$
, and $\iota$![]() is the inclusion map. Consider $\pi ': TL_{R, d}(-2) \to R\mathcal {S}_d/I$
is the inclusion map. Consider $\pi ': TL_{R, d}(-2) \to R\mathcal {S}_d/I$![]() defined by taking $U_i$
defined by taking $U_i$![]() to the image of $T_i-1$
to the image of $T_i-1$![]() in $R\mathcal {S}_d/I$
in $R\mathcal {S}_d/I$![]() . One checks that $\pi '$
. One checks that $\pi '$![]() preserves the defining relations for $TL_{R, d}(-2)$
preserves the defining relations for $TL_{R, d}(-2)$![]() , so that it is a well-defined map. Finally,
, so that it is a well-defined map. Finally,
Therefore, ${\rm ker}\, \Phi = I$![]() .
.
It is nowadays widely known that Temperley–Lieb algebras can be viewed as the centralizer algebras of quantum groups $\mathfrak {sl}_2$![]() in the endomorphism algebra of a tensor power and this goes back to the work of Martin [Reference Martin44] and Jimbo [Reference Jimbo39]. Recall that over $R$
in the endomorphism algebra of a tensor power and this goes back to the work of Martin [Reference Martin44] and Jimbo [Reference Jimbo39]. Recall that over $R$![]() , the Schur algebra $S_R(2, d)$
, the Schur algebra $S_R(2, d)$![]() is defined as the endomorphism algebra $\operatorname {End}_{R\mathcal {S}_d}((R^2)^{\otimes d})$
is defined as the endomorphism algebra $\operatorname {End}_{R\mathcal {S}_d}((R^2)^{\otimes d})$![]() , where $(R^2)^{\otimes d}$
, where $(R^2)^{\otimes d}$![]() affords a right $R\mathcal {S}_d$
affords a right $R\mathcal {S}_d$![]() -module structure via place permutation. In order to relate the Temperley–Lieb algebra to the Schur algebra, we need a suitable action of the Temperley–Lieb algebra on the tensor space. It is as follows.
-module structure via place permutation. In order to relate the Temperley–Lieb algebra to the Schur algebra, we need a suitable action of the Temperley–Lieb algebra on the tensor space. It is as follows.
Theorem 6.4 Let $V$![]() be a free $R$
be a free $R$![]() -module of rank $2$
-module of rank $2$![]() . Then, $V^{\otimes d}$
. Then, $V^{\otimes d}$![]() is a module over $\Lambda = TL_{R, d}(-2)$
is a module over $\Lambda = TL_{R, d}(-2)$![]() where $U_i$
where $U_i$![]() acts as ${\rm id}_V^{\otimes (i-1)}\otimes \tau \otimes {\rm id}_V^{\otimes (d-i-1)}$
acts as ${\rm id}_V^{\otimes (i-1)}\otimes \tau \otimes {\rm id}_V^{\otimes (d-i-1)}$![]() . Here, $\tau$
. Here, $\tau$![]() is the endomorphism of $V^{\otimes 2}$
is the endomorphism of $V^{\otimes 2}$![]() defined by
defined by
(for $v_1, v_2\in V$![]() ). Moreover, there is an algebra isomorphism
). Moreover, there is an algebra isomorphism
Proof. We know that $R\mathcal {S}_d$![]() acts by place permutations on $V^{\otimes d}$
acts by place permutations on $V^{\otimes d}$![]() and we can view this as a right action. With this, $T_i- 1$
and we can view this as a right action. With this, $T_i- 1$![]() acts as $U_i$
acts as $U_i$![]() on the space $V^{\otimes d}$
on the space $V^{\otimes d}$![]() . This shows that it factors through $\Lambda$
. This shows that it factors through $\Lambda$![]() . In particular, to show that $\Lambda \rightarrow {\rm End}_{S(2, d)}(V^{\otimes d})^{op}$
. In particular, to show that $\Lambda \rightarrow {\rm End}_{S(2, d)}(V^{\otimes d})^{op}$![]() is surjective it is enough to check that the canonical map $RS_d\rightarrow {\rm End}_{S(2, d)}(V^{\otimes d})^{op}$
is surjective it is enough to check that the canonical map $RS_d\rightarrow {\rm End}_{S(2, d)}(V^{\otimes d})^{op}$![]() is surjective. But this follows from classical Schur–Weyl duality (see e.g. [Reference König, Slungård and Xi43]). In fact, this can be seen in the following way: let $K$
is surjective. But this follows from classical Schur–Weyl duality (see e.g. [Reference König, Slungård and Xi43]). In fact, this can be seen in the following way: let $K$![]() be a field, then the canonical map $K\mathcal {S}_d\rightarrow \operatorname {End}_{S(2, d)}(V^{\otimes d})^{op}$
be a field, then the canonical map $K\mathcal {S}_d\rightarrow \operatorname {End}_{S(2, d)}(V^{\otimes d})^{op}$![]() fits in the following commutative diagram:
fits in the following commutative diagram:

Here, $\psi$![]() is surjective because $\operatorname {domdim} S_K(d, d)\geq 2$
is surjective because $\operatorname {domdim} S_K(d, d)\geq 2$![]() and $\phi$
and $\phi$![]() is surjective by [Reference Erdmann27, 1.7] and [Reference Donkin20, 4.7] because $(K^d)^{\otimes d}$
is surjective by [Reference Erdmann27, 1.7] and [Reference Donkin20, 4.7] because $(K^d)^{\otimes d}$![]() is a projective–injective module over $S(d, d)$
is a projective–injective module over $S(d, d)$![]() . Observe that $\operatorname {End}_{S_R(2, d)}(V^{\otimes d})^{op}\in R\!\operatorname {-proj}$
. Observe that $\operatorname {End}_{S_R(2, d)}(V^{\otimes d})^{op}\in R\!\operatorname {-proj}$![]() (see e.g. [Reference Cruz9, Proposition A.4.3, Corollary A.4.4]) and it has a base change property (see e.g. [Reference Cruz9, Corollary A.4.6]). In particular, $R(\mathfrak {m})\otimes _R \operatorname {End}_{S_R(2, d)}(V^{\otimes d})^{op}\simeq \operatorname {End}_{S_{R(\mathfrak {m})}(2, d)}(V^{\otimes d})^{op}$
(see e.g. [Reference Cruz9, Proposition A.4.3, Corollary A.4.4]) and it has a base change property (see e.g. [Reference Cruz9, Corollary A.4.6]). In particular, $R(\mathfrak {m})\otimes _R \operatorname {End}_{S_R(2, d)}(V^{\otimes d})^{op}\simeq \operatorname {End}_{S_{R(\mathfrak {m})}(2, d)}(V^{\otimes d})^{op}$![]() for every maximal ideal $\mathfrak {m}$
for every maximal ideal $\mathfrak {m}$![]() of $R$
of $R$![]() . By the above discussion, the maps $R(\mathfrak {m})S_d\rightarrow \operatorname {End}_{S_{R(\mathfrak {m})}(2, d)}(V^{\otimes d})^{op}$
. By the above discussion, the maps $R(\mathfrak {m})S_d\rightarrow \operatorname {End}_{S_{R(\mathfrak {m})}(2, d)}(V^{\otimes d})^{op}$![]() are surjective for every maximal ideal $\mathfrak {m}$
are surjective for every maximal ideal $\mathfrak {m}$![]() of $R$
of $R$![]() . Now, by Nakayama's lemma the map $RS_d\rightarrow \operatorname {End}_{S_R(2, d)}(V^{\otimes d})^{op}$
. Now, by Nakayama's lemma the map $RS_d\rightarrow \operatorname {End}_{S_R(2, d)}(V^{\otimes d})^{op}$![]() is surjective.
is surjective.
It remains to show that the action of $\Lambda$![]() is injective. Let $\sum _i a_iU_i \in \Lambda$
is injective. Let $\sum _i a_iU_i \in \Lambda$![]() acting as zero on $V^{\otimes d}$
acting as zero on $V^{\otimes d}$![]() . The action of $\sum _i a_iU_i$
. The action of $\sum _i a_iU_i$![]() in $y_k$
in $y_k$![]() , defined as the basis element $e_1\otimes \cdots \otimes e_1\otimes e_2\otimes e_1\otimes \cdots \otimes e_1$
, defined as the basis element $e_1\otimes \cdots \otimes e_1\otimes e_2\otimes e_1\otimes \cdots \otimes e_1$![]() where $e_2$
where $e_2$![]() appears in position $k+1$
appears in position $k+1$![]() , yields that $a_k=a_{k+1}=0$
, yields that $a_k=a_{k+1}=0$![]() . This concludes the proof.
. This concludes the proof.
6.2. The $q$ -analogue
-analogue
We shall now discuss the general case of theorem 6.4 and its importance for all Temperley–Lieb algebras.
Let $R$![]() be a commutative Noetherian ring with an invertible element $u\in R$
be a commutative Noetherian ring with an invertible element $u\in R$![]() . We fix a natural number $d$
. We fix a natural number $d$![]() , and we set $q:= u^{-2}$
, and we set $q:= u^{-2}$![]() . We take the Iwahori–Hecke algebra $H=H_{R, q}(d)$
. We take the Iwahori–Hecke algebra $H=H_{R, q}(d)$![]() to be the $R$
to be the $R$![]() -algebra with basis $\{ \widetilde {T}_{w}\mid w\in \mathcal {S}_d\}$
-algebra with basis $\{ \widetilde {T}_{w}\mid w\in \mathcal {S}_d\}$![]() with relations:
with relations:

Here, $s$![]() runs through the set of transpositions $S=\{ (i \ i+1)\mid 1\leq i < d\}$
runs through the set of transpositions $S=\{ (i \ i+1)\mid 1\leq i < d\}$![]() in $\mathcal {S}_d$
in $\mathcal {S}_d$![]() , and $l(w)$
, and $l(w)$![]() is the usual length for $w\in \mathcal {S}_d$
is the usual length for $w\in \mathcal {S}_d$![]() , that is the minimal number of transpositions needed in a factorization of $w$
, that is the minimal number of transpositions needed in a factorization of $w$![]() .
.
This presentation corresponds to the presentation used in [Reference Dipper and Donkin12–Reference Dipper and James14, Reference Donkin20] by
The algebra $H$![]() can also be defined by the braid relations, together with $\widetilde {T}_s^2 = (u-u^{-1})\widetilde {T}_s + 1$
can also be defined by the braid relations, together with $\widetilde {T}_s^2 = (u-u^{-1})\widetilde {T}_s + 1$![]() , that is
, that is
Lemma 6.5 Let $\delta = -u-u^{-1}$![]() . Then, there is a surjective algebra homomorphism
. Then, there is a surjective algebra homomorphism
taking the generator $\widetilde {T}_i:=\widetilde {T}_{(i \ i+1)}$![]() to $U_i+ u$
to $U_i+ u$![]() for $1\leq i \leq d-1$
for $1\leq i \leq d-1$![]() .
.
Proof. We must show that $\Phi$![]() is well-defined, that is it respects the relations of the Hecke algebra. It is clearly surjective. We work with the presentation via the braid relations, together with $(\widetilde {T}_i-u)(\widetilde {T}_i+u^{-1}) = 0$
is well-defined, that is it respects the relations of the Hecke algebra. It is clearly surjective. We work with the presentation via the braid relations, together with $(\widetilde {T}_i-u)(\widetilde {T}_i+u^{-1}) = 0$![]() (for $1\leq i < d-1$
(for $1\leq i < d-1$![]() ). With the definition given, $\Phi (\widetilde {T}_i + u^{-1}) = U_i + u+ u^{-1} = U_i-\delta$
). With the definition given, $\Phi (\widetilde {T}_i + u^{-1}) = U_i + u+ u^{-1} = U_i-\delta$![]() and $\Phi (\widetilde {T}_i-u) = U_i$
and $\Phi (\widetilde {T}_i-u) = U_i$![]() . Hence, we have $\Phi (\widetilde {T}_i + u^{-1})\Phi (\widetilde {T}_i - u) = (U_i-\delta )U_i = 0$
. Hence, we have $\Phi (\widetilde {T}_i + u^{-1})\Phi (\widetilde {T}_i - u) = (U_i-\delta )U_i = 0$![]() .
.
To check the braid relations, we compute:

The coefficient of $U_i$![]() is equal to $u^2$
is equal to $u^2$![]() . With this, the expression is symmetric in $i, i+1$
. With this, the expression is symmetric in $i, i+1$![]() and is therefore equal to $(U_{i+1}+u)(U_i+u)(U_{i+1}+u)$
and is therefore equal to $(U_{i+1}+u)(U_i+u)(U_{i+1}+u)$![]() .
.
We want to determine the kernel of $\Phi$![]() .
.
Theorem 6.6 For each $i=1, 2, \ldots, d-2$![]() define
define
Let $I$![]() be the ideal of $H_{R, q}(d)$
be the ideal of $H_{R, q}(d)$![]() generated by the $x_i$
generated by the $x_i$![]() for $1\leq i\leq d-2$
for $1\leq i\leq d-2$![]() . Fix $\delta = -u-u^{-1}$
. Fix $\delta = -u-u^{-1}$![]() , then there is an exact sequence
, then there is an exact sequence
Proof. From the proof of lemma 6.5 we see that
and with this one gets that $\Phi (x_i) = 0$![]() for all $i$
for all $i$![]() . Hence, $I\subseteq {\rm ker}(\Phi )$
. Hence, $I\subseteq {\rm ker}(\Phi )$![]() . Analogously to the proof of theorem 6.3 replacing the map $\pi '$
. Analogously to the proof of theorem 6.3 replacing the map $\pi '$![]() with the map $TL_{R, d}(\delta )\rightarrow H_{R, q}(d)$
with the map $TL_{R, d}(\delta )\rightarrow H_{R, q}(d)$![]() defined by taking $U_i$
defined by taking $U_i$![]() to the image of $\widetilde {T}_i-u$
to the image of $\widetilde {T}_i-u$![]() in $H_{R, q}(d)/I$
in $H_{R, q}(d)/I$![]() one proves equality.
one proves equality.
Let $V^{\otimes d}$![]() be the free $R$
be the free $R$![]() -module of rank $n$
-module of rank $n$![]() over $R$
over $R$![]() (later we will take $n=2$
(later we will take $n=2$![]() ). Then, $V^{\otimes d}$
). Then, $V^{\otimes d}$![]() is a right $H$
is a right $H$![]() -module, which can be regarded as a deformation of the place permutation action of $\mathcal {S}_d$
-module, which can be regarded as a deformation of the place permutation action of $\mathcal {S}_d$![]() . Denote by $I(n, d)$
. Denote by $I(n, d)$![]() the set of maps $\{1, \ldots, d\}\rightarrow \{1, \ldots, n\}$
the set of maps $\{1, \ldots, d\}\rightarrow \{1, \ldots, n\}$![]() and by $i_j$
and by $i_j$![]() the image $i(j)$
the image $i(j)$![]() . If ${\bf i} \in I(n,d)$
. If ${\bf i} \in I(n,d)$![]() labels the basis element $e_{\bf {i}} = e_{i_1}\otimes \cdots \otimes e_{i_d}$
labels the basis element $e_{\bf {i}} = e_{i_1}\otimes \cdots \otimes e_{i_d}$![]() of $V^{\otimes d}$
of $V^{\otimes d}$![]() and $s=(t \ t+1)\in S$
and $s=(t \ t+1)\in S$![]() we write $e_{\bf i}\cdot s$
we write $e_{\bf i}\cdot s$![]() for the basis element obtained by interchanging $e_{i_t}$
for the basis element obtained by interchanging $e_{i_t}$![]() and $e_{i_{t+1}}$
and $e_{i_{t+1}}$![]() . Then
. Then

Focusing on the Temperley–Lieb algebra, we take $n=2$![]() . Recall that the $q$
. Recall that the $q$![]() -Schur algebra $S_q(2, d)$
-Schur algebra $S_q(2, d)$![]() is the endomorphism algebra ${\rm End}_H(V^{\otimes d})$
is the endomorphism algebra ${\rm End}_H(V^{\otimes d})$![]() via the action as above.
via the action as above.
Theorem 6.7 The $H$![]() -module structure on $V^{\otimes d}$
-module structure on $V^{\otimes d}$![]() factors through $\Phi : H \to \Lambda = TL_{R, d}(\delta ),$
factors through $\Phi : H \to \Lambda = TL_{R, d}(\delta ),$![]() where $\delta = -u-u^{-1}$
where $\delta = -u-u^{-1}$![]() . Hence, $U_s$
. Hence, $U_s$![]() acts as:
acts as:

where $s=(t \ t+1)\in S$![]() . Moreover, there is an algebra isomorphism
. Moreover, there is an algebra isomorphism
Proof. The first statement follows by checking that the elements $x_i$![]() act as zero on $V^{\otimes d}$
act as zero on $V^{\otimes d}$![]() .
.
The element $\widetilde {T}_i-u$![]() acts exactly as the action of $U_i$
acts exactly as the action of $U_i$![]() in $V^{\otimes d}$
in $V^{\otimes d}$![]() , so the canonical map ${H_{R, q}(d)\rightarrow \operatorname {End}_{S_{R, q}(2, d)}(V^{\otimes d})^{op}}$
, so the canonical map ${H_{R, q}(d)\rightarrow \operatorname {End}_{S_{R, q}(2, d)}(V^{\otimes d})^{op}}$![]() factors through $\Lambda$
factors through $\Lambda$![]() , that is, there is an algebra homomorphism $\Lambda \to {\rm End}_{S_{R, q}(2, d)}(V^{\otimes d})^{op}.$
, that is, there is an algebra homomorphism $\Lambda \to {\rm End}_{S_{R, q}(2, d)}(V^{\otimes d})^{op}.$![]() The same argument as the one given in theorem 6.4 works in this case replacing the Schur algebra by the $q$
The same argument as the one given in theorem 6.4 works in this case replacing the Schur algebra by the $q$![]() -Schur algebra and the group algebra of the symmetric group by the Iwahori–Hecke algebra. The injectivity follows again by considering the action of the elements in $\Lambda$
-Schur algebra and the group algebra of the symmetric group by the Iwahori–Hecke algebra. The injectivity follows again by considering the action of the elements in $\Lambda$![]() , acting as zero on $V^{\otimes d}$
, acting as zero on $V^{\otimes d}$![]() , on the elements $y_k$
, on the elements $y_k$![]() defined in the exactly same way as in theorem 6.4.
defined in the exactly same way as in theorem 6.4.
Theorem 6.7 places $V^{\otimes d}$![]() in a central position in the representation theory of Temperley–Lieb algebras where it plays a role similar to that played by $(R^n)^{\otimes d}$
in a central position in the representation theory of Temperley–Lieb algebras where it plays a role similar to that played by $(R^n)^{\otimes d}$![]() in the study of the representation theory of symmetric groups via Schur algebras. In fact, Theorem 8.1.5 of [Reference Cruz10] specializes to the following.
in the study of the representation theory of symmetric groups via Schur algebras. In fact, Theorem 8.1.5 of [Reference Cruz10] specializes to the following.
Corollary 6.8 Let $K$![]() be a field and fix $q=u^{-2}$
be a field and fix $q=u^{-2}$![]() for some element $u\in K^\times$
for some element $u\in K^\times$![]() . Let $T$
. Let $T$![]() be a characteristic tilting module of $S$
be a characteristic tilting module of $S$![]() and let $R(S)$
and let $R(S)$![]() be the Ringel dual of $S:=S_{K, q}(2, d)$
be the Ringel dual of $S:=S_{K, q}(2, d)$![]() over a field $K$
over a field $K$![]() .
.
Then, $(R(S), \operatorname {Hom}_S(T, V^{\otimes d})$![]() is a $(V^{\otimes d}\!\operatorname {-domdim}_S T-2)$
is a $(V^{\otimes d}\!\operatorname {-domdim}_S T-2)$![]() -$\mathcal {F}(\Delta _{R(S)})$
-$\mathcal {F}(\Delta _{R(S)})$![]() quasi-hereditary cover of $TL_{K, d}(-u-u^{-1})$
quasi-hereditary cover of $TL_{K, d}(-u-u^{-1})$![]() , where $\Delta _{R(S)}$
, where $\Delta _{R(S)}$![]() denotes the set of standard modules over $R(S)$
denotes the set of standard modules over $R(S)$![]() . Moreover, the following assertions hold:
. Moreover, the following assertions hold:
(i) If $q+1\neq 0$
 or $d$
or $d$ is odd, then $TL_{K, d}(-u-u^{-1})$
is odd, then $TL_{K, d}(-u-u^{-1})$ is the Ringel dual of $S_{K, q}(2, d)$
is the Ringel dual of $S_{K, q}(2, d)$ , and in particular, it is a split quasi-hereditary algebra over $K$
, and in particular, it is a split quasi-hereditary algebra over $K$ ;
;(ii) If $q+1=0$
 and $d$
and $d$ is even, then $(R(S), \operatorname {Hom}_S(T, V^{\otimes d})$
is even, then $(R(S), \operatorname {Hom}_S(T, V^{\otimes d})$ is a $\left (\frac {d}{2}-2\right )$
is a $\left (\frac {d}{2}-2\right )$ -$\mathcal {F}(\Delta _{R(S)})$
-$\mathcal {F}(\Delta _{R(S)})$ quasi-hereditary cover of $TL_{K, d}(0)$
quasi-hereditary cover of $TL_{K, d}(0)$ and $\operatorname {HNdim}_F \mathcal {F}(\Delta _{R(S)})=\frac {d}{2}-2$
and $\operatorname {HNdim}_F \mathcal {F}(\Delta _{R(S)})=\frac {d}{2}-2$ . In particular, the Schur functor
\[ F:=\operatorname {Hom}_{R(S)}(\operatorname {Hom}_S(T, V^{\otimes d}), - )\colon R(S_{K, q}(2, d))\!\operatorname {-} \operatorname {mod}\rightarrow TL_{K, d}(0)\!\operatorname {-mod} \]induces bijections
. In particular, the Schur functor
\[ F:=\operatorname {Hom}_{R(S)}(\operatorname {Hom}_S(T, V^{\otimes d}), - )\colon R(S_{K, q}(2, d))\!\operatorname {-} \operatorname {mod}\rightarrow TL_{K, d}(0)\!\operatorname {-mod} \]induces bijections \begin{align*} \operatorname{Ext}_{R(S)}^i(M, N)\simeq \operatorname{Ext}_{TL_{K, d}(0)}^i(FM, FN), \quad & \forall M, N\in \mathcal{F}(\Delta_{R(S)}), \notag\\ & 0\leq i\leq \frac{d}{2}-2. \end{align*}
\begin{align*} \operatorname{Ext}_{R(S)}^i(M, N)\simeq \operatorname{Ext}_{TL_{K, d}(0)}^i(FM, FN), \quad & \forall M, N\in \mathcal{F}(\Delta_{R(S)}), \notag\\ & 0\leq i\leq \frac{d}{2}-2. \end{align*}
Proof. The result follows from theorem 5.8, [Reference Cruz10, Theorem 8.1.5] and [Reference Cruz10, Theorem 6.0.1].
7. Uniqueness of the quasi-hereditary cover of $TL_{R, d}(\delta )$
In corollary 6.8, we have constructed a quasi-hereditary cover of $TL_{K, q}(\delta )$![]() using the Ringel dual of a $q$
using the Ringel dual of a $q$![]() -Schur algebra. We will argue now that it is the best quasi-hereditary cover of $TL_{K, d}(\delta )$
-Schur algebra. We will argue now that it is the best quasi-hereditary cover of $TL_{K, d}(\delta )$![]() if $d>2$
if $d>2$![]() (in the sense that there is no other quasi-hereditary cover of the Temperley–Lieb algebra which satisfies (7.3)). For that, going to the integral case is helpful. Assume that $R$
(in the sense that there is no other quasi-hereditary cover of the Temperley–Lieb algebra which satisfies (7.3)). For that, going to the integral case is helpful. Assume that $R$![]() is a commutative Noetherian ring. Let $u$
is a commutative Noetherian ring. Let $u$![]() be an invertible element of $R$
be an invertible element of $R$![]() and fix $q=u^{-2}$
and fix $q=u^{-2}$![]() . If $d=1, 2$
. If $d=1, 2$![]() then the Temperley–Lieb algebra $TL_{R, q}(-u-u^{-1})$
then the Temperley–Lieb algebra $TL_{R, q}(-u-u^{-1})$![]() coincides with the Iwahori–Hecke algebra $H_{R, q}(d)$
coincides with the Iwahori–Hecke algebra $H_{R, q}(d)$![]() and so this case was dealt with in [Reference Cruz9, Subsection 7.2].
and so this case was dealt with in [Reference Cruz9, Subsection 7.2].
Assume from now on that $d>2$![]() . Combining theorem 6.7 with Theorem 8.1.5 of [Reference Cruz10] we obtain the following:
. Combining theorem 6.7 with Theorem 8.1.5 of [Reference Cruz10] we obtain the following:
Corollary 7.1 Let $R$![]() be a commutative Noetherian ring. Fix an element $u\in R^\times$
be a commutative Noetherian ring. Fix an element $u\in R^\times$![]() and $q=u^{-2}$
and $q=u^{-2}$![]() . Let $T$
. Let $T$![]() be a characteristic tilting module of $(S_{R, q}(2, d), \{\Delta (\lambda )_{\lambda \in \Lambda ^+(2, d)} \})$
be a characteristic tilting module of $(S_{R, q}(2, d), \{\Delta (\lambda )_{\lambda \in \Lambda ^+(2, d)} \})$![]() . Denote by $R(S)$
. Denote by $R(S)$![]() the Ringel dual of $(S_{R, q}(2, d), \{\Delta (\lambda )_{\lambda \in \Lambda ^+(2, d)} \})$
the Ringel dual of $(S_{R, q}(2, d), \{\Delta (\lambda )_{\lambda \in \Lambda ^+(2, d)} \})$![]() , that is, $R(S)=\operatorname {End}_{S_{R, q}(2, d)}(T)^{op}$
, that is, $R(S)=\operatorname {End}_{S_{R, q}(2, d)}(T)^{op}$![]() .
.
Then, $(R(S), \operatorname {Hom}_{S_{R, q}(2, d)}(T, V^{\otimes d}) )$![]() is a $(V^{\otimes d}\!\operatorname {-domdim}_{S_{R, q}(2, d), R} T-2)$
is a $(V^{\otimes d}\!\operatorname {-domdim}_{S_{R, q}(2, d), R} T-2)$![]() -$\mathcal {F}(\tilde {\Delta }_{R(S)})$
-$\mathcal {F}(\tilde {\Delta }_{R(S)})$![]() split quasi-hereditary cover of $TL_{R, d}(-u-u^{-1})$
split quasi-hereditary cover of $TL_{R, d}(-u-u^{-1})$![]() .
.
In the following, we will write $R(S)$![]() to denote the Ringel dual $\operatorname {End}_{S_{R, q}(2, d)}(T)^{op}$
to denote the Ringel dual $\operatorname {End}_{S_{R, q}(2, d)}(T)^{op}$![]() . Denote by $F_{R, q}$
. Denote by $F_{R, q}$![]() the Schur functor associated with the quasi-hereditary cover constructed in corollary 7.1. The aim now is to compute $\operatorname {HNdim}_{F_{R, q}}\mathcal {F}(\tilde {\Delta }_{R(S)})$
the Schur functor associated with the quasi-hereditary cover constructed in corollary 7.1. The aim now is to compute $\operatorname {HNdim}_{F_{R, q}}\mathcal {F}(\tilde {\Delta }_{R(S)})$![]() and in particular to determine $V^{\otimes d}\!\operatorname {-domdim}_{S_{R, q}(2, d), R} T$
and in particular to determine $V^{\otimes d}\!\operatorname {-domdim}_{S_{R, q}(2, d), R} T$![]() in terms of the ground ring $R$
in terms of the ground ring $R$![]() .
.
Theorem 7.2 Let $R$![]() be a commutative Noetherian ring. Fix an element $u\in R^\times$
be a commutative Noetherian ring. Fix an element $u\in R^\times$![]() and $q=u^{-2}$
and $q=u^{-2}$![]() . Let $T$
. Let $T$![]() be a characteristic tilting module of $(S_{R, q}(2, d), \{\Delta (\lambda )_{\lambda \in \Lambda ^+(2, d)} \})$
be a characteristic tilting module of $(S_{R, q}(2, d), \{\Delta (\lambda )_{\lambda \in \Lambda ^+(2, d)} \})$![]() . Then,
. Then,

Proof. The algebra $S_{R, q}(2, d)$![]() has the base change property: $S\otimes _R S_{R, q}(2, d)\simeq S_{S, 1_S\otimes q}(2, d)$
has the base change property: $S\otimes _R S_{R, q}(2, d)\simeq S_{S, 1_S\otimes q}(2, d)$![]() as $S$
as $S$![]() -algebras for every commutative ring $S$
-algebras for every commutative ring $S$![]() which is an $R$
which is an $R$![]() -algebra and the standard modules of $S_{S, 1_S\otimes q}(2, d)$
-algebra and the standard modules of $S_{S, 1_S\otimes q}(2, d)$![]() are of the form $S\otimes _R \Delta (\lambda )$
are of the form $S\otimes _R \Delta (\lambda )$![]() , $\lambda \in \Lambda ^+(n, d)$
, $\lambda \in \Lambda ^+(n, d)$![]() (see e.g. [Reference Cruz11, Subsection 3.3, Section 5]). Hence, the result follows from theorem 5.8, [Reference Cruz9, Propositions A.4.7, A.4.3], and [Reference Cruz10, Theorem 3.2.5].
(see e.g. [Reference Cruz11, Subsection 3.3, Section 5]). Hence, the result follows from theorem 5.8, [Reference Cruz9, Propositions A.4.7, A.4.3], and [Reference Cruz10, Theorem 3.2.5].
7.1. Hemmer–Nakano dimension of $\mathcal {F}(\tilde {\Delta }_{R(S)})$
Similarly to the classical case (see also [Reference Cruz9]), there are two cases to be considered.
Following [Reference Cruz9], the commutative Noetherian ring $R$![]() is called $2$
is called $2$![]() -partially $q$
-partially $q$![]() -divisible if $1+q\in R^\times$
-divisible if $1+q\in R^\times$![]() or $1+q=0$
or $1+q=0$![]() .
.
Theorem 7.3 Let $R$![]() be a local regular $2$
be a local regular $2$![]() -partially $q$
-partially $q$![]() -divisible (commutative Noetherian) ring, where $q=u^{-2}$
-divisible (commutative Noetherian) ring, where $q=u^{-2}$![]() , $u\in R^\times$
, $u\in R^\times$![]() . Let $T$
. Let $T$![]() be a characteristic tilting module of $S_{R, q}(n, d)$
be a characteristic tilting module of $S_{R, q}(n, d)$![]() . Then,
. Then,
Proof. By corollary 7.1, $\operatorname {HNdim}_{F_{R, q}} \mathcal {F}(\tilde {\Delta }_{R(S)})\geq V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T -2$![]() .
.
If ${V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T}=+\infty$![]() , then $d$
, then $d$![]() is odd, and then there is nothing to prove. Assume that it is finite. By theorem 7.2, $V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T=\frac {d}{2}$
is odd, and then there is nothing to prove. Assume that it is finite. By theorem 7.2, $V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T=\frac {d}{2}$![]() . In particular, $d$
. In particular, $d$![]() is even and $1+q\notin R^\times$
is even and $1+q\notin R^\times$![]() . Hence, $1+q$
. Hence, $1+q$![]() must be zero. Therefore,
must be zero. Therefore,
where $Q(R)$![]() is a quotient field of $R$
is a quotient field of $R$![]() .
.
By [Reference Cruz10, Corollary 5.3.6], $\operatorname {HNdim}_{Q(R)\otimes _R F_{R, q}} \mathcal {F}(Q(R)\otimes _R \Delta _{R(S)})$![]() cannot be higher than ${V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T-2}$
cannot be higher than ${V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T-2}$![]() . It follows that
. It follows that

Theorem 7.4 Let $R$![]() be a local regular commutative Noetherian ring which is not a $2$
be a local regular commutative Noetherian ring which is not a $2$![]() -partially $q$
-partially $q$![]() -divisible commutative ring, where $q=u^{-2}$
-divisible commutative ring, where $q=u^{-2}$![]() , $u\in R^\times$
, $u\in R^\times$![]() . Let $T$
. Let $T$![]() be a characteristic tilting module of $S_{R, q}(n, d)$
be a characteristic tilting module of $S_{R, q}(n, d)$![]() . Then,
. Then,
Proof. By corollary 7.1, if $V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T$![]() is infinite, then there is nothing to show. So, assume that $V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T$
is infinite, then there is nothing to show. So, assume that $V^{\otimes d}\!\operatorname {-domdim}_{(S_{R, q}(2, d), R)} T$![]() is finite. By theorem 7.2, $d$
is finite. By theorem 7.2, $d$![]() is even and $1+q\notin R^\times$
is even and $1+q\notin R^\times$![]() . By assumption, $1+q\neq 0$
. By assumption, $1+q\neq 0$![]() , otherwise $R$
, otherwise $R$![]() would be a $2$
would be a $2$![]() -partially $q$
-partially $q$![]() -divisible ring. It follows that
-divisible ring. It follows that
is infinite by theorem 7.2. The result for $d=2$![]() follows from [Reference Cruz9, Theorem 7.2.7]. Assume that $d\geq 4$
follows from [Reference Cruz9, Theorem 7.2.7]. Assume that $d\geq 4$![]() . By corollary 7.1 and [Reference Cruz10, Theorem 3.2.5], $\operatorname {HNdim}_{F_{R(\mathfrak {m}), q_\mathfrak {m}}} \mathcal {F}(R(\mathfrak {m})\otimes _R \Delta _{R(S)})\geq 0$
. By corollary 7.1 and [Reference Cruz10, Theorem 3.2.5], $\operatorname {HNdim}_{F_{R(\mathfrak {m}), q_\mathfrak {m}}} \mathcal {F}(R(\mathfrak {m})\otimes _R \Delta _{R(S)})\geq 0$![]() and ${\operatorname {HNdim}_{Q(R)\otimes _R F_{R, q}} \mathcal {F}(Q(R)\otimes _R \Delta _{R(S)})}=+\infty$
and ${\operatorname {HNdim}_{Q(R)\otimes _R F_{R, q}} \mathcal {F}(Q(R)\otimes _R \Delta _{R(S)})}=+\infty$![]() , where $\mathfrak {m}$
, where $\mathfrak {m}$![]() is the unique maximal ideal of $R$
is the unique maximal ideal of $R$![]() , and $q_\mathfrak {m}$
, and $q_\mathfrak {m}$![]() is the image of $q$
is the image of $q$![]() in $R/\mathfrak {m}$
in $R/\mathfrak {m}$![]() . By [Reference Cruz9, Theorem 5.0.9], $\operatorname {HNdim}_{F_{R, q}} \mathcal {F}(\tilde {\Delta }_{R(S)})\geq \frac {d}{2}-1$
. By [Reference Cruz9, Theorem 5.0.9], $\operatorname {HNdim}_{F_{R, q}} \mathcal {F}(\tilde {\Delta }_{R(S)})\geq \frac {d}{2}-1$![]() . The Hemmer–Nakano dimension cannot be higher because similarly to the proof of Theorem 7.2.7 of [Reference Cruz9] there exists a prime ideal of height one $\mathfrak {p}$
. The Hemmer–Nakano dimension cannot be higher because similarly to the proof of Theorem 7.2.7 of [Reference Cruz9] there exists a prime ideal of height one $\mathfrak {p}$![]() such that $1+q\in \mathfrak {p}$
such that $1+q\in \mathfrak {p}$![]() . Hence, $Q(R/\mathfrak {p})\otimes _R V^{\otimes d}\!\operatorname {-domdim}_{S_{Q(R/\mathfrak {p}), q_\mathfrak {p}}(2, d), Q(R/\mathfrak {p})}$
. Hence, $Q(R/\mathfrak {p})\otimes _R V^{\otimes d}\!\operatorname {-domdim}_{S_{Q(R/\mathfrak {p}), q_\mathfrak {p}}(2, d), Q(R/\mathfrak {p})}$![]() is exactly $\frac {d}{2}$
is exactly $\frac {d}{2}$![]() , where $q_\mathfrak {p}$
, where $q_\mathfrak {p}$![]() denotes the image of $q$
denotes the image of $q$![]() in $R/\mathfrak {p}\subset Q(R/\mathfrak {p})$
in $R/\mathfrak {p}\subset Q(R/\mathfrak {p})$![]() . The result follows from [Reference Cruz9, Theorem 5.1.1].
. The result follows from [Reference Cruz9, Theorem 5.1.1].
7.2. Uniqueness
In this part, assume that $R=\mathbb {Z}[x, x^{-1}]$![]() and fix $q=x^{-2}$
and fix $q=x^{-2}$![]() . Assume that $d>2$
. Assume that $d>2$![]() . By [Reference Cruz9, Proposition 5.0.3] and theorem 7.4, $\operatorname {HNdim}_{F_{R, q}} \mathcal {F}(\tilde {\Delta }_{R(S)})\geq \frac {d}{2}-1$
. By [Reference Cruz9, Proposition 5.0.3] and theorem 7.4, $\operatorname {HNdim}_{F_{R, q}} \mathcal {F}(\tilde {\Delta }_{R(S)})\geq \frac {d}{2}-1$![]() . In particular, the Schur functor $F_{R, q}$
. In particular, the Schur functor $F_{R, q}$![]() induces an exact equivalence:
induces an exact equivalence:
Corollary 7.5 $(R(S), \operatorname {Hom}_{S_{R, q}(2, d)}(T, V^{\otimes d}) )$![]() is the unique split quasi-hereditary cover of $TL_{R, d}(-x-x^{-1})$
is the unique split quasi-hereditary cover of $TL_{R, d}(-x-x^{-1})$![]() satisfying property (7.3), where $T$
satisfying property (7.3), where $T$![]() is a characteristic tilting module of $S_{R, q}(2, d)$
is a characteristic tilting module of $S_{R, q}(2, d)$![]() and $R(S)$
and $R(S)$![]() denotes the Ringel dual of $S_{R, q}(2, d)$
denotes the Ringel dual of $S_{R, q}(2, d)$![]() . In particular, $TL_{R, d}(-x-x^{-1})$
. In particular, $TL_{R, d}(-x-x^{-1})$![]() is a split quasi-hereditary algebra over $R$
is a split quasi-hereditary algebra over $R$![]() if and only if $d$
if and only if $d$![]() is odd.
is odd.
Proof. The first statement follows from corollary 2.11 together with [Reference Cruz9, Proposition 5.0.3] and theorem 7.4. For the second statement see for example [Reference Cruz9, Proposition A.4.7] or [Reference Cruz10, Theorem 6.0.1] together with theorem 7.2).
As a consequence, when $d$![]() is odd, the Temperley–Lieb algebra $TL_{R, d}(-x-x^{-1})$
is odd, the Temperley–Lieb algebra $TL_{R, d}(-x-x^{-1})$![]() is exactly a Ringel dual of $S_{\mathbb {Z}[x, x^{-1}], q}(2, d)$
is exactly a Ringel dual of $S_{\mathbb {Z}[x, x^{-1}], q}(2, d)$![]() .
.
Acknowledgements
Part of the collaboration was done during a research visit of the second-named author to the University of Stuttgart, and the authors are grateful for the support given. Some results were obtained during the first-named author's visit to the MPIM at Bonn. The authors would like to thank Steffen Koenig for his comments on an earlier version of this manuscript. The authors are grateful to the anonymous referees for their constructive input and their suggestions to improve the exposition of this manuscript.
Appendix A. More applications of theorem A
In this section, we give two applications of theorem 3.1 showing how it can be a useful tool to understand other problems.
Appendix A.1 Minimality of faithful direct summands of the characteristic tilting module
In this subsection, we prove that there exists a unique minimal direct summand of the characteristic tilting module, $Q$![]() , affording a double centralizer property. Here, minimal means that every other direct summand of the characteristic tilting module affording a double centralizer property has $Q$
, affording a double centralizer property. Here, minimal means that every other direct summand of the characteristic tilting module affording a double centralizer property has $Q$![]() as a direct summand. This fact was first established in [Reference Hu and Xiao36] using a different concept of relative dominant dimension; however, our proof is shorter knowing theorem A. We also refer to [Reference Hu and Xiao36, Reference Mazorchuk and Stroppel46] for previous background on this question.
as a direct summand. This fact was first established in [Reference Hu and Xiao36] using a different concept of relative dominant dimension; however, our proof is shorter knowing theorem A. We also refer to [Reference Hu and Xiao36, Reference Mazorchuk and Stroppel46] for previous background on this question.
Let $M$![]() be an $A$
be an $A$![]() -module and $B$
-module and $B$![]() its endomorphism algebra, then $M$
its endomorphism algebra, then $M$![]() satisfies the double centralizer property if the canonical algebra homomorphism $A\rightarrow \operatorname {End}_B(M)$
satisfies the double centralizer property if the canonical algebra homomorphism $A\rightarrow \operatorname {End}_B(M)$![]() is an isomorphism. There are several characterizations in the literature for this property. If $A$
is an isomorphism. There are several characterizations in the literature for this property. If $A$![]() is a finite-dimensional algebra over a field, $M$
is a finite-dimensional algebra over a field, $M$![]() satisfies the double centralizer property if and only if $M\!\operatorname {-domdim} A\geq 2$
satisfies the double centralizer property if and only if $M\!\operatorname {-domdim} A\geq 2$![]() (see e.g. [Reference Auslander and Solberg1, Corollary 2.4] or [Reference Cruz10, Lemma 5.1.2, Theorem 3.1.1, Corollary 3.1.5]).
(see e.g. [Reference Auslander and Solberg1, Corollary 2.4] or [Reference Cruz10, Lemma 5.1.2, Theorem 3.1.1, Corollary 3.1.5]).
A.1.1. Existence
Let $A$![]() be a split quasi-hereditary algebra (over a field) with a simple preserving duality. Let $T$
be a split quasi-hereditary algebra (over a field) with a simple preserving duality. Let $T$![]() be the characteristic tilting module of $A$
be the characteristic tilting module of $A$![]() and denote by $R(A)$
and denote by $R(A)$![]() the Ringel dual $\operatorname {End}_A(T)^{op}$
the Ringel dual $\operatorname {End}_A(T)^{op}$![]() of $A$
of $A$![]() . We use properties as summarized in § 3.
. We use properties as summarized in § 3.
Let $P_0(DT)$![]() be the projective cover of $DT$
be the projective cover of $DT$![]() as $R(A)$
as $R(A)$![]() -module. Fix $T_0:=T\otimes _{R(A)} P_0(DT)\in \!\operatorname {add}_A T$
-module. Fix $T_0:=T\otimes _{R(A)} P_0(DT)\in \!\operatorname {add}_A T$![]() . We show first that $T_0\!\operatorname {-domdim} A\geq 2$
. We show first that $T_0\!\operatorname {-domdim} A\geq 2$![]() . The projective cover of $DT$
. The projective cover of $DT$![]() gives the exact sequence
gives the exact sequence
of $R(A)$![]() -modules. Recall that $DT$
-modules. Recall that $DT$![]() is the characteristic tilting module of $R(A)$
is the characteristic tilting module of $R(A)$![]() , hence is in $\mathcal {F}(\Delta _{R(A)})$
, hence is in $\mathcal {F}(\Delta _{R(A)})$![]() , and so is $P_0(DT)$
, and so is $P_0(DT)$![]() . Since $\mathcal {F}(\Delta _{R(A)})$
. Since $\mathcal {F}(\Delta _{R(A)})$![]() is closed under kernels of epimorphisms, $\Omega (DT)\in \mathcal {F}(\Delta _{R(A)})$
is closed under kernels of epimorphisms, $\Omega (DT)\in \mathcal {F}(\Delta _{R(A)})$![]() . Therefore, by proposition 2.7, applying $T\otimes _{R(A)} -$
. Therefore, by proposition 2.7, applying $T\otimes _{R(A)} -$![]() to (A.1) gives the exact sequence
to (A.1) gives the exact sequence
Moreover, $T\otimes _{R(A)} \Omega (DT)\in \mathcal {F}(\nabla )$![]() and $T\otimes _{R(A)} DT\simeq DA$
and $T\otimes _{R(A)} DT\simeq DA$![]() , so the exact sequence (A.2) remains exact under $\operatorname {Hom}_A(T_0, -)$
, so the exact sequence (A.2) remains exact under $\operatorname {Hom}_A(T_0, -)$![]() . That is, $T_0\!\operatorname {-codomdim}_A DA\geq 1$
. That is, $T_0\!\operatorname {-codomdim}_A DA\geq 1$![]() . By theorem 3.1, ${T_0\!\operatorname {-domdim} A \geq 2}$
. By theorem 3.1, ${T_0\!\operatorname {-domdim} A \geq 2}$![]() . So, $T_0$
. So, $T_0$![]() affords a double centralizer property.
affords a double centralizer property.
A.1.2. Uniqueness and minimality
Pick another $Q\in \!\operatorname {add}_AT$![]() satisfying $Q\!\operatorname {-domdim} A\geq 2$
satisfying $Q\!\operatorname {-domdim} A\geq 2$![]() . By theorem 3.1, $Q\!\operatorname {-domdim}_A T\geq 1$
. By theorem 3.1, $Q\!\operatorname {-domdim}_A T\geq 1$![]() . Applying proposition 2.6(i) shows that
. Applying proposition 2.6(i) shows that
Therefore, the projective cover of $DT$![]() is in the additive closure of $\operatorname {Hom}_A(T, Q)$
is in the additive closure of $\operatorname {Hom}_A(T, Q)$![]() . Therefore,
. Therefore,
Theorem A.1 Let $A$![]() be a split quasi-hereditary algebra (over a field) with a simple preserving duality. Then, the following assertions hold$:$
be a split quasi-hereditary algebra (over a field) with a simple preserving duality. Then, the following assertions hold$:$![]()
(1) $T_0$
 is the unique minimal direct summand of the characteristic tilting module affording a double centralizer property.
is the unique minimal direct summand of the characteristic tilting module affording a double centralizer property.(2) For every $Q\in \!\operatorname {add}_A T$
 affording a double centralizer property, the following holds:
\[ Q\!\operatorname{-domdim}_A A\geq T_0\!\operatorname{-domdim}_A A\geq 2. \]
affording a double centralizer property, the following holds:
\[ Q\!\operatorname{-domdim}_A A\geq T_0\!\operatorname{-domdim}_A A\geq 2. \]
Proof. Part (1) was proved in the above discussion. By proposition 2.6(i),
where the inequality holds since $T_0\in \!\operatorname {add}_A Q$![]() . By theorem 3.1, part (2) follows.
. By theorem 3.1, part (2) follows.
Appendix A.2 Invariance of dominant dimension under Ringel duality
Given a split quasi-hereditary algebra $A$![]() (over a field) with a simple preserving duality, there are currently at least two methods to see that its dominant dimension remains invariant under Ringel duality.
(over a field) with a simple preserving duality, there are currently at least two methods to see that its dominant dimension remains invariant under Ringel duality.
Indeed, in such a setup, the Ringel dual of $A$![]() also has a simple preserving duality (see e.g. [Reference Fang and Koenig29, Proposition 2.4, Lemma 3.2(1), (2)]) and so the Ringel dual of $A$
also has a simple preserving duality (see e.g. [Reference Fang and Koenig29, Proposition 2.4, Lemma 3.2(1), (2)]) and so the Ringel dual of $A$![]() also has a faithful projective–injective if $A$
also has a faithful projective–injective if $A$![]() has one. Moreover, in such a setup, the Ringel dual of $A$
has one. Moreover, in such a setup, the Ringel dual of $A$![]() has a faithful projective–injective if and only if $A$
has a faithful projective–injective if and only if $A$![]() has one because the Ringel dual of the Ringel dual of $A$
has one because the Ringel dual of the Ringel dual of $A$![]() is up to Morita equivalence $A$
is up to Morita equivalence $A$![]() again. Since the Ringel dual of $A$
again. Since the Ringel dual of $A$![]() and $A$
and $A$![]() are derived equivalent, Theorem 5.5 of [Reference Fang, Hu and Koenig28] states that $A$
are derived equivalent, Theorem 5.5 of [Reference Fang, Hu and Koenig28] states that $A$![]() and the Ringel dual of $A$
and the Ringel dual of $A$![]() have the same dominant dimension.
have the same dominant dimension.
Under the addition of the assumption that $A$![]() has positive dominant dimension so that the endomorphism algebra of the faithful projective–injective module is a symmetric algebra, Fang and Koenig proved in [Reference Fang and Koenig29, Theorem 4.3] that the dominant dimension of $A$
has positive dominant dimension so that the endomorphism algebra of the faithful projective–injective module is a symmetric algebra, Fang and Koenig proved in [Reference Fang and Koenig29, Theorem 4.3] that the dominant dimension of $A$![]() is equal to the dominant dimension of the Ringel dual of $A$
is equal to the dominant dimension of the Ringel dual of $A$![]() .
.
In the rest of this section, we propose a new proof of this fact.
Theorem A.2 Let $(A, \{\Delta (\lambda )_{\lambda \in \Lambda }\})$![]() be a split quasi-hereditary algebra over a field $k$
be a split quasi-hereditary algebra over a field $k$![]() . Suppose that there exists a simple preserving duality ${}^\diamond \!(-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$
. Suppose that there exists a simple preserving duality ${}^\diamond \!(-)\colon A\!\operatorname {-mod}\rightarrow A\!\operatorname {-mod}$![]() . Then
. Then
where $R(A)$![]() denotes the Ringel dual of $A$
denotes the Ringel dual of $A$![]() .
.
Proof. Let $T$![]() be the basic characteristic tilting module of $A$
be the basic characteristic tilting module of $A$![]() . As discussed above, $A$
. As discussed above, $A$![]() has positive dominant dimension if and only if the Ringel dual of $A$
has positive dominant dimension if and only if the Ringel dual of $A$![]() has positive dominant dimension. Assume that $A$
has positive dominant dimension. Assume that $A$![]() has positive dominant dimension and assume that $P$
has positive dominant dimension and assume that $P$![]() is a faithful projective–injective $A$
is a faithful projective–injective $A$![]() -module. Then, $\operatorname {Hom}_A(T, P)$
-module. Then, $\operatorname {Hom}_A(T, P)$![]() is a partial tilting over $R(A)$
is a partial tilting over $R(A)$![]() since $P$
since $P$![]() is injective over $A$
is injective over $A$![]() and it is projective since $P$
and it is projective since $P$![]() is partial tilting over $A$
is partial tilting over $A$![]() . Thus, $\operatorname {Hom}_A(T, P)$
. Thus, $\operatorname {Hom}_A(T, P)$![]() is a projective–injective module since each partial tilting module is self-dual under the simple preserving duality functor (see e.g. [Reference Mazorchuk and Ovsienko45, Section 2]).
is a projective–injective module since each partial tilting module is self-dual under the simple preserving duality functor (see e.g. [Reference Mazorchuk and Ovsienko45, Section 2]).
Then, by theorem 3.1 and proposition 2.6,